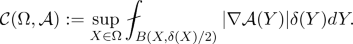Uniform Rectifiability and Elliptic Operators Satisfying a Carleson Measure Condition

Abstract

The present paper establishes the correspondence between the properties of the solutions of a class of PDEs and the geometry of sets in Euclidean space. We settle the question of whether (quantitative) absolute continuity of the elliptic measure with respect to the surface measure and uniform rectifiability of the boundary are equivalent, in an optimal class of divergence form elliptic operators satisfying a suitable Carleson measure condition in uniform domains with Ahlfors regular boundaries. The result can be viewed as a quantitative analogue of the Wiener criterion adapted to the singular $L^p$ data case. The first step is taken in Part I, where we considered the case in which the desired Carleson measure condition on the coefficients holds with sufficiently small constant, using a novel application of techniques developed in geometric measure theory. In Part II we establish the final result, that is, the “large constant case”. The key elements are a powerful extrapolation argument, which provides a general pathway to self-improve scale-invariant small constant estimates, and a new mechanism to transfer quantitative absolute continuity of elliptic measure between a domain and its subdomains.

1 Introduction

1.1 Background and Previous Results.

The present paper, together with its converse in [KP] (see also [DJ]), culminate many years of activity at the intersection of harmonic analysis, geometric measure theory, and PDEs, devoted to the complete understanding of necessary and sufficient conditions on the operator and the geometry of the domain guaranteeing absolute continuity of the elliptic measure with respect to the surface measure of the boundary.

The celebrated 1924 Wiener criterion [Wie] provided the necessary and sufficient conditions on the geometry of the domain responsible for the continuity of the harmonic functions at the boundary. In the probabilistic terms, it characterized the points of the boundary which are “seen" by the Brownian travelers coming from the interior of the domain.

The question of finding necessary and sufficient geometric conditions which could guarantee adequate regularity, so that, roughly speaking, the pieces of the boundary are seen by the Brownian travelers according to their surface measure, turned out to be much more intricate. Curiously, already in 1916 F. & M. Riesz correctly identified the key geometric notion in this context: rectifiability of the boundary $\partial \Omega$, i.e., the existence of tangent planes almost everywhere with respect to arc length $\sigma$ on $\partial \Omega$. In particular, they showed in [RR] that harmonic measure is (mutually) absolutely continuous with respect to $\sigma$ for a simply connected domain in the plane with rectifiable boundary. It took more than a hundred years to establish the converse of the F. & M. Riesz theorem and its higher dimensional analogues. The first such result appeared in 2016 [AHM+], and the question was fully settled for the harmonic functions in 2018 [AHMMT].

The question of what happens in the general PDE setting has been puzzling from the beginning. The Wiener criterion is universal: it applies to all uniformly elliptic divergence form operators with bounded coefficients and characterizes points of continuity of the solution at the boundary. It was realized early on that no such general criterion exists for determining the absolute continuity of elliptic measure with respect to the surface measure to the boundary of a domain. Some of the challenges that arise when considering this question were highlighted by the counterexamples in [CFK, MM]. In 1984 Dahlberg formulated a conjecture concerning optimal conditions on a matrix of coefficients which guarantee absolute continuity of elliptic measure with respect to Lebesgue measure in a half-space. This question was a driving force of a thread of outstanding developments in harmonic analysis in the 80s and 90s due to Dahlberg, Jerison, Kenig, Pipher, and others, stimulating some beautiful and far-reaching new techniques in the theory of weights and singular integral operators, to mention only a few approaches. In [KP], Kenig and Pipher proved Dahlberg’s conjecture, they showed that whenever the gradient of coefficients satisfies a Carleson measure condition (to be defined below in (1.2)) the elliptic measure and the Lebesgue measure are mutually absolutely continuous on a half-space and, by a change of variables argument, above a Lipschitz graph.

Given the aforementioned developments, it was natural to conjecture that the equivalence of rectifiability and regularity of elliptic measure should be valid in the full generality of Dahlberg–Kenig–Pipher (DKP) coefficients. Despite numerous attempts this question turned out to be notoriously resistant to existing methods. The passage from the regularity of the solutions to partial differential equations to rectifiability, or to any geometric information on the boundary, is generally referred to as free boundary problems. This in itself is, of course, a well-studied and rich subject. Unfortunately, the typical techniques arising from minimization of the functionals are both too qualitative and too rigid to treat structural irregularities of rectifiable sets and such weak assumptions as absolute continuity of harmonic measure. The latter became accessible only recently, with the development of the analysis of singular integrals and similar objects on uniformly rectifiable sets. In particular, the first converse of the F. & M. Riesz theorem, [AHM+], directly relies on the 2012 solution of the David-Semmes conjecture regarding the boundedness of the Riesz transforms in $L^2$ [NTV]. At the same time, the techniques stemming from such results for the harmonic functions are not amenable to more general operators of the DKP type, again, due to simple yet fundamental algebraic deficiencies: the derivatives of the coefficients do not offer sufficient cancellations.

The main goal of the present paper is to address the conjecture in full generality for uniform domains with Ahlfors regular boundaries. We establish the equivalence of the absolute continuity of the elliptic measure with respect to the surface measure and the uniform rectifiability of the boundary of a domain under the DKP condition on the coefficients, thus providing the final, optimal geometric results (given the assumed background hypotheses).

We now describe our goal and relevant previous results more precisely. Throughout the paper we shall work under the assumptions that the domain $\Omega$ is uniform, i.e., open and connected in a quantitative way, and that its boundary is $(n-1)$-Ahlfors regular, that is, $(n-1)$-dimensional in a quantitative way (see Section 2.1). Under these conditions one can, for instance, show that scale-invariant absolute continuity of harmonic measure is related to the uniform rectifiability of the boundary and even to the non-tangential accessibility of the exterior domain:

Theorem 1.1

   Let $\Omega \subset {{\mathbb {R}}}^n$, $n\ge 3$, be a uniform domain (bounded or unbounded) with Ahlfors regular boundary (see Definitions 2.8 and 2.1), set $\sigma ={\mathcal {H}}^{n-1}|_{\partial \Omega }$ and let $\omega _{-\Delta }$ denote its associated harmonic measure. The following statements are equivalent:

• (a) $\omega _{-\Delta } \in A_\infty (\sigma )$ (Definition 2.10).

• (b) $\partial \Omega$ is uniformly rectifiable (Definition 2.2).

• (c) $\Omega$ satisfies the exterior corkscrew condition (see Definition 2.3), hence, in particular, it is a chord-arc domain (Definition 2.9).

Postponing all the rigorous definitions to Section 2.1, we remark for the moment that uniform rectifiability is a quantitative version of the notion of rectifiability of the boundary and the Muckenhoupt condition $\omega \in A_\infty (\sigma )$ is, respectively, a quantitative form of the mutual absolute continuity of $\omega$ with respect to $\sigma$. Thus, Theorem 1.1 above is a quantitative form of the rigorous connection between the boundary behavior of harmonic functions and geometric properties of sets that we alluded to above. Returning to the ties with Wiener criterion, we point out that the property of the scale invariant absolute continuity of harmonic measure with respect to surface measure, at least in the presence of Ahlfors regularity of $\partial \Omega$, is equivalent to the solvability of the Dirichlet problem with data in some $L^p(\partial \Omega )$, with $p<\infty$¹; thus, such a characterization is in some sense an analogue of Wiener’s criterion for singular, rather than continuous data.

Theorem 1.1 in the present form appears in [AHMNT, Theorem 1.2]. That (a) implies (b) is the main result in [HMU] (see also [HM2, HLMN]); that (b) yields (c) is [AHMNT, Theorem 1.1]; and the fact that (c) implies (a) was proved in [DJ], and independently in [Sem].

Theorem 1.1 and other recent results² illuminate how the $A_\infty$ condition³ of harmonic measure is related to the geometry of the domain $\Omega$. Unfortunately, as we pointed out above, their proofs do not extend to the optimal class of operators with variable coefficients. Indeed, the best known results in this direction pertain to the “direct" rather than the “free boundary" problem. A description of the elliptic measure in a given geometric environment, is essentially due to C. Kenig and J. Pipher. In 2001 [KP] C. Kenig and J. Pipher proved what they referred to as a 1984 Dahlberg conjecture: if $\Omega \subset {{\mathbb {R}}}^n$ is a bounded Lipschitz domain and the elliptic matrix ${\mathcal {A}}$ satisfies the following Carleson measure condition:

$$\begin{aligned} \sup _{\begin{array}{c} q\in \partial \Omega \\ 0< r<{{\,\mathrm{diam}\,}}(\Omega ) \end{array} } \frac{1}{r^{n-1}} \int _{B(q,r) \cap \Omega } \bigg ( \sup _{Y\in B(X,\frac{\delta (X)}{2})} |\nabla {\mathcal {A}}(Y)|^2 \delta (Y)\bigg )dX <\infty , \end{aligned}$$

(1.2)

where here and elsewhere we write $\delta (\cdot )={\text {dist}}(\cdot ,\partial \Omega )$, then the corresponding elliptic measure $\omega _L\in A_{\infty }(\sigma )$. As observed in [HMT1], one may carry through the proof in [KP], essentially unchanged, with a slightly weakened reformulation of (1.2), namely by assuming, in place of (1.2), the following properties:

• (H1) ${\mathcal {A}}\in {{\,\mathrm{Lip}\,}}_{\mathrm{loc}}(\Omega )$ and $|\nabla {\mathcal {A}}|\delta (\cdot ) \in L^\infty (\Omega )$, where $\delta (\cdot ) := {\text {dist}}(\cdot ,\partial \Omega )$.

• (H2) $|\nabla {\mathcal {A}}|^2 \delta (\cdot )$ satisfies the Carleson measure assumption:

  $$\begin{aligned} \Vert {\mathcal {A}}\Vert _{\mathrm{Car}}:=\sup _{\begin{array}{c} q\in \partial \Omega \\ 0< r<{{\,\mathrm{diam}\,}}(\Omega ) \end{array} } \frac{1}{r^{n-1}} \int _{B(q,r) \cap \Omega } |\nabla {\mathcal {A}}(X)|^2 \delta (X)dX <\infty \,. \end{aligned}$$

  (1.3)

We shall refer to these hypotheses (jointly) as the Dahlberg–Kenig–Pipher condition (DKP condition). Note that each of (H1) and (H2) is implied by (1.2).

Since properties (H1) and (H2) are preserved in subdomains, one can use the method of [DJ] to extend the result of [KP] to chord-arc domains, and hence the analogue of (c) implies (a) (in Theorem 1.1) holds for operators satisfying the DKP condition.

An attempt to address the “free boundary" part of the problem that is to prove that (a) implies (b) or (c) led, the first, second and fourth authors of the present paper (see [HMT1]) to show that under the same background hypothesis as in Theorem 1.1, (a) implies (c) (and hence also (b)) for elliptic operators with variable-coefficient matrices ${\mathcal {A}}$ satisfying (H1) and the Carleson measure estimate

$$\begin{aligned} \sup _{\begin{array}{c} q\in \partial \Omega \\ 0< r<{{\,\mathrm{diam}\,}}(\Omega ) \end{array} } \frac{1}{r^{n-1}} \int _{B(q,r) \cap \Omega } |\nabla {\mathcal {A}}(X)|dX <\infty . \end{aligned}$$

(1.4)

We observe that, in the presence of hypothesis (H1), (1.4) implies (1.3). The weighted $W^{1,2}$ Carleson measure estimate (1.3) is both weaker, and more natural than the $W^{1,1}$ version (1.4). For example, operators verifying (1.3) arise as pullbacks of constant coefficient operators (see [KP, Introduction]), and also in the linearization of “A-harmonic" (i.e., generalized p-harmonic) operators (see [LV, Section 4]). We also mention in passing that a qualitative version of the results in [HMT1] was obtained in [ABHM]. There are also related (quantitative) results in [HMM1] and [AGMT] that are valid in the absence of any connectivity hypothesis.

1.2 Main Result and Proof Techniques.

From the geometric measure theory point of view the main motivation for this paper is to understand whether the elliptic measure of a DKP divergence form elliptic operator distinguishes between a rectifiable and a purely unrectifiable boundary. As in Theorem 1.1, we make the background assumption that $\Omega \subset {\mathbb {R}}^n$, $n\ge 3$, is a uniform domain (see Definition 2.8) with an Ahlfors regular boundary (Definition 2.1). Analytically we consider second order divergence form elliptic operators, that is, $L=-\mathop {{\text {div}}}\nolimits ({\mathcal {A}}(\cdot )\nabla )$, where ${\mathcal {A}}= \big ( a_{ij}\big )_{i,j=1}^n$ is a (not necessarily symmetric) real matrix-valued function on $\Omega$, satisfying the usual uniform ellipticity condition

$$\begin{aligned} \langle {\mathcal {A}}(X)\xi , \xi \rangle \ge \lambda |\xi |^2, \qquad | \langle {\mathcal {A}}(X)\xi , \zeta \rangle | \le \Lambda |\xi \,|\zeta |, \qquad \text {for all } \xi ,\zeta \in {\mathbb {R}}^n\setminus \{0\}\,, \end{aligned}$$

(1.5)

for uniform constants $0<\lambda \le \Lambda <\infty$, and for a.e. $X\in \Omega$. We further assume that ${\mathcal {A}}$ satisfies the Dahlberg–Kenig–Pipher condition, that is, (H1) and (H2), and, additionally, that the associated elliptic measure is an $A_\infty$ weight (see Definition 2.10) with respect to the surface measure $\sigma ={\mathcal {H}}^{n-1}|_{\partial \Omega }$. Our goal is to understand how this analytic information yields insight on the geometry of the domain and its boundary.

Our main result is as follows:

Theorem 1.6

   Let $\Omega \subset {{\mathbb {R}}}^n$, $n\ge 3$, be a uniform domain with Ahlfors regular boundary and set $\sigma ={\mathcal {H}}^{n-1}|_{\partial \Omega }$. Let ${\mathcal {A}}$ be a (not necessarily symmetric) uniformly elliptic matrix on $\Omega$ satisfying (H1) and (H2). Then the following are equivalent:

• (1) The elliptic measure $\omega _L$ associated with the operator $L=-\mathop {{\text {div}}}\nolimits ({\mathcal {A}}(\cdot )\nabla )$ is of class $A_\infty$ with respect to the surface measure.

• (2) $\partial \Omega$ is uniformly rectifiable.

• (3) $\Omega$ is a chord-arc domain.

Remark 1.7

In Corollary 10.3 we show that Theorem 1.6 remains true when we replace the assumptions (H1) and (H2) by a slightly weaker assumption involving the oscillation of the elliptic matrix in place of its gradient.

The equivalence of (2) and (3) (under the stated background hypotheses) was previously known: that (3) $\implies$ (2) follows from the main geometric result of [DJ] (namely, that chord-arc domains can be approximated in a big pieces sense by Lipschitz subdomains), and the converse (2) $\implies$ (3) is proved in [AHMNT]. Moreover, as mentioned above, it was also known that (3) $\implies$ (1), and the proof comprises two main ingredients: first, that the properties (H1) and (H2) are preserved in subdomains, and therefore by the result of [KP],⁴$\omega _L \in A_\infty (\sigma )$ in Lipschitz subdomains of $\Omega$; and second, by the aforementioned big piece approximation result of [DJ], that the $A_\infty$ property may be passed from Lipschitz subdomains to the original chord-arc domain, by use of the maximum principle and a change of pole argument (see [DJ] or, originally, [JK]). In this paper we close the circle by proving the implication (1) $\implies$ (2), thus providing a characterization of chord-arc domains in terms of the properties of the elliptic measure.

We first prove the implication (1) $\implies$ (2) in the “small constant case”, that is, when the Carleson condition (H2) holds with a sufficiently small constant (i.e, $\Vert {\mathcal {A}}\Vert _{\mathrm{Car}}$ is small, see (1.3)). To finish the proof of Theorem 1.6, we then utilize a bootstrapping argument to pass from the case of small Carleson norm to the “large constant case”, in which the Carleson condition (H2) is assumed merely to be finite. The arguments we use to treat the small and large constant cases are quite different in nature, and each is of independent interest in its own right. (For example, what we prove in the small constant case is stronger than what is necessary for Theorem 1.6.) Therefore we divide the proof into two parts, and deal with the small and large constant cases in Parts I and II, respectively. At the end of Part II we also discuss the optimality of the above theorem.

Throughout this paper, and unless otherwise specified, by allowable constants, we mean the dimension $n\ge 3$; the constants involved in the definition of a uniform domain, that is, $M, C_1>1$ (see Definition 2.8); the Ahlfors regular constant $C_{AR}>1$ (see Definition 2.1); the ratio of the ellipticity constants $\Lambda /\lambda \ge 1$ (see (1.5)), and the $A_{\infty }$ constants $C_0>1$ and $\theta \in (0,1)$ (see Definition 2.10).

In Part I, we develop an approach which combines, or rather interlaces, the “classical" free boundary blow-up and compactness arguments (originated in geometric measure theory) with the scale-invariant harmonic analysis methods. This allows us to take advantage of the appropriate amelioration of the coefficients obtained via a compactness approach to show that the desired uniform rectifiability follows from regularity of elliptic measure whenever the coefficients of the underlying equation exhibit small oscillations, in the appropriate Carleson measure sense (see Theorem 1.8 and Corollary 1.13). The smallness condition, while obviously suboptimal, could not be removed directly, for it is essentially built in the nature of the compactness arguments. To be precise, we prove the following:

Theorem 1.8

   Given the values of allowable constants $n\ge 3$, $M, C_1, C_{AR}>1$, $\Lambda \ge \lambda =1$, $C_0>1$, and $0<\theta <1$, there exist N and $\epsilon >0$ depending on the allowable constants, such that the following holds. Let $\Omega \subset {\mathbb {R}}^n$ be a bounded uniform domain with constants $M, C_1$ and whose boundary $\partial \Omega$ is Ahlfors regular with constant $C_{AR}$ and set $\sigma ={\mathcal {H}}^{n-1}|_{\partial \Omega }$. Let $L = -\mathop {{\text {div}}}\nolimits ({\mathcal {A}}(\cdot )\nabla )$ be an elliptic operator with real symmetric matrix ${\mathcal {A}}$ satisfying (1.5) with ellipticity constants $1=\lambda \le \Lambda$ such that the corresponding elliptic measure satisfies $\omega _{L} \in A_{\infty }(\sigma )$ with constants $C_0$ and $\theta$. If ${\mathcal {A}}$ verifies

(1.9)

where $\delta (\cdot )={\text {dist}}(\cdot ,\partial \Omega )$ and $\langle {\mathcal {A}}\rangle _{B(X,\delta (X)/2)}$ denotes the average of ${\mathcal {A}}$ on $B(X,\delta (X)/2)$, then $\Omega$ satisfies the exterior corkscrew condition with constant N, and hence $\Omega$ has uniformly rectifiable boundary.

Remark 1.10

 

• (i) Given ${\mathcal {A}}\in W^{1,1}_{\mathrm{loc }}(\Omega )$ we introduce

  

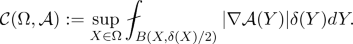  (1.11)

  Poincaré’s inequality easily yields that ${{\,\mathrm{osc}\,}}(\Omega , {\mathcal {A}})\le C_n {\mathcal {C}}(\Omega ,{\mathcal {A}})$ with $C_n$ depending just on dimension. Hence, one can formulate a version of Theorem 1.8 (with a slightly different $\epsilon$) with ${\mathcal {C}}(\Omega ,{\mathcal {A}})<\epsilon$ replacing (1.9).

• (ii) We note that our assumption (1.9) on the matrix ${\mathcal {A}}$ is much weaker than the smallness of the relaxed DKP condition (1.3). To see this, given $X\in \Omega$, let $q_X \in \partial \Omega$ be such that $|X-q_X| = \delta (X)$. Then by Hölder’s inequality

  

  (1.12)

  Hence (1.3) with sufficiently small constant gives smallness of ${\mathcal {C}}(\Omega ,{\mathcal {A}})$ (and hence (1.9)). On the other hand, it is easy to see that the latter is much weaker. Assume for instance that $|\nabla {\mathcal {A}}|\delta \sim \epsilon$ in $\Omega$ in which case ${\mathcal {C}}(\Omega ,{\mathcal {A}})\sim \epsilon$ but (1.3) fails since every integral is infinity.

• (iii) In the hypothesis of Theorem 1.8, boundedness of the domain and symmetry of the operator might seem restrictive and it is very likely that the proof can be modified to remove those restrictions. Nevertheless, Theorem 1.8 as stated is enough to prove Theorem 1.6 and we leave the details to the interested reader.

As a consequence we immediately obtain the “small constant” case of Theorem 1.6:

Corollary 1.13

Under the same background hypothesis as in Theorem 1.8 if ${\mathcal {A}}$ is a symmetric uniformly elliptic matrix on $\Omega$ satisfying (H1) and (H2) with $\Vert {\mathcal {A}}\Vert _{\mathrm{Car}}<\epsilon$ and $\omega _{L} \in A_{\infty }(\sigma )$ then $\partial \Omega$ is uniformly rectifiable.

Remark 1.14

We note that the $A_\infty$ constants for $\omega _L$ are not affected by the normalization $\lambda = 1$, however, the small parameter $\epsilon$ in (1.9) clearly depends upon this normalization.

Remark 1.15

Having fixed the desired ellipticity constants $\lambda =1$ and $\Lambda$ and the geometric parameters $M, C_1, C_{AR}>1$, one may ask whether operators $L= -\mathop {{\text {div}}}\nolimits ({\mathcal {A}}(\cdot )\nabla )$ such that $\omega _L\in A_{\infty }(\sigma )$ and ${\mathcal {A}}$ satisfies (1.9) with small constant $\epsilon$ exist. Choosing a matrix for which the left-hand side of (1.2) is small (e.g., a constant coefficient matrix), we can guarantee that (1.9) holds with a desired $\epsilon$, see Remark 1.10. It is a consequence of the work in [KP] that on a chord arc domain (see Definition 2.9) the $A_{\infty }$ constants of $\omega _L$ only depend on the ellipticity constants, the norm (1.2) and the geometric parameters (which include $M, C_1, C_{AR}>1$). Thus in this case there exist constants $C_0>1$ and $\theta \in (0,1)$ such that all the conditions of Theorem 1.8 are satisfied.

The proof in Part II is based on the method of “extrapolation of Carleson measures", by means of which we bootstrap the small constant case treated in Part I. This method was first introduced in the work of Lewis and Murray [LM], based on the Corona construction which has its origins in the work of Carleson [Car], and Carleson and Garnett [CG]. In order to carry out this procedure, we go back and forth between the original domain $\Omega$ and certain sawtooth domains, taking advantages of the scale-invariant nature of Carleson measures. In particular we need to transfer the $A_\infty$ property of elliptic measure, from the original domain to its sawtooth subdomains. This last step is really the heart of the proof. We note that the use of the Kenig-Pipher condition is key in the latter argument since these operators have the property that the associated elliptic measure for any chord-arc subdomain belongs to $A_\infty$ (see Theorem 9.1 and the comments after it). For the rest of the arguments (at least in the symmetric case) we could have worked with weaker conditions.

2 Preliminaries

In this section we state the definitions and some auxiliary results that will be used throughout the paper.

2.1 Definitions.

Definition 2.1

We say a closed set $E\subset {{\mathbb {R}}}^n$ is Ahlfors regular with constant $C_{AR}>1$ if for any $q\in E$ and $0<r<{{\,\mathrm{diam}\,}}(E)$,

$$\begin{aligned} C_{AR}^{-1}\, r^{n-1} \le {\mathcal {H}}^{n-1}(B(q,r)\cap E) \le C_{AR}\, r^{n-1}. \end{aligned}$$

There are many equivalent characterizations of a uniformly rectifiable set, see [DS2]. Since uniformly rectifiability is not the main focus of our paper, we only state one of the geometric characterizations as its definition.

Definition 2.2

An Ahlfors regular set $E\subset {{\mathbb {R}}}^n$ is said to be uniformly rectifiable, if it has big pieces of Lipschitz images of ${{\mathbb {R}}}^{n-1}$. That is, there exist $\theta , M>0$ such that for each $q\in E$ and $0<r<{{\,\mathrm{diam}\,}}(E)$, there is a Lipschitz mapping $\rho : B_{n-1}(0, r) \rightarrow {{\mathbb {R}}}^n$ such that $\rho$ has Lipschitz norm $\le M$ and

$$\begin{aligned} {\mathcal {H}}^{n-1} \left( E\cap B(q,r) \cap \rho (B_{n-1}(0,r)) \right) \ge \theta r^{n-1}. \end{aligned}$$

Here $B_{n-1}(0,r)$ denote a ball of radius r in ${{\mathbb {R}}}^{n-1}$.

Definition 2.3

An open set $\Omega \subset {\mathbb {R}}^n$ is said to satisfy the (interior) corkscrew condition (resp. the exterior corkscrew condition) with constant $M>1$ if for every $q\in \partial \Omega$ and every $0< r<{{\,\mathrm{diam}\,}}(\Omega )$, there exists $A=A(q,r) \in \Omega$ (resp. $A\in \Omega _{\mathrm{ext}}:={\mathbb {R}}^n\setminus {\overline{\Omega }}$) such that

$$\begin{aligned} B\left( A, \frac{r}{M} \right) \subset B(q,r) \cap \Omega \qquad \Big (\text{ resp. } B\left( A, \frac{r}{M} \right) \subset B(q,r) \cap \Omega _{\mathrm{ext}}. \Big ) \end{aligned}$$

(2.4)

The point A is called a Corkscrew point (or a non-tangential point) relative to $\Delta (q,r)=B(q,r)\cap \partial \Omega$ in $\Omega$ (resp. $\Omega _{\mathrm{ext}}$).

Definition 2.5

An open connected set $\Omega \subset {\mathbb {R}}^n$ is said to satisfy the Harnack chain condition with constants $M, C_1>1$ if for every pair of points $A, A'\in \Omega$ there is a chain of balls $B_1, B_2, \dots , B_K\subset \Omega$ with $K \le M(2+\log _2^+ \Pi )$ that connects A to $A'$, where

$$\begin{aligned} \Pi :=\frac{|A-A'|}{\min \{\delta (A), \delta (A')\}}. \end{aligned}$$

(2.6)

Namely, $A\in B_1$, $A'\in B_K$, $B_k\cap B_{k+1}\ne \emptyset$ and for every $1\le k\le K$,

$$\begin{aligned} C_1^{-1} {{\,\mathrm{diam}\,}}(B_k) \le {\text {dist}}(B_k,\partial \Omega ) \le C_1 {{\,\mathrm{diam}\,}}(B_k). \end{aligned}$$

(2.7)

We note that in the context of the previous definition if $\Pi \le 1$ we can trivially form the Harnack chain $B_1=B(A,3\delta (A)/5)$ and $B_2=B(A', 3\delta (A')/5)$ where (2.7) holds with $C_1=3$. Hence the Harnack chain condition is non-trivial only when $\Pi > 1$.

Definition 2.8

An open connected set $\Omega \subset {{\mathbb {R}}}^n$ is said to be a uniform domain with constants $M, C_1$, if it satisfies the interior corkscrew condition with constant M and the Harnack chain condition with constants $M, C_1$.

Definition 2.9

A uniform domain $\Omega \subset {{\mathbb {R}}}^n$ is said to be NTA if it satisfies the exterior corkscrew condition. If one additionally assumes that $\partial \Omega$ is Ahlfors regular, the $\Omega$ is said to be a chord-arc domain.

For any $q\in \partial \Omega$ and $r>0$, let $\Delta =\Delta (q,r)$ denote the surface ball $B(q,r) \cap \partial \Omega$, and let $T(\Delta )=B(q,r)\cap \Omega$ denote the Carleson region above $\Delta$. We always implicitly assume that $0<r< {{\,\mathrm{diam}\,}}( \Omega )$. We will also write $\sigma ={\mathcal {H}}^{n-1}|_{\partial \Omega }$.

Given an open connected set $\Omega$ and an elliptic operator L we let $\{\omega _L^X\}_{X\in \Omega }$ be the associated elliptic measure. In the statement of Theorem 1.8 we assume that $\omega _L \in A_{\infty }(\sigma )$ in the following sense:

Definition 2.10

The elliptic measure associated with L in $\Omega$ is said to be of class $A_{\infty }$ with respect to the surface measure $\sigma = {\mathcal {H}}^{n-1}|_{\partial \Omega }$, which we denote by $\omega _L\in A_\infty (\sigma )$, if there exist $C_0>1$ and $0<\theta <\infty$ such that for any surface ball $\Delta (q,r)=B(q,r)\cap \partial \Omega$, with $q\in \partial \Omega$ and $0<r<{{\,\mathrm{diam}\,}}(\Omega )$, any surface ball $\Delta '=B'\cap \partial \Omega$ centered at $\partial \Omega$ with $B'\subset B(q,r)$, and any Borel set $F\subset \Delta '$, the elliptic measure with pole at A(q, r) (a corkscrew point relative to $\Delta (q,r)$) satisfies

$$\begin{aligned} \frac{\omega _L^{A(q,r)}(F)}{\omega _L^{A(q,r)}(\Delta ')} \le C_0\left( \frac{\sigma (F)}{\sigma (\Delta ')} \right) ^{\theta }. \end{aligned}$$

(2.11)

Since $\sigma$ is a doubling measure, it is well-known that the condition $\omega _L\in A_\infty (\sigma )$ is equivalent to the fact that $\omega _L\in RH_q(\sigma )$ for some $q>1$ in the following sense: $\omega _L \ll \sigma$ and the Radon-Nikodym derivative $\mathbf{k }_L:= d\omega _L/d\sigma$ satisfies the reverse Hölder estimate

(2.12)

for all $\Delta (q,r)=B(q,r)\cap \partial \Omega$, with $x\in \partial \Omega$ and $0<r<{{\,\mathrm{diam}\,}}(\Omega )$, any surface ball $\Delta '=B'\cap \partial \Omega$ centered at $\partial \Omega$ with $B'\subset B(q,r)$.

Definition 2.13

A domain $\Omega \subset {\mathbb {R}}^n$ with $n\ge 3$ is said to satisfy the capacity density condition (CDC) if there exists a constant $c_0>0$ such that

$$\begin{aligned} \frac{{{\,\mathrm{cap_2}\,}}(B_r(q)\setminus \Omega )}{{{\,\mathrm{cap_2}\,}}(B_r(q))} \ge c_0,\quad \text {for any } q\in \partial \Omega \text { and } 0<r<{{\,\mathrm{diam}\,}}(\Omega ), \end{aligned}$$

(2.14)

where for any set $K\subset {\mathbb {R}}^n$, the capacity is defined as

$$\begin{aligned} {{\,\mathrm{cap_2}\,}}(K) = \inf \bigg \{\int |\nabla \varphi |^2 dX: \varphi \in C_c^{\infty }({\mathbb {R}}^n), K\subset {{\,\mathrm{int}\,}}\{\varphi \ge 1\}\bigg \}. \end{aligned}$$

It was proved in [Zha, Section 3 ] and [HLMN, Lemma 3.27] that a domain in ${\mathbb {R}}^n$, $n\ge 3$, with $(n-1)$-Ahlfors regular boundary satisfies the capacity density condition with constant $c_0$ depending only on n and the Ahlfors regular constant $C_{AR}$. In particular such a domain is Wiener regular and hence for any elliptic operator L, and any function $f\in C(\partial \Omega )$, we can define

$$\begin{aligned} u(X) = \int _{\partial \Omega } f(q) d\omega _L^X(q), \qquad X\in \Omega , \end{aligned}$$

(2.15)

and obtain that $u\in W_{\mathrm{loc}}^{1,2}(\Omega )\cap C({{\overline{\Omega }}})$, $u|_{\partial \Omega }=f$ on $\partial \Omega$ and $Lu = 0$ in $\Omega$ in the weak sense. Moreover, if additionally $f\in {{\,\mathrm{Lip}\,}}(\Omega )$ then $u\in W_{}^{1,2}(\Omega )$.

2.2 Properties of Solutions and Elliptic Measure.

For following lemmas, we always assume that $\Omega$ is a uniform domain with Ahlfors regular boundary (in fact they hold under the weaker assumption that $\Omega$ is a uniform domain satisfying the CDC). Let $L=-\mathop {{\text {div}}}\nolimits ({\mathcal {A}}(\cdot )\nabla )$ be a real uniformly elliptic operator, and we write $\omega =\omega _L$ for the corresponding elliptic measure. Although in our main result we consider non necessarily symmetric uniformly elliptic matrices, we will reduce matters to the symmetric case, in particular all the following properties will be used in that case, hence during this section we assume that ${\mathcal {A}}$ is symmetric. All constants will only depend on the allowable constants, that is, those involved in the fact that the domain in question is uniform and has Ahlfors regularity boundary, and also in the uniform ellipticity of ${\mathcal {A}}$. (Note that we may assume ${\mathcal {A}}$ has been normalized so that $\lambda =1$ in (1.5).) In Part II we will apply these lemmas to $\Omega$ as well as its sawtooth domains $\Omega _{{\mathcal {F}},Q}$.

Under the above assumptions, one can construct the associated elliptic measure $\omega _L$ and Green function G. For the latter the reader is referred to the work of Grüter and Widman [GW], while the existence of the corresponding elliptic measure is an application of the Riesz representation theorem. The behavior of $\omega$ and G, as well as the relationship between them, depends crucially on the properties of $\Omega$, and assuming that $\Omega$ is a uniform domain with the CDC one can follow the program carried out in [JK]. We summarize below the results which will be used later in this paper. For a comprehensive treatment of the subject and the proofs we refer the reader to the forthcoming monograph [HMT2] (see also [Ken] for the case of NTA domains).

Theorem 2.16

   There is a unique non-negative function $G: \Omega \times \Omega \rightarrow {{\mathbb {R}}}\cup \{\infty \}$, the Green function associated with L, and a positive, finite constant C, depending only on dimension, and (given the normalization) $\Lambda$, such that the following hold:

$$\begin{aligned}&G(\cdot , Y) \in W^{1,2}(\Omega \setminus B(Y,s))\cap W^{1,1}_0(\Omega )\cap W_0^{1,r}(\Omega ), \quad \forall \,Y\in \Omega ,\ \forall \,s>0,\ \forall \,r\in \left[ 1,\tfrac{n}{n-1}\right) ; \nonumber \\\end{aligned}$$

(2.17)

$$\begin{aligned}&\int \left\langle {\mathcal {A}}(X)\nabla _X G(X,Y), \nabla \varphi (X) \right\rangle dX = \varphi (Y), \quad \text {for all }\varphi \in C_c^{\infty }(\Omega ); \end{aligned}$$

(2.18)

$$\begin{aligned}&\Vert G(\cdot ,Y)\Vert _{L^{\frac{n}{n-2},\infty }(\Omega )} +\Vert \nabla G(\cdot ,Y)\Vert _{L^{\frac{n}{n-1},\infty }(\Omega )}\le C, \quad \forall \,Y\in \Omega ; \end{aligned}$$

(2.19)

$$\begin{aligned}&G(X,Y) \le C|X-Y|^{2-n}; \end{aligned}$$

(2.20)

and

$$\begin{aligned} G(X,Y) \ge C|X-Y|^{2-n}, \quad \text {if } |X-Y|\le \frac{7}{8}{\delta (Y)}. \end{aligned}$$

(2.21)

Furthermore, if $\Omega$ is a uniform domain satisfying the CDC, for any $\varphi \in C_c^{\infty }({{\mathbb {R}}}^n)$ and for almost all $Y\in \Omega$,

$$\begin{aligned} -\int _{\Omega } \left\langle {\mathcal {A}}(X)\nabla _X G(X,Y), \nabla \varphi (X) \right\rangle dX = \int _{\partial \Omega } \varphi d\omega ^{Y} -\varphi (Y), \end{aligned}$$

(2.22)

where $\{\omega ^Y\}_{Y\in \Omega }$ is the associated elliptic measure.

We observe that (2.19) and Kolmogorov’s inequality give that for every $1\le r<\frac{n}{n-1}$,

$$\begin{aligned} \Vert G(\cdot ,Y)\Vert _{L^r(\Omega )}\le C C_3^{\frac{1}{r}} |\Omega |^{\frac{1}{r}-\frac{n-2}{n}}, \qquad \Vert \nabla G(\cdot ,Y)\Vert _{L^r(\Omega )}\le C C_4^{\frac{1}{r}} |\Omega |^{\frac{1}{r}-\frac{n-1}{n}}, \end{aligned}$$

(2.23)

where C is the constant in (2.19), $C_4=(\frac{n}{(n-2)r})'$, and $C_4=(\frac{n}{(n-1)r})'$.

Lemma 2.24

(Boundary Hölder regularity). There exist constants $C, \beta >0$ (depending on the allowable constants) such that for $q\in \partial \Omega$ and $0<r<{{\,\mathrm{diam}\,}}(\partial \Omega )$, and $u\ge 0$ with $Lu=0$ in $B(q,2r) \cap \Omega$, if u vanishes continuously on $\Delta (q,2r) = B(q,2r) \cap \partial \Omega$, then

$$\begin{aligned} u(X) \le C\left( \frac{|X-q|}{r} \right) ^{\beta } \sup _{B(q, 2r)\cap \Omega } u, \qquad \text {for any } X\in \Omega \cap B(q,r). \end{aligned}$$

(2.25)

Lemma 2.26

(Comparison principle). Let u and v be non-negative solutions to $Lu=Lv=0$ in $B(q,4r)\cap \Omega$ which vanish continuously on $\Delta (q,4r)$. Let $A=A(q,r)$ be a corkscrew point relative to $\Delta (q,r)$. Then

$$\begin{aligned} \frac{u(X)}{v(X)} \approx \frac{u(A)}{v(A)} \quad \text { for any } X\in B(q,r)\cap \Omega . \end{aligned}$$

(2.27)

Lemma 2.28

(Non-degeneracy of elliptic measure). There exists $m_0\in (0,1)$ depending on the allowable constants such that for any $q\in \partial \Omega$ and $0<r<{{\,\mathrm{diam}\,}}(\partial \Omega )$,

$$\begin{aligned} \omega ^{X} (\Delta (q,r)) \ge m_0 \qquad \text {for } X\in B(q,r/2)\cap \Omega . \end{aligned}$$

(2.29)

Lemma 2.30

(Boundary Harnack inequality). Let $\Omega$ be a uniform domain satisfying the CDC. There exists a constant C (depending on the allowable constants) such that for $q\in \partial \Omega$ and $0<r<{{\,\mathrm{diam}\,}}(\partial \Omega )$. If $u\ge 0$ with $Lu=0$ in $\Omega \cap B(q,2r)$ and u vanishes continuously on $\Delta (q,2r)$, then

$$\begin{aligned} u(X) \le C u(A(q,r)), \qquad \text {for any}\ X\in \Omega \cap B(q,r). \end{aligned}$$

(2.31)

Lemma 2.32

(Change of pole formula). Let $q\in \partial \Omega$ and $0<r<{{\,\mathrm{diam}\,}}(\partial \Omega )$ be given, and let $A = A(q,r)$ be a corkscrew point relative to $\Delta (q,r)$. Let $F, F' \subset \Delta (q,r)$ be two Borel subsets such that $\omega ^A(F)$ and $\omega ^A(F')$ are positive. Then

$$\begin{aligned} \frac{\omega ^X(F)}{\omega ^X(F')} \approx \frac{\omega ^A(F)}{\omega ^A(F')}, \quad \text { for any }X\in \Omega \setminus B(q,2r). \end{aligned}$$

(2.33)

In particular with the choice $F=\Delta (q,r)$, we have

$$\begin{aligned} \frac{\omega ^X(F')}{\omega ^X(\Delta (x,r))} \approx \omega ^A(F') \quad \text { for any } X\in \Omega \setminus B(q,2r). \end{aligned}$$

(2.34)

Lemma 2.35

(CFMS estimate). There exists a constant $C\ge 1$, such that for any $q\in \partial \Omega$, $0<r<{{\,\mathrm{diam}\,}}(\partial \Omega )/M$, and $A = A(q,r)$, a corkscrew point relative to $\Delta (q,r)$, the Green’s function $G=G_L$ satisfies

$$\begin{aligned} C^{-1} \frac{G(X_0,A)}{r} \le \frac{\omega ^{X_0}(\Delta (q,r))}{r^{n-1}} \le C ~ \frac{G(X_0,A)}{r} \end{aligned}$$

(2.36)

for any $X_0 \in \Omega \setminus B(q,2r)$.

Lemma 2.37

(Doubling property of the elliptic measure). For every $q\in \partial \Omega$ and $0<r<{{\,\mathrm{diam}\,}}(\partial \Omega )/4$, we have

$$\begin{aligned} \omega ^X(\Delta (q,2r)) \le C \omega ^X(\Delta (q,r)) \end{aligned}$$

(2.38)

for any $X\in \Omega \setminus B(q,4r)$.

Remark 2.39

The following simple observation will be useful. If M denotes the corkscrew constant for $\Omega$, it follows easily from the previous result, Lemma 2.29 and Harnack’s inequality that

$$\begin{aligned} \omega ^X(\Delta (q,2r)) \le C_2\omega ^X(\Delta (q,r)), \end{aligned}$$

(2.40)

for every $q\in \partial \Omega$, $0<r<{{\,\mathrm{diam}\,}}(\partial \Omega )/4$ and for all $X\in \Omega$ with $\delta (X)\ge r/(2M)$. Here $C_2$ is a constant that depends on the allowable parameters associated with $\Omega$ and the ellipticity constants of L.

Our next result establishes that if a domain satisfies the Harnack chain condition then we can modify the chain of balls so that they avoid a non-tangential balls inside:

Lemma 2.41

Let $\Omega \subset {\mathbb {R}}^n$ be an open set satisfying the Harnack chain condition with constants $M, C_1>1$. Given $X_0\in \Omega$, let $B_{X_0}=B(X_0,\delta (X_0)/2)$. For every $X,Y\in \Omega \setminus \overline{B_{X_0}}$, if we set $\Pi =|X-Y|/\min \{\delta (X), \delta (Y)\}$, then there is a chain of open Harnack balls $B_1, B_2, \dots , B_K\subset \Omega$ with $K \le 100 (M+C_1^2)(2+\log _2^+ \Pi )$ that connects X to Y. Namely, $X\in B_1$, $Y\in B_K$, $B_k\cap B_{k+1}\ne \emptyset$ for every $1\le k\le K-1$ and for every $1\le k\le K$,

$$\begin{aligned} (100\,C_1)^{-2} {{\,\mathrm{diam}\,}}(B_k) \le {\text {dist}}(B_k,\partial \Omega ) \le 100\,C_1^2 {{\,\mathrm{diam}\,}}(B_k). \end{aligned}$$

(2.42)

Moreover, $B_k\cap \frac{1}{2} B_{X_0}=\emptyset$ for every $1\le k\le K$.

Proof

Fix X, Y as in the statement and without loss of generality we assume that $\delta (X)\le \delta (Y)$. Use the Harnack chain condition for $\Omega$ to construct the chain of balls $B_1,\dots , B_K$ as in Definition 2.5. If none of $B_k$ meets $B_{X_0}$ then there is nothing to do as this original chain satisfies all the required condition. Hence we may suppose that some $B_k$ meets $B_{X_0}$. The main idea is that then we can modify the chain of balls by adding some small balls that surround $X_0$. To be more precise, we let $k_-$ and $k_+$ be respectively the first and last ball in the chain meeting $B_{X_0}$. Note that $1\le k_-\le k_+\le K$.

We pick $X_{-}\in B_{k_-}\setminus \overline{B_{X_0}}$: If $k_-=1$ we let $X_{-}=X$ or if $k_->1$ we pick $X_{-}\in B_{k_--1}\cap B_{k_-}$. Since $B_{k_-}$ meets $B_{X_0}$ then we can find $Y_{-}\in B_{k_-}\cap \partial B_{X_0}$ such that the open segment joining $X_{-}$ and $Y_{-}$ is contained in $B_{k_-}\setminus \overline{B_{X_0}}$. Analogously we can find $X_{+}\in B_{k_+}\setminus \overline{B_{X_0}}$ and $Y_{+}\in B_{k_+}\cap \partial B_{X_0}$ such that the open segment joining $X_{+}$ and $Y_{+}$ is contained in $B_{k_+}\setminus \overline{B_{X_0}}$.

Next set $r=\delta (X)/(16 C_1)$ and let $N_\pm \ge 0$ be such that $N_\pm \le |X_{\pm }-Y_{\pm }|/r < N_\pm +1$. For $j=0,\dots , N_\pm$, let

$$\begin{aligned} B_\pm ^j=B(X_{\pm }^j,r), \qquad \text {where}\quad X_{\pm }^j= X_\pm +jr \frac{Y_{\pm }-X_{\pm }}{|Y_{\pm }-X_{\pm }|}. \end{aligned}$$

Straightforward arguments show that $N_\pm \le 32 C_1^2$, $X_\pm \in B_\pm ^0$, $Y_\pm \in B_\pm ^{N_\pm }$, $B_\pm ^j\cap B_\pm ^{j+1} \ne \emptyset$ for every $0\le j\le N_\pm -1$, and

$$\begin{aligned} (32 C_1^2)^{-1}{{\,\mathrm{diam}\,}}(B_\pm ^j) \le {\text {dist}}(B_\pm ^j, \partial \Omega ) \le 32 C_1^2{{\,\mathrm{diam}\,}}(B_\pm ^j), \qquad B_\pm ^j\cap \frac{1}{2} B_{X_0}=\emptyset , \end{aligned}$$

for every $0\le j\le N_\pm -1$.

Next, since $X_{\pm }\in \partial B_{X_0}$ we can find a sequence of balls $B^0,\dots , B^{N}$ centered at $\partial B_{X_0}$ and with radius $\delta (X)/16$ (hence $B^j\cap \frac{1}{2} B_{X_0}=\emptyset$) so that $N\le 64$, $Y_-\in B^0$, $Y_+\in B^N$, $B^j\cap B^{j+1}\ne \emptyset$ for $0\le j\le N-1$ and $32^{-1}\le {\text {dist}}(B^j, \partial \Omega )/{{\,\mathrm{diam}\,}}(B^j)\le 32$.

Finally, to form the desired Harnack chain we concatenate the sub-chains $\{B_1, \dots B_{k_--1}\}$, $\{B_{-}^0,\dots B_-^{N_-}\}$, $\{B^0,\dots B^N\}$, $\{B_+^{N},\dots , B_+^0\}$, $\{B_{k_++1},\dots B_K\}$ and the resulting chain have all the desired properties. To complete the proof we just need to observe that the length of the chain is controlled by $K+N_-+N+N_++3\le 100 (M+C_1^2)(2+\log _2^+ \Pi )$.$\square$

2.3 Compactness of Closed Sets and Radon Measures.

The reader may be familiar with the notion of convergence of compact sets in the Hausdorff distance; for general closed sets, not necessarily compact, we use the following notion of convergence, see [DS1, Section 8.2] for details. (It was pointed out to us that this notion is also referred to as the Attouch-Wets topology, see for example [Bee, Chapter 3].)

Definition 2.43

(Convergence of closed sets). Let $\{E_j\}$ be a sequence of non-empty closed subsets of ${{\mathbb {R}}}^n$, and let E be another non-empty closed subset of ${{\mathbb {R}}}^n$. We say that $E_j$ converges to E, and write $E_j \rightarrow E$, if

$$\begin{aligned} \lim _{j\rightarrow \infty } \sup _{x\in E_j \cap B(0,R)} {\text {dist}}(x, E) = 0 \end{aligned}$$

and

$$\begin{aligned} \lim _{j\rightarrow \infty } \sup _{x\in E \cap B(0,R)} {\text {dist}}(x, E_j) = 0 \end{aligned}$$

for all $R>0$. By convention, these suprema are interpreted to be zero when the relevant sets are empty.

We remark that in the above definition, we may replace the balls B(0, R) by arbitrary balls in ${{\mathbb {R}}}^n$. The following compactness property has been proved in [DS1, Lemma 8.2]:

Lemma 2.44

(Compactness of closed sets). Let $\{E_j\}$ be a sequence of non-empty closed subsets of ${{\mathbb {R}}}^n$, and suppose that there exists an $r>0$ such that $E_j \cap B(0,r) \ne \emptyset$ for all j. Then there is a subsequence of $\{E_j\}$ that converges to a nonempty closed subset E of ${{\mathbb {R}}}^n$ in the sense defined above.

Given a Radon measure $\mu$ on ${{\mathbb {R}}}^n$ (i.e., a non-negative Borel such that the measure of any compact set is finite) we define

$$\begin{aligned} {{\,\mathrm{spt}\,}}\mu = \overline{\big \{ x\in {{\mathbb {R}}}^n: \mu (B(x,r))> 0 \text { for any }r>0 \big \}}. \end{aligned}$$

Definition 2.45

We say that a Radon measure $\mu$ on ${{\mathbb {R}}}^n$ is Ahlfors regular with constant $C\ge 1$, if there exits a constant $C\ge 1$ such that for any $x\in E$ and $0<r<{{\,\mathrm{diam}\,}}(E)$,

$$\begin{aligned} C^{-1}\, r^{n-1} \le \mu (B(q,r)) \le C\, r^{n-1}, \qquad \forall \,x\in {{\,\mathrm{spt}\,}}\mu ,\ 0<r<{{\,\mathrm{diam}\,}}({{\,\mathrm{spt}\,}}\mu ). \end{aligned}$$

Definition 2.46

Let $\{\mu _j\}$ be a sequence of Radon measures on ${{\mathbb {R}}}^n$. We say $\mu _j$ converge weakly to a Radon measure $\mu _{\infty }$ and write $\mu _j \rightharpoonup \mu _{\infty }$, if

$$\begin{aligned} \int f d\mu _j \rightarrow \int f d\mu _{\infty } \end{aligned}$$

for any $f\in C_c({{\mathbb {R}}}^n)$.

We finish this section by stating a compactness type lemma for Radon measures which are uniformly doubling and “bounded below”.

Lemma 2.47

([TZ, Lemma 2.19]). Let $\{\mu _j\}_j$ be a sequence of Radon measures. Let $A_1, A_2>0$ be fixed constants, and assume the following conditions:

• (i) $0\in {{\,\mathrm{spt}\,}}\mu _j$ and $\mu _j(B(0,1)) \ge A_1$ for all j,

• (ii) For all $j\in {{\mathbb {N}}}$, $q\in {{\,\mathrm{spt}\,}}\mu _j$ and $r>0$,

  $$\begin{aligned} \mu _j(B(q,2r))\le A_2\mu _j(B(q,r)). \end{aligned}$$

  (2.48)

If there exists a Radon measure $\mu _\infty$ such that $\mu _j\rightharpoonup \mu _\infty$, then $\mu _\infty$ is doubling and

$$\begin{aligned} {{\,\mathrm{spt}\,}}\mu _j\rightarrow {{\,\mathrm{spt}\,}}\mu _\infty , \end{aligned}$$

(2.49)

in the sense of Definition 2.43.

3 Part I. Small Constant Case

The plan of Part I is as follows. We prove Theorem 1.8 by contradiction using a compactness argument. More precisely, we assume that there is a family of bounded uniform domains with Ahlfors regular boundaries and a family of divergence form elliptic operators with associated elliptic measure in the class $A_\infty$ and with all the implicit constants uniformed controlled. We also have that the oscillations of the coefficients convergence to 0 and that the exterior corkscrew condition fails for each domain in the family. This is all detailed in Section 3. The goal is to reach a contradiction and with that goal in mind we show in Section 4 that passing to a subsequence there are a limiting domain which is uniform and has Ahlfors regular boundary and a limiting constant coefficient elliptic operator in that limiting domain whose associated elliptic measure belongs to the class $A_\infty$. With this in hand in Section 5 we are in a position to apply Theorem 1.1 to obtain that the limiting domain satisfies the exterior corkscrew. This in turn leads us to a contradiction since the exterior corkscrew condition fails for any of the domains in the family.

4 Compactness Argument

To prove Theorem 1.8 we will proceed by contradiction. First we discuss the constant N. Recall that, as noted above, the assertion that (a) implies (c) in Theorem 1.1 extends routinely to all constant coefficient second order elliptic operators; alternatively, this fact follows from the results of [HMT1] as (1.4) and (H1) holds trivially in the constant coefficient case. Thus given values of the allowable constants $M, C_1, C_{AR},\Lambda /\lambda$, $C_0,\theta$, let $\Omega \subset {\mathbb {R}}^n$, $n\ge 3$, be a uniform domain with constants $M, C_1$, whose boundary is Ahlfors regular with constant $C_{AR}$, and let $L = -\mathop {{\text {div}}}\nolimits ({\mathcal {A}}_0\nabla )$ be a constant coefficient elliptic operator where the constant real symmetric matrix ${\mathcal {A}}_0$ satisfies (1.5) with ellipticity constants $\lambda , \Lambda$, and such that the corresponding elliptic measure $\omega _{L} \in A_{\infty }(\sigma )$ with constants $C_0$ and $\theta$. Then there exists a constant $N_0=N_0(M, C_1, C_{AR},\Lambda /\lambda ,C_0,\theta )$ such that $\Omega$ satisfies the exterior corkscrew condition with constant $N_0$. We underline that this $N_0$ depends on the ratio of the ellipticity constants rather than the matrix ${\mathcal {A}}_0$ per se.

With this in mind, set

$$\begin{aligned} N=4N_0(4M,2C_1, 2^{5(n-1)}C_{AR}^2,\Lambda /\lambda , C_0 C_2 C_{AR}^{4\theta } 2^{8(n-1)\theta },\theta ) \end{aligned}$$

(3.1)

where the constant $C_2=C_2(M,C_1, C_{AR}, \Lambda /\lambda )$ can be found in Remark 2.39.

We now state the contradiction hypothesis: for fixed $n\ge 3$, we suppose that there exists a set of allowable constants $M, C_1, C_{AR}>1$, $\Lambda \ge \lambda = 1$, $C_0>1$ and $0<\theta <1$, and a sequence $\epsilon _j$ (with $\epsilon _j \rightarrow 0$ as $j\rightarrow \infty$), so that the following holds:

• Assumption (a): For each j there is a bounded domain $\Omega _j\subset {\mathbb {R}}^n$, which is uniform with constants $M, C_1$ and whose boundary is Ahlfors regular with constant $C_{AR}$. Also, there is an elliptic matrix ${\mathcal {A}}_j$ defined on $\Omega _j$, with ellipticity constants $\lambda =1$ and $\Lambda$, and we write $L_j = -\mathop {{\text {div}}}\nolimits ({\mathcal {A}}_j\nabla )$.

• Assumption (b): ${{\,\mathrm{osc}\,}}(\Omega _j, {\mathcal {A}}_j) <\epsilon _j$ (see (1.9)).

• Assumption (c): The elliptic measure of the operator $L_j$ in $\Omega _j$ is of class $A_{\infty }$ with respect to the surface measure $\sigma _j={\mathcal {H}}^{n-1}|_{\partial \Omega _j}$ with constants $C_0$ and $\theta$ (see Definition 2.10).

• Contrary to conclusion: For each j there is $q_j\in \partial \Omega _j$ and $0<r_j<{{\,\mathrm{diam}\,}}(\partial \Omega _j)$ such that $\Omega _j$ has no exterior corkscrew point with constant N (as in (3.1)). That is, there is no ball of radius $r_j/N$ contained in $B(q_j,r_j)\setminus \overline{\Omega _j}$.

Our goal is to obtain a contradiction and as a consequence our main result Theorem 1.8 will be proved. Without loss of generality we may assume $q_j = 0$ and $r_j = 1$ for all j, hence ${{\,\mathrm{diam}\,}}(\partial \Omega _j)>1$. Otherwise, we just replace the domain $\Omega _j$ by $(\Omega _j - q_j)/r_j$, and replace the elliptic matrix ${\mathcal {A}}_j(\cdot )$ by ${\mathcal {A}}_j(q_j + r_j \cdot )$. Note that the new domain and matrix have the same allowable constants, in particular the corresponding $A_{\infty }$ constants stay the same by the scale-invariant nature of Definition 2.10; moreover after rescaling, the above Assumption (b) is still satisfied:

$$\begin{aligned} {{\,\mathrm{osc}\,}}\left( \frac{\Omega _j - q_j}{r_j}, {\mathcal {A}}_j(q_j + r_j \cdot ) \right) = {{\,\mathrm{osc}\,}}(\Omega _j, {\mathcal {A}}_j)<\epsilon _j. \end{aligned}$$

5 Limiting Domains

We want to use a compactness argument similar to the blow-up argument in [TZ]. The crucial difference is that in [TZ], the elliptic operator tends to a constant-coefficient operator as we zoom in on the boundary and blow up the given domain; whereas here we need to work with a sequence of domains and their associated elliptic operators. In particular the geometric convergence of domains does not come for free, and more work is needed to analyze the limiting domain.

To be more precise, getting to the point where we can apply Theorem 1.1 (more precisely, its extension to the elliptic operators with constants coefficients or alternatively [HMT1] applied again to constant coefficient operators) requires showing first that if $\Omega _\infty$ is a “limiting domain” of the domains $\{\Omega _j\}$’s, then $\Omega _\infty$ is an unbounded or bounded uniform domain with Ahlfors regular boundary. To accomplish this we also need to find the limit of the Green functions. Once we have this, to show that $\omega _{L_\infty } \in A_{\infty }(\sigma _{\infty })$ for the limiting domain $\Omega _\infty$ and the limiting operator $L_{\infty }$, we need to construct the elliptic measure $\omega _{L_\infty }^Z$ for any $Z\in \Omega _\infty$ as a limiting measure compatible with the procedure. We will also show that $L_\infty$ is an elliptic operator with constants coefficients.

Throughout the rest of paper we follow the following conventions in terms of notations:

• For any $Z\in \Omega _j$ we write $\delta _j(Z) = {\text {dist}}(Z,\partial \Omega _j)$.

• For any $q\in \partial \Omega _j$ and $r\in (0, {{\,\mathrm{diam}\,}}( \partial \Omega _j))$, we use $A_j(q,r)$ to denote a corkscrew point in $\Omega _j$ relative to $B(q,r)\cap \partial \Omega _j$, i.e.,

  $$\begin{aligned} B\left( A_j(q,r), \frac{r}{M} \right) \subset B(q,r) \cap \Omega _j. \end{aligned}$$

  (4.1)

5.1 Geometric Limit.

Since ${{\,\mathrm{diam}\,}}(\partial \Omega _j) > 1$, modulo passing to a subsequence, one of the following two scenarios occurs:

Case I::

${{\,\mathrm{diam}\,}}(\Omega _j) = {{\,\mathrm{diam}\,}}(\partial \Omega _j) \rightarrow \infty$ as $j\rightarrow \infty$.

Case II::

${{\,\mathrm{diam}\,}}(\Omega _j)={{\,\mathrm{diam}\,}}(\partial \Omega _j) \rightarrow R_0 \in [1,\infty )$ as $j\rightarrow \infty$.

Therefore if $\Omega _j$ “converges” to a limiting domain $\Omega _\infty$, respectively Case I and Case II indicate that $\Omega _\infty$ is unbounded or bounded.

Let $X_j\in \Omega _j$ be a corkscrew point relative to $B(0,{{\,\mathrm{diam}\,}}(\Omega _j)/2)\cap \partial \Omega _j$, then

$$\begin{aligned} |X_j| \sim \delta _j(X_j) \sim {{\,\mathrm{diam}\,}}(\Omega _j), \end{aligned}$$

(4.2)

with constants depending on the uniform constant M. Let $G_j$ be the Green function associated with $\Omega _j$ and the operator $L_j = -\mathop {{\text {div}}}\nolimits ({\mathcal {A}}_j \nabla )$, and $\{\omega _j^X\}_{X\in \Omega _j}$ be the corresponding elliptic measure. In Case I we have

$$\begin{aligned} |X_j| \sim \delta _j(X_j) \sim {{\,\mathrm{diam}\,}}(\Omega _j) \rightarrow \infty , \end{aligned}$$

(4.3)

i.e., the poles $X_j$ tend to infinity eventually. We let

$$\begin{aligned} u_j(Z) = \frac{G_j(X_j,Z)}{\omega _j^{X_j}(B(0,1))}. \end{aligned}$$

(4.4)

In Case II, we may assume that ${{\,\mathrm{diam}\,}}(\Omega _j) \sim R_0$ for all j sufficiently large (one could naively rescale again so that $R_0=1$, should that be the case one may lose the property that $r_j=1$ for all j). Hence, there are constants $0<c_1<c_2$ such that

$$\begin{aligned} c_1 R_0 \le \delta _j(X_j) \le |X_j| \le c_2 R_0 \quad \text { for all } j \text { sufficiently large}. \end{aligned}$$

(4.5)

Thus modulo passing to a subsequence, $X_j$ converges to some point $X_0$ satisfying

$$\begin{aligned} c_1 R_0 \le |X_0| \le c_2 R_0. \end{aligned}$$

(4.6)

Note that (4.5) and (4.6) in particular imply that for any $\rho$ sufficiently small (depending on $R_0$ and $c_1, c_2$), the ball $B(X_0,\rho )$ is contained in $\Omega _j$ and ${\text {dist}}(B(X_0,\rho ),\partial \Omega _j)\ge c_1 R_0/2$. In this case we let

$$\begin{aligned} u_j(Z) = G_j(X_j,Z). \end{aligned}$$

(4.7)

Our next goal is to describe what happens with the objects in question as we let $j\rightarrow \infty$. This is done in Theorems 4.8, 4.78, 4.86 below.

Theorem 4.8

   Under Assumption (a), and using the notation above, we have the following properties (modulo passing to a subsequence which we relabel):

• (1) Case I: there is a function $u_\infty \in C({{\mathbb {R}}}^n)$ such that $u_j\rightarrow u_\infty$ uniformly on compact sets; moreover $\nabla u_j\rightharpoonup \nabla u_\infty$ in $L^2_{\mathrm{loc}}({{\mathbb {R}}}^n)$.

• (2) Case II: there is a function $u_\infty \in C({{\mathbb {R}}}^n\setminus \{X_0\})$ such that $u_j\rightarrow u_{\infty }$ uniformly on compact sets in ${{\mathbb {R}}}^n \setminus \{X_0\}$ and $\nabla u_j\rightharpoonup \nabla u_{\infty }$ in $L_{\mathrm{loc}}^2({{\mathbb {R}}}^n \setminus \{X_0\})$.

• (3) Let $\Omega _\infty =\{Z\in {{\mathbb {R}}}^n: u_\infty >0\}$.⁵ Then ${\overline{\Omega _j}}\rightarrow \overline{\Omega _\infty }$ and $\partial \Omega _j\rightarrow \partial \Omega _\infty$, in the sense of Definition 2.43. Moreover, $\Omega _\infty$ is an unbounded set with unbounded boundary in Case I, and it is bounded with diameter $R_0 \ge 1$ in Case II .

• (4) $\Omega _\infty$ is a nontrivial uniform domain with constants 4M and $2C_1$.

• (5) There is an Ahlfors regular measure $\mu _\infty$ with constant $2^{2(n-1)}C_{AR}$ such that $\sigma _j\rightharpoonup \mu _\infty$. Moreover, ${{\,\mathrm{spt}\,}}\mu _\infty =\partial \Omega _\infty$. In particular, this implies that

  $$\begin{aligned} 2^{-3(n-1)}C_{AR}^{-1} \mu _\infty \le {\mathcal {H}}^{n-1}|_{\partial \Omega _\infty } \le 2^{3(n-1)}C_{AR} \mu _\infty . \end{aligned}$$

  (4.9)

  and hence $\partial \Omega _\infty$ is Ahlfors regular with constant $2^{5(n-1)}C_{AR}^2$.

Remark 4.10

Note that this result is purely geometric. The proof only uses Assumption (a), which states the geometric characters of domains $\Omega _j$ (i.e., they are uniform domains with Ahlfors regular boundaries) and the ellipticity of the matrix operator ${\mathcal {A}}_j$. The other assumptions are irrelevant for this.

Proof of (1) in Theorem 4.8

Let $R>1$ and note that for j large enough (depending on R) we have that $X_j\notin B(0,4R)$ since by (4.3)

$$\begin{aligned} |X_j| = |X_j- 0| \ge \delta _j(X_j) \sim {{\,\mathrm{diam}\,}}(\Omega _j) \rightarrow \infty , \quad \text {as }j\rightarrow \infty . \end{aligned}$$

In particular, $L_ju_j=0$ in $B(0,4R)\cap \Omega _j$ in the weak sense. Recall that all our domains $\Omega _j$ have Ahlfors regular boundary and hence all boundary points are Wiener regular. This in turn implies that $u_j$ is a non-negative L-solution on $B(0,4R)\cap \Omega _j$ which vanishes continuously on $B(0,4R)\cap \partial \Omega _j$.

On the other hand, $0\in \partial \Omega _j$ and, using our convention (4.1), $A_j(0,1)$ is a corkscrew point relative to $B(0,1)\cap \partial \Omega _j$ in the domain $\Omega _j$. Thus, by Lemma 2.35

$$\begin{aligned} u_j(A_j(0,1)) \sim 1. \end{aligned}$$

(4.11)

We can then invoke Lemma 2.30, the fact that $A_j(0,2R)\in \Omega _j$ is a corkscrew point relative to $B(0,2R)\cap \partial \Omega _j$ for the domain $\Omega _j$, Harnack’s inequality, and (4.11) to obtain

$$\begin{aligned} \sup _{Z\in \Omega _j\cap B(0,2R)} u_j(Z) \le C u_j(A_j(0,2R)) \le C_R u_j(A_j(0,1)) \le C_R. \end{aligned}$$

(4.12)

Extending $u_j$ by 0 outside of $\Omega _j$ we conclude that the sequence $\{u_j\}_{j\ge j_0}$ is uniformly bounded in $\overline{B(0,R)}$ for some $j_0$ large enough. Since for each j, ${\mathcal {A}}_{j}$ has ellipticity constants bounded below by $\lambda =1$ and above by $\Lambda$, and $\Omega _j$ is uniform and satisfies the CDC (as $\partial \Omega _j$ is Ahlfors regular) with the same constants as $\Omega _j$, then combining Lemma 2.24 with the DeGiorgi-Nash-Moser estimates we conclude that the sequence $\{u_j\}_j$ is equicontinuous on $\overline{B(0,R)}$ (in fact uniformly Hölder continuous with same exponent). Using Arzela-Ascoli combined with a diagonalization argument applied on a sequence of balls with radii going to infinity, we produce $u_\infty \in C({{\mathbb {R}}}^n)$ and a subsequence (which we relabel) such that $u_j\rightarrow u_\infty$ uniformly on compact sets of ${{\mathbb {R}}}^n$.

As observed before, $u_j$ is a non-negative L-solution on $B(0,4R)\cap \Omega _j$ which vanishes continuously on $B(0,4R)\cap \partial \Omega _j$ and which has been extended by 0 outside of $\Omega _j$. Thus it is a positive L-subsolution on B(0, 4R) and we can use Caccioppoli’s inequality along with (4.12) to conclude that

$$\begin{aligned} \int _{B(0,R)}|\nabla u_j|^2\, dZ \le C\,R^{-2} \int _{B(0,2R)}|u_j|^2\, dZ \le C_R. \end{aligned}$$

(4.13)

This and (4.12) allow us to conclude that

$$\begin{aligned} \sup _j \Vert u_j\Vert _{W^{1,2}(B(0,R))} \le C_R <\infty . \end{aligned}$$

(4.14)

Thus, there exists a subsequence (which we relabel) which converges weakly in $W^{1,2}_{\mathrm{loc}}({{\mathbb {R}}}^n)$. Since we already know that $u_j\rightarrow u_\infty$ uniformly on compact sets of ${{\mathbb {R}}}^n$, we can use again (4.12) to easily see that $u_\infty \in W^{1,2}_{\mathrm{loc}}({{\mathbb {R}}}^n)$, and $\nabla u_j\rightharpoonup \nabla u_{\infty }$ in $L^2_{\mathrm{loc}}({{\mathbb {R}}}^n)$. This completes the proof of (1) in Theorem 4.8. $\square$

Proof of (2) in Theorem 4.8

Recall that in this case $X_j\rightarrow X_0$ as $j\rightarrow \infty$. For any $0<\rho \le c_1R_0/2$ and for all j large enough we have

$$\begin{aligned} B\left( X_j,\frac{\rho }{2} \right) \subset B(X_0,\rho ) \subset B(X_j,2\rho ) \subset \overline{B(X_j,2\rho )} \subset \overline{B(X_j,\delta _j(X_j)/2)} \subset \Omega _j, \end{aligned}$$

(4.15)

where we have used (4.5). Moreover, for j sufficiently large,

$$\begin{aligned} {\text {dist}}(B(X_j,2\rho ),\partial \Omega _j) > \frac{c_1 R_0}{2}. \end{aligned}$$

(4.16)

For any $Z\in \Omega _j\setminus B(X_j,\rho /4)$, using (4.7) and (2.20) it follows that

$$\begin{aligned} u_j(Z) \le \frac{C}{|Z-X_j|^{n-2}} \le \frac{4^{n-2}C}{\rho ^{n-2}}. \end{aligned}$$

(4.17)

Extending $u_j$ by 0 outside $\Omega _j$ the previous estimate clearly holds for every $Z\in {{\mathbb {R}}}^n\setminus \Omega _j$. Thus $\sup _j\Vert u_j\Vert _{L^\infty ({{\mathbb {R}}}^n \setminus B(X_0,\rho ))}\le C(\rho )$. Moreover, as in Case I, the sequence is also equicontinuous (in fact uniformly Hölder continuous). Using Arzela-Ascoli theorem with a diagonalization argument, we can find $u_\infty \in C({{\mathbb {R}}}^n\setminus \{X_0\})$ and a subsequence (which we relabel) such that $u_j\rightarrow u_{\infty }$ uniformly on compact sets of ${{\mathbb {R}}}^n\setminus \{X_0\}$.

Let $0<R\le \sup _{j\gg 1} {{\,\mathrm{diam}\,}}(\Omega _j) \sim R_0$. We claim that

$$\begin{aligned} \int _{B(0,R) \setminus B(X_0,\rho )} |\nabla u_j|^2 dZ \le C(R,\rho ) <\infty . \end{aligned}$$

(4.18)

To prove this, we first take arbitrary $q\in \partial \Omega _j$ and s such that $0<s\le \delta _j(X_j)/5 \sim R_0$. In particular, if $0<\rho <c_1 R_0/10\le \delta _j(X_j)/10$ it follows that $B(q,4s)\subset {{\mathbb {R}}}^n\setminus B(X_j,2 \rho )\subset {{\mathbb {R}}}^n\setminus B(X_0,\rho )$. Thus, proceeding as in Case I, $u_j$ is non-negative subsolution on B(q, 2s) and we can use Caccioppoli’s inequality and (4.17) to obtain

$$\begin{aligned} \int _{B(q,s)\setminus B(X_0,\rho )} |\nabla u_j|^2 dZ = \int _{B(q,s)} |\nabla u_j|^2 dZ \le \frac{C}{s^2} \int _{B(q,2s )} |u_j(Z)|^2 dZ \lesssim \frac{s^{n-2}}{\rho ^{2(n-2)}}. \end{aligned}$$

(4.19)

Note that the previous estimate, with $q=0$ and $s=R$, gives our claim (4.18) when $0<R\le \delta _j(X_j)/5$.

Consider next the case $R_0\sim \delta _j(X_j)/5 < R\le \sup _{j\gg 1} {{\,\mathrm{diam}\,}}(\Omega _j)\sim R_0$. Note first that the set $\Theta _j:=\{Z\in \Omega _j: \delta _j(Z) < \delta _j(X_j)/25\}$ can be covered by a family of balls $\{B(q_i,\delta _j(X_j)/5)\}_i$ with $q_i\in \partial \Omega$ and whose cardinality is uniformly bounded (here we recall that $\delta _j(X_j)\sim {{\,\mathrm{diam}\,}}(\Omega _j)$), Thus, (4.19) applied to these each ball in the family yields

$$\begin{aligned} \int _{\left( B(0,R) \setminus B(X_0,\rho ) \right) \cap \Theta _j } |\nabla u_j|^2 dZ \le \sum _i \int _{B(q_i,\delta _j(X_j)/5) \setminus B(X_0,\rho )} |\nabla u_j|^2 dZ \le C(R, \rho ) <\infty . \end{aligned}$$

(4.20)

On the other hand, the set $\{Z\in \Omega _j\setminus B(X_j,\rho /2): \delta _j(Z) \ge \delta _j(X_j)/25\}$ can be covered by a family of balls $\{B_i\}_i$ so that $r_{B_i}=\rho /16$, $4B_i \subset \Omega _j\setminus B(X_j,\rho /4)$. Moreover, the cardinality of the family is uniformly bounded depending on dimension and the ratio ${{\,\mathrm{diam}\,}}(\Omega _j)/\rho \sim R_0/\rho$. Using (4.15), Caccioppoli’s inequality in each $B_i$ since $4B_i \subset \Omega _j\setminus B(X_j,\rho /4)$, and (4.17) we obtain

$$\begin{aligned} \int _{\left( B(0,R) \setminus B(X_0,\rho ) \right) \setminus \Theta _j } |\nabla u_j|^2 dZ&\le \sum _i\int _{B_i} |\nabla u_j|^2 dZ \nonumber \\&\lesssim \sum _i\frac{1}{r_{B_i}^2} \int _{2B_i} | u_j(Z)|^2 dZ \le C(R,\rho ). \end{aligned}$$

(4.21)

Combining (4.20) and (4.21) we obtain the desired estimate and hence proof of the claim (4.18) is complete.

Next, we combine (4.18) with the fact that $\sup _j\Vert u_j\Vert _{L^\infty ({{\mathbb {R}}}^n \setminus B(X_0,\rho ))}\le C(\rho )$ to obtain that $\sup _j \Vert u_j\Vert _{W^{1,2}(B(0,R)\setminus B(X_0,\rho ))} \le C(R,\rho ) <\infty$. Thus, there exists a subsequence (which we relabel) which converges weakly in $W^{1,2}_{\mathrm{loc}}({{\mathbb {R}}}^n\setminus B(X_0,\rho ))$. Since we already know that $u_j\rightarrow u_\infty$ uniformly on compact sets of ${{\mathbb {R}}}^n\setminus B(X_0,\rho )$, we can easily see that $u_\infty \in W^{1,2}_{\mathrm{loc}}({{\mathbb {R}}}^n\setminus B(X_0,\rho ))$, and $\nabla u_j\rightharpoonup \nabla u_{\infty }$ in $L^2_{\mathrm{loc}}({{\mathbb {R}}}^n\setminus B(X_0,\rho ))$. This completes the proof of (2) in Theorem 4.8. $\square$

Remark 4.22

In the Case II scenario the following remarks will become useful later. In what follows we assume that $0<\rho \le c_1R_0/2$ and j is large enough.

• (i) Let us pick $Y\in \partial B(X_j,3\delta _j(X_j)/4)$ and note that (4.5) gives $Y, A_j(0,c_1 R_0/2) \in \Omega _j\setminus \overline{B(X_j,\delta _j(X_j)/2)}$, $|Y-A_j(0,c_1 R_0/2)|<(c_1+2c_2)R_0$, and $\delta _j(Y)\ge c_1 R_0/4$. Recalling that $\Omega _j$ satisfies the interior corkscrew condition with constant M, it follows by definition that $\delta _j(A_j(0,c_1 R_0/2))\ge c_1 R_0/(2M)$. All these allow us to invoke Lemma 2.41 to then use (2.21) and (4.5) and eventually show

  $$\begin{aligned} u_j\left( A_j\left( 0,\frac{c_1 R_0}{2} \right) \right) \sim u_j(Y) > rsim \left| Y - X_j\right| ^{2-n} \sim \delta _j(X_j)^{2-n}\sim R_0^{2-n}, \end{aligned}$$

  (4.23)

  where the implicit constants are independent of j.

• (ii) The set $\partial B(X_0,\rho )$ is compact and away from $X_0$, so $u_j\rightarrow u_\infty$ uniformly in $\partial B(X_0,\rho )$. Since $X_j\rightarrow X_0$, for any $Z\in \partial B(X_0,\rho )$ we have $\rho /2< |Z-X_j| < 2\rho$ for j sufficiently large. In particular by choosing $\rho <R_0/(16M)$, we have for j large enough

  $$\begin{aligned} |Z-X_j|< 2\rho < \frac{R_0}{8M} \le \frac{{{\,\mathrm{diam}\,}}(\Omega _j)}{4M} \le \frac{\delta _j(X_j)}{2}, \end{aligned}$$

  (4.24)

  where the last estimate uses that $X_j\in \Omega _j$ is a corkscrew point relative to the surface ball $B(0,{{\,\mathrm{diam}\,}}(\Omega _j)/2)\cap \partial \Omega _j$ with constant M. Thus by (2.21) if j is large enough

  $$\begin{aligned} u_j(Z) > rsim |Z-X_j|^{2-n} > rsim \rho ^{2-n}, \qquad \forall \,Z\in \partial B(X_0,\rho ) \end{aligned}$$

  with implicit constants which are independent of j. Therefore,

  $$\begin{aligned} u_\infty (Z) = \lim _{j\rightarrow \infty } u_j(Z) > rsim \rho ^{2-n}, \qquad \forall \,Z\in \partial B(X_0,\rho ) \end{aligned}$$

  (4.25)

  For this reason it is natural to extend the definition of $u_\infty$ to all of ${{\mathbb {R}}}^n$ by simply letting $u_\infty (X_0) =+ \infty$.

• (iii) Since $u_j$ is the Green function in $\Omega _j$ for $L_j$, an elliptic operator with uniform ellipticity constants $\lambda =1$ and $\Lambda$, by (2.23) we know for any $1<r<\frac{n}{n-1}$,

  $$\begin{aligned} \Vert \nabla u_j\Vert _{L^r(\Omega _j)} \lesssim |\Omega _j|^{\frac{1}{r}-\frac{n-1}{n}}\lesssim R_0^{\frac{n}{r}-n+1}<\infty , \end{aligned}$$

  (4.26)

  provided j is large enough and where the implicit constants depend on dimension, r, and $\Lambda$, but are independent of j. Note that $\nabla u_j\equiv 0$ outside of $\Omega _j$ by construction. Thus, one can easily show that passing to a subsequence (and relabeling) $\nabla u_j\rightharpoonup \nabla u_{\infty }$ in $L^r_{\mathrm{loc}}({{\mathbb {R}}}^n)$ for $1<r<n/(n-1)$.

Proof of (3) in Theorem 4.8: Case I. It is clear that $\Omega _\infty$ is an open set in Case I since $u\in C^\infty ({{\mathbb {R}}}^n)$. On the other hand, since $0\in \partial \Omega _j$ for all j, by Lemma 2.44 and modulo passing to a subsequence (which we relabel) we have that there exist non-empty closed sets $\Gamma _{\infty }, \Lambda _{\infty }$ such that ${\overline{\Omega _j}}\rightarrow \Gamma _\infty$ and $\partial \Omega _j\rightarrow \Lambda _\infty$ as $j\rightarrow \infty$, where the convergence is in the sense of Definition 2.43.

We are left with obtaining

$$\begin{aligned} \Lambda _\infty = \partial \Omega _\infty \qquad \text{ and }\qquad \Gamma _\infty ={{\overline{\Omega }}}_\infty . \end{aligned}$$

(4.27)

We first show that $\Lambda _\infty \subset \partial \Omega _\infty$. To that end we take $p\in \Lambda _\infty$, and there is a sequence $p_j\in \partial \Omega _j$ such that $\lim _{j\rightarrow \infty } p_j = p$. Note that $u_\infty (p) =\lim _{j\rightarrow \infty }\ u_j(p)$. On the other hand since the $u_j$’s are uniformly Hölder continuous on compact sets (see the Proof of (1) in Theorem 4.8) and $u_j(p_j)=0$ as $p_j\in \partial \Omega _j$ we have

$$\begin{aligned} 0\le u_\infty (p) \le |u_\infty (p)-u_j(p)|+ |u_j(p)-u_j(p_j)| \lesssim |u_\infty (p)-u_j(p)|+|p-p_j|^\alpha \rightarrow 0, \end{aligned}$$

as $j\rightarrow \infty$. Thus $u_{\infty }(p) = 0$, that is, $p\in {{\mathbb {R}}}^n\setminus \Omega _\infty$.

Our goal is to show that $p\in \partial \Omega _\infty$. Suppose that $p\notin \partial \Omega _\infty$, then $p\in {{\mathbb {R}}}^n\setminus \overline{\Omega _\infty }$ and there exists $\epsilon \in (0,1)$ such that $B(p,\epsilon ) \subset {{\mathbb {R}}}^n\setminus \overline{\Omega _\infty }$, that is, $u_\infty \equiv 0$ on $\overline{B(p,\epsilon )}$. In $\Omega _j$ we have

$$\begin{aligned} \left| A_j\left( p_j,\frac{\epsilon }{2}\right) - A_j(0,1)\right| \le \frac{\epsilon }{2} + | p_j | + 1 \le 2\left( |p| + 1\right) \end{aligned}$$

and

$$\begin{aligned} \delta _j\left( A_j\left( p_j,\frac{\epsilon }{2}\right) \right) \ge \frac{1}{M} \frac{\epsilon }{2}, \qquad \delta _j\left( A_j(0,1)\right) \ge \frac{1}{M}. \end{aligned}$$

Note also that

$$\begin{aligned} \frac{\delta _j\left( A_j\left( p_j,\frac{\epsilon }{2} \right) \right) }{\delta _j(X_j)} + \frac{\delta _j\left( A_j(0,1)\right) }{\delta _j(X_j)} \sim \frac{1}{{{\,\mathrm{diam}\,}}(\Omega _j)}\rightarrow 0, \qquad \text {as }j \rightarrow \infty , \end{aligned}$$

hence for j large enough, $A_j(0,1), A_j\left( p_j,\frac{\epsilon }{2} \right) \notin \overline{B(X_j,\delta _j(X_j)/2})$.

We can then apply Lemma 2.41 and Harnack’s inequality along the constructed chain in $\Omega _j$ to obtain

$$\begin{aligned} G_j\left( X_j,A_j\left( p_j,\frac{\epsilon }{2} \right) \right) \sim G_j(X_j,A_j(0,1)), \end{aligned}$$

where the implicit constants depend on the allowable parameters, $\epsilon$ and |p|, but are uniform on j. Hence by (4.11),

$$\begin{aligned} u_j\left( A_j\left( p_j,\frac{\epsilon }{2}\right) \right) = \dfrac{ G_j \left( X_j,A_j\left( p_j,\frac{\epsilon }{2} \right) \right) }{\omega _j^{X_j}(B(0,1))} > rsim C \dfrac{ G_j\left( X_j,A_j(0,1) \right) }{\omega _j^{X_j}(B(0,1))} = u_j(A_j(0,1)) \ge C_0, \end{aligned}$$

(4.28)

where $C_0$ is independent of j.

Note that since $u_j\rightarrow u_\infty$ on compact sets it follows from our assumption that for j large enough depending on $C_0$

$$\begin{aligned} u_j(Z)=u_j(Z)-u_\infty (Z)<\frac{C_0}{2}, \qquad \forall \,Z\in \overline{B(p,\epsilon )}. \end{aligned}$$

(4.29)

However, for j large enough $A_j(p_j,\epsilon /2) \in B(p_j,\epsilon /2) \subset B(p,\epsilon )$ and then (4.29) contradicts (4.28). Thus, we have shown that necessarily $p\in \partial \Omega _\infty$ and consequently $\Lambda _\infty \subset \partial \Omega _\infty$.

Let us next show that $\partial \Omega _\infty \subset \Lambda _{\infty }$. Assume that $p \notin \Lambda _{\infty }$. Since $\Lambda _{\infty }$ is a closed set, there exists $\epsilon >0$ such that $B(p,2\epsilon )\cap \Lambda _{\infty } = \emptyset$. Since $\Lambda _{\infty }$ is the limit of $\partial \Omega _j$, by Definition 2.43 we have that for j large enough $B(p,\epsilon ) \cap \partial \Omega _j=\emptyset$. Hence, by passing to a subsequence (and relabeling) either $B(p,\epsilon ) \subset \Omega _j$ for all j large enough or $B(p,\epsilon ) \subset {{\mathbb {R}}}^n\setminus {\overline{\Omega _j}}$ for all j large enough.

We first consider the case $B(p,\epsilon ) \subset \Omega _j$. Hence, $\delta _j(p) \ge \epsilon$ and $|A_j(0,1) - p| \le 1+|p|$. Thus there exists a Harnack chain joining $A_j(0,1)$ and p whose length is independent of j and depends on $\epsilon$ and |p|. We next observe that for j large enough $|p-X_j|>\delta _j(X_j)/2$. Indeed, if we take j large enough, using that $0\in \partial \Omega _j$ and (4.3) we clearly have

$$\begin{aligned} 1\le \frac{|X_j|}{\delta _j(X_j)} \le \frac{|X_j-p|}{\delta _j(X_j)} + \frac{|p|}{\delta _j(X_j)} < \frac{|X_j-p|}{\delta _j(X_j)}+\frac{1}{2}, \end{aligned}$$

and we just need to hide to obtain the desired estimate. Once we know that $|p-X_j|>\delta _j(X_j)/2$, we also note that $|\delta _j(A_j(0,1))|\le 1\ll {{\,\mathrm{diam}\,}}(\Omega _j)\sim \delta _j(X_j)$ and hence $A_j(0,1)\notin \overline{B(X_j,\delta (X_j)/2})$ for j large enough.

We can now invoke Lemma 2.41 and Harnack’s inequality along the constructed chain in $\Omega _j$ to obtain that $G_j(X_j,p) \sim G_j(X_j,A_j(0,1))$, which combined with (4.4) and (4.11), yields

$$\begin{aligned} u_j(p) \sim u_j(A_j(0,1)) \sim 1, \end{aligned}$$

(4.30)

where the implicit constants depend on the allowable parameters, p and $\epsilon$, but are uniform on j. Letting $j\rightarrow \infty$ we obtain that $u_\infty (p)\sim 1$ which implies that $p\in \Omega _\infty$, and since we have already shown that $\Omega _\infty$ is open, it follows that $p\notin \partial \Omega _\infty$.

We next consider now the case $B(p,\epsilon ) \subset {{\mathbb {R}}}^n\setminus {\overline{\Omega _j}}$ for all j large enough which implies that by construction $u_j(X) = 0$ for all $X\in B(p,\epsilon )$. By uniform convergence of $u_j$ in compact sets we have that $u_{\infty }(X) = 0$ for $X\in B(p,\epsilon /2)$, which implies $B(p,\epsilon /2) \subset \{u_{\infty }=0\}$ and therefore $p\notin \partial \Omega _\infty$.

In both cases we have shown that if $p \notin \Lambda _{\infty }$ then $p\notin \partial \Omega _\infty$, or, equivalently, $\partial \Omega _\infty \subset \Lambda _{\infty }$. This together with the converse inclusion completes the proof of $\Lambda _{\infty } = \partial \Omega _\infty$.

Our next goal is to show that $\Gamma _\infty ={{\overline{\Omega }}}_\infty$. Note that if $Z\in \Omega _\infty$, then $u_\infty (Z)>0$ and this implies that $u_j(Z)>0$ for j large enough. The latter forces $Z\in \Omega _j$ for all j large enough. This implies that $Z\in \Gamma _\infty$, and we have shown that $\Omega _\infty \subset \Gamma _\infty$. Moreover since $\Gamma _{\infty }$ is closed, we conclude that ${{\overline{\Omega }}}_\infty \subset \Gamma _\infty$.

To obtain the converse inclusion we take $X\in \Gamma _\infty$. Assume that there is $\epsilon >0$ such that $\overline{B(X,2\epsilon )}\subset {{\mathbb {R}}}^n\setminus \overline{\Omega _\infty }$, in particular $B(X,2\epsilon ) \cap \partial \Omega _\infty = \emptyset$. Since we have already shown that $\partial \Omega _\infty$ is the limit of $\partial \Omega _j$’s, for j large enough $B(X,\epsilon ) \cap \partial \Omega _j= \emptyset$. By the definition of $\Gamma _{\infty }$, there is a sequence $\{Y_j\}\subset {{\overline{\Omega _j}}}$ with $Y_j\rightarrow X$ as $j\rightarrow \infty$. Thus, for all j large enough $B(X,\epsilon )$ is a neighborhood of $Y_j$; and in particular $\Omega _j\cap B(X,\epsilon )\not =\emptyset$ since $Y_j \in {\overline{\Omega _j}}$. On the other hand, since $B(X,\epsilon ) \cap \partial \Omega _j= \emptyset$ we conclude that $B(X,\epsilon )\subset \Omega _j$. At this point we follow a similar argument to the one used to obtain (4.30) replacing p by X and obtain for all j large enough

$$\begin{aligned} u_j(X) \sim u_j(A_j(0,1)) \sim 1, \end{aligned}$$

where the implicit constants depend on the allowable parameters, |X| and $\epsilon$, but are uniform on j. Letting $j\rightarrow \infty$ it follows that $u_{\infty }(X)>0$ and hence $X\in \Omega _\infty$, contradicting the assumption that there is $\epsilon >0$ such that $\overline{B(X,2\epsilon )}\subset {{\mathbb {R}}}^n\setminus \overline{\Omega _\infty }$. In sort, we have shown that $\overline{B(X,2\epsilon )}\cap \overline{\Omega _\infty }\ne \emptyset$ for every $\epsilon >0$, that is, $X\in \overline{\Omega _\infty }$. We have eventually proved that $\Gamma _\infty \subset {{\overline{\Omega }}}_\infty$ this completes the proof of (4.27) in the Case I scenario.

Since ${{\,\mathrm{diam}\,}}(\Omega _j) \rightarrow \infty$ and $0\in {\overline{\Omega _j}} \rightarrow {\overline{\Omega _\infty }}$ uniformly on compact set, $\Omega _\infty$ is unbounded. Otherwise we would have ${\overline{\Omega _\infty }} \subset B(0,R)$, and for sufficiently large j one would see that ${\overline{\Omega _j}} \subset B(0,2R)$, which is a contradiction.

On the other hand, it is possible that ${{\,\mathrm{diam}\,}}(\partial \Omega _j) \not \rightarrow {{\,\mathrm{diam}\,}}(\partial \Omega _\infty )$, hence we do not know whether ${{\,\mathrm{diam}\,}}(\partial \Omega _\infty )=\infty$. However, under the assumption that the $\partial \Omega _j$’s are Ahlfors regular with uniform constant, we claim that $\partial \Omega _\infty$ is also unbounded. Assume not, then there is $R>0$ such that $\partial \Omega _\infty \subset B(0,R)$. Let k be a large integer, and notice that $\partial \Omega _j\rightarrow \partial \Omega _\infty$ uniformly on the compact set $\overline{B(0,kR)}$. Thus for j sufficiently large (depending on k)

$$\begin{aligned} \partial \Omega _j\cap \overline{B(0,kR)} \subset B(0,2R). \end{aligned}$$

(4.31)

Since ${{\,\mathrm{diam}\,}}(\partial \Omega _j)\rightarrow \infty$ we can also guarantee that ${{\,\mathrm{diam}\,}}(\partial \Omega _j) > kR$ for j sufficiently large. Recalling that $0\in \partial \Omega _j$, we can then consider the surface ball $\Delta _j(0,kR) = B(0,kR)\cap \partial \Omega _j$. By (4.31) and the Ahlfors regularity of $\partial \Omega _j$,

$$\begin{aligned} C_{AR}^{-1}(kR)^{n-1}\le \sigma _j(\Delta _j(0,kR)) \le \sigma _j(B(0,2R)\cap \partial \Omega _j) \le C_{AR} (2R)^{n-1}. \end{aligned}$$

(4.32)

Letting k large readily leads to a contradiction. $\square$

Proof of (3) in Theorem 4.8: Case II. Take $X\in \Omega _\infty$, that is, $u_\infty (X)>0$. If $X\ne X_0$ then $u_\infty$ is continuous at X and hence $u_\infty (Z)>0$ for every $Z\in B(X,r_x)$ for some $r_x$ small enough. On the other hand, if $X=X_0$, by Remark 4.22 part (ii) we have that $u_\infty (Z)>0$ for all $Z\in B(X_0, \rho )$ with $\rho$ sufficiently small (here we use the convention that $+\infty >0$). Note that this argument show in particular that $B(X_0,\rho )\subset \Omega _\infty$.

On the other hand, since $0\in \partial \Omega _j$ for all j, by Lemma 2.44 and modulo passing to a subsequence (which we relabel), there exist closed sets $\Gamma _{\infty }, \Lambda _{\infty }$ such that ${{\overline{\Omega _j}}}\rightarrow \Gamma _\infty$ and $\partial \Omega _j\rightarrow \Lambda _\infty$ as $j\rightarrow \infty$ in the sense of Definition 2.43. We are going to obtain that

$$\begin{aligned} \Lambda _\infty = \partial \Omega _\infty \qquad \text{ and }\qquad \Gamma _\infty ={{\overline{\Omega }}}_\infty . \end{aligned}$$

(4.33)

Let $p\in \Lambda _\infty$, there is a sequence $\{p_j\}\subset \partial \Omega _j$ such that $p_j\rightarrow p$ as $j\rightarrow \infty$. Note that by (4.5)

$$\begin{aligned} c_1 R_0 \le \delta _j(X_j) \le |X_j-p_j| \le |X_j-p|+|p-p_j|. \end{aligned}$$

Thus, for j large enough, $|X_j-p|> \delta _j(X_j) /2>c_1R_0/2$. In particular, $X_0\ne p$ and $u_j(p)\rightarrow u_\infty (p)$ as $j\rightarrow \infty$. On the other hand since the $u_j$’s are uniformly Hölder continuous on compact sets as observed above, $|u_j(p)|=|u_j(p)-u_j(p_j)| \le C|p-p_j|^\alpha$, thus $u_j(p)\rightarrow 0$ as $j\rightarrow \infty$. Therefore $u_{\infty }(p) = 0$, that is, $p\in {{\mathbb {R}}}^n\setminus \Omega _\infty$.

Suppose now that $p\notin \partial \Omega _\infty$. Then, there exists $0<\epsilon <\delta _j(X_j) /4$ such that $\overline{B(p,\epsilon )} \subset {{\mathbb {R}}}^n\setminus \Omega _\infty$, or, equivalently, $u_\infty \equiv 0$ on $B(p,\epsilon )$. Note that

$$\begin{aligned} \left| A_j\left( p_j,\frac{\epsilon }{2}\right) - A_j\left( 0,\frac{c_1 R_0}{2} \right) \right| \le \frac{\epsilon }{2} + |p_j | + \frac{c_1 R_0}{2} \le C(\epsilon , |p|, R_0). \end{aligned}$$

Also,

$$\begin{aligned} \frac{\epsilon }{2M} \le \delta _j\left( A_j\left( p_j,\frac{\epsilon }{2}\right) \right)< \frac{\epsilon }{2} < \frac{\delta _j(X_j)}{2} \end{aligned}$$

and, by (4.5),

$$\begin{aligned} \frac{c_1 R_0}{2M}\le \delta _j\left( A_j\left( 0,\frac{c_1 R_0}{2} \right) \right) <\frac{c_1 R_0}{2} \le \frac{\delta _j(X_j)}{2}. \end{aligned}$$

(4.34)

Notice that in particular $A_j\left( p_j,\frac{\epsilon }{2}\right)$, $A_j\left( 0,\frac{c_1 R_0}{2} \right) \notin \overline{B(X_j,\delta _j(X_j)/2)}$. We can now invoke Lemma 2.41, Harnack’s inequality along the constructed chain in $\Omega _j$, and (4.23) to see that

$$\begin{aligned} u_j\left( A_j\left( p_j,\frac{\epsilon }{2} \right) \right) \sim u_j\left( A_j\left( 0,\frac{c_1 R_0}{2}\right) \right) > rsim 1, \end{aligned}$$

(4.35)

with implicit constant depending on the allowable parameters, $\epsilon , |p|, R_0$ but independent of j. On the other hand, for all j large enough

$$\begin{aligned} A_j\left( p_j,\frac{\epsilon }{2}\right) \in B\left( p_j,\frac{\epsilon }{2}\right) \subset \overline{B(p,\epsilon )} \subset {{\mathbb {R}}}^n\setminus B(X_j,\delta _j(X_j)/4), \end{aligned}$$

(4.36)

hence $u_j\rightarrow u_\infty$ uniformly on $\overline{B(p,\epsilon )}$ with $u_\infty \equiv 0$ on $\overline{B(p,\epsilon )}$. This and (4.36) contradict (4.35) and therefore we conclude that $p\in \partial \Omega _\infty$, and we have eventually obtained that $\Lambda _\infty \subset \partial \Omega _\infty$.

To show that $\partial \Omega _\infty \subset \Lambda _{\infty }$, we assume that $p \notin \Lambda _{\infty }$. If $p=X_0$, then since we observed above that $B(X_0,\rho ) \subset \Omega _\infty$ (see (4.25)) then $X_0 \notin \partial \Omega _\infty$.

Assume next that $p\ne X_0$. Since $\Lambda _{\infty }$ is a closed set and since $X_j\rightarrow X_0$ as $j\rightarrow \infty$, there exists $\epsilon >0$ such that $B(p,2\epsilon )\cap \Lambda _{\infty } = \emptyset$ and $X_0, X_j\notin B(p, 2 \epsilon )$ for all j large enough. Moreover, since $\Lambda _{\infty }$ is the limit of $\partial \Omega _j$, by Definition 2.43 we have that for all j large enough $B(p,\epsilon ) \cap \partial \Omega _j=\emptyset$. Hence, passing to a subsequence (and relabeling) either $B(p,\epsilon ) \subset \Omega _j$ for j large enough or $B(p,\epsilon ) \subset {{\mathbb {R}}}^n\setminus {\overline{\Omega _j}}$ for j large enough.

Assume first that $B(p,\epsilon ) \subset \Omega _j$ for all j large enough. We consider two subcases. Assume first that $p\notin \overline{B(X_j,\delta _j(X_j)/2}$. Then, proceeding as before, by (4.34) we can apply Lemma 2.41 and Harnack’s inequality along the constructed chain in $\Omega _j$ to get

$$\begin{aligned} u_j(p) \sim u_j\left( A_j\left( 0,\frac{c_1 R_0}{2} \right) \right) > rsim 1, \end{aligned}$$

(4.37)

with implicit constant depending on the allowable parameters, $\epsilon , |p|, R_0$ but independent of j. Suppose next that $p\in \overline{B(X_j,\delta _j(X_j)/2)}$. In that case we can use (4.7), (2.21), and (4.5) to see that for all j large enough

$$\begin{aligned} u_j(p) > rsim |p-X_j|^{2-n} > rsim \delta _j(X_j)^{2-n} > rsim (c_2 R_0)^{2-n}, \end{aligned}$$

(4.38)

with implicit constants which are uniform on j. Combining the two cases together we have shown that $u_j(p) > rsim 1$ uniformly on j. Letting $j\rightarrow \infty$ we conclude that $u_\infty (p) > rsim 1$ and hence $p\in \Omega _\infty$, and since we have already shown that $\Omega _\infty$ is an open set we conclude that $p\notin \partial \Omega _\infty$

We now tackle the second case on which $B(p,\epsilon ) \subset {{\mathbb {R}}}^n\setminus {\overline{\Omega _j}}$ for all j large enough. In this scenario $u_j(X) = 0$ for all $X\in B(p,\epsilon )$. Since $X_0\notin B(p,2\epsilon )$, by uniform convergence of $u_j$ in $\overline{B(p,\epsilon /2)}$ we have that $u_{\infty }(X) = 0$ for $X\in B(p,\epsilon /2)$, which implies $B(p,\epsilon /2) \subset {{\mathbb {R}}}^n\setminus \Omega _\infty$ and eventually $p\notin \partial \Omega _\infty$.

In both cases we have shown that if $p \notin \Lambda _{\infty }$ then $p\notin \partial \Omega _\infty$, or, equivalently, $\partial \Omega _\infty \subset \Lambda _{\infty }$. This together with the converse inclusion completes the proof of $\Lambda _{\infty } = \partial \Omega _\infty$.

Our next task is to show that $\Gamma _\infty ={{\overline{\Omega }}}_\infty$. Let $Z\in \Omega _\infty$ and assume first that $Z=X_0$. By (4.15) and since $X_j\rightarrow X_0$ as $j\rightarrow \infty$ we have that $X_0 \in B(X_j,2\rho ) \subset \Omega _j$ for all j large enough, thus $Z=X_0\in \Gamma _\infty$. On the other hand, if $Z\ne X_0$ since $u_\infty (Z)>0$ we have that $u_j(Z)>0$ for all j large enough. This forces as well that $Z\in \Omega _j$ for j all large enough and again $Z\in \Gamma _\infty$. With this we have shown that $\Omega _\infty \subset \Gamma _\infty$. Moreover, since $\Gamma _{\infty }$ is closed we conclude as well that ${{\overline{\Omega }}}_\infty \subset \Gamma _\infty$.

Next we look at the converse inclusion and take $X\in \Gamma _\infty$. Assume that $X\in {{\mathbb {R}}}^n\setminus \overline{\Omega _\infty }$. Thus, there is $\epsilon >0$ such that $\overline{B(X,2\epsilon )}\subset {{\mathbb {R}}}^n\setminus \overline{\Omega _\infty }$. In particular $B(X,2\epsilon ) \cap \partial \Omega _\infty = \emptyset$ and $B(X_0,\rho ) \cap B(X,2\epsilon ) = \emptyset$ (recall that we showed that $B(X_0,\rho )\subset \Omega _\infty$). Since we have already shown that $\partial \Omega _\infty$ is the limit of $\partial \Omega _j$’s, for j large enough $B(X,\epsilon ) \cap \partial \Omega _j= \emptyset$. By the definition of $\Gamma _{\infty }$, there is a sequence $\{Y_j\}\subset {{\overline{\Omega _j}}}$ so that $Y_j\rightarrow X$ as $j\rightarrow \infty$. Thus, for all j large enough $B(X,\epsilon )$ is a neighborhood of $Y_j$, and, in particular, $\Omega _j\cap B(X,\epsilon )\not =\emptyset$ since $Y_j \in {\overline{\Omega _j}}$. Besides, since $B(X,\epsilon ) \cap \partial \Omega _j= \emptyset$ we conclude that $B(X,\epsilon )\subset \Omega _j$. Using a similar argument to the one used to obtain (4.37) and (4.38) we have (replacing p by X) that

$$\begin{aligned} u_j(X) > rsim 1 \end{aligned}$$

independently of j and with constants that depend on the allowable parameters, $\epsilon , |X|, R_0$. Since $u_j(X)\rightarrow u_\infty (X)$ we conclude that $u_{\infty }(X)>0$ and thus $X\in \Omega _\infty$, contradicting the assumption that $X\in {{\mathbb {R}}}^n\setminus \overline{\Omega _\infty }$. Eventually, $X\in {{\overline{\Omega }}}_\infty$ and we have obtained that $\Gamma _\infty \subset {{\overline{\Omega }}}_\infty$.

Since ${{\,\mathrm{diam}\,}}(\Omega _j) \rightarrow R_0$ is finite and $0\in \partial \Omega _j$, we have $\Omega _j, \Omega _\infty \subset \overline{B(0,2R_0)}$ for j sufficiently large. Hence ${\overline{\Omega _j}} \rightarrow {\overline{\Omega _\infty }}$ uniformly, and thus ${{\,\mathrm{diam}\,}}(\Omega _\infty ) = \lim \limits _{j\rightarrow \infty } {{\,\mathrm{diam}\,}}(\Omega _j) = R_0 \ge 1$. $\square$

For later use let us remark that in the Case II scenario the fact that ${\overline{\Omega _j}}\rightarrow \overline{\Omega _\infty }$ and $\partial \Omega _j\rightarrow \partial \Omega _\infty$ as $j\rightarrow \infty$ in the sense of Definition 2.43 yields

$$\begin{aligned} {{\,\mathrm{diam}\,}}(\Omega _\infty )= & {} {{\,\mathrm{diam}\,}}({\overline{\Omega _\infty }}) = \lim _{j\rightarrow \infty } {{\,\mathrm{diam}\,}}({\overline{\Omega _j}}) = \lim _{j\rightarrow \infty } {{\,\mathrm{diam}\,}}(\Omega _j)= R_0, \end{aligned}$$

(4.39)

$$\begin{aligned} {{\,\mathrm{diam}\,}}(\partial \Omega _\infty )= & {} \lim _{j\rightarrow \infty }{{\,\mathrm{diam}\,}}(\partial \Omega _j) = R_0. \end{aligned}$$

(4.40)

Proof of (4) in Theorem 4.8

Notice that $\Omega _\infty \not =\emptyset$ since $0\in \partial \Omega _\infty$. Next we show that $\Omega$ satisfies the interior corkscrew and the Harnack chain. Let us sketch the argument. For the interior corkscrew condition, fixed $p\in \partial \Omega _\infty$ and $0<r< {{\,\mathrm{diam}\,}}(\partial \Omega _\infty )$, we take a sequence $p_j\in \partial \Omega _j$ so that $p_j\rightarrow p$ and for each j we let $A_j$ be an interior corkscrew relative to $B(p_j,r/2)\cap \partial \Omega _j$ in $\Omega _j$. All the $A_j$’s are contained in B(p, 3r/4), hence, passing to a subsequence, they converge to some point A. Using that the interior corkscrew condition holds for all $\Omega _j$ with the same constant M, it follows that each $A_j$ is uniformly away from $\partial \Omega _j$ and so will be A from $\partial \Omega _\infty$ since $\partial \Omega _j\rightarrow \partial \Omega _\infty$. I turn, this means that A is an interior corkscrew relative to $B(p,r)\cap \partial \Omega _\infty$ in $\Omega _\infty$. Regarding the Harnack chain condition we proceed in a similar fashion. Fixed $X, Y\in \Omega _\infty$ for some fixed j large enough we will have that $X,Y\in \Omega _j$ with $\delta _j(X)\approx \delta _\infty (X)$ and $\delta _j(Y)\approx \delta _\infty (Y)$. We can then construct a Harnack chain to join X and Y within $\Omega _j$ (whose implicit constants are independent of j). Again, since each ball in the constructed Harnack chain is uniformly away from $\partial \Omega _j$, it will also be uniformly away from $\partial \Omega _\infty$ allowing us to conclude that this chain of balls is indeed a Harnack chain within $\Omega _\infty$.

Interior Corkscrew Condition. Recall that each $\Omega _j$ is a uniform domain with constants $M, C_1>1$. Hence, for all $q\in \partial \Omega _j$ and $r\in (0,{{\,\mathrm{diam}\,}}(\partial \Omega _j))$ there is a point $A_j(q,r)\in \Omega _j$ such that

$$\begin{aligned} B\left( A_j(q,r), \frac{r}{M} \right) \subset B(q,r)\cap \Omega _j. \end{aligned}$$

(4.41)

Let $p\in \partial \Omega _\infty$ and $0<r< {{\,\mathrm{diam}\,}}(\partial \Omega _\infty )$. In Case II, by (4.40) we get that $r<{{\,\mathrm{diam}\,}}(\partial \Omega _j)$ for all j sufficiently large. In Case I, either ${{\,\mathrm{diam}\,}}(\partial \Omega _\infty ) = \infty$ or ${{\,\mathrm{diam}\,}}(\partial \Omega _\infty ) < \infty$, but we still have $r<{{\,\mathrm{diam}\,}}(\partial \Omega _j)$ for all j sufficiently large (note that in the latter case ${{\,\mathrm{diam}\,}}(\partial \Omega _j) \not \rightarrow {{\,\mathrm{diam}\,}}(\partial \Omega _\infty )$). Since $\partial \Omega _j\rightarrow \partial \Omega _\infty$, we can find $p_j\in \partial \Omega _j$ converging to p. For each j there exists $A_j(p_j,r/2)$ such that

$$\begin{aligned} B\left( A_j\left( p_j, \frac{r}{2}\right) , \frac{r}{2M}\right) \subset B\left( p_j, \frac{r}{2}\right) \cap \Omega _j. \end{aligned}$$

(4.42)

In particular we deduce that

$$\begin{aligned} \overline{B\left( A_j\left( p_j, \frac{r}{2}\right) , \frac{r}{3M}\right) } \subset \Omega _j\qquad \text{ and }\qquad {\text {dist}}\left( B\left( A_j\left( p_j, \frac{r}{2}\right) , \frac{r}{2M}\right) , \partial \Omega _j\right) \ge \frac{r}{6M}.\nonumber \\ \end{aligned}$$

(4.43)

Note that for j large enough

$$\begin{aligned} A_j\left( p_j, \frac{r}{2}\right) \in B\left( p_j, \frac{r}{2} \right) \subset \overline{B\left( p,\frac{3r}{4}\right) }. \end{aligned}$$

(4.44)

Modulo passing to a subsequence (which we relabel) $A_j\left( p_j, r/2\right)$ converges to some point, which we denote by A(p, r), and for all j sufficiently large (depending on r)

$$\begin{aligned} B\left( A(p,r), \frac{r}{4M} \right) \subset B\left( A_j\left( p_j, \frac{r}{2}\right) , \frac{r}{3M}\right) \subset B(p,r)\cap \Omega _j. \end{aligned}$$

(4.45)

The fact that ${\overline{\Omega _j}} \rightarrow {\overline{\Omega _\infty }}$, the first inclusion in (4.45), and (4.43) give for all j large enough

$$\begin{aligned} B\left( A(p,r),\frac{r}{4M}\right) \subset {\overline{\Omega _\infty }} \qquad \text{ and }\qquad {\text {dist}}\left( B\left( A(p, r), \frac{r}{4M}\right) , \partial \Omega _j\right) \ge \frac{r}{6M}. \end{aligned}$$

(4.46)

This and the fact that $\partial \Omega _j\rightarrow \partial \Omega _\infty$ yield that ${\text {dist}}(B(A(p,r),r/4M), \partial \Omega _\infty )\ge r/6M$, hence B(A(p, r), r/4M) misses $\partial \Omega _\infty$. Combining this with (4.46) and the second inclusion in (4.45), we conclude that

$$\begin{aligned} B\left( A(p,r),\frac{r}{4M} \right) \subset \Omega _\infty \cap B(p,r). \end{aligned}$$

(4.47)

Hence, $\Omega _\infty$ satisfies the interior corkscrew condition with constant 4M.

Harnack Chain Condition. Fix $X,Y\in \Omega _\infty$ and pick $q_X, q_Y\in \partial \Omega _\infty$ such that $|X-q_X| = \delta _{\infty }(X), |Y-q_Y|=\delta _\infty (Y)$. Without loss of generality we may assume that $\delta (X)\ge \delta (Y)$ (otherwise we switch the roles of X and Y). Let us recall that every $\Omega _j$ satisfies the Harnack chain condition with constants $M, C_1>1$. Set

$$\begin{aligned} \Theta :=M\left( 2+\log _2^+\left( \frac{|X-Y|}{\min \{\delta _{\infty }(X),\delta _{\infty }(Y)\}} \right) \right) = M\left( 2+\log _2^+\left( \frac{|X-Y|}{\delta _{\infty }(Y)} \right) \right) . \end{aligned}$$

(4.48)

Choose $R\ge$ large enough (depending on X, Y) so that

$$\begin{aligned} B(q_X,\delta _\infty (X)/2), B\big (X, (2C_1^2)^{4\Theta }\delta _\infty (X)\big ) \subset B(0,R) \end{aligned}$$

(4.49)

and

$$\begin{aligned} B(q_Y,\delta _\infty (Y)/2), B\big (Y, (2C_1^2)^{4\Theta }\delta _\infty (Y)\big )\subset B(0,R). \end{aligned}$$

(4.50)

Take also $d=2^{-1} C_1^{-2\Theta }\le 1$ which also depends on X, Y. Then, by (3) in Theorem 4.8 we can take j large enough (depending on R and d) so that

$$\begin{aligned}&D\big [\partial \Omega _j\cap \overline{B(0,R)}, \partial \Omega _\infty \cap \overline{B(0,R)}\big ], D\big [{{\overline{\Omega _j}}} \cap \overline{B(0,R)}, {{\overline{\Omega _\infty }}}\cap \overline{B(0,R)}\big ] \nonumber \\&\le \frac{d}{2} \delta _{\infty }(Y)\le \frac{d}{2} \delta _{\infty }(X), \end{aligned}$$

(4.51)

By (4.51), (4.49), and (4.50) we have that $X,Y\in \Omega _j$, and

$$\begin{aligned} \frac{\delta _{\infty }(X)}{2} \le \delta _j(X) \le \frac{3\delta _{\infty }(X)}{2}\qquad \text{ and }\qquad \frac{\delta _{\infty }(Y)}{2} \le \delta _j(Y) \le \frac{3\delta _{\infty }(Y)}{2}. \end{aligned}$$

(4.52)

Since $\Omega _j$ satisfies the Harnack chain condition with constants $M, C_1>1$, there exists a collection of balls $B_1,\dots , B_K$ (the choice of balls depend on the fixed j) connecting X to Y in $\Omega _j$ and such that

$$\begin{aligned} C_1^{-1} {\text {dist}}(B_k,\partial \Omega _j) \le {{\,\mathrm{diam}\,}}(B_k) \le C_1 {\text {dist}}(B_k,\partial \Omega _j), \end{aligned}$$

(4.53)

for $k=1,2,\dots ,K$ where

$$\begin{aligned} K \le M\left( 2+\log _2^+\left( \frac{|X-Y|}{\min \{ \delta _j(X), \delta _j(Y) \}} \right) \right) \le 2\Theta . \end{aligned}$$

(4.54)

Combining (4.53) and (4.54), one can see that for every $k = 1,2,\dots ,K$,

$$\begin{aligned} {\text {dist}}(B_k,\partial \Omega _j) \ge d \delta _{\infty }(X), \qquad {{\,\mathrm{diam}\,}}(B_k)\le (2C_1^2)^{2\Theta }\delta _\infty (Y) \end{aligned}$$

(4.55)

and

$$\begin{aligned} {\text {dist}}(X,B_k)\le 2(2C_1^2)^{2\Theta }\delta _{\infty }(X),\qquad {\text {dist}}(Y,B_k) \le 2(2C_1^2)^{2\Theta } \delta _{\infty }(Y). \end{aligned}$$

(4.56)

Given an arbitrary $q_j\in \partial \Omega _j\setminus \overline{B(0,R)}$, by (4.49), (4.55), and (4.56) it follows that

$$\begin{aligned} (2C_1^2)^{4\Theta }\delta _\infty (X)\le & {} |q_j-X|\le {\text {dist}}(q_j,B_k)+{{\,\mathrm{diam}\,}}(B_k)+{\text {dist}}(X,B_k) \nonumber \\\le & {} {\text {dist}}(q_j,B_k)+ 3(2C_1^2)^{2\Theta }\delta _{\infty }(X). \end{aligned}$$

(4.57)

Hiding the last term, using that $\Theta >2$ and taking the infimum over the $q_j$ as above we conclude that

$$\begin{aligned} 4C_1 (2C_1^2)^{2\Theta }\delta _\infty (X)< {\text {dist}}(B_k,\partial \Omega _j\setminus \overline{B(0,R)}). \end{aligned}$$

(4.58)

On the other hand, by (4.53) and (4.55)

$$\begin{aligned} {\text {dist}}(B_k,\partial \Omega _j)\le C_1{{\,\mathrm{diam}\,}}(B_k) \le C_1(2C_1^2)^{2\Theta }\delta _\infty (Y) \le C_1(2C_1^2)^{2\Theta }\delta _\infty (X), \end{aligned}$$

which eventually leads to ${\text {dist}}(B_k,\partial \Omega _j)={\text {dist}}(B_k,\partial \Omega _j\cap \overline{B(0,R)})$. Analogously, replacing $q_j$ by $q\in \partial \Omega _\infty \setminus \overline{B(0,R)}$ in (4.57) we can easily obtain that (4.58) also holds for $\Omega _\infty$:

$$\begin{aligned} 4C_1 (2C_1^2)^{2\Theta }\delta _\infty (X)< {\text {dist}}(B_k,\partial \Omega _\infty \setminus \overline{B(0,R)}). \end{aligned}$$

(4.59)

But, (4.56) yields

$$\begin{aligned} {\text {dist}}(B_k,\partial \Omega _\infty ) \le \delta _\infty (X)+{\text {dist}}(X,B_k) \le \delta _\infty (X)+ 2(2C_1^2)^{2\Theta }\delta _\infty (Y) \le 3(2C_1^2)^{2\Theta }\delta _\infty (Y) , \end{aligned}$$

which eventually leads to ${\text {dist}}(B_k,\partial \Omega _\infty )={\text {dist}}(B_k,\partial \Omega _\infty \cap \overline{B(0,R)})$. Using all these, (4.51), the triangular inequality and (4.51) we can obtain

$$\begin{aligned}&\big |{\text {dist}}(B_k,\partial \Omega _j) -{\text {dist}}(B_k,\partial \Omega _\infty )\big | \\&\quad = \big |{\text {dist}}(B_k,\partial \Omega _j\cap \overline{B(0,R)})-{\text {dist}}(B_k,\partial \Omega _\infty \cap \overline{B(0,R)})\big | \\&\quad \le D\big [\partial \Omega _j\cap \overline{B(0,R)},\partial \Omega _\infty \cap \overline{B(0,R)}\big ] \le \frac{d}{2} \delta _{\infty }(X) \le \frac{1}{2} {\text {dist}}(B_k,\Omega _j). \end{aligned}$$

Thus,

$$\begin{aligned} \frac{2}{3} {\text {dist}}(B_k,\partial \Omega _\infty ) \le {\text {dist}}(B_k,\partial \Omega _j) \le 2 {\text {dist}}(B_k,\partial \Omega _\infty ). \end{aligned}$$

(4.60)

and moreover $B_k\cap \partial \Omega _\infty =\emptyset$. Note that the latter happens for all $k=1,\dots , K$. Recall also that $X\in B_1\cap \Omega _\infty$ and that $B_k\cap B_{k+1}\ne \emptyset$. Consequently, we necessarily have that $B_k \subset \Omega _\infty$ for all $k=1,\dots , K$. Furthermore, (4.60) and (4.53) give

$$\begin{aligned} \frac{2}{3} C_1^{-1} {\text {dist}}(B_k,\partial \Omega _\infty )\le {{\,\mathrm{diam}\,}}(B_k) \le 2C_1 {\text {dist}}(B_k,\partial \Omega _\infty ). \end{aligned}$$

(4.61)

To summarize, we have found a chain of balls $B_1, \dots , B_K$, all contained in $\Omega _\infty$, which verify (4.61), and connect X to Y. Also, K satisfies (4.54) with $\Theta$ given in (4.48). Therefore $\Omega _\infty$ satisfies the Harnack chain condition with constants 2M and $2C_1$. This completes the proof of (4) in Theorem 4.8. $\square$

Proof of (5) in Theorem 4.8

We first recall that for every j, $\sigma _j={\mathcal {H}}^{n-1}|_{\partial \Omega _j}$ is an Ahlfors regular measure with constant $C_{AR}$ and hence ${{\,\mathrm{spt}\,}}\sigma _j=\partial \Omega _j$. In particular the sequence $\{\sigma _j\}$ satisfies conditions (i) and (ii) of Lemma 2.47.

On the other hand, the fact that $\partial \Omega _j$ is Ahlfors regular easily yields, via a standard covering argument, that ${\mathcal {H}}^{n-1}(\partial \Omega _j) \le 2^{n-1}C_{AR} {{\,\mathrm{diam}\,}}(\Omega _j)^n$. Hence, using again that $\partial \Omega _j$ is Ahlfors regular we conclude that for every $R>0$,

$$\begin{aligned} \sup _j \sigma _j(B(0,R)) = \sup _j {\mathcal {H}}^{n-1}(\partial \Omega _j \cap B(0,R)) \le 2^{n-1}C_{AR} R^{n-1}. \end{aligned}$$

Therefore modulo passing to a subsequence (which we relabel), there exists a Radon measure $\mu _\infty$ such that $\sigma _j\rightharpoonup \mu _\infty$ as $j\rightarrow \infty$. Using Lemma 2.47, $\partial \Omega _j={{\,\mathrm{spt}\,}}\sigma _j\rightarrow {{\,\mathrm{spt}\,}}\mu _\infty$ as $j\rightarrow \infty$ in the sense of Definition 2.43. This and (3) in Theorem 4.8 lead to ${{\,\mathrm{spt}\,}}\mu _\infty = \partial \Omega _\infty$.

To show that $\mu _\infty$ is Ahlfors regular take $q\in \partial \Omega _\infty$. Let $q_j\in \partial \Omega _j$ be such that $q_j\rightarrow q$ as $j\rightarrow \infty$. For any $r>0$, using [Mat, Theorem 1.24] and that $\sigma _j$ is Ahlfors regular with constant $C_{AR}$ we conclude that

$$\begin{aligned} \mu _\infty (B(q,r)) \le \liminf _{j\rightarrow \infty } \sigma _j(B(q,r)) \le \liminf _{j\rightarrow \infty } \sigma _j(B(q_j,2r)) \le 2^{n-1} C_{AR}r^{n-1}. \end{aligned}$$

(4.62)

On the other hand, let $0<r<{{\,\mathrm{diam}\,}}(\partial \Omega _\infty )$. In Case II, by (4.40) we get that $r<{{\,\mathrm{diam}\,}}(\partial \Omega _j)$ for all j sufficiently large. In Case I, either ${{\,\mathrm{diam}\,}}(\partial \Omega _\infty ) = \infty$ or ${{\,\mathrm{diam}\,}}(\partial \Omega _\infty ) < \infty$, but we still have $r<{{\,\mathrm{diam}\,}}(\partial \Omega _j)$ for all j sufficiently large. Hence, using again [Mat, Theorem 1.24] and that $\sigma _j$ is Ahlfors regular with constant $C_{AR}$ we obtain

$$\begin{aligned} \mu _\infty (B(q,r))\ge & {} \mu _\infty \left( \overline{B\left( q,\frac{r}{2}\right) }\right) \ge \limsup _{j\rightarrow \infty } \sigma _j\left( \overline{B\left( q,\frac{r}{2}\right) }\right) \nonumber \\\ge & {} \limsup _{j\rightarrow \infty } \sigma _j\left( B\left( q_j,\frac{r}{4}\right) \right) \ge 4^{-(n-1)}C_{R}^{-1}r^{n-1}. \end{aligned}$$

(4.63)

These estimates guarantee that $\mu _\infty$ is Ahlfors regular with constant $2^{2(n-1)}C_{AR}$. Moreover by [Mat, Theorem 6.9],

$$\begin{aligned} 2^{-2(n-1)}C_{AR}^{-1} \mu _\infty \le {\mathcal {H}}^{n-1}|_{\partial \Omega _\infty } \le 2^{3(n-1)}C_{AR} \mu _\infty , \end{aligned}$$

(4.64)

and consequently $\partial \Omega _\infty$ is Ahlfors regular with constant $2^{5(n-1)}C_{AR}^2$. This completes the proof of (5) and hence that of Theorem 4.8. $\square$

5.2 Convergence of Elliptic Matrices.

Our next goal is to show that there exists a constant coefficient real symmetric elliptic matrix ${\mathcal {A}}^*$ with ellipticity constants $1=\lambda \le \Lambda <\infty$ (as in (1.5)) so that for any $0<R<{{\,\mathrm{diam}\,}}(\partial \Omega _\infty )$ and for any $1\le p<\infty$.

$$\begin{aligned} \int _{ B(0,R) \cap \Omega _j} |{\mathcal {A}}_{j}(Z) - {\mathcal {A}}^*|^p dZ \rightarrow 0,\qquad \text { as } j\rightarrow \infty . \end{aligned}$$

(4.65)

Fix $Z_0 \in \Omega _\infty$ and set $B_0 = B(Z_0, 3\delta _{\infty }(Z_0)/8)$. Since $\partial \Omega _j\rightarrow \partial \Omega _\infty$ and ${{\overline{\Omega _j}}} \rightarrow {{\overline{\Omega _\infty }}}$ as $j\rightarrow \infty$, for all sufficiently large j, we can see that $Z_0 \in \Omega _j$,

$$\begin{aligned} \frac{3}{4} \delta _{\infty }(Z_0) \le \delta _j(Z_0) \le \frac{5}{4} \delta _{\infty }(Z_0), \end{aligned}$$

(4.66)

and

$$\begin{aligned} B_0 \subset B\left( Z_0,\frac{\delta _j(Z_0)}{2} \right) \subset \frac{5}{3} B_0 \subset \Omega _j\quad \text {for all } j. \end{aligned}$$

(4.67)

All these, an the oscillation assumption (1.9), yield

(4.68)

Note that all the matrices ${\mathcal {A}}_{j}$ are uniformly elliptic (i.e., all of them satisfy (1.5)), with the same constants $1=\lambda \le \Lambda <\infty$, and in particular $\{\langle {\mathcal {A}}_{j} \rangle _{B_0}\}_j$ is a bounded sequence of constant real matrices. Hence, passing to a subsequence and relabeling $\langle {\mathcal {A}}_{j} \rangle _{B_0}$ converges to some constant elliptic matrix, denoted by ${\mathcal {A}}^*(B_0)$. Combining this with (4.68), the dominated convergence theorem yields

(4.69)

that is, ${\mathcal {A}}_{j}$ converges in $L^1(B_0)$ to a constant elliptic matrix ${\mathcal {A}}^*(B_0)$. Moreover, passing to a further subsequence an relabeling ${\mathcal {A}}_{j}\rightarrow {\mathcal {A}}^*(B_0)$ almost everywhere in $B_0$. In particular, ${\mathcal {A}}^*(B_0)$ is a real symmetric elliptic matrix (i.e., it satisfies (1.5)), with ellipticity constants $1=\lambda \le \Lambda <\infty$. It is important to highlight that all the previous subsequences and relabeling only depends on the choice of $Z_0 \in \Omega _\infty$. In any case, since ${\mathcal {A}}^*(B_0)$ is a constant coefficient matrix we set ${\mathcal {A}}^*:={\mathcal {A}}^*(B_0)$.

Let us pick a countable collection of points $\{Z_k\}\subset \Omega _\infty$ so that $\Omega _\infty =\cup _k B_k$ with $B_k = B(Z_k, 3\delta _{\infty }(Z_k)/8)$. We can repeat the previous argument with any $Z_k$ and define ${\mathcal {A}}^*(B_k)$, a constant real symmetric elliptic matrix satisfying (1.5) so that for some subsequence depending on k, we obtain that ${\mathcal {A}}_{j}\rightarrow {\mathcal {A}}^*(B_k)$ in $L^1(B_k)$ and a.e in $B_k$ as $j\rightarrow \infty$. In particular, ${\mathcal {A}}^*(B_{k_1})={\mathcal {A}}^*(B_{k_2})$ a.e. in $B_{k_1}\cap B_{k_2}$ (in case it is non-empty). Note that $\Omega _\infty$ is path connected (since it satisfies the Harnack chain condition), hence for any k we can find a path joining $Z_k$ and $Z_0$ and cover this path with a finite collection of the previous balls to easily see that ${\mathcal {A}}^*(B_{k})={\mathcal {A}}^*={\mathcal {A}}^*(B_0)$. Moreover, using a diagonalization argument, we can show that there exists a subsequence, which we relabel, so that for all k, we have that ${\mathcal {A}}_{j}\rightarrow {\mathcal {A}}^*$ in $L^1(B_k)$ and a.e in $B_k$ as $j\rightarrow \infty$. From this, and since the matrices concerned are all uniformly bounded, one can prove that for any $1\le p<\infty$ and for all $Z\in \Omega _\infty$,

(4.70)

where $B_Z=B(Z,\delta (Z)/2)$.

We are now ready to start proving our claim (4.65). Recalling that ${\overline{\Omega _j}} \rightarrow {\overline{\Omega _\infty }}$, $\partial \Omega _j\rightarrow \partial \Omega _\infty$ in the sense of Definition 2.43, and that $\partial \Omega _j, \partial \Omega _\infty$ have zero Lebesgue measure since they are Ahlfors regular sets, one can see that

$$\begin{aligned} B(0,R) \cap \left( \Omega _j\triangle \Omega _\infty \right) \subset B(0,R) \cap \left( \left( {{\overline{\Omega _j}}} \triangle {{\overline{\Omega _\infty }}} \right) \cup \left( {{\overline{\Omega _j}}} \cap \partial \Omega _\infty \right) \cup \left( {{\overline{\Omega _\infty }}} \cap \partial \Omega _j\right) \right) \end{aligned}$$

(4.71)

and hence the Lebesgue measure of the set on the left hand side tends to zero as $j\rightarrow \infty$. This and the fact that $\Vert {\mathcal {A}}_{j}\Vert _\infty , \Vert {\mathcal {A}}^*\Vert _\infty \le \Lambda$ give

$$\begin{aligned} \int _{B(0,R) \cap \left( \Omega _j\triangle \Omega _\infty \right) } |{\mathcal {A}}_{j}(Z) - {\mathcal {A}}^*|^p dZ \rightarrow 0,\qquad \text { as } j \rightarrow \infty . \end{aligned}$$

(4.72)

On the other hand, let $\varrho >0$ be arbitrarily small and let $\epsilon = \epsilon (\varrho )>0$ be a small constant to be determined later. Set

$$\begin{aligned}&\Omega _\infty ^{\epsilon ,1} := B(0,R) \cap \{Z\in \Omega _\infty : \delta _{\infty }(Z) < \epsilon \} \\&\quad \text{ and }\quad \Omega _\infty ^{\epsilon ,2} := B(0,R) \cap \{Z\in \Omega _\infty : \delta _{\infty }(Z) \ge \epsilon \}. \end{aligned}$$

Using the notation $\Delta (q,r):=B(q,r)\cap \partial \Omega _\infty$ with $q\in \partial \Omega _\infty$ and $r>0$, Vitali’s covering lemma allows us to find a finite collection of balls $B(q_i,\epsilon )$ with $q_i\in \Delta (0,R+\epsilon )$, such that

$$\begin{aligned} \Omega _\infty ^{\epsilon ,1} \subset \bigcup _{i} B(q_i,5\epsilon ). \end{aligned}$$

(4.73)

Calling the number of balls $L_1$ we get the following estimate,

$$\begin{aligned} L_1\epsilon ^{n-1} \lesssim \sum _{i} \sigma _\infty \left( \Delta (q_i,\epsilon ) \right) = \sigma _\infty \Big ( \bigcup _i\Delta (q_i,\epsilon ) \Big ) \le \sigma _\infty \left( \Delta (0,R+2\epsilon ) \right) \lesssim (R+2\epsilon )^{n-1}, \end{aligned}$$

(4.74)

where we have used that $\partial \Omega _\infty$ is Ahlfors regular and also that $\Delta (q_i, \epsilon ) \subset \Delta (0, R+2\epsilon )$ since $q_i \in \Delta (0,R+\epsilon )$. If we assume that $0<\epsilon <R$ we conclude that $L_1\lesssim (R/\epsilon )^{n-1}$ and moreover by (4.73) we conclude that $|\Omega _\infty ^{\epsilon ,1}|\lesssim \epsilon$ (here the implicit constant depend on R). This and $\Vert {\mathcal {A}}_{j}\Vert _\infty , \Vert {\mathcal {A}}^*\Vert _\infty \le \Lambda$ give at once that for every j,

$$\begin{aligned} \int _{\Omega _\infty ^{\epsilon ,1} \cap \Omega _j} |{\mathcal {A}}_{j}(Z) - {\mathcal {A}}^*|^p dZ \lesssim \Lambda ^p \epsilon <\frac{\varrho }{2}, \end{aligned}$$

(4.75)

provided $\epsilon$ is taken small enough which is fixed from now on.

On the other hand, note that $\overline{\Omega _\infty ^{\epsilon ,2}}$ is compact, hence we can find $Z_1,\dots , Z_{L_2}\in \overline{\Omega _\infty ^{\epsilon ,2}}$ so that $\Omega _\infty ^{\epsilon ,2} \subset \bigcup _{i=1}^{L_2} B_{Z_i}$ where $L_2$ depends on $\epsilon$ and R which have been fixed already. As a result, by (4.70) we arrive at

$$\begin{aligned} \int _{\Omega _\infty ^{\epsilon ,2} \cap \Omega _j} |{\mathcal {A}}_{j}(Z) - {\mathcal {A}}^*|^p dZ \le \sum _{i=1}^{L_2} \int _{B_{Z_i}} |{\mathcal {A}}_{j}(Z) - {\mathcal {A}}^*|^p dZ \rightarrow 0,\quad \text { as } j\rightarrow \infty . \end{aligned}$$

In particular, we can find an integer $j_0 = j_0(R,\epsilon )$ such that

$$\begin{aligned} \int _{\Omega _\infty ^{\epsilon ,2} \cap \Omega _j} |{\mathcal {A}}_{j}(Z) - {\mathcal {A}}^*|^p dZ < \frac{\varrho }{2}, \quad \text { for any } j\ge j_0. \end{aligned}$$

(4.76)

Combining (4.75) and (4.76), we conclude that

$$\begin{aligned} \int _{B(0,R) \cap \left( \Omega _j\cap \Omega _\infty \right) } |{\mathcal {A}}_{j}(Z) - {\mathcal {A}}^*|^p dZ <\varrho , \quad \text { for any } j\ge j_0. \end{aligned}$$

(4.77)

This combined with (4.72) proves the claim (4.65).

5.3 Convergence of Operator.

Theorem 4.78

   The function $u_{\infty }$ solves the Dirichlet problem

$$\begin{aligned} \left\{ \begin{array}{ll} -\mathop {{\text {div}}}\nolimits ({\mathcal {A}}^* \nabla u_\infty ) = 0 &{} \quad \text {in } \Omega _\infty , \\ u_\infty > 0 &{}\quad \text {in }\Omega _\infty , \\ u_\infty = 0 &{} \quad \text {on } \partial \Omega _\infty , \end{array} \right. \end{aligned}$$

(4.79)

in Case I, and solves the Dirichlet problem

$$\begin{aligned} \left\{ \begin{array}{ll} -\mathop {{\text {div}}}\nolimits ({\mathcal {A}}^* \nabla u_\infty ) = \delta _{\{X_0\}} &{}\quad \text {in } \Omega _\infty , \\ u_\infty > 0 &{}\quad \text {in }\Omega _\infty , \\ u_\infty = 0 &{}\quad \text {on } \partial \Omega _\infty , \end{array} \right. \end{aligned}$$

(4.80)

in Case II. Hence, $u_\infty$ is a Green function in $\Omega _\infty$ for a constant-coefficient elliptic operator $L_\infty =-\mathop {{\text {div}}}\nolimits ({\mathcal {A}}^* \nabla )$ with pole at $\infty$ in Case I or at $X_0\in \Omega _\infty$ in Case II.

Proof

Let $\psi \in C^\infty _c(\Omega _\infty )$. Since ${\overline{\Omega _j}}\rightarrow {\overline{\Omega _\infty }}$ and $\partial \Omega _j\rightarrow \partial \Omega _\infty$, it follows that $\psi \in C^\infty _c(\Omega _j)$ for j sufficiently large. In Case I, using (4.4) and (2.22) we have

$$\begin{aligned} \int _{\Omega _j} \langle {\mathcal {A}}_{j}\nabla u_j,\nabla \psi \rangle dZ = \frac{1}{\omega _j^{X_j}(B(0,1)) }\int _{\Omega _j} \langle {\mathcal {A}}_j\nabla G_j(X_j,\cdot ), \nabla \psi \rangle dZ = \frac{\psi (X_j)}{\omega _j^{X_j}(B(0,1))} \rightarrow 0, \end{aligned}$$

(4.81)

as $j\rightarrow \infty$ since $X_j\rightarrow \infty$ by (4.3). Analogously, in Case II, by (4.7) and (2.22) we obtain

$$\begin{aligned} \int _{\Omega _j} \langle {\mathcal {A}}_{j}\nabla u_j,\nabla \psi \rangle dZ = \int _{\Omega _j} \langle {\mathcal {A}}_j\nabla G_j(X_j,\cdot ), \nabla \psi \rangle dZ = \psi (X_j) \rightarrow \psi (X_0). \end{aligned}$$

(4.82)

as $j\rightarrow \infty$ since $X_j\rightarrow X_0$.

Suppose next that ${{\,\mathrm{spt}\,}}\psi \subset B(0,R)$. Let $r=2$ for Case I, and pick $r\in [1,n/(n-1))$ for Case II. By (1) in Theorem 4.8 in Case I and (iii) in Remark 4.22 in Case II it follows that $\nabla u_j\rightharpoonup \nabla u_{\infty }$ in $L^r(B(0,R))$. On the other hand,

$$\begin{aligned}&\left| \int _{\Omega _j} \langle {\mathcal {A}}_{j}\nabla u_j,\nabla \psi \rangle dZ - \int _{\Omega _\infty } \langle {\mathcal {A}}^*\nabla u_\infty ,\nabla \psi \rangle dZ \right| \nonumber \\&\quad \le \Vert \nabla \psi \Vert _{L^{\infty }} \left( \int _{\Omega _j\cap B(0,R)} |{\mathcal {A}}_{j} - {\mathcal {A}}^* |^{r'} dZ \right) ^{\frac{1}{r'}} \left( \int _{\Omega _j\cap B(0,R)} |\nabla u_j|^r \right) ^{\frac{1}{r}} \nonumber \\&\qquad + \left| \int _{\Omega _j\cap B(0,R)} \langle {\mathcal {A}}^* \nabla u_j, \nabla \psi \rangle dZ - \int _{\Omega _\infty \cap B(0,R)} \langle {\mathcal {A}}^* \nabla u_{\infty }, \nabla \psi \rangle dZ \right| . \end{aligned}$$

(4.83)

Using (4.14) in Case I or (4.26) in Case II, and (4.65) with $p=r'$, the term in the second line of (4.83) tends to zero as $j\rightarrow \infty$. Concerning the last term, since ${\mathcal {A}}^*$ is a constant-coefficient matrix, it follows that ${\mathcal {A}}^* \nabla u_j\rightharpoonup {\mathcal {A}}^* \nabla u_{\infty }$ in $L^r(B(0,R))$. Moreover ${{\overline{\Omega _j}}}=\overline{\{u_j> 0 \}} \rightarrow {{\overline{\Omega _\infty }}}=\overline{\{u_{\infty } > 0 \}}$, thus

$$\begin{aligned} \lim _{j\rightarrow \infty } \int _{\Omega _j} \langle {\mathcal {A}}^* \nabla u_j, \nabla \psi \rangle = \int _{\Omega _\infty } \langle {\mathcal {A}}^* \nabla u_{\infty }, \nabla \psi \rangle . \end{aligned}$$

Combining these with (4.81)–(4.83) we eventually conclude that

$$\begin{aligned} \int _{\Omega _\infty } {\mathcal {A}}^* \nabla u_{\infty } \cdot \nabla \psi = 0 \quad \text {for all } \psi \in C_c^\infty (\Omega _\infty ) \end{aligned}$$

(4.84)

in Case I, i.e., $-\mathop {{\text {div}}}\nolimits ({\mathcal {A}}^*\nabla u_{\infty }) = 0$ in $\Omega _\infty$; and in Case II,

$$\begin{aligned} \int _{\Omega _\infty } {\mathcal {A}}^* \nabla u_{\infty } \cdot \nabla \psi = \psi (X_0) \quad \text {for all } \psi \in C_c^\infty (\Omega _\infty ), \end{aligned}$$

(4.85)

i.e., $-\mathop {{\text {div}}}\nolimits ({\mathcal {A}}^*\nabla u_{\infty }) = \delta _{\{X_0\}}$ in $\Omega _\infty$. $\square$

5.4 Analytic Properties of the Limiting Domains.

As mentioned in Section 4, in order to apply Theorem 1.1 we need to study the elliptic measure of the limiting domain with finite poles. In this section we construct this measure by a limiting procedure which is compatible with the procedure used to produce the limiting domain $\Omega _\infty$.

Theorem 4.86

   Under Assumption (a), Assumption (b), Assumption (c), and using the notation from Theorems 4.8 and 4.78, the elliptic measure $\omega _{L_{\infty }}\in A_\infty (\sigma _\infty )$ (see Definition 2.10) with constants ${\widetilde{C}}_0=C_2 C_{AR}^{4\theta } 2^{8(n-1)\theta }$ and ${\widetilde{\theta }}=\theta$, here $C_2$ is the constant in Remark 2.39.

Proof

Our goal is to show that the elliptic measure of $L_{\infty }$ with finite pole can be recovered as a limit of the elliptic measures of $L_j= -\mathop {{\text {div}}}\nolimits ({\mathcal {A}}_{j}(Z)\nabla )$, and the $A_{\infty }$ property of elliptic measures is preserved when passing to a limit.

To set the stage we need to recall how $\omega _{L_\infty }$ is constructed. In Case II, where the domain $\Omega _\infty$ is bounded, one can define $\omega _{L_\infty }$ via the maximum principle and the Riesz representation theorem, after first using the method of Perron (see, e.g., [GT, pp. 24-25]) to construct a harmonic function “associated” to arbitrary continuous boundary data. In Case I, where $\Omega _\infty$ is unbounded, we adapt the construction in [HM1, pg. 588], which is done for the Laplacian but holds for any constant coefficient operator, for the general case see also [HMT2]. Let $0\le f\in {{\,\mathrm{Lip}\,}}(\partial \Omega _\infty )$ with compact support and suppose that $R_0>0$ is large enough so that ${{\,\mathrm{spt}\,}}f\subset B(0,R_0/2)$. For every $R>4R_0$ introduce the bounded open set $\Omega _\infty ^R = \Omega _\infty \cap B(0,2R)$. Extending f by 0 outside of its support, it then follows that $0\le f\in {{\,\mathrm{Lip}\,}}(\partial \Omega _\infty ^R)$. Let $v_R$ be the unique solution to $L_{\infty } v_R = 0$ in $\Omega _\infty ^R$ with boundary value f. Then one can show that there exists $v_\infty \in W^{1,2}_{\mathrm{loc}}(\Omega _\infty )\cap C(\Omega _\infty )$ such that $v_R\rightarrow v_\infty$ uniformly on compacta in $\Omega _\infty$ and on $W^{1,2}_{\mathrm{loc}}(\Omega _\infty )$ as $R\rightarrow \infty$. Also, $v_\infty$ satisfies the maximum principle $0\le \max _{\Omega _\infty }v_\infty \le \max _{\partial \Omega _\infty } f$. Thus, one we can then introduce the elliptic measure $\{\omega _{L_\infty }^Z\}_{Z\in \Omega _\infty }$, via the Riesz transformation theorem, such that

$$\begin{aligned} v_\infty (Z)= \int _{\partial \Omega _\infty } f(q) d\omega _{L_\infty }^Z(q). \end{aligned}$$

(4.87)

In either scenario we have then introduced the elliptic measure $\{\omega _{L_\infty }^Z\}_{Z\in \Omega _\infty }$, so that given $0\le f\in {{\,\mathrm{Lip}\,}}(\partial \Omega _\infty )$ with compact support $v_\infty$ defined as in (4.87) solves the following Dirichlet problem:

$$\begin{aligned} \left\{ \begin{array}{ll} L_\infty v = 0, &{} \text {in }\Omega _\infty , \\ v= f, &{} \text {on }\partial \Omega _\infty . \end{array} \right. \end{aligned}$$

(4.88)

We also observe that since $\partial \Omega _{\infty }$ is Ahlfors regular then $v_\infty \in C(\overline{\Omega _\infty })$.

Our next goal is to see that $\omega _j^Z \rightharpoonup \omega _{L_\infty }^Z$ as Radon measures for every $Z\in \Omega _\infty$, that is,

$$\begin{aligned} \int _{\partial \Omega _j} f(q) d\omega _j^Z(q) \rightarrow \int _{\partial \Omega _\infty } f(q) d\omega _{L_\infty }^Z(q) \quad \text { for any } f\in C_c({{\mathbb {R}}}^n). \end{aligned}$$

With this goal in mind, fix $0\le f\in {{\,\mathrm{Lip}\,}}({{\mathbb {R}}}^n)$ with compact support and suppose that $R_0>0$ is large enough so that ${{\,\mathrm{spt}\,}}f\subset B(0,R_0)$. Define $v_\infty$ as (4.87). For every j we let $h_j\in W^{1,2}_0(\Omega _j)$ be the unique Lax-Milgram solution to the problem $L_j h_j= L_j f$. Initially, $h_j$ is only defined in $\Omega _j$ but we can clearly extend it by 0 outside so that the resulting function, which we call again $h_j$, belongs to $W^{1,2}({{\mathbb {R}}}^n)$. If we next set $v_j=f-h_j\in W^{1,2}({{\mathbb {R}}}^n)$ we obtain that $L_jv_j=0$ in $\Omega _j$ and indeed

$$\begin{aligned} v_j(Z) = \int _{\partial \Omega _j} f d\omega _j^Z, \qquad Z\in \Omega _j, \end{aligned}$$

(4.89)

see [HMT2]. Here $\omega _j^Z$ is the elliptic measure of $L_j$ in $\Omega _j$ with pole Z and, as observed above, the fact that $\partial \Omega _j$ is Ahlfors regular implies in particular that $v_j\in C(\overline{\Omega _j})$ with $v_j|_{\partial \Omega _j}=f$. Note also that $v_j=f\in C({{\mathbb {R}}}^n)$ on ${{\mathbb {R}}}^n\setminus \Omega _j$, hence $v_j\in \ C({{\mathbb {R}}}^n)$. Moreover, by the maximum principle

$$\begin{aligned} 0\le \sup _{\Omega _j} v_j \le \Vert f\Vert _{L^{\infty }(\partial \Omega _j)} \le \Vert f\Vert _{L^{\infty }({{\mathbb {R}}}^n)}, \end{aligned}$$

(4.90)

thus the sequence $\{v_j\}$ is uniformly bounded.

Our next goal is to show that $\{v_j\}$ is equicontinuous. Given an arbitrary $\varrho >0$ let $0<\gamma <\frac{1}{32}$ to be chosen. Since $f\in {{\,\mathrm{Lip}\,}}({{\mathbb {R}}}^n)$, it is uniformly continuous, letting $\gamma$ small enough (depending on f) we can guarantee that

$$\begin{aligned} |f(X)-f(Y)|<\frac{\varrho }{8}, \qquad \text{ provided } \, |X-Y|<\gamma ^{\frac{1}{4}}. \end{aligned}$$

(4.91)

Our first claim is that if $\gamma$ is small enough depending on n, $C_{AR}$, $\Lambda$ (recall that $\lambda = 1$), and $\Vert f\Vert _{L^{\infty }({{\mathbb {R}}}^n)}$, there holds

$$\begin{aligned} |v_j(X)-v_j(Y)|<\frac{\rho }{2}, \qquad \forall \,X\in \Omega _j,\ Y\in \partial \Omega _j,\ |X-Y|<\sqrt{\gamma }. \end{aligned}$$

(4.92)

To see this we recall that $\partial \Omega _j$ is Ahlfors regular with a uniform constant (independent of j), it satisfies the CDC with a uniform constant and [HKM, Theorem 6.18] (see also [HMT2]) yields that for some $\beta >0$ and C depending on n, $C_{AR}$, and $\Lambda$, but independent of j (indeed this is the same $\beta$ as in Lemma 2.24), the following estimate holds:

$$\begin{aligned} \underset{B(Y_j,\sqrt{\gamma })\cap \Omega _j}{{{\,\mathrm{osc}\,}}} v_j \le \underset{B(Y_j,\gamma ^{1/4})\cap \partial \Omega _j}{{{\,\mathrm{osc}\,}}} f + C\Vert f\Vert _{L^{\infty }({{\mathbb {R}}}^n)} \eta ^{\beta }<\frac{\varrho }{2}, \end{aligned}$$

where in the last estimate we have used (4.91) and $\gamma$ has been chosen small enough so that $C\Vert f\Vert _{L^{\infty }({{\mathbb {R}}}^n)} \eta ^{\beta }<\varrho /4$.

We now fix $X, Y\in {{\mathbb {R}}}^n$ so that $|X-Y|<\gamma$ and consider several cases.

Case 1: $X,Y\in \Omega _j$ with $\max \{\delta _j(X),\delta _j(Y)\}<\sqrt{\gamma }/2$.

In this case, we take ${\widehat{x}}\in \partial \Omega _j$ so that $|X-{\hat{x}}|=\delta _j(X)$. Note that $|Y-{\widehat{x}}|<\sqrt{\gamma }$ and we can use (4.92) to obtain

$$\begin{aligned} |v_j(X)-v_j(Y)| \le |v_j(X)-v_j({\widehat{x}})| + |v_j({\widehat{x}})-v_j(Y)|<\rho . \end{aligned}$$

Case 2: $X,Y\in \Omega _j$ with $\max \{\delta _j(X),\delta _j(Y)\}\ge \sqrt{\gamma }/2$.

Assuming without loss of generality that $\delta _j(X)\ge \sqrt{\gamma }/2$, necessarily $Y\in B(X,\delta _j(X)/2)\subset \Omega _j$. Then, by the interior Hölder regularity of $v_j$ in $\Omega _j$ (here $\alpha$ and C depend only on $\Lambda$ and are independent of j) we conclude that

$$\begin{aligned} |v_j(X) - v_j(Y)| \le C\left( \frac{|X-Y|}{\delta _j(X)} \right) ^{\alpha } \Vert v_j\Vert _{L^{\infty }(\Omega _j)} \le C 2^\alpha \gamma ^{\frac{\alpha }{2}}\Vert f\Vert _{L^{\infty }({{\mathbb {R}}}^n)} < \varrho , \end{aligned}$$

provided $\varrho$ is taken small enough (again independently of j).

Case 3: $X,Y\notin \Omega _j$.

Here we just need to use (4.91) and the fact that $v_j=f$ on ${{\mathbb {R}}}^n\setminus \Omega _j$:

$$\begin{aligned} |v_j(X) - v_j(Y)| = |f(X)-f(Y)|< \rho . \end{aligned}$$

Case 4: $X\in \Omega _j$ and $Y\notin \Omega _j$.

Pick $Z\in \partial \Omega _j$ in the line segment joining X and Y (if $Y\in \partial \Omega _j$ we just take $Z=Y$) so that $|X-Z|,|Y-Z|\le |X-Y|<\gamma$. Using (4.92), the fact that $v_j=f$ on ${{\mathbb {R}}}^n\setminus \Omega _j$, and (4.91) we obtain

$$\begin{aligned} |v_j(X) - v_j(Y)| \le |v_j(X) - v_j(Z)| + |v_j(Z) - v_j(Y)|< \frac{\varrho }{2}+|f(Z) - f(Y)| <\varrho . \end{aligned}$$

If we now put all the cases together we have shown that, as desired, $\{v_j\}$ is equicontinuous.

On the other hand, recalling that $h_j\in W_0^{1,2}(\Omega _j)$ satisfies $L_j h_j=L_j f$ in the weak sense in $\Omega _j$, that $f\in W^{1,2}({{\mathbb {R}}}^n)$, and that $\lambda =1$, we see that

$$\begin{aligned} \Vert \nabla h_j\Vert _{L^2(\Omega _j)}^2\le & {} \int _{\Omega _j} \langle {\mathcal {A}}_{j}\nabla h_j,\nabla h_j\rangle dX \\= & {} \int _{\Omega _j} \langle {\mathcal {A}}_{j}\nabla f,\nabla h_j\rangle dX \le \Lambda \Vert \nabla f\Vert _{L^2(\Omega _j)} \Vert \nabla h_j\Vert _{L^2(\Omega _j)}. \end{aligned}$$

We next absorb the last term, use that $v_j=f-h_j$ and that $h_j$ has been extended as 0 outside of $\Omega _j$:

$$\begin{aligned} \Vert \nabla v_j\Vert _{L^2({{\mathbb {R}}}^n)}\le & {} \Vert \nabla f\Vert _{L^2({{\mathbb {R}}}^n)} + \Vert \nabla h_j\Vert _{L^2({{\mathbb {R}}}^n)} = \Vert \nabla f\Vert _{L^2({{\mathbb {R}}}^n)} + \Vert \nabla h_j\Vert _{L^2(\Omega _j)} \\\le & {} (1+\Lambda ) \Vert \nabla f\Vert _{L^2({{\mathbb {R}}}^n)}. \end{aligned}$$

This along with (4.90) yield

$$\begin{aligned} \sup _j \Vert \nabla v_j \Vert _{L^2({{\mathbb {R}}}^n)} \le (1+\Lambda ) \Vert \nabla f\Vert _{L^2({{\mathbb {R}}}^n)}, \quad \text {and } \sup _j \Vert v_j \Vert _{L^2(B(0,R))} \le C_R. \end{aligned}$$

(4.93)

We notice that all these estimates hold for the whole sequence and therefore, so it does for any subsequence.

Let us now fix an arbitrary subsequence $\{v_{j_k}\}_k$. By (4.93) there are a further subsequence and $v\in C({{\mathbb {R}}}^n)\cap W^{1,2}_{\mathrm{loc}}({{\mathbb {R}}}^n)$ with $\nabla v \in L^2({{\mathbb {R}}}^n)$, such that $v_{j_{k_l}} \rightarrow v$ uniformly on compact sets of ${{\mathbb {R}}}^n$ (hence $v\ge 0$) and $\nabla v_{j_{k_l}}\rightharpoonup \nabla v$ in $L^2({{\mathbb {R}}}^n)$ as $l\rightarrow \infty$. Here it is important to emphasize that the choice of the subsequence may depend on the boundary data f and the fixed subsequence, and the same happens with v , and this could be problematic, later we will see that this is not the case.

To proceed we next see that v agrees with f in $\partial \Omega _\infty$. Given $p\in \partial \Omega _\infty$, there exist $p_{j_{k_l}} \in \partial \Omega _{j_{k_l}}$ with $p_{j_{k_l}} \rightarrow p$ as $l\rightarrow \infty$. Using the continuity of v and f at p, the uniform convergence of $v_{j_{k_l}}$ to v on $\overline{B(p,1)}$ and the fact that $v_{j_{k_l}} =f$ on $\partial \Omega _{j_{k_l}}$, we have

$$\begin{aligned}&|v(p) - f(p)| \\&\quad \le |v(p) - v(p_{j_{k_l}})| + |v(p_{j_{k_l}}) - v_{j_{k_l}}(p_{j_{k_l}})| +|f(p_{j_{k_l}} ) - f(p)| \\&\quad \le |v(p) - v( p_{j_{k_l}} )| + \Vert v-v_{j_{k_l}} \Vert _{L^{\infty }(\overline{B(p,1)})} + |f( p_{j_{k_l}}) - f(p)| \rightarrow 0, \quad \text{ as } l\rightarrow \infty , \end{aligned}$$

thus $v(p)=f(p)$ as desired.

Next, we claim the function v solves the Dirichlet problem (4.88). We know that $v\in C({{\mathbb {R}}}^n)$ with $v=f$ in $\partial \Omega _\infty$. Hence, we only need to show that $L_\infty v = 0$ in $\Omega _\infty$. To this aim, let us take $\psi \in C_c^1(\Omega _\infty )$ and let $R>0$ be large enough so that ${{\,\mathrm{spt}\,}}\psi \subset B(0,R)$. Since ${\overline{\Omega _j}} \rightarrow {\overline{\Omega _\infty }}$, for all l large enough we have that $\psi \in C_c^1(\Omega _{j_{k_l}})$ in which case

$$\begin{aligned} \int _{{{\mathbb {R}}}^n} \langle {\mathcal {A}}_{j_{k_l}}\nabla v_{j_{k_l}},\nabla \psi \rangle dZ= 0, \end{aligned}$$

(4.94)

since $L_{j_{k_l}} v_{j_{k_l}}=0$ in $\Omega _{j_{k_l}}$ in the weak sense. Then, by (4.93) and the fact that ${{\,\mathrm{spt}\,}}\psi \subset \Omega _\infty \cap \Omega _{j_{k_l}}\cap B(0,R)$,

$$\begin{aligned}&\left| \int _{{{\mathbb {R}}}^n} \langle {\mathcal {A}}^* \nabla v, \nabla \psi \rangle dZ \right| = \left| \int _{\Omega _{j_k}} \langle {\mathcal {A}}_{j_k}\nabla v_{j_{k_l}},\nabla \psi \rangle dZ - \int _{\Omega _\infty } \langle {\mathcal {A}}^*\nabla v,\nabla \psi \rangle dZ \right| \\&\quad \le (1+\Lambda )\Vert \nabla f\Vert _{L^2({{\mathbb {R}}}^n)}\Vert \nabla \psi \Vert _{L^{\infty }} \left( \int _{\Omega _j\cap B(0,R)} |{\mathcal {A}}_{j_{k_l}} - {\mathcal {A}}^* |^2 dZ \right) ^{\frac{1}{2}} \\&\qquad + \left| \int _{{{\mathbb {R}}}^n} \langle {\mathcal {A}}^* \nabla v_{j_{k_l}}, \nabla \psi \rangle dZ - \int _{{{\mathbb {R}}}^n} \langle {\mathcal {A}}^* \nabla v, \nabla \psi \rangle dZ \right| \rightarrow 0,\quad \text{ as } l\rightarrow \infty , \end{aligned}$$

where we have used (4.65) with $p=2$ for the term in the second line, and the fact that since ${\mathcal {A}}^*$ is a constant-coefficient matrix, it follows that ${\mathcal {A}}^* \nabla v_{j_{k_l}} \rightharpoonup {\mathcal {A}}^* \nabla v$ in $L^2({{\mathbb {R}}}^n)$ as $l\rightarrow \infty$. This eventually shows that $L_\infty v=0$ in $\Omega _\infty$.

In Case II when the domain $\Omega _\infty$ is bounded, the Dirichlet problem (4.88) has a unique solution, and it satisfies the maximum principle, hence we must have that $v=v_\infty$. Therefore, we have shown that given any subsequence $\{v_{j_k}\}_k$ there is a further subsequence $\{v_{j_{k_l}}\}_l$ so that $v_{j_{k_l}}\rightarrow v_\infty$ uniformly on compact sets of ${{\mathbb {R}}}^n$ and $\nabla v_{j_{k_l}} \rightharpoonup \nabla v_\infty$ in $L^2({{\mathbb {R}}}^n)$ as $l\rightarrow \infty$. This eventually shows that entire sequence $\{v_j\}$ satisfies $v_j\rightarrow v_\infty$ uniformly on compact sets of ${{\mathbb {R}}}^n$ and $\nabla v_{j} \rightharpoonup \nabla v_\infty$ in $L^2({{\mathbb {R}}}^n)$ as $j\rightarrow \infty$.

In Case I where the limiting domain $\Omega _\infty$ is unbounded, we need more work to show the solution v is indeed $v_\infty$. Recall that $f\in {{\,\mathrm{Lip}\,}}({{\mathbb {R}}}^n)$ with ${{\,\mathrm{spt}\,}}f\subset B(0,R_0)$. Given $\epsilon >0$, there is an integer $j_0 = j_0(\epsilon , R_0)\in {{\mathbb {N}}}$ such that for $j\ge j_{0}$ and for any $p_j' \in \partial \Omega _j\cap B(0,4R_0)$, there is $p' \in \partial \Omega _\infty \cap B(0,5R_0)$ close enough to $p_j'$ so that $|f(p') -f(p'_j)|<\epsilon$. Consequently,

$$\begin{aligned} \sup _{\partial \Omega _j} |f| = \sup _{\partial \Omega _j\cap B(0,4R_0)} |f| \le \sup _{\partial \Omega _\infty \cap B(0,5R_0)} |f| + \epsilon = \sup _{\partial \Omega _\infty } |f| + \epsilon . \end{aligned}$$

(4.95)

For any $Z\in \Omega _\infty$ there exists a sequence $Z_j \in \Omega _j$ such that $Z_j \rightarrow Z$ and $Z_j\in \overline{B(Z,\delta _\infty (Z)/2)}$ for all j large enough. Since $v\in C({{\mathbb {R}}}^n)$ it follows that for j large enough $|v(Z)-v(Z_j)|<\epsilon$. All these together with (4.90) and the fact that $v_{j_{k_l}} \rightarrow v$ uniformly on compact sets of ${{\mathbb {R}}}^n$ as $l\rightarrow \infty$ give that for all l large enough,

$$\begin{aligned} 0&\le v(Z) \le |v(Z) - v(Z_{j_{k_l}} )| + |v(Z_{j_{k_l}} ) - v_{j_{k_l}} (Z_{j_{k_l}} )| + |v_{j_{k_l}} (Z_{j_{k_l}} )|\nonumber \\&\le 2\epsilon + \sup _{\partial \Omega _j}|f|\le 3\epsilon + \sup _{\partial \Omega _\infty } |f|, \end{aligned}$$

(4.96)

Letting $\epsilon \rightarrow 0$ we get $0\le \sup _{\Omega _\infty }v \le \sup _{\partial \Omega _\infty } |f|$.

As above, let $\Omega _\infty ^R=\Omega _\infty \cap B(0,2R)\subset \Omega _\infty$ and define $v_R$, the unique solution to $L_{\infty } v_R = 0$ in $\Omega _\infty ^R$ with boundary value f. Let us recall that $v_R\rightarrow v_\infty$ uniformly on compacta in $\Omega _\infty$ and on $W^{1,2}_{\mathrm{loc}}(\Omega _\infty )$ as $R\rightarrow \infty$.

Since $0\le v\in C({{\mathbb {R}}}^n)$ with $v|_{\partial \Omega _\infty }=f$, and since ${{\,\mathrm{spt}\,}}f\subset B(0,R_0)$, for every $R>4R_0$ we have that $f|_{\partial \Omega _\infty ^R}\le v|_{\partial \Omega _\infty ^R}$. Maximum principle implies that $v_R \le v$ in $\Omega _R$, and taking limits we conclude that $v_\infty \le v$ on $\Omega _\infty$. Write $0\le {\widetilde{v}}=v- v_\infty \in C(\overline{\Omega _\infty })$ so that $L_{\infty } {\widetilde{v}}=0$ in $\Omega _\infty$ and ${\widetilde{v}}|_{\partial \Omega _\infty }=0$. Fix an arbitrary $Z\in \Omega _\infty$. Since $\Omega _\infty$ is a uniform domain with Ahlfors regular boundary, by Lemma 2.24 we have for any $R'$ such that $\delta _\infty (Z)<R' < {{\,\mathrm{diam}\,}}(\partial \Omega _\infty )=\infty$ (see (3) in Theorem 4.8),

$$\begin{aligned} 0\le {\widetilde{v}}(Z) \lesssim \left( \frac{\delta _{\infty }(Z)}{R'} \right) ^{\beta } \sup _{\Omega _\infty } {\widetilde{v}} \le 2 \left( \frac{\delta _{\infty }(Z)}{R'} \right) ^{\beta } \sup _{\partial \Omega _\infty } f, \end{aligned}$$

(4.97)

Letting $R'\rightarrow \infty$ we conclude that ${\widetilde{v}}(Z) = 0$ and, since Z is arbitrary, we conclude as desired that $v=v_\infty$.

Therefore, we have shown that given a subsequence $\{v_{j_k}\}_k$ there is a further subsequence $\{v_{j_{k_l}}\}_l$ so that $v_{j_{k_l}}\rightarrow v_\infty$ uniformly on compact sets of ${{\mathbb {R}}}^n$ and $\nabla v_{j_{k_l}} \rightharpoonup \nabla v_\infty$ in $L^2({{\mathbb {R}}}^n)$ as $l\rightarrow \infty$. This eventually shows that entire sequence $\{v_j\}$ satisfies $v_j\rightarrow v_\infty$ uniformly on compact sets of ${{\mathbb {R}}}^n$ and $\nabla v_{j} \rightharpoonup \nabla v_\infty$ in $L^2({{\mathbb {R}}}^n)$ as $j\rightarrow \infty$.

Hence, in both Case I and Case II, if $0\le f\in {{\,\mathrm{Lip}\,}}({{\mathbb {R}}}^n)$ has compact support, then

$$\begin{aligned} \lim _{j\rightarrow \infty } \int _{\partial \Omega _j} f(q) d\omega _j^Z(q) =\lim _{j\rightarrow \infty } v_j(Z) = v_\infty (Z)=\int _{\partial \Omega _\infty } f(q) d\omega _{L_\infty }^Z(q), \end{aligned}$$

(4.98)

for any $Z\in \Omega _\infty$.

Fix next $Z\in \Omega _\infty$ and take an arbitrary subsequence $\{\omega _{j_k}\}_{k}$. Take $k_0$ large enough so that $Z\in \Omega _{j_k}$ for every $k\ge k_0$ and note that $\omega _{j_k}^Z({{\mathbb {R}}}^n)=\omega _{j_k}^Z(\partial \Omega _{j_k})=1$ for every $k\ge k_0$. Passing to a subsequence, there exists a Radon measure $\mu ^Z$ with $\mu ^Z({{\mathbb {R}}}^n)\le 1$ so that $\omega _{j_{k_l}}^Z \rightharpoonup \mu ^Z$ as $l\rightarrow \infty$. Thus (4.98) readily leads to

$$\begin{aligned} \int _{\partial \Omega _\infty } f(q) d\omega _{L_\infty }^Z(q)=\int f(q) d\mu ^Z(q). \end{aligned}$$

This equality holds for all $0\le f\in {{\,\mathrm{Lip}\,}}({{\mathbb {R}}}^n)$ with compact support, and one can readily see that this extends to all $f\in C_c({{\mathbb {R}}}^n)$. Hence, $\omega _{j_{k_l}}^Z \rightharpoonup \omega _{L_\infty }^Z$. This eventually shows that the entire sequence $\{\omega _{j}\}$ satisfies $\omega _{j}^Z \rightharpoonup \omega _{L_\infty }^Z$ as Radon measures for any $Z\in \Omega _\infty$.

Our next goal is to see that $\omega _{L_\infty }\in A_{\infty }(\sigma _{\infty })$ (where $\sigma _{\infty } = {\mathcal {H}}^{n-1}|_{\partial \Omega _\infty }$). Fix $p\in \partial \Omega _\infty$ and $0<r<{{\,\mathrm{diam}\,}}(\partial \Omega _\infty )$. Recall that whether ${{\,\mathrm{diam}\,}}(\partial \Omega _\infty )$ is finite or infinite, we always have $r< {{\,\mathrm{diam}\,}}(\Omega _j)$ for all j sufficiently large. Let $\Delta ' = B(m,s)\cap \partial \Omega _\infty$ with $m\in \partial \Omega _\infty$ and $B(m,s)\subset B(p,r) \cap \partial \Omega _\infty$. Let $A(p,r)\in \Omega _\infty$ be a corkscrew point relative to $\Delta (p,r)$ (whose existence is guaranteed by (4) in Theorem 4.8). We can then find $p_j \in \partial \Omega _j$ such that $p_j \rightarrow p$. Thus, for all j large enough $B(p,r)\subset B(p_j,2r)$ and $\delta _j(A(p,r))\ge r/(2M)$. Hence, A(p, r) is also a corkscrew point relative to $B(p_j,2r)\cap \partial \Omega _j$ in $\Omega _j$ with constant 4M. Since $m\in \partial \Omega _\infty$, we can also find $m_j\in \partial \Omega _j$ such that $m_j\rightarrow m$. In particular, for j sufficiently large,

$$\begin{aligned} |m_j - m| < \frac{s}{5}. \end{aligned}$$

(4.99)

Note also that since all the $\Omega _j$’s are uniform and satisfy the CDC with the same constants, and all the operators $L_j$’s have ellipticity constants bounded below and above by $\lambda =1$ and $\Lambda$, we can conclude from Remark 2.39 that there is a uniform constant $C_2$ depending on $M, C_1, C_{AR}>1$, and $\Lambda$, such that (2.40) holds for all $\omega _j$ with the appropriate changes. Using this and [Mat, Theorem 1.24] we obtain

$$\begin{aligned}&\omega _{L_\infty }^{A(p,r)} (\Delta (m,s)) \nonumber \\&\quad \ge \omega _{L_\infty }^{A(p,r)} \left( \overline{B\left( m,\frac{4}{5}s\right) } \right) \ge \limsup _{j\rightarrow \infty } \omega _j^{A(p,r)} \left( \overline{B\left( m,\frac{4}{5}s\right) } \right) \nonumber \\&\quad \ge \limsup _{j\rightarrow \infty } \omega _j^{A(p,r)} \left( \overline{B\left( m_j,\frac{3}{5}s\right) } \right) \ge C_2^{-1} \limsup _{j\rightarrow \infty } \omega _j^{A(p,r)} \left( B\left( m_j,\frac{6}{5}s\right) \right) , \nonumber \\ \end{aligned}$$

(4.100)

where we have used that $\delta _j(A(p,r))\ge r/(2M)\ge \frac{3}{5}s/(2M)$.

Let V be an arbitrary open set in B(m, s), and note that by (4.99)

$$\begin{aligned} V\subset B(m,s) \subset B\left( m_j, \frac{6}{5}s \right) . \end{aligned}$$

Using again [Mat, Theorem 1.24], we see that (4.100) yields

$$\begin{aligned} \frac{\omega _{L_\infty }^{A(p,r)}(V)}{\omega _{L_\infty }^{A(p,r)}(\Delta (m,s))}\le & {} C_2 \dfrac{\liminf _{j\rightarrow \infty } \omega _j^{A(p,r)}(V)}{\limsup _{j\rightarrow \infty } \omega _j^{A(p,r)}\left( B\left( m_j,\frac{6}{5}s\right) \right) } \nonumber \\\le & {} C_2 \liminf _{j\rightarrow \infty } \left( \dfrac{\omega _j^{A(p,r)}(V) }{\omega _j^{A(p,r)}\left( B\left( m_j,\frac{6}{5}s\right) \right) }\right) . \end{aligned}$$

(4.101)

The assumption $B(m,s) \subset B(p,r)$ implies $|m-p|\le r-s$. Using this and that $m_j\rightarrow m$, $p_j\rightarrow p$ as $j\rightarrow \infty$ one can easily see that $|m_j - p_j|<r-\frac{s}{5}$ for all j large enough and hence

$$\begin{aligned} B\left( m_j, \frac{6}{5}s \right) \cap \partial \Omega _j \subset B(p_j,2r)\cap \partial \Omega _j. \end{aligned}$$

(4.102)

As mentioned above A(p, r) is a corkscrew point relative to $B(p_j,2r)\cap \partial \Omega _j$ in $\Omega _j$. This, (4.102) and the fact that by assumption, $\omega _j\in A_\infty (\sigma _j)$ with uniform constants $C_0, \theta$ allow us to conclude that

$$\begin{aligned} \dfrac{\omega _j^{A(p,r)}(V) }{\omega _j^{A(p,r)}\left( B\left( m_j,\frac{6}{5}s\right) \right) } \le C_0 \left( \dfrac{\sigma _j(V)}{\sigma _j\left( B\left( m_j, \frac{6}{5}s \right) \right) } \right) ^\theta \le C_0 C_{AR}^\theta \left( \dfrac{\sigma _j(V)}{s^{n-1}} \right) ^\theta , \end{aligned}$$

(4.103)

where in the last estimate we have used that $\partial \Omega _j$ is Ahlfors regular with constants $C_{AR}$. Combining (4.101), (4.103), the fact that $\sigma _j\rightharpoonup \mu _\infty$, [Mat, Theorem 1.24], and (5) in Theorem 4.8, we finally arrive at

$$\begin{aligned} \frac{\omega _{L_\infty }^{A(p,r)}(V)}{\omega _{L_\infty }^{A(p,r)}(\Delta (m,s))}\le & {} C_0 C_{AR}^\theta \left( \liminf _{j\rightarrow \infty } \dfrac{\sigma _j(V)}{s^{n-1}} \right) ^\theta \\\le & {} C_0 C_{AR}^\theta \left( \frac{\mu _\infty ({{\overline{V}}})}{s^{n-1}} \right) ^\theta \le C_0 C_{AR}^{4\theta } 2^{8(n-1)\theta } \left( \frac{\sigma _\infty ({{\overline{V}}})}{\sigma _\infty (\Delta (m,s))} \right) ^\theta , \end{aligned}$$

and therefore we have shown that for any open set $V\subset B(m,s)$ there holds

$$\begin{aligned} \frac{\omega _{L_\infty }^{A(p,r)}(V)}{\omega _{L_\infty }^{A(p,r)}(\Delta (m,s))} \le C_0 C_{AR}^{4\theta } 2^{8(n-1)\theta } \left( \frac{\sigma _\infty ({{\overline{V}}})}{\sigma _\infty (\Delta (m,s))} \right) ^\theta . \end{aligned}$$

(4.104)

Consider next an arbitrary Borel set $E\subset B(m,s)$. Since $\sigma _{\infty }$ and $\omega _{L_\infty }^{A(p,r)}$ are Borel regular, given any $\epsilon >0$ there is an open set U and a compact set F so that $F\subset E\subset U \subset B(m,s)$ and $\omega _{L_\infty }^{A(p,r)}(U\setminus F)+ \sigma _{\infty }(U\setminus F) <\epsilon$. Note that for any $x\in F$, there is $r_x >0$ such that $B(x,2r_x) \subset U$. Using that F is compact we can then show there exists a finite collection of points $\{x_i\}_{i=1}^m\subset F$ such that $F\subset \bigcup _{i=1}^m B(x_i, r_i) =: V$ and $B(x_i, 2r_i) \subset U$ for $i= 1,\dots ,m$. Consequently, $F\subset V \subset {{\overline{V}}} \subset U$ and $\sigma _{\infty }({{\overline{V}}} \setminus F) \le \sigma _{\infty }(U\setminus F) <\epsilon$. We next use (4.104) with V to see that

$$\begin{aligned} \frac{\omega _{L_\infty }^{A(p,r)}(E)}{\omega _{L_\infty }^{A(p,r)}(\Delta (m,s))}\le & {} \frac{\epsilon +\omega _{L_\infty }^{A(p,r)}(F)}{\omega _{L_\infty }^{A(p,r)}(\Delta (m,s))} \le \frac{\epsilon +\omega _{L_\infty }^{A(p,r)}(V)}{\omega _{L_\infty }^{A(p,r)}(\Delta (m,s))} \\\le & {} \frac{\epsilon }{\omega _{L_\infty }^{A(p,r)}(\Delta (m,s))} + C_0 C_{AR}^{4\theta } 2^{8(n-1)\theta } \left( \frac{\sigma _{\infty }({{\overline{V}}})}{\sigma _{\infty }(\Delta (m,s))} \right) ^\theta \\\le & {} \frac{\epsilon }{\omega _{L_\infty }^{A(p,r)}(\Delta (m,s))} + C_0 C_{AR}^{4\theta } 2^{8(n-1)\theta } \left( \frac{\sigma _{\infty }(E)+\epsilon }{\sigma _{\infty }(\Delta (m,s))} \right) ^\theta . \end{aligned}$$

Letting $\epsilon \rightarrow 0$ we obtain as desired that $\omega _{L_\infty }\in A_\infty (\sigma _\infty )$ with constants $C_0 C_{AR}^{4\theta } 2^{8(n-1)\theta }$ and $\theta$ and the proof is complete. $\square$

6 Proof of Theorem 1.8

Applying Theorem 4.8, we obtain that $\Omega _\infty$ is a uniform domain with constants 4M and $2C_1$, whose boundary is Ahlfors regular with constant $2^{5(n-1)}C_{AR}^2$. Moreover, Theorem 4.86 gives that $\omega _{L_{\infty }}\in A_\infty (\sigma _\infty )$ with constants ${\widetilde{C}}_0=C_2 C_{AR}^{4\theta } 2^{8(n-1)\theta }$ and ${\widetilde{\theta }}=\theta$. Here $L_\infty =-\mathop {{\text {div}}}\nolimits ({\mathcal {A}}^* \nabla )$ with ${\mathcal {A}}^*$ a constant-coefficient real symmetric uniformly elliptic matrix with ellipticity constants $1=\lambda \le \Lambda <\infty$. We can then invoke Theorem 1.1, to see that $\Omega _\infty$ satisfies the exterior corkscrew condition with constant

$$\begin{aligned}N_0=N_0(4M,2C_1, 2^{5(n-1)}C_{AR}^2,\Lambda , C_0 C_2 C_{AR}^{4\theta } 2^{8(n-1)\theta },\theta )\end{aligned}$$

(see introduction to Section 3). Therefore, since $0\in \partial \Omega _\infty$, $0<\frac{1}{2}<{{\,\mathrm{diam}\,}}(\partial \Omega _\infty )$ (recall that ${{\,\mathrm{diam}\,}}(\partial \Omega _\infty ) = \infty$ in Case I, and ${{\,\mathrm{diam}\,}}(\partial \Omega _\infty ) = {{\,\mathrm{diam}\,}}(\Omega _\infty ) = R_0 \ge 1$) there exists $A_0=A^-(0,\frac{1}{2})$ so that

$$\begin{aligned} B\left( A_0,\frac{1}{2N_0} \right) \subset B\left( 0,\frac{1}{2}\right) \setminus {\overline{\Omega _\infty }}. \end{aligned}$$

(5.1)

Hence

$$\begin{aligned} {\text {dist}}\left( B\left( A_0,\frac{1}{4N_0}\right) , {{\mathbb {R}}}^n\setminus {\overline{\Omega _\infty }}\right) \ge \frac{1}{4N_0}. \end{aligned}$$

(5.2)

Since ${\overline{\Omega _j}} \rightarrow {\overline{\Omega _\infty }}$, it follows that for all j large enough

$$\begin{aligned} B\left( A_0,\frac{1}{4N_0} \right) \subset B\left( 0,\frac{1}{2}\right) \setminus {\overline{\Omega _j}} \subset B(0,1)\setminus {\overline{\Omega _j}}. \end{aligned}$$

(5.3)

Hence for all j large enough $A_0$ is a corkscrew point relative to $B(0,1)\cap \partial \Omega _j$ for ${{\mathbb {R}}}^n\setminus {\overline{\Omega _j}}$ with constant $4N_0$. This contradicts our assumption that $\Omega _j$ has no exterior corkscrew point with constant $N=4N_0$ for the surface ball $B(0,1)\cap \partial \Omega _j$ and the proof is complete.

7 Part II. Large Constant Case

The extrapolation argument to augment small Carleson norm is in essence an inductive process combined with delicate stopping time arguments. It requires us to construct the so-called sawtooth domains on which we have better control of the Carleson measure norm. We explain the construction of these sawtooth domains and auxiliary definitions in Section 6, to set the stage for the extrapolation argument. In Section 7 we first state several key ingredients to be used in the proof, namely: the framework of the extrapolation argument in Theorem 7.1 proved in [HMM1]; and Theorem 7.7, a criterion for uniform rectifiability proven as a combination of [HMM1, GMT]. We then outline the proof of Theorem 1.6 using these ingredients and the small constant result proven in Part I (i.e. Corollary 1.13), and in the process reduce matters to two main steps, which are then carried out in two separate sections. In Section 8, we prove a technical estimate showing that a continuous parameter Carleson measure, restricted to a sawtooth subdomain, may be controlled quantitatively by a discretized version of itself. Section 9 contains the most delicate technical part of the proof, involving transference of the $A_\infty$ property to sawtooth subdomains. Finally in Section 10 we discuss the optimality of Theorem 1.6 and present an important corollary.

8 Construction of Sawtooth Domains and Discrete Carleson Measures

Lemma 6.1

(Dyadic decomposition of Ahlfors regular set, [DS1, DS2, Chr]). Let $E\subset {{\mathbb {R}}}^n$ be an Ahlfors regular set. Then there exist constants $a_0, A_1, \gamma >0$, depending only on n and the constants of Ahlfors regularity, such that for each $k\in {\mathbb {Z}}$, there is a collection of Borel sets (“dyadic cubes”)

$$\begin{aligned} {\mathbb {D}}_k : = \{Q_j^k \subset E: j\in {\mathscr {J}}_k \}, \end{aligned}$$

where ${\mathscr {J}}_k$ denotes some index set depending on k, satisfying the following properties.

• (i) $E = \bigcup _{j\in {\mathscr {J}}_k} Q_j^k$ for each $k\in {\mathbb {Z}}$.

• (ii) If $m\ge k$ then either $Q_i^m \subset Q_j^k$ or $Q_i^m \cap Q_j^k = \emptyset$.

• (iii) For each pair (j, k) and each $m<k$, there is a unique $i\in {\mathscr {J}}_m$ such that $Q_j^k \subset Q_i^m$.

• (iv) ${{\,\mathrm{diam}\,}}Q_j^k \le A_1 2^{-k}$.

• (v) Each $Q_j^k$ contains some surface ball $\Delta (x_j^k, a_0 2^{-k}) := B(x_j^k, a_0 2^{-k}) \cap E$.

• (vi) For all (j, k) and all $\rho \in (0,1)$

  $$\begin{aligned}&{\mathcal {H}}^{n-1} \left( \left\{ q\in Q_j^k: {\text {dist}}(q, E\setminus Q_j^k) \le \rho 2^{-k} \right\} \right) \nonumber \\&\quad + {\mathcal {H}}^{n-1} \left( \left\{ q\in E\setminus Q_j^k: {\text {dist}}(q, Q_j^k) \le \rho 2^{-k} \right\} \right) \le A_1 \rho ^{\gamma } {\mathcal {H}}^{n-1} (Q_j^k). \end{aligned}$$

  (6.2)

We shall denote by ${\mathbb {D}} = {\mathbb {D}}(E)$ the collection of all relevant $Q_j^k$, i.e.,

$$\begin{aligned} {\mathbb {D}}= \bigcup _k {\mathbb {D}}_k, \end{aligned}$$

(6.3)

where, if ${{\,\mathrm{diam}\,}}(E)$ is finite, the union runs over those k such that $2^{-k} \lesssim {\mathrm{diam}}(E)$.

Remark 6.4

For a dyadic cube $Q\in {\mathbb {D}}_k$, we shall set $\ell (Q) = 2^{-k}$, and we shall refer to this quantity as the “length” of Q. Evidently, $\ell (Q)\approx {{\,\mathrm{diam}\,}}(Q).$ We will also write $x_Q$ for the “center” of Q, that is, the center of the ball appearing in (v).

Assume from now on that $\Omega$ is a uniform domain with Ahlfors regular boundary and set $\sigma ={\mathcal {H}}^{n-1}|_{\partial \Omega }$. Let ${\mathbb {D}}={\mathbb {D}}(\partial \Omega )$ be the associated dyadic grid from the previous result. We first make a simple observation:

Corollary 6.5

(Doubling property of the kernel). Let $Q\in {\mathbb {D}}$ be a dyadic cube, and ${\widetilde{Q}}\in {\mathbb {D}}$ be such that $C_1^{-1}\ell (Q)\le \ell ({\widetilde{Q}})\le C_1\ell (Q)$ and ${\text {dist}}(Q,{\widetilde{Q}})\le C_1\ell (Q)$ for some $C_1\ge 1$. Suppose $\omega \in RH_p(\sigma )$ for some $p>1$, then for $X_Q$ the corkscrew relative to Q we have

$$\begin{aligned} \int _{{\widetilde{Q}}} \left( {\mathbf{k }}^{X_Q} \right) ^p d\sigma \le C \int _Q \left( {\mathbf{k }}^{X_Q} \right) ^p d\sigma , \end{aligned}$$

(6.6)

with a constant C depending on $C_1$ and the allowable constants and where ${\mathbf{k }}=d\omega /d\sigma$.

The proof is a simple corollary of the doubling property of the elliptic measure (see Lemma 2.37):

Let ${\mathcal {W}}={\mathcal {W}}(\Omega )$ denote a collection of (closed) dyadic Whitney cubes of $\Omega$ (just dyadically divide the standard Whitney cubes from [Ste, Chapter VI] into cubes with side length 1/8 as large), so that the boxes in ${\mathcal {W}}$ form a covering of $\Omega$ with non-overlapping interiors, and which satisfy

$$\begin{aligned} 4\, {\mathrm{diam}}\,(I)\le {\text {dist}}(4 I,\partial \Omega ) \le {\text {dist}}(I,\partial \Omega ) \le 40 \, {\mathrm{diam}}\,(I). \end{aligned}$$

(6.7)

Let X(I) denote the center of I, let $\ell (I)$ denote the side length of I, and write $k=k_I$ if $\ell (I) = 2^{-k}$. We will use “boxes” to refer to the Whitney cubes as just constructed, and “cubes” for the dyadic cubes on $\partial \Omega$. Then for each pair $I, J \in {\mathcal {W}}$,

$$\begin{aligned} \text { if } I\cap J \ne \emptyset , \text { then } 4^{-1} \le \frac{\ell (I)}{\ell (J)} \le 4. \end{aligned}$$

(6.8)

Since I, J are dyadic boxes, then $I\cap J$ is either contained in a face of I, or contained in a face of J. By choosing $\tau _0<2^{-10}$ sufficiently small (depending on n), we may also suppose that there is $t\in (\frac{1}{2},1)$ so that if $0<\tau <\tau _0$, for every distinct pair $I, J\in {\mathcal {W}}(\Omega )$,

$$\begin{aligned} (1+4\tau ) I \cap (1+4\tau ) J \ne \emptyset \iff I\cap J \ne \emptyset ; \end{aligned}$$

(6.9)

and

$$\begin{aligned} t J \cap (1+ 4\,\tau ) I = \emptyset . \end{aligned}$$

(6.10)

Also, $J\cap (1+\tau )I$ contains an $(n-1)$-dimensional cube with side length of the order of $\min \{\ell (I), \ell (J)\}$. This observation will become useful in Section 9. For such $\tau \in (0,\tau _0)$ fixed, we write $I^*=(1+\tau )I$, $I^{**}= (1+2\tau ) I$, and $I^{***}= (1+4\tau ) I$ for the “fattening” of $I\in {\mathcal {W}}$.

Following [HM1, Section 3] we next introduce the notion of Carleson region and discretized sawtooth. Given a cube $Q\in {\mathbb {D}}$, the discretized Carleson region ${\mathbb {D}}_{Q}$ relative to Q is defined by

$$\begin{aligned} {\mathbb {D}}_{Q}=\{Q'\in {\mathbb {D}}:\, \, Q'\subset Q\}. \end{aligned}$$

Let ${\mathcal {F}}$ be family of disjoint cubes $\{Q_{j}\}\subset {\mathbb {D}}$. The global discretized sawtooth region relative to ${\mathcal {F}}$ is the collection of cubes $Q\in {\mathbb {D}}$ that are not contained in any $Q_{j}\in {\mathcal {F}}$;

$$\begin{aligned} {\mathbb {D}}_{{\mathcal {F}}}:={\mathbb {D}}\setminus \bigcup \limits _{Q_{j}\in {\mathcal {F}}}{\mathbb {D}}_{Q_{j}}. \end{aligned}$$

For a given $Q\in {\mathbb {D}}$ the local discretized sawtooth region relative to ${\mathcal {F}}$ is the collection of cubes in ${\mathbb {D}}_{Q}$ that are not in contained in any $Q_{j}\in {\mathcal {F}}$;

$$\begin{aligned} {\mathbb {D}}_{{\mathcal {F}},Q}:={\mathbb {D}}_{Q}\setminus \bigcup \limits _{Q_{j}\in {\mathcal {F}}} {\mathbb {D}}_{Q_{j}}={\mathbb {D}}_{{\mathcal {F}}}\cap {\mathbb {D}}_{Q}. \end{aligned}$$

(6.11)

We also introduce the “geometric” Carleson and sawtooth regions. For any dyadic cube $Q\in {\mathbb {D}}$, pick two parameters $\eta \ll 1$ and $K\gg 1$, and define

$$\begin{aligned} {\mathcal {W}}_Q^0 : = \{I\in {\mathcal {W}}: \eta ^{\frac{1}{4}} \ell (Q) \le \ell (I) \le K^{\frac{1}{2}} \ell (Q),\ {\text {dist}}(I,Q) \le K^{\frac{1}{2}} \ell (Q)\}. \end{aligned}$$

(6.12)

Taking $K\ge 40^2 n$, if $I\in {\mathcal {W}}$ and we pick $Q_I\in {\mathbb {D}}$ so that $\ell (Q_I)=\ell (I)$ and ${\text {dist}}(I,\partial \Omega )={\text {dist}}(I,Q_I)$, then $I\in {\mathcal {W}}^0_{Q_I}$. Let $X_Q$ denote a corkscrew point for the surface ball $\Delta (x_Q, r_Q/2)$. We can guarantee that $X_Q$ is in some $I\in {\mathcal {W}}_Q^0$ provided we choose $\eta$ small enough and K large enough. For each $I\in {\mathcal {W}}_Q^0$, there is a Harnack chain connecting X(I) to $X_Q$, we call it ${\mathcal {H}}_I$. By the definition of ${\mathcal {W}}_Q^0$ we may construct this Harnack chain so that it consists of a bounded number of balls (depending on the values of $\eta , K$). We let ${\mathcal {W}}_Q$ denote the set of all $J\in {\mathcal {W}}$ which meet at least one of the Harnack chains ${\mathcal {H}}_I$, with $I\in {\mathcal {W}}_Q^0$, i.e.

$$\begin{aligned} {\mathcal {W}}_Q := \{J\in {\mathcal {W}}: \text {there exists } I\in {\mathcal {W}}_Q^0 \text { for which } {\mathcal {H}}_I \cap J \ne \emptyset \}; \end{aligned}$$

(6.13)

Besides, it follows from the construction of the augmented collections ${\mathcal {W}}_Q$ and the properties of the Harnack chains that there are uniform constants c and C such that

$$\begin{aligned} c\eta ^{\frac{1}{2} } \ell (Q) \le \ell (I) \le CK^{\frac{1}{2}} \ell (Q), \quad {\text {dist}}(I,Q) \le CK^{\frac{1}{2}} \ell (Q) \end{aligned}$$

(6.14)

for any $I\in {\mathcal {W}}_Q$. In particular once $\eta , K$ are fixed, for any $Q\in {\mathbb {D}}$ the cardinality of ${\mathcal {W}}_Q$ is uniformly bounded. Finally, for every Q we define its associated Whitney region

$$\begin{aligned} U_Q := \bigcup _{I\in \,{\mathcal {W}}_Q} I^*. \end{aligned}$$

(6.15)

We refer the reader to [HM1, Section 3] or [HMM2, Section 2] for additional details.

For a given $Q\in {\mathbb {D}}$, the Carleson box relative to Q is defined by

$$\begin{aligned} T_{Q}:=\text{ int }\left( \bigcup \limits _{Q'\in {\mathbb {D}}_{Q}} U_{Q'}\right) . \end{aligned}$$

(6.16)

For a given family ${\mathcal {F}}$ of disjoint cubes $\{Q_{j}\}\subset {\mathbb {D}}$ and a given $Q\in {\mathbb {D}}$ we define the local sawtooth region relative to ${\mathcal {F}}$ by

$$\begin{aligned} \Omega _{{\mathcal {F}},Q}:=\text{ int }\left( \bigcup \limits _{Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}}U_{Q'}\right) = {\mathrm{int }}\,\left( \bigcup _{I\in \,{\mathcal {W}}_{{\mathcal {F}},Q}} I^*\right) , \end{aligned}$$

where ${\mathcal {W}}_{{\mathcal {F}},Q}:=\bigcup _{Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}}{\mathcal {W}}_{Q'}$. Analogously, we can slightly fatten the Whitney boxes and use $I^{**}$ to define new fattened Whitney regions and sawtooth domains. More precisely,

$$\begin{aligned} T_{Q}^*:=\text{ int }\left( \bigcup \limits _{Q'\in {\mathbb {D}}_{Q}} U_{Q'}^*\right) , \qquad \Omega _{{\mathcal {F}},Q}^*:=\text{ int }\left( \bigcup \limits _{Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}}U_{Q'}^*\right) , \qquad U_{Q'}^*:=\bigcup _{I\in \,{\mathcal {W}}_{Q'}} I^{**}. \end{aligned}$$

(6.17)

Similarly, we can define $T_Q^{**}$, $\Omega _{{\mathcal {F}},Q}^{**}$ and $U_{Q}^{**}$ by using $I^{***}$ in place of $I^{**}$.

One can easily see that there is a constant $\kappa _0>0$ (depending only on the allowable parameters, $\eta$, and K) so that

$$\begin{aligned} T_Q\subset T_{Q}^*\subset T_{Q}^{**}\subset \overline{T_Q^{**}}\subset \kappa _0 B_Q\cap {\overline{\Omega }} =: B_Q^*\cap {\overline{\Omega }}, \qquad \forall \,Q\in {\mathbb {D}}. \end{aligned}$$

(6.18)

Given a pairwise disjoint family ${\mathcal {F}}\subset {\mathbb {D}}$ (we also allow ${\mathcal {F}}$ to be the null set) and a constant $\rho >0$, we derive another family ${\mathcal {F}}({\rho })\subset {\mathbb {D}}$ from ${\mathcal {F}}$ as follows. Augment ${\mathcal {F}}$ by adding all cubes $Q\in {\mathbb {D}}$ whose side length $\ell (Q)\le \rho$ and let ${\mathcal {F}}(\rho )$ denote the corresponding collection of maximal cubes with respect to the inclusion. Note that the corresponding discrete sawtooth region ${\mathbb {D}}_{{\mathcal {F}}(\rho )}$ is the union of all cubes $Q\in {\mathbb {D}}_{{\mathcal {F}}}$ such that $\ell (Q)>\rho$. For a given constant $\rho$ and a cube $Q\in {\mathbb {D}}$, let ${\mathbb {D}}_{{\mathcal {F}}(\rho ),Q}$ denote the local discrete sawtooth region and let $\Omega _{{\mathcal {F}}(\rho ),Q}$ denote the local geometric sawtooth region relative to disjoint family ${\mathcal {F}}(\rho )$.

Given $Q\in {\mathbb {D}}$ and $0<\epsilon <1$, if we take ${\mathcal {F}}_0=\emptyset$, one has that ${\mathcal {F}}_0(\epsilon \,\ell (Q))$ is the collection of $Q'\in {\mathbb {D}}$ such that $\epsilon \,\ell (Q)/2<\ell (Q')\le \epsilon \,\ell (Q)$. We then introduce $U_{Q,\epsilon }=\Omega _{{\mathcal {F}}_0(\epsilon \,\ell (Q)),Q}$, which is a Whitney region relative to Q whose distance to $\partial \Omega$ is of the order of $\epsilon \,\ell (Q)$. For later use, we observe that given $Q_0\in {\mathbb {D}}$, the sets $\{U_{Q,\epsilon }\}_{Q\in {\mathbb {D}}_{Q_0}}$ have bounded overlap with constant that may depend on $\epsilon$. Indeed, suppose that there is $X\in U_{Q,\epsilon }\cap U_{Q',\epsilon }$ with Q, $Q'\in {\mathbb {D}}_{Q_0}$. By construction $\ell (Q)\approx _\epsilon \delta (X)\approx _\epsilon \ell (Q')$ and

$$\begin{aligned} {\text {dist}}(Q,Q')\le {\text {dist}}(X,Q)+{\text {dist}}(X,Q')\lesssim _\epsilon \ell (Q)+\ell (Q')\approx _\epsilon \ell (Q). \end{aligned}$$

The bounded overlap property follows then at once.

Lemma 6.19

([HM1, Lemma 3.61]). Let $\Omega \subset {{\mathbb {R}}}^n$ be a uniform domain with Ahlfors regular boundary. Then all of its Carleson boxes $T_Q$ and sawtooth domains $\Omega _{{\mathcal {F}}, Q}$, $\Omega _{{\mathcal {F}}, Q}^*$ are uniform domains with Ahlfors regular boundaries. In all the cases the implicit constants are uniform, and depend only on dimension and on the corresponding constants for $\Omega$.

We say that ${\mathbb {P}}$ is a fundamental chord-arc subdomain of $\Omega$ if there is $I\in {\mathcal {W}}$ and $m_1$ such that

$$\begin{aligned} {\mathbb {P}}={{\,\mathrm{int}\,}}\left( \bigcup _{j=1}^{m_1} I_j^*\right) \hbox { where } I_j\in {\mathcal {W}}\hbox { and } I\cap I_j \not =\emptyset . \end{aligned}$$

(6.20)

Note that the fact that $I\cap I_j \not =\emptyset$ ensures that $\ell (I)\approx \ell (I_j)$. Moreover ${\mathbb {P}}$ is a chord-arc domain with constants that only depend on n, $\tau$ and the constants used in the construction of ${\mathbb {D}}$ and ${\mathcal {W}}$ (see [HMU, Lemma 2.47] for a similar argument).

Given a sequence of non-negative numbers $\alpha =\{\alpha _Q\}_{Q\in {\mathbb {D}}}$ we define the associated discrete “measure” $m=m_\alpha$:

$$\begin{aligned} m({\mathbb {D}}') := \sum _{Q\in {\mathbb {D}}'} \alpha _Q, \qquad {\mathbb {D}}'\subset {\mathbb {D}}. \end{aligned}$$

(6.21)

Definition 6.22

Let $E\subset {{\mathbb {R}}}^n$ be an Ahlfors regular set, and let $\sigma$ be a dyadically doubling Borel measure on E (not necessarily equal to ${\mathcal {H}}^{n-1}|_{\partial \Omega }$). We say that m as defined in (6.21) is a discrete Carleson measure with respect to $\sigma$, if

$$\begin{aligned} \Vert m\Vert _{{\mathcal {C}}}: = \sup _{Q\in {\mathbb {D}}} \frac{ m({\mathbb {D}}_Q)}{ \sigma (Q) } <\infty . \end{aligned}$$

(6.23)

Also, fixed $Q_0\in {\mathbb {D}}$ we say that m is a discrete Carleson measure with respect to $\sigma$ in $Q_0$ if

$$\begin{aligned} \Vert m\Vert _{{\mathcal {C}}(Q_0)}: = \sup _{Q\in {\mathbb {D}}_{Q_0}} \frac{ m({\mathbb {D}}_Q)}{ \sigma (Q) } <\infty . \end{aligned}$$

(6.24)

9 Proof by Extrapolation

In this section we present some powerful tools which will be key in the proof of our main result. After that we outline the roadmap to pass from the small constant case to the large constant case and thus finish proving Theorem 1.6.

We start with [HMM1, Lemma 4.5], an extrapolation for Carleson measure result which in a nutshell describes how the relationship between a discrete Carleson measure m and another discrete measure ${{\widetilde{m}}}$ yields information about ${{\widetilde{m}}}$.

Theorem 7.1

(Extrapolation, [HMM1, Lemma 4.5]).   Let $\sigma$ be a dyadically doubling Borel measure on $\partial \Omega$ (not necessarily equal to ${\mathcal {H}}^{n-1}|_{\partial \Omega }$), and let m be a discrete Carleson measure with respect to $\sigma$ (defined as in (6.21) and Definition 6.22), with constant $M_0$, that is

$$\begin{aligned} \Vert m\Vert _{{\mathcal {C}}}: = \sup _{Q\in {\mathbb {D}}} \frac{ m({\mathbb {D}}_Q)}{ \sigma (Q) } \le M_0. \end{aligned}$$

(7.2)

Let ${{\widetilde{m}}}$ be another discrete non-negative measure on ${\mathbb {D}}$ defined as in (6.21), by

$$\begin{aligned} {{\widetilde{m}}}({\mathbb {D}}') := \sum _{Q\in {\mathbb {D}}'} \beta _Q, \qquad {\mathbb {D}}'\subset {\mathbb {D}}. \end{aligned}$$

Assume there is a constant $M_1$ such that

$$\begin{aligned} \quad 0\le \beta _Q \le M_1 \sigma (Q)\ \hbox { for any }Q\in {\mathbb {D}}\end{aligned}$$

(7.3)

and that there is a positive constant $\gamma$ such that for every $Q\in {\mathbb {D}}$ and every family of pairwise disjoint dyadic subcubes ${\mathcal {F}}=\{Q_j\}\subset {\mathbb {D}}_Q$ verifying

$$\begin{aligned} \Vert m_{\mathcal {F}}\Vert _{{\mathcal {C}}(Q)}:= \sup _{Q'\in {\mathbb {D}}_Q} \frac{m \left( {\mathbb {D}}_{{\mathcal {F}},Q'} \right) }{\sigma (Q')} \le \gamma , \end{aligned}$$

(7.4)

we have that ${{\widetilde{m}}}$ satisfies

$$\begin{aligned} {{\widetilde{m}}} ({\mathbb {D}}_{{\mathcal {F}},Q}) \le M_1 \sigma (Q). \end{aligned}$$

(7.5)

Then ${{\widetilde{m}}}$ is a discrete Carleson measure, with

$$\begin{aligned} \Vert {{\widetilde{m}}}\Vert _{{\mathcal {C}}}:= \sup _{Q\in {\mathbb {D}}} \frac{\widetilde{m}({\mathbb {D}}_Q)}{\sigma (Q)} \le M_2, \end{aligned}$$

(7.6)

for some $M_2 <\infty$ depending on $n, M_0, M_1, \gamma$ and the doubling constant of $\sigma$.

Theorem 7.7

([HMM1, GMT]).   Let ${\mathcal {D}}$ be an open set satisfying an interior corkscrew condition with Ahlfors regular boundary. Then the following are equivalent:

• (a) $\partial {\mathcal {D}}$ is uniformly rectifiable.

• (b) There exists a constant C such that for every bounded harmonic function u in ${\mathcal {D}}$, i.e. $-\Delta u = 0$ in ${\mathcal {D}}$, and for any $x\in \partial {\mathcal {D}}$ and $0<r\lesssim {{\,\mathrm{diam}\,}}({\mathcal {D}})$, there holds

  $$\begin{aligned} \frac{1}{r^{n-1}} \int _{B(x,r) \cap {\mathcal {D}}} |\nabla u(Y)|^2 {\text {dist}}(Y, \partial {\mathcal {D}})\, dY \le C \Vert u\Vert _\infty ^2. \end{aligned}$$

  (7.8)

Remark 7.9

Condition (7.8) is sometimes referred to as the Carleson measure estimate (CME) for bounded, harmonic functions.

The direction (a) $\implies$ (b) is proved by the first three authors of the present paper [HMM1, Theorem 1.1], and the converse direction is proved by Garnett, Mourgoglou, and Tolsa [GMT, Theorem 1.1]. As we have noted above, see Theorem 1.1, under the uniform domain assumption, the statements (a) and/or (b) are equivalent to the fact that ${\mathcal {D}}$ is a chord-arc domain.

The proof of Theorem 1.6 is rather involved thus we sketch below the plan of the proof.

Proof of Theorem 1.6

We first reduce matters to the case on which ${\mathcal {A}}$ is symmetric. To do so we observe that by [CHMT, Theorem 1.6], under the assumptions (H1) and (H2), if $\omega _L\in A_\infty (\sigma )$ then $\omega _{L^{\mathrm{sym}}}\in A_\infty (\sigma )$ where $L^\mathrm{sym}=-\mathop {{\text {div}}}\nolimits ({\mathcal {A}}^{\mathrm{sym}}\nabla )$ and ${\mathcal {A}}^\mathrm{sym}=(\frac{a_{ij}+a_{ji}}{2})_{i,j=1}^n$ is the symmetric part of ${\mathcal {A}}$. Note that, clearly, ${\mathcal {A}}^{\mathrm{sym}}$ is a symmetric uniformly elliptic matrix in $\Omega$ with the same ellipticity constants as ${\mathcal {A}}$. It also satisfies (H1) and (H2) with constants which are controlled by those of ${\mathcal {A}}$. Hence we only need to show (1) $\implies$ (2) for $L^{\mathrm{sym}}$ which is associated to the symmetric matrix ${\mathcal {A}}^{\mathrm{sym}}$. That is, we may assume to begin with, and we do so, that ${\mathcal {A}}$ is symmetric.

Our main goal is to use the above extrapolation theorem with m and ${\widetilde{m}}$ two discrete measures associated respectively with the sequences $\alpha =\{\alpha _Q\}_{Q\in {\mathbb {D}}}$ and $\beta =\{\beta _Q\}_{Q\in {\mathbb {D}}}$ defined by

$$\begin{aligned} \alpha _Q: = \int _{U_Q^*} |\nabla {\mathcal {A}}(Y)|^2 \delta (Y) dY,\qquad \beta _Q ; = \int _{U_Q} |\nabla u(Y)|^2 \delta (Y) dY, \end{aligned}$$

(7.10)

where u is an arbitrary bounded harmonic function in $\Omega$, such that $\Vert u\Vert _{L^\infty (\Omega )} \le 1$; and $U_Q$ and $U_Q^*$ are as defined in (6.15) and (6.17) respectively. We would like to observe that by the interior Caccioppoli inequality, $\beta _Q$ clearly satisfies the assumption (7.3):

$$\begin{aligned} \beta _Q= & {} \int _{U_Q} |\nabla u(Y)|^2 \delta (Y)\, dY \lesssim \sum _{I\in {\mathcal {W}}_Q} \ell (I)\,\int _{I^*} |\nabla u(Y)|^2\,dY \\\lesssim & {} \sum _{I\in {\mathcal {W}}_Q} \ell (I)^{-1}\,\int _{I^{**}} |u(Y)|^2\,dY \\\lesssim & {} \ell (Q)^{-1}\,\int _{U_Q^*} |u(Y)|^2 \delta (Y) dY \le \ell (Q)^n \approx \sigma (Q), \end{aligned}$$

where we have used (6.14), the bounded overlap of the family $\{I^{**}\}_{I\in {\mathcal {W}}}$, and (6.18). We will take any family of pairwise disjoint dyadic subcubes ${\mathcal {F}}=\{Q_j\}\subset {\mathbb {D}}_Q$ so that (7.4) holds for sufficiently small $\gamma \in (0,1)$ to be chosen and the goal is to obtain (7.5). To achieve this we will carry out the following steps:

• Step 1: We first observe that (7.2) is equivalent to the Carleson measure assumption (H2). This is a simple calculation which uses the fact that the Whitney boxes $I^{**}$ which form $U_Q^*$ have finite overlap and the definition of $T_Q$ in (6.16), details are left to the reader.

• Step 2: Given $\epsilon >0$ we verify that the small Carleson hypothesis (7.4) implies that if $\gamma =\gamma (\epsilon )$ is small enough, ${\mathcal {A}}$ satisfies the small Carleson assumption (with constant $\epsilon$) in the sawtooth domain $\Omega _{{\mathcal {F}},Q}^*$. This is done in Section 8.

• Step 3: We verify that under the hypotheses (H1) and (H2), the assumption $\omega \in A_\infty (\sigma )$ in $\Omega$ is transferable to any sawtooth domain, in particular, if we write $\omega _{*}$ for the elliptic measure associated with L in $\Omega _{{\mathcal {F}},Q}^*$, then $\omega _{*}\in A_\infty ({\mathcal {H}}^{n-1}|_{\partial {\Omega _{{\mathcal {F}},Q}^*}})$ and the implicit constants are uniformly controlled by the allowable constants. See Theorem 9.1 and Corollary 9.3.

• Step 4: We combine Step 2 and Step 3 with Corollary 1.13 applied to the domain $\Omega _{{\mathcal {F}},Q}^*$ and obtain that $\Omega _{{\mathcal {F}},Q}^*$ is a chord-arc domain. More precisely, note first that $\Omega _{{\mathcal {F}},Q}^*$ is a bounded uniform domain with Ahlfors regular boundary (see Lemma 6.19) and all the implicit constants are uniformly controlled by those of $\Omega$, that is, they do not depend on Q or the family ${\mathcal {F}}$. Also, Step 3 says that $\omega _{*}\in A_\infty ({\mathcal {H}}^{n-1}|_{\partial {\Omega _{{\mathcal {F}},Q}^*}})$ and the implicit constants are uniformly controlled by the allowable constants. Hence for the parameter $\epsilon$ given by Corollary 1.13 (recall that we have assumed that ${\mathcal {A}}$ is symmetric), which only depends on the allowable constants and is independent of Q or the family ${\mathcal {F}}$, we can find the corresponding $\gamma =\gamma (\epsilon )$ from Step 2 so that ${\mathcal {A}}$ satisfies the small Carleson assumption (with constant $\epsilon$) in the sawtooth domain $\Omega _{{\mathcal {F}},Q}^*$. Thus Corollary 1.13 applied to the domain $\Omega _{{\mathcal {F}},Q}^*$ yields that $\Omega _{{\mathcal {F}},Q}^*$ is a chord-arc domain with constants that only depend on the allowable constants.

• Step 5: We next apply Theorem 7.7 with ${\mathcal {D}}=\Omega _{{\mathcal {F}},Q}^*$ to obtain that (7.8) holds with ${\mathcal {D}}=\Omega _{{\mathcal {F}},Q}^*$. Seeing that the latter implies (7.5) is not difficult. Indeed, note that any $Y \in \Omega _{{\mathcal {F}},Q}$ satisfies $\delta _*(Y):= {\text {dist}}(Y, \partial \Omega _{{\mathcal {F}},Q}^*) \approx _\tau \delta (Y)$ (here we would like to remind the reader that $\Omega _{{\mathcal {F}},Q}$ is comprised of fattened Whiney boxes $I^*=(1+\tau )I$ while for $\Omega _{{\mathcal {F}},Q}^*$ we use the fatter versions $I^{**}=(1+2\tau )I$). Thus by (7.8), the fact that u is harmonic and bounded by 1 in $\Omega$, and so in $\Omega _{{\mathcal {F}},Q}^*$, and a simple covering argument, we can conclude that

  $$\begin{aligned} {{\widetilde{m}}}_{}( {\mathbb {D}}_{{\mathcal {F}},Q})\lesssim & {} \int _{\Omega _{{\mathcal {F}},Q}} |\nabla u|^2 \delta (Y) dY \approx \int _{\Omega _{{\mathcal {F}},Q}} |\nabla u|^2 \delta _* (Y) dY \\\lesssim & {} \int _{\Omega _{{\mathcal {F}},Q}^*} |\nabla u|^2 \delta _* (Y) dY \lesssim {{\,\mathrm{diam}\,}}(\Omega _{{\mathcal {F}},Q}^*)^{n-1} \approx \ell (Q)^{n-1} \approx \sigma (Q), \end{aligned}$$

  which is (7.5).

After all these steps have been carried out the extrapolation for Carleson measures in Theorem 7.1 allows us to conclude that ${{\widetilde{m}}}$ is a discrete Carleson measure. In other words, we have proved that any bounded harmonic function in $\Omega$ satisfies (7.8) with ${\mathcal {D}}=\Omega$. As a result, and by another use of Theorem 7.7 this time with ${\mathcal {D}}=\Omega$, we derive that $\partial \Omega$ is uniformly rectifiable. This completes the proof of Theorem 1.6 modulo establishing Step 2 and Step 3 and this will be done in the following sections.

$\square$

Remark 7.11

For convenience, we augment ${\mathcal {F}}$ by adding all subcubes of Q of length $2^{-N}\ell (Q)$, and let ${\mathcal {F}}_N$ denote the maximal cubes in the resulting augmented collection. Note that for each $N\ge 2$, the sawtooth domain $\Omega _{{\mathcal {F}}_N,Q}$ is compactly contained in $\Omega$ (indeed is $2^{-N}\ell (Q)$-away from $\partial \Omega$). Note that ${\mathbb {D}}_{{\mathcal {F}}_{N},Q} \subset {\mathbb {D}}_{{\mathcal {F}}_{N'},Q} \subset {\mathbb {D}}_{{\mathcal {F}},Q}$ for every $2\le N\le N'$. In particular, $m_{{\mathcal {F}}_{N}} \le m_{{\mathcal {F}}_{N'}} \le m_{{\mathcal {F}}}$ and thus

$$\begin{aligned} m_{{\mathcal {F}}} \text { satisfies }(7.4) \implies m_{{\mathcal {F}}_N} \text { also satisfies the }(7.4)\text { with a constant independent of }N. \end{aligned}$$

We are going to prove Step 2 and Step 3 for the sawtooth domain $\Omega _{{\mathcal {F}}_N,Q}$, with constants independent of N. Then by Step 4 and Step 5, we will have

$$\begin{aligned} {{\widetilde{m}}}({\mathbb {D}}_{{\mathcal {F}}_N,Q}) \le M_1 \sigma (Q), \end{aligned}$$

(7.12)

with a constant $M_1$ independent of N, and thus (7.5) follows from monotone convergence theorem by letting $N\rightarrow \infty$. To simplify the notations we drop from the index N from now on and write ${\mathcal {F}}={\mathcal {F}}_N$ but we keep in mind that the corresponding sawtooth domain $\Omega _{{\mathcal {F}},Q}$ is compactly contained in $\Omega$.

10 Consequences of the Small Carleson Hypothesis in the Extrapolation Theorem

Set $\Omega _*:= \Omega _{{\mathcal {F}},Q}^*$ and let $\epsilon$ be given. The goal is to see that we can find $\gamma =\gamma (\epsilon )\in (0,1)$ so that (7.4) implies

$$\begin{aligned} \int _{B(x,r) \cap \Omega _*} |\nabla {\mathcal {A}}(Y)|^2 \delta _*(Y) dY \le \epsilon r^{n-1}, \end{aligned}$$

(8.1)

for any $x\in \partial \Omega _*$ and any $0<r<{{\,\mathrm{diam}\,}}(\partial \Omega _*)$. To see this we fix $x\in \partial \Omega _*$ and $0<r<{{\,\mathrm{diam}\,}}(\partial \Omega _*)\approx \ell (Q)$. Using that $\Omega _* \subset \Omega$ one has that $\delta _*(Y) \le \delta (Y)$ and therefore (8.1) follows at once from

$$\begin{aligned} \int _{B(x,r) \cap \Omega _*} |\nabla {\mathcal {A}}(Y)|^2 \delta (Y) dY \le \epsilon r^{n-1}. \end{aligned}$$

(8.2)

To show (8.2), we let $c\in (0,1)$ be a small constant and ${\widetilde{M}}\ge 1$ be a large constant to be determined later, depending on the values of $\eta , K$ used in the definition of ${\mathcal {W}}_Q^0$ in (6.12). We consider two cases depending on the size of r with respect to $\delta (x)$ for $x\in \partial \Omega ^*$. Recall that $\Omega _*$ is compactly contained in $\Omega$, thus $\delta (x)>0$ for any $x\in \partial \Omega _*$.

Case 1. $r\le c\delta (x)$. Since $x\in \partial \Omega _*= \partial \Omega _{{\mathcal {F}},Q}^*$ there exist $Q_x\in {\mathbb {D}}_{{\mathcal {F}},Q}$ and $I_x\in {\mathcal {W}}_{Q_x}$ such that $x\in \partial I_x^{**}$. We choose and fix c sufficiently small (depending just on dimension), so that B(x, r) is contained in $2I_x$. We consider two sub-cases. First if $r\le \gamma ^\frac{1}{n}\delta (x)$ then we can invoke (H1) to obtain

$$\begin{aligned} \int _{B(x,r) \cap \Omega _*} |\nabla {\mathcal {A}}(Y)|^2 \delta (Y) dY\le & {} \int _{B(x,r) \cap 2I_x} |\nabla {\mathcal {A}}(Y)|^2 \delta (Y) dY \nonumber \\\lesssim & {} \int _{B(x,r) \cap 2I_x} \delta (Y)^{-1} dY \nonumber \\\approx & {} \ell (I_x)^{-1} \,r^{n} \approx \delta (x)^{-1} \,r^{n} \lesssim \gamma ^\frac{1}{n}\,r^{n-1}. \end{aligned}$$

(8.3)

On the other hand, if $\gamma ^\frac{1}{n}\delta (x)\le r$ we note that

$$\begin{aligned} B(x,r) \cap \Omega _* \subset 2I_x\cap \Omega _* \subset \bigcup _{Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}} (U_Q^{*}\cap 2I_x). \end{aligned}$$

It is clear that from construction if $U_{Q'}^{*}\cap 2I_x\ne \emptyset$ then $\ell (Q')\approx \ell (I_x)\approx \delta (x)$. Note also that $\#\{I\in {\mathcal {W}}: I\cap 2I_x\ne \emptyset \}\lesssim C_n$ hence $\#\{Q'\in {\mathbb {D}}: U_{Q'}^{*}\cap 2I_x\ne \emptyset \}\lesssim C_{n,\eta ,K}$. Thus, observing that $Q'\in {\mathbb {D}}_{{\mathcal {F}},Q'}$ for every $Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}$ we obtain from (7.4)

$$\begin{aligned}&\int _{B(x,r) \cap \Omega _*} |\nabla {\mathcal {A}}(Y)|^2 \delta (Y) dY \nonumber \\&\quad \le \sum _{\begin{array}{c} Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}\\ U_{Q'}^*\cap 2I_x\ne \varnothing \end{array}} \int _{U_Q^*} |\nabla {\mathcal {A}}(Y)|^2 \delta (Y) dY = \sum _{\begin{array}{c} Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}\\ U_{Q'}^*\cap 2I_x\ne \varnothing \end{array}} \alpha _{Q'} \nonumber \\&\quad \le \sum _{\begin{array}{c} Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}\\ U_{Q'}^*\cap 2I_x\ne \varnothing \end{array}} m({\mathbb {D}}_{{\mathcal {F}},Q'}) \le \gamma \,\sum _{\begin{array}{c} Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}\\ U_{Q'}^*\cap 2I_x\ne \varnothing \end{array}} \sigma (Q') \lesssim \gamma \,\,\delta (x)^{n-1} \lesssim \gamma ^\frac{1}{n}\,r^{n-1}. \end{aligned}$$

(8.4)

Case 2. ${\widetilde{M}}^{-1}\,\ell (Q)<r<{{\,\mathrm{diam}\,}}(\partial \Omega _*)\approx \ell (Q)$. This is a trivial case since by construction and (7.4) we obtain

$$\begin{aligned}&\int _{B(x,r) \cap \Omega _*} |\nabla {\mathcal {A}}(Y)|^2 \delta (Y) dY \nonumber \\&\quad \le \sum _{Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}} \int _{U_{Q'}^*} |\nabla {\mathcal {A}}(Y)|^2 \delta (Y) dY \nonumber \\&\quad = \sum _{Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}} \alpha _{Q'} = m({\mathbb {D}}_{{\mathcal {F}},Q}) \le \gamma \sigma (Q) \approx \gamma \ell (Q)^{n-1} \approx \gamma r^{n-1}. \end{aligned}$$

(8.5)

Case 3. $c\delta (x)<r \le {\widetilde{M}}^{-1}\,\ell (Q)$. Pick ${{\hat{x}}}\in \partial \Omega$ such that $|x-{{\hat{x}}}| = \delta (x)$ and note that $B(x,r)\subset B({\hat{x}}, (1+ c^{-1})r)$. Note also that if $Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}$ is so that $U_{Q'}^*\cap B(x,r)\ne \emptyset$ then we can find $I\in {\mathcal {W}}_{Q'}$ and $Y\in I^{**}\cap B(x,r)$ so that by (6.14)

$$\begin{aligned} \eta ^{\frac{1}{2}}\ell (Q') \lesssim \ell (I) \approx \delta (Y) \le |Y-x|+\delta (x) < (1+c^{-1})\,r. \end{aligned}$$

and for every $y\in Q'$,

$$\begin{aligned} |y-{\hat{x}}|\le & {} {{\,\mathrm{diam}\,}}(Q')+{\text {dist}}(Q',I)+{{\,\mathrm{diam}\,}}(I)+|Y-x|+|x-{\hat{x}}| \\\lesssim & {} K^{\frac{1}{2}}\ell (Q')+r+\delta (x) \lesssim K^{\frac{1}{2}}\,\eta ^{-\frac{1}{2}}(1+ c^{-1})\,r. \end{aligned}$$

Consequently, if we write ${\widetilde{M}}'= C\,K^{\frac{1}{2}}\,\eta ^{-\frac{1}{2}}\,(1+c^{-1})$ and choose ${\widetilde{M}}>{\widetilde{M}}'$, it follows that $\ell (Q')<{\widetilde{M}}'\,r<\ell (Q)$ and $Q'\subset \Delta ({\hat{x}}, {\widetilde{M}}'r)=:\Delta '$.

We can then find a pairwise disjoint family of dyadic cubes $\{Q_k\}_{k=1}^{{\widetilde{N}}}$ with uniform cardinality ${\widetilde{N}}$ (depending on $C_{AR}$ and n) so that $2^{-1}\,{\widetilde{M}}'\,r\le \ell (Q_k)< {\widetilde{M}}'\,r$, $Q_k\cap \Delta '\ne \emptyset$ for every $1\le k\le {\widetilde{N}}$, and $\Delta '\subset \bigcup _{k=1}^{{\widetilde{N}}} Q_k$. Relabeling if necessary, we can assume that there exists ${\widetilde{N}}'\le {\widetilde{N}}$ so that $\Delta '\cap Q\subset \bigcup _{k=1}^{{\widetilde{N}}'} Q_k$ and each $Q_k$ meets $\Delta '\cap Q$ for $1\le k\le {\widetilde{N}}'$. We would like to observe that necessarily ${\widetilde{N}}'\ge 1$ since we have shown that $Q'\subset \Delta '$ for every $Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}$ so that $U_{Q'}^*\cap B(x,r)\ne \emptyset$. Also $Q_k\subset Q$ for $1\le k\le {\widetilde{N}}'$ since $\ell (Q_k)<{\widetilde{M}}'\,r<\ell (Q)$ and $Q_k$ meets Q. Moreover, for every such a $Q'$ we necessarily have $Q'\subset Q_k$ for some $1\le k\le {\widetilde{N}}'$ since $Q'\subset \Delta '\cap Q$, hence $Q'$ meets some $Q_k$ and also $\ell (Q')<{\widetilde{M}}'\,r\le 2\ell (Q_k)$ which forces $Q'\subset Q _k$. All these and (7.4) readily imply

$$\begin{aligned}&\int _{B(x,r) \cap \Omega _*} |\nabla {\mathcal {A}}(Y)|^2 \delta (Y) dY \nonumber \\&\quad \le \sum _{\begin{array}{c} Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}\\ U_{Q'}^*\cap B(x,r)\ne \varnothing \end{array}} \int _{U_{Q'}^*} |\nabla {\mathcal {A}}(Y)|^2 \delta (Y) dY = \sum _{\begin{array}{c} Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}\\ U_{Q'}^*\cap B(x,r)\ne \varnothing \end{array}} \alpha _{Q'} \nonumber \\&\quad \le \sum _{k=1}^{{\widetilde{N}}'} \sum _{\begin{array}{c} Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}\\ Q'\subset Q_k\subset Q \end{array}} \alpha _{Q'} = \sum _{k=1}^{{\widetilde{N}}'} \sum _{Q'\in {\mathbb {D}}_{{\mathcal {F}},Q_k}} \alpha _{Q'} = \sum _{k=1}^{{\widetilde{N}}'} m({\mathbb {D}}_{{\mathcal {F}},Q_k}) \nonumber \\&\quad \le \gamma \sum _{k=1}^{{\widetilde{N}}'} \sigma (Q_k) \lesssim \gamma r^{n-1}. \end{aligned}$$

(8.6)

Combining what we have obtained in all the cases we see that (8.3), (8.4), (8.5), and (8.6) give, since $0<\gamma <1$, that

$$\begin{aligned} \frac{1}{r^{n-1}}\int _{B(x,r) \cap \Omega _*} |\nabla {\mathcal {A}}(Y)|^2 \delta (Y) dY \le C_0\gamma ^{\frac{1}{n}}, \end{aligned}$$

for some constant $C_0\ge 1$ depending on the allowable constants and where we recall that $\gamma$ is at our choice. Hence we just need to pick $\gamma < (C_0^{-1}\epsilon )^n$ to conclude as desired (8.2).

11 Transference of the $A_\infty$ Property to Sawtooth Domains

In this section we show that the $A_\infty$ property for the elliptic operator L in $\Omega$ can be transferred to sawtooth subdomains with constants that only depend on the allowable constants. We first work with sawtooth subdomains which are compactly contained in $\Omega$ and then we consider the general case using that interior sawtooth subdomains exhaust general sawtooth domains.

Theorem 9.1

   Let $\Omega \subset {{\mathbb {R}}}^n$ be a uniform domain with Ahlfors regular boundary. Let ${\mathcal {A}}$ be a symmetric uniformly elliptic matrix on $\Omega$ and $L=-\mathop {{\text {div}}}\nolimits ({\mathcal {A}}\nabla )$ . Assume the following two properties:

• (1) The elliptic measure $\omega _L$ associated with the operator L relative to the domain $\Omega$ is of class $A_\infty$ with respect to the surface measure.

• (2) For every fundamental chord-arc subdomain ${\mathbb {P}}$ of $\Omega$, see (6.20), the elliptic measure associated with L relative to the domain ${\mathbb {P}}$ is also of class $A_\infty$ with respect to the surface measure of ${\mathbb {P}}$, with uniform $A_\infty$ constants.

For every $Q\in {\mathbb {D}}$ and every family of pairwise disjoint dyadic subcubes ${\mathcal {F}}= \{Q_j\} \subset {\mathbb {D}}_Q$, let $\Omega _*=\Omega _{{\mathcal {F}},Q}$ (or $\Omega _*=\Omega _{{\mathcal {F}},Q}^*$) be the associated sawtooth domain, and $\omega _*$ and $\sigma _* = {\mathcal {H}}^{n-1}|_{\partial \Omega _*}$ be the elliptic measure for L and the surface measure of $\Omega _*$. Then $\omega _* \in A_\infty (\sigma _*)$, with the $A_\infty$ constants independent of Q and ${\mathcal {F}}$.

Note that if ${\mathcal {A}}$ is a non necessarily symmetric matrix satisfying hypotheses (H1) and (H2) in $\Omega$, we can easily verify it also satisfies the Kenig-Pipher condition relative to every fundamental chord-arc subdomain. Indeed, since ${\mathbb {P}}\subset \Omega$ then $\delta _{{\mathbb {P}}}(\cdot )\le \delta (\cdot )$ and (H1) in ${\mathbb {P}}$ is automatic. On the other hand, let ${\mathbb {P}}={{\,\mathrm{int}\,}}\left( \bigcup _{j=1}^{m_1} I_j^*\right)$ with $I_j\in {\mathcal {W}}$ and $I\cap I_j \not =\emptyset$ and take $x\in \partial {\mathbb {P}}$ and $r\le {{\,\mathrm{diam}\,}}{\mathbb {P}}\lesssim \ell (I)$. Note that (H1) implies $|\nabla {\mathcal {A}}(Y)|^2\lesssim \ell (I)^{-2}$ for every $Y\in {\mathbb {P}}$ since $\delta (Y)\approx \ell (I)$ , hence

$$\begin{aligned} \frac{1}{r^{n-1}}\int _{B(x,r)\cap {\mathbb {P}}}|\nabla {\mathcal {A}}(Y)|^2 \delta _{{\mathbb {P}}}(Y) dY&\lesssim \frac{1}{r^{n-1}\ell (I)^2}\int _{B(x,r)\cap {\mathbb {P}}} \delta _{{\mathbb {P}}}(Y) dY\lesssim \frac{r^{n+1}}{r^{n-1}\ell (I)^2}.\nonumber \\&\lesssim 1. \end{aligned}$$

(9.2)

That is, (H1) in ${\mathbb {P}}$ holds as well. Thus by [KP] (and the slight improvement in [HMT1]), and the fact that chord-arc domains can be approximated by Lipschitz domains, one obtains that the elliptic measure for L relative to ${\mathbb {P}}$ is also of class $A_\infty$ with respect to the surface measure of ${\mathbb {P}}$ and (2) in the previous result holds. On the other hand, [CHMT, Theorem 1.6] asserts that for any uniform domain $\Omega$, and under the assumptions (H1) and (H2), one has that $\omega _L\in A_\infty (\sigma )$ if and only if $\omega _{L^{\mathrm{sym}}}\in A_\infty (\sigma )$ where $L^{\mathrm{sym}}$ is the operator associated with the symmetric matrix ${\mathcal {A}}^\mathrm{sym}=(\frac{a_{ij}+a_{ji}}{2})_{i,j=1}^n$. Note that ${\mathcal {A}}^\mathrm{sym}$ is also a uniformly elliptic matrix in $\Omega$ with the same ellipticity constants as ${\mathcal {A}}$ and satisfies (H1) and (H2) with constants which are controlled by those of ${\mathcal {A}}$. With all these observations we immediately get the following corollary:

Corollary 9.3

Let $\Omega \subset {{\mathbb {R}}}^n$ be a uniform domain with Ahlfors regular boundary. Suppose that ${\mathcal {A}}$ is a (non necessarily symmetric) uniformly elliptic matrix on $\Omega$ satisfying the hypotheses (H1) and (H2), and that the elliptic measure $\omega _L$ associated with the operator L relative to the domain $\Omega$ is of class $A_\infty$ with respect to the surface measure. Then the elliptic measure associated with L relative to any sawtooth domain is of class $A_\infty$, with uniform constants.

Proof of Theorem 9.1

The proof Theorem 9.1 has several steps. We work with $\Omega _*=\Omega _{{\mathcal {F}}, Q}$ as the proof with $\Omega _{{\mathcal {F}}, Q}^*$ is identical. We first assume that the sawtooth domain $\Omega _*=\Omega _{{\mathcal {F}}, Q}$ is compactly contained in $\Omega$ and show that $\omega _*\in A_\infty (\sigma _*)$, with the $A_\infty$ constants independent of Q and ${\mathcal {F}}$. Here we use $\omega _*$ to denote the elliptic measure associated with L relative to $\Omega _*$.

Under the assumption that $\Omega _*$ is compactly contained in $\Omega$, for Q fixed, let N be an integer such that ${\text {dist}}(\Omega _*,\partial \Omega ) \approx 2^{-N} \ell (Q)$. Then $\Omega _*$ if formed by a union of fattened Whitney boxes of side length controlled from below by $c\,2^{-N} \ell (Q)$ hence $\Omega _*$ clearly satisfies a qualitative exterior corkscrew condition, that is, it satisfies the exterior corkscrew condition for surface balls up to a scale of the order of $2^{-N}\ell (Q)$. In the case of the Kenig-Pipher operators, this information alone does not suffice to derive the desired $A_\infty$ property, with constant independent of N; however this does give us the qualitative absolute continuity $\omega _*^X \ll \sigma _*$ for any $X\in \Omega _*$ (since $\Omega _*$ is a chord-arc domain with constants depending on N). Note that Theorem 9.1 is nonetheless written for a more general class and it is not obvious whether we can automatically have the desired absolute continuity. This will be shown in the course of the proof.

Our main task is to then show that $\omega _* \in A_\infty (\sigma _*)$ with constants that depend only on the allowable constants. If we write $\mathbf{k }_*:=d\omega _*/d\sigma _*$ for the Radon-Nikodym derivative, by the change of pole formula Lemma 2.32, obtaining $\omega _* \in A_\infty (\sigma _*)$, it is equivalent to prove the following: there exists an exponent $p\in (1,\infty )$ and a constant C depending only on the allowable constants such that for any surface ball $\Delta _*=B_*\cap \partial \Omega _*$ centered at $\partial \Omega _*$, with radius smaller than the diameter of $\partial \Omega _*$, and for $X=X_{\Delta _*}\in \Omega _*\cap B_*$, a corkscrew point relative to $\Delta _*$, the following holds

$$\begin{aligned} \int _{\Delta _*} \left( \mathbf{k }_*^X\right) ^p d\sigma _* \le C \sigma _*(\Delta _*)^{1-p}. \end{aligned}$$

(9.4)

Since ${{\,\mathrm{diam}\,}}(\Omega _*) \approx \ell (Q)$, it is easy to see by a standard covering argument and Harnack’s inequality that it suffices to prove (9.4) for $r_* \le M_1^{-1} \ell (Q)$, where $M_1$ is a suitably large fixed constant. By hypothesis (1), $\omega _L\in A_\infty (\sigma )$, hence it belongs to the reverse Hölder class with some exponent $p_1>1$ (see (2.12)). Also, by hypothesis (2) we know that the elliptic measure relative to any fundamental chord-arc subdomain ${\mathbb {P}}$ satisfies an $A_\infty$ condition with respect to the corresponding surface measure with uniform bounds. In turn, there exists $p_2>1$ and a uniform constant so that any of these elliptic measures belong to the reverse Hölder class with this exponent $p_2$ and with the same uniform constant (see (2.12)). We shall henceforth set $p:= \min \{p_1,p_2\}$, and it is for this p that we shall prove (9.4).

To start with the proof, recall that as observed above, since ${\text {dist}}(\Omega _*, \partial \Omega ) \approx 2^{-N}\ell (Q)$, it follows that all the dyadic cubes $Q'\in {\mathbb {D}}_{{\mathcal {F}},Q}$ have length $\ell (Q') > rsim 2^{-N}\ell (Q)$, and the cardinality of ${\mathbb {D}}_{{\mathcal {F}},Q}$ is bounded by a constant C(N). Hence $\Omega _*=\Omega _{{\mathcal {F}},Q}$ is formed by the finite union of Whitney regions $U_{Q'}$ with $Q' \in {\mathbb {D}}_{{\mathcal {F}},Q}$ satisfying $\ell (Q') > rsim 2^{-N}\ell (Q)$. In turn each $U_{Q'}$ is a polyhedral domain consisting of a finite number of fattened Whitney boxes with side length of the order of $\ell (Q')$. In particular there exists a finite index set ${\mathcal {N}}_*$ so that

$$\begin{aligned} \partial \Omega _* \subset \bigcup _{i\in {\mathcal {N}}_*} \partial \left( (I^i)^* \right) \cap \partial \Omega _* = : \bigcup _{i\in {\mathcal {N}}_*} S_*^i. \end{aligned}$$

(9.5)

where $S_*^i \ne \emptyset$ for each $i\in {\mathcal {N}}_*$, ${{\,\mathrm{int}\,}}((I^i)^*)\subset \Omega _*$, and $\ell (I^i) > rsim 2^{-N}$. For each $I^i$, with $i\in {\mathcal {N}}_*$, we pick $Q^i\in {\mathbb {D}}_{{\mathcal {F}},Q}$ such that ${\mathcal {W}}_{Q^i} \ni I^i$ (there could be more than one such a $Q^i$ in which case we just select one). Note that different $I^i$’s may correspond to the same $Q^i$, but each $Q^i$ may only repeat up to a finitely many times, depending only on the allowable constants. Since $S_*^i$ is contained in the boundary of a fattened Whitney box $(I^i)^*$,

$$\begin{aligned} {{\,\mathrm{diam}\,}}(S_*^i) \lesssim \ell (I^i) \approx \ell (Q^i), \text { and } {\text {dist}}(S_*^i, \partial \Omega ) \ge {\text {dist}}((I^i)^*, \partial \Omega ) \approx \ell (Q^i). \end{aligned}$$

(9.6)

On the other hand, the fact that $S_*^i \subset \partial \Omega _*$ means that $I^i$ intersects some $J^i\in {\mathcal {W}}$ so that if $J^i\in {\mathcal {W}}_{Q''}$ then $Q'' \notin {\mathbb {D}}_{{\mathcal {F}},Q}$. If we pick ${\widetilde{Q}}^i\in {\mathbb {D}}$ so that $\ell ({\widetilde{Q}}^i)=\ell (J^i)$ and ${\text {dist}}(J^i,\partial \Omega )={\text {dist}}(J^i, {\widetilde{Q}}^i)$ then as mentioned right below (6.12) we have that $J^i\in {\mathcal {W}}^0_{{\widetilde{Q}}^i}\subset {\mathcal {W}}_{{\widetilde{Q}}^i}$, therefore ${\widetilde{Q}}^i\notin {\mathbb {D}}_{{\mathcal {F}},Q}$. Recalling (6.10) and the comments after it, we know that $tJ^i \subset \Omega \setminus \Omega _*$ and $\partial \left( (I^i)^* \right) \cap \partial \Omega _*$ contains an $(n-1)$-dimensional ball with radius of the order of $\min \{\ell (I^i), \ell (J^i)\}\approx \ell (I^i)$. Denote that $(n-1)$-dimensional ball by $\Delta _*^i \subset S_*^i$. This implies, combined with (9.6), that

$$\begin{aligned} r(\Delta _*^i) \approx {{\,\mathrm{diam}\,}}(S_*^i) \approx \ell (I^i) \approx \ell (Q^i) \approx {\text {dist}}(S_*^i, \partial \Omega ) \approx {\text {dist}}(\Delta _*^i, \partial \Omega ). \end{aligned}$$

(9.7)

At this stage we consider several cases. In the Base case, see Lemma 9.9, we treat surface balls $\Delta _*$ with small radii so that $\Delta _*$ is contained in a uniformly bounded union of Whitney cubes of comparable sides. In the case when $\Delta _*$ is large we decompose the intersection of $\Delta _*$ in small pieces to which the base case can be applied (Step 1). We then put all the local estimates together to obtain a global one (Step 2). This requires Lemma 9.33 and to consider several cases to account for all the small pieces.

Let $\Delta _* = B_*\cap \partial \Omega _* \subset \Omega$, with $B_*=B(x_*,r_*)$, $x_*\in \partial \Omega _*$ and $0<r_*<{{\,\mathrm{diam}\,}}(\partial \Omega _*)$. Since $\Omega _*$ is a uniform domain (see Lemma 6.19), we can pick $X_{\Delta _*}\subset B_*\cap \Omega _*$, a Corkscrew point relative to $\Delta _*$ in $\Omega _*$, so that $\delta _*(X):={\text {dist}}(X,\partial \Omega _*) \approx r_*$. Write

$$\begin{aligned} \Delta _* \subset \bigcup _{i\in {\mathcal {N}}_{\Delta _*}} S_*^i, \quad \text { where } {\mathcal {N}}_{\Delta _*}:=\{i\in {\mathcal {N}}_{*}: \Delta _* \cap S_*^i \ne \emptyset \}. \end{aligned}$$

(9.8)

$\square$

Lemma 9.9

(Base case). Using the notation above we have that $\omega _*\ll \sigma _*$ in $\partial \Omega _*$. Moreover if there exists $i\in {\mathcal {N}}_{\Delta _*}$ such that $r_*\le \frac{\tau }{8} \ell (I^i)$⁶ then

$$\begin{aligned} \int _{\Delta _*} \left( {\mathbf{k }}_*^{X_{\Delta _*}} \right) ^p d\sigma _* \lesssim \sigma _*(\Delta _*)^{1-p}\,, \end{aligned}$$

(9.10)

where ${\mathbf{k }}_* := d\omega _*/d\sigma _*$, p is as above, and the implicit constant only depends on the allowable constants.

Proof

We first claim that

$$\begin{aligned} 2\Delta _* \subset \bigcup _{\begin{array}{c} i'\in {\mathcal {N}}_*\\ I^{i'} \cap I^i \ne \varnothing \end{array} } S_*^{i'} \quad \mathrm{and} \quad 2B_*\cap \Omega _* \subset \bigcup _{\begin{array}{c} i'\in {\mathcal {N}}_* \\ I^{i'} \cap I^i \ne \varnothing \end{array} } (I^{i'})^*. \end{aligned}$$

(9.11)

In fact, for any $i' \in {\mathcal {N}}_*$, if $S_*^{i'}$ intersects $2\Delta _*$, or if $2B_*\cap \Omega _*$ intersects $(I^{i'})^*$, then our current assumption gives

$$\begin{aligned} {\text {dist}}\big ( (I^i)^*, (I^{i'})^* \big ) \le {\text {dist}}\big ((I^i)^* \cap 2B_*, (I^{i'})^* \cap 2B_* \big ) \le {{\,\mathrm{diam}\,}}(2B_*) = 4r_*\le \frac{\tau }{2} \ell (I^i), \end{aligned}$$

and thus

$$\begin{aligned} (I^i)^{**} \cap (I^{i'})^{**}\,\supset \, (I^i)^{**} \cap (I^{i'})^*\, \ne \, \emptyset . \end{aligned}$$

By the choice of $\tau$, i.e., by (6.9), we then have $I^i \cap I^{i'} \ne \emptyset$ and the claim is proved. Next, let $m_1$ denote the maximal number of Whitney boxes intersecting $I^i$. Note that $m_1$ only depends on the constructions of the Whitney cubes, hence just on dimension. By relabeling (9.11) we write

$$\begin{aligned} 2\Delta _* \subset \bigcup _{i'=1}^{m_1} S_*^{i'}\quad \mathrm{and} \quad 2B_*\cap \Omega _* \subset \bigcup _{i'=1}^{m_1}(I^{i'})^*. \end{aligned}$$

(9.12)

Moreover by (9.7), for each $i'=1, \dots , m_1$, we have ${{\,\mathrm{diam}\,}}(S_*^{i'}) \approx \ell (I^{i'}) \approx \ell (I^i)$. Set then

$$\begin{aligned}{\mathbb {P}}:= {{\,\mathrm{int}\,}}\left( \bigcup _{i'=1}^{m_1} (I^{i'})^*\right) \subset \Omega _*,\end{aligned}$$

which by construction is a fundamental chord-arc subdomain ${\mathbb {P}}$ of $\Omega$, see (6.20). Note that since $2B_*\cap \Omega _*$ is open then (9.12) says that $2B_*\cap \Omega _* \subset {\mathbb {P}}$ and hence $2B_*\cap \Omega _* =2B_*\cap {\mathbb {P}}$. This and the fact that $\Omega _*$ and ${\mathbb {P}}$ are open readily implies that $2B_*\cap \partial \Omega _* =2B_*\cap \partial {\mathbb {P}}$. Moreover, $X_{\Delta _*}\in {\mathbb {P}}$ (since $X\in B_*\cap \Omega _*$) and

$$\begin{aligned} {\text {dist}}(X_{\Delta _*},\partial {\mathbb {P}}) \approx \delta _*(X_{\Delta _*}) \approx r_*\le \frac{\tau }{8} \ell (I^i) \le \frac{\tau }{8}{{\,\mathrm{diam}\,}}({\mathbb {P}}) \le \,{{\,\mathrm{diam}\,}}({\mathbb {P}}). \end{aligned}$$

(9.13)

Let $X_{{\mathbb {P}}}$ be a Corkscrew point for the domain ${\mathbb {P}}$, at the scale $\ell (I^i) \approx {{\,\mathrm{diam}\,}}({\mathbb {P}})$, i.e., $X_{\mathbb {P}}$ is a Corkscrew point in ${\mathbb {P}}$ relative to the surface ball consisting of the entire boundary of ${\mathbb {P}}$. Thus in particular, ${\text {dist}}(X_{\mathbb {P}},\partial {\mathbb {P}})\approx {{\,\mathrm{diam}\,}}({\mathbb {P}})\ge \frac{8}{\tau } r_*$, hence ${\text {dist}}(X_{\mathbb {P}},\partial {\mathbb {P}})\ge 2\,c_0\,r_*$ for some uniform $0<c_0<1/4$.

Set $u_1(\cdot ):=G_*(X_{{\mathbb {P}}}, \cdot )$ and $u_2(\cdot ):=G_{{\mathbb {P}}}(X_{{\mathbb {P}}},\cdot )$ in $2B_*\cap \Omega _* =2B_*\cap {\mathbb {P}}$ where $G_*$ and $G_{\mathbb {P}}$ are the Green functions for the operator L and for the domains $\Omega _*$ and ${\mathbb {P}}$ respectively, and where as observed above $X_{\mathbb {P}}\in {\mathbb {P}}\subset \Omega _*$. Fix $y\in \frac{3}{2}B_*\cap \partial \Omega _*=\frac{3}{2}B_*\cap \partial {\mathbb {P}}$ and note that $B(y,c_0 r_*)\subset 2B_*$. Note that if $Z\in B(y,c_0 r_*)$ then

$$\begin{aligned} 2\,c_0r_*\le {\text {dist}}(X_{\mathbb {P}},\partial {\mathbb {P}}) \le |X_{\mathbb {P}}-y| \le |X_{\mathbb {P}}-Z|+|Z-y| < |X_{\mathbb {P}}-Z|+c_0 r_*, \end{aligned}$$

and $|X_{\mathbb {P}}-Z|> c_0 r_*$. As a consequence, $B(y,c_0 r_*)\subset 2B_*\setminus B(X_{{\mathbb {P}}}, c_0 r_*)$. Hence, $L u_1=0$ and $L u_2=0$ in we weak sense in $B(y,c_0 r_*)\cap \Omega _* =B(y,c_0 r_*)\cap {\mathbb {P}}$ and both are continuous in $B(y,c_0 r_*)\cap \overline{\Omega _*} =B(y,c_0 r_*)\cap {\overline{{\mathbb {P}}}}$. In particular both vanish continuously in $B(y,c_0 r_*)\cap \partial \Omega _* =B(y,c_0 r_*)\cap \partial {\mathbb {P}}$. This means that we can use Lemma 2.26 in ${\mathcal {D}}={\mathbb {P}}$ to obtain that for every $Z\in B(y, c_0\,r_*/8)$,

$$\begin{aligned} \frac{u_1(Z)}{u_2(Z)} \approx \frac{u_1(X_{\Delta _{\mathbb {P}}(y,c_0 r_*/2)}^{\mathbb {P}})}{u_2(X_{\Delta _{\mathbb {P}}(y,c_0 r_*/2)}^{\mathbb {P}})} \end{aligned}$$

(9.14)

where $X_{\Delta _{\mathbb {P}}(y,c_0 r_*/2)}^{\mathbb {P}}$ is a corkscrew relative to $B(y,c_0 r_*/2)\cap {\overline{{\mathbb {P}}}}$ for the fundamental chord-arc domain ${\mathbb {P}}$. On the other hand Lemma 2.35 applied in $\Omega _*$ (which is uniform with Ahlfors regular boundary and the implicit constants are uniformly controlled, see Lemma 6.19) and ${\mathbb {P}}$ (a fundamental chord-arc domain) gives for any $0<s\le c_0 r_*/2$,

$$\begin{aligned} u_1(X_{\Delta _*(y,s)}^*)\approx \omega _*^{X_{{\mathbb {P}}}}(\Delta _*(y,s))\,s^{n-2}, \qquad u_2(X_{\Delta _{\mathbb {P}}(y,s)}^{\mathbb {P}})\approx \omega _{\mathbb {P}}^{X_{{\mathbb {P}}}}(\Delta _{\mathbb {P}}(y,s))\,s^{n-2}, \end{aligned}$$

(9.15)

where $X_{\Delta _*(y,s)}^*$ is the corkscrew point relative to $\Delta _*(y,s)= B(y,s)\cap \partial \Omega _*$ for the uniform domain $\Omega _*$, $X_{\Delta _{\mathbb {P}}(y,s)}^{\mathbb {P}}$ is the corkscrew point relative to $\Delta _{\mathbb {P}}(y,s)= B(y,s)\cap \partial {\mathbb {P}}$ for the fundamental chord-arc uniform domain ${\mathbb {P}}$, and $\omega _{\mathbb {P}}$ stands for the elliptic measure associated with the operator L relative to ${\mathbb {P}}$. Note that from the definition of corkscrew condition and the fact that $B(y,s)\cap \Omega _*=B(y,s)\cap {\mathbb {P}}$ it follows that $X_{\Delta _*(y,s)}^*, X_{\Delta _{\mathbb {P}}(y,s)}^*\in B(y,s)\cap \Omega _*=B(y,s)\cap {\mathbb {P}}$ and also

$$\begin{aligned} {\text {dist}}(X_{\Delta _*(y,s)}^*, \partial \Omega _*)\approx {\text {dist}}(X_{\Delta _*(y,s)}^*, \partial {\mathbb {P}})\approx {\text {dist}}(X_{\Delta _{\mathbb {P}}(y,s)}^{\mathbb {P}}, \partial \Omega _*)\approx {\text {dist}}(X_{\Delta _{\mathbb {P}}(y,s)}^{\mathbb {P}}, \partial {\mathbb {P}})\approx s. \end{aligned}$$

Consequently $u_1(X_{\Delta _*(y,s)}^*)\approx u_1(X_{\Delta _{\mathbb {P}}(y,s)}^{\mathbb {P}})$ and $u_1(X_{\Delta _{\mathbb {P}}(y,c_0 r_*/2)}^{\mathbb {P}})\approx u_1(X_{\Delta _*(y,c_0 r_*/2)}^*)$. All these, together with (9.14), (9.15), and Lemma 2.28, give for every $0<s\le c_0 r_*/8$,

$$\begin{aligned}&\frac{\omega _*^{X_{{\mathbb {P}}}}(\Delta _*(y,s))}{\omega _{\mathbb {P}}^{X_{{\mathbb {P}}}}(\Delta _{\mathbb {P}}(y,s))}\nonumber \\&\quad \approx \frac{u_1(X_{\Delta _*(y,s)}^*)}{u_2(X_{\Delta _{\mathbb {P}}(y,s)}^{\mathbb {P}})} \approx \frac{u_1(X_{\Delta _{\mathbb {P}}(y,s)}^{\mathbb {P}})}{u_2(X_{\Delta _{\mathbb {P}}(y,s)}^{\mathbb {P}})} \approx \frac{u_1(X_{\Delta _{\mathbb {P}}(y,c_0 r_*/2)}^{\mathbb {P}})}{u_2(X_{\Delta _{\mathbb {P}}(y,c_0 r_*/2)}^{\mathbb {P}}))} \nonumber \\&\quad \approx \frac{u_1(X_{\Delta _*(y,c_0 r_*/2)}^*)}{u_2(X_{\Delta _{\mathbb {P}}(y,c_0 r_*/2)}^{\mathbb {P}}))} \approx \frac{\omega _*^{X_{\Delta _*(y,c_0 r_*/2)}}(\Delta _*(y,c_0 r_*/2))}{\omega _{\mathbb {P}}^{X_{\Delta _{\mathbb {P}}(y,c_0 r_*/2)}}(\Delta _{\mathbb {P}}(y,c_0r_*/2))} \approx 1 . \end{aligned}$$

(9.16)

With this in hand, we note that since $y\in \Delta _*(x_*,\frac{3}{2}r_*)=\frac{3}{2}B_*\cap \partial \Omega _*=\frac{3}{2}B_*\cap \partial {\mathbb {P}}=\ \Delta _{\mathbb {P}}(x_*,\frac{3}{2}r_*)$ and $0<s\le c_0 r_*/8$ are arbitrary we can easily conclude, using a Vitali covering argument and the fact that both $\omega _*^{X_{{\mathbb {P}}}}$ and $\omega _{\mathbb {P}}^{X_{{\mathbb {P}}}}$ are outer regular and doubling in $\Delta _*(x_*,\frac{3}{2}r_*)=\Delta _{\mathbb {P}}(x_*,\frac{3}{2}r_*)$, that $\omega _*^{X_{{\mathbb {P}}}}(F)\approx \omega _{\mathbb {P}}^{X_{{\mathbb {P}}}}(F)$ for any Borel set $F\subset \Delta _*(x_*,\frac{3}{2}r_*)=\Delta _{\mathbb {P}}(x_*,\frac{3}{2}r_*)$. Hence $\omega _*^{X_{{\mathbb {P}}}}\ll \omega _{\mathbb {P}}^{X_{{\mathbb {P}}}} \ll \omega _*^{X_{{\mathbb {P}}}}$ in $\Delta _*(x_*,\frac{3}{2}r_*)=\Delta _{\mathbb {P}}(x_*,\frac{3}{2}r_*)$. From hypothesis (2) in Theorem 9.1 we know that $\omega _{\mathbb {P}}\ll \sigma _{\mathbb {P}}:={\mathcal {H}}^{n-1}|_{\partial {\mathbb {P}}}$, hence in particular $\omega _*\ll \sigma _*$ in $\Delta _*(x_*,\frac{3}{2}r_*)$. This, (9.16), and Lebesgue’s differentiation theorem readily imply that

$$\begin{aligned} \mathbf{k }_*^{X_{{\mathbb {P}}}} (y) \approx \mathbf{k }_{{\mathbb {P}}}^{X_{{\mathbb {P}}}}(y), \quad \text {for }{\mathcal {H}}^{n-1}\text {-almost all } y\in \Delta _*(x_*,r_*)=\Delta _{\mathbb {P}}(x_*,r_*), \end{aligned}$$

(9.17)

where $\mathbf{k }_{\mathbb {P}}:= d\omega _{\mathbb {P}}/d\sigma _{\mathbb {P}}$ and $\mathbf{k }_* := d\omega _*/d\sigma _{\mathbb {P}}$.

We next observe that Lemma 2.32 applied with ${\mathcal {D}}=\Omega _*$ (along with Harnack’s inequality for the case $r_*\approx \ell (I^i)$) and Lebesgue’s differentiation theorem yield

$$\begin{aligned} \mathbf{k }_*^{X_{\Delta _*}}(y) \approx \frac{1}{\omega _*^{X_{\mathbb {P}}}(\Delta _*)} \, \mathbf{k }_*^{X_{{\mathbb {P}}}}(y)\quad \text {for }\sigma _*\text {-almost all } y\in \Delta _*. \end{aligned}$$

(9.18)

Since ${\mathbb {P}}$ is a fundamental chord-arc subdomain ${\mathbb {P}}$ of $\Omega$, see (6.20), as observed above $\omega _{\mathbb {P}}$ belongs to the reverse Hölder class with exponent $p_2>1$ and so with exponent $p= \min \{p_1, p_2\}$. We find that since ${\sigma _*} ={\sigma _{\mathbb {P}}}$ in $\Delta _*=\Delta _*(x_*,r_*)=\Delta _{{\mathbb {P}}}(x_*,r_*)$,

where we have used (9.18), (9.17), that ${\sigma _*} ={\sigma _{\mathbb {P}}}$, the reverse Hölder estimate with exponent p for $\mathbf{k }_{\mathbb {P}}$, and that both $\partial \Omega _*$ and $\partial {\mathbb {P}}$ are Ahlfors regular sets with uniform bounds.

To complete our proof we need to see that $\omega _*\ll \sigma _*$ in $\partial \Omega _*$. Let us observe that we have already obtained that $\omega _*\ll \sigma _*$ in $\Delta _*(x_*,\frac{3}{2}r_*)$ where $x_*\in \partial \Omega _*$ is arbitrary and $r_*\le \frac{\tau }{8}\ell (I^i)$ for some $i\in {\mathcal {N}}_{\Delta _*}$. We may cover $\partial \Omega _*$ by a finite union of surface balls $\Delta _*(x_j, r_j)$, with $r_j=\frac{2^{-N}}{{\tilde{M}}}\ell (Q)$, where ${\widetilde{M}}$ is large enough to be chosen, whose cardinality may depend on N and ${\widetilde{M}}$. Note that for every $i\in {\mathcal {N}}_*$ we have, as observed before, that $\ell (I^i) > rsim 2^{-N}\ell (Q)> \frac{8}{\tau } \frac{2^{-N}}{{\tilde{M}}}\ell (Q)$ if we pick ${\widetilde{M}}$ large enough. Hence, for every j, it follows that $r_j<\frac{\tau }{8}\ell (I^i)$ for every $i\in {\mathcal {N}}_*$ and in particular for every $i\in {\mathcal {N}}_{\Delta _*(x_j,r_j)}$. Hence the previous argument yields that $\omega _*\ll \sigma _*$ in $\Delta _*(x_j,\frac{3}{2}r_j)$ for every j and consequently $\omega _*\ll \sigma _*$ in $\partial \Omega _*$. $\square$

Remark 9.19

We would like to emphasize that the fact that $\omega _*\ll \sigma _*$ in $\partial \Omega _*$ is automatic for the Kenig-Pipher operators. In fact as observed above $\Omega _*$ is a chord-arc domain and hence $\omega _*\in A_\infty (\sigma _*)$ (albeit with constants which may depend on N). The previous argument proves that the more general hypothesis (2) in Theorem 9.1 also yields $\omega _*\ll \sigma _*$ in $\partial \Omega _*$.

Once the Base case has been established we can focus on proving the $A_\infty$ property for the sawtooth. With this goal in mind we fix a surface ball $\Delta _* = B_*\cap \partial \Omega _* \subset \Omega$, with $B_*=B(x_*,r_*)$, $x_*\in \partial \Omega _*$ and $0<r_*<{{\,\mathrm{diam}\,}}(\partial \Omega _*)$. Let $X:=X_{\Delta _*}\subset B_*\cap \Omega _*$ be a Corkscrew point relative to $\Delta _*$ in $\Omega _*$, so that $\delta _*(X) \approx r_*$. Our goal is to show (9.4). As explained above we may assume that $r_* \le M_1^{-1} \ell (Q)$, for some $M_1$ large enough to be chosen. The Base case (Lemma 9.9) yields (9.4) when $r_* <\frac{\tau }{8} \ell (I^i)$ for some $i\in {\mathcal {N}}_{\Delta _*}$. Hence we may assume from now on that $r_* \ge \frac{\tau }{8} \ell (I^i)$ for every $i\in {\mathcal {N}}_{\Delta _*}$.

Step 1. Show that

$$\begin{aligned} \int _{\Delta _*} \left( \mathbf{k }_*^X \right) ^p d\sigma _* \lesssim \sum _{i\in {\mathcal {N}}_{\Delta _*}} \int _{Q^i} \left( \mathbf{k }^X \right) ^p d\sigma , \end{aligned}$$

(9.20)

where we recall that $Q^i\in {\mathbb {D}}_{{\mathcal {F}},Q}$ is so that $I^i\in {\mathcal {W}}_{Q^i}$ for every $i\in {\mathcal {N}}_{*}$, and where $\mathbf{k }=d\omega _L/d\sigma$.

To see this, by (9.8), it suffices to obtain

$$\begin{aligned} \int _{S_*^i} \left( \mathbf{k }_*^X \right) ^p d\sigma _* \lesssim \int _{Q^i} \left( \mathbf{k }^X \right) ^p d\sigma . \end{aligned}$$

(9.21)

for each $i\in {\mathcal {N}}_{\Delta _*}$. Fix then such an i and cover $S_*^i$ by a uniformly bounded number of surface balls centered at $\partial \Omega _*$ with small radius $\Delta _*^{i,l}=B_*^{i,l}\cap \partial \Omega _*$ where $S_*^i \cap \Delta _*^{i,l} \ne \emptyset$ and $r(\Delta _*^{i,l}) \approx c {{\,\mathrm{diam}\,}}(S_*^i)\approx c\,\ell (I^i)$, the constant c is chosen sufficiently small (depending on $\tau$), so that $r(\Delta _*^{i,l})\ll (\tau /8)\ell (I^i)$. Hence in the present scenario,

$$\begin{aligned} \delta _*(X)\approx r_* \gg r(\Delta _*^{i,l})\,. \end{aligned}$$

(9.22)

We further choose c small enough so that

$$\begin{aligned} 2\Delta _*^{i,l} \subset \bigcup _{\begin{array}{c} i'\in {\mathcal {N}}_* \\ I^{i'} \cap I^i\ne \varnothing \end{array} } S_*^{i'}\quad {\mathrm{and}} \quad 2B^{i,l}_*\cap \Omega _* \subset \bigcup _{\begin{array}{c} i'\in {\mathcal {N}}_* \\ I^{i'} \cap I^i \ne \varnothing \end{array} } (I^{i'})^*. \end{aligned}$$

(9.23)

Note that there are at most a uniformly bounded number of such $i'$, for each l. In each $\Delta _*^{i,l}$ we can use the Base Case, Lemma 9.9, since by construction $r(\Delta _*^{i,l})\ll (\tau /8)\ell (I^i)$ and hence (9.10) implies that

$$\begin{aligned} \int _{\Delta _*^{i,l}} \Big ( \mathbf{k }_*^{X_{\Delta _*^{i,l}}} \Big )^p d\sigma _* \lesssim \sigma _*(\Delta _*^{i,l})^{1-p}. \end{aligned}$$

(9.24)

where $X_{\Delta _*^{i,l}}$ is a corkscrew point relative to $\Delta _*^{i,l}$ in $\Omega _*$. Using Lemma 2.32 applied with ${\mathcal {D}}=\Omega _*$ and Lebesgue’s differentiation theorem we have that $\mathbf{k }_*^{X}(y)\approx \omega _*^X(\Delta _*^{i,l})\,\mathbf{k }_*^{X_{\Delta _*^{i,l}}}(y)$ for $\sigma _*$-a.e. $y\in \Delta _*^{i,l}$. As a result, using (9.24),

$$\begin{aligned} \int _{\Delta _*^{i,l}} \big ( \mathbf{k }_*^X \big )^p d\sigma _*\approx & {} \big (\omega ^X_*(\Delta _*^{i,l})\big )^p \int _{\Delta _*^{i,l}} \Big ( \mathbf{k }_*^{X_{\Delta _*^{i,l}}} \Big )^p d\sigma _* \lesssim \big (\omega ^X_*(\Delta _*^{i,l})\big )^p\,\sigma _*(\Delta _*^{i,l})^{1-p} \nonumber \\= & {} \sigma _*(\Delta _*^{i,l}) \left( \frac{\omega _*^X(\Delta _*^{i,l})}{\sigma _*(\Delta _*^{i,l}) } \right) ^p \lesssim \sigma _*(\Delta _*^i) \left( \frac{\omega _*^X(\Delta _*^{i})}{\sigma _*(\Delta _*^{i}) } \right) ^p , \end{aligned}$$

(9.25)

where we used the Ahlfors regularity of $\sigma _*$ and the doubling properties of $\omega _*$. We claim that

$$\begin{aligned} \frac{\omega _*^X(\Delta _*^{i})}{\sigma _*(\Delta _*^{i}) } \lesssim \frac{ \omega ^X(Q^i) }{\sigma (Q^i)}. \end{aligned}$$

(9.26)

To see this write $u_1(Y)=\omega ^Y_*(\Delta _*^{i} )$ and $u_2(Y)=\omega ^Y(Q^i)$ for every $Y\in \Omega _*$ and note that $L u_1=L u_2=0$ in $\Omega _*\subset \Omega$. For $Y\in \Delta _*^{i}\subset \overline{\Omega _*}\subset \Omega$ we have $u_2(Y) > rsim 1$ by Lemma 2.28 applied in ${\mathcal {D}}=\Omega$, Harnack’s inequality, (9.7), and (6.14). Thus the maximum principle applied in the bounded open set $\Omega _*$ yields that $u_1(Y)\lesssim u_2(Y)$ for every $Y\in \Omega _*$, hence in particular for $Y=X$. This and the fact that $\partial \Omega$ and $\partial \Omega _*$ are Ahlfors regular (see Lemma 6.19) give as desired (9.26).

Combining (9.25) and (9.26), and using Hölder’s inequality and Ahlfors regularity of $\sigma , \sigma _*$, we get

$$\begin{aligned} \int _{\Delta _*^{i,l}} \left( \mathbf{k }_*^X \right) ^p d\sigma _* \lesssim \sigma (Q^i) \left( \frac{ \omega ^X(Q^i) }{\sigma (Q^i)} \right) ^p \lesssim \int _{Q^i} \left( \mathbf{k }^X \right) ^p d\sigma . \end{aligned}$$

(9.27)

We recall that $S_*^i$ is covered by a uniformly bounded number of surface balls $\Delta _*^{i,l}$. Thus summing in l we conclude (9.21) as desired. This completes Step 1.

Step 2. Study the interaction of the elements of the family $\{Q^i: i\in {\mathcal {N}}_{\Delta _*}\}$.

Recall that $Q \in {\mathbb {D}}$ is the fixed cube in $\partial \Omega$ we start with so that $\Omega _* = \Omega _{{\mathcal {F}}, Q}$, and that $Q^i \in {\mathbb {D}}_{{\mathcal {F}}, Q}$. We first note that for every $i\in {\mathcal {N}}_{\Delta _*}$

$$\begin{aligned} {\text {dist}}(\Delta _*, Q) \le {\text {dist}}(S_*^i\cap \Delta _*,Q) \lesssim \ell (Q^i)\approx \ell (I^i)\lesssim r_*. \end{aligned}$$

(9.28)

Pick ${{\hat{x}}}\in {{\overline{Q}}}$ such that ${\text {dist}}({{\hat{x}}}, \Delta _*) = {\text {dist}}(Q, \Delta _*)$. If ${\hat{x}}\in {{\overline{Q}}} \setminus Q$, we replace it by a point, which we call again ${{\hat{x}}}$, belonging to $B({{\hat{x}}}, r_*/2) \cap Q$, so that ${{\hat{x}}} \in Q$ and ${\text {dist}}({{\hat{x}}}, \Delta _*) \lesssim r_*$. We claim that there is a large constant $C>1$ such that $Q^i \subset \Delta _1$ where $\Delta _1:=B({{\hat{x}}}, Cr_*)\cap \partial \Omega$. Indeed if $y\in Q^i$ then

$$\begin{aligned} |y-{{\hat{x}}}|\le {{\,\mathrm{diam}\,}}(Q^i)+{\text {dist}}(Q^i, I^i)+{{\,\mathrm{diam}\,}}(I^i)+|y^i-{{\hat{x}}}|\lesssim r_*, \end{aligned}$$

where we have picked $y^i \in S_*^i \cap \Delta _*$ for each $i\in {\mathcal {N}}_{\Delta _*}$.

Consider next the covering $\Delta _1\subset \cup _{k=1}^{N_1} P_k$, where $N_1$ depends on Ahlfors regularity and dimension, and $\{P_k\}_{k=1}^{N_1}$ is a pairwise disjoint collection of dyadic cubes on $\partial \Omega$, of the same generation, with length $\ell (P_k)\approx r_*$. Since in the present scenario, $\ell (Q^i) \lesssim r_*$, we may further suppose that $\ell (P_k) \ge \ell (Q^i)$ for every i. Moreover, since we have assumed that $r_* \le M_1^{-1} \ell (Q)$, taking $M_1$ large enough we may assume that $\ell (P_k)\le \ell (Q)$ for every $1\le k\le N_1$.

Note that

$$\begin{aligned} \bigcup _{i\in {\mathcal {N}}_{\Delta _*}} Q^i \subset \Delta _1 \subset \bigcup _{k=1}^{N_1} P_k.\end{aligned}$$

By relabeling if needed, we may assume that there exists $N_2$, $1\le N_2\le N_1$, such that $P_k$ meets some $Q^i$, $i\in {\mathcal {N}}_{\Delta _*}$, for each $1\le k\le N_2$. Hence $\bigcup _{i\in {\mathcal {N}}_{\Delta _*}} Q^i \subset \bigcup _{k=2}^{N_2} P_k$ and, necessarily, $Q^i\subset P_k\subset Q$, and since $Q^i \in {\mathbb {D}}_{{\mathcal {F}},Q}$, it follows that $P_k\in {\mathbb {D}}_{{\mathcal {F}},Q}$ for $1\le k\le N_2$.

For future reference, we record the following observation. Recall that X is a Corkscrew point relative to $\Delta _*=B_*\cap \partial \Omega _*$, for the domain $\Omega _*$; i.e., $X\in B_*\cap \Omega _*$, with $\delta _*(X) \approx r_*$. By (9.28) and for every $1\le k\le N_2$ if we pick some i so that $Q^i\subset P_k$ we have

$$\begin{aligned} r_*&\approx \delta _*(X) \le \delta (X) \le {\text {dist}}(X,P_k) \le {\text {dist}}(X, Q^i) \\&\le |X-x_*|+2\,r_*+{\text {dist}}(\Delta _*, Q_i) \lesssim r_* \approx \ell (P_k). \end{aligned}$$

Recalling that $X_{P_k}$ denotes a corkscrew point relative to the dyadic cube $P_k$ we then have that $\delta (X)\approx \ell (P_k)\approx \delta (X_{P_k})$ and also $|X-X_{P_k}|\lesssim \ell (P_k)$, hence by Harnack’s inequality $\omega ^X\approx \omega ^{X_{P_k}}$ and eventually $\mathbf{k }^X\approx \mathbf{k }^{X_{P_k}}$, $\sigma$-a.e. in $\partial \Omega$. On the other hand, we have already mentioned that hypothesis (1) in Theorem 9.1 says that $\omega \in RH_{p_1}(\sigma )$, which clearly implies $\omega \in RH_{p}(\sigma )$ since $p\le p_1$. Note that this reverse Hölder condition is written for surface balls, but it is straightforward to see, using Lemmas 6.1 and 2.37, that the same reverse Hölder estimates hold for any dyadic cube. All these, and the fact that both $\partial \Omega$ and $\partial \Omega _*$ are Ahlfors regular (see Lemma 6.19) lead to

$$\begin{aligned} \int _{P_k} \Big (\mathbf{k }^{X_{P_k}}\Big )^{p} d\sigma \lesssim \sigma (P_k)\bigg (\frac{\omega ^{{X_{P_k}}}(P_k)}{\sigma (P_k)}\bigg )^p \le \sigma (P_k)^{1-p} \approx \sigma _*(\Delta _*)^{1-p}\,, \end{aligned}$$

(9.29)

for each k, with uniform implicit constants.

As mentioned above, for every $i\in {\mathcal {N}}_*$, there exists $J^i\in {\mathcal {W}}$ so that $I^i\cap J^i\ne \emptyset$ and so that if we pick ${\widetilde{Q}}^i\in {\mathbb {D}}$ with $\ell ({\widetilde{Q}}^i)=\ell (J^i)$ and ${\text {dist}}(J^i,\partial \Omega )={\text {dist}}(J^i, {\widetilde{Q}}^i)$ then ${\widetilde{Q}}^i\notin {\mathbb {D}}_{{\mathcal {F}},Q}$. In particular

$$\begin{aligned} \ell ({\widetilde{Q}}^i) \approx \ell (Q^i)\quad \text { and }\quad {\text {dist}}({\widetilde{Q}}^i, Q^i) \lesssim \ell (Q^i). \end{aligned}$$

(9.30)

By the definition of ${\mathbb {D}}_{{\mathcal {F}},Q}$, ${\widetilde{Q}}^i \notin {\mathbb {D}}_{{\mathcal {F}},Q}$ means either ${\widetilde{Q}}^i \subset \partial \Omega \setminus Q$, or ${\widetilde{Q}}^i \subset Q_j$, for some $Q_j\in {\mathcal {F}}$. Given $1 \le k\le N_2$, for each $i\in {\mathcal {N}}_{\Delta _*}$, we say $i\in {\mathcal {N}}_0(k)$, if the first case happens, with $Q^i\subset P_k$; and if the second case happens with $Q_j\in {\mathcal {F}}$, and with $Q^i\subset P_k$, we say $i\in {\mathcal {N}}_j(k)$. For the second case we remark that

$$\begin{aligned} {\text {dist}}(Q_j, P_k) \le {\text {dist}}({\widetilde{Q}}^i, Q^i) \lesssim \ell (Q^i) \le \ell (P_k). \end{aligned}$$

(9.31)

For each k, $1\le k\le N_2$, we set

$$\begin{aligned} {\mathcal {F}}_1(k):=\{Q_j\in {\mathcal {F}}: \exists \, i\in {\mathcal {N}}_j(k),\ \ell (Q_j) \ge \ell (P_k)\} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {F}}_2(k):=\{Q_j\in {\mathcal {F}}: \exists \, i\in {\mathcal {N}}_j(k),\ \ell (Q_j) <\ell (P_k)\}. \end{aligned}$$

With the previous notation, (9.20), and the fact that $\bigcup _{i\in {\mathcal {N}}_{\Delta _*}} Q^i \subset \bigcup _{k=2}^{N_2} P_k$ we obtain

$$\begin{aligned} \int _{\Delta _*} \left( \mathbf{k }_*^X \right) ^p d\sigma _*&\lesssim \sum _{i\in {\mathcal {N}}_{\Delta _*}} \int _{Q^i} \left( \mathbf{k }^X \right) ^p d\sigma \nonumber \\&\le \sum _{k=1}^{N_2} \Bigg (\sum _{i\in {\mathcal {N}}_0(k)}\int _{Q^i} \left( \mathbf{k }^X \right) ^p d\sigma +\sum _{Q_j\in {\mathcal {F}}}\sum _{i\in {\mathcal {N}}_j(k)}\int _{Q^i} \left( \mathbf{k }^X \right) ^p d\sigma \bigg ) \nonumber \\&\lesssim \sum _{k=1}^{N_2} \Bigg (\sum _{i\in {\mathcal {N}}_0(k)}\int _{Q^i} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma +\sum _{Q_j\in {\mathcal {F}}_1(k)}\sum _{i\in {\mathcal {N}}_j(k)}\int _{Q^i} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma \nonumber \\&\quad + \sum _{Q_j\in {\mathcal {F}}_2(k)}\sum _{i\in {\mathcal {N}}_j(k)}\int _{Q^i} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma \bigg ) , \end{aligned}$$

(9.32)

where we have used that $\mathbf{k }^X\approx \mathbf{k }^{X_{P_k}}$, $\sigma$-a.e. in $\partial \Omega$.

At this stage we need the following lemma. We defer its proof until later.

Lemma 9.33

Let ${\mathcal {D}}$ be an open set with Ahlfors regular boundary and write $\sigma ={\mathcal {H}}^{n-1}|_{\partial {\mathcal {D}}}$. Let $Q\in {\mathbb {D}}={\mathbb {D}}(\partial {\mathcal {D}})$ and suppose that ${\mathbb {D}}'\subset {\mathbb {D}}$ is such that each $Q'\in {\mathbb {D}}'$ satisfies one of the following conditions for some $C_1\ge 1$:

• $Q' \subset Q$ and ${\text {dist}}(Q',\partial \Omega \setminus Q) \le C_1 \ell (Q')$.

• $Q' \cap Q = \emptyset$, $\ell (Q') \le C_1 \ell (Q)$ and ${\text {dist}}(Q', Q) \le C_1 \ell (Q')$.

Then there is a subcollection of distinct cubes $\{{\widetilde{Q}}_m\}_{m=1}^{N_2}\subset {\mathbb {D}}$, all of the same generation, with $N_2 = N_2(n,C_{AR}, C_1)$, satisfying $\ell (Q)\le \ell ({{\widetilde{Q}}}_m) \le C_2 \ell (Q)$ and ${\text {dist}}({\widetilde{Q}}_m,Q) \le C_2\ell (Q)$, with $C_2 = C_2(n,C_{AR}, C_1)$, for every m, such that for any $s>1$ if $0\le h\in L_{\mathrm{loc}}^s(\partial {\mathcal {D}},\sigma )$ then

(9.34)

where $C_3=C_3(n,C_{AR}, C_1,s)$.

As a consequence, if there exists $C_1'$ so that for each m, $1\le m\le N_2$, there holds

(9.35)

then

$$\begin{aligned} \sum _{Q' \in {\mathbb {D}}'} \int _{Q'} h d\sigma \le C_3' \sum _{m=1}^{N_2} \int _{{{\widetilde{Q}}}_m } h d\sigma \end{aligned}$$

(9.36)

with $C_3'=C_3'(n,C_{AR}, C_1,s, C_1')$.

Remark 9.37

It follows from the proof of that if $Q'\subset Q$ for all $Q'\in {\mathbb {D}}'$ (i.e., we only consider the first case), then there is only one ${\widetilde{Q}}_m$, namely the unique one containing Q satisfying the given conditions.

Remark 9.38

Suppose that we are under the assumptions of the previous result. Assume further that ${\mathcal {D}}$ is a uniform domain with Ahlfors regular boundary and that $\omega _L\in RH_p(\sigma )$. Then, if $\mathbf{k }_L=d\omega _L/d\sigma$ it follows that

$$\begin{aligned} \sum _{Q' \in {\mathbb {D}}'} \int _{Q'} \left( \mathbf{k }_L^{X_Q}\right) ^p d\sigma \lesssim \int _{Q} \left( \mathbf{k }^{X_Q} \right) ^p d\sigma , \end{aligned}$$

(9.39)

with an implicit constant depending on the allowable constants of ${\mathcal {D}}$, $C_1$, p, and the implicit constant in the condition $\omega _L\in RH_p(\sigma )$.

To see this we recall that from Gehring’s Lemma it follows that there exists $s>1$ such that $\omega _L\in RH_{ps}(\sigma )$. This, combined with Harnack’s inequality, implies that (9.35) holds with $h=\big (\mathbf{k }_L^{X_Q}\big )^p$. As a result (9.36) readily gives (9.39):

$$\begin{aligned} \sum _{Q' \in {\mathbb {D}}'} \int _{Q'}\left( \mathbf{k }_L^{X_Q}\right) ^pd\sigma\lesssim & {} \sum _{m=1}^{N_2} \int _{{{\widetilde{Q}}}_m } \left( \mathbf{k }_L^{X_Q}\right) ^p d\sigma \approx \sum _{m=1}^{N_2} \int _{{{\widetilde{Q}}}_m } \left( \mathbf{k }_L^{X_{\widetilde{Q}_m}}\right) ^p d\sigma \\\lesssim & {} \sum _{m=1}^{N_2} \sigma ({{\widetilde{Q}}}_m)^{1-p} \lesssim \sigma (Q)^{1-p}, \end{aligned}$$

where we have used Harnack’s inequality (to change the pole of the elliptic measure from $X_Q$ to $X_{{{\widetilde{Q}}}_m}$ and the fact that $N_2$ is uniformly bounded).

We will use the previous remark to estimate (9.32). Fixed then $1\le k\le N_2$ and we split the proof in three different steps.

Step 2.1. Estimate for ${\mathcal {N}}_0(k)$.

If $i\in {\mathcal {N}}_0(k)$ we have ${\widetilde{Q}}^i \subset \partial \Omega \setminus Q \subset \partial \Omega \setminus P_k$ and

$$\begin{aligned} {\text {dist}}(Q^i, \partial \Omega \setminus P_k) \le {\text {dist}}(Q^i, {\widetilde{Q}}^i) \lesssim \ell (Q^i). \end{aligned}$$

Since $Q^i \subset P_k$, we may apply Lemma 9.33 to $P_k$ and the collection ${\mathbb {D}}' := \{Q^i: i\in {\mathcal {N}}_0(k)\}$ (note that we are in the first scenario), to obtain by Remark 9.38

$$\begin{aligned} \sum _{i\in {\mathcal {N}}_0(k)} \int _{Q^i} \left( \mathbf{k }^{X_{P_k}}\right) ^p d\sigma \lesssim \int _{P_k} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma \lesssim \sigma _*(\Delta _*)^{1-p}, \end{aligned}$$

(9.40)

where in the last inequality we have used (9.29).

Step 2.2. Estimate for $Q_j\in {\mathcal {F}}_1(k)$.

By (9.31), the cardinality of ${\mathcal {F}}_1(k)$ is uniformly bounded. Moreover, for each $Q_j\in {\mathcal {F}}_1(k)$ we necessarily have $Q_j \cap P_k = \emptyset$, since otherwise, the condition $\ell (Q_j) \ge \ell (P_k)$ guarantees that $P_k\subset Q_j$, and thus $Q^i \subset P_k \subset Q_j\in {\mathcal {F}}$. This contradicts that $Q^i \in {\mathbb {D}}_{{\mathcal {F}},Q}$. On the other hand $Q_j \cap P_k = \emptyset$ implies ${\widetilde{Q}}^i\subset Q_j\subset \partial \Omega \setminus P_k$, for each $i\in {\mathcal {N}}_j(k)$. Combined with (9.30), this yields

$$\begin{aligned} {\text {dist}}(Q^i, \partial \Omega \setminus P_k) \le {\text {dist}}(Q^i, {\widetilde{Q}}^i) \lesssim \ell (Q^i). \end{aligned}$$

Applying Lemma 9.33 to $P_k$ and the collection ${\mathbb {D}}' = \{Q^i: i\in {\mathcal {N}}_j(k)\}$ (note that we are in the first scenario), we obtain from (9.39)

$$\begin{aligned} \sum _{i\in {\mathcal {N}}_j(k)} \int _{Q^i} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma \lesssim \int _{P_k} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma \lesssim \sigma _*(\Delta _*)^{1-p}, \end{aligned}$$

(9.41)

where again we have used (9.29). The above estimate holds for each $Q_j\in {\mathcal {F}}_1(k)$, which as uniformly bounded cardinality, hence

$$\begin{aligned} \sum _{Q_j\in {\mathcal {F}}_1(k)} \sum _{i\in {\mathcal {N}}_j(k)} \int _{Q^i} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma \lesssim \sigma _*(\Delta _*)^{1-p}. \end{aligned}$$

(9.42)

Step 2.3. Estimate for $Q_j\in {\mathcal {F}}_2(k)$.

For each $Q_j\in {\mathcal {F}}_2(k)$ we claim that

$$\begin{aligned} \sum _{i\in {\mathcal {N}}_j(k)} \int _{Q^i} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma \lesssim \int _{Q_j} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma . \end{aligned}$$

(9.43)

In fact, for each $i\in {\mathcal {N}}_j(k)$, by (9.30) and ${\widetilde{Q}}^i \subset Q_j$, we have

$$\begin{aligned} \ell (Q^i) \approx \ell ({\widetilde{Q}}^i) \le \ell (Q_j). \end{aligned}$$

(9.44)

Since $Q^i \in {\mathbb {D}}_{{\mathcal {F}},Q}$, we either have $Q^i \cap Q_j = \emptyset$, or $Q_j \subsetneq Q^i$. In the first case, note that

$$\begin{aligned} {\text {dist}}(Q^i,Q_j) \le {\text {dist}}(Q^i,{\widetilde{Q}}^i))\lesssim \ell (Q^i), \end{aligned}$$

hence $Q^i\cup Q_j\subset \Delta (x_{Q_j}, C\,\ell (Q_j))$ which $x_{Q_j}$ being the center of $Q_j$ an a uniform constant C. By Lemma 2.32 applied with ${\mathcal {D}}=\Omega$ (or Harnack’s inequality if $\ell (Q_j)\approx \ell (P_k)$), Lebesgue’s differentiation theorem, Lemma 2.37, and Harnack’s inequality one can see that

$$\begin{aligned} \mathbf{k }^{X_{P_k}}(y)\approx \omega ^{X_{P_k}}(Q_j)\, \mathbf{k }^{X_{Q_j}}(y), \qquad \text {for }\sigma \text {-a.e. }y\in \Delta (x_{Q_j}, C\,\ell (Q_j)). \end{aligned}$$

This, Lemma 9.33 with $Q_j$ and the collection ${\mathbb {D}}': = \{Q^i: i\in {\mathcal {N}}_j(k), Q^i \cap Q_j = \emptyset \}$ (we are in the second scenario), and Remark 9.38 lead to

$$\begin{aligned}&\sum _{\begin{array}{c} i\in {\mathcal {N}}_j(k) \\ Q^i \cap Q_j = \varnothing \end{array} } \int _{Q^i} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma \approx \left( \omega ^{X_{P_k}}(Q_j)\right) ^p \sum _{\begin{array}{c} i\in {\mathcal {N}}_j(k) \\ Q^i \cap Q_j = \varnothing \end{array} } \int _{Q^i} \left( \mathbf{k }^{X_{Q_j}} \right) ^p d\sigma \nonumber \\&\quad \lesssim \left( \omega ^{X_{P_k}}(Q_j) \right) ^p\int _{Q_j} \left( \mathbf{k }^{X_{Q_j}} \right) ^p d\sigma \approx \int _{Q_j} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma . \end{aligned}$$

(9.45)

On the other hand, if $Q_j \subsetneq Q^i$, then (9.44) gives $\ell (Q_j)\approx \ell (Q^i)$, hence the cardinality of $\{Q^i: i\in {\mathcal {N}}_j(k), Q_j \subsetneq Q^i\}$ is uniformly bounded. On the other hand, by Lemma 2.32 applied with ${\mathcal {D}}=\Omega$ (or Harnack’s inequality if $\ell (Q^i)\approx \ell (P_k)$), Lebesgue’s differentiation theorem, Lemma 2.37, and Harnack’s inequality we readily obtain

$$\begin{aligned} \mathbf{k }^{X_{P_k}}(y)\approx \omega ^{X_{P_k}}(Q_j)\, \mathbf{k }^{X_{Q_j}}(y), \qquad \text {for }\sigma \text {-a.e. }y\in Q^i. \end{aligned}$$

Thus, using Corollary 6.5 we have

$$\begin{aligned} \sum _{\begin{array}{c} i\in {\mathcal {N}}_j(k) \\ Q^i \supsetneq Q_j \end{array}} \int _{Q^i} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma&\approx \left( \omega ^{X_{P_k}}(Q_j)\right) ^p\,\sum _{\begin{array}{c} i\in {\mathcal {N}}_j(k) \\ Q^i \supsetneq Q_j \end{array}} \int _{Q^i} \left( \mathbf{k }^{X_{Q_j}} \right) ^p d\sigma \nonumber \\&\lesssim \left( \omega ^{X_{P_k}}(Q_j)\right) ^p\, \sum _{\begin{array}{c} i\in {\mathcal {N}}_j(k) \\ Q^i \supsetneq Q_j \end{array}} \int _{Q_j} \left( \mathbf{k }^{X_{Q_j}} \right) ^p d\sigma \nonumber \\&\lesssim \left( \omega ^{X_{P_k}}(Q_j)\right) ^p\, \int _{Q_j} \left( \mathbf{k }^{X_{Q_j}} \right) ^p d\sigma \nonumber \\&\approx \int _{Q_j} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma . \end{aligned}$$

(9.46)

The claim (9.43) now follows from (9.45) and (9.46).

To continue, let us recall that for each $Q_j\in {\mathcal {F}}_2(k)$,

$$\begin{aligned} \ell (Q_j) < \ell (P_k)\quad \text { and }\quad {\text {dist}}(Q_j,P_k) \lesssim \ell (P_k), \end{aligned}$$

where the second inequality is (9.31). Consequently, each $Q_j\in {\mathcal {F}}_2(k)$, is contained in some $P\in \mathbf{N}(P_k):= \{P\in {\mathbb {D}}: \ell (P) =\ell (P_k),\ {\text {dist}}(P,P_k) \lesssim \ell (P_k)\}$ and, clearly, the cardinality of $\mathbf{N}(P_k)$ is uniformly bounded. Recalling that ${\mathcal {F}}=\{Q_j\}_j$ is a pairwise disjoint family of cubes, by (9.43), Corollary 6.5, and (9.29), we arrive at

$$\begin{aligned}&\sum _{Q_j\in {\mathcal {F}}_2(k)} \sum _{i\in {\mathcal {N}}_j(k)} \int _{Q^i} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma \lesssim \sum _{Q_j\in {\mathcal {F}}_2(k)} \int _{Q_j} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma \nonumber \\&\quad = \, \int _{\bigcup \limits _{Q_j\in {\mathcal {F}}_2(k)} Q_j} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma \le \sum _{P\in \mathbf{N}(P_k)}\int _{P} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma \lesssim \int _{P_k} \left( \mathbf{k }^{X_{P_k}} \right) ^p d\sigma \lesssim \sigma _*(\Delta _*)^{1-p}. \nonumber \\ \end{aligned}$$

(9.47)

Step 2.4. Final estimate.

We finally combine (9.32) with (9.40), (9.42), and (9.47), and use the fact that $N_2\le N_1=N_1(n, C_{AR})$ to conclude that

$$\begin{aligned} \int _{\Delta _*} \left( \mathbf{k }_*^X \right) ^p d\sigma _* \lesssim \sum _{k=1}^{N_2} \sigma _*(\Delta _*)^{1-p} \lesssim \sigma _*(\Delta _*)^{1-p}. \end{aligned}$$

(9.48)

Hence, we have obtained the desired estimate (9.4), and therefore the proof of Theorem 9.1 is complete, provided that the sawtooth domain $\Omega _*$ is compactly contained in $\Omega$ and modulo the proof of Lemma 9.33.

To consider the general case we need the following theorem which generalizes [KKPT, Theorem 4.1] and [DJK] (see also [DKP, Zha]):

Theorem 9.49

([CHMT, Theorem 1.1]).   Let ${\mathcal {D}}$ be uniform domain ${\mathcal {D}}$ Ahlfors regular boundary, and let ${\mathcal {A}}$ be a real (non necessarily symmetric) uniformly elliptic matrix on ${\mathcal {D}}$. The following are equivalent:

• (1) The elliptic measure $\omega _L$ associated with the operator $L=-\mathop {{\text {div}}}\nolimits ({\mathcal {A}}\nabla )$ is of class $A_\infty$ with respect to the surface measure.

• (2) Any bounded weak solution to $Lu=0$ satisfies the Carleson measure estimate

  $$\begin{aligned} \sup _{\begin{array}{c} x\in \partial {\mathcal {D}} \\ 0<r<\infty \end{array}} \frac{1}{r^n}\int _{B(x,r) \cap {\mathcal {D}}} |\nabla u(Y)|^2 {\text {dist}}(Y,\partial {\mathcal {D}})\, dY \le C\Vert u\Vert _{L^\infty ({\mathcal {D}})}^2. \end{aligned}$$

  (9.50)

The involved constants depend on the allowable constants and the constant appearing in the corresponding hypothesis of the implication in question.

Consider next a general sawtooth domain $\Omega _* = \Omega _{{\mathcal {F}},Q}$ which, although bounded, is not necessarily compactly contained in $\Omega$. By (2) $\implies$ (1) in Theorem 9.49 with ${\mathcal {D}}=\Omega$, in order to obtain that the elliptic measure associated with L relative to $\Omega _*$ belongs to $A_\infty$ with respect to the surface measure, we just need to see that (2) holds with ${\mathcal {D}}=\Omega _*$. With this goal in mind we take u, a bounded weak solution to $Lu=0$ in $\Omega _*$, and let $x\in \partial \Omega$ and $0<r<\infty$.

Given $N\ge 1$ we recall the definition of ${\mathcal {F}}_N:={\mathcal {F}}(2^{-N}\,\ell (Q))$ in Section 6 and write $\Omega _*^N := \Omega _{{\mathcal {F}}_N,Q}$. Note that by construction $\ell (Q')> 2^{-N}\,\ell (Q)$ for every $Q'\in {\mathbb {D}}_{{\mathcal {F}}_N, Q}$, hence $\Omega _*^N$ is compactly contained in $\Omega$ (indeed is at distance of the order $2^{-N}\,\ell (Q)$ to $\partial \Omega$). Then we can apply the previous case to obtain that for each N, the associated elliptic measure associated with L relative to $\Omega _*^N$ satisfies the $A_\infty$ property with respect to the surface measure of $\partial \Omega _*^N$, and the implicit constants depend only on the allowable constants. Hence (1) $\implies$ (2) in Theorem 9.49 with ${\mathcal {D}}=\Omega _*^N$ implies

$$\begin{aligned} \sup _{\begin{array}{c} z\in \partial \Omega _*^N \\ 0<s<\infty \end{array}} \frac{1}{s^n}\int _{B(z,s) \cap \Omega _*^N} |\nabla u(Y)|^2 \delta _*^N(Y)\, dY \lesssim \Vert u\Vert _{L^\infty (\Omega _N^*)}^2 \le C\Vert u\Vert _{L^\infty (\Omega _*)}^2, \end{aligned}$$

(9.51)

since u is a bounded weak solution to $Lu=0$ in $\Omega _*$ and so in each $\Omega _N^*$, where $\delta _*^N={\text {dist}}(\cdot \,,\partial \Omega _*^N)$ and where the implicit constants depend only on the allowable constants.

Let $\omega _*$ and $\omega _*^N$ denote the elliptic measures to L relative to $\Omega _*$ and $\Omega _*^N$ respectively, and let $\sigma _*^N := {\mathcal {H}}^{n-1}|_{\partial \Omega _*^N}$ denote the surface measure of $\partial \Omega _*^N$. By construction $\{\Omega _*^N\}_{N\ge 1}$ is an increasing sequence of sets with $\Omega _*=\cup _{N\ge 1}\Omega _*^N$. Hence, for any $Y\in \Omega _*$ there is $N_Y\ge 1$ such that $Y\in \Omega _*^N$ for all $N\ge N_Y$. Clearly $\delta _*^N(Y) \nearrow \delta _*(Y)$ as $N\rightarrow \infty$ and

$$\begin{aligned} |\nabla u(Y)|^2 \delta _*^N(Y) \chi _{\Omega _*^N}(Y) \nearrow |\nabla u(Y)|^2 \delta _*(Y) \chi _{\Omega _*}(Y), \quad \text { as } N\rightarrow \infty . \end{aligned}$$

On the other hand since $x\in \partial \Omega _*$, using the Corkscrew condition we can find a sequence $\{x_N \}_{N\ge 1}$ with $x_N\in \partial \Omega _*^N$ such that $x_N \rightarrow x$. In particular, $B(x,r) \subset B(x_N,2r)$ for sufficiently large N. By Fatou’s Lemma and (9.51) it then follows

$$\begin{aligned}&\int _{B(x,r) \cap \Omega _*} |\nabla u(Y)|^2 \delta _*(Y)\, dY \le \liminf _{N\rightarrow \infty } \int _{B(x,r) \cap \Omega _*^N} |\nabla u(Y)|^2 \delta _*^N(Y)\, dY \nonumber \\&\quad \le \liminf _{N\rightarrow \infty } \int _{B(x_N,2r) \cap \Omega _*^N} |\nabla u|^2 \delta _*^N(y)\, dY \lesssim r^n\, \Vert u\Vert _{L^\infty (\Omega _*)}^2, \end{aligned}$$

(9.52)

where the implicit constant depend only on the allowable constants. Since x, r, and u are arbitrary we have obtained as desired (2) in Theorem 9.49 for ${\mathcal {D}}=\Omega _*$ and as a result we conclude that $\omega _*\in A_\infty (\sigma _*)$. This completes the proof for an arbitrary sawtooth domain $\Omega _*$, and therefore the proof of Theorem 9.1 modulo the proof of Lemma 9.33. $\square$

Proof of Lemma 9.33

For fixed $k\in {{\mathbb {Z}}}$, write ${\mathbb {D}}'_k:=\{Q'\in {\mathbb {D}}': \ell (Q') = 2^{-k} \ell (Q)\}$, which is a pairwise disjoint family. In the first case since $Q'\subset Q$, we have that $k\ge 0$; in the second case since $\ell (Q') \le C_2 \ell (Q)$, we may assume that $k\ge -\log _2 C_2$. Set then $k_0=0$ in the first case and $k_0$ the integer part of $\log _2 C_1$. We define for $k\ge -k_0$

$$\begin{aligned}&A_k^+ = \{x\in Q: {\text {dist}}(x,\partial \Omega \setminus Q) \lesssim 2^{-k} \ell (Q) \}, \\&\quad A_k^- = \{x\in \partial \Omega \setminus Q: {\text {dist}}(x,Q) \lesssim 2^{-k} \ell (Q) \}, \end{aligned}$$

so that for appropriate choices of the implicit constants, each $Q'\in {\mathbb {D}}'_k$ is contained in either $A_k^+$ (the first case) or $A_k^-$ (the second case). Recall that by the thin boundary property of the dyadic decomposition ${\mathbb {D}}$ (cf. (6.2)), there is $\gamma \in (0,1)$ such that for all k under consideration,

$$\begin{aligned} \sigma (A_k^+) \lesssim 2^{-k\gamma } \sigma (Q), \quad \sigma (A_k^-) \lesssim 2^{-k\gamma }\sigma (Q). \end{aligned}$$

Set

$$\begin{aligned}{\mathcal {F}}_-:= \big \{Q'\subset \partial \Omega \setminus Q: \ell (Q') \le C_1 \ell (Q),\ {\text {dist}}(Q',Q) \le C_1 \ell (Q')\big \}.\end{aligned}$$

Observe that each $Q'\in {\mathcal {F}}_-$ is contained in some dyadic cube ${\widetilde{Q}}$, with $\ell ({{\widetilde{Q}}})\approx \ell (Q)$ and ${\text {dist}}({\widetilde{Q}},Q) \lesssim \ell (Q)$ depending on $C_1$. We may therefore define a collection of distinct cubes ${\mathcal {F}}_*:= \{{\widetilde{Q}}_m\}_{m=1}^{N_2}$, all of the same dyadic generation, one of which (say, ${\widetilde{Q}}_1$) contains Q, with $\ell ({{\widetilde{Q}}}_m) \approx \ell (Q)$, and with ${\text {dist}}({\widetilde{Q}}_m,Q) \lesssim \ell (Q)$ for every m, such that each $Q'\in {\mathcal {F}}_-$ is contained in some ${\widetilde{Q}}_m\in {\mathcal {F}}_*$, and

$$\begin{aligned} \bigcup _k A_k^+ \,\subset \, Q\,\subset \,{\widetilde{Q}}_1\,, \quad \mathrm{and} \quad \bigcup _k A_k^- \subset \, \bigcup _{m=2}^N {\widetilde{Q}}_m. \end{aligned}$$

Clearly, we have $\#{\mathcal {F}}_* = N_2= N_2(n,C_{AR}, C_1)$. Using all the previous observations we get for any $s>1$,

(9.53)

This shows (9.34). To obtain (9.36) we combine (9.53) together with (9.35) and the fact that $\sigma (Q)\approx \sigma (Q_m)$ for every $1\le m\le N_2$ by the Ahlfors regular property and the construction of the family ${\mathcal {F}}_*$. $\square$

12 Optimality

As we mentioned in the introduction, the class of elliptic operators we consider is optimal to guarantee the $A_\infty$ property. In this section we illustrate the optimality from two different points of view. See Proposition 10.2 and Theorem 10.7.

As mentioned right after Definition 2.10, one has that $\omega _L\in A_\infty (\sigma )$ if and only if $\omega _L\in RH_q(\sigma )$ for some $q>1$ in the following sense: $\omega _L \ll \sigma$ and the Radon-Nikodym derivative $\mathbf{k }_L:= d\omega _L/d\sigma$ satisfies the reverse Hölder estimate (2.12). We can then define the $RH_q(\sigma )$-characteristic of $\omega _L$ as folows

(10.1)

where the sup runs over all $q\in \partial \Omega$, $0<r<{{\,\mathrm{diam}\,}}(\Omega )$, and all surface balls $\Delta '=B'\cap \partial \Omega$ centered at $\partial \Omega$ with $B'\subset B(q,r)$.

The following example, based on the work in [MM] and communicated to us by Bruno Guiseppe Poggi Cevallos, illustrates the relationship between the size of the constant in the DKP condition and the $RH_q(\sigma )$-characteristic of elliptic measure.

Proposition 10.2

([MM, Pog]). There exist ${{\mathcal {A}}}$ and a sequence $\{{{\mathcal {A}}}_j\}_j$ of diagonal elliptic matrices with smooth, bounded, real coefficients in ${{\mathbb {R}}}^{n}_+$, uniformly continuous on $\overline{{{\mathbb {R}}}^{n}_+}$, such that ${{\mathcal {A}}}_j$ converges to ${{\mathcal {A}}}$ uniformly on $\overline{{{\mathbb {R}}}^{n}_+}$ and the following hold:

• (1) $\displaystyle { \sup _{\begin{array}{c} q\in {{\mathbb {R}}}^{n-1} \\ 0< r<\infty \end{array} } \frac{1}{r^{n-1}} \int _{B(q,r) \cap {{\mathbb {R}}}^{n}_+} \bigg ( \sup _{Y\in B(X,\frac{\delta (X)}{2})} |\nabla {\mathcal {A}}_j(Y)|^2 \delta (Y)\bigg )dX > rsim j. }$

• (2) For each $q>1$, one has $\omega _j\in RH_q(\sigma )$ with $\displaystyle {\lim _{j\rightarrow \infty }[\omega _j]_{RH_q}=\infty }$, where $\omega _j$ denotes the elliptic measure associated with the operator $L_j=-\mathop {{\text {div}}}\nolimits ({{\mathcal {A}}}_j(\cdot )\nabla )$.

• (3) The elliptic measure associated with the operator $L=-\mathop {{\text {div}}}\nolimits ({{\mathcal {A}}}(\cdot )\nabla )$ is singular with respect to the Lebesgue measure on $\partial {{\mathbb {R}}}^{n}_+={{\mathbb {R}}}^{n-1}$.

On the other hand, we can immediately extend Theorem 1.6 to a larger and optimal class of elliptic operators, pertaining to the condition on the oscillation of the coefficient matrix:

Corollary 10.3

Let $\Omega \subset {{\mathbb {R}}}^n$, $n\ge 3$, be a uniform domain with Ahlfors regular boundary. Let ${\mathcal {A}}$ be a (not necessarily symmetric) uniformly elliptic matrix on $\Omega$ such that

$$\begin{aligned} \sup _{\begin{array}{c} q\in \partial \Omega \\ 0< r<{{\,\mathrm{diam}\,}}(\Omega ) \end{array} } \frac{1}{r^{n-1}} \int _{B(q,r) \cap \Omega } \frac{{{\,\mathrm{osc}\,}}({\mathcal {A}}, X)^2}{\delta (X)} \,dX<\infty , \end{aligned}$$

(10.4)

where ${{\,\mathrm{osc}\,}}({\mathcal {A}}, X) := \sup _{Y,Z\in B(X, \delta (X)/2)} |{\mathcal {A}}(Y) -{\mathcal {A}}(Z)|$. Then the following are equivalent:

• (a) The elliptic measure $\omega _L$ associated with the operator $L=-\mathop {{\text {div}}}\nolimits ({\mathcal {A}}(\cdot )\nabla )$ is of class $A_\infty$ with respect to the surface measure.

• (b) $\partial \Omega$ is uniformly rectifiable.

• (c) $\Omega$ is a chord-arc domain.

Proof

Let $\varphi$ be a non-negative radial, smooth bump function supported in the unit ball, such that $\int _{{{\mathbb {R}}}^n} \varphi \,dX = 1$. We define for $X\in \Omega$ and $t\in (0, \delta (X))$,

$$\begin{aligned} P_t \, {\mathcal {A}}(X) := \varphi _t * {\mathcal {A}}(X) = \int _{{{\mathbb {R}}}^n} \frac{1}{t^n} \,\varphi \left( \frac{X-Y}{t} \right) {\mathcal {A}}(Y) \,dY, \end{aligned}$$

and write for $X\in \Omega$,

$$\begin{aligned} {\mathcal {A}}(X) = P_{\frac{\delta (X)}{4}} \, {\mathcal {A}}(X) + \left( {{\,\mathrm{Id}\,}}- P_{\frac{\delta (X)}{4}} \right) {\mathcal {A}}(X) =: {\widetilde{{\mathcal {A}}}}(X) + \left( {\mathcal {A}}(X) - {\widetilde{{\mathcal {A}}}}(X) \right) . \end{aligned}$$

(10.5)

It is easy to see that ${\widetilde{{\mathcal {A}}}}$ is uniformly elliptic with the same constants as ${\mathcal {A}}$ and also that for every $X\in \Omega$,

$$\begin{aligned} |\nabla {\widetilde{{\mathcal {A}}}}(X)| \le C\, \frac{{{\,\mathrm{osc}\,}}({\mathcal {A}}, X)}{\delta (X)} \qquad \text{ and }\qquad \sup _{Y\in B(X, \delta (X)/4)} |{\mathcal {A}}(Y) - {\widetilde{{\mathcal {A}}}}(Y)| \le {{\,\mathrm{osc}\,}}({\mathcal {A}}, X). \end{aligned}$$

(10.6)

Note that under assumption (10.4), the second estimate in (10.6) allows us to invoke [CHMT, Theorem 1.3] to obtain that $\omega _{L_{\mathcal {A}}} \in A_\infty (\sigma )$ if and only if $\omega _{L_{{\widetilde{{\mathcal {A}}}}}} \in A_\infty (\sigma )$. On the other hand, the first estimate in (10.6) readily implies that ${\widetilde{{\mathcal {A}}}}$ satisfies (H1) and (H2). Hence, Theorem 1.6 applied to ${\widetilde{{\mathcal {A}}}}$ gives at once the desired equivalences. We remark that the direction $(c)\implies (a)$ was also proved earlier in [Rio, Theorem 2.4].

$\square$

Corollary 10.3 is sharp in terms of the class of operators satisfying (10.4). We recall the following examples that illustrate this fact.

Theorem 10.7

[Theorem 4.11][FKP].   Suppose $\alpha$ is a non-negative function defined on ${{\mathbb {R}}}^2_+$ satisfying the doubling condition: $\alpha (X) \le C\alpha (X_0)$ for any $X_0\in {{\mathbb {R}}}^2_+$ and $X\in B(X_0, \delta (X_0)/2)$. Assume that $\alpha ^2(x,t) dx \, dt/t$ is not a Carleson measure in the unit square. Then there exists an elliptic operator $L= - \mathop {{\text {div}}}\nolimits ({\mathcal {A}}(\cdot )\nabla )$ on ${{\mathbb {R}}}^2_+$, such that

• (1) For any interval $I \subset {{\mathbb {R}}}$ and $T(I)=I\times [0,\ell (I)]$,

  $$\begin{aligned} \frac{1}{|I|} \int _{T(I)} \frac{{{\,\mathrm{osc}\,}}^2({\mathcal {A}}(x,t))}{t} dx \, dt \le C\left[ \frac{1}{|I|} \int _{T(2I)} \frac{\alpha ^2(x,t)}{t} dx \, dt + 1 \right] ; \end{aligned}$$

  (10.8)

• (2) The elliptic measure $\omega _{L}$ is not of class $A_\infty (dx)$ on the unit interval [0, 1].

Remarks 10.9

The examples above are constructed using quasi-conformal maps in ${{\mathbb {R}}}^2$. In [FKP] the authors in fact show the estimate (10.8) holds when ${{\,\mathrm{osc}\,}}({\mathcal {A}}(x,t))$ is replaced by the oscillation of elliptic matrix ${\mathcal {A}}(X)$ minus the identity matrix, i.e., $\sup _{Y\in B(X, \delta (X)/2 )} |{\mathcal {A}}(Y) - {{\,\mathrm{Id}\,}}|$; and it is easy to see that for those examples (10.8) follows. As in [CFK, Theorem 3], one can extend the 2 dimensional examples to ${{\mathbb {R}}}^n_+$ with $n\ge 3$ by using the Laplacian operator in the remaining tangential directions.