Abstract
It is well-known that quantitative, scale invariant absolute continuity (more precisely, the weak-\(A_\infty \) property) of harmonic measure with respect to surface measure, on the boundary of an open set \( \Omega \subset \mathbb {R}^{n+1}\) with Ahlfors–David regular boundary, is equivalent to the solvability of the Dirichlet problem in \(\Omega \), with data in \(L^p(\partial \Omega )\) for some \(p<\infty \). In this paper, we give a geometric characterization of the weak-\(A_\infty \) property, of harmonic measure, and hence of solvability of the \(L^p\) Dirichlet problem for some finite p. This characterization is obtained under background hypotheses (an interior corkscrew condition, along with Ahlfors–David regularity of the boundary) that are natural, and in a certain sense optimal: we provide counter-examples in the absence of either of them (or even one of the two, upper or lower, Ahlfors–David bounds); moreover, the examples show that the upper and lower Ahlfors–David bounds are each quantitatively sharp.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A classical criterion of Wiener characterizes the domains in which one can solve the Dirichlet problem for Laplace’s equation with continuous boundary data, and with continuity of the solution up to the boundary. In this paper, we address the analogous issue in the case of singular data. To be more precise, the present work provides a purely geometric characterization of the open sets for which \(L^p\) solvability holds, for some \(p<\infty \), and with non-tangential convergence to the data a.e., thus allowing for singular boundary data. We establish this characterization in the presence of background hypotheses (an interior corkscrew condition [see Definition 2.4 below], and Ahlfors–David regularity of the boundary [Definition 2.1]) that are in the nature of best possible, in the sense that there are counter-examples in the absence of either of them (or of even one of the two, upper or lower, Ahlfors–David bounds); moreover, the examples show that the upper and lower Ahlfors–David bounds are each quantitatively sharp (see the discussion following Theorem 1.2, as well as “Appendix A”, for more details).
Solvability of the \(L^p\) Dirichlet problem is fundamentally tied to quantitative absolute continuity of harmonic measure with respect to surface measure on the boundary: indeed, it is equivalent to the so-called “weak-\(A_\infty \)” property of the harmonic measure (see Definitions 2.14 and 2.15). It is through this connection to quantitative absolute continuity of harmonic measure that we shall obtain our geometric characterization of \(L^p\) solvability.
The study of the relationship between the geometry of a domain, and absolute continuity properties of its harmonic measure, has a long history. A classical result of F. and M. Riesz [47] states that for a simply connected domain \(\Omega \) in the complex plane, rectifiability of \(\partial \Omega \) implies that harmonic measure for \(\Omega \) is absolutely continuous with respect to arclength measure on the boundary. A quantitative version of this theorem was later proved by Lavrentiev [41]. More generally, if only a portion of the boundary is rectifiable, Bishop and Jones [12] have shown that harmonic measure is absolutely continuous with respect to arclength on that portion. They also present a counter-example to show that the result of [47] may fail in the absence of some connectivity hypothesis (e.g., simple connectedness).
In dimensions greater than 2, a fundamental result of Dahlberg [18] establishes a quantitative version of absolute continuity, namely that harmonic measure belongs to the class \(A_\infty \) in an appropriate local sense (see Definitions 2.14 and 2.15 below), with respect to surface measure on the boundary of a Lipschitz domain.
The result of Dahlberg was extended to the class of Chord-arc domains (see Definition 2.7) by David and Jerison [21], and independently by Semmes [48]. The Chord-arc hypothesis was weakened to that of a two-sided corkscrew condition (Definition 2.4) by Bennewitz and Lewis [11], who then drew the conclusion that harmonic measure is weak-\(A_\infty \) (in an appropriate local sense, see Definitions 2.14 and 2.15) with respect to surface measure on the boundary; the latter condition is similar to the \(A_\infty \) condition, but without the doubling property, and is the best conclusion that can be obtained under the weakened geometric conditions considered in [11]. We note that weak-\(A_\infty \) is still a quantitative, scale invariant version of absolute continuity.
More recently, one of us (Azzam) has given in [6] a geometric characterization of the \(A_\infty \) property of harmonic measure with respect to surface measure for domains with n-dimensional Ahlfors–David regular (n-ADR) boundary (see Definition 2.1). Azzam’s results are related to those of the present paper, so let us describe them in a bit more detail. Specifically, he shows that for a domain \(\Omega \) with n-ADR boundary, harmonic measure is in \(A_\infty \) with respect to surface measure, if and only if 1) \(\partial \Omega \) is uniformly rectifiable (n-UR)Footnote 1, and 2) \(\Omega \) is semi-uniform in the sense of Aikawa and Hirata [1]. The semi-uniform condition is a connectivity condition which states that for some uniform constant M, every pair of points \(x\in \Omega \) and \(y\in \partial \Omega \) may be connected by a rectifiable curve \(\gamma =\gamma (y,x)\), with \(\gamma {\setminus } \{y\} \subset \Omega \), with length \(\ell (\gamma ) \le M|x-y|\), and which satisfies the “cigar path” condition
Semi-uniformity is a weak version of the well known uniform condition, whose definition is similar, except that it applies to all pairs of points \(x,y\in \Omega \). For example, the unit disk centered at the origin, with the slit \(\{-1/2\le x\le 1/2, y=0\}\) removed, is semi-uniform, but not uniform. It was shown in [1] that for a domain satisfying a John condition and the Capacity Density Condition (in particular, for a domain with an n-ADR boundary), semi-uniformity characterizes the doubling property of harmonic measure. The method of [6] is, broadly speaking, related to that of [21], and of [11]. In [21], the authors show that a Chord-arc domain \(\Omega \) may be approximated in a “Big Pieces” sense (see [21] or [11] for a precise statement; also cf. Definition 2.12 below) by Lipschitz subdomains \(\Omega '\subset \Omega \); this fact allows one to reduce matters to the result of Dahlberg via the maximum principle (a method which, to the present authors’ knowledge, first appears in [39] in the context of \(BMO_1\) domains). The same strategy, i.e., Big Piece approximation by Lipschitz subdomains, is employed in [11]. Similarly, in [6], matters are reduced to the result of [21], by showing that for a domain \(\Omega \) with an n-ADR boundary, \(\Omega \) is semi-uniform with a uniformly rectifiable boundary if and only if it has “Very Big Pieces” of Chord-arc subdomains (see [6] for a precise statement of the latter condition). As mentioned above, the converse direction is also treated in [6]. In that case, given an interior corkscrew condition (which holds automatically in the presence of the doubling property of harmonic measure), and provided that \(\partial \Omega \) is n-ADR, the \(A_\infty \) (or even weak-\(A_\infty \)) property of harmonic measure was already known to imply uniform rectifiability of the boundary [32] (although the published version appears in [28]; see also [44] for an alternative proof, and a somewhat more general result); as in [1], semi-uniformity follows from the doubling property, although in [6], the author manages to show this while dispensing with the John domain background assumption (given a harmlessly strengthened version of the doubling property).
Thus, in [6], the connectivity condition (semi-uniformity), is tied to the doubling property of harmonic measure, and not to absolute continuity. On the other hand, in light of the example of [12], and on account of the aforementioned connection to solvability of the Dirichlet problem, it has been an important open problem to determine the minimal connectivity assumption which, in conjunction with uniform rectifiability of the boundary, yields quantitative absolute continuity of harmonic measure with respect to surface measure. In the present work, we present a connectivity condition, significantly milder than semi-uniformity, which we call the weak local John condition (see Definition 2.11 below), and which solves this problem. Thus, we obtain a geometric characterization of the domains for which one has quantitative absolute continuity of harmonic measure; equivalently, for which one has solvability of the Dirichlet problem with singular (\(L^p\)) data (see Theorem 1.1 below). In fact, we provide two geometric characterizations of such domains, one in terms of uniform rectifiability combined with the weak local John condition, the other in terms of approximation of the boundary in a big pieces sense, by boundaries of Chord-arc subdomains.
Let us now describe the weak local John condition, which says, roughly speaking, that from each point \(x\in \Omega \), there is local non-tangential access to an ample portion of a surface ball at a scale on the order of \(\delta _{\Omega }(x):={\text {dist}}(x,\partial \Omega )\). Let us make this a bit more precise. A “carrot path” (aka non-tangential path) joining a point \(x\in \Omega \), and a point \(y \in \partial \Omega \), is a connected rectifiable path \(\gamma =\gamma (y,x)\), with endpoints y and x, such that for some \(\lambda \in (0,1)\) and for all \(z\in \gamma \),
where \(\ell \big (\gamma (y,z)\big )\) denotes the arc-length of the portion of the original path with endpoints y and z. For \(x\in \Omega \), and \(N\ge 2\), set
We assume that every point \(x\in \Omega \) may be joined by a carrot path to each y in a “Big Piece” of \(\Delta _x\), i.e., to each y in a Borel subset \(F \subset \Delta _x\), with \(\sigma (F)\ge \theta \sigma (\Delta _x)\), where \(\sigma \) denotes surface measure on \(\partial \Omega \), and where the parameters \(N\ge 2\), \(\lambda \in (0,1)\), and \(\theta \in (0,1]\) are uniformly controlled. We refer to this condition as a “weak local John condition”, although “weak local semi-uniformity” would be equally appropriate. See Definitions 2.8, 2.9 and 2.11 for more details. We remark that a strong version of the local John condition (i.e., with \(\theta =1\)) has appeared in [37], in connection with boundary Poincaré inequalities for non-smooth domains.
Let us observe that the weak local John condition is strictly weaker than semi-uniformity: for example, the unit disk centered a the origin, with either the cross \(\{-1/2\le x\le 1/2, y=0\}\cup \{-1/2\le y\le 1/2, x=0\}\) removed, or with the slit \(\{0\le x\le 1, y=0 \}\) removed, satisfies the weak local John condition, although semi-uniformity fails in each case.
The main result in the present work is the following geometric characterization of quantitative absolute continuity of harmonic measure, and of the \(L^p\) solvability of the Dirichlet problem. The terminology used here will be defined in the sequel.
Theorem 1.1
Let \(\Omega \subset \mathbb {R}^{n+1}\), \(n\ge 1\), be an open set satisfying an interior corkscrew condition (see Definition 2.4 below), and suppose that \(\partial \Omega \) is n-dimensional Ahlfors–David regular (n-ADR; see Definition 2.1 below). Then the following are equivalent:
-
(1)
\(\partial \Omega \) is Uniformly Rectifiable (n-UR; see Definition 2.2 below) and \(\Omega \) satisfies the weak local John condition (see Definition 2.11 below).
-
(2)
\(\Omega \) satisfies an Interior Big Pieces of Chord-Arc Domains (IBPCAD) condition (see Definition 2.12 below).
-
(3)
Harmonic measure \(\omega \) is locally in weak-\(A_\infty \) (see Definition 2.15 below) with respect to surface measure \(\sigma \) on \(\partial \Omega \).
-
(4)
The \(L^p\) Dirichlet problem is solvable for some \(p<\infty \), i.e., for some \(p<\infty \), there is a constant C such that if \(g\in L^p(\partial \Omega )\), then the solution to the Dirichlet problem with data g, is well defined as \(u(x):=\int _{\partial \Omega } g d\omega ^x\) for each \(x\in \Omega \), converges to g non-tangentially, and enjoys the estimate
$$\begin{aligned} \Vert N_*u\Vert _{L^{p}(\partial \Omega )}\, \le \,C\, \Vert g\Vert _{L^p(\partial \Omega )}, \end{aligned}$$(1.3)where \(N_*u\) is a suitable version of the non-tangential maximal function of u.
Some explanatory comments are in order. The proof has two main new ingredients: the implication (1) implies (2), and the fact that the weak-\(A_\infty \) property of harmonic measure implies the weak local John condition (this is the new part of (3) implies (1)). In turn, we split these main new results into two theorems: the first implication is the content of Theorem 1.2 below, and the second is the content of Theorem 1.3. We remark that the interior corkscrew condition is not needed for (1) implies (2) (nor for (2) implies (3) if and only if (4)). Rather, it is crucial for (3) implies (1) (see “Appendix A”).
As regards the other implications, the fact that (2) implies (3) follows by a well-known argument using the maximum principle and the result of [21] and [48] for Chord-arc domainsFootnote 2, along with the criterion for weak-\(A_\infty \) obtained in [11]; the equivalence of (3) and (4) is well known, and we refer the reader to, e.g., [27, Section 4], and to [26] for details. The implication (3) implies (1) has two parts. As mentioned above, the fact that weak-\(A_\infty \) implies weak local John is new, and is the content of Theorem 1.3. The remaining implication, namely that weak-\(A_\infty \) implies n-UR, is the main result of [32]; an alternative proof, with a more general result, appears in [44], and see also [28] for the final published version of the results of [32], along with an extension to the p-harmonic setting.
We note that our background hypotheses (upper and lower n-ADR, and interior corkscrew) are in the nature of best possible: one may construct a counter-example in the absence of any one of them, for at least one direction of this chain of implications, as we shall discuss in “Appendix A”. In addition, in the case of the n-ADR condition, given any \(\varepsilon >0\), the counter-examples for the upper (respectively, lower) n-ADR property can be constructed in such a way as to show that no weaker condition of the form \(H^n(B(x,r)\cap \partial \Omega ) \lesssim r^{n -\varepsilon }\) (resp., \(H^n(B(x,r)\cap \partial \Omega ) \gtrsim r^{n+ \varepsilon }\)), with \(r<1\), may be substituted for a true n-ADR upper or lower bound. Moreover, the first example shows that one cannot substitute the Capacity Density Condition (CDC)Footnote 3 in place of the n-ADR condition: indeed, the example is an NTA domain, in particular, it satisfies an exterior corkscrew condition, and thus also the CDC.
As regards our assumption of the interior corkscrew condition, we point out that, as is well known, the n-ADR condition implies that the open set \(\mathbb {R}^{n+1}{\setminus } \partial \Omega \) satisfies a corkscrew condition, with constants depending only on n and ADR, i.e., at every scale r, and for every point \(x\in \partial \Omega \), there is at least one component of \(\mathbb {R}^{n+1}{\setminus } \partial \Omega \) containing a corkscrew point relative to the ball B(x, r). Our last example shows that such a component should lie inside \(\Omega \) itself, for each x and r; i.e., that \(\Omega \) should enjoy an interior corkscrew condition.
As explained above, the main new contributions of the present work are contained in the following pair of theorems:
Theorem 1.2
Let \(\Omega \subset \mathbb {R}^{n+1}\), \(n\ge 1\), be an open set, not necessarily connected, with an n-dimensional Ahlfors–David regular (n-ADR) boundary. Then the following are equivalent:
-
(i)
\(\partial \Omega \) is uniformly rectifiable (n-UR), and \(\Omega \) satisfies the weak local John condition.
-
(ii)
\(\Omega \) satisfies an Interior Big Pieces of Chord-Arc Domains (IBPCAD) condition.
Only the direction (i) implies (ii) is new. For the converse, the fact that IBPCAD implies the weak local John condition is immediate from the definitions. Moreover, the boundary of a Chord-arc domain is n-UR, and an n-ADR set with big pieces of n-UR is also n-UR (see [23]). As noted above, that (ii) implies the weak-\(A_\infty \) property follows by well known arguments.
Theorem 1.3
Let \(\Omega \subset \mathbb {R}^{n+1}\), \(n\ge 1\), be an open set satisfying an interior corkscrew condition and suppose that \(\partial \Omega \) is n-dimensional Ahlfors–David regular (n-ADR). If the harmonic measure for \(\Omega \) satisfies the weak-\(A_\infty \) condition, then \(\Omega \) satisfies the weak local John condition.
Let us mention that the present paper is a combination of unpublished work of two different subsets of the present authors: Theorem 1.2 is due to the second and third authors, and was first posted in the draft manuscript [34]Footnote 4; Theorem 1.3 is due to the first, fourth and fifth authors, and appeared first in the draft manuscript [9].
The paper is organized as follows. In the next section, we set notation and give some definitions. In Part 1 of the paper (Sects. 3–8), we give the proof of Theorem 1.2. In Part 2 of the paper (Sects. 9–16) we give the proof of Theorem 1.3. Finally, in “Appendix A”, we discuss some counter-examples which show that our background hypotheses are in the nature of best possible.
We thank the referee for a careful reading of the paper, and for several helpful suggestions that have led us to clarify certain matters, and to make improvements in the presentation.
2 Notation and definitions
-
Unless otherwise stated, we use the letters c, C to denote harmless positive constants, not necessarily the same at each occurrence, which depend only on dimension and the constants appearing in the hypotheses of the theorems (which we refer to as the “allowable parameters”). We shall also sometimes write \(a\lesssim b\), \(a \gtrsim b\), and \(a \approx b\) to mean, respectively, that \(a \le C b\), \(a \ge c b\), and \(0< c \le a/b\le C\), where the constants c and C are as above, unless explicitly noted to the contrary. In some occasions we will employ the notation \(a\lesssim _\lambda b\), \(a \gtrsim _\lambda b\) and \(a \approx _\lambda b\) to emphasize that the previous implicit constants c and/or C may depend on some relevant parameter \(\lambda \). At times, we shall designate by M a particular constant whose value will remain unchanged throughout the proof of a given lemma or proposition, but which may have a different value during the proof of a different lemma or proposition.
-
Our ambient space is \(\mathbb {R}^{n+1}\), \(n\ge 1\).
-
\(\Omega \) will always denote an open set in \(\mathbb {R}^{n+1}\), not necessarily connected unless otherwise specified.
-
We use the notation \(\gamma (x,y)\) to denote a rectifiable path with endpoints x and y, and its arc-length will be denoted \(\ell (\gamma (x,y))\). Given such a path, if \(z\in \gamma (x,y)\), we use the notation \(\gamma (z,y)\) to denote the portion of the original path with endpoints z and y.
-
We let \(e_j\), \(j=1,2,\dots ,n+1,\) denote the standard unit basis vectors in \(\mathbb {R}^{n+1}\).
-
The open \((n+1)\)-dimensional Euclidean ball of radius r will be denoted B(x, r). For \(x\in \partial \Omega \), a surface ball is denoted \(\Delta (x,r):= B(x,r) \cap \partial \Omega .\)
-
Given a Euclidean ball B or surface ball \(\Delta \), its radius will be denoted \(r_B\) or \(r_\Delta \), respectively.
-
Given a Euclidean or surface ball \(B= B(x,r)\) or \(\Delta = \Delta (x,r)\), its concentric dilate by a factor of \(\kappa >0\) will be denoted \(\kappa B := B(x,\kappa r)\) or \(\kappa \Delta := \Delta (x,\kappa r).\)
-
Given an open set \(\Omega \subset \mathbb {R}^{n+1}\), for \(x \in \Omega \), we set \(\delta _{\Omega }(x):= {\text {dist}}(x,\partial \Omega )\).
-
We let \(H^n\) denote n-dimensional Hausdorff measure, and let \(\sigma := H^n\big \lfloor _{\,\partial \Omega }\) denote the surface measure on \(\partial \Omega \).
-
For a Borel set \(A\subset \mathbb {R}^{n+1}\), we let \(\chi _A\) denote the usual indicator function of A, i.e. \(\chi _A(x) = 1\) if \(x\in A\), and \(\chi _A(x)= 0\) if \(x\notin A\).
-
For a Borel set \(A\subset \mathbb {R}^{n+1}\), we let \({{\,\mathrm{int}\,}}(A)\) denote the interior of A.
-
Given a Borel measure \(\mu \), and a Borel set A, with positive and finite \(\mu \) measure, we set
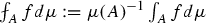 .
. -
We shall use the letter I (and sometimes J) to denote a closed \((n+1)\)-dimensional Euclidean dyadic cube with sides parallel to the co-ordinate axes, and we let \(\ell (I)\) denote the side length of I. If \(\ell (I) =2^{-k}\), then we set \(k_I:= k\). Given an n-ADR set \(E\subset \mathbb {R}^{n+1}\), we use Q (or sometimes P or R) to denote a dyadic “cube” on E. The latter exist (see [17, 22, 38]), and enjoy certain properties which we enumerate in Lemma 2.16 below.
Definition 2.1
(n-ADR) (aka n-Ahlfors–David regular). We say that a set \(E \subset \mathbb {R}^{n+1}\), of Hausdorff dimension n, is n-ADR if it is closed, and if there is some uniform constant C such that
where \({{\,\mathrm{diam}\,}}(E)\) may be infinite. Here, \(\Delta (x,r):= E\cap B(x,r)\) is the surface ball of radius r, and as above, \(\sigma := H^n\lfloor _{\,E}\) is the “surface measure” on E.
Definition 2.2
(n-UR) (aka n-uniformly rectifiable). An n-ADR (hence closed) set \(E\subset \mathbb {R}^{n+1}\) is n-UR if and only if it contains “Big Pieces of Lipschitz Images” of \(\mathbb {R}^n\) (“BPLI”). This means that there are positive constants \(c_1\) and \(C_1\), such that for each \(x\in E\) and each \(r\in (0,{{\,\mathrm{diam}\,}}(E))\), there is a Lipschitz mapping \(\rho = \rho _{x,r}: \mathbb {R}^n\rightarrow \mathbb {R}^{n+1}\), with Lipschitz constant no larger than \(C_1\), such that
We recall that n-dimensional rectifiable sets are characterized by the property that they can be covered, up to a set of \(H^n\) measure 0, by a countable union of Lipschitz images of \(\mathbb {R}^n\); we observe that BPLI is a quantitative version of this fact.
We remark that, at least among the class of n-ADR sets, the n-UR sets are precisely those for which all “sufficiently nice” singular integrals are \(L^2\)-bounded [22]. In fact, for n-ADR sets in \(\mathbb {R}^{n+1}\), the \(L^2\) boundedness of certain special singular integral operators (the “Riesz Transforms”), suffices to characterize uniform rectifiability (see [43] for the case \(n=1\), and [45] in general). We further remark that there exist sets that are n-ADR (and that even form the boundary of a domain satisfying interior corkscrew and Harnack Chain conditions), but that are totally non-rectifiable (e.g., see the construction of Garnett’s “4-corners Cantor set” in [23, Chapter 1]). Finally, we mention that there are numerous other characterizations of n-UR sets (many of which remain valid in higher co-dimensions); cf. [22, 23].
Definition 2.3
(“UR character”). Given an n-UR set \(E\subset \mathbb {R}^{n+1}\), its “UR character” is just the pair of constants \((c_1,C_1)\) involved in the definition of uniform rectifiability, along with the ADR constant; or equivalently, the quantitative bounds involved in any particular characterization of uniform rectifiability.
Definition 2.4
(Corkscrew condition). Following [39], we say that an open set \(\Omega \subset \mathbb {R}^{n+1}\) satisfies the corkscrew condition if for some uniform constant \(c>0\) and for every surface ball \(\Delta :=\Delta (x,r),\) with \(x\in \partial \Omega \) and \(0<r<{{\,\mathrm{diam}\,}}(\partial \Omega )\), there is a ball \(B(x_\Delta ,cr)\subset B(x,r)\cap \Omega \). The point \(x_\Delta \subset \Omega \) is called a corkscrew point relative to \(\Delta .\) We note that we may allow \(r<C{{\,\mathrm{diam}\,}}(\partial \Omega )\) for any fixed C, simply by adjusting the constant c. In order to emphasize that \(B(x_\Delta ,cr) \subset \Omega \), we shall sometimes refer to this property as the interior corkscrew condition.
Definition 2.5
(Harnack Chains, and the Harnack Chain condition [39]). Given two points \(x,x' \in \Omega \), and a pair of numbers \(M,N\ge 1\), an (M, N)-Harnack Chain connecting x to \(x'\), is a chain of open balls \(B_1,\dots ,B_N \subset \Omega \), with \(x\in B_1,\, x'\in B_N,\) \(B_k\cap B_{k+1}\ne \emptyset \) and \(M^{-1}{{\,\mathrm{diam}\,}}(B_k) \le {\text {dist}}(B_k,\partial \Omega )\le M{{\,\mathrm{diam}\,}}(B_k).\) We say that \(\Omega \) satisfies the Harnack Chain condition if there is a uniform constant M such that for any two points \(x,x'\in \Omega \), there is an (M, N)-Harnack Chain connecting them, with N depending only on M and the ratio \(|x-x'|/\left( \min \big (\delta _{\Omega }(x),\delta _{\Omega }(x')\big )\right) \).
Definition 2.6
(NTA). Again following [39], we say that a domain \(\Omega \subset \mathbb {R}^{n+1}\) is NTA (Non-tangentially accessible) if it satisfies the Harnack Chain condition, and if both \(\Omega \) and \(\Omega _\mathrm{ext}:= \mathbb {R}^{n+1}{\setminus } \overline{\Omega }\) satisfy the corkscrew condition.
Definition 2.7
(CAD). We say that a connected open set \(\Omega \subset \mathbb {R}^{n+1}\) is a CAD (Chord-arc domain), if it is NTA, and if \(\partial \Omega \) is n-ADR.
Definition 2.8
(Carrot path). Let \(\Omega \subset \mathbb {R}^{n+1}\) be an open set. Given a point \(x\in \Omega \), and a point \(y \in \partial \Omega \), we say that a connected rectifiable path \(\gamma =\gamma (y,x)\), with endpoints y and x, is a carrot path (more precisely, a \(\lambda \)-carrot path) connecting y to x, if \(\gamma {\setminus }\{y\}\subset \Omega \), and if for some \(\lambda \in (0,1)\) and for all \(z\in \gamma \),
With a slight abuse of terminology, we shall sometimes refer to such a path as a \(\lambda \)-carrot path in \(\Omega \), although of course the endpoint y lies on \(\partial \Omega \).
A carrot path is sometimes referred to as a non-tangential path.
Definition 2.9
(\((\theta ,\lambda ,N)\)-weak local John point). Let \(x\in \Omega \), and for constants \(\theta \in (0,1]\), \(\lambda \in (0,1)\), and \(N\ge 2\), set
We say that a point \(x\in \Omega \) is a \((\theta ,\lambda ,N)\)-weak local John point if there is a Borel set \(F\subset \Delta ^N_x\), with \(\sigma (F)\ge \theta \sigma (\Delta ^N_x)\), such that for every \(y\in F\), there is a \(\lambda \)-carrot path connecting y to x.
Thus, a weak local John point is non-tangentially connected to an ample portion of the boundary, locally. We observe that one can always choose N smaller, for possibly different values of \(\theta \) and \(\lambda \), by moving from x to a point \(x'\) on a line segment joining x to the boundary.
Remark 2.10
We observe that it is a slight abuse of notation to write \(\Delta _x\), since the latter is not centered on \(\partial \Omega \), and thus it is not a true surface ball; on the other hand, there are true surface balls, \(\Delta '_x:=\Delta (\hat{x},(N-1)\delta _{\Omega }(x))\) and \(\Delta ''_x:=\Delta (\hat{x},(N+1)\delta _{\Omega }(x))\), centered at a “touching point” \(\hat{x}\in \partial \Omega \) with \(\delta _{\Omega }(x)=|x-\hat{x}|\), which, respectively, are contained in, and contain, \(\Delta _x\).
Definition 2.11
(Weak local John condition). We say that \(\Omega \) satisfies a weak local John condition if there are constants \(\lambda \in (0,1)\), \(\theta \in (0,1]\), and \(N\ge 2\), such that every \(x\in \Omega \) is a \((\theta ,\lambda ,N)\)-weak local John point.
Definition 2.12
(IBPCAD). We say that a connected open set \(\Omega \subset \mathbb {R}^{n+1}\) has Interior Big Pieces of Chord-Arc Domains (IBPCAD) if there exist positive constants \(\eta \) and C, and \(N\ge 2\), such that for every \(x\in \Omega \), with \(\delta _{\Omega }(x)<{{\,\mathrm{diam}\,}}(\partial \Omega )\), there is a Chord-arc domain \(\Omega _x\subset \Omega \) satisfying
-
\(x\in \Omega _x\).
-
\({\text {dist}}(x,\partial \Omega _x) \ge \eta \delta _{\Omega }(x)\).
-
\({{\,\mathrm{diam}\,}}(\Omega _x) \le C\delta _{\Omega }(x)\).
-
\(\sigma (\partial \Omega _x\cap \Delta ^N_x) \ge \,\eta \, \sigma (\Delta ^N_x) \,\approx _N\, \eta \,\delta _{\Omega }(x)^n\).
-
The Chord-arc constants of the domains \(\Omega _x\) are uniform in x.
Remark 2.13
In the presence of an interior corkscrew condition, Definition 2.12 is easily seen to be essentially equivalent to the following more standard “Big Pieces” condition: there are positive constants \(\eta \) and C (perhaps slightly different to that in Definition 2.12), such that for each surface ball \(\Delta :=\Delta (x,r) = B(x,r) \cap \partial \Omega \), \(x\in \partial \Omega \) and \(r <{{\,\mathrm{diam}\,}}(\partial \Omega )\), and for any corkscrew point \(x_\Delta \) relative to \(\Delta \) there is a Chord-arc domain \(\Omega _\Delta \) satisfying
-
\(x_\Delta \in \Omega _\Delta \)
-
\({\text {dist}}(x_\Delta ,\partial \Omega _\Delta ) \ge \eta r\).
-
\(\Omega _\Delta \subset B(x,Cr) \cap \Omega \).
-
\(\sigma (\partial \Omega _\Delta \cap \Delta (x,Cr)) \ge \,\eta \, \sigma (\Delta (x,Cr))\approx \eta r^n\).
-
The Chord-arc constants of the domains \(\Omega _\Delta \) are uniform in \(\Delta \).
Definition 2.14
(\(A_\infty \), weak-\(A_\infty \), and weak-\(RH_q\)). Given an n-ADR set \(E\subset \mathbb {R}^{n+1}\), and a surface ball \(\Delta _0:= B_0 \cap E\) centered on E, we say that a Borel measure \(\mu \) defined on E belongs to \(A_\infty (\Delta _0)\) if there are positive constants C and s such that for each surface ball \(\Delta = B\cap E\) centered on E, with \(B\subseteq B_0\), we have
Similarly, we say that \(\mu \in \) weak-\(A_\infty (\Delta _0)\) if for each surface ball \(\Delta = B\cap E\) centered on E, with \(2B\subseteq B_0\),
We recall that, as is well known, the condition \(\mu \in \) weak-\(A_\infty (\Delta _0)\) is equivalent to the property that \(\mu \ll \sigma \) in \(\Delta _0\), and that for some \(q>1\), the Radon–Nikodym derivative \(k:= d\mu /d\sigma \) satisfies the weak reverse Hölder estimate

with B centered on E. We shall refer to the inequality in (2.5) as a “weak-\(RH_q\)” estimate, and we shall say that \(k\in \) weak-\(RH_q(\Delta _0)\) if k satisfies (2.5).
Definition 2.15
(Local \(A_\infty \) and local weak-\(A_\infty \)). We say that harmonic measure \(\omega \) is locally in \(A_\infty \) (resp., locally in weak-\(A_\infty \)) on \(\partial \Omega \), if there are uniform positive constants C and s such that for every ball \(B=B(x,r)\) centered on \(\partial \Omega \), with radius \(r<{{\,\mathrm{diam}\,}}(\partial \Omega )/4\), and associated surface ball \(\Delta =B\cap \partial \Omega \),
or, respectively, that
equivalently, if for every ball B and surface ball \(\Delta =B\cap \partial \Omega \) as above, and for each point \(p\in \Omega {\setminus } 4B\), \(\omega ^p\in \) \(A_\infty (\Delta )\) (resp., \(\omega ^p\in \) weak-\(A_\infty (\Delta )\)) with uniformly controlled \(A_\infty \) (resp., weak-\(A_\infty \)) constants.
Lemma 2.16
(Existence and properties of the “dyadic grid”) [17, 22, 23]. Suppose that \(E\subset \mathbb {R}^{n+1}\) is an n-ADR set. Then there exist constants \( a_0>0,\, s>0\) and \(C_1<\infty \), depending only on n and the ADR constant, such that for each \(k \in \mathbb {Z},\) there is a collection of Borel sets (“cubes”)
where \(\mathfrak {I}_k\) denotes some (possibly finite) index set depending on k, satisfying
-
(i)
\(E=\cup _{j}Q_{j}^k\) for each \(k\in {\mathbb Z}\).
-
(ii)
If \(m\ge k\) then either \(Q_{i}^{m}\subset Q_{j}^{k}\) or \(Q_{i}^{m}\cap Q_{j}^{k}=\emptyset \).
-
(iii)
For each (j, k) and each \(m<k\), there is a unique i such that \(Q_{j}^k\subset Q_{i}^m\).
-
(iv)
\({{\,\mathrm{diam}\,}}\big (Q_{j}^k\big )\le C_1 2^{-k}\).
-
(v)
Each \(Q_{j}^k\) contains some “surface ball” \(\Delta \big (x^k_{j},a_02^{-k}\big ):= B\big (x^k_{j},a_02^{-k}\big )\cap E\).
-
(vi)
\(H^n\big (\big \{x\in Q^k_j:\mathrm{dist}(x,E{\setminus } Q^k_j)\le \vartheta \,2^{-k}\big \}\big )\le C_1\,\vartheta ^s\,H^n\big (Q^k_j\big ),\) for all k, j and for all \(\vartheta \in (0,a_0)\).
A few remarks are in order concerning this lemma.
-
In the setting of a general space of homogeneous type, this lemma has been proved by Christ [17] (see also [38]), with the dyadic parameter 1/2 replaced by some constant \(\delta \in (0,1)\). In fact, one may always take \(\delta = 1/2\) (see [36, Proof of Proposition 2.12]). In the presence of the Ahlfors–David property (2.1), the result already appears in [22, 23]. Some predecessors of this construction have appeared in [19] and [20].
-
For our purposes, we may ignore those \(k\in \mathbb {Z}\) such that \(2^{-k} \gtrsim \mathrm{diam}(E)\), in the case that the latter is finite.
-
We shall denote by \(\mathcal {D}=\mathcal {D}(E)\) the collection of all relevant \(Q^k_j\), i.e.,
$$\begin{aligned} \mathcal {D}:= \cup _{k} \mathcal {D}_k, \end{aligned}$$where, if \({{\,\mathrm{diam}\,}}(E)\) is finite, the union runs over those k such that \(2^{-k} \lesssim \mathrm{diam}(E)\).
-
Properties (iv) and (v) imply that for each cube \(Q\in \mathcal {D}_k\), there is a point \(x_Q\in E\), a Euclidean ball \(B(x_Q,r_Q)\) and a surface ball \(\Delta (x_Q,r_Q):= B(x_Q,r_Q)\cap E\) such that \(r_Q\approx 2^{-k} \approx \mathrm{diam}(Q)\) and
$$\begin{aligned} \Delta (x_Q,r_Q)\subset Q \subset \Delta (x_Q,Cr_Q), \end{aligned}$$(2.8)for some uniform constant C. We shall refer to the point \(x_Q\) as the “center” of Q.
-
For a dyadic cube \(Q\in \mathcal {D}_k\), we shall set \(\ell (Q) = 2^{-k}\), and we shall refer to this quantity as the “length” of Q. Evidently, by adjusting if necessary some parameters, we can assume that
$$\begin{aligned} {{\,\mathrm{diam}\,}}(Q)\le \ell (Q)\lesssim {{\,\mathrm{diam}\,}}(Q). \end{aligned}$$We shall denote
$$\begin{aligned} B_Q:= B(x_Q,4\ell (Q)),\qquad \Delta _Q:= \Delta (x_Q,4\ell (Q)). \end{aligned}$$(2.9)Notice that \(Q\subset \Delta _Q\subset B_Q\).
-
For a dyadic cube \(Q \in \mathcal {D}\), we let k(Q) denote the dyadic generation to which Q belongs, i.e., we set \(k = k(Q)\) if \(Q\in \mathcal {D}_k\); thus, \(\ell (Q) =2^{-k(Q)}\).
-
Given \(R\in \mathcal {D}\), we set
$$\begin{aligned} \mathcal {D}(R):=\{Q\in \mathcal {D}:Q\subset R\}. \end{aligned}$$(2.10)For \(j\ge 1\), we also let
$$\begin{aligned} \mathcal {D}_j(R):=\left\{ Q\in \mathcal {D}(R): \, \ell (Q)=2^{-j}\,\ell (R)\right\} . \end{aligned}$$(2.11) -
For a pair of cubes \(Q',Q \in \mathcal {D}\), if \(Q'\) is a dyadic child of Q, i.e., if \(Q'\subset Q\), and \(\ell (Q) =2\ell (Q')\), then we write \(Q'\lhd Q\).
-
For \(\lambda >1\), we write
$$\begin{aligned} \lambda Q = \bigl \{x\in E:\, {\text {dist}}(x,Q)\le (\lambda -1)\,\ell (Q)\bigr \}. \end{aligned}$$
With the dyadic cubes in hand, we may now define the notion of a corkscrew point relative to a cube Q.
Definition 2.17
(Corkscrew point relative to Q). Let \(\Omega \) satisfy the corkscrew condition (Definition 2.4), suppose that \(\partial \Omega \) is n-ADR, and let \(Q\in \mathcal {D}(\partial \Omega )\). A corkscrew point relative to Q is simply a corkscrew point relative to the surface ball \(\Delta (x_Q,r_Q)\) defined in (2.8).
Definition 2.18
(Coherency and Semi-coherency). [23]. Let \(E\subset \mathbb {R}^{n+1}\) be an n-ADR set. Let \({\mathsf T}\subset \mathcal {D}(E)\). We say that \({\mathsf T}\) is coherent if the following conditions hold:
-
(a)
\({\mathsf T}\) contains a unique maximal element \(Q({\mathsf T})\) which contains all other elements of \({\mathsf T}\) as subsets.
-
(b)
If Q belongs to \({\mathsf T}\), and if \(Q\subset \widetilde{Q}\subset Q({\mathsf T})\), then \(\widetilde{Q}\in {{\mathsf T}}\).
-
(c)
Given a cube \(Q\in {\mathsf T}\), either all of its children belong to \({\mathsf T}\), or none of them do.
We say that \({\mathsf T}\) is semi-coherent if conditions (a) and (b) hold. We shall refer to a coherent or semi-coherent collection \({\mathsf T}\) as a tree.
3 Part 1: Proof of Theorem 1.2
4 Preliminaries for the Proof of Theorem 1.2
We begin by recalling a bilateral version of the David-Semmes “Corona decomposition” of an n-UR set. We refer the reader to [35] for the proof.
Lemma 3.1
( [35, Lemma 2.2]) Let \(E\subset \mathbb {R}^{n+1}\) be an n-UR set. Then given any positive constants \(\eta \ll 1\) and \(K\gg 1\), there is a disjoint decomposition \(\mathcal {D}(E) = \mathcal {G}\cup \mathcal {B}\), satisfying the following properties.
-
(1)
The “Good” collection \(\mathcal {G}\) is further subdivided into disjoint trees, such that each such tree \({\mathsf T}\) is coherent (Definition 2.18).
-
(2)
The “Bad” cubes, as well as the maximal cubes \(Q({\mathsf T})\), \({\mathsf T}\subset \mathcal {G}\), satisfy a Carleson packing condition:
$$\begin{aligned} \sum _{Q'\subset Q, \,Q'\in \mathcal {B}} \sigma (Q') \,\,+\,\sum _{{\mathsf T}\subset \mathcal {G}: Q({\mathsf T})\subset Q}\sigma \big (Q({\mathsf T})\big )\,\le \, C_{\eta ,K}\, \sigma (Q), \quad \forall Q\in \mathcal {D}(E). \end{aligned}$$ -
(3)
For each \({\mathsf T}\subset \mathcal {G}\), there is a Lipschitz graph \(\Gamma _{{\mathsf T}}\), with Lipschitz constant at most \(\eta \), such that, for every \(Q\in {\mathsf T}\),
$$\begin{aligned} \sup _{x\in \Delta _Q^*} {\text {dist}}(x,\Gamma _{{\mathsf T}} )\, +\,\sup _{y\in B_Q^*\cap \Gamma _{{\mathsf T}}}{\text {dist}}(y,E) < \eta \,\ell (Q), \end{aligned}$$(3.1)where \(B_Q^*:= B(x_Q,K\ell (Q))\) and \(\Delta _Q^*:= B_Q^*\cap E\), and \(x_Q\) is the “center” of Q as in (2.8)–(2.9).
We remark that in [35], the trees \({\mathsf T}\) were denoted by \(\mathbf{S}\), and were called “stopping time regimes” rather than trees.
We mention that David and Semmes, in [22], had previously proved a unilateral version of Lemma 3.1, in which the bilateral estimate (3.1) is replaced by the unilateral bound
Next, we make a standard Whitney decomposition of \(\Omega _E:=\mathbb {R}^{n+1}{\setminus } E\), for a given n-UR set E (in particular, \(\Omega _E\) is open, since n-UR sets are closed by definition). Let \(\mathcal {W}=\mathcal {W}(\Omega _E)\) denote a collection of (closed) dyadic Whitney cubes of \(\Omega _E\), so that the cubes in \(\mathcal {W}\) form a pairwise non-overlapping covering of \(\Omega _E\), which satisfy
(just dyadically divide the standard Whitney cubes, as constructed in [49, Chapter VI], into cubes with side length 1/8 as large) and also
whenever \(I_1\) and \(I_2\) touch.
We fix a small parameter \(\tau _0>0\), so that for any \(I\in \mathcal {W}\), and any \(\tau \in (0,\tau _0]\), the concentric dilate
still satisfies the Whitney property
Moreover, for \(\tau \le \tau _0\) small enough, and for any \(I,J\in \mathcal {W}\), we have that \(I^*(\tau )\) meets \(J^*(\tau )\) if and only if I and J have a boundary point in common, and that, if \(I\ne J\), then \(I^*(\tau )\) misses (3/4)J.
Pick two parameters \(\eta \ll 1\) and \(K\gg 1\) (eventually, we shall take \(K=\eta ^{-3/4}\)). For \(Q\in \mathcal {D}(E)\), define
Remark 3.2
We note that \(\mathcal {W}^0_Q\) is non-empty, provided that we choose \(\eta \) small enough, and K large enough, depending only on dimension and ADR, since the n-ADR condition implies that \(\Omega _E\) satisfies a corkscrew condition. In the sequel, we shall always assume that \(\eta \) and K have been so chosen.
Next, we recall a construction in [35, Section 3], leading up to and including in particular [35, Lemma 3.24]. We summarize this construction as follows.
Lemma 3.3
Let \(E\subset \mathbb {R}^{n+1}\) be n-UR, and set \(\Omega _E:= \mathbb {R}^{n+1}{\setminus } E\). Given positive constants \(\eta \ll 1\) and \(K\gg 1\), as in (3.6) and Remark 3.2, let \(\mathcal {D}(E) = \mathcal {G}\cup \mathcal {B}\), be the corresponding bilateral Corona decomposition of Lemma 3.1. Then for each \({\mathsf T}\subset \mathcal {G}\), and for each \(Q\in {\mathsf T}\), the collection \(\mathcal {W}^0_Q\) in (3.6) has an augmentation \(\mathcal {W}^*_Q\subset \mathcal {W}\) satisfying the following properties.
-
(1)
\(\mathcal {W}^0_Q\subset \mathcal {W}^*_Q = \mathcal {W}_Q^{*,+}\cup \mathcal {W}_Q^{*,-}\), where (after a suitable rotation of coordinates) each \(I \in \mathcal {W}_Q^{*,+}\) lies above the Lipschitz graph \(\Gamma _{{\mathsf T}}\) of Lemma 3.1, each \(I \in \mathcal {W}_Q^{*,-}\) lies below \(\Gamma _{{\mathsf T}}\). Moreover, if \(Q'\) is a child of Q, also belonging to \({\mathsf T}\), then \(\mathcal {W}_Q^{*,+}\) (resp. \(\mathcal {W}_Q^{*,-}\)) belongs to the same connected component of \(\Omega _E\) as does \(\mathcal {W}_{Q'}^{*,+}\) (resp. \(\mathcal {W}_{Q'}^{*,-}\)) and \(\mathcal {W}_{Q'}^{*,+}\cap \mathcal {W}_{Q}^{*,+}\ne \emptyset \) (resp., \(\mathcal {W}_{Q'}^{*,-}\cap \mathcal {W}_{Q}^{*,-}\ne \emptyset \)).
-
(2)
There are uniform constants c and C such that
$$\begin{aligned} \begin{array}{c} c\eta ^{1/2} \ell (Q)\le \ell (I) \le CK^{1/2}\ell (Q), \quad \forall I\in \mathcal {W}^*_Q, \\ {\text {dist}}(I,Q)\le CK^{1/2} \ell (Q),\quad \forall I\in \mathcal {W}^*_Q, \\ c\eta ^{1/2} \ell (Q)\le {\text {dist}}(I^*(\tau ),\Gamma _{{\mathsf T}}),\quad \forall I\in \mathcal {W}^*_Q,\quad \forall \tau \in (0,\tau _0]. \end{array} \end{aligned}$$(3.7)
Moreover, given \(\tau \in (0,\tau _0]\), set
and given \({\mathsf T}'\), a semi-coherent subtree of \({\mathsf T}\), define
Then each of \(\Omega ^\pm _{{\mathsf T}'}\) is a CAD, with Chord-arc constants depending only on \(n,\tau ,\eta , K\), and the ADR/UR constants for \(\partial \Omega \) (see Fig. 1).
Remark 3.4
In particular, for each \({\mathsf T}\subset \mathcal {G}\), if \(Q'\) and Q belong to \({\mathsf T}\), and if \(Q'\) is a dyadic child of Q, then \(U_{Q'}^+\cup U_{Q}^+\) is Harnack Chain connected, and every pair of points \(x,y\in U_{Q'}^+\cup U_Q^+\) may be connected by a Harnack Chain in \(\Omega _E\) of length at most \(C= C(n,\tau ,\eta ,K,\hbox {ADR/UR})\). The same is true for \(U_{Q'}^-\cup U_{Q}^-\).
Remark 3.5
Let \(0<\tau \le \tau _0/2\). Given any \({\mathsf T}\subset \mathcal {G}\), and any semi-coherent subtree \({\mathsf T}'\subset {\mathsf T}\), define \(\Omega _{{\mathsf T}'}^\pm =\Omega _{{\mathsf T}'}^\pm (\tau )\) as in (3.9), and similarly set \(\widehat{\Omega }_{{\mathsf T}'}^\pm =\Omega _{{\mathsf T}'}^\pm (2\tau )\). Then by construction, for any \(x\in \overline{\Omega _{{\mathsf T}'}^\pm }\),
where of course the implicit constants depend on \(\tau \).
As in [35], it will be useful for us to extend the definition of the Whitney region \(U_Q\) to the case that \(Q\in \mathcal {B}\), the “bad” collection of Lemma 3.1. Let \(\mathcal {W}_Q^*\) be the augmentation of \(\mathcal {W}_Q^0\) as constructed in Lemma 3.3, and set
For \(Q \in \mathcal {G}\) we shall henceforth simply write \(\mathcal {W}_Q^\pm \) in place of \(\mathcal {W}_Q^{*,\pm }\). For arbitrary \(Q\in \mathcal {D}(E)\), good or bad, we may then define
Let us note that for \(Q\in \mathcal {G}\), the latter definition agrees with that in (3.8). Note that by construction
for some uniform constants \(C\ge 1\) and \(0<c<1\) (see (3.3), (3.6), and (3.7)). In particular, for every \(Q\in \mathcal {D}\) if follows that
where we recall that \(\mathcal {D}(Q)\) is defined in (2.10).
For future reference, we introduce dyadic sawtooth regions as follows. Given a family \(\mathcal {F}\) of disjoint cubes \(\{Q_j\}\subset \mathcal {D}\), we define the global discretized sawtooth relative to \(\mathcal {F}\) by
i.e., \(\mathcal {D}_{\mathcal {F}}\) is the collection of all \(Q\in \mathcal {D}\) that are not contained in any \(Q_j\in \mathcal {F}\). We may allow \(\mathcal {F}\) to be empty, in which case \(\mathcal {D}_\mathcal {F}=\mathcal {D}\). Given some fixed cube Q, we also define the local discretized sawtooth relative to \(\mathcal {F}\) by
Note that with this convention, \(\mathcal {D}(Q)=\mathcal {D}_{{\emptyset }}(Q)\) (i.e., if one takes \(\mathcal {F}=\emptyset \) in (3.15)).
5 Step 1: the set-up
In the proof of Theorem 1.2, we shall employ a two-parameter induction argument, which is a refinement of the method of “extrapolation” of Carleson measures. The latter is a bootstrapping scheme for lifting the Carleson measure constant, developed by J. L. Lewis [42], and based on the corona construction of Carleson [15] and Carleson and Garnett [16] (see also [4, 5, 29,30,31, 35]).
5.1 Reduction to a dyadic setting
To set the stage for the induction procedure, let us begin by making a preliminary reduction. It will be convenient to work with a certain dyadic version of Definition 2.12. To this end, let \(x\in \Omega \), with \(\delta _{\Omega }(x) < {{\,\mathrm{diam}\,}}(\partial \Omega )\), and set \(\Delta _x=\Delta _x^N=B(x,N\delta _{\Omega }(x))\cap \partial \Omega \), for some fixed \(N\ge 2\) as in Definition 2.9.
Let \(\hat{x}\in \partial \Omega \) be a touching point for x, i.e., \(|x-\hat{x}|=\delta _{\Omega }(x)\). Choose \(x_1\) on the line segment joining x to \(\hat{x}\), with \(\delta _{\Omega }(x_1) = \delta _{\Omega }(x)/2\), and set \(\Delta _{x_1}=B(x_1,N\delta _{\Omega }(x)/2)\cap \partial \Omega \). Note that \(B(x_1,N\delta _{\Omega }(x)/2)\subset B(x,N\delta _{\Omega }(x))\), and furthermore,
We may therefore cover \(\Delta _{x_1}\) by a disjoint collection \(\{Q_i\}_{i=1}^M\subset \mathcal {D}(\partial \Omega )\), of equal length \(\ell (Q_i)\approx \delta _{\Omega }(x)\), such that each \(Q_i\subset \Delta _x\), and such that the implicit constants depend only on n and ADR, and thus the cardinality M of the collection depends on n, ADR, and N. With \(E=\partial \Omega \), we make the Whitney decomposition of the set \(\Omega _E =\mathbb {R}^{n+1}{\setminus } E\) as in Sect. 3 (thus, \(\Omega \subset \Omega _E\)). Moreover, for sufficiently small \(\eta \) and sufficiently large K in (3.6), we then have that \(x\in U_{Q_i}\) for each \(i=1,2,\dots ,M\). By hypothesis, there are constants \(\theta _0\in (0,1],\lambda _0\in (0,1)\), and \(N\ge 2\) as above, such that every \(z\in \Omega \) is a \((\theta _0,\lambda _0,N)\)-weak local John point (Definition 2.9). In particular, this is true for \(x_1\), hence there is a Borel set \(F\subset \Delta _{x_1}\), with \(\sigma (F) \ge \theta _0 \sigma (\Delta _{x_1})\), such that every \(y\in F\) may be connected to \(x_1\) via a \(\lambda _0\)-carrot path. By n-ADR, \(\sigma (\Delta _{x_1})\approx \sum _{i=1}^M\sigma (Q_i)\) and thus by pigeon-holing, there is at least one \(Q_i=:Q\) such that \(\sigma (F\cap Q) \ge \theta _1\sigma (Q)\), with \(\theta _1\) depending only on \(\theta _0\), n and ADR. Moreover, the \(\lambda _0\)-carrot path connecting each \(y\in F\) to \(x_1\) may be extended to a \(\lambda _1\)-carrot path connecting y to x, where \(\lambda _1\) depends only on \(\lambda _0\).
We have thus reduced matters to the following dyadic scenario: let \(Q\in \mathcal {D}(\partial \Omega )\), let \(U_Q=U_{Q,\tau }\) be the associated Whitney region as in (3.11), with \(\tau \le \tau _0/2\) fixed, and suppose that \(U_Q\) meets \(\Omega \) (recall that by construction \(U_Q\subset \Omega _E=\mathbb {R}^{n+1}{\setminus } E\), with \(E=\partial \Omega \)). For \(x\in U_Q\cap \Omega \), and for a constant \(\lambda \in (0,1)\), let
denote the set of \(y\in Q\) which may be joined to x by a \(\lambda \)-carrot path \(\gamma (y,x)\), and for \(\theta \in (0,1]\), set
Remark 4.1
Our goal is to prove that, given \(\lambda \in (0,1)\) and \(\theta \in (0,1]\), there are positive constants \(\eta \) and C, depending on \(\theta ,\lambda \), and the allowable parameters, such that for each \(Q\in \mathcal {D}(\partial \Omega )\), and for each \( x\in T_Q(\theta ,\lambda )\), there is a Chord-arc domain \(\Omega _x\), with uniformly controlled Chord-arc constants, constructed as a union \(\cup _kI_k^*\) of fattened Whitney boxes \(I_k^*\), such that
where \(U_Q^i\) is the particular connected component of \(U_Q\) containing x, and
For some \(Q\in \mathcal {D}(\partial \Omega )\), it may be that \(T_Q\) is empty. On the other hand, by the preceding discussion, each \(x\in \Omega \) belongs to \(T_Q(\theta _1,\lambda _1)\) for suitable \(Q,\theta _1\) and \(\lambda _1\), so that (4.3) (with \(\theta =\theta _1, \lambda =\lambda _1\)) implies
with \(\eta _1\approx \eta \), where Q is the particular \(Q_i\) selected in the previous paragraph. Moreover, since \(x\in T_Q\subset U_Q\), we can modify \(\Omega _x\) if necessary, by adjoining to it one or more fattened Whitney boxes \(I^*\) with \(\ell (I) \approx \ell (Q)\), to ensure that for the modified \(\Omega _x\), it holds in addition that \({\text {dist}}(x,\partial \Omega _x) \gtrsim \ell (Q) \approx \delta _{\Omega }(x)\), and therefore \(\Omega _x\) verifies all the conditions in Definition 2.12.
The rest of this section is therefore devoted to proving that there exists, for a given Q and for each \(x\in T_Q(\theta ,\lambda )\), a Chord-arc domain \(\Omega _x\) satisfying the stated properties (when the set \(T_Q(\theta ,\lambda )\) is not vacuous). To this end, we let \(\lambda \in (0,1)\) (by Remark 4.1, any fixed \(\lambda \le \lambda _1\) will suffice). We also fix positive numbers \(K\gg \lambda ^{-4}\), and \(\eta \le K^{-4/3}\ll \lambda ^4\), and for these values of \(\eta \) and K, we make the bilateral Corona decomposition of Lemma 3.1, so that \(\mathcal {D}(\partial \Omega )=\mathcal {G}\cup \mathcal {B}\). We also construct the Whitney collections \(\mathcal {W}^0_Q\) in (3.6), and \(\mathcal {W}_Q^*\) of Lemma 3.3 for this same choice of \(\eta \) and K.
Given a cube \(Q\in \mathcal {D}(\partial \Omega )\), we set
Thus, \(\mathcal {D}_*(Q)\) consists of the cube Q itself, along with its dyadic children and grandchildren. Let
denote the collection of cubes which are the maximal elements of the trees \({\mathsf T}\) in \(\mathcal {G}\). We define
Given any collection \(\mathcal {D}'\subset \mathcal {D}(\partial \Omega )\), we set
Then \(\mathfrak {m}\) is a discrete Carleson measure, i.e., recalling that \(\mathcal {D}(R)\) is the discrete Carleson region relative to R defined in (2.10), we claim that there is a uniform constant C such that
Indeed, note that for any \(Q'\in \mathcal {D}\), there are at most 3 cubes Q such that \(Q'\in \mathcal {D}_*(Q)\) (namely, \(Q'\) itself, its dyadic parent, and its dyadic grandparent), and that by n-ADR, \(\sigma (Q)\approx \sigma (Q')\), if \(Q'\in \mathcal {D}_*(Q)\). Thus, given any \(R\in \mathcal {D}(\partial \Omega )\),
by Lemma 3.1 part (2). Here, and throughout the remainder of this section, a generic constant C, and implicit constants, are allowed to depend upon the choice of the parameters \(\eta \) and K that we have fixed, along with the usual allowable parameters.
With (4.7) in hand, we therefore have
5.2 Induction hypothesis and outline of proof
As mentioned above, our proof will be based on a two parameter induction scheme. Given \(\lambda \in (0,\lambda _1]\) fixed as above, we recall that the set \(F_{car}(x,Q,\lambda )\) is defined in (4.1). The induction hypothesis, which we formulate for any \(a\ge 0\), and any \(\theta \in (0,1]\) is as follows:

Let us briefly sketch the strategy of the proof. We first fix \(\theta =1\), and by induction on a, establish \(H[M_0,1]\). We then show that there is a fixed \(\zeta \in (0,1)\) such that \(H[M_0,\theta ]\) implies \(H[M_0,\zeta \theta ]\), for every \(\theta \in (0,1]\). Iterating, we then obtain \(H[M_0,\theta _1]\) for any \(\theta _1\in (0,1]\). Now, by (4.8), we have (4.10) with \(a=M_0\), for every \(Q\in \mathcal {D}(\partial \Omega )\). Thus, \(H[M_0,\theta _1]\) may be applied in every cube Q such that \(T_Q(\theta _1,\lambda )\) (see (4.2)) is non-empty, with \(V_Q=\{x\}\), for any \(x\in T_Q(\theta _1,\lambda )\). For \(\lambda \le \lambda _1\), and an appropriate choice of \(\theta _1\), by Remark 4.1, we obtain the existence of a Chord-arc domain \(\Omega _x\) verifying the conditions of Definition 2.12, and thus that Theorem 1.2 holds, as desired.
6 Some geometric observations
We begin with some preliminary observations. In what follows we have fixed \(\lambda \in (0,\lambda _1]\) and two positive numbers \(K\gg \lambda ^{-4}\), and \(\eta \le K^{-4/3}\ll \lambda ^4\), for which the bilateral Corona decomposition of \(\mathcal {D}(\partial \Omega )\) in Lemma 3.1 is applied. We now fix \(k_0\in \mathbb {N}\), \(k_0\ge 4\), such that
Lemma 5.1
Let \(Q\in \mathcal {D}(\partial \Omega )\), and suppose that \(Q'\subset Q\), with \(\ell (Q')\le 2^{-k_0}\ell (Q)\). Suppose that there are points \(x\in U_Q\cap \Omega \) and \(y\in Q'\), that are connected by a \(\lambda \)-carrot path \(\gamma =\gamma (y,x)\) in \(\Omega \). Then \(\gamma \) meets \(U_{Q'}\cap \Omega \).
Proof
By construction (see (3.6), Lemma 3.3, (3.10) and (3.11)), \(x\in U_Q\) implies that
Since \(2^{-k_0}\ll \eta \), and \(\ell (Q')\le 2^{-k_0}\ell (Q)\), we then have that \(x\in \Omega {\setminus } B\big (y,2\ell (Q')\big )\), so \(\gamma (y,x)\) meets \(B\big (y,2\ell (Q')\big ){\setminus } B\big (y,\ell (Q')\big )\), say at a point z. Since \(\gamma (y,x)\) is a \(\lambda \)-carrot path, and since we have previously specified that \(\eta \ll \lambda ^4\),
On the other hand
In particular then, the Whitney box I containing z must belong to \(\mathcal {W}^0_{Q'}\) (see (3.6)), so \(z\in U_{Q'}\). Note that \(z\in \Omega \) since \(\gamma \subset \Omega \). \(\square \)
We shall also require the following. We recall that by Lemma 3.3, for \(Q\in {\mathsf T}\subset \mathcal {G}\), the Whitney region \(U_Q\) has the splitting \(U_Q = U_Q^+\cup U_Q^-\), with \(U_Q^+\) (resp. \(U_Q^-\)) lying above (resp., below) the Lipschitz graph \(\Gamma _{\mathsf T}\) of Lemma 3.1.
Lemma 5.2
Let \(Q'\subset Q\), and suppose that \(Q'\) and Q both belong to \(\mathcal {G}\), and moreover that both \(Q'\) and Q belong to the same tree \({\mathsf T}\subset \mathcal {G}\). Suppose that \(y\in Q'\) and \(x\in U_Q\cap \Omega \) are connected via a \(\lambda \)-carrot path \(\gamma (y,x)\) in \(\Omega \), and assume that there is a point \(z\in \gamma (y,x) \cap U_{Q'}\cap \Omega \) (by Lemma 5.1 we know that such a z exists provided \(\ell (Q')\le 2^{-k_0} \ell (Q)\)). Then \(x\in U_Q^+\) if and only if \(z\in U_{Q'}^+\) (thus, \(x\in U_Q^-\) if and only if \(z\in U_{Q'}^-\)).
Proof
We suppose for the sake of contradiction that, e.g., \(x\in U_Q^+\), and that \(z\in U_{Q'}^-\). Thus, in traveling from y to z and then to x along the path \(\gamma (y,x)\), one must cross the Lipschitz graph \(\Gamma _{\mathsf T}\) at least once between z and x. Let \(y_1\) be the first point on \(\gamma (y,x)\cap \Gamma _{\mathsf T}\) that one encounters after z, when traveling toward x. By Lemma 3.3,
where we recall that we have fixed \(K\gg \lambda ^{-4}\). Consequently, \(\ell \big (\gamma (y,x)\big ) \ll K^{3/4} \ell (Q)\), so in particular, \(\gamma (y,x)\subset B_Q^*:= B\big (x_Q,K\ell (Q)\big )\), as in Lemma 3.1. On the other hand, \(y_1\notin B^*_{Q'}\). Indeed, \(y_1\in \Gamma _{\mathsf T}\), so if \(y_1 \in B^*_{Q'}\), then by (3.1), \(\delta _{\Omega }(y_1) \le \eta \ell (Q')\). However,
where in the last step we have used Lemma 3.3. This contradicts our choice of \(\eta \ll \lambda ^4\).
We now form a chain of consecutive dyadic cubes \(\{P_i\}\subset \mathcal {D}(Q)\), connecting \(Q'\) to Q, i.e.,
where the introduced notation \(P_i\lhd P_{i+1}\) means that \(P_i\) is the dyadic child of \(P_{i+1}\), that is, \(P_i\subset P_{i+1}\) and \(\ell (P_{i+1})=2\ell (P_i)\). Let \(P:=P_{i_0}\), \(1\le i_0\le M+1\), be the smallest of the cubes \(P_i\) such that \(y_1 \in B_{P_i}^*\). Setting \(P':= P_{i_0-1}\), we then have that \(y_1 \in B_P^*\), and \(y_1\notin B_{P'}^*\). By the coherency of \({\mathsf T}\), it follows that \(P\in {\mathsf T}\), so by (3.1),
On the other hand,
and therefore, since \(y\in Q' \subset P'\),
Combining (5.2) and (5.3), we see that \(\lambda \lesssim \eta /K\), which contradicts that we have fixed \(\eta \ll \lambda ^4\), and \(K\gg \lambda ^{-4}\). \(\square \)
Lemma 5.3
Fix \(\lambda \in (0,1)\). Given \(Q\in \mathcal {D}(\partial \Omega )\) and a non-empty set \(V_Q\subset U_Q\cap \Omega \), such that each \( x \in V_Q\) may be connected by a \(\lambda \)-carrot path to some \(y\in Q\), set
where we recall that \(F_{car}(x,Q,\lambda )\) is the set of \(y\in Q\) that are connected via a \(\lambda \)-carrot path to x (see (4.1)). Let \(Q'\subset Q\) be such that \(\ell (Q')\le 2^{-k_0} \ell (Q)\) and \(F_Q\cap Q'\ne \emptyset \). Then, there exists a non-empty set \(V_{Q'}\subset U_{Q'}\cap \Omega \) such that if we define \(F_{Q'}\) as in (5.4) with \(Q'\) replacing Q, then \( F_Q\cap Q'\subset F_{Q'}\). Moreover, for every \(y\in V_{Q'}\), there exist \(x\in V_Q\), \(y\in Q'\) (indeed \(y\in F_Q\cap Q'\)) and a \(\lambda \)-carrot path \(\gamma =\gamma (y,x)\) such that \(y\in \gamma \).
Proof
For every \(y\in F_Q\cap Q'\), by definition of \(F_Q\), there exist \(x\in V_Q\) and a \(\lambda \)-carrot path \(\gamma =\gamma (y,x)\). By Lemma 5.1, there is a point \(y'=y'(y)\in \gamma \cap U_{Q'}\cap \Omega \) (there can be more than one \(y'\), but we just pick one). Note that the sub-path \(\gamma (y,y')\subset \gamma (y,x)\) is also a \(\lambda \)-carrot path, for the same constant \(\lambda \). All the conclusions in the lemma follow easily from the construction by letting \(V_{Q'}=\bigcup _{y\in F_Q\cap Q'} y'(y)\). \(\square \)
Remark 5.4
It follows easily from the previous proof that under the same assumptions, if one further assumes that \(\ell (Q')<2^{-k_0}\,\ell (Q)\), we can then repeat the argument with both \(Q'\) and \((Q')^*\) (the dyadic parent of \(Q'\)) to obtain respectively \(V_{Q'}\) and \(V_{(Q')^*}\). Moreover, this can be done in such a way that every point in \(V_{Q'}\) (resp. \(V_{(Q')^*}\)) belongs to a \(\lambda \)-carrot path which also meets \(V_{(Q')^*}\) (resp. \(V_{Q'}\)), connecting \(U_Q\) and \(Q'\).
Given a family \(\mathcal {F}:=\{Q_j\}\subset \mathcal {D}(\partial \Omega )\) of pairwise disjoint cubes, we recall that the “discrete sawtooth” \(\mathcal {D}_\mathcal {F}\) is the collection of all cubes in \(\mathcal {D}(\partial \Omega )\) that are not contained in any \(Q_j\in \mathcal {F}\) (see (3.14)), and we define the restriction of \(\mathfrak {m}\) (cf. (4.5), (4.6)) to the sawtooth \(\mathcal {D}_\mathcal {F}\) by
We then set
Let us note that we may allow \(\mathcal {F}\) to be empty, in which case \(\mathcal {D}_\mathcal {F}=\mathcal {D}\) and \(\mathfrak {m}_\mathcal {F}\) is simply \(\mathfrak {m}\). We note that the following claim, and others in the sequel, remain true when \(\mathcal {F}\) is empty; sometimes trivially so, and sometimes with some straightforward changes that are left to the interested reader.
Claim 5.5
Given \(Q\in \mathcal {D}(\partial \Omega )\), and a family \(\mathcal {F}=\mathcal {F}_Q:=\{Q_j\}\subset \mathcal {D}(Q){\setminus } \{Q\}\) of pairwise disjoint sub-cubes of Q, if \(\Vert \mathfrak {m}_\mathcal {F}\Vert _{\mathcal {C}(Q)} \le 1/2\), then each \(Q' \in \mathcal {D}_{\mathcal {F}}\cap \mathcal {D}(Q)\), each \(Q_j\in \mathcal {F}\), and every dyadic child \(Q_j'\) of any \(Q_j\in \mathcal {F}\), belong to the good collection \(\mathcal {G}\), and moreover, every such cube belongs to the same tree \({\mathsf T}\subset \mathcal {G}\). In particular, \({\mathsf T}' :=\mathcal {D}_\mathcal {F}\cap \mathcal {D}(Q)\) is a semi-coherent subtree of \({\mathsf T}\), and so is \({\mathsf T}'':= (\mathcal {D}_\mathcal {F}\cup \mathcal {F}\cup \mathcal {F}')\cap \mathcal {D}(Q)\), where \(\mathcal {F}'\) denotes the collection of all dyadic children of cubes in \(\mathcal {F}\).
Indeed, if any \(Q' \in \mathcal {D}_{\mathcal {F}}\cap \mathcal {D}(Q)\) were in \(\mathcal {M}\cup \mathcal {B}\) (recall that \(\mathcal {M}:=\{Q({\mathsf T})\}_{{\mathsf T}\subset \mathcal {G}}\) is the collection of cubes which are the maximal elements of the trees \({\mathsf T}\) in \(\mathcal {G}\)), then by construction \(\alpha _{Q'}=\sigma (Q')\) for that cube (see (4.5)), so by definition of \(\mathfrak {m}\) and \(\mathfrak {m}_\mathcal {F}\), we would have
a contradiction. Similarly, if some \(Q_j\in \mathcal {F}\) (respectively, \(Q_j'\in \mathcal {F}'\)) were in \(\mathcal {M}\cup \mathcal {B}\), then its dyadic parent (respectively, dyadic grandparent) \(Q_j^*\) would belong to \(\mathcal {D}_{\mathcal {F}}\cap \mathcal {D}(Q)\), and by definition \(\alpha _{Q_j^*}=\sigma (Q_j^*)\), so again we reach a contradiction. Consequently, \(\mathcal {F}\cup \mathcal {F}'\cup (\mathcal {D}_\mathcal {F}\cap \mathcal {D}(Q))\) does not meet \(\mathcal {M}\cup \mathcal {B}\), and the claim follows.
7 Construction of chord-arc subdomains
For future reference, we now prove the following. Recall that for \(Q\in \mathcal {G}\), \(U_Q\) has precisely two connected components \(U_Q^\pm \) in \(\mathbb {R}^{n+1}{\setminus } \partial \Omega \).
Lemma 6.1
Let \(Q\in \mathcal {D}(\partial \Omega )\), let \(k_1\) be such that \(2^{k_1}> 2^{k_0}\gg 100 K\), see (5.1), and suppose that there is a family \(\mathcal {F}=\mathcal {F}_Q:=\{Q_j\}\subset \mathcal {D}(Q){\setminus } \{Q\}\) of pairwise disjoint sub-cubes of Q, with \(\Vert \mathfrak {m}_\mathcal {F}\Vert _{\mathcal {C}(Q)} \le 1/2\) (hence by Claim 5.5, there is some \({\mathsf T}\subset \mathcal {G}\) with \({\mathsf T}\supset (\mathcal {D}_\mathcal {F}\cup \mathcal {F}\cup \mathcal {F}')\cap \mathcal {D}(Q)\)), and a non-empty subcollection \(\mathcal {F}^*\subset \mathcal {F}\), such that:
-
(i)
\(\ell (Q_j) \le 2^{-k_1}\ell (Q)\), for each cube \(Q_j\in \mathcal {F}^*\);
-
(ii)
the collection of balls \(\big \{\kappa B^*_{Q_j}:= B\big (x_{Q_j},\kappa K \ell (Q_j)\big ):\, Q_j \in \mathcal {F}^* \big \}\) is pairwise disjoint, where \(\kappa \gg K^4 \) is a sufficiently large positive constant; and
-
(iii)
\(\mathcal {F}^*\) has a disjoint decomposition \(\mathcal {F}^*=\mathcal {F}^*_+ \cup \mathcal {F}^*_-\), where for each \(Q_j \in \mathcal {F}_\pm ^*\), there is a Chord-arc subdomain \(\Omega _{Q_j}^\pm \subset \Omega \), consisting of a union of fattened Whitney cubes \(I^*\), with \(U_{Q_j}^\pm \subset \Omega _{Q_j}^\pm \subset B^*_{Q_j}:= B(x_{Q_j},K \ell (Q_j))\), and with uniform control of the Chord-arc constants.
Define a semi-coherent subtree \({\mathsf T}^*\subset {\mathsf T}\) by
and for each choice of ± for which \(\mathcal {F}^*_\pm \) is non-empty, set
Then for \(\kappa \) large enough, depending only on allowable parameters, \(\Omega _Q^\pm \) is a Chord-arc domain, with chord arc constants depending only on the uniformly controlled Chord-arc constants of \(\Omega _{Q_j}^\pm \) and on the other allowable parameters. Moreover, \( \Omega _Q^\pm \subset B_Q^*\cap \Omega = B(x_Q,K\ell (Q))\cap \Omega \), and \(\Omega _Q^\pm \) is a union of fattened Whitney cubes.
Remark 6.2
Note that we define \(\Omega _Q^\pm \) if and only if \(\mathcal {F}^*_\pm \) is non-empty. It may be that one of \(\mathcal {F}^*_+, \mathcal {F}^*_-\) is empty, but \(\mathcal {F}^*_+\) and \(\mathcal {F}^*_-\) cannot both be empty, since \(\mathcal {F}^*\) is non-empty by assumption.
Proof of Lemma 6.1
Without loss of generality we may assume that \(\Omega _{Q_j}^{\pm }\) is not contained in \(\Omega _{{\mathsf T}^*}^\pm \) for all \(Q_j\in \mathcal {F}^*\) (otherwise we can drop those cubes from \(\mathcal {F}^*\)). On the other hand, we notice that \(\Omega _Q^\pm \) is a union of (open) fattened Whitney cubes (assuming that it is non-empty): each \(\Omega _{Q_j}^\pm \) has this property by assumption, as does \(\Omega _{{\mathsf T}^*}^\pm \) by construction.
We next observe that if \(\Omega _Q^+\) (resp. \(\Omega _Q^-\)) is non-empty, then it is contained in \(\Omega \). Indeed, by construction, \(\Omega _Q^+\) is non-empty if and only if \(\mathcal {F}^*_+\) is non-empty. In turn, \(\mathcal {F}^*_+\) is non-empty if and only if there is some \(Q_j\in \mathcal {F}^*\) such that \(U_{Q_j}^+\subset \Omega _{Q_j}^+ \subset \Omega \), and moreover, the latter is true for every \(Q_j \in \mathcal {F}^*_+\), by definition. But each such \(Q_j\) belongs to \({\mathsf T}^*\), hence \(U_{Q_j}^+\subset \Omega ^+_{{\mathsf T}^*}\), again by construction (see (3.9)). Thus, \(\Omega _{{\mathsf T}^*}^+\) meets \(\Omega \), and since \(\Omega _{{\mathsf T}^*}^+\subset \mathbb {R}^{n+1}{\setminus } \partial \Omega \), therefore \(\Omega _{{\mathsf T}^*}^+\subset \Omega \). Combining these observations, we see that \(\Omega _Q^+\subset \Omega \). Of course, the same reasoning applies to \(\Omega _Q^-\), provided it is non-empty.
In addition, since \({\mathsf T}^*\subset {\mathsf T}\), and since \(K \gg K^{1/2}\), by Lemma 3.3 we have \(\Omega _{{\mathsf T}^*}^\pm \subset B_Q^*= B(x_Q,K\ell (Q))\). Furthermore, \(\Omega _{Q_j}^\pm \subset B^*_{Q_j}:= B(x_{Q_j},K \ell (Q_j))\), and since \(\ell (Q_j) \le 2^{-k_1}\ell (Q)\le (100K)^{-1}\ell (Q)\), we obtain
Thus, in particular, \(\Omega _{Q_j}^\pm \subset B_Q^*\), and therefore also \(\Omega _Q^\pm \subset B_Q^*\).
It therefore remains to establish the Chord-arc properties. It is straightforward to prove the interior corkscrew condition and the upper n-ADR bound, and we omit the details. Thus, we must verify the Harnack Chain condition, the lower n-ADR bound, and the exterior corkscrew condition.
7.1 Harnack Chains
Suppose, without loss of generality, that \(\Omega _Q^+\) is non-empty, and let \(x,y\in \Omega _Q^+\), with \(|x-y|= r\). If x and y both lie in \(\Omega _{{\mathsf T}^*}^+\), or in the same \(\Omega _{Q_j}^+\), then we can connect x and y by a suitable Harnack path, since each of these domains is Chord-arc. Thus, we may suppose either that 1) \(x\in \Omega _{{\mathsf T}^*}^+\) and y lies in some \(\Omega _{Q_j}^+\), or that 2) x and y lie in two distinct \(\Omega _{Q_{j_1}}^+\) and \(\Omega _{Q_{j_2}}^+\). We may reduce the latter case to the former case: by the separation property (ii) in Lemma 6.1, we must have \(r\gtrsim \kappa \max \big ({{\,\mathrm{diam}\,}}(\Omega _{Q_{j_1}}^+),{{\,\mathrm{diam}\,}}(\Omega _{Q_{j_2}}^+)\big )\), so given case 1), we can connect \(x\in \Omega _{Q_{j_1}}^+\) to the center \(z_1\) of some \(I_1^*\subset U^+_{Q_1}\), and \(y\in \Omega _{Q_{j_2}}^+\) to the center \(z_2\) of some \(I_2\subset U^+_{Q_2}\), where \(Q_1,Q_2 \in {\mathsf T}^*\), with \(Q_{j_i}\subset Q_i\subset Q\), and \(\ell (Q_i)\approx r\), \(i=1,2\). Finally, we can connect \(z_1\) and \(z_2\) using that \(\Omega _{{\mathsf T}^*}^+\) is Chord-arc.
Hence, we need only construct a suitable Harnack Chain in Case 1). We note that by assumption and construction, \(U_{Q_j}^+ \subset \Omega _{{\mathsf T}^*}^+ \cap \Omega _{Q_j}^+\).
Suppose first that
where \(c'\le 1\) is a sufficiently small positive constant to be chosen. Since \(y \in \Omega ^+_{Q_j} \subset B_{Q_j}^*\), we then have that \(x \in 2 B_{Q_j}^*\), so by the construction of \(\Omega _{{\mathsf T}^*}^+\) and the separation property (ii), it follows that \(\delta _{\Omega }(x) \ge c \ell (Q_j)\), where c is a uniform constant depending only on the allowable parameters (in particular, this fact is true for all \(x \in \Omega _{{\mathsf T}^*}^+ \cap 2 B_{Q_j}^*\), so it does not depend on the choice of \(c'<1\)). Now choosing \(c'\le c/2\) (eventually, it may be even smaller), we find that \(\delta _{\Omega }(y) \ge (c/2)\ell (Q_j)\). Moreover, \(y \in \Omega _{Q_j}^+ \subset B_{Q_j}^*\) implies that \(\delta _{\Omega }(y) \le K\ell (Q_j)\). Also, since \(x\in 2B_{Q_j}^*\) we have that \(\delta _{\Omega }(x) \le 2K\ell (Q_j)\). Since \(\Omega _{Q_j}^+\) and \(\Omega _{{\mathsf T}^*}^+\) are each the interior of a union of fattened Whitney cubes, it follows that there are Whitney cubes I and J, with \(x\in I^*\), \(y\in J^*\), and
where the implicit constants depend on K. For \(c'\) small enough in (6.2), depending on the implicit constants in the last display, and on the parameter \(\tau \) in (3.4), this can happen only if \(I^*\) and \(J^*\) overlap (recall that we have fixed \(\tau \) small enough that \(I^*\) and \(J^*\) overlap if and only if I and J have a boundary point in common), in which case we may trivially connect x and y by a suitable Harnack Chain.
On the other hand, suppose that
Let \(z \in U_{Q_j}^+ \subset \Omega _{{\mathsf T}^*}^+ \cap \Omega _{Q_j}^+\), with \({\text {dist}}(z, \partial \Omega _Q^+) \gtrsim \ell (Q_j)\) (we may find such a z, since \(U_{Q_j}^+\) is a union of fattened Whitney cubes, all of length \(\ell (I^*) \approx \ell (Q_j)\); just take z to be the center of such an \(I^*\)). We may then construct an appropriate Harnack Chain from y to x by connecting y to z via a Harnack Chain in the Chord-arc domain \(\Omega _{Q_j}^+\), and z to x via a Harnack Chain in the Chord-arc domain \(\Omega _{{\mathsf T}^*}^+\).
7.2 Lower n-ADR and exterior corkscrews
We will establish these two properties essentially simultaneously. Again suppose that, e.g., \(\Omega _Q^+\) is non-empty. Let \(x \in \partial \Omega _Q^+\), and consider B(x, r), with \(r < {{\,\mathrm{diam}\,}}\Omega _Q^+ \approx _K\ell (Q)\). Our main goal at this stage is to prove the following:
with c a uniform positive constant depending only upon allowable parameters (including \(\kappa \)). Indeed, momentarily taking this estimate for granted, we may combine (6.3) with the interior corkscrew condition to deduce the lower n-ADR bound via the relative isoperimetric inequality [24, p. 190]. In turn, with both the lower and upper n-ADR bounds in hand, (6.3) implies the existence of exterior corkscrews (see, e.g., [31, Lemma 5.7]).
Thus, it is enough to prove (6.3). We consider the following cases.
Case 1: B(x, r/2) does not meet \(\partial \Omega _{Q_j}^+\) for any \(Q_j \in \mathcal {F}^*_+\). In this case, the exterior corkscrew for \(\Omega _{{\mathsf T}^*}^+\) associated with B(x, r/2) easily implies (6.3).
Case 2: B(x, r/2) meets \(\partial \Omega _{Q_j}^+\) for at least one \(Q_j \in \mathcal {F}^*_+\), and \(r \le \kappa ^{1/2} \ell (Q_{j_0})\), where \(Q_{j_0}\) is chosen to have the largest length \(\ell (Q_{j_0})\) among those \(Q_j\) such that \(\partial \Omega _{Q_j}^+\) meets B(x, r/2). We now further split the present case into subcases.
Subcase 2a: B(x, r/2) meets \(\partial \Omega ^+_{Q_{j_0}}\) at a point z with \(\delta _{\Omega }(z) \le (M\kappa ^{1/2})^{-1} \ell (Q_{j_0})\), where M is a large number to be chosen. Then \(B(z, (M\kappa ^{1/2})^{-1} r) \subset B(x,r)\), for M large enough. In addition, we claim that \(B(z, (M\kappa ^{1/2})^{-1} r)\) misses \(\Omega _{{\mathsf T}^*}^+\cup \big (\cup _{j\ne j_0} \Omega _{Q_j}^+\big )\). The fact that \(B(z, (M\kappa ^{1/2})^{-1} r)\) misses every other \(\Omega _{Q_j}^+, j\ne j_0\), follows immediately from the restriction \(r \le \kappa ^{1/2} \ell (Q_{j_0})\), and the separation property (ii). To see that \(B(z, (M\kappa ^{1/2})^{-1} r)\) misses \(\Omega _{{\mathsf T}^*}^+\), note that if \(|z-y|< (M\kappa ^{1/2})^{-1} r\), then
for M large. On the other hand,
by the construction of \(\Omega _{{\mathsf T}^*}^+\) and the separation property (ii). Thus, the claim follows, for a sufficiently large (fixed) choice of M. Since \(B(z, (M\kappa ^{1/2})^{-1} r)\) misses \(\Omega _{{\mathsf T}^*}^+\) and all other \(\Omega _{Q_j}^+\), we inherit an exterior corkscrew point in the present case (depending on M and \(\kappa \)) from the Chord-arc domain \(\Omega _{Q_{j_0}}^+\). Again (6.3) follows.
Subcase 2b: \(\delta _{\Omega }(z) \ge (M\kappa ^{1/2})^{-1} \ell (Q_{j_0})\), for every \(z\in B(x,r/2)\cap \partial \Omega _{Q_{j_0}}^+\) (hence \(\delta _{\Omega }(z) \approx _{\kappa ,K} \ell (Q_{j_0})\), since \(\Omega ^+_{Q_{j_0}} \subset B^*_{Q_{j_0}}\)). We claim that consequently, \(x\in \partial I^*\), for some I with \(\ell (I) \approx \ell (Q_{j_0}) \gtrsim r\), such that \(\text {int}\, I^* \subset \Omega _Q^+\). To see this, observe that it is clear if \(x\in \partial \Omega _{Q_{j_0}}^+\) (just take \(z=x\)). Otherwise, by the separation property (ii), the remaining possibility in the present scenario is that \(x\in \partial U_{Q'}^+\cap \partial \Omega _{{\mathsf T}^*}^+\), for some \(Q'\in {\mathsf T}^*\) with \(Q_{j_0}\subset Q'\), in which case \(\delta _{\Omega }(x)\approx \ell (Q')\ge \ell (Q_{j_0})\). Since also \(\delta _{\Omega }(x)\le |x-z|+\delta _{\Omega }(z)\lesssim _{\kappa , K}\ell (Q_{j_0})\), for any \(z\in B(x,r/2)\cap \partial \Omega ^+_{Q_{j_0}}\), the claim follows.
On the other hand, since \(x\in \partial \Omega _Q^+\), there is a \(J\in \mathcal {W}\) with \(\ell (J) \approx \ell (Q_{j_0})\), such that \(J^*\) is not contained in \(\Omega _Q^+\). We then have an exterior corkscrew point in \(J^* \cap B(x,r)\), and (6.3) follows in this case.
Case 3: B(x, r/2) meets \(\partial \Omega _{Q_j}^+\) for at least one \(Q_j \in \mathcal {F}^*_+\), and \(r > \kappa ^{1/2} \ell (Q_{j_0})\), where as above \(Q_{j_0}\) has the largest length \(\ell (Q_{j_0})\) among those \(Q_j\) such that \(\partial \Omega _{Q_j}^+\) meets B(x, r/2). In particular then, \(r \gg 2K \ell (Q_{j_0})={{\,\mathrm{diam}\,}}(B^*_{Q_{j_0}})\ge {{\,\mathrm{diam}\,}}(\Omega ^+_{Q_{j_0}})\), since we assume \(\kappa \gg K^4\).
We next claim that B(x, r/4) contains some \(x_1 \in \partial \Omega _{{\mathsf T}^*}^+ \cap \partial \Omega _Q^+\). This is clear if \(x\in \partial \Omega _{{\mathsf T}^*}^+\) by taking \(x_1=x\). Otherwise, \(x\in \partial \Omega _{Q_j}^+\) for some \(Q_j\in \mathcal {F}^*\). Note that \(U_{Q_j}^{\pm }\subset B(x_{Q_j}, K\ell (Q_j))\subset B(x, 2 K\ell (Q_{j}))\). Also, \(U_{Q_j}^{\pm }\subset \Omega _{{\mathsf T}^*}^\pm \), by construction. On the other hand we note that if \(z\in U_Q^{\pm }\) we have by (3.12)
by our choice of \(k_1\). By this fact, and the definition of \(\Omega _{{\mathsf T}^*}\), we have
Using then that \(\Omega _{{\mathsf T}^*}^\pm \) is connected, we see that a path within \(\Omega _{{\mathsf T}^*}^\pm \) joining \(U_{Q_j}^{\pm }\) with \(U_{Q}^{\pm }\) must meet \(\partial B(x,3K\ell (Q_{j}))\). Hence we can find \(y^\pm \in \Omega _{{\mathsf T}^*}^\pm \cap \partial B(x,3K\ell (Q_{j}))\). By Lemma 3.3, \(\Omega _{{\mathsf T}^*}^+\) and \(\Omega _{{\mathsf T}^*}^-\) are disjoint (they live respectively above and below the graph \(\Gamma _{{\mathsf T}}\)), so a path joining \(y^+\) and \(y^-\) within \(\partial B(x,3K\ell (Q_{j}))\) meets some \(x_1\in \partial \Omega _{{\mathsf T}^*}^+\cap \partial B(x,3K\ell (Q_{j}))\). On the other hand, \(x_1\notin \overline{\Omega _{Q_j}^+}\), since \(\overline{\Omega _{Q_j}^+}\subset \overline{B_{Q_j}^*}\subset B(x,3K\ell (Q_{j}))\). Furthermore, \(x_1\in \partial B(x,3K\ell (Q_{j}))\subset \kappa B_{Q_j}^*\), so by assumption (ii), we necessarily have that \(x_1\notin \overline{\Omega _{Q_k}^+}\) for \(k\ne j\). Thus, \(x_1\in \partial \Omega _Q^+\), and moreover, since B(x, r/2) meets \(\partial \Omega _{Q_j}^+\) (at x) we have \(\ell (Q_j)\le \ell (Q_{j_0})\). Therefore, \(x_1\) is the claimed point, since in the current case \(3K\ell (Q_{j})\le 3K\ell (Q_{j_0}) \ll r\).
With the point \(x_1\) in hand, we note that
By the exterior corkscrew condition for \(\Omega _{{\mathsf T}^*}^+\),
for some constant \(c_1\) depending only on n and the ADR/UR constants for \(\partial \Omega \), by Lemma 3.3. Also, for each \(\Omega ^+_{Q_j}\) whose boundary meets \(B(x_1,r/4) {\setminus } \overline{\Omega _{{\mathsf T}^*}^+}\) (and thus meets B(x, r/2)),
in the present scenario. Consequently, \(\kappa ^{1/4}B_{Q_j}^* \subset B(x_1,r/2)\), for all such \(Q_j\).
We now make the following claim.
Claim 6.3
On has
for some \(c_2>0\) depending only on allowable parameters.
Observe that by the second containment in (6.4), we obtain (6.3) as an immediate consequence of (6.7), and thus the proof will be complete once we have established Claim 6.3.
Proof of Claim 6.3
To prove the claim, we suppose first that
where the sum runs over those j such that \(\overline{B_{Q_j}^*}\) meets \(B(x_1,r/4){\setminus } \overline{\Omega _{{\mathsf T}^*}^+}\), and \(c_1\) is the constant in (6.5). In that case, (6.7) holds with \(c_2 = c_1/2\) (and even with \(B(x_1,r/4)\)), by definition of \(\Omega ^+_Q\) (see (6.1)), and the fact that \(\Omega _{Q_j} \subset B_{Q_j}^*\). On the other hand, if (6.8) fails, then summing over the same subset of indices j, we have
We now make a second claim:
Claim 6.4
For j appearing in the previous sum, we have
for some uniform \(c>0\).
Taking the latter claim for granted momentarily, we insert estimate (6.10) into (6.9) and sum, to obtain
By the separation property (ii), the balls \(\kappa ^{1/4} B^*_{Q_{j}}\) are pairwise disjoint, and by assumption \(\Omega _{Q_j}^+\subset B_{Q_j}^*\). Thus, for any given \(j_1\), \(\kappa ^{1/4} B^*_{Q_{j_1}} {\setminus } \overline{B^*_{Q_{j_1}}}\) misses \(\cup _j \overline{\Omega ^+_{Q_j}}\). Moreover, as noted above (see (6.6) and the ensuing comment), \(\kappa ^{1/4}B_{Q_j}^* \subset B(x_1,r/2)\) for each j under consideration in (6.8)–(6.11). Claim 6.3 now follows. \(\square \)
Proof of Claim 6.4
There are two cases: if \(\frac{1}{2} \kappa ^{1/4} B_{Q_j}^* \subset \mathbb {R}^{n+1}{\setminus } \overline{\Omega _{{\mathsf T}^*}^+}\), then (6.10) is trivial, since \(\kappa \gg 1\). Otherwise, \(\frac{1}{2} \kappa ^{1/4} B_{Q_j}^*\) contains a point \(z\in \partial \Omega _{{\mathsf T}^*}^+\). In the latter case, by the exterior corkscrew condition for \(\Omega _{{\mathsf T}^*}^+\),
since \(\kappa \gg 1\). On the other hand, \( B\big (z, 2^{-1}\kappa ^{1/4}K \ell (Q_j)\big ) \subset \kappa ^{1/4} B_{Q_j}^*\), and (6.10) follows, finishing the proof of Claim 6.4. \(\square \)
Next, (6.4) and (6.7) yield (6.3) in the present case and hence the proof of Lemma 6.1 is complete. \(\square \)
8 Step 2: Proof of \(H[M_0,1]\)
We shall deduce \(H[M_0,1]\) (see Sect. 4.2) from the following pair of claims.
Claim 7.1
\(H[0,\theta ]\) holds for every \(\theta \in (0,1]\).
Proof of Claim 7.1
If \(a=0\) in (4.10), then \(\Vert \mathfrak {m}\Vert _{\mathcal {C}(Q)}=0\), whence it follows by Claim 5.5, with \(\mathcal {F}=\emptyset \), that there is a tree \({\mathsf T}\subset \mathcal {G}\), with \(\mathcal {D}(Q)\subset {\mathsf T}\). Hence \({\mathsf T}':=\mathcal {D}(Q)\) is a coherent subtree of \({\mathsf T}\), so by Lemma 3.3, each of \(\Omega _{{\mathsf T}'}^\pm \) is a CAD, containing \(U_Q^\pm \), respectively, with \(\Omega _{{\mathsf T}'}^\pm \subset B_Q^*\) by (3.13). Moreover, by [35, Proposition A.14]
so that \(\sigma (Q)\le \sigma (\partial \Omega _{{\mathsf T}'}^\pm \cap \partial \Omega ).\) Thus, \(H[0,\theta ]\) holds trivially. \(\square \)
Claim 7.2
There is a uniform constant \(b>0\) such that \(H[a,1] \implies H[a+b,1]\), for all \(a\in [0,M_0)\).
Combining Claims 7.1 and 7.2, we find that \(H[M_0,1]\) holds.
To prove Claim 7.2, we shall require the following.
Lemma 7.3
[31, Lemma 7.2] Suppose that E is an n-ADR set, and let \(\mathfrak {m}\) be a discrete Carleson measure, as in (4.6)–(4.8) above. Fix \(Q\in \mathcal {D}(E)\). Let \(a\ge 0\) and \(b>0\), and suppose that \(\mathfrak {m}\big (\mathcal {D}(Q)\big )\le (a+b)\,\sigma (Q).\) Then there is a family \(\mathcal {F}=\{Q_j\}\subset \mathcal {D}(Q)\) of pairwise disjoint cubes, and a constant C depending only on n and the ADR constant such that
where \(\mathcal {F}_{bad}:= \{Q_j\in \mathcal {F}:\,\mathfrak {m}\big (\mathcal {D}(Q_j){\setminus } \{Q_j\}\big )>\,a\sigma (Q_j)\}\).
We refer the reader to [31, Lemma 7.2] for the proof. We remark that the lemma is stated in [31] in the case that E is the boundary of a connected domain, but the proof actually requires only that E have a dyadic cube structure, and that \(\sigma \) be a non-negative, dyadically doubling Borel measure on E. In our case, we shall of course apply the lemma with \(E=\partial \Omega \), where \(\Omega \) is open, but not necessarily connected.
Proof of Claim 7.2
We assume that H[a, 1] holds, for some \(a\in [0,M_0)\). Let us set \(b= 1/(2C)\), where C is the constant in (7.1). Consider a cube \(Q\in \mathcal {D}(\partial \Omega )\) with \(\mathfrak {m}(\mathcal {D}(Q)) \le (a+b) \sigma (Q)\). Suppose that there is a set \(V_Q\subset U_Q\cap \Omega \) such that (4.11) holds with \(\theta =1\). We fix \(k_1>k_0\) (see (5.1)) large enough so that \(2^{k_1}> 100 K\).
Case 1: There exists \(Q'\in \mathcal {D}_{k_1}(Q)\) (see (2.11)) with \(\mathfrak {m}\big (\mathcal {D}(Q')\big ) \le a\sigma (Q')\).
In the present scenario \(\theta =1\), that is, \(\sigma (F_Q)=\sigma (Q)\) (see (4.11) and (5.4)), which implies \(\sigma (F_Q\cap Q')=\sigma (Q')\). We apply Lemma 5.3 to obtain \(V_{Q'}\subset U_{Q'}\cap \Omega \) and the corresponding \(F_{Q'}\) which satisfies \(\sigma (F_{Q'})=\sigma (Q')\). That is, (4.11) holds for \(Q'\), with \(\theta =1\). Consequently, we may apply the induction hypothesis to \(Q'\), to find \(V^*_{Q'}\subset V_{Q'}\), such that for each \(U_{Q'}^i\) meeting \(V^*_{Q'}\), there is a Chord-arc domain \(\Omega _{Q'}^i \supset U_{Q'}^i\) formed by a union of fattened Whitney cubes with \(\Omega ^i_{Q'}\subset B(x_Q',K\ell (Q'))\cap \Omega \), and
By Lemma 5.3, and since \(k_1>k_0\), each \(y\in V^*_{Q'}\) lies on a \(\lambda \)-carrot path connecting some \(y\in Q'\) to some \(x\in V_Q\); let \(V^{**}_Q\) denote the set of all such x, and let \(\mathbf{U}^{**}_Q\) (respectively, \(\mathbf{U}^*_{Q'}\)) denote the collection of connected components of \(U_Q\) (resp., of \(U_{Q'}\)) which meet \(V^{**}_Q\) (resp., \(V^*_{Q'}\)). By construction, each component \(U_{Q'}^i \in \mathbf{U}^*_{Q'}\) may be joined to some corresponding component in \(\mathbf{U}^{**}_Q\), via one of the carrot paths. After possible renumbering, we designate this component as \(U_Q^i\), we let \(x_i, y_i\) denote the points in \(V_Q^{**}\cap U_Q^i\) and in \(V_Q^*\cap U_{Q'}^i\), respectively, that are joined by this carrot path, and we let \(\gamma _i\) be the portion of the carrot path joining \(x_i\) to \(y_i\) (if there is more than one such path or component, we just pick one). We also let \(V_Q^*=\{x_i\}_i\) be the collection of all of the selected points \(x_i\). We let \(\mathcal {W}_i\) be the collection of Whitney cubes meeting \(\gamma _i\), and we then define
By the definition of a \(\lambda \)-carrot path, since \(\ell (Q')\approx _{k_1}\ell (Q)\), and since \( \Omega ^i_{Q'}\) is a CAD, one may readily verify that \(\Omega ^i_Q\) is also a CAD consisting of a union \(\cup _k I_k^*\) of fattened Whitney cubes \(I_k^*\). We omit the details. Moreover, by construction,
so that the analogue of (7.3) holds with \(Q'\) replaced by Q, and with \(c_a\) replaced by \(c_{k_1} c_a\).
It remains to verify that \(\Omega _Q^i \subset B_Q^* = B(x_Q, K \ell (Q))\). By the induction hypothesis, and our choice of \(k_1\), since \(\ell (Q')=2^{-k_1}\ell (Q)\) we have
Moreover, \(U_Q\subset B_Q^*\), by (3.13). We therefore need only to consider \(I^*\) with \(I\in \mathcal {W}_i\). For such an I, by definition there is a point \(z_i\in I\cap \gamma _i\) and \(y_i\in Q'\), so that \(z_i\in \gamma (y_i,x_i)\) and thus,
where in the last inequality we have used (3.12) and the fact that \(x_i\in U_Q\). Hence, for every \(z\in I^*\) by (3.3)
by our choice of the parameters K and \(\lambda \).
We then obtain the conclusion of \(H[a+b,1]\) in the present case.
Case 2: \(\mathfrak {m}\big (\mathcal {D}(Q')\big ) > a\sigma (Q')\) for every \(Q'\in \mathcal {D}_{k_1}(Q)\).
In this case, we apply Lemma 7.3 to obtain a pairwise disjoint family \(\mathcal {F}=\{Q_j\}\subset \mathcal {D}(Q)\) such that (7.1) and (7.2) hold. In particular, by our choice of \(b=1/(2C)\),
so that the conclusions of Claim 5.5 hold.
We set
define
and let
Then by (7.2)
where \(\rho \in (0,1)\) is defined by
We claim that
Indeed, if this were not true for some \(Q_j\), then by definition of \(\mathcal {F}_{good}\) and pigeon-holing there will be \(Q_j'\in \mathcal {D}(Q_j)\) with \(\ell (Q_j')=2^{-k_1}\,\ell (Q)\) such that \(\mathfrak {m}\big (\mathcal {D}(Q_j')\big )\le a\,\sigma (Q_j')\). This contradicts the assumptions of the current case.
Note also that \(Q\notin \mathcal {F}_{good}\) by (7.9) and \(Q\notin \mathcal {F}_{bad}\) by (7.2), hence \(\mathcal {F}\subset \mathcal {D}(Q){\setminus }\{Q\}\). By (7.4) and Claim 5.5, there is some tree \({\mathsf T}\subset \mathcal {G}\) so that \({\mathsf T}''=(\mathcal {D}_\mathcal {F}\cup \mathcal {F}\cup \mathcal {F}')\cap \mathcal {D}(Q)\) is a semi-coherent subtree of \({\mathsf T}\), where \(\mathcal {F}'\) denotes the collection of all dyadic children of cubes in \(\mathcal {F}\).
Case 2a: \(\sigma (F_0) \ge \frac{1}{2}\, \rho \sigma (Q)\).
In this case, Q has an ample overlap with the boundary of a Chord-arc domain with controlled Chord-arc constants. Indeed, let \({\mathsf T}'=\mathcal {D}_\mathcal {F}\cap \mathcal {D}(Q)\) which, by (7.4) and Claim 5.5, is a semi-coherent subtree of some \({\mathsf T}\subset \mathcal {G}\). Hence, by Lemma 3.3, each of \(\Omega _{{\mathsf T}'}^\pm \) is a CAD with constants depending on the allowable parameters, formed by the union of fattened Whitney boxes, which satisfies \(\Omega _{{\mathsf T}'}^\pm \subset B_Q^*\cap \Omega \) (see (3.8), (3.9), and (3.13)). Moreover, by [35, Proposition A.14] and [31, Proposition 6.3] and our current assumptions,
Recall that in establishing \(H[a+b,1]\), we assume that there is a set \(V_Q\subset U_Q\cap \Omega \) for which (4.11) holds with \(\theta =1\). Pick then \(x\in V_Q\) and set \(V_Q^*:=\{x\}\subset V_Q\). Note that since \(U_Q=U_Q^+\cup U_Q^-\) it follows that x belongs to either \(U_Q^+\cap \Omega \) or \(U_Q^-\cap \Omega \). For the sake of specificity assume that \(x\in U_Q^+\cap \Omega \) hence, in particular, \(U_Q^+\subset \Omega _{{\mathsf T}'}^+\subset \Omega \). Note also that \(U_Q^+\) is the only component of \(U_Q\) meeting \(V_Q^*\). All these together give at once that the conclusion of \(H[a+b,1]\) holds in the present case.
Case 2b: \(\sigma (F_0) < \frac{1}{2} \,\rho \sigma (Q)\).
In this case by (7.7)
In addition, by the definition of \(\mathcal {F}_{good}\) (7.6), and pigeon-holing, every \(Q_j\in \mathcal {F}_{good}\) has a dyadic child \(Q_j'\) (there could be more children satisfying this, but we just pick one) so that
Under the present assumptions \(\theta =1\), that is, \(\sigma (F_Q)=\sigma (Q)\) (see (4.11) and (5.4)), hence \(\sigma (F_Q\cap Q_j')=\sigma (Q_j')\). We apply Lemma 5.3 (recall (7.9)) to obtain \(V_{Q_j'}\subset U_{Q_j'}\cap \Omega \) and \(F_{Q_j'}\) which satisfies \(\sigma (F_{Q_j'})=\sigma (Q_j')\). That is, (4.11) holds for \(Q_j'\), with \(\theta =1\). Consequently, recalling that \(Q_j'\in {\mathsf T}\subset \mathcal {G}\) (see Claim 5.5), and applying the induction hypothesis to \(Q_j'\), we find \(V^*_{Q_j'}\subset V_{Q_j'}\), such that for each \(U_{Q_j'}^\pm \) meeting \(V^*_{Q_j'}\), there is a Chord-arc domain \(\Omega _{Q_j'}^\pm \supset U_{Q_j'}^\pm \) formed by a union of fattened Whitney cubes with \(\Omega ^\pm _{Q_j'}\subset B_{Q_j'}^*\cap \Omega \). Moreover, since in particular, the cubes in \(\mathcal {F}\) along with all of their children belong to the same tree \({\mathsf T}\) (see Claim 5.5), the connected component \(U_{Q_j}^\pm \) overlaps with the corresponding component \(U^\pm _{Q_j'}\) for its child, so we may augment \(\Omega _{Q_j'}^\pm \) by adjoining to it the appropriate component \(U_{Q_j}^\pm \), to form a chord arc domain
Moreover, since \(K\gg 1\), and since \(Q_j'\subset Q_j\), we have that \(B^*_{Q_j'} \subset B^*_{Q_j}\), hence \(\Omega ^\pm _{Q_j}\subset B_{Q_j}^*\) by construction.
By a covering lemma argument, for a sufficiently large constant \(\kappa \gg K^4\), we may extract a subcollection \(\mathcal {F}_{good}^*\subset \mathcal {F}_{good}\) so that \( \{ \kappa B_{Q_j}^*\}_{Q_j\in \mathcal {F}_{good}^*}\) is a pairwise disjoint family, and
In particular, by (7.10),
where the implicit constants depend on ADR, K, and the dilation factor \(\kappa \).
By the induction hypothesis, and by construction (7.12) and n-ADR,
where \(\Omega _{Q_j} \) is equal either to \(\Omega _{Q_j}^+\) or to \(\Omega _{Q_j}^-\) (if (7.14) holds for both choices, we arbitrarily set \(\Omega _{Q_j}=\Omega _{Q_j}^+\)).
Combining (7.14) with (7.13), we obtain
We now assign each \(Q_j\in \mathcal {F}_{good}^*\) either to \(\mathcal {F}^*_+\) or to \(\mathcal {F}^*_-\), depending on whether we chose \(\Omega _{Q_j}\) satisfying (7.14) to be \(\Omega _{Q_j}^+\), or \(\Omega _{Q_j}^-\). We note that at least one of the sub-collections \(\mathcal {F}^*_\pm \) is non-empty, since for each j, there was at least one choice of “+’ or “-” such that (7.14) holds for the corresponding choice of \(\Omega _{Q_j}\). Moreover, the two collections are disjoint, since we have arbitrarily designated \(\Omega _{Q_j} = \Omega _{Q_j}^+\) in the case that there were two choices for a particular \(Q_j\).
To proceed, as in Lemma 6.1 we set
which is semi-coherent by construction.
For \(\mathcal {F}^*_\pm \) non-empty, we now define
Observe that by the induction hypothesis, and our construction (see (7.12) and the ensuing comment), for an appropriate choice of ±, \(U_{Q_j}^\pm \subset \Omega _{Q_j} \subset B_{Q_j}^*\), and since \(\ell (Q_j) \le 2^{-k_1} \ell (Q)\), by (7.15) and Lemma 6.1, with \(\mathcal {F}^*=\mathcal {F}^*_{good}\), each (non-empty) choice of \(\Omega _Q^\pm \) defines a Chord-arc domain with the requisite properties.
Thus, we have proved Claim 7.2 and therefore, as noted above, it follows that \(H[M_0,1]\) holds. \(\square \)
9 Step 3: Bootstrapping \(\theta \)
In this last step, we shall prove that there is a uniform constant \(\zeta \in (0,1)\) such that for each \(\theta \in (0,1]\), \(H[M_0,\theta ]\implies H[M_0,\zeta \theta ]\). Since we have already established \(H[M_0,1]\), we then conclude that \(H[M_0,\theta _1]\) holds for any given \(\theta _1\in (0,1]\). As noted above, it then follows that Theorem 1.2 holds, as desired.
In turn, it will be enough to verify the following.
Claim 8.1
There is a uniform constant \(\beta \in (0,1)\) such that for every \(a\in [0,M_0)\), \(\theta \in (0,1]\), \(\vartheta \in (0,1)\), and \(b=1/(2C)\) as in Step 2/Proof of Claim 7.2, if \(H[M_0,\theta ]\) holds, then
Let us momentarily take Claim 8.1 for granted. Recall that by Claim 7.1, \(H[0,\theta ]\) holds for all \(\theta \in (0,1]\). In particular, given \(\theta \in (0,1]\) fixed, for which \(H[M_0,\theta ]\) holds, we have that \(H[0,\theta /2]\) holds. Combining the latter fact with Claim 8.1, and iterating, we obtain that \(H[kb, (1-2^{-1}\beta ^k)\theta ]\) holds. We eventually reach \(H[M_0,(1-2^{-1}\beta ^\nu )\theta ]\), with \(\nu \approx M_0/b\). The conclusion of Step 3 now follows, with \(\zeta := 1-2^{-1}\beta ^\nu \).
Proof of Claim 8.1
The proof will be a refinement of that of Claim 7.2. We are given some \(\theta \in (0,1]\) such that \(H[M_0,\theta ]\) holds, and we assume that \(H[a,(1-\vartheta )\theta ]\) holds, for some \(a\in [0,M_0)\) and \(\vartheta \in (0,1)\). Set \(b= 1/(2C)\), where as before C is the constant in (7.1). Consider a cube \(Q\in \mathcal {D}(\partial \Omega )\) with \(\mathfrak {m}(\mathcal {D}(Q)) \le (a+b) \sigma (Q)\). Suppose that there is a set \(V_Q\subset U_Q\cap \Omega \) such that (4.11) holds with \(\theta \) replaced by \((1-\vartheta \beta )\theta \), for some \(\beta \in (0,1)\) to be determined. Our goal is to show that for a sufficiently small, but uniform choice of \(\beta \), we may deduce the conclusion of the induction hypothesis, with \(\mathcal {C}_{a+b}, c_{a+b}\) in place of \(C_a,c_a\).
By assumption, and recalling the definition of \(F_Q\) in (5.4), we have that (4.11) holds with constant \((1-\vartheta \beta )\theta \), i.e.,
As in the proof of Claim 7.2, we fix \(k_1>k_0\) (see (5.1)) large enough so that \(2^{k_1}> 100K\). There are two principal cases. The first is as follows.
Case 1: There exists \(Q'\in \mathcal {D}_{k_1}(Q)\) (see (2.11)) with \(\mathfrak {m}\big (\mathcal {D}(Q')\big ) \le a\sigma (Q')\).
We split Case 1 into two subcases.
Case 1a: \(\sigma (F_Q\cap Q') \ge (1-\vartheta )\theta \sigma (Q')\).
In this case, we follow the Case 1 argument for \(\theta =1\) in Sect. 7mutatis mutandis, so we merely sketch the proof. By Lemma 5.3, we may construct \(V_{Q'}\) and \(F_{Q'}\) so that \(F_Q\cap Q' = F_{Q'}\) and hence \(\sigma (F_{Q'})\ge (1-\vartheta )\theta \sigma (Q')\). We may then apply the induction hypothesis \(H[a,(1-\vartheta )\theta ]\) in \(Q'\), and then proceed exactly as in Case 1 in Section 7 to construct a subset \(V_Q^*\subset V_Q\) and a family of Chord-arc domains \(\Omega _Q^i\) satisfying the various desired properties, and such that
The conclusion of \(H[a+b, (1-\vartheta \beta )\theta ]\) then holds in the present scenario.
Case 1b: \(\sigma (F_Q\cap Q') < (1-\vartheta )\theta \sigma (Q')\).
By (8.1)
In the scenario of Case 1b, this leads to
that is,
Note that we have the dyadic doubling estimate
where \(M_1=M_1(k_1,n, ADR)\). Combining this estimate with (8.2), we obtain
We now choose \(\beta \le 1/(M_1+1)\), so that \((1-\beta )/M_1 \ge \beta \), and therefore the expression in square brackets is at least 1. Consequently, by pigeon-holing, there exists a particular \(Q''_0\in \mathcal {D}_{k_1}(Q){\setminus }\{Q'\}\) such that
By Lemma 5.3, we can find \(V_{Q''_0}\) such that \(F_Q\cap Q_0'' = F_{Q_0''}\), where the latter is defined as in (5.4), with \(Q_0''\) in place of Q. By assumption, \(H[M_0,\theta ]\) holds, so combining (8.3) with the fact that (4.10) holds with \(a=M_0\) for every \(Q\in \mathcal {D}(\partial \Omega )\), we find that there exists a subset \(V^*_{Q''_0}\subset V_{Q''_0}\), along with a family of Chord-arc domains \(\{\Omega _{Q_0''}^i\}_i\) enjoying all the appropriate properties relative to \(Q_0''\). Using that \(\ell (Q_0'')\approx _{k_1} \ell (Q)\), we may now proceed exactly as in Case 1a above, and also Case 1 in Section 7, to construct \(V_Q^*\) and \(\{\Omega _Q^i\}_i\) such that the conclusion of \(H[a+b, (1-\vartheta \beta )\theta ]\) holds in the present case also.
Case 2: \(\mathfrak {m}\big (\mathcal {D}(Q')\big ) > a\sigma (Q')\) for every \(Q'\in \mathcal {D}_{k_1}(Q)\).
In this case, we apply Lemma 7.3 to obtain a pairwise disjoint family \(\mathcal {F}=\{Q_j\}\subset \mathcal {D}(Q)\) such that (7.1) and (7.2) hold. In particular, by our choice of \(b=1/(2C)\), \(\Vert \mathfrak {m}_\mathcal {F}\Vert _{\mathcal {C}(Q)}\le 1/2\).
Recall that \(F_Q\) is defined in (5.4), and satisfies (8.1). We define \(F_0 =Q{\setminus } (\bigcup _\mathcal {F}Q_j)\) as in (7.5), and \(\mathcal {F}_{good}:= \mathcal {F}{\setminus } \mathcal {F}_{bad}\) as in (7.6). Let \(G_0:= \bigcup _{\mathcal {F}_{good}}Q_j\). Then as above (see (7.7)),
where again \(\rho =\rho (M_0,b)\in (0,1)\) is defined as in (7.8). Just as in Case 2 for \(\theta =1\) in Sect. 7, we have that
(see (7.9)). Hence, the conclusions of Claim 5.5 hold.
We first observe that if \(\sigma (F_0) \ge \varepsilon \sigma (Q)\), for some \(\varepsilon >0\) to be chosen (depending on allowable parameters), then the desired conclusion holds. Indeed, in this case, we may proceed exactly as in the analogous scenario in Case 2a in Sect. 7: the promised Chord-arc domain is again simply one of \(\Omega _{{\mathsf T}'}^\pm \), since at least one of these contains a point in \(V_Q\) and hence in particular is a subdomain of \(\Omega \). The constant \(c_{a+b}\) in our conclusion will depend on \(\varepsilon \), but in the end this will be harmless, since \(\varepsilon \) will be chosen to depend only on allowable parameters.
We may therefore suppose that
Next, we refine the decomposition \(\mathcal {F}= \mathcal {F}_{good}\cup \mathcal {F}_{bad}\). With \(\rho \) as in (7.8) and (8.4), we choose \(\beta < \rho /4\). Set
and define \(\mathcal {F}^{(2)}_{good}:= \mathcal {F}_{good}{\setminus } \mathcal {F}_{good}^{(1)}\). Let
and define \(\mathcal {F}^{(2)}_{bad}:= \mathcal {F}_{bad}{\setminus } \mathcal {F}_{bad}^{(1)}\).
We split the remaining part of Case 2 into two subcases. The first of these will be easy, based on our previous arguments.
Case 2a: There is \(Q_j\in \mathcal {F}^{(1)}_{bad}\) such that \(\ell (Q_j)>2^{-k_1}\,\ell (Q)\).
By definition of \(\mathcal {F}_{bad}^{(1)}\), one has \(\sigma (F_Q\cap Q_j)\ge \theta \sigma (Q_j)\). By pigeon-holing, \(Q_j\) has a descendant \(Q'\) with \(\ell (Q') = 2^{-k_1}\ell (Q)\), such that \(\sigma (F_Q\cap Q')\ge \theta \sigma (Q')\). We may then apply \(H[M_0,\theta ]\) in \(Q'\), and proceed exactly as we did in Case 1b above with the cube \(Q_0''\), which enjoyed precisely the same properties as does our current \(Q'\). Thus, we draw the desired conclusion in the present case.
The main case is the following.
Case 2b: Every \(Q_j\in \mathcal {F}^{(1)}_{bad}\) satisfies \(\ell (Q_j)\le 2^{-k_1}\,\ell (Q)\).
Observe that by definition,
and also
Set \(\mathcal {F}_*:=\mathcal {F}{\setminus } \mathcal {F}_{good}^{(2)}\). For future reference, we shall derive a certain ampleness estimate for the cubes in \(\mathcal {F}_*\). By (8.1),
where in the last step have used (8.6) and (8.7). Observe that
Using (8.9) and (8.10), for \(\varepsilon \ll \big (4\rho ^{-1}-1\big )\vartheta \beta \theta \), we obtain
and thus
We now make the following claim. \(\square \)
Claim 8.2
For \(\varepsilon \) chosen sufficiently small,
Proof of Claim 8.2
If \(\sum _{\mathcal {F}_{good}^{(1)}}\sigma (Q_j)\ge \varepsilon \sigma (Q)\), then we are done. Therefore, suppose that
We have made the decomposition
Consequently
where we have used (8.6), and (8.12) to estimate the contributions of \(F_0\), and of \(\mathcal {F}_{good}^{(1)}\), respectively. This, (8.1), (8.7), and (8.8) yield
In turn, applying (8.10) in the latter estimate, and rearranging terms, we obtain
Recalling that \(G_0=\cup _{\mathcal {F}_{good}}Q_j\), and that \(\mathcal {F}_{good}= \mathcal {F}^{(1)}_{good} \cup \mathcal {F}^{(2)}_{good}\), we further note that by (8.4), choosing \(\varepsilon \ll \rho \), and using (8.6) and (8.12), we find in particular that
Applying (8.15) and the trivial estimate \( \sum _{\mathcal {F}_{bad}^{(2)}}\sigma (Q_j)\le \sigma (Q)\) in (8.14), we then have
Since \(\rho <1\), we conclude, for \(\varepsilon \le (4C)^{-1}\vartheta \beta \theta \), that
and Claim 8.2 follows.
With Claim 8.2 in hand, let us return to the proof of Case 2b of Claim 8.1. We begin by noting that by definition of \(\mathcal {F}_{bad}^{(1)}\), and Lemma 5.3, we can apply \(H[M_0,\theta ]\) to any \(Q_j \in \mathcal {F}_{bad}^{(1)}\), hence for each such \(Q_j\) there is a family of Chord-arc domains \(\{\Omega ^i_{Q_j}\}_i\) satisfying the desired properties.
Now consider \(Q_j\in \mathcal {F}^{(1)}_{good}\). Since \(\mathcal {F}^{(1)}_{good}\subset \mathcal {F}_{good}\), by pigeon-holing \(Q_j\) has a dyadic child \(Q_j'\) satisfying
(there may be more than one such child, but we just pick one). Our immediate goal is to find a child \(Q_j''\) of \(Q_j\), which may or may not equal \(Q_j'\), for which we may construct a family of Chord-arc domains \(\{\Omega ^i_{Q''_j}\}_i\) satisfying the desired properties. To this end, we assume first that \(Q_j'\) satisfies
In this case, we set \(Q_j'':=Q_j'\), and using Lemma 5.3, by the induction hypothesis \(H[a,(1-\vartheta )\theta ]\), we obtain the desired family of Chord-arc domains.
We therefore consider the case
In this case, we shall select \(Q_j''\ne Q_j'\). Recall that we use the notation \(Q''\lhd Q\) to mean that \(Q''\) is a dyadic child of Q. Set
Note that we have the dyadic doubling estimate
where \(M_1=M_1(n, ADR)\). We also note that
By definition of \(\mathcal {F}_{good}^{(1)}\),
By (8.18), it follows that
In turn, using (8.20), we obtain
By the dyadic doubling estimate (8.19), this leads to
Choosing \(\beta \le \rho / (4 (M_1+1))\), we find that the expression in square brackets is at least 1, and therefore, by pigeon holing, we can pick \(Q_j''\in \mathcal {F}_j''\) satisfying
Hence, using Lemma 5.3, we see that the induction hypothesis \(H[M_0,\theta ]\) holds for \(Q''_j\in \mathcal {F}_j''\), and once again we obtain the desired family of Chord-arc domains.
Recall that we have constructed our packing measure \(\mathfrak {m}\) in such a way that each \(Q_j\in \mathcal {F}\), as well as all of its children, along with the cubes in \(\mathcal {D}_\mathcal {F}\cap \mathcal {D}(Q)\), belong to the same tree \({\mathsf T}\); see Claim 5.5. This means in particular that for each such \(Q_j\), the Whitney region \(U_{Q_j}\) has exactly two components \(U_{Q_j}^\pm \subset \Omega _{\mathsf T}^\pm \), and the analogous statement is true for each child of \(Q_j\). This fact has the following consequences:
Remark 8.3
For each \(Q_j \in \mathcal {F}_{bad}^{(1)}\), and for the selected child \(Q_j''\) of each \(Q_j\in \mathcal {F}_{good}^{(1)}\), the conclusion of the induction hypothesis produces at most two Chord-arc domains \(\Omega ^\pm _{Q_j} \supset U_{Q_j}^\pm \) (resp. \(\Omega _{Q_j''}^\pm \supset U_{Q_j''}^\pm \)), which we enumerate as \(\Omega ^i_{Q_j}\) (resp. \(\Omega _{Q_j''}^i)\), \(i=1,2\), with \(i=1\) corresponding “+”, and \(i=2\) corresponding to “-”, respectively.
Remark 8.4
For each \(Q_j\in \mathcal {F}_{good}^{(1)}\), the connected component \(U_{Q_j}^\pm \) overlaps with the corresponding component \(U^\pm _{Q_j''}\) for its child, so we may augment \(\Omega _{Q_j''}^i\) by adjoining to it the appropriate component \(U_{Q_j}^\pm \), to form a chord arc domain
By the induction hypothesis, for each \(Q_j \in \mathcal {F}_{bad}^{(1)} \cup \mathcal {F}_{good}^{(1)}\) (and by n-ADR, in the case of \(\mathcal {F}_{good}^{(1)}\)), the Chord-arc domains \(\Omega ^i_{Q_j}\) that we have constructed satisfy
where the sum has either one or two terms, and where the implicit constant depends either on \(M_0\) and \(\theta \), or on a and \((1-\vartheta )\theta \), depending on which part of the induction hypothesis we have used. In particular, for each such \(Q_j\), there is at least one choice of index i such that \(\Omega ^i_{Q_j}=:\Omega _{Q_j}\) satisfies
(if the latter is true for both choices \(i=1,2\), we arbitrarily choose \(i=1\), which we recall corresponds to “+”). Combining the latter bound with Claim 8.2, and recalling that \(\varepsilon \) has now been fixed depending only on allowable parameters, we see that
For \(Q_j \in \mathcal {F}_{bad}^{(1)} \,\cup \, \mathcal {F}_{good}^{(1)}\), as above set \(B^*_{Q_j}:= B(x_{Q_j}, K \ell (Q_j))\). By a covering lemma argument, we may extract a subfamily \(\mathcal {F}^*\subset \mathcal {F}_{bad}^{(1)} \,\cup \, \mathcal {F}_{good}^{(1)}\) such that \( \{\kappa B^*_{Q_j}\}_{Q_j\in \mathcal {F}^*}\) is pairwise disjoint, where again \(\kappa \gg K^4\) is a large dilation factor, and such that
Let us now build (at most two) Chord-arc domains \(\Omega ^i_Q\) satisfying the desired properties. Recall that for each \(Q_j \in \mathcal {F}^*\), we defined the corresponding Chord-arc domain \(\Omega _{Q_j}:= \Omega _{Q_j}^i\), where the choice of index i (if there was a choice), was made so that (8.22) holds. We then assign each \(Q_j\in \mathcal {F}^*\) either to \(\mathcal {F}^*_+\) or to \(\mathcal {F}^*_-\), depending on whether we chose \(\Omega _{Q_j}\) satisfying (8.22) to be \(\Omega _{Q_j}^1=\Omega _{Q_j}^+\), or \(\Omega _{Q_j}^2 =\Omega _{Q_j}^-\). We note that at least one of the sub-collections \(\mathcal {F}^*_\pm \) is non-empty, since for each j, there was at least one choice of index i such that (8.22) holds with \(\Omega _{Q_j}:= \Omega _{Q_j}^i\). Moreover, the two collections are disjoint, since we have arbitrarily designated \(\Omega _{Q_j} = \Omega _{Q_j}^1\) (corresponding to “+”) in the case that there were two choices for a particular \(Q_j\). We further note that if \(Q_j \in \mathcal {F}^*_\pm \), then \(\Omega _{Q_j} = \Omega _{Q_j}^\pm \supset U_{Q_j}^\pm \).
We are now in position to apply Lemma 6.1. Set
which is a semi-coherent subtree of \({\mathsf T}\), with maximal cube Q. Without loss of generality, we may suppose that \(\mathcal {F}^*_+\) is non-empty, and we then define
and similarly with “+” replaced by “−”, provided that \(\mathcal {F}^*_-\) is also non-empty. Observe that by the induction hypothesis, and our construction (see Remarks 8.3 and 8.4, and Lemma 3.3), for an appropriate choice of “±”, \(U_{Q_j}^\pm \subset \Omega _{Q_j} \subset B_{Q_j}^*\), and since \(\ell (Q_j) \le 2^{-k_1} \ell (Q)\), by (8.23) and Lemma 6.1, each (non-empty) choice defines a Chord-arc domain with the requisite properties. This completes the proof of Case 2b of Claim 8.1 and hence that of Theorem 1.2. \(\square \)
10 Part 2: Proof of Theorem 1.3
11 Preliminaries for the Proof of Theorem 1.3
11.1 Uniform rectifiability
Recall the definition of n-uniform rectifiable (n-UR) sets in Definition 2.2. Given a ball \(B\subset {\mathbb {R}}^{n+1}\), we denote
where the infimum is taken over all the affine n-planes that intersect B. The following result is due to David and Semmes:
Theorem 9.1
Let \(E\subset {\mathbb {R}}^{n+1}\) be n-ADR. Denote \(\sigma ={H}^n\lfloor _{\,E}\) and let \(\mathcal {D}\) be the associated dyadic lattice. Then, E is n-UR if and only if, for any \(\varepsilon >0\),
For the proof, see [23, Theorem 2.4, p.32] (this provides a slight variant of Theorem 9.1, and it is straightforward to check that both formulations are equivalent). Remark that the constant 3 multiplying \({B}_Q\) in the estimate above can be replaced by any number larger than 1.
Recall also the following result (see [28] or [44]).
Theorem 9.2
Let \(\Omega \subset {\mathbb {R}}^{n+1}\), \(n\ge 1\), be an open set satisfying an interior corkscrew condition, with n-ADR boundary, such that the harmonic measure in \(\Omega \) belongs to weak-\(A_\infty \). Then \(\partial \Omega \) is n-UR.
11.2 Harmonic measure
From now on we assume that \(\Omega \subset {\mathbb {R}}^{n+1}\) is an open set with n-ADR boundary such that the harmonic measure in \(\Omega \) belongs to weak-\(A_\infty \). We denote by \(\sigma \) the surface measure in \(\partial \Omega \), that is, \(\sigma = {H}^n\lfloor _{\,\partial \Omega }\). We also consider the dyadic lattice \(\mathcal {D}\) associated with \(\sigma \) as in Lemma 2.16. The AD-regularity constant of \(\partial \Omega \) is denoted by \(C_0\).
We denote by \(\omega ^p\) the harmonic measure with pole at p of \(\Omega \), and by \(g(\cdot ,\cdot )\) the Green function. Much as before we write \(\delta _\Omega (x) = {\text {dist}}(x,\partial \Omega )\).
The following well known result is sometimes called “Bourgain’s estimate”:
Lemma 9.3
[13]. Let \(\Omega \subsetneq {\mathbb {R}}^{n+1}\) be open with n-ADR boundary, \(x\in \partial \Omega \), and \(0<r\le {{\,\mathrm{diam}\,}}(\partial \Omega )/2\). Then
where c depends on n and the n-ADRity constant of \(\partial \Omega \).
The following is also well known.
Lemma 9.4
Let \(\Omega \subsetneq {\mathbb {R}}^{n+1}\) be open with n-ADR boundary. Let \(p,q\in \Omega \) be such \(|p-q|\ge 4\,\delta _\Omega (q)\). Then,
We remark that the previous lemma is also valid in the case \(n>1\) without the n-ADR assumption. In the case \(n=1\) this holds under the 1-ADR assumption, and also in the more general situation where \(\Omega \) satisfies the CDC. This follows easily from [1, Lemmas 3.4 and 3.5]. Notice that n-ADR implies the CDC in \({\mathbb {R}}^{n+1}\) (for any n), by standard arguments.
The following lemma is also known. See [28, Lemma 3.14], for example.
Lemma 9.5
Let \(\Omega \subsetneq {\mathbb {R}}^{n+1}\) be open with n-ADR boundary and let \(p\in \Omega \). Let B be a ball centered at \(\partial \Omega \) such that \(p\not \in 8B\). Then
Lemma 9.6
Let \(\Omega \subsetneq {\mathbb {R}}^{n+1}\) be open with n-ADR boundary. Let \(x\in \partial \Omega \) and \(0<r<{{\,\mathrm{diam}\,}}(\Omega )\). Let u be a non-negative harmonic function in \(B(x,4r)\cap \Omega \) and continuous in \(B(x,4r)\cap \overline{\Omega }\) such that \(u\equiv 0\) in \(\partial \Omega \cap B(x,4r)\). Then extending u by 0 in \(B(x,4r){\setminus } \overline{\Omega }\), there exists a constant \(\alpha >0\) such that, for all \(y,z\in B(x,r)\),
where C and \(\alpha \) depend on n and the AD-regularity of \(\partial \Omega \). In particular,
The next result provides a partial converse to Lemma 9.4.
Lemma 9.7
Let \(\Omega \subsetneq {\mathbb {R}}^{n+1}\) be open with n-ADR boundary. Let \(p\in \Omega \) and let \(Q\in \mathcal {D}\) be such that \(p\not \in 2B_Q\). Suppose that \(\omega ^p(Q)\approx \omega ^p(2Q)\). Then there exists some \(q\in \Omega \) such that
and
Proof
For a given \(k_0\ge 2\) to be fixed below, we can pick \(P\in \mathcal {D}(Q)\) with \(\ell (P)= 2^{-k_0}\ell (Q)\) such that
Let \({\varphi }_P\) be a \(C^\infty \) function supported in \({B}_P\), \({\varphi }_P\equiv 1\) on P, and such that \(\Vert \nabla {\varphi }_P\Vert _\infty \lesssim 1/\ell (P)\). Then, choosing \(k_0\) small enough so that \(p\not \in 50{B}_P\), say, and applying Caccioppoli’s inequality,
Applying now Lemmas 9.6 and 9.5 and taking \(k_0\) small enough so that \(24{B}_P\cap \partial \Omega \subset 2Q\), for any \(a\in (0,1)\) we get
From the estimates above we infer that
Hence, for a small enough, we derive
which implies the existence of the point q required in the lemma. \(\square \)
11.3 Harnack chains and carrots
It will be more convenient for us to work with Harnack chains instead of curves. The existence of a carrot curve is equivalent to having what we call a good chain between points.
Let \(x\in \Omega \), \(y\in \overline{\Omega }\) be such that \(\delta _\Omega (y)\le \delta _\Omega (x)\), and let \(C>1\). A C-good chain (or C-good Harnack chain) from x to y is a sequence of balls \(B_{1},B_{2},\dots \) (finite or infinite) contained in \(\Omega \) such that \(x\in B_1\) and either
-
\(\lim _{j\rightarrow \infty } {\text {dist}}(y,B_j)=0\) if \(y\in \partial \Omega \), or
-
\(y\in B_N\) if \(y\in \Omega \), where N is the number of elements of the sequence if this is finite,
and moreover the following hold:
-
\(B_j\cap B_{j+1}\ne \varnothing \) for all j,
-
\(C^{-1}\,{\text {dist}}(B_j,\partial \Omega ) \le r(B_j)\le C\,{\text {dist}}(B_j,\partial \Omega )\) for all j,
-
\(r(B_j)\le C\,r(B_i)\) if \(j>i\),
-
for each \(t>0\) there are at most C balls \(B_j\) such that \(t< r(B_j)\le 2t\).
Abusing language, sometimes we will omit the constant C and we will just say “good chain” or “good Harnack chain”.
Observe that in the definitions of carrot curves and good chains, the order of x and y is important: having a carrot curve from x to y is not equivalent to having one from y to x, and similarly with good chains.
Lemma 9.8
There is a carrot curve from \(x\in \Omega \) to \(y\in \overline{\Omega }\) if and only if there is a good Harnack chain from x to y.
Proof
Let \(\gamma \) be a carrot curve from x to y. We can assume \(y\in \Omega \), since if \(y\in \partial \Omega \), we can obtain this case by taking a limit of points \(y_{j}\in \Omega \) converging to y. Let \(\{B_{j}\}_{j=1}^{N}\) be a Vitali subcovering of the family \(\{B(z,\delta _{\Omega }(z)/10): z\in \gamma \}\) and let \(r_{B_j}\) stand for the radius and \(x_{B_j}\) for the center of \(B_j\). So the balls \(B_j\) are disjoint and \(5B_{j}\) cover \(\gamma \). Note that for \(t>0\), if \(t< r_{B_{j}}\le 2t\),
In particular, since the \(B_{j}\)’s are disjoint, by volume considerations, there can only be boundedly many \(B_{j}\) of radius between t/2 and t, say. Moreover, we may order the balls \(B_j\) so that \(x\in 5B_1\) and \(B_{j+1}\) is a ball \(B_k\) such that \(5B_k\cap 5B_j\ne \varnothing \) and \(5\overline{B_k}\) contains the point from \(\gamma \cap \bigcup _{h:5B_h\cap 5B_j\ne \varnothing }5\overline{B}_h\) which is maximal in the natural order induced by \(\gamma \) (so that x is the minimal point in \(\gamma \)). Then for \(j>i\),
This implies \(5B_1,5B_2,\ldots \) is a C-good chain for a sufficiently big C.
Now suppose that we can find a good chain from x to y, call it \(B_{1},\dots ,B_{N}\). Let \(\gamma \) be the path obtained by connecting their centers in order. Let \(z\in \gamma \). Then there is a j such that \(z\in [x_{B_{j}},x_{B_{j+1}}]\), the segment joining \(x_{B_{j}}\) and \(x_{B_{j+1}}\). Since \(\{B_{i}\}_i\) is a good chain,
We would like to note that the implicit constants do not depend on N. Indeed, from the properties of the good chain it easily follows that
Thus, \(\gamma \) is a carrot curve from x to y. \(\square \)
12 The main lemma for the Proof of Theorem 1.3
Because of the absence of doubling conditions on harmonic measure under the weak-\(A_\infty \) assumption, to prove Theorem 1.3 we cannot use arguments similar to the ones in [1] or [6]. Instead, we prove a local result which involves only one pole and one ball which has its own interest. This is the Main Lemma 10.2 below.
Let \(B\subset {\mathbb {R}}^{n+1}\) be a ball centered at \(\partial \Omega \) and let \(p \in \Omega \). We restate Definition 2.15 in the following form: \(\omega ^p\) satisfies the weak-\(A_\infty \) condition in B if for every \(\varepsilon _0 \in (0,1)\) there exists \(\delta _0 \in (0,1)\) such that the following holds: for any subset \(E \subset B\cap \partial \Omega \),
In the next sections we will prove the following.
Main Theorem 10.2 Let \(\Omega \subset {\mathbb {R}}^{n+1}\) have n-uniformly rectifiable boundary. Let \(R_0\in \mathcal {D}\) and let \(p\in \Omega {\setminus } 4{B}_{R_0}\) be a point such that
and \(\omega ^{p}(R_0)\ge c'>0\). Suppose that \(\omega ^p\) satisfies the weak-\(A_\infty \) condition in \({B}_{R_0}\). Then there exists a subset \({\mathrm {Con}}(R_0)\subset R_0\) and a constant \(c''>0\) with \(\sigma ({\mathrm {Con}}(R_0))\ge c''\,\sigma (R_0)\) such that each point \(x\in {\mathrm {Con}}(R_0)\) can be joined to p by a carrot curve. The constant \(c''\) and the constants involved in the carrot condition only depend on \(c,c',n\), the weak-\(A_\infty \) condition, and the n-UR character of \(\partial \Omega \).
The notation \({\mathrm {Con}}(\cdot )\) stands for “connectable”.
It is easy to check that Theorem 1.3 follows from this result. First notice that the assumptions of the theorem imply that \(\partial \Omega \) is n-uniformly rectifiable by Theorem 9.2. Consider now any \(x\in \Omega \) and take a point \(\xi \in \partial \Omega \) such that \(|x-\xi |=\delta _\Omega (x)\). Then we consider the point p in the segment \([x,\xi ]\) such that \(|p-\xi |=\frac{1}{16}\,\delta _\Omega (x)\). By Lemma 9.3, we have
because \(p\in \overline{\frac{1}{2}B(\xi ,\tfrac{1}{8}\delta _\Omega (x))}\). Hence, by covering \(B(\xi ,\tfrac{1}{8}\delta _\Omega (x))\cap \partial \Omega \) with cubes \(R\in \mathcal {D}\) contained in \(B(\xi ,\tfrac{1}{4}\delta _\Omega (x))\cap \partial \Omega \) with side length comparable to \(\delta _\Omega (x)\) we deduce that at least one these cubes, call it \(R_0\), satisfies \(\omega ^p(R_0)\gtrsim 1\). Further, by taking the side length small enough, we may also assume that \(p\not \in 4{B}_{R_0}\). Since \(\omega ^p\) satisfies the weak-\(A_\infty \) property in \(B_{R_0}\) (by the assumptions in Theorem 1.3), we can apply the Main Lemma 10.2 above and infer that there exists a subset \(F:={\mathrm {Con}}(R_0)\subset R_0\) with \(\sigma (F)\ge c'\,\sigma (R_0)\gtrsim \delta _\Omega (x)^n\) such that all \(y\in F\) can be joined to x by a carrot curve, which proves that \(\Omega \) satisfies the weak local John condition and concludes the proof of Theorem 1.3.
Two essential ingredients of the proof of the Main Lemma 10.2 are a corona type decomposition (whose existence is ensured by the n-uniform rectifiability of the boundary) and the Alt–Caffarelli–Friedman monotonicity formula [3]. This formula is used in some of the connectivity arguments below. This allows to connect by carrot curves corkscrew points where the Green function is not too small to other corkscrew points at a larger distance from the boundary where the Green function is still not too small (see Lemma 11.6 for the precise statement). The use of the Alt–Caffarelli–Friedman formula is not new to problems involving harmonic measure and connectivity (see, for example, [7]). However, the way it is applied here is new, as far as we know.
Two important steps of the proof of the Main Lemma 10.2 (and so of Theorem 1.3) are the Geometric Lemma 14.3 and the Key Lemma 15.1. An essential idea consists of distinguishing cubes with “two well separated big corkscrews” (see Sect. 13.4 for the precise definition). In the Geometric Lemma 10.2 we construct two disjoint open sets satisfying a John condition associated to trees involving this type of cubes, so that the boundaries of the open sets are located in places where the Green function is very small. This construction is only possible because the associated tree involves only cubes with two well separated big corkscrews. The existence of these cubes is an obstacle for the construction of carrot curves. However, in a sense, in the Key Lemma 15.1 we take advantage of their existence to obtain some delicate estimates for the Green function on some corkscrew points.
We claim now that to prove he Main Lemma 10.2 we can assume that \(\Omega ={\mathbb {R}}^{n+1}{\setminus } \partial \Omega \). To check this, let \(\Omega \), p, and \(R_0\) satisfy the assumptions in the Main Lemma. Consider the open set \(V=\mathbb {R}^{n+1}{\setminus } \partial \Omega \). Then the harmonic measure \(\omega ^p\) in \(\Omega \) coincides with the harmonic measure \(\omega _V^p\) in V (the fact that V is not connected does not disturb us). Thus V, p, and \(R_0\) satisfy the assumptions in the Main Lemma, and moreover \(V=\mathbb {R}^{n+1}{\setminus } \partial \Omega ={\mathbb {R}}^{n+1}{\setminus } \partial V\). Assuming the Main Lemma to be valid in this particular case, we deduce that there exists a subset \({\mathrm {Con}}(R_0)\subset R_0\) and a constant \(c''>0\) with \(\sigma ({\mathrm {Con}}(R_0))\ge c''\,\sigma (R_0)\) such that each point \(x\in {\mathrm {Con}}(R_0)\) can be joined to p by a carrot curve in V. Now just observe that if \(\gamma \) is one of this carrot curves and it joints p and \(x\in {\mathrm {Con}}(R_0)\subset \partial V=\partial \Omega \), then \(\gamma \) is contained in V except for its end-point x. By connectivity, since \(p \in \Omega \cap \gamma \), \(\gamma \) must be contained in \(\Omega \), except for the end-point x. Hence, \(\gamma \) is a carrot curve with respect to \(\Omega \).
Sections 11–16 are devoted to the proof of Main Lemma 10.2. To this end, we will assume that \(\Omega ={\mathbb {R}}^{n+1}{\setminus } \partial \Omega \).
13 The Alt–Caffarelli–Friedman formula and the existence of short paths
13.1 The Alt–Caffarelli–Friedman formula
Recall the following well known result of Alt–Caffarelli–Friedman (see [14, Theorems 12.1 and 12.3]):
Theorem 11.1
Let \(B(x,R)\subset {\mathbb {R}}^{n+1}\), and let \(u_1,u_2\in W^{1,2}(B(x,R))\cap C(B(x,R))\) be nonnegative subharmonic functions. Suppose that \(u_1(x)=u_2(x)=0\) and that \(u_1\cdot u_2\equiv 0\). Set
and
Then J(x, r) is a non-decreasing function of \(r\in (0,R)\) and \(J(x,r)<\infty \) for all \(r\in (0,R)\). That is,
Further,
In the case of equality we have the following result (see [46, Theorem 2.9]).
Theorem 11.2
Let B(x, R) and \(u_1,u_2\) be as in Theorem 11.1. Suppose that \(J(x,r_a)=J(x,r_b)\) for some \(0<r_a<r_b<R\). Then either one or the other of the following holds:
-
(a)
\(u_1=0\) in \(B(x,r_b)\) or \(u_2=0\) in \(B(x,r_b)\);
-
(b)
there exists a unit vector e and constants \(k_1,k_2>0\) such that
$$\begin{aligned} u_1(y)= k_1\,((y-x)\cdot e)^+,\qquad u_2(y)= k_2\,((y-x)\cdot e)^-, \qquad \text {in }B(x,r_b). \end{aligned}$$
We will also need the following auxiliary lemma.
Lemma 11.3
Let \(B(x,R)\subset {\mathbb {R}}^{n+1}\), and let \(\{u_i\}_{i\ge 1} \subset W^{1,2}(B(x,R))\cap C(B(x,R))\) a sequence of functions which are nonnegative, subharmonic, such that each \(u_i\) is harmonic in \(\{y\in B(x,R):u_i(y)>0\}\) and \(u_i(x)=0\). Suppose also that
for all \(i\ge 1\). Then, for every \(0<r<R\) there exists a subsequence \(\{u_{i_k}\}_{k\ge 1}\) which converges uniformly in B(x, r) and weakly in \(W^{1,2}(B(x,r))\) to some function \(u\in W^{1,2}(B(x,r))\cap C(B(x,r))\), and moreover,
Proof
The existence of a subsequence \(\{u_{i_k}\}_{k\ge 1}\) converging weakly in \(W^{1,2}(B(x,r))\) and uniformly in B(x, r) to some function \(u\in W^{1,2}(B(x,r))\cap C(B(x,r))\) is an immediate consequence of the Arzelà–Ascoli and the Banach–Alaoglu theorems. The identity (11.4) is clear when \(n=1\), and quite likely, for \(n>1\) this is also well known. However, for completeness, we will show the details (for \(n>1\)).
Consider a non-negative subharmonic function \(v\in W^{1,2}(B(x,R))\cap C(B(x,R))\) which is harmonic in \(\{y\in B(x,R):v(y)>0\}\) so that \(v(x)=0\). For \(0<r<R\) and \(0<\delta <R-r\), let \({\varphi }\) be a radial \(C^\infty \) function such that \(\chi _{B(x,r)} \le {\varphi }\le \chi _{B(x,r+\delta )}\). Let \(\mathcal {E}(y)=c_n^{-1}\,|y|^{1-n}\) be the fundamental solution of the Laplacian. For \(\varepsilon >0\), denote \(v_\varepsilon =\max (v,\varepsilon )-\varepsilon \). Then we have
Using the fact that \(v_\varepsilon \) is harmonic in \(\{v_\varepsilon >0\}\) and that \(\mathcal {E}(x-\cdot )\,v_\varepsilon \,{\varphi }\in W^{1,2}_0(\{v_\varepsilon >0\} \cap B(x,R))\) since \({\varphi }\) is compactly supported in B(x, R), \(v_\varepsilon =0\) on \(\partial \{v_\varepsilon >0\}\), and x is far away from \(\overline{\{v_\varepsilon >0\}}\), it follows easily that \(I_1=0\). On the other hand, we have
Thus,
Taking into account that \({{\,\mathrm{supp}\,}}\nabla {\varphi }\) is far away from x, letting \(\varepsilon \rightarrow 0\), we obtain
Using the preceding identity, it follows easily that
Indeed, \(\lim _{k\rightarrow \infty }u_{i_k}(x)^2 = u(x)^2\). Also, it is clear that
Further,
by the weak convergence of \(u_{i_k}\) in \(W^{1,2}(B(x,R))\) and the uniform convergence in \(B(x,r+\delta )\), since \({{\,\mathrm{supp}\,}}\nabla {\varphi }\) is far away from x.
Let \(\psi \) be a radial \(C^\infty \) function such that \(\chi _{B(x,r-\delta )} \le \psi \le \chi _{B(x,r)}\). The same argument as above shows that
Consequently,
and also
Since \(\delta >0\) can be taken arbitrarily small, (11.4) follows. \(\square \)
Lemma 11.4
Let \(B(x,2R)\subset {\mathbb {R}}^{n+1}\), and let \(u_1,u_2\in W^{1,2}(B(x,2R))\cap C(B(x,2R))\) be nonnegative subharmonic functions such that each \(u_i\) is harmonic in \(\{y\in B(x,2R):u_i(y)>0\}\). Suppose that \(u_1(x)=u_2(x)=0\) and that \(u_1\cdot u_2\equiv 0\). Assume also that
For any \(\varepsilon >0\), there exists some \(\delta >0\) such that if
with \(J(\cdot ,\cdot )\) defined in (11.1), then either one or the other of the following holds:
-
(a)
\(\Vert u_1\Vert _{\infty ,B(x,R)}\le \varepsilon \,R\) or \(\Vert u_2\Vert _{\infty ,B(x,R)}\le \varepsilon \,R\);
-
(b)
there exists a unit vector e and constants \(k_1,k_2>0\) such that
$$\begin{aligned}&\Vert u_1- k_1\,((\cdot -x)\cdot e)^+\Vert _{\infty ,B(x,R)}\le \varepsilon \,R ,\\&\Vert u_2-k_2\,((\cdot -x)\cdot e)^-\Vert _{\infty ,B(x,R)}\le \varepsilon \,R. \end{aligned}$$
The constant \(\delta \) depends only on \(n,\alpha ,C_1,\varepsilon \).
Proof
Suppose that the conclusion of the lemma fails. Then, by replacing \(u_i(y)\) by \(\frac{1}{R}\,u_i(Ry+x)\), we can assume that \(x=0\) and \(R=1\). Let \(\varepsilon >0\), and for each \(\delta =1/k\) and \(i=1,2\), consider functions \(u_{i,k}\) satisfying the assumptions of the lemma and such that neither (a) nor (b) holds for them. By Lemma 11.3, there exist subsequences (which we still denote by \(\{u_{i,k}\}_k\)) which converge uniformly in \(B(0,\frac{3}{2})\) and weakly in \(W^{1,2}(B(0,\frac{3}{2}))\) to some functions \(u_i\in W^{1,2}(B(0,\frac{3}{2}))\cap C(B(0,\frac{3}{2}))\), and moreover,
both for \(r=1\) and \(r=1/2\). Clearly, the functions \(u_i\) are non-negative, subharmonic, and \(u_1\cdot u_2=0\). Hence, by Theorem 11.2, one of the following holds:
- (a’):
-
\(u_1=0\) in B(0, 1) or \(u_2=0\) in B(0, 1);
- (b’):
-
there exists a unit vector e and constants \(k_1,k_2>0\) such that
$$\begin{aligned} u_1(y)= k_1\,(y\cdot e)^+,\qquad u_2(y)= k_2\,(y\cdot e)^-, \qquad \text {in }B(0,1). \end{aligned}$$
However, the fact that neither (a) nor (b) holds for any pair \(u_{1,k}\), \(u_{2,k}\), together with the uniform convergence of \(\{u_{i,k}\}_k\), implies that neither (a’) nor (b’) can hold, and thus we get a contradiction. \(\square \)
13.2 Existence of short paths
Let \(p\in \Omega \) and \(\Lambda >1\). For \(x\in \partial \Omega \), we write \(x\in {{\mathsf {WA}}}(p,\Lambda )\) if for all \(0<r\le \delta _\Omega (p)\),
We will see in Sect. 12 that, under the assumptions of the Main Lemma 10.2, for some \(\Lambda \) big enough,
Lemma 11.5
Let \(p\in \Omega \), \(x_0\in {{\mathsf {WA}}}(p,\Lambda )\), and \(r\in (0,\delta _\Omega (p))\). Then there exists \(q\in B(x_0,r)\) such that, for some constant \(\kappa \in (0,1/10)\),
-
(a)
\(\delta _\Omega (q) \ge \kappa \,r\), and
-
(b)
$$\begin{aligned} \kappa \,\frac{\omega ^p(B(x_0,r))}{r^{n-1}} \le g(p,q)\le \kappa ^{-1}\,\frac{\omega ^p(B(x_0,r))}{r^{n-1}}. \end{aligned}$$
The constant \(\kappa \) depends only on \(\Lambda \), n, and \(C_0\), the AD-regularity constant of \(\partial \Omega \).
Proof
This follows easily from Lemmas 9.4 and 9.7. \(\square \)
Lemma 11.6
(Short paths). Let \(p\in \Omega \), \(x_0\in {{\mathsf {WA}}}(p,\Lambda )\), and for \(0<r_0\le \delta _\Omega (p)/4\), \(0<\tau _0,\lambda _0 \le 1\), let \(q\in \Omega \) be such that
Then there exist constants \(A_1>1\) and \(0<a_1,\lambda _1<1\) such that for every \(r\in (r_0,\delta _\Omega (p)/2)\), there exists some point \(q'\in \Omega \) such that
(with \(\kappa \) as in Lemma 11.5) and such that q and \(q'\) can be joined by a curve \(\gamma \) such that
The parameters \(\lambda _1,A_1,a_1\) depend only on \(C_0,\Lambda ,\lambda _0,\tau _0\) and the ratio \(r/r_0\).
Proof
All the parameters in the lemma will be fixed along the proof. We assume that \(A_1\gg \kappa ^{-1}>1\). First note that we may assume that \(r< 2A_1^{-1} |x_0-p|\). Otherwise, we just take a point \(q'\in \Omega \) such that \(|p-q'|=\delta _\Omega (p)/2\), which clearly satisfies the properties in (11.7). Further, both q and \(q'\) belong to the open connected set
for a sufficiently small \(c_2>0\). The fact that U is connected is well known. This follows from the fact that, for any \(\lambda >0\), any connected component of \(\{g(p,\cdot )>\lambda \}\) should contain p. Otherwise there would be a connected component where \(g(p,\cdot )-\lambda \) is positive and harmonic with zero boundary values. So, by maximum principle, \(g(p,\cdot )-\lambda \) should equal \(\lambda \) in the whole component, which is a contradiction. So there is only one connected component.
We just let \(\gamma \) be a curve contained in U. Note that
for a sufficiently small \(a>0\) because, by boundary Hölder continuity,
if \({\text {dist}}(x,\partial \Omega )\le \delta _\Omega (p)/2\). Further, the fact that \(g(p,x)\le c|x-p|^{1-n}\) ensures that \(U\subset B(p,C\delta _\Omega (p))\), for a sufficiently big constant C depending on \(r/r_0\).
So from now on we assume that \(r< 2A_1^{-1} |x_0-p|\). By Lemma 11.5 we know there exists some point \({\widetilde{q}}\in \Omega \) such that
with c depending on \(\kappa \) and \(\Lambda \).
Assume that q and \({\widetilde{q}}\) cannot be joined by a curve \(\gamma \) as in the statement of the lemma. Otherwise, we choose \(q'={\widetilde{q}}\) and we are done. For \(t>0\), consider the open set
We fix \(t>0\) small enough such that \(q,{\widetilde{q}}\in V^{2t}\subset V^t\). Such t exists by (11.6) and (11.8), and it may depend on \(\Lambda ,\lambda ,r/r_0\).
Let \(V_1\) and \(V_2\) be the respective components of \(V^t\) to which q and \({\widetilde{q}}\) belong. We have
because otherwise there is a curve contained in \(V^t\subset B(x_0,\tfrac{1}{4}A_1r)\) which connects q and \({\widetilde{q}}\), and further this is far away from \(\partial \Omega \). Indeed, we claim that
To see this, note that by the Hölder continuity of \(g(p,\cdot )\) in \(B(x_0,\tfrac{1}{2}A_1r)\), for all \(x\in V^t\), we have
where in the last inequality we used Lemma 9.5 and that \(x_0 \in {{\mathsf {WA}}}(p,\Lambda )\). This yields our claim.
Next we wish to apply the Alt–Caffarelli–Friedman formula with
It is clear that both satisfy the hypotheses of Theorem 11.1. For \(i=1,2\) and \(0<s<A_1r\), we denote
so that \(J(x_0,s) = J_1(x_0,s)\,J_2(x_0,s)\). We claim that:
-
(i)
\(J_i(x_0,s)\lesssim _\Lambda 1\) for \(i=1,2\) and \(0<s<\tfrac{1}{4}A_1r\).
-
(ii)
\(J_i(x_0,2r) \gtrsim _{\Lambda ,\lambda ,r/r_0} 1\) for \(i=1,2\).
The condition (i) follows from (11.3) and the fact that
which holds by Lemma 9.5 and subharmonicity, since \(x_0 \in {{\mathsf {WA}}}(p,\Lambda )\). Concerning (ii), note first that
where we first used Cauchy estimates and then the pointwise bounds of \(g(\cdot ,\cdot )\) in (11.10) with \(s\approx \delta _\Omega (y)\). Thus, using also that \(q \in V^{2t}\), we infer that \(u_1(y)>t\,r_0/2 \) in some ball \(B(q,ctr_0)\) with c possibly depending on \(\Lambda ,\lambda ,r/r_0\). Analogously, we deduce that \(u_2(y)>t\,r_0/2\) in some ball \(B({\widetilde{q}},ctr_0)\). Let B be the largest open ball centered at q not intersecting \(\partial V_1\) and let \(y_{0}\in \partial V_1\cap \partial B\). Then, by considering the convex hull \(H\subset B\) of \(B(q,ctr_0)\) and \(y_0\) and integrating in spherical coordinates (with the origin in \(y_0\)), one can check that
An analogous estimate holds for \(u_2\), and then it easily follows that
which implies (ii). We leave the details for the reader.
From the conditions (i) and (ii) and the fact that J(x, r) is non-decreasing we infer that
and also
Assume that \(\tfrac{1}{4}A_1=2^m\) for some big \(m>1\). Since \(J(x_0,s)\) is non-decreasing we infer that there exists some \(h\in [1,m-1]\) such that
because otherwise, by iterating the reverse inequality, we get a contradiction. Now from Lemma 11.4 we deduce that, given any \(\varepsilon >0\), for m big enough, there are constant \(k_i\approx _{\Lambda ,\lambda ,r/r_0} 1\) and a unit vector e such that
As a matter of fact, \(\Vert u_i\Vert _{\infty ,B(x_0,2^{h+1}r)}\approx _{\Lambda ,\lambda ,r/r_0} 2^hr\) by (11.3), (11.11), and (11.10); \(\Vert u_i\Vert _\mathrm{{Lip}^\alpha ,B(x_0,2^{h+1}r)}\lesssim _{\Lambda ,\lambda ,r/r_0}(2^{h}r)^{1-\alpha }\) by Lemma 9.6; and the option (a) in Lemma 11.4 cannot hold (since we have \(\Vert u_i\Vert _{\infty ,B(x_0,2^hr)}\approx _{\Lambda ,\lambda ,r/r_0} 2^hr\)).
In particular, for \(\varepsilon \) small, (11.12) implies that if \(q':=x_0 + 2^{h-1}re\), then one has \(u_1(q') \approx _{\Lambda ,\lambda ,r/r_0} 2^{h-1}r\), and also that
Thus \(B(q',2^{h-2}r)\subset \Omega \) and so \(q'\) is at a distance at least \(2^{h-2}r\) from \(\partial \Omega \), and also
Further, since q and \(q'\) are both in \(V_1\) by definition, there is a curve \(\gamma \) which joins q and \(q'\) contained in \(V_1\) satisfying
by (11.9). So \(q'\) satisfies all the required properties in the lemma and we are done. \(\square \)
14 Types of cubes
From now on we fix \(R_0\in \mathcal {D}\) and \(p\in \Omega \) and we assume that we are under the assumptions of the Main Lemma 10.2.
We need now to define two families \({\mathsf {HD}}\) and \({\mathsf {LD}}\) of high density and low density cubes, respectively. Let \(A\gg 1\) be some fixed constant. We denote by \({\mathsf {HD}}\) (high density) the family of maximal cubes \(Q\in \mathcal {D}\) which are contained in \(R_0\) and satisfy
We also denote by \({\mathsf {LD}}\) (low density) the family of maximal cubes \(Q\in \mathcal {D}\) which are contained in \(R_0\) and satisfy
(notice that \(\omega ^{p}(R_0)\approx \omega ^{p}(2R_0)\approx 1\) by assumption). Observe that the definition of the family \({\mathsf {HD}}\) involves the density of 2Q, while the one of \({\mathsf {LD}}\) involves the density of Q.
We denote
Lemma 12.1
We have
Proof
By Vitali’s covering theorem, there exists a subfamily \(I\subset {\mathsf {HD}}\) so that the cubes 2Q, \(Q\in I\), are pairwise disjoint and
Then, since \(\sigma \) is doubling, we obtain
Next we turn our attention to the low density cubes. Since the cubes from \({\mathsf {LD}}\) are pairwise disjoint, we have
\(\square \)
From the above estimates and the fact that the harmonic measure belongs to weak-\(A_\infty \) (cf. (10.1)), we infer that if A is chosen big enough, then
and thus
As a consequence, denoting \(G_0= R_0{\setminus } (B_H\cup B_L))\), we deduce that
which implies that
again using the fact that \(\omega ^p\) belongs to weak-\(A_\infty \) in \({B}_{R_0}\). So we have:
Lemma 12.2
Assuming A big enough, the set \(G_0:= R_0{\setminus } (B_H\cup B_L))\) satisfies
with the implicit constants depending on \(C_0\) and the weak-\(A_\infty \) condition in \({B}_{R_0}\).
We denote by \(\mathsf {G}\) the family of those cubes \(Q\in \mathcal {D}(R_0)\) which are not contained in \(\bigcup _{P\in {\mathsf {HD}}\cup {\mathsf {LD}}}P\). In particular, such cubes \(Q\in \mathsf {G}\) do not belong to \({\mathsf {HD}}\cup {\mathsf {LD}}\) and
From this fact, it follows easily that \(G_0\) is contained in the set \({{\mathsf {WA}}}(p,\Lambda )\) defined in Sect. 11.2, assuming \(\Lambda \) big enough, and so Lemma 12.2 ensures that (11.5) holds.
The following lemma is an immediate consequence of Lemma 11.5.
Lemma 12.3
For every cube \(Q\in \mathsf {G}\) there exists some point \({z}_Q\in 2{B}_Q\cap \Omega \) such that \(\delta _\Omega ({z}_Q)\ge \kappa _0\,\ell (Q)\) and
for some \(\kappa _0,c_3>0\), which depend on A and on the weak-\(A_\infty \) constants in \({B}_{R_0}\).
If \({z}_Q\in 2{B}_Q\cap \Omega \) and \(\delta _\Omega ({z}_Q)\ge \kappa _0\,\ell (Q)\), we say that \({z}_Q\) is \(\kappa _0\)-corkscrew for Q. If (12.2) holds, we say that \({z}_Q\) is a \(c_3\)-good corkscrew for Q. Abusing notation, quite often we will not write “for Q”.
We will need the following auxiliary result:
Lemma 12.4
Let \(Q\in \mathcal {D}\) and let \({z}_Q\) be a \(\lambda \)-good \(c_4\)-corkscrew, for some \(\lambda ,c_4>0\). Suppose that \(\ell (Q)\ge c_5\,\ell (R_0)\). Then there exists some C-good Harnack chain that joins \({z}_Q\) and p, with C depending on \(\lambda ,c_5\).
Proof
Consider the open set \(U=\{x\in \Omega :g(p,x)>\lambda \,\ell (Q)/\sigma (R_0)\}\). This is connected and thus there exists a curve \(\gamma \subset U\) that connects \({z}_Q\) and p. By Hölder continuity, any point \(x\in \Omega \) such that \(\delta _\Omega (x)\le \delta _\Omega (p)/2\), satisfies
Since \(g(p,x)>\lambda \,\ell (Q)/\sigma (R_0)\gtrsim _{c_5,\lambda }\ell (R_0)^{1-n}\) for all \(x\in U\), we then deduce that \({\text {dist}}(U,\partial \Omega )\ge c_6\,\ell (R_0)\) for some \(c_6>0\) depending on \(\lambda \) and \(c_5\). Thus,
From the fact that \(g(p,x)\le |p-x|^{1-n}\) for all \(x\in \Omega \), we infer that any \(x\in U\) satisfies
Therefore,
So \(U\subset B(p,C_2\,\ell (R_0))\) for some \(C_2\) depending on \(\lambda \) and \(c_5\). Next we consider a Besicovitch covering of \(\gamma \) with balls \(B_i\) of radius \(c_6\ell (R_0)/2\). By volume considerations, it easily follows that the number of balls \(B_i\) is bounded above by some constant \(C_3\) depending on \(\lambda \) and \(c_5\), and thus this is a C-good Harnack chain, with \(C=C(\lambda ,c_5)\). \(\square \)
Lemma 12.5
There exists some constant \(\kappa _1\) with \(0<\kappa _1\le \kappa _0\) such that the following holds for all \(\lambda >0\). Let \(Q\in \mathsf {G}\), \(Q\ne R_0\), and let \({z}_Q\) be a \(\lambda \)-good \(\kappa _1\)-corkscrew. Then there exists some cube \(R\in \mathsf {G}\) with \(Q\subsetneq R\subset R_0\) and \(\ell (R)\le C\,\ell (Q)\) and a \(\lambda '\)-good \(\kappa _1\)-corkscrew \({z}_R\) such that \({z}_Q\) and \({z}_R\) can be joined by a \(C'(\lambda )\)-good Harnack chain, with \(\lambda '>0\) and C depending on \(\lambda \).
The proof below yields a constant \(\lambda '<\lambda \). On the other hand, the lemma ensures that \({z}_R\) is still a \(\kappa _1\)-corkscrew, which will be important for the arguments to come.
Proof
This follows easily from Lemma 11.6. For completeness we will show the details.
By choosing \(\Lambda =\Lambda (A)>0\) big enough, \(G_0\cap Q\subset {{\mathsf {WA}}}(p,\Lambda )\) and thus there exists some \(x_0\in Q\cap {{\mathsf {WA}}}(p,\Lambda )\). We let
where \(\kappa _0\) is defined in Lemma 12.3 and \(\kappa \) in Lemma 11.5 (and thus it depends only on A and \(C_0\)). We apply Lemma 11.6 to \(x_0\), \(q=z_Q\), with \(r_0=3r({B}_Q)\), \(\lambda _0\approx \lambda \), and \(r=4r({B}_Q)\). To this end, note that
Hence there exists \(q'\in B(x_0,A_1r)\) such that
and such that q and \(q'\) can be joined by a curve \(\gamma \) such that
with \(\lambda _1,A_1,a_1\) depending on \(C_0,A,\lambda ,\kappa _1\). Now let \(R\in \mathcal {D}\) be the cube containing \(x_0\) such that
Observe that
Also, we may assume that \(\ell (R)\le \ell (R_0)\) because otherwise we have \(\ell (Q)\gtrsim A_1\, \delta _\Omega (p)\) and then the statement in the lemma follows from Lemma 12.4. So we have \(Q\subsetneq R\subset R_0\).
From (12.3) we get
and
Hence, \(q'\) is a \(\lambda '\)-good \(\kappa _1\)-corkscrew, for \(\lambda ' = c\lambda _12\kappa \).
From (12.4) and arguing as in the end of the proof of Lemma 12.4 we infer that \({z}_Q=q\) and \({z}_R=q'\) can be joined by a \(C(\lambda )\)-good Harnack chain. \(\square \)
From now on we will assume that all corkscrew points for cubes \(Q\in \mathsf {G}\) are \(\kappa _1\)-corkscrews, unless otherwise stated.
15 The corona decomposition and the Key Lemma
15.1 The corona decomposition
Recall that the \(b\beta \) coefficient of a ball was defined in (9.1). For each \(Q\in \mathcal {D}\), we denote
Now we fix a constant \(0<\varepsilon \ll \min (1,\kappa _1)\). Given \(R\in \mathcal {D}(R_0)\), we denote by \({\mathsf {Stop}}(R)\) the maximal family of cubes \(Q\in \mathcal {D}(R){\setminus } \{R\}\) satisfying that either \(Q\not \in \mathsf {G}\) or \(b\beta \bigl ({\widehat{Q}}\bigr )>\varepsilon \), where \({\widehat{Q}}\) is the parent of Q. Recall that the family \(\mathsf {G}\) was defined in (12.1). Note that, by maximality, \({\mathsf {Stop}}(R)\) is a family of pairwise disjoint cubes.
We define
In particular, note that \({\mathsf {Stop}}(R)\not \subset {\mathsf {T}}(R)\).
We now define the family of the top cubes with respect to \(R_0\) as follows: first we define the families \({\mathsf {Top}}_k\) for \(k\ge 1\) inductively. We set
Assuming that \({\mathsf {Top}}_k\) has been defined, we set
and then we define
Notice that the family of cubes \(Q\in \mathcal {D}(R_0)\) with \(\ell (Q)\le 2^{-10}\ell (R_0)\) which are not contained in any cube \(P\in {\mathsf {HD}}\cup {\mathsf {LD}}\) is contained in \(\bigcup _{R\in {\mathsf {Top}}}{\mathsf {T}}(R)\), and this union is disjoint. Also, all the cubes in that union belong to \(\mathsf {G}\).
The following lemma is an easy consequence of our construction. Its proof is left for the reader.
Lemma 13.1
We have
Also, for each \(R\in {\mathsf {Top}}\),
Further, for all \(Q\in {\mathsf {T}}(R)\cup {\mathsf {Stop}}(R)\),
Remark that the last inequality holds for any cube \(Q\in {\mathsf {Stop}}(R)\) because its parent \({\widehat{Q}}\) belongs to \({\mathsf {T}}(R)\) and so \({\widehat{Q}}\) is not contained in any cube from \({\mathsf {HD}}\), which implies that \(\omega ^p(2Q)\le \omega ^p(2{\widehat{Q}})\lesssim A\,\frac{\sigma ({\widehat{Q}})}{\sigma (R_0)}\approx A\,\frac{\sigma (Q)}{\sigma (R_0)}.\)
Using that \(\partial \Omega \) is n-UR (by the assumption in the Main Lemma 10.2), it is easy to prove that the cubes from \({\mathsf {Top}}\) satisfy a Carleson packing condition. This is shown in the next lemma.
Lemma 13.2
We have
Proof
For each \(Q\in {\mathsf {Top}}\) we have
Then we get
Note now that, because of the stopping conditions, for all \(Q\in {\mathsf {Top}}\), if \(P\in {\mathsf {Stop}}(Q)\cap \mathsf {G}\), then the parent \({\widehat{P}}\) of P satisfies \(b\beta _{\partial \Omega }(100{B}_{{\widehat{P}}})>\varepsilon \). Hence, by Theorems 9.1 and 9.2,
On the other hand, the cubes \(P\in {\mathsf {Stop}}(Q){\setminus }\mathsf {G}\) with \(Q\in {\mathsf {Top}}\) do not contain any cube from \({\mathsf {Top}}\), by construction. Hence, they are disjoint and thus
By an analogous reason,
Using (13.1) and the estimates above, the lemma follows. \(\square \)
Given a constant \(K\gg 1\), next we define
By Chebyshev and the preceding lemma, we have
Therefore, if K is chosen big enough (depending on \(M(\varepsilon )\) and the constants on the weak-\(A_\infty \) condition), by Lemma 12.2 we get
and thus
We distinguish now two types of cubes from \({\mathsf {Top}}\). We denote by \({\mathsf {Top}}_a\) the family of cubes \(R\in {\mathsf {Top}}\) such that \({\mathsf {T}}(R)=\{R\}\), and we set \({\mathsf {Top}}_b={\mathsf {Top}}{\setminus } {\mathsf {Top}}_a\). Notice that, by construction, if \(R\in {\mathsf {Top}}_b\), then \(b\beta (R)\le \varepsilon \). On the other hand, this estimate may fail if \(R\in {\mathsf {Top}}_a\).
15.2 The truncated corona decomposition
For technical reasons, we need now to define a truncated version of the previous corona decomposition. We fix a big natural number \(N\gg 1\). Then we let \({\mathsf {Top}}^{(N)}\) be the family of the cubes from \({\mathsf {Top}}\) with side length larger than \(2^{-N}\ell (R_0)\). Given \(R\in {\mathsf {Top}}^{(N)}\) we let \({\mathsf {T}}^{(N)}(R)\) be the subfamily of the cubes from \({\mathsf {T}}(R)\) with side length larger than \(2^{-N}\ell (R_0)\), and we let \({\mathsf {Stop}}^{(N)}(R)\) be a maximal subfamily from \({\mathsf {Stop}}(R)\cup \mathcal {D}_{N}(R_0)\), where \(\mathcal {D}_{N}(R_0)\) is the subfamily of the cubes from \(\mathcal {D}(R_0)\) with side length \(2^{-N}\ell (R_0)\). We also denote \({\mathsf {Top}}_a^{(N)} ={\mathsf {Top}}^{(N)}\cap {\mathsf {Top}}_a\) and \({\mathsf {Top}}_b^{(N)} ={\mathsf {Top}}^{(N)}\cap {\mathsf {Top}}_b\).
Observe that, since \({\mathsf {Top}}^{(N)}\subset {\mathsf {Top}}\), we also have
15.3 The key lemma
The main ingredient for the proof of the Main Lemma 10.2 is the following result.
Lemma 13.3
(Key Lemma). Given \(\eta \in (0,1)\) and \(\lambda \in (0,c_3]\) (with \(c_3\) as in (12.2)), there exists an exceptional family \(\mathsf {Ex}(R)\subset {\mathsf {Stop}}(R)\cap \mathsf {G}\) satisfying
such that, for every \(Q\in {\mathsf {Stop}}(R)\cap \mathsf {G}{\setminus } \mathsf {Ex}(R)\), any \(\lambda \)-good corkscrew for Q can be joined to some \(\lambda '\)-good corkscrew for R by a \(C(\lambda ,\eta )\)-good Harnack chain, with \(\lambda '\) depending on \(\lambda ,\eta \).
This lemma will be proved in the next Sects. 14 and 15. Using this result, in Sect. 16 we will build the required carrot curves for the Main Lemma 10.2, which join the pole p to points from a suitable big piece of \(R_0\). If the reader prefers to see how this is applied before its long proof, they may go directly to Sect. 16. A crucial point in the Key Lemma is that the constant \(\varepsilon \) in the definition of the stopping cubes of the corona decomposition does not depend on the constants \(\lambda \) or \(\eta \) above.
To prove the Key Lemma 13.3 we will need first to introduce the notion of “cubes with well separated big corkscrews” and we will split \({\mathsf {T}}^{(N)}(R)\) into subtrees by introducing an additional stopping condition involving this type of cubes. Later on, in Sect. 14 we will prove the “Geometric Lemma”, which relies on a geometric construction which plays a fundamental role in the proof of the Key Lemma.
15.4 The cubes with well separated big corkscrews
Let \(Q\in \mathcal {D}\) be a cube such that \(b\beta (Q)\le C_4\varepsilon \). For example, Q might be a cube from \(Q\in {\mathsf {T}}^{(N)}(R)\cup {\mathsf {Stop}}^{(N)}(R)\), with \(R\in {\mathsf {Top}}^{(N)}_b\) (which in particular implies that \(b\beta (R)\le \varepsilon \)). We denote by \(L_Q\) a best approximating n-plane for \(b\beta (Q)\), and we choose \({z}_Q^1\) and \({z}_Q^2\) to be two fixed points in \({B}_Q\) such that \({\text {dist}}({z}_Q^i,L_Q) = r({B}_Q)/2\) and lie in different components of \({\mathbb {R}}^{n+1}{\setminus } L_Q\). So \({z}_Q^1\) and \({z}_Q^2\) are corkscrews for Q. We will call them “big corkscrews”.
Since any corkscrew x for Q satisfies \(\delta _\Omega (x)\ge \kappa _1\,\ell (Q)\) and we have chosen \(\varepsilon \ll \kappa _1\), it turns out that
As a consequence, x can be joined either to \({z}_Q^1\) or to \({z}_Q^2\) by a C-good Harnack chain, with C depending only on \(n,C_0,\kappa _1\), and thus only on n, \(C_0\) and the weak-\(A_\infty \) constants in \({B}_{R_0}\). The following lemma follows by the same reasoning:
Lemma 13.4
Let \(Q,Q'\in \mathcal {D}\) be cubes such that \(b\beta (Q),b\beta (Q')\le C_4\varepsilon \) and \(Q'\) is the parent of Q. Let \({z}_Q^i,{z}_{Q'}^i\), for \(i=1,2\), be big corkscrews for Q and \(Q'\) respectively. Then, after relabeling the corkscrews if necessary, \({z}_Q^i\) can be joined to \({z}_{Q'}^i\) by a C-good Harnack chain, with C depending only on \(n,C_0,\kappa _1\).
Given \(\Gamma >0\), we will write \(Q\in {{\mathsf {WSBC}}}(\Gamma )\) (or just \(Q\in {{\mathsf {WSBC}}}\), which stands for “well separated big corkscrews”) if \(b\beta (Q)\le C_4\varepsilon \) and the big corkscrews \({z}_Q^1\), \({z}_Q^2\) can not be joined by any \(\Gamma \)-good Harnack chain. The parameter \(\Gamma \) will be chosen below. For the moment, let us say that \(\Gamma ^{-1}\ll \varepsilon \). The reader should think that in spite of \(b\beta (Q)\le C_4\varepsilon \), the possible existence of “holes of size \(C\,\varepsilon \ell (Q)\) in \(\partial \Omega \)” makes possible the connection of the big corkscrews by means of \(\Gamma \)-Harnack chains passing through these holes. Note that if \(b\beta (Q)\le C_4\varepsilon \) and \(Q\not \in {{\mathsf {WSBC}}}(\Gamma )\), then any pair of corkscrews for Q can be connected by a \(C(\Gamma )\)-good Harnack chain, since any of these corkscrews can be joined by a good chain to one of the big corkscrews for Q, as mentioned above.
15.5 The tree of cubes of type \({{\mathsf {WSBC}}}\) and the subtrees
Given \(R\in {\mathsf {Top}}^{(N)}_b\), denote by \({\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\) the maximal subfamily of cubes \(Q\in \mathcal {D}(R)\) which satisfy that either
-
\(Q\not \in {{\mathsf {WSBC}}}(\Gamma )\), or
-
\(Q\not \in {\mathsf {T}}^{(N)}(R)\).
Also, denote by \({\mathsf {T}}_{{\mathsf {WSBC}}}(R)\) the cubes from \(\mathcal {D}(R)\) which are not contained in any cube from \({\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\). So this tree is empty if \(R\not \in {{\mathsf {WSBC}}}(\Gamma )\). Notice also that \({\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\not \subset {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\).
Observe that if \(Q\in {\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\), it may happen that \(Q\not \in {{\mathsf {WSBC}}}(\Gamma )\). However, unless \(Q=R\), it holds that \(Q\in {{\mathsf {WSBC}}}(\Gamma ')\), with \(\Gamma '>\Gamma \) depending only on \(\Gamma \) and \(C_0\) (because the parent of Q belongs to \({{\mathsf {WSBC}}}(\Gamma )\)).
For each \(Q\in {\mathsf {Stop}}_{{\mathsf {WSBC}}}(R){\setminus }{\mathsf {Stop}}(R)\), we denote
So we have
and the union is disjoint. Observe also that we have the partition
16 The geometric lemma
16.1 The geometric lemma for the tree of cubes of type \({{\mathsf {WSBC}}}\)
Let \(R\in {\mathsf {Top}}^{(N)}_b\) and suppose that \({\mathsf {T}}_{{\mathsf {WSBC}}}(R)\ne \varnothing \). We need now to define a family \({\mathsf {End}}(R)\) of cubes from \(\mathcal {D}\), which in a sense can be considered as a regularized version of \({\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\). The first step consists of introducing the following auxiliary function:
Observe that \(d_R\) is 1-Lipschitz.
For each \(x\in \partial \Omega \) we take the largest cube \(Q_x\in \mathcal {D}\) such that \(x\in Q_x\) and
We consider the collection of the different cubes \(Q_x\), \(x\in \partial \Omega \), and we denote it by \({\mathsf {End}}(R)\).
Lemma 14.1
Given \(R\in {\mathsf {Top}}^{(N)}_b\), the cubes from \({\mathsf {End}}(R)\) are pairwise disjoint and satisfy the following properties:
-
(a)
If \(P\in {\mathsf {End}}(R)\) and \(x\in 50{B}_P\), then \(100\,\ell (P)\le d_R(x) \le 900\,\ell (P)\).
-
(b)
There exists some absolute constant C such that if \(P,P'\in {\mathsf {End}}(R)\) and \(50{B}_P\cap 50{B}_{P'} \ne \varnothing \), then \(C^{-1}\ell (P)\le \ell (P')\le C\,\ell (P).\)
-
(c)
For each \(P\in {\mathsf {End}}(R)\), there at most N cubes \(P'\in {\mathsf {End}}(R)\) such that \(50{B}_P\cap 50{B}_{P'} \ne \varnothing ,\) where N is some absolute constant.
-
(d)
If \(P\in {\mathsf {End}}(R)\) and \({\text {dist}}(P,R)\le 20\,\ell (R)\), then there exists some \(Q\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\) such that \(P\subset 22Q\) and \(\ell (Q)\le 2000\,\ell (P)\).
Proof
The proof is a routine task. For the reader’s convenience we show the details. To show (a), consider \(x\in 50 {B}_P\). Since \(d_R(\cdot )\) is 1-Lipschitz and, by definition, \(d_R({x}_{P})\ge 300\,\ell (P)\), we have
To prove the converse inequality, by the definition of \({\mathsf {End}}(R)\), there exists some \(z'\in {\widehat{P}}\), the parent of P, such that
Also, we have
Thus,
The statement (b) is an immediate consequence of (a), and (c) follows easily from (b). To show (d), observe that, for any \(S\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\),
Thus,
In particular, choosing \(S=R\), we deduce
and thus, using again that \({\text {dist}}(P,R)\le 20\ell (R)\), it follows that \(P\subset 22R\). Let \(S_0\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\) be such that \(d_R({x}_P)=\ell (S_0) + {\text {dist}}({x}_P,S_0)\), and let \(Q\in \mathcal {D}\) be the smallest cube such that \(S_0\subset Q\) and \(P\subset 22Q\). Since \(S_0\subset R\) and \(P\subset 22R\), we deduce that \(S_0\subset Q\subset R\), implying that \(Q\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\).
So it just remains to check that \(\ell (Q)\le 2000\,\ell (P)\). To this end, consider a cube \({\widetilde{Q}}\supset S_0\) such that
From the first inequality, it is clear that \(P\subset 2{\widetilde{Q}}\) and then, by the definition of Q, we infer that \(Q\subset {\widetilde{Q}}\). This inclusion and the second inequality above imply that
By (a) we know that \(d_R({x}_P)\le 900\,\ell (P)\), and so we derive \(\ell (Q) \le 2000\,\ell (P)\). \(\square \)
Lemma 14.2
Given \(R\in {\mathsf {Top}}^{(N)}_b\), if \(Q\in {\mathsf {End}}(R)\) and \({\text {dist}}(P,R)\le 20\,\ell (R)\), then \(b\beta (Q)\le C\,\varepsilon \) and \(Q\in {{\mathsf {WSBC}}}(\Gamma ')\), with \(\Gamma '=c_6\,\Gamma \), for some absolute constants \(C,c_6>0\).
Proof
This immediate from the fact that, by (d) in the previous lemma, there exists some cube \(Q'\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\) such that \(Q\subset 22Q'\) and \(\ell (Q')\le 2000\,\ell (Q)\), so that \(b\beta (Q')\le \varepsilon \) and \(Q'\in {{\mathsf {WSBC}}}(\Gamma )\). \(\square \)
As in Sect. 3, we make a standard Whitney decomposition of the open set \(\Omega \). With a harmless abuse of notation we let \(\mathcal {W}=\mathcal {W}(\Omega )\) denote a collection of (closed) dyadic Whitney cubes of \(\Omega \), so that the cubes in \(\mathcal {W}\) form a pairwise non-overlapping covering of \(\Omega \), which satisfy for some \(M_0>20\) and \(D_0\ge 1\)
-
(i)
\(10I \subset \Omega \);
-
(ii)
\(M_0 I \cap \partial \Omega \ne \varnothing \);
-
(iii)
there are at most \(D_0\) cubes \(I'\in \mathcal {W}\) such that \(10I \cap 10I' \ne \varnothing \). Further, for such cubes \(I'\), we have \(\ell (I')\approx \ell (I)\), where \(\ell (I')\) stands for the side length of \(I'\).
From the properties (i) and (ii) it is clear that \({\text {dist}}(I,\partial \Omega )\approx \ell (I)\). We assume that the Whitney cubes are small enough so that
To construct this Whitney decomposition one just needs to replace each cube \(I\in \mathcal {W}\), as in [49, Chapter VI], by its descendants \(I'\in \mathcal {D}_k(I)\), for some fixed \(k\ge 1\).
For each \(I\in \mathcal {W}\), as much as in Lemma 9.4, we denote by \(B^I\) a ball concentric with I and radius \(C_5\ell (I)\), where \(C_5\) is a universal constant big enough so that
and whenever \(p\notin 5I\). Obviously, the ball \(B^I\) intersects \(\partial \Omega \), and the family \(\{B^I\}_{I\in \mathcal {W}}\) does not have finite overlapping.
Given a bounded measurable set \(F\subset \mathbb R^{n+1}\) with \(|F|>0\), and a function \(f\in L^1_\mathrm{loc}({\mathbb {R}}^{n+1})\), we denote by \(m_F f\) the mean of f in F with respect to Lebesgue measure. That is,
To state the Geometric Lemma we need some additional notation. Given a cube \(R'\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\), we denote by \({\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\) the family of cubes from \(\mathcal {D}\) with side length at most \(\ell (R')\) which are contained in \(100{B}_{R'}\) and are not contained in any cube from \({\mathsf {End}}(R)\). We also denote by \({\widetilde{{\mathsf {End}}}}(R')\) the subfamily of the cubes from \({\mathsf {End}}(R)\) which are contained in some cube from \({\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\). Note that \({\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\) is not a tree, in general, but a union of trees. Further, from Lemma 14.1(a), it follows easily that
Lemma 14.3
(Geometric Lemma). Let \(0<\gamma <1\), and assume that the constant \(\Gamma =\Gamma (\gamma )\) in the definition of \({{\mathsf {WSBC}}}\) is big enough. Let \(R\in {\mathsf {Top}}^{(N)}_b\cap {{\mathsf {WSBC}}}(\Gamma )\) and let \(R'\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\) be such that \(\ell (R')=2^{-k_0}\ell (R)\), with \(k_0=k_0(\gamma )\ge 1\) big enough. Then there are two open sets \(V_1,V_2\subset C{B}_{R'}\cap \Omega \) with disjoint closures which satisfy the following properties:
-
(a)
There are subfamilies \(\mathcal {W}_i\subset \mathcal {W}\) such that \(V_i=\bigcup _{I\in \mathcal {W}_i} 1.1{{\,\mathrm{int}\,}}(I).\)
-
(b)
Each \(V_i\) contains a ball \(B_i\) with \(r(B_i)\approx \ell (R')\), and each corkscrew point for \(R'\) contained in \(2{B}_{R'}\cap V_i\) can be joined to the center \(z_i\) of \(B_i\) by a good Harnack chain contained in \(V_i\). Further, any point \(x\in V_i\) can be joined to \(z_i\) by a good Harnack chain (not necessarily contained in \(V_i\)).
-
(c)
For each \(Q\in \big ({\mathsf {T}}_{{\mathsf {WSBC}}}(R)\cup {\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\big ) \cap \mathcal {D}(R')\) there are big corkscrews \({z}_Q^1\in V_1\cap 2{B}_Q\) and \({z}_Q^2\in V_2\cap 2{B}_Q\), and if \({\widehat{Q}}\) is an ancestor of Q which also belongs to \({\mathsf {T}}_{{\mathsf {WSBC}}}(R)\cap \mathcal {D}(R')\), then \({z}_Q^i\) can be joined to \({z}_{{\widehat{Q}}}^i\) by a good Harnack chain, for each \(i=1,2\).
-
(d)
\((\partial V_1\cup \partial V_2)\cap 10{B}_{R'} \subset \bigcup _{P\in {\widetilde{{\mathsf {End}}}}(R')}2{B}_P\).
-
(e)
For each \(P\in {\widetilde{{\mathsf {End}}}}(R')\) such that \(2{B}_P\cap 10{B}_{R'}\ne \varnothing \), let \(\mathcal {W}_P\) be the family of Whitney cubes \(I\subset V_1\cup V_2\) such that \(1.1\overline{I}\cap \partial (V_1\cup V_2)\cap 2{B}_P\ne \varnothing \), so that
$$\begin{aligned} \partial V_i\cap 2{B}_P \subset \bigcup _{I\in \mathcal {W}_P}1.1\overline{I}. \end{aligned}$$Then
-
(i)
$$\begin{aligned} m_{4I} g(p,\cdot )\le \gamma \,\frac{\ell (P)}{\sigma (R_0)}\quad \text{ for } \text{ each } I\in \mathcal {W}_P, \end{aligned}$$
and
-
(ii)
$$\begin{aligned} \sum _{I\in \mathcal {W}_P} \ell (I)^n \lesssim \ell (P)^n \quad \text { and }\quad \sum _{I\in \mathcal {W}_P} \omega ^p(B^I) \lesssim \omega ^p(C{B}_P), \end{aligned}$$
for some universal constant \(C>1\).
-
(i)
The constants involved in the Harnack chain and corkscrew conditions may depend on \(\varepsilon \), \(\Gamma \), and \(\gamma \).Footnote 5
16.2 Proof of the geometric Lemma 14.3
In this whole subsection we fix \(R\in {\mathsf {Top}}^{(N)}_b\) and we assume \({\mathsf {T}}_{{\mathsf {WSBC}}}(R)\ne \varnothing \), as in Lemma 14.3. We let \(R'\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\) be such that \(\ell (R')=2^{-k_0}\ell (R)\), with \(k_0=k_0(\gamma )\ge 1\) big enough, as in Lemma 14.3, and we consider the associated families \({\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\) and \({\widetilde{{\mathsf {End}}}}(R')\).
Remark 14.4
By arguments analogous to the ones in Lemma 14.2, it follows easily that if \(Q\in {\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\), for \(R'\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\) such that \(\ell (R')=2^{-k_0}\ell (R)\), then there exists some cube \(S\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\) such that \(Q\subset 22S\) and \(\ell (S)\le 2000\ell (Q)\). This implies that \(b\beta (Q)\le C\,\varepsilon \) and \(Q\in {{\mathsf {WSBC}}}(c_6\Gamma )\) too.
In order to define the open sets \(V_1\), \(V_2\) described in the lemma, first we need to associate some open sets \(U_1(Q)\), \(U_2(Q)\) to each \(Q\in {\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\cup {\widetilde{{\mathsf {End}}}}(R')\). We distinguish two cases:
-
For \(Q\in {\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\), we let \(\mathcal J_i(Q)\) be the family of Whitney cubes \(I\in \mathcal {W}\) which intersect
$$\begin{aligned} \{y\in \ 20{B}_Q:{\text {dist}}(y,L_Q)>\varepsilon ^{1/4}\,\ell (Q)\} \end{aligned}$$and are contained in the same connected component of \({\mathbb {R}}^{n+1}{\setminus } L_Q\) as \({z}_Q^i\), and then we set
$$\begin{aligned} U_i(Q) = \bigcup _{I\in \mathcal J_i(Q)} 1.1{{\,\mathrm{int}\,}}(I). \end{aligned}$$ -
For \(Q\in {\widetilde{{\mathsf {End}}}}(R')\) the definition of \(U_i(Q)\) is more elaborated. First we consider an auxiliary ball \({\widetilde{{B}}}_Q\), concentric with \({B}_Q\), such that \(19{B}_Q\subset {\widetilde{{B}}}_Q\subset 20{B}_Q\) and having thin boundaries for \(\omega ^p\). This means that, for some absolute constant C,
$$\begin{aligned} \omega ^p\bigl (\bigl \{x\in 2{\widetilde{{B}}}_Q:{\text {dist}}(x,\,\partial {\widetilde{{B}}}_Q)\le t\,r({\widetilde{{B}}}_Q)\bigr \}\bigr ) \le C\, t\,\omega ^p(2{\widetilde{{B}}}_Q) \quad \text{ for } \text{ all } t>0\text{. } \end{aligned}$$(14.3)The existence of such ball \({\widetilde{{B}}}_Q\) follows by well known arguments (see for example [50, p.370]).
Next we denote by \(\mathcal J(Q)\) the family of Whitney cubes \(I\in \mathcal {W}\) which intersect \({\widetilde{{B}}}_Q\) and satisfy \(\ell (I)\ge \theta \,\ell (Q)\) for \(\theta \in (0,1)\) depending on \(\gamma \) (the reader should think that \(\theta \ll \varepsilon \) and that \(\theta =2^{-j_1}\) for some \(j_1\gg 1\)), and we set
$$\begin{aligned} U(Q) = \bigcup _{I\in \mathcal J(Q)} 1.1{{\,\mathrm{int}\,}}(I). \end{aligned}$$(14.4)For a fixed \(i=1\) or 2, let \(\{D_j^i(Q)\}_{j\ge 0}\) be the connected components of U(Q) which satisfy one of the following properties:
-
either \({z}_Q^i\in D_j^i(Q)\) (recall that \({z}_Q^i\) is a big corkscrew for Q), or
-
there exists some \(y\in D_j^i(Q)\) such that \(g(p,y)> \gamma \,\ell (Q)\,\sigma (R_0)^{-1}\) and there is a \(C_6(\gamma ,\theta )\)-good Harnack chain that joins y to \({z}_Q^i\), for some constant \(C_6(\gamma ,\theta )\) to be chosen below.
Then we let \(U_i(Q)=\bigcup _j D_j^i(Q)\). After reordering the sequence, we assume that \({z}_Q^i\in D_0^i(Q)\). We let \(\mathcal J_i(Q)\) be the subfamily of cubes from \(\mathcal J(Q)\) contained in \(U_i(Q)\).
-
In the case \(Q\in {\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\), from the definitions, it is clear that the sets \(U_i(Q)\) are open and connected and
In the case \(Q\in {\widetilde{{\mathsf {End}}}}(R')\), the sets \(U_i(Q)\) may fail to be connected. However, (14.5) still holds if \(\Gamma \) is chosen big enough (which will be the case). Indeed, if some component \(D_j^i\) can be joined by \(C_6(\gamma ,\theta )\)-good Harnack chains both to \({z}_Q^1\) and \({z}_Q^2\), then there is a \(C(\gamma ,\theta )\)-good Harnack chain that joins \({z}_Q^1\) to \({z}_Q^2\), and thus Q does not belong to \({{\mathsf {WSBC}}}(c_6\Gamma )\) if \(\Gamma \) is taken big enough, which cannot happen by Lemma 14.2. Note also that the two components of
are contained in \(D_0^1(Q)\cup D_0^2(Q)\), because \(b\beta (Q)\le C\varepsilon \) and we assume \(\theta \ll \varepsilon \).
The following is immediate:
Lemma 14.5
Assume that we relabel appropriately the sets \(U_i(P)\) and corkscrews \({z}_P^i\) for \(P\in {\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\cup {\widetilde{{\mathsf {End}}}}(R')\). Then for all \(Q,{\widehat{Q}}\in {\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\cup {\widetilde{{\mathsf {End}}}}(R')\) such that \({\widehat{Q}}\) is the parent of Q we have
Further,
where c depends at most on n and \(C_0\).
The labeling above can be chosen inductively. First we fix the sets \(U_i(T)\) and corkscrews \(x_{T}^i\) for every maximal cube T from \({\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\) (contained in \(100{B}_{R'}\) and with side length equal to \(\ell (R')\)). Further we assume that, for any maximal cube T, the corkscrew \(x^i_T\) is at the same side of \(L_{R'}\) as \({z}_{R'}^i\), for each \(i=1,2\) (this property will be used below). Later we label the sons of each T so that (14.6) holds for any son Q of T. Then we proceed with the grandsons of T, and so on. We leave the details for the reader.
The following result will be used later to prove the property (e)(i).
Lemma 14.6
Suppose that the constant \(k_0(\gamma )\) in Lemma 14.3 is big enough. Let \(Q\in {\widetilde{{\mathsf {End}}}}(R')\) and assume \(\theta \) small enough and \(C_6(\gamma ,\theta )\) big enough in the definition of \(U_i(Q)\). If \(y\in {\widetilde{{B}}}_Q\) satisfies \(g(p,y)> \gamma \,\ell (Q)\,\sigma (R_0)^{-1}\), then \(y\in U_1(Q)\cup U_2(Q)\).
Recall \({\widetilde{{B}}}_Q\) is the ball with thin boundary appearing in (14.3).
Proof
By the definition of \(U_i(Q)\), it suffices to show that y belongs to some component \(D_j^i(Q)\) and that there is a \(C_6(\gamma ,\theta )\)-good Harnack chain that joins y to \({z}_Q^i\). To this end, observe that by the boundary Hölder continuity of \(g(p,\cdot )\),
where in the last inequality we used Lemma 9.5. Thus,
and if \(\theta \) is small enough, then y belongs to some connected component of the set U(Q) in (14.4). By Lemma 14.1(d) there is a cube \(Q'\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\) such that \(Q\subset 22Q'\) and \(\ell (Q')\approx \ell (Q)\). In particular, \({{\mathsf {WA}}}(p,\Lambda )\cap Q'\supset G_0\cap Q'\ne \varnothing \) and thus, by applying Lemma 11.6 with \(q=y\) and \(r_0=Cr({B}_Q)\) (for a suitable \(C>1\)), it follows that there exists a \(\kappa _1\)-corkscrew \(y'\in C(\gamma )\,{B}_Q\), with \(C(\gamma )>20\) say, such that y can be joined to \(y'\) by a \(C'(\gamma )\)-good Harnack chain. Assuming that the constant \(k_0(\gamma )\) in Lemma 14.3 is big enough, it turns out that \(y'\in 2{B}_{Q''}\) for some \(Q''\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\) such that \(22Q''\supset Q\). Since all the cubes S such that \(Q\subset S\subset 22Q''\) satisfy \(b\beta (S)\le C\,\varepsilon \), by applying Lemma 13.4 repeatedly, it follows that \(y'\) can be joined either to \({z}_Q^1\) or \({z}_Q^2\) by a \(C''(\gamma )\)-good Harnack chain. Then, joining both Harnack chains, it follows that y can be joined either to \({z}_Q^1\) or \({z}_Q^2\) by a \(C'''(\gamma )\)-good Harnack chain. So y belongs to one of the components \(D_j^i\), assuming \(C_6(\gamma ,\theta )\) big enough. \(\square \)
From now on we assume \(\theta \) small enough and \(C_6(\gamma ,\theta )\) big enough so that the preceding lemma holds. Also, we assume \(\theta \ll \varepsilon ^4\). We define
Next we will show that
Since the number of cubes \(Q\in {\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\cup {\widetilde{{\mathsf {End}}}}(R')\) is finite (because of the truncation in the corona decomposition), this is a consequence of the following:
Lemma 14.7
Suppose \(\Gamma \) is big enough in the definition of \({{\mathsf {WSBC}}}\) (depending on \(\theta \)). For all \(P,Q\in {\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\cup {\widetilde{{\mathsf {End}}}}(R')\), we have
Proof
We suppose that \(\ell (Q)\ge \ell (P)\) We also assume that \(\overline{U_1(P)} \cap \overline{U_2(Q)}\ne \varnothing \) and then we will get a contradiction. Notice first that if \(\ell (P)=\ell (Q)=2^{-j}\ell (R')\) for some \(j\ge 0\), then the corkscrews \({z}_P^i\) and \({z}_Q^i\) are at the same side of \(L_Q\) for each \(i=1,2\). This follows easily by induction on j.
Case 1. Suppose first that \(P,Q\in {\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\). Since the cubes from \(\mathcal J_2(Q)\) have side length at least \(c\,\varepsilon ^{1/4}\,\ell (Q)\), it follows that at least one of the cubes from \(\mathcal J_1(P)\) has side length at least \(c'\,\varepsilon ^{1/4}\,\ell (Q)\), which implies that \(\ell (P)\ge c''\,\varepsilon ^{1/4}\,\ell (Q)\), by the construction of \(U_1(P)\).
Since \(U_1(P) \cap U_2(Q)\ne \varnothing \), there exists some curve \(\gamma =\gamma ({z}_P^1,{z}_Q^2)\) that joins \({z}_P^1\) and \({z}_Q^2\) such that \({\text {dist}}(\gamma ,\partial \Omega )\ge c\,\varepsilon ^{1/2}\,\ell (Q)\) because all the cubes from \(\mathcal J_2(Q)\) have side length at least \(c\,\varepsilon ^{1/4}\,\ell (Q)\), and the ones from \(\mathcal J_1(P)\) have side length \(\ge c\,\varepsilon ^{1/4}\,\ell (P)\ge c\,\varepsilon ^{1/2}\,\ell (Q)\).
Let \({\widehat{P}}\) be the ancestor of P such that \(\ell ({\widehat{P}})=\ell (Q)\). From the fact that \(\overline{U_1(P)} \cap \overline{U_2(Q)}\ne \varnothing \), we deduce that \(20{B}_P\cap 20{B}_Q\ne \varnothing \) and thus \(20{B}_{{\widehat{P}}}\cap 20{B}_Q\ne \varnothing \), and so \(20{B}_{{\widehat{P}}}\subset 60{B}_Q\). This implies that \({z}_{{\widehat{P}}}^1\) is in the same connected component as \({z}_Q^1\) and also that \({\text {dist}}([{z}_Q^1,{z}_{{\widehat{P}}}^1],\partial \Omega )\gtrsim \ell (Q)\), because \(b\beta (100{B}_Q)\le \varepsilon \ll 1\) and they are at the same side of \(L_Q\).
Consider now the chain \(P=P_1\subset P_2\subset \cdots \subset P_m={\widehat{P}}\), so that \(P_{i+1}\) is the parent of \(P_i\). Form the curve \(\gamma '= \gamma '({z}_{{\widehat{P}}}^1,{z}_P^1)\) with endpoints \({z}_{{\widehat{P}}}^1\) and \({z}_P^1\) by joining the segments \([{z}_{P_i}^1,{z}_{P_{i+1}}^1]\). Since these segments satisfy
it is clear that \({\text {dist}}(\gamma ',\partial \Omega )\ge c\,\varepsilon ^{1/4}\,\ell (Q)\).
Next we form a curve \(\gamma ''= \gamma ''({z}_Q^1,{z}_Q^2)\) which joins \({z}_Q^1\) to \({z}_Q^2\) by joining \([{z}_Q^1,{z}_{{\widehat{P}}}^1]\), \(\gamma '({z}_{{\widehat{P}}}^1,{z}_P^1)\), and \(\gamma ({z}_P^1,{z}_Q^2)\). It follows easily that this is contained in \(90{B}_Q\) and that \({\text {dist}}(\gamma '',\partial \Omega )\ge c\,\varepsilon ^{1/2}\,\ell (Q)\). However, this is not possible because \({z}_Q^1\) and \({z}_Q^2\) are in different connected components of \({\mathbb {R}}^{n+1}{\setminus } L_Q\) and \(b\beta (Q)\le \varepsilon \ll \varepsilon ^{1/2}\) (since we assume \(\varepsilon \ll 1\)).
Case 2. Suppose now that \(Q\in {\widetilde{{\mathsf {End}}}}(R') \). The arguments are quite similar to the ones above. In this case, the cubes from \(\mathcal J_2(Q)\) have side length at least \(\theta \,\ell (Q)\) and thus at least one of the cubes from \(\mathcal J_1(P)\) has side length at least \(c\,\theta \,\ell (Q)\), which implies that \(\ell (P)\ge c'\,\theta \,\ell (Q)\).
Now there exists a curve \(\gamma =\gamma ({z}_P^1,{z}_Q^2)\) that joints \({z}_P^1\) and \({z}_Q^2\) such that \({\text {dist}}(\gamma ,\partial \Omega )\ge c\,\theta ^2\,\ell (Q)\) because all the cubes from \(\mathcal J_2(Q)\) have side length at least \(\theta \,\ell (Q)\), and the ones from \(\mathcal J_1(P)\) have side length \(\theta \,\ell (P)\ge c\,\theta ^2\,\ell (Q)\).
We consider again cubes \({\widehat{P}}\) and \(P_1,\ldots ,P_m\) defined exactly as above. By the same reasoning as above, \({\text {dist}}([{z}_Q^1,{z}_{{\widehat{P}}}^1],\partial \Omega )\gtrsim \ell (Q)\). We also define the curve \(\gamma ' =\gamma '({z}_{{\widehat{P}}}^1,{z}_P^1)\) which joins \({z}_{{\widehat{P}}}^1\) to \({z}_P^1\) in the same way. In the present case we have
Again construct a curve \(\gamma ''= \gamma ''({z}_Q^1,{z}_Q^2)\) which joins \({z}_Q^1\) to \({z}_Q^2\) by gathering \([{z}_Q^1,{z}_{{\widehat{P}}}^1]\), \(\gamma '({z}_{{\widehat{P}}}^1,{z}_P^1)\), and \(\gamma ({z}_P^1,{z}_Q^2)\). This is contained in \(C{B}_Q\) (for some \(C>1\) possibly depending on \(\gamma \)) and satisfies \({\text {dist}}(\gamma '',\partial \Omega )\ge c\,\theta ^2\,\ell (Q)\). From this fact we deduce that \({z}_Q^1\) and \({z}_Q^2\) can be joined by \(C(\theta )\)-good Harnack chain. Taking \(\Gamma \) big enough (depending on \(C(\theta )\)), this implies that the big corkscrews for Q can be joined by a \((c_6\Gamma )\)-good Harnack chain, which contradicts Lemma 14.2.
Case 3. Finally suppose that \(P\in {\widetilde{{\mathsf {End}}}}(R')\). We consider the same auxiliary cube \({\widehat{P}}\) and the same curve \(\gamma =\gamma ({z}_P^1,{z}_Q^2)\) satisfying \({\text {dist}}(\gamma ,\partial \Omega )\ge c\,\theta \,\ell (P)\). By joining the segments \([{z}_{P_i}^2,{z}_{P_{i+1}}^2]\), we construct a curve \(\gamma '_2=\gamma '_2({z}_{{\widehat{P}}}^2,{z}_P^2)\) analogous to \(\gamma '=\gamma '({z}_{{\widehat{P}}}^1,{z}_P^1)\) from the case 2, so that this joins \({z}_{{\widehat{P}}}^2\) to \({z}_P^2\) and satisfies \({\text {dist}}(\gamma '_2,\partial \Omega )\gtrsim \ell (P)\).
We construct a curve \(\gamma '''\) that joins \({z}_P^1\) to \({z}_P^2\) by joining \(\gamma ({z}_P^1,{z}_Q^2)\), \([{z}_Q^2,{z}_{{\widehat{P}}}^2]\), and \(\gamma '_2({z}_{{\widehat{P}}}^2,{z}_P^2)\). Again this is contained in \(C{B}_Q\) and it holds \({\text {dist}}(\gamma ''',\partial \Omega )\ge c\,\theta \,\ell (P)\). This implies that \({z}_P^1\) and \({z}_P^2\) can be joined by \(C(\theta )\)-good Harnack chain. Taking \(\Gamma \) big enough, we deduce the big corkscrews for P can be joined by a \((c_6\Gamma )\)-good Harnack chain, which is a contradiction. \(\square \)
By the definition of \(V_1\) and \(V_2\) it is clear that the properties (a), (b) and (c) in Lemma 14.3 hold. So to complete the proof of the lemma it just remains to prove (d) and (e).
Proof of Lemma 14.3(d)
Let \(x\in (\partial V_1\cup \partial V_2)\cap 10{B}_{R'}\). We have to show that there exists some \(S\in {\widetilde{{\mathsf {End}}}}(R')\) such that \(x\in 2{B}_S\). To this end we consider \(y\in \partial \Omega \) such that \(|x-y|=\delta _\Omega (x)\). Since \({x}_{R'}\in \partial \Omega \), it follows that \(y\in 20{B}_{R'}\). Let \(S\in {\widetilde{{\mathsf {End}}}}(R')\) be such that \(y\in S\). Observe that
We claim that \(x\in 2{B}_S\). Indeed, if \(x\not \in 2{B}_S\), taking also into account (14.7), there exists some ancestor Q of S contained in \(100{B}_{R'}\) such that \(x\in 2{B}_Q\) and \(\delta _\Omega (x)=|x-y|\approx \ell (Q)\). From the fact that \(S\subsetneq Q\subset 100 {B}_{R'}\) we deduce that \(Q\in {\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\). By the construction of the sets \(U_i(Q)\), it is immediate to check that the condition that \(\delta _\Omega (x)\approx \ell (Q)\) implies that \(x\in U_1(Q)\cup U_2(Q)\). Thus \(x\in V_1\cup V_2\) and so \(x\not \in \partial (V_1\cup V_2) = \partial V_1 \cup \partial V_2\) (for this identity we use that \({\text {dist}}(V_1,V_2)>0\)), which is a contradiction. \(\square \)
To show (e), first we need to prove the next result:
Lemma 14.8
For each \(i=1,2\), we have
Proof
Clearly, we have
So it suffices to show that
Let \(x\in \partial U_i(P)\cap \partial V_i\cap 10{B}_{R'}\), with \(P\in {\widetilde{{\mathsf {T}}}}_{{\mathsf {WSBC}}}(R')\), \(P\cap 10{B}_{R'}\ne \varnothing \). From the definition of \(U_i(P)\), it follows easily that
On the other hand, by Lemma 14.3(d), there exists some \(Q\in {\widetilde{{\mathsf {End}}}}(R')\) such that \(x\in 2{B}_Q\). By the definition of \(U_i(Q)\), since \(\theta \ll \varepsilon \), it also follows easily that
Hence, \({\text {dist}}(\partial V_i\cap 2{B}_Q,\partial \Omega )\le \varepsilon ^{1/2}\,\ell (Q),\) and so
We claim that \(\ell (Q)\lesssim \ell (P)\). Indeed, from the fact that \(x\in \partial U_i(P)\subset 30{B}_P\), we infer that
Suppose that \(\ell (Q)\ge \ell (P)\). This implies that \({B}_P\subset 33{B}_Q\). Consider now a cube \(S\subset P\) belonging to \({\widetilde{{\mathsf {End}}}}(R')\). Since \({B}_S\cap 33{B}_Q\ne \varnothing \), by Lemma 14.1 (b) we have
which proves our claim. Together with (14.9) and (14.10), this yields
which is a contradiction for \(\varepsilon \) small enough. So there does not exist any \(x\in \partial U_i(P)\cap \partial V_i\cap 10{B}_{R'}\), which proves (14.8). \(\square \)
Proof of Lemma 14.3(e)
Let \(P\in {\widetilde{{\mathsf {End}}}}(R')\) be such that \(2{B}_P\cap 10{B}_{R'}\ne \varnothing \). The statement (i) is an immediate consequence of Lemma 14.6. In fact, this lemma implies that any \(y\in 2{B}_P\) such that \(g(p,y)> \gamma \,\ell (P)\,\sigma (R_0)^{-1}\) is contained in \(U_1(P)\cup U_2(P)\) and thus in \(V_1\cup V_2\). In particular, \(y\not \in \partial (V_1\cup V_2)= \partial V_1 \cup \partial V_2\). Thus, if \(y\in 2{B}_P\cap \partial V_i\), then
It is easy to check that this implies the statement (i) in Lemma 14.3(e) (possibly after replacing \(\gamma \) by \(C\gamma \)).
Next we turn our attention to (ii). To this end, denote by \(J_P\) the subfamily of the cubes \(Q\in {\widetilde{{\mathsf {End}}}}(R')\) such that \(30{B}_Q\cap 2{B}_P\ne \varnothing \). By Lemma 14.8,
We will show that
where \(\mathcal {W}_P\) is the family of Whitney cubes \(I\subset V_1\cup V_2\) such that \(1.1\overline{I}\cap \partial (V_1\cup V_2)\cap 2{B}_P\ne \varnothing \). To this end, observe that, by (14.11) and the construction of \(U_i(Q)\), for each \(I\in \mathcal {W}_P\) there exists some \(Q\in J_P\) such that \(I\subset 30{B}_Q\) and either \(\ell (I)\approx \theta \ell (Q)\) or \(1.1\overline{I}\cap \partial {\widetilde{{B}}}_Q\ne \varnothing \). Using the n-ADRity of \(\sigma \), it is immediate to check that for each \(Q\in J_P\),
Also,
Since the number of cubes \(Q\in J_P\) is uniformly bounded (by Lemma 14.1(b)) and \(\ell (Q)\approx \ell (P)\), the above inequalities yield the first estimate in (14.12).
To prove the second one we also distinguish among the two types of cubes \(I\in J_P\) above. First, by the bounded overlap of the balls \(B^I\) such that \(\ell (I)=\theta \,\ell (Q)\), we get
since the balls \(B^I\) in the sum are contained \(C{B}_P\) for a suitable universal constant \(C>1\). To deal with the cubes \(I\in \mathcal {W}\) such that \(1.1\overline{I}\cap \partial {\widetilde{{B}}}_Q\ne \varnothing \) we intend to use the thin boundary property of \({\widetilde{{B}}}_Q\) in (14.3). To this end, we write
where \(\mathcal U_d(A)\) stands for the d-neighborhood of A. By (14.3) it follows that
and thus
for a suitable \(C>1\). Together with (14.13), this yields the second inequality in (14.12), which completes the proof of Lemma 14.3(e). \(\square \)
17 Proof of the key lemma
We fix \(R_0\in \mathcal {D}\) and a corkscrew point \(p\in \Omega \) as in the preceding sections. We consider \(R\in {\mathsf {Top}}^{(N)}_b\) and we assume \({\mathsf {T}}_{{\mathsf {WSBC}}}(R)\ne \varnothing \), as in Lemma 14.3. We let \(R'\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\) be such that \(\ell (R')=2^{-k_0}\ell (R)\), with \(k_0=k_0(\gamma )\ge 1\) big enough. Given \(\lambda >0\) and \(i=1,2\), we set
so that by Lemma 12.3, \({\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\cap \mathcal {D}(R')\cap \mathsf {G}= {\mathsf {H}}_1(R')\cup {\mathsf {H}}_2(R')\). Here we are assuming that the corkscrews \({z}_Q^i\) belong to the set \(V_i\) from Lemma 14.3, that \(\lambda \) is small enough, and we are taking into account that, by the arguments in Sect. 13.4, any corkscrew for Q can be joined to one of the big corkscrews \({z}_Q^1\) by some C-good Harnack chain.
Lemma 15.1
(Baby Key Lemma). Let \(p,R_0,R,R'\) be as above. Given \(\lambda >0\), define also \({\mathsf {H}}_i(R')\) as above. For a given \(\tau >0\), suppose that
If \(\gamma \) is small enough in the definition of \(V_i\) in Lemma 14.3 (depending on \(\tau \) and \(\lambda \)), then
Remark that \(\Gamma \) depends on \(\gamma \) (see Lemma 14.3), and thus the families \({{\mathsf {WSBC}}}(\Gamma )\), \({\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\), \({\mathsf {H}}_i(R')\) also depend on \(\gamma \). The reader should thing that \(\Gamma \rightarrow \infty \) as \(\gamma \rightarrow 0\).
A key fact in this lemma is that the constants \(\lambda ,\tau \) can be taken arbitrarily small, without requiring \(\varepsilon \rightarrow 0\) as \(\lambda \tau \rightarrow 0\). Instead, the lemma requires \(\gamma \rightarrow 0\), which does not affect the packing condition in Lemma 13.2.
We denote
with \(\mathcal {W}_P\) as in the Lemma 14.3. That is, \(\mathcal {W}_P\) is the family of Whitney cubes \(I\subset V_1\cup V_2\) such that \(1.1\overline{I}\cap \partial (V_1\cup V_2)\cap 2{B}_P\ne \varnothing \). So the family \({\mathsf {Bdy}}(R')\) contains Whitney cubes which intersect the boundaries of \(V_1\) or \(V_2\) and are close to \(10{B}_{R'}\).
Let us introduce some extra piece of notation. Given \(q\in \mathbb {R}^{n+1}\) and \(0<r<s\) we let
To prove Lemma 15.1, first we need the following auxiliary result.
Lemma 15.2
Let \(p,R_0,R,R'\) be as above and, for \(i=1\) or 2, let \(Q\in {\mathsf {H}}_i(R')\). Let \(V_i\) be as in Lemma 14.3 and let \(q\in \Omega \) be a corkscrew point for Q which belongs to \(V_i\). Denote \(r=2\ell (R')\) and for \(\delta \in (0,1/100)\) set
Then we have
Let us note that the fact that q is a corkscrew for Q contained in \(V_i\) implies that \({\text {dist}}(q,\partial V_i)\approx \ell (Q)\), by the construction of the sets \(V_i\) in Lemma 14.3.
Proof
We fix \(i=1\), for definiteness. Recall that \(V_1=\bigcup _{I\in \mathcal {W}_1} 1.1{{\,\mathrm{int}\,}}(I)\). For each \(I\in \mathcal {W}_1\), consider a smooth function \(\eta _I\) such that \(\chi _{0.9I}\le \eta _I\le \chi _{1.09I}\) with \(\Vert \nabla \eta _I\Vert _\infty \lesssim \ell (I)^{-1}\) and
It follows that \({{\,\mathrm{supp}\,}}\eta \subset V_1\) and so \({{\,\mathrm{supp}\,}}\eta \cap V_2=\varnothing ,\) and also
Let \({\varphi }_0\) be a smooth function such that \(\chi _{B(q,1.2r)}\le {\varphi }_0\le \chi _{B(q,1.8r)}\), with \(\Vert \nabla {\varphi }_0\Vert _\infty \lesssim 1/r\). Then we set
So \({\varphi }\) is smooth, and it satisfies
Observe that, in a sense, \({\varphi }\) is a smooth version of the function \(\chi _{B(q,r)\cap V_1}\).
Since \(g(p,q) = g(p,q)\,{\varphi }(q)\) and \(g(p,\cdot )\,{\varphi }\) is a continuous function from \(W_0^{1,2}(\Omega )\), we have
First we estimate \(I_2\). For \(\varepsilon \) with \(0<\varepsilon <1/10\), we consider a smooth function \({\varphi }_\varepsilon \) such that \(\chi _{B(q,\varepsilon \delta _\Omega (q))}\le {\varphi }_\varepsilon \le \chi _{B(q,2\varepsilon \delta _\Omega (q))}\), with \(\Vert \nabla {\varphi }_\varepsilon \Vert _\infty \lesssim 1/(\varepsilon \delta _\Omega (q))\). Since \({\varphi }_\varepsilon \,{\varphi }= {\varphi }_\varepsilon \), we have
To deal with \(I_{2,a}\) we use the fact that for \(x\in B(q,2\varepsilon \delta _\Omega (q))\) we have
Then we get
Let us turn our attention to \(I_{2,b}\). We denote \(\psi = {\varphi }(1-{\varphi }_\varepsilon )\). Integrating by parts, we get
Observe now that the first integral vanishes because \(\psi \, g(q,\cdot )\in W_0^{1,2}(\Omega )\cap C(\overline{\Omega })\) and vanishes at \(\partial \Omega \) and at p. Hence, since \(\nabla \psi = \nabla {\varphi }- \nabla {\varphi }_\varepsilon \), we derive
To estimate \(I_4\) we take into account that \(|\nabla {\varphi }_\varepsilon |\lesssim \chi _{A(q,\varepsilon \delta _\Omega (q),2\varepsilon \delta _\Omega (q))}/ (\varepsilon \delta _\Omega (q))\), and then we derive
Using now that, for x in the domain of integration,
we obtain
From the above estimates we infer that
Since neither \(I_1\) nor \(I_3\) depend on \(\varepsilon \), letting \(\varepsilon \rightarrow 0\) we get
We denote
and
Next we split the last integral as follows:
Concerning \(J_1\), we have
Thus, using also that \(|\nabla {\varphi }|\lesssim 1/r\) outside \({\widetilde{F}}\),
Regarding \(J_2\), using Cauchy–Schwarz, we get
To estimate the integral \(\int _{{\widetilde{A}}_{r,\delta }} g(p,x)^2\,dx\), we take into account that, for all \(x\in {\widetilde{A}}_{r,\delta }\),
Then we deduce
Next we estimate the integral \(\int _{{\widetilde{A}}_{r,\delta }} |\nabla g(q,x)|^2\,dx\). By covering \({\widetilde{A}}_{r,\delta }\) by a finite family of balls of radius r/100 and applying Caccioppoli’s inequality to each one, it follows that
Since
we get
So we obtain
By interchanging, p and q, it is immediate to check that an analogous estimate holds for the second summand on the right hand side of (15.4). Thus we get
Concerning \(J_3\), we just take into account that \(|\nabla {\varphi }|\lesssim 1/\ell (I)\) in 2I, and then we obtain
Together with (15.2), (15.3), and (15.5), this yields the lemma. \(\square \)
Proof of Lemma 15.1
We fix \(i=1\), for definiteness. By a Vitali type covering theorem, there exists a subfamily \({\widetilde{{\mathsf {H}}}}_1(R')\subset {\mathsf {H}}_1(R')\) such that the balls \(\{8{B}_Q\}_{Q\in {\widetilde{{\mathsf {H}}}}_1(R')}\) are disjoint and
By Lemma 15.2, for each \(Q\in {\widetilde{{\mathsf {H}}}}_1(R')\) we have
with \(r=2\ell (R')\). Since \(g(p,{z}_{Q}^1)> \lambda \,\ell (Q)/\sigma (R_0)\), we derive
17.1 Estimate of \(\sum _{Q\in \tilde{\mathcal {W}}{\mathsf {H}}_{1}(R')} I_{1}(Q)\,\ell (Q)^{n-1}\)
We have
Note now that
where we used the fact that the cubes 4Q, with \(Q\in {\widetilde{{\mathsf {H}}}}_1(R')\), are pairwise disjoint. Since \(r\approx \ell (R')\), we derive
17.2 Estimate of \(\sum _{Q\in \tilde{\mathcal {W}}{\mathsf {H}}_{1}(R')} I_{2}(Q)\,\ell (Q)^{n-1}\)
First we estimate \(\int _{A({z}_Q^1,r,2r)}g(p,x)\,dx\) by applying Lemma 9.5:
So we have
17.3 Estimate of \(\sum _{Q\in \tilde{\mathcal {W}}{\mathsf {H}}_{1}(R')} I_{3}(Q)\,\ell (Q)^{n-1}\)
Note first that, for each \(I\in {\mathsf {Bdy}}(R')\), since \({z}_Q^1\not \in 4I\), using the subharmonicity of \(g(p,\cdot )\) and \(g({z}_Q^1,\cdot )\) in 4I, and Caccioppoli’s inequality,
By very similar estimates, we also get
Recall now that, by Lemma 14.3(e)(i),
for each \(I\in \mathcal {W}_P\), with \(P\in {\widetilde{{\mathsf {End}}}}(R')\) such that \(2{B}_P\cap 10{B}_{R'}\ne \varnothing \).
We distinguish two types of Whitney cubes \(I\in {\mathsf {Bdy}}(R')\). We write \(I\in T_1\) if \(\ell (I)\ge \gamma ^{1/2}\ell (P)\) for some P such that \(I\in \mathcal {W}_P\) and \(2{B}_P\cap 10{B}_{R'}\ne \varnothing \), and we write \(I \in T_2\) otherwise (there may exist more than one P such that \(I\in \mathcal {W}_P\), but if \(\mathcal {W}_P\cap \mathcal {W}_{P'}\ne \varnothing \), then \(\ell (P)\approx \ell (P')\)). So we split
Concerning the sum \(S_1\) we have
Next we take into account that
where \(x_I\) stands for the center of I and \(C>1\) is some absolute constant. This follows from Lemma 9.5 if \(x_I\) is far from Q, and it can be deduced from Lemma 9.3 when \(x_I\) is close to Q (in this case, \(\omega ^{x_I}(4Q)\approx 1\)). Then we derive
Since \(\sum _{Q\in {\widetilde{{\mathsf {H}}}}_1(R')}\omega ^{x_I}(4Q)\lesssim 1\) for each I, we get
By Lemma 14.3(e)(ii), we have \(\sum _{I\in \mathcal {W}_P} \ell (I)^n\lesssim \ell (P)^n\), and so we deduce
Next we turn our attention to the sum \(S_2\) in (15.7). Recall that
Let us remark that we assume the condition that \(I\in \mathcal {W}_P\) for some \(2P\in {\widetilde{{\mathsf {End}}}}(R')\) such that \(2{B}_P\cap 10{B}_{R'}\ne \varnothing \) to be part of the definition of \(I\in T_2\). Using the estimate \(m_{4I}g(p,\cdot ) \lesssim \omega ^p(B^I)\,\ell (I)^{1-n}\), we derive
To estimate the term A we take into account that if \(20I\cap 20{B}_Q\ne \varnothing \) and \(I\in \mathcal {W}_P\), then \(\ell (P)\lesssim \ell (Q)\) and thus \(\ell (I)\lesssim \gamma ^{1/2}\,\ell (Q)\) because \(I\in T_2\). As a consequence, \(I\subset 21{B}_Q\) and also, by the Hölder continuity of \(g({z}_Q^1,\cdot )\), if we let B be a ball concentric with \(B^I\) with radius comparable to \(\ell (Q)\) and such that \({\text {dist}}({z}_Q^1,B)\approx \ell (Q)\), we obtain
where \(\alpha >0\) is the exponent of Hölder continuity. Hence,
By Lemma 14.3(e)(ii), we have \(\sum _{I\in \mathcal {W}_P} \omega ^p(B^I)\lesssim \omega ^p(C{B}_P)\), and using also that, for P as above, \(C{B}_P\subset C'{B}_Q\) for some absolute constant \(C'\), we obtain
Finally, we turn our attention to the term B. We have
We claim now that, in the last sum, if one assumes that \(20I\cap 20{B}_Q=\varnothing \), then \({\text {dist}}(I,8{B}_Q)\ge c\,\gamma ^{-1/2}\,\ell (I)\). To check this, take \(P\in {\widetilde{{\mathsf {End}}}}(R')\) such that \(I\in \mathcal {W}_P\). Then note that
Using that \(I\cap 2{B}_P\ne \varnothing \), \({{\,\mathrm{diam}\,}}(I)\le C\gamma ^{1/2}\ell (P)\ll \ell (P)\), and \(\ell (Q)\le {\text {dist}}(I,8{B}_Q)\), we get
which implies that
and yields our claim.
Taking into account that the balls \(\{8{B}_Q\}_{Q\in {\widetilde{{\mathsf {H}}}}_1(R')}\) are disjoint and the Hölder continuity of \(\omega ^{(\cdot )}(\partial \Omega {\setminus } c\gamma ^{-1/2} I)\), for all \(x\in 4I\) we get
Thus,
Recalling again that \(\sum _{I\in \mathcal {W}_P} \omega ^p(B^I)\lesssim \omega ^p(C{B}_P)\), we deduce
Remark that for the second inequality we took into account that P is contained in a cube of the form \(22P'\) with \(P'\in {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\) and \(\ell (P')\approx \ell (P)\), by Lemma 14.1. This implies that \(\omega ^p(C{B}_P)\le \omega ^p(C'{B}_{P'})\lesssim \sigma (P')\,\sigma (R_0)^{-1}\lesssim \sigma (P)\,\sigma (R_0)^{-1}\).
Gathering the estimates above and recalling (15.6), we deduce
So, if \(\delta \) and \(\gamma \) are small enough (depending on \(\lambda ,\tau \)), we infer that
That is, there exists some \(y_0\in 2{B}_{R'}\cap V_1\) with \(\delta _\Omega (y_0)\ge \delta \,\ell (R')\) such that
with \(\delta \) depending on \(\lambda ,\tau \). Since \({z}_{R'}^1\) and \(y_0\) can be joined by a C-good Harnack chain (for some C depending on \(\delta \) and \(\gamma \), and thus on \(\lambda ,\tau \)), we deduce that
as wished. \(\square \)
Lemma 15.3
Let \(\eta \in (0,1)\) and \(\lambda >0\). Choose \(\gamma =\gamma (\lambda ,\tau )\) small enough as in Lemma 15.1 with \(\tau =\eta /2\). Assume that the family \({{\mathsf {WSBC}}}(\Gamma )\) is defined by choosing \(\Gamma \) big enough depending on \(\gamma \) (and thus on \(\lambda \) and \(\eta \)) as in Lemma 14.3. Let \(R\in {\mathsf {Top}}^{(N)}_b\) and suppose that \({\mathsf {T}}_{{\mathsf {WSBC}}}(R)\ne \varnothing \). Then, there exists an exceptional family \(\mathsf {Ex}_{{\mathsf {WSBC}}}(R)\subset {\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\cap \mathsf {G}\) satisfying
such that, for every \(Q\in {\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\cap \mathsf {G}{\setminus } \mathsf {Ex}_{{\mathsf {WSBC}}}(R)\), any \(\lambda \)-good corkscrew for Q can be joined to some \(\lambda '\)-good corkscrew for R by a \(C(\lambda ,\eta )\)-good Harnack chain, with \(\lambda '\) depending on \(\lambda ,\eta \).
Proof
For any \(R'\in \mathcal {D}_{k_0}(R)\cap {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\), with \(k_0=k_0(\gamma )\), we define \({\mathsf {H}}_i(R')\) as in (15.1), so that
For each \(R'\), we set
That is, for fixed \(i=1\) or 2, if \(\sum _{P\in {\mathsf {H}}_i(R')} \sigma (P)\le \tau \,\sigma (R')\), then all the cubes from \({\mathsf {H}}_i(R')\) belong to \(\mathsf {Ex}_{{\mathsf {WSBC}}}(R')\). In this way, it is clear that
We claim that the \(\lambda \)-good corkscrews of cubes from \({\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\cap \mathsf {G}\cap \mathcal {D}(R'){\setminus } \mathsf {Ex}_{{\mathsf {WSBC}}}(R')\) can be joined to some \({\widetilde{\lambda }}\)-good corkscrew for \(R'\) by a \({\widetilde{C}}\)-good Harnack chain, with \({\widetilde{\lambda }}\) depending on \(\lambda ,\eta \), and \({\widetilde{C}}\) depending on \(\Gamma \) and thus on \(\lambda ,\eta \) too. Indeed, if \(Q\in {\mathsf {H}}_i(R'){\setminus } \mathsf {Ex}_{{\mathsf {WSBC}}}(R')\) and \({z}_Q^i\) is \(\lambda \)-good corkscrew belonging to \(V_i\) (we use the notation of Lemma 15.1 and 14.3), then \(\sum _{P\in {\mathsf {H}}_i(R')} \sigma (P)> \tau \,\sigma (R')\) by the definition above and thus Lemma 15.1 ensures that \(g(p,{z}_{R'}^i)\ge c(\lambda ,\tau )\,\frac{\ell (R')}{\sigma (R_0)}\). So \({z}_{R'}^i\) is a \({\widetilde{\lambda }}\)-good corkscrew, which by Lemma 14.3(c) can be joined to \({z}_Q^i\) by a \({\widetilde{C}}\)-good Harnack chain. In turn, this \({\widetilde{\lambda }}\)-good corkscrew for \(R'\) can be joined to some \(\lambda '\)-good corkscrew for R by a \(C'\)-good Harnack chain, by applying Lemma 13.4\(k_0\) times, with \(C'\) depending on \(k_0\) and thus on \(\lambda \) and \(\eta \).
On the other hand, the cubes \(Q\in {\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\cap \mathsf {G}\) which are not contained in any cube \(R'\in \mathcal {D}_{k_0}(R)\cap {\mathsf {T}}_{{\mathsf {WSBC}}}(R)\) satisfy \(\ell (Q)\ge 2^{-k_0}\ell (R)\), and then, arguing as above, their associated \(\lambda \)-good corkscrews can be joined to some \(\lambda '\)-good corkscrew for R by a \(C'\)-good Harnack chain, by applying Lemma 13.4 at most \(k_0\) times. Hence, if we define
taking into account (15.8), the lemma follows. \(\square \)
Proof of the Key Lemma 13.3
We choose \(\Gamma =\Gamma (\lambda ,\eta )\) as in Lemma 15.3 and we consider the associated family \({{\mathsf {WSBC}}}(\Gamma )\). In case that \({\mathsf {T}}_{{\mathsf {WSBC}}}(R)= \varnothing \), we set \(\mathsf {Ex}(R)=\varnothing \). Otherwise, we consider the family \(\mathsf {Ex}_{{\mathsf {WSBC}}}(R)\) from Lemma 15.3, and we define
It may be useful for the reader to compare the definition above with the partition of \({\mathsf {Stop}}(R)\) in (13.3). By Lemma 15.3 we have
Next we show that for every \(P\in {\mathsf {Stop}}(R)\cap \mathsf G{\setminus } \mathsf {Ex}(R)\), any \(\lambda \)-good corkscrew for P can be joined to some \(\lambda '\)-good corkscrew for R by a \(C(\lambda ,\eta )\)-good Harnack chain. In fact, if \(P\in {\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\), then \(P\in {\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\cap \mathsf G{\setminus } \mathsf {Ex}_{{\mathsf {WSBC}}}(R)\) since such cube P cannot belong to \({\mathsf {SubStop}}(Q)\) for any \(Q\in {\mathsf {Stop}}_{{\mathsf {WSBC}}}(R){\setminus } {\mathsf {Stop}}(R)\) (recall the partition (13.3)), and thus the existence of such Harnack chain is ensured by Lemma 15.3. On the other hand, if \(P\not \in {\mathsf {Stop}}_{{\mathsf {WSBC}}}(R)\), then P is contained in some cube \(Q(P)\in {\mathsf {Stop}}_{{\mathsf {WSBC}}}(R){\setminus }{{\mathsf {WSBC}}}(\Gamma )\). Consider the chain \(P=S_1\subset S_2\subset \cdots \subset S_m=Q(P)\), so that each \(S_i\) is the parent of \(S_{i-1}\). For \(1\le i\le m\), choose inductively a big corkscrew \(x_i\) for \(S_i\) in such a way that \(x_1\) is at the same side of \(L_P\) as the good \(\lambda \) corkscrew \({z}_P\) for P, and \(x_{i+1}\) is at the same side of \(L_{S_i}\) as \(x_i\) for each i. Using that \(b\beta (S_i)\le C\varepsilon \ll 1\) for all i, it easy to check that the line obtained by joining the segments \([{z}_P,x_1]\), \([x_1,x_2]\),...,\([x_{m-1},x_m]\) is a good carrot curve and so gives rise to a good Harnack chain that joins \({z}_P\) to \(x_m\). It may happen that \(x_m\) is not a \(\lambda \)-good corkscrew. However, since \(Q(P)\not \in {{\mathsf {WSBC}}}(\Gamma )\), it turns out that \(x_m\) can be joined to some \(c_3\)-good corkscrew \({z}_{Q(P)}\) for Q(P) by some \(C(\Gamma )\)-good Harnack chain, with \(c_3\) given by (12.2) (and thus independent of \(\lambda \) and \(\eta \)), because \(Q(P)\in \mathsf {G}\). Note that since \(\lambda \le c_3\), \({z}_{Q(P)}\) is also a \(\lambda \)-good corkscrew. In turn, since \(Q(P)\not \in \mathsf {Ex}_{{\mathsf {WSBC}}}(R)\), \({z}_{Q(P)}\) can be joined to some \(\lambda '\)-good corkscrew for R by another \(C'(\lambda ,\eta )\)-good Harnack chain. Altogether, this shows that \({z}_P\) can be connected to some \(\lambda '\)-good corkscrew for R by a \(C''(\lambda ,\eta )\)-good Harnack chain, which completes the proof of the lemma. \(\square \)
Below we will write \(\mathsf {Ex}(R,\lambda ,\eta )\) instead of \(\mathsf {Ex}(R)\) to keep track of the dependence of this family on the parameters \(\lambda \) and \(\eta \).
18 Proof of the main Lemma 10.2
18.1 Notation
Recall that by the definition of \(G_0^K\) in (13.2), \(\sum _{R\in {\mathsf {Top}}}\chi _R(x) \le K\) for all \(x\in G_0^K\). For such x, let Q be the smallest cube from \({\mathsf {Top}}\) that contains x, and denote \(n_0(x) = \log _2\frac{\ell (R_0)}{\ell (Q)}\), so that \(Q\in \mathcal {D}_{n_0(x)}(R_0)\). Next let \(N_0\in {\mathbb {Z}}\) be such that
and denote
Fix
and set
and also
(recall that \({\mathsf {Top}}^{(N)}_a\) and \({\mathsf {Top}}^{(N)}_b\) were defined in Section 13.2). So if \(R\in {\mathsf T}_a'{\setminus } \mathcal {D}_{N}(R_0)\), then \({\mathsf {Stop}}^{N}(R)\) coincides the family of sons of R, and it \(R\in {\mathsf T}_b'\) this will not be the case, in general. Next we denote by \({\mathsf T}_a\) and \({\mathsf T}_b\) the respective subfamilies of cubes from \({\mathsf T}_a'\) and \({\mathsf T}_b'\) which intersect \({\widetilde{G}}_0^K\).
For \(j\ge 0\), we set
We also denote
and we let \({\mathsf T}_a^j\) be the subfamily of cubes \(R\in {\mathsf T}_a\) such that there exists some \(Q\in {\mathsf {S}}_b^{j-1}\) such that \(Q\supset R\) and R is not contained in any cube from \({\mathsf {S}}_b^{k}\) with \(k\ge j\).
18.2 Two auxiliary lemmas
Lemma 16.1
The following properties hold for the family \({\mathsf T}_b^1\):
-
(a)
The cubes from \({\mathsf T}_b^1\) are pairwise disjoint and cover \({\widetilde{G}}_0^K\), assuming \(N_0\) big enough.
-
(b)
If \(R\in {\mathsf T}_b^1\), then \(\ell (R)\approx _K\ell (R_0)\).
-
(c)
Given \(R\in \mathcal {D}(R_0)\) with \(\ell (R)\ge c\,\ell (R_0)\) (for example, \(R\in {\mathsf T}_b^1\)) and \(\lambda >0\), if \({z}_R\) is a \(\lambda \)-good corkscrew point for R, then there is a \(C(\lambda ,c)\)-good Harnack chain that joins \({z}_R\) to p.
Proof
Concerning the statement (a), the cubes from \({\mathsf T}_b^1\) are pairwise disjoint by construction. Suppose that \(x\in {\widetilde{G}}_0^K\) is not contained in any cube from \({\mathsf T}_b^1\). By the definition of the family \({\mathsf {Top}}^{N}\), this implies that all the cubes \(Q\subset R_0\) with \(2^{-N}\ell (R_0)\le \ell (Q)\le 2^{-10}\ell (R_0)\) containing x belong to \({\mathsf T}_a\). However, there are at most K cubes Q of this type, which is not possible if N is taken big enough. So the cubes from \({\mathsf T}_b^1\) cover \({\widetilde{G}}_0^K\).
The proof of (b) is analogous. Given \(R\in {\mathsf T}_b^1\), all the cubes Q which contain R and have side length smaller or equal that \(2^{-10}\ell (R_0)\) belong to \({\mathsf T}_a\). Hence there at most \(K-1\) cubes Q of this type, because \({\widetilde{G}}_0^K \cap R\ne \varnothing \). Thus, \(\ell (R)\ge 2^{-K-10}\ell (R_0)\).
The statement (c) is an immediate consequence of (b) and Lemma 12.4. \(\square \)
Lemma 16.2
Let \(Q\in {\mathsf T}_a^j\cup {\mathsf T}_b^j\) for some \(j\ge 2\) and let \({z}_Q\) be a \(\lambda \)-good corkscrew for Q, with \(\lambda >0\). There exists some constant \(\gamma _0(\lambda ,K)>0\) such if \(\ell (Q)\le \gamma _0(\lambda ,K)\,\ell (R_0)\), then there exists some cube \(R\in {\mathsf {S}}_b\) such that \(R\supset Q\) with a \(\lambda '\)-good corkscrew \({z}_R\) for R such that \({z}_R\) can be joined to \({z}_Q\) by a \(C(\lambda ,K)\)-good Harnack chain, with \(\lambda '\) depending on \(\lambda \) and K.
Proof
We assume \(\gamma _0(\lambda ,K)>0\) small enough. Then we can apply Lemma 12.5\(K+1\) times to get cubes \(R_1,\ldots ,R_{K+1}\) satisfying:
-
\(Q\subsetneq R_1\subsetneq R_2\subsetneq \cdots \subsetneq R_{K+1}\) and \(\ell (R_{K+1})\le 2^{-10}\ell (R_0)\),
-
each \(R_j\) has an associated \(\lambda '\)-good corkscrew \({z}_{R_i}\) (with \(\lambda '\) depending on \(\lambda ,K\)) and there exists a \(C(\lambda ,K)\)-good Harnack chain joining \({z}_Q\) and \({z}_{R_1}, \ldots ,{z}_{R_{K+1}}\).
Since \(Q\cap {\widetilde{G}}_0^K\ne \varnothing \), at least one of the cubes \(R_1,\ldots ,R_{K+1}\), say \(R_j\), does not belong to \({\mathsf {Top}}\). This implies that \(R_j\in {\mathsf {T}}^{(N)}({\widetilde{R}})\) for some \({\widetilde{R}}\in {\mathsf T}_b\). Let \(R\in {\mathsf {Stop}}^{(N)}({\widetilde{R}})\) be the stopping cube that contains Q. Then Lemma 14.3 ensures that there is a good Harnack chain that connects \({z}_{R_j}\) to some corkscrew \({z}_R\) for R. Notice that \(\ell (R_j)\approx _{\lambda ,K}\ell (Q)\approx _{\lambda ,K} \ell (R)\) because \(Q\subset R\subset R_j\). This implies that \(g(p,{z}_R)\approx _{K,\lambda } g(p,{z}_{R_j})\approx _{K,\lambda } g(p,{z}_Q)\). Further, gathering the Harnack chain that joins \({z}_Q\) to \({z}_{{\widetilde{R}}}\) and the one that joins \({z}_{R_j}\) to \({z}_R\), we obtain the good Harnack chain required by the lemma. \(\square \)
18.3 The algorithm to construct good Harnack chains
We will construct good Harnack chains that join good corkscrews from “most” cubes from \(\mathcal {D}_{N}(R_0)\) that intersect \({\widetilde{G}}_0^K\) to good corkscrews from cubes belonging to \(R\in {\mathsf T}_b^1\), and then we will join these latter good corkscrews to p using the fact that \(\ell (R)\approx \ell (R_0)\). To this end we choose \(\eta >0\) such that
and we denote
(so that \(m\le K\)) and we apply the following algorithm: we set \(a_{m+1}=c_3\), so that (12.2) ensures that for each \(Q\in {\mathsf T}_a\cup {\mathsf T}_b\) there exists some good \(a_{m+1}\)-good corkscrew \({z}_Q\). For \(j=m,m-1,\ldots ,1\), we perform the following procedure:

After iterating the procedure above for \(j=m,m-1\ldots ,1\) and joining some Harnack chains arisen in the different iterations, we will have constructed C-good Harnack chains that join \(a_{m+1}\)-good corkscrew points for all cubes \(Q\in {\mathsf T}_a\) not contained in \(\bigcup _{j=1}^m\bigcup _{P\in {\mathsf {NC}}_j}P\) to \(a_{1}\)-good corkscrews of some ancestors R(Q) belonging either \({\mathsf T}_b^1\) or, more generally, such that \(\ell (R(Q))\gtrsim \ell (R_0)\). The constants \(c_j'\), \(a_j'\), \(a_j\), \(C_j\) worsen at each step j. However, this is not harmful because the number of iterations of the procedure is at most m, and \(m\le K\).
Denote by \(I_N\) the cubes from \(\mathcal {D}_{N}(R_0)\) which intersect \({\widetilde{G}}_0^K\) and are not contained in any cube from \(\{P\in {\mathsf {NC}}_j:j=1,\cdots m\}\). By the algorithm above we have constructed good Harnack chains that join \(a_{m+1}\)-good corkscrew points for all cubes \(Q\in I_N\) to some \(a_1\)-good corkscrew for cubes \(R(Q)\in \mathcal {D}(R_0)\) with \(\ell (R(Q))\approx \ell (R_0)\). Also, by applying Lemma 16.1 (c) we can connect the \(a_1\)-good corkscrew for R(Q) to p by a good Harnack chain.
Consider now an arbitrary point \(x\in {\widetilde{G}}_0^K\cap Q\), with \(Q\in I_N\). By the definition of \({\widetilde{G}}_0^K\) and the choice \(N=N_0\), all the cubes \(P\in \mathcal {D}\) containing x with side length smaller or equal than \(\ell (Q)\) satisfy \(b\beta (P)\le \varepsilon \). Then, by an easy geometric argument (see the proof of Lemma 13.3 for a related one) it is easy to check that there is a good Harnack chain joining any good corkscrew for Q to x. Hence, for all the points \(x\in \bigcup _{Q\in I_N}Q\cap {\widetilde{G}}_0^K\) there is a good Harnack chain that joins x to p.
Finally, observe that, for each j, by Lemma 13.3,
Therefore,
and thus
This finishes the proof of the Main Lemma 10.2. \(\square \)
Notes
This is a quantitative, scale-invariant version of rectifiability, see Definition 2.2 and the ensuing comments.
The CDC is a scale invariant potential theoretic “thickness” condition, i.e., a quantitative version of Weiner regularity; see, e.g., [1].
To guarantee the existence of the sets \(V_i\) and the fact that they are contained in \(\Omega \) we use the assumption that \(\Omega =\mathbb {R}^{n+1}{\setminus }\partial \Omega \).
References
Aikawa, H., Hirata, K.: Doubling conditions for harmonic measure in John domains. Ann. Inst. Fourier (Grenoble) 58(2), 429–445 (2008)
Akman, M., Bortz, S., Hofmann, S., Martell, J.M.: Rectifiability, interior approximation and Harmonic Measure. Ark. Mat. 57(1), 1–22 (2019)
Alt, H.W., Caffarelli, L.A., Friedman, A.: Variational problems with two phases and their free boundaries. Trans. Am. Math. Soc. 282(2), 431–461 (1984)
Auscher, P., Hofmann, S., Lewis, J.L., Tchamitchian, P.: Extrapolation of Carleson measures and the analyticity of Kato’s square-root operators. Acta Math. 187(2), 161–190 (2001)
Auscher, P., Hofmann, S., Muscalu, C., Tao, T., Thiele, C.: Carleson measures, trees, extrapolation, and \(T(b)\) theorems. Publ. Mat. 46(2), 257–325 (2002)
Azzam, J.: Semi-uniform domains and a characterization of the \(A_\infty \) property for harmonic measure. Preprint, arXiv:1711.03088
Azzam, J., Garnett, J., Mourgoglou, M., Tolsa, X.: Uniform rectifiability, elliptic measure, square functions, and \(\varepsilon \)-approximability via an ACF monotonicity formula. Preprint arXiv:1612.02650 (2016)
Azzam, J., Mourgoglou, M., Tolsa, X.: Singular sets for harmonic measure on locally flat domains with locally finite surface measure. Int. Math. Res. Not. 2017(12), 3751–3773 (2017)
Azzam, J., Mourgoglou, M., Tolsa, X.: Harmonic measure and quantitative connectivity: geometric characterization of the \(L^p\)-solvability of the Dirichlet problem. Part II. Preprint arXiv:1803.07975
Badger, M.: Null sets of harmonic measure on NTA domains: Lipschitz approximation revisited. Math. Z. 270(1–2), 241–262 (2012)
Bennewitz, B., Lewis, J.L.: On weak reverse Hölder inequalities for nondoubling harmonic measures. Complex Var. Theory Appl. 49(7-9), 571–582 (2004)
Bishop, C., Jones, P.: Harmonic measure and arclength. Ann. Math. (2) 132, 511–547 (1990)
Bourgain, J.: On the Hausdorff dimension of harmonic measure in higher dimensions. Invent. Math. 87, 477–483 (1987)
Caffarelli, L., Salsa, S.: A geometric approach to free boundary problems. Graduate Texts in Math. 64. Am. Math. Soc. (2005)
Carleson, L.: Interpolation by bounded analytic functions and the corona problem. Ann. Math. (2) 76, 547–559 (1962)
Carleson, L., Garnett, J.: Interpolating sequences and separation properties. J. Anal. Math. 28, 273–299 (1975)
Christ, M.: A \(T(b)\) theorem with remarks on analytic capacity and the Cauchy integral. Colloq. Math. LX/LXI, 601–628 (1990)
Dahlberg, B.: On estimates for harmonic measure. Arch. Ration. Mech. Anal. 65, 272–288 (1977)
David, G.: Morceaux de graphes lipschitziens et intégrales singulières sur une surface (French) [Pieces of Lipschitz graphs and singular integrals on a surface]. Rev. Mat. Iberoam. 4(1), 73–114 (1988)
David, G.: Wavelets and Singular Integrals on Curves and Surfaces. Lecture Notes in Mathematics, vol. 1465. Springer, Berlin (1991)
David, G., Jerison, D.: Lipschitz approximation to hypersurfaces, harmonic measure, and singular integrals. Indiana Univ. Math. J. 39(3), 831–845 (1990)
David, G., Semmes, S.: Singular integrals and rectifiable sets in \(\mathbb{R}^n\). Au-delà des graphes lipschitziens. Asterisque 193, 152 (1991)
David, G., Semmes, S.: Analysis of and on Uniformly Rectifiable Sets. Mathematical Monographs and Surveys, vol. 38, AMS (1993)
Evans, L.C., Gariepy, R.F.: Measure Theory and Fine Properties of Functions. Studies in Advanced Mathematics. CRC Press, Boca Raton (1992)
Heinonen, J., Kilpeläinen, T., Martio, O.: Nonlinear Potential Theory of Degenerate Elliptic Equations (Rev. ed.). Dover, New York (2006)
Hofmann, S.: Quantitative absolute continuity of harmonic measure and the Dirichlet problem: a survey of recent progress. To appear in special volume in honor of the 65th birthday of Carlos Kenig
Hofmann, S., Le, P.: BMO solvability and absolute continuity of harmonic measure. J. Geom. Anal. 28(4), 3278–3299 (2018)
Hofmann, S., Le, P., Martell, J.M., Nyström, K.: The weak-\(A_\infty \) property of harmonic and \(p\)-harmonic measures implies uniform rectifiability. Anal. PDE. 10(3), 513–558 (2017)
Hofmann, S., Lewis, J.L.: The Dirichlet problem for parabolic operators with singular drift terms. Mem. Am. Math. Soc. 151, 719 (2001)
Hofmann, S., Martell, J.M.: \(A_\infty \) estimates via extrapolation of Carleson measures and applications to divergence form elliptic operators. Trans. Am. Math. Soc. 364(1), 65–101 (2012)
Hofmann, S., Martell, J.M.: Uniform rectifiability and harmonic measure I: Uniform rectifiability implies Poisson kernels in \(L^p\). Ann. Sci. École Norm. Sup. 47(3), 577–654 (2014)
Hofmann, S., Martell, J.M.: Uniform Rectifiability and harmonic measure IV: Ahlfors regularity plus Poisson kernels in \(L^p\) implies uniform rectifiability. Preprint, arXiv:1505.06499
Hofmann, S., Martell, J.M.: A sufficient geometric criterion for quantitative absolute continuity of harmonic measure. Preprint arXiv:1712.03696v1
Hofmann, S., Martell, J.M.: Harmonic measure and quantitative connectivity: geometric characterization of the \(L^p\) solvability of the Dirichlet problem. Part I. Preprint arXiv:1712.03696v3 (2018)
Hofmann, S., Martell, J.M., Mayboroda, S.: Uniform rectifiability, Carleson measure estimates, and approximation of harmonic functions. Duke Math. J. 165(12), 2331–2389 (2016)
Hofmann, S., Mitrea, D., Mitrea, M., Morris, A.J.: \(L^p\)-square function estimates on spaces of homogeneous type and on uniformly rectifiable sets. Mem. Am. Math. Soc. 245, 1159 (2017)
Hofmann, S., Mitrea, M., Taylor, M.: Singular integrals and elliptic boundary problems on regular Semmes-Kenig-Toro domains. Int. Math. Res. Not. 2010, 2567–2865 (2010)
Hytönen, T., Kairema, A.: Systems of dyadic cubes in a doubling metric space. Colloq. Math. 126(1), 1–33 (2012)
Jerison, D., Kenig, C.: Boundary behavior of harmonic functions in nontangentially accessible domains. Adv. Math. 46(1), 80–147 (1982)
Kenig, C.E., Toro, T.: Harmonic measure on locally flat domains. Duke Math. J. 87(3), 509–551 (1997)
Lavrentiev, M.: Boundary problems in the theory of univalent functions (Russian). Math Sb. 43, 815–846 (1936); AMS Transl. Series 2 32 , 1–35 (1963)
Lewis, J., Murray, M.: The method of layer potentials for the heat equation in time-varying domains. Mem. Am. Math. Soc. 114, 545 (1995)
Mattila, P., Melnikov, M., Verdera, J.: The Cauchy integral, analytic capacity, and uniform rectifiability. Ann. Math. (2) 144(1), 127–136 (1996)
Mourgoglou, M., Tolsa, X.: Harmonic measure and Riesz transform in uniform and general domains. J. Reine Angew. Math. 758, 183–221 (2020)
Nazarov, F., Tolsa, X., Volberg, A.: On the uniform rectifiability of ad-regular measures with bounded Riesz transform operator: the case of codimension 1. Acta Math. 213(2), 237–321 (2014)
Petrosyan, A., Shahgholian, H., Uraltseva, N.: Regularity of free boundaries in obstacle-type problems. Regularity of free boundaries in obstacle-type problems. Graduate Studies in Mathematics, vol. 136. American Mathematical Society, Providence, RI (2012)
Riesz, F. and M.: Über die randwerte einer analtischen funktion. Compte Rendues du Quatrième Congrès des Mathématiciens Scandinaves, Stockholm 1916, Almqvists and Wilksels, Uppsala (1920)
Semmes, S.: A criterion for the boundedness of singular integrals on on hypersurfaces. Trans. Am. Math. Soc. 311, 501–513 (1989)
Stein, E.M.: Singular Integrals and Differentiability Properties of Functions. Princteon University Press, Princeton (1970)
Tolsa, X.: Analytic capacity, the Cauchy transform, and non-homogeneous Calderón-Zygmund theory. Progress in Mathematics, vol. 307. Birkhäuser Verlag, Basel (2014)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
S.H. was supported by NSF Grant DMS-1664047. J.M.M. acknowledges financial support from the Spanish Ministry of Economy and Competitiveness, through the “Severo Ochoa” Programme for Centres of Excellence in R&D (SEV-2015- 0554). He also acknowledges that the research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ ERC Agreement No. 615112 HAPDEGMT. In addition, S.H. and J.M.M. were supported by NSF Grant DMS-1440140 while in residence at the MSRI in Berkeley, California, during Spring semester 2017. M.M. was supported by IKERBASQUE and partially supported by the Grant MTM-2017-82160-C2-2-P of the Ministerio de Economía y Competitividad (Spain), and by IT-641-13 (Basque Government). X.T. was supported by the ERC Grant 320501 of the European Research Council (FP7/2007-2013) and partially supported by MTM-2016-77635-P, MDM-2014-044 (MICINN, Spain), 2017-SGR-395 (Catalonia), and by Marie Curie ITN MAnET (FP7-607647).
Appendix A: Some counter-examples
Appendix A: Some counter-examples
We shall discuss some counter-examples which show that our background hypotheses in Theorem 1.1 (namely, n-ADR and interior corkscrew condition) are natural, and in some sense in the nature of best possible. In the first two examples, \(\Omega \) is a domain satisfying an interior corkscrew condition, such that \(\partial \Omega \) satisfies exactly one (but not both) of the upper or the lower n-ADR bounds, and for which harmonic measure \(\omega \) fails to be weak-\(A_\infty \) with respect to surface measure \(\sigma \) on \(\partial \Omega \). In this setting, in which full n-ADR fails, there is no established notion of uniform rectifiability, but in each case, the domain will enjoy some substitute property which would imply uniform rectifiability of the boundary in the presence of full n-ADR. Moreover, these examples may be constructed in such a way that the failure of the condition (either upper or lower n-ADR) can be expressed quantitatively, with a bound that may be taken arbitrarily close to a true n-ADR bound; see (A.3) and (A.6) below.
In the last example, we construct an open set \(\Omega \) with n-ADR boundary, and for which \(\omega \in \) weak-\(A_\infty \) with respect to surface measure, but for which the interior corkscrew condition fails, and \(\partial \Omega \) is not n-UR.
Example 1
Failure of the upper n-ADR bound. In [8], the authors construct an example of a Reifenberg flat domain \(\Omega \subset \mathbb {R}^{n+1}\) for which surface measure \(\sigma = H^n\lfloor _{\,\partial \Omega }\) is locally finite on \(\partial \Omega \), but for which the upper n-ADR bound
fails, and for which harmonic measure \(\omega \) is not absolutely continuous with respect to \(\sigma \). Note that the hypothesis of Reifenberg flatness implies in particular that \(\Omega \) and \(\Omega _{ext}:= \mathbb {R}^{n+1}{\setminus } \overline{\Omega }\) are both NTA domains, hence both enjoy the corkscrew condition, so by the relative isoperimetric inequality, the lower n-ADR bound
holds. Thus, it is the failure of (A.1) which causes the failure of absolute continuity: in the presence of (A.1), the results of [21] apply, and one has that \(\omega \in A_\infty (\sigma )\), and that \(\partial \Omega \) satisfies a “big pieces of Lipschitz graphs” condition (see [21] for a precise statement), and hence is n-UR. We note that by a result of Badger [10], a version of the Lipschitz approximation result of [21] still holds for NTA domains with locally finite surface measure, even in the absence of the upper n-ADR condition.
In addition, given any \(\varepsilon >0\), the construction in [8] can be made in such a way that (A.1) fails “within \(\varepsilon \)”, i.e., so that
Let us sketch an argument to explain why this is so; we refer the interested reader to [8] for more details.
The domain \(\Omega \) in [8] is obtained by enlarging a Wolff snowflake, that we will denote here by D. Both \(\Omega \) and D are \(\delta \)-Reifenberg flat, with \(\delta \) as small as wished in the construction (recall that Wolff snowflakes can be taken \(\delta \)-Reifenberg flat, with \(\delta \) as small as wished).
It is shown in [8, Theorem 3.1] that for all \(x\in \partial \Omega \) and \(r<1\),
where \(\mu \) is some measure supported on \(\partial D\) satisfying \(\mu (B(x,r)) \gtrsim r^{n-\alpha }\) for all x in some compact set \(E \subset \partial \Omega \cap \partial D\), and some \(\alpha >0.\) In the construction in [8], the authors take \(\mu =\omega _D\), the harmonic measure for D. Further, from results of Kenig and Toro it follows that harmonic measure in a \(\delta \)-Reifenberg flat domain D satisfies
with \(\varepsilon \rightarrow 0\) as \(\delta \rightarrow 0\) (see [40, Theorem 4.1]). As a consequence, the measure \(\mu \) satisfies
with \(\varepsilon \) as small as wished depending on \(\delta \). From (A.4), it follows that
Example 2
Failure of the lower n-ADR bound. In [2, Example 5.5], the authors give an example of a domain satisfying the interior corkscrew condition, whose boundary is rectifiable (indeed, it is contained in a countable union of hyperplanes), and satisfies the upper n-ADR condition (A.1), but not the lower n-ADR condition (A.2), but for which surface measure \(\sigma \) fails to be absolutely continuous with respect to harmonic measure, and in fact, for which the non-degeneracy condition
fails to hold uniformly for \(x\in \Omega \), for any fixed positive \(\eta \) and c, and therefore \(\omega \) cannot be weak-\(A_\infty \) with respect to \(\sigma \). We note that in the presence of the full n-ADR condition, if \(\partial \Omega \) were contained in a countable union of hyperplanes (as it is in the example), then in particular it would satisfy the “BAUP” condition of [23], and thus would be n-UR [23, Theorem I.2.18, p. 36].
Moreover, given any \(\varepsilon >0\), the parameters in the example of [2] can be chosen in such a way that the lower ADR bound fails “within \(\varepsilon \)”, i.e., so that
To see this, we proceed as follows. We follow closely the construction in [2, Example 5.5], with some modification of the parameters. Fix \(\varepsilon >0\), and set
For \(k\ge 1\), and \(n\ge 2\), set
where for \(x\in \mathbb {R}^n\), \(\Delta (x,r):= \{y\in \mathbb {R}^n:\, |x-y|<r\}\) is the usual n-disk of radius r centered at x. Define
each of which is clearly open and connected. Notice that \(\Omega \) satisfies the interior Corkscrew condition (since the sets \(\Sigma _k\) are located at heights which are sufficently separated). Moreover, it is easy to see that \(\partial \Omega \) satisfies the upper ADR condition and that \(\mathbb {R}^n\times \{0\}\subset \partial \Omega \).
On the other hand, the lower ADR bound fails. To see this, let \(X=(x,0)\in \partial \Omega \), and choose \(\mathbf {m}_{k,x}\in {\mathbb {Z}}^n\) and \(X_k=(c_k\,\mathbf {m}_{k,x}, 2^{-k})\in \Sigma _k\subset \partial \Omega \) such that \(X_k\rightarrow X\). Set \(B_k=B(X_k, 2^{-k-2})\), and observe that \(H^n(B_k\cap \partial \Omega )/(2^{-kn})\approx 2^{-kn\varepsilon }\rightarrow 0\) as \(k\rightarrow \infty \), or equivalently
where \(B_k\) has radius \(r_k \approx 2^{-k}\), and \(\varepsilon '=n\varepsilon \). We shall show that this behavior is in fact typical, and that (A.6) holds, with \(\varepsilon '\) in place of \(\varepsilon \).
Let \(\omega ^{(\cdot )}:= \omega ^{(\cdot )}_\Omega \) and \(\omega _k^{(\cdot )}:= \omega ^{(\cdot )}_{\Omega _k}\) denote harmonic measure for the domains \(\Omega \) and \(\Omega _k\) respectively.
Claim
\(\omega ^{(\cdot )}(F) = 0\), with \(F:=\mathbb {R}^n\times \{0\}\). Thus, in particular (A.5) fails.
It remains to verify (A.6), and the claim. As regards the former, note that for \(X=(x,0)\in F\), we have the trivial standard lower n-ADR bound \(H^n(\Delta (X,r))\gtrsim r^n\), whereas for \(X=(x,2^{-k}) \in \Sigma _k\), we have
The first and fourth of these estimates are of course the standard lower n-ADR bound. For \(r\le c_k\), the second estimate is bounded below by \(2^{-kn\varepsilon }r^n\), and in turn, with \(r\lesssim 2^{-k}\), the second and third estimates are therefore bounded below by
which yields (A.6) with \(\varepsilon '=n\varepsilon \) in place of \(\varepsilon \).
Let us now prove the claim. We first recall some definitions. Given an open set \(O\subset \mathbb {R}^{n+1}\), and a compact set \(K\subset O\), we define the capacity of K relative to O as
Also, the inhomogeneous capacity of K is defined as
Combining [25, Theorem 2.38], [1, Theorem 2.2.7] and [1, Theorem 4.5.2] we have that if K is a compact subset of \(\overline{B}\), where B is a ball with radius smaller than 1, then
where the implicit constants depend only on n, the sup runs over all Radon positive measures \(\mu \) supported on K, for which
Fix \(k\ge 2\), and set
by definition of \(c_k\). Our next goal is to show that
For a fixed \(X_0\) and s, write \(K=\overline{B(X_0,s)}\cap \Sigma _k\), set \(\mu = 2^{kn\varepsilon } s^{-1} \, H^n\lfloor _K,\) and note that for \(X\in K\), similarly to (A.7), we have
To compute \(W(\mu )(X)\) for \(X\in K\) write
Then, since \(s\ge \beta = 2^{k(n-1)} c_k = 2^{-k(1+\varepsilon )}\),
Furthermore, the last two estimates in (A.10) easily imply that \(III+IV\lesssim 1\) and hence \(W(\mu )(X)\lesssim 1\) for every \(X\in K\). This, (A.8), and (A.10) imply as desired (A.9):
Set
and observe that for \(X\in P_k\),
Recall that \(F=\mathbb {R}^n\times \{0\}\), and define
Observe that \(u\in W^{1,2}(\Omega _k)\cap C(\overline{\Omega _k})\) since \(\partial \Omega _k\) is ADR (constants depend on k but we just use this qualitatively) and \(\chi _F\) is a Lipschitz function on \(\partial \Omega _k\). Fix \(Z_0\in P_k\) and let \(Z_0'\in \Sigma _k\) be such that \(|Z_0-Z_0'|={\text {dist}}(Z_0, \partial \Omega _k)\le 2\beta \). Let \(\Omega _{Z_0}= \Omega _k\cap B(Z_0', \frac{3}{4} 2^{-k})\), which is an open connected bounded set. We can now apply the usual capacitary estimates (see, e.g., [25, Theorem 6.18]) to find a constant \(\alpha =\alpha (n)>0\) such that
where we have used (A.9), the definition of \(\beta \), and the fact that \(u\equiv 0\) on \(\partial \Omega _k \cap B(Z_0',2^{-k-1})\). Note that the last estimate holds for any \(Z_0\in P_k\) and therefore, by the maximum principle,
In particular, if we set \(X_0:= (0,\dots ,0,1) \in \mathbb {R}^{n+1}_+\), then by another application of the maximum principle,
as \(k \rightarrow \infty \), and the claim is established.
Example 3
Failure of the interior corkscrew condition. The example is based on the construction of Garnett’s 4-corners Cantor set \(\mathcal {C}\subset \mathbb {R}^2\) (see, e.g., [23, Chapter 1]). Let \(I_0\) be a unit square positioned with lower left corner at the origin in the plane, and in general for each \(k = 0, 1,2,\dots \), we let \(I_k\) be the unit square positioned with lower left corner at the point (2k, 0) on the x-axis. Set \(\Omega _0:= I_0\). Let \(\Omega _1\) be the first stage of the 4-corners construction, i.e., a union of four squares of side length 1/4, positioned in the corners of the unit square \(I_1\), and similarly, for each k, let \(\Omega _k\) be the k-th stage of the 4-corners construction, positioned inside \(I_k\). Note that \({\text {dist}}(\Omega _k, \Omega _{k+1}) = 1\) for every k. Set \(\Omega := \cup _k \Omega _k\). It is easy to check that \(\partial \Omega \) is n-ADR, and that the non-degeneracy condition (A.5) holds in \(\Omega \) for some uniform positive \(\eta \) and c, and thus by the criterion of [11], \(\omega \in \) weak-\(A_\infty (\sigma )\). On the other hand, the interior corkscrew condition clearly fails to hold in \(\Omega \) (it holds only for decreasingly small scales as k increases), and certainly \(\partial \Omega \) cannot be n-UR: indeed, if it were, then \(\partial \Omega _k\) would be n-UR, with uniform constants, for each k, and this would imply that \(\mathcal {C}\) itself was n-UR, whereas in fact, as is well known, it is totally non-rectifiable. One can produce a similar set in 3 dimensions by simply taking the cylinder \(\Omega '=\Omega \times [0,1]\). Details are left to the interested reader.
Rights and permissions
About this article
Cite this article
Azzam, J., Hofmann, S., Martell, J.M. et al. Harmonic measure and quantitative connectivity: geometric characterization of the \(L^p\)-solvability of the Dirichlet problem. Invent. math. 222, 881–993 (2020). https://doi.org/10.1007/s00222-020-00984-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-020-00984-5



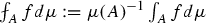 .
.