1 Introduction

The signal from CMOS/CCD image sensors is often contaminated by noise, which can appear during the image acquisition process, as well as from various environmental and mechanical factors of the imaging instrument. The amount of noise in the captured image is presented as a random variation of brightness or color information and may hide or alter important details in the image. As a consequence, the noise-affected images become much more difficult to interpret and analyze. To fulfill the need for noise-free images in a variety of practical contexts, the image denoising process is generally used to clear out as much as possible the noise [13]. Therefore, it is very difficult to remove it from images without prior knowledge of its model. Indeed, according to recent works in the literature, the most performant existing image denoising algorithms are those that rely heavily on the accurate estimation of noise parameters [1, 3, 41, 104]. That means that noise parameters are taken as inputs in these denoising models. For early and traditional denoising methods, the noise model is supposed as known beforehand as additive or multiplicative, its parameter is represented by a constant value of the variance on the whole of the image, which is also invariant according to the color components [17, 98]. Unfortunately, these assumptions simplify the effect of the denoising algorithms, because they give usually not convincing denoising results. As a consequence, in some cases, the practical use of the filter becomes severely limited. However, the real noise model (or noise level) is spatially variant, spatially correlated, signal-dependent, and even device-dependent. Since an accurate noise-level estimator is an important premise in the denoising process to obtain high-quality images. Generally, it is possible to estimate the noise model by detecting several images of the same scene and then, for each pixel, compute its standard deviation and mean intensity. Hence, estimated noise model is obtained by plotting each standard deviation against its mean value on the graph. The lower envelope that comes just below the cloud of points is the curve of the noise model. This technique is tedious and time-consuming [59]. Thus, it is preferable to estimate it from one image. During the past decades, several works on noise estimation from a single image contaminated by CCD/CMOS noise are elaborated in the literature [31, 57, 77]. The common noise estimation for signal-dependent from one image consists of firstly extracting, from the noisy image, the homogeneous areas [5, 11, 55, 72, 93, 107, 115]. Then, for each area, local means and standard deviations are computed and plotted as a scatter plot on a graph. To estimate the curve of the noise model, a global parametric model is adjusted to specific points of the cloud and describes the dependence of the standard deviation of the noise with the mean of the signal [76]. However, most of these methods assume that the processed image contains a sufficient amount of homogeneous areas, which is not necessarily always true for natural image processing. Recently, new noise estimation algorithms have been developed in [56, 63, 76] with state-of-the-art performance. The authors [63, 76] argue that these methods can effectively estimate the noise of images without flat areas. Noise parameter estimation algorithms are used for many well-known denoising algorithms including Wiener filtering [101], nonlocal means (NLM) [18, 106], BM3D [24], sparse representation-based denoising [28], matching method [103], Kalman filter [77], robust Kalman filter [84,85,86], and deep learning denoising methods [38, 112]. In a similar context, the main idea of this work is to integrate the SDN estimation of [63, 89] into the SRAD filter to achieve high accuracy in noise removal. SRAD filter is a variant of Perona–Malik (P–M) anisotropic diffusion technique [12, 91, 105] and a most popular especially in the extraction of multiplicative (or speckle) noise in synthetic aperture radar (SAR) images [50]. Also, it enhances, in particular, images with flat areas [27, 108]. Due to the significant role played by SRAD in image filtering, several strategies and ideas have been proposed to improve it in order to suppress spurious image features, including noise and disturbing artifacts and to adapt it to numerous image processing techniques and modality images. Here are some recent approaches to improve flexibility and performance of conventional SRAD method: In [22], a speckle noise reduction algorithm is proposed to denoise SAR images with speckle noise. This study is first used traditional SRAD filter and then followed by the application of logarithmic transformation to convert the speckle noise to additive. After that, in order to further remove the additive noise, discrete wavelet transform (DWT) is used to convert obtained image into one approximate sub-band image and six detailed sub-band images, and finally, a weighted guided image filter (WGIF) is applied as post-treatment for removing much of the noise. This method showed good effectiveness in removing speckle noise while preserving edge information. In [45], a modified SRAD model is developed using gradient domain-guided image filtering (GDGIF) to remove speckle noise in synthetic aperture radar (SAR) images. In [111], an improved P–M filter for speckle noise based on the PDE of SRAD is developed to enhance SAR images, which used different edge detection operators to obtain a more effective diffusion function for removing speckle noise close to the edges. In [49], a denoising framework based on an SRAD filter is proposed to denoise images corrupted by speckle noise. The process consists of a succession of several steps: Firstly, the image is treated by the traditional SRAD filter, then logarithmic and wavelet transformations are applied over the filter output. Four sub-band images are obtained where three ones are processed by soft thresholding whereas the fourth is by a guided filter, followed by the application of inverse wavelet transform (IWT) over the combined output results. Finally, exponential transformation is applied to obtain the final denoised image. In [45], Hyunho et al. have proposed an algorithm to reduce speckle noise in synthetic aperture radar (SAR) images using traditional SRAD filter and gradient domain-guided image filtering (GDGIF). GDGIF is an edge-aware weighting applied adaptively to images obtained after SRAD to further reduce speckle noise. Most of the above-mentioned denoising algorithms, including SRAD, simply consider the noise level as known and are approximated as purely additive or multiplicative noise. However, these assumptions simplify the effect of the filter, as they generally lead to unsatisfactory denoising results, especially for images corrupted by general type of noise and including intricate details and rich textured regions. Particularly, the SRAD assumes that the type of noise is known in advance as multiplicative, uncolored, and constant (or uniform) for each pixel in the image. In addition, it estimates the noise model over a manually selected homogeneous region. The hypothesis of using uniform noise variance on the whole image leads to over-smooth images or leave some noise unfiltered. Also, the manual selection of a homogeneous region in the image is not always obvious, especially in the case of images containing complex textures. The noise model assumed by SRAD is not realistic in practice, because the noise of a real digital camera sensor is typically not pure white multiplicative. Such noise can be modeled as color-dependent, a mixture of additive and multiplicative signal-dependent components. Therefore, it is important to model the noise as realistically as possible to achieve better denoising results. Given the mentioned problems above and the status of SRAD algorithm, the present paper suggests a new denoising system designed for more general signal-dependent noise based on references of Acton [6, 108].

The proposed algorithm, named SDN-reducing anisotropic diffusion (SDN-RAD), is based on an SRAD filter and an SDN noise estimator to enhance the CCD image sensor. The proposed filter out most of the noises, and at the same time, maintains boundaries and most principal details such as textures. The most important highlights of the proposed work can be summarized as follows:

  • General signal-dependent noise (SDN) is adopted by our system

  • Iterative select patch-based framework to estimate the parameters of the SDN is used, which is based on principal component analysis (PCA) and a texture strength metric to select the weak textured patches.

  • The outputs of the select patch-based framework (SDN estimator) are used as input parameters for the SRAD filter to deal with a variety of images captured by the CCD camera.

SDN-RAD algorithm is effective for the removal of general mixed noise present in images captured by CCD/CMOS sensors, which varies with pixel intensity in an image and color components (i.e., signal-dependent noise). Furthermore, it smooths out homogeneous areas and maintains the contours and textured features in the image. First, a more accurate noise model is automatically estimated for the signal-dependent noise image, resulting in improved parameter estimation. Second, the model is combined with the classical SRAD filter to further enhance the image denoising effect. Therefore, an effective and remarkable improvement in the ability to suppress mixed noise for images containing most principal details such as textures and those with flat regions. The present document is structured as follows: After reviewing the literature related to the topic of the proposed work in Sect. 2, a brief review of the SRAD and DPAD filters is developed in Sect. 3.1. The SDN-reducing anisotropic diffusion (SDN-RAD) method and its proposed noise model are developed in Sect. 3.2. The estimation steps of SDN parameters are explained in Sect. 3.3. Section 4 presents both the results of the noise model estimation and denoising process. Section 5 provides concluding remarks on the proposed work.

2 Related Work

A careful examination of the literature allows us to explore different denoising works since their existence. These methods can generally be roughly classified as classical denoising methods, wavelet-based methods, partial differential equation (PDE)-based methods, and deep learning-based approaches, which are cited in more detail in the rest of this section focusing on their advantages and drawbacks.

Classical denoising methods processed the image pixels directly, which means that it is looking for removing noise by calculating the gray level intensity of each pixel based on the correlation between pixels of patches in the observed image. Traditional classical denoising approaches include mean filtering, median filtering, Gaussian filtering, and bilateral filtering [10, 17, 21, 26, 97]. These filters can be further classified into two types: linear and nonlinear filters. Linear filters were destined to remove noise in the spatial domain, but they cannot save image textures. Examples of linear filters include mean filtering [30, 39] and Wiener filters [75, 99] that have been adopted especially for additive white Gaussian noise. However, they can over-smooth images with high noise, easily blur sharp edges and may lead to loss details. To overcome these disadvantages, nonlinear filters have further been employed for image denoising and edge-preserving such as median filtering and bilateral filtering [73, 90, 97]. Median filter, weighted median filtering [42] and adaptive total variation median filter [47], has been used to attenuate the effects of a salt and pepper type noise. The limitations of such filters that are in the presence of a lot of noise in the data they tend to destroy the image edges and create false edge pixels, and they cannot suppress several other types of noise like speckle noise in ultrasound images [53]. In [65], an adaptive median filter is proposed, where a dynamic adjustment of the size window of the filter and depending on the detected defects in the image is included in the traditional median filter. This method is destined to remove speckle noise or in the case of noise when spots are larger than one pixel. The major inconvenience of this method is that it is computationally expensive, which can make it slower for high-resolution images with large dimensions, and it is not suitable for other types of noises commonly seen in captured images such as additive noise, Poisson noise, etc. Likewise, a traditional bilateral filter [97] is a non-iterative scheme for edge-preserving and smoothing, which used a weighted average of each pixel in the image within a local neighborhood. The weights vary according to the spatial distance between the pixels and the difference in pixel intensity values. This filter is a fast tool to reduce noise while preserving image details, and it treats images with varying contrast and non-uniform lighting. However, it can cause some limitations, such as sensitivity to parameter selection, and the possibility of introducing color changes or artifacts in the processed image. As a consequence, many extensions of bilateral filter have been developed over the years to enhance image quality for different imaging modalities, including photographic images [25, 96, 110], point cloud images [81], computed tomography (CT) images to minimize radiation dose in while maintaining data integrity [102], satellite imaginary for real-time application [72], and infrared images [32]. Nonlocal means (NLM) algorithm is also a popular filter-based classical method [18, 48, 107, 113]. It uses characteristics of several similar patches in the image based on Euclidean distance to reduce image noise. Afterward, a lot of improvements in NLM algorithm denoising methods are mainly applied for feature extraction, compressed sensing, and image denoising [40, 44]. On the other side, different denoising methods based on nonlocal mean operator are developed [54, 82]. Among them, Himanshu algorithm [82] is image adaptive-guided image filtering using a modified cuckoo search algorithm to obtain optimal kernel size and smoothing degree. This method has a good effect for removing the Gaussian noise. Total variation (TV) regularization methods are proposed and are widely used in denoising images with speckles. The basic idea of these techniques is to minimize the sum of the absolute differences between neighboring pixel values of an image. TV regularization allows to denoise an image using piecewise smooth solutions with sharp edges, which permits an effective reduction of noise while preserving important features. However, the areas with significant backscatter in SAR images limit the effectiveness of TV regularization. In [87], an example of TV regularization method is proposed, where it is based on hybrid variation model (Fisher–Tippett (FT) distribution-p-norm) first- and second-order hybrid TVs (called HTpVs) to remove the speckle noise after removing the backscatter. In [80], authors have proposed a speckle suppression technique using at first a logarithmic transformation to the noisy images, then by mapping of local blocks based on gray theory is used to regroup similar blocks of reference patches into approximate low-rank matrices, and finally, weighted nuclear norm minimization (WNNM) method is employed to denoise image.

Several wavelet-based methods have been presented over the past several years. The main idea of the basic wavelets denoising technique is to decompose signals into different frequency components. Since noise is often concentrated in the high-frequency components and features are usually in the low-frequency components. Therefore, this method is very effective in maintaining important details while suppressing noise. Moreover, it is commonly easy to implement, which means that it can treat large images in a reasonable amount of time. As well, it can be used in different contexts because it can be applied to a wide range of signals, such as images, signal data, and time-series data and adapted to different types of noise. Wavelet denoising algorithms are computationally intensive because the decomposition and reconstruction stages needed in wavelet transforms consume significant computational resources. Also, they assume a noise model like AWGN. This assumption does not allow for accurate modeling of noise characteristics in all scenarios. Consequently, these methods may not perform optimally when confronted with mixed and spatially correlated noise. In [15], a wavelet denoising approach using an unsupervised learning model is developed, which aims at exploiting the merits of the wavelet transforms such as sparsity, similarity with the human visual system, multi-resolution structure, and to adapt an unsupervised dictionary learning algorithm, in order to create a dictionary destined to a noise reducing. Chang et al. developed an adaptive data-driven threshold for the image denoising process using wavelet soft thresholding [20]. The threshold is given in a Bayesian framework, and the prior used on the wavelet coefficients is the generalized Gaussian distribution (GGD) which is widely used in image processing applications. In [9], a wavelet denoising algorithm-based noise model is developed. The authors proved that the grating-based X-ray interferometry technique, which is traditional mammography positively complemented by phase contrast and scattering X-ray imaging, can provide images superior to conventional mammography. This technology can produce the obtained images, absorption, differential phase contrast (DPC), and scattering signals of the sample. The noise level associated with the DPC and scattering signals is significant. Since noise models for three signals have been investigated, and the noise variance has been computed and translated from the spatial to the wavelet domain.

For several decades, partial differential equation (PDE)-based denoising methods have been studied and improved [14, 70]. A variety of PDE-based denoising techniques have been suggested to treat only Gaussian additive or multiplicative noises [36]. In particular, these techniques have received much attention because of their ability to preserve and even enhance edges in the processed image. The most popular and applied filter in this category is Perona–Malik diffusion [74], which is a method aiming at filtering image corrupted with additive Gaussian noise without losing significant details of the original image, such as edges, lines, corners, or other fin structures that are useful for the interpretation of the image. Perona–Malik model is based on a diffusion process, where the diffusion function varies spatially in such a way that the smoothing degree increases close to edges and other most prominent structures in the image, but decreases in homogeneous regions. Motivated by the efficiency of the Perona–Malik technique in the suppression of additive noise, researchers are addressed to reduce multiplicative speckle noise. For instance, Yu and Acton [108] developed a speckle reducing anisotropic diffusion (SRAD) filter, which is an improved version of the diffusion method adapted for images damaged by speckle noise such as ultrasonic and radar imaging. SRAD exploited the instantaneous coefficient of variation in adaptive filtering as in Lee and Frost filters [35, 54] for removing multiplicative noise in imagery. Afterward, Aja-Fernández et al. derived another version of the anisotropic diffusion filter that is based on SRAD filter and called it details preserving anisotropic diffusion (DPAD) [6]. DPAD uses another diffusion function (taken from Kuan’s filter) based on the estimation of the signal and noise statistics. For the same purpose, Karl et al. extended the simple anisotropic diffusion process to a matrix diffusion [51], allowing different levels of smoothing along different directions such as the contours and the principal curvature directions of 3D structures. For images containing tubular structures such as blood vessels, they have chosen the gradient and the principal curvature directions as a basis for the diffusion matrix.

Over the years, PDE-based denoising methods continue to be an active area of research, so some of previous methods have been refined and new algorithms have been developed. For instance, in [66], authors have proposed diffusion-driven method for reducing noise using two diffusion functions that properly guided the diffusion process across regions in the image.

Nair et al. have integrated a low arithmetic complexity image smoothing model for anisotropic diffusion smoothing of images [69]. An operating approach based on the anisotropic diffusion method is proposed in [37] to deal satellite remote sensing images.

Recently, deep learning-based approaches have achieved good performance improvement in image denoise processing [58, 61, 94]. The reason for the great success of a convolutional neural network (CNN) in the area of noise removal can be attributed to understanding complex patterns in data and its strong modeling ability but that does not mean these types of methods do not have drawbacks. CNNs require significant volumes of labeled training data to produce accurate denoising results. Collecting and processing a large dataset comprising both clean and noisy image pairs can be time-consuming, costly or, in some cases, impractical. Insufficient or incorrect training data can limit performance or make generalization to different noise types or levels more difficult.

Most of the aforementioned denoising algorithms simply consider the noise level as known and purely AWGN or multiplicative noise. That is, the performances of the image denoising technique are limited due to the poor estimate of the noise and thus the output denoised image loses most of the critical details. Signal-dependent noise, used to refer model of noise, is a function of how standard deviation varies with respect to intensity mean value in the observed image. In addition, for image containing high-frequency components such noise, textures, edges, and corners, it is difficult to distinguish them from noise during the denoising process. However, the denoising task often relies on the knowledge of the noise distribution and its parameters.

3 Anisotropic Diffusion Scheme for Signal-Dependent Noise Filtering

3.1 Overview on SRAD and DPAD Filters

Yu and Acton [108] proposed speckle reducing anisotropic diffusion filter (SRAD), which is an anisotropic diffusion equation to denoise, especially, images corrupted by multiplicative noise (speckle noise). In fact, SRAD is obtained by combining anisotropic diffusion with the Lee filter [54] and is expressed as the following:

$$\left\{\begin{array}{l}\frac{\partial {I}_{n}\left(i,j;t+\nabla t\right)}{\partial t}=div\left[c\left(q\left(i,j;t\right)\right).\nabla {I}_{n}\left(i,j;t\right)\right]\\ {I}_{n}\left(i,j;t=0\right)={I}_{0}\end{array}\right.$$
(1)

where \(\partial\) is the first-order partial derivative, \({I}_{n}\) is the processed image, \(\nabla\) is the gradient operator, \((i,j)\) are the space position of the pixel in the image, t is the iteration number, \(\nabla t\) is the step time, \({I}_{0}\) is the noisy image at \(t=0\), \(\mathrm{div}\) is refer to divergence operator, and c(.) is the diffusion coefficient, and there are two functions to express it:

$${c\left(q\left(i,j;t\right)\right)}_{\mathrm{SRAD}}=\frac{1}{1+\left[{q}^{2}\left(i,j;t\right)-{q}_{0}^{2}\left(t\right)\right]/\left[{q}_{0}^{2}\left(t\right)\left(1+{q}_{0}^{2}\left(i,j;t\right)\right)\right]}$$
(2)
$${c\left(q\left(i,j;t\right)\right)}_{\mathrm{SRAD}}=\mathrm{exp}\left\{-\left[{q}^{2}\left(i,j;t\right)-{q}_{0}^{2}\left(t\right)\right]/\left[{q}_{0}^{2}\left(t\right)\left(1+{q}_{0}^{2}\left(t\right)\right)\right]\right\}$$
(3)

According to Eqs. (2) and (3), \({q}_{0}\) is the instantaneous speckle scale function or coefficient of variation of noise, which controls the degree of smoothing applied to the image by the SRAD filter. The computation of \({q}_{0}\) will be discussed later in this section. \(q\) is the instantaneous coefficient of variation, where its expression can be written as follows:

$${q\left(i,j;t\right)}_{\mathrm{SRAD}}=\sqrt{\frac{\left(1/2\right){\left(\left|\nabla {I}_{n}\left(i,j;t\right)\right|/{I}_{n}\left(i,j;t\right)\right)}^{2}- \left(1/{4}^{2}\right){\left[\left|{\nabla }^{2}{I}_{n}\left(i,j;t\right)\right|/{I}_{n}\left(i,j;t\right)\right]}^{2}}{{\left[1+\left(1/4\right)\left(\left|{\nabla }^{2}{I}_{n}\left(i,j;t\right)\right|/{I}_{n}\left(i,j;t\right)\right)\right]}^{2}}}$$
(4)

where \(|\bullet |\) is the magnitude.

SRAD filter uses Jacobi iteration method to solve numerically the partial differential equation (PDE) given in Eq. (1). Specific solution steps are formulated by Yu and Acton in [108]. The PDE of the SRAD filter can be approximated as follows:

$${I}_{n}\left(i,j;t+\Delta t\right)={I}_{n}\left(i,j;t+\Delta t\right)+\frac{\Delta t}{\left|{\eta }_{s}\right|} d\left(i,j;t\right)$$
(5)

where \(\left|{\eta }_{s}\right|=4\) is the four direct neighborhoods and

$$\begin{aligned} d\left(i,j;t\right)&=\frac{1}{{h}^{2}}\left[ c\left(i+1,j;t\right)\left( {I}_{n}\left(i+1,j;t\right)- {I}_{n} \left(i,j;t\right)\right)\right.\\ &\quad+c\left(i-1,j;t\right)\left({I}_{n}\left(i-1,j;t\right)- {I}_{n} \left(i,j;t\right)\right)\\ &\quad+c\left(i,j+1;t\right)\left({I}_{n}\left(i,j+1;t\right)- {I}_{n}\left(i,j;t\right) \right)\\ &\quad\left.+c\left(i,j-1;t\right)\left({I}_{n}\left(i,j-1;t\right)- {I}_{n}\left(i,j;t\right)\right)\right]\end{aligned}$$
(6)

Here\(t\) and \(\Delta t\) denote, respectively, the number of iterations and step of the time. \(h\) is the spatial step size and was chosen equal to 1. \(c\left(i+1,j;t\right)\) is the coefficient of variation in the east of the central pixel at time\(t\). This method not only shows effectiveness in removing speckle noise from a corrupted image at different levels, but also retains and refines the boundary information in the observed image. Similar to SRAD, Aja-Fernandez et al. proposed another version of anisotropic diffusion filter by combining conventional anisotropic diffusion with Kuan filter [52]. They called their filter as detail preserving anisotropic diffusion (DPAD) [6]. DPAD is similar to SRAD with a few modifications. For example, it computes the local coefficient of variation of the image of each pixel in the image as follows:

$${q\left(i,j;t\right)}_{\mathrm{DPAD}}=\sqrt{\frac{\frac{1}{\left|{\eta }_{p}\right|-1}\sum_{p\in {\eta }_{P}}{\left({I}_{p}-\overline{{I }_{n}\left(i,j;t\right)}\right)}^{2})}{{\overline{{I }_{n}\left(i,j;t\right)}}^{2}}}=\sqrt{\frac{Var({I}_{n}\left(i,j;t\right))}{{\overline{{I }_{n}\left(i,j;t\right)}}^{2}}}$$
(7)

where \(\left|{\eta }_{p}\right|\) is chosen as a window of 5 × 5 neighbor of the current pixel \({I}_{n}\left(i,j;t\right)\), \(p\) is the neighbor pixel, \({I}_{p}\) is the intensity of \(p\), \({\overline{{I }_{n}\left(i,j;t\right)}}^{2}\), and \(\mathrm{Var}({I}_{n}\left(i,j;t\right))\) are, respectively, the square of local mean value of current pixel and its local variance. Furthermore, the diffusion coefficient function adopted by DPAD is written as follows:

$${c\left(q\left(i,j;t\right)\right)}_{\mathrm{DPAD}}=\frac{1+\frac{1}{{q(i,j;t)}^{2}}}{1+\frac{1}{{{q}_{0}\left(t\right)}^{2}}}$$
(8)

In smoothing prediction rate \(c(.)\), it is necessary to accuracy estimate the noise level \({q}_{0}\), there are several manners which have been proposed by Yu and Acton. In the first one, they manually selected an homogeneous region in the image, and then, they computed from it, iteratively, the mean and variance values of noise. These values represent the noise characteristics (or noise parameters) and will be used in computation of the noise coefficient of variation, whose expression is given by:

$${{q}_{0}\left(t\right)}_{\mathrm{SRAD}}=\sqrt{\frac{{\sigma }_{n}^{2}}{{\overline{n} }^{2}}}$$
(9)

where \(n\) is the multiplicative noise in the observed homogeneous region, \({\sigma }_{n}^{2}\) and \(\overline{n }\) are the noise characteristics that are, respectively, the variance and mean value. In the second one, they estimated \({q}_{0}(t)\) automatically and without homogeneous region selection. First of all, they stated that \({q}_{0}\left(t\right)\) can be expressed by [108]:

$${{q}_{0}\left(t\right)}_{\mathrm{SRAD}}={q}_{0}(0) .\mathrm{exp}(-\rho t)$$
(10)

where \(\mathrm{exp}(.)\) is the exponential function, \(\rho\) is a constant less than \(1\), and \({q}_{0}(0)\) is the initial noise level in the observed image. \({q}_{0}(0)\) is assumed equal to \(1\) for ultrasound images, \(1/\sqrt{N}\) for N-look SAR images. However, Eq. (10) is analytical form of a linear approximation of the speckle noise estimation, so predicted noise statistics are far from being realistic. In a parallel context, Yu and Acton tried to improve the filter by applying another noise estimator [109], where the expression is as follows:

$${{q}_{0}\left(t\right)}_{\mathrm{MAD}}^{\mathrm{SRAD}}=\left(\frac{Cst}{\sqrt{2}}\right) \mathrm{MAD}\left(\nabla \mathrm{log}({I}_{n}(i,j;t)\right))$$
(11)

Here \(\mathrm{log}(.)\) is the logarithmic function, \(Cst=1.4826\) and \(\mathrm{MAD}\left(x\right)=\{ \left| x-\mathrm{med}|x| \right| \}\), refers to the median absolute deviation, with \(x\) is a vector, and \(med\) is median value of\(|x|\). Aja-Fernández et al. in their paper [6] estimate \({q}_{0}(t)\) in the same way of computing \({q\left(i,j;t\right) }_{\mathrm{DPAD}}\), not on the whole of image, but within a selected homogenous area, or even they have taken the minimum, or the average, or the median of all \({q\left(i,j;t\right) }_{\mathrm{DPAD}}\) values computed on the whole image.

Although the above adopted methods of noise estimation have been very simple to implement and they achieved reasonably performance in image denoising, they suffered from several drawbacks. During the past decade, in several reference methods [23, 55, 59, 60], some experiments have taken place in order to have a better overview of several noise estimator performances. For instance, the manual selection of homogeneous region by user is possible but it is nontrivial for a computer, also the selected region may contain information, leading to an overestimation of noise, the amount of noise removed is uniform throughout the image, whether at the edges, or in a homogeneous or textured region. In addition, the minimum is biased toward zero due to the presence of aberrant values. That is why, the minimum operator is considered as a lower bound for \({q}_{0}\). The average operator, on the other side, tends to overestimate \({q}_{0}(t)\) and is considered as an upper bound. The median operator, however, behaves very closely to \({{q}_{0}}_{\mathrm{MAD}}\) using a \(5\times 5\) neighborhood and indicates less variability about the real value.

3.2 SDN-Reducing Anisotropic Diffusion Method

SRAD and DPAD filters proposed the noise model with some assumptions, such noise is a purely signal-independent multiplicative white noise (SIMWN). Generally, authors used the simplification in order to make more easier the implementation of filter but obtained results will always be unsatisfactory. However, noise is not realistic in practice and is more complicate to estimate. The noise produced in images by a real digital camera is usually non-white, not purely multiplicative, and should be modeled as signal-dependent noise (SDN). Indeed, the assumption of using a uniform noise variance (a single parameter) over the whole image leads denoising algorithms to over-blur the image or to leave part of the noise unfiltered. In the proposed work, such noise can be a mixture of additive and signal-dependent multiplicative components. Only three parameters are sufficient to completely describe the suggested noise model. These parameters are explained in relation to the hardware characteristics of the sensor and the image acquisition process. As a consequence, a noise estimation step becomes complicated, and the challenge is to estimate it, accurately and without manual intervention, from a single noisy image.

In the following sub-sections, first, it is provided an overview on different kinds of noise alterations during the image acquisition and processing chain. Next, it is described the technique for the estimation of noise parameters from a single SDN corrupted image. Finally, a new coefficient of variation of noise \({{q}_{0}\left(i,j;t\right)}_{\mathrm{SDN}}\) is developed.

3.2.1 Digital Image Sensors

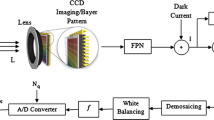
The two main technologies of camera sensors are charge-coupled device (CCD) and a complementary metal–oxide–semiconductor (CMOS) sensors (Figs. 1 and 2). In CCD sensor, an amount of charge is generated at each sensing element (or photo diode and is referred to a "pixel") and is transported from pixel to pixel and is converted into analog voltage at the output node. Then, an analog to digital converter (ADC) is used to convert the analog value of each pixel to a digital value. Unlike CCD sensors, CMOS sensors work by converting charge to voltage inside each sensing element which is coupled with individual amplifier to amplify the electric signal from the sensing element. Not only that, but each column of array has its own ADC and each pixel's value is converted into a digital value. Some of the main advantages are that CMOS sensors have lower power consumption than their CCD counterparts, they are much less expensive to manufacture than CCDs, and they provide faster readout than CCDs. They are, therefore, suitable for fast image acquisition. Additionally, CMOS sensors can be done with semiconductors materials besides silicon such as gallium arsenide, indium gallium arsenide, and silicon germanium [83]. These materials allow for CMOS devices to be sensitive to wavelengths outside the visible spectrum. All these are great benefits, especially when it comes to design consumer electronic devices where battery life and cost are quite important like digital cameras or cell phones. Based on these differences, it is clear that CCDs are generally used in cameras that offer high-quality images with high-resolution and excellent sensitivity to light. CMOS sensors are traditionally known for their lower image quality, lower resolution, and lower sensitivity to light. CCD sensors are widely used in the current times and have become popular in the fields of consumer and automotive electronics, space exploration, telemedicine, video surveillance, fluorescence detection, etc. Their main disadvantage is that all those integrated extra amplifiers and ADCs generate a lot of noise. Noise is a random signal, which is always presents in digital images during the image processing pipeline of the sensor. Therefore, noise has been studied for decades in image processing due to its effect in different applications such as image denoising. To achieve optimal performance in this application, it is essential to identify the characteristics of noise in advance. In some literature review, noise models can be divided into two categories: signal-independent noise (SIN) and signal-dependent noise (SDN). The basic used model for SIN is approximated as additive white Gaussian noise (AWGN) [55, 92]. However, this model is not pertinent due to the dominant presence of Poisson/multiplicative noise that alters a natural image acquired by an imaging system. While SIN models assume that the noise level is stationary in the whole natural image, independently of the intensity of the original pixel, SDN models consider that the noise level depends proportionally on the original pixel value [71].

Fig. 1
figure 1

CCD camera sensor

Full size image
Fig. 2
figure 2

CMOS camera sensor

Full size image

3.3 CCD Camera Sources Noise

As mentioned in the previous sub-section, the CCD camera converts the photons (or the irradiance) which arrive in the image sensor, in electrons, in electrical voltage, and finally in bits. The real CCD camera noise model was developed from existing studies on the various sources of camera noise [16, 29, 95, 100]. Before addressing the noise modeling, a general overview of the nature of the different transformations and the main sources of error in a typical color CCD camera is provided below [46, 68]. Noise in raw images can come from different sources which is divided into two broad types: shot noise and digital noise. The first type is actually related to the nature of the light and optical artifacts, while the second is caused by the internal electronics of the camera sensor. As noise reduces perceived image quality, several models have been developed to model noise at various steps of image acquisition process in order to reduce or remove it later. Shot noise includes in particular the dark shot noise and photon shot noise. The word "Dark Shot Noise" is employed to describe accumulation of electrons generated by the heat in the sensor. It depends upon the temperature and therefore can be reduced by cooling down the sensor. The photon shot noise also known as Poisson multiplicative noise, and it is linked with the quantum properties of light. Photon noise results from the fact that light arrives in photons on the individual sensing elements which are subject to random fluctuations, i.e., even with a constant light source the exact number of photons, being absorbed by the sensing element, may vary from unit time to unit time and from sensing element to sensing element. The signal intensity, i.e., the number of photons captured by the sensing element, during a given exposure time is stochastic and can be described by zero-mean Poisson distribution with a variance that depends on the number of generated photoelectrons and the number of dark electrons [43]. The effect of photon shot noise decreases with exposure time.

Digital noise refers to sensor electronic limitations which is randomness caused by imperfections and variations in the sensing elements and electronic circuitry which ultimately transform the photons into a digital signal. This type of noise contains fixed pattern noise (FPN) [64, 67, 79], photon response non-uniformity (PRNU), and quantification noise. Both noises PRNU and FPN, also known as pattern noise (PN), are a component that remains practically the same if several photos of the same scene are taken. FPN is caused by dark currents and depends on exposure and temperature [64]. The dark current consists of thermally generated electrons that discharge the pixel as if a photon had hit it. Even, it can be detected in obscurity. FPN is generated at different locations in the sensor, and it is related to irregularities in the fundamental crystal structure of the silicon [4]. PRNU refers to the non-uniform pixel response across the sensor's surface. The dominant part of PN is PRNU which is an intrinsic property of all digital camera sensors. It is mainly due to the inhomogeneity of the silicon wafers, which implies little variations between individual sensor pixels in their ability to convert light into electrons [34]. When taking a long exposure time, the image sensor heats up and PRNU becomes more visible. Therefore, it does not exist in the absence of a signal, because it depends on the signal. After that, the charge is collected at each pixel, it is then moved to the output amplifier to be read. The amplifier amplifies sequentially the charge accumulated at each pixel into a measurable voltage value. To create a numerical image that can be saved on a computer, voltage measurements are quantized both spatially and in magnitude by the analogic–numeric converter (ADC). The quantization process can be accompanied by a quantization noise. Following that the obtained raw image is processed by some typical post-acquisition processes, such as demosaicing, white balancing, and gamma correction. During the demosaicing process, false colors, known as "demosaicing noise," can be introduced in the output image. Demosaicing is an algorithm for reconstructing a full color image from the incomplete color samples output of RGB color filter array (CFA) implemented in image sensors. Indeed, each color channel of generated output image has different characteristics of noise properties.

3.4 General Signal-Dependent Noise Model

Captured image by a typical CCD camera can be modeled by taking into account of different types of noises observed during its acquisition process. Usually, the digital image model is composed of two mutually independent parts, a multiplicative signal-dependent component that includes the photon shot noise, dark current, etc., and a signal-independent component for stationary disturbances such as PN noise, read-out noise, and thermal noise. In this work, let us propose the generic signal-dependent noise model of the form:

$${I}_{n}\left(i,j\right)=I\left(i,j\right)+{\eta }_{w}\left(I,\left(i,j\right)\right)+{\eta }_{G}\left(i,j\right)$$
(13)

with \({I}_{n}(i,j)\) is the intensity pixel \((i,j)\) in the noisy image, \(I(i,j)\) is the intensity at \((i,j)\) pixel in the noise free image (is unknown), \((i,j)\) are the indices of pixels in the raw image, \(i = 1, \dots , M, j = 1, \dots , N\), \(M\times N\) is the image resolution, and \({\eta }_{G}\) is stationary noise throughout the image and is assumed as white and zero-mean Gaussian distribution with constant standard deviation \({\sigma }_{G}.\) As pixel intensities are generally non-stationary in the image\(, {\eta }_{w}\) is modeled as a signal-dependent noise with a varying variance that depends on the value of the pixel intensity \(I\), which will be non-stationary too, and it is spatially auto-correlated [33] and may can be written as \({\eta }_{w}\left(I,\left(i,j\right)\right)={I\left(i,j\right)}^{\gamma }.\omega (i,j)\). The term \(\omega (i,j)\) defines multiplicative noise component obeying Gaussian distribution with zero-mean and relative variance \({\sigma }_{\omega }^{2}\), and \(\gamma\) is the exponential parameter belonging to \([\mathrm{0,1}]\) [98]. The standard deviation of the proposed noisy signal is a function, namely \({\sigma }_{{I}_{n}}\), of the expectation of the model (13), i.e., \({\mathrm{std}\left[{I}_{n}(i,j)\right]=\sigma }_{{I}_{n}}\left({\mathbb{E}}\left[{I}_{n}(i,j)\right]\right)\). Consequently, the overall variance is given by following affine form:

$${\sigma }_{{I}_{n}}^{2}\left(i,j\right)={\sigma }_{I}^{2}\left(i,j\right)+{\mathbb{E}}\left[{I\left(i,j\right)}^{2\gamma }\right].{\sigma }_{\omega }^{2}(i,j)+{\sigma }_{G}^{2}\left(i,j\right)$$
(14)

If the variance is computed on homogeneous sequence of pixels, thus \({\sigma }_{I}^{2}\left(i,j\right)=0\). Since, the variance of noise, also known as noise level function (NLF), can be expressed as follows:

$${\sigma }_{{I}_{n}}^{2}\left(i,j\right)={\mathbb{E}}\left[{I(i,j)}^{2\gamma }\right].{\sigma }_{\omega }^{2}(i,j)+{\sigma }_{G}^{2}\left(i,j\right)$$
(15)

Let's the symbol \({\tau }_{n}^{t}\) is used exclusively to denote the function of the noise variance \({\sigma }_{{I}_{n}}^{2}\). A Taylor series approximation [98] of the function \({I}^{2\gamma }\) is used to evaluate \({\mathbb{E}}\left[{I\left(i,j\right)}^{2\gamma }\right]:\)

\({\mathbb{E}}\left[{I}^{2\gamma }\left(i,j\right)\right]\simeq {{\mathbb{E}}\left[I\left(i,j\right)\right]}^{2\gamma }\) and \({{\mathbb{E}}\left[I\left(i,j\right)\right]}^{2\gamma }\simeq I(i,j)\). Hence, coming again to a model of Eq. (15) with a form

$${\tau }_{n}^{t}\left(I;{\gamma ,\sigma }_{\omega },{\sigma }_{\mathrm{G}}\right)={I}^{2\gamma }.{\sigma }_{\omega }^{2}+{\sigma }_{\mathrm{G}}^{2}$$
(16)

This noise model is proposed to account for several different acquisition systems. Since, by changing the values of three noise parameters \(({\gamma ,\sigma }_{\omega },{\sigma }_{\mathrm{G}})\), \({\tau }_{n}^{t}\) can modelize various types of noise such as multiplicative speckle noise, Poisson noise, film-grain noise, and others [5]. Therefore, the noise coefficient of variation in the traditional SRAD/DPAD filter adjusted for signal-dependant noise takes the new following form:

$${{q}_{0}\left(I,i,j;t\right)}_{\mathrm{SDN}}=\sqrt{\frac{{\tau }_{n}^{t}\left(I;{\gamma ,\sigma }_{\omega },{\sigma }_{{\eta }_{G}}\right)}{{\overline{{I }_{n}\left(i,j;t\right)}}^{2}}}$$
(17)

\({{q}_{0}\left(.\right)}_{\mathrm{SDN}}\) can vary from pixel to pixel in the image, also across different color components due to the demosaicing process. The 3 × 3 neighborhood shown in Fig. 3a is used to compute the new noise coefficient of variation in order to discriminate accurately the textured regions and the edges from noise. The proposed algorithm is similar to the SRAD filter, but with a few distinctions. Such as, Eq. (17) is used to compute the new noise coefficient of variation for each pixel instead of a single value for the whole image, the SDN instantaneous coefficient of variation is calculated using Eq. (4), the new diffusion function \(c(.)\) is given following Eq. (2), and the proposed PDE can be approximated by the \(4\) direct neighbors \((i,e. \left|{\eta }_{\mathrm{SDN}}\right|= 4)\) (Fig. 3b).

Fig. 3
figure 3

Neighbors of pixel \(I\left(i,j\right)\) in the 8- and 4-neighborhoods

Full size image

3.5 Estimation of SDN Parameters

The current sub-section describes a procedure of the estimation of the three parameters of the proposed noise model. For images with homogeneous simple structures, to estimate the noise level for practical use, many early researchers, in the field of SDN estimation, have taken the smallest standard deviation of the most homogeneous sub-blocks in the observed image as the overall noise level. However, the assumption of constant noise variance across the whole image leads to an over-smoothing of the image or some noise is unfiltered, especially in the case of textured images; for that reason, proposed algorithm is oriented to accurately estimate the real noise level, for the variety of input images, especially for those with rich textures [63]. A block diagram, in Fig. 4, illustrates the structure of the proposed algorithm, where blocks are explained below:

  1. a.

    The input noisy image is clipped into blocks of size \(K\times K\)

  2. b.

    A pair of local parameters (local mean and variance) are calculated for each block.

    • Local variance of each block is estimated as a power of noisy block along to the minimum variance direction \({X}_{\mathrm{min}}\).

    • Local mean is the mean of the intensities in each block

  3. c.

    Once local means and variances of all blocks in the observed image are calculated, the SDN parameters of the NLF are estimated by ML-Estimator.

    However, the initial estimated NLF, denoted by (\({{\tau }_{n}}^{0}\)), is an overestimate of the noise level because it may contain signal. In order to optimize the estimated noise model, an integrated framework based on the texture strength for optimal weak textured patches selection is applied. To provide further explanation, a series of steps are illustrated below:

  4. d.

    For each block, a texture strength metric is calculated using local parameters

  5. e.

    A threshold \(th\) on the texture strengths is calculated to discriminate the weak textured blocks

  6. f.

    The variances of selected weak textured blocks are used to make iterative estimates the new parameters of NLF in the same manner as previously mentioned (step c).

In the rest of the section, all these steps are formulated, below with more details, in mathematical terms.

Fig. 4
figure 4

Different steps of the noise estimation procedure (NEP) applied on each channel: red, green, and blue and each iteration

Full size image

Firstly, block or patch-based approach [2] is used where the input noisy image is divided into blocks of size \(K\times K\) and is defined by their center pixel \({I}_{n}^{k}\) (\(k\) is the indice of patch). The noise-free pixel values of patches are estimated by their mean values, and the patches are supposed flat with zero-mean noise. For each block \({B}_{k}\), a \(k\) pair of local parameters (i.e., the local mean and local variance) are calculated respectively as outlined below:

$${\widetilde{I}}_{k}=\frac{1}{{K}^{2}}\sum_{i,j\epsilon {B}_{k}}{I}_{n}\left(i,j\right)$$
(18)
$${\widetilde{\sigma }}_{k}^{2}={\Vert {X}_{\mathrm{min}}^{T} .{Y}_{n}^{k}\Vert }^{2}$$
(19)

where \({\widetilde{I}}_{k}\) is the approximate local mean or the noise-free signal of \(\mathrm{k{\prime}}\mathrm{ block}\), \({\widetilde{\sigma }}_{k}^{2}\), is the estimated noise variance of each patch, which is also defined as a power of noisy patch along to the vector \({X}_{\mathrm{min} }(\)or the minimum variance direction. \({X}_{\mathrm{min}}\) is computed using the principal component analysis (PCA), i.e., it is the eigenvector associated to the minimum eigenvalue of the following covariance matrix of all patches of noisy image:

$${\Sigma }_{{I}_{n}}=\frac{1}{M\times N}\sum_{k=1}^{M\times N}{Y}_{n}^{k} .{{Y}_{n}^{k}}^{T}$$
(20)

The letter ‘\(T\)’ indicates the transpose operator. \({Y}_{n}^{k}\) is the vector of the observed pixel values into \(k\)-th noisy patch\({\left\{{{\varvec{I}}}_{{\varvec{n}}}\left(i,j\right)\right\}}_{k}\). \({Y}^{k}\) refers to the set of pixel values in k-th noise-free patch \({\left\{\mathrm{I}\left(i,j\right)\right\}}_{k}\).

Once local means and variances of all sub-blocks in the observed image are calculated, the SDN parameters of NLF are estimated by the maximum likelihood estimator (ML-Estimator). The likelihood of NLF is derived as follows:

$$\mathcal{L}=\prod_{k=1}^{S}\frac{1}{\sqrt{2\uppi {\tau }_{n}^{t}\left({\widetilde{I}}_{k};\gamma ,{\sigma }_{\omega }^{2},{\sigma }_{{\eta }_{G}}^{2} \right)}} \mathrm{exp}\left\{- \frac{{\widetilde{\sigma }}_{k}^{2}}{2{\tau }_{n}^{t}\left({\widetilde{I}}_{k};\gamma ,{\sigma }_{\omega }^{2},{\sigma }_{{\eta }_{G}}^{2}\right)}\right\}$$
(21)

Here S indicates the number of selected patches, \({\widetilde{I}}_{k}\) and \({\widetilde{\sigma }}_{k}^{2}\) are, respectively, mean value and variance of selected patch. The cost function \(\mathcal{F}\) to be minimized can be derived from negative log-likelihood function as follows:

$$\mathcal{F}\left(\gamma ,{\sigma }_{\omega }^{2},{\sigma }_{{\eta }_{G}}^{2}\right)=\sum_{k=1}^{S}log\left({\tau }_{n}^{t}\left({\widetilde{I}}_{k};\gamma ,{\sigma }_{\omega }^{2},{\sigma }_{{\eta }_{G}}^{2} \right)\right)+ \frac{{\widetilde{\sigma }}_{k}^{2}}{2{\tau }_{n}^{t}\left({\widetilde{I}}_{k};\gamma ,{\sigma }_{\omega }^{2},{\sigma }_{{\eta }_{G}}^{2} \right)}$$
(22)

To minimize the cost function with respect to \(\gamma ,{\sigma }_{\omega }^{2},\) and \({\sigma }_{\mathrm{G}}^{2}\), the gradient-descent technique is applied, including the three parameters are initialized to zero in the algorithm. However, the obtained estimated NLF (\({{\tau }_{n}}^{0}\)) is an overestimate of the noise level because sub-blocks may contain information, and it is a real problem especially for images with a rich texture or images with fine details. To avoid overestimating the noise level for images with textures, a weak textured patches selection algorithm based on the texture strength is used [62]. The proposed algorithm selects suitable patches to evaluate the homogeneity of image patches. For each sub-block in observed image, a texture strength metric is calculated using the following formula:

$${\rm T}_{s}=\mathrm{tr}(G.{G}^{T})$$
(23)

where \(\mathrm{tr}(.)\) is the trace of a matrix, and \(G\) is expressed as follows:

$$G=\left[H{Y}_{N}^{k} V{Y}_{N}^{k}\right]$$
(24)

\(H , V\), are, respectively, the matrices of the horizontal and vertical first derivative operators for the image patch. Therefore, to extract weak textured patches, a threshold for the texture strength is calculated in the algorithm. The threshold \(\mathrm{th}\) has been expressed as

$$\mathrm{th}={{\tau }_{n}}^{0} . {\Gamma }^{-1}\left(\beta ,\frac{{K}^{2}}{2},\frac{2}{{K}^{2}} \mathrm{tr}\left({H}^{T} H+{V}^{T}V\right)\right)$$
(25)

Here \({\Gamma }^{-1}\left(\upbeta ,{\vartheta },\upzeta )\right)\) represents the inverse gamma cumulative distribution function with \(\vartheta\) is the shape parameter, \(\upzeta\) is the scale parameter, and \(\beta\) is the confidence level which is equal to 0.99. \({{\tau }_{n}}^{0}\) is the noise variance of patches in the observed image, \({K}^{2}\) represents the number of pixels in the patch. As mentioned in Eq. (25), the threshold \(th\) requires the noise level \({{\tau }_{n}}^{0}\) as a variable. Once the textured patches image is thresholded with \(\mathrm{th}\), the variances of selected weak textured patches are used to estimate the parameters of NLF using the same expressions (21) and (22). This latest process is iterated until obtaining the unchanged estimated NLF, which is the final and required \({\tau }_{n}\). In the same manner, the variances of selected week textured patches are given by expression (19).

4 Numerical Results

The numerical experiments were performed with MATLAB 2015a on an Intel Core i7–7500CPU 2.90 GHz with 8.00 GB memory.

In the current section, several experiments are effected on test images from BSD dataset because it is known as the most popular and complete dataset available for our aims [8]. Therefore, it has been used in several publications and has the advantage of providing several human-labeled segmentations for each image. The BSD68 dataset consists of 68 images from the separate test set of the BSD dataset. Some images from this database are presented in Fig. 5. Before applying our algorithm, a synthetic signal-dependent noise was added to the chosen test image according to Eq. (16). In our experiments, to generate synthetic noise, the three parameters of NLF for noise model are set and expressed as a three wise combination of \(\upgamma\) ∈ [0, 1], \({\sigma }_{\omega }=\left[0.5, 1.5\right]\) and \({\sigma }_{\mathrm{G}}=\left[\mathrm{5,20}\right]\) for 8-bit images. Figure 6 is displayed an example of synthetic noisy image corrupted by following parameters \({\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{{\eta }_{G}}=15\).

Fig. 5
figure 5

Some test images from BSD68 dataset

Full size image
Fig. 6
figure 6

a '65019.jpg' original image. b Noisy image with \({\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{{\eta }_{G}}=15\) and c noisy sub-image

Full size image
Fig. 7
figure 7

a Noised green channel of '65019.jpg' test image and b selected weak textured patches in noised green image

Full size image

Before performing the denoising process, it is necessary to estimate for each iteration the noise model. The goal of noise estimation is to accurately estimate the function \({\tau }_{n}\) (i.e., the three parameters \(\upgamma\), \({\sigma }_{\omega }\), and \({\sigma }_{G}\)) of the observation model (16) from a noisy image. The proposed noise estimator is divided into three main steps: local estimation of mean/standard deviation pairs, select week textured regions, and global parametric model fitting to the selected local estimates.

First experiments are started with homogeneous images. An example is shown in Fig. 7, where, Fig. 7a corresponding to the green channel of original image '65019.jpg,' and Fig. 7b shows its obtained image after applying the weak textured patches selection process. In this last image, black regions correspond to pixels having the most high texture strength, while the others regions are lightly textured. As we have already explained, the noise in an image is colored through the demosaicing step in the image acquisition process (see Fig. 8). So three RGB noise components will be estimated for noise. Therefore, the proposed noise estimator algorithm will provide three curves of NLFs for red, green, and blue channels.

Fig. 8
figure 8

Color image. From top to bottom and from left to right: original sub-image, noisy sub-image, and color noise in sub-image; red, green, and blue channels of color sub-image; red, green, and blue channels of color image noise

Full size image

The three curves of noise model of image in Fig. 6 are shown in Fig. 9, and their estimated parameters of \({\gamma , \sigma }_{\omega },{\sigma }_{G}\) are illustrated through Table 1. In accordance with Fig. 9, the three NLF curves overlap considerably with the real noise models (blue curves) with a small distinction. Also, the test values of three parameters exhibit perfect congruence with their corresponding real values. Considering these outcomes, it is clear that the noise estimation process accurately estimates the noise parameters of mixed noise. Figure 10 shows another result of the same image but corrupted by other parameters of synthetic noise where \({\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{G}=5\). Table 2 presents the estimated parameters for the three-color channels.

Fig. 9
figure 9

Model noise of image '65019.jpg': noised with \({\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{{\eta }_{G}}=15\); RMSE = Red: (17.03) Green: (18.47) Blue: (8.60)

Full size image
Table 1 Parameters of model noise of image '65019.jpg': noised with \({\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{G}=15\);
Full size table
Fig. 10
figure 10

Model noise of image '65019.jpg': noised with \({\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{G}=5\); RMSE = Red: (12.85) Green: (13.98) Blue: (10.96)

Full size image
Table 2 Parameters of model noise of image '65019.jpg': noised with \({\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{G}=5\);
Full size table

Afterwards, the test image, refers to '27059.jpg' from BSD dataset, is chosen to deal image containing textured regions (Fig. 11—left). This image is damaged by following synthetic noise parameters: \({\gamma =0.5,\sigma }_{\omega }=1.5,{\sigma }_{G}=15\) (see Fig. 11—right). Their corresponding results of noise estimator are presented in Fig. 12 and Table 3. The two estimated red and green NLF curves are correctly superimposed on the real curves, while the blue curve shows a few differences from the real curve, and their three estimated noise parameters are displayed in Table 3.

Fig. 11
figure 11

Test image '27059.jpg' from BSD300 dataset from standard BSD68 dataset: right: original free noise image and left: Image corrupted with synthetic noise with following parameters: \(\left({\gamma =0.5,\sigma }_{\omega }=1.5,{\sigma }_{G}=15\right)\)

Full size image
Fig. 12
figure 12

Noise level estimation on '27059.jpg' image, the proposed method estimates the noise level correctly for red, green, and blue channels

Full size image
Table 3 Parameters of model noise of image '27059.jpg': noised with \({\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{{\eta }_{G}}=15\);
Full size table

To ensure the algorithm's applicability across various images, we have chosen Lena image that is one of the most widely used standard test images for image denoising. It is considered as a good test image because it contains flat regions, a nice mixt of details, textures, and shading. Firstly, original Lena test image (Fig. 13) is corrupted by a signal-dependent noise with the following parameters:\({\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{G}=15\)). Then, SDN noise estimation algorithm is applied on it with the size of the patch fixed to\(7\times 7\). The estimated three curves of NLF are shown at last line of Fig. 14, where obtained NLF of green channel gives the best-fit curve with the true NLF. The second line of Fig. 14 illustrates the red, green, and blue images for week textured selection pixels of RGB noised image (first line of Fig. 14). The selection of pixels with a high variance value in the green channel is better than that of the other two, since the grayscale image provides a clear view of the contours and textured areas in the image. Therefore, the results obtained by modeling the noise parameters are better than those obtained for the red and blue components. The green NLF curve is closer to the real curve than the other curves, and the estimated noise parameters are better than those of the red and blue channels. To examine the efficiency of the algorithm of noise estimation, different modelizations were carried out for different levels of noise on the original image. The obtained results are arranged in Table 4. The table reports true and estimated noise parameters for Lena images corrupted with three combinations of values of the parameters which are: \({\sigma }_{G}=15,{ \sigma }_{\omega }=1.5, \gamma =0.5\); \({\sigma }_{G}=5,{ \sigma }_{\omega }=1.5, \gamma =0.5\) and \({\sigma }_{G}=0.5,{ \sigma }_{\omega }=0.5, \gamma =1\). The experimental results are close to the real values, in particular for the green channel. Throughout all these tests and results, it has already been shown that the noise variance varies as a function of intensity in the image.

Fig. 13
figure 13

Lena test image; from left to right: original Lena image, noised image, and noised sub-image (\({\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{G}=15\)),

Full size image
Fig. 14
figure 14

Noise level estimation on noisy Lena image \({(\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{G}=15\)), for red, green, and blue channels. From top to bottom and from left to right: red, green, and blue channels of noisy Lena image. Red, green, and blue images for week textured selection pixels and the three estimated NLFs: RMSE = Red: (10.19) Green: ( 7.43) Blue: (32.31)

Full size image
Fig. 15
figure 15

From left to right: original noise free image and noise free ROI; noisy image \({(\gamma =0.5, \sigma }_{\omega }=0.5,{\sigma }_{{\eta }_{G}}=10)\); and noisy ROI

Full size image
Table 4 Estimated parameters of noise model of noised Lena image for different values of the parameters \({(\sigma }_{G}, { \sigma }_{\omega } \mathrm{and} \gamma )\)
Full size table

Once the efficiency of the noise estimation algorithm has been verified for different images and different types of noise, let us now proceed to the denoising of these images based on the obtained noise parameters, which will serve as inputs for the proposed denoising method. Indeed, in this part of section, the proposed filter is evaluated in comparison with SRAD and DPAD methods. The SRAD and DPAD codes can be obtained from Mathworks website at (https://fr.mathworks.com/matlabcentral/fileexchange/36906-detail-preserving-anosotropic-diffusion-for-speckle-filtering-dpad) [7]. The input parameters of SDN-RAD are the original image with synthetic noise, the step time \(\Delta {\varvec{t}}\), the kernel size for computing instantaneous noise coefficient of variation is equal to\(3\times 3\), the number of iteration \(iter\) and automatic and instantaneous noise parameters:\({\sigma }_{G}, { \sigma }_{\omega }\mathrm{ and }\gamma\). Experiments are carried out to show the performance of noise reduction and the capability of structure preserving. Drawing from several references on image processing, two measurement indexes are often used to assess the effect of denoising algorithms, which are the root-mean-square error (RMSE) and the signal-to-noise ratio (SNR). RMSE stands for root-mean-square error [19, 31, 56, 78, 88, 114]. It is a commonly used metric to measure the differences between the processed image and its original image. The lower the value of RMSE, the lower the error and it designates a better filtered image. RMSE is calculated as follows:

$$\mathrm{RMSE}=\sqrt{\frac{1}{M\times N}\sum_{i=1}^{M}\sum_{j=1}^{N}{\left[{I}_{p}\left(i,j\right)-I\left(i,j\right)\right]}^{2}}$$

Here \(M\) and \(N\) are, respectively, the width and the height of the image, \({I}_{p}\) is the enhanced image, and \(I\) is the free noise/original image. \((i,j)\) are the pixel locations. SNR is a well-known quantitative measure in image processing and is widely used for evaluating the quality of denoising algorithms, image compression techniques, and image acquisition systems. It provides the ratio of the desired image information to the undesired noise that may corrupt the image quality, which allows to offer an objective evaluation for easy interpretation and comparison of denoising techniques (i.e., SNR quantifies the power of the noise present in the image). A higher SNR value indicates a better the image quality.

SNR is defined by the ratio between the variance of the noise free image and the variance of processed image where formula is expressed as follows:

$$\mathrm{SNR}=10\bullet {\mathrm{log}}_{10}\left[\frac{\sum_{i=1}^{M}\sum_{j=1}^{N}{\left[I\left(i,j\right)\right]}^{2}}{\sum_{i=1}^{M}\sum_{j=1}^{N}{\left[{I}_{p}\left(i,j\right)-I\left(i,j\right)\right]}^{2}}\right]$$

Firstly, experiments are performed on the '65019.jpg' image, which is corrupted with synthetic noise by the following parameters: \({(\gamma =0.5, \sigma }_{\omega }=0.5,{\sigma }_{{\eta }_{G}}=10\)). Zoomed region of interest (ROI) is used to show more details for small objects after denoising (see Fig. 15).

Figure 16 shows the results of zoomed restored sub-images after application of the three filters, SRAD, DPAD, and the proposed one (SDN-RAD) for red, green, and blue components. In view of these outcomes, we can observe that SDN-RAD preserves image structures much better than SRAD and DPAD filters for three channels. Also, its correspondent result of colored sub-image is very well denoised without changing the content of the original image. In addition, it has a better visual quality in comparison with the other filters. Indeed, the color of the obtained image, edges, and fine structures is better preserved. Table 1 includes setting parameters of each filter (SRAD, DPAD, and SDN-RAD) and their simulation results of SNR and RMSE.

Fig. 16
figure 16

From top to bottom and from left to right: noisy sub-image for red channel and its correspond results obtained by DPAD, SRAD, and the proposed method; results for green channel, red channel, and colored noisy sub-image; and denoised sub-image by DPAD, SRAD, and the proposed method

Full size image

The term \("\Delta {\varvec{t}}"\) is the step time, and \("\mathrm{Runtime}"\) is the period of time during which the algorithm is running. From the data presented in the table, SDN-RAD shows good results for both SNR and RMSE for the three channels, since it has reached a good performance with the greatest SNR value and the lowest RMSE score.

In order to enhance the assessment of the effectiveness of the proposed algorithm, simulation studies were performed using other image corrupted with different parameters of synthetic noise. Figures 17, 18, and 19 show obtained results of the smooth out of Lena image for red, green, and blue channels corrupted with noise characteristics: \({\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{{\eta }_{G}}=15\). To provide a clear visual demonstration of the algorithm's effectiveness, two regions of interest (ROI) are selected in noisy Lena image. By placing, side by side, the both noisy, and denoised ROI images, it can be directly compare the changes in noise level, detail preservation for each algorithm (see Figs. 17, 18, 19, and 20). Interpretation of the results obtained by our algorithm shows that noise has been considerably reduced from the original image, producing in a cleaner and more visually appealing results than SRAD and DPAD. From results in Tables 5 and 6, our algorithm is expensive in execution time (highest runtime) against SRAD and DPAD filters, this is due particularly to the noise estimation process. Indeed, noise estimation in SRAD and DPAD is a matter of a few instructions, but for our method, noise estimation requires several steps, such as calculating the statistics pair (variance and mean intensity value) for each pixel, selection of weak textured regions (by PCA and a texture strength metric), and adjusting the parameter values that make the observed data most likely according to the assumed statistical model by the ML-Estimator approach.

Fig. 17
figure 17

Denoised red Lena image (Fig. 14); noisy red channel and obtained results, respectively, of SDN-RAD, SRAD, DPAD-Median, and DPAD-Moda

Full size image
Fig. 18
figure 18

Denoised green Lena image (Fig. 14); green component of noisy Lena image (Fig. 16); noisy green channel and its correspondent results of SDN-RAD, SRAD, DPAD-Median, and DPAD-Moda

Full size image
Fig. 19
figure 19

Experiment outputs on blue component of noised Lena image (Fig. 14); noisy blue channel and its correspondent results of SDN-RAD, SRAD, DPAD-Moda, and DPAD-Median

Full size image
Fig. 20
figure 20

Experiment outputs on color noisy Lena image (Fig. 14); from top to bottom and from left to right: color free image, noisy image, and its correspondent results with: SRAD, proposed method, DPAD-Moda, and DPAD-Median

Full size image
Table 5 Simulation results of the three filters of '65019.jpg' image for synthetic noise with \({(\gamma =0.5, \sigma }_{\omega }=0.5,{\sigma }_{{\eta }_{G}}=10)\)
Full size table
Table 6 Simulation results of the three filters of Lena image for synthetic noise with \({(\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{G}=15)\)
Full size table

Now, the image with textured regions in Fig. 11 is used to showcase the effectiveness of present algorithm in preserving fine textures while reducing noise during denoising process. Experimental results were applied and displayed in Fig. 21. The simulation results are shown in Table 7. From the performance of each denoising algorithm, our improved algorithm has clear advantages over other filters for mixed noise suppression and a visual effect, as well as the SNR and RMSE characteristics have reached a good level. However, both the DPAD-Median, DPAD-Moda algorithms, and the SRAD algorithm can only filter clear regions in the image with specific noise and cannot better deal other regions, especially the slightly dark areas, containing complex noise. In contrast with SDN-RAD, that can suppress complex noise from any area of the image.

Fig. 21
figure 21

Experiment outputs of Fig. 11 (test image '27059.jpg' from BSD300 dataset); noisy image and its correspondent results of proposed method, SRAD, DPAD-Median, and DPAD-Moda

Full size image
Table 7 Simulation results on three channels of Fig. 21 for characteristics synthetic noise \({(\gamma =0.5, \sigma }_{\omega }=1.5,{\sigma }_{G}=15)\)
Full size table

5 Conclusions

Despite extensive research on removing synthetic noises such as AWGN and speckle noise, few have focused on real image denoising. However, real noise is a combining of several kind of noises such as additive and multiplicative noises. The biggest challenge is the complexity of real noise because experimental usual noise is much simpler than real one. It is pixel-independent, also simplified as single component and not related to color components. On the other hand, real noise is pixel-dependent and mostly spatially correlated and channel-variant. Therefore, the noise analysis and accurate modeling of noise guarantee an accurate estimation of the noise and then the development of an effective denoising scheme. In this paper, an improved version of the SRAD filter is developed to optimize the performance of removing a real noise in CCD images. The characteristics of the SRAD filter makes it perfectly suitable for noise removing in the case of images with smooth areas, but when the image is textured, the edge and texture information in the enhanced image cannot be well preserved. In addition, it is adopted for ultrasonic and radar imaging affected by noise with some assumptions, such as a purely signal-independent, multiplicative, and white. However, these assumptions simplify the effect of the filter, as they generally lead to unsatisfactory denoising results, especially for images with the general type of noise and intricate details. To overcome these limitations, the present paper has suggested a new denoising system, designed for more general signal-dependent noise. It is based heavily on the accurate estimation of noises parameters. This is a typical SRAD filter approach, but with the insertion of an iterative select patch-based framework to accurately estimate the parameters of the SDN. Extensive experiments demonstrate a significant increase in the image denoising performance in terms of SNR and RMSE. The proposed new filter has shown great potential for denoising images without blurring them, preserving texture details, edges, and small details. However, the main problem with performance here is the fact that the method is slow and requires the time-consuming computation of noise parameters. In summary, this study is about using a variant of the anisotropic diffusion technique with estimating general noise models for image denoising purposes. The noise model estimation not only has a good denoising effect but also can retain fine details of the noisy image.

For future work, the proposed method can be improved and expanded to other applications in the fields of feature recognition, segmentation, and others. Furthermore, the proposed technique involves numerous operations such as estimation steps of noise parameters, image gradients, and partial differential equations during the removal of noise from the image. Therefore, the next work will be to determine whether the algorithm can be further improved to reduce the time spent.