1 Introduction

Fractional-order derivatives (FODs) have become a hot topic during the past decades because they are widely used in the control of dynamical processes [9, 13], and lots of real-world physical systems can be well described by FODs. There are three commonly used definitions of FODs named Riemann–Liouville derivative, Grünward–Letnikov derivative, and Caputo derivative. During the past 2 decades, various types of the stability and stabilization of linear time-invariant fractional-order systems (LTI-FOSs) have been widely investigated and many results are obtainable; for example, see [8, 16, 19, 20, 22, 25]. The robust stability and stabilization of fractional-order interval systems with the order \(\alpha \in (0,1)\) was investigated in [19]. The Mikhailov stability criterion and finite-time Lyapunov stability criterion for fractional-order linear time-delay systems were derived in [8] and [22], respectively. The robust stability and stabilization with the case \(\alpha \in (0,1)\) of fractional-order interval systems combined with coupling relationships were considered in [16]. Additionally, the control problems of fractional-order descriptor systems are widely studied by many scholars. The robust stabilization of uncertain descriptor fractional-order systems were solved by designing fractional-order controllers [25]. Both state and output feedback controllers were presented to stabilize the fractional-order singular uncertain systems with the order \(\alpha \in (0,2)\) [20]. Moreover, the stabilization criterion of the fractional-order triangular system was derived and the obtained stabilization results were utilized to consider the control problems of fractional-order chaotic systems in three cases [26]. The linear feedback controllers were proposed to address the synchronization and anti-synchronization of a class of fractional-order chaotic systems based on the triangular structure [27]. The passivity was considered for fractional-order neural network which is affected by time-varying delay [31]. The sliding controller was designed for the synchronization of fractional-order chaotic systems with disturbances [28].

It is worth mentioning that since Luenberger introduced the concept of observer for dynamic systems, which has become one of the fundamental system concepts in the modern control theory. The observer is a dynamic system which utilizes the available information of inputs and outputs to reconstruct the unmeasured states of the original system. Observer design for linear systems is a popular problem in control theory that has been studied in many aspects. This is due to the fact that a state estimation is generally required for the control when all states of the system are not available. The observer, observer-based controller and observer-based compensator were designed for the integer-order systems with applications can be found in [17, 18, 32]. More recently, many types of full-order and reduced-order observers for LTI-FOSs are obtainable. The observers were designed for LTI-FOSs with unknown inputs [24]. By decomposing the parameter matrixes, an observer was derived for the LTI-FOSs with \(0<\alpha \le 1\) without considering the unknown input [2]. On the basis of the solutions to generalized inverted matixes, the observer was presented for singular LTI-FOSs [23]. To satisfy the fault sensitivity, disturbance robustness and admissibility of singular LTI-FOSs, an H_/\(H_\infty \) fault detection observer was considered [6]. In addition, a nonasymptotic pseudo-state estimator was proposed for a class of LTI-FOSs which can be transformed into the Brunovsky’s observable canonical form of pseudo-state space representation with unknown initial conditions and \(H_\infty \)-like observer [33]. The dynamic compensator was designed based on disturbance estimator for fractional-order time-delay fuzzy systems with nonlinearities and unknown external disturbances in [12]. The robust fractional-order observer was designed for a class of disturbed LTI-FOSs in the form of time domains and frequency domains, respectively [3]. Notice that the above observers are under the definition of Caputo derivative, [34] designed observers for LTI-FOSs under the definitions of Riemann–Liouville derivative and Grünwald–Letnikov derivative. On the other hand, observer-based controllers (OBCs) have been applied to the control of LTI-FOSs effectively. The robust \(H_\infty \) OBCs were derived by use of the generalized Kalman–Yakubovich–Popov lemma [4], and the novel sufficient criterion was given by means of linear matrix inequalities (LMIs) to guarantee the stabilization of disturbed uncertain LTI-FOSs [10]. Several LMIs were presented to obtain the stabilization for uncertain LTI-FOSs on the ground of robust OBCs [11, 14]. The observer-based event-triggered output feedback controller was given to investigate fractional-order cyber-physical systems with \(0<\alpha <1\), in which the system was affected by stochastic network attacks [35]. The OBCs was derived for the stabilization of LTI-FOSs with the input delay [7].

Additionally, state estimation of LTI-FOSs in the presence of unknown inputs has been another fascinating and relevant topic in the modern control theory. Two different observers, \(H_\infty \) filter for the estimation of the states, and fractional-order sliding model uncertain input observer for the simultaneous estimation of both states and unknown inputs, have been addressed for LTI-FOSs with the consideration of proper initial memory effect [15]. A high-order sliding mode observer was proposed for the simultaneous estimation of the pseudo-state and the unknown input of LTI-FOSs with the single unknown input and the single output systems in both noisy and noise-free cases, respectively [1]. Nevertheless, the problem on the reconstruction of unknown inputs is still open. The reason for the reconstruction of unknown inputs is that, in some applications, it is either a costly task or not basically doable to measure some of the inputs. There are many situations where an input observer is required to estimate the cutting force of a machine tool or the exerting force/torque of a robotic system. In chaotic systems, one wishes to estimate not only the state for chaos synchronization but also the information signal input for the secure communication. Compared with the state estimation, less research has been carried out on estimating simultaneously the state of a dynamic system and its inputs. Notice that not only the state estimation but also the unknown inputs are of significance because the state estimation is generally required for the control when all states of the system are not available and the unknown input can represent the impact of the failure of actuators or plant components, and thus worth to be estimated and used in the field of fault detection and isolation. Consequently, a new fractional-order observer is presented to estimate both states and unknown inputs simultaneously. To the author’s best knowledge, this kind of observer for LTI-FOSs is quiet new and not fully investigated. Motivated by the above discussions, we investigate the interesting problem that both states and unknown inputs are simultaneously estimated for LTI-FOSs by reconstructing the original systems. In comparison with the aforementioned papers, the main contributions of this work are generalized as follows.

  1. 1.

    Necessary and sufficient conditions are presented to guarantee the stabilization of LTI-FOSs with the case \(\alpha \in (0,1)\). Note that the stability criterion obtained can be applied to [23] but it is incorrect when it comes to the result in [19].

  2. 2.

    A novel fractional-order dynamic observer consists of state vectors, ancillary vectors and the estimations is presented which shows that the observers designed in [2,3,4, 10, 11, 23, 24, 33, 34] are the special form of the observer obtained in this paper.

  3. 3.

    Not only the states but also the unknown inputs are simultaneously estimated compared with [2, 3, 23, 24, 33]. The reconstruction of the initial LTI-FOSs makes the estimation more efficient than the results derived in [14, 15].

The rest of this paper is arranged as follows. The definition of Caputo derivative and the stability criteria for LTI-FOSs are proposed in Sect. 2. To estimate the states and unknown inputs simultaneously, a fractional-order dynamic observer is proposed, and the parameter matrices of the observer are solved by the solutions to the generalized inverse matrix in Sect. 3. In Sect. 4, an illustrated example is given to verify the correctness and efficiency of the obtained results. Section 5 draws the conclusion of the paper.

Notation: \(A^T\): the transpose of a matrix A; \(R^n\): the real n-dimensional Euclidean space; \(R^{n\times m}\) (\({\mathbb {C}}^{n\times m}\)): the set of all \(n\times m\) matrices defined in the real (complex) plane; \(A^*\): the conjugate transpose of Hermitian matrix A; \(\otimes \): the Kronecker product; \({\mathcal {Y}}^+\): the generalized inverse of matrix \({\mathcal {Y}}\); Re(A) (Im(A)): the real (imaginary) part of Hermitian matrix A; sym(A): \(A^T+A\).

2 Preliminaries and Problem Formulation

There are three mainly used definitions of fractional-order derivative: Riemann–Liouville derivative, Grünward–Letnikov derivative and Caputo derivative. In this paper, only Caputo derivative is used since this Laplace transform allows using initial values of classical integer-order derivatives with clear physical interpretations. Caputo derivative with \(\alpha \)-order is defined as

$$\begin{aligned} D_t^\alpha f(t)=\frac{D^\alpha f(t)}{\textrm{d}t^\alpha } = {\left\{ \begin{array}{ll} \frac{1}{\Gamma (\alpha -n)}\int _a^t\frac{f^{(n)}(\tau )}{{(t-\tau )}^{\alpha +1-n}}\textrm{d}\tau , &{} \quad n-1<\alpha <n \\ \frac{\textrm{d}^n{f(t)}}{\textrm{d}t^n}, &{} \quad \alpha =n \end{array}\right. } \end{aligned}$$

where \(n=[\alpha ]\), and the notation \(\Gamma (\cdot )\) denotes the Gamma function which is presented as

$$\begin{aligned} \Gamma (z)=\int _{0}^{\infty }{e^{-t}t^{z-1}\textrm{d}t}. \end{aligned}$$

In the sequel, the following system is considered

$$\begin{aligned} D_t^\alpha x(t)=A x(t), \end{aligned}$$
(1)

where \(\alpha \in (0,2)\), \(x(t)\in R^n\) denotes the state, and \(A\in R^{n\times n}\).

To proceed, we begin with the following Lemmas.

Lemma 1

System (1) is stable with the order \(\alpha \in (0,2)\) iff [21]

$$\begin{aligned} \mid arg(spec(A))\mid >\alpha \frac{\pi }{2}. \end{aligned}$$

Lemma 2

When \(\alpha \in (0,1)\), (1) is stable iff [30]

$$\begin{aligned} e^{i\theta }Q_1A+e^{-i\theta }A^{*}Q_1+e^{-i\theta }Q_2A+e^{i\theta }A^{*}Q_2<0, \end{aligned}$$
(2)

where \(\theta =(1-\alpha )\frac{\pi }{2}\), matrixes \(Q_1, Q_2\) are Hermitian matrixes such that \(Q_1=Q_1^*\in {\mathbb {C}}^{n \times n}\), \(Q_2=Q_2^*\in {\mathbb {C}}^{n \times n}\), and \(Q_1>0, Q_2>0\).

Lemma 3

If (1) with the order \(\alpha \in (0,1)\) satisfies the following conditions

$$\begin{aligned}{} & {} \sum \limits _{m=1}^{2}\sum \limits _{n=1}^{2}sym\left\{ \sigma _{mn}\otimes P_{mn}A\right\} <0, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \quad \left[ \begin{array}{ll} P_{11} &{} \quad P_{12}\\ {-}P_{12} &{} \quad P_{11} \end{array}\right]>0, \left[ \begin{array}{ll} P_{12} &{} \quad P_{22}\\ {-}P_{22} &{} \quad P_{12} \end{array}\right] >0, \end{aligned}$$
(4)

where

$$\begin{aligned}&\sigma _{11}= \left[ \begin{matrix} \sin \left( \alpha \frac{\pi }{2}\right) &{}\quad \cos \left( \alpha \frac{\pi }{2}\right) \\ -\cos \left( \alpha \frac{\pi }{2}\right) &{}\quad \sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] ,\ \sigma _{12}= \left[ \begin{matrix} -\cos \left( \alpha \frac{\pi }{2}\right) &{}\quad \sin \left( \alpha \frac{\pi }{2}\right) \\ {-}\sin \left( \alpha \frac{\pi }{2}\right) &{}\quad {-}\cos \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] ,\\&\sigma _{21}= \left[ \begin{matrix} \sin \left( \alpha \frac{\pi }{2}\right) &{}\quad -\cos \left( \alpha \frac{\pi }{2}\right) \\ \cos \left( \alpha \frac{\pi }{2}\right) &{}\quad \sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] ,\ \sigma _{22}= \left[ \begin{matrix} \cos \left( \alpha \frac{\pi }{2}\right) &{}\quad \sin \left( \alpha \frac{\pi }{2}\right) \\ {-}\sin \left( \alpha \frac{\pi }{2}\right) &{}\quad \cos \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] , \end{aligned}$$

then it is stable, where \(P_{\kappa 1}\in R^{n \times n}\), \(\kappa =1,2\) are positive symmetric matrices, and \(P_{\kappa 2} \in R^{n \times n}\) are skew-symmetric matrices.

Proof

To begin with, we define \(P_{\kappa 1}=Re(Q_{\kappa })\), \(P_{\kappa 2}=Im(Q_{\kappa })\), \(\kappa =1,2\). It follows form Lemma 2 that \(P_{\kappa 1}-iP_{\kappa 2}^T=P_{\kappa 1}+iP_{\kappa 2}\). Moreover, the asymptotic stability of (1) can be guaranteed iff there exist two skew-symmetric matrices \(P_{\kappa 2} \in R^{n \times n}\) and two positive symmetric matrices \(P_{\kappa 1}\in R^{n \times n}\) such that

$$\begin{aligned} Q_1=P_{11}+iP_{12}>0, \quad Q_2=P_{21}+iP_{22}>0. \end{aligned}$$
(5)

Substituting (5) in (3) and combining with the Euler formulae yields that

$$\begin{aligned}&(\cos \theta +i \sin \theta )(P_{11}+iP_{12})A+(\cos \theta -i\sin \theta )A^T(P_{11}-iP_{12}^T)\nonumber \\&\qquad +(\cos \theta -i\sin \theta )(P_{21}+iP_{22})A+(\cos \theta +i \sin \theta )A^T(P_{21}-iP_{22}^T)\nonumber \\&\quad =(\cos \theta +i\sin \theta )(P_{11}+iP_{12})A+(\cos \theta -i\sin \theta )A^T(P_{11}-iP_{12}^T)\nonumber \\&\qquad +(\cos \theta -i\sin \theta )(P_{21}+iP_{22})A+(\cos \theta +i\sin \theta )A^T (P_{21}-iP_{22}^T)\nonumber \\&\quad =P_{11}A \cos \theta +i P_{12}A \cos \theta +i P_{11}A \sin \theta - P_{12}A \sin \theta \nonumber \\&\qquad +A^TP_{11}\cos \theta -i A^TP_{12}^T \cos \theta -i A^TP_{11}\sin \theta -A^TP_{12}^T \sin \theta \nonumber \\&\qquad + P_{21}A \cos \theta +i P_{22}A \cos \theta -i P_{21}A \sin \theta +P_{22}A \sin \theta \nonumber \\&\qquad +A^TP_{21}\cos \theta -i A^TP_{22}\cos \theta +iA^TP_{21}\sin \theta +A^TP_{22}^T\sin \theta \nonumber \\&\quad =P_{11}A \cos \theta +iP_{11}A \sin \theta +A^TP_{11}\cos \theta -iA^TP_{11}\sin \theta \nonumber \\&\qquad -P_{12}A \sin \theta +iP_{12}A \cos \theta -A^TP_{12}^T\sin \theta -iA^TP_{12}^T\cos \theta \nonumber \\&\qquad +P_{21}A \cos \theta -i{\mathcal {P}}_{21}A \sin \theta +A^TP_{21}\cos \theta +iA^TP_{21}\sin \theta \nonumber \\&\qquad +A^TP_{22}^T-iA^TP_{22}^T\cos \theta +P_{22}A \sin \theta +iP_{22}A \cos \theta \nonumber \\&\quad =P_{11}A \sin \left( \alpha \frac{\pi }{2}\right) +iP_{11}A \cos \left( \alpha \frac{\pi }{2}\right) +A^TP_{11}\sin \left( \alpha \frac{\pi }{2}\right) -iA^TP_{11} \cos \left( \alpha \frac{\pi }{2}\right) \nonumber \\&\qquad -P_{12}A \cos \left( \upsilon \frac{\pi }{2}\right) +iP_{12}A \sin \left( \alpha \frac{\pi }{2}\right) -\alpha ^TP_{12}^T\cos (\alpha \frac{\pi }{2}) +i\alpha ^TP_{12}\sin \left( \alpha \frac{\pi }{2}\right) \nonumber \\&\qquad +P_{21}A \sin \left( \alpha \frac{\pi }{2}\right) -iP_{21}A \cos \left( \alpha \frac{\pi }{2}\right) +A^TP_{21}\sin \left( \alpha \frac{\pi }{2}\right) +iA^TP_{21} \cos \left( \alpha \frac{\pi }{2}\right) \nonumber \\&\qquad +P_{22}A \cos \left( \alpha \frac{\pi }{2}\right) +iP_{22}A \sin \left( \alpha \frac{\pi }{2}\right) -A^TP_{22}\sin \left( \alpha \frac{\pi }{2}\right) +iA^TP_{22}\cos \left( \alpha \frac{\pi }{2}\right) \nonumber \\&\quad <0. \end{aligned}$$
(6)

Considering that a Hermitian matrix Q is positive iff \(\left[ \begin{matrix} Re(Q)&\quad Im(Q) \Im (Q)&\quad Re(Q) \end{matrix}\right] >0\), thus the above inequality is equivalent to

$$\begin{aligned}&\left[ \begin{matrix} \sin \left( \alpha \frac{\pi }{2}\right) &{} \quad \cos \left( \alpha \frac{\pi }{2}\right) \\ cos\left( \alpha \frac{\pi }{2}\right) &{} \quad \sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \otimes P_{11}A+\left[ \begin{matrix} \sin \left( \alpha \frac{\pi }{2}\right) &{} \quad \cos \left( \alpha \frac{\pi }{2}\right) \\ {-}\cos \left( \alpha \frac{\pi }{2}\right) &{} \quad \sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \otimes A^TP_{11}\nonumber \\&\qquad +\left[ \begin{matrix} -\cos \left( \alpha \frac{\pi }{2}\right) &{} \quad \sin \left( \alpha \frac{\pi }{2}\right) \\ -\sin \left( \alpha \frac{\pi }{2}\right) &{} \quad -\cos \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \otimes P_{12}A+\left[ \begin{matrix} -\cos \left( \alpha \frac{\pi }{2}\right) &{} \quad -\sin \left( \alpha \frac{\pi }{2}\right) \\ \sin \left( \alpha \frac{\pi }{2}\right) &{} \quad -\cos \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \otimes A^TP_{12}^T\nonumber \\&\qquad +\left[ \begin{matrix} \sin \left( \alpha \frac{\pi }{2}\right) &{} \quad -\cos \left( \alpha \frac{\pi }{2}\right) \\ \cos \left( \alpha \frac{\pi }{2}\right) &{} \quad \sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \otimes P_{21}A+\left[ \begin{matrix} \sin \left( \alpha \frac{\pi }{2}\right) &{} \quad \cos \left( \alpha \frac{\pi }{2}\right) \\ {-}\cos \left( \alpha \frac{\pi }{2}\right) &{} \quad \sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \otimes A^TP_{21}^T\nonumber \\&\qquad +\left[ \begin{matrix} \cos \left( \alpha \frac{\pi }{2}\right) &{} \quad \sin \left( \frac{\pi }{2}\alpha \right) \\ sin\left( \alpha \frac{\pi }{2}\right) &{} \quad \cos \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \otimes P_{22}A+\left[ \begin{matrix} \cos \left( \alpha \frac{\pi }{2}\right) &{} \quad -\sin \left( \alpha \frac{\pi }{2}\right) \\ \sin \left( \alpha \frac{\pi }{2}\right) &{} \quad \cos \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \otimes A^TP_{22}^T\nonumber \\&\quad =sym\left\{ \left[ \begin{matrix} \sin \left( \alpha \frac{\pi }{2}\right) &{} \quad \cos \left( \alpha \frac{\pi }{2}\right) \\ {-}\cos \left( \alpha \frac{\pi }{2}\right) &{} \quad \sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \otimes P_{11}A\right\} \nonumber \\&\qquad +sym\left\{ \left[ \begin{matrix} -\cos \left( A\frac{\pi }{2}\right) &{} \quad \sin \left( \alpha \frac{\pi }{2}\right) \\ sin\left( \alpha \frac{\pi }{2}\right) &{} \quad -\cos \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \otimes P_{12}A\right\} \nonumber \\&\qquad +sym\left\{ \left[ \begin{matrix} \sin \left( \alpha \frac{\pi }{2}\right) &{} \quad -\cos \left( \alpha \frac{\pi }{2}\right) \\ \cos \left( \alpha \frac{\pi }{2}\right) &{} \quad \sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \otimes P_{21}A\right\} \nonumber \\&\qquad +sym\left\{ \left[ \begin{matrix} \cos \left( \alpha \frac{\pi }{2}\right) &{} \quad \sin \left( \alpha \frac{\pi }{2}\right) \\ sin\left( \alpha \frac{\pi }{2}\right) &{} \quad \cos \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \otimes P_{22}A\right\} \nonumber \\&\quad =\sum \limits _{m=1}^{2}\sum \limits _{n=1}^{2}sym\left\{ \sigma _{mn}\otimes P_{ij}A\right\} \nonumber \\&\quad <0, \end{aligned}$$
(7)

which completes the proof. \(\square \)

Lemma 4

(1) is stable with the order \(\alpha \in [1,2)\) iff

$$\begin{aligned} \left[ \begin{matrix} (A^TP+PA)\sin \left( \alpha \frac{\pi }{2}\right) &{} \quad (A^TP-PA)\cos \left( \alpha \frac{\pi }{2}\right) \\ (PA-A^TP)\cos \left( \alpha \frac{\pi }{2}\right) &{} \quad (A^TP+PA)\sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] <0, \end{aligned}$$
(8)

where \(P=P^T>0\) [5].

Consider the following fractional-order system

$$\begin{aligned} \begin{aligned} D_t^\alpha x(t)&={\mathcal {A}}x(t)+{\mathcal {B}}u(t)+{\mathcal {F}}d(t),\\ y(t)&={\mathcal {C}}x(t)+{\mathcal {D}}d(t), \end{aligned} \end{aligned}$$
(9)

where \(\alpha \in (0,2)\), \(x(t)\in R^n\) is the state vector, \(y(t)\in R^p\) is the output vector, \(u(t)\in R^m\) is the control input, \(d(t)\in R^r\) is the unknown input vector, and \(\mathcal {A}\in R^{n\times n}, {\mathcal {B}}\in R^{n\times m}, {\mathcal {F}}\in R^{n\times r}, {\mathcal {C}}\in R^{p\times n}, {\mathcal {D}}\in R^{p\times r}\) are the known matrixes with appropriate dimensions.

Lemma 5

Consider the following matrix equation

$$\begin{aligned} {\mathcal {X}}{\mathcal {Y}}={\mathcal {Z}}. \end{aligned}$$

The above equation has a solution iff [29]

$$\begin{aligned} rank\left[ \begin{matrix} {\mathcal {Y}}\\ {\mathcal {Z}} \end{matrix} \right] =rank \ {\mathcal {Y}}, \end{aligned}$$

and the general solution can be expressed as

$$\begin{aligned} {\mathcal {X}}={\mathcal {Z}}{\mathcal {Y}}^++{\mathcal {U}}[I_n-\mathcal {Y}({\mathcal {Y}})^+], \end{aligned}$$

where \({\mathcal {U}}\) can be selected arbitrarily and \(I_n\) is an \(n\times n\) identity matrix. In addition, some solution of the matrix equation can be expressed as

$$\begin{aligned} {\mathcal {X}}={\mathcal {Z}}{\mathcal {Y}}^+, \end{aligned}$$

where \({\mathcal {Y}}^+=({\mathcal {Y}}^T{\mathcal {Y}})^{-1}\mathcal {Y}^T\).

3 Main Results

To cope with the simultaneous estimations of the states and unknown inputs, system (9) can be rewritten as

$$\begin{aligned} \begin{aligned} {\mathcal {E}} D_t^\alpha \xi (t)&={\mathbb {A}}\xi (t)+{\mathcal {B}}u(t),\\ y(t)&={\mathbb {C}}\xi (t), \end{aligned} \end{aligned}$$
(10)

where \(\xi (t)=\left[ \begin{matrix} x(t)\\ d(t) \end{matrix}\right] \), \({\mathbb {A}}=[{\mathcal {A}} \quad {\mathcal {F}}]\), \({\mathbb {C}}=[{\mathcal {C}} \quad {\mathcal {D}}]\), \(\mathcal {E}=[I_{n\times n} \quad 0_{n\times r}]\).

To make the estimation meaningful, we first give the following assumption.

Assumption 1

rank \(\left[ \begin{matrix} {\mathcal {E}}\\ {\mathbb {C}} \end{matrix}\right] =n+r.\)

3.1 Observer Design for LTI-FOSs with Unknown Inputs

Consider the following fractional-order observer

$$\begin{aligned} D_t^\alpha z(t)&={\mathbb {N}}z(t)+{\mathbb {J}}y(t)+{\mathbb {H}}u(t)+{\mathbb {M}}\psi (t),\nonumber \\ D_t^\alpha \psi (t)&={\mathbb {P}}z(t)+{\mathbb {Q}}y(t)+{\mathbb {G}}\psi (t),\nonumber \\ {\hat{\xi }}(t)&={\mathbb {R}}z(t)+{\mathbb {S}}y(t), \end{aligned}$$
(11)

where \(z(t)\in R^n\) is the state vector, \(\psi (t)\in R^n\) is the ancillary vector, and \({\hat{\xi }}(t)\in R^{n+r}\) is the estimation of x(t) and d(t). \({\mathbb {N}}\), \({\mathbb {J}}\), \({\mathbb {H}}\), \({\mathbb {M}}\), \({\mathbb {P}}\), \({\mathbb {Q}}\), \({\mathbb {G}}\), \({\mathbb {R}}\) and \({\mathbb {S}}\) are unknown matrices with appropriate dimensions requiring to be figured out in the following.

Remark 1

Without considering the unknown input and the ancillary vector, i.e., \(d(t)=0\), \(\psi (t)=0\), system (10) and observer (11) can degrade into the usual form. Specifically, (11) can generalize several existing observers in the following two forms.

  1. 1.

    When \({\mathbb {R}}=I\), \({\mathbb {P}}=0\), \({\mathbb {Q}}=0\), \({\mathbb {G}}=0\) and \({\mathbb {M}}=0\), (11) gives that

    $$\begin{aligned} D_t^{\alpha }z(t)&={\mathbb {N}}z(t)+{\mathbb {H}}u(t)+{\mathbb {J}}y(t),\\ {\hat{x}}(t)&=z(t)+{\mathbb {S}}y(t),\nonumber \end{aligned}$$

    this kind of observer can be found in [14, 24].

  2. 2.

    When \({\mathbb {R}}=I\), \({\mathbb {S}}=0\), \({\mathbb {P}}=0\), \({\mathbb {Q}}=0\), \({\mathbb {G}}=0\), \({\mathbb {M}}=0\) and \(\mathcal {A}-{\mathbb {J}}{\mathcal {C}}={\mathbb {N}}\), we present the following observer

    $$\begin{aligned} D_t^{\alpha }{\hat{x}}(t)&={{\mathcal {A}}{\hat{x}}(t)}+\mathcal {B}u(t)+{\mathbb {J}}(y(t)-{\mathcal {C}}{\hat{x}}(t)),\\ {\hat{y}}(t)&={\mathcal {C}}{\hat{x}}(t), \end{aligned}$$

    this kind of observer can be found in [3, 10, 11, 14, 24].

Lemma 6

Observer (11) is effective for system (10) if there exists a matrix \({\mathbb {T}}\) such that

$$\begin{aligned}&{\mathbb {N}}{\mathbb {T}}{\mathcal {E}}+{\mathbb {J}}{\mathbb {C}}-{\mathbb {T}}{\mathbb {A}}=0, \end{aligned}$$
(12a)
$$\begin{aligned}&{\mathbb {H}}-{\mathbb {T}}{\mathcal {B}}=0, \end{aligned}$$
(12b)
$$\begin{aligned}&{\mathbb {P}}{\mathbb {T}}{\mathcal {E}}+{\mathbb {Q}}{\mathbb {C}}=0, \end{aligned}$$
(12c)
$$\begin{aligned}&{\mathbb {R}}{\mathbb {T}}{\mathcal {E}}+{\mathbb {S}}{\mathbb {C}}=I, \end{aligned}$$
(12d)

and the matrix

$$\begin{aligned} \Xi =\left[ \begin{array}{ccc} {\mathbb {N}} &{} \quad {\mathbb {M}} \\ {\mathbb {P}} &{} \quad {\mathbb {G}} \\ \end{array} \right] \nonumber \end{aligned}$$

satisfies

$$\begin{aligned} \mid arg(spec(\Xi ))\mid >\alpha \frac{\pi }{2}. \end{aligned}$$

Proof

We define the following error

$$\begin{aligned} \zeta (t)=z(t)-{\mathbb {T}} {\mathcal {E}}\xi (t), \end{aligned}$$

where the matrix \({\mathbb {T}}\in R^{n\times n}\) is arbitrary with an appropriate dimension. Thus

$$\begin{aligned} D_t^\alpha \zeta (t)&=D_t^\alpha z(t)-{\mathbb {T}}{\mathcal {E}} D_t^\alpha \xi (t)\\&={\mathbb {N}}z(t)+{\mathbb {J}}y(t)+{\mathbb {H}}u(t) +{\mathbb {M}}\psi (t)-{\mathbb {T}}{\mathbb {A}}\xi (t)-{\mathbb {T}}{\mathcal {B}}u(t)\\&={\mathbb {N}}\zeta (t)+{\mathbb {N}}{\mathbb {T}}{\mathcal {E}}\xi (t) +{\mathbb {J}}{\mathbb {C}}\xi (t) +{\mathbb {H}}u(t)-{\mathbb {T}}{\mathbb {A}}\xi (t)-{\mathbb {T}}{\mathcal {B}}u(t)+{\mathbb {M}}\psi (t)\\&={\mathbb {N}}\zeta (t)+({\mathbb {N}}{\mathbb {T}}\mathcal {E}+{\mathbb {J}}{\mathbb {C}}-{\mathbb {T}}{\mathbb {A}})\xi (t)+({\mathbb {H}}-{\mathbb {T}}\mathcal {B})u(t)+{\mathbb {M}}\psi (t) \end{aligned}$$

and

$$\begin{aligned} D_t^\alpha \psi (t)&={\mathbb {P}} \zeta (t) +{\mathbb {P}}{\mathbb {T}}{\mathcal {E}}\xi (t)+{\mathbb {Q}}{\mathbb {C}}\xi (t)+{\mathbb {G}}\psi (t)\\&={\mathbb {P}}\zeta (t)+({\mathbb {P}}{\mathbb {T}}\mathcal {E}+{\mathbb {Q}}{\mathbb {C}})\xi (t)+{\mathbb {G}}\psi (t),\\ {\hat{\xi }}(t)&={\mathbb {R}}z(t)+{\mathbb {S}}{\mathbb {C}}\xi (t)\\&={\mathbb {R}}\zeta (t)+({\mathbb {R}}{\mathbb {T}}\mathcal {E}+{\mathbb {S}}{\mathbb {C}})\xi (t). \end{aligned}$$

If there exists a matrix \({\mathbb {T}}\) such that

$$\begin{aligned}&{\mathbb {N}}{\mathbb {T}}\mathcal {E}+{\mathbb {J}}{\mathbb {C}}-{\mathbb {T}}{\mathbb {A}}=0,\\&{\mathbb {H}}-{\mathbb {T}}{\mathcal {B}}=0,\\&{\mathbb {P}}{\mathbb {T}}{\mathcal {E}}+{\mathbb {Q}}{\mathbb {C}}=0,\\&{\mathbb {R}}{\mathbb {T}}{\mathcal {E}}+{\mathbb {S}}{\mathbb {C}}=I, \end{aligned}$$

then it holds that

$$\begin{aligned} \left[ \begin{array}{ccc} D_t^\alpha \zeta (t) \\ D_t^\alpha \psi (t) \\ \end{array} \right] =\left[ \begin{array}{ccc} {\mathbb {N}} &{} \quad {\mathbb {M}} \\ {\mathbb {P}} &{} \quad {\mathbb {G}} \\ \end{array} \right] \left[ \begin{array}{ccc} \zeta (t) \\ \psi (t) \\ \end{array} \right] = \Xi \left[ \begin{array}{ccc} \zeta (t) \\ \psi (t) \\ \end{array} \right] . \end{aligned}$$
(13)

Moreover, let

$$\begin{aligned} e(t)={\mathbb {R}}\zeta (t), \end{aligned}$$
(14)

which yields that if \(\zeta (t)\rightarrow 0\), then \(e(t)\rightarrow 0\). In addition, the errors \(\zeta (t)\rightarrow 0\) and \(\psi (t)\rightarrow 0\) iff the matrix \(\Xi \) satisfies Lemma 1, which completes the proof. \(\square \)

3.2 Parameterization of the Observer

Actually, the design of observer (11) is to work out the matrices \({\mathbb {N}}\), \({\mathbb {J}}\), \({\mathbb {H}}\), \({\mathbb {M}}\), \({\mathbb {P}}\), \({\mathbb {Q}}\), \({\mathbb {G}}\), \({\mathbb {R}}\) and \({\mathbb {S}}\) appropriately. In the following, we will solve those matrices step by step.

Firstly, it follows from (12c) and (12d) that

$$\begin{aligned} \left[ \begin{array}{ccc} {\mathbb {P}} &{} \quad {\mathbb {Q}} \\ {\mathbb {R}} &{} \quad {\mathbb {S}} \\ \end{array} \right] \left[ \begin{array}{ccc} {\mathbb {T}}{\mathcal {E}} \\ {\mathbb {C}} \\ \end{array} \right] = \left[ \begin{array}{ccc} 0_{n\times (n+r)} \\ I_{(n+r)\times (n+r)} \\ \end{array} \right] , \end{aligned}$$
(15)

In light of Lemma 5, (15) has a solution iff

$$\begin{aligned} rank \left[ \begin{matrix} {\mathbb {T}}{\mathcal {E}}\\ {\mathbb {C}} \end{matrix}\right] =rank \left[ \begin{matrix} {\mathbb {T}}\mathcal {E}\\ {\mathbb {C}}\\ 0\\ I \end{matrix}\right] =n+r. \end{aligned}$$

Let \({\mathbb {E}}\in R^{{n\times (n+r)}}\) be an arbitrary matrix with full row rank such that

$$\begin{aligned} rank\left[ \begin{matrix} {\mathbb {T}}{\mathcal {E}}\\ {\mathbb {C}} \end{matrix}\right] =rank \left[ \begin{matrix} {\mathbb {E}}\\ {\mathbb {C}} \end{matrix}\right] =n+r, \end{aligned}$$
(16)

that is, \(\left[ \begin{matrix} {\mathbb {E}}\\ {\mathbb {C}} \end{matrix}\right] \) is equivalent to \(\left[ \begin{matrix} {\mathbb {T}}{\mathcal {E}}\\ {\mathbb {C}} \end{matrix}\right] \). Hence, there exists a matrix \({\mathbb {K}}\) such that

$$\begin{aligned} \left[ \begin{array}{ccc} {\mathbb {T}}{\mathcal {E}} \\ {\mathbb {C}} \\ \end{array} \right] =\left[ \begin{array}{ccc} I &{} \quad -{\mathbb {K}} \\ 0 &{} \quad I \\ \end{array} \right] \left[ \begin{array}{ccc} {\mathbb {E}} \\ {\mathbb {C}} \\ \end{array} \right] , \end{aligned}$$

which yields that

$$\begin{aligned} {\mathbb {T}}{\mathcal {E}}={\mathbb {E}}-{\mathbb {K}}{\mathbb {C}}, \end{aligned}$$

i.e.,

$$\begin{aligned} \left[ \begin{array}{ccc} {\mathbb {T}} \quad {\mathbb {K}} \end{array} \right] \left[ \begin{array}{ccc} {\mathcal {E}} \\ {\mathbb {C}} \\ \end{array} \right] = {\mathbb {E}}. \end{aligned}$$
(17)

By Lemma 5, (17) has a solution iff

$$\begin{aligned} rank\left[ \begin{matrix} {\mathcal {E}}\\ {\mathbb {C}} \end{matrix}\right] =rank \left[ \begin{matrix} {\mathbb {E}}\\ {\mathcal {E}}\\ {\mathbb {C}} \end{matrix}\right] =n+r,\nonumber \end{aligned}$$

and the solutions to (17) can be expressed as

$$\begin{aligned} {\mathbb {T}}= & {} {\mathbb {E}}\left[ \begin{array}{ccc} {\mathcal {E}} \\ {\mathbb {C}}\\ \end{array} \right] ^+ \left[ \begin{array}{ccc} I_{n \times n} \\ 0 \\ \end{array} \right] , \end{aligned}$$
(18)
$$\begin{aligned} {\mathbb {K}}= & {} {\mathbb {E}}\left[ \begin{array}{ccc} {\mathcal {E}} \\ {\mathbb {C}}\\ \end{array} \right] ^+ \left[ \begin{array}{ccc} 0 \\ I_{p \times p} \\ \end{array} \right] . \end{aligned}$$
(19)

Secondly, since \(\left[ \begin{matrix} {\mathbb {E}}\\ {\mathbb {C}} \end{matrix}\right] \) is of full column rank, (15) can be rewritten as

$$\begin{aligned} \left[ \begin{array}{ccc} {\mathbb {P}} &{} \quad {\mathbb {Q}} \\ {\mathbb {R}} &{} \quad {\mathbb {S}} \\ \end{array} \right] \left[ \begin{array}{ccc} I &{} \quad -{\mathbb {K}} \\ 0 &{} \quad I \\ \end{array} \right] \left[ \begin{array}{ccc} {\mathbb {E}} \\ {\mathbb {C}} \\ \end{array} \right] =\left[ \begin{array}{ccc} 0 \\ I \\ \end{array} \right] , \end{aligned}$$
(20)

which admits a solution iff

$$\begin{aligned} rank\left[ \begin{matrix} {\mathbb {E}}\\ {\mathbb {C}} \end{matrix}\right] =rank \left[ \begin{matrix} {\mathbb {E}}\\ {\mathbb {C}}\\ 0\\ I \end{matrix}\right] =n+r. \end{aligned}$$
(21)

Furthermore, on the basis of Lemma 5, the general solution to (20) is given as

$$\begin{aligned} \left[ \begin{array}{ccc} {\mathbb {P}} &{} \quad {\mathbb {Q}} \\ {\mathbb {R}} &{} \quad {\mathbb {S}} \\ \end{array} \right] = \left\{ \left[ \begin{array}{ccc} 0 \\ I \\ \end{array} \right] {\Upsilon }^+ + \left[ \begin{array}{ccc} O_1 \\ O_2 \\ \end{array} \right] (I-\Upsilon {\Upsilon }^+)\right\} \left[ \begin{array}{ccc} I &{} \quad {\mathbb {K}} \\ 0 &{} \quad I \\ \end{array} \right] , \end{aligned}$$
(22)

where \(\Upsilon =\left[ \begin{array}{ccc} {\mathbb {E}} \\ {\mathbb {C}}\\ \end{array} \right] \), \(O_1\), \(O_2\) are arbitrary matrices with appropriate dimensions.

Finally, the solution to (22) can be described specifically as

$$\begin{aligned} {\mathbb {P}}&=O_1V_1, \end{aligned}$$
(23a)
$$\begin{aligned} {\mathbb {Q}}&=O_1V_2, \end{aligned}$$
(23b)
$$\begin{aligned} {\mathbb {R}}&=U_1+O_2V_1, \end{aligned}$$
(23c)
$$\begin{aligned} {\mathbb {S}}&=U_2+O_2V_2, \end{aligned}$$
(23d)

where

$$\begin{aligned} U_1&={\Upsilon }^+\left[ \begin{array}{ccc} I_{n \times n} \\ 0 \\ \end{array} \right] , \end{aligned}$$
(24a)
$$\begin{aligned} U_2&={\Upsilon }^+\left[ \begin{array}{ccc} {\mathbb {K}} \\ I_{p \times p} \\ \end{array} \right] , \end{aligned}$$
(24b)
$$\begin{aligned} V_1&=(I-\Upsilon {\Upsilon }^+)\left[ \begin{array}{ccc} I_{n \times n} \\ 0 \\ \end{array} \right] , \end{aligned}$$
(24c)
$$\begin{aligned} V_2&=(I-\Upsilon {\Upsilon }^+)\left[ \begin{array}{ccc} {\mathbb {K}} \\ I_{p \times p} \\ \end{array} \right] . \end{aligned}$$
(24d)

Remark 2

It follows from Assumption 1 and \({\mathbb {E}}\) with full row rank that (17) holds. Additionally, once \({\mathbb {E}}\) is given, \({\mathbb {T}}\) and \({\mathbb {K}}\) can be calculated directly.

Remark 3

It follows from (14) that if \(\zeta (t) \rightarrow 0\), then \(e(t)\rightarrow 0\), i.e., e(t) is independent of \({\mathbb {R}}\). If we set \(O_2=0\) then (23c) and (23d) yield that

$$\begin{aligned} {\mathbb {R}}=U_1, \end{aligned}$$
(25a)
$$\begin{aligned} {\mathbb {S}}=U_2. \end{aligned}$$
(25b)

Notice that (12a) is equal to

$$\begin{aligned} \left[ \begin{array}{ccc} {\mathbb {N}} \quad {\mathbb {J}} \end{array} \right] \left[ \begin{array}{ccc} {\mathbb {T}}{\mathcal {E}} \\ {\mathbb {C}} \\ \end{array} \right] = {\mathbb {T}}{\mathbb {A}}, \end{aligned}$$
(26)

or equivalently,

$$\begin{aligned} \left[ \begin{array}{ccc} {\mathbb {N}} \quad {\mathbb {J}} \end{array} \right] \left[ \begin{array}{ccc} I &{} \quad -{\mathbb {K}} \\ 0 &{} \quad I \\ \end{array} \right] \left[ \begin{array}{ccc} {\mathbb {E}} \\ {\mathbb {C}} \\ \end{array} \right] ={\mathbb {T}}{\mathbb {A}}. \end{aligned}$$
(27)

According to Lemma 5, the solution to (27) is presented as

$$\begin{aligned} \left[ \begin{array}{ccc} {\mathbb {N}} \quad {\mathbb {J}} \end{array} \right] = \left[ {\mathbb {T}}{\mathbb {A}}{\Upsilon }^++O_3(I-\Upsilon {\Upsilon }^+)\right] \left[ \begin{array}{ccc} I &{} \quad {\mathbb {K}} \\ 0 &{} \quad I \\ \end{array} \right] , \end{aligned}$$

in which \(O_3\) is an arbitrary matrix with an appropriate dimension. As a consequence,

$$\begin{aligned} {\mathbb {N}}=U_3+O_3V_1, \end{aligned}$$
(28a)
$$\begin{aligned} {\mathbb {J}}=U_4+O_3V_2, \end{aligned}$$
(28b)

where

$$\begin{aligned} U_3= & {} {\mathbb {T}}{\mathbb {A}}{\Upsilon }^+\left[ \begin{array}{ccc} I_{n \times n} \\ 0 \\ \end{array} \right] , \end{aligned}$$
(29)
$$\begin{aligned} U_4= & {} {\mathbb {T}}{\mathbb {A}}{\Upsilon }^+\left[ \begin{array}{ccc} {\mathbb {K}} \\ I_{p \times p} \\ \end{array} \right] , \end{aligned}$$
(30)

Based on the above discussions, (13) can be rewritten as

$$\begin{aligned} D_t^\alpha \eta (t)=\left[ \begin{array}{ccc} {\mathbb {N}} &{} \quad {\mathbb {M}} \\ {\mathbb {P}} &{} \quad {\mathbb {G}} \\ \end{array} \right] \eta (t)=\bar{{\mathbb {A}}}\eta (t)=({\mathbb {A}}_{11}+Z{\mathbb {A}}_{12})\eta (t) \end{aligned}$$
(31)

where

$$\begin{aligned} \eta (t)=\left[ \begin{matrix} \zeta (t)\\ \psi (t) \end{matrix}\right] , \quad {\mathbb {A}}_{11}=\left[ \begin{array}{ccc} U_3 &{} \quad 0 \\ 0 &{} \quad 0 \\ \end{array} \right] , \quad {\mathbb {A}}_{12}=\left[ \begin{array}{ccc} V_1 &{} \quad 0 \\ 0 &{} \quad I \\ \end{array} \right] ,\quad Z=\left[ \begin{array}{ccc} O_3 &{} \quad {\mathbb {M}} \\ O_1 &{} \quad {\mathbb {G}} \\ \end{array} \right] . \end{aligned}$$

Consequently, the design of observer (11) is reduced to the determination of the matrix Z such that (31) is stable. The matrix Z can be obtained in the following two cases.

3.2.1 \(\alpha \in (0,1)\)

Theorem 1

There exists a matix Z such that (31) is stable iff there exist a symmetric positive definite matrix \(P_1\) and a matrix \(Y_1\) such that

$$\begin{aligned}&\left[ \begin{matrix} (2P_1{\mathbb {A}}_{11}+2{\mathbb {A}}_{11}^TP_1+2Y_1{\mathbb {A}}_{12} +2{\mathbb {A}}_{12}^TY_1^T)\sin \left( \alpha \frac{\pi }{2}\right) \\ 0 \end{matrix}\right. \nonumber \\&\quad \left. \begin{matrix} 0 \\ (2P_1{\mathbb {A}}_{11}+2{\mathbb {A}}_{11}^TP_1+2Y_1{\mathbb {A}}_{12} +2{\mathbb {A}}_{12}^TY_1^T)\sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] <0. \end{aligned}$$
(32)

In this case, Z is determined by \(Z=P_1^{-1}Y_1\).

Proof

Substituting (31) in (3) in Lemma 3 yields that

$$\begin{aligned}&\sum \limits _{i=1}^{2}\sum \limits _{j=1}^{2}sym\left\{ \sigma _{ij}\otimes P_{ij}{\bar{{\mathbb {A}}}}\right\} \\&\quad =\sum \limits _{i=1}^{2}\sum \limits _{j=1}^{2}sym\left\{ \sigma _{ij}\otimes P_{ij}({\mathbb {A}}_{11}+Z{\mathbb {A}}_{12})\right\} \\&\quad =\sum \limits _{i=1}^{2}\sum \limits _{j=1}^{2}sym\left\{ \sigma _{ij}\otimes P_{ij}{\mathbb {A}}_{11}+\sigma _{ij}P_{ij}Z{\mathbb {A}}_{12}\right\} \\&\quad =\sum \limits _{i=1}^{2}\sum \limits _{j=1}^{2}sym\left\{ \sigma _{ij}\otimes P_{ij}{\mathbb {A}}_{11}\right\} +\sum \limits _{i=1}^{2} \sum \limits _{j=1}^{2}sym\left\{ \sigma _{ij}\otimes P_{ij}Z{\mathbb {A}}_{12}\right\} \end{aligned}$$

To simplify the calculation, by setting \( P_{12}=P_{22}=0\), \(P_{11}=P_{21}=P_1\), we have

$$\begin{aligned}&sym\{\sigma _{11}\otimes P_1{\mathbb {A}}_{11}\}+sym\{\sigma _{21}\otimes P_1{\mathbb {A}}_{11}\}\\&\qquad +sym\{\sigma _{11}\otimes P_1Z{\mathbb {A}}_{12}\}+sym\{\sigma _{21}\otimes P_1Z{\mathbb {A}}_{12}\}\\&\quad =\left[ \begin{matrix} (P_1{\mathbb {A}}_{11}+{\mathbb {A}}_{11}^TP_1)\sin \left( \alpha \frac{\pi }{2}\right) &{} \quad (P_1{\mathbb {A}}_{11}-{\mathbb {A}}_{11}^TP_1)\cos \left( \alpha \frac{\pi }{2}\right) \\ (-P_1{\mathbb {A}}_{11}+{\mathbb {A}}^T_{11}P_1)\cos \left( \alpha \frac{\pi }{2}\right) &{} \quad (P_1{\mathbb {A}}_{11}+{\mathbb {A}}_{11}^TP_1)\sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \\&\qquad +\left[ \begin{matrix} (P_1{\mathbb {A}}_{11}+{\mathbb {A}}_{11}^TP_1)\sin \left( \alpha \frac{\pi }{2}\right) &{} \quad (-P_1{\mathbb {A}}_{11}+{\mathbb {A}}_{11}^TP_1)\cos \left( \alpha \frac{\pi }{2}\right) \\ (P_1{\mathbb {A}}_{11}-{\mathbb {A}}^T_{11}P_1)\cos \left( \alpha \frac{\pi }{2}\right) &{} \quad (P_1{\mathbb {A}}_{11}+{\mathbb {A}}_{11}^TP_1)\sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \\&\qquad +\left[ \begin{matrix} (P_1Z{\mathbb {A}}_{12}+{\mathbb {A}}_{12}^TZ^TP_1)\sin \left( \alpha \frac{\pi }{2}\right) &{} \quad (P_1Z{\mathbb {A}}_{12}-{\mathbb {A}}_{12}^TZ^TP_1)\cos \left( \alpha \frac{\pi }{2}\right) \\ (-P_1Z{\mathbb {A}}_{12}+{\mathbb {A}}^T_{12}Z^TP_1)\cos \left( \alpha \frac{\pi }{2}\right) &{} \quad (P_1Z{\mathbb {A}}_{12}+{\mathbb {A}}_{12}^TZ^TP_1)\sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \\&\qquad +\left[ \begin{matrix} (P_1Z{\mathbb {A}}_{12}+{\mathbb {A}}_{12}^TZ^TP_1)\sin \left( \alpha \frac{\pi }{2}\right) &{} \quad (-P_1Z{\mathbb {A}}_{12}+{\mathbb {A}}_{12}^TZ^TP_1)\cos \left( \alpha \frac{\pi }{2}\right) \\ (P_1Z{\mathbb {A}}_{12}-{\mathbb {A}}^T_{12}Z^TP_1)\cos \left( \alpha \frac{\pi }{2}\right) &{} \quad (P_1Z{\mathbb {A}}_{12}+{\mathbb {A}}_{12}^TZ^TP_1)\sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \\&\quad =\left[ \begin{matrix} (2P_1{\mathbb {A}}_{11}+2{\mathbb {A}}_{11}^TP_1+2Y_1{\mathbb {A}}_{12} +2{\mathbb {A}}_{12}^TY_1^T)\sin \left( \alpha \frac{\pi }{2}\right) \\ 0 \end{matrix}\right. \\&\qquad \left. \begin{matrix} 0 \\ (2P_1{\mathbb {A}}_{11}+2{\mathbb {A}}_{11}^TP_1+2Y_1{\mathbb {A}}_{12} +2{\mathbb {A}}_{12}^TY_1^T)\sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] <0 \end{aligned}$$

where \(Y_1=P_1Z\), which completes the proof. \(\square \)

3.2.2 \(\alpha \in [1,2)\)

Theorem 2

There exists a parameter matrix Z such that (31) is stable iff there exist a symmetric positive definite matrix \(P_2\) and a matrix \(Y_2\) such that

$$\begin{aligned}&\left[ \begin{matrix} ({\mathbb {A}}_{11}^TP_2+P_2{\mathbb {A}}_{11}- {\mathbb {A}}_{12}^TY_2^T-Y_2{\mathbb {A}}_{12})\sin \left( \alpha \frac{\pi }{2}\right) \\ (P_2{\mathbb {A}}_{11}-{\mathbb {A}}^T_{11}P_2- Y_2{\mathbb {A}}_{12}+{\mathbb {A}}_{12}^TY_2^T)\cos \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right. \nonumber \\&\quad \left. \begin{matrix} ({\mathbb {A}}_{11}^TP_2-P_2{\mathbb {A}}_{11}-{\mathbb {A}}_{12}^TY_2^T +Y_2{\mathbb {A}}_{12})\cos \left( \alpha \frac{\pi }{2}\right) \\ ({\mathbb {A}}_{11}^TP_2+P_2{\mathbb {A}}_{11}-{\mathbb {A}}_{12}^TY_2^T -Y_2{\mathbb {A}}_{12})\sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] <0. \end{aligned}$$
(33)

In such a case, Z is determined by \(Y_2=P_2^{-1}Z\).

Proof

Substituting (31) in Lemma 4, we have that

$$\begin{aligned}&\left[ \begin{matrix} [({\mathbb {A}}_{11}-Z{\mathbb {A}}_{12})^TP_2+P_2({\mathbb {A}}_{11}- Z{\mathbb {A}}_{12})]\sin \left( \alpha \frac{\pi }{2}\right) \\ [P_2({\mathbb {A}}_{11}-Z{\mathbb {A}}_{12})-({\mathbb {A}}_{11}- Z{\mathbb {A}}_{12})^TP_2]\cos \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right. \\&\quad \ \ \left. \begin{matrix} ({\mathbb {A}}_{11}^TP_2-P_2{\mathbb {A}}_{11}-{\mathbb {A}}_{12}^TZ^TP_2+ P_2Z{\mathbb {A}}_{12})\cos \left( \alpha \frac{\pi }{2}\right) \\ [({\mathbb {A}}_{11}-Z{\mathbb {A}}_{12})^TP_2+P_2({\mathbb {A}}_{11}- Z{\mathbb {A}}_{12})]\sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \\&=\left[ \begin{matrix} ({\mathbb {A}}_{11}^TP_2-{\mathbb {A}}_{12}^TZ^TP_2+P_2{\mathbb {A}}_{11}- P_2Z{\mathbb {A}}_{12})\sin \left( \alpha \frac{\pi }{2}\right) \\ (P_2{\mathbb {A}}_{11}-P_2Z{\mathbb {A}}_{12}-{\mathbb {A}}_{11}^TP_2- {\mathbb {A}}_{12}^TZ^TP_2)\cos \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right. \\&\quad \ \ \left. \begin{matrix} ({\mathbb {A}}_{11}^TP_2-P_2{\mathbb {A}}_{11}-{\mathbb {A}}_{12}^TZ^TP_2+ P_2Z{\mathbb {A}}_{12})\cos \left( \alpha \frac{\pi }{2}\right) \\ ({\mathbb {A}}_{11}^TP_2-{\mathbb {A}}_{12}^TZ^TP_2+P_2{\mathbb {A}}_{11}- P_2Z{\mathbb {A}}_{12})\sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \\&=\left[ \begin{matrix} ({\mathbb {A}}_{11}^TP_2+P_2{\mathbb {A}}_{11}-{\mathbb {A}}_{12}^TY_2^T- Y_2{\mathbb {A}}_{12})\sin \left( \alpha \frac{\pi }{2}\right) \\ (P_2{\mathbb {A}}_{11}-{\mathbb {A}}^T_{11}P_2-Y_2{\mathbb {A}}_{12}+ {\mathbb {A}}_{12}^TY_2^T)\cos \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right. \\&\quad \ \ \left. \begin{matrix} ({\mathbb {A}}_{11}^TP_2-P_2{\mathbb {A}}_{11}-{\mathbb {A}}_{12}^TY_2^T+ Y_2{\mathbb {A}}_{12})\cos \left( \alpha \frac{\pi }{2}\right) \\ ({\mathbb {A}}_{11}^TP_2+P_2{\mathbb {A}}_{11}-{\mathbb {A}}_{12}^TY_2^T- Y_2{\mathbb {A}}_{12})\sin \left( \alpha \frac{\pi }{2}\right) \end{matrix}\right] \\&<0, \end{aligned}$$

where \(Y_2=P_2Z\), which completes the proof. \(\square \)

Within the above results, we present the following design algorithm to determine the desired fractional-order observer.

Algorithm 1
figure a

Fractional-Order Observer Design Algorithm

Full size image

4 Simulation Results

The following numerical example is presented to verify the derived theoretical results.

Example 1

The parameters of fractional-order system (9) are chosen as

$$\begin{aligned} {\mathcal {A}}=\left[ \begin{matrix} -2 &{} \quad 1 &{} \quad 2\\ 0 &{} \quad -2 &{} \quad -1\\ 0 &{} \quad 0 &{} \quad -1 \end{matrix}\right] ,\ {\mathcal {B}}=0,\ {\mathcal {F}}=\left[ \begin{matrix} 1 &{} \quad 0 \\ 0 &{} \quad 1 \\ 0 &{} \quad -1 \end{matrix}\right] ,\ {\mathcal {C}}=\left[ \begin{matrix} -1 &{} \quad 1 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 1 \end{matrix}\right] ,\ {\mathcal {D}}=\left[ \begin{matrix} -1 &{} \quad 0 \\ 0 &{} \quad 1 \end{matrix}\right] , \end{aligned}$$

then we have that

$$\begin{aligned} {\mathbb {A}}=[{\mathcal {A}}\ {\mathcal {F}}]= \left[ \begin{matrix} -2 &{} \quad 1 &{} \quad 2 &{} \quad 1 &{} \quad 0 \\ 0 &{} \quad -2 &{} \quad 1 &{} \quad 0 &{} \quad 1 \\ 0 &{} \quad 0 &{} \quad -1 &{} \quad 0 &{} \quad -1 \end{matrix}\right] ,\ {\mathbb {C}}=[{\mathcal {C}}\ {\mathcal {D}}]= \left[ \begin{matrix} -1 &{} \quad 1 &{} \quad 0 &{} \quad -1 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 1 &{} \quad 0 &{} \quad 1 \end{matrix}\right] . \end{aligned}$$

Clearly, \(rank \left[ \begin{matrix} {\mathcal {E}}\\ {\mathbb {C}} \end{matrix}\right] =5\), which satisfies Assumption 1.

Moreover, set

$$\begin{aligned} {\mathbb {E}}= \left[ \begin{matrix} 1 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 1 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 1 &{} \quad 0 \end{matrix}\right] \end{aligned}$$

such that \(rank \left[ \begin{matrix} {\mathbb {E}}\\ {\mathbb {C}} \end{matrix}\right] =n+r\).

It follows from step 2 in Algorithm 1 that

$$\begin{aligned} {\mathbb {T}}= \left[ \begin{matrix} 1 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 1 \\ -1 &{} \quad 1 &{} \quad 0 \end{matrix}\right] ,\ {\mathbb {K}}= \left[ \begin{matrix} 0 &{} \quad 0 \\ 0 &{} \quad 0 \\ -1 &{} \quad 0 \end{matrix}\right] ,\ {\mathbb {H}}=0. \end{aligned}$$

According to step 4, we obtain that

$$\begin{aligned} U_1= \left[ \begin{matrix} 1 &{} \quad 0 &{} \quad 0 \\ 1 &{} \quad 0 &{} \quad 1 \\ 0 &{} \quad 1 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 1 \\ 0 &{} \quad -1 &{} \quad 0 \end{matrix}\right] ,\ U_2= \left[ \begin{matrix} 0 &{} \quad 0 \\ 0 &{} \quad 0 \\ 0 &{} \quad 0 \\ -1 &{} \quad 0 \\ 0 &{} \quad 1 \end{matrix}\right] ,\ V_1=0,\ V_2=0. \end{aligned}$$

Furthermore, step 5 deduces that

$$\begin{aligned} U_3= \left[ \begin{matrix} -1 &{} \quad 2 &{} \quad 2 \\ 0 &{} \quad 0 &{} \quad 0 \\ -1 &{} \quad -2 &{} \quad -4 \end{matrix}\right] ,\ U_4= \left[ \begin{matrix} -1 &{} \quad 0 \\ 0 &{} \quad -1 \\ 1 &{} \quad 1 \end{matrix}\right] . \end{aligned}$$

Hence, by step 6, \({\mathbb {R}}=U_1\) and \({\mathbb {S}}=U_2\).

In the sequel, set \(d(t)=[0.2\ 0.2]^T\). In such a case, by Theorem 1, we achieve that

$$\begin{aligned}&P_1=10^6\times \left[ \begin{matrix} 0.4286 &{} \quad -0.1851 &{} \quad 0.1509 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ -0.1851 &{} \quad 3.3696 &{} \quad 0.0399 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0.1509 &{} \quad 0.0399 &{} \quad 0.2107 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 3.4796 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 3.4796 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 3.4796 \end{matrix}\right] ,\\&Y_1=10^5\times \left[ \begin{matrix} 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad -4.4038 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad -4.4038 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad -4.4038 \end{matrix}\right] , \end{aligned}$$

As a consequence,

$$\begin{aligned} Z=\left[ \begin{matrix} 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad -0.1266 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad -0.1266 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad -0.1266 \end{matrix}\right] . \end{aligned}$$

Therefore, \({\mathbb {M}}=O_1=O_3={\textbf {0}}_{3\times 3}\), and

$$\begin{aligned} {\mathbb {G}}= \left[ \begin{matrix} -0.1266 &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad -0.1266 &{} \quad 0 \\ 1 &{} \quad 0 &{} \quad -0.1266 \end{matrix}\right] . \end{aligned}$$

It is easy to see that by step 9, \({\mathbb {P}}={\mathbb {Q}}={\textbf {0}}_{3\times 3}\). Finally, step 10 indicates that \({\mathbb {N}}=U_3\) and \({\mathbb {J}}=U_4\).

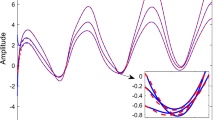
Based on the above calculations, the simulation results are presented as Figs. 1, 2 and 3 with \(\alpha =0.9\) and the initial states \((x_1(t),x_2(t),x_3(t))=(15,-5,5)\), \((z_1(t),z_2(t),z_3(t))=(0,5,5)\) and \((\psi _1(t),\psi _2(t),\psi _3(t))=(5,-10,5)\). The simulation results show that the designed fractional-order observer can simultaneously estimate both the states (see Figs. 1, 2) and the unknown inputs (see Fig. 3), effectively. Furthermore, within the same initial states, the simulation results with \(\alpha =0.6\) and \(\alpha =0.8\) are shown in Figs. 4 and 5, respectively. It follows from the simulation results that the convergence rate is faster when the order is more and more big.

Fig. 1
figure 1

The estimation of state \(x_1(t)\)

Full size image
Fig. 2
figure 2

The estimation of state \(x_2(t)\)

Full size image
Fig. 3
figure 3

The estimation of unknown input \(d_1(t)\)

Full size image
Fig. 4
figure 4

The estimation of \(x_1(t)\), \(x_2(t)\) and \(d_1(t)\) with \(\alpha =0.6\)

Full size image
Fig. 5
figure 5

The estimation of \(x_1(t)\), \(x_2(t)\) and \(d_1(t)\) with \(\alpha =0.8\)

Full size image

5 Conclusion

In this paper, a fractional-order observer has been proposed to estimate both the states and the unknown inputs for LTI-FOSs with \(0<\alpha <2\). A necessary and sufficient criterion has been derived to guarantee the stability of LTI-FOSs with \(0<\alpha <1\). The parameterized matrices of the derived fractional-order observer have been solved on the basis of the stability theorems and the solution to the generalized inverse matrix. The fractional-order observer design algorithm has been presented to verify the correctness and effectiveness of the designed observer. Simulation results have shown that the desired observer can estimate both the states and the unknown inputs, simultaneously.

For future investigations, we may consider the simultaneous estimations of both states and unknown inputs for fractional-order nonlinear system and related fractional-order observer-based controller designed problems.