1 Introduction

In recent years, FONNs have attracted considerable research attention. Compared with integer-order neural networks (IONNs), FONNs can represent the real dynamic characteristics of actual network systems more accurately. As a consequence, many important and interesting results on FONNs have been reported and various issues have been studied by many authors, such as asymptotic stability [18, 19, 30, 37, 47, 51], finite-time stability [7, 36, 41, 45, 49], guaranteed cost control [39, 42], synchronization analysis [1, 5, 26,27,28,29, 32, 46, 52, 53, 56, 57], \(H_{\infty }\) control problem [43] and so on.

On the other hand, passivity theory plays an important role in network control theory [31]. Passivity performance analysis has also been extensively applied in various areas such as signal processing, fuzzy control, power system, robot system and so on. In the recent years, many important results on passivity analysis for continuous-time or discrete-time integer-order dynamical systems have been reported in the literature [3,4,5, 8, 10, 14, 20, 22,23,24, 40, 48, 50, 54, 55, 58]. For example, by using a second-order Bessel–Legendre inequality, the authors in [58] derived some improved passivity criterion for neural networks with a bounded time-varying delay. The conditions were expressed in terms of linear matrix inequality (LMI). Some passivity criteria for IONNs with discrete bounded time-varying delay were presented in [24] by constructing a suitable augmented Lyapunov–Krasovskii functional with an extended free-weighting matrices integral inequality. By constructing an improved Lyapunov–Krasovskii functional with a novel delay-produce-type term and combining with a free-matrix-based integral inequality, the problem of passivity analysis for uncertain IONNs with mixed bounded time-varying delays was addressed in the work of Ge at el. [13]. The authors in [5] investigated the passivity analysis problem for BAM neural networks with leakage, discrete, distributed delays and uncertainties by using a Wirtinger-based integral inequality combined with some novel summation inequalities. Based on the stochastic analysis theory combined with the LMI techniques, passive synchronization problems for Markov jump neural networks with randomly occurring gain variations have been considered in the work of Dai et al. [10]. With the help of stochastic analysis theory and the Lyapunov–Krasovskii functional method, the authors in [34] considered the problem of passive gain-scheduling filtering for Markov jump linear parameter varying systems with fading channels. Recently, reliable event-triggered asynchronous extended passive control problems for semi-Markov jump fuzzy systems have been considered by Shen et al. [35]. Summarizing these results, we can see that the methods used in existing works mainly based on the Lyapunov–Krasovskii functional method combined with the LMI techniques. Noting that the passivity analysis problem of fractional-order dynamical systems is more complex and difficult than that of integer-order dynamical systems due to the fact that fractional derivatives are nonlocal and have weakly singular kernels. This is the main reason that there have been very few results on passivity analysis for fractional-order systems [9, 11, 33]. Very recently, the authors in [11] solved the passivity analysis problem for FONNs for the first time by using the LMI techniques and control theories. Note that the results derived in [11] were for FONNs without time delays and applied only for order-independent passivity analysis. It is well known that time delay is very encountered in various systems, and its existence may cause undesirable system transient response and instability. When time delay is small, it is obvious that delay-dependent stability conditions are less conservative than delay-independent ones. To the best of our knowledge, the problem of passivity analysis for FONNs with a time-varying delay has not yet been investigated in the literature. Therefore, the main goal of this paper is to present a simple and easily verifiable delay-dependent and order-dependent criteria for the passivity analysis problem of FONNs with a bounded time-varying delay.

In this paper, we study the passivity analysis problem for FONNs with a bounded time-varying delay. The main contributions of this paper are summarized as follows:

  • A less conservative delay-dependent and order-dependent stability criteria for asymptotic stability of FONNs with a bounded time-varying delay is investigated based on Razumikhin fractional-order theorem and the LMI techniques;

  • Based on the proposed stability criteria and some auxiliary properties of fractional calculus, the problem of passivity analysis for FONNs with a time-varying delay is solved for the first time;

  • Some new sufficient criterion is derived in terms of LMI, which can be effectively solved in polynomial time by various computational tools;

  • Some numerical examples are given to show that our results are less conservative compared to some existing works.

The organization of this paper is as follows. In Sect. 2, we provide some definitions, notations and auxiliary lemmas which will be used in the proof of the main results. We present our main results on passivity analysis for FONNs with a bounded time-varying delay in Sect. 3. Four numerical examples are provided in Sect. 4 to illustrate the effectiveness of the proposed method.

Notations The notation used in this paper is standard. Let \(\mathbb {R}^n\) and \(\mathbb {R}^{n \times m}\) denote the n-dimensional Euclidean space with vector norm \(\Vert .\Vert \) and the set of \(n\times m\) matrices, respectively. \(I_n\) and \(0_n\) denote the \(n \times n\) dimensional identity and zero matrix, respectively. \(0_{n \times m}\) denote the \(n \times m\) dimensional zero matrix. For matrices \(P, Q \in \mathbb {R}^{n \times m}\), \({{\,\mathrm{diag}\,}}\{P, Q\}\) denotes the block matrices \(\begin{bmatrix} P &{} 0 \\ 0 &{} Q \end{bmatrix}\). \(\mathsf {sym}(P)\) stands for \(P + P^T\). A matrix P is symmetric positive definite, write \(P > 0\), if \(P = P^T\) and \(x^TPx > 0, \forall x \in \mathbb {R}^n, x \not = 0\). A matrix Q is symmetric semi-positive-definite, write \(Q \ge 0\), if \(Q = Q^T\) and \(x^TQx \ge 0, \forall x \in \mathbb {R}^n\). \(L_p([0, T]), p \ge 1\) denotes the space of all \(p-\) integrable functions on [0, T]. The segment of the trajectory x(t) is denoted by \(x_t = \{x(t+s): s \in [-\delta , 0]\}\) with its norm \(\Vert x_t\Vert = \sup \nolimits _{s \in [-\delta , 0]}\Vert x(t+s)\Vert \). Let \(\mathbb {S}_{+}^n\) and \(\mathbb {S}_{++}^n\) denote the set of symmetric semi-positive-definite and the set of symmetric positive definite matrices in \(\mathbb {R}^{n \times n}\), respectively. We also denote by \(\mathbb {D}_{++}^n\) the set of positive diagonal matrices, that is, a matrix \(\varLambda = {{\,\mathrm{diag}\,}}\{\lambda _1, \ldots , \lambda _n\} \in \mathbb {D}_{++}^n\) if \(\lambda _i > 0 \, (i = 1, 2, \ldots , n)\).

2 Problem Statement and Preliminaries

We first give some basic concepts of fractional calculus from [17] for later use. The Riemann–Liouville integral \(I_t^{\mu }f(t)\), the Riemann–Liouville derivative \(_RD_t^{\mu }\) and the Caputo fractional derivative \(D_t^{\mu }f(t)\) are defined for \(f \in L^1[0, +\infty ), \mu \in (0, 1)\) as follows, respectively:

$$\begin{aligned}&I_t^{\mu }f(t) = \frac{1}{\varGamma (\mu )}\int _{0}^{t}(t-s)^{\mu - 1}f(s)\,ds,\\&_RD_t^{\mu }f(t) = \frac{d}{dt}\left( I_t^{1-\mu }f(t)\right) ,\\&D_t^{\mu }f(t) =\, _RD_t^{\mu }\left( f(t) - f(0)\right) , \end{aligned}$$

where \(\varGamma (.)\) is the gamma function, \(\varGamma (s) = \int \limits _{0}^{\infty }e^{-t}t^{s-1}dt, s > 0.\)

We recall some useful properties about fractional-order calculus.

P1 ([17]): For any constants \(\lambda _1, \lambda _2\), and two functions f(t), g(t), we have

$$\begin{aligned} D_t^{\mu }\left( \lambda _1 f(t) + \lambda _2 g(t)\right) = \lambda _1D_t^{\mu }f(t) + \lambda _2D_t^{\mu }g(t). \end{aligned}$$

P2 ([17]): If \(f(t) \in C^{n}([0, +\infty ), \mathbb {R})\) and \(n-1< \mu < n, (n \ge 1, n \in \mathbb {Z}^{+}),\) then

$$\begin{aligned} I_{t}^{\mu }\left( D_t^{\mu }f(t)\right) = f(t) - \sum \limits _{j=0}^{n-1}\frac{t^j}{j!}f^{(j)}(0). \end{aligned}$$

In particular, when \(0< \mu < 1,\) we have

$$\begin{aligned} I_{t}^{\mu }\left( D_t^{\mu }f(t)\right) = f(t) - f(0). \end{aligned}$$

P3 ([17]): If f(t) is a continuous function, then we have

$$\begin{aligned} I_{t}^{\mu _1}\left( I_{t}^{\mu _2}f(t)\right) = I_{t}^{\mu _2}\left( I_{t}^{\mu _1}f(t)\right) = I_{t}^{\mu _1+\mu _2}(f(t)), \forall t \ge t_0. \end{aligned}$$

Consider the following Caputo fractional-order neural networks with a time-varying delay:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} D_t^{\mu }x(t) = -Ax(t) + W_1g(x(t)) + W_2g(x(t-\delta (t))) + u(t) \\ &{} z(t) = C_1g(x(t)) + C_2g(x(t-\delta (t)) + C_3u(t),\\ &{} x(t) = \phi (t), t \in [-\delta , 0], \end{array}\right. } \end{aligned}$$
(1)

where \(\mu \in (0, 1]\), \(x(t) \in \mathbb {R}^n\) is the neuron state vector, n is the number of neurons in FONNs, \(z(t) \in \mathbb {R}^n\) is the output vector and \(u(t) \in \mathbb {R}^n\) is the external input of the network, \(g(x(t)) = \left( g_1(x_1(t)), g_2(x_2(t)), \ldots , g_n(x_n(t))\right) ^T \in \mathbb {R}^n\) denotes the neuron activation function, \(W_1 = (w_{ij}^1)_{n \times n}, W_2 = (w_{ij}^2)_{n \times n}, C_1, C_2, C_3 \in \mathbb {R}^{n \times n}, A = {{\,\mathrm{diag}\,}}\{a_1, \ldots , a_n\} \in \mathbb {D}_{++}^{n}\, (a_i > 0, i = 1, 2, \ldots , n),\) are known constant matrices, the initial condition \(\phi (t)\) is a vector-valued continuous function.

Before proceeding further, we need the following assumptions:

(H1): The time-varying delay function \(\delta (t)\) is continuous and satisfying

$$\begin{aligned} \begin{aligned}&0 \le \delta (t) \le \delta , \end{aligned} \end{aligned}$$
(2)

where \(\delta \) is known constant.

(H2): The activation functions \(g_i(.)\) are continuous, \(g_i(0) = 0 (i = 1, 2, \ldots , n)\) and satisfy the following condition

$$\begin{aligned} l_i^{-} \le \frac{g_i(a) - g_i(b)}{a-b} \le l_i^{+}, \, i = 1, 2, \ldots , n, \end{aligned}$$
(3)

where \(a, b \in \mathbb {R}, a \not = b,\) and \(l_i^{-}, l_i^{+}\) are known real scalars.

Remark 1

The constants \(l_i^{-}\) and \(l_i^{+}\) are allowed to be positive, negative or zero. Therefore, condition (2) is less restrictive than the descriptions on both Lipschitz-type activation functions and sigmoid activation functions when analyzing the stability or stabilization of FONNs.

Definition 1

([55]) System (1) is said to be passive if the following conditions are satisfied:

  1. (i)

    With zero output vector and zero external input vector, system (1) is asymptotically stable.

  2. (ii)

    With zero initial condition, i.e., \(\phi (t) = 0, \forall t \in [-\delta , 0]\), there exists a positive number \(\gamma > 0\) such that

    $$\begin{aligned} 2\int _{0}^{t_f}z^T(t)u(t)dt \ge -\gamma \int _{0}^{t_f}u^T(t)u(t)dt, \forall t_f \ge 0, \end{aligned}$$

    where z(t) is the output vector of the system and u(t) is external input in the system which belongs to \(L_2[0, \infty )\).

Now, we present several technical lemmas which are essential in order to prove the main results of this paper.

Lemma 1

([12]) Let \(x(t) \in \mathbb {R}^n\) be a vector of differentiable function. Then, for any time instant \(t \ge t_0,\) the following relationship holds

$$\begin{aligned} \frac{1}{2}D_{t}^{\alpha }\left( x^T(t)Px(t)\right) \le x^T(t)P D_{t}^{\alpha }x(t), \quad \forall \alpha \in (0, 1), \forall t \ge 0. \end{aligned}$$

where \(P \in \mathbb {R}^{n \times n}\) is a symmetric positive definite matrix.

Lemma 2

[21] Assume that there exist three positive constants \({\mathsf {a}}_1, {\mathsf {a}}_2, {\mathsf {a}}_3\) and a quadratic Lyapunov function \(V(.): \mathbb {R}^{+} \times \mathbb {R}^n \rightarrow \mathbb {R}^{+}\) such that

\((i) \quad {\mathsf {a}}_1\Vert x(t)\Vert ^2 \le V(t, x(t)) \le {\mathsf {a}}_2\Vert x(t)\Vert ^2, t\ge 0, x\in \mathbb {R}^n\) and

\((ii) \quad D^{\mu }_tV(t,x(t)) \le - {\mathsf {a}}_3\Vert x(t)\Vert ^2\, \) whenever \(\, V(t+s,x(t+s)) < \rho V(t,x(t)), \forall s\in [-h,0], t\ge 0,\) for some \(\rho > 1\), then the zero solution of delayed fractional-order system \(D^{\mu }_tx(t) = f(t,x_t), \, \mu \in (0, 1),\) is asymptotically stable.

3 Main Results

In order to solve the problem of passivity analysis for FONNs with a time-varying delay (1), we first present a new stability result for system (1) with zero output vector and zero external input vector. Let us denote

$$\begin{aligned}&{\mathsf {e}}_j = \begin{bmatrix} 0_{n \times (j-1)n}&I_n&0_{n \times (5-j)n} \end{bmatrix}, \, j = 1, \ldots , 5. \end{aligned}$$

Theorem 1

Assume that the assumptions (H1)–H(2) hold. System (1) with \(u(t) \equiv 0, z(t) \equiv 0\) is asymptotically stable if there exist matrices \(P, Q \in \mathbb {S}_{++}^n\), a matrix \(X \in \mathbb {S}_{+}^{5n}\), three matrices \(\varLambda _i = {{\,\mathrm{diag}\,}}\{\lambda _{i1}, \lambda _{i2}, \ldots , \lambda _{in}\} \in \mathbb {D}_{++}^{n} \, (i = 1, 2, 3)\) such that the following LMI holds

$$\begin{aligned} \begin{aligned}&\varOmega = \delta ^{\mu }\mu ^{-1}\varUpsilon ^T X \varUpsilon + \sum \limits _{i=1}^{3}\varOmega _i < 0, \end{aligned} \end{aligned}$$
(4)

where

$$\begin{aligned}&\varUpsilon = \begin{bmatrix} {\mathsf {e}}_1^T&{\mathsf {e}}_2^T&{\mathsf {e}}_3^T&{\mathsf {e}}_4^T&{\mathsf {e}}_5^T \end{bmatrix}^T, \, \varSigma _1 = {{\,\mathrm{diag}\,}}\{l_1^-, \ldots , l_n^-\}, \, \varSigma _2 = {{\,\mathrm{diag}\,}}\{l_1^+, \ldots , l_n^+\}, \\&\varUpsilon _1 = {\mathsf {e}}_3 - \varSigma _1{\mathsf {e}}_1, \, \varUpsilon _2 = \varSigma _2{\mathsf {e}}_1 - {\mathsf {e}}_3,\\&\varUpsilon _3 = {\mathsf {e}}_4 - \varSigma _1{\mathsf {e}}_2, \, \varUpsilon _4 = \varSigma _2{\mathsf {e}}_2 - {\mathsf {e}}_4,\\&\varUpsilon _5 = {\mathsf {e}}_3 - {\mathsf {e}}_4 - \varSigma _1 \left( {\mathsf {e}}_1 -{\mathsf {e}}_2 \right) , \, \varUpsilon _6 = \varSigma _2\left( {\mathsf {e}}_1 - {\mathsf {e}}_2\right) - {\mathsf {e}}_3 + {\mathsf {e}}_4,\\&\varOmega _1 = \mathsf {sym} \left( {\mathsf {e}}_1^TP{\mathsf {e}}_5 - e_1^TQe_5 + {\mathsf {e}}_1^TQW_1{\mathsf {e}}_3 + {\mathsf {e}}_1^TQW_2{\mathsf {e}}_4 - {\mathsf {e}}_5^TQA{\mathsf {e}}_1 +\right. \\&\left. {\mathsf {e}}_5^TQW_1{\mathsf {e}}_3 + {\mathsf {e}}_5^TQW_2{\mathsf {e}}_4 \right) ,\\&\varOmega _2 = {\mathsf {e}}_1^T\left[ -QA - A^TQ + P\right] {\mathsf {e}}_1 - {\mathsf {e}}_2^TP{\mathsf {e}}_2 + {\mathsf {e}}_5^T(-2Q){\mathsf {e}}_5,\\&\varOmega _3 = \mathsf {sym} \left( \varUpsilon _1^T \varLambda _1\varUpsilon _2 + \varUpsilon _3^T \varLambda _2\varUpsilon _4 + \varUpsilon _5^T \varLambda _3\varUpsilon _6\right) . \end{aligned}$$

Proof

Consider the following Lyapunov function for the system (1) with \(u(t) \equiv 0, y(t) \equiv 0:\)

$$\begin{aligned} V(t) = V(t, x(t)) = x^T(t) Px(t). \end{aligned}$$

It is easy to check that

$$\begin{aligned} \lambda _{\min }(P)\Vert x(t)\Vert ^2 \le V(t) \le \lambda _{\max }(P)\Vert x(t)\Vert ^2. \end{aligned}$$

Hence, condition (i) in Lemma 2 is guaranteed. By using Lemma 1, the Caputo fractional derivative order \(\mu \) of system (1) with \(u(t) \equiv 0, z(t) \equiv 0\) is calculated as follow:

$$\begin{aligned} \begin{aligned} D_t^{\mu }V(t)&\le 2 x^T(t)PD_t^{\mu } x(t) = \xi ^T(t)\mathsf {sym}\left( {\mathsf {e}}_1^TP{\mathsf {e}}_5\right) \xi (t), \end{aligned} \end{aligned}$$
(5)

where \(\xi (t) = \begin{bmatrix} x^T(t)&x^T(t-\delta (t))&g^T(x(t))&g^T(x(t-\delta (t)))&\left( D_{t}^{\mu }x(t)\right) ^T \end{bmatrix}^T\). For any a matrix \(Q \in \mathbb {S}_{++}^{n}\), the following equation can be obtained by using FONNs system (1) with zero output vector and zero external input vector

$$\begin{aligned} \begin{aligned} \left[ 2x^T(t) + 2(D_{t}^{\mu }x(t))^T\right] Q\left[ -D_{t}^{\mu }x(t) - Ax(t) + W_1g(x(t)) + W_2g(x(t-\delta (t)))\right] = 0. \end{aligned}\nonumber \\ \end{aligned}$$
(6)

For any a matrix \(X \in \mathbb {S}_{+}^{5n}\), the following estimate holds

$$\begin{aligned} \begin{aligned}&\delta ^{\mu }\mu ^{-1}\xi ^T(t)X\xi (t) - \int _{t-\delta (t)}^{t}(t-s)^{\mu - 1}\xi ^T(t)X\xi (t)ds \\&= \delta ^{\mu }\mu ^{-1}\xi ^T(t)X\xi (t) + \xi ^T(t)X \xi (t)\frac{(t-s)^{\mu }}{\mu }\bigg |_{s = t - \delta (t)}^{s=t}\\&= \delta ^{\mu }\mu ^{-1}\xi ^T(t)X\xi (t) - \delta ^{\mu }(t)\mu ^{-1}\xi ^T(t)X\xi (t) \\&\ge 0. \end{aligned} \end{aligned}$$
(7)

From Assumption (H2), it can be deduced that for any \(\lambda _{ji} > 0, \, (j=1, 2, 3, i = 1, 2, \ldots , n)\),

$$\begin{aligned}&2\left( g_i(x_i(t)) - l_i^{-}x_i(t)\right) \lambda _{1i}\left( l_{i}^{+}x_i(t) - g_i(x_i(t))\right) \ge 0,\\&2\left( g_i(x_i(t-\delta (t))) - l_{i}^{-}x_i(t-\delta (t))\right) \lambda _{2i} \left( l_i^{+}x_i(t-\delta (t)) - g_i(x_i(t-\delta (t)))\right) \ge 0,\\&2\left( g_i(x_i(t)) - g_i(x_i(t-\delta (t))) - l_i^{-}(x_i(t) - x_i(t-\delta (t)))\right) \lambda _{3i}\\&\times \left( l_i^{+}(x_i(t) - x_i(t-\delta (t))) - g_i(x_i(t)) + g_i(x_i(t-\delta (t)))\right) \ge 0, \end{aligned}$$

which imply

$$\begin{aligned} \begin{aligned}&2\xi ^T(t)\varUpsilon _1^T\varLambda _1\varUpsilon _2\xi (t) \ge 0, \\&2\xi ^T(t)\varUpsilon _3^T\varLambda _2\varUpsilon _4\xi (t) \ge 0, \\&2\xi ^T(t)\varUpsilon _5^T\varLambda _3\varUpsilon _6\xi (t) \ge 0. \end{aligned} \end{aligned}$$
(8)

Since \(V(t, x(t)) = x^T(t)Px(t)\), in the light of Lemma 2, we assume that for some real number \(\rho > 1\) such that

$$\begin{aligned} V(t+s, x(t+s)) < \rho V(t, x(t)), \forall s \in [-\delta , 0], \end{aligned}$$

we obtain

$$\begin{aligned} \begin{aligned}&\rho x^T(t)Px(t) - x^T(t-\delta (t))Px(t-\delta (t)) > 0. \end{aligned} \end{aligned}$$
(9)

Combining estimates (5)–(9), we then obtain

$$\begin{aligned} \begin{aligned}&D_t^{\mu }V(t, x(t)) \le \xi ^T(t){\hat{\varOmega }}\xi (t) - \int _{t-\delta (t)}^{t}(t-s)^{\mu - 1}\xi ^T(t)X\xi (t)ds, \end{aligned} \end{aligned}$$
(10)
$$\begin{aligned}&{\hat{\varOmega }} = \delta ^{\mu }\mu ^{-1}\varUpsilon ^T X \varUpsilon + \varOmega _1 + {\hat{\varOmega }}_2 + \varOmega _3,\\&{\hat{\varOmega }}_2 = {\mathsf {e}}_1^T\left[ -QA - A^TQ + \rho P\right] {\mathsf {e}}_1 -{\mathsf {e}}_2^TP{\mathsf {e}}_2 + {\mathsf {e}}_5^T[-2Q]{\mathsf {e}}_5. \end{aligned}$$

Since \(\rho > 1\) is an arbitrary parameter and the left-hand side function \(D_{t}^{\mu }V(t, x(t))\) does not dependent on \(\rho \), then taking \(\rho \rightarrow 1^{+}\), the inequality (10) leads to

$$\begin{aligned} \begin{aligned}&D_t^{\mu }V(t, x(t)) \le \xi ^T(t)\varOmega \xi (t) - \int _{t-\delta (t)}^{t}(t-s)^{\mu - 1}\xi ^T(t)X\xi (t)ds, \end{aligned} \end{aligned}$$
(11)

Since \(\int _{t-\delta (t)}^{t}(t-s)^{\mu - 1}\xi ^T(t)X\xi (t)ds \ge 0\), we have

$$\begin{aligned} \begin{aligned}&D_t^{\mu }V(t, x(t)) \le \xi ^T(t)\varOmega \xi (t). \end{aligned} \end{aligned}$$
(12)

From (4), we have \(D_t^{\mu }V(t, x(t)) < 0.\) Thus, condition (ii) in Lemma 2 is also satisfied. Thus, system (1) with zero output vector and zero external input vector is asymptotically stable. The proof of theorem is completed. \(\square \)

Remark 2

In [51], the authors considered the problem of stability analysis for system (1) with zero output vector and zero external input. However, they derived delay-independent stability criteria for the considered system with a constant time delay. In Theorem 1, we proposed delay-dependent and order-dependent stability criteria for system (1) (\(u(t) \equiv 0, z(t) \equiv 0\)) with a time-varying delay by using the fractional-order Razumikhin theorem and the LMI approach. Therefore, the obtained result in Theorem 1 is less conservative than the existing results [6, 51].

Based on the proposed stability criteria of Theorem 1 and some auxiliary properties of fractional calculus, we will solve the problem of passivity analysis for FONNs (1). For the simplicity of matrix representation, we denote

$$\begin{aligned}&{\mathsf {r}}_j = \begin{bmatrix} 0_{n \times (j-1)n}&I_n&0_{n \times (6-j)n} \end{bmatrix}, \, j = 1, \ldots , 6. \end{aligned}$$

Theorem 2

Assume that the assumptions (H1)–H(2) hold. System (1) is passive if there exist matrices \(P, Q \in \mathbb {S}_{++}^n\), a matrix \(X \in \mathbb {S}_{+}^{5n}\), three matrices \(\varLambda _i = {{\,\mathrm{diag}\,}}\{\lambda _{i1}, \lambda _{i2}, \ldots , \lambda _{in}\} \in \mathbb {D}_{++}^{n} \, (i = 1, 2, 3)\) and a scalar \(\gamma > 0\) such that the following LMI holds

$$\begin{aligned} \begin{aligned}&\varXi = \delta ^{\mu }\mu ^{-1}\varPi ^T X \varPi + \sum \limits _{i=1}^{3}\varXi _i < 0 \\ \end{aligned} \end{aligned}$$
(13)

where

$$\begin{aligned}&\varPi = \begin{bmatrix} {\mathsf {r}}_1^T&{\mathsf {r}}_2^T&{\mathsf {r}}_3^T&{\mathsf {r}}_4^T&{\mathsf {r}}_5^T \end{bmatrix}^T,\\&\varPi _1 = {\mathsf {r}}_3 - \varSigma _1{\mathsf {r}}_1, \, \varPi _2 = \varSigma _2{\mathsf {r}}_1 - {\mathsf {r}}_3,\\&\varPi _3 = {\mathsf {r}}_4 - \varSigma _1{\mathsf {r}}_2, \, \varPi _4 = \varSigma _2{\mathsf {r}}_2 - {\mathsf {r}}_4,\\&\varPi _5 = {\mathsf {r}}_3 - {\mathsf {r}}_4 - \varSigma _1 \left( {\mathsf {r}}_1 -{\mathsf {r}}_2 \right) , \, \varPi _6 = \varSigma _2\left( {\mathsf {r}}_1 - {\mathsf {r}}_2\right) - {\mathsf {r}}_3 + {\mathsf {r}}_4,\\&\varSigma _1 = {{\,\mathrm{diag}\,}}\{l_1^-, \ldots , l_n^-\}, \, \varSigma _2 = {{\,\mathrm{diag}\,}}\{l_1^+, \ldots , l_n^+\}, \\&\varXi _1 = \mathsf {sym}\bigg ( {\mathsf {r}}_1^TP{\mathsf {r}}_5 - r_1^TQr_5 + {\mathsf {r}}_1^TQW_1{\mathsf {r}}_3 + {\mathsf {r}}_1^TQW_2{\mathsf {r}}_4 + {\mathsf {r}}_1^TQ{\mathsf {r}}_6 - {\mathsf {r}}_5^TQA{\mathsf {r}}_1 \\&\qquad + {\mathsf {r}}_5^TQW_1{\mathsf {r}}_3 + {\mathsf {r}}_5^TQW_2{\mathsf {r}}_4 + {\mathsf {r}}_5^TQ{\mathsf {r}}_6 - {\mathsf {r}}_3^TC_1^T{\mathsf {r}}_6 - {\mathsf {r}}_4^TC_2^T{\mathsf {r}}_6\bigg ),\\&\varXi _2 = {\mathsf {r}}_1^T\left[ -QA - A^TQ + P\right] {\mathsf {r}}_1 - {\mathsf {r}}_2^TP{\mathsf {r}}_2 + {\mathsf {r}}_5^T(-2Q){\mathsf {r}}_5 + {\mathsf {r}}_6^T\left( -C_3 - C_3^T - \gamma I\right) {\mathsf {r}}_6,\\&\varXi _3 = \mathsf {sym}\left( \varPi _1^T\varLambda _1\varPi _2 + \varPi _3^T\varLambda _2\varPi _4 + \varPi _5^T\varLambda _3\varPi _6\right) . \end{aligned}$$

Proof

Whenever \(u(t) \equiv 0, z(t) \equiv 0\), (13) implies (4). It follows from Theorem 1, system (1) with zero output vector and zero external input vector is asymptotically stable. To show the passivity analysis of system (1), we consider the Lyapunov function as considered in the proof of Theorem 1. By using the same technique as in Theorem 1, we obtain the following estimate

$$\begin{aligned} \begin{aligned}&D_t^{\mu }V(t) -2z^T(t)u(t) - \gamma u^T(t)u(t) \le \eta ^T(t)\varXi \eta (t), \end{aligned} \end{aligned}$$
(14)

where \(\eta (t) = \begin{bmatrix} x^T(t)&x^T(t-\delta (t))&g^T(x(t))&g^T(x(t-\delta (t)))&\left( D_{t}^{\mu }x(t)\right) ^T&u^T(t) \end{bmatrix}^T\). From (13), we get

$$\begin{aligned} \begin{aligned}&D_t^{\mu }V(t) -2z^T(t)u(t) - \gamma u^T(t)u(t) < 0, \, \forall t \ge 0. \end{aligned} \end{aligned}$$
(15)

Integrating (15) with respect to t from 0 to \(t_f\), we get

$$\begin{aligned} \begin{aligned}&I_{t_f}^{1}D_{t_f}^{\mu }V(t_f) - 2\int _{0}^{t_f}z^T(t)u(t)dt - \int _{0}^{t_f}\gamma u^T(t)u(t)dt < 0. \end{aligned} \end{aligned}$$
(16)

By using properties P2 and P3 on fractional-order calculus, we obtain

$$\begin{aligned} I_{t_f}^{1}D_{t_f}^{\mu }V(t_f)&= I_{t_f}^{1-\mu }I_{t_f}^{\mu }D_{t_f}^{\mu }V(t_f)\\&= I_{t_f}^{1-\mu }\left( I_{t_f}^{\mu }D_{t_f}^{\mu }V(t_f)\right) \\&= I_{t_f}^{1-\mu }\left( V(t_f) - V(0)\right) \\&= I_{t_f}^{1-\mu }V(t_f) - I_{t_f}^{1-\mu }V(0). \end{aligned}$$

On the other hand, we have

$$\begin{aligned}&I_{t_f}^{1-\mu }V(t_f)\\&= \frac{1}{\varGamma (1-\mu )}\int _{0}^{t_f}(t_f -t)^{-\mu }x^T(t)Px(t)dt \ge 0, \forall t_f \ge 0. \end{aligned}$$

Under zero initial condition, we can get the following estimate

$$\begin{aligned}&I_{t_f}^{1-\mu }V(0) \\&= \frac{1}{\varGamma (1-\mu )}\int _{0}^{t_f}(t_f -t)^{-\mu }x^T(0)Px(0)dt = 0, \forall t_f \ge 0. \end{aligned}$$

Hence, \(I_{t_f}^{1}D_{t_f}^{\mu }V(t_f) \ge 0, \forall t_f \ge 0\) with zero initial condition. Therefore, we have

$$\begin{aligned} J = \int _{0}^{t_f}\left( -2z^T(t)u(t) - \gamma u^T(t)u(t)\right) dt < 0, \forall t_f \ge 0. \end{aligned}$$

Hence,

$$\begin{aligned} 2\int _{0}^{t_f}z^T(t)u(t)dt> -\gamma \int _{0}^{t_f}u^T(t)u(t)dt, \, \forall t_f > 0. \end{aligned}$$

This completes the proof. \(\square \)

Remark 3

In [11], the authors used the Lyapunov direct method to derive order-independent passivity analysis criteria for FONNs without time delays. Here, we use the fractional Razumikhin theorem combined with some auxiliary properties of fractional calculus to obtain delay-dependent and order-dependent passivity analysis criteria for Caputo fractional-order neural networks with a time-varying delay. The model considered in this paper is more general, and our results are less conservative than the results in [11].

Remark 4

LMIs are useful tool for solving a wide variety of optimization and control problems. LMI-based conditions are solvable in polynomial time. In the literature, many efficient software packages such as Matlab’s LMI Control Toolbox, SP program and LMITOOL [44] have been developed to solve LMI problems. The LMI condition (4) in Theorem 1 (or (13) in Theorem 2) contains only five unknown matrices, one weighting-free matrix (or five unknown matrices, one weighting-free matrix, and a scalar) and depends on the parameters of the system under consideration as well as the delay bound. Therefore, these conditions can be easily verified by using existing efficient software packages. To find the feasible solution of the LMI in the case of bigger LMIs in size, it can be solved by the interior point algorithms in convex optimization technique and the LMI toolbox in MATLAB. Yet, there is an increase in computational time.

Remark 5

The bounded time-varying delay is considered in Theorem 1 and Theorem 2, if system (1) degenerates into ones with constant time delays, i.e., \(\delta (t) = \delta \), these results are still new and available. In future works, we will consider the problem of passivity analysis for some kind of FONNs with unbounded time-varying delays by using the method in [15] combined with LMI approach.

Remark 6

In the recent years, many results have been presented for passivity analysis of integer-order dynamical systems with time-varying delays [14, 22,23,24, 38, 40, 48, 50, 54, 58]. Since the fact that fractional derivatives are nonlocal and have weakly singular kernels, these approaches could not be extended to FONNs easily. This is the main reason that there are very few results on passivity analysis for FONNs. By using fractional-order Razumikhin theorem and some auxiliary properties on fractional calculus, we have solved the problem of passivity analysis for Caputo FONNs with a bounded time-varying delay for the first time. The method used in Theorem 2 can be regarded as an extension of the problem of passivity analysis for IONNs with bounded time-varying delays to fractional-order ones. Theorem 2 of this paper is new and has not been reported anywhere else in the literature.

Remark 7

In this paper, we consider the problem of passivity analysis for Caputo FONNs with a bounded time-varying delay. For the passive control problem of FONNs with bounded or unbounded time-varying delays, how to construct the output feedback controller, dynamic output feedback controller [9], the observer-based controller [25] or adaptive feedback controller [28] to solve the problem are interesting problems. These require further investigation in future works.

4 Numerical Examples

This section provides four numerical examples to show the effectiveness of the obtained results in this paper.

Example 1

Consider the FONNs (1) with \(u(t) \equiv 0, z(t) \equiv 0\) and the following parameters

$$\begin{aligned}&A = \begin{bmatrix} 0.8 &{} 0 \\ 0 &{} 0.9 \end{bmatrix}, \, W_1 = \begin{bmatrix} -0.05 &{} 0.01 \\ 0.23 &{} 0.01 \end{bmatrix}, \, W_2 = \begin{bmatrix} -0.01 &{} 0.12\\ 0.11 &{} 0.01 \end{bmatrix}, \\&C_1 = C_2 = C_3 = 0_2,\\&\mu = 0.9. \end{aligned}$$
Fig. 1
figure 1

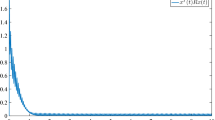
State trajectories of the system in Example 1

Full size image

The time delay is chosen as \(\delta (t) \equiv \delta = 1\). The activation function is given by

$$\begin{aligned} g(x(t)) = (\tanh x_1(t), \tanh x_2(t))^T \in \mathbb {R}^2. \end{aligned}$$

Hence, \(l_1^{-} = l_2^{-} = -1, l_1^+ = l_2^+ = 1\). We will show that the result in [6] cannot be applied in this example. By computing, we have \(\Vert W_1^*\Vert = \sum \limits _{i=1}^{2}\max \limits _{1 \le j \le 2}\{|w_{ij}^1|l_j^+\} = 0.24, \Vert W_2^*\Vert = \sum \limits _{i=1}^{2}\max \limits _{1 \le j \le 2}\{|w_{ij}^2|l_j^+\} = 0.23\) and \({\overline{a}} = \min \{1 - a_{\max }, a_{\min }\}\), where \(a_{\max } = \max \limits _{1\le i \le 2}\{a_{i}\} = 0.9\), \(a_{\min }= \min \limits _{1\le i \le 2}\{a_{i}\} = 0.8\). Hence, \({\overline{a}} = 0.1\). Therefore, \(\Vert W_1^*\Vert + \Vert W_2^*\Vert = 0.47 > {\overline{a}} = 0.1\) fails to satisfy the condition \(\Vert W_1^*\Vert + \Vert W_2^*\Vert < {\overline{a}}\) of Theorem 1 in [6]. However, by using LMI Control Toolbox in MATLAB [2], the LMI (4) in Theorem 1 is feasible with

$$\begin{aligned}&P = \begin{bmatrix} 35.6448 &{} -0.0734 \\ -0.0734 &{} 25.8804 \end{bmatrix}, \, Q = \begin{bmatrix} 38.1943 &{} 4.6044 \\ 4.6044 &{} 22.5124 \end{bmatrix}, \, \varLambda _1 = \begin{bmatrix} 2.1203 &{} 0 \\ 0 &{} 1.1505 \end{bmatrix}, \\&\varLambda _2 = \begin{bmatrix} 8.6505 &{} 0 \\ 0 &{} 6.8448 \end{bmatrix}, \, \varLambda _3 = \begin{bmatrix} 1.1170 &{} 0 \\ 0 &{} 0.6274 \end{bmatrix},\\&X = \left[ {\begin{matrix} 10.6959 &{} 1.5725 &{} 1.0797 &{} 0.0045 &{} -0.0107 &{} -0.0090 &{} -0.0866 &{} -2.3619 &{} 17.7301 &{} 4.5257 \\ 1.5725 &{} 5.1638 &{} 0.0129 &{} 0.5905 &{} -0.0603 &{} -0.0061 &{} -1.1958 &{} -0.4250 &{} 4.8263 &{} 8.5187 \\ 1.0797 &{} 0.0129 &{} 7.4599 &{} -0.0403 &{} -0.0065 &{} -0.0008 &{} 0.0039 &{} -0.0013 &{} 0.0536 &{} -0.0115\\ 0.0045 &{} 0.5905 &{} -0.0403 &{} 5.0246 &{} -0.0025 &{} -0.0003 &{} -0.0014 &{} 0.0010 &{} 0.0081 &{} 0.0113 \\ -0.0107 &{} -0.0603 &{} -0.0065 &{} -0.0025 &{} 2.9745 &{} 0.0005 &{} -1.0441 &{} 0.0025 &{} 0.3998 &{} -2.4481\\ -0.0090 &{} -0.0061 &{} -0.0008 &{} -0.0003 &{} 0.0005 &{} 1.6119 &{} 0.0008 &{} -0.5833 &{} -0.2196 &{} -0.1372 \\ -0.0866 &{} -1.1958 &{} 0.0039 &{} -0.0014 &{} -1.0441 &{} 0.0008 &{} 9.1402 &{} 0.0025 &{} -0.1055 &{} -1.2516\\ -2.3619 &{} -0.4250 &{} -0.0013 &{} 0.0010 &{} 0.0025 &{} -0.5833 &{} 0.0025 &{} 6.9571 &{} -2.5768 &{} -0.4562\\ 17.7301 &{} 4.8263 &{} 0.0536 &{} 0.0081 &{} 0.3998 &{} -0.2196 &{} -0.1055 &{} -2.5768 &{} 40.4116 &{} 5.4179\\ 4.5257 &{} 8.5187 &{} -0.0115 &{} 0.0113 &{} -2.4481 &{} -0.1372 &{} -1.2516 &{} -0.4562 &{} 5.4179 &{} 22.3863 \end{matrix}}\right] . \end{aligned}$$

By Theorem 1 and Remark 5, the system is asymptotically stable.

In order to obtain simulation results, let us choose initial value as \(\phi (t) = (0.5, -0.5)^T \in \mathbb {R}^2, \forall t \in [-1, 0]\). From Fig. 1, we can see that the states of the system are asymptotically stable.

Example 2

Consider the FONNs (1) with \(u(t) \equiv 0, z(t) \equiv 0\) and the following parameters

$$\begin{aligned}&A = \begin{bmatrix} 0.6 &{} 0 \\ 0 &{} 1 \end{bmatrix}, \, W_1 = \begin{bmatrix} 0.01 &{} 0.02 \\ -0.06 &{} 0.08 \end{bmatrix}, \, W_2 = \begin{bmatrix} 0.09 &{} 0.8 \\ -0.05 &{} 0.01 \end{bmatrix}, \\&C_1 = C_2 = C_3 = 0_2,\\&\mu = 0.8. \end{aligned}$$
Fig. 2
figure 2

State trajectories of the system in Example 2

Full size image

The activation functions are given by

$$\begin{aligned} g_i(x_i) = 0.5\left( |x_i + 1| - |x_i - 1|\right) , (i = 1, 2). \end{aligned}$$

It is easy to verify that condition (3) is satisfied with \(\varSigma _1 = {{\,\mathrm{diag}\,}}\{0, 0\}, \varSigma _2 = {{\,\mathrm{diag}\,}}\{1, 1\}.\) We let the time delay \(\delta (t) = |\sin (\omega t)|\), where \(\omega > 0\) is scalar. Note that \(\delta (t)\) is a continuous function but nondifferentiable at arbitrarily many points \(t_k = \frac{k\pi }{\omega }, k \in \mathbb {Z}^{+}\). As a consequence, the existing results, for example, in [6, 21, 47, 51, 57] cannot directly ensure stability of the system. By using the Matlab LMI toolbox [2], we obtain a set of feasible solutions as follows:

$$\begin{aligned}&P = \begin{bmatrix} 125.9724 &{} 91.1017 \\ 91.1017 &{} 812.9082 \end{bmatrix}, \, Q = \begin{bmatrix} 225.0191 &{} 63.9701 \\ 63.9701 &{} 578.4119 \end{bmatrix},\\&\varLambda _1 = \begin{bmatrix} 4.4149 &{} 0 \\ 0 &{} 53.7355 \end{bmatrix}, \, \varLambda _2 = \begin{bmatrix} 106.1268 &{} 0 \\ 0 &{} 538.3481 \end{bmatrix}, \, \varLambda _3 = \begin{bmatrix} 3.3803 &{} 0 \\ 0 &{} 20.2852 \end{bmatrix},\\&X = \left[ {\begin{matrix} 68.2618 &{} 16.9373 &{} 0.0586 &{} 7.3939 &{} -3.1959 &{} 0.2170 &{} -6.1585 &{} -93.8508 &{} 108.5540&{} 9.3645 \\ 16.9373 &{} 115.4775 &{} -0.2334 &{} 1.3804 &{} 0.9317 &{} -33.4051 &{} 10.7739 &{}-20.9265 &{} 21.6569 &{} 178.6727 \\ 0.0586 &{} -0.2334 &{} 53.3757 &{} 42.0356 &{} 1.5102 &{} 0.0595 &{}-47.1683 &{} -2.7751 &{} 0.3854 &{} 0.5384 \\ 7.3939 &{} 1.3804 &{} 42.0356 &{}390.6252 &{} 0.3321 &{} 11.1656 &{} -1.1784&{} -297.5324 &{} 9.5420 &{} 7.4973 \\ -3.1959 &{} 0.9317 &{} 1.5102 &{} 0.3321 &{} 6.3509 &{} -0.0866 &{} -2.8054 &{} -0.1412 &{} 0.7909 &{} 16.6528 \\ 0.2170 &{} -33.4051 &{} 0.0595 &{} 11.1656 &{} -0.0866 &{} 61.8614 &{} -0.2296 &{} -20.9664 &{} -4.2554 &{} -25.5241 \\ -6.1585 &{} 10.7739 &{} -47.1683 &{} -1.1784 &{} -2.8054 &{} -0.2296 &{} 92.9970 &{} 0.4991 &{} -7.7493 &{} 12.4623 \\ -93.8508 &{} -20.9265 &{} -2.7751 &{} -297.5324 &{} -0.1412 &{} -20.9664 &{} 0.4991 &{} 566.3696 &{} -100.4306 &{} -37.5642 \\ 108.5540 &{} 21.6569 &{} 0.3854 &{} 9.5420 &{} 0.7909 &{} -4.2554 &{} -7.7493 &{} -100.4306 &{} 205.9427 &{} 68.3705 \\ 9.3645 &{} 178.6727 &{} 0.5384 &{} 7.4973 &{} 16.6528 &{} -25.5241 &{} 12.4623 &{} -37.5642 &{} 68.3705 &{} 580.9007 \end{matrix}}\right] . \end{aligned}$$

According to Theorem 1, the system is asymptotically stable.

In order to obtain simulation results, let us choose the time delay as \(\delta (t) = |\sin t|\), initial value as \( \phi (t) = (1, -1)^T \in \mathbb {R}^2, \forall t \in [-1, 0]\). From Fig. 2, we can see that the states of the system are asymptotically stable.

Example 3

Consider the following two-dimensional FONNs with a time-varying delay

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} D_t^{0.7}x(t) = -Ax(t) + W_1g(x(t)) + W_2g(x(t-\delta (t))) + u(t), \, t \ge 0,\\ &{} z(t) = C_1g(x(t)) + C_2g(x(t-\delta (t))) + C_3u(t), \end{array}\right. } \end{aligned}$$
(17)

where \(x(t) = (x_1(t), x_2(t))^T \in \mathbb {R}^2\) is pseudo-state, \(u(t) \in \mathbb {R}^2\) is the external input of the network, \(z(t) \in \mathbb {R}^2\) is the output vector, and

$$\begin{aligned}&A = \begin{bmatrix} 1 &{} 0 \\ 0 &{} 1 \end{bmatrix}, \, W_1 = \begin{bmatrix} 0.02 &{} 0.03\\ 0.02 &{} -0.08 \end{bmatrix}, \, W_2 = \begin{bmatrix} 0.08 &{} 0.07 \\ -0.02 &{} 0.03 \end{bmatrix}, \\&C_1 = C_2 = C_3 = I_2. \end{aligned}$$

The activation functions are given by

$$\begin{aligned} g_i(x_i) = \tanh (x_i), \, (i = 1, 2). \end{aligned}$$

It is easy to verify that condition (3) is satisfied with \(\varSigma _1 = {{\,\mathrm{diag}\,}}\{-1, -1\}, \varSigma _2 = {{\,\mathrm{diag}\,}}\{1, 1\}.\) We let the time delay \(\delta (t) = \frac{t}{1+t}, \, t \ge 0\). By using the MATLAB LMI Control Toolbox, we can find a solution to the LMI (13) as follows \(\gamma = 942.1760\) and

$$\begin{aligned}&P = \begin{bmatrix} 434.5651 &{} -10.4605 \\ -10.4605 &{} 495.5811 \end{bmatrix}, \, Q = \begin{bmatrix} 470.1122 &{} 8.0855 \\ 8.0855 &{} 498.3805 \end{bmatrix}, \\&\varLambda _1 = \begin{bmatrix} 36.6030 &{} 0 \\ 0 &{} 56.0828 \end{bmatrix}, \, \varLambda _2 = \begin{bmatrix} 111.0305 &{} 0 \\ 0 &{} 122.0611 \end{bmatrix}, \, \varLambda _3 = \begin{bmatrix} 11.4239 &{} 0 \\ 0 &{} 17.1571 \end{bmatrix}, \\&X = \left[ \begin{matrix} 63.7531 &{} -0.8560 &{} 8.6797 &{} -0.0467 &{} 1.3715 &{} 0.3164 &{} -14.4626 &{} -13.3236 &{} 115.3794&{} 7.8165 \\ -0.8560 &{} 67.4771 &{} -0.0334 &{} 13.0923 &{} 0.1675 &{} 2.0417 &{} 3.9256 &{} -5.5215 &{} 8.0434 &{} 100.8383 \\ 8.6797 &{} -0.0334 &{} 69.6759 &{} -4.0231 &{} -0.0768 &{} 0.0046 &{} -0.0866 &{} -0.0390 &{} 0.4128 &{} -0.0239 \\ -0.0467 &{} 13.0923 &{} -4.0231 &{} 80.2866 &{} 0.0049 &{} -0.1324 &{} 0.0469 &{} -0.1432 &{} -0.0315 &{} 0.7677 \\ 1.3715 &{} 0.1675 &{} -0.0768 &{} 0.0049 &{} 36.9037 &{} -0.0240 &{} -6.8740 &{} 0.0966 &{} -4.8688 &{} -3.6488 \\ 0.3164 &{} 2.0417 &{} 0.0046 &{} -0.1324 &{} -0.0240 &{} 55.8719 &{} -0.1146 &{} -11.1018 &{} -5.0095 &{} 14.0761 \\ -14.4626 &{} 3.9256 &{} -0.0866 &{} 0.0469 &{} -6.8740 &{} -0.1146 &{} 92.4922 &{} -0.0287 &{} -17.1314 &{} 4.9761 \\ -13.3236 &{} -5.5215 &{} -0.0390 &{} -0.1432 &{} 0.0966 &{} -11.1018 &{} -0.0287 &{} 106.3481 &{} -14.3922 &{} -9.4709 \\ 115.3794 &{} 8.0434 &{} 0.4128 &{} -0.0315 &{} -4.8688 &{} -5.0095 &{} -17.1314 &{} -14.3922 &{} 295.5900 &{} 3.0156 \\ 7.8165 &{} 100.8383 &{} -0.0239 &{} 0.7677 &{} -3.6488 &{} 14.0761 &{} 4.9761 &{} -9.4709 &{} 3.0156 &{} 311.1612 \end{matrix}\right] . \end{aligned}$$

According to Theorem 2, we know that system (17) is passivity.

In order to obtain simulation results, let us choose initial value as \(\phi (t) = (0.5, -0.6)^T \in \mathbb {R}^2, \forall t \in [-1, 0]\). Figure 3 shows the state trajectories of system (17) with external input \(u(t) = (1-2\sin t, 1-3\cos t )^T \in \mathbb {R}^2\). Figure 4 displays the trajectories state of system (17) with zero external input, i.e., \(u(t) \equiv 0\), which shows that the FONNs with a bounded time-varying delay without external input is asymptotically stable.

Fig. 3
figure 3

State trajectories of the system in Example 3 with external input

Full size image
Fig. 4
figure 4

State trajectories of the system in Example 3 without external input

Full size image

Example 4

Consider the following three-dimensional FONNs with hub structure and a bounded time-varying delay [16]

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} D_t^{\mu }x(t) = -Ax(t) + W_1g(x(t)) + W_2g(x(t-\delta (t))) + u(t),\, t \ge 0,\\ &{} z(t) = C_1g(x(t)) + C_2g(x(t-\delta (t))) + C_3u(t), \end{array}\right. } \end{aligned}$$
(18)

where the order \(\mu \in {\mathbf {S}}: = \{0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1\}\), \(x(t) = (x_1(t), x_2(t), x_3(t))^T \in \mathbb {R}^3\) is pseudo-state, \(u(t) \in \mathbb {R}^3\) is the external input of the network, \(z(t) \in \mathbb {R}^3\) is the output vector, the time-varying function \(\delta (t) = \frac{t}{1+t}, t \ge 0\), \(A = {{\,\mathrm{diag}\,}}\{9, 8, 9\}\) and

$$\begin{aligned}&W_1 = \begin{bmatrix} 3 &{} -2 &{} -2 \\ 1 &{} 1 &{} 0 \\ 1 &{} 0 &{} 1 \end{bmatrix},\, W_{2} = I_3, \, C_1 = C_2 = C_3 = I_3. \end{aligned}$$

The activation functions are given by

$$\begin{aligned} g_i(x_i) = 0.5\left( |x_i + 1| - |x_i - 1|\right) , (i = 1, 2, 3). \end{aligned}$$

It is easy to verify that the time-varying function \(\delta (t)\) satisfies the condition (2) with \(\delta = 1\), the activation functions \(g_i(x_i)\) satisfy the condition (3) with \(\varSigma _{1} = \{0, 0, 0\}, \varSigma _2 = \{1,1,1\}\). Applying Theorem 2, it is found the FONNs under study are passive with the order \(\mu \in {\mathbf {S}}\). Table 1 shows the relationship between the order \(\mu \) and the passivity performance \(\gamma \).

Table 1 The relationship between the order \(\mu \) and the passivity performance \(\gamma \)
Full size table

In order to obtain simulation results, let us choose initial value as \(\phi (t) = (1, -1, -0.5)^T \in \mathbb {R}^3, \forall t \in [-1, 0]\). We consider three cases: \(\mu = 0.4\), \(\mu = 0.8\) and \(\mu = 1\). Figures 5, 6 and 7 display the trajectories of system (18) with zero external input and the order \(\mu = 0.4, \mu = 0.8\) and \(\mu = 1\), respectively. It is clear that the system is asymptotically stable.

Fig. 5
figure 5

State trajectories of the system in Example 4 with zero external input and order \(\mu = 0.4\)

Full size image
Fig. 6
figure 6

State trajectories of the system in Example 4 with zero external input and order \(\mu = 0.8\)

Full size image
Fig. 7
figure 7

State trajectories of the system in Example 4 with zero external input and order \(\mu = 1\)

Full size image

5 Conclusions

In this paper, we have investigated the problem of passivity analysis of FONNs with a time-varying delay. By using some auxiliary properties of fractional calculus and Razumikhin fractional-order theorem, new sufficient conditions for solving the passivity analysis problem have been presented in terms of LMIs. Some numerical examples with simulation results are given to illustrate the effectiveness of the proposed results. The method of studying delay-dependent passivity in this paper can be extended to other types of FONNs, such as switched FONNs with time-varying delays and fractional-order memristive neural networks. It is notable that the time-varying function in the considered system is bounded, then our future work is to extent the proposed results to FONNs with unbounded time-varying delays. The second proposal for future work is the study of observer-based control or adaptive feedback control problems for FONNs with bounded or unbounded time-varying delay.