1 Introduction

The fractional Fourier transform (FrFT) corresponds to a generalization of the ordinary Fourier transform, where noninteger powers of the respective operator are admitted. The FrFT was first exploited in quantum mechanics [18] and further used in several application scenarios, such as image encryption, optical signal processing, velocity estimation and vibration on SAR imagery, filtering, biomedical signal and image processing [6, 7, 9, 16, 20, 29]. Hardware FrFT implementations are frequently required in some of the aforementioned scenarios. Such implementations are normally designed from discrete versions of the transform (DFrFT), which should satisfy the following requirements: (i) numerical approximation of the continuous FrFT; (ii) unitarity; (iii) additivity; (iv) reduction to discrete Fourier transform (DFT) when the fractional order equals one. Additionally, it is expected that a DFrFT can be computed using some efficient algorithm [27].

Among the DFrFT approaches documented in the literature, the eigendecomposition-based DFrFT (ED-DFrFT) fulfills all the above listed requirements. On the other hand, the computational complexity of a N-point ED-DFrFT is \(\mathcal {O}(N^{2})\). The sampling-type DFrFT involves less computational complexity than ED-DFrFT, but they cannot satisfy additivity criterion (iii); this is critical, for example, in applications related to signal recovery, as demonstrated in [27]. Therefore, the scope of this work is restricted to ED-DFrFT implementations, due to the preservation of most requirements of a legitimate DFrFT.

Although subquadratic computational complexity algorithms for computing ED-DFrFT are still a shortcoming in the literature, recent studies promote reduced arithmetic complexity approaches [8, 17]; such a reduction can be achieved, for instance, by choosing suitable HGL DFT (Hermite–Gaussian-like) eigenbases that provide significant number of entries equal (or approximately) to zero in the eigenvectors [8]. In particular, HGL DFT eigenbases generated by closed-form expressions can perform the computation of ED-DFrFT with reducedFootnote 1 arithmetic complexity [7, 8, 14, 15]. On the other hand, eigenvectors based on matrices commuting with the DFT matrix operator generated by nonclosed-form procedures are not suitable for this task [3, 4, 10, 19, 25].

The scarce number of publications related to hardware architectures for ED-DFrFT computations does not address the development of dedicated hardware for generalized cases. For example, Sinha et al. [26], Acharya and Mukherjee [1] suggested similar architectures for computing the DFrFT of real-valued input vector. Cariow et al. [5] proposed processing unit structures for small size N-point DFrFTs (\(N<8\)). Although Prasad et al. [21] and Ray et al. [22] propose N-points DFrFT (N is odd or even positive integer) and \(2^{m}\)-points DFrFT (m is a positive integer) architectures, respectively, they do not exploit properly the error analysis of the proposed architectures and the arithmetic hardware complexity scales up as the number of points increase. Moreover, the method in [22] employs a simplified version of the DFrFT matrix, which may compromise the DFrFT accuracy. Therefore, the current literature still lacks of reliable, low complexity and no constrain hardware architectures for general cases of ED-DFrFT. In this paper, we intend to address this issue by introducing two different architectures for computing the DFrFT of a N-length complex-valued vector \(\textbf{x}\), where \(N = 4L\) and L is a positive integer, based on recent studies of ED-DFrFT with reduced arithmetic complexity [8]. We consider \(N = 4L\) or \(N = 2^{m}\) cases, \(m \in \{2,3,4,\ldots \}\), due to their practical usage in signal processing. However, without loss of generality, the proposed DFrFT architectures can also cover \(N \ne 4L\) cases with slight hardware changes.

We propose an architecture for DFrFT computation and then consider the implementation of this architecture using two different HGL DFT eigenbases. More precisely, we consider a DFrFT computation method that exploits symmetry and sparsity properties of HGL DFT eigenvectors used to define the DFrFT [8]. The considered HGL DFT eigenbases are those proposed in [3] and [15], which are, respectively, identified as \(\hbox {HGL}_1\) and \(\hbox {HGL}_2\). Thus, we refer to the considered implementation alternatives by means of the acronyms \(\hbox {HGL}_1\) and \(\hbox {HGL}_2\).

In this context, it is relevant to emphasize that our work does not constitute a direct hardware implementation of existing methods, but involves a series of decisions and architecture choices to achieve the results documented throughout our text. In particular, we confirm that the potential computational benefits suggested in the references we consider have repercussions on a practical implementation, which takes into account not only complexity in terms of numbers of arithmetic operations, but memory /registers, logic elements, percentage consumption of reconfigurable hardware resources, best datapath optimization, etc. Moreover, compared to other papers focused on implementing DFrFT in hardware, our proposal has the smallest footprint, whose value is also constant, regardless of the transform length.

The next sections of this paper are summarized as follows:

  • In Sect. 2, we describe the basic fixed-point arithmetic modules and the hardware architecture for computing an eigenvalue used in the proposed architectures;

  • In Sect. 3, we describe the \(\hbox {HGL}_1\) and \(\hbox {HGL}_2\) architectures for computing a N-point DFrFT, for \(N = 4L\) (L is a positive integer);

  • In Sect. 4, we validate the proposed hardware architectures by means of several tests for \(N \in \{8,16,32,64,128,256\}\). We carry out a comparative analysis taking into account software/hardware requirements, evaluating implementation complexity, latency and performance of the architectures when applied to signal compaction. In the analyzed scenarios, we verify that the \(\hbox {HGL}_2\) architecture achieved the best memory usage and speed performance among the proposed architectures.

2 Basic Modules

In the implemented architectures, we adopt the 32-bit two’s complement fixed-point number representation, where the first and the second most significant bits (MSB) are the signed integer part and the 30 lowest significant bits (LSB) are the fractional part of the number. The resolution is given by \(\delta = 2^{-30}\). In this manner, a real-valued number y represented as a 32-bit fixed-point number is limited by the range \(-2.0\le y \le 2.0 - \delta \) and has its fractional part given by the sum of negative powers of 2. This approach aims to reduce the hardware complexity usually associated with floating-point operations. We evaluate the approximation error propagation of each architecture in Sect. 4.

In what follows, we present the fixed-point arithmetic modules and a module to compute an eigenvalue used in the architectures.

2.1 Fixed-Point Arithmetic Modules

We describe the fixed-point arithmetic modules as follows:

  • Adder/subtractor: the sum/subtraction operation between 32-bit two’s complement fixed-point numbers is equivalent to sum/subtraction between 32-bit integers;

  • Fixed-point multiplier and bit shifting: the multiplier module performs the multiplication of two two’s complement 32-bit fixed-point numbers, whose output also gives a two’s complement 32-bit fixed-point number. Although the multiplication of two 32-bit numbers can generate a 64-bit number, the multiplier output provides a 32-bit two’s complement fixed-point number. Right/left-bit shifting represents multiplication/division by two in fixed-point;

  • RCM (real-complex multiplier) module: this module consists of two fixed-point multipliers, which perform two real multiplications between a real number represented as a 32-bit fixed-point number, x, and real/imaginary parts of a complex number represented as two 32-bit fixed-point numbers, u and v. Let \(z=x(u+jv)\), \(j\overset{\triangle }{=}\sqrt{-1}\,\), the outputs of the RCM module are two 32-bit fixed-point numbers, \(\Re (z)=x u\) and \(\Im (z)=x v\);

  • CCM (complex-complex multiplier) module: this module consists of three fixed-point multipliers, two subtractors and three adders. This module is based on [2], where a low complexity complex multiplication algorithm is described; it performs three real multiplications between sums/subtractions of real/imaginary parts of two complex numbers represented as 32-bit fixed-point numbers, x, y, u and v. Let \(z=(x+jy)(u+jv)\,\), the outputs of CCM module are two 32-bit fixed-point numbers, \(\Re (z)=(x-y)v + x(u-v)\) and \(\Im (z)=(x-y)v + y(u+v)\).

  • CORDIC module: this module consists of a lookup table, adders and shift registers (based on Volder’s algorithm [11, 28]). It computes cosine and sine of a fixed-point angle \(\theta \), \(0\le \theta <\pi /2\) rad. In this work, we use the CORDIC module imported from Altera IP core library ALTERA_CORDIC IP core [12].

2.2 Computation of an Eigenvalue \(\lambda _{n}^{a}\)

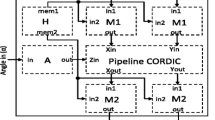
Let \(a\in \mathbb {R}\), \(-2.0\le a <2.0\), be the fractional order and \(\mathbf {\Lambda }^{a}=[\lambda _{0}^{a}, \lambda _{1}^{a}, \lambda _{2}^{a},\ldots , \lambda _{N-1}^{a}]^{T}\) be a column vector formed by the eigenvalues of the corresponding DFrFT matrix (the superscript T denotes row-column transposition of the argument). The Lambda module computes an eigenvalue

$$\begin{aligned} \lambda _{n}^{a}=e^{-j\frac{\pi }{2}\alpha }=\cos \left( \frac{\pi }{2}\alpha \right) -j\sin \left( \frac{\pi }{2}\alpha \right) , \end{aligned}$$
(1)

\(n \in \{0,1,2,\ldots ,N-1\}\), \(\alpha \in \{0,a,2a,\ldots ,(N-2)a, Na\}\) [8], by means of a fixed-point multiplier, one adder, a CORDIC module (see Fig. 1a) and a finite state machine (FSM) with 3 states (see Fig. 1b). From this point forward, in order to visually simplify the proposed architectures, in the figures, the labeled arrows containing the same name or symbol are physically connected and the [\(\cdot \); \(\cdot \)] notation means physical bit-array concatenation of two fixed-point numbers. The output data are two fixed-point numbers, \(\Re (\lambda _{n}^{a})\) and \(\Im (\lambda _{n}^{a})\), \(n \in \{0,1,2,\ldots ,N-1\}\). A controller external to this module loads the input a and enables/disables the start pin. In particular, the following states are specified:

  • State S1: if start pin is enabled, disable done pin and accumulate the a bus value to the \(\alpha \)-register accumulator. After \((N - 3)\) cycles of the state machine shown in Fig. 1b, the accumulated value will correspond to \((N - 2)a\);

  • State S2: verify trivial eigenvalue possibilities. If yes, update the \(\lambda _{n}^{a}\) bus output according to \(\alpha \)-register value, enable done pin and the next state is S1. Otherwise multiply the \(\alpha \)-register value by \(\pi /2\) and the next state is S3;

  • State S3: after 15 clock cycles, route the CORDIC module outputs to \(\lambda _{n}^{a}\) bus output. Enable done pin and the next state is S1.

Fig. 1
figure 1

Lambda module that computes an eigenvalue \(\lambda _{n}^{a}\): a architecture; b FSM

Full size image

3 DFrFT Hardware Architectures

In this section, we describe two architectures for computing the N-point DFrFT (\(N=4L\), L is a positive integer). We consider the DFrFT computation method proposed in [8] using the HGL eigenbases proposed in [3, 15]: (i) Architecture HGL\(_1\); (ii) Architecture HGL\(_2\), whose memory block structures, data path and FSM of each architecture are presented.

3.1 Architecture \(\hbox {HGL}_1\)

Considering the method proposed in [8], we can compute the DFrFT of a vector \(\textbf{x} \in \mathbb {C}^N\) through right-to-left matrix multiplications between \(\textbf{x}\), \(\textbf{V}^{T}\), \(\textrm{diag}(\mathbf {\Lambda }^{a})\) and \(\textbf{V}\), that is,

$$\begin{aligned} \textbf{X}^{a}=(\textbf{V}\textrm{diag}(\mathbf {\Lambda }^{a})\textbf{V}^{T})\textbf{x}, \end{aligned}$$
(2)

with reduced arithmetic complexity by generating intermediate vectors

$$\begin{aligned} \textbf{x}'= & {} \textbf{V}^{T}\textbf{x}, \end{aligned}$$
(3)
$$\begin{aligned} \textbf{x}''= & {} \mathbf {\Lambda }^{a}\circ \textbf{x}', \end{aligned}$$
(4)
$$\begin{aligned} \textbf{X}^{a}= & {} \textbf{V}\textbf{x}'', \end{aligned}$$
(5)

where \(\textrm{diag}(\;)\) is a diagonal matrix, whose main diagonal consists of the argument elements [23].

3.1.1 Memory Blocks

In order to synthesize a hardware architecture based on the method described in [8] using the HGL eigenbasis proposed in [3], we design 6 memory blocks aiming to optimize the memory usage, memory access and latency, during the computation of the intermediate vector \(\textbf{x}'\) and output \(\textbf{X}^{a}\):

  • Two memory blocks store nonzero distinct absolute elements of the matrix \(\textbf{V}^{T}\): (i) the memory block sram-\(V^{T}\) consists of \((N/2-1)N\) memory addresses, where each address stores a fixed-point number, \(\textbf{V}^{T}_{n,i}\), \(n \in \{0,1,2,\ldots ,N-1\}\), \(i \in \{1,2,3,\ldots ,N/2-1\}\); and (ii) the memory block sram-\(V_{0\vert N/2}^{T}\) consists of \(N/2+1\) memory addresses, where each address stores two fixed-point numbers, \(\textbf{V}^{T}_{p,0}\) and \(\textbf{V}^{T}_{p,N/2}\,\), \(p \in \{0,2,4,\ldots ,N-2,N-1\}\);

  • Two memory blocks store elements of \(\textbf{x}\) and \(\textbf{X}^{a}\): (i) the memory block sram-x consists of N/2 memory addresses, where the content of the first memory address stores four fixed-point numbers, \(\Re (\textbf{x}_{0})\), \(\Im (\textbf{x}_{0})\), \(\Re (\textbf{x}_{N/2})\), \(\Im (\textbf{x}_{N/2})\), and the remaining addresses store \(\Re (\textbf{x}_{i})\), \(\Im (\textbf{x}_{i})\), \(\Re (\textbf{x}_{N-i})\), \(\Im (\textbf{x}_{N-i})\), \(i \in \{1,2,\ldots ,N/2-1\}\); and (ii) a memory block with the same structure as sram-x, sram-\(X^{a}\), stores the elements of \(\textbf{X}^{a}\), where the content of the first memory address stores four fixed-point numbers, \(\Re (\textbf{X}_{0}^{a})\), \(\Im (\textbf{X}_{0}^{a})\), \(\Re (\textbf{X}_{N/2}^{a})\), \(\Im (\textbf{X}_{N/2}^{a})\), and the remaining addresses store \(\Re (\textbf{X}^{a}_{i})\), \(\Im (\textbf{X}^{a}_{i})\), \(\Re (\textbf{X}^{a}_{N-i})\), \(\Im (\textbf{X}^{a}_{N-i})\), \(i \in \{1,2,\ldots ,N/2-1\}\);

  • Two memory blocks store elements of \(\textbf{x}'\) and \(\textbf{x}''\): two memory blocks, sram-x’ and sram-x”, consist of N memory addresses, where each memory address stores two fixed-point numbers, \(\Re (\textbf{x}'_{n})\) and \(\Im (\textbf{x}'_{n})\), \(\Re (\textbf{x}''_{n})\) and \(\Im (\textbf{x}''_{n})\), \(n \in \{0,1,2,\ldots ,N-1\}\), respectively.

3.1.2 Computation of the Intermediate Vector \(\textbf{x}'\)

In this section, we describe the synthesized module that executes the arithmetic operations in (3). For optimization purposes, we take into account the symmetry properties of \(\hbox {HGL}_1\) eigenvectors (rows of matrix \(\textbf{V}^{T}\)). We implement a RCM module, a CCM module and 8 adders, as shown in Fig. 2a. We adopt \(\Re (\;\cdot \;\vert \;\cdot \;)\) or \(\Im (\;\cdot \;\vert \;\cdot \;)\) notations to label a bus/register that is assigned to either the first or the second argument according to the memory address of the respective memory block structures of each variable as described in Sect. 3.1.1.

A FSM with 3 states, orchestrated by the Control module, computes the elements of \(\textbf{x}'\), as shown in Fig. 2b. Through the sram-\(V^{T}\)-address, sram-\(V_{0\vert N/2}^{T}\)-address and sram-x-address output buses, the Control module recursively selects the respective memory block addresses to be read; and they are loaded in the sram-\(V^{T}\)-readdata, sram-\(V_{0\vert N/2}^{T}\)-readdata, sram-x-readdata input buses according to machine states routines. Moreover, after the recursive computation of each \(\textbf{x}'\) component, the Control module selects the respective memory address, sram-x’-address, and writes into it through the sram-x’-writedata bus. In particular, the following states are specified:

  • State S1: set the write/\(\overline{\text{ read }}\) enable pin to low. Update the RCM and CCM inputs with elements of \(\textbf{V}^{T}\) and sum/subtraction of \(\textbf{x}_{0}\) or \(\textbf{x}_{N/2}\), and \(\textbf{x}_{i}\) or \(\textbf{x}_{N-i}\), \(i \in \{1,2,3..,N/2-1\}\) (according to the current value of sram-x’-address) stored into their respective registers. Update the sram-x-address and sram-\(V^{T}\)-address buses. The next state is S2;

  • State S2: update the x-registers and \(V^{T}\)-registers. If the sram-x-address value is zero, the mac-registers accumulators initialize with the sum of RCM and CCM outputs. Otherwise accumulate the RCM outputs in the mac-registers. If the Control module reads the last sram-x memory address, then the next state is S3. Otherwise the next state is S1;

  • State S3: route the mac-registers values to the sram-x’-writedata buffer of the sram-x’ current address and set the write/\(\overline{\text{ read }}\) enable pin to high. Clear the mac-registers. If the current value of sram-x’-address is \(N-1\), then the computation of \(\textbf{x}'\) is finished. Otherwise the next state is S1;

Fig. 2
figure 2

Module for computing the intermediate vector \(\textbf{x}'\): a architecture; b FSM

Full size image

3.1.3 Computation of the Intermediate Vector \(\textbf{x}''\) and the Elements \(\textbf{X}_{0}^{a}\) and \(\textbf{X}_{N/2}^{a}\)

In this section, we describe the synthesized module that executes the arithmetic operations in (4), where the computation of each element of \(\Lambda ^{a}\) and the element-wise multiplication between the elements of \(\Lambda ^{a}\) and \(\textbf{x}'\) are performed. Moreover, for latency optimization purpose, this module also computes the elements \(\textbf{X}_{0}^{a}\) and \(\textbf{X}_{N/2}^{a}\) using the elements stored in the memory block sram-\(V_{0\vert N/2}^{T}\) described in Sect. 3.1.1. We implement a Lambda module, RCM and CCM modules (shared with the architecture explored in Sect. 3.1.2), 4 adders and a left-bit shift register, as shown in Fig. 3a.

A FSM with 5 states, orchestrated by Control module, computes the elements of \(\textbf{x}''\), \(\textbf{X}_{0}^{a}\) and \(\textbf{X}_{N/2}^{a}\), as shown in Fig. 3b. Through the sram-x’-address and sram-\(V_{0\vert N/2}^{T}\)-address output buses, the Control module recursively selects the respective memory block addresses to be read; and they are loaded in the sram-x’-readdata and sram-\(V_{0\vert N/2}^{T}\)-readdata input buses according to machine states routines. Moreover, after the recursive computation of each element of \(\Lambda ^{a}\), followed by the computation of each element of \(\textbf{x}''\), the Control module selects the respective memory address, sram-x”-address, and writes into it through the sram-x”-writedata bus. Furthermore, the Control module selects the first address of the memory block sram-\(X^{a}\) and write into it through the sram-\(X^{a}\)-writedata bus. As the selected fractional order a is constant during the computation of a DFrFT, the value stored in a-register remains the same. In particular, the following states are specified:

  • State S1: if the current value of sram-x’-address is equal to \(N-1\), then load 2a to the a input port of Lambda module. Otherwise, load a. Enable start pin. The next state is S2;

  • State S2: compute an eigenvalue \(\lambda _{n}^{a}\) and store it in the \(\lambda _{n}^{a}\)-registers. Update the CCM inputs with the values of \(\lambda _{n}^{a}\)-registers and x’\(_{n}\)-registers. The next state is S3;

  • State S3: route the values stored in the \(V_{p,0}^{T}\)-register, \(V_{p,N/2}^{T}\)-register and CCM outputs to the RCM and CCM inputs. Route the CCM outputs to the sram-x”-writedata buffer for writing into the current address sram-x”-address and set the write/\(\overline{\text{ read }}\) enable pin to high. The next state is S4;

  • State S4: set the write/\(\overline{\text{ read }}\) enable pin to low. Accumulate the RCM and CCM output values in the \(X_{0}^{a}\)-registers and \(X_{N/2}^{a}\)-registers. Update sram-x’-address and sram-x”-address. If the current value of sram-x”-address is \(N-1\), then the computation of \(\textbf{x}''\) is finished and the next state is S5. Otherwise the next state is S1;

  • State S5: route the \(X_{0}^{a}\)-registers and \(X_{N/2}^{a}\)-registers values to the sram-\(X^{a}\) -writedata buffer for writing into the first address of sram-\(X^{a}\) and set the write / \(\overline{\text{ read }}\) enable pin to high.

Fig. 3
figure 3

Module for computing the intermediate vector \(\textbf{x}''\): a architecture; b FSM

Full size image

3.1.4 Computation of Vector \(\textbf{X}^{a}\)

In this section, we describe the synthesized module that executes the arithmetic operations in (5), except for the elements \(\textbf{X}_{0}^{a}\) and \(\textbf{X}_{N/2}^{a}\), which are computed in the module described in Sect. 3.1.3. Thus, this module recursively and simultaneously computes each element of \(\textbf{X}_{i}^{a}\) and \(\textbf{X}_{N-i}^{a}\), \(i \in \{1,2,\ldots ,N/2-1\}\). We implement 6 adders and a RCM module (shared with the architectures explored in Sects. 3.1.2 and 3.1.3) for arithmetic operations in (5) regarding the computation of \(\textbf{X}^{a}\), as shown in Fig. 4a.

A FSM with 3 states, orchestrated by the Control module, computes the remaining elements of \(\textbf{X}^{a}\), as shown in Fig. 4b. Through the sram-\(V^{T}\)-address and sram-x”-address output buses, the Control module selects recursively the respective memory block addresses to be read; and they are loaded in the sram-\(V^{T}\)-readdata, sram-x”-readdata input buses according to machine states routines. Moreover, after the recursive computation of each \(\textbf{X}^{a}\) component, the Control module selects the respective memory address, sram-\(X^{a}\)-address, and writes into it through the sram-\(X^{a}\)-writedata bus. In particular, the following states are specified:

  • State S1: update the RCM inputs with the values of x”\(_{n}\)-registers and \(V_{n,i}^{T}\)-register. Update the addresses sram-x”-address and sram-\(V^{T}\)-address. The next state is S2;

  • State S2: if the current value of sram-x”-address is equal to \(N-1\), then route the values of \(X_{i}^{a}\)-registers and \(X_{N-i}^{a}\)-registers to the sram-\(X^{a}\)-writedata bus for writing into the current memory address sram-\(X^{a}\)-address, set the write/\(\overline{\text{ read }}\) enable pin to high and the next state is S3. Otherwise accumulate the values provided in the RCM outputs positively or negatively (for odd or even values of sram-x”-address, respectively) to the \(X_{i}^{a}\)-registers and \(X_{N-i}^{a}\)-registers and the next state is S1;

  • State S3: set the write/\(\overline{\text{ read }}\) enable pin to low. If sram-\(X^{a}\)-address value is equal to \(N/2-1\), then the computation of \(\textbf{X}^{a}\) is finished. Otherwise clear the accumulators \(X_{i}^{a}\)-registers and \(X_{N-i}^{a}\)-registers, update the sram-\(X^{a}\)-address and the next state is S1.

Fig. 4
figure 4

Module for computing the \(\textbf{X}^{a}\): a architecture; b FSM

Full size image

3.2 Architecture \(\hbox {HGL}_2\)

The architecture proposed in this section is also based on the DFrFT computation method given in [8] method, which employs intermediate vectors. Therefore, it is similar to the architecture described in Sect. 3.1. However, in the current case, the eigenbasis proposed in [15] is used. The changes resulting from this choice are detailed below.

3.2.1 Memory Blocks

In order to minimize the memory usage and the memory access during the DFrFT computation, we design three memory blocks that store nonzero distinct absolute elements of \(\textbf{V}^{T}\): (i) the memory block sram-\(V^{T}\) stores nonzero distinct absolute elements of \(\textbf{V}^{T}_{m,i}\), \(m \in \{0,1,2,\ldots ,N-3\}\), \(i \in \{1,2,3,\ldots , N/2 - 1\}\), where each address stores a fixed-point number; (ii) the memory block sram-\(V_{N/2}^{T}\) consists of \(N/2 - 1\) memory addresses, where each memory address stores a fixed-point number, \(\textbf{V}^{T}_{q,N/2}\), \(q \in \{0,2,4,\ldots ,N-4\}\); and (iii) the memory block sram-\(V^{T}_{\Phi _{N-2}\vert \Phi _{N-1}}\) stores four fixed-point numbers, \(\textbf{V}^{T}_{N-2,0}\), \(\textbf{V}^{T}_{N-1,0}\), \(\textbf{V}^{T}_{N-2,1}\) and \(\textbf{V}^{T}_{N-1,2}\), that represent the distinct absolute elements of the eigenvectors \(\Phi _{N-2}\) and \(\Phi _{N-1}\) [8].

Furthermore, we implement the same memory block structures described in Sect. 3.1 for \(\textbf{x}\), \(\textbf{x}'\), \(\textbf{x}''\) and \(\textbf{X}^{a}\) storage, but with slight changes of \(\textbf{x}\) and \(\textbf{X}^{a}\) indexes as described in the following steps.

3.2.2 Computation of the Intermediate Vectors \(\textbf{x}'\)

The computation of the intermediate vector \(\textbf{x}'\) employs an architecture and FSM similar to those explored in Sect. 3.1.2, where the elements \(\textbf{x}_{0}\,\), \(\textbf{x}_{N/2}\) become \(\textbf{x}_{N/2-1}\,\), \(\textbf{x}_{N-1}\), respectively, and \(\textbf{x}_{i}\,\), \(\textbf{x}_{N-i}\,\), \(i \in \{1,2,3,\ldots ,N/2-1\}\), become \(\textbf{x}_{i}\,\), \(\textbf{x}_{N-2-i}\,\), \(i \in \{0,1,2,\ldots ,N/2-2\}\), respectively.

Moreover, we increment two accumulators and a second CCM module for a fast computation of \(\textbf{x}'_{N-2}\) and \(\textbf{x}'_{N-1}\). Due to repeated components of eigenvectors \(\Phi _{N-2}\) and \(\Phi _{N-1}\) [8], we can compute \(\textbf{x}'_{N-2}\) and \(\textbf{x}'_{N-1}\) through positive/negative accumulation of the \(\textbf{x}\) elements and four multiplications.

3.2.3 Computation of the Intermediate Vector \(\textbf{x}''\) and the Elements \(\textbf{X}_{N/2-1}^{a}\) and \(\textbf{X}_{N-1}^{a}\)

The computation of the intermediate vector \(\textbf{x}''\) follows the same architecture and FSM explored in Sect. 3.1.3. However, the elements \(\textbf{X}^{a}_{0}\,\), \(\textbf{X}^{a}_{N/2}\) become \(\textbf{X}^{a}_{N/2-1}\,\), \(\textbf{X}^{a}_{N-1}\,\), respectively. Using two CCM modules, we recursively compute the elements of \(\textbf{x}''\), \(\textbf{X}^{a}_{N/2-1}\) and \(\textbf{X}^{a}_{N-1}\).

3.2.4 Computation of \(\textbf{X}^{a}\)

The computation of \(\textbf{X}^{a}\) employs an architecture and a FSM similar to those explored in Sect. 3.1.4. However, the elements \(\textbf{X}^{a}_{i}\,\), \(\textbf{X}^{a}_{N-i}\,\), \(i \in \{1,2,3,\ldots ,N/2-1\}\), become \(\textbf{X}^{a}_{i}\,\), \(\textbf{X}^{a}_{N-2-i}\,\), \(i \in \{0,1,2,\ldots ,N/2-2\}\), respectively.

4 Implementation and Results

We design the hardware architectures in Verilog on the Intel Cyclone V field-programmable gate array (FPGA) SoC 5CSEMA5F31C6 [13], using Quartus Prime 18.1 Standard Edition. The FPGA has 32,070 logic elements and 4,065,280 bits of on-chip SRAM. The 5CSEMA5F31C6 chip also includes a hard processor unit (HPS), represented by a Dual-Core ARM Cortex-A9 processor. A Linux-distributed operational system (OS) runs in the HPS, where programs (written in C programming language) establish Ethernet/UDP communication between computer and HPS. The HPS also exchanges data with the FPGA architectures through a shared dual-port on-chip SRAM.

In particular, for test purposes of each architecture, the HPS stores once into the shared on-chip SRAM the elements of the matrix \(\textbf{V}^{T}\) of eigenvectors through memory mapping; it receives the complex-valued vector \(\textbf{x}\) and fractional order a from the computer; performs vector normalization and floating-point to fixed-point conversions; stores a and \(\textbf{x}\) into the shared on-chip SRAM; and enables the DFrFT computation of the respective values of a and \(\textbf{x}\). Later, the HPS performs fixed-point to floating-point conversions; sends the output vector \(\textbf{X}^{a}\) and FPGA latency (in clock cycles) to the computer. Additionally, in the application related to compact representation in fractional Fourier domain (see details in Sect. 4.4), the HPS also executes an optimum fractional order searching algorithm; sends the optimum fractional order, measurement of compactness and searching time delay (in seconds) to the computer.

In this way, we can validate the proposed architectures using a high level programming language. In this work, we use the MATLAB to perform such a task. Figure 5 illustrates the hardware setup designed to validate the architectures and applications. The computer USB terminal performs debugging procedures and sends commands to the HPS.

Fig. 5
figure 5

Hardware setup for testing the implemented designs and communication between computer, HPS and FPGA

Full size image

4.1 Synthesis Results

In Table 1, the synthesis results of the architectures described in Sect. 3 are presented; it provides the number of logical elements (LE), number of registers, number of 32-bit Adders/Subtractors and 32-bit fixed-point multipliers used in each architecture. We observe that the \(\hbox {HGL}_2\)-based architecture requires a larger number of hardware elements than the \(\hbox {HGL}_1\)-based architecture. This is in line with the fact that, due to the distinct symmetry and outperforming sparsity of \(\hbox {HGL}_2\) eigenbasis compared to \(\hbox {HGL}_1\) eigenbasis [8], we enhance the memory access and parallel arithmetic operations of \(\hbox {HGL}_2\)-based architecture aiming to optimize the latency performance.

Table 1 Synthesis results for the proposed DFrFT architectures
Full size table

Table 2 provides the number of memory bits used by the architectures in the Cyclone V and their usage percentages (in parentheses) provided by Quartus for \(N = 8,16,32,64,128,256\). We remark that the \(\hbox {HGL}_2\)-based architecture requires smaller memory allocation than the \(\hbox {HGL}_1\)-based architecture due to the smaller number of nonzero distinct absolute elements of \(\hbox {HGL}_2\) eigenbasis matrix \(\textbf{V}^{T}\) stored in SRAM and required to compute a DFrFT.

Table 2 Memory usage (bits) for the proposed DFrFT architectures
Full size table

For test purposes, we generate in MATLAB a set of 1000 random input vectors \(\textbf{x}\in \mathbb {C}^N\), where each element of \(\textbf{x}\), \(\textbf{x}_{n}\), is bounded by \(-1.0\le \Re (\textbf{x}_{n}) \le 1.0\) and \(-1.0 \le \Im (\textbf{x}_{n})\le 1.0\), and a set of 1000 random fractional orders a, \(-2.0\le a<2.0\). In order to compare the architectures in terms of accuracy, we compute 1000 N-DFrFTs of \(\textbf{x}\) for \(N \in \{{8,16,32,64,128,256}\}\) in MATLAB with double-precision floating-point number representation, using the \(\hbox {HGL}_{1}\) and \(\hbox {HGL}_{2}\) eigenbases, and consider the obtained results as a reference.

On the HPS side, a program stores once nonzero distinct absolute elements of eigenvectors matrix \(\textbf{V}^{T}\) in 32-bit fixed-point format into the shared SRAM memory blocks, according to the DFrFT architecture. For each DFrFT computation, the computer sends to the HPS a respective input vector \(\textbf{x}\) and a fractional order a in double-precision floating-point number format.

Before each DFrFT computation procedure, the HPS normalizes each input vector \(\textbf{x}\), converts the 64-bit floating-point elements of a and \(\textbf{x}\) to 32-bit fixed-point numbers, stores into the sram-x memory block and enables the DFrFT computation according to the respective DFrFT architecture. The normalization approach avoids fixed-point overflows during arithmetic operations performed by the FPGA.

The HPS reads the sram-\(X^{a}\) memory block and converts the \(\textbf{X}^{a}\) elements (computed by the FPGA running at a clock frequency of 100 MHz) from fixed to floating-point and multiplies the \(\textbf{X}^{a}\) by the norm of the input vector \(\textbf{x}\). The HPS sends the DFrFT of a respective input vector \(\textbf{x}\) and latency in clock cycles (counted by the FPGA) to the computer. The computer then performs the latency and accuracy analysis.

In Table 3, the root mean squared error (RMSE) and latency (in clock cycles) of each DFrFT architecture computed by the HPS-FPGA are shown. The DFrFT latency of integer fractional orders \(a = 0, 1, -1, -2\) is shown in parentheses. We observe that the \(\hbox {HGL}_{2}\)-based architecture achieved better accuracy and latency than \(\hbox {HGL}_{1}\)-based architecture to compute a N-point DFrFT. We suggest that this fact is caused by the lowest required number of arithmetic operations to calculate a DFrFT [8].

Table 3 RMSE and latency of each proposed DFrFT architecture
Full size table

During this research, we also synthesized a DFrFT computation architecture based on the method proposed in [17] using the \(\hbox {HGL}_1\) and \(\hbox {HGL}_2\) eigenbases. We observed that such an architecture requires a larger number of hardware elements and is significantly slower than the proposed architecture. This is in line with the fact that, according to the method given in [17], the \(N\times N\) DFrFT matrix can be decomposed into two (for an odd N) or three (for an even N) matrices. Then, the DFrFT of an input vector can be written as sums of low complexity matrix products. However, the elements of these complex-valued matrices need to be computed. Therefore, the hardware requirements and timing performance for the DFrFT computation are compromised.

4.2 Comparative Analysis

In order to compare the results obtained by the proposed DFrFT architectures, we also compute in MATLAB the continuous FrFT of the rectangular pulse [7, 18]. In Fig. 6, we use \(N=256\) and plot the DFrFT magnitudes (computed by the HPS-FPGA) and sampled versions of continuous FrFT magnitudes of the rectangular pulse. Inspecting Fig. 6a–c, one can observe that the graphs have similar visual aspects. In Fig. 6d, the graphs overlap each other, assuming, in all cases, the aspect of a sync function.

Fig. 6
figure 6

Comparison of normalized absolute values of continuous FrFT (computed in MATLAB), \(\hbox {HGL}_1\) and \(\hbox {HGL}_2\) architectures (computed by HPS-FPGA) for \(N = 256\) points: a \(a = 0.25\); b \(a = 0.50\); c \(a = 0.75\); d \(a = 1.00\)

Full size image

In order to evaluate the accuracy of DFrFTs compared to continuous FrFT of the rectangular pulse, we vary the fractional order a at a step of 0.01 and compute the RMSE. The result is shown in Fig. 7, where we observe no significant differences between the DFrFTs computed by the architectures.

Fig. 7
figure 7

RMSE of \(\hbox {HGL}_1\) and \(\hbox {HGL}_2\)-based DFrFTs compared to continuous FrFT for \(N = 256\)

Full size image

Due to similar odd/even symmetry patterns of the matrices \(\textbf{V}^{T}\) of eigenvectors, verified in [3, 15], the strategies described in Sect. 3 are fully applicable to DFrFT for \(N \ne 4L\), L is a positive integer. We just have to modify the variable indexes of the memory blocks and FSM to adapt the memory accesses based on strategies mentioned in [8].

4.3 Comparison with Related Works

Except the implementations presented in [5], which covers small size DFrFTs (\(N<8\)), and [1, 26], which are discussed in [22] and cover DFrFTs of real-valued input vectors, we can compare the proposed architectures with approaches given in [21, 22]. The hardware complexity and latency details of the proposed and existing architectures [21, 22] are presented in Table 4 for 256-point DFrFT case. Other cases covered in this paper can be compared by means of hardware requirement formulas presented in [21, 22]. The arithmetic hardware complexity (number of adders/subtractors and multipliers) of our architectures is constant and significantly lower (at least, a 96% and 88% reduction of multipliers and adders/subtractors, respectively, for 256-point DFrFT computation) than the increasing complexity of [21, 22] architectures (limited to \(\mathcal {O}(4N)\) and \(\mathcal {O}(2N)\), respectively). Although the memory usage of our architectures is higher than [22] and lower than [21] architectures, the number of registers is significantly lower than [21, 22] methods. Due to pipelined approaches proposed in [21, 22], they achieved higher throughput. However, the existing ED-DFrFT architectures in the literature do not provide detailed error analysis (similar to those discussed in Sects. 4.1 and 4.2) to compare the accuracy of their methods with ours regarding a paramount feature of a DFrFT, the numerical approximation of the continuous FrFT. They also do not carry out tests with distinct values of N, complex-valued input vector \(\textbf{x}\) and fractional order a. In view of the above, a complete comparison, in terms of accuracy, between our proposal and those presented in the cited papers is not feasible, considering the scope of the current paper.

In summary, comparing our architectures with similar existing architectures (i.e., no input constrains nor limited values of N) in the literature [21, 22] regarding the hardware requirements, we conclude that the appropriate architecture depends on the application priority. If timing optimization is required, then [22] reaches the best latency. Otherwise, if a circuit area minimal solution is required, our architectures are more suitable.

Table 4 Comparison of hardware complexity and latency of the proposed architectures with the existing architectures for 256-point DFrFT
Full size table

We can also compare our architectures with that proposed in [30]. In this context, it is relevant to point out that, in the cited paper, a sampling-type DFrFT is considered (please, see the second paragraph of Sect. 1). Moreover, in [30], the architecture is restricted to the computation of a 256-point DFrFT, without a report of how the hardware complexity behaves for general N-point transforms, nor numerical error analysis (only a qualitative architecture error analysis for a small set of input signal and parameters is provided). A fair comparison of latency in clock cycles between [30] and our architectures is unfeasible, because, although the cited paper provides the latency in microseconds (\(=2.819 \mu s\)), it does not inform the running clock frequency. The proposed \(\hbox {HGL}_2\) architecture has memory requirements (in bits) similar to those given in [30], \(\approx 848\) kbits and 828 kbits, respectively [31]. Although the arithmetic hardware complexity is not properly detailed (numbers of adders and multipliers) in [30], according to the FPGA documentation used in the referred work [31], we can deduce that the number of required arithmetic hardware component is significantly higher than that required in our architectures. Finally, the number of registers used in the referred architecture is, at least, 7 times greater than ours. In brief, even taking into account the caveats outlined above and the incompleteness of some experiments and records in [30], our preliminary conclusion is that, in terms of hardware complexity, our architectures outperform that described in the cited paper.

4.4 Compact Fractional Fourier Domains

In order to analyze the searching performance of an optimum fractional order for compact fractional Fourier domain, \(a_{opt.}\), and measurement of compactness, \(l_{1}\)-norm, of each DFrFT architecture, we apply the minimum norm method (MNM) proposed in [24] considering the same synthetic bi-component chirp signal used in [8] for \(N = 256\). A program runs the MNM algorithm in the HPS, while the FPGA computes the DFrFTs through the proposed DFrFT architectures.

Based on the method given in [8], we can search the \(a_{opt.}\) using the same intermediate vector \(\textbf{x}'\). Therefore, the proposed architectures compute \(\textbf{x}'\) only once, saving approximately 40% of computational arithmetic operations of the remaining DFrFTs before the algorithm convergence.

In Table 5, one can observe the respective \(a_{opt.}\), \(l_{1}\)-norm, number of DFrFTs required to find \(a_{opt.}\) and algorithm time-convergence according to each DFrFT architectures. We observe that the optimal fractional orders achieved by the proposed architectures are close to the results obtained in [8]. Additionally, the \(\hbox {HGL}_{2}\)-based architecture reached the lowest \(l_{1}\)-norm, i.e., the greatest compactness performance. Due to inherent errors of floating-point to fixed-point conversions (and vice-versa) and fixed-point arithmetic operations used in the DFrFT architectures, we believe that the proposed method requires 4 additional DFrFTs for convergence of the MNM algorithm, when compared to the results given in [8].

Table 5 Application of the MNM to a bi-component chirp signal by using the \(\hbox {HGL}_1\) and \(\hbox {HGL}_2\) architectures
Full size table

The results can be visually compared by using Fig. 8, where the squared magnitude of the original chirp signal (black line) and the corresponding compact representation in fractional Fourier domain computed by the DFrFT architectures are plotted. Although the \(\hbox {HGL}_{1}\)-based DFrFT (blue line) have a central portion narrower than that of the \(\hbox {HGL}_{2}\)-based DFrFT (red line), side fluctuations contribute to higher \(l_{1}\)-norm [8].

Fig. 8
figure 8

Magnitude squared of chirp signal in original (time) and fractional Fourier domains encountered by using the MNM algorithm

Full size image

5 Conclusion

We presented two hardware architectures for computing ED-DFrFTs of N-length complex-valued vectors, where \(N=4L\) and L is a positive integer. The proposed architectures can be generalized for \(N \ne 4L\) with slight changes of variable indexes of the memory blocks. By means of comparative analyses, we demonstrated that reliable DFrFTs can be achieved with low error through fixed-point numerical representations and appropriate conversions, instead of floating-point numerical representations. Among the proposed architectures in this study, the \(\hbox {HGL}_2\)-based architecture achieved better speed performance and memory usage than \(\hbox {HGL}_1\)-based architecture, but additional arithmetic hardware elements are required. Moreover, the \(\hbox {HGL}_{2}\)-based architecture achieved a smaller \(l_{1}\)-norm, i.e., a greater compactness performance associated with a lower latency, when compared to \(\hbox {HGL}_{1}\)-based architecture. Although pipelined architectures presented in the literature outperform \(\hbox {HGL}_2\) architecture regarding latency performance, the proposed architectures have the lowest arithmetic hardware complexity among the existing architectures. Therefore, choosing a specific architecture depends on the application and involves aspects related to area and timing performance.

We are currently investigating the possibility of decreasing the latency of the \(\hbox {HGL}_2\) architecture through pipelined approaches and implementing rounding strategies in \(\hbox {HGL}_2\) eigenbasis, as proposed in [8], in order to reduce the number of arithmetic operations without significantly compromising the accuracy of the DFrFT architecture.

The proposed methods are also suitable for application-specific integrated circuit (ASIC) design, which can be considered to achieve speed performance in real-time applications with low hardware complexity, i.e., minimal circuit area, such as filtering in the fractional domain, time–frequency analysis, chirp-rate estimation, compressive sensing, velocity and vibration estimation on SAR imagery and similar applications.