1 Introduction

Adaptive filtering theory is an optimal filtering method developed based on linear filtering theories such as Wiener filtering theory [31] and Kalman filtering theory [7]. The Wiener filter is designed based on the known signal statistical properties to obtain optimal estimates in practical applications. However, this design is unsuitable for signal statistical properties are unknown or non-stationary. The Kalman filter is applicable when the input signal is non-stationary. However, this requires the previous estimate and the current observation to estimate the signal value. In practical applications of signal processing, a priori knowledge of the statistical properties of the signal and noise is often unavailable. Thus, the adaptive filter is required in the absence of a priori statistics. The adaptive filter can learn and adjust its parameters adaptively according to the signal sampling value, which finally achieves optimal filtering. Thus, the adaptive filter shows excellent adaptive and real-time characteristics for signal processing problems in unknown or non-stationary environments. The adaptive filter also has broad applicability in a range of fields, such as distributed linear cyber-physical system [10], wireless sensor networks [29] and other adaptive signal processing [32, 33, 35,36,37,38,39,40,41]. In linear adaptive filtering algorithms, the standard algorithms are the least mean square (LMS) algorithm with low computational complexity, the normalized LMS (NLMS) algorithm with strong tracking performance, and the affine projection algorithm with fast convergence speed. Although linear filtering algorithm has flourished, the linear adaptive filter is no longer suitable for practical applications. Therefore, research on nonlinear filters is on the agenda.

Many scholars have developed nonlinear filter models, proposing the Volterra adaptive filtering [1, 16, 34], functional link adaptive filtering [5] and neural network adaptive filtering [6] algorithms. The spline adaptive filtering (SAF) algorithm was developed to achieve high efficiency in nonlinear adaptive filtering algorithms, obtain lower computational complexity, and obtain better adaptability [18, 26, 31]. The SAF consists of a linear combiner and spline interpolation, with the spline control points stored in a set of discrete look-up tables (LUTs). The SAF adjusts the filter’s coefficients and spline control points through the error signal and input signal to identify the nonlinear system.

According to the different orders of nonlinearization, the SAF can be divided into the Wiener model [11], Hammerstein model [20], and variants arising from these two types according to different topology structures [24]. In recent years, some scholars have combined block-oriented architecture with spline interpolation function to propose a new Wiener model, called Wiener SAF [23]. The spline adaptive algorithms in this study are all Wiener-type structures.

The SAF-LMS algorithm is proposed based on the SAF. The SAF-LMS algorithm significantly solves nonlinear problems based on previous simulations and steady-state performance analysis [25]. However, LMS-type algorithms use the second-order statistical information of the error that deviates from the optimal solution in the face of non-Gaussian signals. The shortcomings of the LMS-type algorithm in non-Gaussian environment are still inevitable in the SAF, thus requiring explorations of the nonlinear SAF algorithm.

Studies have proposed many improved spline-type algorithms to solve various problems. Peng applied the maximum correntropy criterion (MCC) to the SAF algorithm, named SAF-MCC algorithm [18], taking advantage of the MCC criterion anti-mutation signal characteristic and performing excellently in a heavy-tailed non-Gaussian environment. Subsequently, algorithms suitable for non-Gaussian environments have continued to be proposed to combat impulsive interference; successfully proposed algorithms include the spline set-membership normalized least M-estimate algorithm [12], the spline algorithm based on the Versoria function criterion [14], and a family of logarithmic spline adaptive algorithm with hyperbolic cosine as the core [17].

Active noise control (ANC) technology integrates various modern advanced science and technology to alleviate the limitation of passive noise control due to space and cost reasons. Its advantages are the small size of the equipment, low cost, easy installation, debugging ability, and remarkable control effect on low-frequency noise. As the application of today’s control technology of mainstream noise has become increasingly mature, the ANC algorithm has played a critical role in the controlling ability. For example, the classic filtered-x LMS algorithm has been widely used for ANC. However, this algorithm generally assumes the secondary channel loudspeaker as an ideal linear distortion-free model. In real solutions, ANC systems are probably nonlinear. The specific manifestation of this nonlinearity is that the model input and output signals exhibit a nonlinear relationship. Moreover, harmonics are found in the output signal, and the original signal spectrum changes [19]. The linear ANC system is inapplicable in these cases, while the above SAF is a good solution.

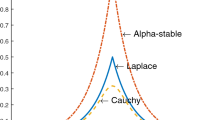
In general, the kernel function of the MCC defaults to the Gaussian kernel. Despite not being impeccable, the Gaussian kernel is accepted as maximally noncommittal to outliers. It also expresses maximum uncertainty concerning missing information [3, 28]. Thus, one is confronted with the problem of choosing a suitable kernel width value through the kernel approach. An inappropriate choice of width will significantly deteriorate the algorithm’s behavior. The generalized correntropy, which adopts the generalized Gaussian density function as kernel, was proposed. The study focuses on the problem of unsatisfactory simple spline filtering effect under non-Gaussian noise. The SAF-GMCC algorithm is proposed by introducing the generalized maximum correntropy criterion (GMCC) to the SAF. Then, the variable step-size is introduced, and the SAF-VGMCC algorithm is proposed to improve the SAF-GMCC algorithm’s performance. This performance is achieved after theoretically analyzing the SAF-GMCC and SAF-VGMCC algorithms and comparing the performance of the proposed new spline algorithms through simulations in an impulsive interference environment. This study proposes the filtered-c generalized maximum correntropy criterion (FcGMCC) and variable step-size filtered-c generalized maximum correntropy criterion (FcVGMCC) algorithms given the ANC system nonlinear problem. Finally, the effectiveness of the proposed algorithms in the nonlinear and non-Gaussian noise environments is verified through simulation in an alpha noise environment with different impulsive strengths.

The rest of this paper is structured as follows: Sect. 2 introduces the SAF and GMCC. Section 3 proposes the SAF-GMCC and SAF-VGMCC algorithms. Section 4 analyzes the range of the step-size and the steady-state of the SAF-GMCC algorithm under some simplifying assumptions. Section 5 provides some numerical simulations and Sect. 6 introduces the FcGMCC and FcVGMCC algorithms. Finally, Sect. 7 concludes this paper.

2 Spline Adaptive Filter and Generalized Correntropy

2.1 Spline Adaptive Filter

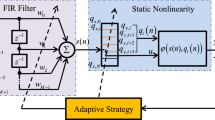
Figure 1 shows a structural schematic of the SAF. The main components are the cascade of a fair number of linear filters and a memoryless nonlinear function implemented by the spline interpolation scheme [22]. In Fig. 1, \(n\) is the instantaneous moment, and \({\mathbf{x}}\left( n \right)\) is the input signal of the whole system and the input of the linear adaptive filter. The \(s\left( n \right)\) is the output of the linear network. The spline interpolation function and the LUT address the input of the nonlinear network \(s\left( n \right)\). Finally, the output signal of the system is generated.

$$ s\left( n \right) = {\mathbf{w}}^{{\mathbf{T}}} \left( n \right){\mathbf{x}}\left( n \right) $$
(1)

where \({\mathbf{w}}\left( n \right) = \left[ {w_{0} , \, w_{1} , \ldots ,w_{N - 1} } \right]^{T}\) is the adaptive weight vector for the finite impulse response filter. The tapped delayed input signal is represented as \({\mathbf{x}}\left( n \right) = \left[ {x\left( n \right), \, x\left( {n - 1} \right), \ldots , \, x\left( {n - N + 1} \right)} \right]^{T}\), where \(N\) is the number of filter taps. The input signal of the nonlinear spline filter, namely \(s\left( n \right)\), is the output signal of the linear time-invariant filter, and the final system output signal is \(y\left( n \right)\). The parameters \(i\) and \(u\) are the span index and local parameters, respectively, where \(u \in \left[ {0,1} \right]\).

Fig. 1
figure 1

Spline adaptive filter structural model

Full size image

The calculation formula of the local parameter \(u\left( n \right)\) is as follows

$$ u\left( n \right) = \frac{s\left( n \right)}{{\Delta x}} - \left\lfloor {\frac{s\left( n \right)}{{\Delta x}}} \right\rfloor $$
(2)

The formula for calculating the span index \(i(n)\) is as follows

$$ i(n) = \left\lfloor {\frac{s\left( n \right)}{{\Delta x}}} \right\rfloor + \frac{H - 1}{2} $$
(3)

where \(H\) is the total number of control points, \(\vartriangle x\) is the sampling interval, and \(\left\lfloor \bullet \right\rfloor\) is rounded down. For notation simplicity, we use \(i \equiv i(n)\).

The output of the SAF is as follows:

$$ y\left( n \right) = \varphi_{i} \left( u \right) = {\mathbf{u}}_{n}^{T} {\mathbf{Ch}}_{i,n} $$
(4)

where \({\mathbf{u}}_{n} = \left[ {u^{3} \left( n \right), \, u^{2} \left( n \right), \, u\left( n \right),1} \right]^{T}\). For notation simplicity, we use \({\mathbf{u}} \equiv {\mathbf{u}}_{n}\) to determine the starting position of a group of continuous control points in the LUT through the span index to form a control point vector \({\mathbf{h}}_{i} = \left[ { \, h_{i} , \, h_{i + 1} , \, h_{i + 2} , \, h_{i + 3} } \right]^{T}\). \({\mathbf{C}}\) is the spline basis matrix. CR-spline and B-spline basis matrices are the most widely used among SAFs. Moreover, the CR-spline basis matrix [2] produces a more local approximation than the B-spline basis matrix [22]. To improve the accuracy of the estimation of nonlinear quantities, the CR-spline basis matrix is given as follows:

$$ C_{CR} = \frac{1}{2}\left( {\begin{array}{*{20}c} { - 1} & 3 & { - 3} & 1 \\ 2 & { - 5} & 4 & { - 1} \\ { - 1} & 0 & 1 & 0 \\ 0 & 2 & 0 & 0 \\ \end{array} } \right) $$
(5)

2.2 Generalized Maximum Correntropy Criterion

Given two random variables X and Y, the correlation entropy is defined by [4]

$$ V\left( {X,Y} \right) = E\left[ {\varphi \left( X \right)^{T} \varphi \left( Y \right)} \right] $$
(6)

where \(\varphi ( \cdot )\) represents the nonlinear mapping determined by the kernel function. Additionally, \(\varphi ( \cdot )\) satisfies the following equation

$$ \varphi \left( X \right)^{T} \varphi \left( Y \right) = \kappa \left( {X,Y} \right) $$
(7)

where \(\kappa \left( { \cdot , \cdot } \right)\) denotes the Mercer nucleus. The kernel function of the GMCC is as follows:

$$ G_{\alpha ,\beta } \left( e \right) = \frac{\alpha }{{2\beta \Gamma \left( {1/\alpha } \right)}}\exp \left( { - \left| {\frac{e}{\beta }} \right|^{\alpha } } \right) = \gamma_{\alpha ,\beta } \exp \left( { - \lambda |e|^{\alpha } } \right) $$
(8)

where \(e = x - y\), \(\Gamma ( \cdot )\) represents the gamma function, \(\alpha\) is the shape parameter greater than zero, \(\beta\) is the scale coefficient, \(\lambda = 1/\beta^{\alpha }\) represents the kernel parameter, \(\gamma_{\alpha ,\beta }\) is the normalization constant, and the expression of \(\gamma_{\alpha ,\beta }\) is as follows:

$$ \gamma_{\alpha ,\beta } = \alpha /\left( {2\beta \cdot \Gamma \left( {1/\alpha } \right)} \right) $$
(9)

From the above formulas, the entropy function of GMCC is

$$ V_{\alpha ,\beta } \left( {X,Y} \right) = E_{\alpha ,\beta } [G\left( {X - Y} \right)] $$
(10)

3 Proposed Algorithms

3.1 Proposed SAF-GMCC Algorithm

A sample-averaged estimate of the GMCC is given as follows

$$ \hat{V}_{\alpha ,\beta } \left( {X,Y} \right) = \frac{1}{N}\sum\limits_{i = 1}^{N} {G_{\alpha ,\beta } } \left( {x_{i} - y_{i} } \right) $$
(11)

Under the condition of adaptive filtering, the cost function is defined as follows:

$$ J = E_{\alpha ,\beta } [G\left( {e\left( n \right)} \right)] = \gamma_{\alpha ,\beta } E\left[ {\exp \left( { - \lambda |e(n)|^{\alpha } } \right)} \right] $$
(12)

When \(\alpha = 2\), the GMCC-type algorithms will degenerate into the MCC-type algorithms. The cost function of the SAF-GMCC algorithm is as follows:

$$ J\left( {{\mathbf{w}}_{n} ,{\mathbf{h}}_{i,n} } \right) = E\left[ {\gamma_{\alpha ,\beta } \exp \left( { - \lambda |e(n)|^{\alpha } } \right)} \right] \approx \gamma_{\alpha ,\beta } \exp \left( { - \lambda |e(n)|^{\alpha } } \right) $$
(13)

Some studies [4, 28, 30] have evaluated whether the absolute value function in \(J\left( {{\mathbf{w}}_{n} ,{\mathbf{h}}_{i,n} } \right)\) is differentiable inferring that the kernel functions about GMCC are differentiable. Through the gradient descent method, the updated method of the filter weight coefficient is as follows:

$$ {\mathbf{w}}_{n + 1} = {\mathbf{w}}_{n} - \mu_{{\mathbf{w}}} \frac{{\partial J\left( {{\mathbf{w}}_{n} ,{\mathbf{h}}_{i,n} } \right)}}{{\partial {\mathbf{w}}_{n} }} $$
(14)
$$ \frac{{\partial J\left( {{\mathbf{w}}_{n} ,{\mathbf{h}}_{i,n} } \right)}}{{\partial {\mathbf{w}}_{n} }} = - f\left( {e\left( n \right)} \right) \cdot \frac{{\partial \varphi_{i} \left( u \right)}}{\partial u\left( n \right)}\frac{\partial u\left( n \right)}{{\partial s\left( n \right)}}\frac{\partial s\left( n \right)}{{\partial {\mathbf{w}}_{n} }} = - f\left( {e\left( n \right)} \right) \cdot \varphi^{\prime}_{i} \left( u \right){\mathbf{x}}(n) $$
(15)

where \(\varphi^{\prime}_{i} \left( u \right) = {\dot{\mathbf{u}}}^{T} {\mathbf{Ch}}_{i,n}\), \({\dot{\mathbf{u}}} = \frac{{\partial {\mathbf{u}}}}{\partial u} = \left[ {3u^{2} \left( n \right),2u\left( n \right),1,0} \right]^{T}\) and \(f\left( {e\left( n \right)} \right)\) expresses

$$ f\left( {e\left( n \right)} \right) = \alpha \lambda \cdot \gamma_{\alpha ,\beta } \exp \left( { - \lambda |e(n)|^{\alpha } } \right)\left| {e\left( n \right)} \right|^{\alpha - 1} \cdot sign\left( {e\left( n \right)} \right) $$
(16)

Similarly, it is deduced that the control point update method is as follows

$$ {\mathbf{h}}_{i,n + 1} = {\mathbf{h}}_{i,n} - \mu_{{\mathbf{h}}} \frac{{\partial J\left( {{\mathbf{w}}_{n} ,{\mathbf{h}}_{i,n} } \right)}}{{\partial {\mathbf{h}}_{i,n} }} $$
(17)
$$ \frac{{\partial J\left( {{\mathbf{w}}_{n} ,{\mathbf{h}}_{i,n} } \right)}}{{\partial {\mathbf{h}}_{i,n} }} = - f\left( {e\left( n \right)} \right) \cdot \frac{{\partial \varphi_{i} \left( u \right)}}{{\partial {\mathbf{h}}_{i,n} }} = - f\left( {e\left( n \right)} \right) \cdot {\mathbf{C}}^{T} {\mathbf{u}} $$
(18)

In summary, the updated formulas of the SAF-GMCC algorithm are as follows:

$$ {\mathbf{w}}_{n + 1} = {\mathbf{w}}_{n} + \mu_{{\mathbf{w}}} f\left( {e\left( n \right)} \right) \cdot \varphi^{\prime}_{i} \left( u \right){\mathbf{x}}(n) $$
(19)
$$ {\mathbf{h}}_{i,n + 1} = {\mathbf{h}}_{i,n} + \mu_{{\mathbf{h}}} f\left( {e\left( n \right)} \right) \cdot {\mathbf{C}}^{T} {\mathbf{u}} $$
(20)

where \(\mu_{{\mathbf{w}}}\) and \(\mu_{{\mathbf{h}}}\) represent the step-size convergence factor of the weights and control points, respectively.

3.2 Proposed SAF-VGMCC Algorithm

Like the linear adaptive filter algorithm, the SAF algorithm also has a problem because the convergence speed and the steady-state error cannot be considered simultaneously. Inspired by a previous study [13], in this study we introduce the variable step-size into the SAF-GMCC algorithm, and propose a variable step-size SAF-VGMCC algorithm.

In the SAF-GMCC algorithm, the weight \(\mu_{{\varvec{w}}}\) and the step-size of the control point \(\mu_{{\varvec{h}}}\) are fixed values. We use \(\mu_{{\varvec{w}}} \left( n \right)\) and \(\mu_{{\varvec{h}}} \left( n \right)\) to replace the fixed values. Then, (19) and (20) are rewritten as follows:

$$ {\mathbf{w}}_{n + 1} = {\mathbf{w}}_{n} + \mu_{{\varvec{w}}} \left( n \right)f\left( {e\left( n \right)} \right) \cdot \varphi^{\prime}_{i} \left( u \right){\mathbf{x}}(n) $$
(21)
$$ {\mathbf{h}}_{i,n + 1} = {\mathbf{h}}_{i,n} + \mu_{{\varvec{h}}} \left( n \right)f\left( {e\left( n \right)} \right) \cdot {\mathbf{C}}^{T} {\mathbf{u}} $$
(22)

In addition, the adjustments of the variable step-sizes are all controlled by the squared value of the impulsive-free error.

$$ \mu_{{\text{w}}} \left( n \right) = a\mu_{{\text{w}}} \left( {n - 1} \right) + \left( {1 - a} \right)\min \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{o}^{2} \left( n \right),\mu_{{\text{w}}} \left( {n - 1} \right)} \right] $$
(23)
$$ \mu_{{\text{h}}} \left( n \right) = a\mu_{{\text{h}}} \left( {n - 1} \right) + \left( {1 - a} \right)\min \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{o}^{2} \left( n \right),\mu_{h} \left( {n - 1} \right)} \right] $$
(24)

where \(a < 1\) is a forgetting factor which is close to one. Furthermore, \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{o}^{2} \left( n \right)\) is an estimate of the squared value of the impulse-free error [42], used to adjust the variable step process obtained by [13].

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{o}^{2} (n) = \lambda \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e}_{o}^{2} (n - 1) + c_{1} (1 - \lambda )med(\gamma_{n} ) $$
(25)

where \(\lambda\) is another forgetting factor close to one but less than one; \(c_{1} = 1.483\left( {1 + 5/\left( {N - 1} \right)} \right)\) is a finite correction factor; \(med(.)\) represents the median operator; and \(\gamma_{{\text{n}}}\) is expressed as follows

$$ \gamma_{n} = \left[ {e^{2} \left( n \right),e^{2} \left( {n - 1} \right), \cdots ,e^{2} \left( {n - N + 1} \right)} \right] $$
(26)

Table 1 shows the pseudocode of the SAF-VGMCC algorithm.

Table 1 The pseudocode of the SAF-VGMCC algorithm
Full size table

3.3 Proposed Algorithms Applied to ANC

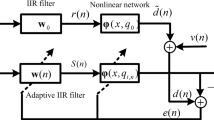
Figure 2 shows a schematic of a nonlinear ANC system based on the SAF algorithm.

Fig. 2
figure 2

Spline nonlinear active noise control structural model

Full size image

The residual noise sensed by the error microphone is mathematically obtained as follows:

$$ e\left( n \right) = d\left( n \right) - y\left( n \right) * s_{N} \left( n \right) $$
(27)

where \(*\) represents the linear convolution operator and \(s_{N} \left( n \right)\) is the impulse response of the secondary path.

This section discussed the practical applications of the proposed algorithms. In the ANC model, we propose a new ANC algorithm against impulsive interference, namely the FcGMCC algorithm. Its cost functions are the same as (21) and (22). The derivation process of the FcVGMCC algorithm is similar to that of the FcGMCC algorithm. The difference is that the FcVGMCC step-size satisfies (23) and (24). The updated formulas of the FcGMCC algorithm are as follows:

$$\begin{aligned} {\mathbf{w}}_{{n + 1}} & = {\mathbf{w}}_{n} - \mu _{{\mathbf{w}}} \frac{{\partial J\left( {{\mathbf{w}}_{n} ,{\mathbf{h}}_{{i,n}} } \right)}}{{\partial {\mathbf{w}}_{n} }} \\ & {\text{ = }}{\mathbf{w}}_{n} {\text{ + }}\mu _{{\mathbf{w}}} f\left( {e\left( n \right)} \right)\frac{{\partial \left[ {y\left( n \right) * s_{N} \left( n \right)} \right]}}{{\partial {\mathbf{w}}\left( n \right)}} \\ & = {\mathbf{w}}_{n} {\text{ + }}\mu _{{\mathbf{w}}} f\left( {e\left( n \right)} \right)\left[ {{\mathbf{\dot{u}}}^{T} {\mathbf{Cq}}_{i} \frac{1}{{\Delta x}}{\mathbf{x}}\left( n \right) * s_{N} \left( n \right)} \right] \\ & = {\mathbf{w}}_{n} {\text{ + }}\mu _{{\mathbf{w}}} f\left( {e\left( n \right)} \right)x^{{\mathbf{'}}} (n) \\ \end{aligned} $$
(28)
$$\begin{aligned} {\mathbf{w}}_{{n + 1}} = & {\mathbf{w}}_{n} - \mu _{{\mathbf{w}}} \frac{{\partial J\left( {{\mathbf{w}}_{n} ,{\mathbf{h}}_{{i,n}} } \right)}}{{\partial {\mathbf{w}}_{n} }} \\ = & {\mathbf{w}}_{n} + \mu _{{\mathbf{w}}} f\left( {e\left( n \right)} \right)\frac{{\partial \left[ {y\left( n \right)*s_{N} \left( n \right)} \right]}}{{\partial {\mathbf{w}}\left( n \right)}} \\ = & {\mathbf{w}}_{n} + \mu _{{\mathbf{w}}} f\left( {e\left( n \right)} \right)\left[ {{\mathbf{\dot{u}}}^{T} {\mathbf{Cq}}_{i} \frac{1}{{\Delta x}}{\mathbf{x}}\left( n \right)*s_{N} \left( n \right)} \right] \\ = & {\mathbf{w}}_{n} + \mu _{{\mathbf{w}}} f\left( {e\left( n \right)} \right)x^{'} (n) \\ \end{aligned} $$
(29)

where \(x^{{\mathbf{^{\prime}}}} (n) = {\dot{\mathbf{u}}}^{T} {\mathbf{Cq}}_{i} \frac{1}{\Delta x}{\mathbf{x}}\left( n \right) * s_{N} \left( n \right)\) and \(u^{\prime} = {\mathbf{u}} * s_{N} \left( n \right)\).

4 Mean Analysis of SAF-GMCC

This section analyzes the range of step-sizes which makes the SAF-GMCC algorithm stable.

4.1 Mean Analysis of \(\mu_{{\mathbf{w}}}\)

Averaging two sides of (19) yields

$$ E\left\{ {{\mathbf{w}}_{n + 1} } \right\} = E\left\{ {{\mathbf{w}}_{n} } \right\} + \mu_{{\mathbf{w}}} E\left\{ {f\left( {e\left( n \right)} \right)\varphi^{\prime}(r\left( n \right)){\mathbf{x}}(n)} \right\} $$
(30)

Referring to Fig. 3, \({\mathbf{w}}_{0}\) and \(\varphi_{0} (p(n),{\mathbf{h}}_{0} )\) are the unknown systems to be identified and \(v(n)\) denotes additional ambient noise. The output error of the adaptive structure is as follows:

$$ e\left( n \right) = \tilde{d}\left( n \right) - y\left( n \right) = \varphi_{0} \left( {p\left( n \right)} \right) - \varphi \left( {s\left( n \right)} \right) + v\left( n \right) $$
(31)
Fig. 3
figure 3

Nonlinear system identification model

Full size image

Since the noise signal \(v(n)\) is independent of \(x(n)\), using the Taylor formula in (30) yields:

$$ E\left\{ {{\mathbf{w}}_{n + 1} } \right\} = E\left\{ {{\mathbf{w}}_{n} } \right\} + \mu_{{\mathbf{w}}} E\left\{ {{\mathbf{x}}(n)\varphi^{\prime}\left( {s\left( n \right)} \right)\left( {f\left( {v\left( n \right)} \right)} \right.} \right.\left. {\left. { + f^{\prime } \left( {v\left( n \right)} \right)\left[ {\varphi_{0} \left( {p\left( n \right)} \right) - \varphi \left( {s\left( n \right)} \right)} \right]} \right)} \right\} $$
(32)

Since \(f\left( {v\left( n \right)} \right)\) is an odd function, (32) is rewritten as follows:

$$ E\left\{ {{\mathbf{w}}_{n + 1} } \right\} = E\left\{ {{\mathbf{w}}_{n} } \right\} + \mu_{{\mathbf{w}}} E\left\{ {{\mathbf{x}}(n)\varphi^{\prime}\left( {s\left( n \right)} \right)\left[ {f^{\prime } \left( {v\left( n \right)} \right)\left[ {\varphi_{0} \left( {p\left( n \right)} \right) - \varphi \left( {s\left( n \right)} \right)} \right]} \right]} \right\} $$
(33)

Gaussian distribution is the probability distribution of the process \(p\left( n \right)\), \({\mathbf{x}}\left( n \right)\) is a Gaussian signal, and the mode \({\mathbf{w}}_{0}\) is non-random. Furthermore, the Lyapunov version of the central limit theorem [21] guarantees that the probability distribution of \(s\left( n \right)\) is close to the Gaussian distribution as long as the length of \({\mathbf{w}}_{n}\) grows. The above assumptions and the extension of the Bussgang theorem are used to evaluate the second term on the right side of (33), stated as follows.

Corollary: Let \({{\varvec{\Theta}}} = \left[ {\theta_{1} , \ldots ,\theta_{n} } \right]\) represent an n-dimensional Gaussian variate and \(G\left( z \right)\) is any analysis function defined in the subspace \({\mathbf{z}} = \left[ {\theta_{2} , \ldots ,\theta_{n} } \right]\) [21]. Then, the expectation of multiplying \(\theta_{1}\) by \(G\left( z \right)\) is described as follows:

$$ E\left\{ {\theta_{1} \cdot G\left( {\theta_{2} , \ldots ,\theta_{n} } \right)} \right\} = m_{{\theta_{1} }} \cdot E\left\{ {G\left( {\theta_{2} , \ldots ,\theta_{n} } \right)} \right\} + \sum\limits_{i = 2}^{n} E \left\{ {\frac{{\partial G\left( {\theta_{2} , \ldots ,\theta_{n} } \right)}}{{\partial \theta_{i} }}} \right\}K_{1,i} $$
(34)

where \(m_{\theta 1}\) denotes the average value of \(\theta_{1}\) and \(K_{1,i}\) expresses the covariance between \(\theta_{1}\) and \(\theta_{{\text{ i}}}\).

Using the corollary in (33), we derive the following expression:

$$ \begin{gathered} \, E\left\{ {{\mathbf{x}}(n)\varphi^{\prime}\left( {s\left( n \right)} \right)f^{\prime } \left( {v\left( n \right)} \right)\varphi_{0} \left( {p\left( n \right)} \right)\} } \right. \hfill \\ \quad= E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}\left( {E\left\{ {\varphi^{\prime}\left( {s\left( n \right)} \right)\varphi^{\prime}_{0} \left( {p\left( n \right)} \right)} \right\}{\mathbf{R}}_{x} {\mathbf{w}}_{0} } \right.\left. { + E\left\{ {\varphi^{\prime\prime}\left( {s\left( n \right)} \right)\varphi_{0} \left( {p\left( n \right)} \right)} \right\}{\mathbf{R}}_{x} E\left\{ {{\mathbf{w}}_{n} } \right\}} \right) \hfill \\ \end{gathered} $$
(35)
$$ \begin{gathered} \, E\left\{ {{\mathbf{x}}(n)\varphi^{\prime}\left( {s\left( n \right)} \right)f^{\prime } \left( {v\left( n \right)} \right)\varphi \left( {s\left( n \right)} \right)} \right\} \hfill \\ = E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}E\left\{ {\varphi^{{\prime}{2}} \left( {s\left( n \right)} \right)} \right.\left. { + \varphi^{\prime\prime}\left( {s\left( n \right)} \right)\varphi \left( {s\left( n \right)} \right)} \right\}{\mathbf{R}}_{x} E\left\{ {{\mathbf{w}}_{n} } \right\} \hfill \\ \end{gathered} $$
(36)

where \({\mathbf{R}}_{x} = E\{ {\mathbf{x}}(n){\mathbf{x}}^{T} (n)\}\) represents the autocorrelation matrix of the input signal. Combining (34), (35) and (36), the following equation is calculated as:

$$ E\left\{ {{\mathbf{w}}_{n + 1} } \right\} = \left[ {{\mathbf{I}} - \mu_{{\mathbf{w}}} a{\mathbf{R}}_{x} E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}} \right]E\left\{ {{\mathbf{w}}_{n} } \right\} + \mu_{{\mathbf{w}}} b{\mathbf{R}}_{x} E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}{\mathbf{w}}_{0} $$
(37)

where

$$ a = E\left\{ {\varphi^{{\prime}{2}} \left( {s\left( n \right)} \right)} \right\} + E\left\{ {\varphi^{\prime\prime}\left( {s\left( n \right)} \right)\left[ {\varphi \left( {s\left( n \right)} \right) - \varphi_{0} \left( {p\left( n \right)} \right)} \right]} \right\} $$
(38)
$$ b = E\left\{ {\varphi^{\prime}\left( {s\left( n \right)} \right)\varphi^{\prime}_{0} \left( {p\left( n \right)} \right)} \right\} $$
(39)

The expectation of \({\text{w}}_{n}\) is solved using the recursive iteration equation after ignoring the expected time dependency, as follows:

$$ \begin{gathered} E\left\{ {{\mathbf{w}}_{n} } \right\} = \left[ {{\mathbf{I}} - \mu_{{\mathbf{w}}} a{\mathbf{R}}_{x} E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}} \right]^{n} E\left\{ {{\mathbf{w}}_{ - 1} } \right\} \hfill \\ \, + \mu_{{\mathbf{w}}} b\sum\limits_{r = 0}^{n - 1} {\left[ {{\mathbf{I}} - \mu_{{\mathbf{w}}} a{\mathbf{R}}_{x} E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}} \right]^{n - 1 - r} } \times E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}{\mathbf{R}}_{x} {\mathbf{w}}_{0} \hfill \\ \end{gathered} $$
(40)

where \({\mathbf{w}}_{ - 1}\) is the original condition of the linear filter.

If and only if the matrix \(\left[ {{\mathbf{I}} - \mu_{{\mathbf{w}}} a{\mathbf{R}}_{x} E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}} \right]\) is stable, unbiased estimates are obtained. Thus, \(\left[ {{\mathbf{I}} - \mu_{{\mathbf{w}}} a{\mathbf{R}}_{x} E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}} \right]\) is equivalent to \(\left| {{\mathbf{I}} - \mu_{{\mathbf{w}}} a{\mathbf{R}}_{x} E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}} \right| < 1\), and the following equation is obtained:

$$ 0 < \mu_{{\mathbf{w}}} < \frac{2}{{a\lambda_{\max } \left( {{\mathbf{R}}_{x} } \right)E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}}} $$
(41)

Therefore, if the nonlinearity converges to the actual value at the steady-state, namely \(\varphi (s(n)) \to \varphi_{0} (p(n))\), then we derive this expression:

$$ \mathop {\lim }\limits_{n \to \infty } E\left\{ {{\mathbf{w}}_{n} } \right\} = {\mathbf{w}}_{0} $$
(42)

4.2 Mean Analysis of \(\mu_{{\mathbf{h}}}\)

The mean analysis of \(\mu_{{\mathbf{h}}}\) is obtained similar to that of the previous subsection. The output error of the adaptive structure is as follows:

$$ e(n) = \tilde{d}(n) - y(n) = {\mathbf{u}}_{l,n}^{T} {\mathbf{Ch}}_{i,n} - {\mathbf{u}}_{s,n}^{T} {\mathbf{Ch}}_{i,n} + v(n) $$
(43)

where \({\mathbf{u}}_{l,n}^{{}}\) and \({\mathbf{u}}_{s,n}^{{}}\) are the local variables \({\mathbf{u}}_{n}^{{}}\) for evaluating \(p\left( n \right)\) and \(s\left( n \right)\), respectively.

Similar to (34), the expectation of \({\mathbf{h}}_{i,n}\) is calculated as follows:

$$ E\left\{ {{\mathbf{h}}_{i,n + 1} } \right\} = \left[ {{\mathbf{I}} - \mu_{{\mathbf{h}}} {\mathbf{C}}^{{\text{T}}} {\mathbf{U}}_{s} {\mathbf{C}}E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}} \right]E\left\{ {{\mathbf{h}}_{i,n} } \right\} + \mu_{{\mathbf{h}}} {\mathbf{C}}^{{\text{T}}} {\mathbf{U}}_{sp} {\mathbf{C}}E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}{\mathbf{h}}_{i,0} $$
(44)

where \({\mathbf{U}}_{s} = E\left\{ {{\mathbf{u}}_{s,n} {\mathbf{u}}_{s,n}^{T} } \right\}\) is the autocorrelation matrix and \({\mathbf{U}}_{sp} = E\left\{ {{\mathbf{u}}_{s,n} {\mathbf{u}}_{p,n}^{T} } \right\}\) is a cross correlation matrix. The recursion Eq. (44) is solved by

$$ \begin{gathered} E\left\{ {{\mathbf{h}}_{i,n} } \right\} = \left[ {{\mathbf{I}} - \mu_{{\mathbf{h}}} {\mathbf{C}}^{{\text{T}}} {\mathbf{U}}_{s} {\mathbf{C}}E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}} \right]^{n} E\left\{ {{\mathbf{h}}_{ - 1} } \right\} \hfill \\ \quad\quad\quad\; + \mu_{{\mathbf{h}}} \sum\limits_{r = 0}^{n - 1} {\left[ {{\mathbf{I}} - \mu_{{\mathbf{h}}} {\mathbf{C}}^{{\text{T}}} {\mathbf{U}}_{s} {\mathbf{C}}E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}} \right]^{n - 1 - r} } \times E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}{\mathbf{C}}^{{\text{T}}} {\mathbf{U}}_{sp} {\mathbf{Ch}}_{i,0} \hfill \\ \end{gathered} $$
(45)

where \({\mathbf{h}}_{ - 1}\) indicates the original condition of the spline control point.

Similar to the linear case, if and only if the matrix \(\left[ {{\mathbf{I}} - \mu_{{\mathbf{h}}} {\mathbf{C}}^{{\text{T}}} {\mathbf{U}}_{s} {\mathbf{C}}E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}} \right]\) is stable, the SAF-GMCC algorithm is stable. Thus, \(\left| {{\mathbf{I}} - \mu_{{\mathbf{h}}} \lambda \left( {{\mathbf{C}}^{{\text{T}}} {\mathbf{U}}_{s} {\mathbf{C}}} \right)E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}} \right| < 1\) can be obtained. The following equation can be obtained:

$$ 0 < \mu_{{\mathbf{h}}} < \frac{2}{{\lambda_{\max } \left( {{\mathbf{C}}^{T} {\mathbf{U}}_{s} {\mathbf{C}}} \right)E\left\{ {f^{\prime } \left( {v\left( n \right)} \right)} \right\}}} $$
(46)

At the same time, when the system converges to the steady state value, its stable state solution is

$$ \mathop {\lim }\limits_{n \to \infty } E\left\{ {{\mathbf{h}}_{i,n} } \right\} = {\mathbf{h}}_{i,0} $$
(47)

4.3 Selection of Optimal Parameters

The trial-and-error determines the selection of parameters. However, this approach is unrealistic in practical application. Finding the optimal solution of the parameters is necessary for accurate signals. Thus, (28) and (29) are the cost functions of the SAF-GMCC algorithm. First, \(\mu_{{\mathbf{w}}}\), \(\mu_{{\mathbf{h}}}\), \(\alpha\) and \(\beta\) are replaced in (28) and (29), and \(\mu_{{\mathbf{w}}} (n)\), \(\mu_{{\mathbf{h}}} (n)\), \(\alpha (n)\) and \(\beta (n)\) are used to indicate that these variables are all time-varying. Let \({{\varvec{\upomega}}}_{n} = {\mathbf{w}}_{n} - {\mathbf{w}}_{0}\) and \({\mathbf{\rm H}}_{n} = {\mathbf{h}}_{i,n} - {\mathbf{h}}_{i,0}\), and then, \({\mathbf{w}}_{0}\) and \({\mathbf{h}}_{i,0}\) are subtracted from both sides of (28) and (29):

$$ {{\varvec{\upomega}}}_{n + 1} = {{\varvec{\upomega}}}_{n} + \mu_{{\mathbf{w}}} (n)f(e\left( n \right))\varphi_{i}^{\prime } \left( u \right){\mathbf{x}}(n) $$
(48)
$$ {\mathbf{\rm H}}_{n + 1} = {\mathbf{\rm H}}_{n} + \mu_{{\mathbf{h}}} (n)f(e\left( n \right)){\mathbf{C}}^{T} {\mathbf{u}} $$
(49)

From a previous study [25], we have

$$ e(n) = v(n) - \frac{{{\mathbf{c}}_{3} {\mathbf{h}}_{i,0} }}{\vartriangle x}{\mathbf{x}}_{{}}^{T} (n){{\varvec{\upomega}}}_{n}^{{}} - ({\mathbf{C}}^{T} {\mathbf{u}})^{T} {\mathbf{\rm H}}_{n}^{{}} $$
(50)

where \({\mathbf{c}}_{k}\) expresses the k-th row of \({\mathbf{C}}\). \(v(n)\) is the measurement noise. Substituting (50) into (48) and (49), we obtain

$$ \begin{aligned} {{\varvec{\upomega}}}_{n + 1}^{{}} & = {{\varvec{\upomega}}}_{n}^{{}} + \mu_{w}^{{}} (n)f(e\left( n \right))\varphi_{i}^{\prime } \left( u \right){\mathbf{x}}(n) \\ & = [I - \mu_{w}^{{}} (n)g(e(n))\frac{{\varphi_{i}^{\prime } \left( u \right){\mathbf{c}}_{3} {\mathbf{h}}_{i,0} }}{\vartriangle x}{\mathbf{x}}(n){\mathbf{x}}^{T} (n)]{{\varvec{\upomega}}}_{n}^{{}} \\ & \quad { + }\mu_{w}^{{}} (n)g(e(n))\varphi_{i}^{\prime } \left( u \right)(v(n){\mathbf{x}}(n) - {\mathbf{x}}(n)({\mathbf{C}}^{T} {\mathbf{u}})^{T} {\mathbf{\rm H}}_{n}^{{}} \\ & = [I - \mu_{w}^{{}} (n)g(e(n))m\varphi_{i}^{\prime } \left( u \right){\mathbf{x}}(n){\mathbf{x}}^{T} (n)]{{\varvec{\upomega}}}_{n}^{{}} \\ & \quad { + }\mu_{w}^{{}} (n)g(e(n))\varphi_{i}^{\prime } \left( u \right)(v(n){\mathbf{x}}(n) - {\mathbf{x}}(n)({\mathbf{C}}^{T} {\mathbf{u}})^{T} {\mathbf{\rm H}}_{n}^{{}} \\ \end{aligned} $$
(51)
$$ \begin{aligned} {\mathbf{\rm H}}_{n + 1} & = {\mathbf{\rm H}}_{n} + \mu_{{\mathbf{h}}} (n)f(e\left( n \right)){\mathbf{C}}^{T} {\mathbf{u}} \\ & = {\mathbf{\rm H}}_{n} + \mu_{{\mathbf{h}}} (n)g(e\left( n \right)){\mathbf{C}}^{T} {\mathbf{u}}(v(n) - \frac{{{\mathbf{c}}_{3} {\mathbf{h}}_{i,0} }}{\vartriangle x}{\mathbf{x}}_{{}}^{T} (n){{\varvec{\upomega}}}_{n}^{{}} - ({\mathbf{C}}^{T} {\mathbf{u}})^{T} {\mathbf{\rm H}}_{n}^{{}} ) \\ & = (I - \mu_{{\mathbf{h}}} (n)g(e\left( n \right))\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} ){\mathbf{\rm H}}_{n} \\ \, & + \mu_{{\mathbf{h}}} (n)g(e\left( n \right))(v(n)({\mathbf{C}}^{T} {\mathbf{u}})^{T} - m({\mathbf{C}}^{T} {\mathbf{u}})^{T} {\mathbf{x}}_{{}}^{T} (n){{\varvec{\upomega}}}_{n}^{{}} ) \end{aligned} $$
(52)

where \(m = \frac{{{\mathbf{c}}_{3} {\mathbf{h}}_{i,0} }}{\vartriangle x}\) and \(g(e(n)) = \lambda_{1} \exp \left( { - \lambda_{2} |e(n)|^{\alpha } } \right)\left| {e\left( n \right)} \right|^{\alpha - 2}\). Multiplying (51) and (52) by their transpose from the left and taking expectation with the above approximations, we obtain

$$ \begin{gathered} {{\varvec{\upomega}}}_{n + 1}^{2} = [I - 2\mu_{w}^{{}} (n)mg(e(n))\varphi_{i}^{\prime } \left( u \right){\mathbf{x}}(n){\mathbf{x}}^{T} (n) + \mu_{w}^{2} (n)m^{2} g^{2} (e(n))\varphi_{i}^{2\prime } \left( u \right)({\mathbf{x}}(n){\mathbf{x}}^{T} (n))^{2} ]{{\varvec{\upomega}}}_{n}^{2} \hfill \\ \quad\quad\quad\; - 2[\mu_{w}^{2} (n)mg^{2} (e(n))\varphi_{i}^{2\prime } \left( u \right)v(n){\mathbf{x}}(n){\mathbf{x}}^{T} (n){\mathbf{x}}(n) + \mu_{w}^{{}} (n)mg(e(n))\varphi_{i}^{\prime } \left( u \right)v(n){\mathbf{x}}(n)]{{\varvec{\upomega}}}_{n}^{{}} \hfill \\ \quad\quad\quad\; { + }2[\mu_{w}^{2} (n)mg^{2} (e(n))\varphi_{i}^{2\prime } \left( u \right){\mathbf{x}}(n){\mathbf{x}}^{T} (n){\mathbf{x}}(n) + \mu_{w}^{{}} (n)mg(e(n))\varphi_{i}^{\prime } \left( u \right){\mathbf{x}}(n)]{{\varvec{\upomega}}}_{n}^{{}} ({\mathbf{C}}^{T} {\mathbf{u}})^{T} {\mathbf{\rm H}}_{n} \hfill \\ \quad\quad\quad\; - 2\mu_{w}^{2} (n)g^{2} (e(n))\varphi_{i}^{2\prime } \left( u \right)v(n)({\mathbf{C}}^{T} {\mathbf{u}}_{n} )^{T} {\mathbf{\rm H}}_{n} \left\| {{\mathbf{x}}(n)} \right\|^{2} \hfill \\ \quad\quad\quad\; { + }\mu_{w}^{{2}} (n)g^{2} (e(n)))\varphi_{i}^{2\prime } \left( u \right)\left\| {{\mathbf{x}}(n)} \right\|^{2} \left\| {({\mathbf{C}}^{T} {\mathbf{u}}_{n} )^{T} {\mathbf{\rm H}}_{n} } \right\|^{2} + \mu_{w}^{2} (n)g^{2} (e(n))\varphi_{i}^{2\prime } \left( u \right)v^{2} (n)\left\| {{\mathbf{x}}(n)} \right\|^{2} \hfill \\ \end{gathered} $$
(53)
$$ \begin{gathered} {\mathbf{\rm H}}_{n + 1}^{2} = (I - 2\mu_{{\mathbf{h}}}^{{}} (n)g(e(n))\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} + \mu_{{\mathbf{h}}}^{2} (n)g^{2} (e(n))\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{4} ){\mathbf{\rm H}}_{n}^{2} \\ \quad\quad\quad\; + \mu_{{\mathbf{h}}}^{2} (n)g^{2} (e(n))v^{2} (n)\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} + \mu_{{\mathbf{h}}}^{2} (n)m^{2} g^{2} (e(n))\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} \left\| {{\mathbf{x}}_{{}}^{T} (n){{\varvec{\upomega}}}_{n}^{{}} } \right\|^{2} \\ \quad - 2[\mu_{{\mathbf{h}}}^{{}} (n)g(e(n))v(n) + \mu_{{\mathbf{h}}}^{2} g^{2} (e(n))v(n)\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} ]({\mathbf{C}}^{T} {\mathbf{u}})^{T} {\mathbf{\rm H}}_{n}^{{}} \\ \quad\quad\quad\; { + }2[\mu_{{\mathbf{h}}}^{{}} (n)mg(e(n)) + \mu_{{\mathbf{h}}}^{2} (n)m^{2} g^{2} (e(n))\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} ]{\mathbf{x}}_{{}}^{T} (n){{\varvec{\upomega}}}_{n}^{{}} ({\mathbf{C}}^{T} {\mathbf{u}})^{T} {\mathbf{\rm H}}_{n} \\ - 2\mu_{{\mathbf{h}}}^{2} (n)mg^{2} (e(n))v(n)\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} {\mathbf{x}}_{{}}^{T} (n){{\varvec{\upomega}}}_{n}^{{}} \\ \end{gathered} $$
(54)

We aim to optimize the step-sizes and other variable factors for the SAF-GMCC algorithm by minimizing \({\mathbf{\rm H}}_{n + 1}^{2}\) and \({{\varvec{\upomega}}}_{n + 1}^{2}\). We take the partial derivative of (53) and (54) concerning all variables, and set them to zero. After simplifying, the following equation is obtained.

$$ \left\{ {\begin{array}{llll} {0 = \frac{{\partial \lambda_{1} }}{\partial \alpha (n)} - \lambda_{1} \frac{{\partial \lambda_{2} }}{\partial \alpha (n)}|e(n)|^{\alpha (n)} + \lambda_{1} \ln |e(n)|(1 - \lambda_{2} |e(n)|^{\alpha (n)} )} \hfill \\ {0 = \frac{{\partial \lambda_{1} }}{\partial \beta (n)} - \lambda_{1} \frac{{\partial \lambda_{2} }}{\partial \beta (n)}|e(n)|^{\alpha (n)} + \lambda_{1} \ln |e(n)|(1 - \lambda_{2} |e(n)|^{\alpha (n)} )} \hfill \\ \begin{array}{llllll} 0 = [ - m{\mathbf{x}}(n){\mathbf{x}}^{T} (n) + m^{2} \mu_{w}^{{}} (n)g(e(n))\varphi_{i}^{\prime } \left( u \right)({\mathbf{x}}(n){\mathbf{x}}^{T} (n))^{2} ]{{\varvec{\upomega}}}_{n}^{2} \hfill \\ - [2m\mu_{w}^{{}} (n)g(e(n))\varphi_{i}^{\prime } \left( u \right)v(n){\mathbf{x}}(n){\mathbf{x}}^{T} (n){\mathbf{x}}(n) + mv(n){\mathbf{x}}(n)]{{\varvec{\upomega}}}_{n}^{{}} \hfill \\ { + }[2m\mu_{w}^{{}} (n)g(e(n))\varphi_{i}^{\prime } \left( u \right){\mathbf{x}}(n){\mathbf{x}}^{T} (n){\mathbf{x}}(n) + m{\mathbf{x}}(n)]{{\varvec{\upomega}}}_{n}^{{}} ({\mathbf{C}}^{T} {\mathbf{u}})^{T} {\mathbf{\rm H}}_{n} \hfill \\ - 2\mu_{w}^{{}} (n)g(e(n))\varphi_{i}^{\prime } \left( u \right)v(n)({\mathbf{C}}^{T} {\mathbf{u}})^{T} {\mathbf{\rm H}}_{n} \left\| {{\mathbf{x}}(n)} \right\|^{2} \hfill \\ { + }\mu_{w}^{{}} (n)g(e(n))\varphi_{i}^{\prime } \left( u \right)\left\| {{\mathbf{x}}(n)} \right\|^{2} \left\| {({\mathbf{C}}^{T} {\mathbf{u}})^{T} {\mathbf{\rm H}}_{n} } \right\|^{2} + \mu_{w}^{{}} (n)g(e(n))\varphi_{i}^{\prime } \left( u \right)v^{2} (n)\left\| {{\mathbf{x}}(n)} \right\|^{2} \hfill \\ \end{array} \hfill \\ \begin{array}{llll} 0 = ( - \left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} + \mu_{{\mathbf{h}}}^{{}} (n)g(e(n))\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{4} ){\mathbf{\rm H}}_{n}^{2} + \mu_{{\mathbf{h}}}^{{}} (n)g(e(n))v^{2} (n)\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} \\ + \mu_{{\mathbf{h}}}^{{}} (n)m^{2} g(e(n))\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} \left\| {{\mathbf{x}}_{{}}^{T} (n){{\varvec{\upomega}}}_{n}^{{}} } \right\|^{2} \\ - [v(n) + 2\mu_{{\mathbf{h}}}^{{}} (n)g(e(n))v(n)\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} ]({\mathbf{C}}^{T} {\mathbf{u}})^{T} {\mathbf{\rm H}}_{n}^{{}} \\ { + }[m + 2\mu_{{\mathbf{h}}}^{{}} (n)m^{2} g(e(n))\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} ]{\mathbf{x}}_{{}}^{T} (n){{\varvec{\upomega}}}_{n}^{{}} ({\mathbf{C}}^{T} {\mathbf{u}})^{T} {\mathbf{\rm H}}_{n} \\ - 2\mu_{{\mathbf{h}}}^{{}} (n)mg(e(n))v(n)\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} {\mathbf{x}}_{{}}^{T} (n){{\varvec{\upomega}}}_{n}^{{}} \\ \end{array} \hfill \\ \end{array} } \right. $$
(55)

where

$$ \left\{ {\begin{array}{*{20}l} {\lambda_{1} = \alpha (n)\lambda \cdot \gamma_{\alpha (n),\beta (n)} = \frac{{\alpha^{2} (n)}}{{2\beta (n)^{\alpha (n) + 1} \Gamma \left( {1/\alpha (n)} \right)}},\lambda_{2} = 1/\beta (n)^{\alpha (n)} } \hfill \\ {\frac{{\partial \lambda_{1} }}{\partial \alpha (n)} = \frac{{2\alpha (n) - \alpha^{2} (n)\ln (\beta (n)) + \varphi (1/\alpha (n))}}{{2\beta (n)^{\alpha (n) + 1} \Gamma \left( {1/\alpha (n)} \right)}},\frac{{\partial \lambda_{2} }}{\partial \alpha (n)} = - \frac{\ln (\beta (n))}{{\beta (n)^{\alpha (n)} }}} \hfill \\ {\frac{{\partial \lambda_{1} }}{\partial \beta (n)} = - \frac{{\alpha^{2} (n)(\alpha (n) + 1)}}{{2\beta (n)^{\alpha (n) + 2} \Gamma \left( {1/\alpha (n)} \right)}},\frac{{\partial \lambda_{2} }}{\partial \beta (n)} = - \frac{\alpha (n)}{{\beta (n)^{\alpha (n) + 1} }}} \hfill \\ \end{array} } \right. $$
(56)
$$ E[\left\| {{\mathbf{C}}^{T} {\mathbf{u}}} \right\|^{2} ] \approx \frac{1}{2}E[u^{2} (n)] + \left\| {{\mathbf{c}}_{4} } \right\|^{2} $$
(57)

Like the method used in the previous study [9], we estimate \({{\varvec{\upomega}}}_{n}^{{}}\) and \({\mathbf{\rm H}}_{n}\) through one-step approximation as follows:

$$ {{\varvec{\upomega}}}_{n}^{{}} \approx - \tilde{\mu }_{w}^{{}} (n)\tilde{f}(e\left( n \right))\varphi_{i}^{\prime } \left( u \right){\mathbf{x}}(n) $$
(58)
$$ {\mathbf{\rm H}}_{n} \approx - \tilde{\mu }_{{\mathbf{h}}} (n)\tilde{f}(e\left( n \right)){\mathbf{C}}^{T} {\mathbf{u}} $$
(59)

where \(\tilde{\mu }_{w}^{{}} (n)\) and \(\tilde{\mu }_{{\mathbf{h}}} (n)\) are the optimal step-sizes for estimating \({{\varvec{\upomega}}}_{n}^{{}}\) and \({\mathbf{\rm H}}_{n}\), respectively. \(\tilde{f}(e\left( n \right))\) is the value of \(\alpha (n)\) and \(\beta (n)\) when taking the optimal solutions.

When a unique solution exists (55), and the functions of the different parameters are convex functions in the vicinity of the solution, the time-varying optimal solution of the variables is solved [8, 34].

5 Numerical Simulations

MATLAB simulation experiments evaluate the performance of the proposed algorithms [15]. Let the unknown system order be N = 4. The weight vector of the unknown adaptive system, namely \({\mathbf{w}}_{0} = \left[ {0.6, - 0.4,0.25, - 0.15} \right]^{T}\), consists of linear components. The nonlinear memoryless objective function implemented by the 21-point length LUT control points takes the following values:

$$ \begin{gathered} {\mathbf{h}}_{0} = \{ - 2, - 1.8, \ldots , - 1.0, - 0.8, - 0.91,0.42, - 0.01,\; \hfill \\ \quad\quad - 0.1,0.1, - 0.15,0.58,1.2,1.0,1.2, \ldots ,2.0\} \hfill \\ \end{gathered} $$
(60)

where sample interval \(\vartriangle x = 0.2\).

In this experiment, a Gaussian signal and a first-order color signal (\(AR(1) = [1, - 0.8]\) model) are used as the input signals to the system. The desired signal is expressed as follows:

$$ \tilde{d}\left( n \right) = \varphi_{0} \left( {p(n),{\mathbf{h}}_{0} } \right) + v\left( n \right) $$
(61)

where \(v\left( n \right)\) is the observation noise, that contains the background noise and the impulsive noise \(v\left( n \right) = v_{A}^{{}} \left( n \right) + v_{B}^{{}} \left( n \right)\). The background noise \(v_{A} \left( n \right)\) is a Gaussian white noise with a signal-to-noise ratio (\(SNR = 10\log_{10} ({{\sigma_{x}^{2} } \mathord{\left/ {\vphantom {{\sigma_{x}^{2} } {\sigma_{v}^{2} }}} \right. \kern-0pt} {\sigma_{v}^{2} }})\)) of 30 dB; \(\sigma_{x}^{2}\) indicates the variance of the input signal; and \(\sigma_{{\text{v}}}^{2}\) represents the variance of Gaussian white noise. The impulsive noise \(v_{B} \left( n \right)\) is a Bernoulli Gaussian (BG) process, i.e., \(v_{B} \left( n \right) = b\left( n \right)q\left( n \right)\), where \(q\left( n \right)\) is a Gaussian process with zero mean variance \(\sigma_{B}^{2}\) and has \(\sigma_{B}^{2} \gg \sigma_{A}^{2}\). Moreover, \(b\left( n \right)\) represents a Bernoulli process. Its probability density function is as follows:

$$ P(w) = \left\{ {\begin{array}{*{20}c} {1 - {\text{P}}_{r} , \, w = 0} \\ {{\text{P}}_{r} , \, w = 1} \\ \end{array} } \right. $$
(62)

where \({\text{P}}_{r}\) represents represent the average power of the BG signal, which determines the probability of impulsive interference. The larger the \({\text{P}}_{r}\) value, the stronger the impact. \({\text{P}}_{r} = 0\) and \({\text{P}}_{r} = 0.01\) are chosen for comparing simulation results.

Mean square derivation (\({\text{MSD}} = 10\log_{10} \left\| {{\mathbf{w}}(n) - {\mathbf{w}}_{0} } \right\|_{2}^{2}\)) measures the algorithm’s performance [23].

Figure 4a, b, and c shows the algorithms’ performance with different SNRs. The parameters of each algorithm are shown in Table 2. As the SNR decreases, the performance of the two proposed algorithms is consistently better than other algorithms. As the SNR decreases, the effect of the variable step-size strategy is no longer evident, as shown in Fig. 4a, b, and c. This decrease may be because the stability range of the step-sizes becomes narrow when the SNR is small, resulting in the variable step-size strategy not being performed correctly. The possible causes and their analysis will be part of our future research.

Fig. 4
figure 4

The curves of SAF-type algorithms for estimating time-varying unknown systems with different SNRs: \(AR(1) = [1,0],{\text{P}}_{r} = 0[1,0]\)\(,{\text{P}}_{r} = 0\): a SNR = 15 dB; b SNR = 10 dB; and c SNR = 5 dB

Full size image
Table 2 Choice of parameters in Fig. 4
Full size table

Figure 5a and b shows the MSD curves of all algorithms in different environments where the impulsive interference frequencies are 0 and 0.01, respectively. The setting parameters of all algorithms are shown in Table 3. The SAF-LMS algorithm has diverged in an impulsive interference environment. The SAF-SNLMS and SAF-VSNLMS algorithms can keep the convergence. However, the proposed SAF-GMCC and SAF-VGMCC algorithms remain stable under impulsive interference, and the performance is significantly better than several other algorithms. In addition, the SAF-VGMCC algorithm has better performance than the SAF-GMCC algorithm (Fig. 6).

Fig. 5
figure 5

The curves of SAF-type algorithms for estimating time-varying unknown system under BG noise environment for different probabilities of occurrence of impulsive noise: \(AR(1) = [1, - 0.8]\), SNR = 30 dB: a \({\text{P}}_{r} = 0\) and b \({\text{P}}_{r} = 0.01\)

Full size image
Table 3 Choice of parameters in Fig. 5
Full size table
Fig. 6
figure 6

The curves of the experimental signal and the filtered signal in the time domain and frequency domain for estimating time-varying unknown system: \(AR(1) = [1, - 0.8]\), SNR = 30 dB, \({\text{P}}_{r} = 0.01\): a SAF-GMCC and b SAF-VGMCC

Full size image

However, the step-size variation of the original variable step-size algorithm does not effectively track the mutation signal. Thus, we propose an improvement strategy for the original variable step-size algorithm; as shown in Fig. 7, when \(n = 15000\), \({\mathbf{w}}_{0} = \left[ {0.6, - 0.4,0.25, - 0.15} \right]^{T}\) is reversed. The improved variable step-size algorithm exhibits excellent mutation tracking ability, where \(\mu_{{\mathbf{w}}} { = }\mu_{{\mathbf{h}}} { = }0.05\) and the other parameters are the same as in Fig. 6.

Fig. 7
figure 7

a Comparison of the tracking step-size curves of the original SAF-VGMCC and improved SAF-VGMCC algorithms; b comparison of the MSD curves of the original SAF-VGMCC and improved SAF-VGMCC algorithms: \(AR(1) = [1, - 0.8]\), SNR = 30 dB, and \({\text{P}}_{r} = 0\)

Full size image

The improved variable step-size strategy adds a part to detect mutations; when \(\left| {e(n) - e(n - 1)} \right| \ge \vartheta_{n}\), the step-size jumps to the initial step-size \(\mu_{{\mathbf{w}}} { = }\mu_{{\mathbf{h}}} { = }0.05\), and the variable step-size process is repeated, where \(\vartheta_{n} = Mmed(\kappa_{n} )\) and \(\kappa_{n} = [\left| {e(n - 1) - e(n - 2)} \right|,\left| {e(n - 2) - e(n - 3)} \right|,...,\left| {e(n - M) - e(n - M - 1)} \right|]\).

6 Application of ANC

6.1 Comparative Experiment of ANC

This experiment shows that the secondary channel of the system is a non-minimum phase. The first step is to set N = 6 for the nonlinear spline structure. The standard averaged noise reduction (ANR) is used as the evaluation index to unify the criteria for judging the performance of these algorithms, and its expression is as follows:

$$ {\text{ANR}} \left( n \right) = 20\log \left( {\frac{{A_{e} \left( n \right)}}{{A_{d} \left( n \right)}}} \right) $$
(63)
$$ A_{e} \left( n \right) = \lambda A_{e} \left( {n - 1} \right) + \left( {1 - \lambda } \right)|e\left( n \right)|,A_{e} \left( 0 \right) = 0 $$
(64)
$$ A_{d} \left( n \right) = \lambda A_{d} \left( {n - 1} \right) + \left( {1 - \lambda } \right)|e\left( n \right)|,A_{d} \left( 0 \right) = 0 $$
(65)

where \({\uplambda }\) is a smoothing parameter, and \(\lambda \to 1,\;\lambda \ne 1\). In this experiment, \(\lambda = 0.999\).

In the experiment, we select the ubiquitous \(\alpha\)-stable noise defined as follows:

$$ \varphi \left( {\text{t}} \right) = \exp \left\{ {j\vartheta {\text{t}} - \gamma |t|^{\alpha } [1 + j\beta {\text{sign}} \left( {\text{t}} \right)\omega \left( {{\text{t,}}\alpha } \right)]} \right\} $$
(66)

where

$$ \omega \left( {t,\alpha } \right) = \left\{ {\begin{array}{*{20}l} {\frac{\pi }{2}\log |t|,} \hfill & {\alpha = 1} \hfill \\ {\tan \frac{\alpha \pi }{2},} \hfill & {\alpha \ne 1} \hfill \\ \end{array} } \right. $$
(67)
$$ {\text{sign}} \left( {\text{t}} \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {t > 0} \hfill \\ {0,} \hfill & {t = 0} \hfill \\ { - 1,} \hfill & {t < 0} \hfill \\ \end{array} } \right. $$
(68)

The simulation is based on the standard \(\alpha\)-stable distribution [27], whose parameter values are \(\beta { = 0, }\gamma { = 1}\), and \(\vartheta { = 0}\), and the characteristic function is as follows:

$$ \varphi \left( t \right) = \exp \left( { - |t|^{\alpha } } \right) $$
(69)

The noise intensity is controlled by adjusting the \(\alpha\)-parameter. The smaller the \(\alpha\), the greater the impact strength. The primary channel noise observed by the error microphone is given by [19]

$$ d\left( n \right) = u\left( {n - 2} \right) + \delta_{1} u^{2} \left( {n - 2} \right) - \delta_{2} u^{3} \left( {n - 1} \right) $$
(70)

The function \({\updelta }_{{\text{i}}} ,{\text{i = 1,2,}}...\) is to measure the strength of the nonlinear secondary channel, and this simulation takes \({\updelta }_{1} { = 0}{\text{.08}}\) and \({\updelta }_{2} { = 0}{\text{.04}}\). The input signal \({\mathbf{x}}\left( n \right)\) is the alpha-stable distributed noise. \(u\left( n \right){\text{ = x}}\left( n \right) * p\left( n \right)\), \(p\left( n \right)\) is the impulsive response of the transfer function of the primary channel. Afterward \(\alpha \equiv \alpha^{ * }\), in \(\alpha\)-stable noise to achieve ease of differentiation. The transfer functions of the primary and the secondary channels with non-minimum phase characteristics are as follows:

$$ P\left( z \right) = z^{ - 3} - 0.3z^{ - 4} + 0.2z^{ - 5} $$
(71)
$$ S\left( z \right) = z^{ - 2} + 1.5z^{ - 3} - z^{ - 4} $$
(72)

Figure 5 shows the performance of the FcNLMS, FcSNLMS, FcMCC, FcGMCC, and FcVGMCC algorithms based on the SAF-NLMS, SAF-SNLMS, SAF-MCC, SAF-GMCC, and SAF-VGMCC algorithms, respectively, where the impact strength is 2, 1.9, 1.8, and 1.7. Table 4 shows the parameters (Fig. 8).

Table 4 Choice of parameters in ANC
Full size table
Fig. 8
figure 8

ANR curves under different alpha impulsive noises

Full size image

The FcGMCC and FcVGMCC algorithms maintain stable convergence under the non-minimum phase channel, when the input signal does not contain impulsive noise. Under comprehensive comparison, the new algorithms’ convergence speed and steady-state ANR are better than other algorithms. The FcVGMCC algorithm shows better performance than the FcGMCC algorithm. The FcGMCC and FcVGMCC algorithms have superior performance, when \(\alpha = 1.9\). The steady-state ANR of the proposed FcVGMCC algorithm is better than that of other algorithms. When the input contains impulsive noise, the FcNLMS algorithm shows severe divergence state with the same step-size parameter. When \(\alpha = 1.8\) and \(\alpha = 1.7\), the FcGMCC and FcVGMCC algorithms offer clear advantages. Although the steady-state of the FcVGMCC algorithm is similar to that of the FcGMCC algorithm, the FcVGMCC algorithm convergence speed is faster than that of the FcGMCC algorithm.

7 Conclusions

This study proposes the SAF-GMCC and SAF-VGMCC algorithms, to improve the robustness of the traditional SAF-type algorithms. Unlike the algorithms based on the error mean square criterion, which relies on the Gaussian environment, the SAF-GMCC algorithm is not too sensitive to abnormal data because of the presence of the kernel function. Thus, the SAF-GMCC algorithm offers good robustness in impulsive interference. In addition, the variable step-size is introduced to improve the SAF-GMCC algorithm’s performance, and the SAF-VGMCC algorithm is proposed. Compared with the fixed step-size algorithm, the SAF-VGMCC algorithm has theoretically improved both convergence rate and steady-state error. Simulation in impulsive interference shows that the performance of the above algorithms is effective in impulsive interference. Finally, this study presents the practical applications of the proposed algorithms. Then, the SAF-GMCC and SAF-VGMCC algorithms are applied to nonlinear ANC, and the FcGMCC and FcVGMCC algorithms are proposed. The nonlinear problem in the ANC model is solved by introducing the nonlinear spline adaptive structure. In addition, a better noise removal effect is achieved with the algorithms’ robustness, even when the noise source contains impulsive interference. Simulation experiments shows the feasibility of the proposed FcGMCC and FcVGMCC algorithms in nonlinear and non-Gaussian noise environments.