Nonlinear Spline Adaptive Filtering Against Non-Gaussian Noise

Abstract

In this paper, a generalized maximum Versoria criterion algorithm (GMVC) based on wiener spline adaptive filter, called SAF–GMVC, is proposed. The proposed algorithm is used for nonlinear system identification under non-Gaussian environment. To improve the convergence performance of the SAF–GMVC, the momentum stochastic gradient descent (MSGD) is introduced. In order to further reduce the steady-state error, the variable step-size algorithm is introduced, called as SAF–GMVC–VMSGD. Simulation results demonstrate that SAF–GMVC–VMSGD achieves better filtering effective against non-Gaussian noise.

1 Introduction

Adaptive filtering (AF) algorithm is widely used in signal processing, which has been utilized for system identification [20], prediction model [5], interference elimination [19], inverse modeling [23]. Least mean square (LMS) is one of the most popular AF algorithms due to its simplicity and good performance [7]. However, it cannot deal with nonlinear structure. One solution is the spline adaptive filter (SAF), which uses spline interpolation to interpolate data from known nodes, formed SAF–LMS [14]. Some constructs have been proposed of the SAF algorithm, examples as: Wiener SAF [10], Hammerstein SAF [15], Sandwich 1 SAF, Sandwich 2 SAF [16].

However, the SAF–LMS performance degradation in the presence of the non-Gaussian environment, due to the use of the mean square error (MSE) criterion [14]. To achieve better robuster filtering performance, various nonlinear optimization criteria have been proposed. Examples include: the LMS adaptive scheme has been extended to the normalized version, called SAF–NLMS [6]. Peng et al. propose SAF–MCC algorithm, combining SAF with maximum correntropy criterion (MCC), which shown robust to large outliers [12]. The reference [24] proposed a novel algorithm, under the impulsive environment. That algorithm through introduce momentum in stochastic gradient descent, called SAF–ARC–MMSGD. The reference [4] proposed a sign normalised least mean square algorithm (SNLMS) based on Wiener spline adaptive filter, and the variable step-size scheme is introduced, SAF–VSS–SNLMS. Moreover, the weight update of the normalized subband spline adaptive filter algorithm is conducted using the principle of minimum disturbance [22]. Referring to [2, 8], compared with the maximum correntropy criterion, the Versoria criterion has faster convergence speed and stronger robustness when applied to adaptive filtering. Huang et al. applied the Versoria function to the adaptive filtering to improve the robustness [8]. In order to further improve the robustness of the system, a robust weight-constraint decorrelation normalized maximum Versoria algorithm is designed [25]. Jain et al. applied the Versoria function to the research of kernel adaptive filtering [9]. Other researchers applied the maximum Versoria adaptive filtering algorithm to the study of power energy [1, 18]. The filter algorithm based on Generalized maximum Versoria criterion (GMVC) has strong robustness, so this paper chooses GMVC algorithm as the adaptive strategy.

In this paper, we propose a novel robust wiener type spline adaptive filter algorithm, which is called SAF–GMVC–VMSGD. Through variable step size-momentum stochastic gradient descent update the loss function weight. Generalized maximum Versoria criterion as a loss function. Compared with the SAF-MCC algorithm, it does not require exponential operation. Under non-Gaussian noise, compare with SAF–MCC, simulation results demonstrate better efficiency of the proposed SAF–GMVC–VMSGD algorithm.

2 Wiener Spline Adaptive Filter

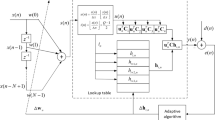
Wiener spline adaptive filter architecture consists of the cascade of a suitable number of linear filter, and a memoryless nonlinear function implemented by the spline interpolation scheme [17].

The input signal of SAF at instant n is x(n), the input signal x(n) passes through a FIR filter, obtaining an intermediate output s(n). Input signal defined as ${\mathbf {x}}_n = \left[ \begin{array}{cccc}x_{n}&x_{n-1}&\ldots&x_{n-M+1} \end{array}\right] ^T$. M represents the order of tap weights of the FIR filter. Intermediate output s(n) is defined as

$$\begin{aligned} s(n) = \mathbf{{w}}_n^T \mathbf{{x}}_n \end{aligned}$$

(1)

where ${\mathbf {w}}_n = \left[ \begin{array}{cccc}w_{0}&w_{1}&\ldots&w_{M-1} \end{array}\right] ^T$ is the weight vector of FIR filter at instant n.

Interpolation functions are smooth parametric curves that interpolate by collecting defined control points in a lookup table (LUT). Cubic spline curve mainly includes B spline and CR spline [3]. Since CR spline has the characteristic of passing all control nodes, Therefore, CR splines are the only objects considered in this article. The interpolation process starts with the calculation of normalized horizontal coordinates u and interval indexes i based on the LUT.

Let ${\mathbf {Q}}_i = \left[ \begin{array}{cccc}q_{x,i}, q_{y,i} \end{array}\right] ^T$ for $i=0,1,2,\ldots ,N$ represent the $N+1$ control points (knots), where the $x-axis$ value $q_{x,j}$ are uniformly distributed and order to $q_{x,N}> \cdots>q_{x,1}>q_{x,0}$. Then we can obtain i and u by the following equations

$$\begin{aligned} i= & {} \left\lfloor \frac{s(n)}{\Delta x} \right\rfloor + \frac{N}{2} \end{aligned}$$

(2)

$$\begin{aligned} u_n= & {} \frac{s(n)}{\Delta x} - \left\lfloor \frac{s(n)}{\Delta x} \right\rfloor \end{aligned}$$

(3)

where $\Delta x = q_{i+1} - q_{i}$ is the uniform space between knots, $\lfloor \cdot \rfloor$ is the floor operator.

To calculate the filter output y(n), suppose that $y_{n} = \varphi (x_{n})$ is the spline function to be estimated. Which is a spline interpolation of four adaptive control points of the ith interval contained in a LUT, which can be expressed

$$\begin{aligned} y_{n} = \varphi _{i}(u_{n}) = \mathbf{{u}}_{n}^T\mathbf{{C}}{} \mathbf{{q_{i}}}(n) \end{aligned}$$

(4)

where the vector $\mathbf{{u}}_n$ is defined as $\mathbf{{u}}_n = [ u^3,u^2,u,1 ]^T$, the vector $\mathbf{{q_{i}}}(n)$ is defined by $\mathbf{{q_{i}}}(n) =[q_{i},q_{i+1},q_{i+2},q_{i+3}]^T$, at the instant n. And $\mathbf{{C}}$ is the basis matrix of CR-spline defined [6]

$$\begin{aligned} \mathbf{{C}}&= \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {-1} &{} {3} &{} {-3} &{} {1} \\ 2 &{} {-5} &{} 4 &{} {-1} \\ {-1} &{} 0 &{} 1 &{} 0 \\ 0 &{} 2 &{} 0 &{} 0 \\ \end{array}} \right] \end{aligned}$$

(5)

The derivative of $y_{n}$ with respect to $u_{n}$ is calculated

$$\begin{aligned} \frac{\partial y_{n}}{\partial u} = \frac{\partial \varphi _{i}(u)}{\partial u} = {{\dot{\mathbf {u}}}^\mathbf {T} \mathbf {C q_{i}}}(n) \end{aligned}$$

(6)

where ${\dot{\mathbf{u}}}= [3u^2, 2u, 1, 0]^T$.

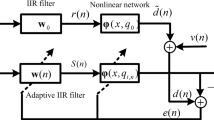
In this work, Wiener spline adaptive filter consists that the cascade of an adaptive FIR filter and cubic CR-spline. The basic block diagram of SAF is shown in Fig. 1.

Fig. 1

Structure of Wiener spline adaptive filter

With reference to Fig. 1, the priori error $e_{n}$ is defined

$$\begin{aligned} e_{n}= & {} d(n) - y_{n} \end{aligned}$$

(7)

Based on the basic framework above, the adaptive strategy of SAF is derived by minimizing the instantaneous square error which is given [14].

$$\begin{aligned} J({{\mathbf {w}_{n},\mathbf {q_{i}}}}(n)) = e_{n}^2 \end{aligned}$$

(8)

Derivative of $J(\mathbf {w}_{n},\mathbf {q_{i}}(n))$ as regards $\mathbf {w}_{n}$ and $\mathbf {q_{i}}(n)$, and using the stochastic gradient descent (SGD) method, the adaptive process of SAF can be expressed

$$\begin{aligned} {\mathbf {w}_{n+1}} = {\mathbf {w}_{n}} + \mu _{w} e_{n} {\dot{\mathbf {u}}}^{\mathbf {T} \mathbf {C q_{i}}}(n) {\mathbf {x_{n}}} / \Delta x \end{aligned}$$

(9)

$$\begin{aligned} \mathbf{{q_{i}}}(n+1) = \mathbf{{q_{i}}}(n) + \mu _{q} e_{n} \mathbf{{C^T u_{n}}} \end{aligned}$$

(10)

where $\mu _{w}$ and $\mu _{q}$ represent the learning rates for the weights and for the control points, separately. The above traditional SAF method, called SAF–LMS [14].

3 SAF–GMVC–VMSGD Algorithm

In this part, in order to improve the robustness of SAF against non-Gaussian noise, we introduce the generalized Versoria criterion (GMVC) combines with the SAF, present the proposed algorithm SAF–GMVC. And then, to further improve the convergence performance, the variable step-size momentum stochastic gradient descent (VMSGD) algorithm is introduced, the algorithm called SAF–GMVC–VMSGD.

3.1 Generalized Versoria Function

In non-Gaussian noise environment, in order to more effectively use the system output error information to improve the convergence speed or steady-state error of the filter. Many error nonlinear adaptive filtering algorithms with saturation characteristics have been proposed. For example, adaptive filtering algorithm based on maximum correntropy criterion (MCC). When non-Gaussian noise appears, the system output error is very large. The error nonlinearity of MCC algorithm approaches the saturation value 0. At this time, the weight coefficient vector of MCC algorithm is almost not updated, thus suppressing the non-Gaussian noise. However, since MCC algorithms uses Gaussian probability density function (GPDF) as the cost function, it has a large computational complexity. An adaptive filtering algorithm with stronger robustness in non-Gaussian noise environment is proposed, namely maximum Versoria criterion (MVC) algorithm. Compared with MCC algorithm, this algorithm does not contain exponential operation and has lower steady-state error.

The cost function of the maximum correntropy criterion (MCC) algorithm is the GPDF, which can be written as[21]

$$\begin{aligned} f(e_{n}) = \mathrm{exp}(-\frac{e_n^2}{2\varpi ^2}) \end{aligned}$$

(11)

where $\varpi >0$ is the kernel width. The GPDF is high calculation cost when it used in signal processing, especially in adaptive filtering.

For adaptive filtering, designing a suitable and high-efficiency cost framework is an important issue. In order to draw forth the proposed cost function, we first introduce the standard Versoria criterion, which is defined as [8, 13, 25],

$$\begin{aligned} f(e_{n})= \frac{8a^3}{4a^2+e_{n}^2} = \frac{2a}{1+{\left( \frac{e_{n}}{2a} \right) }^2} \end{aligned}$$

(12)

where $e_n$ represent error, $a>0$ is the radius of the generating circle of Versoria. The centroid of the generating circle is located at (0, a). A larger value of the radius a leads to a steeper Versoria [8]. The loss function of Geman–McClure estimator defined as $f(e_{n})=\frac{e_{n}^2}{\vartheta ^2+e_{n}^2}$, $\vartheta$ denotes the positive parameter which modulates the shape of the loss function [11].

Fig. 2

Comparison of steepness of the GPDF, the Versoria function, the Geman–McClure function

As a comparison, Fig. 2 plots the GPDF $(\varpi =0.5)$, the Geman–McClure function $(\vartheta =0.5)$ and the standard Versoria function $(a=0.5)$. From this figure, we can observe that the Versoria function is less steep than the two other functions for the error $e_{n}$. This means that the error along the direction of the gradient ascent of the Versoria is faster to reach the optimal point than do the GPDF and the Geman–McClure function. From the perspective of the adaptive filter, the gradient ascent algorithm based on the Versoria function has a faster convergence rate to reach the same steady-state error than do the GPDF and the Geman–McClure function algorithm.

Generalized Versoria criterion can be regarded as [1, 2, 9, 18],

$$\begin{aligned} f(e_{n}) = \frac{2a}{1+{\left| \frac{e_{n}}{2a} \right| }^p} = \frac{2a}{1+\tau {\left| e_{n} \right| }^p} \end{aligned}$$

(13)

$p>0$ is the shape parameter, and $\tau = (2a)^{-p}$. As a special case, it reduced to the standard Versoria function when $p = 2$.

3.2 SAF–GMVC

According to the generalized Versoria function in linear adaptive filtering show stronger robustness, and there is no exponential operation in the formula, thus reducing the computational complexity of the system. Used Versoria function as the cost function:

$$\begin{aligned} \begin{aligned} J(e_{n})= & {} J(\mathbf {w}_{n},\mathbf {q_{i}}(n))= & {} E \left[ \frac{1}{1+\tau {\left| e_{n} \right| }^p} \right] \end{aligned} \end{aligned}$$

(14)

The gradient of Eq. (14) with respect to $e_{n}$, and denoting the result by $e_{d}(n)$,

$$\begin{aligned} \begin{aligned} e_{d}(n)= & {} \nabla J(\mathbf {w}_{n},\mathbf {q_{i}}(n))= & {} \frac{\tau p}{(1+\tau {\left| e_{n} \right| }^p)^2} {\left| e_{n} \right| }^{p-1} \mathrm{sign}(e_{n}) \end{aligned} \end{aligned}$$

(15)

where $E\left[ \cdot \right]$ denotes the expectation operator. As can be seen from Eq. (14), when an non-Gaussian interference corrupted $e_{n}$ appears, leads to $J(e_{n})\rightarrow 0$, which plays the role of suppressing non-Gaussian interference. Eliminate the updating of weight vector based on the non-Gaussian interference.

Fig. 3

Slope curves of the cost function with different parameters

Figure 3 shows the derivative curves for different parameters, the slope curves dropping gradually to zero, which will reduce the effect of non-Gaussian noise interference on cost function.

SAF combine with generalized Versoria cost function. Taking the derivative of Eq. (14) with respect to $\mathbf {w_{n}}$.

$$\begin{aligned} \begin{aligned} \mathbf{{g_{w}}}(n)= & {} \frac{\partial J(e_{n})}{\partial \mathbf {w}_{n}}= & {} \frac{J{{(\mathbf {w}_{n},\mathbf {q_{i}}}}(n))}{\partial \mathbf {w}_{n}}= & {} -e_{d}(n) {\frac{\partial \varphi _{i}(u)}{\partial u}}{\frac{\partial u}{\partial s(n)}}{\frac{\partial s(n)}{\partial \mathbf {w}_{n}}} \end{aligned} \end{aligned}$$

(16)

Through Eqs. (1), (3), (6), can get

$$\begin{aligned} \begin{aligned} \mathbf {{g_{w}}}(n)=&{} - e_{d}(n){{\dot{\mathbf {u}}}^\mathbf {T} \mathbf {C q_{i}}}(n) \mathbf {x_{n}} / \Delta x \end{aligned} \end{aligned}$$

(17)

Taking the derivative of Eq. (14) with respect to $\mathbf {q_{i}}(n)$,

$$\begin{aligned} \begin{aligned} \mathbf{{g_{q}}}(n)= & {} \frac{\partial J(e_{n})}{\partial \mathbf{{q_{i}}}(n)}= & {} \frac{J\mathbf{{(w_{n},q_{i}}}(n))}{\partial \mathbf{{q_{i}}}(n)}= & {} -e_{d}(n) {\frac{\partial \varphi _{i}(u)}{\partial \mathbf{{q_{i}}}(n)}} \end{aligned} \end{aligned}$$

(18)

Through Eq. (4), we can get

$$\begin{aligned} \begin{aligned} \mathbf{{g_{q}}}(n)= & {} - e_{d}(n)\mathbf{{{C}^T u_{n}}} \end{aligned} \end{aligned}$$

(19)

Using gradient descent method can be to obtain the iterative learning rules of SAF–GMVC.

$$\begin{aligned} \begin{aligned} \mathbf {w}_{n+1}=&{} {\mathbf {w}_{n}} + \mu _{w} e_{d}(n) {\dot{\mathbf {u}}}^\mathbf {T} \mathbf {C q_{i}}(n) {\mathbf {x_{n}}} / \Delta x \end{aligned} \end{aligned}$$

(20)

$$\begin{aligned} \begin{aligned} \mathbf{{q_{i}}}(n+1)= & {} \mathbf{{q_{i}}}(n) + \mu _{q} e_{d}(n) \mathbf{{C^T u_{n}}} \end{aligned} \end{aligned}$$

(21)

where the parameters $\mu _{w}$ and $\mu _{q}$ represent the learning rates for the weights and for the control points, respectively, for simplicity, incorporate the others constant values.

3.3 Variable Step-Size Momentum SGD Algorithm

In order to improve the convergence performance, the momentum term and variable step-size term are introduced. The specific operation is as follows. In order to increase the convergence speed, the momentum stochastic gradient descent algorithm is introduced, called SAF–GMVC–MMSGD. In this method, the exponential moving average value of the historical gradients are defined as the momentum term, and the actual modification of the weight vector at current instant depends on both the current gradient and the momentum term [24], which can be expressed

$$\begin{aligned} \begin{aligned} {\mathbf {m}}(n)= & {} \sigma {\mathbf {m}(n-1)} + \mu {\mathbf {g}}(n) \end{aligned} \end{aligned}$$

(22)

$$\begin{aligned} \begin{aligned} {\mathbf {w}_{n+1}}= & {} {\mathbf {w}_{n}} - {\mathbf {m}(n)} \end{aligned} \end{aligned}$$

(23)

where $\mathbf {m}(n)$ represents the momentum term also the actual modification of the weight vector at instant n, $\mathbf {w}_{n}$ and $\mathbf {g}(n)$ are the weight vector and gradient vector, respectively, $\sigma$ is the momentum parameter, and $\mu$ is the learning rate.

In order to further reduce the steady-state error, the variable step-size algorithms is introduced, named SAF–GMVC–VMSGD. $\mu _{w}(n)$ and $\mu _{q}(n)$ represent the learning rates for the weights and for the control points, respectively.

$$\begin{aligned} \begin{aligned} \mu _{w}(n)= & {} \rho \mu _{w}(n-1) + (1- \rho ) \min {\left[ {\hat{e}^2_{o}(n)}, \mu _{w}(n-1) \right] } \end{aligned} \end{aligned}$$

(24)

$$\begin{aligned} \begin{aligned} \mu _{q}(n)= & {} \rho \mu _{q}(n-1) + (1- \rho ) \min {\left[ {\hat{e}^2_{o}(n)}, \mu _{q}(n-1) \right] } \end{aligned} \end{aligned}$$

(25)

where $\rho$ is the forgetting factor approaching one. $\hat{e}^2_{o}(n)$ is the estimate of squared value of the non-Gaussian noise error [4].

$$\begin{aligned} \begin{aligned} \hat{e}^2_{o}(n)= & {} \lambda {\hat{e}^2_{o}(n-1)} + c_{1}(1-\lambda ){med(\gamma _{n})} \end{aligned} \end{aligned}$$

(26)

where $\lambda$ is forgetting factor close to but smaller than one, $c_{1} = 1.483(1+\frac{5}{N_{w}-1})$ is a finite correction factor [4] and $N_{w}$ is the data window. $\gamma _{n} = \left[ e^2_{n},e^2_{n-1},\ldots ,e^2_{n-N_{w}+1} \right]$ and $med(\cdot )$ denotes the median operator.

$\mu (n)$ bring Eq. (22), we can get

$$\begin{aligned} \begin{aligned} \mathbf {m}(n)= & {} \sigma \mathbf {m}(n-1) + \mu (n) \mathbf {g}(n) \end{aligned} \end{aligned}$$

(27)

Due to the momentum term will cause oscillations at the neighborhood of minimum value, two algorithms are introduced. First, the decay technique about momentum factor $\sigma$.

$$\begin{aligned} \begin{aligned} \sigma _{n}= & {} c_{0} \sigma _{n-1} \end{aligned} \end{aligned}$$

(28)

where $c_{0}$ is the decay coefficient $(0.9995 \sim 1)$. When $c_{0}= 1$ , the decay technique will be ineffective.

Second, the direction compare of the momentum term and the current gradient by their inner product. If the inner product is non-negative, we use the momentum method. In reverse, it means the momentum term and current gradient orient to opposite directions. We only choose current gradient [24]. Expressed as

$$\begin{aligned} \begin{aligned} \mathbf { m_{w}}(n) = \left\{ \begin{array}{ll} \mu _{w}(n)\mathbf {g_{w}}(n), &{} {\left\langle {\mathbf {m_{w}}(n-1),\mathbf {g_{w}}(n)} \right\rangle } < 0 \\ \sigma _{n}\mathbf {m_{w}}(n-1) + \mu _{w}(n)\mathbf {g_{w}}(n), &{} {\left\langle {\mathbf {m_{w}}(n-1),\mathbf {g_{w}}(n)} \right\rangle } \ge 0 \end{array} \right. \end{aligned} \end{aligned}$$

(29)

$$\begin{aligned} \begin{aligned} \mathbf {m_{q}}(n) = \left\{ \begin{array}{ll} \mu _{q}(n)\mathbf {g_{q}}(n), &{} {\left\langle {\mathbf {m_{q}}(n-1),\mathbf {g_{q}}(n)} \right\rangle } < 0 \\ \sigma _{n}\mathbf {m_{q}}(n-1) + \mu _{q}(n)\mathbf {g_{q}}(n), &{} {\left\langle {\mathbf {m_{q}}(n-1),\mathbf {g_{q}}(n)} \right\rangle } \ge 0 \end{array} \right. \end{aligned} \end{aligned}$$

(30)

where $\mathbf {g_{w}}(n)$ and $\mathbf {g_{q}}(n)$ are defined at Eqs. (17), (19), $\mathbf {m_{w}}(n)$ and $\mathbf {m_{q}}(n)$ represent the momentum terms at instant n with regard to w and $q_{i}$.The updating equations can be rewritten as

$$\begin{aligned} \begin{aligned} \mathbf {w_{n+1}}= & {} \mathbf { w_{n}} - \mathbf {m_{w}}(n) \end{aligned} \end{aligned}$$

(31)

$$\begin{aligned} \begin{aligned} \mathbf {q_{i}}(n+1)= & {} \mathbf {q_{i}}(n) - \mathbf {m_{q}}(n) \end{aligned} \end{aligned}$$

(32)

3.4 The Proposed SAF–GMVC–VMSGD Algorithm Brief

The proposed algorithm SAF–GMVC–VMSGD, combine the generalized Versoria cost function is adopted to increase the robustness against non-Gaussian noises, with the variable step-size momentum stochastic gradient descent (VMSGD) is introduced to further improve the convergence performance. The proposed algorithm is summarized in Algorithm 1.

4 Convergence Analysis

In this section, we analyzed the convergence property of the proposed algorithm in nonlinear identification system. As shown in Fig. 4, $w^*$ is the weight vector and $q^*$ is the control point, of real system. We take ${\left| e_{n+1} \right| } < {\left| e_{n} \right| }$ as a condition for judging whether the algorithm convergence. The convergence analysis of the proposed algorithm can be implemented in two separate phases with regard to $\mathbf {w}$ and $\mathbf {q_{i}}$.

Fig. 4

Block diagram of the system identification using Wiener SAF

4.1 Convergence Analysis of $\mathbf {w}$

Taking a first-order Taylor series expansion of the error $e_{n+1}$ at instant n.

$$\begin{aligned} \begin{aligned} e_{n+1}= & {} e_{n} + \frac{\partial e_{n}}{\partial \mathbf {w}_{n}^T} \Delta \mathbf {w}_{n} +h.o.t \end{aligned} \end{aligned}$$

(33)

where h.o.t. represents the high-order term of Taylor series. The second term can be expressed as

$$\begin{aligned} \begin{aligned} \frac{\partial e_{n}}{\partial \mathbf {w}_{n}^T}=&{} - {\frac{\partial y_{n}}{\partial u}}{\frac{\partial u}{\partial s(n)}}{\frac{\partial s(n)}{\partial \mathbf {w}_{n}^T}}=&{} -{\dot{\mathbf {u}_{n}}}^{\mathbf {T} \mathbf {C q_{i}}}(n) \mathbf {x_{n}}^T/ \Delta x \end{aligned} \end{aligned}$$

(34)

$$\begin{aligned} \begin{aligned} \Delta \mathbf {w}_{n}= & {} \mathbf {w}_{n+1} - \mathbf {w}_{n} \end{aligned} \end{aligned}$$

(35)

Then reference to Eqs. (29), (31), (35) can be expressed as

$$\begin{aligned} \begin{aligned} \Delta \mathbf {w_{n}} = \left\{ \begin{array}{ll} - \mu _{w}(n)\mathbf {g_{w}}(n), &{} {\left\langle {\mathbf {m_{w}}(n-1),\mathbf {g_{w}}(n)} \right\rangle } < 0 \\ - \sigma _{n}\mathbf {m_{w}}(n-1) - \mu _{w}(n)\mathbf {g_{w}}(n), &{} {\left\langle {\mathbf {m_{w}}(n-1),\mathbf {g_{w}}(n)} \right\rangle } \ge 0 \end{array} \right. \end{aligned} \end{aligned}$$

(36)

Consider the case of ${\left\langle {\mathbf {m_{w}}(n-1),\mathbf {g_{w}}(n)} \right\rangle } \ge 0$, substituting Eqs. (34), (36) into Eq. (33) and ignoring the higher order terms, then we can get

$$\begin{aligned} \begin{aligned} e_{n+1}&= e_{n} + {\left[ \sigma _{n} \mathbf {m_{w}}(n-1) + \mu _{w}(n) \mathbf {g_{w}}(n) \right] } {\dot{\mathbf {u}_{n}}}^{\mathbf {T} \mathbf {C q_{i}}}(n) \mathbf {x_{n}}^T/ \Delta x \end{aligned} \end{aligned}$$

(37)

Bring Eq. (17) into Eq. (37),

$$\begin{aligned} \begin{aligned} e_{n+1}= & {} e_{n}{\left[ 1- \frac{\sigma _{n}\mathbf {g^T_{w}}(n)\mathbf {m_{w}}(n-1) + \mu _{w}(n)\mathbf {g^T_{w}}(n) \mathbf {g_{w}}(n)}{e_{d}(n)e_n}\right] } \end{aligned} \end{aligned}$$

(38)

${\left| e_{n+1} \right| } < {\left| e_{n} \right| }$ ensure the convergence of the algorithm. The following relation holds

$$\begin{aligned} \begin{aligned} \left| 1- \frac{\sigma _{n}\mathbf {g^T_{w}}(n)\mathbf {m_{w}}(n-1) + \mu _{w}(n)\mathbf {g^T_{w}}(n) \mathbf {g_{w}}(n)}{e_{d}(n)e_n} \right| <1 \end{aligned} \end{aligned}$$

(39)

It is derive that

$$\begin{aligned} \begin{aligned} 0< { \frac{\sigma _{n}\mathbf {g^T_{w}}(n)\mathbf {m_{w}}(n-1) + \mu _{w}(n)\mathbf {g^T_{w}}(n) \mathbf {g_{w}}(n)}{e_{d}(n)e_n} } <2 \end{aligned} \end{aligned}$$

(40)

$\mathbf {g^T_{w}}(n)\mathbf {m_{w}}(n-1)$ and $\mathbf {g^T_{w}}(n) \mathbf {g_{w}}(n)$ is non-negative, $e_n$ and $e_{d}(n)$ are of the same sign, the bound of the learning rate under convergence condition is

$$\begin{aligned} 0< \mu _{w}(n) < { \frac{2e_{d}(n)e_n - \sigma _{n}\mathbf {g^T_{w}}(n)\mathbf {m_{w}}(n-1)}{\mathbf {g^T_{w}}(n) \mathbf {g_{w}}(n)}} \end{aligned}$$

(41)

Consider the case of ${\left\langle {\mathbf {m_{w}}(n-1),\mathbf {g_{w}}(n)} \right\rangle }< 0$, substituting Eqs. (34), (36) into Eq. (33) and ignoring the higher order terms, then we can get.

$$\begin{aligned} \begin{aligned} e_{n+1}=&{} e_{n} + \mu _{w}(n) \mathbf {g_{w}}(n) {\dot{\mathbf {u}_{n}}}^{\mathbf {T} \mathbf {C q_{i}}}(n) \mathbf {x_{n}}^T/ \Delta x \end{aligned} \end{aligned}$$

(42)

Bring Eq. (17) into Eq. (42), i.e.,

$$\begin{aligned} \begin{aligned} e_{n+1}= & {} e_{n}{\left[ 1- \frac{\mu _{w}(n)\mathbf {g^T_{w}}(n) \mathbf {g_{w}}(n)}{e_{d}(n)e_n}\right] } \end{aligned} \end{aligned}$$

(43)

The bound of the learning rate is

$$\begin{aligned} \begin{aligned} 0< \mu _{w}(n) < { \frac{2e_{d}(n)e_n}{\mathbf {g^T_{w}}(n) \mathbf {g_{w}}(n)}} \end{aligned} \end{aligned}$$

(44)

The learning rate should satisfy

$$\begin{aligned} \begin{aligned} 0<\mu _{w}(n)<\min (\frac{2e_{d}(n)e_n}{\mathbf {g^T_{w}}(n) \mathbf {g_{w}}(n)},\frac{2e_{d}(n)e_n - \sigma _{n}\mathbf {g^T_{w}}(n)\mathbf {m_{w}}(n-1)}{\mathbf {g^T_{w}}(n) \mathbf {g_{w}}(n)}) \end{aligned} \end{aligned}$$

(45)

4.2 Convergence Analysis of $\mathbf {q_{i}}$

The convergence analysis of $\mathbf {q_{i}}$ is similar to convergence analysis of $\mathbf {w}$. Taking a first-order Taylor series expansion of the error $e_{n+1}$ at instant n, we can get

$$\begin{aligned} \begin{aligned} e_{n+1}= & {} e_{n} + \frac{\partial e_{n}}{\partial \mathbf {q^T_{i}}(n)} \Delta \mathbf {q_{i}}(n) +h.o.t \end{aligned} \end{aligned}$$

(46)

where h.o.t. represents the high order terms of the first-order Tylor series expansion. The second term can be expressed as

$$\begin{aligned} \begin{aligned} \frac{\partial e_{n}}{\partial \mathbf {q^T_{i}}(n)}= & {} -{\frac{\partial y_{n}}{\partial \mathbf {q^T_{i}}(n)}}= & {} -\mathbf {u_{n}^T C} \end{aligned} \end{aligned}$$

(47)

$$\begin{aligned} \begin{aligned} \Delta \mathbf {q_{i}}(n)= & {} \mathbf {q_{i}}(n+1) - \mathbf {q_{i}}(n) \end{aligned} \end{aligned}$$

(48)

Then, reference to Eqs. (30), (32), (48) can be expressed as

$$\begin{aligned} \begin{aligned} \Delta \mathbf {q_{i}}(n) = \left\{ \begin{array}{ll} -\mu _{q}(n)\mathbf {g_{q}}(n), &{} {\left\langle {\mathbf {m_{q}}(n -1 ),\mathbf {g_{q}}(n)} \right\rangle } < 0 \\ -\sigma _{n}\mathbf {m_{q}}(n-1) - \mu _{q}(n)\mathbf {g_{q}}(n), &{} {\left\langle {\mathbf {m_{q}}(n-1),\mathbf {g_{q}}(n)} \right\rangle } \ge 0 \end{array} \right. \end{aligned} \end{aligned}$$

(49)

Consider the case of ${\left\langle {\mathbf {m_{q}}(n -1 ),\mathbf {g_{q}}(n)} \right\rangle } < 0$, substituting Eqs. (47), (49) and (19) into Eq. (46) and ignoring the higher order terms, then we can get

$$\begin{aligned} \begin{aligned} e_{n+1}= & {} e_{n}{\left[ 1- \frac{\mu _{q}(n)\mathbf {g^T_{q}}(n) \mathbf {g_{q}}(n)}{e_{d}(n)e_n}\right] } \end{aligned} \end{aligned}$$

(50)

Satisfy the convergence condition ${\left| e_{n+1} \right| } < {\left| e_{n} \right| }$, obtained

$$\begin{aligned} \begin{aligned} \left| 1- \frac{\mu _{q}(n)\mathbf {g^T_{q}}(n) \mathbf {g_{q}}(n)}{e_{d}(n)e_n} \right| <1 \end{aligned} \end{aligned}$$

(51)

The other case is similar to the above $\mathbf {w}$ convergence analysis process, the convergence condition of the learning rate $\mathbf {q_{i}}$,

$$\begin{aligned} \begin{aligned} 0<\mu _{q}(n)<\min \left( \frac{2e_{d}(n)e_n}{\mathbf {g^T_{q}}(n) \mathbf {g_{q}}(n)},\frac{2e_{d}(n)e_n - \sigma _{n}\mathbf {g^T_{q}}(n)\mathbf {m_{q}}(n-1)}{\mathbf {g^T_{q}}(n) \mathbf {g_{q}}(n)} \right) \end{aligned} \end{aligned}$$

(52)

5 Numerical Simulations

Several numerical simulations are performed, observing the convergence speed and the steady-state error, to verify the effectiveness of the proposed algorithm. The input signal $x_{n}$ is generated by the following relationship.

$$\begin{aligned} \begin{aligned} x_{n}= & {} r x_{n-1} + \sqrt{1-r^2} \xi (n) \end{aligned} \end{aligned}$$

(53)

where $\xi (n)$ is a zero mean white Gaussian noise with unitary variance, and $r \in \left[ 0,1\right)$ is a correlation factor that determines the correlation between adjacent input signal $x_{n}$ values.

The algorithm performance is measured by use of mean square error (MSE),

$$\begin{aligned} \begin{aligned} \mathrm{MSE}= & {} 10 \lg {\left[ e_{n} \right] }^2 \end{aligned} \end{aligned}$$

(54)

In this paper, the weight vectors of the FIR filter in all SAF type related algorithms are typically initialized to $\mathbf {w}_{0} = { \left[ 1,0,\ldots ,0 \right] }^T$. In addition, an independent white Gaussian noise v(n) with different signal to noise ratio (SNR), that is added to the output of the real unknown system. In the simulation, according to the theoretical boundary of the step size and the simulation experiment value, the step size range of the experiment simulation is obtained $0<\mu _{w}<0.056$, $0<\mu _{q}<1.65$. The initialized learning rate $\mu _{w} = \mu _{q} = 0.01$. The control points of CR-spline are initialized as a straight line with unitary slope, which is the same as [14] [6] [24]. The following experiment results are obtained by 100 independent Monte Carlo trials.

5.1 With White Gaussian Noise

Assuming that the wiener system to be identified consists of a FIR filter with $w^* = {\left[ 0.6,-0.4,0.25.-0.15,0.1 \right] }$, with a uniform interval $\Delta x = 0.2$, a nonlinear spline function interpolated by a 23 knots vector [6]. Set $q^* = [ -2.2,-2.0,\ldots , -0.8,-0.91,0.42,-0.01,-0.1,0.1,-0.15,\ldots ,2.0,2.2]$, $N_{w}=11$, $a = 1.6$, $p = 1.9$. The parameters of all kinds of algorithms are listed in Table 1.

Table 1 Parameters of three kinds of algorithms in simulation

Fig. 5

The profiles curve of nonlinearity using SAF–GMVC–VMSGD (SNR = 30 dB) (Color figure online)

Fig. 6

MSE of SAF–GMVC–VMSGD under different correlation factors r (SNR = 30 dB)

Fig. 7

MSE curves of proposed algorithms compared with each other (SNR = 30 dB)

Fig. 8

Compare the three proposed algorithms with the different SNR (Color figure online)

Fig. 9

The simulation of the step size boundary

The profiles curve of nonlinearity using the proposed algorithm are shown in Fig. 5. It can be seen that the proposed algorithm (the red dashed line) can accurately converge to profiles of nonlinearity (the solid blue line) of the system to be identified. Figure 6 shows the MSE curves of SAF–GMVC–VMSGD under different correlation factors $r = 0.1, r= 0.3, r=0.5, r=0.8, r= 0.9, r=0.98$. When the input signal under different correlation factors $r = 0.1, r= 0.3, r=0.5, r=0.8, r= 0.9$, show the better performance of the convergence speed and the steady-state error. When $r= 0.98$, the steady-state error not better than other factors. Figure 7 the proposed algorithms are compared with each other (SAF–GMVC, SAF–GMVC–MMSGD, SAF–GMVC–VMSGD). SAF–GMVC–MMSGD compare with SAF–GMVC improved the convergence speed, which much the same steady-state error. SAF–GMVC–VMSGD compare with SAF–GMVC–MMSGD reduced the steady-state error, which have the same convergence speed. The experiment is performed to verify the performance of the proposed algorithms with the different signal-to-noise ratio (SNR) of 30 dB, 20 dB, 15 dB, 10 dB. In Fig. 8 the proposed algorithms are compared with each other under different SNR, $a=0.32$, $p=2.5$, the blue curve represents the SAF–GMVC, the red curve represents the SAF–GMVC–MMSGD, the black curve represents the SAF–GMVC–VMSGD. With different SNR, the proposed SAF–GMVC–VMSGD algorithms shown the convergence performance better under different SNR, especially SNR = 30 dB. When SNR = 30 dB, $\mu _{w}=0.056$, $\mu _{q}=1.65$, the simulation results of the step size theoretical boundary are shown in Fig. 9. (a) Represents the tracking of filter weight value. Slight deviation appears in the tracking of the first and second weight values. The filtering of the other weights is consistent with the desired. (b) Represents the tracking of control points. Deviation in the front and back of the control points. The filtering of the middle section control points is consistent with the desired. (c) The system identifies the MSE curve of the test. The convergence value of MSE curve is far from the level line of noise. The tail of the MSE curve shows an upward trend.

5.2 With Non-Gaussian Noise

The experiment is performed to further verify the performance of the proposed algorithm under non-Gaussian noise environment. The experiment include two non-Gaussian noises types, impulse noise and Cauchy noise. The impulse noise is generated by an alpha-stable distribution, with $\alpha \in \left( 0,2\right]$ is a characteristic exponent representing the stability index which determines the strength of impulse, $\beta \in \left[ -1,1 \right]$ is a symmetry parameter, $\iota >0$ is a dispersion parameter, and $\varrho$ is a location parameter [12]. which can be expressed as

$$\begin{aligned} \begin{aligned} f(t)= & {} \exp {\left\{ j\varrho t - \iota {\left| t \right| }^\alpha {\left[ 1 + j \beta \mathrm{sign}(t) S(t,\alpha ) \right] } \right\} } \end{aligned} \end{aligned}$$

(55)

where

$$\begin{aligned} \begin{aligned} {\begin{matrix} S(t,\alpha )&{}=&{} \left\{ \begin{array}{ll} \tan {\left( \frac{\alpha \pi }{2} \right) }, &{} \alpha \ne 1 \\ \left( \frac{2}{\pi } \right) \log \left| t \right| , &{} \alpha =1 \end{array} \right. \end{matrix}} \end{aligned} \end{aligned}$$

(56)

The parameters of alpha-stable distribution are set as follows, $\alpha = 1.6$, $\beta = 0$, $\iota = 0.05$, $\varrho = 0$.

Fig. 10

MSE curves of six different algorithms with impulsive noises

Fig. 11

MSE curves of SAF–GMVC–VMSGD with different p, a under impulsive noise

The experimental parameters are the same as those in Table 1, $a = 0.32$, $p = 2.5$, $N_{w}=11$, SNR = 30 dB. Figure 10 shows the MSE curves of different algorithms under impulsive noise environment. Specially, the proposed algorithm SAF–GMVC–VMSGD performs better than other algorithms due to the fast convergence speed and small steady-state error. Figure 11 MSE curves of SAF–GMVC–VMSGD with different factors p, a under impulsive noise. In the same shape factor $p=2.5$, which is shown that the larger parameter a, the steady-state error worse. However, $p=4$, which is shown that the steady-state error not better with the factor a smaller. To sum up, when the parameter p is selected suitable, the steady-state error will vary with factor a. No matter how the steady-state error changes, the convergence speed is faster. In the above experiment simulations, using different parameters also getting the better performance, show the robustness of the nonlinearity identified system.

The Cauchy noise also described by an alpha-stable distribution, with $\alpha = 1$, $\beta = 0$, $r = 0.9$, other parameters are same to the impulsive noise. This experiment result is obtained by 150 independent Monte Carlo trials. Figure 12 shows the MSE curves of different algorithms under Cauchy noise environments. The proposed SAF–GMVC–VMSGD algorithm shows better convergence performance. The experimental results show that the proposed SAF–GMVC–VMSGD algorithm performs well in the above two non-Gaussian noise type.

Fig. 12

MSE curves of proposed algorithms under Cauchy noise environments

6 Conclusion

This paper proposed a novel Wiener SAF type robust adaptive filtering algorithm, named SAF–GMVC–VMSGD, for nonlinear system identification. The algorithm substitutes a generalized Versoria as cost function, improving the robustness against non-Gaussian noises. Meanwhile, it adopts the variable step-size momentum SGD to further improve the convergence performance. It can be concluded from the numerical simulations that: (1) Compared with the other Wiener SAF type algorithm, the proposed algorithm has the fastest convergence speed and the smallest steady-state error both in the with and without of non-Gaussian noise. (2) The suitable factors lead to stronger robustness in nonlinear identification system. (3) The proposed algorithm not only suitable for Wiener SAF type, but also suitable for other kinds of SAF type. The future work may be devoted to giving the steady-state analysis of the proposed algorithm.