Correction-Based Diffusion LMS Algorithms for Distributed Estimation

Abstract

In this paper, we consider distributed estimation problems where a set of agents are used for jointly estimating an interesting parameter from the noise measurements. By using the adaptation-then-combination rule in the traditional diffusion least mean square (DLMS), a DLMS is proposed by introducing a correction step with a gain factor between the adaptation and combination steps. An explicit expression for the network mean-square deviation is derived for the proposed algorithm, and a sufficient condition is established to guarantee the mean stability. Simulation results are provided to verify theoretical results, and it is shown that the proposed algorithm outperforms the traditional DLMS.

1 Introduction

Distributed estimation, that estimates the unknown parameter vector of interest through the noisy observation data of each node, has recently received much attention. Adaptive networks are attractive solutions for distributed estimation problems. An adaptive network consists of a group of nodes with data processing, learning, and data transmission capabilities. These nodes are connected together in a variety of topologies to form an interconnected network. Nodes in the network can interact with their neighbors to exchange information and collaborate to estimate common target parameters. As a research hotspot in distributed networks, distributed estimation has a wide range of practical applications, including biomedicine, sensory networks, environmental monitoring, target location, smart agriculture, and counter-terrorism [20].

The problem of distributed estimation in adaptive networks has received more and more attention, and a large number of distributed estimation algorithms have been proposed. In addition, there are at least two types of the communication modes between nodes in a distributed network: the consensus strategy [2, 17, 19, 25] and the diffusion strategy [5,6,7, 22, 23]. However, it is known that traditional diffusion strategy outperforms traditional consensus strategy [26]. Therefore, we choose the diffusion network structure in this paper. Diffusion networks are sought after by researchers and have been widely applied in cognitive radio, environmental monitoring, and industrial automation. In [24], the diffusion least mean-square (DLMS) algorithm was proposed to improve the estimation performance of the algorithm. The adapt-then-combine (ATC) DLMS algorithm and the combine-then-adapt (CTA) DLMS algorithm were proposed according to the order of fusion and adaptation in [3]. In order to improve the convergence speed of the algorithm, the researchers presented a variable step size DLMS algorithm to accelerate the convergence speed by dynamically changing the step size in real time [18]. Aiming at the problem of noise influence in regression vector, a compensatory diffusion LMS algorithm was studied in [1]. In [9], a DLMS algorithm based on data selection, which enabled nodes to decide whether to spread data according to transmission criteria, was designed to reduce the communication volume of nodes to a certain extent. In [10], the authors considered the influence of malicious nodes on the network under specific attacks and have introduced a DLMS algorithm based on reputation mechanism. The principle is to assign the corresponding reputation value according to the contribution made by the node. In wireless sensor networks, energy saving is an important research content, and the regression vector may be a non-Gaussian distribution. Therefore, a quantized minimum error entropy criterion was proposed in the literature [4], which was only used to transmit error signals between nodes and effectively reduced the amount of information transmission.

It is worth pointing out that improving the estimation performance of the least mean-square algorithm itself has been largely ignored despite their irreplaceable significance in parameter estimation. As a result, we focus on designing an effective strategy to improve the steady-state performance of the algorithm. In [26], the author proposed an exact diffusion strategy with guaranteed exact convergence for deterministic optimization problems. The exact diffusion algorithm has proven to remove the bias that is characteristic of distributed solutions for deterministic optimization problems [26]. In addition, the algorithm was shown to be applicable to a larger set of combination policies than earlier approaches in the literature [26]. The exact diffusion resembles standard diffusion strategy, with the addition of a “correction” step between the adaptation and combination step. Inspired by this paper, we directly add the “correction” step between the adaptation and combination in the DLMS algorithm. Nevertheless, the estimated performance of the algorithm is not improved. Therefore, we have thought of adding a gain factor to the correction step as shown in the third part and propose correction-based diffusion LMS Algorithms. In comparison with [24] which have focused on DLMS algorithms, the correction-based diffusion LMS algorithm performs estimating unknown parameters more efficiently. Simulation results illustrate the theoretical findings and reveal the enhanced learning abilities of the proposed filters.

The structure of this paper is as follows. In Sect. 2, we develop an estimation problem and propose a solution. The algorithm is presented in Sect. 3. In Sect. 4, we analyze the performance of the algorithm. In Sect. 5, we simulate the algorithms and theoretical results.

Notation: In this paper, we adopt normal font letters for scalars, boldface lowercase letters for column vectors, and boldface uppercase letters for matrices. The symbol $(\cdot )^T$ denotes matrix transpose, and the symbol $(\cdot )^{-1}$ denotes matrix inverse. The operators diag$\{\cdot \}$, col$\{\cdot \}$, tr$(\cdot )$, and ${\mathbb {E}}\{\cdot \}$ denote the (block) diagonal matrix, the column vector, the trace of a matrix, the expectation, respectively. The symbol $\otimes$ denotes the Kronecker product. The symbol vec$\{\cdot \}$ refers to the standard vectorization operator that stacks the columns of a matrix on top of each other. The notation ${\left\| \cdot \right\| _2}$ denotes the Euclidean norm of a vector, and ${\left| \cdot \right| }$ denotes the (element-wised) ${L_1}$-norm of a scalar or vector. We use indexes k and $\ell$ to denote nodes and use i to denote time. Other notations will be introduced if necessary.

2 Problem Formulation

Consider a network of N wireless sensors, spatially distributed over some region. At every time instant i, each node k can access to a zero-mean observation ${d_k(i)}$, and a zero-mean $M-$dimensional row regression vector ${{\varvec{u}}_k(i)}$. We assume the data to be related via a linear model as follows:

$$\begin{aligned} {d_k(i)} = {{\varvec{u}}_k(i)}{{\varvec{w}}^o} + {v_k(i)} \end{aligned}$$

(1)

where ${{\varvec{w}}^o}$ is an $M-$dimensional unknown column vector, and ${v_k(i)}$ is a zero-mean measurement noise of variance $\sigma _{v,k}^2$. We assume covariance matrix ${\varvec{\mathcal R}_{u,k}}= {\mathbb {E}}\{{{{\varvec{u}}_k(i)^T}{\varvec{u}}_k(i)}\}$ is positive definite, and let ${\varvec{{\mathcal {R}}}_{\mathrm{d}u,k}}= \mathbb E\{{{d_k(i)}{\varvec{u}}_k(i)^T}\}$, where ${\varvec{\mathcal R}_{\mathrm{d}u,k}}$ is a cross-correlation vector.

We estimate the unknown parameter ${{\varvec{w}}^o}$ by minimizing the following cost function:

$$\begin{aligned} {\varvec{w}^o} = \mathop {\arg \min }\limits _{\varvec{w} \in { R^M}}\ {J^{\mathrm{glob}}}(\varvec{w}) = \sum \limits _{k = 1}^N {\mathbb {E}}{\{ |{d_k}(i) - {\varvec{u}_k}(i)\varvec{w}{|^2}\} } \end{aligned}$$

(2)

which is strongly convex, second-order differentiable, and minimized at ${{\varvec{w}}^o}$.

The optimal estimator is given by [21]

$$\begin{aligned} {{\varvec{w}}^o} = {\left( \sum \limits _{k = 1}^N {{\varvec{{\mathcal {R}}}_{u,k}}} \right) ^{ - 1}}{\left( \sum \limits _{k = 1}^N {{\varvec{{\mathcal {R}}}_{\mathrm{d}u,k}}} \right) } \end{aligned}$$

(3)

It is worth pointing out that centralized networks have the disadvantages of the poor performance in dealing emergencies and in processing the transmitted data in real time [3]. Hence, we focus on designing distributed network topology for estimating unknown parameters.

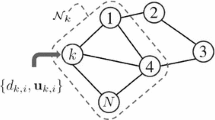
Note the entry $a_{\ell ,k}$ of the matrix ${\varvec{A}}$, which can represent the topology of a network, satisfies

$$\begin{aligned} \mathbb {1}^T{\varvec{A}}=\mathbb {1}^T,\ \varvec{A}\mathbb {1}=\mathbb {1},\ \ a_{\ell ,k}=0 \ \text{ if } \ \ell \notin {\mathcal {N}}_k \end{aligned}$$

(4)

where $\mathbb {1}$ denotes an $N-$dimensional column vector consisting of all ones. Let $a_{\ell ,k}$ denotes the weight that is used to scale the data that flows from node $\ell$ to k. Let $\varvec{A} \buildrel \varDelta \over = [{a_{\ell ,k}}] \in { R^{N \times N}}$ denotes the matrix that collects all these coefficient.

Now, we consider that it is feasible to replace the global cost with the local costs as follows:

$$\begin{aligned} {J^{\mathrm{glob}}}(\varvec{w}) = \sum \limits _{\ell = 1}^N {{J_\ell }(\varvec{w})} \end{aligned}$$

(5)

where $J^{\mathrm{glob}}(\varvec{w})={\mathbb {E}}\{|d_{\ell }(i)-\varvec{u}_{\ell }(i)\varvec{w}|^2\}$ denotes the cost function in $\ell$ node.

By using the property of combination coefficients $a_{\ell ,k}=a_{k,\ell }$ and ${\sum \limits _{k = 1}^N {{a_{k,\ell }}} }=1$, we can rewrite Eq. (5) as follows:

$$\begin{aligned} {J^{\mathrm{glob}}}(\varvec{w})= \sum \limits _{\ell = 1}^N {\left( {\sum \limits _{k = 1}^N {{a_{k,\ell }}} } \right) {J_\ell }(\varvec{w})} \end{aligned}$$

(6)

It only exchanges the order and data with neighbor nodes in k node, so

$$\begin{aligned} {J^{\mathrm{glob}}}(\varvec{w})&= \sum \limits _{k = 1}^N {\left( {\sum \limits _{\ell \in {{\mathcal {N}}_k}} {{a_{\ell ,k}}} } \right) {J_\ell }(\varvec{w})} \nonumber \\&= \sum \limits _{k = 1}^N {J_\ell ^{loc}(\varvec{w})} \end{aligned}$$

(7)

Thus, when the combination coefficients are symmetric and convex, we will find out that optimizing the global cost in view of individual costs (2) is equivalent to optimizing the global cost in view of local costs (7). Hence, we can represent the global optimization problem in terms of the local optimization problem. In the following papers, we only give the algorithm of each node k.

3 Diffusion Adaptive Solutions

In order to estimate ${{\varvec{w}}^o}$ more accurately, the diffusion least mean-square algorithms are proposed, which include the ATC algorithm and the CTA algorithm. Here, we focus on the algorithm using the adapt-then-combine cooperation rule as it shows better performance than the combine-then-adapt cooperation strategy. The ATC diffusion LMS is implemented by [11]

where $\mu$ is a constant step size parameter, ${\varvec{w}}_{k,i}$ is an estimate at i iteration for each node k, and $\varphi _{k,i}$ is the intermediate variable. The coupling coefficient $a_{\ell ,k}$, which is the $\ell$ and k entity of the matrix ${\varvec{A}}$ that is a double-stochastic matrix satisfied Eq. (4).

We note that the mean-square error value of DLMS algorithm still needs to be reduced, although it already has good estimation performance. It is of importance to design an effective strategy to improve the performance of the algorithm. Therefore, we hope to design a distributed algorithm to improve steady-state performance of the algorithm. The exact diffusion algorithm has been proposed to remove the bias that is characteristic of distributed solution for deterministic optimization problems, and the algorithm is as follows [26, 27]:

where ${\bar{a}}_{\ell ,k}$ is the $\ell$ and k entry of the matrix $\bar{A}$ that satisfies $\bar{A}=(I_N+A)/2$. The symbol $\nabla {J_k}({{\varvec{w}}_{k,i - 1}})$ denotes the gradient vector of $J_k$ relative to w, which is a convex and differentiable function for deterministic optimization problems. $\phi _{k,i}$ and $\varphi _{k,i}$ are intermediate variables.

It is observed that the “correction” step has been added to the algorithm between the adaptation and combination step.

We apply this idea of adding “correction” step between combination and adaptation to the DLMS algorithm. Therefore, we design a correction-based diffusion LMS algorithm by adding a gain factor before the difference between ${\varvec{w}}_{k,i-1}$ and $\varphi _{k,i-1}$ from the previous iteration. The algorithm is as follows:

where both $\varphi _{k,i}$ and $\phi _{k,i}$ are intermediate variables, $\lambda$ is a positive gain factor, and $a_{\ell ,k}$ is the coupling coefficient.

It is observed that correction-based diffusion LMS algorithm is different from the exact diffusion strategy, with the addition of a gain factor. Another difference is that the exact diffusion is to study deterministic optimization problem, while diffusion LMS is to study parameter estimation problem with noise in measurement equation.

Before proceeding with this paper, we introduce the following assumptions:

Assumption 1

The regressor vector ${\varvec{u}}_{k,i}$ arises from a zero-mean random process that is temporally stationary, temporally white, and independent in time and space.

Assumption 2

The noise ${\varvec{v}}_{k,i}$ is zero-mean Gaussian, which is identically independent distributed in time and also spatially independent and is independent of other signals.

Assumption 3

The regressor vectors $\{{\varvec{u}}_{k,i}\}$ are independent of $\{ {\varvec{w}}_{\ell ,i}\}$ for all $\ell$ and for $j<i$.

These assumptions are commonly used in the adaptive filtering literature since they help simplify the analysis, and the performance results obtained under this assumption match well the actual performance of stand-alone filters for sufficiently small step sizes.

4 Performance Analysis

In this section, we will analyze the convergence and mean-square error performance of the algorithm (10) which is proposed in the third part.

4.1 Error Vector Recursion

We define the error quantities

$$\begin{aligned} {{{\tilde{w}}}_{k,i}} = {{\varvec{w}}^o} - {{\varvec{w}}_{k,i}}\ ,\ {{{\tilde{\varphi }}} _{k,i}} = {{\varvec{w}}^o} - {\varphi _{k,i}}\ ,\ {{{\tilde{\phi }}} _{k,i}} = {{\varvec{w}}^o} - {\phi _{k,i}} \end{aligned}$$

(11)

By substituting Eq. (11) into Eq. (10), we get the following

Then, by doing the dimension expansion, we have

where

$$\begin{aligned} \varvec{{\mathcal {A}}}&{\buildrel \varDelta \over =}\varvec{A} \otimes {\varvec{I}_M} \end{aligned}$$

(14)

$$\begin{aligned} {\varvec{{\tilde{w}}}_i}&{\buildrel \varDelta \over =} \text{ col }\{ {\varvec{{\tilde{w}}}_{1,i}},{\varvec{{\tilde{w}}}_{2,i}},.......,{\varvec{{\tilde{w}}}_{N,i}}\} \end{aligned}$$

(15)

$$\begin{aligned} {{{\tilde{\varphi }}} _i}&{\buildrel \varDelta \over =} \text{ col }\{ {{{\tilde{\varphi }} }_{1,i}},{{{\tilde{\varphi }} }_{2,i}},.......,{{\tilde{\varphi }}_{N,i}}\} \end{aligned}$$

(16)

$$\begin{aligned} {{{\tilde{\phi }}} _i}&{\buildrel \varDelta \over =} \text{ col }\{ {{\tilde{\phi }}_{1,i}},{{{\tilde{\phi }} }_{2,i}},.......,{{{\tilde{\phi }} }_{N,i}}\} \end{aligned}$$

(17)

$$\begin{aligned} {\varvec{g_i}}&{\buildrel \varDelta \over =} \text{ col }\{ \varvec{u}_{1,i}^T{v_{1,i}},.......,\varvec{u}_{N,i}^T{v_{N,i}}\} \end{aligned}$$

(18)

$$\begin{aligned} {\varvec{{\mathcal {D}}}_i}&{\buildrel \varDelta \over =} \text{ diag }\{ \varvec{u}_{1,i}^T{\varvec{u}_{1,i}},.......,\varvec{u}_{N,i}^T{\varvec{u}_{N,i}}\} \end{aligned}$$

(19)

Then, it can be verified that the network error vector ${\varvec{\tilde{w}_i}}$ for the diffusion strategy (10) evolves according to the following recursion:

$$\begin{aligned} {\varvec{{\tilde{w}}}_i} = {{\varvec{{\mathcal {B}}}}_{1,i}}{\varvec{{\tilde{w}}}_{i - 1}} + {\varvec{{\mathcal {B}}}_{2,i - 1}}{\varvec{{\tilde{w}}}_{i - 2}} - \mu {\varvec{{\mathcal {A}}}^T}{\varvec{g}_i} + \lambda \mu {\varvec{\mathcal A}^T}{\varvec{g}_{i - 1}} \end{aligned}$$

(20)

where

$$\begin{aligned} {\varvec{{\mathcal {B}}}_{1,i}} = {\varvec{{\mathcal {A}}}^T}\left[ {\left( {\lambda + 1} \right) {\varvec{I}_{MN}} - \mu {\varvec{{\mathcal {D}}}_i}} \right] \end{aligned}$$

(21)

$$\begin{aligned} {\varvec{{\mathcal {B}}}_{2,i - 1}} = - \lambda {\varvec{{\mathcal {A}}}^T}\left( {{\varvec{I}_{MN}} - \mu {\varvec{{\mathcal {D}}}_{i - 1}}} \right) \end{aligned}$$

(22)

Remark 1

In an extreme case when $\lambda =0$, the error vector recursion (20) of the correction-based diffusion LMS algorithm equals to the error vector recursion of the DLMS algorithm.

4.2 Mean Stability Analysis

Since $\{ {\varvec{v}}_{k,i}\}$ is a zero-mean measurement noise and is independent of the regressor vectors $\{\varvec{u}_{k,i}\}$. Therefore, taking the expectation of both sides of (20), we get

$$\begin{aligned} {\mathbb {E}}\{{\varvec{{\tilde{w}}}_i}\} = {\varvec{{\mathcal {B}}}_1}\mathbb E\{{\varvec{{\tilde{w}}}_{i - 1}}\} + {\varvec{{\mathcal {B}}}_2}{\mathbb {E}}\left\{ {{\varvec{{\tilde{w}}}_{i - 2}}} \right\} \end{aligned}$$

(23)

where

$$\begin{aligned} \varvec{{\mathcal {B}}}_1&={\mathbb {E}}\{{\varvec{{\mathcal {B}}}_{1,i}}\}={\varvec{{\mathcal {A}}}^T}\left[ {\left( {\lambda + 1} \right) {\varvec{I}_{MN}} - \mu {\varvec{{\mathcal {R}}}_u}} \right] \end{aligned}$$

(24)

$$\begin{aligned} \varvec{{\mathcal {B}}}_2&={\mathbb {E}}\{{\varvec{{\mathcal {B}}}_{2,i-1}}\}=- \lambda {\varvec{{\mathcal {A}}}^T}\left( {{\varvec{I}_{MN}} - \mu {\varvec{{\mathcal {R}}}_u}} \right) \end{aligned}$$

(25)

$$\begin{aligned} \varvec{{\mathcal {R}}}_u&={\mathbb {E}}\{\varvec{{\mathcal {D}}}_i\}=\text{ diag }\{\varvec{R}_{u,1}, \varvec{R}_{u,2},......,\varvec{R}_{u,N}\} \end{aligned}$$

(26)

In order to facilitate the analysis below, we extend the equation (23) as follows

$$\begin{aligned} {\mathbb {E}}\left\{ {\left[ {\begin{array}{c} {\varvec{{\tilde{w}}}_i}\\ {{\varvec{{\tilde{w}}}_{i\mathrm{{ - }}1}}} \end{array}} \right] } \right\}&= \left[ {\begin{array}{cc} {{\varvec{{\mathcal {B}}}_1}}&{}{{\varvec{{\mathcal {B}}}_2}}\\ {{\varvec{I}_{MN}}}&{}{{\varvec{0}_{MN}}} \end{array}} \right] {\mathbb {E}}\left\{ {\left[ {\begin{array}{c} {{\varvec{{\tilde{w}}}_{i\mathrm{{ - }}1}}}\\ {{\varvec{{\tilde{w}}}_{i\mathrm{{ - 2}}}}} \end{array}} \right] } \right\} \nonumber \\&= \varvec{B}{\mathbb {E}}\left\{ {\left[ {\begin{array}{c} {{\varvec{{\tilde{w}}}_{i\mathrm{{ - }}1}}}\\ {{\varvec{{\tilde{w}}}_{i\mathrm{{ - 2}}}}} \end{array}} \right] } \right\} \end{aligned}$$

(27)

Recursion (27) converges as $i \rightarrow \infty$ if the matrix $\varvec{B}$ is stable. Since $\varvec{{\mathcal {A}}}$ is a double random matrix, we get

$$\begin{aligned} \rho \left( \varvec{B} \right)&= \rho \left( {\left[ {\begin{array}{cc} {{\varvec{{\mathcal {B}}}_1}}&{}{{\varvec{{\mathcal {B}}}_2}}\\ {{\varvec{I}_{MN}}}&{}{{\varvec{0}_{MN}}} \end{array}} \right] } \right) \nonumber \\&\le \rho \left( {\left[ {\begin{array}{cc} {(\lambda + 1){\varvec{I}_{MN}} - \mu {\varvec{{\mathcal {R}}}_u}}&{}{ - \lambda ({\varvec{I}_{MN}} - \mu {\varvec{{\mathcal {R}}}_u})}\\ {{\varvec{I}_{MN}}}&{}{{\varvec{0}_{MN}}} \end{array}} \right] } \right) \nonumber \\&\le \rho \left( {\left[ {\begin{array}{cc} {\lambda {\varvec{I}_{MN}}}&{}{ - {\varvec{I}_{MN}}}\\ {{\varvec{0}_{MN}}}&{}{{\varvec{I}_{MN}} - \mu {\varvec{{\mathcal {R}}}_u}} \end{array}} \right] } \right) \nonumber \\&< 1 \end{aligned}$$

(28)

Thus, the stability of the algorithm (10) is ensured by choosing $\mu$ and $\lambda$ such that:

$$\begin{aligned} 0< \mu< \frac{2}{{{\lambda _{\max }}({\varvec{R}_{u,k}})}} \ \ \mathrm{and}\ \ 0< \lambda < 1 \end{aligned}$$

(29)

where ${\lambda _{\max }}({\varvec{R}_{u,k}})$ is the maximum eigenvalue of $\varvec{R}_{u,k}$. We observe that the deviation reduces to 0, when $i \rightarrow \infty$.

It can be seen from condition (29) that the gain factor $\lambda$ is not directly related to the step size $\mu$, but only when the conditions of the step size and the gain factor are simultaneously established, the algorithm (10) converges.

Remark 2

When the gain factor satisfies the constraint condition (29), the step size condition of the algorithm is the same as the step size condition of the DLMS algorithm to guarantee stability.

4.3 Mean-Square Deviation Behavior Analysis

To perform the mean-square-error analysis, we shall use the Kronecker product operator [8] and the vectorization operator vec$(\cdot )$. First, we write the results by extending the equation (20).

$$\begin{aligned} {{{\tilde{w}}}_{i-1}^i}&={B}_i {{{\tilde{w}}}_{i-2}^{i-1}} + {{ {A}}_2}{{ {g}}_{i-1}^i} \nonumber \\&= \left( {{ { { A}}_1} + {{ { A}}_2} \cdot \left( {{{ {{\mathcal D}}}_{1,i}} + {{ {{{\mathcal {D}}}}}_{2,i-1}}} \right) } \right) {{\tilde{w}}_{i - 2}^{i-1}} + {{ { A}}_2}{{ { g}}_{i-1}^i} \end{aligned}$$

(30)

where

$$\begin{aligned}&{\varvec{{\tilde{w}}}_{i-1}^i} = \left[ {\begin{array}{c} {{\varvec{{\tilde{w}}}_i}}\\ {{\varvec{{\tilde{w}}}_{i - 1}}} \end{array}} \right] \end{aligned}$$

(31)

$$\begin{aligned}&{\varvec{g}_{i-1}^i} = \left[ {\begin{array}{c} {{\varvec{ g}_i}}\\ {{\varvec{ g}_{i - 1}}} \end{array}} \right] \end{aligned}$$

(32)

$$\begin{aligned}&{\varvec{B}}_i =\left[ {\begin{array}{cc} {{\varvec{{\mathcal {B}}}_{1,i}}}&{}{{\varvec{{\mathcal {B}}}_{2,i - 1}}}\\ {{\varvec{I}_{MN}}}&{}{{\varvec{0}_{MN}}} \end{array}} \right] \end{aligned}$$

(33)

$$\begin{aligned}&{ {\varvec{A}}}_1={\left[ {\begin{array}{cc} {(\lambda + 1){\varvec{{\mathcal {A}}}^T}}&{}{ - \lambda {\varvec{{\mathcal {A}}}^T}}\\ {{\varvec{I}_{MN}}}&{}{{\varvec{0}_{MN}}} \end{array}} \right] } \end{aligned}$$

(34)

$$\begin{aligned}&{ {\varvec{A}}}_2={\left[ {\begin{array}{cc} { - \mu {\varvec{{\mathcal {A}}}^T}}&{}{\lambda \mu {\varvec{{\mathcal {A}}}^T}}\\ {{\varvec{0}_{MN}}}&{}{{\varvec{0}_{MN}}} \end{array}} \right] } \end{aligned}$$

(35)

$$\begin{aligned}&{ {\varvec{D}}}_{1,i}={\left[ {\begin{array}{cc} {{\varvec{{\mathcal {D}}}_i}}&{}{{\varvec{0}_{MN}}}\\ {{\varvec{0}_{MN}}}&{}{{\varvec{0}_{MN}}} \end{array}} \right] } \end{aligned}$$

(36)

$$\begin{aligned}&{ {\varvec{D}}}_{2,i-1}={\left[ {\begin{array}{cc} {{\varvec{0}_{MN}}}&{}{{\varvec{0}_{MN}}}\\ {{\varvec{0}_{MN}}}&{}{{\varvec{{\mathcal {D}}}_{i - 1}}} \end{array}} \right] } \end{aligned}$$

(37)

To analyze the convergence in mean-square-error sense, we consider evaluating a weighted variance of the error vector $\varvec{{\tilde{w}}}_i$. Let $\varvec{\varSigma }_1$ denotes an arbitrary nonnegative definite matrix that we are free to choose.

Let

$$\begin{aligned} \varvec{\varSigma }=\left[ {\begin{array}{cc}{\varvec{\varSigma }_1} &{}\varvec{0}\\ \varvec{0}&{}\varvec{0}\end{array}} \right] \end{aligned}$$

(38)

We have

$$\begin{aligned}&{\mathbb {E}}\left\| {{\varvec{{\tilde{w}}}_i}} \right\| _{{\varvec{\varSigma }_1}} ^2 ={\mathbb {E}}\left\| {{\varvec{{\tilde{w}}}_{i-1}^i}} \right\| _{\varvec{\varSigma }}^2 \end{aligned}$$

(39)

Thus, we consider the variance of the weight error vector ${\varvec{{\tilde{w}}}_{i-1}^i}$, weighted by any positive-definite matrix $\varvec{\varSigma }$. According to assumption 1, 2, and 3, we obtain:

$$\begin{aligned} {\mathbb {E}}\left\| {{\varvec{{\tilde{w}}}_i}} \right\| _{\varvec{\varSigma }_1} ^2&={\mathbb {E}}\left\| {{\varvec{{\tilde{w}}}_{i-1}^i}} \right\| _{\varvec{\varSigma }}^2 \nonumber \\&={\mathbb {E}}\left\{ {\left\| {\left( {{\varvec{A}_1} + {\varvec{A}_2} \cdot \left( {{\varvec{D}_{1,i}} + {\varvec{D}_{2,i - 1}}} \right) } \right) \varvec{{\tilde{w}}}_{i - 2}^{i - 1}} \right. } {\left. { + {\varvec{A}_2}\varvec{g}_{i - 1}^i} \right\| _{\varvec{\varSigma }}^2} \right\} \nonumber \\&= {\mathbb {E}}\left\| {{{\varvec{{\tilde{w}}}}_{i-2}^{i - 1}}} \right\| _{{\varvec{\varSigma }^\prime } }^2 +{\mathbb {E}}\left\| {{{\varvec{A}}_2}{{\varvec{g}}_{i-1}^i}} \right\| _{{\varvec{\varSigma }}}^2 + 2\mathbb E\left\{ {({{\varvec{{\tilde{w}}}}}_{i-2}^{i - 1})^T{{{{\varvec{B}}_{i} }}^T}{\varvec{\varSigma }}{{\varvec{A}}_2}{{\varvec{g}}_{i-1}^i}} \right\} \end{aligned}$$

(40)

where matrix ${{\varvec{\varSigma }} '}$ is give by:

$$\begin{aligned} {{{\varvec{\varSigma }} '}}&= {{ \varvec{B}}^T}{\varvec{\varSigma }}{ \varvec{B}} - {{\varvec{R}}_{u,1}}{\varvec{A}^T_{2}}{\varvec{\varSigma }}{{{\varvec{A}}}_2}{{\varvec{R}}_{u,1}} - {{\varvec{R}}_{u,2}}{{\varvec{A}}}^T_{2}{\varvec{\varSigma }}{{{\varvec{A}}}_2}{{\varvec{R}}_{u,2}} \nonumber \\&\quad + {\mathbb {E}}\left\{ {\varvec{D}^T_{1,i}{{\varvec{A}}}^T_{2}{\varvec{\varSigma }}{{{\varvec{A}}}_{2}}{{{\varvec{D}}}_{1,i}}} \right\} + {\mathbb {E}}\left\{ {{{\varvec{D}}}^T_{2,i-1}{{\varvec{A}}}^T_{2}{\varvec{\varSigma }}{{{\varvec{A}}}_{2}}{{\varvec{D}}_{2,i-1}}} \right\} \end{aligned}$$

(41)

where

$$\begin{aligned} {\varvec{B}}&= { {\varvec{A}}_1} + { {\varvec{A}}_2} \cdot \left( {{{ {\varvec{R}}}_{u,1}} + {{ {\varvec{R}}}_{u,2}}} \right) \end{aligned}$$

(42)

$$\begin{aligned}&=\left[ {\begin{array}{cc} {{\varvec{{\mathcal {B}}}_{1}}}&{}{{\varvec{{\mathcal {B}}}_{2}}}\\ {{\varvec{I}_{MN}}}&{}{{\varvec{0}_{MN}}} \end{array}} \right] \end{aligned}$$

(43)

$$\begin{aligned} { {\varvec{R}}_{u,1}}&= {\mathbb {E}}\left\{ {{ {\varvec{D}}}^T_{1,i}} \right\} ={\left[ {\begin{array}{cc} {{\varvec{{\mathcal {R}}}_u}}&{}{{\varvec{0}_{MN}}}\\ {{\varvec{0}_{MN}}}&{}{{\varvec{0}_{MN}}} \end{array}} \right] } \end{aligned}$$

(44)

$$\begin{aligned} { {\varvec{R}}_{u,2}}&= {\mathbb {E}}\left\{ {{ {\varvec{D}}_{2,i - 1}}} \right\} ={\left[ {\begin{array}{cc} {{\varvec{0}_{MN}}}&{}{{\varvec{0}_{MN}}}\\ {{\varvec{0}_{MN}}}&{}{{\varvec{{\mathcal {R}}}_u}} \end{array}} \right] } \end{aligned}$$

(45)

By performing the vectorization operator of the positive definite matrix ${\varvec{\varSigma }}$, we obtain $\sigma$=vec($\varvec{\varSigma }$). Similarly, let $\sigma '$=vec($\varvec{\varSigma }'$). According to the property vec$(\varvec{A}\varSigma \varvec{B})=({\varvec{B}}^T\otimes \varvec{A})\sigma$, where $\varvec{A}$ and $\varvec{B}$ are the arbitrary matrices, we get

$$\begin{aligned} \text{ vec }( {{{ {\varvec{B}}}^T}{\varvec{\varSigma }}{\varvec{B}}} )&= ( {{{\varvec{B}}}^T} \otimes {{{\varvec{B}}}^T} )\sigma \end{aligned}$$

(46)

$$\begin{aligned} {vec}( {{{{\varvec{R}}}_{u,1}}{{\varvec{A}}}^T_2{\varvec{\varSigma }}{{{\varvec{A}}}_2}{{{\varvec{R}}}_{u,1}}} )&= \left( {{{{\varvec{R}}}_{u,1}}{{\varvec{A}}}^T_2 \otimes {{{\varvec{R}}}_{u,1}}{{\varvec{A}}}^T_2} \right) {\sigma }\nonumber \\&= \left( {{{{\varvec{R}}}_{u,1}} \otimes {{{\varvec{R}}}_{u,1}}} \right) \left( {{{\varvec{A}}}^T_2 \otimes {{\varvec{A}}}^T_2} \right) {\sigma } \end{aligned}$$

(47)

$$\begin{aligned} \text{ vec }( {{{{\varvec{R}}}_{u,2}}{{\varvec{A}}}^T_2{\varvec{\varSigma }}{{{\varvec{A}}}_2}{{{\varvec{R}}}_{u,2}}} )&= \left( {{{{\varvec{R}}}_{u,2}}{{\varvec{A}}}^T_2 \otimes {{{\varvec{R}}}_{u,2}}{{\varvec{A}}}^T_2} \right) {\sigma }\nonumber \\&= \left( {{{{\varvec{R}}}_{u,2}} \otimes {{{\varvec{R}}}_{u,2}}} \right) \left( {{{\varvec{A}}}^T_2 \otimes {{\varvec{A}}}^T_2} \right) {\sigma } \end{aligned}$$

(48)

Assume now that the regressors are Gaussian zero-mean random vectors. Then, for any Hermitian matrix H it holds [21]:

$$\begin{aligned} {\mathbb {E}}\left\{ {\varvec{u}_{k,i}^T{\varvec{u}_{k,i}}\varvec{H}\varvec{u}_{\ell ,i}^T{\varvec{u}_{\ell ,i}}} \right\}&= {\varvec{R}_{u,k}}\varvec{H}{\varvec{R}_{u,\ell }} + \beta {\delta _{k\ell }}{\varvec{R}_{u,k}}\text{ Tr }(\varvec{H}{\varvec{R}_{u,k}}) \end{aligned}$$

(49)

where $\beta =1$ if the regressors are complex, and $\beta =2$ if the regressors are real. And $\delta _{k\ell }$ indicates the correlation coefficient of $\varvec{u}_{k,i}$ and $\varvec{u}_{\ell ,i}$.

Consider the matrices $\varvec{K}_{1}={\mathbb {E}}\left\{ {{{\varvec{D}}}^T_{1,i}\varvec{Q}{{{\varvec{D}}}_{1,i}}} \right\}$ and $\varvec{K}_{2}=\mathbb E\left\{ {{{\varvec{D}}}^T_{2,i-1}\varvec{Q}{{{\varvec{D}}}_{2,i-1}}} \right\}$, where $\varvec{Q}={{\varvec{A}}}^T_2{\varvec{\varSigma }}{{\varvec{A}}_2}$, we obtain

$$\begin{aligned} {\varvec{K}}&= \left[ {\begin{array}{ccc} {\varvec{{\mathcal {R}}}_{u,1}^T{\varvec{Q}_{11}}{\varvec{{\mathcal {R}}}_{u,1}}}&{} \cdots &{}{\varvec{{\mathcal {R}}}_{u,1}^T{\varvec{Q}_{1N}}{\varvec{\mathcal R}_{u,N}}}\\ \vdots &{} \ddots &{} \vdots \\ {\varvec{{\mathcal {R}}}_{u,N}^T{\varvec{Q}_{N1}}{\varvec{{\mathcal {R}}}_{u,1}}}&{} \cdots &{}{\varvec{{\mathcal {R}}}_{u,N}^T{\varvec{Q}_{NN}}{\varvec{\mathcal R}_{u,N}}} \end{array}} \right] \nonumber \\&\quad + \left[ {\begin{array}{ccc} {{\varvec{{\mathcal {R}}}_{u,1}}\varvec{r}_{1}^T}\varvec{q}_{1,1}&{} \cdots &{}{{\varvec{0}_M}}\\ \vdots &{} \ddots &{} \vdots \\ {{\varvec{0}_M}}&{} \cdots &{}{{\varvec{{\mathcal {R}}}_{u,N}}\varvec{r}_{N}^T}\varvec{q}_{N,N} \end{array}} \right] \end{aligned}$$

(50)

$$\begin{aligned} \varvec{q}_{k,\ell }&=\text{ vec }(\varvec{Q}_{k,\ell }), \varvec{r}_{k}=\text{ vec }(\varvec{{\mathcal {R}}}_{u,k})\end{aligned}$$

(51)

$$\begin{aligned} \varvec{K}_{1}&=\text{ diag }\{\varvec{K},\varvec{0}_{MN}\}\nonumber \\&={\varvec{R}}_{u,1}^T\varvec{Q} {\varvec{R}}_{u,1}+{\varvec{R}}_{u,1}\varvec{Z}_{m} \end{aligned}$$

(52)

where $\varvec{Z}_{m}=$diag$\{\varvec{r}_{1}^T\varvec{q}_{1,1},\cdots ,\varvec{r}_{N}^T\varvec{q}_{N,N},0,\cdots ,0\}$. Taking the vector operator of the above matrix $\varvec{K}$, we get

$$\begin{aligned} \text{ vec }(\varvec{K}_{1})&=\left( {{{{\varvec{R}}}_{u,1}} \otimes {{{\varvec{R}}}_{u,1}}} \right) \text{ vec }(\varvec{Q}) +(\varvec{I}_{2MN}\otimes {\varvec{R}}_{u,1})\varvec{{\mathcal {L}}}_{m}\text{ vec }(\varvec{Q}) \nonumber \\&=\left( {{{{\varvec{R}}}_{u,1}} \otimes {{{\varvec{R}}}_{u,1}}} +(\varvec{I}_{2MN}\otimes {\varvec{R}}_{u,1})\varvec{{\mathcal {L}}}_{m}\right) \times \left( {{{\varvec{A}}}^T_2 \otimes {{\varvec{A}}}^T_2} \right) {\sigma } \end{aligned}$$

(53)

where $\varvec{{\mathcal {L}}}_{m}$ is given as follows:

$$\begin{aligned} \varvec{{\mathcal {L}}}_{m}&=\text{ diag }\{\varvec{{\mathcal {L}}}_{m,1},\cdots ,\varvec{{\mathcal {L}}}_{m,N},0,\cdots ,0\} \end{aligned}$$

(54)

$$\begin{aligned} \varvec{{\mathcal {L}}}_{m,k}&=\left[ {\begin{array}{c} {{\varvec{I}_k} \otimes { e_1}}\\ \vdots \\ {{\varvec{I}_k} \otimes { e_M}} \end{array}} \right] \otimes \varvec{r}_k^T \end{aligned}$$

(55)

Similarly, we also have

$$\begin{aligned} \text{ vec }(\varvec{K}_{2})&=\left( {{{{\varvec{R}}}_{u,2}} \otimes {{{\varvec{R}}}_{u,2}}} \right) \text{ vec }(\varvec{Q}) +(\varvec{I}_{2MN}\otimes {\varvec{R}}_{u,2})\varvec{{\mathcal {L}}}_{n}\text{ vec }(\varvec{Q}) \nonumber \\&=\left( {{{{\varvec{R}}}_{u,2}} \otimes {{{\varvec{R}}}_{u,2}}} +(\varvec{I}_{2MN}\otimes {\varvec{R}}_{u,2})\varvec{{\mathcal {L}}}_{n}\right) \times \left( {{{\varvec{A}}}^T_2 \otimes {{\varvec{A}}}^T_2} \right) {\sigma } \end{aligned}$$

(56)

where $\varvec{{\mathcal {L}}}_{n}$ is given as follows:

$$\begin{aligned} \varvec{{\mathcal {L}}}_{n}&=\text{ diag }\{0,\cdots ,0,\varvec{\mathcal L}_{n,1},\cdots ,\varvec{{\mathcal {L}}}_{n,N}\} \end{aligned}$$

(57)

$$\begin{aligned} \varvec{{\mathcal {L}}}_{n,k}&=\left[ {\begin{array}{c} {{\varvec{I}_{N+k}} \otimes { e_1}}\\ \vdots \\ {{\varvec{I}_{N+k}} \otimes { e_M}} \end{array}} \right] \otimes \varvec{r}_k^T \end{aligned}$$

(58)

where $\varvec{I}_{k}$ is a $2N\times 2N$ matrix with a unit entry at position K and zeros elsewhere, $e_k$ is a $M\times 1$ column vector with a unit entry at position K and zeros elsewhere.

Then, we have

$$\begin{aligned} \mathrm{{vec}}\left( {\varvec{\varSigma }'} \right) = \varvec{{\mathcal {F}}}\sigma \end{aligned}$$

(59)

where

$$\begin{aligned} \varvec{{\mathcal {F}}}=&\left( {{\varvec{B}}^T \otimes {\varvec{B}}^T} \right) + ((\varvec{I}_{2MN}\otimes {\varvec{R}}_{u,1})\varvec{{\mathcal {L}}}_{m} +(\varvec{I}_{2MN}\otimes {\varvec{R}}_{u,2})\varvec{{\mathcal {L}}}_{n}) \left( {{{\varvec{A}}}^T_2 \otimes {{\varvec{A}}}^T_2} \right) {\sigma } \end{aligned}$$

(60)

The second term of Eq. (40) can be written as:

$$\begin{aligned} {\mathbb {E}}\left\| {{{{\varvec{A}}}_2}{{ {\varvec{g}}}_{i-1}^i}} \right\| _{\varvec{\varSigma }} ^2&= {\mathbb {E}}\left\{ {( {\varvec{g}}_{i-1}^i)^T {\varvec{A}}_2^T\varvec{\varSigma }{{ {\varvec{A}}}_2}{{ {\varvec{g}}}_{i-1}^i}} \right\} \nonumber \\&= \mathrm{{vec}}{((\lambda ^2+1){\varvec{H}_1})^T}\sigma \end{aligned}$$

(61)

where

$$\begin{aligned} {\varvec{H}_1} = \left[ {\begin{array}{cc} {{\mu ^2}\sigma _v^2{\varvec{{\mathcal {A}}}^T}{\varvec{{\mathcal {R}}}_u}\varvec{{\mathcal {A}}}}&{}{{\varvec{0}_{MN}}}\\ {{\varvec{0}_{MN}}}&{}{{\varvec{0}_{MN}}} \end{array}} \right] \end{aligned}$$

(62)

The third term of Eq. (35) can be written as:

$$\begin{aligned} {\mathbb {E}}\left\{ {{{\varvec{B}}_{i} }^T{\varvec{\varSigma }}{{{\varvec{A}}}_2}{{{\varvec{G}}}_{i-1}^i}} \right\} = \mathrm{{vec}}{\left( -\lambda {{\varvec{H}_2}} \right) ^T}{\sigma } \end{aligned}$$

(63)

where

$$\begin{aligned} {\varvec{H}_2} = \left[ {\begin{array}{cc} { {\mu ^2}\sigma _v^2{\varvec{{\mathcal {B}}}_1}{\varvec{\mathcal A}^T}{\varvec{{\mathcal {R}}}_u}\varvec{{\mathcal {A}}}}&{}{{\varvec{0}_{MN}}}\\ { {\mu ^2}\sigma _v^2{\varvec{{\mathcal {A}}}^T}{\varvec{\mathcal R}_u}\varvec{{\mathcal {A}}}}&{}{{\varvec{0}_{MN}}} \end{array}} \right] \end{aligned}$$

(64)

Finally, we have

$$\begin{aligned} {\mathbb {E}}\left\| {{{\varvec{{\tilde{w}}}}_{i-1}^i}} \right\| _{\sigma } ^2 = {\mathbb {E}}\left\| {{{\varvec{{\tilde{w}}}}_{i-2}^{i-1}}} \right\| _{\varvec{{\mathcal {F}}}\sigma }^2 + \mathrm{{vec}}\left( {{(\lambda ^2+1)\varvec{H}_1} -2{\lambda \varvec{H}_2}} \right) \sigma \end{aligned}$$

(65)

4.3.1 Convergence Analysis

A necessary and sufficient condition for the convergence of $E\left\| {{{\varvec{{\tilde{w}}}}_{i-1}^i}} \right\| _{\sigma } ^2$ is that $\varvec{{\mathcal {F}}}$ is a stable matrix, namely, $\rho (\varvec{{\mathcal {F}}})<1$. A simpler, approximate condition as shown below can be obtained for small step sizes [16]:

$$\begin{aligned} \varvec{{\mathcal {F}}} = {{\mathbb {E}}}\{ {{{\varvec{B}}}^T}{ \otimes }{{{\varvec{B}}}^T}\} \approx {{\varvec{B}}}^T{ \otimes }{{\varvec{B}}^T} \end{aligned}$$

(66)

which $\varvec{{\mathcal {F}}}$ is stable if ${\varvec{B}}$ is stable. This condition is the same as the condition for mean stability (29) and can be easily checked.

4.3.2 Steady-State Performance

Notice that the stability of $\varvec{{\mathcal {F}}}$ guarantees that $\varvec{I}-\varvec{{\mathcal {F}}}$ will be invertible. Thus, we have

$$\begin{aligned} \mathop {\lim }\limits _{i \rightarrow \infty } {\mathbb {E}}\left\| {{{ {\varvec{w}}}_{i-1}^i }} \right\| _{(\varvec{I} - \varvec{{\mathcal {F}}})\sigma }^2 = \mathrm{{vec}}((\lambda ^2+1){\varvec{H}_1} - 2\lambda {\varvec{H}_2})\sigma \end{aligned}$$

(67)

Then, choosing

$$\begin{aligned} \sigma = {(\varvec{I} -\varvec{{\mathcal {F}}})^{ - 1}}\mathrm{{vec(diag}}({\varvec{e}_k}) \otimes {\varvec{I}_M}) \end{aligned}$$

(68)

where ${\varvec{e}_k}$ is a $2N-$dimension column vector that has a position unit entry at k and zeros elsewhere. Then,

$$\begin{aligned} \mathrm{MSD}_k&= {\mathbb {E}}{\left\| {{{\tilde{\varvec{w}}}_{k,\infty }}} \right\| ^2} \nonumber \\&= \mathrm{{vec}}((\lambda ^2+1){\varvec{H}_1} - 2\lambda {\varvec{H}_2}){(\varvec{I} - \varvec{{\mathcal {F}}})^{ - 1}} \times \mathrm{{vec}}(\text{ diag }({\varvec{e}_k}) \otimes {\varvec{I}_M}) \end{aligned}$$

(69)

where MSD$_k$ denotes the mean-square deviation of node k. Then, the network mean-square deviation (MSD) as follows:

$$\begin{aligned} MS{D^{network}}&\buildrel \varDelta \over = \frac{1}{N}\sum \limits _{k = 1}^N {MS{D_k}} \nonumber \\&=\frac{1}{N}\sum \limits _{k = 1}^N {\mathrm{{vec}}((\lambda ^2+1){\varvec{H}_1} - 2\lambda {\varvec{H}_2}){(\varvec{I} - \varvec{{\mathcal {F}}})^{ - 1}}} \times \mathrm{{vec}}(\text{ diag }({\varvec{e}_k}) \otimes {\varvec{I}_M}) \end{aligned}$$

(70)

Remark 3

From Eq. (70), we can see that the performance of the correction-based diffusion LMS algorithm is related to the gain factor. In an extreme case when $\lambda =0$, the performance of the correction-based diffusion LMS algorithm equals to the performance of the DLMS algorithm.

5 Simulation Results

5.1 Example 1

In this section, in order to analyze the performance of correction-based diffusion LMS algorithm, we choose a network topology consisting of 20 nodes. The combination matrix $\varvec{A}$ satisfies the double-stochastic property. The entry $a_{\ell ,k}$ satisfies the Metropolis rule [11,12,13,14] as follows:

$$\begin{aligned} {a_{\ell ,k}} = \left\{ {\begin{array}{ll} \frac{1}{{\max ({n_k},{n_\ell })}},&{}\quad \mathrm{if} \;\ell \ne k,\ell \in {N_k}\\ \\ 1 - \sum \limits _{\begin{array}{c} \ell \in {N_k}\\ \ell \ne k \end{array}} {{a_{\ell ,k}}} ,&{}\quad \mathrm{if} \;\ell = k\\ 0,&{}\quad \mathrm{if}\;\ell \notin {N_k} \end{array}} \right. \end{aligned}$$

(71)

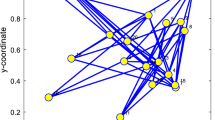
Figure 1 depicts the network topology that is generated according to matrix A with $N=20$ nodes.

The initial estimate $\varvec{w}_{k,1}$ and the initial intermediate value $\varvec{\varphi }_{k,1}$ in the k node are, respectively, selected to be $\varvec{w}_{k,1}={[0,0]}^{T}$, $\varvec{\varphi }_{k,1}={[0,0]}^{T}$. The regression vectors $\varvec{u}_{k,i}$ are a 1$\times$2 zero-mean Gaussian distributed with covariance matrix $\varvec{R}_{u,k}=\varvec{I}_2$. The noises $v_{k,i}$ are a zero-mean Gaussian random variable, independent of any other signal with variance ${\sigma _{v,k}^2=0.25}$. In addition, we assume the estimated parameter $w^o=[1,2]^T$.

We compared the proposed algorithm when gain factor is taken different values. To guarantee almost the same initial convergence rate, we set the step size at $\mu =0.02$ for all the algorithms. And the results are averaged over 100 independent experiments. Figure 2 shows the learning curve for correction-based DLMS algorithm when the gain factor is taken $\lambda =0$, $\lambda =0.2$, $\lambda =0.4$, and $\lambda =0.6$, and $\lambda =0.8$, respectively. Figure 3 shows the learning curve for correction-based DLMS algorithm when the gain factor is taken $\lambda =0.8$, $\lambda =0.85$, $\lambda =0.9$, $\lambda =0.95$, and $\lambda =0.98$, respectively. As can be seen from the figure, when the gain factor takes different values, learning curve will also be different. From Fig. 2, we can observe that when the gain factor is between 0 and 0.8, the MSD gradually decreases as the gain factor increases. From Fig. 3, we can observe that the MSD is proportional to the gain factor if the gain factor is chosen between 0.8 and 0.98. Therefore, we obtain that the learning curve with a gain factor of 0.8 exhibits better performance than learning curves with other gain values.

Fig. 1

Network topology consisting of 20 nodes

Fig. 2

The learning curve for correction-based DLMS algorithm when the gain factor is taken $\lambda =0$, $\lambda =0.2$, $\lambda =0.4$, $\lambda =0.6$, and $\lambda =0.8$, respectively

Fig. 3

The learning curve for correction-based DLMS algorithm when the gain factor is taken $\lambda =0.8$, $\lambda =0.85$, $\lambda =0.9$, $\lambda =0.95$, and $\lambda =0.98$, respectively

Fig. 4

The theoretical MSD when the gain factor $\lambda$ takes different values

Fig. 5

Simulation values and theoretical values of two algorithms include DLMS algorithm [11] and C-DLMS algorithm

We paint the theoretical mean-square deviation that was derived in Sect. 4. Figure 4 shows the theoretical MSD when the gain factor $\lambda$ takes different values. By contrast, it is obvious that theoretical value of the MSD with a gain factor of 0.8 outperforms the theoretical MSD with other gain values.

We simulate the theoretical value of the MSD analyzed in Sect. 4 and compare the theoretical value with the simulated value of the algorithm as shown in Fig. 5. It can be observed from the figure that the theoretical value of the DLMS algorithm is − 33.161dB, and the theoretical value of our proposed algorithms is − 34.236dB when the gain factor is 0.8. The difference between the two is about 1dB. It is obvious that our theoretical results are well matched to the simulation results. In addition, we compare the adapt-then-combine (ATC) DLMS algorithm, the combine-then-adapt (CTA) DLMS algorithm, and the correction-based diffusion LMS algorithm, as shown in Fig. 5, we can observe that correction-based diffusion LMS algorithm has better convergence performance than the other two algorithms.

5.2 Example 2

To verify the performance of the proposed algorithm in different networks, consider a distributed sensor network consisting of 12 nodes. These sensors are randomly distributed in an area of $100\times 100$. When the distance between two sensors is less than $R=20$ m, data transmission is allowed. The final network topology is shown in Fig. 6 [15].

The unknown parameter $\varvec{w}^o$ is set to a $4\times 1$ random vector, the measurement noise $v_{k,i}$ is randomly selected between (0.1, 0.2), and the regression vector is set to a $0-$mean Gaussian vector with $\varvec{R}_{u,k}=\varvec{I}_2$, and the step size $\mu$ is chosen to be 0.02.

Figure 7 shows the learning curve for correction-based DLMS algorithm when the gain factor is taken $\lambda =0$, $\lambda =0.2$, $\lambda =0.4$, and $\lambda =0.6$, and $\lambda =0.8$, respectively.

Figure 8 shows the learning curve for correction-based DLMS algorithm when the gain factor is taken $\lambda =0.8$, $\lambda =0.85$, $\lambda =0.9$, $\lambda =0.95$, and $\lambda =0.98$, respectively.

It is obvious that theoretical value of the MSD with a gain factor of 0.8 outperforms the theoretical MSD with other gain values.

Simulation results suggest that our proposed algorithm performs better than the least mean-square algorithm when the gain factor is chosen to be appropriate.

Fig. 6

Network topology consisting of 12 nodes

Fig. 7

The learning curve for correction-based DLMS algorithm when the gain factor is taken $\lambda =0$, $\lambda =0.2$, $\lambda =0.4$, $\lambda =0.6$, and $\lambda =0.8$, respectively

Fig. 8

The learning curve for correction-based DLMS algorithm when the gain factor is taken $\lambda =0.8$, $\lambda =0.85$, $\lambda =0.9$, $\lambda =0.95$, and $\lambda =0.98$, respectively

6 Conclusion

In this paper, we proposed a correction-based diffusion least mean-square algorithm. Then, we analyzed the stability and mean-square error performance of the algorithm and derived sufficient conditions to ensure the convergence of the algorithm.

• 1. The correction-based diffusion least mean-square algorithm proposed outperforms the original diffusion LMS, and better performance can be obtained if the correction factor is properly selected.

• 2. In the traditional LMS algorithm, the convergence of the algorithm is only related to the step size. However, the convergence of the proposed algorithm is affected not only by the step size but also by the gain factor.

Finally, we expect our proposed algorithm to be applied to other situations, such as cyber attacks, equality constraints, and so on. Next, we will study the algorithm in the case of cyber attacks.