Dynamical analysis of an age-structured SEIR model with relapse

Abstract

Mathematical models play a crucial role in controlling and preventing the spread of diseases. Based on the communication characteristics of diseases, it is necessary to take into account some essential epidemiological factors such as the time delay that takes an individual to progress from being latent to become infectious, the infectious age which refers to the duration since the initial infection and the occurrence of reinfection after a period of improvement known as relapse, etc. Moreover, age-structured models serve as a powerful tool that allows us to incorporate age variables into the modeling process to better understand the effect of these factors on the transmission mechanism of diseases. In this paper, motivated by the above fact, we reformulate an SEIR model with relapse and age structure in both latent and infected classes. Then, we investigate the asymptotic behavior of the model by using the stability theory of differential equations. For this purpose, we introduce the basic reproduction number $\mathcal {R}_0$ of the model and show that this threshold parameter completely governs the stability of each equilibrium of the model. Our approach to show global attractivity is based on the fluctuation lemma and Lyapunov functionals method with some results on the persistence theory. The conclusion is that the system has a disease-free equilibrium which is globally asymptotically stable if $\mathcal {R}_0<1$, while it has only a unique positive endemic equilibrium which is globally asymptotically stable whenever $\mathcal {R}_0>1$. Our results imply that early diagnosis of latent infection with decrease in both transmission and relapse rates may lead to control and restrict the spread of disease. The theoretical results are illustrated with numerical simulations, which indicate that the age variable is an essential factor affecting the spread of the epidemic.

1 Introduction

Infectious diseases have posed a significant threat to human health and economic growth. Consequently, controlling and reducing these diseases is becoming an increasingly collective priority. Mathematical modeling is a useful tool to investigate various characteristics of diseases such as their rapid spread, transmission routes, incubation period, relapse phase, and more. Compartmental models are an elegant method to understand how infectious diseases spread and identify the epidemiological factors that influence the propagation of the disease throughout the population [1,2,3]. Usually, epidemiological models assume that the population of susceptible individuals can progress to different categories of infection, such as exposed, infected, reinfected, and recovered. Among many models used to study the transmission dynamics of infectious diseases, the susceptible-infective-recovered (SIR) models have received more attention. In 1927, Kermack and McKendrick [4] were the first to develop the SIR model, where the total population is divided into three classes: susceptible, infective, and recovered. The model was initially designed to study infectious diseases such as measles, chickenpox, or mumps, where getting infected provides immunity. Since then, several versions of the SIR compartmental model have been created and developed to study different characteristics of infectious diseases, some of which are described in [5,6,7,8,9] and references therein.

In some infectious disease, there is a significant incubation period during which an individual has been infected but is not yet infectious [10]. For example, tuberculosis may take several months to develop into the infectious stage. Taking into account this fact, an additional category of individuals who have been exposed to the disease but are not yet capable of transmitting it has been added to the SIR epidemic model and then the novel epidemic model known as SEIR was introduced (see, e.g., [11,12,13]). Moreover, due to several factors, a recovered individual can be reinfected again after a period of improvement which is known as the relapse phase (see, e.g., [14,15,16]). Identifying the related factors that affect reinfection in recovered individuals allows public health services to create prevention programs and develop control strategies that eliminate such factors and reduce the relapse rate [17, 18].

Most of these models are based on differential equations (ODE), which assume that all individuals in different categories have the same waiting time. Otherwise, it is crucial to indicate that, for example, the duration of the latent period of exposed individuals may vary significantly among several elements and factors, such as the specificity of infections and the individual’s health status. For example, latent tuberculosis can remain in the inactive stage without causing disease for months, years, or even decades before becoming infectious, potentially developing into a severe stage, highly contagious, and deadly disease if left untreated or incompletely treated [19, 20]. Furthermore, the infection age period, which refers to the duration since the initial infection, is an important epidemiological element that plays a vital role in the modeling process of infectious diseases, particularly HIV/AIDS and hepatitis B (see, e.g., [21,22,23,24]).

In fact, age-structured models serve as a puissant tool to study the epidemiology of infectious disease ( see, e.g., [24,25,26]). Moreover, by investigating the global dynamics of these epidemic models, we can understand how the disease spreads through the population with the aim of developing some control strategies to reduce or even eradicate the spread of diseases. For example, Magal et al. [27] have investigated the global stability of endemic equilibrium for an age-structured model with infection age using the classic Volterra-type Lyapunov functions. These functions were also used to get the global stability of a delay SIR (susceptible-infected-removed) model with a fixed infection period in McCluskey [28] and Melnik and Korobeinikov [29] used them to obtain the global stability for SIR and SEIR models with age-dependent susceptibility. More details concerning the development of the Lyapunov functionals approach to study the global dynamics of infectious diseases, we name a few references [1, 18, 30,31,32,33,34,35,36,37].

Motivated by the above works, this paper introduces and analyzes an SEIR epidemic model with latency, infection age structure, and relapse. This model is appropriate for diseases that have latent periods and can also relapse, such as tuberculosis and herpes virus infection. To the best of our knowledge, our model is new, which lies in the fact that both latency and infection individuals are to be continuous age-dependent, with a relapse phase.

This study aims to clarify the global asymptotic behavior of the model by using the Lyapunov function method, which consists of constructing an appropriate Lyapunov function. For this purpose, we establish the threshold parameter $\mathcal {R}_0$ in connection with the existence of the endemic equilibrium of the model. Then, we show that it determines the global asymptotic stability (or attractivity) of each equilibrium, that is, if $\mathcal {R}_0<1$, then the disease-free equilibrium is globally asymptotically stable, whereas if $\mathcal {R}_0>1$, then the endemic equilibrium uniquely exists and it is globally attractive.

The rest of this paper is organized as follows: In Sect. 2, we reformulate the mathematical model and provide some important preliminary concepts. Then, in Sect. 3, we show the existence of both disease-free and endemic equilibria of the model. Then, we analyze their local asymptotic stability by using the linearization approach. Furthermore, Sect. 4 is devoted to the relative compactness of solution semi-flow and the existence of a global attractor. Moreover, In Sect. 5, we prove the uniform persistence of the model. Section 6 discusses the global asymptotic stability of disease-free and endemic equilibria by employing the Lyapunov functional technique. Finally, Sect. 7 is dedicated to perform some numerical simulations that illustrate our theoretical results.

2 Model formulation

To create our model, we assume that the population can be divided into four subsets, namely, susceptible, exposed, infected, and recovered. Let S(t) be the size of the susceptible individual at time t, e(t, a) represent the density of exposed individuals who are infected but not yet infectious at time t with latency age a, i(t, b) denote the density of infected individual at time t with infection age b, and R(t) the size of recovered individuals at time t. Then, we suppose that the model to be studied is based on the following assumptions:

• i. Susceptible individuals become infected when they come into contact with infectious individuals. In this context, we consider the bilinear form $\displaystyle S(t) \int \nolimits _{0}^{\infty } \vartheta (b) i(t,b) \text {d} b$ as the incidence rate for our model, where $\vartheta (b)$ represents the age-dependent transmission coefficient, which describes the contact process between susceptible and infectious individuals.

• ii. Exposed individuals can leave the latent classe and become infected at rate of $\varphi (a)$. Thus, the total rate at which exposed individuals progress into the infectious class alive may be given by $\displaystyle \int \nolimits _{0}^{\infty } \varphi (a) e(t,a) \text {d} a$.

• iii. Infected individuals move to the recovered class at an age-dependent rate of $\psi (b)$. As a result, the total rate at which the infected individuals become recovered can be determined by $\displaystyle \int \nolimits _{0}^{\infty } \psi (b) i(t,b)\text {d} b$.

• iv. After the improvement period, there is a possibility of relapse, and hence, the recovered individual may get reinfected again at a rate denoted by $\delta$. Consequently, the quantity of the reinfected individual can be presented by the linear relapse rate $\delta R(t)$.

• v. The natural mortality rate for all individuals is given by $\mu$. Moreover, the death rates of exposed and infectious individuals because of the disease are given by $\nu _1(a)$ and $\nu _2(b)$, respectively.

Therefore, the disease spread model according to the above assumptions is represented as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\text {d} S(t)}{\text {d} t}= A- \mu S(t) - S(t) \int \nolimits _{0}^{\infty } \vartheta (b) i(t,b)\text {d} b, &{} \\ \displaystyle \frac{\partial e(t,a)}{\partial t } + \frac{\partial e(t,a)}{\partial a} = - (\varphi (a) + \nu _1(a) +\mu ) e(t,a), &{} \\ \displaystyle \frac{\partial i(t,b) }{\partial t } + \frac{\partial i(t,b) }{\partial b } = -(\psi (b) +\nu _2(b)+\mu ) i(t,b), &{} \\ \displaystyle \frac{\text {d} R(t)}{\text {d} t}= \int \limits _{0}^{\infty } \psi (b) i(t,b) \text {d} b -(\delta + \mu )R(t), \end{array} \right. \end{aligned}$$

(1)

with boundary conditions

$$\begin{aligned} \displaystyle e(t,0) =S(t) J(t), \quad \text {and} \quad \displaystyle i(t,0) = W(t), \end{aligned}$$

(2)

and initial condition, by biological reasons, are the positive continuous functions

$$\begin{aligned} S(0)=S_0, \quad e(0, a)=e_0(a), \quad i(0, b) = i_0(b), \quad \text {and} \quad R(0)=R_0, \end{aligned}$$

(3)

where

$$\begin{aligned} J(t)= & {} \int \limits _{0}^{\infty } \vartheta (b) i(t,b)\text {d} b, \end{aligned}$$

(4)

$$\begin{aligned} W(t)= & {} \int \limits _{0}^{\infty } \varphi (a) e(t,a) \text {d} a + \delta R(t). \end{aligned}$$

(5)

Throughout this paper, we consider the following assumptions and notations:

Assumption A

Assume that

i.:

A, $\mu$, $\delta >0$, and $\nu _1, \nu _2, \varphi , \psi , \vartheta \in L_{+}^{\infty }(0, \infty )$.

ii.:

$\vartheta$ and $\varphi$ are Lipschitz continuous functions on $\mathbb {R}_+$, with Lipschitz coefficients $L_\vartheta$ and $L_\varphi$, respectively.

iii.:

For any function $\pi \in L_{+}^{\infty }(0, \infty )$, we denote

$$\begin{aligned} \underline{\pi }:={\text {ess}}\inf \limits _{\tau \in \mathbb {R}_+} \pi (\tau )<+\infty , \quad \text {and} \quad \overline{\pi }:={\text {ess}}\sup \limits _{\tau \in \mathbb {R}_+} \pi ({\tau })<+\infty . \end{aligned}$$

Let us define the following functional space:

$$\begin{aligned} X:= \mathbb {R}_+ \times L_{+}^1(0, \infty ) \times L_{+}^1(0, \infty ) \times \mathbb {R}_+, \end{aligned}$$

equipped with the norm

$$\begin{aligned} \big \Vert (x_1, x_2, x_3, x_4) \big \Vert _X = \vert x_1 \vert + \int \nolimits _{0}^{\infty } \vert x_2(a) \vert \text {d} a + \int \limits _{0}^{\infty } \vert x_3(b) \vert \text {d} b + \vert x_4\vert . \end{aligned}$$

Notice that the initial condition of system (1)–(3) can be expressed as follows:

$$\begin{aligned} x_0 = (S_0, e_0(\cdot ), i_0(\cdot ), R_0) \in X. \end{aligned}$$

By the standard theory of functional differential equations (see, e.g., [38, 39]), we can verify that system (1) with boundary conditions (2) and initial condition (3) has a unique nonnegative continuous solution (S, e, i, R).

Next, we define a continuous semi-flow $\Phi \,: \, \mathbb {R}_+ \times X \rightarrow X$ generated by system (1)–(3) by

$$\begin{aligned} \Phi (t,x_0)= (S(t), e(t, \cdot ), i(t, \cdot ), R(t)), \quad t\ge 0, \, x_0 \in X. \end{aligned}$$

(6)

Hence,

$$\begin{aligned} \big \Vert \Phi (t, x_0) \big \Vert _X = \big \Vert (S(t), e(t, \cdot ), i(t, \cdot ), R(t)) \big \Vert _X = S(t)+ \int \nolimits _{0}^{\infty } e(t,a) \text {d} a + \int \nolimits _{0}^{\infty } i(t,b)\text {d} b +R(t). \end{aligned}$$

Denote

$$\begin{aligned} p_1(a)=\varphi (a) + \tilde{\nu }_1(a), \quad \text {and} \quad p_2(b)= \psi (b) + \tilde{\nu }_2(b), \end{aligned}$$

(7)

where

$$\begin{aligned} \tilde{\nu }_1(a)= \nu _1(a)+\mu , \quad \text {and} \quad \tilde{\nu }_2(b)= \nu _2(b)+\mu . \end{aligned}$$

Let

$$\begin{aligned} \mu _0= \min \{ \mu , \underline{\tilde{\nu }}_1, \underline{\tilde{\nu }}_2 \}. \end{aligned}$$

(8)

Then, we define the following biologically feasible region

$$\begin{aligned} \Gamma = \left\{ (S, e, i, R) \in X\;: \; S(t) + \int \nolimits _{0}^{\infty }e(t,a)\text {d} a + \int \nolimits _{0}^{\infty }i(t,b)\text {d} b +R(t) \le \frac{A}{\mu _0} \right\} . \end{aligned}$$

Now, we can prove the following result:

Proposition 2.1

Considering system (1)–(3), then we have

i.:

$\Gamma$ is positively invariant for $\{\Phi (t,x_0) \}_{t\ge 0}$, that is, $\Phi (t,x_0) \in \Gamma$, for $x_0 \in \Gamma$ and $t\ge 0$;

ii.:

$\{\Phi (t,x_0)\}_{t\ge 0}$ is point dissipative and $\Gamma$ attract all points in X.

Proof

First, by the definition of the semi-flow $\Phi$ given by (6), we have

$$\begin{aligned} \frac{\text {d} }{\text {d} t} \big \Vert \Phi (t,x_0)\big \Vert _{X}= \frac{\text {d} S(t)}{\text {d} t} + \int \limits _{0}^{\infty }\frac{\partial e(t,a)}{\partial t} \,\text {d} a + \int \limits _{0}^{\infty } \frac{\partial i(t,b) }{\partial t} \text {d} b + \frac{\text {d} R(t)}{\text {d} t}. \end{aligned}$$

Then, system (1)–(3) provides

$$\begin{aligned} \frac{\text {d} }{\text {d} t} \big \Vert \Phi (t)x_0 \big \Vert _{X}= & {} A-\mu S(t) - S(t)\int \limits _{0}^{\infty } \vartheta (b) i(t,b)\text {d} b + e(t,0) - \int \limits _{0}^{\infty } p_1(a) e(t,a) \text {d} a \\{} & {} +i(t,0) - \int \limits _{0}^{\infty } p_2(b) i(t,b) \text {d} b + \int \limits _{0}^{\infty } \psi (b) i(t,b) \text {d} b -(\mu +\delta ) R(t). \end{aligned}$$

where $p_1$ and $p_2$ are provided by (7). Therefore, by using the boundary conditions (2), we can get

$$\begin{aligned} \frac{\text {d} }{\text {d} t} \big \Vert \Phi (t,x_0) \big \Vert _{X} \le A- \mu _0 \big \Vert \Phi (t,x_0) \big \Vert _{X}. \end{aligned}$$

(9)

where $\mu _0$ is given by (8). Hence, by the variation of the constants, we find

$$\begin{aligned} \big \Vert \Phi (t,x_0) \big \Vert _{X} \le \frac{A}{\mu _0} - e^{- \mu _0 t} \left( \frac{A}{\mu _0} - \big \Vert x_0 \big \Vert _X\right) , \end{aligned}$$

(10)

which implies that $\Phi (t,x_0) \in \Gamma$, $t\ge 0$, for any solution of system (1)–(3) satisfying $x_0 \in \Gamma$. Thus, we have $\{\Phi (t,x_0)\}_{t\ge 0}$ is positively invariant for the set $\Gamma$. Moreover, if follows from (10) that $\displaystyle \limsup _{t\rightarrow \infty }\big \Vert \Phi (t,x_0) \big \Vert _{X} \le \frac{A}{\mu _0}$, for any $x_0 \in \Gamma$. Consequently, it can be concluded that $\{\Phi (t,x_0)\}_{t\ge 0}$ is point dissipative and $\Gamma$ is an attracting set for all points in X. This completes the proof. $\square$

The following properties are direct consequences of Proposition 2.1.

Proposition 2.2

If $x_0 \in X$ and $\Vert x_0 \Vert _X \le \eta$ for some constant $\eta \ge \frac{A}{\mu _0}$, then the following statements hold true for $t\ge 0$:

i.:

$0 \le S(t), \, \displaystyle \int \limits _{0}^{\infty } e(t,a) \text {d} a, \, \displaystyle \int \limits _{0}^{\infty } i(t,b) \text {d} b, \, R(t) \le \eta$;

ii.:

$e(t,0) \le \overline{\vartheta }\, \eta ^2$, and $i(t,0) \le (\overline{\varphi } + \delta )\eta$;

iii.:

$\displaystyle \liminf _{t \rightarrow \infty } S(t) \ge \frac{A}{\mu + \underline{\vartheta } \eta }$.

3 Existence and local stability of equilibria

In this section, we will establish the existence of both disease-free and endemic equilibria of system (1)–(3). Furthermore, we will analyze the local asymptotic stability of these equilibria by using the linearization technique described in Webb [26, Section 4.5]. Before going on, for the sake of clarity, let us introduce the following notations:

$$\begin{aligned} \zeta _1 = \int \limits _{0}^{\infty }\varphi (a) \phi _1(a) \text {d} a, \quad \zeta _2 = \int \limits _{0}^{\infty } \vartheta (b) \phi _2(b) \text {d} b, \quad \text {and} \quad \zeta _3 = \int \limits _{0}^{\infty } \psi (b) \phi _2(b) \text {d} b, \end{aligned}$$

(11)

with

$$\begin{aligned} \phi _1(a) = e^{- \int \limits _{0}^{a}p_1(\sigma )\text {d} \sigma }, \quad \text {and} \quad \phi _2(b) = e^{- \int \limits _{0}^{b}p_2(\sigma )\text {d} \sigma }, \quad \text {for all } a,b \in \mathbb {R}_+. \end{aligned}$$

(12)

Evidently, it can be observed that $\zeta _1, \zeta _3 \le 1$. Now, we could state the following result about the existence of the disease-free equilibrium:

Lemma 3.1

System (1)–(3) has always a unique disease-free equilibrium $E^0 = (S^0, 0, 0, 0)$, where

$$\begin{aligned} S^0= \frac{A}{\mu }. \end{aligned}$$

(13)

Proof

When there is no disease-transmission (i.e., $e(t,a)=i(t,b) =R(t)=0$ for all $t,a,b \in \mathbb {R}_{+}$), the disease-free equilibrium of system (1)–(3) must satisfy the following equation $A-\mu S^0=0$, which implies that $S^0 = \frac{A}{\mu }$. Then, without any restrictions, system (1)–(3) admits a unique disease-free equilibrium, denoted by $E^0=(S^0, 0, 0,0)$. This proves Lemma 3.1. $\square$

Next, we pass to study the local asymptotic stability of the disease-free equilibrium $E^0$ given in Lemma 3.1. It is worth noting that investigating the dynamical behavior of the disease-free equilibrium aims to identify the impact of disease elimination on the population.

Theorem 3.2

Let $\mathcal {R}_0$ be given by (21). Then, the disease-free equilibrium $E^0$ of system (1)–(3) is locally asymptotically stable if $\mathcal {R}_0<1$, whereas it is unstable if $\mathcal {R}_0>1$.

Proof

Let $S^0$ be given by (13). Consider the following pertubation variables: $\tilde{S}(t) = S(t)-S^0$, $\tilde{e}(t,a)=e(t,a)$, $\tilde{i}(t,b)= i(t,b)$, and $\tilde{R}(t)=R(t)$. Then, by linearizing system (1)–(3) around $E^0$, we could find

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\text {d} \tilde{S}(t)}{\text {d} t}= -\mu \tilde{S} - S^0 \int \limits _{0}^{\infty } \vartheta (b) \tilde{i}(t,b) \text {d} b, &{} \\ \displaystyle \frac{\partial \tilde{e}(t,a)}{\partial t } + \frac{\partial \tilde{e}(t,a)}{\partial a} = - p_1(a) \tilde{e}(t,a), &{} \\ \displaystyle \frac{\partial \tilde{i}(t,b)}{\partial t } + \frac{\partial \tilde{i}(t,b)}{\partial b } = - p_2(b) \tilde{ i} (t,b), &{} \\ \displaystyle \frac{\text {d} \tilde{R}(t)}{\text {d} t}= \int \limits _{0}^{\infty } \psi (b) \tilde{i}(t,b) \text {d} b -(\delta + \mu )\tilde{R}(t), &{} \\ \displaystyle e(t,0) = S^0 \int \limits _{0}^{\infty } \vartheta (b) \tilde{i}(t,b) \text {d} b, \\ \displaystyle i(t,0) = \int \limits _{0}^{\infty } \varphi (a) \tilde{e}(t,a) \text {d} a + \delta \tilde{R}(t). \end{array} \right. \end{aligned}$$

(14)

Furthermore, consider the following exponential solution functions $\tilde{S}(t)= x_1 e^{\lambda t}$, $\tilde{e}(t,a) = x_2(a) e^{\lambda t}$, $\tilde{i}(t,b) = x_3(b) e^{\lambda t}$, and $\tilde{R}(t)= x_4 e^{\lambda t}$, where $(x_1, x_2(a), x_3(b), x_4) \in X$ is to be determined later, and $\lambda \in \mathbb {\mathbb {R}}$. Therefore, by substituting them into system (14), it yields

$$\begin{aligned} \left\{ \begin{array}{ll} { (\lambda + \mu ) x_1 = - S^0 \displaystyle \int \limits _{0}^{\infty } \vartheta (b) x_3(b) \text {d} b, }\\ \displaystyle \frac{\text {d} x_2(a)}{\text {d} a} = - (\lambda + p_1(a)) x_2(a), &{} \\ \displaystyle \frac{\text {d} x_3(b)}{\text {d} b} =-(\lambda + p_2 (b) ) x_3(b), &{} \\ (\lambda + \mu + \delta ) x_4 = \displaystyle \int \limits _{0}^{\infty } \psi (b) x_3(b) \text {d} b, &{} \\ x_2(0)= S^0 \displaystyle \int \limits _{0}^{\infty } \vartheta (b) x_3(b) \text {d} b, \\ x_3(0) = \displaystyle \int \limits _{0}^{\infty } \varphi (a) x_2(a) \text {d} a + \delta x_4. \end{array} \right. \end{aligned}$$

(15)

Solving the second and third differential equations of system (15), we obtain

$$\begin{aligned} x_2(a) = x_2(0) e^{- \int \limits _{0}^{a} (\lambda +p_1(\sigma )) \text {d} \sigma }, \quad \end{aligned}$$

(16)

and

$$\begin{aligned} x_3(b) = x_3(0) e^{- \int \limits _{0}^{b} (\lambda +p_2(\sigma )) \text {d} \sigma }. \quad \end{aligned}$$

(17)

Before going on, we need to show that $\lambda + \mu \not =0$ and $\lambda + \mu +\delta \not =0$. To this end, we suppose by contradiction that $\lambda +\mu +\delta =0$. Then, by inserting (17) into the fourth equation of system (15), we get $x_3(0)=0$. This together with the first equation of system (15) gives $\lambda +\mu =0$, which is a contradiction. Similarly, we can also show that $\lambda +\mu \not =0$. According to the fourth equation of system (15), we could obtain

$$\begin{aligned} x_4 = \frac{x_3(0)}{\lambda +\mu + \delta } \int \limits _{0}^{\infty } \psi (b) e^{- \int \limits _{0}^{b} (\lambda + p_2(\sigma )) \text {d} \sigma } \text {d} b. \end{aligned}$$

(18)

Next, by substituting (16), (17) and (18) into the last equation of system (15), we find

$$\begin{aligned} x_3(0) = S^0 \widehat{\zeta }_1( \lambda ) \widehat{\zeta }_2( \lambda ) x_3(0) +\frac{\delta }{\lambda +\mu + \delta } \widehat{\zeta }_3( \lambda ) x_3(0), \end{aligned}$$

where $\widehat{\zeta }_1( \lambda )$, $\widehat{\zeta }_2( \lambda )$, and $\widehat{\zeta }_3( \lambda )$ are the Laplace transform of functions $\varphi \phi _1$, $\vartheta \phi _2$ and $\psi \phi _1$, respectively. Thus, the characteristic equation of the linear system (15) at $E^0$ can be expressed as follows:

$$\begin{aligned} G(\lambda ) = S^0 \widehat{\zeta }_1( \lambda ) \widehat{\zeta }_2( \lambda ) + \frac{\delta }{\lambda +\mu + \delta } \widehat{\zeta }_3( \lambda ) =1. \end{aligned}$$

(19)

Note that G is continuously differentiable function and satisfies

$$\begin{aligned} \lim _{\lambda \rightarrow -\infty } G(\lambda )= +\infty , \quad \lim _{\lambda \rightarrow +\infty } G(\lambda )= 0, \quad \text {and} \quad G'(\lambda )<0. \end{aligned}$$

Therefore, G is monotonically decreasing of $\lambda \in \mathbb {R}$. Thus, with the help of the intermediate value theorem, we can deduce that any eigenvalue $\lambda$ of the equation $G(\lambda )=1$ has a positive real part if $G(0) > 1$. Hence, the disease-free equilibrium $E^0$ of system (1)–(3) is unstable when $G(0)>1$. Next, we consider $G(0)<1$, and we claim that all roots of Eq. (19) have negative real parts. To this end, we suppose that $\lambda$ is a complex root satisfying $G(\lambda ) = 1$, such that $\text {Re} (\lambda )\ge 0$. Therefore, by taking the real part of Eq. (19), it yields the following

$$\begin{aligned} 1= \text {Re} G(\lambda )= & {} \text {Re} \left[ S^0 \, \widehat{\zeta }_1( \lambda ) \, \widehat{\zeta }_2( \lambda ) + \frac{\delta }{\lambda +\mu + \delta } \widehat{\zeta }_3( \lambda ) \right] \\\le & {} S^0\, \widehat{\zeta }_1 ( \text {Re} (\lambda ) ) \, \widehat{\zeta }_2( \text {Re} (\lambda )) + \frac{\delta \left[ \text {Re} (\lambda )+\mu +\delta \right] }{ \left[ \text {Re} (\lambda )+\mu + \delta \right] ^2 + \text {Im} ^2(\lambda ) } \, \widehat{\zeta }_3( \text {Re} (\lambda ) )\\\le & {} G(\text {Re} (\lambda )), \end{aligned}$$

where we have used $\text {Re} (\lambda )\ge 0$. Hence, we have

$$\begin{aligned} 1= \text {Re} G(\lambda ) \le G(\text {Re} (\lambda )) \le G(0), \end{aligned}$$

(20)

which contradicts the assumption of $G(0)<1$. Thus, we conclude that any eigenvalue $\lambda$ of Eq. (19) has a negative real part if $G(0) < 1$. At this stage, we define the basic reproduction number of (1)–(3) by

$$\begin{aligned} \mathcal {R}_0 = G(0) = S^0 \zeta _1 \zeta _2 + \frac{\delta }{\mu + \delta } \zeta _3, \end{aligned}$$

(21)

which is the average number of secondary infections produced by an infected individual in a population completely susceptible (see, e.g., [3] for more details). In conclusion, from the above analysis, it follows that the disease-free equilibrium $E^0$ of system (1)–(3) is locally asymptotically stable whenever $\mathcal {R}_0 < 1$, and unstable if $\mathcal {R}_0 >1$. This completes the proof. $\square$

Remark 3.3

Denote

$$\begin{aligned} \tilde{\zeta }_3 = \frac{\delta }{\mu +\delta } \zeta _3. \end{aligned}$$

(22)

According to (11), we have $\zeta _3 = \displaystyle \int \limits _{0}^{\infty } \psi (b) e^{-\int \limits _{0}^{b}(\psi (\sigma ) + \nu _2(\sigma )+\mu ) \text {d} \sigma } \text {d} b \le 1$. Therefore, it can be readily deduced that $\tilde{\zeta }_3 <1$.

Remark 3.4

Recall that $\vartheta (b)$ represents the disease-transmission function rate, and $\varphi (a)$ denotes the rate at which the exposed individual becomes infectious. Thus, we have

$$\begin{aligned} \mathcal {R}_{01}=\underbrace{ S^0}_{i } \underbrace{\int \limits _{0}^{\infty } \varphi (a) \phi _1(a) \text {d} a}_{ii } \times \underbrace{\int \limits _{0}^{\infty } \vartheta (b) \phi _2(b) \text {d} b}_{iii } \end{aligned}$$

is the number of infectious individuals produced by the primary cases after the incubation period, where

i.:

Denotes the initial susceptible population size.

ii.:

Denotes the probability refers to the likelihood of an exposed individual becoming infectious.

iii.:

Represents the total transmission rate of an infectious individual who can transmit the disease during their infectious period.

Moreover, since $\psi (b)$ is the function rate at which the infectious individual becomes recovered, and $\delta$ is the relapse rate, we have

$$\begin{aligned} \mathcal {R}_{02}=\underbrace{\frac{\delta }{\mu +\delta } }_{iv }\underbrace{\int \limits _{0}^{\infty } \psi (b) \phi _2(b) \text {d} b}_{v } \end{aligned}$$

is the number of infectious cases produced by the primary case after the relapse phase, where

iv.:

Refers to the proportion of individuals who return to being infectious after having recovered.

v.:

It represents the likelihood of infectious individuals surviving an infectious disease and becoming recovered.

Consequently, the basic reproduction number $\mathcal {R}_0$ of system (1)–(3) can be expressed in the following way $\mathcal {R}_0 = \mathcal {R}_{01} + \mathcal {R}_{02}$.

Next, we move to investigate the existence and local asymptotic stability of the endemic equilibrium of system (1)–(3). First, we introduce the following result which ensures the existence of the endemic equilibrium under some conditions.

Lemma 3.5

Let $\mathcal {R}_0$ be defined by (21). Then, system (1)–(3) has a unique endemic equilibrium $E^*= (S^*, e^*(a), i^*(b), R^*)$, if $\mathcal {R}_0>1$, where

$$\begin{aligned} S^* = \frac{1- \tilde{\zeta }_3}{ \zeta _1 \zeta _2}, \; e^*(a)= \frac{\mu (\mathcal {R}_0 -1)}{\zeta _1 \zeta _2}\phi _1(a), \; i^*(b)= \frac{\mu (\mathcal {R}_0-1)}{ (1 - \tilde{\zeta }_3) \zeta _2 } \phi _2(b), \, \text {and} \, R^* = \frac{\mu (\mathcal {R}_0-1) \zeta _3}{ (\mu +\delta ) ( 1-\tilde{\zeta }_3) \zeta _2}, \end{aligned}$$

where $\tilde{\zeta }_3<1$ is given by (22).

Proof

For system (1)–(3), an endemic equilibrium $E^* = (S^*, e^*(a), i^*(b), R^*)$ should verify the following system

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle 0=A -\mu S^* - S^* \int \limits _{0}^{\infty } \vartheta (b) i^*(b)\text {d} b, &{}\\ \displaystyle \frac{\text {d} e^*(a)}{\text {d} a} = - p_1(a) e^*(a), &{}\\ \displaystyle \frac{\text {d} i^*(b)}{\text {d} b} = - p_2(b) i^*(b), &{} \\ \displaystyle 0= \int \limits _{0}^{\infty } \psi (b) i^*(b)\text {d} b -(\mu + \delta ) R^*, \\ \displaystyle e^*(0) =S^* \int \limits _{0}^{\infty } \vartheta (b) i^*(b)\text {d} b, &{} \\ \displaystyle i^*(0) = \int \limits _{0}^{\infty } \varphi (a) e^*(a) \text {d} a + \delta R^*. &{} \end{array} \right. \end{aligned}$$

(23)

In view of the second and third differential equations of system (23), it yields

$$\begin{aligned} e^*(a)= e^*(0)\phi _1(a), \quad \text {for all } a \in \mathbb {R}_+, \end{aligned}$$

(24)

and

$$\begin{aligned} i^*(b)= i^*(0)\phi _2(b), \quad \text {for all } b \in \mathbb {R}_+, \end{aligned}$$

(25)

where $\phi _1(a)$ and $\phi _2(b)$ are provided by (12). Furthermore, from the fourth equation of system (23) and by using (25), we can obtain

$$\begin{aligned} R^* = \frac{\zeta _3}{\mu + \delta } i^*(0). \end{aligned}$$

(26)

Next, by inserting (26) into the last equation of (23) and by using (24) and (25), we find

$$\begin{aligned} i^*(0)= & {} \int \limits _{0}^{\infty } \varphi (a) e^*(a)\text {d} a + \delta R^* \\= & {} \zeta _1 e^*(0) + \frac{\delta \zeta _3 }{\mu + \delta } i^*(0) \\= & {} S^* \zeta _1 \zeta _2 i^*(0) + \frac{\delta \zeta _3}{\mu + \delta } i^*(0), \end{aligned}$$

which implies that

$$\begin{aligned} S^* = \frac{ 1 - \tilde{\zeta _3} }{ \zeta _1 \zeta _2}. \end{aligned}$$

(27)

Notice that the fact that $\tilde{\zeta }_3 <1$ ensures the nonnegativity of $S^*$. Moreover, by substituting (27) into the first equation of system (23), it results

$$\begin{aligned} i^*(0) = \frac{\mu (\mathcal {R}_0 -1) }{(1- \tilde{\zeta }_3) \zeta _2}. \end{aligned}$$

(28)

Then, from the fifth equation of system (23) and by using (28), it follows

$$\begin{aligned} e^*(0)= \frac{\mu (\mathcal {R}_0 -1)}{\zeta _1 \zeta _2}. \end{aligned}$$

Lastly, by inserting (28) into Eq. (26), we get

$$\begin{aligned} R^* = \frac{\mu (\mathcal {R}_0-1) \zeta _3}{ (\mu +\delta ) ( 1-\tilde{\zeta }_3) \zeta _2}. \end{aligned}$$

This completes the proof of Lemma 3.5. $\square$

Remark 3.6

Note that $e^*(0)$ and $i^*(0)$ can be written as follows: $e^*(0) = S^* J^*$ and $i^*(0)= W^*$, where

$$\begin{aligned} J^*=\frac{\mu (\mathcal {R}_0-1)}{1- \tilde{\zeta _3}}, \quad \text {and} \quad W^*= \zeta _1 S^* J^*+\delta R^*. \end{aligned}$$

(29)

We can also observe that when $J^*=0$, the endemic equilibrium $E^*$ becomes the disease-free equilibrium $E^0$.

In what follows, we analyze the local asymptotic stability of $E^*$. Notice that the study of the dynamical behavior of the endemic equilibrium is intended to determine how disease spreads when it becomes endemic in a population.

Theorem 3.7

Suppose $\mathcal {R}_0>1$. Then, the endemic equilibrium $E^*$ is locally asymptotically stable.

Proof

Let $S^*$, $e^*(a)$, $i^*(b)$, and $R^*$ be given in Lemma 3.5. Consider the following perturbation variables: $\bar{S}(t) = S(t)- S^*$, $\bar{e}(t,a) = e(t,a) - e^*(a)$, $\bar{i}(t,b) = i(t,b) -i^*(b)$, and $\bar{R}(t)= R(t)- R^*$. Then, through linearization of system (1)–(3) around $E^*$, we obtain the following linearized system:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\text {d} \bar{S}(t)}{\text {d} t}= -\mu \bar{S}(t) - J^* \bar{S}(t) -S^* \int \limits _{0}^{\infty } \vartheta (b) \bar{i}(t,b)\text {d} b, &{} \\ \displaystyle \frac{\partial \bar{e}(t,a)}{\partial t } + \frac{\partial \bar{e}(t,a)}{\partial a} = - p_1 (a)\bar{e}(t,a), &{} \\ \displaystyle \frac{\partial \bar{i}(t,b)}{\partial t } + \frac{\partial \bar{i}(t,b)}{\partial b } = - p_2(b) \bar{i}(t,b), &{}\\ \displaystyle \frac{\text {d} \bar{R}(t)}{\text {d} t} = \int \limits _{0}^{\infty } \psi (b) \bar{i}(t,b)\text {d} b - (\mu +\delta )\bar{R} (t), \\ \displaystyle \bar{e}(t,0) = J^* \bar{S}(t) + S^* \int \limits _{0}^{\infty } \vartheta (b) \bar{i}(t,b)\text {d} b, &{}\\ \displaystyle \bar{i}(t,0) = \int \limits _{0}^{\infty } \varphi (a) \bar{e}(t,a)\text {d} a + \delta \bar{R}(t), &{} \end{array} \right. \end{aligned}$$

(30)

where $J^*$ is given by (29). Next, we consider the following exponential functions: $\bar{S}(t)= y_1 e^{\omega t}$, $\bar{e}(t,a) = y_2(a) e^{\omega t}$, $\bar{i}(t,b) = y_3(b) e^{\omega t}$ and $\bar{R}(t)= y_4 e^{\omega t}$, where $(y_1, y_2(a), y_3(b), y_4) \in X$ is to be determined later, and $\omega \in \mathbb {\mathbb {R}}$. Then, by substituting them into system (30), it yields

$$\begin{aligned} \left\{ \begin{array}{ll} (\omega + \mu + J^*)y_1= -S^* \displaystyle \int \limits _{0}^{\infty } \vartheta (b) y_3(b)\text {d} b, &{} \\ \displaystyle \frac{\text {d} y_2(a)}{\text {d} a}=- (\omega +p_1 (a) ) y_2(a), &{} \\ \displaystyle \frac{\text {d} y_3(b)}{\text {d} b}=- (\omega +p_2 (b) ) y_3(b), &{}\\ (\omega + \mu + \delta )y_4 = \displaystyle \int \limits _{0}^{\infty } \psi (b) y_3(b)\text {d} b, &{}\\ y_2(0) = J^* y_1 + S^* \displaystyle \int \limits _{0}^{\infty } \vartheta (b) y_3(b)\text {d} b, &{}\\ y_3(0) = \displaystyle \int \limits _{0}^{\infty } \varphi (a) y_2(a)\text {d} a + \delta y_4.&{} \end{array} \right. \end{aligned}$$

(31)

Therefore, the solutions of the second and third differential equations of system (31) are given, respectively, by

$$\begin{aligned} y_2(a) = y_2(0) e^{- \int \limits _{0}^{a} (\omega +p_1(\sigma )) \text {d} \sigma }, \quad \text { for all } a \in \mathbb {R}_+, \end{aligned}$$

(32)

and

$$\begin{aligned} y_3(b) = y_3(0) e^{- \int \limits _{0}^{b} (\omega +p_2(\sigma )) \text {d} \sigma }. \quad \quad \text { for all } b \in \mathbb {R}_+, \end{aligned}$$

(33)

Now, we show that $\omega +\mu +J^*\not =0$ and $\omega + \mu +\delta \not =0$. To this end, we assume that $\omega +\mu +\delta =0$. Then, it results from (33) and the fourth equation of system (31) that $y_3(0)=0$. Hence, from the first equation of system (31), it follows that $\omega +\mu +J^*=0$, which results in a contradiction. In the same way, we can also show that $\omega +\mu +J^* \not =0$. Next, in view of system (31), we can express the characteristic equation corresponding to $E^*$ of the linearized system (30) as follows:

$$\begin{aligned} (\omega +\mu ) (\omega + \mu + \delta )S^* \widehat{\zeta }_1(\omega ) \widehat{\zeta }_2(\omega ) - (\omega +\mu +J^*)(\omega +\mu +\delta - \delta \widehat{\zeta }_3(\omega ))=0, \end{aligned}$$

(34)

where $\widehat{\zeta }_1( \omega )$, $\widehat{\zeta }_2( \omega )$ and $\widehat{\zeta }_3( \omega )$ are the Laplace transform of the functions $\varphi \phi _1$, $\vartheta \phi _2$ and $\psi \phi _1$, respectively. Thus, Eq. (34) can be rewritten as follows:

$$\begin{aligned} H(\omega )= \frac{\omega +\mu }{\omega +\mu +J^*}S^* \widehat{\zeta }_1(\omega ) \widehat{\zeta }_2(\omega ) + \frac{\delta }{\omega +\mu +\delta } \widehat{\zeta }_3(\omega )=1. \end{aligned}$$

(35)

It is clearly to see that if $\mathcal {R}_0>1$, then we have

$$\begin{aligned} H(0)= \frac{1- \tilde{\zeta }_3 }{1 + \frac{\mathcal {R}_0 -1}{1-\tilde{\zeta }_3}} + \tilde{\zeta }_3 <1. \end{aligned}$$

(36)

Assume that the equation $H(\omega )=1$ has a complex root $\omega$ such that $\text {Re} (\omega )\ge 0$. Then, by taking the real part of Eq. (35), we have

$$\begin{aligned} 1= \text {Re} H(\omega ) \le H(\text {Re} (\omega )) \le H(0); \end{aligned}$$

which goes against the inequality (36), and this contradicts the assumption of $\mathcal {R}_0>1$. Consequently, any eigenvalue $\omega$ of $H(\omega ) = 1$ has a negative real part, if $\mathcal {R}_0 > 1$. Therefore, the endemic equilibrium $E^*$ is considered to be locally asymptotically stable, if $\mathcal {R}_0>1$. This completes the proof. $\square$

Remark 3.8

Biologically speaking, Theorem 3.2 and Theorem 3.7 imply that the disease can be eliminated from the community when the basic reproduction number $\mathcal {R}_0<1$; while the disease will be able to start spreading through a population when $\mathcal {R}_0>1$, if the initial sizes of the populations of the model are in the basin of attraction of the equilibria $E^0$ and $E^*$, respectively. However, to ensure that the elimination or spreading of the disease is independent of the initial sizes of the populations, it is necessary to show that the equilibria $E^0$ and $E^*$ are globally asymptotically stable, respectively (see, Theorem 6.1 and Theorem 6.6 obtained below).

4 Existence of compact global attractor

In this section, we will show that the semi-flow generated by system (1)–(3) admits a compact global attractor, which is necessary to study the attractivity of the endemic equilibrium in Sect. 6. According to the approach presented in the monograph of Hale [40, Chapter 3], the existence of the global attractor is established with the help of the following

Lemma 4.1

[40, Theorem 3.4.6] If $T(t) \,: \, X\rightarrow X$, $t \in \mathbb {R}_+$ is asymptotically smooth, point dissipative and orbits of bounded sets are bounded, then there exists a global attractor.

One can observe that the second and third statements of Lemma 4.1 are obtained directly by Proposition 2.1. Then, to derive the first statement of Lemma 4.1 (i.e., asymptotic smoothness of the semi-flow $\Phi$ ), we will use the following

Lemma 4.2

[40, Lemma 3.2.3] For each $t\in \mathbb {R}_+$, suppose $T(t) = S(t) + U(t) \,: \, X \rightarrow X$ has the property that U(t) is completely continuous and there is a continuous function $k: \, \mathbb {R}_+ \times \mathbb {R}_+ \rightarrow \mathbb {R}_+$ such that $k(t, r) \rightarrow 0$ as $t \rightarrow \infty$, and $\vert S(t)x \vert \le k(t, r)$ if $\vert x \vert < r$. Then, T(t), $t\in \mathbb {R}_+$, is asymptotically smooth.

Before we proceed, it is necessary to state some essential ingredients. Firstly, by applying the characteristic method [26, Chapter 1], we can solve the second and third first-order hyperbolic partial differential equations of system (1) with boundary condition (2) and initial condition (3) along the characteristic lines $t - a = const$, and $t-b=const$, respectively, as follows:

$$\begin{aligned} e(t,a) = \left\{ \begin{array}{ll} S(t-a) J(t-a)\phi _1(a), &{} \quad t >a, \\ e_0(a-t)\displaystyle \frac{\phi _1(a)}{\phi _1(a-t)}, &{} \quad t \le a, \end{array} \right. \end{aligned}$$

(37)

and

$$\begin{aligned} i(t,b) = \left\{ \begin{array}{ll} W(t-b) \phi _2(b), &{} \quad t > b, \\ i_0(b-t) \displaystyle \frac{\phi _2(b)}{\phi _2(b-t)}, &{} \quad t \le b. \end{array} \right. \end{aligned}$$

(38)

Furthemorer, we introduce the following proposition:

Proposition 4.3

The functions J(t) and W(t) given by (4) and (5), respectively, are Lipschitz continous on $\mathbb {R}_+$, with Lipschitz constants $L_J$ and $L_W$, respectively.

Now, based on the above preparations, we are able to state the main result of this section.

Theorem 4.4

Assume $\mathcal {R}_0>1$. Then, there exists a global attractor $\textbf{A}$ for the solution semi-flow $\Phi$ of system (1)–(3) in $\Gamma$.

Proof

To show the asymptotic smoothness of the semi-flow $\Phi$ defined by (6), we only need to apply Lemma 4.2. Specifically, for each $t\in \mathbb {R}_+$ and $x_0 \in \Gamma$, we define $\Phi _1$ and $\Phi _2$ by

$$\begin{aligned} \Phi _1(t,x_0) = (S(t), \tilde{e}(t, \cdot ), \tilde{i}(t, \cdot ), R(t) ), \quad \text {and} \quad \Phi _2(t,x_0) =(0, \widehat{e}(t, \cdot ), \widehat{i}(t, \cdot ), 0 ), \end{aligned}$$

where

$$\begin{aligned}{} & {} \widehat{e}(t,a)= \left\{ \begin{array}{ll} 0, &{} \quad t> a, \\ e_0(a-t)\frac{\phi _1(a)}{\phi _1(a-t)}, &{} \quad t \le a, \end{array} \right. \end{aligned}$$

(39)

$$\begin{aligned}{} & {} \widehat{i}(t,b)= \left\{ \begin{array}{ll} 0, &{} \quad t > b, \\ i_0(b-t)\frac{\phi _2(b)}{\phi _2(b-t)}, &{} \quad t \le b, \end{array} \right. \end{aligned}$$

(40)

and

$$\begin{aligned} \tilde{e}(t,a)= & {} e(t,a) - \widehat{e}(t,a) = \left\{ \begin{array}{ll} S(t-a)J(t-a) \phi _1(a), &{} \quad t> a, \\ 0, &{} \quad t \le a, \end{array} \right. \end{aligned}$$

(41)

$$\begin{aligned} \tilde{i}(t,b)= & {} i(t,b) - \widehat{i}(t,b)= \left\{ \begin{array}{ll} W(t-b) \phi _2(b), &{} \quad t > b, \qquad \qquad \qquad \\ 0, &{} \quad t \le b, \end{array} \right. \end{aligned}$$

(42)

where J(t) and W(t) are given by (4) and (5), respectively. Then, we have $\Phi =\Phi _1 + \Phi _2$ and it is clearly to observe that $\widehat{e}$, $\widehat{i}$, $\tilde{e}$ and $\tilde{i}$ are nonnegatives. By using (39) and (40), we could find

$$\begin{aligned} \Vert \Phi _2(t,x_0) \Vert _X= & {} \Vert \widehat{e}(t,\cdot ) \Vert _1 + \Vert \widehat{i}(t,\cdot ) \Vert _1 \\= & {} \int \limits _{t}^{\infty } e_0(a-t) \frac{\phi _1(a)}{\phi _1(a-t)}\text {d} a + \int \limits _{t}^{\infty } i_0(b-t) \frac{\phi _2 (b)}{\phi _2(b-t)}\text {d} b \\= & {} \int \limits _{0}^{\infty } e_0(a) \frac{\phi _1(a+t)}{\phi _1(a)}\text {d} a+ \int \limits _{0}^{\infty } i_0(b) \frac{\phi _2(b+t)}{\phi _2(b)}\text {d} b \\\le & {} \Vert e_0 \Vert _1 e^{- \underline{p}_1 t } + \Vert i_0 \Vert _1 e^{- \underline{p}_2 t } \\\le & {} e^{- p_0 t } \Vert x_0\Vert _X, \quad t \ge 0, \end{aligned}$$

where $p_0= \min \{ \underline{p}_1, \underline{p}_2 \}$, which means that the assumption on $\Phi _2$ stated in Lemma 4.2 is satisfied. Next, we show that $\Phi _1$ is completely continuous. Let $t\in \mathbb {R}_+$ and $E \subseteq \Gamma$ be a bounded set. Define

$$\begin{aligned} \Gamma _t = \left\{ \Phi _1(t,x_0) \; \vert \quad x_0\in E \right\} . \end{aligned}$$

To claim that $\Phi _1$ is completely continuous, it suffices to show that $\Gamma _t$ is precompact set. To to this, it is enough to prove that

$$\begin{aligned} \Gamma _t (e,i)= \left\{ (\tilde{e}(t,\cdot ), \tilde{i}(t,\cdot )) \; \vert \; (S(t), \tilde{e}(t,\cdot ), \tilde{i}(t,\cdot ), R(t)) \in \Gamma _t \right\} \end{aligned}$$

is precompact set with the help of Fréchet–Kolmogrov Theorem [41, Page 275] in Yosida’s monograph. So, from the definitions of $\Phi _1$ and $\Gamma$, it follows that $\Gamma _{t}(e,i)$ is bounded. Therefore, the first condition stated in the Fréchet–Kolmogrov Theorem is satisfied. Moreover, according to (41) and (42), it is obvious to see that

$$\begin{aligned} \int \limits _{t}^{\infty } \tilde{e}(t,a) \text {d} a = \int \limits _{t}^{\infty } \tilde{i}(t,b)\text {d} b =0, \quad \text {for all } a,b \ge t, \end{aligned}$$

which implies the third condition stated also satisfied. Lastly, we need to verify the second condition of the Fréchet–Kolmogrov Theorem. This involves to show that

$$\begin{aligned} \lim _{h \rightarrow 0} \big \Vert \tilde{e}(t,\cdot +h) - \tilde{e}(t,\cdot ) \big \Vert _1 =0, \end{aligned}$$

(43)

and

$$\begin{aligned} \lim _{h \rightarrow 0} \big \Vert \tilde{i}(t,\cdot +h) - \tilde{i}(t,\cdot ) \big \Vert _1 =0, \end{aligned}$$

(44)

uniformly in $\Gamma _{t}(e,i)$. So, according to (42) we have $\tilde{i}(0, \cdot ) = 0$. Thus, the expression (44) is automatically satisfied when $t = 0$. Assume $t > 0$ and $h \in (0, t)$. Then, from (42), we have

$$\begin{aligned} \big \Vert \tilde{i}(t,\cdot +h) - \tilde{i}(t,\cdot ) \big \Vert _1= & {} \int \limits _{0}^{\infty } \big \vert \tilde{i}(t, b+h) - \tilde{i}(t,b) \big \vert \text {d} b \\= & {} \int \limits _{0}^{t-h} \big \vert W(t-b-h)\phi _2(b+h) -W(t-b) \phi _2(b) \big \vert \text {d} b \\{} & {} \quad + \int \limits _{t-h}^{h} W(t-b) \phi _2(b) \text {d} b \\\le & {} \ell _1+\ell _2+\ell _3. \end{aligned}$$

Then, in view of Proposition 2.2, it follows

$$\begin{aligned} \ell _1= & {} \int \limits _{0}^{t-h} W(t-b-h) \big \vert \phi _2(b+h) - \phi _2(b) \big \vert \text {d} b \nonumber \\\le & {} (\overline{\varphi } + \delta ) \eta \int \limits _{0}^{t-h} \big \vert \phi _2(b+h) - \phi _2(b) \big \vert \text {d} b \nonumber \\= & {} (\overline{\varphi } + \delta ) \eta \left( \int \limits _{0}^{t-h} \phi _2(b) \text {d} b - \int \limits _{0}^{t-h} \phi _2(b+h) \text {d} b \right) \nonumber \\= & {} (\overline{\varphi } + \delta ) \eta \left( \int \limits _{0}^{h} \phi _2(b) \text {d} b - \int \limits _{t-h}^{t} \phi _2(b) \text {d} b \right) \nonumber \\\le & {} (\overline{\varphi } + \delta ) \eta h. \end{aligned}$$

(45)

Next, with the help of Proposition 4.3, we obtain

$$\begin{aligned} \ell _2= & {} \int \limits _{0}^{t-h} \big \vert W(t-b-h) -W(t-b) \big \vert \phi _2(b) \text {d} b \nonumber \\\le & {} L_W h \int \limits _{0}^{t-h} \phi _2(b) \text {d} b \nonumber \\\le & {} \frac{L_W }{\underline{p}_2}h, \end{aligned}$$

(46)

where we have used W(t) is Lipschitz function with constant $L_W$. Further, we have

$$\begin{aligned} \ell _3 = \int \limits _{t-h}^{h} W(t-b) \phi _2(b) \text {d} b \le (\overline{\varphi } + \delta ) \eta h. \end{aligned}$$

(47)

In summary, by collecting the inequalities (45), (46) and (47), we get

$$\begin{aligned} \big \Vert \tilde{i}(t,\cdot +h) - \tilde{i}(t,\cdot ) \big \Vert _1 \le C_i h, \quad C_i= 2(\overline{\varphi }+ \delta ) \eta + L_W/ \underline{p}_2, \end{aligned}$$

which implies that (44) is satisfied. Similarly, by repeating the same calculations as above, we could get

$$\begin{aligned} \big \Vert \tilde{e}(t,\cdot +h) - \tilde{e}(t,\cdot ) \big \Vert _1 \le C_e h, \quad C_e= 2\overline{\vartheta } \eta ^2 + \eta (\overline{\vartheta }L_S + L_J)/\underline{p}_1. \end{aligned}$$

(48)

Thus, Eq. (43) is also satisfied. This completes the proof of Theorem 4.4. $\square$

5 Uniform persistence

This section aims to show that system (1)–(3) is uniformly persistent whenever $\mathcal {R}_0>1$ by using the approach developed in [42, Chapter 9]. Before going further, for the sake of convenience, we consider the function $\mathcal {H}\,: \, \mathbb {R}_+ \rightarrow \mathbb {R}$, and denote

$$\begin{aligned} \mathcal {H}_\infty = \liminf _{t \rightarrow \infty } \mathcal {H}(t), \quad \text {and} \quad \mathcal {H}^\infty = \limsup _{t \rightarrow \infty } \mathcal {H}(t). \end{aligned}$$

Then, we state the following two Lemmas, which will assist in the discussion ahead.

Lemma 5.1

[43, Lemma 4.2] Let $\mathcal {H}\,: \, \mathbb {R}_+ \rightarrow \mathbb {R}$ be a bounded and continuously differentiable function. Then, there exist sequences $\{t_n\}$ and $\{r_n \}$ such that $t_n \rightarrow \infty$ and $r_n \rightarrow \infty$, $\mathcal {H}(t_n) \rightarrow \mathcal {H}_{\infty }$, $\mathcal {H}(r_n)\rightarrow \mathcal {H}^{\infty }$, $\mathcal {H}'(t_n)\rightarrow 0$, and $\mathcal {H}'(r_n) \rightarrow 0$ as $n \rightarrow \infty$.

Lemma 5.2

[38, Chapter 7] Suppose $\mathcal {H}\,: \, \mathbb {R}_+ \rightarrow \mathbb {R}$ is bounded function and $y\in L^{1}_{+}(0, +\infty )$. Then, we have

$$\begin{aligned} \limsup _{t \rightarrow \infty } \int \limits _{0}^{t} \mathcal {H}(\tau ) y(t-\tau ) \text {d} \tau \le \mathcal {H}^{\infty } \Vert y \Vert _1. \end{aligned}$$

Now, let us define the persistence function $\rho \,: \, \Gamma \rightarrow \mathbb {R}_+$, as follows

$$\begin{aligned} \rho (S, e(\cdot ), i(\cdot ), R) = \int \limits _{0}^{\infty } \vartheta (b) i(t,b)\text {d} b=J(t), \end{aligned}$$

which provides the infective force at time t. Furthermore, we set

$$\begin{aligned} \Gamma _0 = \left\{ x_0 \in \Gamma \, \left| \right. \text { There exists } t_0 \in \mathbb {R}_+ \text { such that } \rho (\Phi (t_0,x_0 )) >0 \right\} . \end{aligned}$$

Hence, it can be clearly seen that, for any $x_0 \in \Gamma {\setminus } \Gamma _0$, we have $\displaystyle \lim _{t \rightarrow \infty } \Phi (t, x_0) =E^0$. Moreover, let us introduce the following definition of the uniform persistence concept.

Definition 5.3

[42, Page 61] System (1)–(3) is said to be uniformly weakly $\rho$-persistent (respectively, uniformly strongly $\rho$-persistent) if there exists an $\varepsilon > 0$, independent of the initial condition, such that

$$\begin{aligned} \limsup _{t \rightarrow \infty } \rho (\Phi (t, x_0))>\varepsilon , \quad \left( \text {respectively } \liminf _{t \rightarrow \infty } \rho (\Phi (t, x_0)) >\varepsilon \right) , \end{aligned}$$

for any $x_0 \in \Gamma _0$.

Now we are in a position to state the following result:

Theorem 5.4

Assume $\mathcal {R}_0>1$. Then, system (1)–(3) is uniformly weakly $\rho$-persistent.

Proof

Since $\mathcal {R}_0>1$, there exists a small $\varepsilon _0>0$ such that

$$\begin{aligned} \varepsilon _1 \triangleq \frac{A}{\mu +\varepsilon _0} - \varepsilon _0>0, \end{aligned}$$

and

$$\begin{aligned} \varepsilon _2 \triangleq \varepsilon _1 \widehat{\zeta }_1(\varepsilon _0) \widehat{\zeta }_2(\varepsilon _0) + \frac{\delta }{\mu +\delta + \varepsilon _0 } \widehat{\zeta }_3(\varepsilon _0) >1. \end{aligned}$$

(49)

In what follows, by a way of contradiction, we will show that system (1)–(3) is uniformly weakly $\rho$-persistent. Otherwise, there exists $x_0 \in \Gamma _0$ such that

$$\begin{aligned} \limsup _{t \rightarrow \infty } \int \limits _{0}^{\infty } \vartheta (b) i(t,b)\text {d} b \le \frac{\varepsilon _0}{2}. \end{aligned}$$

(50)

Then, there exists $t_0 \ge 0$ such that

$$\begin{aligned} \int \limits _{0}^{\infty } \vartheta (b) i(t,b)\text {d} b \le \varepsilon _0, \quad \text { for all } t \ge t_0. \end{aligned}$$

(51)

Without loss of generality, we can assume that $t_0 = 0$ since we can replace the initial condition with $\Phi (t_0, x_0)$. Next, the first equation in (1) together with (51) provides

$$\begin{aligned} \frac{\text {d} S(t)}{\text {d} t} \ge A - (\mu + \varepsilon _0) S(t), \quad \text { for all } t \ge t_0=0. \end{aligned}$$

(52)

Thus, we have $S_\infty \ge \frac{A}{\mu + \varepsilon _0}$. Therefore, there exists $t_1\ge 0$ suc that

$$\begin{aligned} S(t) \ge \varepsilon _1, \quad \text { for all } t \ge t_1=0. \end{aligned}$$

(53)

Furthermore, the fourth equation of system (1) with (38), gives

$$\begin{aligned} \frac{\text {d} R(t)}{\text {d} t} \ge \int \limits _{0}^{t }\psi (b) \phi _2(b) W(t-b) \text {d} b - (\mu + \delta ) R(t). \end{aligned}$$

(54)

Then, by applying the Laplace transform on the inequality (54), we get

$$\begin{aligned} \lambda \widehat{R}(\lambda ) - R(0) \ge \widehat{\zeta }_3(\lambda ) \widehat{W}(\lambda ) - (\mu +\delta ) \widehat{R}(\lambda ), \end{aligned}$$

(55)

where $\widehat{\zeta }_3$, $\widehat{R}$, and $\widehat{W}$ are the Laplace transform of $\psi \phi _2$, R(t), and W(t), respectively. Hence, we have

$$\begin{aligned} \widehat{R}(\lambda ) \ge \frac{ \widehat{\zeta }_3(\lambda ) }{\lambda +\mu + \delta } \widehat{W}(\lambda ). \end{aligned}$$

(56)

Moreover, (5) together with (53) provides

$$\begin{aligned} W(t)\ge & {} \int \limits _{0}^{t} \varphi (a) \phi _1(a) S(t-a) J(t-a) \text {d} a + \delta R(t) \nonumber \\\ge & {} P(t) + \delta R(t), \end{aligned}$$

(57)

where

$$\begin{aligned} P(t)= \varepsilon _1 \int \limits _{0}^{t}\varphi (a) \phi _1(a) \int \limits _{0}^{t-a} \vartheta (b) \phi _2(b) W(t-a-b) \text {d} b \text {d} a. \end{aligned}$$

Now, by taking the Laplace transform again on both sides of (57), we find

$$\begin{aligned} \widehat{W}(\lambda ) \ge \widehat{P}(\lambda ) + \delta \widehat{R}(\lambda ), \end{aligned}$$

(58)

where $\widehat{W}$, $\widehat{P}$ and $\widehat{R}$ are the Laplace transform of W(t), P(t), and R(t), respectively, with

$$\begin{aligned} \widehat{P}(\lambda )= & {} \varepsilon _1 \int \limits _{0}^{\infty } e^{- \lambda t}\int \limits _{0}^{t } \varphi (a) \phi _1(a) \int \limits _{0}^{t-a} \vartheta (b) \phi _2(b) W(t-a-b) \text {d} b \text {d} a \text {d} t \\= & {} \varepsilon _1 \int \limits _{0}^{\infty } \varphi (a) \phi _1(a) e^{- \lambda a } \text {d} a \int \limits _{0}^{\infty }\vartheta (b) \phi _2(b) e^{- \lambda b} \text {d} b \int \limits _{0}^{\infty } W(\sigma ) e^{- \lambda \sigma }\text {d} \sigma . \end{aligned}$$

Thus, we have

$$\begin{aligned} \widehat{P}(\lambda ) = \varepsilon _1 \widehat{\zeta }_1(\lambda ) \widehat{\zeta }_2(\lambda ) \widehat{W}(\lambda ), \end{aligned}$$

(59)

where $\widehat{\zeta }_1$ and $\widehat{\zeta }_2$ are the Laplace transforms of $\varphi \phi _1$ and $\vartheta \phi _2$, respectively. Next, inserting (59) into (58) and using (56), it yields

$$\begin{aligned} \widehat{W}(\lambda ) \ge \left( \varepsilon _1 \widehat{\zeta }_1(\lambda ) \widehat{\zeta }_2(\lambda ) + \frac{\delta }{\lambda +\mu +\delta } \widehat{\zeta }_3(\lambda ) \right) \widehat{W}(\lambda ). \end{aligned}$$

(60)

Note that $\widehat{W}(\lambda )<+\infty$ because W(t) is bounded function; further, since $x_0\in \Gamma _0$, we have $\widehat{W}(\lambda )>0$ for all $\lambda >0$. Then, dividing both sides by $\widehat{W}(\lambda )$ and letting $\lambda \rightarrow \varepsilon _0$ in (60), we immediately obtain

$$\begin{aligned} 1 \ge \varepsilon _1 \widehat{\zeta }_1(\varepsilon _0) \widehat{\zeta }_2(\varepsilon _0) + \frac{\delta }{\varepsilon _0+\mu +\delta } \widehat{\zeta }_3(\varepsilon _0), \end{aligned}$$

which contradicts (49), and hence the proof is complete. $\square$

Now, in order to move from uniform weak persistence to uniform strong persistence, we follow the approach described in [42, Chapter 9], (see also, McCluskey [33, Section 8]). We consider total $\Phi$-trajectories of system (1)–(3) in space X, where $\Phi$ is a continuous semi-flow defined by (6). Let $\textbf{x}(t)\,:\, \mathbb {R} \rightarrow X$ be a total $\Phi$-trajectory such that $\textbf{x}(t)= (S(t), e(t, \cdot ), i(t, \cdot ), R(t))$, for all $t \in \mathbb {R}$. Then, it follows that $\textbf{x}(t+r)=\Phi (r, \textbf{x}(t))$ for all $t\in \mathbb {R}$, and all $r\in \mathbb {R}_+$. Hence, we have

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\text {d} S(t)}{\text {d} t}= A- \mu S(t) - S(t) \int \limits _{0}^{\infty } \vartheta (b) i(t,b)\text {d} b, &{} \\ e(t,a)= S(t-a) J(t-a) \phi _1(a), &{} \\ i(t,b) = W(t-b) \phi _2(b), &{} \\ J(t) = \displaystyle \int \limits _{0}^{\infty } \vartheta (b)W(t-b) \phi _2(b)\text {d} b, &{} \\ W(t) = \displaystyle \int \limits _{0}^{\infty }\varphi (a) S(t-a) J(t-a)\phi _1(a) \text {d} a+ \delta R(t), &{} \\ \displaystyle \frac{\text {d} R(t)}{\text {d} t}= \int \limits _{0}^{\infty } \psi (b) i(t,b)\text {d} b -(\delta + \mu )R(t), \end{array} \right. \end{aligned}$$

(61)

for all $t\in \mathbb {R}$, and $a,b \in \mathbb {R}_+$. Now, let us introduce the following lemmas which will be used later to show the uniform strong persistence result.

Lemma 5.5

Let $\textbf{x}(t)$ be a total trajectory in $\Gamma$ for all $t \in \mathbb {R}$. Then, the following statements hold: i. S(t) is strictly positive on $\mathbb {R}$; ii. if $\rho (\Phi (t))=0$ for all $t \le 0$, then $\rho (\Phi (t))=0$ for all $t \ge 0$.

Proof

• i. Firstly, we show that $S(t)>0$, for all $t\in \mathbb {R}$. By way of contradiction, suppose (i) is not true. Then, there exists a fixed $t^*\in \mathbb {R}$ such that $S(t^*)=0$. Therefore, from (61) we have $\frac{\text {d} S(t^*)}{\text {d} t}=A>0$. Hence, by the continuity of S(t), there exists a sufficiently small $\epsilon >0$ such that $S(t^*- \epsilon ) < 0$, which contradicts $S(t)\in \Gamma$. Thus, S(t) is strictly positive on $\mathbb {R}$.

• ii. Assume that $J(t) = 0$, for all $t\le 0$. Then, from fourth to fifth equations of system (61), it yields that $R(t) \le 0$, for all $t\le 0$. This together with last equation of system (61) provides

  $$\begin{aligned} R(t)=0, \quad \text {for all } t \in \mathbb {R}. \end{aligned}$$

  (62)

  From fourth to fifth equations in system (61), we can obtain

  $$\begin{aligned} J(t) = \int \limits _{0}^{\infty } \vartheta (b) \phi _2(b) \int \limits _{0}^{\infty } \varphi (a) \phi _1(a) S(t-a-b) J(t-a-b) \text {d} a \text {d} b + F(t), \end{aligned}$$

  (63)

  where

  $$\begin{aligned} F(t)= \delta \int \limits _{0}^{\infty } \vartheta (b) \phi _2(b) R(t-b) \text {d} b. \end{aligned}$$

  By changing the variables, we can rewrite (63) as follows:

  $$\begin{aligned} J(t)= & {} \int \limits _{-\infty }^{t} \vartheta (t-\sigma ) \phi _2(t-\sigma ) \int \limits _{0}^{\infty } \varphi (a) \phi _1(a) S(\sigma - a) J(\sigma -a) \text {d} a \text {d} \sigma +F(t) \\= & {} \int \limits _{-\infty }^{t} \vartheta (t-\sigma ) \phi _2(t-\sigma ) \int \limits _{-\infty }^{\sigma } \varphi (\sigma -\upsilon ) \phi _1(\sigma -\upsilon ) S(\upsilon ) J(\upsilon ) \text {d} \upsilon \text {d} \sigma +F(t). \end{aligned}$$

  Here, if $J(t)=0$, for all $t\le 0$, it can be deduced from Eq. (62) that $F(t)=0$, for all $t \in \mathbb {R}$; in addition, with the help of Proposition 2.1, we obtain

  $$\begin{aligned} J(t) \le \overline{\vartheta } \eta \int \limits _{0}^{t} \int \limits _{0}^{\sigma }J(\upsilon ) \text {d} \upsilon d \sigma , \quad \text { for all } t\ge 0. \end{aligned}$$

  (64)

  Next, denote

  $$\begin{aligned} \mathcal {B}(t) = \int \limits _{0}^{t} J(\upsilon )\text {d} \upsilon + \int \limits _{0}^{t} \int \limits _{0}^{\sigma }J(\upsilon ) \text {d} \upsilon \text {d} \sigma , \quad \text {for all } t\ge 0. \end{aligned}$$

  Thus, we have

  $$\begin{aligned} \frac{\text {d} \mathcal {B}(t)}{\text {d} t}= & {} J(t) + \int \limits _{0}^{t} J(\upsilon )\text {d} \upsilon \\\le & {} \overline{\vartheta } \eta \int \limits _{0}^{t} \int \limits _{0}^{\sigma }J(\upsilon ) \text {d} \upsilon \text {d} \sigma + \int \limits _{0}^{t} J(\upsilon )\text {d} \upsilon \\\le & {} \gamma \mathcal {B}(t), \end{aligned}$$

  where $\gamma =\max \left\{ \overline{\vartheta } \eta ,1\right\}$. Hence, we get $\mathcal {B}(t) \le \mathcal {B}(0)e^{\gamma t}$, for all $t\ge 0$. Notice that since $\mathcal {B}(0)=0$, it results then $\mathcal {B}(t)=0$, for all $t\ge 0$, and hence $J(t)=0$, for all $t\ge 0$. Proof is complete. $\square$

Lemma 5.6

Let $\textbf{x}(t)$ be a total trajectory in $\Gamma$ for all $t \in \mathbb {R}$. Then, $\rho (\Phi (t))$ is either strictly positive or identical to zero on $\mathbb {R}$.

Proof

Note that, for any $t^* \in \mathbb {R}$, with the help of Lemma 5.5, we may observe $J(t)=0$ for all $t\ge t^*$, if $J(t)=0$ for all $t\le t^*$. This means that either

i.:

J(t) is identically zero on $\mathbb {R}$; or

ii.:

there exists a decreasing sequence $\{t_n\}_{n \ge 1}$ such that $t_n \rightarrow -\infty$ as $n \rightarrow \infty$ and $J(t_n) >0$.

For the second statement (ii.), let us denote

$$\begin{aligned} J_n(t)= J(t+t_n), \quad \text {for all } t \ge 0. \end{aligned}$$

(65)

From (4) we have

$$\begin{aligned} J_n(t) = \int \limits _{0}^{t} \vartheta (b) \phi _2(b) W_n(t-b) \text {d} b + \tilde{J}_n(t), \end{aligned}$$

(66)

where

$$\begin{aligned} \tilde{J}_n(t)= & {} \int \limits _{t}^{\infty }\vartheta (b) i_{0n}(t-b) \frac{\phi _2(b)}{\phi _2(t-b)}\text {d} b \nonumber \\= & {} \int \limits _{0}^{\infty } \vartheta (t+b) i_{0n}(b) \frac{\phi _2(t+b)}{\phi _2(b)}\text {d} b, \end{aligned}$$

(67)

Moreover, in view of (5) it yields

$$\begin{aligned} W_n(t)= & {} \int \limits _{0}^{t} \varphi (a) \phi _1(a) S_n(t-a) J_n(t-a) \text {d} a +\delta R_n(t) + \tilde{W}_n(t) \nonumber \\\ge & {} \int \limits _{0}^{t} \varphi (a) \phi _1(a) S_n(t-a) J_n(t-a) \text {d} a, \end{aligned}$$

(68)

where

$$\begin{aligned} \tilde{W}_n(t)=\int \limits _{t}^{\infty } \varphi (a) e_{0n}(t-a) \frac{\phi _1(a)}{\phi _1(t-a)}\text {d} a. \end{aligned}$$

Next, combining (66) and (68), we find

$$\begin{aligned} J_n(t) \ge \int \limits _{0}^{t} \vartheta (b) \phi _2(b) \int \limits _{0}^{t-b}\varphi (a) \phi _1(a) S_n(t-a-b) J_n(t-a-b) \text {d} a \text {d} b +\tilde{J}_n(t). \end{aligned}$$

Denote $\displaystyle \inf _{t\in \mathbb {R}}S(t)=\underline{S}$. Then, after making some changes of variables, we can get

$$\begin{aligned} J_n(t)\ge & {} \underline{S} \int \limits _{0}^{t} \vartheta (t-\sigma ) \phi _2(t-\sigma ) \int \limits _{0}^{\sigma }\varphi (a) \phi _1(a) J_n(\sigma -a) \text {d} a \text {d} \sigma +\tilde{J}_n(t) \\= & {} \underline{S} \int \limits _{0}^{t} \vartheta (t-\sigma ) \phi _2(t-\sigma ) \int \limits _{0}^{\sigma }\varphi (\sigma - \upsilon ) \phi _1(\sigma - \upsilon ) J_n(\upsilon ) \text {d} \upsilon \text {d} \sigma +\tilde{J}_n(t) \\= & {} \underline{S} \int \limits _{0}^{t} \left( \int \limits _{0}^{t-\upsilon } \vartheta (t-\upsilon -s) \phi _2(t-\upsilon -s) \varphi (s) \phi _1(s) ds \right) J_n(\upsilon ) \text {d} \upsilon +\tilde{J}_n(t). \end{aligned}$$

Therefore, we have

$$\begin{aligned} J_n(t)\ge & {} \int \limits _{0}^{t}\gamma (t-\upsilon ) J_n(\upsilon ) \text {d} \upsilon + \tilde{J}_n(t) \\= & {} \int \limits _{0}^{t}\gamma (\upsilon ) J_n(t-\upsilon ) \text {d} \upsilon + \tilde{J}_n(t), \end{aligned}$$

where

$$\begin{aligned} \gamma (t) = \underline{S} \int \limits _{0}^{t} \vartheta (t-s) \phi _2(t-s) \varphi (s) \phi _1(s)ds, \quad t\ge 0. \end{aligned}$$

Note that from (66) to (67), we have $\tilde{J}_n(0)= J(t_n)>0$, and $\tilde{J}_n$ is a continuous function at 0. By applying the result described in the monograph of Smith and Thiem [42, Corollary B.6], we can show that there is a positive constant $\xi > 0$ that depends only on the function $\gamma (t)$, such that $J_n(t) > 0$ for all $t > \xi$. Furthermore, using the definition of $J_n(t)$ given by (65), we can easily see that $J(t) > 0$ for all $t > \xi +t_n$. Since $t_n \rightarrow -\infty$ as $n\rightarrow \infty$, it follows that $J(t)>0$ for all $t\in \mathbb {R}$. Consequently, J(t) is strictly positive on $\mathbb {R}$. This proves Lemma 5.6. $\square$

Now, based on the above preparations, we will state the main result of this section.

Theorem 5.7

Assume $\mathcal {R}_0>1$. Then, system (1)–(3) is uniformly strongly $\rho$-persistent.

Proof

In view of Theorem 4.4, the semi-flow $\Phi$ generated by system (1)–(3) has a global compact attractor $\textbf{A}$. Additionally, when $\mathcal {R}_0>1$, Theorem 5.4 shows that system (1)–(3) is uniformly weakly $\rho$-persistence. This combined with Lemma 5.5, Lemma 5.6, and [42, Theorem 5.2] leads immediately to conclude that system (1)–(3) is uniformly strongly $\rho$-persistence. $\square$

Next, in accordance with [42, Theorem 5.7], we introduce the following

Theorem 5.8

There exists a compact attractor $\mathbf{\tilde{A}}$ that attracts every solution with initial condition in $\Gamma _0$. Moreover $\mathbf{\tilde{A}}$ is uniformly $\rho$-positive, i.e., there exists a positive constant $\varpi$, such that

$$\begin{aligned} \rho (\Phi (t, x_0) \ge \varpi , \quad \text {for all } x_0 \in \mathbf{\tilde{A}}. \end{aligned}$$

(69)

Remark 5.9

In epidemiology, the uniform persistence concept means, roughly speaking, that the proportion of infected individuals is bounded away from 0 and the bound does not depend on the initial condition after a sufficient long time, if the basic reproduction number is larger than unity.

6 Global stability

In this section, we will discuss the main results of this paper. Firstly, we will start by studying the global stability of the disease-free equilibrium $E^0$ of system (1)–(3) with the help of the Fluctuation Lemma 5.1. To this end, let us state the following result:

Theorem 6.1

Assume $\mathcal {R}_0<1$. Then, the disease-free equilibrium $E^0$ of system (1)–(3) is globally asymptotically stable in $\Gamma$.

Proof

By Theorem 3.2, we only need to get the global attractivity of $E^0$. Let $(S,e(t,\cdot ),i(t, \cdot ), R)$ be a solution of system (1)–(3), with the initial condition $(S_0, e_0, i_0,R_0)$ in $\Gamma$. We first claim that $W^\infty = J^\infty = R^\infty = 0$, which means that

$$\begin{aligned} \displaystyle \limsup _{t \rightarrow \infty } W(t) = \displaystyle \limsup _{t \rightarrow \infty } J(t) = \displaystyle \limsup _{t \rightarrow \infty } R(t)=0.\end{aligned}$$

In view of Lemma 5.1, there exists a sequence $\{t_n \}$ such that $t_n \rightarrow \infty$, $R(t_n) \rightarrow R^\infty$ and $\frac{\text {d} R(t_n)}{\text {d} t} \rightarrow 0$ as $n \rightarrow \infty$. Last equation of system (1) with (38) gives

$$\begin{aligned} \frac{\text {d} R(t_n)}{\text {d} t}= & {} \int \limits _{0}^{t_n} \psi (b) \phi _2(b) W(t_n-b) \text {d} b + \int \limits _{t_n}^{\infty } \psi (b) i_0(b-t_n) \frac{\phi _2(b)}{\phi _2(b-t_n)} \text {d} b - (\mu + \delta ) R(t_n) \\\le & {} \int \limits _{0}^{t_n} \psi (b) \phi _2(b) W(t_n-b) \text {d} b + \overline{\psi } \Vert i_0 \Vert _1 e^{- \underline{p}_2 t_n} - (\mu +\delta ) R(t_n). \end{aligned}$$

Passing to the limite as $n \rightarrow \infty$ and by using Lemma 5.2, we find

$$\begin{aligned} 0 \le \zeta _3 W^\infty -(\mu +\delta ) R^\infty , \end{aligned}$$

which implies

$$\begin{aligned} R^\infty \le \frac{\zeta _3}{\mu +\delta } W^\infty . \end{aligned}$$

(70)

Moreover, from (4) to (38), we can write

$$\begin{aligned} J(t)= & {} \int \limits _{0}^{t}\vartheta (b) \phi _2(b) W(t-b) \text {d} b + \int \limits _{t}^{\infty } \vartheta (b) i_0(b-t) \frac{\phi _2(b)}{\phi _2(b-t)}\text {d} b \\\le & {} \int \limits _{0}^{t}\vartheta (b) \phi _2(b) W(t-b) \text {d} b + \overline{\vartheta } \Vert i_0 \Vert _1 e^{- \underline{p}_2 t }. \end{aligned}$$

With the help of Lemma 5.2 again, it results

$$\begin{aligned} J^\infty \le \zeta _2 W^\infty . \end{aligned}$$

(71)

Furthermore, the formula of W(t) in (5) with (37) provides

$$\begin{aligned} W(t)= & {} \int \limits _{0}^{t} \varphi (a) \phi _1(a) S(t-a) J(t-a) \text {d} a + \int \limits _{t}^{\infty } \varphi (a) e_0(a-t) \frac{\phi _1(a)}{\phi _1(a-t)}\text {d} a + \delta R(t) \\\le & {} \int \limits _{0}^{t} \varphi (a) \phi _1(a) S(t-a) J(t-a) \text {d} a + \overline{\varphi } \Vert e_0 \Vert _1 e^{-\underline{p}_1 t } + \delta R(t). \end{aligned}$$

According to Lemma 5.2, we can obtain

$$\begin{aligned} W^\infty \le S^0 \zeta _1 J^\infty + \delta R^\infty , \end{aligned}$$

(72)

where we have used $S^\infty \le S^0$. Now, by combining (70), (71) and (72), it yields

$$\begin{aligned} W^\infty \le \mathcal {R}_0 W^\infty . \end{aligned}$$

(73)

Due to $\mathcal {R}_0<1$, it follows immediately that $W^\infty =0$. This together with (70) and (71) leads to obtain $R^\infty =J^\infty =0$. Therefore, it can be deduced that

$$\begin{aligned} \limsup _{t \rightarrow \infty }\Vert e(t,\cdot ) \Vert _1 =0, \quad \limsup _{t \rightarrow \infty }\Vert i(t,\cdot ) \Vert _1 =0, \quad \text {and} \quad \limsup _{t \rightarrow \infty } R(t)= 0. \end{aligned}$$

Lastly, recall that $S^0=\frac{A}{\mu }$. Then, we move to show that $\displaystyle \limsup _{t \rightarrow \infty } S(t) =S^0$. To this end, it suffices to prove that $S^\infty \ge S^0$ since it is straightforward to observe that $S^\infty \le S^0$.

By Lemma 5.1, there exists a sequence $\{t_n \}$ such that $t_n \rightarrow \infty$, $S(t_n) \rightarrow S^\infty$ and $\frac{\text {d} S(t_n)}{\text {d} t} \rightarrow 0$ as $n \rightarrow \infty$. First equation of (1) together with (37) allows to write

$$\begin{aligned} \frac{\text {d} S(t_n)}{\text {d} t}= & {} A - \mu S(t_n) - S(t_n) \int \limits _{0}^{t_n} \vartheta (b) W(t_n- b)\phi _2(b)\text {d} b \\{} & {} \hspace{2.2cm} - S(t_n) \int \limits _{t_n}^{\infty } \vartheta (b) i_0(b-t_n) \frac{\phi _2(b)}{\phi _2(b-t_n)}\text {d} b \\\ge & {} A - \mu S(t_n) - S(t_n) \int \limits _{0}^{t_n} \vartheta (b) W(t_n- b)\phi _2(b) \text {d} b - S(t_n) \underline{\vartheta } \Vert i_0 \Vert _1 e^{-\underline{p}_2 t_n}. \end{aligned}$$

Letting $n \rightarrow \infty$ with the help of Lemma 5.2, we can obtain $0 \ge A - \mu S^\infty$, which implies that $S^\infty \ge S^0$, where we have used $W^\infty =0$. Therefore, based on the above discussion, we have derived the following conclusion

$$\begin{aligned}\displaystyle \limsup _{t\rightarrow \infty } \left( S(t), e(t,\cdot ), i(t, \cdot ), R(t) \right) =E^0.\end{aligned}$$

Thus, the proof is complete. $\square$

In what follows, based on the Lyapunov functionals technique and LaSalle invariance principle (we may refer to [44, 45], for more details), we will derive the global stability of the endemic equilibrium $E^*$ of system (1)–(3). Before going on, it is necessary define the function $g\,: \, (0, +\infty ) \longrightarrow \mathbb {R}_+$, as follows

$$\begin{aligned} g(x)= x-1-\ln x, \end{aligned}$$

(74)

which is a well-known ingredient to build the Lyapunov functional in Volterra–Lotka systems [46]. Note that $g'(x)= 1-\frac{1}{x}$. Therefore, the function g is decreasing on (0, 1], and increasing on $[1, +\infty )$, and it has only one extremum, which is a global minimum at $x=1$. Additionally, we have $1-x+\ln x \le 0$ for $x>0$, and the equality holds if and only if $x=1$.

The following lemma ensures the well definition of the constructive Lyapunov functional defined by (78).

Lemma 6.2

Consider $\mathcal {R}_0>1$. Let $\mathbf{{x}}(t)$ be a total trajectory in $\mathbf{\tilde{A}}$ for all $t \in \mathbb {R}$. Then, the following estimates hold:

$$\begin{aligned} S(t) \ge \varpi _1, \quad \frac{e(t,a)}{e^*(a)}\ge \frac{\varpi \varpi _1}{S^* J^*}, \quad \frac{i(t,b) }{i^*(b)} \ge \frac{ \varpi \varpi _1}{W^*} \zeta _1, \text { and } R(t) \ge \varpi _2, \end{aligned}$$

where $\varpi _1 = \frac{A}{\mu + \varpi }$, $\varpi _2= \frac{ \varpi \varpi _1 }{\mu + \delta } \zeta _1 \zeta _3$, and $\varpi$ is given in Theorem 5.8.

Proof

In view of (61) and by using (69), we obtain

$$\begin{aligned} \frac{\text {d} S(t)}{\text {d} t} \ge A -(\mu + \varpi )S(t), \end{aligned}$$

which means that $\displaystyle \liminf _{t \rightarrow \infty }S(t) \ge \frac{A}{\mu +\varpi }=\varpi _1$, for each point in $\mathbf{\tilde{A}}$. Thus, by invariance, we get

$$\begin{aligned} S(t) \ge \varpi _1, \text { for all } t \in \mathbb {R}. \end{aligned}$$

(75)

Moreover, we have $e(t,a)= S(t-a) J(t-a)\phi _1(a)$. Then, according to (69) and (75), we can write

$$\begin{aligned} \frac{e(t,a)}{e^*(a)} = \frac{S(t-a) J(t-a)}{S^* J^*}\ge \frac{\varpi \varpi _1}{S^* J^*}, \quad \text {for all } t \in \mathbb {R}. \end{aligned}$$

(76)

Next, we have $i(t,b) = W(t-b)\phi _2(b)$, for all $t \in \mathbb {R}$, where

$$\begin{aligned} W(t) = \int \limits _{0}^{\infty } \varphi (a) S(t-a) J(t-a) \text {d} a + \delta R(t) \ge \varpi \varpi _1 \zeta _1, \end{aligned}$$

and hence, we have

$$\begin{aligned} \frac{i(t,b) }{i^*(b)} = \frac{W(t)}{W^*} \ge \frac{ \varpi \varpi _1}{W^*} \zeta _1, \quad \text {for all } t \in \mathbb {R}. \end{aligned}$$

(77)

Finally, from equation of R in (61) and with the help of (77), we find

$$\begin{aligned} \frac{\text {d} R(t)}{\text {d} t}= & {} \int \limits _{0}^{\infty }\psi (b) i(t,b)\text {d} b -(\mu +\delta ) R(t) \\= & {} \int \limits _{0}^{\infty }\psi (b) \phi _2(b) W(t-b)\text {d} b -(\mu +\delta ) R(t) \\\ge & {} \varpi \varpi _1 \zeta _1 \zeta _3 - (\mu +\delta ) R(t). \end{aligned}$$

Hence, we have $\displaystyle R_{\infty } \ge \frac{ \varpi \varpi _1}{\mu + \delta } \zeta _1 \zeta _3=\varpi _2$. Therefore, we have

$$\begin{aligned} R(t) \ge \varpi _2, \quad \text {for all } t \in \mathbb {R}. \end{aligned}$$

The proof of Lemma 6.2 is complete for all $t \in \mathbb {R}$. The proof is complete. $\square$

Furthermore, some straightforward lemmas are summarized below, which will be used in proving Theorem 6.6.

Lemma 6.3

Each solution of system (1)–(3) satisfies

$$\begin{aligned} \int \limits _{0}^{\infty } \vartheta (b) i^*(b) \left[ \frac{S(t) i(t,b) e^*(0) }{S^* i^*(b)e(t,0) }-1\right] \text {d} b=0. \end{aligned}$$

Lemma 6.4

Set $\delta ^*= \frac{\delta }{(\mu +\delta ) \zeta _1 S^*}$. Then, we have

$$\begin{aligned} \int \limits _{0}^{\infty } \left[ \vartheta (b) +\delta ^* \psi (b) \right] i^*(b) \text {d} b = \frac{i^*(0)}{\zeta _1 S^*}. \end{aligned}$$

Lemma 6.5

Each solution of system (1)–(3) satisfies

$$\begin{aligned} \frac{1 }{\zeta _1 S^* } \int \limits _{0}^{\infty } \varphi (a) e^*(a) \left[ \frac{e(t,a) i^*(0) }{ i(t,0) e^*(a)} -1 \right] \text {d} a + \delta ^* \int \limits _{0}^{\infty } \psi (b) i^*(b) \left[ \frac{R(t)i^*(0)}{R^* i(t,0)}-1 \right] \text {d} b =0. \end{aligned}$$

After setting the above preparations, we are about to show the global asymptotic stability of the endemic equilibrium $E^*$.

Theorem 6.6

Assume $\mathcal {R}_0>1$. Then, the endemic equilibrium $E^*$ of system (1)–(3) is globally asymptotically stable.

Proof

By Theorem 3.7, $E^*$ is locally asymptotically stable and there exists a global attractor $\mathbf{\tilde{A}} \in \Gamma$. Hence, our aim is showing $\mathbf{\tilde{A}} = \{ E^*\}$. Let $\textbf{x}(t)=(S(t), e(t, \cdot ), i(t, \cdot ), R(t))$ be a total $\Phi$-trajectory in $\mathbf{\tilde{A}}$ for all $t\in \mathbb {R}$. By Lemma 6.2, there exists $\varpi _0$ such that $0 \le g(x) \le \varpi _0$ with x being any of $\frac{S(t)}{S^*}$, $\frac{e(t,a)}{e^*(a)}$, $\frac{i(t,b) }{i^*(b)}$, and $\frac{R(t)}{R^*}$, for any $t\in \mathbb {R}$ and $a \in \mathbb {R}_+$.

Define

$$\begin{aligned} V(t)= V_1(t) + V_2(t) + V_3 (t) + V_4(t), \end{aligned}$$

(78)

where

$$\begin{aligned} V_1(t)= & {} g\left( \frac{S(t)}{S^*}\right) , \\ V_2(t)= & {} \frac{1}{\zeta _1 S^*} \int \limits _{0}^{\infty } \upsilon _1(a) e^*(a) g \left( \frac{e(t,a)}{e^*(a)}\right) \text {d} a, \\ V_3(t)= & {} \int \limits _{0}^{\infty } \upsilon _2(b) i^*(b) g \left( \frac{i(t,b) }{i^*(b)}\right) \text {d} b, \\ V_4(t)= & {} \delta ^* R^* g \left( \frac{R(t)}{R^*}\right) , \end{aligned}$$

with

$$\begin{aligned} \upsilon _1(a) = \int \limits _{a}^{\infty } \varphi (\sigma ) e^{- \int \limits _{a}^{\sigma } p_1(s) ds} \text {d} \sigma , \quad \text {and} \quad \upsilon _2(b) = \int \limits _{b}^{\infty } \left[ \vartheta (\sigma ) +\delta ^* \psi (\sigma ) \right] e^{- \int \limits _{b}^{\sigma } p_2(s) ds} \text {d} \sigma , \end{aligned}$$

where $\delta ^*$ is given in Lemma 6.4. Note that for all $a,b \in \mathbb {R}_{+}$, we have

$$\begin{aligned} \left\{ \begin{array}{ll} \upsilon _1(0)=\zeta _1, &{} \\ \upsilon _2(0)= \zeta _2 +\delta ^* \zeta _3, &{} \\ \upsilon '_1(a)= p_1(a) \upsilon _1(a) - \varphi (a), &{} \\ \upsilon '_2(b)= p_2(b) \upsilon _2(b)- [\vartheta (b)+\delta ^* \psi (b)].&{} \end{array} \right. \end{aligned}$$

(79)

Now, we move to show that $\frac{\text {d} V(t)}{\text {d} t}$ is nonnegative. Here, we will independently calculate the derivatives $\frac{\text {d} V_1}{\text {d} t}$, $\frac{\text {d} V_2}{\text {d} t}$, $\frac{\text {d} V_3}{\text {d} t}$, and $\frac{\text {d} V_4}{\text {d} t}$, then we collect them all up. Firstly, by differentiating $V_1$ along the solution of system (1)–(3), we obtain

$$\begin{aligned} \frac{\text {d} V_1}{\text {d} t} = - \mu \frac{(S(t)-S^*)^2}{S(t) S^*} + \int \limits _{0}^{\infty } \vartheta (b) i^*(b) \left( 1- \frac{S^*}{S(t)} - \frac{S(t) i(t,b) }{S^* i^*(b)} + \frac{i(t,b) }{i^*(b)} \right) \text {d} b, \end{aligned}$$

where we have used $A= \mu S^* + S^* \displaystyle \int \limits _{0}^{\infty }\vartheta (b) i^*(b) \text {d} b$. Then, after some calculations and rearrangement, we find

$$\begin{aligned} \frac{\text {d} V_1}{\text {d} t}= & {} - \mu \frac{(S(t)-S^*)^2}{S(t) S^*} +\int \limits _{0}^{\infty } \vartheta (b) i^*(b) \left[ \frac{i(t,b) }{i^*(b)} -\frac{S(t) i(t,b) }{S^* i^*(b)} + \ln \frac{e(t,0)}{e^*(0)} - \ln \frac{i(t,b) }{i^*(b)} \right] \text {d} b\\{} & {} \quad - \int \limits _{0}^{\infty } \vartheta (b) i^*(b) \left[ g\left( \frac{S^*}{S(t)} \right) + g\left( \frac{S(t) i(t,b) e^*(0) }{S^* i^*(b)e(t,0) }\right) \right] \text {d} b \\{} & {} \quad + \int \limits _{0}^{\infty } \vartheta (b) i^*(b) \left[ \frac{S(t) i(t,b) e^*(0) }{S^* i^*(b)e(t,0) }-1\right] \text {d} b. \end{aligned}$$

With the help of Lemma 6.3, we can obtain

$$\begin{aligned} \frac{\text {d} V_1}{\text {d} t}= & {} - \mu \frac{(S(t)-S^*)^2}{S(t) S^*} +\int \limits _{0}^{\infty } \vartheta (b) i^*(b) \left[ \frac{i(t,b) }{i^*(b)} -\frac{S(t) i(t,b) }{S^* i^*(b)} + \ln \frac{e(t,0)}{e^*(0)} - \ln \frac{i(t,b) }{i^*(b)} \right] \text {d} b \nonumber \\{} & {} \quad - \int \limits _{0}^{\infty } \vartheta (b) i^*(b) \left[ g\left( \frac{S^*}{S(t)} \right) + g\left( \frac{S(t) i(t,b) e^*(0) }{S^* i^*(b)e(t,0) }\right) \right] \text {d} b. \end{aligned}$$

(80)

Next, by differentiating $V_2(t)$ along the solution of system (1)–(3), it follows

$$\begin{aligned} \frac{\text {d} V_2(t)}{\text {d} t}= & {} - \frac{1}{\zeta _1 S^*}\int \limits _{0}^{\infty } \upsilon _1(a) \left( 1-\frac{e^*(a)}{e(t,a)} \right) \left( \frac{\partial e(t,a) }{\partial a} + p_1(a) e(t,a) \right) \text {d} a \nonumber \\= & {} - \frac{1}{\zeta _1 S^*} \int \limits _{0}^{\infty } \upsilon _1(a) e^*(a) \frac{\partial }{\partial a} g\left( \frac{e(t,a)}{e^*(a)}\right) \text {d} a, \end{aligned}$$

(81)

where we have used

$$\begin{aligned} \frac{\partial }{\partial a} g\left( \frac{e(t,a)}{e^*(a)}\right) = \frac{1}{e^*(a)} \left( 1-\frac{e^*(a)}{e(t,a)} \right) \left( \frac{\partial e(t,a) }{\partial a} + p_1(a) e(t,a) \right) . \end{aligned}$$

Applying integration by parts on (81) and taking into account (79), we can get

$$\begin{aligned} \frac{\text {d} V_2 (t)}{\text {d} t}= & {} - \frac{1}{\zeta _1 S^*} \left[ \upsilon _1(a) e^*(a) g \left( \frac{e(t,a)}{e^*(a)} \right) \Bigr |_{0}^{\infty } - \int \limits _{0}^{\infty } \left( \upsilon '_1(a) -p_1(a) \upsilon _1(a) \right) e^*(a) g \left( \frac{e(t,a)}{e^*(a)} \right) \text {d} a \right] \\= & {} -\frac{1}{\zeta _1 S^*} \left[ \int \limits _{0}^{\infty } \varphi (a) e^*(a) g \left( \frac{e(t,a)}{e^*(a)} \right) \text {d} a - \zeta _1 e^*(0) g\left( \frac{e(t,0)}{e^*(0)} \right) \right] . \end{aligned}$$

Thus, we have

$$\begin{aligned} \frac{\text {d} V_2}{\text {d} t} = \frac{1 }{\zeta _1 S^*} \int \limits _{0}^{\infty } \varphi (a) e^*(a) \left( \frac{e(t,0)}{e^*(0)} - \ln \frac{e(t,0)}{e^*(0)} - \frac{e(t,a)}{e^*(a)} + \ln \frac{e(t,a)}{e^*(a)} \right) \text {d} a. \end{aligned}$$

After doing some calculations and simplifying, we have consequently got

$$\begin{aligned} \frac{\text {d} V_2}{\text {d} t}= & {} \frac{1 }{\zeta _1 S^* } \int \limits _{0}^{\infty } \varphi (a) e^*(a) \left[ \ln \frac{i^*(0)}{i(t,0) } +\frac{e(t,0)}{e^*(0)} -\ln \frac{e(t,0)}{e^*(0)} -\frac{e(t,a)}{e^*(a)}\right] \text {d} a \nonumber \\{} & {} \quad - \frac{1 }{\zeta _1 S^* } \int \limits _{0}^{\infty } \varphi (a) e^*(a)g \left( \frac{e(t,a) i^*(0) }{ i(t,0) e^*(a)} \right) \text {d} a \nonumber \\{} & {} \quad + \frac{1 }{\zeta _1 S^* } \int \limits _{0}^{\infty } \varphi (a) e^*(a) \left[ \frac{e(t,a) i^*(0) }{ i(t,0) e^*(a)} -1 \right] \text {d} a. \end{aligned}$$

(82)

Similarly, the derivative of $V_3(t)$ can be expressed as follows

$$\begin{aligned} \frac{\text {d} V_3}{\text {d} t} = \int \limits _{0}^{\infty } \left[ \vartheta (b) + \delta ^* \psi (b) \right] i^*(b) \left( \frac{i(t,0)}{i^*(0)} - \ln \frac{i(t,0)}{i^*(0)} - \frac{i(t,b) }{i^*(b)} + \ln \frac{i(t,b) }{i^*(b)} \right) \text {d} b. \end{aligned}$$

Then, by performing some rearrangements, it yields

$$\begin{aligned} \frac{\text {d} V_3}{\text {d} t}= & {} \int \limits _{0}^{\infty } [\vartheta (b) +\delta ^* \psi (b) ] i^*(b) \frac{i(t,0)}{i^*(0)} \text {d} b - \delta ^* \int \limits _{0}^{\infty } \psi (b) i^*(b) g \left( \frac{R(t)i^*(0)}{R^* i(t,0)} \right) \text {d} b \nonumber \\{} & {} + \int \limits _{0}^{\infty } \vartheta (b) i^*(b) \left[ \ln \frac{i(t,b) }{i^*(b)} - \frac{i(t,b) }{i^*(b)} - \ln \frac{i(t,0)}{i^*(0)} \right] \text {d} b \nonumber \\{} & {} + \delta ^* \int \limits _{0}^{\infty } \psi (b) i^*(b) \left[ \ln \frac{R^*}{R(t)}+\ln \frac{i(t,b) }{i^*(b)} - \frac{i(t,b) }{i^*(b)} \right] \text {d} b \nonumber \\{} & {} + \delta ^* \int \limits _{0}^{\infty } \psi (b) i^*(b) \left[ \frac{R(t)i^*(0)}{R^* i(t,0)}-1 \right] \text {d} b. \end{aligned}$$

(83)

Next, differentiating $V_4$ and considering that $\mu + \delta =\displaystyle \frac{1}{R^*} \int \limits _{0}^{\infty } \psi (b) i^*(b) \text {d} a$, we obtain

$$\begin{aligned} \frac{\text {d} V_4 }{\text {d} t} = \delta ^* \int \limits _{0}^{\infty } \psi (b) i^*(b) \left[ 1- \frac{R(t)}{R^*} - \frac{R^* i(t,b) }{R(t) i^*(b)}+\frac{i(t,b) }{i^*(b)} \right] \text {d} b. \end{aligned}$$

Through some computations, we can get

$$\begin{aligned} \frac{\text {d} V_4 }{\text {d} t}= & {} - \delta ^* \int \limits _{0}^{\infty } \psi (b) i^*(b) g\left( \frac{R^* i(t,b) }{R(t) i^*(b)}\right) \text {d} b - \delta ^* \int \limits _{0}^{\infty } \psi (b) i^*(b) \frac{R(t)}{R^*}\text {d} b \nonumber \\{} & {} + \delta ^* \int \limits _{0}^{\infty } \psi (b) i^*(b) \left[ \frac{i(t,b) }{i^*(b)} -\ln \frac{i(t,b) }{i^*(b)} - \ln \frac{R^* }{R(t) } \right] \text {d} b. \end{aligned}$$

(84)

In summary, by combining and rearranging the expressions (80), (82), (83), and (84) with the help of Lemma 6.4 and Lemma 6.5, the derivative of V(t) can be expressed as follows:

$$\begin{aligned} \frac{\text {d} V(t)}{\text {d} t}= & {} -\mu \frac{(S(t)-S^*)^2}{S(t) S^*} - \int \limits _{0}^{\infty } \vartheta (b) i^*(b) \left[ g\left( \frac{S^*}{S(t)} \right) + g\left( \frac{S(t) i(t,b) e^*(0) }{S^* i^*(b)e(t,0) }\right) \right] \text {d} b \nonumber \\{} & {} \quad - \frac{1 }{\zeta _1 S^* } \int \limits _{0}^{\infty } \varphi (a) e^*(a)g \left( \frac{e(t,a) i^*(0) }{ i(t,0) e^*(a)} \right) \text {d} a \nonumber \\{} & {} \quad - \delta ^* \int \limits _{0}^{\infty } \psi (b) i^*(b) \left[ g \left( \frac{R(t)i^*(0)}{R^* i(t,0)} \right) + g\left( \frac{R^* i(t,b) }{R(t) i^*(b)}\right) \right] \text {d} b. \end{aligned}$$

(85)

Therefore, it follows that $\frac{\text {d} V(t)}{\text {d} t } \le 0$, which implies that the function V(t) is non-increasing. Further, we can observe that V(t) is bounded function on any solution $\textbf{x}(\cdot )$, which means that $\alpha$-limit set of solution $\textbf{x}(\cdot )$ must be contained in the largest invariance subset $\mathcal {M}$ in $\left\{ \frac{\text {d} V(t)}{\text {d} t}=0 \right\}$. Now, let us proceed to determine the subset $\mathcal {M}$. To this end, it follows from $\frac{\text {d} V(t)}{\text {d} t}=0$ that $S(t)=S^*$, for all $t \in \mathbb {R}$. Then, by taking into account $S(t)=S^*$, it yields from the first equation of system (61) that

$$\begin{aligned} 0 =A -\mu S^* - S^* \int \limits _{0}^{\infty } \vartheta (b) i(t,b)\text {d} b, \quad \text {for all } t \in \mathbb {R}. \end{aligned}$$

(86)

In addition, from the first equation of system (23), we have

$$\begin{aligned} 0=A-\mu S^* - S^* \int \limits _{0}^{\infty } \vartheta (b) i^*(b)\text {d} b. \end{aligned}$$

(87)

Fig. 1

The evolution of solutions S(t), $E(t) = \displaystyle \int \limits _{0}^{\infty } e(t,a)\text {d} a$, $I(t)= \displaystyle \int \limits _{0}^{\infty }i(t,b)\text {d} b$, and R(t) when $\beta _1=7.5\times 10^{-4}$, $\delta =1/78.5$and $\mathcal {R}_0 =0.7564< 1$

Equation (86) with (87) provides that $\displaystyle \int \limits _{0}^{\infty } \vartheta (b) i(t,b)\text {d} b = \displaystyle \int \limits _{0}^{\infty } \vartheta (b) i^*(b)\text {d} b$. Moreover, we have

$$\begin{aligned} e(t,0)= S(t)\int \limits _{0}^{\infty } \vartheta (b) i(t,b)\text {d} b = S^* \int \limits _{0}^{\infty } \vartheta (b) i^*(b)\text {d} b =e^*(0), \end{aligned}$$

(88)

which implies that $e(t,a)=e^*(a)$, for all $t\in \mathbb {R}$. Thus, it can be deduced that $i(t,b) =i^*(b)$, and $R(t)=R^*$, for all $t \in \mathbb {R}$. Consequently, $\mathcal {M}=\{E^*\}$ is the largest invariant subset of $\left\{ \frac{\text {d} V(t)}{\text {d} t}=0 \right\}$. Hence, according to the Lyapunov–LaSalle invariance principle, the endemic equilibrium $E^*$ can be considered globally asymptotically stable whenever $\mathcal {R}_0>1$. This completes the proof of Theorem 6.6. $\square$

7 Numerical simulations

In this section, we will illustrate some numerical analysis to provide the theoretical results obtained in previous sections. We will consider herpes disease as an illustrative example that aligns well with the SEIR model (1)–(3). To this end, the backward Euler and linearized finite difference method will be used to discretize the ODEs and PDE in system (1)–(3), and the integral will be numerically calculated using Simpson’s rule.

Fig. 2

The evolution of solutions $e(t,a)\text {d} a$ and i(t, b) when $\beta _1=7.5\times 10^{-4}$, $\delta =1/78.5$ and $\mathcal {R}_0 =0.7564< 1$

Fig. 3

The evolution of solutions S(t), $E(t) = \displaystyle \int \limits _{0}^{\infty } e(t,a)\text {d} a$, $I(t)= \displaystyle \int \limits _{0}^{\infty }i(t,b)\text {d} b$, and R(t) when $\beta _1=7.5\times 10^{-3}$, $\delta =1/97.2$ and $\mathcal {R}_0 = 1.4502>1$

Fig. 4

The evolution of solutions e(t, a) and i(t, b) when $\beta _1=7.5\times 10^{-3}$, $\delta =1/97.2$ and $\mathcal {R}_0 = 1.4502>1$

We use parameters from previous research by Foss et al. [47]. The parameters A, $\mu$, and $\delta$ in system (1)–(3) take the following values: $A=275$, $\mu =0.014$, and $\delta$ is assumed to be varied.

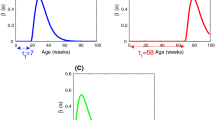
The functions $\nu _1(a)$, and $\nu _2(b)$ are considered to be constants, and $\nu _1(a)=\nu _2(b)=\nu =0.019$. Moreover, the functions $\vartheta (b)$, $\varphi (a)$, and $\psi (b)$ are chosen to be

$$\begin{aligned} \vartheta (b)= \beta _1 \left( 1+\sin \frac{(b-5)\pi }{10} \right) , \; \varphi (a)= \beta _2 \left( 1+\sin \frac{(a-1)\pi }{2} \right) , \; \psi (b)= \beta _3 \left( 1+\sin \frac{(b-15)\pi }{30} \right) , \end{aligned}$$

where $\beta _1$ is assumed to be varied, $\beta _2 =0.03$, and $\beta _3=0.09$. Moreover, the initial condition is chosen as

$$\begin{aligned} S(0)= 1200,\quad e_0(a)=50(a + 3) e^{0.2(a+3)}, \quad i_0(b)=(b + 3) e^{0.2(b+3)}, \quad \text {and} \quad R(0)= 50. \end{aligned}$$

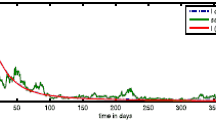
• i. When $\beta _1= 7\times 10^{-4}$ and $\delta =1/78.5$, then we have $\mathcal {R}_0=0.7564<1$. Thus, according to Theorem 6.1 the disease-free equilibrium $E^0$ is globally asymptotically stable (see, Figs. 1 and 2). This means that the disease eventually tends to go extinct.

• ii. When $\beta _1= 7\times 10^{-3}$ and $\delta =1/87.2$, then we have $\mathcal {R}_0=1.4502>1$. In view of Theorem 6.6, the endemic equilibrium $E^*$ is globally asymptotically stable (see Figs. 3 and 4). This indicates that the disease can start spreading through the population.

8 Discussion

In this paper, we have created and analyzed an SEIR epidemic model with continuous age structure for both latently infected individuals and infectious individuals with relapse to understand how these epidemiological factors affect the spread of the infectious disease. We then studied the global asymptotic stability of each equilibrium of the model by constructing the appropriate Lyapunov functional. Our theoretical results showed that the threshold parameter $\mathcal {R}_0$ completely governs the spread of diseases. That is, if $\mathcal {R}_0<1$, then the disease-free equilibrium is globally asymptotic stable, which means that the disease can be eradicated from the community, while the endemic equilibrium of the model is considered to be globally asymptotic stable whenever $\mathcal {R}_0>1$, indicating that the disease will continue to spread through the population. To control the transmission of the disease, we should take related strategies to reduce the basic reproduction number to below one. From the expression of $\mathcal {R}_0$, that is,

$$\begin{aligned} \mathcal {R}_0 = \frac{A}{\mu }\zeta _1 \zeta _2+ \frac{\delta }{\mu +\delta } \zeta _3. \end{aligned}$$

Notice that we must work on both terms to reduce the $\mathcal {R}_0$ value. The first term can be reduced by decreasing the quantities of $\zeta _1$ and $\zeta _2$. However, the relapse rate $\delta$ must be reduced to decrease the second term, as it has a direct effect, while the treatment rate $\zeta$ does not. Thus, strategies for controlling the disease may include early diagnosis of latent infections, decreasing both transmission and relapse rates.