1 Introduction

Mathematical models make it possible to project the evolution of contagious diseases to highlight the probable consequence of an epidemic and to assist inform the necessity of the public health interventions. The models utilize basal presumptions or gathered statistics as well as mathematics to obtain the responsible parameters for different contagious diseases and utilize these parameters to determine the outcome of various interventions, such as mass immunization programs. Modeling can assist to determine which intervention is required and which one to avoid or can predict next or future evolution patterns, so on. This projection was very helpful in predicting the newly discovered COVID-19 disease we cite for instance the paper [1, 2], and other diseases as bovine Babesiosis disease [3], HIV [4], so on. Further, the application of fractional calculus in understanding and predicting the evolution of infectious diseases and evolution of species attract the attention of numerous scholars we cite for instance the papers [5,6,7,8,9,10,11,12]. For more information about different methods for mathematical modeling of some other natural problems, we invite the readers to check the following papers [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]

In the literature, modeling the spread of infectious diseases using differential equations occupies a remarkable portion of the newly research achievements as example the researches [4, 22, 31,32,33], where each population is considered that evolutes in terms of time only. Indeed, if we presume that the studied population split into four different classes of populations namely: S-class S, E-class E, I-class I, R-class R, the infected person can pass through many stages which depends on the degree of the contagion of the person and the severity on the infectious disease, modeling this effect is tough using only ordinary differential equations. In these regards, we can consider in the mathematical modeling the time spend in the I-class which it can be called by age of infection, which means that the infected class depends on time denoted t and the infection age denoted a, such as approximation is investigated at the first time in [4, 31] for SIR model. There are many leading works in this context, such as modeling incubation period in [34], vaccination-age (quarantine) [24], addiction models [22, 32, 33], treat age [33], diffusion effect [35], which proves the huge importance of age-dependent models in predicting the outbreak of infectious diseases.

In fact, the crucial responsible component for the manner of transmission infected-susceptible is the incidence functional, where there are many types of incidence functional that been suggested and investigated we mention as example ratio-dependent type, Holling I-III type, Beddington–DeAngelis type, Hassell–Varley type, so on, which highlights the diversity in the transmission mode of many infectious diseases. In this research, we will consider a very wide class of incidence function that includes the previously mentioned incidence functions for determining the threshold dynamic of the investigated model. Before proposing our investigated model, and for the purpose of highlighting the achievement done in treating the global behavior of age structure models, we take as a starting point the following age-structured model considered by Rost et al. [36] and McCluskey [34]

$$\begin{aligned} \left\{ \begin{array}{lll} S'(t)=\Gamma - S(t)\int _0^{\infty }\beta (\eta ) i(t,\eta )\mathrm{d}\eta -\mu S(t),\\ E'(t)= S(t)\int _0^{\infty }\beta (\eta )i(t,\eta )\mathrm{d}\eta -(\mu +\alpha )E(t), \\ i_t(t,\eta )+i_\eta (t,\eta )=-(\mu +\gamma (\eta ))i(t,\eta ),\\ R'(t)=\int _0 ^\infty \gamma (\eta ) i(t,\eta )\mathrm{d} \eta -\mu R(t),\\ i(t,0)=\mu E(t). \end{array} \right. \end{aligned}$$
(1.1)

S(t),   (resp.   E(t)) is the susceptible population (resp. exposed population) density at t (which represents the time). R(t) is the removal population density at t. i(t, a) is the density of the infected population a time t and infection age a. \(\Gamma \) represents the constant entering flux, and \(\mu \) stands for the constant mortality-rate, \(1/\alpha \) is the incubation duration. \(\int _0 ^\infty \gamma (\eta ) i(t,\eta )\mathrm{d} \eta \) is the total density of persons entered into the R-class at t, \(\beta (\eta )\) represents the transmission rate which highlight the degree of the contagion of the infected person in the I-class. In the recently investigated SEIR model [34, 37], it is explained how the function \(\beta \) can take into count the incubation stage, but the age-structured SIR models as [23, 38] can provide a very good accuracy in the cases of contagious diseases with a small length of incubation stage as seasoner flu, COVID-19 disease, so on and loses its epidemiological accuracy in the cases of large latency stage contagious diseases, as an example tuberculose, HIV where the infected person can spend months in latency stage before becoming a fully contagious person. In this case, the age-structured SEIR model can provide better epidemiological precision results than the classical SIR model. Our purpose is to introduce a nonlinear incidence function into the system (1.1); hence, we obtain the system:

$$\begin{aligned} \left\{ \begin{array}{lll} S'(t)= \Gamma -\mu S(t)-K\big (S(t),W(t)\big ), \;\;\ t \ge 0,\\ E'(t)=K\big (S(t),W(t)\big )-(\mu +\alpha )E(t),\\ i_t(t,\eta )+i_\eta (t,\eta )=-(\mu +\gamma (\eta )) i(t,\eta ), \\ R'(t)=\int _{0}^{\infty }\gamma (\eta )i(t,\eta ) \mathrm{d}\eta ,\\ W(t)=\int _{0}^{\infty }\beta (\eta )i(t,\eta ) \mathrm{d}\eta ,\\ i(t,0)=\alpha E(t),\;\ t>0,\\ S(0)={\tilde{S}}\ge 0, ~~E(0)={\tilde{E}}\ge 0, ~~R(0)={\tilde{R}}\ge 0, ~~i(0,.)=i_0(.). \end{array} \right. \end{aligned}$$
(1.2)

All the parameters of the system (1.2) have the same epidemiological relevance as the model (1.1), and for simplicity we considered that \(\gamma (\eta )=\nu (\eta )+r(\eta )\). Further, the main mathematical assumption on the NIF \(K\big (S(t), W(t)\big )\) will be set in the next section. In [7] an SEIR model is also investigated with age-dependent in the exposed and the infected classes, the main result in the said paper is to investigate the model directly. Here, we will transform the model (1.2) into a difference equation with infinite delay, where the mathematical analysis will be transformed radically. The main idea behind using such as transformation is to obtain some information about the method of studying or analyzing global behavior of equilibria for difference equation, and how to construct a LF for this kind of systems. It is widely known that delay can generate interesting behavior as Hopf bifurcation [39, 40]. Further, there are few works that deals with the global behavior of some epidemiological models with time delay as [41,42,43,44,45,46,47,48,49]. Here, we will prove that the infinite delay will not affect the behavior of the solution, and based on the best of our knowledge investigating global behavior for an age-structured SEIR using difference equation is never been achieved before, and we strongly believe that this method will be very helpful in determining global behavior for different difference systems. Furthermore, we are interested in studying the global behavior of a system with difference equations and nonlinear incidence function, which never been achieved before for the SEIR model, which motivates our paper. Also, we will use the trajectory system to analyze the proprieties of the \(\alpha \)-limit and \(\omega \)-limit sets for proving the global stability of the equilibria without passing the local stability of them, which is more adequate in our case. Motivated by the previous mentioned points we organize the research in the manuscript as the form:

The next section is set to rewrite the system (1.2) as a system of difference equations, and providing the necessary conditions on the NIF K with various examples, also, we use some simplifications of the model. Next, we will prove that the solution of the investigated model has a global compact attractor (GCA) denoted \({\mathbf {A}}\), and write the total trajectory (TT) system. The GAS of the DFE is the subject of interest in Sect. 3 whereby the help of the trajectory system and a proper LF is achieved for proving the GAS of this equilibrium in the case of \(R_0<1\). In the fourth section, the uniqueness of the EE is provided for \(R_0>1\), next to the uniform persistence. The GAS of the unique EE is shown in Sect. 5 using the total trajectory system and a proper LF. The threshold dynamics are proved also numerical for confirming the obtained mathematical results.

2 Transformation of system (1.2) into system of difference equations and preliminary results

Before starting with the transformation of the model (1.2) into a system of difference equations that contains infinite delay, we put the following assumptions that fit with the epidemiological relevance on the model parameters:

  • We will consider in the whole paper that the function \(\beta \) is an integrable positive function. The function \(\gamma \in L_{+}^{\infty }({\mathbb {R}}^{+})\).

  • Assuming that K satisfies :

    1. 1.

      If \(J\ge 0,\) K(S, .) is an increasing for \(S\ge 0\) and if \(S\ge 0,\) K(., W) is an increasing for \(W\ge 0.\) Further, \(K(0,W)=K(S,0)=0\) \(\forall S, W\ge 0.\)

    2. 2.

      \(\dfrac{\partial K}{\partial W}(.,0)\ge 0\) and continuous on every compact set M.

    3. 3.

      K verifies the Lipschitz condition, which means that there exist \(L>0,\) where \(\forall C>0\), \(\exists L:=L_C>0\) verifying:

      $$\begin{aligned} |K(S_2,W_2)-K(S_1,W_1)|\le L(|S_2-S_1|+|W_2-W_1|), \end{aligned}$$
      (2.1)

      whenever \(0\le S_2,S_1, W_2, W_1\le C.\)

  • We denote \(N(t)=S(t)+E(t)+I(t)+R(t)\) where \(I(t)= \int _0^{\infty } i(t,\eta )d\eta \), be the total population, which verifies:

    $$\begin{aligned} N'(t)=\Gamma -\mu N(t). \end{aligned}$$

    Clearly, N(t) tends to \(\dfrac{\Gamma }{\mu },\) as \(t\rightarrow \infty \) then, the fourth eq. in (1.2) can be neglected.

  • We denote

    $$\begin{aligned} {\bar{N}}=\dfrac{\Gamma }{\mu }, \end{aligned}$$

    and

    $$\begin{aligned} \digamma (\eta )=e^{-\int _0^{\eta }\gamma (\sigma )d\sigma }. \end{aligned}$$

Now, let us focus on transforming (1.2) into a system of difference equations. The integration of i equation in (1.2), using the characteristic method we get:

$$\begin{aligned} i(t,\eta )=\left\{ \begin{array}{lll} \alpha E(t-\eta )e^{-\mu \eta }\digamma (\eta ), \;\;\ t>\eta \ge 0,\\ i_0(\eta -t)e^{-\mu t} \dfrac{\digamma (\eta )}{\digamma (\eta -t)}, \;\;\ \eta >t\ge 0. \end{array} \right. \end{aligned}$$
(2.2)

and

$$\begin{aligned} \left\{ \begin{array}{lll} S'(t)=\Gamma -\mu S(t)-K(S(t),W(t))\\ E'(t)=K(S(t),W(t))-(\mu +\alpha )E(t),\\ W(t)=\int _0^{\infty }\beta (\eta )i(t,\eta )\mathrm{d}\eta .\\ S(0)=S_0,\;\ E(0)=E_0. \end{array} \right. \end{aligned}$$
(2.3)

Hence, we arrive to the following form of the system (1.2) (system of difference equations):

$$\begin{aligned} \left\{ \begin{array}{lll} S'(t)=\Gamma -\mu S(t)-K\big (S(t),W(t)\big ), \,\\ E'(t)=K\big (S(t),W(t)\big )-(\mu +\alpha )E(t),\\ W(t)=\alpha \int _0^{\infty }\beta (\eta )e^{-\mu \eta }\digamma (\eta )E(t-\eta )\mathrm{d}\eta , \end{array} \right. \end{aligned}$$
(2.4)

with

$$\begin{aligned} \left\{ \begin{array}{lll} S(0)=S_0,\\ E(t)=\phi (t), \;\ \text{ for }\;\ t\le 0. \end{array} \right. \end{aligned}$$
(2.5)

We denote

$$\begin{aligned} C_{\Delta }:=\{\phi :{\mathbb {R}}_-\rightarrow {\mathbb {R}}, \;\ \phi e^{\Delta s}\;\ \text{ is } \text{ bounded } \text{ and } \text{ uniformly } \text{ continuous } \text{ on }\;\ {\mathbb {R}}_-\}. \end{aligned}$$

with \(0<\Delta <\mu +\inf (\gamma ).\)

With the norm

$$\begin{aligned} ||\chi ||=\sup _{s\le 0}|\chi (s)e^{\Delta s}|. \end{aligned}$$

Let the notation \(E_t\) stands for E(t), this means that \(E_t(\theta )=E(t+\theta ),\) with \(\theta \le 0.\) The positive functions cone in \(C_{\Delta }\) is highlighted by Y;  that means

$$\begin{aligned} Y:=\{\phi \in C_{\Delta } : \phi (\theta )\ge 0\;\ \text{ for }\;\ \theta \le 0\}. \end{aligned}$$

We presume that \((S_0,\phi ) \in {\mathbb {R}}^{+}\times Y\) then from [50] the existence and the regularity and the uniqueness of solution for (2.4)–(2.5) in \({\mathbb {R}}^{+}\times Y\) is guaranteed.

Proposition 2.1

\(\exists P>0\) such that for any solution of (2.4)–(2.5) \(\exists T>0\) verifying

$$\begin{aligned} S(t)\le P,\; E(t)\le P,\; ||E_t||\le P,\;\ \; W(t)\le M, \;\ \;\ \forall t\ge T. \end{aligned}$$
(2.6)

Moreover,

$$\begin{aligned} \Lambda \le \liminf _{t\rightarrow \infty } S(t), \end{aligned}$$
(2.7)

with \(\Lambda :=\frac{\Gamma }{\mu +L}.\)

Proof

First of all, a simple computation, yields

$$\begin{aligned} \limsup _{t\rightarrow \infty }N(t)\le {\bar{N}}. \end{aligned}$$

as \(S+E+I+R=N\) then

$$\begin{aligned} \limsup _{t\rightarrow \infty } (S(t)+E(t))\le {\bar{N}}. \end{aligned}$$

Therefore, \(\exists T>0\) such \(\forall t\ge T\) we get

$$\begin{aligned} S(t)\le {\bar{N}},\;\ I(t)\le {\bar{N}}\;\ \text{ and }\;\ E(t)\le {\bar{N}}. \end{aligned}$$

In addition,

$$\begin{aligned} ||E_t||= & {} \sup _{\theta \le 0} E_t(\theta )=\sup _{u\le t} E(u)e^{\Delta u}e^{-\Delta t}\\\le & {} \max \{{e^{-\Delta t}||\phi ||,Ke^{\Delta T}e^{-\Delta t}, {\bar{N}}}\}, \end{aligned}$$

where \(K=\sup _{0\le u\le T} E(u).\) Further,

$$\begin{aligned} W(t)\le & {} \alpha \int _0^{\infty }\beta (\eta )e^{\Delta \eta }e^{-\mu \eta }e^{-\Delta \eta }E_t(-\eta )\mathrm{d}\eta ,\\\le & {} \dfrac{\alpha ||\beta ||}{\mu +\inf (\gamma )-\Delta }||E_t||. \end{aligned}$$

Consequently, we can choose M so large in such a way (2.6) is satisfied. For the second estimation (2.7), we put \(\liminf _{t\rightarrow \infty } S(t)=S_{\infty }\), \(\limsup _{t\rightarrow \infty } W(t)=W^{\infty },\) the fluctuation method [51] yields the existence of a sequence denoted \(t_k\), verifying \(S'(t_k)\rightarrow 0\), \(\lim _{t_k\rightarrow \infty } S(t_k)=S_{\infty },\) thus

$$\begin{aligned} 0 \ge \Gamma -\mu S_{\infty }-K(S_{\infty },W^{\infty }), \end{aligned}$$

due to (2.1), we obtain

$$\begin{aligned} 0\ge \Gamma -\mu S_{\infty }-LS_{\infty }, \end{aligned}$$

so,

$$\begin{aligned} S_{\infty }\ge \dfrac{\Gamma }{\mu +L}. \end{aligned}$$

\(\square \)

For the model (1.2), the BRN \(R_0\) is defined by

$$\begin{aligned} R_0=\dfrac{\alpha }{\mu +\alpha }\dfrac{\partial K}{\partial W}({\bar{N}},0)\int _0^{\infty }\beta (\eta )e^{-\mu \eta }e^{-\int _0^\eta \gamma (\sigma )\mathrm{d}\sigma }\mathrm{d}\eta , \end{aligned}$$
(2.8)

3 GCA and TT

First, we define the following semiflow

$$\begin{aligned} \Phi (t,(S_0,\phi ))=(S(t),E_t(.)), \end{aligned}$$
(3.1)

with \((S,E_t)\) is solution of (2.4)–(2.5).

We choose \(X={\mathbb {R}}^{+} \times Y\) and we show the presence of a compact attractor (CA) of all bounded sets (BS) of X, (for more details see [51, 52]).

Theorem 3.1

The semi-flow \(\Phi \) has a compact attractor denoted \({\mathbf {A}}\) of bounded sets of X.

Proof

using Proposition 2.1, the semi-flow \(\Phi \) is point-dissipative. Hence, by Theorem 2.33 in [51], we only need to prove that \(\Phi \) is eventually bounded on BS and verifying asymptotical smoothness condition in order to prove our Theorem. These two properties are checked by employing the same ideas as in proof of Theorem 6.1 [36]. \(\square \)

The remained part of the section is devoted to describe some estimates for bounded TT of (2.4)–(2.5) for the purpose of avoiding analyzing the local behavior of (2.4)–(2.5). These system has a crucial role in avoiding proving the GAS of the equilibria without passing by the local stability analysis, see, e.g., [51].

TT system

We put \({\bar{\phi }}\) that verifies \({\bar{\phi }}(t)=(S(t),E_t(.)).\) Hence, \({\bar{\phi }}(r+t)=\Phi (t,{\bar{\phi }}(r)),\) \(t\ge 0,\) \(r\in {\mathbb {R}}.\) Thus, by a simple computation, a total trajectories satisfy, for all \(t\in {\mathbb {R}},\) the system

$$\begin{aligned} \left\{ \begin{array}{lll} S'(t)=\Gamma -\mu S(t)-K(S(t),W(t)),\\ E'(t)=K(S(t),W(t))-(\mu +\alpha )E(t),\\ W(t)=\alpha \int _0^{\infty }\beta (\eta )e^{-\mu \eta }\digamma (\eta ) E(t-\eta )\mathrm{d}\eta . \end{array} \right. \end{aligned}$$
(3.2)

Next, we will provide some important proprieties for TT system through the following lemma:

Lemma 3.2

For all \((S_0,\phi )\in {\mathbf {A}},\) we have

$$\begin{aligned} \begin{array}{lll} S(t)+E(t) \le {\bar{N}},\;\;\;\ \text{ and }\;\ S(t)\ge \dfrac{\Gamma }{\mu +L},\;\ \text{ where } \text{ L } \text{ is } \text{ the } \text{ Lipschitz } \text{ constant, }\\ \text{ and } \;\ W(t)\le \dfrac{\alpha {\bar{N}}}{\mu }||\beta ||, \end{array} \end{aligned}$$

for all \( t\in {\mathbb {R}}.\)

Proof

By summing the first and second equations of (3.2), we arrive at

$$\begin{aligned} S'(t)+E'(t)\le \Gamma -\mu (S(t)+E(t)), \end{aligned}$$

for \(t\ge r\) we get

$$\begin{aligned} (S(t)+E(t))e^{\mu t}\le (S(r)+E(r))e^{\mu r}+\dfrac{\Gamma }{\mu }(e^{\mu t}-e^{\mu r}), \end{aligned}$$

putting \(r\rightarrow -\infty \) we find

$$\begin{aligned} S(t)+E(t) \le \dfrac{\Gamma }{\mu }, \;\ \text{ for } \text{ all }\;\ t\in {\mathbb {R}}. \end{aligned}$$

Also,

$$\begin{aligned} W(t)=\int _0^{\infty }\beta (\eta )e^{-\mu \eta }\digamma (\eta )\alpha E(t-\eta )\mathrm{d}\eta \le \dfrac{\alpha \Gamma }{\mu ^2}||\beta ||. \end{aligned}$$

Next, we determine the persistence of S in (3.2). Using the fact that W is bounded and (2.1), we get

$$\begin{aligned} \begin{array}{lll} S'(t)&{}\ge &{} \Gamma -\mu S(t)-K(S(t),\dfrac{\alpha A}{\mu ^2}||\beta ||), \\ &{}\ge &{} \Gamma -\mu S(t)-LS(t). \end{array} \end{aligned}$$

Finally, some calculations yield:

$$\begin{aligned} S(t) \ge \dfrac{\Gamma }{\mu +L} \;\;\ \forall t\in {\mathbb {R}}. \end{aligned}$$
(3.3)

\(\square \)

4 The GAS of DFE

Here, we determine the global behavior of the solution of (2.4)–(2.5) in the case of \(R_0<1\), note that the DFE \( ({\bar{N}}, 0 )\) is the unique equilibrium state in this case. Through this section, the assumption of concavity of K(S, W) with respect to W is mandatory.

Theorem 4.1

For \(R_0\le 1\), we get the global asymptotic stability of DFE \(({\bar{N}}, 0 )\)

Proof

Introducing the function

$$\begin{aligned} \psi (\eta )=\alpha \dfrac{\partial K}{\partial W}({\bar{N}},0)\int _{\eta }^{\infty }\beta (\sigma )e^{-\mu \sigma }\digamma (\sigma )\mathrm{d}\sigma . \end{aligned}$$

For \((S_0,\phi )\in {\mathbf {A}},\) we set the LF as the form \(V(S_0,\phi )=V_1(S_0,\phi )+V_2(S_0,\phi )+\phi (0)\) where

$$\begin{aligned} V_1(S_0,\phi )=S_0-\int ^{S_0}_{{\bar{N}}}\lim _{W\rightarrow 0^{+}}\dfrac{f({\bar{N}},W)}{f(\eta ,W)}\mathrm{d}\eta -{\bar{N}}, \end{aligned}$$

and

$$\begin{aligned} V_2(S_0,\phi )=\int _0^{\infty }\psi (\eta )\phi (-\eta )\mathrm{d}\eta , \end{aligned}$$

Putting\(\Psi : {\mathbb {R}}\rightarrow {\mathbf {A}}\) be a \(\Phi -\)TT, \(\Psi (t)=(S(t),E_t),\) \(S(0)=S_0\) and \(E_0=\phi ,\) with \((S(t),E_t)\) is solution of (3.2).

$$\begin{aligned} \dfrac{\mathrm{d}}{\mathrm{d}t}V_1(\Psi (t))= & {} \left( 1-\lim _{W\rightarrow 0^{+}}\dfrac{K({\bar{N}},W)}{f(S(t),W)}\right) (A-\mu S(t)-K(S(t),W(t)))\\= & {} \mu \left( 1-\lim _{W\rightarrow 0^{+}}\dfrac{K({\bar{N}},W)}{f(S(t),W)}\right) \left( {\bar{N}}-S(t)\right) \\&-K(S(t),W(t))\left( 1-\lim _{W\rightarrow 0^{+}}\dfrac{K({\bar{N}},W)}{K(S(t),W)}\right) . \end{aligned}$$

Concerning \(V_2\), we have

$$\begin{aligned} \dfrac{\mathrm{d}}{\mathrm{d}t}V_2(\Psi (t))= & {} \int _0^{\infty }\psi (\eta )\dfrac{\mathrm{d}}{\mathrm{d}t}E(t-\eta )\mathrm{d}\eta ,\\= & {} -\int _0^{\infty }\psi (a)\dfrac{\mathrm{d}}{\mathrm{d}a}E(t-\eta )\mathrm{d}\eta ,\\= & {} \psi (0)E(t)+\int _0^{\infty }\psi '(a)E(t-\eta )\mathrm{d}\eta ,\\= & {} R_0(\mu +\alpha ) E(t)-\alpha \dfrac{\partial K}{\partial W}({\bar{N}},0)\int _0^{\infty }\beta (a)e^{-\mu \eta }\digamma (a)E(t-\eta )\mathrm{d}\eta . \end{aligned}$$

Adding \(V'_1,\) \(V'_2,\) and E(t) yields

$$\begin{aligned} \dfrac{\mathrm{d}}{\mathrm{d}t}V(\Psi (t))= & {} \mu \left( 1-\lim _{W\rightarrow 0^{+}}\dfrac{K({\bar{N}},W)}{K(S(t),W)}\right) \big ({\bar{N}}-S(t)\big )-\big (1-R_0\big )(\mu +\alpha ) E(t),\\&+K(S(t),W(t))\lim _{J\rightarrow 0^{+}}\dfrac{K({\bar{N}},W)}{K(S(t),W)}-\dfrac{\partial K({\bar{N}},0)}{\partial W}W(t). \end{aligned}$$

Clearly, the first two terms of the previous equation are nonpositive, and yield that the third term is also nonpositive. In fact, the concavity of K for J gives

$$\begin{aligned} K(S,W)\le W\dfrac{\partial K}{\partial W}(S,0). \end{aligned}$$

Hence,

$$\begin{aligned}&K(S(t),W(t))\lim _{W\rightarrow 0^{+}}\dfrac{K({\bar{N}},W)}{K(S(t),W)}-W(t)\dfrac{\partial K}{\partial W}({\bar{N}},0) \\&\quad =K(S(t),W(t))\dfrac{\dfrac{\partial K}{\partial W}({\bar{N}},0)}{\dfrac{\partial K}{\partial W}(S(t),0)}-W(t)\dfrac{\partial K}{\partial W}({\bar{N}},0),\\&\quad =\dfrac{\dfrac{\partial K}{\partial W}({\bar{N}},0)}{\dfrac{\partial K}{\partial W}(S(t),0)}\big (K(S(t),W(t))-W(t)\dfrac{\partial K}{\partial W}(S(t),0)\big )\le 0. \end{aligned}$$

Clearly, \(\dfrac{\mathrm{d}}{\mathrm{d}t}V(\Psi (t))=0\) yields \(S(t)={\bar{N}}\) \(\forall t\in {\mathbb {R}}.\) Employing this result in the S eq. yields \(W(t)=0\), \(\forall t\in {\mathbb {R}}.\) From (3.2), we easily find \(E(t)=0\), \(\forall t\in {\mathbb {R}}.\) Using the compactness of \({\mathbf {A}}\) is compact, respectively, \(\omega (x)\) and \(\alpha (x)\) are non-empty, compact, invariant and attract \(\Psi (t)\) as \(t\rightarrow \pm \infty \). Using also the fact that \(V(\Psi (t))\) is decreasing in t,  V is nonvariable on the \(\omega (x)\) and \(\alpha (x),\) and hence \(\omega (x)=\alpha (x)=\{({\bar{N}},0)\}.\) As a result, \(\lim \limits \nolimits _{t\longrightarrow \pm \infty }\Psi (t)=({\bar{N}},0)\) and

$$\begin{aligned} \lim \limits _{t\longrightarrow - \infty }V(\Psi (t))=\lim \limits _{t\longrightarrow + \infty }V(\Psi (t))=V({\bar{N}},0). \end{aligned}$$

Then, \(V(\Psi (t))=V({\bar{N}},0)\), \(\forall t\in {\mathbb {R}}.\) Using the fact that \(\alpha (x)=\{({\bar{N}},0)\}\) hence \(V(\Psi (t))\le V({\bar{N}},0)\) \(\forall t\in {\mathbb {R}}.\) Further, the minimum of \(\Psi \) at \(({\bar{N}},0),\) then \(\Psi (t)=({\bar{N}},0)\), \(\forall t\in {\mathbb {R}}.\) More precisely, \((S_0,\phi )=({\bar{N}},0).\) Consequently, \({\mathbf {A}},\) is the singleton set contains only the DFE \(({\bar{N}},0).\) Theorem 2.39 in [51] yields the globally asymptotically stability of the DFE. \(\square \)

5 Existence of EE and uniform persistence

Here, we deal with some proprieties of the system (2.4)–(2.5) in the case of \(R_0>1\). At first, we demonstrate the existence of EE and then, we determine the uniform persistence of the solution of (3.2).

Lemma 5.1

Let \(\lim _{W\rightarrow 0^{+}}\dfrac{K({\bar{N}},W)}{K(S,W)}>1\), \(S\in [0,{\bar{N}}).\) Hence, for \(R_0>1,\) (2.4) has a unique EE.

Proof

EE verifies the following equality

$$\begin{aligned} \Phi (t,(S^{*},E^{*}))=(S^{*},E^{*}), \;\ \text{ where } \;\ E^{*}\ne 0,\;\ \forall t\ge 0. \end{aligned}$$

where \(S^{*}, E^{*}\) verify

$$\begin{aligned} \left\{ \begin{array}{lll} \Gamma -\mu S^{*}-K(S^{*},W^{*})=0, \\ (\mu +\alpha )E^{*}=K(S^{*},W^{*}),\\ W^{*}=\alpha E^{*}\int _0^{\infty }\beta (\eta )e^{-\mu \eta }\digamma (\eta )\mathrm{d}\eta . \end{array} \right. \end{aligned}$$
(5.1)

Combining the equations of (5.1), we arrive at

$$\begin{aligned} \left\{ \begin{array}{lll} A=\mu S^{*}+K(S^{*},W^{*}), \\ {\bar{D}}K(S^{*},W^{*})=W^{*}, \end{array} \right. \end{aligned}$$

with

$$\begin{aligned} {\bar{D}}:=\dfrac{\alpha }{\mu +\alpha }\int _0^{\infty }\beta (\eta )e^{-\mu \eta }\digamma (\eta )\mathrm{d}\eta . \end{aligned}$$
(5.2)

using the same calculation as in [53], we arrive to the existence of EE. \(\square \)

Now, investigate the uniform persistence; where Theorem 5.2 in [51] is been used. At first, we see the hypostypsis on the NIF K. We presume the existence of EE denoted \((S^{*},W^{*})\) verifying (5.1) such that

$$\begin{aligned} \left\{ \begin{array}{lll} \dfrac{x}{W^{*}}< \dfrac{K(S,x)}{K(S,W^{*})}< 1 \;\ \text{ for }\;\ x<W^{*},\\ 1< \dfrac{K(S,x)}{K(S,W^{*})}< \dfrac{x}{W^{*}} \;\ \text{ for }\;\ x> W^{*}. \end{array} \right. \end{aligned}$$
(5.3)

\(\exists \varepsilon >0\), \(\eta >0\) where, \(\forall S\in [{\bar{N}}-\varepsilon ,{\bar{N}}+\varepsilon ]\), hence

$$\begin{aligned} \dfrac{K(S,W_1)}{W_1}\ge \dfrac{K(S,W_2)}{W_2}, \end{aligned}$$
(5.4)

for all \(0< W_1 \le W_2\le \eta .\)

Finally, we presume that

$$\begin{aligned} \phi (\eta )>0,\;\ \text{ for } \text{ some } \;\ \eta \le 0. \end{aligned}$$
(5.5)

Remark 5.2

If K verifies both the differentiability and the concavity conditions for W, hence (5.3) and (5.4) are checked automatically.

Setting a persistence function \(\rho : {\mathbb {R}}^{+}\times Y_{+}\rightarrow {\mathbb {R}}^{+}\) as

$$\begin{aligned} \rho (S_0,\phi )=E(0), \end{aligned}$$

then for \(x=(S_0,\phi ),\)

$$\begin{aligned} \rho (\Phi (t,x))=E(t). \end{aligned}$$

The next Lemma insures that (H1) in Theorem 5.2 ( [51]) is checked.

Lemma 5.3

Using (5.5), \(\rho \) is nonnegative anywhere on \({\mathbb {R}}.\)

Proof

Presuming that \(\exists r\in {\mathbb {R}}\) in such a way \(E(t)=0\) \(\forall t\le r.\) Then, \(E(t)=0\), \(\forall t>r.\) In fact, for \(t>r\) and by a change of variable we find

$$\begin{aligned} (E(t)e^{(\mu +\alpha )t})'= & {} \alpha e^{(\mu +\alpha )t} \int _{-\infty }^{t}\beta (t-\sigma )e^{-\mu (t-\sigma )}\digamma (t-\sigma )E(\sigma )\mathrm{d}\sigma ,\\= & {} \alpha e^{(\mu +\alpha )t}\int _{r}^{t}\beta (t-\sigma )e^{-\mu (t-\sigma )}\digamma (t-\sigma )E(\sigma )\mathrm{d}\sigma , \end{aligned}$$

by integration and Fubini’s theorem we obtain

$$\begin{aligned} E(t)e^{(\mu +\alpha )t}\le & {} \alpha {\bar{N}} ||\beta ||\int _r^{t}e^{(\mu +\alpha )\theta }\int _r^{\theta }e^{-\mu (\theta -\sigma )}E(\sigma )\mathrm{d}\sigma \mathrm{d}\theta ,\\\le & {} \alpha {\bar{N}} ||\beta ||\int _r^{t}e^{\mu \sigma }E(\sigma )\int _{\theta }^{t}e^{\alpha \theta }\mathrm{d}\theta \mathrm{d}\sigma , \end{aligned}$$

thus, by a straightforward calculation, we get

$$\begin{aligned} E(t)\le {\bar{N}} ||\beta ||\int _r^tE(\sigma )\mathrm{d}\sigma . \end{aligned}$$

Using Gronwall Lemma and the fact that \(E(r)=0\), we conclude that \(E(t)=0\), \(\forall t>r\). This is a contradiction with (5.5). Now, we suppose that \(\exists t_n\) verifying \(t_n\rightarrow \infty \) and \(E(t_n)>0.\) We set \(E_n(t)=E(t+t_n)\) and \(S_n(t)=S(t+t_n).\) So, by a simple computation

$$\begin{aligned} E_n(t)e^{(\mu +\alpha )t}\ge & {} E_n(0)+ \alpha \dfrac{A}{\mu +L} \int _0^{t}e^{(\mu +\alpha )\theta }\int _{-\infty }^{\theta }\beta (\theta -\sigma )e^{-\mu (\theta -\sigma )}E(\sigma )\mathrm{d}\sigma \mathrm{d}\theta , \end{aligned}$$

by \(E_n(0)=E(t_n)>0\) then \(E_n(t)>0\) \(\forall t\ge 0.\) Finally, using \(t_n\rightarrow -\infty \) as \(n\rightarrow \infty \) then

$$\begin{aligned} E(t)>0, \;\ \forall t\in {\mathbb {R}}. \end{aligned}$$

\(\square \)

Using the fact that (H1) in Section 5.1. [51] holds, and using Theorem 5.2. in [51], it is sufficient to demonstrate the weak uniform persistence for establishing the uniform persistence.

Theorem 5.4

Assume that (5.3), (5.4), (5.5) are checked. Then, \(\exists \eta >0\) verifying

$$\begin{aligned} \liminf _{t\rightarrow \infty } E(t)>\eta , \end{aligned}$$

for any positive sol. of (2.4) we have \(R_0>1.\)

Proof

Using contradiction, we suppose that

$$\begin{aligned} \lim _{t\rightarrow \infty }E(t)=0, \end{aligned}$$

then

$$\begin{aligned} \lim _{t\rightarrow \infty }W(t):=\lim _{t\rightarrow \infty }\int _0^{\infty }\alpha \beta (\eta )e^{-\mu \eta }\digamma (a)E(t-\eta )\mathrm{d}\eta =0. \end{aligned}$$

Now, handling the S eq. in (1.2) and for t sufficiently large

$$\begin{aligned} S'(t)\ge & {} A-\mu S(t)-K({\bar{N}},W),\\\ge & {} A-\mu S(t)-K({\bar{N}},\varepsilon ), \end{aligned}$$

hence

$$\begin{aligned} S(t)\ge \left( S_0-\dfrac{A-K({\bar{N}},\varepsilon )}{\mu }\right) e^{-\mu t}+\dfrac{A-K({\bar{N}},\varepsilon )}{\mu }, \end{aligned}$$

thus

$$\begin{aligned} \liminf _{t\rightarrow \infty } S(t)\ge {\bar{N}}-\psi (\varepsilon ), \end{aligned}$$

with \(\psi (\varepsilon )=\dfrac{K({\bar{N}},\varepsilon )}{\mu }.\) We have

$$\begin{aligned} \limsup _{t\rightarrow \infty }S(t)\le {\bar{N}}, \end{aligned}$$

as a result, we presume

$$\begin{aligned} |S(t)-{\bar{N}}|<\psi (\varepsilon ),\;\ t\ge T. \end{aligned}$$

Otherwise, since \(R_0>1\) then for \(\varepsilon \) so small and \(t^{*}\) so large we get

$$\begin{aligned} \dfrac{K({\bar{N}}-\psi (\varepsilon ),\varepsilon )}{\varepsilon }\int _0^{t^{*}}\alpha \beta (a)e^{-\mu a}\digamma (a)\mathrm{d}a>\mu +\alpha . \end{aligned}$$

Now, using the equation of E

$$\begin{aligned} E'(t)= & {} K(S(t),w(t))-(\mu +\alpha )E(t),\\\ge & {} K({\bar{N}}-\psi (\varepsilon ),W(t))-(\mu +\alpha )E(t), \end{aligned}$$

In view of (5.4) and the fact that \(W(t)<\varepsilon \) where t is sufficiently large, we obtain,

$$\begin{aligned} K({\bar{N}}-\psi (\varepsilon ),W(t))\ge \dfrac{K({\bar{N}}-\psi (\varepsilon ),\varepsilon )}{\varepsilon }W(t), \end{aligned}$$

thus

$$\begin{aligned} E'(t)\ge & {} \dfrac{K({\bar{N}}-\psi (\varepsilon ),\varepsilon )}{\varepsilon }W(t)-(\mu +\alpha )E(t),\\\ge & {} \dfrac{K({\bar{N}}-\psi (\varepsilon ),\varepsilon )}{\varepsilon }\int _0^{t^{*}}\alpha \beta (a)e^{-\mu a}\digamma (\eta )E(t-\eta )\mathrm{d}\eta -(\mu +\alpha )E(t). \end{aligned}$$

Now, by employing a similar method as in the proof of Theorem 6.1. ( [36]) we reach to a contradiction. The proof is completed. \(\square \)

Letting \(X_0\) be a set which is:

$$\begin{aligned} X_0=\{ (S_0,\phi )\in X ; \phi (\eta )=0,\;\ \text{ for } \text{ all }\;\ \eta \le 0 \}. \end{aligned}$$

From Theorem 5.7 in [51], we get:

Theorem 5.5

\(\exists \mathbf {A_1}\) (GCA) that entices all solutions with initial data in \(X\setminus X_0.\) Further, \(\mathbf {A_1}\) is \(\rho -\) uniformly positive, that is, \(\exists \delta >0\) in such a way,

$$\begin{aligned} E(t)\ge \delta , \;\ \forall t\in {\mathbb {R}},\;\ \text{ and }\;\ \forall (S_0,\phi )\in \mathbf {A_1}. \end{aligned}$$
(5.6)

6 The GAS and uniqueness of the EE

Her, we deal with the BAS of EE \(E^{*}\) of (3.2). At first, we need to check what if all solutions of (3.2) with initial condition verifying (5.5), and verifying the boundedness and the persistence prosperities.

Corollary 6.1

\(\exists {\bar{\delta }}>0\) where, \(\forall (S_0,\phi )\in \mathbf {A_1},\)

$$\begin{aligned} W(t):=\alpha \int _0^{\infty }\beta (\eta )e^{-\mu \eta }\digamma (\eta )E(t-\eta )\mathrm{d}\eta \ge {\bar{\delta }}, \;\ \end{aligned}$$

and

$$\begin{aligned} K(S(t),W(t))\ge K(\dfrac{A}{\mu +L},{\bar{\delta }}), \end{aligned}$$
(6.1)

for all \(t\in {\mathbb {R}},\) and \({\bar{\delta }}:=\delta \alpha \int _0^{\infty }\beta (\eta )e^{-\mu \eta }\digamma (\eta )\mathrm{d}\eta .\)

Proof

Since \(\mathbf {A_1}\) is invariant, \(\exists \Psi :{\mathbb {R}}\rightarrow \mathbf {A_1},\) \(\Psi (t)=(S(t),E_t)\) with \(S(0)=S_0\) and \(E_0(a)=\phi (a)\) for \(a\le 0.\) In view of the estimation (5.6), \(\forall t\in {\mathbb {R}}\) we obtain,

$$\begin{aligned} W(t):=\alpha \int _0^{\infty }\beta (\eta )e^{-\mu \eta }\digamma (\eta )E(t-\eta )\mathrm{d}\eta \ge \delta \alpha \int _0^{\infty }\beta (\eta )e^{-\mu \eta }\digamma (\eta )\mathrm{d}\eta , \end{aligned}$$

From Lemma 3.2, we easily obtain (6.1). \(\square \)

Theorem 6.2

By the presumptions of Theorem 5.4, the EE \((S^{*},E^{*})\) is unique and it is GAS in \(\mathbf {A_1}\).

Proof

Let \(\Psi : {\mathbb {R}}\rightarrow \mathbf {A_1}\) be a \(\Phi -\)TT, \(\Psi (t)=(S(t),E_t(.)),\) \(S(0)=S_0\) and \(E_0(.)=\phi ,\) with \((S(t),E_t(.))\) is solution of (3.2). Putting \(H(\chi )=\chi -ln(\chi )-1,\) also

$$\begin{aligned} \psi (\eta )=K(S^{*},W^{*})\int _\eta ^{\infty }\mathrm{d}m(\vartheta ),\;\ \text{ with } \;\ \mathrm{d}m(\vartheta )=\dfrac{\beta (\vartheta )e^{-\mu \vartheta }\digamma (\vartheta )}{{\bar{D}}}\mathrm{d}\vartheta . \end{aligned}$$
(6.2)

with \({\bar{D}}:=\int _0^{\infty }\beta (\vartheta )e^{-\mu \vartheta }\digamma (\vartheta )\mathrm{d}\vartheta .\) We mention that \(\int _0^{\infty }\mathrm{d}m(\sigma )=1.\)

For \((S_0,\phi )\in A_1,\) we set the LF as \(V(S_0,\phi )= V_1(S_0,\phi )+V_2(S_0,\phi )+E^{*}V_3(S_0,\phi )\) with

$$\begin{aligned} V_1(S_0,\phi )=S_0- \int _{S^{*}}^{S_0}\dfrac{K(S^{*},W^{*})}{K(\eta ,W^{*})}\mathrm{d}\eta -S^{*}, \end{aligned}$$

and

$$\begin{aligned} V_2(S_0,\phi )= & {} \int _0^{\infty }\psi (a)H\left( \dfrac{\phi (-a)}{E^{*}}\right) \mathrm{d}a. \\ V_3(S_0,\phi )= & {} H\left( \dfrac{\phi (0)}{E^{*}}\right) , \end{aligned}$$

Firstly,

$$\begin{aligned} \dfrac{\mathrm{d}}{\mathrm{d}t}V_1(\Psi (t))= & {} \mu (1-\dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})})(S^{*}-S(t))+ \left( 1-\dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}\right) K(S^{*},W^{*}) \nonumber \\&-\left( 1-\dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}\right) K(S(t),W(t)). \end{aligned}$$
(6.3)

Concerning \(V_2\), we have

$$\begin{aligned} \dfrac{\mathrm{d}}{\mathrm{d}t}V_2(\Psi (t))= & {} H\left( \dfrac{E(t)}{E^{*}}\right) \psi (0)+\int _0^{\infty }H\left( \dfrac{E(t-a)}{E^{*}}\right) \psi '(a)\mathrm{d}a,\nonumber \\= & {} K(S^{*},W^{*})H\left( \dfrac{E(t)}{E^{*}}\right) +\int _0^{\infty }H\left( t\dfrac{E(t-a)}{E^{*}}\right) \psi '(a)\mathrm{d}a. \end{aligned}$$
(6.4)

Now,

$$\begin{aligned} E^{*}V'_3(t)=\left( 1-\dfrac{E^{*}}{E(t)}\right) \big (K(S(t),W(t))-(\mu +\alpha )E(t)\big ), \end{aligned}$$
(6.5)

adding \(V'_1,\) \(V'_2\) and \(E^{*}V'_3\) we obtain

$$\begin{aligned} V'(\Psi (t))= & {} \mu \left( 1-\dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}\right) (S^{*}-S(t))+K(S^{*},W^{*})\left( 1 -\dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}\right) \\&-K(S(t),W(t))\left( 1-\dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}\right) \\&+K(S^{*},W^{*})\left( \dfrac{E(t)}{E^{*}}-\ln \dfrac{E(t)}{E^{*}}-1\right) +\left( 1-\dfrac{E^{*}}{E(t)}\right) K(S(t),W(t)) \\&-(\mu +\alpha )E(t)\left( 1-\dfrac{E^{*}}{E(t)}\right) \\&+\int _0^{\infty }H\left( \dfrac{E(t-a)}{E^{*}}\right) \psi '(a)\mathrm{d}a. \end{aligned}$$

Recall that \((\mu +\alpha )E^{*}=K(S^{*},w^{*}),\) and reorganizing our terms, we have

$$\begin{aligned} V'(\Psi (t))= & {} \mu \left( 1-\dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}\right) (S^{*}-S(t))+K(S(t),W(t))\dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}\\&+ \int _0^{\infty }H\left( \dfrac{E(t-a)}{E^{*}}\right) \psi '(a)\mathrm{d}a\\&+K(S^{*},W^{*})\left( 1-\dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}\right) -K(S^{*},W^{*})\ln \dfrac{E(t)}{E^{*}}-\dfrac{E^{*}}{E(t)}K(S(t),W(t)). \end{aligned}$$

Adding and subtracting the term

$$\begin{aligned} K(S^{*},W^{*})\left( \ln \dfrac{K(S(t),W(t))}{K(S(t),W^{*})}+1\right) , \end{aligned}$$

and the explicit expression of H yields

$$\begin{aligned} V'(\Psi (t))= & {} \mu \left( 1-\dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}\right) (S^{*}-S(t))+\int _0^{\infty }H\left( \dfrac{E(t-a)}{E^{*}}\right) \psi '(a)\mathrm{d}a\\&+K(S^{*},W^{*})H\left( \dfrac{K(S(t),W(t))}{K(S(t),W^{*})}\right) \\&+K(S^{*},W^{*})\left( \ln \dfrac{K(S(t),W(t))}{K(S(t),W^{*})}-\ln \dfrac{E(t)}{E^{*}}\right. \\&\left. -\dfrac{E^{*}K(S(t),W(t))}{E(t)K(S^{*},W^{*})}-\dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}+2\right) , \end{aligned}$$

from this and the following equality

$$\begin{aligned} \ln \dfrac{K(S(t),W(t))}{K(S(t),W^{*})}=\ln \dfrac{K(S(t),W(t))}{K(S^{*},W^{*})}+\ln \dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}, \end{aligned}$$

we find,

$$\begin{aligned} V'(\Psi (t))= & {} \mu \left( 1-\dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}\right) (S^{*}-S(t))+ \int _0^{\infty }H\left( \dfrac{E(t-a)}{E^{*}}\right) \psi '(a)\mathrm{d}a \\&+K(S^{*},W^{*})H\left( \dfrac{K(S(t),W(t))}{K(S(t),W^{*})}\right) \\&+K(S^{*},W^{*})\left( \ln \dfrac{E^{*}K(S(t),W(t))}{E(t)K(S^{*},W^{*})}-\dfrac{E^{*}K(S(t),W(t))}{E(t)K(S^{*},W^{*})}\right. \\&\left. +\ln \dfrac{f(S^{*},W^{*})}{f(S(t),W^{*})} -\dfrac{f(S^{*},W^{*})}{K(S(t),W^{*})}+2\right) , \end{aligned}$$

therefore, in view of the definition of the function \(\psi ,\)

$$\begin{aligned} V'(\Psi (t))= & {} \mu \left( 1-\dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}\right) (S^{*}-S(t))K(S^{*},W^{*})\left( H\left( \dfrac{K(S(t),W(t))}{K(S(t),W^{*})}\right) \right. \\&\left. -\int _0^{\infty }H\left( \dfrac{E(t-a)}{E^{*}}\right) \mathrm{d}m(a)\mathrm{d}a\right) \\&-K(S^{*},W^{*})\left\{ H\left( \dfrac{E^{*}K(S(t),W(t))}{E(t)K(S^{*},W^{*})}\right) +H\left( \dfrac{K(S^{*},W^{*})}{K(S(t),W^{*})}\right) \right\} . \end{aligned}$$

Since K is nondecreasing in S, the first term is nonpositive. Now, we set

$$\begin{aligned} X=H\left( \dfrac{K(S(t),W(t))}{K(S(t),W^{*})}\right) -\int _0^{\infty }H\left( \dfrac{E(t-a)}{E^{*}}\right) \mathrm{d}m(a), \end{aligned}$$

and we claim that X is negative. Indeed, using concaveness of H, and using Jensen inequality see [4], we get

$$\begin{aligned} X\le & {} H\left( \dfrac{K(S(t),W(t))}{K(S(t),W^{*})}\right) -H\left( \int _0^{\infty }\dfrac{E(t-a)}{E^{*}}\mathrm{d}m(a)\right) , \end{aligned}$$

from the definition of \(\mathrm{d}m(a)\) and J we have,

$$\begin{aligned} X\le & {} H\left( \dfrac{K(S(t),W(t))}{K(S(t),W^{*})}\right) -H\left( \dfrac{W(t)}{W^{*}}\right) . \end{aligned}$$

Considering t verifying \(Z:=\dfrac{W(t)}{W^{*}}<1;\) and according to the hypothesis (5.3), we obtain

$$\begin{aligned} \dfrac{K(S(t),W(t))}{K(S(t),W^{*})}\ge \dfrac{W(t)}{W^{*}}. \end{aligned}$$

Then, using \(H(1)=0,\) H is nonincreasing in (0, 1),  and K is nondecreasing with respect to J we get,

$$\begin{aligned} H\left( \dfrac{K(S(t),W(t))}{K(S(t),W^{*})}\right) \le H\left( \dfrac{W(t)}{W^{*}}\right) , \end{aligned}$$

hence \(X\le 0.\)

For the remained values of t,  means \(Z>1,\) using (5.3), we have

$$\begin{aligned} \dfrac{K(S(t),W(t))}{K(S(t),W^{*})}\le \dfrac{W(t)}{W^{*}}, \end{aligned}$$

hence, (H is nondecreasing in \((1,\infty )\))

$$\begin{aligned} H\left( \dfrac{K(S(t),W(t))}{K(S(t),W^{*})}\right) \le H\left( \dfrac{W(t)}{W^{*}}\right) . \end{aligned}$$

As a result, the result is shown and hence \(\dfrac{\mathrm{d}V}{\mathrm{d}t}\le 0.\)

Remarking \(\dfrac{\mathrm{d}}{\mathrm{d}t}V(\Psi (t))=0\) leads to \(S(t)=S^{*},\) \(\forall t\in {\mathbb {R}}\) also

$$\begin{aligned} H\left( \dfrac{K(S(t),W(t))E^{*}}{K(S(t),W^{*})E(t)}\right) =0. \end{aligned}$$

and thus

$$\begin{aligned} K(S^{*},W(t))E^{*}=K(S^{*},W^{*})E(t) \end{aligned}$$
(6.6)

The first eq. in (3.2) yields

$$\begin{aligned} A-\mu S^{*}=K(S^{*},W(t)), \end{aligned}$$

combined with (5.1) we arrive at

$$\begin{aligned} K(S^{*},W(t))=K(S^{*},W^{*}), \end{aligned}$$

then \(W(t)=W^{*}\) \(\forall t\in {\mathbb {R}}.\) Substituting this result in (6.6), we get

$$\begin{aligned} E(t)=E^{*}, \;\ \;\ \forall t\in {\mathbb {R}}. \end{aligned}$$

Using the same procedures used in the proof of Theorem 4.1 leads to the GAS of the EE. As the equality \(\frac{\mathrm{d}}{\mathrm{d}t}V(\Psi (t))=0\) only checked if \(S=S^{*},\) hence EE is unique. \(\square \)

7 Graphical representations

Here, we will offer some illustrations of the obtained results in the previous sections. Further, we will give the method of choosing some parameters. At first, using euler explicit formula for approximating the first-order derivative to the system (1.2) we get

$$\begin{aligned} \left\{ \begin{array}{l} S(t+\triangle t)=S(t)+\triangle t(\Lambda -\mu S(t)-G(S(t),W(t))), \\ E(t+\triangle t)=E(t)+\triangle t\left( K(S(t),W(t))-(\mu +\alpha )E(t)\right) , \\ J(t)=\alpha \sum _0 ^\infty \triangle \eta \beta (\eta \triangle \eta ) \mathrm{e}^{-\mu \eta \triangle \eta }\digamma (\eta \triangle \eta )E(t-\eta ), \\ S(0)=S_0 , \quad E(t)=\phi (t), t<0, \end{array} \right. \end{aligned}$$
(7.1)

Now, let us discuss the method of choosing the transmission rate \(\beta (a)\). It is been shown in the first section that the age structured SIR system can lose its epidemiological precision in the case of infection with a large (or variable) latency stage. In several papers (such as [54]), the following transmission functional is considered

$$\begin{aligned} \beta (a)=\left\{ \begin{array}{ll}{0,} &{} { \text{ if } a \le \tau _{1}} \\ {\beta _1\left( a-\tau _{1}\right) ^{2} e^{-0.2\left( a-\tau _{1}\right) },} &{} { \text{ if } a>\tau _{1}.}\end{array}\right. , \end{aligned}$$
(7.2)

where in fact, for \(0<a<\tau _1\) it represents the latency stage. This kind of functionals cannot be considered for age structured SEIR system (1.2). In Fig. 1, the choice of transmission functional depends on the average of the latency stage where for (A) the latency stage is small (\(a_1=7 \) weeks) which means that the SIR model can be used with a very good epidemiological precision. For (B), the latency stage is very long (\(a_2=68 \) week) which means that the SIR model is not suitable for this case of infections; in this case, the SEIR is more precise then the SIR model. In fact, for the reason of modeling the latency stage it is better to consider the transmission functional used in (C) (which means that \(\tau _1 =0\)) for the SEIR model

Fig. 1
figure 1

The method of choosing the transmission functional with \(\beta _1=40.10^{-3}\)

Full size image

Now, we will provide some examples for various incidence functional to confirm the obtained mathematical results:

Example 1

we consider the Beddington–DeAngelis incidence,

$$\begin{aligned} K(S,W)=\frac{SW}{1+c_1 S + c_2 W}, \end{aligned}$$

Using this nonlinear incidence, we will verify the global behavior of the system (2.4). At first, the associated BRN is

$$\begin{aligned} R_0= \frac{\alpha {\bar{N}}}{(1+C_1 {\bar{N}})(\mu + \alpha )}\int _0^{\infty }\beta (\eta )\mathrm{e}^{-\mu \eta -\int _0 ^\eta \gamma (\sigma )\mathrm{d}\sigma } \mathrm{d}\eta . \end{aligned}$$
(7.3)

for Fig. 2 we utilize the following parameter set:

$$\begin{aligned} \Gamma= & {} 3\times 10^{-3},~~\mu =0.1,~~\alpha =10^{-6},~~c_1=0.01,~~c_2=0.01,~~\gamma (\eta )=\gamma ^*=0.01, ~~ \nonumber \\ S_0= & {} 0.080,~~E(t)=0.05,~~ t\in ]-\infty ,0]. \end{aligned}$$
(7.4)
Fig. 2
figure 2

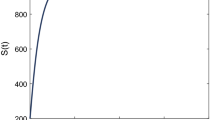
The global behavior of the SEIR system with difference equations with the Beddington–DeAngelis incidence function in both cases \(R_0<1\) and \(R_0>1\) where we use the set of parameters (7.4) for a we used \(\beta _1=3\times 10^3\) and for b we used \(\beta _1=\times 10^3\)

Full size image

Example 2

Now, we consider a second example of another incidence functional that our analysis can fit, which is the ratio-dependent incidence function which is expressed as

$$\begin{aligned} K(S,W)=\frac{SW}{S+W}, \end{aligned}$$

Using the same arguments, we can calculate the BRN which is written as

$$\begin{aligned} R_0= \frac{\alpha }{(\mu + \alpha )}\int _0^{\infty }\beta (\eta \triangle \eta )\mathrm{e}^{-\mu \eta -\int _0 ^\eta \gamma (\sigma )d\sigma } d\eta . \end{aligned}$$
(7.5)

In Fig. 3, we use the set:

$$\begin{aligned} \Gamma= & {} 3\times 10^{-3},~~\mu =0.1,~~\alpha =10^{-6},~~\gamma (\eta )=\gamma ^*=0.01, ~~ \nonumber \\ S_0= & {} 0.080,~~E(t)=0.05,~~ t\in ]-\infty ,0]. \end{aligned}$$
(7.6)
Fig. 3
figure 3

The global behavior of the SEIR system with difference equations with the ratio-dependent incidence function in both cases \(R_0<1\) and \(R_0>1\) where we use the set (7.6) and for a we used \(\beta _1=10^2\) and for b we used \(\beta _1=40\)

Full size image

Example 3

For the last example that we will consider is the Crowley–Martin which is expressed as

$$\begin{aligned} K(S,W)=\frac{SW}{1+c_1S+c_2W+c_1 c_2 SW}, \end{aligned}$$

Using the same arguments, we can calculate the BRN which is written as

$$\begin{aligned} R_0= \frac{\alpha {\bar{N}}}{(1+C_1 {\bar{N}})(\mu + \alpha )}\int _0^{\infty }\beta (\eta )\mathrm{e}^{-\mu \eta -\int _0 ^\eta \gamma (\sigma )\mathrm{d}\sigma } \mathrm{d}\eta . \end{aligned}$$
(7.7)

In Fig. 4, we use the set:

$$\begin{aligned} \Gamma= & {} 3\times 10^{-3},~~\mu =0.1,~~\alpha =10^{-6},~~c_1=0.01,~~c_2=0.01,~~\gamma (\eta )=\gamma ^*=0.01, ~~\nonumber \\ S_0= & {} 0.080,~~E(t)=0.05,~~ t\in ]-\infty ,0]. \end{aligned}$$
(7.8)
Fig. 4
figure 4

The global behavior of the SEIR system with difference equations with the Crowley–Martin incidence function in both cases \(R_0<1\) and \(R_0>1\) where we use the set (7.8) and for a we used \(\beta _1=2\times 10^3\) and for b we used \(\beta _1=2.5\times 10^3\)

Full size image

8 Discussion

We investigate in this research with a new approach for determining the global conduct of difference equations with infinite delay. Our starting point was an age-structured SEIR model, and by applying the characteristic method and some calculations, we transformed the aged structured model (1.2) into a system with difference equations and infinite delay. In the literature, there many works that deal with the dynamical conduct of age-structured models we mention a few [23, 24, 31,32,33, 38], but they analyze the age-structured model directly. But here we investigate the system with difference equations and infinite delay. To mention the global conduct of these kind of models is not very known, where through this paper we arrived to put the first steps in determining the global dynamics for this kind of systems. To mention that the construction method of LF is radically different where the infinite delay plays a crucial role in the building method. Indeed, our global analysis is entirely governed by the value of BRN where for \(R_0\le 1\) we get the GAS of the DFE and for \(R_0>1\) we obtain the GAS of the EE. Also, we can highlight that the very well-known method for proving the GAS of equilibria is to show the global attraction of an equilibrium using Lyapunov function and the local stability of the same equilibrium, but here we use a different approach, where the local stability is very tough to be achieved; hence, we use the total trajectory system (see chapter 9 in [51]), also the uniform persistence (for the EE) for avoiding analyzing the local behavior of the equilibria, where determining the proprieties of the \(\alpha \)-limit and \(\omega \)-limit sets is more handseled in our case, where the main purpose is to prove that these sets contain only the DFE (for \(R_0<1\)) and the EE (for \(R_0>1\)) as it has been shown in the Proof of Theorem 4.1, also Theorem 6.2, which is the main motivation of our research. Furthermore, A wide class of nonlinear incidence functions is included which means that the incidence functional has no influence on the threshold dynamics of this research. In fact, this result is confirmed numerically, where we considered three examples the first is the Beddington–DeAngelis functional response in Fig. 2, which highlights the achievement of the threshold behavior of the SEIR system with difference Eq. (2.4). The second example is the ratio-dependent functional response where the same results are achieved in Fig. 3. The last example is the Crowley–Martin incidence function, where the conduct of solution is affected by the value of BRN and it is shown through Fig. 4.

The main result achieved in this research is not confined to determine the global behavior of age-structured models only (this result is already achieved through many types of research as it is been mentioned in the first section) but is to put a background for treating systems with differential equations and infinite delay. This result can be applied to many other fields as ecological, eco-epidemiological systems [55].