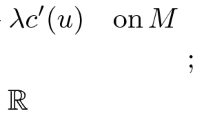Abstract
In this paper, by using variational methods we investigate the existence of solutions for the following system of elliptic equations
where (M, g) is a smooth closed Riemannian manifold of dimension \(n\ge 3, \Delta _{g}\) is the Laplace–Beltrami operator, a, b and c are functions Hölder continuous in M, f is a smooth function and \(\alpha>1, \beta >1\) are two real numbers such that \(\alpha + \beta = 2^*,\) where \( 2^{*}= 2n/(n-2)\) denotes the critical Sobolev exponent. We get these results by assuming sufficient conditions on the function \(h= \frac{\alpha }{2^{*}} a + \frac{2\sqrt{\alpha \beta }}{2^{*}}b + \frac{\beta }{2^{*}} c\) related to the linear geometric potential \(\frac{n-2}{4(n-1)}R_{g}\), where \(R_{g}\) is the scalar curvature associated to the metric g.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let (M, g) be a smooth closed Riemannian manifold of dimension \(n\ge 3\). We are concerned with the existence of solutions of the following system:
where \(\Delta _{g}\) is the Laplace–Beltrami operator, a, b and c are functions Hölder continuous in M, f is a smooth function, and \(\alpha>1, \beta >1\) are real constants satisfying \(\alpha + \beta = 2^*\), where \(2^{*}= 2n/(n-2)\) is the critical Sobolev exponent.
Coupled systems of nonlinear equations like (1.1) are now parts of several important branches of mathematical physics. They appear in the Hartree-Fock theory for Bose–Einstein double condensates, in fiber-optic theory, in the theory of Langmuir waves in plasma physics, and in the behavior of deep water waves and freak waves in the ocean. A general reference in book form on such systems and their role in physics is by Ablowitz et al. [1].
Motivated by the varied applications the existence of solutions and their qualitative properties have been the object of study by many researchers, see for instance, [2, 6, 7, 21] for problems in Euclidean domains and [10, 11, 18, 20] in Riemannian context.
Next, we would like to mention some works that are strongly related to the system we propose to study. We begin with work due to Alves et al. [2], which the authors looked for positive solutions of the elliptic differential system
where \(\Omega \) is a bounded domain in \({\mathbb {R}}^n, n\ge 3\), with smooth boundary and Dirichlet homogeneous boundary conditions. The main point is to compare the value of \(\alpha + \beta \) with the Sobolev critical exponent. Depending on how the parameters \(\tau , \mu , \sigma \in {\mathbb {R}}\) relate to \(\lambda _1\) (the first eigenvalue of the Laplacian operator), existence and nonexistence results are provided and compared with the classical result of Brezis and Nirenberg concerning elliptic differential equations with Sobolev critical exponent. The second paper is due to Hebey [18], which the author considers elliptic systems of Yamabe-type equations
where \(A=(A_{ij}): M \rightarrow M_p\) is a smooth function, \(p \in {\mathbb {Z}}, p \ge 1\), and \(M_p^s({\mathbb {R}})\) denotes the vector space of symmetric \(p \times p\) real matrices. Assuming sufficient conditions on the matrix A related to the linear geometric potential \(\frac{n-2}{4(n-1)}R_{g}\), the author studies the existence of minimizing solutions for this system, the existence of high-energy solutions, blow-up theory and its compactness properties.
The system (1.1) is strongly related to the equation
which has been intensively studied in literature, see for instance, Druet [8] and Vétois [27]. When we have \( a=\frac{n-2}{4(n-1)}R_{g}\) in the equation above, we obtain the prescribe scalar curvature equation
which is a generalization of the well-known Yamabe equation (when f is constant) whose positive solutions are such that the scalar curvature of the conformal metric \({\tilde{g}}=u^{2^{*} - 2}g\) is constant. The Eq. (1.2) has been studied, for example, by Aubin [3], Aubin and Hebey [5], Escobar and Schoen [13], Hebey and Vaugon [16, 17], Schoen [24], Trudinger [26] and Yamabe [28]. The study of this equation both in the classical form as in the prescribed form, motivated us in this research about the existence of solutions for system (1.1) in a compact Riemannian manifold.
Before presenting our main results, we need to introduce some notations and definitions. Throughout this work, we will denote by \(H^{1}(M)\) the Sobolev space of all functions in \(L^{2}(M)\) with one derivative (in the weak sense) in \(L^{2}(M)\). We equip \(H^{1}(M)\) with the standard \(\Vert \cdot \Vert _{H^1}-\)norm, that is, \( \Vert u\Vert _{H^{1}}^2 = \Vert \nabla u\Vert ^{2}_{2} + \Vert u\Vert ^{2}_{2}, \) where \(\Vert \cdot \Vert _{q}\) denotes the norm of the Lebesgue space \(L^{q}(M)\), whenever \(q\ge 1\). The norm of \(L^{q}(M)\times L^{q}(M)\) will be defined by \(\Vert (u,v)\Vert _{q}=\left( \Vert u\Vert _{q}^{q}+\Vert v\Vert _{q}\right) ^{1/q}.\)
We shall work with the space \(H = H^{1}(M)\times H^{1}(M)\) endowed with the norm
In this context, we say that a pair of functions \((u,v)\in H\) is a weak solution of (1.1), if for all \((\varphi , \psi ) \in H\), it holds
By elliptic regularity theory (for example, see Lee and Parker [23, Theorem 4.1]), any weak solution (u, v) of (1.1), is in \(C^{2}\times C^{2}\) when a, b and c are Hölder continuous, and is in \(C^{\infty }\times C^{\infty }\) when a, b and c are smooth functions.
An important relation obtained by Alves et al. [2] that we will use in this work is the following:
whenever \(\alpha + \beta \le 2^{*}\), where \(S_{\alpha +\beta }\) is the best Sobolev constant defined by
and \({\mathcal {S}}_{(\alpha ,\beta )}\) is defined by
When \(\alpha + \beta = 2^{*}\), we denote by \(S_{2^{*}}=K_{n}^{-2}\) and \({\mathcal {S}}_{(\alpha ,\beta )} = {\mathcal {S}}_{*}\), where \(K_{n}\) is the sharp constant for the embedding of \(H^{1}({\mathbb {R}}^{n})\) into \(L^{2^{*}}({\mathbb {R}}^{n})\).
Throughout this work we assume some very general hypotheses on the functions a, b, c and f that will allow us to obtain some existence results for system (1.1) through variational methods. Precisely, we assume that the function f satisfies
and the functions a, b and c satisfy the following coercivity condition: there exists \(C_{0}>0\) such that
Our first result in this work can be stated as follows:
Theorem 1.1
Let (M, g) be a closed Riemannian manifold of dimension \(n\ge 3\). Let \(\alpha ,\beta >1\) be two real numbers such that \(\alpha + \beta = 2^*\), and let a, b and c be functions Hölder continuous in M, and \(f\in C ^{\infty }\), with a, b and c satisfying (1.6) and f satisfying (1.5), writing \(h=\frac{ \alpha }{2^{*}} a + \frac{2\sqrt{\alpha \beta }}{2^{*}}b + \frac{\beta }{2^{*}} c\). Let \(x_{0}\) be some point in M such that \(f(x_{0})=\max _{M}f\). If, in addition, we assume that
Then, system (1.1) has a nontrivial solution.
Theorem 1.1 will be proved using the Mountain Pass Theorem without the Palais-Smale compactness condition. A delicate part is the estimating the minimax level in order to overcome the lack of compactness of the functional associated to system (1.1) caused by the critical growth of the nonlinearities. We achieve this objective following some ideas developed in [3, 4, 9]. Here we face some extra difficulties due to the tight coupling of the system.
As a consequence of Theorem 1.1, we prove the following results.
Corollary 1.2
Suppose the same assumptions of Theorem 1.1. Let \(x_{0}\) be some point in M such that \(f(x_{0})=\max _{M}f\). If, in addition, we assume \(b\le 0\) and
Then, system (1.1) has a pair of positive solutions.
Corollary 1.3
Suppose the same assumptions of Theorem 1.1 and that f is constant and positive. Let \(x_{0}\) be some point in M such that
Then, system (1.1) has a nontrivial solution.
For the next results, consider the functional \(E_h: H \rightarrow {\mathbb {R}}\) given by
and let
Define
Remark 1.4
When f is constant and equal to \(1, \lambda _{f}(M, g)\) is called of Yamabe invariant of the manifold (M, g), and is usually denoted by \(\lambda (M,g)\). In the particular case of the unit \(n-\)sphere \({\mathbb {S}}^{n}\) with the standard metric is denoted by \(\lambda ({\mathbb {S}}^{n})\). It is well known that when \(\lambda _{f}(M, g)<\frac{\lambda ({\mathbb {S}}^{n})}{(\max _{M}f)^{2/2^{*}}}\), there exists \(\varphi \in C^{\infty }(M)\) with \(\varphi >0\) and \(\int _{M}f\varphi ^{2^{*}}dv_{g}=1\) such that
with \(\lambda _{f}(M,g) = \int _{M}\left( |\nabla \varphi |^{2}_{g} + \frac{n-2}{4(n-1)}R_{g}\varphi ^{2}\right) dv_{g}.\) It is also known that \(\lambda ({\mathbb {S}}^{n}) = K_{n}^{-2}\), with
where \(\omega _{n}\) is the volume of the unit \(n-\)sphere (see [3, 8, 9]).
In the next results we deal with the case where the functions a, b and c satisfy the condition:
Remark 1.5
The coercivity condition (1.6) and (1.14) imply that given \(\psi \in H^{1}(M)\) and \(\xi , \zeta >0\) such that \(\left( \frac{\xi }{\zeta }\right) ^{2}= \frac{\alpha }{\beta }\), then
Therefore, \(-\Delta _{g} + \frac{n-2}{4(n-1)}R_{g}\) is also coercive. In particular we are dealing with the case where the Yamabe invariant is positive.
We can state the following result.
Theorem 1.6
Let (M, g) be a closed Riemannian manifold of dimension \(n\ge 3\). Let \(\alpha ,\beta >1\) be two real numbers such that \(\alpha + \beta = 2^*\), and let a, b and c be functions Hölder continuous in M, and \(f\in C ^{\infty }\), with a, b and c satisfying (1.6) and (1.14), and f satisfying (1.5). Let \(x_{0}\) be some point in M such that \(f(x_{0})=\max _{M}f\). If \(S_{f,h}^{(\alpha ,\beta )} < \frac{{\mathcal {S}}_{*}}{f(x_{0})^{2/2^{*}}}\), where \({\mathcal {S}}_{*}\) is defined in (1.4). Then, system (1.1) has a nontrivial solution.
Complementing Theorem 1.6 and inspired by [5, 13, 17], we prove the following theorems:
Theorem 1.7
Let (M, g) be a closed Riemannian manifold of dimension \(n\ge 3\). Let a, b and c be functions Hölder continuous in M satisfying (1.6) and (1.14). Assume that \(n\ge 6\) and M is not locally conformally flat. If at a point \(x_{0}\) where \(f(x_{0})=\max _{M}f\) is such that the Weyl tensor is nonvanishing (that is, \(|W_g(x_{0})|\ne 0\)). If we assume that
Then, \(S_{f,h}^{(\alpha ,\beta )} < \frac{{\mathcal {S}}_{*}}{f(x_{0})^{2/2^{*}}}\). Consequently, system (1.1) has a nontrivial solution.
Theorem 1.8
Let (M, g) be a closed Riemannian manifold of dimension \(n\ge 3\). Let a, b and c be functions Hölder continuous in M satisfying (1.6) and (1.14). Assume that \(n=3, 4\) or 5, or M is locally conformally flat, when \(n\ge 6\). Let \(x_{0}\in M\) be a point such that \(f(x_{0})=\max _{M}f> 0\). We have the following cases:
Then, \(S_{f,h}^{(\alpha ,\beta )} < \frac{{\mathcal {S}}_{*}}{f(x_{0})^{2/2^{*}}}\) unless M is conformal to the standard \({\mathbb {S}}^{n}\). Consequently, system (1.1) has a nontrivial solution. When \(n > 8\) the same conclusion holds if \(|\nabla W_g(x_{0})|\ne 0\) and \(\Delta ^{3}_{g} f(x_{0}) = 0\) or when \(|\nabla W_g(x_{0})|=0\) if \(|\nabla ^{2} W_g(x_{0})| \ne 0\) and \(\Delta ^{3}_{g} f(x_{0}) = \Delta ^{4}_{g} f(x_{0}) = 0\), or when all derivatives of \(W_g\) vanish at \(x_{0}\) if \(\Delta ^{m}_{g} f(x_{0}) = 0\) for all \(1\le m \le \frac{n}{2} - 1\).
Corollary 1.9
Suppose the same assumptions of Theorems 1.7 or 1.8. In addition, if \(b\le 0\) and the functions a and c satisfy
Then, system (1.1) has a pair of positive solutions.
Corollary 1.10
Suppose the same assumptions of Theorems 1.7 or 1.8. In addition, if we assume that \(f\ge 0, b=0\) and \(a= c = \frac{n-2}{4(n-1)}R_{g}\). Then, system (1.1) has a nontrivial solution. Moreover, we have that
Therefore, the pair \((\xi \varphi ,\zeta \varphi )\) (up to rescaling) is solution for the system, for any positive solution \(\varphi \in C^{\infty }\) of (1.13), where \(\int _{M}f\varphi ^{2^{*}}dv_{g}=1\) and \(\frac{\xi }{\zeta }=\left( \frac{\alpha }{\beta }\right) ^{1/2}\).
A special case is when we consider the unit \(n-\)sphere \({\mathbb {S}}^{n}\) with the standard metric \(g_{0}\), that is, the scalar curvature is \(R_{g_{0 } }= n(n-1)\). Note that this case is included in Theorem 1.1 when we assume the same hypotheses. Therefore the following theorem is a case special of Theorem 1.8, when \(M = {\mathbb {S}}^{n}/\Gamma \).
Theorem 1.11
Let \(\Gamma \) be a nontrivial finite group of isometries of \({\mathbb {S}}^{n}\) acting without fixed point on \({\mathbb {S}}^{n}\). Write \(M={\mathbb {S}}^{n}/\Gamma \), and let a, b, c and f be functions invariant under \(\Gamma \) and satisfying the same assumptions of Theorem 1.8. Then \(S_{f,h}^{(\alpha ,\beta )}({\mathbb {S}}^{n}/\Gamma ) < \frac{{\mathcal {S}}_{*}}{f(x_{0})^{2/2^{*}}}\), and therefore, system (1.1) has a nontrivial solution on \({\mathbb {S}}^{n}\).
Remark 1.12
Note that from [13], when f is invariant under \(\Gamma \) and \(\lambda _{f}({\mathbb {S}}^{n}/\Gamma )<\frac{\lambda ({\mathbb {S}}^{n})}{(\max _{M}f)^{2/2^{*}}}\), there is a positive solution \(\varphi \in C^{\infty }({\mathbb {S}}^{n})\) to the equation
where \(\int _{{\mathbb {S}}^{n}}f\varphi ^{2^{*}}dv_{g_{0}}=1\).
Corollary 1.13
Suppose the same assumptions of Theorem 1.11. In addition, if we assume that \(b=0, a= c = \frac{n(n-2)}{4}\) and \(f\ge 0\). Then, system (1.1) has a nontrival solution. Moreover, we have
Therefore, the pair \((\xi \varphi ,\zeta \varphi )\) (up to rescaling) is solution for system (1.1), where \(\varphi \in C^{\infty }\) is a positive solution of Eq. (1.17).
Corollary 1.14
Suppose the same assumptions of Theorem 1.11. In addition, if we assume that \(b=0, f=1\) and \(a= c = \frac{n(n-2)}{4}\) then we get that \(S^{(\alpha ,\beta )}({\mathbb {S}}^{n}) ={\mathcal {S}}_{*}\) and system (1.1) has infinitely many pair of positive solutions. Moreover, if (u, v) is a minimizer for \(S^{(\alpha ,\beta )}({\mathbb {S}}^{n})\) with \(u, v>0\), then up to rescaling u and v will have the following forms:
where \({\overline{x}} \in {\mathbb {S}}^{n}\), \(r=d_{g_{0}}(x,{\overline{x}}), \xi _{1},\zeta _{1}>0, \rho _{0}>1\) and \(\frac{\xi _{1}}{\zeta _{1}} = \left( \frac{\alpha }{\beta }\right) ^{1/2}\).
Corollary 1.15
Suppose the same assumptions of Theorem 1.11. In addition, if \(b\le 0\) and the functions a and c satisfy the following hypothesis
Then, system (1.1) has a pair of positive solutions on \({\mathbb {S}}^{n}\).
The paper is organized as follows. In Sect. 2 we prove an essential Sobolev inequality to prove the main results. In Sect. 3 we prove Theorem 1.1 and its consequences. In Sect. 4 we prove Theorems 1.6, 1.7 and 1.8. We dedicate Sect. 5 for the case of the sphere \({\mathbb {S}}^{n}\).
2 Some Preliminary Results
In [19], Hebey and Vaugon have established that the best constant for the Sobolev inequality is \(K^{2}_{n}\). Precisely, they proved that there is a positive constant B such that
for all \(u\in H^1(M)\). Moreover, if \(\Vert u\Vert _{2^{*}}^{2}\le K\Vert \nabla u\Vert _{2}^{2} + C\Vert u\Vert ^{2}_{2}\) for all \(u\in H^{1}(M)\), where K and C are positive constants, then \(K\ge K^{2}_{n}\).
Initially, we establish an inequality that will be used in the proof of the main results.
Lemma 2.1
Let \({\mathcal {S}}_{*}\) be the constant defined in (1.4) when \(\alpha + \beta = 2^{*}\). Then, there is a positive constant \(B_{0}\) such that
for all \((u,v)\in H\). Moreover, \(\left( {\mathcal {S}}_{*}\right) ^{-1}\) is the best constant such that the inequality holds.
Proof
Given \(u,v\in H^{1}(M)\), since \(\frac{\alpha }{2^{*}} + \frac{\beta }{2^{*}} = 1\), by Hölder’s inequality,
that is,
On the other hand, by Young’s inequality,
Choosing \(\varepsilon = \left[ \left( \frac{\alpha }{\beta }\right) ^{\beta /2^{*}} + \left( \frac{\beta }{\alpha }\right) ^{\alpha /2^{*}}\right] ^{-1} \frac{2^{*}}{\alpha }\), by a straightforward calculation, we get
and consequently,
Using (2.3) and the Sobolev inequality (2.1), we can find \(B>0\) such that
Therefore, we get that
for all \((u,v)\in H\), where \(B_{0}=B\left[ \left( \frac{\alpha }{\beta }\right) ^{\beta /2^{*}} + \left( \frac{\beta }{\alpha }\right) ^{\alpha /2^{*}}\right] ^{-1}\).
Finally, if \(S_{0}\) is a positive constant such that
for all \((u,v)\in H\), where \(B_{1}\) is some positive constant. We claim that \(S_{0}\ge {\mathcal {S}}_{*}^{-1}\). Indeed, given \(\varphi \in H^{1}(M)\) and writing \(u=\alpha ^{1/2}\varphi \) and \(v=\beta ^{1/2}\varphi \), by (2.4) we have
which gives us
for some \(B_2>0\). Since \(K_{n}^{-2}\) is the best constant in the Sobolev embedding theorem (see [4, 19]), we reach that
and since \({\mathcal {S}}_{*} = \left[ \left( \frac{\alpha }{\beta }\right) ^{\beta /2^{*}} + \left( \frac{\beta }{\alpha }\right) ^{\alpha /2^{*}}\right] K_{n}^{-2}\), we conclude the proof of the Lemma. \(\square \)
An immediate consequence this result is the following inequality.
Corollary 2.2
Let \(C=\max \{{\mathcal {S}}_{*}^{-1}, B_{0}\}\), then we have
Another result that will be important later on is the following Brezis-Lieb type lemma.
Lemma 2.3
Let \(u_{m}\rightharpoonup u\) and \(v_{m}\rightharpoonup v\) in \(H^{1}(M)\) and let \(\ell \in L^{\infty }(M)\). Then we have
where \(o_{m}(1) \rightarrow 0\) as \(m \rightarrow \infty \).
Proof
The proof is similar to [6, Lemma 2.1] and we omit it. \(\square \)
3 Proof of Theorem 1.1
We begin this section by introducing some notations and definitions. First, consider the functional \(I: H\rightarrow {\mathbb {R}}\) associated to system (1.1) given by
Since the functions a, b and c are Hölder continuous and f is a smooth function, we have that I is well defined and by standard arguments \(I\in C^{1}(H, {\mathbb {R}})\) with
Hence, a critical point of I is a weak solution of system (1.1) and reciprocally. Moreover, by the coercivity condition (1.6), it is easy to see that I satisfies the geometry of the Mountain Pass Theorem, that is, there exist \(\rho >0\) and \(R>0\) such that
and there exists some \(({\tilde{u}},{\tilde{v}})\in H\) with \(\Vert ({\tilde{u}},{\tilde{v}})\Vert >R\) and such that \(I({\tilde{u}},{\tilde{v}})<0\).
Now, for some pair \(({\tilde{u}},{\tilde{v}})\) satisfying the second condition above, we consider the set \( \Gamma = \left\{ \gamma \in C([0,1], H) \,: \, \gamma (0) = 0 \ \text {and} \ \gamma (1)= ({\tilde{u}},{\tilde{v}})\right\} \), and so we can define the minimax level
Next, we will estimate the level c. This will be a very delicate result.
Lemma 3.1
Suppose that (1.7) holds, then
for some par \(({\tilde{u}},{\tilde{v}})\in H\), where c is defined in (3.2).
Proof
Initially, we will verify that there exists \(({\overline{u}},{\overline{v}}) \in H\) such that
where Q is defined by
for \((u, v)\in H\) with \(\int _{M}f(x)|u|^{\alpha }|v|^{\beta }dv_{g}>0\).
The proof will be done considering the cases \(n\ge 4\) and \(n=3\).
Let \(x_{0}\in M\) be a point such that \(f(x_{0})=\max \{f(x)\,:\, x \in M\}\). We denote by \(B_{\delta }(x_{0})\) the geodesic ball of center \(x_{0}\) and radius \(\delta \), with \(\delta \in (0,i_{g})\), where \(i_g\) is the injective radius of (M, g). We choose \(\delta \) enough small if necessary such that \(f(x)>0\) on \(B_{2\delta }(x_{0})\). In normal coordinates we can write the following expansions
where \(\det (g)\) is the determinant of the components of the metric g and \(h=\frac{\alpha }{2^{*}} a + \frac{2\sqrt{\alpha \beta }}{2^{*}}b + \frac{\beta }{2^{*}} c \), with \(\theta \in (0,1)\) such that \(h\in C^{0,\theta }(M)\), and \(\eta \in C^{\infty }_{0}([-2\delta ,2\delta ])\), with \(\eta = 1\) in \([-\delta ,\delta ]\) and \(0\le \eta \le 1\).
Now, for \(n \ge 4\) and \(\epsilon >0\), we consider the following sequence of functions
For \(0<p,q<\infty \), we put \(I^{p}_{q}:= \displaystyle {\int _{0}^{\infty }t^{p}(1+ t)^{-q}dt}\), and then it holds that
When \(n=4\), from [3, 4], we get
Now considering \(\xi , \zeta >0\) such that \(\frac{\xi }{\zeta }= \sqrt{\frac{\alpha }{\beta }}\), we obtain
Then, by (3.8) and (3.7), it follows that (for \(\epsilon \) enough small):
where \(\kappa (\alpha ,\beta )=\left[ \left( \frac{\alpha }{\beta }\right) ^{\beta /2^{*}} + \left( \frac{\beta }{\alpha }\right) ^{\alpha /2^{*}}\right] \). Consequently, as \(I_{4}^{2}=\int _{0}^{\infty }\frac{t^{2}}{(1+t)^{4}}dt=\frac{1}{3}\) we reach
For \(n>4\), from [3, 4], we have
Thus, similarly to what we did above, we find that
Now, we recall, by (1.7), that
for \(n\ge 4\). Then, by (3.9) and (3.10), it follows, for \(\epsilon \) sufficient small, that (3.4) holds.
Now, we consider the case \(n=3\). As a, b and c satisfy the condition (1.6), it follows that \(-\Delta _{g} + h\) is a coercive operator. Then we can consider \(G_{x_{0}}:M\backslash \{x_{0}\}\longrightarrow {\mathbb {R}}\) the Green function this operator, that is,
where \(\delta _{x_{0}}\) is the Dirac mass at \(x_{0}\). It is well known that for x close to \(x_{0}\) we can write
Next, we will use Druet’s idea [9]. By using the cut-off function \(\eta \), we can write \(G_{x_{0}}\) as follows:
where \(w_{h}\in C^{\infty }_{loc}(M\backslash \{x_{0}\})\). In \(M\backslash B_{\delta }(x_{0})\), we have
And, in \(B_{\delta }(x_{0})\), we write in normal coordinates
In particular, we have that the right side of the above equation is in \(L^{s}(M)\) for all \(1<s<3\), so by standard elliptic theory, \(w_{h}\in C^{0}(M)\cap H^{1}(M)\) and moreover \(w_{h}(x_{0}) = \omega _{2}m(x_{0})\) (for more details see Druet [9]).
As we have assumed that \(h\le \frac{1}{8}R_{g}\) (see (1.7)), there exists \({\overline{G}}_{x_{0}}\) the Green function of \(-\Delta _{g} + \frac{1}{8}R_{g}\), and as above we can write
Now, note that
Green’s Formula and the hypothesis \(h \le \frac{1}{8}R_{g}\) (but not equal) gives us
so, \({\overline{w}}(y) < w_{h}(y)\), for all \(y\in M\), in particular, as \({\overline{w}}(x_{0})= \omega _{2}{\overline{m}}(x_{0})\ge 0\) it follows that \(w_{h}(x_{0})>0\) (here \({\overline{m}}(x_{0})\) is given by the expansion of \({\overline{G}}_{x_{0}}\) in a neighborhood of \(x_{0}\), and the positive mass theorem garantee that \({\overline{m}}(x_{0})\ge 0\), see [24, 25].
For \(\epsilon >0\) and \(x\in M\), we define the function
where \(u_{\epsilon }\) is the test-function defined as (3.6).
As we did in case \(n\ge 4\), we estimate \(Q (\xi v_{\epsilon },\zeta v_{\epsilon })\). For this we will estimate \(\int _{M}(|\nabla v_{\epsilon }|_{g}^{2} + hv_{\epsilon }^{2})d{g}\) and \(\int _{M}f(x)v_{\epsilon }^{6}dv_{g}\). First, note that
where \(U_{\epsilon }(x)=\frac{1}{(\epsilon + d_{g}(x,x_{0})^{2})^{1/2}}\).
Note that we can write
With that we calculate:
Now, as in normal coordinates the Laplacian of a radial function F can be written as follows \(-\Delta _{g}F = \frac{1}{r^{n-1}\sqrt{\det (g)}}\partial _{r}(r^{n-1}\sqrt{\det (g)}\partial _{r}F)\), we have
where \(-\Delta \) is the Euclidian Laplacian. Since \(-\Delta U_{\epsilon } = 3\epsilon U_{\epsilon }^{5}\), and using (3.17), we get that
So,
Now, writing that
we have
So, we get that
Finally, we calculate
first, by (3.11), we have
Second, we get from Eqs. (3.12) and (3.13) that
so, we have
Now, using the obtained in (3.18), (3.19), (3.20), (3.25) and (3.27) in the Eq. (3.16), gives us the following estimate
Now, we estimate \(\int _{M}f(x)v_{\epsilon }^{6}dv_{g}\).
Using the expansion (3.5) in normal coordinate,
so, we have
Similarly, we get
Also, we calculate
From what was obtained in (3.30)–(3.32) and the fact that \(\omega _{2}I_{5/2}^{1/2} = 2\int _{{\mathbb {R}}^{n}}U_{1}^{5}dx = 2\int _{{\mathbb {R}}^{n}}(-\Delta U_{1})dx = \frac{2}{3}\omega _{2}\), we have that
Now, we can calculate \(Q (\xi v_{\epsilon }, \zeta v_{\epsilon })\) for \(\epsilon \) enough small, by the Eqs. (3.28) and (3.33),
as \(I_{3}^{1/2}=\frac{1}{3}I_{3}^{3/2}\) and \(\left( \frac{1}{6}\omega _{2}I_{3}^{3/2}\right) ^{1/3}=\frac{K_{3}^{2}}{2}\omega _{2}I_{3}^{3/2}\) (see (3.7)), we get that
As \(w_{h}(x_{0})>0\), then
Therefore, we obtain (3.4), when \(n=3\).
Now, in order to prove (3.3), we define for any \(t>0\) the following functional:
where \(X_{u}=(\xi ^{2} + \zeta ^{2})\int _{M}|\nabla u|^{2}_{g}dv_{g} + \int _{M}\left[ \xi ^{2}a + 2\xi \zeta b+ \zeta ^{2}c\right] u^{2}dv_{g}\) and \(Y_{u}=\xi ^{\alpha }\zeta ^{\beta }\int _{M}f(x)u^{2^*}dv_{g}\).
We want to find \(t_{0}>0\) such that \(\Phi '(t_{0})=0\), that is, such that \(t_{0}X - t_{0}^{2^{*} - 1}Y = 0\). Hence,
Therefore, \(t_{0}\) is the only critical point of \(\Phi \) and since \(\Phi (t)\rightarrow -\infty \) as \(t\rightarrow \infty \), then \(t_{0}\) is a maximum point for \(\Phi \).
Note that, by the above calculations, we get
Choose \(t_{1}>t_{0}\) large such that \(\Phi (t_{1})<0\) and write \({\tilde{u}}=t_{1}\xi u_{\epsilon }(x)\) and \({\tilde{v}}=t_{1}\zeta u_{\epsilon }(x)\) when \(n\ge 4\) (and \({\tilde{u}}=t_{1}\xi v_{\epsilon }\) and \({\tilde{v}}=t_{1}\zeta v_{\epsilon }\) when \(n=3\)). So,
which proves (3.3). This completes the proof. \(\square \)
We now have the tools for the proof of Theorem 1.1.
Proof of the Theorem 1.1
By Ekeland Variational Principle, there is a sequence \(\{(u_{m},v_{m})\}\) in H such that
Now note that
Thus, by the coercivity hypothesis (1.6), we obtain that \(\{(u_{m},v_{m})\}\) is bounded in H. Hence, there exists \((u_{0},v_{0}) \) in H such that, up to a subsequence,
It is easy to see that \(f(x)|u_{m}|^{\alpha - 2}u_{m}|v_{m}|^{\beta } \) is an uniformly bounded sequence in \(L^{2^{*}/(2^{*} -1)}(M)\) and converges pointwisely to \(f(x)|u_{0}|^{\alpha - 2}u_{0}|v_{0}|^{\beta } \), from Lemma 4.8 in [22], we have
Similarly we obtain the same for the sequence \(f(x)|u_{m}|^{\alpha }v_{m} |v_{m}|^{\beta -2}\). As \(I'(u_{m},v_{m})\cdot (\varphi ,\psi )= o_{m}(1)\), for all \((\varphi ,\psi )\in H\), by using (3.36), (3.37) and letting \(m \rightarrow \infty \), we reach that \(I'(u_{0},v_{0})=0\), that is, \((u_{0},v_{0})\) is a weak solution of (1.1).
The next step is to prove that \(u_{0}\not = 0\) and \(v_{0}\not = 0\).
First, let us see that \(u_{0} = 0\), if and only if, \(v_{0}= 0\). Indeed, if \(u_{0} = 0\), then \(-\Delta _g v_{0} + c(x)v_{0} = 0\ \ \text {in} \ \ M\). So by coercivity hypothesis (1.6), we have that \(v_{0}=0\).
If \(u_{0} = 0\) and \(v_{0} = 0\), we write \(\tau = \displaystyle {\lim _{m\longrightarrow 0}\int _{M} \left( |\nabla u_{m}|^{2}_{g} + |\nabla v_{m}|^{2}_{g}\right) dv_{g}}\). Since \(I'(u_{m},v_{m})\cdot (u_{m},v_{m})=o_{m}(1)\), then we get
On the other hand, since \(I(u_{m},v_{m})= \textrm{c} + o_{m}(1)\), then we get \(\tau =n\textrm{c}\).
Now, by Lemma 2.1, we know that there is a positive constant \(B_{0}\) such that
Thus, passing to the limit in the inequality above and using (3.36), we get \( (n\textrm{c})^{2/2^{*}}\le f(x_{0})^{(n-2)/n}{\mathcal {S}}_{*}^{-1}n\textrm{c}\). Hence,
But, this contradicts the estimate obtained for the level \(\textrm{c}\) in Lemma 3.1. Therefore, \(u_{0}\ne 0\) and \(v_{0}\not = 0\). Thus, we conclude the proof of Theorem 1.1. \(\square \)
Proof of Corollary 1.2
Consider the functional \(J: H \rightarrow {\mathbb {R}}\) defined by
This functional satisfies the same properties of I. Using the same test functions to estimate the minimax level and using the same steps as in the previous proof, one obtains that there exists \((u_{0},v_{0}) \in H\) a nontrivial critical point of the functional J. Now, we will prove that \(u_{0}\) and \(v_{0}\) are positive solutions. First, we denote by \(u^{+}=\max \{u,0\}\) and \(u^{-}=\min \{u,0\}\). Then, since \(J'(u_{0},v_{0})\cdot (u_{0}^{-},v_{0}^{-})=0\), we get
As \(b\le 0 \) and \(u_{0}^{+}v_{0}^{-} + u_{0}^{-}v_{0}^{+}\le 0\), we deduce that
and consequently by (1.6), we reach \(u_{0}^{-}= 0\) and \(v_{0}^{-}=0\). Therefore, \(u_{0}\ge 0\) and \(v_{0}\ge 0\). By elliptic regularity theory and maximum principle follows that \(u_{0}>0\) and \(v_{0} >0\). \(\square \)
4 Proof of Theorems 1.6, 1.7 and 1.8
In this section, we will study the case where the combination \(h=\frac{\alpha }{2^{*}}a + \frac{2\sqrt{\alpha \beta }}{2^{*}}b + \frac{\beta }{2^{*}}c\) is less than or equal to \(\frac{n-2}{4(n-1)}R_{g}\). We will begin by recalling some notations and definitions. Considering the functional \(E_h: H \rightarrow {\mathbb {R}}\) given by
and constraint set \( \Lambda ^{\alpha ,\beta }_{f}:= \left\{ (u,v) \in H\,:\, \int _{M}f(x)|u|^{\alpha }|v|^{\beta }dv_{g} = 1\right\} . \)
Note that \(E_h\) is bounded from below on \(\Lambda ^{\alpha ,\beta }_{f}\). Indeed, by the coercivity condition (1.6) and Corollary 2.2, we have
for all \((u,v)\in \Lambda ^{\alpha ,\beta }_{f}\). Thus, we can consider
If there exists \((u,v)\in \Lambda ^{\alpha ,\beta }_{f}\) which achieves the infimum \(S_{f,h}^{(\alpha ,\beta )}\), it turns out that (u, v) will be a weak solution of the following system
In order to achieve the existence result we need to recall some results due to Escobar–Schoen [13], Aubin–Hebey [5] and Hebey–Vaugon [17] for Prescribe scalar curvature problem, which prove that f is the scalar curvature of a conformal metric (see also [4]).
Before, let us remember that, when \(\max _{M} f>0\) it is known that \(\lambda _{f}(M, g)\le \frac{\lambda ({\mathbb {S}}^{n})}{(\max _{M} f)^{2/2^{*}}}\), where \(\lambda _{f}(M, g)\) is defined in (1.12), and if \(\lambda _{f}(M, g) < \frac{\lambda ({\mathbb {S}}^{n})}{(\max _{M} f)^{2/2^{*}}}\), then there is \(\varphi \in C^{\infty }\) with \(\varphi >0, \int _{M}f(x)\varphi ^{2^{*}}dv_{g}=1\), and such that
that is, \(\varphi \) is a positive solution of the equation \(-\Delta _{g}u + \frac{n-2}{4(n-1)}R_{g}u=\lambda _{f}(M, g)fu^{2^{*}-1}\). Therefore, \({\hat{\textrm{g}}}=\varphi ^{2^{*}-2}g\) is a conformal metric to g, where \(f=R_{{\hat{\textrm{g}}}}\) is the scalar curvature of the metric \({\hat{\textrm{g}}}\), and moreover, \(\lambda _{f}(M,{\hat{\textrm{g}}}) = \lambda _{f}(M, g)\).
Theorem A
(Escobar–Schoen [13]). Let f be a \(C^{\infty }\) function with \(\max _{M} f > 0\) on a compact riemannian manifold (M, g) not conformal to the sphere with the standard metric. Then if \(n=3\),
and consequently f is the scalar curvature of a conformal metric. The same conclusion holds for the locally conformally flat manifolds when \(n \ge 4\) if at a point \(x_{0}\) where f is maximal, all its derivatives up to order \(n - 2\) vanish.
Theorem B
(Aubin–Hebey [5]). Assume that \(n\ge 6\) and (M, g) is not locally conformally flat. Let f be a smooth function with \(\max _{M}f>0\). If at a point \(x_{0}\) where \(f(x_{0})=\max _{M}f\) is such that the Weyl tensor is nonvanishing (that is, \(|W_g(x_{0})|\ne 0\)) and \(\Delta _{g} f(x_{0})=0\), then if \(n=6\),
and consequently f is the scalar curvature of a conformal metric. When \(n>6\) the same conclusion holds. If in addition \(\left| \Delta _{g}^{2}f(x_{0})\right| \big /f(x_{0})\) is small enough.
Theorem C
(Hebey–Vaugon [17]). Let f be a \(C^{\infty }\) function satisfying \(\max _{M}f> 0\) and \(\Delta _g f(x_{0}) = 0\) at a point \(x_{0}\) where f is maximum. Then
and consequently f is the scalar curvature of a conformal metric when \(n=4\) or 5, unless M is conformal to the standard \({\mathbb {S}}^{n}\). When \(n\ge 6\) we suppose that \(|W_g(x_{0})|=0\). The same conclusion holds if \(\Delta _g^{2}f(x_{0})=0\), when \(n=6\) or \(n=7\), and when \(n=8\) if in addition \(\Delta _g^{3} f(x_{0}) = 0\) or \(|\nabla W_g(x_{0})|\ne 0\). When \(n > 8\) the same conclusion holds if \(|\nabla W_g(x_{0})|\ne 0\) and \(\Delta _g^{3} f(x_{0}) = 0\) or when \(|\nabla W_g(x_{0})|=0\) if \(|\nabla ^{2} W_g(x_{0})| \ne 0\) and \(\Delta _g^{3} f(x_{0}) = \Delta _g^{4} f(x_{0}) = 0\), or when all derivatives of \(W_g\) vanish at \(x_{0}\) if \(\Delta _g^{m} f(x_{0}) = 0\) for all \(1\le m \le \frac{n}{2} - 1\).
The next result is the first step to prove Theorems 1.7 and 1.8.
Lemma 4.1
If \(\lambda _{f}(M,g)<\frac{\lambda ({\mathbb {S}}^{n})}{f(x_{0})^{2/2^{*}}}\), then \(S_{f,h}^{(\alpha ,\beta )} < \dfrac{{\mathcal {S}}_{*}}{f(x_{0})^{2/2^{*}}}\), where \({\mathcal {S}}_{*}\) is given in (1.4).
Proof
Since \(\lambda _{f}(M,g)<\frac{\lambda ({\mathbb {S}}^{n})}{f(x_{0})^{2/2^{*}}}\), from theorems A, B and C, there exists \(\varphi \in C^{\infty }(M)\) with \(\varphi >0, \int _{M}f(x)\varphi ^{2^{*}}dv_{g}=1\) and such that
Now, consider the following pair of functions \((w_{1},w_{2})\in \Lambda ^{\alpha ,\beta }_{f}\), where \(w_{1}=\xi \left( \xi ^{\alpha }\zeta ^{\beta }\right) ^{-1/2^{*}} \varphi \) and \(w_{2}=\zeta \left( \xi ^{\alpha }\zeta ^{\beta }\right) ^{-1/2^{*}}\varphi \), with \(\frac{\xi }{\zeta }= \sqrt{\frac{\alpha }{\beta }}\), thus
As \(h=\frac{\alpha }{2^{*}}a + \frac{2\sqrt{\alpha \beta }}{2^{*}}b+ \frac{\beta }{2^{*}}c\le \frac{n-2}{4(n-1)}R_{g}\), it follows that
Consequently,
hence \(S_{f,h}^{(\alpha ,\beta )}< \frac{{\mathcal {S}}_{*}}{f(x_{0})^{2/2^{*}}}\) as desired. Finishing the proof. \(\square \)
We will now prove the second auxiliary result of this section.
Lemma 4.2
If \(S_{f,h}^{(\alpha ,\beta )}<\dfrac{{\mathcal {S}}_{*}}{f(x_{0})^{2/2^{*}}}\), then there exists (u, v) in \(\Lambda ^{\alpha ,\beta }_{f}\) such that \(E_{h}(u, v)=S_{f,h}^{(\alpha ,\beta )}\).
Proof
Let \(\{(u_{m},v_{m})\}\subset \Lambda ^{\alpha ,\beta }_{f}\) be a minimizing sequence for \(S_{f,h}^{(\alpha ,\beta )}\), that is,
where \(o_{m}(1) \rightarrow 0\) as \(m\rightarrow \infty \). By the coercivity hypothesis (1.6), it follows that \(\{(u_{m},v_{m})\}\) is bounded in H. Thus, there exists (u, v) in H such that, up to a subsequence, \((u_{m},v_{m})\rightharpoonup (u,v)\) in \(H, (u_{m},v_{m}) \rightarrow (u,v)\) in \(L^{2}(M) \times L^2(M)\), and \((u_{m}(x),v_{m}(x)) \rightarrow (u(x),v(x))\) a.e in M. From Lemma 2.1 and (4.5), we get
where \(B_{0}>0\). Letting \(m \rightarrow \infty \), we obtain that
Then, since \(S_{f,h}^{(\alpha ,\beta )} <\dfrac{ {\mathcal {S}}_{*}}{f(x_{0})^{2/2^{*}}}\), we find that \(0 < \Vert (u,v)\Vert ^{2}_{2}\), and consequently, \(u\ne 0\) or \(v\ne 0\).
We claim that \(u\ne 0\) and \(v\ne 0\). Moreover, \((u,v)\in \Lambda _f^{\alpha ,\beta }\) is a minimizing for \(S_{f,h}^{(\alpha ,\beta )}\). Indeed, rewriting (4.5), we have
On the other hand, since \(1=\int _{M}f(x)|u_{m}|^{\alpha }|v_{m}|^{\beta }dv_{g}\), Lemma 2.3 gives us
Now, note that \(\int _{M}f(x)|u|^{\alpha }|v|^{\beta }dv_{g}>0\), otherwise, by (4.7) and Lemma 2.1, we would have
hence,
But, using the inequality above in (4.6), we get
again as \(S_{f,h}^{(\alpha ,\beta )} <\frac{ {\mathcal {S}}_{*}}{f(x_{0})^{2/2^{*}}}\), we reach that \(E_{h}(u,v)\le 0\), and so \(u= v=0\), which is a contradiction. Therefore, \(\int _{M}f(x)|u|^{\alpha }|v|^{\beta }dv_{g}>0\).
Now, returning to (4.7) we get
as \(S_{f,h}^{(\alpha ,\beta )}>0\), then
By using (4.6), it follows that
Since \(S_{f,h}^{(\alpha ,\beta )}f(x_{0})^{2/2^{*}}{\mathcal {S}}_{*}^{-1}-1<0\), we have
The lower semicontinuity of \(E_{h}\) implies \(E_{h}(u,v)\le \lim \inf E_{h}(u_{m},v_{m})=S_{f,h}^{(\alpha ,\beta )}\), and hence \(0<\tau =\int _{M}f(x)|u|^{\alpha }|v|^{\beta }dv_{g}\le 1\), now writing \(u_{0}= \tau ^{-1/2^{*}}u\) and \(v_{0}=\tau ^{-1/2^{*}}v\), we have
with \((u_{0},v_{0})\in \Lambda ^{\alpha ,\beta }_{f}\). By definition of \(S_{f,h}^{(\alpha ,\beta )}\) it follows that \(E_{h}(u_{0},v_{0}) = S_{f,h}^{(\alpha ,\beta )}\), so we prove that \(E_{h}(u,v) = S_{f,h}^{(\alpha ,\beta )}\tau ^{2/2^*}\).
Finally, we can check that \(\tau =\int _{M}f(x)|u|^{\alpha }|v|^{\beta }dv_{g}=1\), for this, we return to (4.6) and (4.8). Then
Hence,
As \(f(x_{0})^{2/2^{*}}S_{f,h}^{(\alpha ,\beta )}<{\mathcal {S}}_{*}\), then \( \int _{M}f(x)|u|^{\alpha }|v|^{\beta }dv_{g}=1\).
Consequenlty, we get that \((u,v)\in \Lambda ^{\alpha ,\beta }_{f}\), which proves that (u, v) is a minimizer for \(S_{f,h}^{(\alpha ,\beta )}\). \(\square \)
Now we can prove the main results of this section.
Proof of Theorem 1.6
Since \(S_{f,h}^{(\alpha ,\beta )} < \frac{{\mathcal {S}}_{*}}{f(x_{0})^{2/2^{*}}}\), by Lemma 4.2 there exists \((u_0,v_0)\in \Lambda ^{\alpha ,\beta }_{f}\) such that \(E_{h}(u_0,v_0) = S_{f,h}^{(\alpha ,\beta )}\). Denote by \(G(u,v)= \int _{M}f(x)|u|^{\alpha }|v|^{\beta }dv_{g} - 1\), where \((u,v) \in H\). Then, there is a Lagrange multiplier \(\lambda \) that satisfies
Taking \(\varphi = u_0\) and \(\psi =v_0\) above, we have that \(2E_{h}(u_0,v_0) = 2^{*}\lambda \), hence \(\lambda = \frac{2}{2^{*}}S_{f,h}^{(\alpha ,\beta )}>0\). Therefore, by (4.9), we have that \((u_0,v_0)\) is a weak solution of the following system
It is easy to see that the pair \(((2S_{f,h}^{(\alpha ,\beta )})^{1/(2^{*}-2)}u_0,(2S_{f,h}^{(\alpha ,\beta )})^{1/(2^{*}-2)}v_0)\) is a weak solution of system 1.1. This completes the proof of the theorem. \(\square \)
Proof of Theorems 1.7 and 1.8
From Theorem B and Theorem C together with Lemma 4.1, it follows that \(S_{f,h}^{(\alpha ,\beta )} < \frac{{\mathcal {S}}_{*}}{f(x_{0})^{2/2^{*}}}\). Thus the proof follows similar to Theorem 1.6. \(\square \)
Let us introduce some notations before of the proof of Corollary 1.9. Let
Then, if \(b\le 0\) in M, it is easy to see that \(E_{h}(|u|,|v|)\le E_{h}(u,v)\), so if \((u,v)\in \Lambda ^{\alpha ,\beta }_{f}\) then \((|u|,|v|)\in \Lambda ^{\alpha ,\beta }_{f,+}\), and therefore, we deduce that \(S_{f,h,+}^{(\alpha ,\beta )} \le S_{f,h}^{(\alpha ,\beta )}\). Then, by Lemma 4.1, we have \(S_{f,h,+}^{(\alpha ,\beta )} < \frac{{\mathcal {S}}_{*}}{f(x_{0})^{2/2^{*}}}\). Moreover, we claim that \(S_{f,h}^{(\alpha ,\beta )}>0\), indeed,
for all \((u,v)\in \Lambda ^{\alpha ,\beta }_{f,+}\).
Proof of Corollary 1.9
Let \(\{(u_{m},v_{m})\}\subset \Lambda ^{\alpha ,\beta }_{f,+}\) be a minimizing sequence for \(S_{f,h,+}^{(\alpha ,\beta )}\). Arguing similarly to Lemma 4.2, we obtain a pair \((u,v)\in \Lambda ^{\alpha ,\beta }_{f,+}\) such that \(E_{h}(u,v)=S_{f,h,+}^{(\alpha ,\beta )}\), with \(u\ne 0\) and \(v\ne 0\), where \(u_{m}\rightharpoonup u\) and \(v_{m}\rightharpoonup v\) in \(H^{1}(M)\). Now, we claim that \(u\ge 0\) and \(v\ge 0\) in M. Indeed, if we consider \(G_+(u,v) = \int _{M}f(x)(u^{+})^{\alpha }(v^{+})^{\beta }dv_{g} - 1\), there is a Lagrange multiplier \(\lambda \) such that
Taking \(\varphi =u^{-}\) and \(\psi =v^{-}\) as test functions above, we have
Since \(b\le 0\), it follows that \(E_{h}(u^{-},v^{-})\le 0\), hence \(u^{-} = v^{-}= 0\). Thus, we conclude that \(u\ge 0\) and \(v\ge 0\). Considering \(\varphi =u\) and \(\psi =v\) as test functions in (4.11), we get \(2E_{h}(u,v) = 2^{*} \lambda >0\), and consequently \(\lambda =\frac{2}{2^{*}}S_{f,A,+}^{(\alpha ,\beta )}>0\). Therefore, \(((2S_{f,h,+}^{(\alpha ,\beta )})^{1/(2^{*}-2)}u,(2S_{f,h,+}^{(\alpha ,\beta )})^{1/(2^{*}-2)}v)\) is a weak positive solution of system (1.1), because the elliptic regularity theory gives us \(u>0\) and \(v>0\) in M. \(\square \)
Proof of Corollary 1.10
Here, we assume that \(b=0, a= c= \frac{(n-2)}{4(n-1)}R_{g}\) and \(f\ge 0\). We claim that
Indeed, from of the proof of Lemma 4.1 (see (4.4)), it is sufficient to prove that
In order to achieve this goal, let \(\{(u_{m},v_{m})\}\subset \Lambda ^{\alpha ,\beta }_{f}\) be a minimizing sequence for \(S_{f,h}^{(\alpha ,\beta )}\), that is,
Define \(w_{m}=t_{m}v_{m}\), where \(t_m>0\) is chosen so that
By Young’s inequality, we get that
Using (4.13) in (4.12), we have
On the other hand, it is easy to see that \(t^{2\beta /2^{*}} + t^{(2\beta /2^{*})-2}\ge \left( \sqrt{\frac{\alpha }{\beta }}\right) ^{2\beta /2^{*}}+\left( \sqrt{\frac{\beta }{\alpha }}\right) ^{2\alpha /2^{*}},\) for all \(t>0\). Therefore,
5 Case \({\mathbb {S}}^{n}\)
Let \(({\mathbb {S}}^{n}, g_{0})\) be the \(n-\)sphere, where \(g_{0}\) is standard metric of \({\mathbb {S}}^{n}\). Due to the argument of Escobar and Schoen in [13] we can prove:
Lemma 5.1
Let \(\Gamma \) be a nontrivial finite group of isometries of \({\mathbb {S}}^{n}\) acting without a fixed point on \({\mathbb {S}}^{n}\). Write \((M={\mathbb {S}}^{n}/\Gamma , g )\), where g is the metric induced by \(\pi :{\mathbb {S}}^{n}\longrightarrow {\mathbb {S}}^{n}/\Gamma \) covering map. Let \({\overline{a}}, {\overline{b}}, {\overline{c}}\) and \({\overline{f}}\) be functions in M satisfying the same assumptions of Theorem 1.8. Then we have that
Proof
By hypotheses about \(\Gamma \) it is known that \(M={\mathbb {S}}^{n}/\Gamma \) is a compact Riemannian manifold locally conformally flat, which is not conformally diffeomorphic to \({\mathbb {S}}^{n}\). From Theorem C, we have \(\lambda _{{\overline{f}}}(M, g)<{\lambda ({\mathbb {S}}^{n})}/{{\overline{f}}(x_{0})^{ 2 /2^{*}}}\), and consequently
as desired. \(\square \)
Proof of Theorem 1.11
By Lemma 4.2 and Lemma 5.1, it follows that there exists \(({\overline{u}}_{0},{\overline{v}}_{0})\in H\) weak solution of system (1.1) for \((M={\mathbb {S}}^{n}/\Gamma , g )\). Since a, b, c and f are invariant under \(\Gamma \) (and recall that \(\pi ^{*}g=g_{0}\) and \(\Delta _{g_{0}}(u\circ \pi )=(\Delta _{g}u)\circ \pi \), for \(u\in C^{2}(M)\)), then writing \(u_{0}= {\overline{u}}_{0}\circ \pi \) and \(v_{0}= {\overline{v}}_{0}\circ \pi \) we have that \((u_{0},v_{0})\in H^{1}({\mathbb {S}}^{n}) \times H^{1}({\mathbb {S}}^{n})\) is a weak solution of the system
which ends the proof of the theorem. \(\square \)
Proof of Corollary 1.14
As a consequence of the assumptions, from corollary 1.13 we immediately have that \(S^{(\alpha ,\beta )}({\mathbb {S}}^{n}) = {\mathcal {S}}_{*}\). Let \(\varphi \in C^{\infty }({\mathbb {S}}^{n})\) be a minimizer for \(\lambda ({\mathbb {S}}^{n})\), we can to see that \((\xi \varphi ,\zeta \varphi )\) is a minimizer for \(S^{(\alpha ,\beta )}({\mathbb {S}}^{n})\). Indeed, notice that
So, \((\xi \varphi ,\zeta \varphi )\) is a solution of the system
Hence the rescaling \(((S^{(\alpha ,\beta )}({\mathbb {S}}^{n}))^{1/(2^{*}-2)}\xi \varphi ,(S^{(\alpha ,\beta )}({\mathbb {S}}^{n}))^{1/(2^{*}-2)}\zeta \varphi )\) is solution of system (1.1). Therefore, we have infinite positive solutions for system (1.1), because for \(x_{0}\in {\mathbb {S}}^{n}\) fixed, and any \(\rho >1\), the functions
are minimizer for \(\lambda ({\mathbb {S}}^{n})\), with \(r=d_{g_{0}}(x,x_0)\) (for more details see Theorem 5.1 in [15]).
On the other hand, if (u, v) is a minimizer for \(S^{(\alpha ,\beta )}({\mathbb {S}}^{n})\), with \(u,v\in C^{\infty }\), \(u,v>0\) and \(\int _{{\mathbb {S}}^{n}}u^{\alpha }v^{\beta }dg_{0}=1\). Let \(\sigma :{\mathbb {S}}^{n}\backslash \{P_{N}\}\longrightarrow {\mathbb {R}}^{n}\) be the stereographic projection, where \(P_{N}\) is the north pole of \({\mathbb {S}}^{n}\), since \((\sigma ^{-1})^{*}(g_{0}) = U^{4/(n-2)}g_{e}\), where \(U(y) = \left( \frac{2}{1+|y|^{2}}\right) ^{(2-n)/2}\) and \(g_{e}\) is the Euclidian metric. So, we have
and
Consequently, \(({\overline{u}},{\overline{v}})\) is a minimizer for \({\mathcal {S}}_{*}\), where \({\overline{u}}=(u\circ \sigma ^{-1})U\) and \({\overline{v}}=(v\circ \sigma ^{-1})U\), that is,
From Theorem 1.3 in [12], it follows that
where \(y_{0}\in {\mathbb {R}}^{n}, \varepsilon _{0}>0\) and \(\xi _{1},\zeta _{1}>0\) satisfying
so, a simple calculation gives us
Therefore, by definition of \({\overline{u}}\) and \({\overline{v}}\) we get that \(u = \frac{\xi _{1}}{\zeta _{1}}v \). Then \(\xi _{1}^{-1}u\) is positive solution (up to a rescaling) of the equation \(-\Delta _{g_{0}}w + \frac{n(n-2)}{4}w = w^{2^{*}-1}\) in \({\mathbb {S}}^{n}\). From Theorem 5.1 in [15] then up to a constant scale factor, u is of the following form, \(u(x) = \xi _{1}(\rho _{0} - \cos r)^{\frac{2-n}{2}}\), so, \(v(x) = \zeta _{1}(\rho _{0} - \cos r)^{\frac{2-n}{2}}\), where \(r=d_{g_{0}}(x,x_0)\) and \(\rho _{0}>1\). This complete the proof. \(\square \)
Data Availibility
All data generated or analysed during this study are included in this published article.
References
Ablowitz, M.J., Prinari, B., Trubatch, A.D.: Discrete and Continuous Nonlinear Schrödinger Systems. Cambridge University Press, Cambridge (2004)
Alves, C.O., de Morais Filho, D.C., Souto, M.A.S.: On systems of equations involving subcritical or critical Sobolev exponents. Nonlinear Anal. 42, 771–787 (2000)
Aubin, T.: Equations différentielles non linéaires et problème de Yamabe concernant la courbure scalaire. J. Math. Pures Appl. 55, 269–296 (1976)
Aubin, T.: Some Nonlinear Problems in Riemannian Geometry. Springer, Berlin (1998)
Aubin, T., Hebey, E.: Courbure scalaire prescrite. Bull. Sci. Math. 115, 125–132 (1991)
Chabrowski, J., Yang, J.: On the Neumann problem for an elliptic system of equation involving the Sobolev expoent. Colloq. Math. 90, 1–35 (2001)
Deng, S., Yang, J.: Critical Neumann problem for nonlinear elliptic systems in exterior domains. Electron. J. Differ. Equ. 153, 1–13 (2008)
Druet, O.: Generalized scalar curvature type equations on compact Riemannian manifolds. Proc. R. Soc. Edinb. Sect. A 130, 767–788 (2000)
Druet, O.: Optimal Sobolev inequalities and extremal functions the three-dimensional case. Indiana Univ. Math. J. 51, 69–88 (2002)
Druet, O., Hebey, E.: Sharp asymptotics and compactness for local low energy solutions of critical elliptic systems in potential form. Calc. Var. Partial Differ. Equ. 31, 205–230 (2008)
Druet, O., Hebey, E., Vétois, J.: Bounded stability for strongly coupled critical elliptic systems below the geometric threshold of the conformal Laplacian. J. Funct. Anal. 258, 999–1059 (2010)
Dou, J., Qu, C.: Classification of positive solutions for an elliptic system with a higher-order fractional Laplacian. Pac. J. Math. 261, 311–334 (2013)
Escobar, J.F., Schoen, R.M.: Conformal metrics with prescribed scalar curvature. Invent. Math. 86, 243–254 (1986)
Gilbarg, D., Trudinger, N.: Elliptic Partial Differential Equations of Second Order. Springer, Berlin (1983)
Hebey, E.: Nonlinear Analysis on Manifolds: Sobolev Spaces and Inequalities. Courant Institute of Mathematical Sciences, New York (2000)
Hebey, E., Vaugon, M.: Courbure scalaire prescrite pour des variétés non conformément difféomorphes à la sphŕe. C.R. Acad. Sci. 316, 281 (1993)
Hebey, E., Vaugon, M.: Le problème de Yamabe équivariant. Bull. Sci. Math. 117, 241–286 (1993)
Hebey, E.: Critical elliptic systems in potential form. Adv. Differ. Equ. 11, 511–600 (2006)
Hebey, E., Vaugon, M.: Meilleures constantes dans le théorème d’inclusion de Sobolev. Ann. Inst. H. Poincaré. Anal. Non Linéaire 13, 57–93 (1996)
Hebey, E., Vétois, J.: Multiple solutions for critical elliptic systems in potential form. Commun. Pure. Appl. Anal. 7, 715–741 (2008)
Ishiwata, M.: Multiple solutions for semilinear elliptic systems involving critical Sobolev exponent. Differ. Integr. Equ. 20, 1237–1252 (2007)
Kavian, O.: Introduction à la Thèorie des Points Critiques: et Applications aux Problèmes Elliptiques. Springer, Berlin (1993)
Lee, J.M., Parker, T.H.: The Yamabe problem. Bull. Am. Math. Soc. New Ser. 17, 37–91 (1987)
Schoen, R.: Conformal deformation of a Riemannian metric to constant scalar curvature. J. Differ. Geom. 20, 479–495 (1984)
Schoen, R., Yau, S.-T.: Lectures on Differential Geometry. International Press, Cambridge (2010)
Trudinger, N.: Remarks concerning the conformal deformation of Riemannian structures on compact manifolds. An. Scuola Norm. Sup. Pisa 22, 265–274 (1968)
Vétois, J.: Multiple solutions for nonlinear elliptic equations on compact Riemannian manifolds. Int. J. Math. 9, 1071–1111 (2007)
Yamabe, H.: On a deformation of Riemannian structures on compact manifolds. Osaka J. Math. 12, 21–37 (1960)
Funding
This work were supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Grant 309998/2020-4, and by Paraíba State Research Foundation (FAPESQ), Grant 3034/2021.
Author information
Authors and Affiliations
Contributions
All authors have contributed equally to this work for writing, review and editing. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
de Oliveira Sousa, N., de Souza, M. On Solutions for Strongly Coupled Critical Elliptic Systems on Compact Riemannian Manifolds. Results Math 78, 91 (2023). https://doi.org/10.1007/s00025-023-01866-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00025-023-01866-x