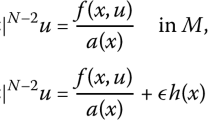Blow-up solutions for Hardy–Sobolev equations on compact Riemannian manifolds

Abstract

Let (M, g) be a smooth compact Riemannian manifold of dimension $n\ge 6$, $\xi _0\in M$, and we are concerned with the following Hardy–Sobolev elliptic equations:

$$\begin{aligned} -\Delta _gu+h(x)u=\frac{u^{2^{*}(s)-1-\epsilon }}{d_{g}(x,\xi _0)^s},\ \ \ \ u>0\ \ \mathrm{in} \ \ M, \end{aligned}$$

(0.1)

where $\Delta _g\,=\,\mathrm{div}_g(\nabla )$ is the Laplace–Beltrami operator on M, h(x) is a $C^1$ function on M, $\epsilon$ is a sufficiently small real parameter, $2^{*}(s):=\frac{2(n-s)}{n-2}$ is the critical Hardy–Sobolev exponent with $s\in (0,2)$, and $d_{g}$ is the Riemannian distance on M. Performing the Lyapunov–Schmidt reduction procedure, we obtain the existence of blow-up families of positive solutions of problem (0.1).

1 Introduction

Let (M, g) be a smooth compact Riemannian manifold of dimension $n\ge 6$ without boundary. Given $\xi _0\in M$, we consider the asymptotically critical Hardy–Sobolev elliptic equation

$$\begin{aligned} -\Delta _gu+h\left( x\right) u=\frac{u^{2^{*}\left( s\right) -1-\epsilon }}{d_{g}\left( x,\xi _0\right) ^s},\ \ \ \ u>0\ \ \mathrm{in} \ \ M, \end{aligned}$$

(1.1)

where $\Delta _g=\,\mathrm{div}_g(\nabla )$ is the Laplace–Beltrami operator on M, h(x) is a $C^1$ function on M, $\epsilon$ is a small real parameter, $d_{g}$ is the Riemannian distance on (M, g), and $2^{*}(s):=\frac{2(n-s)}{n-2}$ is the critical Hardy–Sobolev exponent with $s\in (0,2)$ in the following sense: let $H_1^2( M)$ be the completion of $C^\infty ( M)$ for the norm defined by (2.1); the Sobolev space $H_1^2( M)$ is continuously embedded in the weighted Lebesgue space $L^p( M,d_{g}(\cdot ,\xi _0)^{-s})$ if and only if $1\le p \le 2^{*}(s)$, and this embedding is compact if and only if $1\le p <2^{*}(s)$.

In the case $s=0$, problem (1.1) is related to the well-known Yamabe problem. That is, if $h\equiv \frac{n-2}{4(n-1)}\mathrm{Scal}_g$, where $\mathrm{Scal}_g$ is the scalar curvature of the manifold, Eq. (1.1) with $s=0$ and $\varepsilon =0$ is intensively studied as the Yamabe equation whose positive solutions u are such that the scalar curvature of the conformal metric $u^{2^*-2}g$ is constant (See, [1, 16, 17]). On the other hand, Micheletti, Pistoia, and Vétois in [13] showed that for giving any $C^1-$stable critical point of $h(\xi _0)-\frac{n-2}{4(n-1)}Scal_g(\xi _0),$ there exists a single peak solution for problem (1.1) with $s=0$. In [3], the author considered the existence of multi-peak solutions which are separate from each other for (1.1) with $s=0$. Sign-changing bubble towers solutions has been established by Pistoia and Vétois in [14].

In the case $s\ne 0$, there are many studies on Hardy–Sobolev equations in the Euclidean space; we refer to [2, 5, 6, 11] and references therein. Recently, Jaber obtained some results about the existence of positive solutions for Hardy–Sobolev equations on compact Riemannian manifolds. In particular, Jaber in [9] studied optimal Hardy–Sobolev inequalities on compact Riemannian manifolds, and then in [8] investigated the existence of positive solutions for the following equation:

$$\begin{aligned} -\Delta _gu+h(x)u=\frac{u^{2^{*}(s)-1}}{d_{g}(x,\xi _0)^s},\ \ \ \ u>0\ \ \mathrm{in} \ \ M. \end{aligned}$$

(1.2)

The author obtained the existence of positive solutions of (1.2) when the potential h satisfies $h(\xi _0)<\frac{(n-2)(6-s)}{12(2n-2-s)}Scal_g(\xi _0)$. In [10], the author proved the existence of solution for Eq. (1.2) with a perturbation term $u^{q-1}$ for $2<q<\frac{2n}{n-2}$ by mountain pass theorem.

Inspired by the above-mentioned works, we study the existence of peak solutions for Eq. (1.1) when $\epsilon$ small enough. To the best of our knowledge, it seems that this is the first result about the existence of blow-up solutions for elliptic equations with Hardy–Sobolev term on manifolds. Our main result can be stated as follows.

Theorem 1.1

Let (M, g) be a smooth compact Riemannian manifold of dimension $n\ge 6$, let h be a $C^1$ function on M such that the operator $-\Delta _g+h$ is coercive, and let $\xi _0 \in \mathcal {M}$ satisfy

$$\begin{aligned} \left\{ \begin{array}{ll} h\left( \xi _0\right)>\frac{\left( n-2\right) \left( 6-s\right) }{12\left( 2n-2-s\right) }Scal_g\left( \xi _0\right) , &{} \hbox {if}\ \ \epsilon >0; \\ h\left( \xi _0\right)<\frac{\left( n-2\right) \left( 6-s\right) }{12\left( 2n-2-s\right) }Scal_g\left( \xi _0\right) , &{} \hbox {if}\ \ \epsilon <0, \end{array} \right. \end{aligned}$$

and if $\epsilon$ is small enough, then Eq. (1.1) admits a solution $u_\epsilon$ such that the family $(u_\epsilon )_\epsilon$ is bounded in $H_1^2( M)$ and blows up at $\xi _0$ as $\epsilon \rightarrow 0$.

The proof of our result relies on a very well-known Lyapunov–Schmidt reduction procedure, introduced in [4] and used in many of the quoted papers. In particular, [3] and [13] for the existence of blow-up solutions for asymptotically critical elliptic equations on Riemannian manifolds.

The paper is organized as follows: We give some preliminaries in Sect. 2. Section 3 is devoted to the existence result. The proof of the main theorem will be given in Sect. 4.

In this paper, C denotes a generic positive constant, which may also vary from line to line.

2 The framework and preliminary results

In this section, we give some preliminary results. Let M be a compact Riemannian manifold of class $C^{\infty }$. On the tangent bundle of M, we define the exponential map $\exp : T\mathcal {M}\rightarrow M$, which has the following properties:

• (i) $\exp$ is of class $C^{\infty }$;

• (ii) there exists a constant $r>0$ such that $\mathrm{exp}_{\xi _0}\big |_{B(0,r)}: B(0,r)\rightarrow B_{g}(\xi _0,r)$ is a diffeomorphism for all $\xi _0\in M$, where B(0, r) denotes the ball in $\mathbb {R}^{n}$ centered at 0 with radius r, and $B_{g}(\xi _0,r)$ denotes the ball in $\mathcal {M}$ centered at $\xi _0$ with radius r with respect to the distance induced by the metric g.

From now on, we fix such r with $r<i_g/2$, where $i_g$ denotes the injectivity radius of (M, g). Let $\mathfrak {C}$ be the atlas on M whose charts are given by the exponential map and $\mathcal {P}=\{\psi _{\omega }\}_{\omega \in \mathfrak {C} }$ be a partition of unity subordinate to the atlas $\mathfrak {C}$.

Let $H_1^2( M)$ be the Sobolev space with the inner product

$$\begin{aligned} \left\langle u,v\right\rangle =\int _{ M}\left\langle \nabla u,\nabla v\right\rangle _g\ \mathrm{d}\upsilon _g+\int _{ M}huv \mathrm{d}\upsilon _g, \end{aligned}$$

with the norm

$$\begin{aligned} \Vert u\Vert _h^2=\int _{ M}\left( |\nabla _g u|^2+hu^2\right) \ \mathrm{d}\upsilon _g. \end{aligned}$$

(2.1)

For $u\in H_1^2( M)$, we have

$$\begin{aligned} \int _{ M}|\nabla _{g}u|^2\ \mathrm{d}\upsilon _g=\sum \limits _{\omega \in \mathfrak {C}}\int _{\omega }\psi _{\omega }(x)|\nabla _{g}u|^2\ \mathrm{d}\upsilon _g, \end{aligned}$$

where $d\upsilon _g=\sqrt{\mathrm{det}\ g}\ \mathrm{d}z$ denotes the volume form on M associated with the metric g. Moreover, if u has support inside one chart $\omega =B_{g}(\xi _0,r)$, then

$$\begin{aligned}&\int _{ M}|\nabla _{g}u|^2\ \mathrm{d}\upsilon _g\nonumber \\&\quad =\sum \limits _{\omega \in \mathfrak {C}}\int _{B(0, r)}\psi _{\omega }(\exp _{\xi _0}(z)) \sum \limits _{i,j=1}^ng_{\xi _0}^{ij}(z)\frac{\partial u(\mathrm{exp}_{\xi _0}(z))}{\partial z_{i}}\frac{\partial u(\mathrm{exp}_{\xi _0}(z))}{\partial z_{j}} |g_{\xi _0}(z)|^{\frac{1}{2}}\ \mathrm{d}z, \end{aligned}$$

(2.2)

where $g_{\xi _0}$ denotes the Riemannian metric reading in B(0, r) through the normal coordinates defined by the exponential map $\mathrm{exp}_{\xi _0}$ at $\xi _0$. We denote $|g_{\xi _0}(z)|:=\mathrm{det}(g_{\xi _0}(z))$ and $(g_{\xi _0})^{ab}(z)$ is the inverse matrix of $g_{\xi _0}(z)$. In particular, it holds

$$\begin{aligned} g_{\xi _0}^{\mathrm{ab}}(0)=\delta _{\mathrm{ab}},\quad \ g_{\xi _0}(0)=\,\mathrm{Id},\qquad \frac{\partial g_{\xi _0}^{\mathrm{ab}}}{\partial z_c}(0)=0\ \ \ \ \mathrm{for}\ \ \mathrm{any}\ \ a,b,c, \end{aligned}$$

where $\delta _{ab}$ is the Kronecker symbol. Since M is compact, there are two strictly positive constants C and $\tilde{C}$ such that

$$\begin{aligned} \forall \ \xi _0\in M, \quad \forall \ \upsilon \in T_{\xi _0} M, \quad C\Vert \upsilon \Vert ^2\le g_{\xi _0}\left( \upsilon , \upsilon \right) \le \tilde{C}\Vert \upsilon \Vert ^2. \end{aligned}$$

Hence, we have

$$\begin{aligned} \forall \ \xi _0\in M, \quad C_1\le |g_{\xi _0}|\le C_2. \end{aligned}$$

Let $L^q( M,d_g(x,\xi _0)^{-s})$ be the weighted Lebesgue space equipped with the norm

$$\begin{aligned} |u|_{q,s}=\left( \int _{ M}d_g(x,\xi _0)^{-s}|u|^q\ \mathrm{d}\upsilon _g\right) ^{1/q}. \end{aligned}$$

It will be useful to rewrite problem (1.1) in a different setting. We first introduce the following operator. Let $i^{*}:L^{2(n-s)/(n+2-2s)}( M,d_g(x,\xi _0)^{-s}) \hookrightarrow H^2_1( M)$ be the adjoint operator of the embedding $i: H^2_1( M)\hookrightarrow L^{2^*(s)}( M,d_g(x,\xi _0)^{-s})$, i.e., for any $w \in L^{2(n-s)/(n+2-2s)}( M,d_g(x,\xi _0)^{-s})$, the function $u=i^{*}(w)\in H^2_1( M)$ is the unique solution of the equation $\Delta _gu+hu=w$ in M. By the continuity of the embedding $H^2_1( M)$ into $L^{2^{*}(s)}( M,d_g(x,\xi _0)^{-s})$, we have

$$\begin{aligned} \Vert i^{*}(w)\Vert _h\le C|w|_{\frac{2(n-s)}{n+2-2s},s} \end{aligned}$$

(2.3)

for some positive constant C independent of w.

To study the supercritical case, by the standard elliptic estimates (see, [7]), given a real number $q>2(n-s)/(n-2)$, that is

$$\begin{aligned} \frac{\left( n-s\right) q}{n-s+\left( 2-s\right) q}>\frac{2\left( n-s\right) }{n+2-2s} \end{aligned}$$

for any w in $L^{2(n-s)/(n+2-2s)}( M,d_g(x,\xi _0)^{-s})$, the function $i^{*}(w)$ belongs to $L^{q}( M,d_g(x,\xi _0)^{-s})$ and satisfies

$$\begin{aligned} |i^{*}(w)|_{q,s}\le C|w|_{\frac{2(n-s)}{n+2-2s},s} \end{aligned}$$

(2.4)

for some positive constant C independent of w. For $\varepsilon$ small, we set

$$\begin{aligned} q_{\varepsilon }:=\left\{ \begin{array}{ll} 2^{*}\left( s\right) -\frac{n-s}{2-s}\varepsilon \quad &{} \mathrm{if} \quad \varepsilon <0;\\ 2^{*}(s) \quad &{} \mathrm{if} \quad \varepsilon >0, \end{array} \right. \end{aligned}$$

and set $\mathcal {H}_{\varepsilon }=H^2_1( M)\cap L^{q_\varepsilon }( M,d_g(x,\xi _0)^{-s})$ to be the Banach space provided with the norm

$$\begin{aligned} \Vert u\Vert _{h,q_{\varepsilon }}=\Vert u\Vert _h+|u|_{q_{\varepsilon },s}. \end{aligned}$$

If $\varepsilon >0$, the subcritical case, the space $\mathcal {H}_{\varepsilon }$ is the Sobolev space $H^2_1( M)$, and the norm $\Vert \cdot \Vert _{h,q_{\varepsilon }}$ is equivalent to the norm $\Vert \cdot \Vert _h$. A simple calculation gives that

$$\begin{aligned} \frac{(n-s)q_{\varepsilon }}{n-s+(2-s)q_{\varepsilon }}=\left\{ \begin{array}{ll} \frac{q_{\varepsilon }}{2^{*}(s)-1-\varepsilon } \quad &{} \mathrm{if} \quad \varepsilon <0;\\ \frac{2(n-s)}{n+2-2s} \quad &{} \mathrm{if} \quad \varepsilon >0, \end{array} \right. \end{aligned}$$

(2.5)

and by (2.3) [or (2.4) in the supercritical case], we can write problem (1.1) as

$$\begin{aligned} u=i^{*}\left( f_{\varepsilon }(u)\right) , \ \ \ \ u\in \mathcal {H}_{\varepsilon }, \end{aligned}$$

(2.6)

where $f_{\varepsilon }(u)=\frac{u_{+}^{2^{*}(s)-1-\epsilon }}{d_{g}(x,\xi _0)^s}$, with $u_+=\max \{u,0\}$.

We introduce the following equation which corresponds to the limit equation of problem (1.1).

$$\begin{aligned} -\Delta u(z)=\frac{u^{2^{*}(s)-1}(z)}{|z|^s},\ \ \ \ u>0 \ \ \ \ \mathrm{in}\ \ \ \mathbb {R}^n, \end{aligned}$$

(2.7)

where $\Delta =\mathrm{div}(\nabla )$ is the Laplace–Beltrami operator associated with the Euclidean metric. In [12], it is known that Eq. (2.7) possesses the following family of radial solutions $\delta ^{(2-n)/2}U(\delta ^{-1}|z|)$, where

$$\begin{aligned} U(z)=\alpha _n\Big (\frac{1}{1+|z|^{2-s}}\Big )^{\frac{n-2}{2-s}},\quad \text{ with } \ \ \alpha _n=\left( (n-s)(n-2)\right) ^\frac{n-2}{2(2-s)}. \end{aligned}$$

(2.8)

Let us define a smooth cutoff function $\chi _r$ that satisfies $\chi _r(z)=1$ for $z\in \bar{B}(0, \frac{r}{2})$; $0<\chi _r(z)<1$ for $z\in B(0, r)\backslash B(0, \frac{r}{2})$; $\chi _r(z)=0$ for $z\in \mathbb {R}^n\backslash \bar{B}(0, r)$, and $|\nabla \chi _r(z)|\le \frac{2}{r}$, $|\nabla ^2\chi _r(z)|\le \frac{2}{r^2}$. For any $\xi _0\in M$ and any positive real number $\delta$, we define

$$\begin{aligned} W_{\delta , \xi _0}(x):= \left\{ \begin{array}{ll} \chi _r(\mathrm{exp}_{\xi _0}^{-1}(x))\delta ^{\frac{2-n}{2}}U\Big (\delta ^{-1}\mathrm{exp}_{\xi _0}^{-1}(x)\Big ) &{} \ \mathrm{if}\ x\in B_{g}(\xi _0, r);\\ 0 &{} \ \mathrm{otherwise}. \end{array} \right. \end{aligned}$$

(2.9)

From the work of [15], we know that every solution of the linear equation

$$\begin{aligned} -\Delta v=(2^{*}(s)-1)\frac{U^{2^{*}(s)-2}}{|z|^s}v,\ \ \ \ \ v\in \mathcal {D}^{1,2}_0(\mathbb {R}^n), \end{aligned}$$

(2.10)

is the linear combination of the function

$$\begin{aligned} V(z) = \frac{d\left( \delta ^{(2-n)/2}U(\delta ^{-1}z)\right) }{d\delta }\Big |_{\delta =1} = \frac{1}{2} (n-s)^{\frac{n-2}{2(2-s)}}(n-2)^{\frac{n+2-2s}{2(2-s)}}\frac{|z|^{2-s}-1}{(1+|z|^{2-s})^{\frac{n-s}{2-s}}}.\nonumber \\ \end{aligned}$$

(2.11)

We introduce the functions

$$\begin{aligned} Z_{\delta ,\xi _0}(x):= \left\{ \begin{array}{ll} \chi _r\left( \mathrm{exp}_{\xi _0}^{-1}(x)\right) \delta ^{\frac{2-n}{2}}V\left( \delta ^{-1}\mathrm{exp}_{\xi _0}^{-1}(x)\right) &{} \ \mathrm{if}\ x\in B_{g}(\xi _0, r);\\ 0 &{} \ \mathrm{otherwise}. \end{array} \right. \end{aligned}$$

(2.12)

Define

$$\begin{aligned} K_{\delta , \xi _0}=\mathrm{Span}\left\{ Z_{\delta , \xi _0}\right\} , \end{aligned}$$

and

$$\begin{aligned} K_{\delta , \xi _0}^{\bot }=\left\{ \phi \in \mathcal {H}_{\varepsilon }:\ \langle \phi , Z_{\delta , \xi _0}\rangle =0\right\} . \end{aligned}$$

We will look for the solution of (2.6), or equivalent to (1.1), of the form

$$\begin{aligned} u_{\varepsilon }= W_{\delta _\epsilon (t),\xi _0}+\phi _{\epsilon ,t},\quad \delta _\epsilon (t) =\sqrt{| \epsilon | t},\quad t>0, \end{aligned}$$

(2.13)

where the rest term $\phi _{\epsilon ,t}\in \mathcal {H}_{\varepsilon } \cap K_{\delta _\epsilon (t), \xi _0}^{\bot }$ and $W_{\delta _\epsilon (t),\xi _0}$ is as in (2.9).

Let $\Pi _{\delta _\epsilon (t), \xi _0}: \mathcal {H}_{\varepsilon }\rightarrow K_{\delta _\epsilon (t), \xi _0}$ and $\Pi _{\delta _\epsilon (t), \xi _0}^{\bot }: \mathcal {H}_{\varepsilon }\rightarrow K_{\delta _\epsilon (t), \xi _0}^{\bot }$ be the orthogonal projections. To solve problem (2.6), we will solve the following system:

$$\begin{aligned}&\Pi _{\delta _\epsilon (t), \xi _0}^{\bot }\left\{ W_{\delta _\epsilon (t), \xi _0} +\phi _{\epsilon ,t}-i^{*}\left[ f_{\epsilon }\left( W_{\delta _\epsilon (t), \xi _0} +\phi _{\epsilon ,t}\right) \right] \right\} =0, \end{aligned}$$

(2.14)

$$\begin{aligned}&\Pi _{\delta _\epsilon (t), \xi _0}\left\{ W_{\delta _\epsilon (t), \xi _0} +\phi _{\epsilon ,t}-i^{*}\left[ f_{\epsilon }\left( W_{\delta _\epsilon (t), \xi _0} +\phi _{\epsilon ,t}\right) \right] \right\} =0. \end{aligned}$$

(2.15)

3 The existence result

The first step in the proof consists in solving Eq. (2.14). This is done in Proposition 3.1. We skip the proof of this result, which is rather standard in the literature on Lyapunov–Schmidt reduction; we refer the readers to [13].

Proposition 3.1

If $n\ge 6$ and $\delta _\varepsilon (t)$ is as in (2.13), for any $a,b>0$ satisfying $a< b$, if $\epsilon$ is small enough, for any $t\in [a,b]$, Eq. (2.14) has a unique solution $\phi _{\epsilon ,t}$ in $\mathcal {H}_{\varepsilon } \cap K_{\delta _\epsilon (t), \xi _0}^{\bot }$, which is continuously differentiable with respect to t. Moreover,

$$\begin{aligned} \Vert \phi _{\epsilon ,t}\Vert _{h,q_\varepsilon } \le C\left\{ \begin{array}{ll} |\epsilon |\left| \ln |\epsilon |\ \right| ^{2/3} \quad &{} \quad \mathrm{if}\ \ n=6\ \ \mathrm{and}\ \ \epsilon >0;\\ |\epsilon |\left| \ln |\epsilon |\ \right| \quad &{} \quad \mathrm{otherwise}, \end{array} \right. \end{aligned}$$

(3.1)

where C is a positive constant.

We define the functional $J_{\epsilon }: \mathcal {H}_\epsilon \rightarrow \mathbb {R}$ by

$$\begin{aligned} J_\epsilon \left( u(x)\right) =&\frac{1}{2}\int _{M} |\nabla _g u(x)|^2d\upsilon _g+\frac{1}{2}\int _{M} h(x)u(x)^2d\upsilon _g -\frac{1}{2^{*}(s)-\epsilon }\int _{M} \frac{u_+^{2^{*}(s)-\epsilon }}{d_g(x,\xi _0)^s}d\upsilon _g, \end{aligned}$$

(3.2)

where $u_+=\max \{u,0\}\in \mathcal {H}_\epsilon$. It is well known that any critical point of $J_{\epsilon }$ is the solution to problem (1.1). We also define the functional $\widetilde{J}_{\epsilon }: \mathbb {R}^+ \rightarrow \mathbb {R}$ by

$$\begin{aligned} \widetilde{J}_{\epsilon }(t)=J_{\epsilon }\left( W_{\delta _\epsilon (t),\xi _0}+\phi _{\epsilon ,t}\right) , \end{aligned}$$

(3.3)

where $W_{\delta _\epsilon (t),\xi _0}$ is defined in (2.9) and $\phi _{\epsilon ,t}$ is given by Proposition 3.1.

The next result allows to solve Eq. (2.15), by reducing the problem to a finite dimensional one.

Proposition 3.2

• (i) For $\epsilon$ small, if t is a critical point of the functional $\widetilde{J}_\epsilon$, then $W_{\delta _\epsilon (t),\xi _0}+\phi _{\epsilon ,t}$ is a solution of (2.6), or equivalent of problem (1.1).

• (ii) If $n\ge 6$ and $\delta _\varepsilon (t)$ is as in (2.13), for $a<t<b$, there holds

  $$\begin{aligned} \tilde{J}_{\epsilon }(t)=&\frac{2-s}{2(n-s)}c_0 -c_1\epsilon -c_2\epsilon \ln |\epsilon | +c_3\varphi _{\xi _0}(t)\epsilon +o(|\epsilon |) \end{aligned}$$

  (3.4)

  as $\epsilon \rightarrow 0$, $\mathcal {C}^1$-uniformly with respect to $\xi _0$ in M, where $c_i$, $i=0,1,\cdots ,4$ are positive constants, and $\varphi _{\xi _0}(t)$ is defined by

  $$\begin{aligned} \varphi _{\xi _0}(t)=&\text{ sign }(\epsilon )\Big ( h(\xi _0)-\frac{(n-2)(6-s)}{12(2n-2-s)}Scal_g(\xi _0)\Big )t - c_4 \ln t. \end{aligned}$$

  (3.5)

Proof

First, by using the same argument as in [13], we have that for $\epsilon$ small, if t is a critical point of the functional $\widetilde{J}_\epsilon$, then $W_{\delta _\epsilon (t),\xi _0}+\phi _{\epsilon ,t}$ is a solution of (2.6), or equivalently of problem (1.1). Moreover, if $n\ge 6$ and for $a<t<b$, there holds

$$\begin{aligned} \tilde{J}_{\epsilon }(t)= J_\epsilon \left( W_{\delta _\epsilon (t), \xi _0}(x)\right) +o(|\epsilon |), \end{aligned}$$

(3.6)

as $\epsilon \rightarrow 0$, $\mathcal {C}^1$-uniformly with respect to $\xi _0$ in M.

We now give the expansion of the energy $J(W_{\delta _\epsilon (t),\xi _0}(x))$. We have

$$\begin{aligned} J_\epsilon \left( W_{\delta _\epsilon (t), \xi _0}(x)\right) =&\frac{1}{2}\int _{M} |\nabla _g W_{\delta _\epsilon (t), \xi _0}(x)|^2\mathrm{d}\upsilon _g+\frac{1}{2}\int _{M} h(x)W_{\delta _\epsilon (t), \xi _0}(x)^2\mathrm{d}\upsilon _g \nonumber \\&\quad -\frac{1}{2^{*}(s)-\epsilon }\int _{M} \frac{ W_{\delta _\epsilon (t), \xi _0}^{2^{*}(s)-\epsilon }}{d_g(x,\xi _0)^s}\mathrm{d}\upsilon _g. \end{aligned}$$

(3.7)

We estimate each term as follows.

$$\begin{aligned}&\int _{M} |\nabla _g W_{\delta _\epsilon (t), \xi _0}(x)|^2\mathrm{d}\upsilon _g\nonumber \\&\quad = \int _{\mathbb {R}^n}\left( \delta ^{ij}-\frac{\delta _\epsilon (t)^2}{3}R_{iklj}z_iz_j+o(\delta _\epsilon (t)^2)\right) \left( 1-\frac{\delta _\epsilon (t)^2}{6}R_{kl}z_kz_l\right) \nonumber \\&\quad \times \frac{\partial U(z) }{\partial z_i} \frac{\partial U(z) }{\partial z_j} \mathrm{d}z+o(\delta _\epsilon (t)^2)\nonumber \\&\quad =\int _{\mathbb {R}^n}|\nabla U|^2\mathrm{d}z-|\epsilon |\frac{ t }{6n}Scal_{g}(\xi _0)\int _{\mathbb {R}^n}|z|^2|\nabla U|^2\mathrm{d}z+o( |\epsilon | ),\nonumber \\ \end{aligned}$$

(3.8)

and

$$\begin{aligned}&\frac{d}{dt}\Big (\int _{M} |\nabla _g W_{\delta _\epsilon (t), \xi _0}(x)|^2\mathrm{d}\upsilon _g\Big )\nonumber \\&\quad =-\delta _\epsilon (t)\delta '_\epsilon (t) \frac{ 1 }{3n}Scal_{g}(\xi _0)\int _{\mathbb {R}^n}|z|^2|\nabla U|^2\mathrm{d}z+o(\delta _\epsilon (t)\delta '_\epsilon (t) ),\nonumber \\&\quad = -|\epsilon | \frac{ 1 }{6n}Scal_{g}(\xi _0)\int _{\mathbb {R}^n}|z|^2|\nabla U|^2\mathrm{d}z+o(|\epsilon |), \end{aligned}$$

(3.9)

where $\delta '_\epsilon (t)$ denotes the derivative of $\delta _\epsilon (t)$ with respect to t. Moreover,

$$\begin{aligned} \int _{M} h(x)W_{\delta _\epsilon (t), \xi _0}(x)^2d\upsilon _g =&\delta _\epsilon (t)^2h(\xi _0)\int _{\mathbb {R}^n} U^2\mathrm{d}z+o(\delta _\epsilon (t)^2)\nonumber \\ =&|\epsilon | t h(\xi _0)\int _{\mathbb {R}^n} U^2\mathrm{d}z+o( |\epsilon |), \end{aligned}$$

(3.10)

and

$$\begin{aligned} \frac{d}{\mathrm{d}t}\Big (\int _{M} h(x)W_{\delta _\epsilon (t), \xi _0}(x)^2\mathrm{d}\upsilon _g \Big )=&2\delta _\epsilon (t) \delta '_\epsilon (t)h(\xi _0)\int _{\mathbb {R}^n} U^2\mathrm{d}z+o(\delta _\epsilon (t)^2)\nonumber \\ =&|\epsilon | h(\xi _0)\int _{\mathbb {R}^n} U^2\mathrm{d}z+o( |\epsilon | ). \end{aligned}$$

(3.11)

Furthermore, by (2.13), we have

$$\begin{aligned}&\frac{1}{2^{*}(s)-\epsilon }\int _{M} \frac{ W_{\delta _\epsilon (t), \xi _0}^{2^{*}(s)-\epsilon }}{d_g(x,\xi _0)^s}\mathrm{d}\upsilon _g\nonumber \\&\quad =\frac{1}{2^{*}(s)} \int _{\mathbb {R}^n}\frac{U(z)^{2^{*}(s)}}{|z|^s}\mathrm{d}z+\epsilon \ln |\epsilon |\frac{1}{2^{*}(s)} \frac{n-2}{4}\int _{\mathbb {R}^n}\frac{U(z)^{2^{*}(s)}}{|z|^s}\mathrm{d}z\nonumber \\&\quad +\epsilon \Big [\frac{1}{(2^{*}(s))^2} \int _{\mathbb {R}^n}\frac{U(z)^{2^{*}(s)}}{|z|^s}\mathrm{d}z-\text{ sign }(\epsilon )\frac{1}{2^{*}(s)} \int _{\mathbb {R}^n}\frac{U(z)^{2^{*}(s)}}{|z|^s}\ln U(z)\mathrm{d}z\Big ]\nonumber \\&\quad +\epsilon \Big [\Big (\frac{1}{2^{*}(s)} \frac{n-2}{4}\int _{\mathbb {R}^n}\frac{U(z)^{2^{*}(s)}}{|z|^s}\mathrm{d}z\Big )\ln t\nonumber \\&\quad -\text{ sign }(\epsilon )\Big (\frac{1}{2^{*}(s)}\frac{Scal_g(\xi _0)}{6n}\int _{\mathbb {R}^n}|z|^{2-s}U(z)^{2^{*}(s)}\mathrm{d}z\Big )\ t\Big ]\nonumber \\&\quad +o(|\epsilon |), \end{aligned}$$

(3.12)

and

$$\begin{aligned}&\frac{d}{\mathrm{d}t}\Big (\frac{1}{2^{*}(s)-\epsilon }\int _{M} \frac{ W_{\delta _\epsilon (t), \xi _0}^{2^{*}(s)-\epsilon }}{d_g(x,\xi _0)^s}\mathrm{d}\upsilon _g\Big )\nonumber \\&\quad = \epsilon \frac{\delta '_\epsilon (t)}{\delta _\epsilon (t)}\frac{1}{2^{*}(s)} \frac{n-2}{2}\int _{\mathbb {R}^n}\frac{U(z)^{2^{*}(s)}}{|z|^s}\mathrm{d}z\nonumber \\&\quad -\delta _\epsilon (t)\delta '_\epsilon (t)\frac{1}{2^{*}(s)}\frac{Scal_g(\xi _0)}{3n} \int _{\mathbb {R}^n}|z|^{2-s}U(z)^{2^{*}(s)}\mathrm{d}z\nonumber \\&\quad +o(\delta _\epsilon (t)\delta '_\epsilon (t))\nonumber \\&\quad =\epsilon \Big [\Big (\frac{1}{2^{*}(s)} \frac{n-2}{4}\int _{\mathbb {R}^n}\frac{U(z)^{2^{*}(s)}}{|z|^s}\mathrm{d}z\Big )\frac{ 1}{t}\nonumber \\&\quad -\text{ sign }(\epsilon )\Big (\frac{1}{2^{*}(s)}\frac{Scal_g(\xi _0)}{6n}\int _{\mathbb {R}^n}|z|^{2-s}U(z)^{2^{*}(s)}\mathrm{d}z\Big )\Big ]+o(|\epsilon |). \end{aligned}$$

(3.13)

Since U is the solution of problem (2.7), we have that

$$\begin{aligned} \int _{\mathbb {R}^n}|\nabla U|^2\mathrm{d}z=\int _{\mathbb {R}^n}\frac{U(z)^{2^{*}(s)}}{|z|^s}\mathrm{d}z. \end{aligned}$$

Thus, from (3.7), (3.8), (3.10) and (3.12), we get

$$\begin{aligned} J_\epsilon \left( W_{\delta _\epsilon (t), \xi _0}(x)\right) =&\frac{2-s}{2(n-s)}c_0 -c_1\epsilon -c_2\epsilon \ln |\epsilon | +c_3\varphi _{\xi _0}(t)\epsilon +o(|\epsilon |), \end{aligned}$$

(3.14)

as $\epsilon \rightarrow 0$, $\mathcal {C}^0$-uniformly with respect to $\xi _0$ in M, where

$$\begin{aligned} c_0=&\int _{\mathbb {R}^n}|\nabla U|^2\mathrm{d}z,\\ c_1=&\frac{1}{(2^{*}(s))^2} \int _{\mathbb {R}^n}\frac{U(z)^{2^{*}(s)}}{|z|^s}\mathrm{d}z-\text{ sign }(\epsilon )\frac{1}{2^{*}(s)} \int _{\mathbb {R}^n}\frac{U(z)^{2^{*}(s)}}{|z|^s}\ln U(z)\mathrm{d}z,\\ c_2=&\frac{1}{2^{*}(s)} \frac{n-2}{4}\int _{\mathbb {R}^n}\frac{U(z)^{2^{*}(s)}}{|z|^s}\mathrm{d}z,\\ c_3=&\frac{1}{2}\int _{\mathbb {R}^n} U^2\mathrm{d}z, \end{aligned}$$

and

$$\begin{aligned} \varphi _{\xi _0}(t)=\,&\text{ sign }(\epsilon )\Big [ h(\xi _0)-\Psi (U)Scal_g(\xi _0)\Big ]t - c_4 \ln t, \end{aligned}$$

where

$$\begin{aligned} \Psi (U)= \frac{1 }{6n} \frac{\int _{\mathbb {R}^n}|z|^2|\nabla U|^2\mathrm{d}z}{\int _{\mathbb {R}^n} U^2\mathrm{d}z}-\frac{1}{2^{*}(s)}\frac{1}{3n}\frac{\int _{\mathbb {R}^n}|z|^{2-s}U(z)^{2^{*}(s)}\mathrm{d}z}{\int _{\mathbb {R}^n} U^2\mathrm{d}z}, \end{aligned}$$

and

$$\begin{aligned} c_4=\frac{1}{2^{*}(s)} \frac{n-2}{2}\frac{\int _{\mathbb {R}^n}\frac{U(z)^{2^{*}(s)}}{|z|^s}\mathrm{d}z}{\int _{\mathbb {R}^n} U^2\mathrm{d}z} . \end{aligned}$$

Next, we compute $\Psi (U)$ by using similar ideas of Jaber in [8]. For any positive real numbers p and q satisfying $p-q>1$, we set

$$\begin{aligned} I_p^q=\int _0^{+\infty }\frac{t^q}{(1+t)^p}dt. \end{aligned}$$

Then we find

$$\begin{aligned} I_{p+1}^q=\frac{p-q-1}{p}I_p^q,\qquad \text{ and }\quad \ \ I_{p+1}^{q+1}=\frac{q+1}{p-q-1}I_{p+1}^q. \end{aligned}$$

(3.15)

Using (2.8), we derive

$$\begin{aligned} \frac{\int _{\mathbb {R}^n}|z|^2|\nabla U|^2\mathrm{d}z}{\int _{\mathbb {R}^n} U^2\mathrm{d}z} =&\frac{(n-2)^2\int _0^{+\infty }\frac{r^{n+3-2s}}{(1+r^{2-s})^{\frac{2(n-s)}{2-s}}}\mathrm{d}r}{\int _0^{+\infty }\frac{r^{n-1}}{(1+r^{2-s})^{\frac{2(n-2)}{2-s}}}\mathrm{d}r}\\ =&\frac{(n-2)^2\int _0^{+\infty }\frac{t^{\frac{n}{2-s}+1}}{(1+t)^{\frac{2(n-s)}{2-s}}}\mathrm{d}t}{\int _0^{+\infty }\frac{t^{\frac{n}{2-s}-1}}{(1+t)^{\frac{2(n-2)}{2-s}}}\mathrm{d}t}\\ =&\frac{(n-2)^2I_{\frac{2(n-s)}{2-s}}^{\frac{n}{2-s}+1}}{I_{\frac{2(n-2)}{2-s}}^{\frac{n}{2-s}-1}}\\ =&\frac{n(n-2)(n+2-s)}{2(2n-2-s)}, \end{aligned}$$

and

$$\begin{aligned} \frac{\int _{\mathbb {R}^n}|z|^{2-s}U(z)^{2^{*}(s)}\mathrm{d}z}{\int _{\mathbb {R}^n} U^2\mathrm{d}z} =&(n-s)(n-2)\frac{ \int _0^{+\infty }\frac{r^{n+1-s}}{(1+r^{2-s})^{\frac{2(n-s)}{2-s}}}\mathrm{d}r}{\int _0^{+\infty }\frac{r^{n-1}}{(1+r^{2-s})^{\frac{2(n-2)}{2-s}}}\mathrm{d}r}\\ =&(n-s)(n-2) \frac{ \int _0^{+\infty }\frac{t^{\frac{n=2}{2-s} }}{(1+t)^{\frac{2(n-s)}{2-s}}}\mathrm{d}t}{\int _0^{+\infty }\frac{t^{\frac{n}{2-s}-1}}{(1+t)^{\frac{2(n-2)}{2-s}}}\mathrm{d}t}\\ =&(n-s)(n-2)\frac{ I_{\frac{2(n-s)}{2-s}}^{\frac{n-2}{2-s} }}{I_{\frac{2(n-2)}{2-s}}^{\frac{n}{2-s}-1}}\\ =&\frac{n(n-4)(n -s)}{2(2n-2-s)}. \end{aligned}$$

Then,

$$\begin{aligned} \Psi (U)=\frac{(n-2)(6-s)}{12(2n-2-s)}. \end{aligned}$$

Thus, we can rewrite $\varphi _{\xi _0}(t)$ as in (3.5).

Finally, (3.9), (3.11) together with (3.13) yield that (3.14) holds in $\mathcal {C}^1$-sense with respect to t. $\square$

4 Proof of the main result

Proof of Theorem 1.1

From Proposition 3.2 (i), it follows that $W_{\delta _\epsilon (t),\xi _0}+\phi _{\epsilon ,t}$, where $W_{\delta _\epsilon (t),\xi _0}$ is defined in (2.9) and the existence of $\phi _{\epsilon ,t}$ is guaranteed by Proposition 3.1, is a solution of (1.1) if t is a critical point of the functional $\widetilde{J}_\epsilon$, which is equivalent to finding a critical point of the function $\varphi _{\xi _0}(t)$.

In fact, by assumption,

$$\begin{aligned} \text{ sign }(\epsilon )\Big (h(\xi _0)-\frac{(n-2)(6-s)}{12(2n-2-s)}Scal_g(\xi _0)\Big )>0, \end{aligned}$$

then $\varphi _{\xi _0}(t)$ has a minimal point

$$\begin{aligned} t_0=c_4\Big [\text{ sign }(\epsilon )( h(\xi _0)-\frac{(n-2)(6-s)}{12(2n-2-s)}Scal_g(\xi _0))\Big ]^{-1}, \end{aligned}$$

which is a stable critical point of $\varphi _{\xi _0}(t)$. Then there exists $t_\varepsilon$ such that $t_\varepsilon \rightarrow t_0$ as $\varepsilon \rightarrow 0$ and $t_\varepsilon$ is the critical point of $\widetilde{J}_\epsilon$. $\square$