1 Introduction

The great advantage in the establishment of elastic mechanics that is the basis of classical seismology lies in the introduction of a “set system of free particles,” nested within the framework of conventional continuum mechanics theory, then obtaining the widely used elastic wave equation without the independent free term of rotational motion. Although the wave equation derived from conventional continuum mechanics theory has made immense contributions to humankind, anyone engaged in actual work, such as the operators of data processing and interpretation from petroleum companies and oil service technology companies, know its huge unknown and unknowable factors. Scholars have been deepening exploration of the field of forward modeling, imaging, and inversion (Li et al., 2022; Liu, 2019; Liu et al., 2020; Wang et al., 2022), especially the study of wave theory in rock and soil media which affects the propagation of seismic waves. A trend in the development of geophysics is to seek wave theory closer to the physical reality and derive corresponding wave equations to achieve highly accurate imaging and inversion of complex structures.

Classical seismology is based on the framework of conventional continuum mechanics theory, which is considered a local theory, meaning that the stress at a material point depends only on the strain at that material point. Additionally, it is assumed that the strain energy density function for the medium contains only the classical strain (the first-order derivative of the displacements). It requires an idealized model and assumes that the materials making up the medium are uniformly and continuously distributed. In other words, the material is represented by a continuous mass rather than as discrete particles (Zhu et al., 2020). In reality, complicated internal micro-defects/microstructures commonly exist for both natural rock and soil media and human-made materials. In rock and soil media, micro-defects/microstructures generally refer to the structures characterized by the micro-pores, micro-cracks, and micro-voids, while for metal, the micro-defects/microstructures refer to the crystal dislocations. It is difficult to describe the complex microstructural interactions by the conventional continuum mechanics theory under its continuity assumption. One feasible solution is to consider every microstructure separately with conventional continuum theory. However, this may compromise the efficiency and accuracy in such a model. For some complex structures, ill-conditioned problems may occur, especially for the localized deformation and fracture and long-range interactions. The conventional continuum mechanics theory is never capable of adequately handling these problems (Askes & Gutierrez, 2006; Bonnell & Shao, 2003). It is worth emphasizing that the scale of micro-defects/microstructures varies with the observation target, and it is a relative concept. Although the different scales of observation have straightforward boundaries, shorter scales of observation (e.g., microscale, nanoscale) have an influence on longer scales of observation (e.g., macro-scale) and vice versa, resulting in heterogeneous responses (Askes & Metrikine, 2005). For rock and soil media, microscale differences in the pore and grain geometry of rocks result in macro-scale differences in wave responses and characteristics.

The generalized continuum mechanics (GCM) theory enriches the context of the conventional continuum mechanics theory by introducing additional higher than first-order displacement gradients and first-order rotation gradients (de Borst & Muhlhaus, 1992; Chang & Ma, 1992; Chang et al., 1998; De Domenico et al., 2019; Karparvarfard et al., 2015; Kong et al., 2009; Lam et al., 2003; Peerlings et al., 1996; Yang et al., 2002), increasing the degrees of freedom of the material point (Eringen, 1966, 1967, 1990), or taking the non-local effects into account (Ari & Eringen, 1983; Eringen, 1999, 2002; Eringen et al., 1977), which are usually accompanied by additional characteristic length scale parameters (or higher-order constants) to represent the microstructural properties of the medium. Moreover, the elastic wave equations derived from GCM theory can handle the influence of heterogeneity of a medium caused by the microstructural interactions on propagation of seismic waves. The term "generalized" in GCM theory refers to the further relaxation of the basic assumptions and principles of the conventional continuum mechanics theory. Therefore, these two theories are not mutually contradictory, but rather complementary. In contrast to conventional continuum mechanics theory, the GCM theory imparts volume properties to the material point, allowing it to be driven by forces and couples (a force drives the material point to translate and a couple drives the material point to rotate). Due to the interactions between the material points, the body couple and the surface couple are introduced, leading to the asymmetry of the stress tensors. If the volume of the material point vanishes, the GCM theory becomes the conventional continuum mechanics theory.

The history of GCM theory development can be traced back to the end of the nineteenth century, when the existence of the body couple and the surface couple in a medium was originally postulated by Voigt (1887). Since then, numerous theories and approaches have been proposed as extensions of the conventional continuum mechanics theory. Among them, the couple stress theory (Toupin, 1962), strain gradient theory (Toupin, 1964), second strain gradient theory (Mindlin, 1965), micro-polar theory and micro-stretch theory (Eringen, 1966, 1990), and non-local theory (Eringen, 1983; Eringen & Edelen, 1972) are relatively successful and widely used. These theories accurately describe the underlying microstructure by introducing factors of certain characteristic length scale parameters that represent the lower scales, while effectively saving computing resources compared with the conventional theory. Despite being short of the universally acknowledged physical interpretation and unified understanding of the characteristic length scale parameters with different definitions and numbers, it faces some difficulties in large-scale applications. In 1964, Mindlin (1964) proposed a more generalized theory containing 903 characteristic length scale parameters. In order to further promote the practical application of theories and approaches, pioneering researchers have for decades explored a variety of methods to reduce the number of characteristic length scale parameters while effectively describing microstructural interactions. Aifantis (1999) proposed one-parameter second strain gradient theory, in which the second-order strain gradients are considered as an additional effect of strain energy density. However, the Aifantis theory is phenomenological, rather than derived from the microstructure. Yang et al. (2002) introduced an additional equilibrium relation to govern the behavior of the couples and presented a modified couple stress theory with one characteristic length scale parameter. Chakraborty (2008) also presented a non-local extension of Biot’s theory of poroelasticity, which has only one characteristic length scale parameter. This parameter can be estimated by comparing the theoretical dispersion rate with experimental observation, and Chakraborty’s theory has been successfully applied to the diagnosis of osteoporosis. Wang et al. (2020) derived the asymmetric wave equations based on the modified couple stress theory (Yang et al., 2002) and performed numerical modeling for seismic wave propagation in a viaduct system. The coefficient reflecting the connection between the characteristic length scale parameter of the medium and the characteristic length scale parameter of the micro-pore was obtained through the analysis of field data and synthetic data.

To date, relatively few studies have been conducted to derive the elastic wave equations in the frame of GCM theory with numerical modeling or analytical solutions, especially in the frequency band of seismic exploration. In addition, there are few studies in the existing literature that incorporate multiple theories and methods of the GCM theory into an integrated frame. In this work, we introduce the concept of the multi-scale microstructural interactions and consider the characteristic length scale parameter as a comprehensive parameter affected by multiple factors, including the localized deformation phenomenon, stress concentration effect, and the geometric characteristics of the material that make up the medium. We incorporate the modified couple stress theory and the one-parameter second strain gradient theory into a unified framework to describe microstructural interactions at different scales, and analyze the influence of multi-scale microstructural characteristics on seismic waves. Specifically, we first derive asymmetric elastic wave equations based on modified couple stress and one-parameter second strain gradient theory under the same definition of the characteristic length scale parameter of the medium. Second, we perform numerical modeling for a layered model and salt model using three different wave equations and analyze the influence on the propagation of seismic waves caused by the complex microstructural interactions in the medium under different theories. Finally, we draw conclusions based on the findings.

2 Asymmetric Elastic Wave Equations

In the frame of the GCM theory, the characteristic length scale parameter l of the medium along with the high-order spatial derivative terms of the state variables (strain or stress) is used to describe the influence of the microstructural interactions in the medium on the propagation of seismic waves. In general, the characteristic length scale parameter of the medium is affected by multiple factors, such as localized deformation phenomenon, stress concentration effect in the medium, and the geometric characteristics of the materials. In ideal conditions, that is, without considering the influence of other factors, the characteristic length scale parameter lm of the micro-pore can be regarded as the characteristic length scale of the medium, and the coefficient \(\gamma\) between the l and the lm can be calculated by comparing the field data with synthetic data (Wang et al., 2020).

In this section, we first define the characteristic length scale parameter lm of the micro-pore as the mean particle diameter; through the quantitative relationship \(l = \gamma l_{m} ,\gamma \ge 1\), the characteristic length scale parameter l of the medium can be expressed, and then under the same characteristic length scale parameter l, we derive the asymmetric elastic wave equations based on the modified couple stress theory and one-parameter second strain gradient theory.

2.1 Asymmetric Elastic Wave Equations Based on the Modified Couple Stress Theory

According to the couple stress theory (Koiter, 1964), the interaction between the material micro-elements is transmitted through the surface stress \(p_{i}^{\left( n \right)}\) and the surface force couple \(m_{i}^{\left( n \right)}\), which can be expressed by the stress tensor \(\sigma_{ij}\) and couple stress tensor \(\mu_{ij}\):

$$p_{i}^{\left( n \right)} = \sigma_{ji} n_{j} ,$$
(1)
$$m_{i}^{\left( n \right)} = \mu_{ji} n_{j} ,$$
(2)

where \(n_{j}\) is the unit normal vector.

At the same time, the stress tensor and the couple stress tensor both satisfy the equilibrium equation of linear momentum and the equilibrium equation of angular momentum:

$$\frac{d}{dt}\int\limits_{{V_{a} }} {V_{i} dv} = \oint\limits_{{S_{a} }} {p_{i}^{\left( n \right)} ds} + \int\limits_{{V_{a} }} {F_{i} dv} = 0\left( { = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }}} \right),$$
(3)
$$\frac{d}{dt}\int\limits_{{V_{a} }} {\Omega_{i} dv} = \oint\limits_{{S_{a} }} {\left[ {e_{ijk} r_{j} p_{k}^{\left( n \right)} + m_{i}^{\left( n \right)} } \right]ds} + \int\limits_{{V_{a} }} {\left[ {e_{ijk} r_{j} F_{k} + M_{i} } \right]dv} = 0,$$
(4)

where \(V_{a}\) is the volume of the material and \(S_{a}\) is the boundary; \(V_{i} ,\Omega_{i}\) are the linear momentum and angular momentum, respectively; \(F_{i} ,M_{i}\) are the body force and body couple; \(e_{ijk}\) is the permutation symbol, \(r_{j}\) is the position vector, \(u_{i}\) is the displacement vector, and \(\rho\) is the density.

Applying the divergence theorem, transforming from surface integral to volume fraction, and ignoring high-order traces, the differential expression of the equilibrium equations can be obtained:

$$\sigma_{ji,j} + F_{i} = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }},$$
(5)
$$\mu_{ji,j} + e_{ist} \sigma_{st} + M_{i} = 0.$$
(6)

Decomposing the stress tensor into the sum of the symmetric stress tensor and the antisymmetric stress tensor (Yang et al., 2002), we obtain

$$\begin{gathered} \sigma_{ij} = \tau_{ij} + r_{ij} , \\ \tau_{ij} = \frac{1}{2}\left( {\sigma_{ij} + \sigma_{ji} } \right), \\ r_{ij} = \frac{1}{2}\left( {\sigma_{ij} - \sigma_{ji} } \right). \\ \end{gathered}$$
(7)

Thus, the equilibrium equations can be expressed as follows:

$$\tau_{ji,j} + r_{ji,j} + F_{i} = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }},$$
(8)
$$\mu_{ji,j} + e_{ist} r_{st} + M_{i} = 0.$$
(9)

According to Eq. (9), we can derive the relationship between the antisymmetric stress tensor and the couple stress tensor:

$$r_{st} = \frac{1}{2}\left( {\mu_{ji,j} + M_{i} } \right)e_{its} .$$
(10)

Now, the couple stress tensor is decomposed into the sum of the deflection part and the spherical part (Yang et al., 2002):

$$\mu_{ij} = m_{ij} + \frac{1}{3}\mu_{kk} \delta_{ij} .$$
(11)

Taking the divergence of Eq. (10), and substituting Eq. (11), we have

$$r_{ts,t} = \frac{1}{2}\left( {m_{ji,jt} + M_{i,t} } \right)e_{ist} .$$
(12)

Substituting Eqs. (7) and 12) into Eq. (8), to eliminate the antisymmetric stress tensor, the equilibrium equation containing the symmetric stress tensor and the deflection part of the couple stress tensor has the following relationship:

$$\tau_{ji,j} + \frac{1}{2}e_{ikt} m_{st,sk} + \frac{1}{2}e_{ist} M_{t,s} + F_{i} = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }}.$$
(13)

Further, we consider the boundary conditions in the frame of couple stress theory.

Then, applying the principle of virtual work, we derive the constitutive relations of the modified couple stress theory (Yang et al, 2002). The work done by the external loads through the virtual displacement \(\delta u_{i}\) and the virtual rotation \(\delta \omega_{i}\) is expressed as follows (Hadjesfandiari & Dargush, 2011):

$$\int\limits_{{V_{a} }} {\left( {\sigma_{ji,j} + F_{i} } \right)\delta u_{i} dv} = 0,$$
(14)
$$\int\limits_{{V_{a} }} {\left( {\mu_{ji,j} { + }e_{ist} \sigma_{st} + M_{i} } \right)\delta \omega_{i} dv} = 0.$$
(15)

According to the principle of virtual work, the change in the deformation energy is equal to the work done by the external loads through the virtual displacement and the virtual rotation.

$$\begin{gathered} \int\limits_{{V_{a} }} {\sigma_{ji} \delta \varepsilon_{ij} dv} + \int\limits_{{V_{a} }} {\mu_{ji} \delta \omega_{i,j} dv} = \int\limits_{{V_{a} }} {\delta wdv} \\ = \int\limits_{{S_{a} }} {p_{i}^{\left( n \right)} \delta u_{i} ds} + \int\limits_{{S_{a} }} {m_{i}^{\left( n \right)} \delta \omega_{i} ds} + \int\limits_{{V_{a} }} {F_{i} \delta u_{i} dv} + \int\limits_{{V_{a} }} {M_{i} \delta \omega_{i} dv} \\ = \int\limits_{{V_{a} }} {\left( {F_{i} \delta u_{i} + M_{i} \delta \omega_{i} } \right)dv} + \int\limits_{{V_{a} }} {\left( {\sigma_{ji,j} \delta u_{i} + \sigma_{ji} \delta u_{i,j} + m_{ji,j} \delta \omega_{i} + m_{ji} \delta \omega_{i,j} } \right)dv} \\ = \int\limits_{{V_{a} }} {\left[ {\delta u_{i} \left( {\sigma_{ji,j} + F_{i} } \right) + \delta \omega_{i} \left( {m_{ji,j} + M_{i} } \right) + \sigma_{ji} \delta u_{i,j} + m_{ji} \delta \omega_{i,j} } \right]dv} , \\ \end{gathered}$$
(16)

where \(w\) is the deformation energy density.

Under the assumption of small deformation, the relative displacement between two points in a Cartesian coordinate system is expressed as follows (Aki & Richards, 2002):

$$du_{i} = u_{i,j} dx_{j} ,$$
(17)

where \(u_{i,j}\) is the displacement gradient tensor and can be decomposed into the sum of the symmetric strain tensor \(\varepsilon_{ij}\) and antisymmetric rotation tensor \(\omega_{ij}\).

$$\begin{gathered} \varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right), \\ \omega_{ij} = \frac{1}{2}\left( {u_{i,j} - u_{j,i} } \right). \\ \end{gathered}$$
(18)

The rotation vector \(\omega_{i}\) corresponding to the antisymmetric rotation tensor \(\omega_{ij}\) is defined as

$$\omega_{i} = \frac{1}{2}e_{ijk} u_{k,j} = - \frac{1}{2}e_{ijk} \omega_{jk} .$$
(19)

In the frame of couple stress theory, the rotation gradient tensor \(\omega_{i,j}\) is introduced to describe the torsional and bending deformation of the material. We define the symmetric curvature tensor \(\chi_{ij}\) and the antisymmetric curvature tensor \(\kappa_{ij}\), respectively, as follows (Yang et al., 2002):

$$\begin{gathered} \chi_{ij} = \frac{1}{2}\left( {\omega_{i,j} + \omega_{j,i} } \right) = \frac{1}{2}\left( {\frac{1}{2}e_{jkl} u_{l,ki} + \frac{1}{2}e_{ikl} u_{l,kj} } \right), \hfill \\ \kappa_{ij} = \frac{1}{2}\left( {\omega_{i,j} - \omega_{j,i} } \right) = \frac{1}{2}\left( {\frac{1}{2}e_{jkl} u_{l,ki} - \frac{1}{2}e_{ikl} u_{l,kj} } \right). \hfill \\ \end{gathered}$$
(20)

Substituting the equilibrium equation (Eq. (13)) and Eq. (18), (20) into Eq. (16), we obtain

$$\begin{gathered} \int\limits_{{V_{a} }} {\delta wdv} = \int\limits_{{V_{a} }} {\left[ {\delta u_{i} \left( {\sigma_{ji,j} + F_{i} } \right) + \delta \omega_{i} \left( {\mu_{ji,j} + M_{i} } \right) + \sigma_{ji} \delta u_{i,j} + m_{ji} \delta \omega_{i,j} } \right]dv} \\ = \int\limits_{{V_{a} }} {\left( {\delta \varepsilon_{ij} \tau_{ij} + \delta \chi_{ij} m_{ij} } \right)dv} . \\ \end{gathered}$$
(21)

Then we derive the conjugate relationship between the deformation energy density and the displacement and the torsional and bending deformation. The deformation energy density depends only on the symmetric strain tensor and the symmetric curvature tensor.

$$\begin{gathered} \tau_{ij} = \frac{\partial w}{{\partial \varepsilon_{ij} }}, \\ m_{ij} = \frac{\partial w}{{\partial \chi_{ij} }}. \\ \end{gathered}$$
(22)

As for the isotropic medium, the deformation energy density can be written as follows:

$$\begin{gathered} w = \frac{1}{2}\lambda \left( {\varepsilon_{ii} } \right)^{2} + \mu \varepsilon_{ij} \varepsilon_{ij} + \mu l^{2} \chi_{ij} \chi_{ij} \\ = \frac{1}{2}\lambda \left( {\varepsilon_{ii} } \right)^{2} + \mu \varepsilon_{ij} \varepsilon_{ij} + \eta \chi_{ij} \chi_{ij} , \\ \end{gathered}$$
(23)

where \(\lambda ,\mu\) are the Lamé constants, \(\eta\) is a parameter reflecting the characteristics of the medium's rotational movement, \(\eta = \mu l^{2}\), and \(l\) is the characteristic length scale parameter of the medium.

Then we derive the constitutive relations for the isotropic medium.

$$\begin{gathered} \tau_{ij} = \lambda \delta_{ij} \varepsilon_{kk} + 2\mu \varepsilon_{ij} , \\ m_{ij} = 2\mu l^{2} \chi_{ij} = 2\eta \chi_{ij} . \\ \end{gathered}$$
(24)

Substituting the constitutive relations (Eq. (24)) into the equilibrium equation (Eq. (13)), the elastic wave equations based on the modified couple stress theory (Yang et al., 2002) are given as follows (without consideration of body force and body force couple):

$$\left( {\lambda + \mu } \right)u_{j,ji} + \mu u_{i,jj} + \frac{1}{2}e_{ijk} \eta \left( {\frac{1}{2}e_{kmn} u_{n,mllj} + \frac{1}{2}e_{lmn} u_{n,mklj} } \right) = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }}.$$
(25)

2.2 Asymmetric Elastic Wave Equations Based on the One-Parameter Second Strain Gradient Theory

According to the non-local theory, the state variables of a point are weighted by the state variables of all points in its neighborhood (Eringen, 1972).

$${\tilde{\mathbf{A}}}\left( {\mathbf{x}} \right) = \frac{1}{V}\int\limits_{V} {{\mathbf{h}}\left( {\mathbf{n}} \right){\mathbf{A}}\left( {{\mathbf{x}} + {\mathbf{n}}} \right)dV} ,$$
(26)

where \(V\) is the volume of the neighborhood, and for a spherical neighborhood, we consider the characteristic length scale parameter \(l\) of the medium as the radius of the spherical neighborhood, \(V = \frac{4}{3}\pi l^{3}\), \({\tilde{\mathbf{A}}}\left( {\mathbf{x}} \right)\) is an equivalent state variable of a point, \({\mathbf{A}}\left( {{\mathbf{x}} + {\mathbf{n}}} \right)\) is the state variable of each point in the neighborhood, \({\mathbf{h}}\left( {\mathbf{n}} \right)\) is an empirical weighting function subject to the normalization condition \(\int\limits_{V} {{\mathbf{h}}\left( {\mathbf{n}} \right)dV} = V\), and when \({\mathbf{A}}\left( {{\mathbf{x}} + {\mathbf{n}}} \right)\) is constant, \({\tilde{\mathbf{A}}}\left( {\mathbf{x}} \right) = {\mathbf{A}}\left( {{\mathbf{x}} + {\mathbf{n}}} \right)\). Assuming \({\mathbf{h}}\left( {\mathbf{n}} \right) = 1\), Eq. (26) can be rewritten as

$${\tilde{\mathbf{A}}}\left( {\mathbf{x}} \right) = \frac{1}{V}\int\limits_{V} {{\mathbf{A}}\left( {{\mathbf{x}} + {\mathbf{n}}} \right)dV} .$$
(27)

Applying the Taylor series expansion algorithm, keeping the derivative term below the second order, and substituting the volume of the neighborhood, we derive

$${\tilde{\mathbf{A}}}\left( {\mathbf{x}} \right) = {\mathbf{A}}\left( {\mathbf{x}} \right) + \frac{{l^{2} }}{10}\nabla^{2} {\mathbf{A}}\left( {\mathbf{x}} \right) = \left( {1 + \frac{{l^{2} }}{10}\nabla^{2} } \right){\mathbf{A}}\left( {\mathbf{x}} \right).$$
(28)

According to the generalized Hooke's law, the expression of the constitutive equation is as follows:

$$\sigma_{ij} = C_{ijkl} \varepsilon_{kl} ,$$
(29)

where \(\sigma_{ij}\) is the stress tensor, \(\varepsilon_{kl}\) is the strain tensor, and \(C_{ijkl}\) is the elastic coefficient tensor.

Thus, we define the non-local strain tensor as (Voyiadjis & Dorgan, 2004):

$${\tilde{\mathbf{\varepsilon }}} = \left( {1 + \frac{{l^{2} }}{10}\nabla^{2} } \right){{\varvec{\upvarepsilon}}} = \left( {{1} + c\nabla^{2} } \right){{\varvec{\upvarepsilon}}},$$
(30)

where \(c\) is the coefficient of the second-order gradient tensor, \(c = {{l^{2} } \mathord{\left/ {\vphantom {{l^{2} } {10}}} \right. \kern-0pt} {10}}\).

Substituting the non-local strain tensor and the non-local stress tensor for the strain tensor and the stress tensor, respectively, we obtain

$$\tilde{\sigma }_{ij} = C_{ijkl} \tilde{\varepsilon }_{kl} = C_{ijkl} (\varepsilon_{kl} + c\nabla^{2} \varepsilon_{kl} ).$$
(31)

As for isotropic medium, the constitutive equation can be rewritten as

$$\tilde{\sigma }_{ij} = \lambda \left( {\varepsilon_{kk} + c\nabla^{2} \varepsilon_{kk} } \right)\delta_{ij} + 2\mu \left( {\varepsilon_{ij} + c\nabla^{2} \varepsilon_{ij} } \right) = \left( {1 + c\nabla^{2} } \right)\left( {\lambda \delta_{ij} \varepsilon_{kk} + 2\mu \varepsilon_{ij} } \right).$$
(32)

The equilibrium equation is given as

$$\sigma_{ji,j} + F_{i} = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }}.$$
(33)

In the case of equivalent stress, the equilibrium equation can be rewritten as

$$\tilde{\sigma }_{ji,j} + F_{i} = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }}.$$
(34)

Substituting the constitutive equation based on the non-local theory into the equilibrium equation, we derive the asymmetric elastic wave equations based on the one-parameter second strain gradient theory (without consideration of body force):

$$\left( {1 + c\nabla^{2} } \right)\left( {\left( {\lambda + \mu } \right)u_{j,ij} + \mu u_{i,jj} } \right) = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }}.$$
(35)

According to Eqs. (25) and (35), it is worth noting that the independent free terms in the asymmetric wave equations derived from the two different theories are not exactly the same. For Eq. (25), the independent free term is \(\frac{1}{2}e_{ijk} \eta \left( {\frac{1}{2}e_{kmn} u_{n,mllj} + \frac{1}{2}e_{lmn} u_{n,mklj} } \right)\), whereas for Eq. (35), the independent free term is \(c\nabla^{2} \left( {\left( {\lambda + \mu } \right)u_{j,ij} + \mu u_{i,jj} } \right)\). The independent free term is used to describe the internal microstructural interactions. Compared with the modified couple stress theory, the one-parameter second strain gradient theory in which the strain energy density function contains a higher-order spatial derivative of strain can describe the heterogeneity of a medium caused by smaller-scale microstructural interactions. Assuming that the scale of the internal microstructure of the medium is the characteristic length scale parameter l of the medium, the asymmetric elastic wave equation based on the modified couple stress theory can represent the microstructural interactions with scale l, and the asymmetric elastic wave equation based on the one-parameter second strain gradient can represent the smaller-scale microstructural interactions inside the spherical neighborhood with scale l as the radius. Therefore, the concept of multi-scale microstructural interactions can be introduced.

In the next section, by setting the same characteristic length scale parameter for the micro-pore, we perform numerical modeling for the layered model and salt model using the conventional elastic wave equations and the asymmetric elastic wave equations based on the modified couple stress theory and one-parameter second strain gradient theory, and we analyze the influence of the microstructural interactions described by the different theories on the propagation of seismic waves. Compared with the conventional elastic wave equations, the asymmetric elastic wave equations only introduce an additional characteristic length scale parameter of the medium and an independent free term describing the microstructural interactions in the medium. As a result, the demand for computing resources is not greatly increased. In addition, to avoid the influence of numerical dispersion and boundary reflections on the modeling results, we use a higher-order optimized finite-difference operator and optimized perfectly matched layer (PML) boundary conditions for numerical modeling.

3 Numerical Modeling

3.1 Layered Model

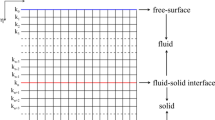
First, we perform numerical modeling of the two-layered model, as shown in Fig. 1. Both the horizontal and vertical sizes of the model are 3.2 km, and the grid interval is dx = dz = 8 m. For the first layer of the model, the P-wave velocity, S-wave velocity, and density are 2.4 km/s, 1.3856 km/s, and 1400 kg/m3, and for the second layer they are 4.2 km/s, 2.4249 km/s, and 2600 kg/m3, respectively. The characteristic length scale of the micro-pore of the first layer is set to 700 μm, and the second layer is set to 300 μm. A Ricker wavelet with a dominant frequency of 25 Hz is located at (1.6 km, 0 km), as shown in the red pentacle in Fig. 1. The time interval is 0.001 s, and the record length is 3 s.

Fig. 1
figure 1

Two-layered model used for numerical modeling. The thickness of the first layer is 1.6 km. The source position is shown by the red pentacle

Full size image

We perform numerical modeling for the two-layered model using the conventional elastic wave equations and the asymmetric elastic wave equations based on the modified couple stress theory. Figure 2 shows the snapshots generated by different elastic wave equations at a moment of 1.25 s. Figure 2a and d are the snapshots (x and z component) generated by the conventional elastic wave equations, Fig. 2b and e are the snapshots (x and z component) generated by the asymmetric elastic wave equations based on the modified couple stress theory, and Fig. 2c and f are the difference between Fig. 2a and b and between Fig. 2d and e, respectively.

Fig. 2
figure 2

a Snapshots generated by the conventional elastic wave equations (x component); b snapshots generated by the elastic wave equations based on the modified couple stress theory (x component); c the difference between a and b; d snapshots generated by the conventional elastic wave equations (z component); e snapshots generated by the elastic wave equations based on the modified couple stress theory (z component); f the difference between d and e

Full size image

As shown in Fig. 2, due to the addition of an independent free term containing the characteristic length scale parameters of the medium to the asymmetric elastic wave equation based on the modified couple stress theory, some new components of wavefields appear in both the x and z components of the synthetic snapshots, which can be regarded as the displacement disturbance caused by the heterogeneity of the medium. In Fig. 2c and f, the changes in wavefields can be observed more clearly. However, the changes are only reflected in the propagation of S-waves and have no effect on the propagation of P-waves.

The numerical modeling results of the layered model show that the elastic wave equation derived from the modified couple stress theory, containing the independent free term embedded in the characteristic length scale parameter of the medium, can describe the propagation of displacement disturbances generated by considering the microstructural interactions in the medium. The propagation of displacement disturbances can be clearly observed in the synthetic snapshots. At the same time, the heterogeneity of the medium caused by the microstructural interaction described by the modified couple stress theory has no effect on the propagation of the P-wave; however, it will cause new components to appear in the wavefields of the S-wave, causing the S-wave to propagate in a dispersive manner.

Next, a comparison of the synthetic snapshots generated by the conventional elastic wave equation and the asymmetric elastic wave equation based on the one-parameter second strain gradient theory is shown in Fig. 3. Similarly, all the snapshots are computed at 1.25 s. Figure 3a and d present the snapshots (x and z component) generated by the conventional elastic wave equations, Fig. 3b and e show the snapshots (x and z component) generated by the asymmetric elastic wave equations based on the one-parameter second strain gradient theory, and Fig. 3c and f show the difference between Fig. 3a and b and between Fig. 3d and e, respectively.

Fig. 3
figure 3

a Snapshots generated by the conventional elastic wave equations (x component); b snapshots generated by the elastic wave equations based on the one-parameter second strain gradient theory (x component); c the difference between a and b; d snapshots generated by the conventional elastic wave equations (z component); e snapshots generated by the elastic wave equations based on the one-parameter second strain gradient theory (z component); f the difference between d and e

Full size image

As shown in Fig. 3, whether in the x component or the z component of the synthetic snapshots, the influence of displacement disturbance caused by the heterogeneity of the medium described by the second-order strain gradient on the propagation of seismic waves can be clearly observed. That is, new components of wavefields appear in the synthetic snapshots. Comparing the differences in the snapshots as shown in Fig. 3c and f, we can more clearly observe the changes in the wavefields. The changes are reflected not only in the propagation of the S-wave, but also in the propagation of the P-wave, and the P-wave and S-wave both propagate in a dispersive manner. At the same time, under the framework of the one-parameter second strain gradient theory, the influence of microstructural interactions in the medium on the S-wave is significantly greater than that on the P-wave.

Further, we extract single-trace synthetic seismograms at the position (x, z) = (0.8 km, 0.4 km) for analysis, as shown in Fig. 4. Figure 4a–c depicts the x component and Fig. 4d–f the z component of single-trace synthetic seismograms. The blue, red, and green lines represent the seismograms generated by the conventional elastic wave equations, the elastic wave equations based on the modified couple stress theory, and the one-parameter second strain gradient theory, respectively.

Fig. 4
figure 4

Seismograms generated by different elastic wave equations: a-d x component; e–h z component

Full size image

In order to facilitate comparison, the single-trace synthetic seismograms generated by different elastic wave equations are shown together in Fig. 4d and h. Figure 4d indicates that the spatial derivative term of rotation introduced by the modified couple stress theory only affects the S-wave and converted wave, new information appears in the S-wave and converted wave, and both the amplitudes and the travel time have changed. While the second-order gradient of strain introduced by the one-parameter second strain gradient theory affects the S-wave, P-wave, and converted wave, although the changes in seismograms are weaker, the changes in the amplitudes and the travel time of the S-wave, P-wave, and converted wave can still be observed in Fig. 4h.

In addition, we note that even though the characteristic length scale parameters of the micro-pore are set the same, the heterogeneity of the medium described by the modified couple stress theory has a larger influence on the seismograms, which also shows that the modified couple stress theory and the one-parameter second strain gradient theory derived from the non-local theory describe the heterogeneity with different scales. Compared with the modified couple stress theory, the one-parameter second strain gradient theory can reflect the heterogeneity at smaller scale; however, the influence on seismic waves is weaker.

We capture seven regions (black dotted bordered rectangle) of Fig. 4d and h to zoom in, respectively, as shown in Fig. 5b–f and Fig. 6b–f. The influence of the heterogeneity of the medium caused by the microstructural interactions on the propagation of seismic waves can be observed more clearly, and the conclusions drawn are consistent with the above analysis.

Fig. 5
figure 5

Magnification of seismograms generated by different elastic wave equations (x component). a Seismograms generated by different elastic wave equations; b–h zoomed-in views of blocks 1–7, respectively

Full size image
Fig. 6
figure 6

Magnification of seismograms generated by different elastic wave equations (z component). a Seismograms generated by different elastic wave equations; b–h zoomed-in views of blocks 1–7, respectively

Full size image

3.2 Salt Model

We then perform additional numerical modeling of the SEG/EAGE (Society of Exploration Geophysicists/European Association of Geoscientists and Engineers) salt model to further examine the different elastic wave equations. The grid dimensions of the salt model are nx = 676, nz = 201, and the grid spacing is 8 m in both the x- and z-axis. The P-wave velocity model is shown in Fig. 7. The S-wave velocity is a scaled version of the P-wave velocity, with \(v_{S} = {{v_{P} } \mathord{\left/ {\vphantom {{v_{P} } {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}.\). The seismic source is a Ricker wavelet with a dominant frequency of 25 Hz, located at the red pentacle in Fig. 7. The record length is 5 s with a time step of 0.001 s. The characteristic length scale parameter of the micro-pore of the salt model is set to 700 μm.

Fig. 7
figure 7

The SEG/EAGE salt P-wave velocity model

Full size image

Figure 8 shows the x and z components of the synthetic shot records for the salt model generated by the conventional elastic wave equation and the asymmetric elastic wave equation based on the modified couple stress theory. Figure 8c is the record of Fig. 8a subtracted from Fig. 8b, and Fig. 8f is the record of Fig. 8d subtracted from Fig. 8e.

Fig. 8
figure 8

Synthetic shot records of the SEG/EAGE salt model, generated by the different elastic wave equations. a Synthetic shot records generated by the conventional elastic wave equations (x component); b synthetic shot records generated by the elastic wave equations based on the modified couple stress theory (x component); c the difference between a and b; d synthetic shot records generated by the conventional elastic wave equations (z component); e synthetic shot records generated by the elastic wave equations based on the modified couple stress theory (z component); f the difference between d and e

Full size image

We noted that even when the model is more complex, the displacement disturbance caused by the heterogeneity of the medium described by the spatial derivative of rotation still has an obvious influence on the propagation of seismic waves, as shown in Fig. 8. Compared with the shot records generated by the conventional elastic wave equation, the shot records generated by the asymmetric elastic wave equation have obvious differences in some regions, marked with the red arrows. It is easier to observe from the results of the subtraction, that is, as shown in Fig. 8c and f, new components appear in the records of the S-wave and surface wave. These new components are generated by considering the heterogeneity of the medium caused by the microstructural interactions.

Figure 9 shows the x and z components of the synthetic shot records for the salt model generated by the conventional elastic wave equation and the asymmetric elastic wave equation based on the one-parameter second strain gradient theory. Figure 9c is the record of Fig. 9a subtracted from Fig. 9b, and Fig. 9f is the record of Fig. 9d subtracted from Fig. 9e.

Fig. 9
figure 9

Synthetic shot records of the SEG/EAGE salt model, generated by the different elastic wave equations. a Synthetic shot records generated by the conventional elastic wave equations (x component); b synthetic shot records generated by the elastic wave equations based on the one-parameter second strain gradient theory (x component); c the difference between a and b; d synthetic shot records generated by the conventional elastic wave equations (z component); e synthetic shot records generated by the elastic wave equations based on the one-parameter second strain gradient theory (z component); f the difference between d and e

Full size image

Similarly, for complex models, the displacement disturbance described by the second-order gradient of strain also has an obvious influence on the propagation of seismic waves (see the regions marked by the red arrows in Fig. 9). If the shot records generated by the two elastic wave equations are subtracted, as shown in Fig. 9c and f, new components appear not only in the records of the S-wave and the surface wave, but also the records of the P-wave, which shows that the smaller-scale heterogeneity of the medium has an influence on the P-wave.

In summary, whether for the layered model or more complex salt model, compared with the numerical modeling results generated by the conventional elastic wave equations, the results generated by the asymmetric elastic wave equations contain new components which are very closely related to the characteristic length scale parameter of the medium. It is worth noting that in the frequency band of seismic exploration, the wavefield responses caused by the multiple-scale heterogeneity of the medium can still be clearly observed.

4 Conclusions

Complicated internal micro-defects/microstructures exist in both natural earth media and human-made materials. However, it is difficult to describe the complex microstructural interactions by the conventional continuum mechanics theory under its continuity assumption. In addition, it is worth emphasizing that the scale of micro-defects/microstructures varies with the observation target, and it is a relative concept. In this paper, we integrate the modified couple stress theory and the one-parameter second strain gradient theory into a unified framework for analyzing the complex microstructural interactions in the medium. Then we derive the asymmetric elastic wave equations based on the modified couple stress theory and the one-parameter second strain gradient theory under the same characteristic length scale parameter and perform numerical modeling. We can draw the following conclusions.

  1. 1.

    The complex microstructural interactions in the medium have an influence on the propagation of seismic waves. In the frequency band of seismic exploration, the influence of the microstructural interactions on the propagation of seismic waves can be obviously observed in seismic wave responses.

  2. 2.

    For the modified couple stress theory, the spatial derivative of rotation is introduced to describe the complex microstructural interactions, which causes the S-wave to propagate in a dispersive manner and has no effect on the P-wave propagation.

  3. 3.

    For the one-parameter second strain gradient theory, the second-order gradient of strain is introduced, which can represent smaller-scale microstructural interactions in the medium. New components appear in the P-wave and S-wave responses, while the amplitude and travel time also change.

  4. 4.

    The influence of the microstructural interactions described by the one-parameter second strain gradient theory on the propagation of seismic waves is weaker, and smaller microscale differences in the pore and grain geometry of rocks result in smaller macro-scale differences in wave responses and characteristics.