A Generalized 2.5-D Time-Domain Seismic Wave Equation to Accommodate Various Elastic Media and Boundary Conditions

Abstract

The 2.5-D seismic wave numerical simulation method employs point sources from 2-D geological models, enabling the calculation of point source wavefields at pseudo-2-D computational cost. We present herein a generalized 2.5-D first-order time-domain governing equation to model seismic wave propagation in different (acoustic, elastic isotropic, and anisotropic) media, then derive different formulae that incorporate topographic free-surface and fluid–solid interfaces. Furthermore, by assigning different model parameters from point to point, accommodating different boundary conditions, and applying the finite difference approach, we achieve the numerical simulation of seismic wave propagation with just one computer program. Comparisons with 3-D analytic and numerical solutions obtained using different full-space homogeneous models (acoustic, elastic isotropic, and anisotropic) verify the correctness of the 2.5-D method. Comparison of the results with a 3-D pseudospectral method show that the proposed 2.5-D method can simulate seismic wave propagation in various media with different boundary conditions. In addition, unlike the problems encountered when using 2-D numerical solutions for real 3-D applications, the 2.5-D method can be employed directly as a forward modeling method in seismic reverse-time migration and an efficient wavefield conversion tool between practical point source data and artificial line source data for 2-D seismic full waveform inversion.

1 Introduction

The numerical simulation of seismic wave propagation has always been considered a crucial step towards a more detailed understanding and interpretation of seismic data, as well as for imaging the Earth’s shallow or deep interior. With the rapid development of computer technology, various kinds of numerical methods, such as the finite-difference method (Moczo et al., 2014), finite-element method (Zhang et al., 2007), pseudospectral method (Fornberg, 1988), boundary element method (Bouchon & Coutant, 1994), discontinuous Galerkin method (Hesthaven & Warburton, 2008), finite volume element method (Su et al., 2020), and spectral element method (e.g., Seriani & Priolo, 1994; Faccioli et al., 1997; Komatitsch & Tromp, 1999) have been successfully applied to 2-D and 3-D seismic wave modeling.

Although 3-D seismic wave modeling can be applied to more complex problem (e.g., 3-D heterogeneous systems), it is usually very time-consuming and requires huge amounts of computer memory, leading to inefficiency for seismic imaging techniques in large models. To efficiently obtain high-resolution images of the Earth’s interior, seismic imaging techniques are mostly performed using computationally attractive 2-D models in either the time or frequency domain, such as diffraction tomography (Gelius, 1995; Pratt & Worthington, 1988; Wu & Toksöz, 1987), reverse time migration (Baysal et al., 1983; Dai et al., 2011; Zhang et al., 2015), and full-waveform inversion (Li & Demanet, 2016; Pratt & Worthington, 1990; Tarantola, 1984; Vigh et al., 2014; Virieux & Operto, 2009).

However, in 2-D seismic wave modeling, the point source used in practice is replaced with an artificial line source to achieve high computational efficiency, meaning that the magnitude of the source is constant along the strike direction, e.g., y-direction, while the wavefield becomes two-dimensional (Zhou et al., 2012). This is not true in seismic practice and results in difficulty in matching the 3-D dynamic features of real observed seismograms with such 2-D numerical solutions (Auer et al., 2013). Although 3-D to 2-D data transformation methods can be applied to convert realistic point source data into line source data and thereby obtain synthetic seismograms comparable to observed ones, such transformation filters can only be reliably applied to very simplistic models, e.g., homogeneous or flat-layered isotropic media in the far-field approximation with no overlapping arrivals (Williamson & Pratt, 1995).

To overcome the line-source assumption in 2-D wave modeling while avoiding the inefficient computations of 3-D wave modeling, one can apply a 2.5-D wave modeling approach, which employs a 3-D point source in a 2-D geological model (Song et al., 1995; Furumura & Takenaka, 1996; Zhou & Greenhalgh, 1998a, 1998b; Novais & Santos, 2005; Sinclair et al., 2007; Sinclair et al., 2012; Zhou et al., 2012; Xiong et al., 2013; Baker & Roecker, 2014). The 2.5-D forward-modeling method assumes a medium that is symmetric in the out-of-plane direction, allowing the application of a Fourier transform with respect to the out-of-plane direction and reducing the 3-D problem to a repeated 2-D computational problem, which is much more economical than full 3-D wave modeling (Zhou & Greenhalgh, 2006). Song et al. (1995) reconstructed the 3-D wavefield by applying the 2.5-D finite-difference scheme in the frequency domain. Zhou and Greenhalgh (1998a, b) applied a finite-element method to obtain the numerical solution of the 2.5-D frequency-domain wave equation with explicit 2.5-D absorbing boundary conditions. Doyon and Giroux (2014) demonstrated a finite-difference method to solve a 2.5-D frequency-domain wave equation in viscoelastic isotropic media. Takenaka and Kennett (1996) solved a 2.5-D elastodynamic equation in the time domain, but for incident plane waves. Novais and Santos (2005) improved the wavenumber sampling strategy for the time-domain finite-difference method. In addition, Zhou and Greenhalgh (2011b) developed numerical computations of sensitivity kernels for 2.5-D seismic full-waveform inversion. Roecker et al. (2010) and Baker and Roecker (2014) described a 2.5-D frequency-domain viscoelastic wavefield simulation method for their full-waveform inversion applications. Xiong et al. (2013) solved the 2.5-D problem by first transforming the elastic wave equation from the spatial into the wavenumber domain. Then, for each wavenumber, it becomes possible to solve a 2-D problem using the FD method with staggered grids.

In addition, the seismic wave velocity is direction dependent because of the existence of thin isotropic layers (Backus, 1962), fluid-filled cracks, and fractured rocks (Crampin et al., 1984). Seismic wavefield propagation modeling in anisotropic media has been widely studied (e.g., Igel et al., 1995; Lisitsa & Vishnevskiy, 2010; Saenger & Bohlen, 2004; Zhang et al., 2012a; Zhou & Greenhalgh, 2011a; Zhu & Dorman, 2000) due to the significant effects of seismic anisotropy on the arrival time, propagation direction, amplitude, and phases of the seismic wavefield (Christensen, 1984; Crampin, 1985; Martin & Thomas, 1987). As a practical way to understand the seismic anisotropy, synthetic seismic waveforms in anisotropic media are important for seismic exploration and Earth structure investigations (Heibig & Thomsen, 2005; Silver & Chan, 1991; Tsvankin et al., 2010). Furthermore, correct implementation of fluid–solid interfaces is helpful to investigate the physical phenomena that occur when a seismic wave propagates across complex fluid–solid interfaces, which can improve understanding of the generation and propagation of T-waves (e.g., de Groot-Hedlin & Orcutt, 2001; Jamet et al., 2013; Okal, 2008), Scholte and leaky Rayleigh waves (e.g., de Hoop & van der Hijden, 1983; Padilla et al., 1999; Zhu & Popovics, 2004), and seismic scattering caused by the seafloor (e.g., Greaves & Stephen, 2000; Robertsson & Levander, 1995).

However, the above-mentioned 2.5-D seismic wavefield numerical simulation methods in both the time and frequency domains are only applicable for a single (acoustic, elastic, or anisotropic) medium, while there is no generalized wave equation that can describe different types of medium (elastic, viscoelastic, and anisotropic) under different boundary conditions (acoustic free surface, solid free surface, and solid–liquid). This is the problem to be solved herein, that is, the development of a generalized 2.5-D first-order wave equation in the time domain and its solution, being suitable for complex mixed models with different boundary conditions. This is because the resulting generalized wavefield simulation method can deal with mutual coupling or merging phenomena between different types of waves, for example, a body (P or S) wave excited in an elastic isotropic medium penetrating into an elastic anisotropic medium and splitting and transforming into quasi-P (qP) or quasi-S (qSV, qSH) waves. Furthermore, it captures the change in the seismic wave velocity with the direction of propagation, the splitting of the shear wave, the dispersion of the surface wave velocity depending on the propagation direction, and the apparent anisotropy caused by the thin interlayer and the directional distribution of cracks in elastic anisotropic media. Such problems can be tackled with a single computer program, as illustrated by the solutions of the generalized 2.5-D first-order wave equation discussed in this paper.

In this paper, we present a generalized 2.5-D first-order time-domain wave equation (concise form) that accommodates acoustic, elastic isotropic, and anisotropic media, as well as the boundary conditions at free-surface and fluid–solid interfaces. We then solve the generalized wave equation using the DRP/opt MacCormack finite-difference method, a popular and well-tested nonstaggered scheme that has been successfully applied by Zhang and Chen (2006), Zhang et al. (2012a, 2012b) and Sun et al. 2016), and Sun and Zhang (2018) for 2-D and 3-D seismic wave modeling. The MacCormack-type scheme has inherent dissipation, which damps the spurious short-wavelength numerical waves generated by media discontinuities, computational domain boundaries, grid discontinuities, and other computational irregularities (Zhang & Chen, 2006). The generalized 2.5-D seismic wave equation is formulated in a concise matrix form, which is valid for different media and boundary conditions at different interfaces, then several numerical examples are given to show the correctness of the proposed wave equation and the effectiveness of the numerical method.

2 Generalized 2.5-D Seismic Wave Equation

Considering a geological model that is constant in the strike direction then taking the Fourier transformation with respect to the out-of-plane coordinate of the 3-D seismic wave equations (Novais & Santos, 2005; Zhou & Greenhalgh, 1998a, b), one obtains a generalized governing equation for 2.5-D seismic wave modeling in a concise matrix form that is suitable for different boundary conditions. By defining different wavefield vectors, assigning variable model parameters from point-to-point to three coefficient matrices, and employing either a pressure or force vector as a point source, one can achieve 2.5-D seismic wave modeling in complex geological models using a single computer software.

2.1 Elastic Anisotropic Media

In a 3-D elastic anisotropic medium, the first-order governing equation for wave propagation is given by Sun and Zhang (2018) as

$$ \begin{aligned} \dot{v}_{x} & = \rho^{ - 1} \left( {\sigma_{xx,x} + \sigma_{xz,z} + \sigma_{xy,y} + s_{x} } \right), \\ \dot{v}_{y} & = \rho^{ - 1} \left( {\sigma_{xy,x} + \sigma_{yz,z} + \sigma_{yy,y} + s_{y} } \right), \\ \dot{v}_{z} & = \rho^{ - 1} \left( {\sigma_{xz,x} + \sigma_{zz,z} + \sigma_{yz,y} + s_{z} } \right), \\ \end{aligned} $$

(1)

and

$$ \begin{aligned} \dot{\sigma }_{xx} & = c_{11} v_{x,x} + c_{16} v_{x,y} + c_{15} v_{x,z} + c_{16} v_{y,x} + c_{12} v_{y,y} + c_{14} v_{y,z} + c_{15} v_{z,x} + c_{14} v_{z,y} + c_{13} v_{z,z} , \\ \dot{\sigma }_{xy} & = c_{16} v_{x,x} + c_{66} v_{x,y} + c_{56} v_{x,z} + c_{66} v_{y,x} + c_{26} v_{y,y} + c_{46} v_{y,z} + c_{56} v_{z,x} + c_{46} v_{z,y} + c_{36} v_{z,z} , \\ \dot{\sigma }_{yy} & = c_{12} v_{x,x} + c_{26} v_{x,y} + c_{25} v_{x,z} + c_{26} v_{y,x} + c_{22} v_{y,y} + c_{24} v_{y,z} + c_{25} v_{z,x} + c_{24} v_{z,y} + c_{23} v_{z,z} , \\ \dot{\sigma }_{xz} & = c_{15} v_{x,x} + c_{56} v_{x,y} + c_{55} v_{x,z} + c_{56} v_{y,x} + c_{25} v_{y,y} + c_{45} v_{y,z} + c_{55} v_{z,x} + c_{45} v_{z,y} + c_{35} v_{z,z} , \\ \dot{\sigma }_{yz} & = c_{14} v_{x,x} + c_{46} v_{x,y} + c_{45} v_{x,z} + c_{46} v_{y,x} + c_{24} v_{y,y} + c_{44} v_{y,z} + c_{45} v_{z,x} + c_{44} v_{z,y} + c_{34} v_{z,z} , \\ \dot{\sigma }_{zz} & = c_{13} v_{x,x} + c_{36} v_{x,y} + c_{35} v_{x,z} + c_{36} v_{y,x} + c_{23} v_{y,y} + c_{34} v_{y,z} + c_{35} v_{z,x} + c_{34} v_{z,y} + c_{33} v_{z,z} , \\ \end{aligned} $$

(2)

in which $v_{x}$, $v_{{\text{y}}}$, and $v_{{\text{z}}}$ are particle velocity components; $\sigma_{xx}$, $\sigma_{yy}$,$\sigma_{zz}$, $\sigma_{xz}$,$\sigma_{xy}$, and $\sigma_{yz}$ are stress tensor components; $s_{x}$, $s_{{\text{y}}}$, and $s_{{\text{z}}}$ are source components; $\rho$ is mass density; $c_{ij}$ are components of the elastic matrix, the overdot represents the partial derivative with respect to time, and “$,x_{i}$” represents a derivative with respective to the $x_{i}$-coordinate. Applying Fourier transformation to Eqs. (1) and (2) along the y-axis to obtain equations in the wavenumber domain yields the 2.5-D governing equations

$$ \begin{gathered} \dot{\tilde{v}}_{x} = \rho^{ - 1} \left( {\tilde{\sigma }_{xx,x} + \tilde{\sigma }_{xz,z} + \mathrm{i}k_{y} \tilde{\sigma }_{xy} + s_{x} } \right), \hfill \\ \dot{\tilde{v}}_{y} = \rho^{ - 1} \left( {\tilde{\sigma }_{xy,x} + \tilde{\sigma }_{yz,z} + \mathrm{i}k_{y} \tilde{\sigma }_{yy} + s_{y} } \right), \hfill \\ \dot{\tilde{v}}_{z} = \rho^{ - 1} \left( {\tilde{\sigma }_{xz,x} + \tilde{\sigma }_{zz,z} + \mathrm{i}k_{y} \tilde{\sigma }_{yz} + s_{z} } \right), \hfill \\ \end{gathered} $$

(3)

and

$$ \begin{aligned} \dot{\tilde{\sigma }}_{xx} & = c_{11} \tilde{v}_{x,x} + c_{15} \tilde{v}_{x,z} + c_{16} \tilde{v}_{y,x} + c_{14} \tilde{v}_{y,z} + c_{15} \tilde{v}_{z,x} + c_{13} \tilde{v}_{z,z} + \mathrm{i}k_{y} \left( {c_{16} \tilde{v}_{x} + c_{12} \tilde{v}_{y} + c_{14} \tilde{v}_{z} } \right), \\ \dot{\tilde{\sigma }}_{xy} & = c_{16} \tilde{v}_{x,x} + c_{56} \tilde{v}_{x,z} + c_{66} \tilde{v}_{y,x} + c_{46} \tilde{v}_{y,z} + c_{56} \tilde{v}_{z,x} + c_{36} \tilde{v}_{z,z} + \mathrm{i}k_{y} \left( {c_{66} \tilde{v}_{x} + c_{26} \tilde{v}_{y} + c_{46} \tilde{v}_{z} } \right), \\ \dot{\tilde{\sigma }}_{yy} & = c_{12} \tilde{v}_{x,x} + c_{25} \tilde{v}_{x,z} + c_{26} \tilde{v}_{y,x} + c_{24} \tilde{v}_{y,z} + c_{25} \tilde{v}_{z,x} + c_{23} \tilde{v}_{z,z} + \mathrm{i}k_{y} \left( {c_{26} \tilde{v}_{x} + c_{22} \tilde{v}_{y} + c_{24} \tilde{v}_{z} } \right), \\ \dot{\tilde{\sigma }}_{xz} & = c_{15} \tilde{v}_{x,x} + c_{55} \tilde{v}_{x,z} + c_{56} \tilde{v}_{y,x} + c_{45} \tilde{v}_{y,z} + c_{55} \tilde{v}_{z,x} + c_{35} \tilde{v}_{z,z} + \mathrm{i}k_{y} \left( {c_{56} \tilde{v}_{x} + c_{25} \tilde{v}_{y} + c_{45} \tilde{v}_{z} } \right), \\ \dot{\tilde{\sigma }}_{yz} & = c_{14} \tilde{v}_{x,x} + c_{45} \tilde{v}_{x,z} + c_{46} \tilde{v}_{y,x} + c_{44} \tilde{v}_{y,z} + c_{45} \tilde{v}_{z,x} + c_{34} \tilde{v}_{z,z} + \mathrm{i}k_{y} \left( {c_{46} \tilde{v}_{x} + c_{24} \tilde{v}_{y} + c_{44} \tilde{v}_{z} } \right), \\ \dot{\tilde{\sigma }}_{zz} & = c_{13} \tilde{v}_{x,x} + c_{35} \tilde{v}_{x,z} + c_{36} \tilde{v}_{y,x} + c_{34} \tilde{v}_{y,z} + c_{35} \tilde{v}_{z,x} + c_{33} \tilde{v}_{z,z} + \mathrm{i}k_{y} \left( {c_{36} \tilde{v}_{x} + c_{23} \tilde{v}_{y} + c_{34} \tilde{v}_{z} } \right). \\ \end{aligned} $$

(4)

Defining the wavefield vector and source vector as

$$ \begin{aligned} {\tilde{\mathbf{y}}}^{(\mathrm{S})} & = \left( {{\tilde{\mathbf{v}}},{\tilde{\mathbf{\sigma }}}_{{\mathbf{1}}} ,{\tilde{\mathbf{\sigma }}}_{{\mathbf{2}}} } \right)^{{\text{T}}} , \, {\tilde{\mathbf{s}}}^{(\mathrm{S})} = ({\mathbf{s,0,0}})^{{\text{T}}} , \\ {\tilde{\mathbf{\nu }}} & = \left( {\tilde{\nu }_{x} ,\tilde{\nu }_{y} ,\tilde{\nu }_{z} } \right)^{T} , \, {\mathbf{s}} = \rho^{ - 1} \left( {s_{x} ,s_{y} ,s_{z} } \right)^{{\text{T}}} , \\ {\tilde{\mathbf{\sigma }}}_{1} & = \left( {\tilde{\sigma }_{xx} ,\tilde{\sigma }_{xy} ,\tilde{\sigma }_{yy} } \right)^{{\text{T}}} , \, {\tilde{\mathbf{\sigma }}}_{2} = \left( {\tilde{\sigma }_{xz} ,\tilde{\sigma }_{yz} ,\tilde{\sigma }_{zz} } \right)^{{\text{T}}} {,} \\ \end{aligned} $$

(5)

then Eqs. (3) and (4) can be simplified to the matrix form

$$ {\mathbf{\dot{\tilde{y}}}}^{(\mathrm{S})} = {\mathbf{A}}^{(\mathrm{S})} \partial_{x} {\tilde{\mathbf{y}}}^{(\mathrm{S})} + {\mathbf{B}}^{(\mathrm{S})} \partial_{z} {\tilde{\mathbf{y}}}^{(\mathrm{S})} + {\mathbf{C}}^{(\mathrm{S})} {\tilde{\mathbf{y}}}^{(\mathrm{S})} + {\tilde{\mathbf{s}}}^{(\mathrm{S})} , $$

(6)

which is valid for 2.5-D seismic wave modeling in arbitrary elastic anisotropic media. The coefficient matrices ${\mathbf{A}}^{(\mathrm{S})}$, ${\mathbf{B}}^{(\mathrm{S})}$, and ${\mathbf{C}}^{(\mathrm{S})}$ are given in Appendix 1, and the superscript “(S)” stands for the solid media, which may be elastic isotropic and anisotropic.

2.2 Acoustic Medium

In a 3-D acoustic medium, the first-order governing equation of wave propagation is given by Landau and Lifshitz (1959) as

$$ \begin{aligned} \dot{v}_{x} & = \rho^{ - 1} ( - \partial_{x} P), \\ \dot{v}_{y} & = \rho^{ - 1} ( - \partial_{y} P), \\ \dot{v}_{z} & = \rho^{ - 1} ( - \partial_{z} P) \\ \end{aligned} $$

(7)

and

$$ \dot{P} = - K(\partial_{x} v_{x} + \partial_{y} v_{y} + \partial_{z} v_{z} ) + s(t)\delta ({\mathbf{x}} - {\mathbf{x}}_{{\mathbf{s}}} ), $$

(8)

where P is pressure, $v_{i}$ is velocity component, K is the bulk modulus, $\rho$ is density of the medium, and s(t) is a point source at x_s.

After taking the Fourier transform with respect to the y-coordinate, Eqs. (7) and (8) become

$$ \begin{aligned} \dot{\tilde{v}}_{x} & = \rho^{ - 1} \left( { - \partial_{x} \tilde{P}} \right), \\ \dot{\tilde{v}}_{y} & = \rho^{ - 1} \left( { - \mathrm{i}k_{y} \tilde{P}} \right), \\ \dot{\tilde{v}}_{z} & = \rho^{ - 1} \left( { - \partial_{z} \tilde{P}} \right), \\ \end{aligned} $$

(9)

and

$$ \dot{\tilde{P}} = - K\left( {\partial_{x} \tilde{v}_{x} + \mathrm{i}k_{y} \tilde{v}_{y} + \partial_{z} \tilde{v}_{z} } \right) + s(t)\delta \left( {{\mathbf{x}} - {\mathbf{x}}_{{\mathbf{s}}} } \right). $$

(10)

Defining the wavefield vector and source vector as

$$ {\tilde{\mathbf{y}}}^{(\mathrm{W})} = \left( {\tilde{v}_{x} ,\tilde{v}_{y} ,\tilde{v}_{z} ,\tilde{P}} \right)^{T} , \, {\tilde{\mathbf{s}}}^{(\mathrm{W})} = \left( {0,0,0,s(t)\delta ({\mathbf{x}} - {\mathbf{x}}_{s} )} \right)^{T} , $$

(11)

the combined matrix form of Eqs. (9) and (10) becomes

$$ {\mathbf{\dot{\tilde{y}}}}^{(\mathrm{W})} = {\mathbf{A}}^{(\mathrm{W})} \partial_{x} {\tilde{\mathbf{y}}}^{(\mathrm{W})} + {\mathbf{B}}^{(\mathrm{W})} \partial_{z} {\tilde{\mathbf{y}}}^{(\mathrm{W})} + {\mathbf{C}}^{(\mathrm{W})} {\tilde{\mathbf{y}}}^{(\mathrm{W})} + {\tilde{\mathbf{s}}}^{(\mathrm{W})} , $$

(12)

which is valid for 2.5-D seismic wave modeling in arbitrary acoustic media; the coefficient matrices ${\mathbf{A}}^{(\mathrm{W})}$, ${\mathbf{B}}^{(\mathrm{W})}$, and ${\mathbf{C}}^{(\mathrm{W})}$ are given in Appendix 2. The superscript “(W)” stands for an acoustic medium such as water.

2.3 Free Surface of Acoustic Medium

On the free surface of an acoustic medium (strictly speaking, it should be an air–fluid interface, which can be approximated as a vacuum–fluid interface in seismological applications), the pressure P vanishes. Consequently, Eqs. (9) and (10) become

$$ \begin{aligned} \dot{\tilde{v}}_{x} & = \rho^{ - 1} \left( { - \partial {}_{x}\tilde{P}} \right), \\ \dot{\tilde{v}}_{y} & = 0, \\ \dot{\tilde{v}}_{z} & = \rho^{ - 1} \left( { - \partial {}_{z}\tilde{P}} \right), \\ \dot{\tilde{P}} & = 0, \\ \end{aligned} $$

(13)

which can also be written in matrix form as

$$ {\mathbf{\dot{\tilde{y}}}}^{{({\text{AW}})}} = {\mathbf{A}}^{{({\text{AW}})}} \partial_{x} {\tilde{\mathbf{y}}}^{(\mathrm{W})} + {\mathbf{B}}^{{({\text{AW}})}} \partial_{z} {\tilde{\mathbf{y}}}^{(\mathrm{W})} + {\mathbf{C}}^{{({\text{AW}})}} {\tilde{\mathbf{y}}}^{{({\text{AW}})}} + {\tilde{\mathbf{s}}}^{(\mathrm{W})} , $$

(14)

where the coefficient matrices are

$$ {\mathbf{A}}^{{(AW)}} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 & { - \rho ^{{ - 1}} } \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right),\;{\mathbf{B}}^{{(AW)}} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & { - \rho ^{{ - 1}} } \\ 0 & 0 & 0 & 0 \\ \end{array} } \right),\;{\mathbf{C}}^{{(AW)}} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right). $$

(15)

The superscript “(AW)” represents the free surface of the acoustic medium. Comparing Eqs. (15)–(71) reveals that Eq. (14) is a special case of Eq. (12).

2.4 Free Surface of Elastic Medium

On the free surface of an elastic medium (strictly speaking, it should be an air–solid interface, which can be approximated by a vacuum–solid interface in seismological applications), the normal component of the stress vanishes,

$$ {{\varvec{\upsigma}}} \cdot {\mathbf{n}} = {\mathbf{0}}, $$

(16)

which means

$$ \begin{gathered} \sigma_{xx} n_{1} + \sigma_{xy} n_{2} + \sigma_{xz} n_{3} = 0, \hfill \\ \sigma_{xy} n_{1} + \sigma_{yy} n_{2} + \sigma_{yz} n_{3} = 0, \hfill \\ \sigma_{xz} n_{1} + \sigma_{yz} n_{2} + \sigma_{zz} n_{3} = 0. \hfill \\ \end{gathered} $$

(17)

Here, n = (n₁, n₂, n₃) is the normal vector of the free surface. Equation (17) can be rewritten in matrix form as

$$ \left( {\begin{array}{*{20}c} {n_{1} } & \quad {n_{2} } & \quad 0 & \quad {n_{3} } & \quad 0 & \quad 0 \\ 0 & \quad {n_{1} {\mkern 1mu} } & \quad {n_{2} {\mkern 1mu} } & \quad 0 & \quad {n_{3} {\mkern 1mu} } & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad {n_{1} {\mkern 1mu} } & \quad {n_{2} {\mkern 1mu} } & \quad {n_{3} {\mkern 1mu} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\sigma _{{xx}} } \\ {\sigma _{{xy}} } \\ {\sigma _{{yy}} } \\ {\sigma _{{xz}} } \\ {\sigma _{{yz}} } \\ {\sigma _{{zz}} } \\ \end{array} } \right) = 0, $$

(18)

which may be changed into the submatrix form

$$ {\mathbf{B}}_{2} {{\varvec{\upsigma}}}_{2} = - {\mathbf{B}}_{1} {{\varvec{\upsigma}}}_{1} , $$

(19)

where

$$ {{\varvec{\upsigma}}}_{1} { = }\left( {\sigma_{xx} ,\sigma_{xy} ,\sigma_{yy} } \right),\quad {{\varvec{\upsigma}}}_{2} { = }\left( {\sigma_{xz} ,\sigma_{yz} ,\sigma_{zz} } \right), $$

(20)

$$ {\mathbf{B}}_{1} = \left( {\begin{array}{*{20}c} {n_{1} } & {n_{2} } & 0 \\ 0 & {n_{1} } & {n_{2} } \\ 0 & 0 & 0 \\ \end{array} } \right),\quad {\mathbf{B}}_{2} = \left( {\begin{array}{*{20}c} {n_{3} } & 0 & 0 \\ 0 & {n_{3} } & 0 \\ {n_{1} } & {n_{2} } & {n_{3} } \\ \end{array} } \right). $$

(21)

From Eq. (21), the inverse matrix of B₂ and its multiplication with B₁ gives

$$ \begin{gathered} {\mathbf{S}} = - {\mathbf{B}}_{2}^{ - 1} {\mathbf{B}}_{1} = - \left( {\begin{array}{*{20}c} {n_{3}^{ - 1} } & 0 & 0 \\ 0 & {n_{3}^{ - 1} } & 0 \\ { - n_{1} n_{3}^{ - 2} } & { - n_{2} n_{3}^{ - 2} } & {n_{3}^{ - 1} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {n_{1} } & {n_{2} } & 0 \\ 0 & {n_{1} } & {n_{2} } \\ 0 & 0 & 0 \\ \end{array} } \right) \hfill \\ \, = \left( {\begin{array}{*{20}c} { - n_{1} n_{3}^{ - 1} } & { - n_{2} n_{3}^{ - 1} } & 0 \\ 0 & { - n_{1} n_{3}^{ - 1} } & { - n_{2} n_{3}^{ - 1} } \\ {n_{1}^{2} n_{3}^{ - 2} } & {2n_{1} n_{2} n_{3}^{ - 2} } & {n_{2}^{2} n_{3}^{ - 2} } \\ \end{array} } \right), \hfill \\ \end{gathered} $$

(22)

so that we have

$$ {{\varvec{\upsigma}}}_{2} { = }{\mathbf{S\sigma }}_{1} , $$

(23)

which shows that the stress component ${{\varvec{\upsigma}}}_{2}$ can be calculated from ${{\varvec{\upsigma}}}_{1}$ with a known normal vector n, and only the stress component ${{\varvec{\upsigma}}}_{1}$ is independent.

Assuming that the free surface is given by z = z₀(x) and z₀ is differentiable, one has the slopes $tg\alpha = z^{\prime}_{0} (x)$ and the normal vector ${\mathbf{n}} = ( - \sin \alpha ,0,\cos \alpha )$, which changes Eq. (22) to

$$ {\mathbf{S}} = \left( {\begin{array}{*{20}c} {z^{\prime}_{0} (x)} & 0 & 0 \\ 0 & {z^{\prime}_{0} (x)} & 0 \\ {z^{\prime}_{0} (x)^{2} } & 0 & 0 \\ \end{array} } \right). $$

(24)

According to Eqs. (23) and (24), one may calculate the following partial derivatives:

$$ \begin{aligned} & {\dot{\mathbf{\sigma }}}_{2} = {\mathbf{S\dot{\sigma }}}_{1} , \hfill \\ & \partial_{x} {{\varvec{\upsigma}}}_{2} = (\partial_{x} {\mathbf{S}}){{\varvec{\upsigma}}}_{1} + {\mathbf{S}}(\partial_{x} {{\varvec{\upsigma}}}_{1} ), \hfill \\ & \partial_{z} {{\varvec{\upsigma}}}_{2} = {\mathbf{S}}(\partial_{z} {{\varvec{\upsigma}}}_{1} ). \hfill \\ \end{aligned} $$

(25)

Substituting Eq. (25) for (3) results in

$$ \begin{aligned} \dot{\tilde{v}}_{x} & = \rho^{ - 1} \left[ {\tilde{\sigma }_{xx,x} + z^{\prime}_{0} (x)\tilde{\sigma }_{xx,z} + \mathrm{i}k_{y} \tilde{\sigma }_{xy} + s_{x} } \right], \\ \dot{\tilde{v}}_{y} & = \rho^{ - 1} \left[ {\tilde{\sigma }_{xy,x} + z^{\prime}_{0} (x)\tilde{\sigma }_{xy,z} + \mathrm{i}k_{y} \tilde{\sigma }_{yy} + s_{y} } \right], \\ \dot{\tilde{v}}_{z} & = \rho^{ - 1} \left[ {z^{\prime}_{0} (x)\tilde{\sigma }_{xx,x} + z^{\prime}_{0} (x)^{2} \tilde{\sigma }_{xx,z} + \mathrm{i}k_{y} z^{\prime}_{0} (x)\tilde{\sigma }_{xy} + z^{\prime\prime}_{0} (x)\tilde{\sigma }_{xx} + s_{z} } \right]. \\ \end{aligned} $$

(26)

From Eq. (4), we have

$$ \begin{aligned} \dot{\tilde{\sigma }}_{xx} & = c_{11} \tilde{v}_{x,x} + c_{15} \tilde{v}_{x,z} + c_{16} \tilde{v}_{y,x} + c_{14} \tilde{v}_{y,z} + c_{15} \tilde{v}_{z,x} + c_{13} \tilde{v}_{z,z} + \mathrm{i}k_{y} \left( {c_{16} \tilde{v}_{x} + c_{12} \tilde{v}_{y} + c_{14} \tilde{v}_{z} } \right), \\ \dot{\tilde{\sigma }}_{xy} & = c_{16} \tilde{v}_{x,x} + c_{56} \tilde{v}_{x,z} + c_{66} \tilde{v}_{y,x} + c_{46} \tilde{v}_{y,z} + c_{56} \tilde{v}_{z,x} + c_{36} \tilde{v}_{z,z} + \mathrm{i}k_{y} \left( {c_{66} \tilde{v}_{x} + c_{26} \tilde{v}_{y} + c_{46} \tilde{v}_{z} } \right), \\ \dot{\tilde{\sigma }}_{yy} & = c_{12} \tilde{v}_{x,x} + c_{25} \tilde{v}_{x,z} + c_{26} \tilde{v}_{y,x} + c_{24} \tilde{v}_{y,z} + c_{25} \tilde{v}_{z,x} + c_{23} \tilde{v}_{z,z} + \mathrm{i}k_{y} \left( {c_{26} \tilde{v}_{x} + c_{22} \tilde{v}_{y} + c_{24} \tilde{v}_{z} } \right). \\ \end{aligned} $$

(27)

Defining the wavefield vector and the source vector as

$$ {\tilde{\mathbf{y}}}^{{({\text{AS}})}} = \left( {\tilde{v}_{x} ,\tilde{v}_{y} ,\tilde{v}_{z} ,\tilde{\sigma }_{xx} ,\tilde{\sigma }_{xy} ,\tilde{\sigma }_{yy} } \right)^{{\text{T}}} , \, {\tilde{\mathbf{s}}}^{{({\text{AS}})}} = \rho^{ - 1} \left( {s_{x} ,s_{y} ,s_{z} ,0,0,0} \right)^{{\text{T}}} , $$

(28)

we obtain the matrix form of Eqs. (26) and (27) as

$$ {\mathbf{\dot{\tilde{y}}}}^{{({\text{AS}})}} = {\mathbf{A}}^{{({\text{AS}})}} \partial_{x} {\tilde{\mathbf{y}}}^{{({\text{AS}})}} + {\mathbf{B}}^{{({\text{AS}})}} \partial_{z} {\tilde{\mathbf{y}}}^{{({\text{AS}})}} + {\mathbf{C}}^{{({\text{AS}})}} {\tilde{\mathbf{y}}}^{{({\text{AS}})}} + {\tilde{\mathbf{s}}}^{{({\text{AS}})}} , $$

(29)

where the coefficient matrices ${\mathbf{A}}^{{({\text{AS}})}}$,${\mathbf{B}}^{{({\text{AS}})}}$, and ${\mathbf{C}}^{{({\text{AS}})}}$ are given in Appendix 3. The superscript “(AS)” means the free surface of the elastic medium. Comparing Eqs. (28) and (29) with Eqs. (5) and (6) reveals that Eq. (29) excludes the stress components ${\tilde{\mathbf{\sigma }}}_{2}$ from Eq. (6) due to the free-surface boundary condition of Eq. (23), and only the stress components ${\tilde{\mathbf{\sigma }}}_{1}$ and velocity vector ${\tilde{\mathbf{v}}}$ are independent and need to be solved from Eq. (29).

2.5 Fluid–Solid Interface

At a fluid–solid interface, e.g., a 2-D seafloor defined by $z = z_{0} (x)$ where z₀ is twice differentiable, the boundary conditions include the continuity of the normal stress and normal velocity vector, while the tangential traction vanishes, i.e.,

$$ {\tilde{\mathbf{\sigma }}}(t,x,z_{0} (x)) \cdot {\mathbf{n}} = - \tilde{P}(t,x,z_{0} (x)) \cdot {\mathbf{n}}, $$

(30)

$$ {\tilde{\mathbf{v}}}^{(\mathrm{S})} (t,x,z_{0} (x)) \cdot {\mathbf{n}} = {\tilde{\mathbf{v}}}^{(\mathrm{W})} (t,x,z_{0} (x)) \cdot {\mathbf{n}}, $$

(31)

_and

$$ \begin{gathered} {\tilde{\mathbf{\sigma }}}(t,x,z_{0} (x)) \cdot {{\varvec{\uptau}}}^{(1)} = {\mathbf{0}}, \hfill \\ {\tilde{\mathbf{\sigma }}}(t,x,z_{0} (x)) \cdot {{\varvec{\uptau}}}^{(2)} = {\mathbf{0}}, \hfill \\ \end{gathered} $$

(32)

where ${\tilde{\mathbf{\sigma }}}$ is the stress on the solid side, $\tilde{P}$ is the pressure on the fluid side, and the vectors ${\tilde{\mathbf{v}}}^{(\mathrm{S})}$ and ${\tilde{\mathbf{v}}}^{(\mathrm{W})}$ stand for the velocity vectors of solid and fluid at the interface, respectively. Applying the slope $tg\alpha = z^{\prime}_{0} (x)$ of the interface, we have the tangential vectors

$$ {{\varvec{\uptau}}}^{(1)} = \left( {\begin{array}{*{20}c} 0 \\ 1 \\ 0 \\ \end{array} } \right), \, {{\varvec{\uptau}}}^{(2)} = \left( {\begin{array}{*{20}c} {\cos \alpha } \\ 0 \\ {\sin \alpha } \\ \end{array} } \right). $$

(33)

Equation (32) implies

$$ \begin{gathered} \tilde{\sigma }_{xy} = 0, \, \tilde{\sigma }_{yy} = 0, \, \tilde{\sigma }_{yz} = 0, \hfill \\ \tilde{\sigma }_{xx} = - z^{\prime}_{0} (x)\tilde{\sigma }_{xz} , \, \tilde{\sigma }_{xz} = - z^{\prime}_{0} (x)\tilde{\sigma }_{zz} , \hfill \\ \end{gathered} $$

(34)

which shows that only $\tilde{\sigma }_{zz}$ is independent and that the other nonzero components $(\tilde{\sigma }_{xx} ,\tilde{\sigma }_{xz} )$ depend on $\tilde{\sigma }_{zz}$ and $z^{\prime}_{0} (x)$. Applying Eqs. (34)–(30) gives

$$ \tilde{\sigma }_{zz} = \frac{ - 1}{{1 + z^{\prime}_{0} (x)^{2} }}\tilde{P}. $$

(35)

This shows that the stress component $\tilde{\sigma }_{zz}$ is defined by the pressure on the fluid side. In the particular case $z^{\prime}_{0} (x) = 0$ (a flat interface), we have $\tilde{\sigma }_{zz} = - \tilde{P}$ and Eq. (34) shows that all the stress components except for $\tilde{\sigma }_{zz}$ vanish. Equation (35) gives

$$ \dot{\tilde{P}} = - \left[ {1 + z^{\prime}_{0} (x)^{2} } \right]\tilde{\sigma }_{zz} . $$

(36)

For simplicity, considering no extra source at the fluid–solid interface, we substitute Eqs. (4) and (14) for (36) and obtain

$$ \begin{aligned} \partial_{x} \tilde{v}_{x}^{(\mathrm{W})} & + \mathrm{i}k_{y} \tilde{v}_{y}^{(\mathrm{W})} + \partial_{z} \tilde{v}_{z}^{(\mathrm{W})} \\ & = \frac{{1 + z^{\prime}_{0} (x)^{2} }}{K}\left[ {(c_{13} ,c_{36} ,c_{35} ) \cdot \partial_{x} {\tilde{\mathbf{v}}}^{(\mathrm{S})} + (c_{35} ,c_{34} ,c_{33} ) \cdot \partial_{z} {\tilde{\mathbf{v}}}^{(\mathrm{S})} { + }\mathrm{i}k_{y} (c_{36} ,c_{23} ,c_{34} ) \cdot {\tilde{\mathbf{v}}}^{(\mathrm{S})} } \right], \\ \end{aligned} $$

(37)

which leads to

$$ \tilde{v}_{y}^{(\mathrm{W})} = \frac{{1 + z^{\prime}_{0} (x)^{2} }}{K}\left( {c_{36} \tilde{v}_{x}^{(\mathrm{S})} + c_{23} \tilde{v}_{y}^{(\mathrm{S})} + c_{34} \tilde{v}_{z}^{(\mathrm{S})} } \right), $$

(38)

for any $k_{y}$. Also, Eq. (31) gives

$$ \tilde{v}_{z}^{(\mathrm{W})} = z^{\prime}_{0} (x)\left( {\tilde{v}_{x}^{(\mathrm{W})} - \tilde{v}_{x}^{(\mathrm{S})} } \right) + \tilde{v}_{z}^{(\mathrm{S})} . $$

(39)

Equations (38) and (39) show that the water velocity components $\tilde{v}_{y}^{(\mathrm{W})}$ and $\tilde{v}_{z}^{(\mathrm{W})}$ are not independent and can be calculated from the solid velocity vector ${\tilde{\mathbf{v}}}^{(\mathrm{S})} = (\tilde{v}_{x}^{(\mathrm{S})} ,\tilde{v}_{y}^{(\mathrm{S})} ,\tilde{v}_{z}^{(\mathrm{S})} )$ and the x-component $\tilde{v}_{x}^{(\mathrm{W})}$ of the water velocity vector at the interface.

Substituting Eq. (37) for (4) results in

$$ \begin{aligned} \dot{\tilde{P}} & = \\- \left( {1 + z^{\prime}_{0} (x)^{2} } \right)\left[ {(c_{13} ,c_{36} ,c_{35} ) \cdot \partial_{x} {\tilde{\mathbf{v}}}^{(\mathrm{S})} \quad + (c_{35} ,c_{34} ,c_{33} ) \cdot \partial_{z} {\tilde{\mathbf{v}}}^{(\mathrm{S})} } \right. \\ & \quad + \left. {ik_{y} (c_{36} ,c_{23} ,c_{34} ) \cdot {\tilde{\mathbf{v}}}^{(\mathrm{S})} } \right]. \\ \end{aligned} $$

(40)

In addition, employing Eqs. (34) and (35) for Eq. (3), we have

$$ \begin{aligned} \dot{\tilde{v}}_{x}^{(\mathrm{S})} & = \rho_{{\text{S}}}^{ - 1} \left( {\frac{{ - z_{0}^{^{\prime}} (x)^{2} }}{{z_{0}^{^{\prime}} (x)^{2} + 1}}\partial_{x} \tilde{P} + \frac{{z_{0}^{^{\prime}} (x)}}{{z_{0}^{^{\prime}} (x)^{2} + 1}}\partial_{z} \tilde{P} + \frac{{ - z_{0}^{^{\prime}} (x)z_{0}^{^{\prime\prime}} (x)}}{{\left( {z_{0}^{^{\prime}} (x)^{2} + 1} \right)^{2} }}\tilde{P}} \right), \\ \dot{\tilde{v}}_{y}^{(\mathrm{S})} & = \rho_{{\text{S}}}^{ - 1} \left( { - z_{0}^{^{\prime}} (x)\tilde{\sigma }_{xy,z} + \tilde{\sigma }_{yz,z} } \right), \\ \dot{\tilde{v}}_{z}^{(\mathrm{S})} & = \rho_{{\text{S}}}^{ - 1} \left( {\frac{{z_{0}^{^{\prime}} (x)}}{{z_{0}^{^{\prime}} (x)^{2} + 1}}\partial_{x} \tilde{P} + \frac{ - 1}{{z_{0}^{^{\prime}} (x)^{2} + 1}}\partial_{z} \tilde{P} + \frac{{z_{0}^{^{\prime\prime}} (x)\left( {1 - z_{0}^{^{\prime}} (x)^{2} } \right)}}{{\left( {z_{0}^{^{\prime}} (x)^{2} + 1} \right)^{2} }}\tilde{P}} \right), \\ \end{aligned} $$

(41)

where $\rho_{{\text{S}}}$ is the solid density. From Eq. (13), we also have

$$ \dot{\tilde{v}}_{x}^{(\mathrm{W})} = \rho_{{\text{W}}}^{ - 1} ( - \partial_{x} \tilde{P}), $$

(42)

where $\rho_{{\text{W}}}$ is the water density. By employing the following wavefield vectors and a source vector on the interface

$$ \begin{aligned} {\tilde{\mathbf{y}}}^{{\left( {{\text{WS}}} \right)}} & = \left( {{\tilde{\mathbf{v}}}^{{{\text{WS}}}} ,\tilde{P},\tilde{\sigma }_{xy} ,\tilde{\sigma }_{yz} } \right)^{{\text{T}}} , \\ {\tilde{\mathbf{v}}}^{{\left( {{\text{WS}}} \right)}} & = \left( {\tilde{v}_{x}^{\left( W \right)} ,\tilde{v}_{x}^{\left( S \right)} ,\tilde{v}_{y}^{\left( S \right)} ,\tilde{v}_{z}^{\left( S \right)} } \right), \\ {\tilde{\mathbf{s}}}^{{\left( {{\text{WS}}} \right)}} & = \left\{ \begin{gathered} \left( {0,0,0,0,\dot{s}\left( t \right)\delta \left( {{\mathbf{x}} - {\mathbf{x}}_{{\mathbf{s}}} } \right),0,0} \right)^{{\text{T}}} ,\left( {{\text{fluid}}} \right) \hfill \\ \left( {0,s_{x} ,s_{y} ,s_{z} ,0,0,0} \right)^{T} ,\left( {{\text{solid}}} \right) \hfill \\ \end{gathered} \right.. \\ \end{aligned} $$

(43)

Equations (38), (40), and (41) can thus be reduced to the matrix form

$$ {\mathbf{\dot{\tilde{y}}}}^{{({\text{WS}})}} = {\mathbf{A}}^{{({\text{WS}})}} \partial_{x} {\tilde{\mathbf{y}}}^{{({\text{WS}})}} + {\mathbf{B}}^{{({\text{WS)}}}} \partial_{z} {\tilde{\mathbf{y}}}^{{({\text{WS}})}} + {\mathbf{C}}^{{({\text{WS}})}} {\tilde{\mathbf{y}}}^{{({\text{WS}})}} + {\tilde{\mathbf{s}}}^{{({\text{WS}})}} , $$

(44)

where the coefficient matrices ${\mathbf{A}}^{{({\text{WS}})}}$, ${\mathbf{B}}^{{({\text{WS}})}}$, and ${\mathbf{C}}^{{({\text{WS}})}}$ are given in Appendix 4. After solving Eq. (44), one can apply Eqs. (34), (35), (38), and (39) to calculating the solid stress components $\left( {\tilde{\sigma }_{xx} ,\tilde{\sigma }_{xz} ,\tilde{\sigma }_{zz} } \right)$ and the water velocity components $(\tilde{v}_{y}^{(\mathrm{W})} ,\tilde{v}_{z}^{(\mathrm{W})} ),$ respectively.

3 Numerical Methods

The previous section showed that the generalized 2.5-D time-domain first-order governing equations of seismic waves in various media and at different interfaces have the generalized concise matrix form

$$ \dot{\tilde{y}} = {\mathbf{A}}\partial_{x} \tilde{y} + {\mathbf{B}}\partial_{z} \tilde{y} + {\mathbf{C}}\tilde{y} + {\tilde{\mathbf{s}}}, $$

(45)

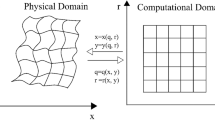
where the wavefield vector ${\tilde{\mathbf{y}}}$, source vector ${\tilde{\mathbf{s}}}$, and the matrices A, B, and C depend on the media and vary from point to point. To better describe the undulating surface topography, the curvilinear finite-difference method is applied, enabling one to divide the geological model by curvilinear coordinates and the body-conforming grid (Zhang & Chen, 2006) to make the grid lines exactly match the free-surface topography and undulating subsurface interfaces. The first step of the curvilinear finite difference approach is to map the curvilinear grids in physical space $\left( {x,z} \right)$ to the uniform rectangular grids in the computational space $\left( {\xi ,\eta } \right)$ by coordinate transformations (Thompson et al., 1985). Thus, Eq. (45) becomes

$$ \dot{\tilde{y}} = {\mathbf{A}}_{1} \partial_{\xi } \tilde{y} + {\mathbf{B}}_{1} \partial_{\eta } \tilde{y} + {\mathbf{C}}_{1} \tilde{y} + {\tilde{\mathbf{s}}}, $$

(46)

where

$$ \begin{aligned} {\mathbf{A}}_{1} & = \partial_{x} \xi (x,z) \cdot {\mathbf{A}} + \partial_{z} \xi (x,z) \cdot {\mathbf{B}}, \\ {\mathbf{B}}_{1} & = \partial_{x} \eta (x,z) \cdot {\mathbf{A}} + \partial_{z} \eta (x,z) \cdot {\mathbf{B}}, \\ {\mathbf{C}}_{1} & = {\mathbf{C}}. \\ \end{aligned} $$

(47)

The detail of the mapping from the curvilinear coordinate to the Cartesian coordinates and the method to obtain the derivatives $\partial_{x} \xi (x,z),$ $\partial_{z} \xi (x,z),$ $\partial_{x} \eta (x,z)$ and $\partial_{z} \eta (x,z)$ have been reported in literature (Zhang & Chen, 2006; Sun et al., 2016; Sun & Zhang, 2018; Yang et al., 2020), and $z^{\prime}_{0}$ and $z^{\prime\prime}_{0}$ are also calculated numerically by the finite-difference method.

3.1 Spatial Differential Format

Hixon and Turkel (2000) applied the dispersion relation preserving (DRP, Tam & Webb, 1993) method to optimize the coefficients of the finite difference operator and obtained a DRP/opt MacCormack format in terms of low dispersion and dissipation. Here, we adopt the DRP/opt MacCormack finite difference formats to discrete Eq. (46); e.g., the spatial derivatives with respect to $\xi -$ and $\eta -$ axis can be approximated by the forward and backward finite-difference operators (Hixon, 1997; Hixon & Turkel, 2000)

$$ \begin{aligned} L_{\xi }^{\rm F} ({\tilde{\mathbf{y}}})_{i} & = \frac{1}{\Delta x}\sum\limits_{j = - 1}^{3} {a_{j} {\tilde{\mathbf{y}}}_{i + j,k} ,} \\ L_{\xi }^{\rm B} ({\tilde{\mathbf{y}}})_{i} & = \frac{1}{\Delta x}\sum\limits_{j = - 1}^{3} { - a_{j} {\tilde{\mathbf{y}}}_{i - j,k} ,} \\ L_{\eta }^{\rm F} ({\tilde{\mathbf{y}}})_{k} & = \frac{1}{\Delta z}\sum\limits_{j = - 1}^{3} {a_{j} {\tilde{\mathbf{y}}}_{i,k + j} ,} \\ L_{\eta }^{\rm B} ({\tilde{\mathbf{y}}})_{k} & = \frac{1}{\Delta z}\sum\limits_{j = - 1}^{3} { - a_{j} {\tilde{\mathbf{y}}}_{i,k - j} ,} \\ \end{aligned} $$

(48)

where $L_{\xi }$ and $L_{\eta }$ represent the spatial difference with respect to the $\xi -$ and $\eta -$axis, the subscripts i and k are indices of the grid point, and the superscripts “F” and “B” denote forward and backward operators, respectively. The coefficients are given by $a_{ - 1} = - 0.30874$, $a_{0} = - 0.6326$, $a_{1} = 1.2330$, $a_{2} = - 0.3334$, and $a_{3} = 0.04168$.

The spatial derivatives in Eq. (46) can be approximated by the following forms if the DRP/opt MacCormack differential formats are applied (Zhang & Chen, 2006)

$$ \left\{ \begin{gathered} \hat{L}^{{{\text{FF}}}} ({\tilde{\mathbf{y}}}) = {\mathbf{A}}L_{\xi }^{\rm F} ({\tilde{\mathbf{y}}}) + {\mathbf{B}}L_{\eta }^{\rm F} ({\tilde{\mathbf{y}}}) + {\mathbf{C}}({\tilde{\mathbf{y}}}), \hfill \\ \hat{L}^{{{\text{BB}}}} ({\tilde{\mathbf{y}}}) = {\mathbf{A}}L_{\xi }^{\rm B} ({\tilde{\mathbf{y}}}) + {\mathbf{B}}L_{\eta }^{\rm B} ({\tilde{\mathbf{y}}}) + {\mathbf{C}}({\tilde{\mathbf{y}}}), \hfill \\ \hat{L}^{{{\text{FB}}}} ({\tilde{\mathbf{y}}}) = {\mathbf{A}}L_{\xi }^{\rm F} ({\tilde{\mathbf{y}}}) + {\mathbf{B}}L_{\eta }^{\rm B} ({\tilde{\mathbf{y}}}) + {\mathbf{C}}({\tilde{\mathbf{y}}}), \hfill \\ \hat{L}^{{{\text{BF}}}} ({\tilde{\mathbf{y}}}) = {\mathbf{A}}L_{\xi }^{\rm B} ({\tilde{\mathbf{y}}}) + {\mathbf{B}}L_{\eta }^{\rm F} ({\tilde{\mathbf{y}}}) + {\mathbf{C}}({\tilde{\mathbf{y}}}), \hfill \\ \end{gathered} \right. $$

(49)

in which $\hat{L}^{{{\text{FF}}}}$, $\hat{L}^{{{\text{BB}}}}$, $\hat{L}^{{{\text{FB}}}}$, and $\hat{L}^{{{\text{BF}}}}$ are 2-D DRP/opt MacCormack differential operators.

The derivatives with respect to the $\eta$-axis on grid points near the free surface (k₂) and near the water–solid interface (k_n−2 and k_n+2) are calculated by the 4–2 MacCormack differential operators,

$$ \begin{aligned} L_{\eta }^{\rm F} ({\tilde{\mathbf{y}}})_{k} & = \frac{1}{\Delta z}\sum\limits_{j = 0}^{2} {a_{j} {\tilde{\mathbf{y}}}_{i,k + j} ,} \\ L_{\eta }^{\rm B} ({\tilde{\mathbf{y}}})_{k} & = \frac{1}{\Delta z}\sum\limits_{j = 0}^{2} { - a_{j} {\tilde{\mathbf{y}}}_{i,k - j} ,} \\ \end{aligned} $$

(50)

in which $a_{0} = - 7/6$, $a_{1} = 8/6$, and $a_{2} = - 1/6$. The model mesh is shown in Fig. 1. The derivatives with respect to the $\eta$-axis on the grid near the free surface (k₁) and near the water–solid interface (k_n−1 and k_n+1) are calculated by 2–2 MacCormack differential operators, which are the simplest classical FD operator,

$$ \begin{aligned} L_{\xi }^{\rm F} ({\tilde{\mathbf{y}}})_{k} & = \frac{1}{\Delta z}\sum\limits_{j = 0}^{1} {a_{j} {\tilde{\mathbf{y}}}_{i,k + j} ,} \\ L_{\xi }^{\rm B} ({\tilde{\mathbf{y}}})_{k} & = \frac{1}{\Delta z}\sum\limits_{j = 0}^{1} { - a_{j} {\tilde{\mathbf{y}}}_{i,k - j} ,} \\ \end{aligned} $$

(51)

with coefficients $a_{0} = - 1.0$ and $a_{1} = 1.0$.

Fig. 1

Model meshing illustration; the blue line (k₀) and red line (k_n) represent the free surface and fluid–solid interface, respectively

For free-surface grids (k₀) and acoustic wave equation parameters on water–solid interface grids (k_n), the derivatives with respect to the $\eta -$axis are calculated by one-sided differential operators,

$$ L_{\eta } ({\tilde{\mathbf{y}}})_{k} = \frac{1}{\Delta z}\sum\limits_{j = 0}^{1} { - a_{j} {\tilde{\mathbf{y}}}_{i,k - j} ,} $$

(52)

with coefficients $a_{0} = - 1.0$ and $a_{1} = 1.0$, but for elastic wave equation parameters on water–solid interface grids (k_n), the derivatives with respect to the $\eta$-axis are calculated by one-sided differential operators,

$$ L_{\eta } ({\tilde{\mathbf{y}}})_{k} = \frac{1}{\Delta z}\sum\limits_{j = 0}^{1} {a_{j} {\tilde{\mathbf{y}}}_{i,k + j} ,} $$

(53)

with coefficients $a_{0} = - 1.0$ and $a_{1} = 1.0$. The derivatives with respect to the $\xi$-axis on these surface and near surface grids are calculated by DRP/opt MacCormack differential operators.

3.2 Time Integration Method

The fourth-order Runge–Kutta scheme is used to update the wavefields (Hixon, 1997; Hixon & Turkel, 2000), which has low dispersion and dissipation. To avoid numerical bias in each of the multistage Runge–Kutta schemes, the order of the one-sided difference operator is interchanged every step (Zhang & Chen, 2006). The implementation of the DRP/opt MacCormack scheme and the four-stage low-dispersion and low-dissipation Runge–Kutta scheme for Eq. (46) is described below (Zhang et al., 2012a, 2012b):

Time integration loop

(i) Sub time step 1:

$$ \begin{aligned} {\mathbf{h}}_{1}^{(n)} & = \Delta t\hat{L}^{{{\text{FF}}}} \left( {{\tilde{\mathbf{y}}}^{n} } \right), \\ {\mathbf{h}}_{2}^{(n)} & = \Delta t\hat{L}^{{{\text{BB}}}} \left( {{\tilde{\mathbf{y}}}^{n} + \alpha_{2} {\mathbf{h}}_{1}^{(n)} } \right), \\ {\mathbf{h}}_{3}^{(n)} & = \Delta t\hat{L}^{{{\text{FF}}}} \left( {{\tilde{\mathbf{y}}}^{n} + \alpha_{3} {\mathbf{h}}_{2}^{(n)} } \right), \\ {\mathbf{h}}_{4}^{(n)} & = \Delta t\hat{L}^{{{\text{BB}}}} \left( {{\tilde{\mathbf{y}}}^{n} + \alpha_{4} {\mathbf{h}}_{3}^{(n)} } \right), \\ {\tilde{\mathbf{y}}}^{n + 1} & = {\tilde{\mathbf{y}}}^{n} + \beta_{1} {\mathbf{h}}_{1}^{(n)} + \beta_{2} {\mathbf{h}}_{2}^{(n)} + \beta_{3} {\mathbf{h}}_{3}^{(n)} + \beta_{4} {\mathbf{h}}_{4}^{(n)} , \\ \end{aligned} $$

(54)

(ii) Sub time step 2:

$$ \begin{aligned} {\mathbf{h}}_{1}^{(n + 1)} & = \Delta t\hat{L}^{{{\text{FB}}}} \left( {{\tilde{\mathbf{y}}}^{n + 1} } \right), \\ {\mathbf{h}}_{2}^{(n + 1)} & = \Delta t\hat{L}^{{{\text{BF}}}} \left( {{\tilde{\mathbf{y}}}^{n + 1} + \alpha_{2} {\mathbf{h}}_{1}^{(n + 1)} } \right), \\ {\mathbf{h}}_{3}^{(n + 1)} & = \Delta t\hat{L}^{{{\text{FB}}}} \left( {{\tilde{\mathbf{y}}}^{n + 1} + \alpha_{3} {\mathbf{h}}_{2}^{(n + 1)} } \right), \\ {\mathbf{h}}_{4}^{(n + 1)} & = \Delta t\hat{L}^{{{\text{BF}}}} \left( {{\tilde{\mathbf{y}}}^{n + 1} + \alpha_{4} {\mathbf{h}}_{3}^{(n + 1)} } \right), \\ {\tilde{\mathbf{y}}}^{n + 2} & & = {\tilde{\mathbf{y}}}^{n} + \beta_{1} {\mathbf{h}}_{1}^{(n + 1)} + \beta_{2} {\mathbf{h}}_{2}^{(n + 1)} + \beta_{3} {\mathbf{h}}_{3}^{(n + 1)} + \beta_{4} {\mathbf{h}}_{4}^{(n + 1)} , \\ \end{aligned} $$

(55)

(iii) Sub time step 3:

$$ \begin{aligned} {\mathbf{h}}_{1}^{(n + 2)} & = \Delta t\hat{L}^{{{\text{BB}}}} \left( {{\tilde{\mathbf{y}}}^{n + 2} } \right), \\ {\mathbf{h}}_{2}^{(n + 2)} & = \Delta t\hat{L}^{{{\text{FF}}}} \left( {{\tilde{\mathbf{y}}}^{n + 2} + \alpha_{2} {\mathbf{h}}_{1}^{(n + 2)} } \right), \\ {\mathbf{h}}_{3}^{(n + 2)} & = \Delta t\hat{L}^{{{\text{BB}}}} \left( {{\tilde{\mathbf{y}}}^{n + 2} + \alpha_{3} {\mathbf{h}}_{2}^{(n + 2)} } \right), \\ {\mathbf{h}}_{4}^{(n + 2)} & = \Delta t\hat{L}^{{{\text{FF}}}} \left( {{\tilde{\mathbf{y}}}^{n + 2} + \alpha_{4} {\mathbf{h}}_{3}^{(n + 2)} } \right), \\ {\tilde{\mathbf{y}}}^{n + 3} & = {\tilde{\mathbf{y}}}^{n + 2} + \beta_{1} {\mathbf{h}}_{1}^{(n + 2)} + \beta_{2} {\mathbf{h}}_{2}^{(n + 2)} + \beta_{3} {\mathbf{h}}_{3}^{(n + 2)} + \beta_{4} {\mathbf{h}}_{4}^{(n + 2)} , \\ \end{aligned} $$

(56)

(iv) Sub time step 4:

$$ \begin{aligned} {\mathbf{h}}_{1}^{(n + 3)} & = \Delta t\hat{L}^{{{\text{BF}}}} \left( {{\tilde{\mathbf{y}}}^{n + 3} } \right), \\ {\mathbf{h}}_{2}^{(n + 3)} & = \Delta t\hat{L}^{{{\text{FB}}}} \left( {{\tilde{\mathbf{y}}}^{n + 3} + \alpha_{2} {\mathbf{h}}_{1}^{(n + 3)} } \right), \\ {\mathbf{h}}_{3}^{(n + 3)} & = \Delta t\hat{L}^{{{\text{BF}}}} \left( {{\tilde{\mathbf{y}}}^{n + 3} + \alpha_{3} {\mathbf{h}}_{2}^{(n + 3)} } \right), \\ {\mathbf{h}}_{4}^{(n + 3)} & = \Delta t\hat{L}^{{{\text{FB}}}} \left( {{\tilde{\mathbf{y}}}^{n + 3} + \alpha_{4} {\mathbf{h}}_{3}^{(n + 3)} } \right), \\ {\tilde{\mathbf{y}}}^{n + 4} & = {\tilde{\mathbf{y}}}^{n + 3} + \beta_{1} {\mathbf{h}}_{1}^{(n + 3)} + \beta_{2} {\mathbf{h}}_{2}^{(n + 3)} + \beta_{3} {\mathbf{h}}_{3}^{(n + 3)} + \beta_{4} {\mathbf{h}}_{4}^{(n + 3)} , \\ \end{aligned} $$

(57)

Stopping criteria.

End of time integration

In the above equations, The coefficients are $\alpha_{1} = 0$, $\alpha_{2} = 0.5$, $\alpha_{3} = 0.5$, $\alpha_{4} = 1$, $\beta_{1} = 1/6$, $\beta_{2} = 1/3$, $\beta_{3} = 1/3$, and $\beta_{4} = 1/6$. Note that this DRP/opt MacCormack finite difference method should satisfy the stability condition (Hixon & Turkel, 2000)

$$ \Delta t < 0.93\frac{\Delta h}{{c_{\max } }}, $$

(58)

where $\Delta t$ is the time sampling rate, $c_{\max }$ is the maximum wave velocity of the model, and $\Delta h$ is the grid spacing

$$ \Delta h = \frac{{c_{{{\text{min}}}} }}{{2.5f_{{\text{c}}} {\text{PPW}}}}, $$

(59)

where $c_{\min }$ is the minimum wave velocity of the model, $f_{{\text{c}}}$ is the center frequency of the source signal, and PPW is the number of points per wavelength. Numerical tests by Sun et al. (2016) showed that the DRP/opt MacCormack scheme finite difference method on curvilinear grids can be effectively applied to nonflat free-surface models when PPW exceeds 7.2.

3.3 Source and Absorbing Boundary Conditions

We apply a concentrated force source on the grid point and use the Ricker wavelet as the source signal,

$$ s(t) = \left( {1 - 2\pi^{2} f_{{\text{c}}}^{2} (t - t_{0} )^{2} } \right)\exp \left( { - \pi^{2} f_{{\text{c}}}^{2} (t - t_{0} )^{2} } \right), $$

(60)

for which a center frequency of $f_{{\text{c}}} = 30\,\mathrm{Hz}$ and a delay time of t₀ = 0.03 s are applied. Note that all the time steps are 0.5 ms for the following numerical tests, which satisfies the stability condition in Eq. (58) for the medium used and the source function has been added to the $\tilde{v}_{z}$ component for elastic media (but could also be added to the $\tilde{v}_{x}$ or $\tilde{v}_{y}$ component). To remove the artificial edge effects of the computational grid, we apply the generalized stiffness reduction method (GSRM, Zhou et al., 2020), which is applicable for various media, such as acoustic, elastic isotropic, and anisotropic.

3.4 Inverse Fourier Transform

After solving Eq. (46), one obtains the k_y-domain wavefield solution ${\tilde{\mathbf{y}}}(\tau_{n} ,x,k_{y} ,z)$ at $\tau_{n} = n\Delta \tau$. To recover the complete spatial-domain wavefield vector ${\mathbf{y}}(\tau_{n} ,x,y,z)$, the inverse Fourier transform of the solution ${\tilde{\mathbf{y}}}(\tau_{n} ,x,k_{y} ,z)$ must be implemented, i.e.

$$ {\mathbf{y}}(\tau_{n} ,x,y,z) \approx \frac{{2k_{y}^{c} }}{{\left( {N_{ky} - 1} \right)\pi }}\sum\limits_{m = 1}^{{N_{ky} }} {{\tilde{\mathbf{y}}}\left( {\tau_{n} ,x,k_{y}^{m} ,z} \right)e^{{i\left( {k_{y}^{m} y} \right)}} ,} \, k_{y}^{m} \in \left[ { - k_{y}^{c} ,k_{y}^{c} } \right]. $$

(61)

According to the definition of the wavefield vector y, the components $(\tilde{v}_{x} ,\tilde{v}_{y} ,\tilde{v}_{z} )$ can be calculated by the Green’s function tensor $\dot{\tilde{G}}_{sj}$, satisfying the symmetric or antisymmetric property (Zhou et al. 2012),

$$ \dot{\tilde{G}}_{sj} (\tau_{n} ,x,k_{y} ,z) = ( - 1)^{s + j} \dot{\tilde{G}}_{sj} (\tau_{n} ,x, - k_{y} ,z) $$

(62)

where s = 1, 2, or 3 stands for the source in the x, y, or z direction, while j = 1, 2, or 3 stands for the velocity component in the x, y, or z direction. Consequently, the velocity components $v_{sj} (\tau_{n} ,x,y,z)$ are calculated by

$$ v_{sj} (\tau_{n} ,x,y,z) = \left\{ {\begin{array}{*{20}c} {\frac{{k_{y}^{c} }}{{\left( {N_{ky} - 1} \right)\pi }}\sum\limits_{m = 1}^{{N_{ky} }} {\tilde{v}_{sj} \left( {\tau_{n} ,x,k_{y}^{m} ,z} \right)} \cos \left( {k_{y}^{m} y} \right), \, (s + j = {\text{oven}});} \\ {\frac{{k_{y}^{c} }}{{\left( {N_{ky} - 1} \right)\pi }}\sum\limits_{m = 1}^{{N_{ky} }} {i\tilde{v}_{sj} \left( {\tau_{n} ,x,k_{y}^{m} ,z} \right)} \sin \left( {k_{y}^{m} y} \right), \, (s + j = {\text{odd}}).} \\ \end{array} } \right. $$

(63)

It is not difficult to show that the k_y-domain pressure $\tilde{P}(\tau_{n} ,x,k_{y} ,z)$ is always symmetric about the xz-plane in an acoustic medium, so that the spatial-domain pressure can be calculated by

$$ P(\tau_{n} ,x,y,z) = \frac{{k_{y}^{c} }}{{\left( {N_{ky} - 1} \right)\pi }}\sum\limits_{m = 1}^{{N_{ky} }} {\tilde{P}\left( {\tau_{n} ,x,k_{y}^{m} ,z} \right)\cos \left( {k_{y}^{m} y} \right)} , $$

(64)

where

$$ k_{y}^{c} = \frac{\pi }{\Delta x}, \, N_{ky} = N_{x} , $$

(65)

and $\Delta x$ and N_x are the grid sampling distance and grid number in the x-direction, respectively.

4 Verification by Analytic Solutions

To validate the proposed 2.5-D numerical method, we first conduct three numerical tests for full-space homogeneous models that have an analytical solution (Appendix 5). In this way, we can examine how the 2.5-D numerical simulation effectively matches the 3-D analytical solutions in these media. To verify that the 2.5-D method is more efficient than the 3-D method, we also compare the 2.5-D numerical results with 3-D numerical results obtained by using the 3-D DRP/opt MacCormack finite difference method (Sun et al. 2018) to solve the 3-D elastic wave equation (Eqs. 1 and 2) and acoustic wave equation (Eqs. 7 and 8). The global measurement of a single-valued envelop misfit (EM) and phase misfit (PM) developed by Kristeková et al., (2006, 2009) is used to evaluate the misfit between the 2.5-D FDM numerical solutions and the reference solutions. Kristeková et al. (2009) defined that misfit criteria EM < 0.22 and PM < 0.2 indicate excellent levels while misfit criteria EM < 0.51 and PM < 0.40 indicate good levels of misfit.

The three full-space homogeneous models represent an acoustic, elastic isotropic, and elastic vertical transversely isotropic (VTI) medium, respectively. The model dimensions and grids are shown in Fig. 2, in which the source and receivers are indicated by a red star and blue triangles. These layouts of source and receivers may not be applicable to seismic practice, but they are helpful to illustrate the details of the solutions. For the 3-D numerical tests, the model size is $500\;{\text{m}} \times 500\;{\text{m}} \times 500\;{\text{m}}$, the model slices at y = 0 are shown as Fig. 2a, and the receiver and source locations are the same as in the 2.5-D models. The independent model parameters of the four media used are presented in Table 1. The rest of the nonzero elastic moduli are calculated from these independent model parameters; e.g., for the isotropic medium, we have elastic parameters C₁₂ = C₁₃ = C₂₃ = C₁₁ − 2C₄₄, C₂₂ = C₃₃ = C₁₁, and C₅₅ = C₆₆ = C₄₄, and for the VTI-1 medium we calculate C₁₂ = C₁₁ − 2C₆₆, C₁₃ = C₂₃ = C₁₁–2C₄₄, C₂₂ = C₃₃ = C₁₁, and C₅₅ = C₄₄, while for the VTI-2 medium we employ C₁₂ = C₁₁–2C₆₆, C₂₂ = C₁₁, C₂₃ = C₁₃, and C₅₅ = C₄₄.

Fig. 2

Geometric illustrations of 2.5-D numerical simulations for a full space model, b, c free-surface acoustic/elastic isotropic and VTI models, and d fluid–solid interface model. Red stars and blue triangles indicate source and receiver locations, respectively, and grid spaces are Δx = Δz = 2 m

Table 1 Model parameters used for numerical experiments

Figure 3a shows the P-wave snapshot of the 2.5-D wavefield solutions at time t = 0.14 s for the homogeneous acoustic model (model of Fig. 2a), from which one can clearly see the P-wave in the wavefields. To verify the correctness of the 2.5-D numerical solutions, we compare the P-component synthetic seismograms (receiver location x = 100 m, z = 100 m) generalized from the 2.5-D numerical solutions with the 3-D analytic solutions and 3-D numerical solutions (Fig. 3b), from which one can observe that the synthetic seismogram of the 2.5-D numerical simulation matches reasonably well with the 3-D analytic solutions and 3-D numerical solutions.

Fig. 3

Snapshots of the compressed P-wave (a) of the 2.5-D wavefield solutions at t = 0.14 s and comparison of the compressed P-wave synthetic seismograms between the 3-D analytic solution, 3-D FDM, and 2.5-D FDM numerical solutions (b) in the homogeneous acoustic medium given in Table 1. The black star indicates source location

Figure 4a and b respectively show the V_x- and V_z-component snapshots of the 2.5-D wavefield solutions at time t = 0.09 s in the homogeneous elastic isotropic medium, where the P- and S-wavefront are clearly presented. Figure 4c, d shows a comparison of the 2.5-D numerical solutions with the 3-D analytic solutions and 3-D numerical solutions (receiver location x = 100 m, z = 100 m) for the V_x- and V_z-component, respectively, from which one can see that the three solutions coincide with each other very well, regardless of the 2.5-D and 3-D numerical solutions. Such observations are similar to the case of the homogeneous acoustic medium shown in Fig. 3 except for the presence of S-wave.

Fig. 4

Snapshots of V_x- (a) and V_z-component (b) of 2.5-D wavefield solutions at t = 0.09 s and comparison of the V_x- (c) and V_z-component (d) synthetic seismogram between the 3-D analytic solution, 3-D FDM numerical solution, and 2.5-D FDM numerical solution for the homogeneous elastic isotropic medium given in Table 1. The black star indicates source location

Figure 5a and b respectively show V_x- and V_z-component snapshots of the 2.5-D wavefield solutions at time t = 0.08 s for the homogeneous elastic VTI-1 medium given in Table 1. Note that Fig. 5a, b does not show any cusp because we choose a simple VTI model that has an analytic solution. Figure 5c and d are similar to Fig. 4c and d except that they are for the VTI model. Moreover, the quantitative comparisons of the waveforms of the 2.5-D FDM numerical solutions and 3-D analytic solutions in Table 3 (where columns 1–5 correspond to Figs. 3b, 4c, d, and 5c, d, respectively) indicate that both the PM and EM of the comparisons are below 0.07 and 0.049, above the excellent level for the misfit criteria (Kristeková et al., 2009). Therefore, these three tests (homogeneous acoustic, elastic isotropic, and elastic VTI-1 medium) verify the correctness of the proposed 2.5-D numerical simulations. In addition, Table 2 also provides a comparison of the CPU memory cost and CPU running time for the 2.5-D and 3-D numerical simulations calculated on the same CPU (Intel Xeon Gold 6248 CPU at 2.50 GHz). From Table 2, it can be concluded that the CPU time and computer memory used by the 2.5-D numerical simulation are much less than those of the 3-D numerical simulation, especially for computer memory. Because the 2.5-D method can calculate point source solutions at 2-D memory cost and is easy to parallelize, it is an economic method to obtain point source numerical solutions for some specific geological models, such as sedimentary strata whose attributes remain approximately unchanged along the strike direction, in which case there is no need to use the inefficient 3-D modeling method.

Fig. 5

Snapshots of the V_x- (a) and V_z-component (b) of the 2.5-D wavefield solutions at t = 0.08 s and comparison of the V_x- (c) and V_z-component (d) synthetic seismogram between the 3-D analytic solution, 3-D FDM, and 2.5-D FDM numerical solutions in the homogeneous elastic VTI-1 model given in Table 1. The black star indicates source location

Table 2 Comparison of CPU time and memory cost between the 2.5-D and 3-D numerical simulation methods in a homogeneous model

5 Tests for Interface Models

To verify the adaptability of the proposed 2.5-D numerical simulation method to different models including different interfaces, we selected four models: three (acoustic, isotropic, and VTI medium) flat free-surface models and one fluid–solid interface model. We choose these flat free-surface models only to provide a clear view of the wavefronts reflected from the free surfaces. To verify that the proposed 2.5-D method is valid for the free surface, we compared the 2.5-D numerical results with the 3-D pseudospectral method (PSM) (Furumura et al., 1998) for the three free-surface models. For the acoustic and isotropic free-surface models, the source is located at point (x = 500 m, z = 350 m) and 101 receivers are located equidistantly along the depth of 500 m (Fig. 2b). For the VTI free-surface model (Fig. 2c), the source is located at point (x = 500 m, z = 400 m), and 101 receivers are located equidistantly at the depth of 800 m. For 3-D PSM numerical modeling, the size of the three free-surface models is 1000 m × 1000 m × 1000 m, the model slice at y = 0 m is shown in Fig. 2b for the acoustic and isotropic model and in Fig. 2c for VTI model, and the receiver and source locations are the same as in the 2-D models. For the water–solid interface model (Fig. 2d), the first layer is acoustic, the second layer is elastic VTI-1, the source is located at point (x = 500 m, z = 300 m), and six receivers are located along the vertical line at x = 300 m crossing the interface. All the model parameters are presented in Table 1.

Figure 6a, b shows snapshots of the V_x- and V_z-component of the 2.5-D wavefield solutions at time t = 0.4 s in the acoustic free-surface model. Figure 6c, d shows seismogram of the velocity components at the line of receivers. From Fig. 6, one can clearly see the direct P-wave and its reflection from the free surface. Figure 7 shows a comparison of two components of the synthetic seismograms (receiver location: x = 300 m, z = 500 m) between the 2.5-D FDM and the 3-D PSM numerical solutions in an acoustic free-surface model. It is clearly seen that the 2.5-D numerical solution matches well with the 3-D PSM solution, regardless of the V_x- and V_z-component synthetic seismograms. Figure 8 shows 2.5-D wavefield solutions in the elastic isotropic free-surface model, which is similar to Fig. 6 except that the snapshot time is 0.32 s. From Fig. 8 one can observe six seismic phases that include the direct P and S, reflected PP and SS, converted PS and SP waves, identified by the numbers from 1 to 6. Figure 9 is similar to Fig. 7 except that it is for the elastic isotropic free-surface model.

Fig. 6

Snapshots of V_x- (a) and V_z-component (b) of the 2.5-D wavefield solutions and the V_x- (c) and V_z-component (d) synthetic seismograms of the 2.5-D wavefield solutions in an acoustic free-surface model. The black star indicates source location

Fig. 7

Comparison of V_x- (a) and V_z- (b) component synthetic seismograms between the 3-D PSM and 2.5-D FDM numerical solution in an acoustic free-surface model

Fig. 8

V_x- (a) and V_z-component (b) snapshots and V_x- (c) and V_z-component (d) synthetic seismograms of the 2.5-D wavefield solutions in an elastic isotropic free-surface model. In (c) the numbers 1–6 indicate the direct P and S, reflected PP, converted SP and PS, and reflected SS waves, respectively. The black star indicates source location

Fig. 9

Comparison of V_x- (a) and V_z-component (b) synthetic seismograms generalized between the 3-D PSM and 2.5-D FDM numerical solution in an elastic isotropic free-surface model. In (a) the numbers 1–6 indicate the direct P and S, reflected PP, converted SP and PS, and reflected SS waves, respectively

Figure 10 shows 2.5-D wavefield solutions in the elastic VTI free-surface model, which is similar to Fig. 8 except that the snapshot time is 0.30 s. From Fig. 10, one can find six seismic phases: direct qP and qSV, reflected qPqP and qSVqSV, and converted qPqSV and qSVqP waves, which are indicated by numbers from 1 to 6. Figure 11 is similar to Fig. 9 except that it is for a VTI free-surface model and the receiver location is (x = 300 m, z = 800 m). From Figs. 9 and 11, we reach a similar observation that the 2.5-D numerical solutions matches well with the 3-D PSM solutions, regardless of the V_x- and V_z-component synthetic seismograms. These seismic waves exhibit anisotropic propagation in the VTI medium, being quite different from the waves shown in Figs. 8 and 9 that propagate at constant speed in all directions. All these observations are similar to the results for the previous two free-surface models. The quantitative comparisons of the waveforms of the 2.5-D FDM numerical solutions and 3-D PSM numerical solutions in Table 3 (where columns 6–11 correspond to Figs. 7a, b, 9a, b, and 11a, b, respectively) indicate that both the PM and EM of the comparisons are below 0.30 and 0.22, being better than the good level for the misfit criteria (Kristeková et al., 2009). Due to the difference not only between 2.5-D and 3-D methods, but also between FDM and PSM, the errors between the 2.5-D FDM and 3-D PSM solutions (Table 3, columns 6–11) are greater than those between the 2.5-D FDM numerical solutions and 3-D analytic solutions ( Table 3, columns 1–5), and in particular the error increases with time (Figs. 7, 9 and 11).

Fig. 10

V_x- (a) and V_z-component (b) snapshots and V_x- (c) and V_z-component (d) synthetic seismograms generalized by the 2.5-D wavefield solutions in an elastic VTI free-surface model. In (c) the numbers 1–6 indicate the direct qP and qSV, reflected qPqP, converted qSVqP and qPqSV, and reflected qSVqSV wave, respectively. The black star indicates source location

Fig. 11

Comparison of V_x- (a) and V_z-component (b) synthetic seismograms generalized between the 3-D PSM and 2.5-D FDM numerical solution in an elastic VTI free-surface model. In (a) the numbers 1–6 indicate the direct P and S, reflected PP, converted SP and PS, and reflected SS waves, respectively

Table 3 Envelop misfit (EM) and phase misfit (PM) values for receivers

Figure 12 shows snapshots of the V_x- and V_z-component 2.5-D wavefield solutions at time t = 0.28 s in the fluid–solid interface model. Figure 13a and b respectively show the V_x- and V_z-component synthetic seismograms at the three hydrophones located in the fluid, where receivers 1–3 are located at points (x = 300 m, z = 200 m), (x = 300 m, z = 300 m), and (x = 300 m, z = 400 m), respectively, while Fig. 13c, d show the corresponding synthetic seismograms at the three hydrophones located in the solid Earth, where receivers 4–6 are located at points (x = 300 m, z = 600 m), (x = 300 m, z = 700 m), and (x = 300 m, z = 800 m), respectively. From these results, one can see that the three hydrophones located in the fluid only receive two seismic phases, viz. the direct P and the PP reflection, while the three geophones located in solid Earth also pick up two seismic phases but, different from the hydrophones, one is the transmitted qP arrival and the other is the transmitted qPqP and converted qPqS. In addition, one can also see that the V_z-component of the fluid and solid velocities is continuous at the interface, but the V_x-components are different. This can be seen from Eqs. 39, 41, and 42 with $z_{0}^{^{\prime}} = 0$ (for a flat interface).

Fig. 12

V_x- and V_z-component snapshots of the 2.5-D wavefield solutions in a fluid–solid interface model. The black star indicates source location

Fig. 13

V_x- (a, c) and V_z-component (b, d) synthetic seismograms at the three receivers located in fluid (a, b) and solid Earth (c, d) predicted by the 2.5-D simulation method

6 Complex Model

To examine the capability of our proposed 2.5-D numerical method for complex models, we selected a mixed three-layer (acoustic, elastic isotropic, and VTI-2) model having a fluid free surface and an irregular fluid–solid interface (Fig. 14). The source is located at point (x = 1000 m, z = 450 m), with three receivers (Fig. 14) located in the acoustic medium (x = 500 m, z = 200 m), the elastic isotropic medium (x = 500 m, z = 500 m), and the VTI medium (x = 500 m, z = 800 m); all the medium parameters are presented in Table 1. Figures 15 and 16 respectively show the V_x- and V_z-component snapshots of the 2.5-D wavefield solutions in the mixed three-layer model for six continuous time steps, from which one can see clear reflection, conversion, transmission waveforms and multiples. From the results at time t = 0.12 s and 0.2 s given by Figs. 15 and 16, the transmitted and converted P-waves show up in the first layer (acoustic medium) when the P- and S-waves pass through the fluid–solid interface, and the converted qP- and qSV-waves go downward in the third layer (VTI medium) as the P- and S- wave pass through the solid–solid interface. From the results at time t = 0.36 s to 0.52 s, the reflected P-wave appears due to the arrivals of the upward P-wave at the free surface in the first layer, and also one can see clear multiples in the second layer from the results at time t = 0.28–0.52 s. Figure 17 shows the V_x- and V_z-component synthetic seismograms predicted by the 2.5-D simulation method for receivers located in the first layer (acoustic case, Fig. 17a, b), the second layer (isotropic case, Fig. 17c, d), and the third layer (VTI case, Fig. 17e, f). Similarly, we can observe the different arrivals at the three differently located receivers.

Fig. 14

Three-layered mixed (acoustic, elastic isotropic, and VTI-2) model with the moduli presented in Table 1. The red star and yellow triangles indicate source and receiver locations, respectively. The undulating interfaces are generated by a sinusoidal function: $z = z_{0} + b_{0} \sin \left[ {\left( {x + x_{0} } \right)/a_{0} } \right]$; for the first interface, z₀ = 300 m, b₀ = − 50 m, x₀ = 100 m, a₀ = 100; for the second interface, z₀ = 600 m, b₀ = 50 m, x₀ = 100 m, a₀ = 100

Fig. 15

V_x-component snapshots of the 2.5-D wavefield solutions in a mixed three-layer model at six different time steps. The black star indicates source location

Fig. 16

V_z-component snapshots of the 2.5-D wavefield solutions in a mixed three-layer model at six different time steps. The black star indicates source location

Fig. 17

V_x- and V_z-component synthetic seismograms predicted by the 2.5-D simulation method for receiver located in the first layer (acoustic case, a, b), second layer (isotropic case, c, d), and third layer (VTI case, e, f)

7 Conclusions

A generalized 2.5-D first-order matrix-form wave equation is established and solved using a high-order finite-difference scheme. We demonstrate that the wave equation is valid for various media and different interface conditions. By defining different wavefield vectors, assigning variable model parameters from point-to-point to three coefficient matrices, and employing a point source of either pressure or force vector, 2.5-D seismic wave modeling in complex geological models can be accomplished by a single computer software. Our numerical results show that the 2.5-D numerical solutions match reasonably well with 3-D analytical solutions and also 3-D numerical solutions in different media and display correct responses to various interfaces. Such a 2.5-D numerical simulation technique can be directly employed as the forward modeling method for seismic reverse-time migration and efficient full-waveform inversion. The proposed 2.5-D numerical technique may become an effective tool to simulate 3-D seismic wave propagation in 2-D geological models and investigate the conversion of point source data to line source data in different (acoustic, elastic isotropic, and anisotropic) 2-D models which may include a free-surface topography and fluid–solid interfaces.

Appendices

Appendix 1: Coefficient Matrices for Elastic Anisotropic Medium

Equations (3) can be rewritten in the following form:

$$ \begin{aligned} \left( {\begin{array}{*{20}c} {\dot{\tilde{v}}_{x} } \\ {\dot{\tilde{v}}_{y} } \\ {\dot{\tilde{v}}_{z} } \\ \end{array} } \right) & = \left( {\begin{array}{*{20}c} {\rho^{ - 1} } & 0 & 0 & 0 & 0 & 0 \\ 0 & {\rho^{ - 1} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\rho^{ - 1} } & 0 & 0 \\ \end{array} } \right)\partial_{x} \left( {\begin{array}{*{20}c} {\tilde{\sigma }_{xx} } \\ {\tilde{\sigma }_{xy} } \\ {\tilde{\sigma }_{yy} } \\ {\tilde{\sigma }_{xz} } \\ {\tilde{\sigma }_{yz} } \\ {\tilde{\sigma }_{zz} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} 0 & 0 & 0 & {\rho^{ - 1} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {\rho^{ - 1} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {\rho^{ - 1} } \\ \end{array} } \right)\partial_{z} \left( {\begin{array}{*{20}c} {\tilde{\sigma }_{xx} } \\ {\tilde{\sigma }_{xy} } \\ {\tilde{\sigma }_{yy} } \\ {\tilde{\sigma }_{xz} } \\ {\tilde{\sigma }_{yz} } \\ {\tilde{\sigma }_{zz} } \\ \end{array} } \right) \\ & + \left( {\begin{array}{*{20}c} 0 & {ik_{y} \rho^{ - 1} } & 0 & 0 & 0 & 0 \\ 0 & 0 & {ik_{y} \rho^{ - 1} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {ik_{y} \rho^{ - 1} } & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\tilde{\sigma }_{xx} } \\ {\tilde{\sigma }_{xy} } \\ {\tilde{\sigma }_{yy} } \\ {\tilde{\sigma }_{xz} } \\ {\tilde{\sigma }_{yz} } \\ {\tilde{\sigma }_{zz} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\rho^{ - 1} s_{x} } \\ {\rho^{ - 1} s_{y} } \\ {\rho^{ - 1} s_{z} } \\ \end{array} } \right). \\ \end{aligned} $$

(66)

Similarly, Eq. (4) becomes

$$ \left( {\begin{array}{*{20}c} {\dot{\tilde{\sigma }}_{xx} } \\ {\dot{\tilde{\sigma }}_{xy} } \\ {\dot{\tilde{\sigma }}_{yy} } \\ {\dot{\tilde{\sigma }}_{xz} } \\ {\dot{\tilde{\sigma }}_{yz} } \\ {\dot{\tilde{\sigma }}_{zz} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {c_{11} } & {c_{16} } & {c_{15} } \\ {c_{16} } & {c_{66} } & {c_{56} } \\ {c_{12} } & {c_{26} } & {c_{25} } \\ {c_{15} } & {c_{56} } & {c_{55} } \\ {c_{14} } & {c_{46} } & {c_{45} } \\ {c_{13} } & {c_{36} } & {c_{35} } \\ \end{array} } \right)\partial_{x} \left( {\begin{array}{*{20}c} {\tilde{v}_{x} } \\ {\tilde{v}_{y} } \\ {\tilde{v}_{z} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {c_{15} } & {c_{14} } & {c_{13} } \\ {c_{56} } & {c_{46} } & {c_{36} } \\ {c_{25} } & {c_{24} } & {c_{23} } \\ {c_{55} } & {c_{45} } & {c_{35} } \\ {c_{45} } & {c_{44} } & {c_{34} } \\ {c_{35} } & {c_{34} } & {c_{33} } \\ \end{array} } \right)\partial_{z} \left( {\begin{array}{*{20}c} {\tilde{v}_{x} } \\ {\tilde{v}_{y} } \\ {\tilde{v}_{z} } \\ \end{array} } \right) + \mathrm{i}k_{y} \left( {\begin{array}{*{20}c} {c_{16} } & {c_{12} } & {c_{14} } \\ {c_{66} } & {c_{26} } & {c_{46} } \\ {c_{26} } & {c_{22} } & {c_{24} } \\ {c_{56} } & {c_{25} } & {c_{45} } \\ {c_{46} } & {c_{24} } & {c_{44} } \\ {c_{36} } & {c_{23} } & {c_{34} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\tilde{v}_{x} } \\ {\tilde{v}_{y} } \\ {\tilde{v}_{z} } \\ \end{array} } \right). $$

(67)

Accordingly, we obtain the following coefficient matrices for Eq. (6):

$$ {\mathbf{A}}^{(\mathrm{S})} = \left( {\begin{array}{*{20}c} {\mathbf{0}} & {{\mathbf{M}}_{1} } & {{\mathbf{M}}_{2} } \\ {{\mathbf{S}}_{1} } & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{S}}_{4} } & {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right), \, {\mathbf{B}}^{(\mathrm{S})} = \left( {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{M}}_{3} } \\ {{\mathbf{S}}_{2} } & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{S}}_{5} } & {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right), \, {\mathbf{C}}^{(\mathrm{S})} = \left( {\begin{array}{*{20}c} {\mathbf{0}} & {{\mathbf{M}}_{4} } & {{\mathbf{M}}_{5} } \\ {{\mathbf{S}}_{3} } & {\mathbf{0}} & {\mathbf{0}} \\ {{\mathbf{S}}_{6} } & {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right), $$

(68)

where

$$ \begin{aligned} {\mathbf{M}}_{1} & = \left( {\begin{array}{*{20}c} {\rho^{ - 1} } & 0 & 0 \\ 0 & {\rho^{ - 1} } & 0 \\ 0 & 0 & 0 \\ \end{array} } \right), \, {\mathbf{M}}_{2} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ {\rho^{ - 1} } & 0 & 0 \\ \end{array} } \right), \, {\mathbf{M}}_{3} = \left( {\begin{array}{*{20}c} {\rho^{ - 1} } & 0 & 0 \\ 0 & {\rho^{ - 1} } & 0 \\ 0 & 0 & {\rho^{ - 1} } \\ \end{array} } \right), \, \\ {\mathbf{M}}_{4} & = \left( {\begin{array}{*{20}c} 0 & {ik_{y} \rho^{ - 1} } & 0 \\ 0 & 0 & {ik_{y} \rho^{ - 1} } \\ 0 & 0 & 0 \\ \end{array} } \right), \, {\mathbf{M}}_{5} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & {ik_{y} \rho^{ - 1} } & 0 \\ \end{array} } \right), \, {\mathbf{S}}_{1} = \left( {\begin{array}{*{20}c} {c_{11} } & {c_{16} } & {c_{15} } \\ {c_{16} } & {c_{66} } & {c_{56} } \\ {c_{12} } & {c_{26} } & {c_{25} } \\ \end{array} } \right), \, \\ {\mathbf{S}}_{2} & = \left( {\begin{array}{*{20}c} {c_{15} } & {c_{14} } & {c_{13} } \\ {c_{56} } & {c_{46} } & {c_{36} } \\ {c_{25} } & {c_{24} } & {c_{23} } \\ \end{array} } \right), \, {\mathbf{S}}_{3} = \mathrm{i}k_{y} \left( {\begin{array}{*{20}c} {c_{16} } & {c_{12} } & {c_{14} } \\ {c_{66} } & {c_{26} } & {c_{46} } \\ {c_{26} } & {c_{22} } & {c_{24} } \\ \end{array} } \right), \, {\mathbf{S}}_{4} = \left( {\begin{array}{*{20}c} {c_{15} } & {c_{56} } & {c_{55} } \\ {c_{14} } & {c_{46} } & {c_{45} } \\ {c_{13} } & {c_{36} } & {c_{35} } \\ \end{array} } \right), \, \\ {\mathbf{S}}_{5} & = \left( {\begin{array}{*{20}c} {c_{55} } & {c_{45} } & {c_{35} } \\ {c_{45} } & {c_{44} } & {c_{34} } \\ {c_{35} } & {c_{34} } & {c_{33} } \\ \end{array} } \right), \, {\mathbf{S}}_{6} = \mathrm{i}k_{y} \left( {\begin{array}{*{20}c} {c_{56} } & {c_{25} } & {c_{45} } \\ {c_{46} } & {c_{24} } & {c_{44} } \\ {c_{36} } & {c_{23} } & {c_{34} } \\ \end{array} } \right){.} \\ \end{aligned} $$

(69)

Appendix 2: Coefficient Matrices for Acoustic Medium

We combine Eqs. (9) and (10) into the following form:

$$ \begin{aligned} \left( \begin{gathered} \dot{\tilde{v}}_{{\text{x}}} \hfill \\ \dot{\tilde{v}}_{y} \hfill \\ \dot{\tilde{v}}_{z} \hfill \\ {\dot{\tilde{P}}} \hfill \\ \end{gathered} \right) & = \left( \begin{gathered} { 0 0 0 } - \rho^{ - 1} \hfill \\ { 0 0 0 0} \hfill \\ { 0 0 0 0} \hfill \\ - K{ 0 0 0} \hfill \\ \end{gathered} \right)\partial_{x} \left( \begin{gathered} \tilde{v}_{x} \hfill \\ \tilde{v}_{y} \hfill \\ \tilde{v}_{z} \hfill \\ {\tilde{P}} \hfill \\ \end{gathered} \right) + \left( \begin{gathered} {0 0 0 0} \hfill \\ {0 0 0 0} \hfill \\ {0 0 0 } - \rho^{ - 1} \hfill \\ {0 0 } - K { 0} \hfill \\ \end{gathered} \right)\partial_{z} \left( \begin{gathered} \tilde{v}_{x} \hfill \\ \tilde{v}_{y} \hfill \\ \tilde{v}_{z} \hfill \\ {\tilde{P}} \hfill \\ \end{gathered} \right) \\ & + \left( \begin{gathered} {0 0 0 0} \hfill \\ {0 0 0 } - \mathrm{i}k_{y} \rho^{ - 1} \hfill \\ {0 0 0 }0 \hfill \\ {0 } - \mathrm{i}k_{y} K \, 0{ 0} \hfill \\ \end{gathered} \right)\left( \begin{gathered} \tilde{v}_{x} \hfill \\ \tilde{v}_{y} \hfill \\ \tilde{v}_{z} \hfill \\ {\tilde{P}} \hfill \\ \end{gathered} \right) + \left( \begin{gathered} { 0} \hfill \\ { 0} \hfill \\ { 0} \hfill \\ \dot{s}(t)\delta ({\mathbf{x}} - {\mathbf{x}}_{s} ) \hfill \\ \end{gathered} \right). \\ \end{aligned} $$

(70)

Consequently, we obtain the following coefficient matrices for Eq. (12):

$$ {\mathbf{A}}^{(\mathrm{W})} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 & { - \rho^{ - 1} } \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ { - K} & 0 & 0 & 0 \\ \end{array} } \right),{\mathbf{B}}^{(\mathrm{W})} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & { - \rho^{ - 1} } \\ 0 & 0 & { - K} & 0 \\ \end{array} } \right),{\mathbf{C}}^{(\mathrm{W})} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & { - \mathrm{i}k_{y} \rho^{ - 1} } \\ 0 & 0 & 0 & 0 \\ 0 & { - \mathrm{i}k_{y} K} & 0 & 0 \\ \end{array} } \right). $$

(71)

Appendix 3: Coefficient Matrices for the Free Surface of Elastic Medium

Combing Eqs. 26 and 27, we obtain

$$ \begin{aligned} \left( \begin{gathered} \dot{\tilde{v}}_{{\text{x}}} \hfill \\ \dot{\tilde{v}}_{y} \hfill \\ \dot{\tilde{v}}_{z} \hfill \\ \dot{\tilde{\sigma }}_{xx} \hfill \\ \dot{\tilde{\sigma }}_{xy} \hfill \\ \dot{\tilde{\sigma }}_{yy} \hfill \\ \end{gathered} \right) & = \left( \begin{gathered} {0 0 0 } \rho^{ - 1} { 0 } 0 \hfill \\ {0 0 0 0 }\rho^{ - 1} \, 0 \hfill \\ {0 0 0 (}\partial_{x} {\text{z}}_{{0}} )\rho^{ - 1} { 0 } 0 \hfill \\ c_{11} \, c_{16} \, c_{15} { 0 0 } 0 \hfill \\ c_{16} \, c_{66} \, c_{56} { 0 0 } 0 \hfill \\ c_{12} \, c_{26} \, c_{25} { 0 0 } 0 \hfill \\ \end{gathered} \right)\partial_{x} \left( \begin{gathered} \tilde{v}_{x} \hfill \\ \tilde{v}_{y} \hfill \\ \tilde{v}_{z} \hfill \\ \tilde{\sigma }_{xx} \hfill \\ \tilde{\sigma }_{xy} \hfill \\ \tilde{\sigma }_{yy} \hfill \\ \end{gathered} \right) + \left( \begin{gathered} {0 0 0 (}\partial_{x} {\text{z}}_{{0}} )\rho^{ - 1} { 0 } 0 \hfill \\ {0 0 0 0 (}\partial_{x} {\text{z}}_{{0}} )\rho^{ - 1} \, 0 \hfill \\ {0 0 0 (}\partial_{x} {\text{z}}_{{0}} )^{2} \rho^{ - 1} { 0 } 0 \hfill \\ c_{15} \, c_{14} \, c_{13} { 0 0 } 0 \hfill \\ c_{56} \, c_{46} \, c_{36} { 0 0 } 0 \hfill \\ c_{25} \, c_{24} \, c_{23} { 0 0 } 0 \hfill \\ \end{gathered} \right)\partial_{z} \left( \begin{gathered} \tilde{v}_{x} \hfill \\ \tilde{v}_{y} \hfill \\ \tilde{v}_{z} \hfill \\ \tilde{\sigma }_{xx} \hfill \\ \tilde{\sigma }_{xy} \hfill \\ \tilde{\sigma }_{yy} \hfill \\ \end{gathered} \right) \\ & + \left( \begin{gathered} {0 0 0 } 0 \, \mathrm{i}k_{y} \rho^{ - 1} \, 0 \hfill \\ {0 0 0 0 0 } \mathrm{i}k_{y} \rho^{ - 1} \hfill \\ {0 0 0 (}\partial_{xx} {\text{z}}_{{0}} )\rho^{ - 1} { (}\partial_{x} {\text{z}}_{{0}} )ik_{y} \rho^{ - 1} \, 0 \hfill \\ \mathrm{i}k_{y} c_{16} \, \mathrm{i}k_{y} c_{12} \, \mathrm{i}k_{y} c_{14} { 0 0 }0 \hfill \\ \mathrm{i}k_{y} c_{66} \, \mathrm{i}k_{y} c_{26} \, \mathrm{i}k_{y} c_{46} { 0 0 }0 \hfill \\ \mathrm{i}k_{y} c_{26} \, \mathrm{i}k_{y} c_{22} \, \mathrm{i}k_{y} c_{24} { 0 0 }0 \hfill \\ \end{gathered} \right)\left( \begin{gathered} \tilde{v}_{x} \hfill \\ \tilde{v}_{y} \hfill \\ \tilde{v}_{z} \hfill \\ \tilde{\sigma }_{xx} \hfill \\ \tilde{\sigma }_{xy} \hfill \\ \tilde{\sigma }_{yy} \hfill \\ \end{gathered} \right) + \left( \begin{gathered} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{gathered} \right). \\ \end{aligned} $$

(72)

We thus obtain the following coefficient matrices for Eq. (29):

$$ \begin{aligned} {\mathbf{A}}^{{({\text{AS}})}} & = \left( \begin{gathered} {0 0 0 } \, \rho^{ - 1} { 0 } 0 \hfill \\ {0 0 0 0 }\rho^{ - 1} \, 0 \hfill \\ {0 0 0 (}\partial_{x} {\text{z}}_{{0}} )\rho^{ - 1} { 0 } 0 \hfill \\ c_{11} \, c_{16} \, c_{15} { 0 0 } 0 \hfill \\ c_{16} \, c_{66} \, c_{56} { 0 0 } 0 \hfill \\ c_{12} \, c_{26} \, c_{25} { 0 0 } 0 \hfill \\ \end{gathered} \right),\begin{array}{*{20}c} {} & {} \\ \end{array} {\mathbf{B}}^{{({\text{AS}})}} = \left( \begin{gathered} {0 0 0 (}\partial_{x} {\text{z}}_{{0}} )\rho^{ - 1} { 0 } 0 \hfill \\ {0 0 0 0 (}\partial_{x} {\text{z}}_{{0}} )\rho^{ - 1} \, 0 \hfill \\ {0 0 0 (}\partial_{x} {\text{z}}_{{0}} )^{2} \rho^{ - 1} { 0 } 0 \hfill \\ c_{15} \, c_{14} \, c_{13} { 0 0 } 0 \hfill \\ c_{56} \, c_{46} \, c_{36} { 0 0 } 0 \hfill \\ c_{25} \, c_{24} \, c_{23} { 0 0 } 0 \hfill \\ \end{gathered} \right), \\ {\mathbf{C}}^{{({\text{AS}})}} & = \left( \begin{gathered} {0 0 0 } 0 \, \mathrm{i}k_{y} \rho^{ - 1} \, 0 \hfill \\ {0 0 0 0 0 } \mathrm{i}k_{y} \rho^{ - 1} \hfill \\ {0 0 0 (}\partial_{xx} {\text{z}}_{{0}} )\rho^{ - 1} { (}\partial_{x} {\text{z}}_{{0}} )ik_{y} \rho^{ - 1} \, 0 \hfill \\ \mathrm{i}k_{y} c_{16} \, \mathrm{i}k_{y} c_{12} \, \mathrm{i}k_{y} c_{14} { 0 0 } 0 \hfill \\ \mathrm{i}k_{y} c_{66} \, \mathrm{i}k_{y} c_{26} \, \mathrm{i}k_{y} c_{46} { 0 0 } 0 \hfill \\ \mathrm{i}k_{y} c_{26} \, \mathrm{i}k_{y} c_{22} \, \mathrm{i}k_{y} c_{24} { 0 0 } 0 \hfill \\ \end{gathered} \right), \\ \end{aligned} $$

(73)

Appendix 4: Coefficient Matrices for a Fluid–Solid Interface

Combining Eqs. 40, 41, and 42, we obtain the following form:

$$ \begin{gathered} \left( \begin{gathered} \dot{\tilde{v}}_{x}^{(\mathrm{W})} \hfill \\ \dot{\tilde{v}}_{x}^{(\mathrm{S})} \hfill \\ \dot{\tilde{v}}_{y}^{(\mathrm{S})} \hfill \\ \dot{\tilde{v}}_{z}^{(\mathrm{S})} \hfill \\ {\dot{\tilde{P}}} \hfill \\ \dot{\tilde{\sigma }}_{xy} \hfill \\ \dot{\tilde{\sigma }}_{yz} \hfill \\ \end{gathered} \right) = \left( {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & { - \rho_{w}^{ - 1} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{{ - \rho_{s}^{ - 1} \partial_{x} z_{0}^{2} }}{{\partial_{x} z_{0}^{2} + 1}}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{{ - \rho_{s}^{ - 1} \partial_{x} z_{0} }}{{\partial_{x} z_{0}^{2} + 1}}} & 0 & 0 \\ { - K} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right)\partial_{x} \left( \begin{gathered} \tilde{v}_{x}^{(\mathrm{W})} \hfill \\ \tilde{v}_{x}^{(\mathrm{S})} \hfill \\ \tilde{v}_{y}^{(\mathrm{S})} \hfill \\ \tilde{v}_{z}^{(\mathrm{S})} \hfill \\ {\tilde{P}} \hfill \\ \tilde{\sigma }_{xy} \hfill \\ \tilde{\sigma }_{yz} \hfill \\ \end{gathered} \right) + \left( {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{{\rho_{s}^{ - 1} \partial_{x} z_{0} }}{{\partial_{x} z_{0}^{2} + 1}}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & { - \rho_{s}^{ - 1} \partial_{x} z_{0} } & {\rho_{s}^{ - 1} } \\ 0 & 0 & 0 & 0 & {\frac{{ - \rho_{s}^{ - 1} }}{{\partial_{x} z_{0}^{2} + 1}}} & 0 & 0 \\ { - K\partial_{x} z_{0} } & {K\partial_{x} z_{0} } & 0 & { - K} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right)\partial_{z} \left( \begin{gathered} \tilde{v}_{x}^{(\mathrm{W})} \hfill \\ \tilde{v}_{x}^{(\mathrm{S})} \hfill \\ \tilde{v}_{y}^{(\mathrm{S})} \hfill \\ \tilde{v}_{z}^{(\mathrm{S})} \hfill \\ {\tilde{P}} \hfill \\ \tilde{\sigma }_{xy} \hfill \\ \tilde{\sigma }_{yz} \hfill \\ \end{gathered} \right) \hfill \\ + \left( {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{{ - 2\rho_{s}^{ - 1} \partial_{x} z_{0} \partial_{xx} z_{0} }}{{(\partial_{x} z_{0}^{2} + 1)^{2} }}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{{ - \rho_{s}^{ - 1} \partial_{xx} z_{0} (1 - \partial_{x} z_{0}^{2} )}}{{(\partial_{x} z_{0}^{2} + 1)^{2} }}} & 0 & 0 \\ 0 & { - \mathrm{i}k_{y} (\partial_{x} z_{0}^{2} + 1)c_{36} } & { - \mathrm{i}k_{y} (\partial_{x} z_{0}^{2} + 1)c_{23} } & { - \mathrm{i}k_{y} (\partial_{x} z_{0}^{2} + 1)c_{34} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right)\left( \begin{gathered} \tilde{v}_{x}^{(\mathrm{W})} \hfill \\ \tilde{v}_{x}^{(\mathrm{S})} \hfill \\ \tilde{v}_{y}^{(\mathrm{S})} \hfill \\ \tilde{v}_{z}^{(\mathrm{S})} \hfill \\ {\tilde{P}} \hfill \\ \tilde{\sigma }_{xy} \hfill \\ \tilde{\sigma }_{yz} \hfill \\ \end{gathered} \right) + \left( {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right). \hfill \\ \end{gathered} $$

(74)

We then obtain the following coefficient matrices for Eq. 44:

$$ {\mathbf{A}}^{(WS)} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & { - \rho_{w}^{ - 1} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{{ - \rho_{s}^{ - 1} \partial_{x} z_{0}^{2} }}{{\partial_{x} z_{0}^{2} + 1}}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{{ - \rho_{s}^{ - 1} \partial_{x} z_{0} }}{{\partial_{x} z_{0}^{2} + 1}}} & 0 & 0 \\ { - K} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right), \, {\mathbf{B}}^{(WS)} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{{\rho_{s}^{ - 1} \partial_{x} z_{0} }}{{\partial_{x} z_{0}^{2} + 1}}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & { - \rho_{s}^{ - 1} \partial_{x} z_{0} } & {\rho_{s}^{ - 1} } \\ 0 & 0 & 0 & 0 & {\frac{{ - \rho_{s}^{ - 1} }}{{\partial_{x} z_{0}^{2} + 1}}} & 0 & 0 \\ { - K\partial_{x} z_{0} } & {K\partial_{x} z_{0} } & 0 & { - K} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right), $$

(75)

$$ {\mathbf{C}}^{(WS)} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{{ - 2\rho_{s}^{ - 1} \partial_{x} z_{0} \partial_{xx} z_{0} }}{{(\partial_{x} z_{0}^{2} + 1)^{2} }}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{{ - \rho_{s}^{ - 1} \partial_{xx} z_{0} (1 - \partial_{x} z_{0}^{2} )}}{{(\partial_{x} z_{0}^{2} + 1)^{2} }}} & 0 & 0 \\ 0 & { - \mathrm{i}k_{y} (\partial_{x} z_{0}^{2} + 1)c_{36} } & { - \mathrm{i}k_{y} (\partial_{x} z_{0}^{2} + 1)c_{23} } & { - \mathrm{i}k_{y} (\partial_{x} z_{0}^{2} + 1)c_{34} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right). $$

(76)

Appendix 5: Analytical Solutions in 3-D Homogeneous Medium

The analytical solutions in homogeneous acoustic media are given by

$$ F(r,t) = {\text{IFFT}}\left( {\mathrm{i} \cdot w \cdot R(w) \cdot G(w)} \right), $$

(77)

where $R(w)$ is the Fourier transform of the Ricker wavelet function (Wang, 2015),

$$ R(w) = \frac{{2w^{2} }}{{\sqrt \pi w_{{\text{p}}}^{3} }}\exp \left( {\frac{{ - w^{2} }}{{w_{{\text{p}}}^{2} }} + \mathrm{i}wt_{0} } \right). $$

(78)

$G(w)$ is the Green’s function in acoustic media (Aki & Richard, 1980).

The analytical solutions in homogeneous isotropic and VTI media are given by

$$ v_{kl} (x,y,z,t) = {\text{IFFT}}\left( {\mathrm{i} \cdot w \cdot R(w) \cdot G_{kl} ({\mathbf{x}},w)} \right), $$

(79)

where $w_{{\text{p}}}$ is the domain frequency corresponding to the maximum amplitude and t₀ is the delay time. IFFT the is fast inverse Fourier transform. $G_{kl} ({\mathbf{x}},w)$ is an asymptotic Green’s function in homogeneous anisotropic medium (Eq. 72, Vavryčuk, 2007).