Epistemic Uncertainty in PSHA and Seismic Hazard Characterization Using the Logic Tree Approach: Part I, Developing the Framework

Abstract

Epistemic uncertainty offers alternatives on decision making and various possibilities of computing the hazard integral. Generally, the logic tree approach is used while treating the epistemic uncertainty. Logic tree weight calculation is a subjective decision based on the degree of belief of the analyst on the possible contributors to the epistemic uncertainty and often leads to a different set of values by different researchers. This paper aims to develop a framework of accounting for the epistemic uncertainty in probabilistic seismic hazard analysis (PSHA) by minimizing the subjectivity involved in weight calculation. Guidelines/rules are developed for the weight calculation at each node of the logic tree. Recurrence parameters, magnitude and distance probability distributions, maximum magnitude, and selection of ground motion predictive equations (GMPEs) are considered the possible sources of epistemic uncertainty. A GMPE rule is proposed to be used with the PSHA framework to account for the propagation of epistemic uncertainty. The north-east region of India is chosen for the purpose of illustration. The study region is divided into seven seismic source zones (five in the active crustal region and two in the subduction zone). Seismic hazard is characterized in terms of the weighted mean and fractile representation of hazards using the logic tree approach. Only one sample illustration of the results are reported in terms of weighted mean and fractile representation of hazard curves and uniform hazard spectra (UHS). Further illustration of the PSHA results with possible implications from the epistemic uncertainty is reported in the companion paper.

1 Introduction

Uncertainties are generally categorized into two groups, namely, the aleatory variability and epistemic uncertainty, though the physical basis of distinction is somewhat debatable (Bommer & Scherbaum, 2008; Der Kiureghian & Ditlevsen, 2009). Aleatory variability refers to the intrinsic/congenital component, which is irreducible (stems from the Latin ‘alea’ meaning dice). Epistemic uncertainty is subjective, stemming from incomplete knowledge and, in fact, reducible with more relevant information. In addition to the location and magnitude of future earthquakes and scatter in the GMPEs (precisely the residuals), several other components can also be considered under aleatory variability, for example, the focal depth, and is generally included in the PSHA directly through the hazard integral. Sources of epistemic uncertainty that stems from the decision making can be categorized into two broad groups, namely, (i) the decisions pertaining to earthquake rupture prediction, i.e., seismic source characterization; and (ii) the decision on ground motion characterization models (Bradley, 2009; Rodriguez-Marek et al., 2021). Decision making in seismic source characterization includes the possible alternatives of source zone boundaries, recurrence models and their parameters, assigning maximum magnitude to each fault, rules for defining magnitude distribution, and distance metrics. Decision making is also involved in source-to-site distance characterization whenever fault geometry is not completely known, such as strike or dip. (Yaghmaei-Sabegh & Ebrahimi-Aghabagher, 2019). Decision making on the selection of GMPEs was detailed by Cotton et al. (2006) and subsequently revised by Bommer et al. (2010), while Scherbaum et al. (2009) reported a framework for ranking the selected GMPEs. Accounting for the effects of local site amplification also needs decision making and hence is attributed to the epistemic uncertainty. Most GMPEs account for this effect in an average sense through period-dependent site amplification factors over the prediction at the bedrock level. Average shear wave velocity in the top 30 m, denoted as Vs₃₀, is often used as a proxy of the shear wave velocity profile at the site. Another alternative is to arrive at the detailed velocity profile through geotechnical and geophysical investigations followed by a 1D (one dimensional) site response analysis with reasonable accuracy (Rodriguez-Marek et al., 2021).

Epistemic uncertainty offers alternatives on decision making and various possibilities of computing the hazard integral and subsequently results in a suite of hazard curves. Generally, the logic tree approach, derived from the probability tree, is employed while treating the epistemic uncertainty. Opinion differs in interpreting the weights assigned to each terminal branch of the logic/probability tree. While the probability tree works on the total probability theorem under the assumption of mutually exclusive and collectively exhaustive (MECE) events, the weights associated with each terminal branch represent its probability of occurrence. Along this line, the weighted mean representation of the hazard curve is only recommended to be used in seismic design (McGuire et al., 2005; Musson, 2005). Logic tree interpretation was introduced by Kulkarni et al. (1984) and subsequently defended by Abrahamson and Bommer (2005) though used by various researchers. The weights associated with the terminal branches represent the relative degree of belief of the analyst on each model instead of frequentist interpretation. Subsequently, these weights are considered subjective probability of the consequence of each model and enables a fractile representation of the hazard curve. Marzocchi et al. (2015) presented a nice example illustrating the difference of two interpretations. Bommer and Scherbaum (2008) recommended two possible interpretations of the fractile/weighted mean representation of a hazard (as the case may be) from the suite of hazard curves contingent on the intended application. Bommer et al. (2005) discussed the implementation of the logic tree to account for the propagation on epistemic uncertainty through selection and compatibility of GMPEs. More recent investigation recommends a representative suite approach for GMPEs instead of multiple GMPEs with weights (Atkinson et al., 2014), though the framework is arguably still in its infancy and requires unmanageable complexity for generalization. Finally, populating the nodes of the logic tree with possible alternatives needs thorough understanding on the part of analyst. For example, providing equal weights should be avoided, correlated alternatives (such as a- and b-values of recurrence relation) should not be selected as independent branches, aleatory variables (alternatives on focal depth) should not be considered in the logic tree, etc. Bommer and Scherbaum (2008) discussed the possible use and misuse of the logic tree in PSHA.

A large number of PSHA studies have been reported using the logic tree approach in different parts of the world. In most of the studies, logic tree weights are taken as either equal or based on degree of belief from expert/group of experts. For example, Bradley (2009) and Kalakonas et al. (2020) considered equal weights for GMPEs. Delavaud et al. (2012) considered the logic tree weights for GMPEs as a combination of the log-likelihood (LLH) method (Scherbaum et al., 2009) and judgement from six different experts. Anderson (2018) considered the equal weights for GMPEs and random/expert judgement-based weights for branches at other nodes of the logic tree. Grünthal et al. (2018) considered the equal weights at most of the nodes of a logic tree and expert judgement at the remaining. Anbazhagan et al. (2019) considered the logic tree weight by the LLH method for GMPEs and expert judgement for branches at other nodes of the logic tree. Tromans et al. (2019) considered weights based on expert judgement of the analyst. Epistemic uncertainty in site response analysis is considered by Rodriguez-Marek et al. (2021) and logic tree weights are taken as equal and discrete representations of a log-normal distribution.

Assigning equal weights to different terminal branches of a logic tree reflects more on the ‘lack of relevant information’ rather than ‘equal confidence’ on each alternative. Logic tree weight calculation is a subjective decision based on the degree of belief of the analyst on the possible contributors to the epistemic uncertainty and often leads to a different set of values by different researchers. However the weight should be logically deducible in a peer review process and, in other words, conform to the terminal goal of SSHAC (1997): ‘the center, the body, and the range of technical interpretations that the larger technical community would have if they were to conduct the study’ and that of USNRC (2018): ‘the center, the body, and the range of technically defensible interpretations of the available data, methods and models (CBR of TDI)’.

This paper aims to develop a framework of accounting for the epistemic uncertainties in PSHA. Minimizing the subjectivity involved in weight calculation is another complementary objective. Hence, guidelines/rules are developed for the weight calculation at each node of the logic tree. Sources of epistemic uncertainty considered here are (1) recurrence relation parameter, (2) magnitude probability distribution, (3) distance probability distribution, (4) maximum magnitude, and (5) selection of GMPEs. Proposed methodology of accounting for the epistemic uncertainty and constructing the weighted mean and fractile representation of hazards using the suite of hazard curves (denoted as model hazard curves; MHCs) as outcome from various branches of the logic tree is explained under a separate heading. So North-east India is chosen for the purpose of illustrating the proposed framework. While one set of sample results is used in the paper for the purpose of illustrating the application of proposed framework, further details on hazard analysis and results are presented in the companion paper (Gurjar and Basu, 2022).

For example, topography, tectonic setup, earthquake catalogue, seismicity, and delineation of source zones of the study region are reported in the companion paper. PSHA is then performed in the companion paper using the logic tree approach and taking into account the sources of epistemic uncertainties addressed above. Weighted mean and fractile representation of hazard of the region are estimated at 2% (maximum considered earthquake, MCE) and 10% (design basis earthquake, DBE) probability of exceedance in 50 years for the NEHRP (National Earthquake Hazard Reduction Program) soil types of B, C, and D. Hazard analysis also reports the weighted mean and fractile representation of uniform hazard spectra (UHS) for 112 district headquarters from seven states of North-east India.

2 Proposed Methodology of Accounting for the Epistemic Uncertainty and Characterization of Seismic Hazard

A step-by-step framework is proposed here to enable inclusion of the epistemic uncertainty in seismic hazard characterization.

2.1 Defining the Sources of Epistemic Uncertainty: Earthquake Rupture Forecast

Let $L$ be the number of source zones and $q\left( { = 1,L} \right)$ denotes a typical source zone with $a_{q}$ number of possible candidates for GMPE using a standard selection procure, for example, the log-likelihood method. Further, $b_{m} ,c,d,$ and $e_{r}$ are the number of possible rules used to define the maximum magnitude, probability distribution of magnitude, sets of recurrence relation parameters, and probability distribution of source-to-site distance, respectively. Any possible combination of these four rules constitutes a scenario that is defined here as earthquake rupture forecast (ERF). Clearly, $N = b_{m} .c.d.e_{r}$ is the number of ERFs that define the sources of epistemic uncertainty. Ideally, $N$ is the number of hazard curves that can be generated to describe the distribution of seismic hazard at a site.

One single GMPE may not adequately describe the attenuation of intensity measure for the entire study area if comprising different source zones. In such a case, each source zone may be best described by an individual set of GMPEs. Given this understanding, PSHA framework must include the provision of using multiple GMPEs for the hazard estimation. The GMPE rule is required to combine the contribution of applicable GMPEs if the end objective is to compute the fractile hazard (considering different sets of GMPEs in different source zones). However, the GMPE rule is not required if the end objective is only to compute the weighted mean rate hazard. Further, it should be noted that any typical ERF above does not explicitly refer to one GMPE or a set of GMPEs. One typical ERF should be assigned with a ‘GMPE rule’ that identifies the GMPE for each source zone. Hence, any ERF is further discretized into a set of sub-earthquake rupture forecasts (SERFs) conforming to the assigned GMPE rule as described below.

2.2 GMPE Rule and Its Implementation: Sub-Earthquake Rupture Forecast

The applicable GMPE rule may have multiple interpretations. For example: (i) considering only one GMPE from all the source zones and replacing only one at a time, and (ii) considering one GMPE from any one source zone and weighted attributes of all possible GMPEs in other source zones. The former leads to a large number of MHCs (same as the multiplication of the number of GMPEs over all the contributing source zones). In comparison, the latter leads to the same number of MHCs as the summation of the number of GMPEs over all the contributing source zones. However, both the interpretations lead to a consistent weighted mean hazard.

The first interpretation includes only a single GMPE from each source zone and hence does not account for the epistemic uncertainty (due to the selection of GMPEs) in an MHC. In contrast, the second interpretation (i.e., the proposed GMPE rule recommending a single GMPE from one source zone and weighted attributes of all possible GMPEs in other source zones) indirectly accounts for the epistemic uncertainty (due to the selection of GMPEs) in an MHC. Hence, the second interpretation is considered in this paper for further processing.

Consider, for example, the$u^{th}$ SERF and the$p^{th}$ ERF. Note that the GMPE rule is defined for the SERFs and hence remains the same in all ERFs, i.e., regardless of $p$. The GMPE rule is implemented as follows:

• (a) $u^{th}$ SERF: All ruptures ($m - r$ pair) in $q^{th}$ source zone will be governed by only $v^{th}$ of the $a_{q}$ number of possible candidates for GMPE, whereas other ruptures in any other source zone ($1,L$ but $\ne q$) will be contributed by the weighted attributes of all possible GMPEs in the respective source zone.

• (b) Repeat this rule for all the GMPEs in the$q^{th}$ source zone, i.e., $v = 1,a_{q}$. This will lead to a set of $a_{q}$ number of SERFs.

• (c) Follow a similar assignment in all source zones $q = 1,L$. This will lead to a set of $\sum\nolimits_{q = 1}^{L} {a_{q} } = N_{GMPE}$ number of SERFs. Here, $N_{GMPE}$ denotes the total number of GMPEs considered provided no GMPE is common between two zones. However, $\sum\nolimits_{q = 1}^{L} {a_{q} }$ holds for the number of SERFs in general.

Therefore, any of the $\sum\nolimits_{q = 1}^{L} {a_{q} }$ number of SERFs is defined as the $q^{th}$ source zone governed by its $v^{th}$ GMPE, $q = 1,L$, and $v = 1,a_{q}$. Clearly, the number of possible MHCs contributing to the epistemic uncertainty with due consideration of the attributes from GMPEs is given by $N_{MHC} = N\sum\nolimits_{q = 1}^{L} {a_{q} }$.

2.3 Construction of a Typical Model Hazard Curve

PSHA has been the focus of interdisciplinary research and is reported by a wide spectrum of researchers. Contingent on the discipline specific needs, many often simplified frameworks are adopted that defy the basic rule of probability. Regardless of the scenario, the following general assumptions are made in this paper for an MHC in the absence of epistemic uncertainty:

• (a) Number of occurrences of an earthquake exceeding a magnitude within a time interval (defined as the recurrence model) and hence the number of exceedance of a specific hazard level in a specific site within a time interval follows Poisson distribution. By virtue, ‘Poisson’s distribution generates itself under the addition of independent random variables’ and hence, under the assumption of mutually exclusive and collectively exhaustive causal ruptures, the exceedance rate contributed by all causal ruptures can be added to calculate that of a specific hazard level in a specific site.

• (b) Given the occurrence of a causal rupture, aleatory variability of an intensity measure (IM) closely follows log-normal distribution. This is specified through GMPEs by predicting the logarithmic mean and standard deviation of the considered IM.

Defining the geomean spectral acceleration at any specified time period $\left( {T^{ * } } \right)$ as the IM, $Sa\left( {T^{ * } } \right)$, the rate of exceedance of a given hazard level $Sa^{ * }$ can be expressed as

$$\lambda \left( {\ln Sa\left( {T^{ * } } \right) > \ln Sa^{ * } } \right) = \sum\limits_{k} {P\left( {\ln Sa\left( {T^{ * } } \right) > \ln Sa^{ * } \left| {Rup_{k} } \right.} \right)} \lambda \left( {Rup_{k} } \right).$$

(1)

Here $\lambda \left( {Rup_{k} } \right)$ denotes the rate of triggering the $k^{th}$ rupture.

While accounting for the epistemic uncertainty in the proposed framework, the contribution of the$k^{th}$ rupture is reiterated here for better clarity: (i) with one single GMPE to some SERFs contingent on the containing source zone; and (ii) with weighted GMPEs to remaining SERFs. Regardless of these two scenarios, assuming that the set of considered GMPEs constitutes a mutually exclusive and collectively exhaustive set, one may write using the theorem of total probability

$$P\left( {\ln Sa\left( {T^{ * } } \right) > \ln Sa^{ * } \left| {Rup_{k} } \right.} \right) = \sum\limits_{j = 1}^{{\sum\limits_{q = 1}^{L} {a_{q} } }} {P\left( {\ln Sa\left( {T^{ * } } \right) > \ln Sa^{ * } \left| {GMPE_{j} ,Rup_{k} } \right.} \right)P\left( {GMPE_{j} \left| {Rup_{k} } \right.} \right)} .$$

(2)

Equation (2) precisely accounts for the propagation of epistemic uncertainty through GMPE, which when substituted into Eq. (1) results in

$$\lambda \left( {\ln Sa\left( {T^{ * } } \right) > \ln Sa^{ * } } \right) = \sum\limits_{k} {\left[ {\sum\limits_{j = 1}^{{\sum\limits_{q = 1}^{L} {a_{q} } }} {P\left( {\ln Sa\left( {T^{ * } } \right) > \ln Sa^{ * } \left| {GMPE_{j} ,Rup_{k} } \right.} \right)P\left( {GMPE_{j} \left| {Rup_{k} } \right.} \right)} } \right]\lambda \left( {Rup_{k} } \right)} .$$

(3)

Here $P\left( {GMPE_{j} \left| {Rup_{k} } \right.} \right)$ defines, given the triggering of the$k^{th}$ rupture, the probability that the$j^{th}$ GMPE would control the propagation of intensity measure from the source to the site. According to the GMPE rule, $P\left( {GMPE_{j} \left| {Rup_{k} } \right.} \right)$ is 1.0 if the $k^{th}$ rupture contributes to one single GMPE, and otherwise, the weight should be specified for all GMPEs such that sum of the weights is unity. Finally, Eq. (3) is the manifestation of total probability theorem and the weight discussed here has the ‘frequentist interpretation’.

2.4 Construction of a Fractile Representation of Hazard Curve

Prior to describing the construction of a fractile representation of a hazard curve, a discussion on assigning weight to each MHC is relevant.

2.4.1 Assigning Weight to MHCs

With respect to the two ‘irreconcilable attitudes’, namely, the probability tree vs. the logic tree, and the resulting controversy between the weighted mean vs. fractile representation of a hazard, this paper stands by the fractile representation of hazard. In other words, each terminal branch of the logic tree is considered as a ‘possible alternative’ without any ‘frequentist interpretation’, and hence the weight assigned to the resulting MHC reflects merely the confidence of analyst on that alternative. Nevertheless, the weights assigned to each MHC should be logically deducible in a peer review process and, in other words, conform to the terminal goal of SSHAC (1997): ‘the center, the body, and the range of technical interpretations that the larger technical community would have if they were to conduct the study’, and that of USNRC (2018): ‘the center, the body, and the range of technically defensible interpretations of the available data, methods and models (CBR of TDI)’.

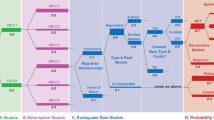
A typical terminal branch of the logic tree in this paper comprises five nodes as shown in Fig. 1a. Referring to Sect. 2.1, the first four nodes represent the alternative ERFs, and referring to Sect. 2.2, the fifth node considers the alternative SERFs. Nodes associated with ERFs are recommended to be populated with weights conforming to the standard practice but in compliance with the CBR of TDI. Some site-specific information is needed that precludes further generalization at this stage. However, the consideration of SERFs representing the propagation of epistemic uncertainty through GMPEs is somewhat unique in this paper and demands a generalized discussion on populating and assigning the weights. First, the candidate GMPEs will be selected conforming to the selection criteria recommended by Bommer et al. (2010). Next, the selected GMPEs will be ranked according to the log-likelihood (LLH) as reported by Scherbaum et al. (2009). The procedure computes the LLH of each GMPE that passed the selection criteria of Bommer et al. (2010). The weight is next assigned to each candidate inversely proportional to the LLH and all GMPEs with weight higher the ‘uniform weight’ (reciprocal of the number of candidates) are selected. These two steps are repeated for each source zone.

Fig. 1

Logic tree diagram

To explain it further, let $N_{q}$ be the number of candidate GMPEs for the $q^{th}$ source zone screened through the criteria of Bommer et al. (2010) and $w_{iq}$ represents the associated weights, $i = 1,N_{q}$. Let $a_{q}$ be the number of GMPEs with weight $w_{iq} > {1 \mathord{\left/ {\vphantom {1 {N_{q} }}} \right. \kern-\nulldelimiterspace} {N_{q} }}$ and finally selected for PSHA. The weights assigned to these selected $a_{q}$ number of GMPEs are rescaled such that sum of the weights is unity. Let us denote these final weights as $\overline{w}_{jq}$, $j = 1,a_{q}$.

Further, an additional step is considered to quantify the confidence in the selected set of GMPEs (through the criteria of Bommer et al., 2010) in any source zone. It should be noted that this additional step is useful only for the estimation of fractile hazard and does not affect the estimation of weighted mean hazard. A hypothetical case of equal LLH (or weights) for all the GMPEs within a source zone is first considered for further illustration. In other words, all the GMPEs lead to a nearly identical exceedance rate and hence do not account for the epistemic uncertainty effectively. Conversely, the greater the variation in weights within a source zone, the better is the effectiveness in capturing the epistemic uncertainty in that source zone.

Consider, for example, only the $q^{th}$ source zone. The weight $\left( {W_{q} } \right)$ is a random variable with realizations, $w_{1q} ,w_{2q} , \cdots ,w_{{N_{q} q}}$, depending on (i) the total number of GMPEs considered, and (ii) the observed data set. Parameters of the random variable can be estimated using the moments of different orders. Consider the variance $\left( {\sigma_{q}^{2} } \right)$ representing the confidence in capturing the epistemic uncertainty (and a spike representing no epistemic uncertainty). In other words, confidence in the sets of selected GMPEs across the source zones in capturing the epistemic uncertainty can be considered directly proportional to the variance of weights, which is denoted as the source zone weightage in this study. For example, the variance for the $q^{{{\text{th}}}}$ source zone may be estimated as

$$s_{q}^{2} = \frac{1}{{N_{q} - 1}}\sum\limits_{i = 1}^{{N_{q} }} {\left( {w_{iq} - \frac{1}{{N_{q} }}\sum\limits_{i = 1}^{{N_{q} }} {w_{iq} } } \right)}^{2} .$$

(4)

Rationale behind this assignment is intrinsic to the motivation of adopting the logic-tree framework. Assigning equal weights to all terminal branches of the logic tree reflects more on the ‘lack of relevant information’ rather than ‘equal confidence’ (should not be confused with ‘equally likely’ in the probability tree) in each alternative. Therefore, the weight assigned to the $q^{th}$ source zone is proposed to be

$$w_{q} = \frac{{s_{q}^{2} }}{{\sum\nolimits_{q = 1}^{L} {s_{q}^{2} } }}.$$

(5)

Finally, the weight associated with any of the $\sum\nolimits_{q = 1}^{L} {a_{q} }$ number of SERFs, defined through the $q^{th}$ source zone governed by its $j^{th}$ GMPE, consists of two parts, i.e., within the source zone $\left( {\overline{w}_{jq} } \right)$ and across the source zone $\left( {w_{q} } \right)$, and is expressed as

$$w_{SERF} = w_{q} \overline{w}_{jq} .$$

(6)

Therefore, the weight associated with any typical MHC is given by

$$w_{MHC} = w_{ERF} w_{SERF} .$$

(7)

where $w_{ERF}$ denotes the weight of the defining ERF.

One should not be confused between the (i) seven total source zones (five for active crustal region, ACR, and two for subduction zone, SZ) defined initially (refer Fig. 1 in the companion paper) and (ii) the only two (one each for ACR and SZ) considered in Fig. 1a. The reason is the paucity of available strong motion data for ranking and selection of GMPEs in the north-east region of India to divide it into seven source zones. Hence, the entire ACR is considered for the selection and ranking of one set of GMPEs, whereas the entire SZ is considered for another set. Therefore, the GMPE rule is implemented using two source zones, whereas all other sources of epistemic uncertainty account for the seven source zones.

One may also argue that the source zones should not be considered as logic tree branches (Fig. 1a). However, as per the GMPE rule associated with a particular SERF, total hazard at the site is governed by a single GMPE from one source zone (contribution 1) and the weighted attributes of all the GMPEs in all other source zones (contribution 2). Hence, each branch of the GMPE in any of the source zones (i.e., contribution 1) is further added to the weighted attributes of all the GMPEs in all other source zones (i.e., contribution 2). Since the GMPE rule considers each source zone twice, it is represented by two branches (SZ + ΣACR and ACR + ΣSZ; here, ΣACR and ΣSZ represent the weighted attributes of ACR and SZ, respectively) such that the weighted sum is unity. This is also consistent with the estimation of weighted mean hazard. Figure 1b sequentially represents the steps to be followed in the logic tree application for performing PSHA: (i) identification of the site where PSHA is required to be performed, (ii) identification of the sources in the surrounding contributing hazard to the site, (iii) identification of the applicable SERF and ERF based on the type of source zones, and (iv) computation of the mean annual rate of exceedance contributed from all potential sources in the surrounding.

2.4.2 Choice of Dissecting Ensemble MHCs

Consider all the $N_{{{\text{MHC}}}}$ number of MHCs that are collectively defined as the ensemble, referring back to the frequentist interpretation, two possible alternatives for conditional random variable exist contingent on the possible usage. For example, conditioned to the exceedance of IM by a specified level, ‘rate’ can be treated as a random variable if the EDP-hazard (engineering demand parameter-hazard) or loss computation is the end objective. This is denoted as the ‘vertical dissection’. Alternatively, conditioned to a given exceedance rate, IM can be considered a random variable if the design seismic hazard is the end objective. This is denoted as the ‘horizontal dissection’.

With design seismic hazard as the end objective, consider the ensemble MHC and a rate of exceedance, say, $\lambda = \lambda_{k}$ of an IM describing the seismic hazard. A vector of the IM is constructed with one element from each MHC. Since the IM vector is treated as independent, possible alternatives (independent random variables) from various terminal branches of the logic tree with branch factors indicating their probability of occurrence, referring to Fig. 2a, the weighted mean representation of hazard is given by

$$E\left( {IM} \right) = \mu_{IM} = \int\limits_{ - \infty }^{\infty } {im.f\left( {im} \right)\dim } = \sum\limits_{i = 1}^{{N_{MHC} }} {im_{i} f\left( {im_{i} } \right)\dim_{i} } = \sum\limits_{i = 1}^{{N_{MHC} }} {W_{MHC}^{i} im_{i} } ,$$

(8)

Here, $im_{i} \,\,\left( {i = 1,n} \right)$ is the realization of the IM vector from horizontal dissection of all the MHCs and $W_{MHC}^{i} \,\,\left( {i = 1,n} \right)$ is the branch factor (weight) from the logic tree associated with $i^{th}$ MHC.

Fig. 2

Weighted mean and fractile representation of hazard

Similarly, the fractile representation of hazard is given by

$$P\left( {IM \le im_{p} } \right) = \Phi \left( {im_{p} } \right) = \int\limits_{ - \infty }^{{im_{p} }} {f\left( {im} \right)\dim } = \sum\limits_{i = 1}^{{im_{p} }} {W_{MHC}^{i} } \Rightarrow im_{p} = \Phi^{ - 1} \left( {\sum\limits_{i = 1}^{{im_{p} }} {W_{MHC}^{i} } } \right).$$

(9)

Here, $im_{p}$ is the $p^{th}$ fractile estimate of the hazard, which can be estimated from cumulative distribution function (CDF) of the IM vector constructed nonparametrically (Fig. 2b) considering cumulative branch factors $\left( {\sum\limits_{i} {W_{MHC}^{i} } } \right)$ as the cumulative probability. Similar process is repeated for several discrete realization of rate of exceedance $\left( {k = 1,2, \cdots } \right)$ and the same z-fractile estimate is noted. Rate of exceedance when plotted against these z-fractile estimates leads to a fractile representation of the hazard curve, which is denoted here for better clarity as the fractile representation of the IM-hazard curve. A similar procedure can be adopted with vertical dissection and the resulting fractile hazard curve is defined here as the fractile representation of rate-hazard curve.

2.5 Construction of a Fractile Representation of the Uniform Hazard Spectrum and Design Seismic Hazard

IM is next considered at several discrete time periods and the associated z-fractile representation of IM-hazard curves is constructed. These z-fractile representations of IM-hazard curves are utilized to construct the z-fractile representation of the uniform hazard spectrum (z-UHS) representing a specified rate of exceedance. While the rate of exceedance is usually considered 10PE50 (475-year return period, DBE) or 2PE50 (2475-year return period, MCE), the design seismic hazard accounting for the epistemic uncertainty may be characterized by mean or appropriate fractile representation of UHS.

Further, there is a dividend in studying this fractile representation of IM-hazard. The ratio between the appropriate fractile and weighted mean representation of hazard (not median!) explains an alternate viewpoint of the ‘importance factor’ commonly used in seismic standards. In such a case, it would be interesting to see the importance factor as period- and site-dependent, as opposed to a constant.

Referring to Sect. 2.4, the weight calculation for a typical MHC $\left( {w_{MHC} } \right)$, resulting from any branch of the logic tree (Fig. 1a) is given by Eq. (7) which requires the $w_{SERF}$ and $w_{ERF}$ to be calculated. Here $w_{SERF}$ is given by Eq. (6) and can be calculated if $w_{iq}$ (associated weights of GMPEs, $i = 1,N_{q}$ in $q^{th}$ source zone) are known. Hence, the selection of GMPEs and their weight calculation ($w_{iq}$ and $\overline{w}_{jq}$) are explained in the next section.

3 GMPE Selection and Weight Calculation

Proper selection of GMPE is an important step for evaluating the seismic hazard at any site. A few GMPEs are reported to date for North-east India including the Himalayan region due to the limited recordings of strong ground motion data, such as Sharma et al. (2009), Nath et al. (2012), Anbazhagan et al. (2013), and Gupta (2010). However, several GMPEs have been reported around the world for similar tectonic features and site characteristics. Douglas (2020) reported a nice collection of GMPEs developed all around the world to the date of publication.

Generally, three to four GMPEs are good enough for the consideration of epistemic uncertainty due to selection of GMPEs (Stewart et al., 2013). Selection criteria recommended by Bommer et al. (2010) is applied to the database of GMPEs (Douglas, 2020) in the reverse chronological order (starting from the recent), to the selection of ten to 15 GMPEs in each source zone. Hence, a set of 14 and 12 GMPEs are selected for ACR and SZ, respectively, and summarized in Appendix A. All these screened GMPEs use different measures of source-to-site distance such as Joyner-Boore distance $\left( {R_{jb} } \right)$, epicentral distance $\left( {R_{{{\text{epi}}}} } \right)$, hypocentral distance $\left( {R_{{{\text{hypo}}}} } \right)$ and rupture distance $\left( {R_{{{\text{rup}}}} } \right)$.

Final selection of the GMPEs is based on the ranking using an information theoretic or log-likelihood (LLH) approach reported by Scherbaum et al. (2009), and implementation of which in the present context is briefly described here. Let $N_{q}$ be the number of candidates GMPEs for ranking in the $q^{{{\text{th}}}}$ source zone after preliminary screening. Recorded strong motion data at PESMOS (Program for Excellence in Strong Motion Studies) and COSMOS (Consortium of Organizations for Strong Motion Observation Systems) stations in the north-east region with moment magnitude greater than 4 and $R_{jb}$ less than 300 km (reduced if GMPE is not applicable) are considered for log-likelihood estimation. However, $R_{jb}$ is not reported in the database. Therefore, $R_{hypo}$ and $R_{epi}$ are first computed from the information of latitude and longitude of the source and station and focal depth reported in the database. Associated $R_{jb}$ is next constructed using the algorithm of Petersen et al. (2008). Appendix B summarizes the selected database which is used in the ranking process.

The candidate GMPEs use different intensity measures for the horizontal component of seismic excitation including GMRotI50, RotD50 and geomean. Five percent damped absolute acceleration response spectra are constructed using GMRotI50, RotD50 and geomean as the intensity measure for each recording. Geomean is defined in this paper over the ‘as-recorded’ pair (without any rotation for along and normal to the principal plane). Other intensity measures such as random, vectorial composition, and horizontal unspecified, if used in the GMPEs, are assumed as geomean in this paper. The observed sample data set for each GMPE is constructed using the associated spectral ordinates sampled at the period of 0.005 s over a period range of zero to the specified maximum.

Let the observed sample data set be defined as $X = \left\{ {x_{k} } \right\}$, with $k = 1,2,3, \cdots ,n$. Here $k^{th}$ realization is associated with a given triplet of magnitude $\left( {M_{k} } \right)$, source-to-site distance $\left( {R_{k} } \right)$ and the time period $\left( {T_{k} } \right)$. Associated with this $k^{th}$ triplet, each GMPE returns the median $\left( {\overline{Y}_{k} } \right)$ and logarithmic dispersion $\left( {\sigma_{k} } \right)$ of the respective intensity measures that are assumed to be log normally distributed. Hence, conditioned to a governing GMPE, the probability of $k^{th}$ observed data is given by

$$p\left( {X = x_{k} \left| {\overline{Y}_{k} ,\sigma_{k} } \right.} \right) = f\left( {x_{k} } \right)dx = \frac{1}{{\sigma_{k} \sqrt {2\pi } }}e^{{ - \frac{{\left[ {\ln \left( {x_{k} } \right) - \ln \left( {\overline{Y}_{k} } \right)} \right]^{2} }}{{2\sigma_{k}^{2} }}}} dx.$$

(10)

It should be noted that source-to-site distance for the observed events is available in $R_{hypo}$, $R_{epi}$ and also in $R_{jb}$ using the algorithm of Petersen et al. (2008). In addition, $R_{rup}$ is also required for some GMPEs and, in such cases, $R_{jb}$ is converted into $R_{rup}$ as recommended by Tavakoli et al. (2018). Average sample log-likelihood is next given by the negative of the average of logarithm of joint probability as follows:

$${\text{LLH}} = - \frac{1}{n}\sum\limits_{k = 1}^{n} {log_{B} \left\{ {f\left( {x_{k} } \right)} \right\}} .$$

(11)

Here $B$ denotes the base of the logarithm which is taken as 2. Associated weight for the $i^{th}$(out of $N_{q}$) GMPE in $q^{th}$ source zone is given by

$$w_{iq} = \frac{{B^{{ - LLH_{iq} }} }}{{\sum\nolimits_{i = 1}^{{N_{q} }} {B^{{ - LLH_{iq} }} } }}.$$

(12)

Higher the weight better is the ranking and Table 1 presents the GMPEs according to ranking for both ACR and SZ. The GMPEs with weight less than uniform weight, i.e., $w_{iq} < {1 \mathord{\left/ {\vphantom {1 {N_{q} }}} \right. \kern-\nulldelimiterspace} {N_{q} }}$, are rejected (Anbazhagan et al., 2016). GMPEs are also rejected based on the exclusive requirements of this paper. For example, Sharma et al. (2009) is only applicable to rock and soil sites (NEHRP B and C) and $R_{jb} \le 100$ km, and hence is not considered in ACR. Similarly, some of the GMPEs are rejected in SZ: 1) Anbazhagan et al. (2013) is applicable to the bedrock only; 2) Gupta (2010) is developed based on only three earthquake data and applicable to Intraslab only; 3) Youngs et al. (1997) is applicable to rock and soil sites. Finally, a cap of four GMPEs is imposed on both ACR and SZ and that leads to i) Rank-1, -3, -4 and -5 GMPEs for the ACR; and ii) Rank-4 and -5 GMPEs for the SZ. The GMPEs that are finally selected for PSHA are highlighted by bold letters in Table 1 with their rescaled weights ($\overline{w}_{jq}$).

Table 1 Ranking and final selection of candidate GMPEs for ACR and SZ

4 Earthquake Rupture Forecast (ERF)

The logic tree consists of two parts, ERF and SERF, as shown in the Fig. 1a. SERF refers to the GMPE rule comprising two sections, (i) within the source zone (explained in the Sect. 3), and (ii) across the source zone (explained in the Sect. 2.4). Hence, this section is devoted to the ERF only. ERF is primarily contributed from the first four nodes of the logic tree, namely, (i) distance probability distribution, (ii) recurrence relation parameters, (iii) magnitude distribution, and (iv) maximum magnitude. Any possible combination from these four nodes leads to one realization of ERF. The weight calculations for the first four nodes of the logic tree (Sect. 2.1, Fig. 1a) are explained in the subsequent sections. Finally, the weight associated with any realization of ERF, $w_{ERF}$, is given by the product of the weights contributed from the constituting nodes of the logic tree.

It should be noted that the logic tree starts in a sequence: (i) distance probability distribution, (ii) recurrence relation parameters, (iii) magnitude distribution, (iv) maximum magnitude and (v) selection of GMPEs. However, these sections are explained in a different sequence. Nevertheless, it is instructive to note the interdependence of some of these sections. For example, (i) weight calculation for maximum magnitude depends on the magnitude distribution and the recurrence relation parameters, and (ii) the weight calculation for magnitude distribution depends on the maximum magnitude and the recurrence relation parameters. Hence, for better clarity, the independent sections, for example, selection of GMPEs (Sect. 3) and recurrence relation parameters (Sect. 4.1) are discussed first. Interdependent sections are explained next, for example, magnitude distribution (Sect. 4.2), distance probability distribution (Sect. 4.3), and maximum magnitude (Sect. 4.4).

4.1 Estimation of Recurrence Relation Parameters

Gutenberg-Richter (1944) recurrence relation is expressed as $\log_{10} \left( {\lambda_{m} } \right) = a - bm$ with $a$ and $b$ as the recurrence parameters, whereas $\lambda_{m}$ is the mean annual rate of exceedance of magnitude $m$. Two of the most widely used methods of computing the recurrence parameters, namely (i) the least squares method of fitting a straight line (SL) and (ii) the maximum log-likelihood (LLH) method (Kijko & Smit, 2012), are considered in this paper as the possible contributors to epistemic uncertainty. While the first method is generally used and a sample illustration for the first zone of ACR is presented in Fig. 3, the maximum log-likelihood method requires some discussion on fundamentals for its implementation in this paper. This is explained with an illustration presented in Table 2 for the first zone of ACR.

Fig. 3

Frequency magnitude relationship for ACR Zone 1 by straight line fitting

Table 2 Sub-catalogues for ACR Zone-1

Let a catalogue over a period of $T_{c}$ years be known for the $q^{th}$ source zone. The catalogue is discretised into a set of $s$ magnitude intervals and Stepp’s (Stepp, 1972) method is employed for the evaluation of associated completion periods ($T_{m}^{1} ,T_{m}^{2} ,T_{m}^{3} , \ldots ,T_{m}^{s} )$. With reference to Table 2 (rows 2 and 3), the completion periods of 30, 50, 190 and 220 years from recent (31/07/2020) are obtained for magnitude intervals of 4–5, 5–6, 6–7 and > 7, respectively. The information of completion period and associated magnitude intervals are recast to construct a set of sub-catalogues of duration $T_{1} ,T_{2} ,T_{3} , \ldots ,T_{s}$ with minimum (complete) magnitude in each sub-catalogue as $m_{\min }^{1} ,m_{\min }^{2} ,m_{\min }^{3} , \ldots ,m_{\min }^{s}$, respectively, and total number of events as $n_{1} ,n_{2} ,n_{3} , \ldots ,n_{s}$, respectively. Unlike Stepp’s method, here the time is measured from the oldest, and hence, $m_{\min }^{1} > m_{\min }^{2} > m_{\min }^{3} > \cdots > m_{\min }^{s}$. Rows 4 and 5 of Table 2 illustrate this calculation from the results of Stepp’s method. The complete catalogue is then reconstructed by compiling all the sub-catalogues such that: (i) duration $\sum_{i = 1}^{s} {T_{i} = T_{c} }$; and (ii) number of events $\sum_{i = 1}^{s} {n_{i} = N}$.

Let $m_{1}^{i} ,m_{2}^{i} ,m_{3}^{i} , \ldots ,m_{{n_{i} }}^{i}$ represent the observed magnitudes in the$i^{th}$ sub-catalogue. Under the assumption of mutual independency, the joint probability density function for the $i^{th}$ sub-catalogue conditioned to $\beta = b\ln \left( {10} \right)$ is given by

$$f\left( {m\left| \beta \right.} \right) = f\left( {m_{1}^{i} \left| \beta \right.} \right)f\left( {m_{2}^{i} \left| \beta \right.} \right)f\left( {m_{3}^{i} \left| \beta \right.} \right) \cdots f\left( {m_{{n_{i} }}^{i} \left| \beta \right.} \right) = \prod\limits_{j = 1}^{{n_{i} }} {f\left( {m_{j}^{i} \left| \beta \right.} \right)} .$$

(13)

Therefore, likelihood of the entire catalogue may be constructed as

$$L\left( \beta \right) = \prod\limits_{i = 1}^{s} {\prod\limits_{j = 1}^{{n_{i} }} {f\left( {m_{j}^{i} \left| \beta \right.} \right)} } .$$

(14)

The parameter $\beta$ can be evaluated by maximizing the likelihood and, alternatively, the logarithm of likelihood. Hence, by taking natural logarithm of Eq. (14) and for the maxima,

$$\ln \left[ {L\left( \beta \right)} \right] = \sum\limits_{i = 1}^{s} {\sum\limits_{j = 1}^{{n_{i} }} {\ln \left[ {f\left( {m_{j}^{i} \left| \beta \right.} \right)} \right]} } \to \frac{d}{d\beta }\ln \left[ {L\left( \beta \right)} \right] = 0.$$

(15)

Using the lower bound Gutenberg-Richter recurrence relation, one may write,

$$f\left( {m_{j}^{i} \left| {\hat{\beta }} \right.} \right) = \hat{\beta }e^{{ - \hat{\beta }\left( {m_{j}^{i} - m_{\min }^{i} } \right)}} \to \ln \left[ {f\left( {m_{j}^{i} \left| {\hat{\beta }} \right.} \right)} \right] = \ln \left( {\hat{\beta }} \right) + \hat{\beta }\left( {m_{\min }^{i} - m_{j}^{i} } \right).$$

(16)

Using Eq. (16) into Eq. (15) and after some simplifications, one may write

$$\sum\limits_{i = 1}^{s} {\sum\limits_{j = 1}^{{n_{i} }} {\frac{1}{{\hat{\beta }}}} } + \sum\nolimits_{i = 1}^{s} {\sum\nolimits_{j = 1}^{{n_{i} }} {\left[ { - \left( {m_{j}^{i} - m_{\min }^{i} } \right)} \right]} } = 0 \to \frac{{\sum\nolimits_{i = 1}^{s} {n_{i} } }}{{\hat{\beta }}} = \sum\nolimits_{i = 1}^{s} {n_{i} } \left[ {\left( {\frac{1}{{n_{i} }}\sum\nolimits_{j = 1}^{{n_{i} }} {m_{j}^{i} } } \right) - m_{\min }^{i} } \right].$$

(17)

Further, assuming $\left( {\frac{1}{{n_{i} }}\sum\nolimits_{j = 1}^{{n_{i} }} {m_{j}^{i} } } \right) - m_{\min }^{i} = \overline{m}^{i} - m_{\min }^{i} = \frac{1}{{\hat{\beta }_{i} }}$ and $r_{i} = {{n_{i} } \mathord{\left/ {\vphantom {{n_{i} } {\sum\nolimits_{i = 1}^{s} {n_{i} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{i = 1}^{s} {n_{i} } }}$, Eq. (17) may be solved for

$$\frac{1}{{\hat{\beta }}} = \sum\limits_{i = 1}^{s} {\frac{{r_{i} }}{{\hat{\beta }_{i} }}} .$$

(18)

Equation (18) is known as the generalized Aki-Utsu b value estimator and also well explained by Kijko and Smit (2012).

Estimated mean annual rate of exceedance corresponding to $m_{\min }$ is given by

$$\hat{\lambda }_{{m_{\min } }} = {{\hat{N}} \mathord{\left/ {\vphantom {{\hat{N}} {T_{c} }}} \right. \kern-\nulldelimiterspace} {T_{c} }}.$$

(19)

Here, $\hat{N} = \sum\limits_{i = 1}^{s} {\hat{N}_{i} }$ and $\hat{N}_{i}$ is the total number of events in the$i^{th}$ sub-catalogue between $m_{\min }^{i}$ to $m_{\max }$, which can be estimated using the probability distribution of magnitude as follows

$$\hat{N}_{i} = \frac{{n_{i} }}{{F_{M} \left( {m_{\min }^{i} \le m \le m_{\max } \left| {m_{\min } ,m_{\max } } \right.} \right)}} = \frac{{n_{i} }}{{1 - F_{M} \left( {m_{\min } \le m \le m_{\min }^{i} \left| {m_{\min } ,m_{\max } } \right.} \right)}}.$$

(20)

Here, $F_{M} \left( {m_{\min } \le m \le m_{\min }^{i} \left| {m_{\min } ,m_{\max } } \right.} \right) = \frac{{1 - e^{{ - \beta \left( {m_{\min }^{i} - m_{\min } } \right)}} }}{{1 - e^{{ - \beta \left( {m_{\max } - m_{\min } } \right)}} }}$ is given by the doubly truncated Gutenberg-Richter recurrence relation with $m_{\min } = 4$(events below which can be ignored due to lack of engineering importance) and $m_{\max } = m_{\max }^{obs}$ (maximum observed magnitude), and $n_{i}$ is the number of events in the$i^{th}$ sub-catalogue between $m_{\min }^{i}$ to $m_{\max }$. Values of a and b can be estimated using the relations $\hat{\beta } = b\ln \left( {10} \right)$ and $\hat{\lambda }_{{m_{\min } }} = 10^{{a - bm_{\min } }}$.

With reference to Table 2, for the sample illustration, $N_{c} = 1402$ and $m_{\max }^{obs} = 8$, with $m_{\min } = 4$. Using Eqs. (18) and (19), one may calculate $\hat{\beta } = 1.9386$ and $\hat{\lambda }_{{m_{\min } }} = 35.0418$, respectively, and finally $b = 0.84$ and $a = 4.91$. Recurrence parameters obtained by both the methods for all the source zones are reported in Table 3.

Table 3 Seismicity parameters for the north-east region

4.1.1 Weight Calculation for the Process of Estimating Recurrence Relation Parameters

Weights associated with each method of estimating recurrence relation parameters for the logic tree approach are proposed to be inversely proportional to mean squared error over all the source zones. For example, consider one of the source zones, say $q^{th}$. Let $T_{m}^{k}$ be the completion period of the$k^{th}$ magnitude interval with $N_{m}^{k}$ number of events within the completion period. Table 4 presents a sample illustration for the first zone of ACR. Recurrence parameters are estimated using the procedure described above. Associated mean rate of occurrence is estimated as $\lambda_{m} = 10^{{\left( {a - bm} \right)}}$ for both the methods (for example, the last two columns of Table 4). The observed mean annual rate of exceedance $\left( {\lambda^{obs} } \right)$ is estimated using the cumulative sum of ${{N_{m}^{k} } \mathord{\left/ {\vphantom {{N_{m}^{k} } {T_{m}^{k} }}} \right. \kern-\nulldelimiterspace} {T_{m}^{k} }}$ starting from the highest magnitude interval (for example, column 5 of Table 4). Mean squared error for both the methods, namely, SL and LLH, are given by $E_{SL}^{q} = \frac{1}{s}\sum\limits_{k = 1}^{s} {\left( {\lambda^{k,obs} - \hat{\lambda }_{m}^{k,SL} } \right)^{2} }$ and $E_{LLH}^{q} = \frac{1}{s}\sum\limits_{k = 1}^{s} {\left( {\lambda^{k,obs} - \hat{\lambda }_{m}^{k,LLH} } \right)^{2} }$, respectively. Table 5 compares the mean squared error using both the methods for each source zone.

Table 4 Observed and estimated mean annual rate (λ) from (a, b values) of SL and LLH method for ACR Zone-1

Table 5 Mean squared error between the observed and estimated rates of SL and LLH methods

Both errors in all source zones are compared and the best-fit linear relation is constructed with a constraint of zero intercept, i.e., $E_{LLH} = \theta \times E_{SL}$ (Fig. 4). The first source zone of SZ is neglected as an outlier and $\theta$ is estimated as 0.85. Finally, the weights are computed as inversely proportional to the mean squared error as follows:

$$W_{SL} = \frac{{{1 \mathord{\left/ {\vphantom {1 {E_{SL} }}} \right. \kern-\nulldelimiterspace} {E_{SL} }}}}{{\left( {{1 \mathord{\left/ {\vphantom {1 {E_{SL} }}} \right. \kern-\nulldelimiterspace} {E_{SL} }} + {1 \mathord{\left/ {\vphantom {1 {E_{LLH} }}} \right. \kern-\nulldelimiterspace} {E_{LLH} }}} \right)}} = \frac{\theta }{1 + \theta } = \frac{0.85}{{1 + 0.85}} = 0.46,\,W_{LLH} = \frac{{{1 \mathord{\left/ {\vphantom {1 {E_{LLH} }}} \right. \kern-\nulldelimiterspace} {E_{LLH} }}}}{{\left( {{1 \mathord{\left/ {\vphantom {1 {E_{SL} }}} \right. \kern-\nulldelimiterspace} {E_{SL} }} + {1 \mathord{\left/ {\vphantom {1 {E_{LLH} }}} \right. \kern-\nulldelimiterspace} {E_{LLH} }}} \right)}} = \frac{1}{1 + \theta } = \frac{1}{1 + 0.85} = 0.54.$$

(21)

Fig. 4

Zero-intercept best-fit straight-line relationship between the mean squared error of SL and LLH methods

4.2 Magnitude Distribution/Recurrence Relation

Recurrence relation defines a relation between the mean annual rate of exceedance and magnitude and hence the magnitude distribution as well. Since the study is applied to the north-east region which does not have any documented characteristic events in any of the source zones, the characteristic earthquake model is not included. Therefore, two alternatives of magnitude distribution are considered in this paper as the possible contributors to epistemic uncertainty, namely, (i) bounded Gutenberg-Richter (GR) (1944) and (ii) Main and Burton (MB) (1984). Associated magnitude distributions, $f_{1} \left( {m_{i} } \right)$ and $f_{2} \left( {m_{i} } \right)$, respectively, are given by

$$p\left( {M = m_{i} \left| {m_{\max } ,\beta ,m_{\min } \le m_{i} \le m_{\max } } \right.} \right) = f_{1} \left( {m_{i} } \right)dm_{i} = \frac{{\beta e^{{ - \beta \left( {m_{i} - m_{\min } } \right)}} }}{{1 - e^{{ - \beta \left( {m_{\max } - m_{\min } } \right)}} }}dm_{i} \,\,\left( {{\text{Gutenberg}} - {\text{Richter}},{1944}} \right)$$

(22)

$$\begin{gathered} p\left( {M = m_{i} \left| {m_{\max } ,\beta ,m_{\min } \le m_{i} \le m_{\max } } \right.} \right) = f_{2} \left( {m_{i} } \right)dm_{i} \hfill \\ = \frac{{\beta \left[ {e^{{ - \beta \left( {m_{i} - m_{\min } } \right)}} - e^{{ - \beta \left( {m_{\max } - m_{\min } } \right)}} } \right]H\left( {m_{\max } - m_{i} } \right) + \left[ {e^{{ - \beta \left( {m_{i} - m_{\min } } \right)}} - e^{{ - \beta \left( {m_{\max } - m_{\min } } \right)}} \left\{ {1 + \beta \left( {m_{\max } - m_{i} } \right)} \right\}} \right]\delta \left( {m_{\max } - m_{i} } \right)}}{{\left[ {1 - e^{{ - \beta \left( {m_{\max } - m_{\min } } \right)}} - \beta e^{{ - \beta \left( {m_{\max } - m_{\min } } \right)}} \left( {m_{\max } - m_{\min } } \right)} \right]}}dm_{i} \,\,\left( {\text{Main and Burton, 1984}} \right) \hfill \\ \end{gathered}$$

(23)

Similarly, the mean annual rate of exceedance, ${\lambda _1}\left( {{m_i}} \right)$ and ${\lambda _2}\left( {{m_i}} \right)$respectively, are given by

$$ {\lambda _1}\left( {{m_i}} \right) = \nu \frac{{{e^{ - \beta \left( {{m_i} - {m_{\min }}} \right)}} - {e^{ - \beta \left( {{m_{\max }} - {m_{\min }}} \right)}}}}{{1 - {e^{ - \beta \left( {{m_{\max }} - {m_{\min }}} \right)}}}}$$

(24)

(Gutenberg-Richter, 1944)

$${\lambda _2}\left( {{m_i}} \right) = \nu \left[ {{e^{ - \beta \left( {{m_i} - {m_{\min }}} \right)}} - {e^{ - \beta \left( {{m_{\max }} - {m_{\min }}} \right)}}\left\{ {1 + \beta \left( {{m_{\max }} - {m_i}} \right)} \right\}} \right]H\left( {{m_{\max }} - {m_i}} \right)$$

(25)

(Main and Burton 1984) Here, $\nu = {{e^{\left( \alpha- \beta {m_{min}}\right)} \; \text {and}\; \alpha = a1n }}$ (10).

Probability density function (PDF) (magnitude distribution) and mean annual rate of exceedance are plotted against magnitude in Fig. 5a and 5b, respectively, for the purpose of illustration.

Fig. 5

Variation of probability density function and mean annual rate with magnitude for Gutenberg-Richter (1944) and Main and Burton (1984) recurrence relations [m_min = 4, m_max = 8, a = 4 and b = 1]

4.2.1 Weight Calculation for Magnitude Distribution

Weights associated with each alternative are computed for the logic tree using a log-likelihood approach similar to that employed in the case of GMPEs. Let $M = \left\{ {m_{i} } \right\}$, with $i = 1,2,3, \cdots ,n$ be the sample data set of observed events (seismic catalogue) in any of the source zones, say $q^{th}$. Since all the observed events are independent, denoting $g\left( {m_{i} } \right) = f\left( {m_{i} } \right)dm_{i}$ as the likelihood of model $g$[$g_{1}$ or $g_{2}$] for the observed sample $m_{i}$, the associated joint probability is given by $L\left( {g\left| M \right.} \right) = \prod\limits_{i = 1}^{n} {g\left( {m_{i} } \right)}$. Negative of the average sample log-likelihood is considered here to define the log-likelihood (LLH):

$$LLH\left( g \right) = - \left\langle {log_{B} \left( {L\left( {g\left| M \right.} \right)} \right)} \right\rangle = - \frac{1}{n}\sum\limits_{i = 1}^{n} {log_{B} \left( {g\left( {m_{i} } \right)} \right)} .$$

(26)

Here, $B$ refers to the base of the logarithm and is taken as 2 (can also be taken as 10, Scherbaum et al., 2009). The negative sign is considered here, as the logarithm of probability is always non-positive. Clearly, the LLH is superior and is the method of recurrence relation. Associated weightage of recurrence relations is given by

$$W_{{g_{j} }} = {{B^{{ - LLH\left( {g_{j} } \right)}} } \mathord{\left/ {\vphantom {{B^{{ - LLH\left( {g_{j} } \right)}} } {\sum\limits_{j = 1}^{2} {B^{{ - LLH\left( {g_{j} } \right)}} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{j = 1}^{2} {B^{{ - LLH\left( {g_{j} } \right)}} } }}.$$

(27)

Since PDFs of both methods are identical at low magnitudes with a little difference near the maximum magnitude, none of the observed events ($m_{\min }$ to $m_{\max }^{obs}$) should be considered while calculating the LLH, which would otherwise appear as nearly identical. It is reasonable to consider events in the range of [$\hat{m}_{\max }$–1.5 ~ $m_{\max }^{obs}$] for the computation of LLH (Fig. 5a). Weights are calculated in this paper separately for each source zone by considering the observed events within magnitude range [$\hat{m}_{\max }$–1.5 ~ $m_{\max }^{obs}$]. Four possible combinations are also considered for each source zone, for example, two sets of recurrence parameters [(a1, b1), (a2, b2) or $\beta_{1} ,\,\beta_{2}$] and two sets of maximum magnitude [$\hat{m}_{\max }^{1}$ and $\hat{m}_{\max }^{2}$]. Three alternatives for maximum magnitudes are discussed later in Sect. 4.4. However, the third maximum magnitude is dropped here since it is dependent on the fault length and, therefore, has an unreasonably higher order of complexity. Final weights for both the magnitude distributions are taken as the weighted average (by number of events) over all the source zones and all possible combinations.

4.3 Distance Probability Distribution

Distribution of source-to-site distance also contributes to the epistemic uncertainty. While assuming all the points on a fault plane are equiprobable to rupture (Iyengar & Ghosh, 2004), two alternatives are considered in this paper as the possible contributors to epistemic uncertainty: the distribution of source-to-site distance is independent or dependent on magnitude of the event. Magnitude independent probability distribution is based on the point-source model, and hence, rupture length of the fault due to causal magnitude for the earthquake is ignored. The magnitude-dependent model accounts for the finite rupture length, and hence, the distribution is conditioned to the magnitude of event.

All the faults are assumed to be linear with known length in the study region and $R_{jb}$ is considered as the measure of source-to-site distance $\left( R \right)$ in this paper. $P\left( {R|M = m} \right)$ due to a rupture segment uniformly distributed over the fault plane was reported by Der Kiureghian and Ang (1977) and simplified by Iyengar and Ghosh (2004) for the hypocentral distance. The same model is extended in this paper to account for $R_{jb}$ as the distance metric. While Fig. 6 illustrates the conceptual development of CDF for a fault located at one side of the site, the mathematical model is given by

$$\left. \begin{gathered} \begin{array}{*{20}c} {P\left( {R < r\left| {M = m} \right.} \right)} & = & 0 & {for} & {r < \left( {L_{0}^{2} + D^{2} } \right)^{0.5} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {P\left( {R < r\left| {M = m} \right.} \right)} & = & {\frac{{\left( {r^{2} - D^{2} } \right)^{0.5} - L_{0} }}{{L_{f} - X\left( m \right)}} \, \begin{array}{*{20}c} {for} & {\left( {L_{0}^{2} + D^{2} } \right)^{0.5} < r < \left[ {D^{2} + \left\{ {L_{f} + L_{0} - X\left( m \right)} \right\}^{2} } \right]^{0.5} } \\ \end{array} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {P\left( {R < r\left| {M = m} \right.} \right)} & = & 1 & {for} & {r > \left[ {D^{2} + \left\{ {L_{f} + L_{0} - X\left( m \right)} \right\}^{2} } \right]^{0.5} } \\ \end{array} \hfill \\ \end{gathered} \right\}.$$

(28)

Fig. 6

Fault rupture model

Here, $X\left( m \right)$ is the rupture length in km given by Wells and Coppersmith (1994) for different fault types but not exceeding the fault length:

$$\begin{array}{*{20}c} {X\left( m \right)} & = \\ \end{array} \left\{ {\begin{array}{*{20}c} {{\text{Min}}\left( {L_{f} ,10^{ - 3.22 + 0.69m} } \right)} & {{\text{Min}}\left( {L_{f} ,10^{ - 3.55 + 0.74m} } \right)} & {{\text{Min}}\left( {L_{f} ,10^{ - 2.01 + 0.50m} } \right)} & {{\text{Min}}\left( {L_{f} ,10^{ - 2.86 + 0.63m} } \right)} \\ {{\text{Undefined}}} & {\text{Strike - slip}} & {{\text{Normal}}} & {{\text{Reverse}}} \\ \end{array} } \right..$$

(29)

Other recent recommendations may also be used in place of Wells and Coppersmith (1994) leading to another source of epistemic uncertainty, which, however, is not considered in this paper for simplicity.

For a general case with the fault located at both sides of the site, conditional probabilities for the segments on each side are calculated separately and added with a weight as the fraction of total fault length. The same formulation also applies to the magnitude-independent model with $X\left( m \right) = 0$. Sample comparison of both probability density functions (PDF), i.e., $p(r)$ and $p(r|m)$, is presented in Fig. 7 for an arbitrary source and site in the study region with moment magnitude M_w 6.4.

Fig. 7

Source-to-site distance probability distribution (arbitrary source and site, Mw = 6.4)

4.3.1 Weight Calculation for the Type of Distance Probability Distribution

Proposed procedure for weight calculation of distance probability distribution is slightly complicated. However, it is also based on the log-likelihood approach. Let $M = \left\{ {m_{i} } \right\}$, with $i = 1,2,3, \cdots ,n$ be the sample data set of observed events (seismic catalogue) in the magnitude interval ${\text{Min}}\left( {\hat{m}_{\max }^{1} ,\hat{m}_{\max }^{2} } \right) - 1.5\sim m_{\max }^{obs}$ in the complete study region including all the source zones. Each observed event must be assigned to a particular source (fault) since the distance probability distribution depends on relative location of source and site. With limited information available, one may assign an event to the nearest fault or a few faults (say 3 or 5) nearby. The former approach is adopted throughout this paper to avoid subjectivity. It is desirable to consider only the events occurring within the area of influence around a particular site to avoid unnecessary computation. Area of influence is defined in this paper as the maximum radial distance of 300 km around a site under the assumption that an event above certain magnitude $\left( {m_{\min } } \right)$ triggering outside it would cause negligible effect to the structure located at the site.

Each observed event with the source assigned will have a total of 24 possible combinations of calculating the PDF: 12 combinations each for ${g_{j} \left( {r_{i} ,m_{i} } \right) = p\left( {r_{i} } \right)f\left( {m_{i} } \right)dm_{i} dr_{i} }$ and ${g_{j} \left( {r_{i} ,m_{i} } \right) = p\left( {r_{i} \left| {m_{i} } \right.} \right)f\left( {m_{i} } \right)dm_{i} dr_{i} }$. For example, three alternatives for maximum magnitude (Sect. 4.4), two for recurrence parameters and two for magnitude distribution. Hence, three probability density functions, namely, $p\left( r \right)$ and $p\left( {r\left| m \right.} \right)$ (as above) and $f\left( m \right)$(as in Sect. 4.2), are computed in each of the 24 possible combinations and evaluated for each observed event with a given $m - r$ pair within the area of influence for each site followed by the computation of log-likelihood. This step is repeated for all the site locations considered (2302 locations with 0.1° grid spacing) in the study region followed by an estimate of the sample size independent average log-likelihood as follows:

$$\left. {\begin{array}{*{20}c} {{\text{LLH}}_{g\left( r \right)} = - \frac{1}{{N_{sc} }}\left[ {\sum\limits_{k = 1}^{2302} {\sum\limits_{j = 1}^{12} {\sum\limits_{i = 1}^{{n_{k} }} {log_{B} \left\{ {g_{j} \left( {r_{i} ,m_{i} } \right)} \right\}} } } } \right]} & {with} & {g_{j} \left( {r_{i} ,m_{i} } \right) = p\left( {r_{i} } \right)f\left( {m_{i} } \right)dm_{i} dr_{i} } \\ {{\text{LLH}}_{{g\left( {r\left| m \right.} \right)}} = - \frac{1}{{N_{sc} }}\left[ {\sum\limits_{k = 1}^{2302} {\sum\limits_{j = 13}^{24} {\sum\limits_{i = 1}^{{n_{k} }} {log_{B} \left\{ {g_{j} \left( {r_{i} ,m_{i} } \right)} \right\}} } } } \right]} & {with} & {g_{j} \left( {r_{i} ,m_{i} } \right) = p\left( {r_{i} \left| {m_{i} } \right.} \right)f\left( {m_{i} } \right)dm_{i} dr_{i} } \\ \end{array} } \right\}.$$

(30)

Here, $n_{k}$ is the total number of events within the influence area of $k^{th}$ site, $p\left( r \right)$ and $p\left( {r\left| m \right.} \right)$ are magnitude independent and dependent distance probabilities, respectively, and calculated using the CDF given by Eq. (28), whereas $f\left( m \right)$ is the magnitude probability density function as defined in Eqs. (22) and (23). Further, ${1 \mathord{\left/ {\vphantom {1 {N_{sc} }}} \right. \kern-\nulldelimiterspace} {N_{sc} }}$ is used for a sample size independent estimate with $N_{sc}$ as total sample count $\left( {2302 \times 12 \times n_{k} } \right)$ and $B = 2$ is taken as the base of logarithm. Associated weights are calculated as:

$$\begin{array}{*{20}c} {W_{g\left( r \right)} = \frac{{B^{{ - LLH_{g\left( r \right)} }} }}{{B^{{ - LLH_{g\left( r \right)} }} + B^{{ - LLH_{{g\left( {r\left| m \right.} \right)}} }} }},} & {W_{{g\left( {r\left| m \right.} \right)}} = \frac{{B^{{ - LLH_{{g\left( {r\left| m \right.} \right)}} }} }}{{B^{{ - LLH_{g\left( r \right)} }} + B^{{ - LLH_{{g\left( {r\left| m \right.} \right)}} }} }}} \\ \end{array} .$$

(31)

4.4 Maximum Magnitude

Opinion differs while considering the maximum magnitude in PSHA, and several terminologies are interchangeably used in the prior art, for example, maximum characteristic, expected or possible earthquake magnitude. However, writing a simple terminology such as ‘maximum magnitude’ is often preferred followed by explaining the way of defining it (Abrahamson, 2000). Seven possible alternatives (five alternatives from Gupta, 2002; Kijko & Singh, 2011; and proportional to fault length) are initially selected for the estimation of maximum magnitude. Since five alternatives from Kijko and Singh, (2011) result in nearly identical estimation, the maximum of these five is considered a single alternative. Finally, three possible alternatives (maximum of five alternatives from Gupta, 2002; Kijko & Singh, 2011; and proportional to fault length) are considered in this paper as the contributors to epistemic uncertainty as explained below.

• A. Maximum of five methods from Kijko and Singh (2011)

  Several procedures for maximum magnitude estimation (statistically) are well explained and summarized by Kijko and Singh (2011), out of which following five methods are selected in this paper:

  • (a) Tate–Pisarenko:

    $$\hat{m}_{\max } = m_{\max }^{obs} + \frac{{1 - e^{{ - \hat{\beta }\left( {\hat{m}_{\max } - m_{\min } } \right)}} }}{{\hat{N}\hat{\beta }e^{{ - \hat{\beta }\left( {m_{\max }^{obs} - m_{\min } } \right)}} }}.$$

    (32)

  • (b) Kijko–Sellevoll:

    $$\hat{m}_{\max } = m_{\max }^{obs} + \int\limits_{{m_{\min } }}^{{m_{\max } }} {\left[ {\frac{{1 - e^{{ - \hat{\beta }\left( {m - m_{\min } } \right)}} }}{{1 - e^{{ - \hat{\beta }\left( {\hat{m}_{\max } - m_{\min } } \right)}} }}} \right]}^{{\hat{N}}} dm.$$

    (33)

  • (c) Tate–Pisarenko–Bayes:

    $$\begin{gathered} \hat{m}_{\max } = m_{\max }^{obs} + \frac{1}{{\hat{N}\hat{\beta }C_{\beta } }}\left( {\frac{{p_{G} }}{{p_{G} + m_{\max }^{obs} - m_{\min } }}} \right)^{{ - \left( {q_{G} + 1} \right)}} \hfill \\ C_{\beta } = \frac{1}{{1 - \left[ {{{p_{G} } \mathord{\left/ {\vphantom {{p_{G} } {\left( {p_{G} + \hat{m}_{\max } - m_{\min } } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {p_{G} + \hat{m}_{\max } - m_{\min } } \right)}}} \right]^{{q_{G} }} }};p_{G} = \frac{{\hat{\beta }}}{{\left( {\sigma_{{\hat{\beta }}} } \right)^{2} }};q_{G} = \left( {\frac{{\hat{\beta }}}{{\sigma_{{\hat{\beta }}} }}} \right)^{2} ;\sigma_{{\hat{\beta }}} = \frac{{\hat{\beta }}}{\sqrt N }. \hfill \\ \end{gathered}$$

    (34)

  • (d) Kijko–Sellevoll–Bayes:

    $$\hat{m}_{\max } = m_{\max }^{obs} + \left( {C_{\beta } } \right)^{{\hat{N}}} \int\limits_{{m_{\min } }}^{{m_{\max } }} {\left[ {1 - \left\{ {{{p_{G} } \mathord{\left/ {\vphantom {{p_{G} } {\left( {p_{G} + m - m_{\min } } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {p_{G} + m - m_{\min } } \right)}}} \right\}^{{q_{G} }} } \right]^{{\hat{N}}} dm}$$

    (35)

  • (e) Non-parametric with Gaussian kernel

After arranging observed magnitudes in ascending order,

$$\hat{m}_{\max } = m_{\max }^{obs} + \sum\limits_{i = 1}^{{N_{c} - 1}} {\left( {{\raise0.7ex\hbox{$i$} \!\mathord{\left/ {\vphantom {i {N_{c} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${N_{c} }$}}} \right)^{{N_{c} }} \left( {m_{i + 1} - m_{i} } \right)} .$$

(36)

Here, $\hat{\beta }$ and $\hat{N}$ are given by Eqs (18) and (20), respectively, and $N_{c}$ is the total number of events observed between minimum magnitude $\left( {m_{\min } = 4} \right)$ to maximum observed magnitude $\left( {m_{\max }^{obs} } \right)$. Maximum estimated magnitude $\left( {\hat{m}_{\max } } \right)$ appears on both sides of the governing expression in the first four methods [(a) to (d)], and hence, an iterative scheme is adopted with initial guess as $\hat{m}_{\max } = m_{\max }^{obs}$. Care should be exercised while implementing these methods: any one or even more of these methods may not necessarily converge owing to the incompleteness or insufficient number of events in some catalogues leading to unrealistic estimates of maximum magnitude even exceeding 10 and such cases should be discarded.

• B. Maximum observed magnitude + 0.5 (Gupta, 2002)

This is the simplest method recommended by Gupta (2002) for the maximum magnitude of a source zone:

$$\hat{m}_{\max } = m_{\max }^{obs} + 0.5$$

(37)

• III. Proportional to fault length

Maximum magnitude of earthquake depends on fault area (Wyss, 1979) and hence may be considered proportional to the fault length in some sense. Maximum magnitude for the$j^{th}$ fault of length $L_{f}^{j}$ is proposed in this paper as the third alternative:

$$m_{\max }^{j} = \hat{m}_{\max }^{3} - m_{0} \left( {1 - {{L_{f}^{j} } \mathord{\left/ {\vphantom {{L_{f}^{j} } {L_{f}^{\max } }}} \right. \kern-\nulldelimiterspace} {L_{f}^{\max } }}} \right);\,\,\,\,m_{0} = \hat{m}_{\max }^{3} \left[ {{{L_{f}^{{{\text{m}} edian}} } \mathord{\left/ {\vphantom {{L_{f}^{{{\text{m}} edian}} } {L_{f}^{\max } }}} \right. \kern-\nulldelimiterspace} {L_{f}^{\max } }}} \right].$$

(38)

Here, $\hat{m}_{\max }^{3}$ is the larger of the above two methods; $L_{f}^{\max }$ and $L_{f}^{{{\text{m}} edian}}$ are maximum and median length of all the faults in a source zone. Maximum magnitudes estimated by the first and second methods considered here are summarized in Table 6 along with larger of the two. Note that the third method allows different maximum magnitudes in the faults located even within the same source zone and hence is not included in Table 6.

Table 6 Maximum magnitude for all the source zones by different methods

4.4.1 Weight Calculation for Maximum Magnitude

Weight associated with each alternative of maximum magnitude may be calculated in a similar way as explained with the distance probability model. A set of 12 possible combinations (four for each alternative of maximum magnitude, i.e., two for magnitude distributions with two for recurrence parameters) are considered. The framework is applied over the entire study area considering the events within the magnitude interval $Min\left( {\hat{m}_{\max }^{1} ,\hat{m}_{\max }^{2} } \right) - 1.5\sim m_{\max }^{obs}$ for respective source zones. Log-likelihood is estimated as follows:

$$LLH_{{f\left( {m\left| {\hat{m}_{\max }^{l} } \right.} \right)}} = - \frac{1}{{N_{sc} }}\left[ {\sum\limits_{j = 1}^{2} {\sum\limits_{k = 1}^{2} {\sum\limits_{i = 1}^{{n_{e} }} {log_{B} \left\{ {f_{j} \left( {m_{i} \left| {\hat{m}_{\max }^{l} ,\beta_{k} } \right.} \right)dm_{i} } \right\}} } } } \right]\,\,;{\text{ with}}\,l = 1,2,3.$$

(39)

Here, $n_{e}$ is the number of events within the magnitude range considered and $N_{sc} = 2 \times 2 \times n_{e}$ denotes the total sample count. Weights associated with each alternative of maximum magnitude is given by

$$W_{{\hat{m}_{\max }^{l} }} = \frac{{B^{{ - LLH_{{f\left( {m\left| {\hat{m}_{\max }^{l} } \right.} \right)}} }} }}{{\sum_{l = 1}^{3} {B^{{ - LLH_{{f\left( {m\left| {\hat{m}_{\max }^{l} } \right.} \right)}} }} } }}.$$

(40)

Sample illustration of an MHC contributed from a typical branch of logic tree and its weight calculation is explained in the next section.

5 Typical Model Hazard Curve and Weight Calculation

Construction of a typical model hazard curve with weight calculation is explained in the Sect. 2. This section presents one sample illustration for better clarity.

5.1 Model Hazard Curve

Hazard integral or PSHA computational framework in terms of discrete summations can be expressed as (Kramer, 1996)

$$\lambda \left( {\ln Sa\left( {T^{ * } } \right) > \ln Sa^{ * } } \right) = \sum\limits_{i = 1}^{{N_{S} }} {\sum\limits_{j = 1}^{{N_{M} }} {\sum\limits_{k = 1}^{{N_{R} }} {\nu_{i} \left( {m_{\min } } \right)P\left( {\ln Sa\left( {T^{ * } } \right) > \ln Sa^{ * } \left| {m_{j} ,r_{k} } \right.} \right)} } } f\left( {m_{j} ,r_{k} } \right)\Delta m\Delta r.$$

(41)

Here, $N_{S}$ represents the number of potential earthquake sources in a region around the site; $N_{M}$ and $N_{R}$ are the number of discrete magnitude and distance segments considered in the$i^{th}$ potential earthquake source; $\nu_{i} \left( {m_{\min } } \right)$ is the mean annual rate of exceedance of events with magnitude greater than $m_{\min }$ in the$i^{th}$ source; $P\left( {\ln Sa\left( {T^{ * } } \right) > \ln Sa^{ * } \left| {m_{j} ,r_{k} } \right.} \right)$ is given by GMPE for an earthquake of magnitude $Mw = m_{j}$ triggered at a distance of $R_{jb} = r_{k}$; and $f\left( {m_{j} ,r_{k} } \right)\Delta m\Delta r$ is the probability of triggering an earthquake of magnitude $m_{j}$ at a distance of $r_{k}$. In the case of magnitude-independent distance probability distribution, $f\left( {m_{j} ,r_{k} } \right) = f\left( {m_{j} } \right)p\left( {r_{k} } \right)$ with $f\left( {m_{j} } \right)$ and $p\left( {r_{k} } \right)$ as the probability density functions of magnitude and distance, respectively, given by Eq. (22)/Eq. (23) and Eq. (28) with $X\left( m \right) = 0$, respectively. In the case of magnitude-dependent distance probability distribution, $p\left( {r_{k} } \right)$ is replaced by $p\left( {r_{k} \left| {m_{j} } \right.} \right)$, which can be obtained from the first derivative of Eq. (28).

In this study, North-east India is divided into two types of source zones, namely, SZ and ACR, which are further subdivided into two and five source zones, respectively. Referring to Fig. 1a, one branch of the logic tree with the following details is considered here for sample illustration: (i) magnitude-independent distance probability distribution; (ii) recurrence parameters using straight line method; (iii) magnitude distribution by Gutenberg-Richter (1944); and (iv) maximum magnitude as $m_{\max }^{1}$(Table 6). This explains one alternative for the first four nodes of the logic tree, which is defined as ERF (Sect. 2.1). The selected ERF is further divided into a set of SERFs conforming to the GMPE rule (Sect. 2.2).

Rate of exceedance of an intensity measure given a threshold, $\lambda \left( {\ln Sa\left( {T^{ * } } \right) > \ln Sa^{ * } } \right)$ (denoted as $\lambda$ hereafter for brevity) is first computed by summing up the contributions from all the potential sources in SZ around a particular site considering (i) ERF as above and (ii) BCHY16 (Table 1) as the GMPE. Next, $\lambda$ contributed by the potential sources of ACR with same ERF and all four GMPEs (in ACR) are computed separately followed by taking a weighted (Table 1) sum. Total exceedance rate is given by the sum of the two computed above. Repeating the same procedure for different values of threshold intensity measure $\left( {\ln Sa^{ * } } \right)$ enables the construction of one MHC corresponding to a single terminal branch of the logic tree.

Further, GMPEs considered in this computation if uses the source-to-site distance other than $R_{jb}$, a conversion of distance metric is performed prior to using the GMPE: $R_{jb}$ is converted into (i) $R_{rup}$ and $R_{hypo}$ using the algorithm of Kaklamanos et al. (2011); and (ii) $R_{epi}$ using the recommendation of Tavakoli et al. (2018).

5.2 Weight Calculation

Weight associated with each MHC $\left( {w_{MHC} } \right)$ is required for the computation of weighted mean representation of rate hazard curve. With reference to Fig. 1, for the same MHC considered above, $w_{ERF} = 0.43 \times 0.46 \times 0.55 \times 0.339 = 0.0368$ and $w_{SERF} = 0.28 \times 0.51 = 0.1428$. Therefore, weight of the MHC is computed as $w_{MHC} = 0.0368 \times 0.1428 = 5.266 \times 10^{ - 3}$.

6 Results and Discussion

PSHA is performed in the companion paper using the logic tree approach to consider the possible effects of epistemic uncertainty. The sources of epistemic uncertainty considered are the (i) recurrence parameters, (ii) magnitude distribution, (iii) distance probability distribution, (iv) maximum magnitude and (v) selection of GMPEs. PSHA is carried out for three NEHRP soil sites of class B (V_s30 760–1500 m/s), C (V_s30 360–760 m/s) and D (V_s30 180–360 m/s) with an average shear wave velocity of 1100, 550 and 250 m/s, respectively. Only one sample illustration of PSHA results out of 112 district headquarters of seven states in North-east India is reported in this paper in terms of the weighted mean and fractile representation of hazard curves and UHS for brevity (50th, 84.13th and 99.86th percentile). Computation of weighted mean and fractile representation of hazards may lead to an alternate perspective of ‘importance factor’ used in seismic design. As opposed to a structure specific decision, importance factor is likely to be dependent on the natural period and seismicity of the location as well. Further exploration of PSHA results and the ‘importance factor’ is reported in the companion paper.

6.1 Weighted Mean and Fractile Representation of Hazard Curves

A typical MHC represents the mean annual rate of exceedance of a selected intensity measure at a particular site. Several MHCs can be generated from various terminal branches of the logic tree as a possible alternative. A sample illustration of the MHCs (peak ground acceleration, PGA, T = 0) at site class B for Champhai district in Mizoram is presented in Fig. 8a as an outcome from different branches of the logic tree. Thick outer lines indicate the spread of the hazard curves. Figure 8b represents the weighted mean and different fractile estimates of the hazard curves illustrated in Fig. 8a. Both IM and rate hazard curves resulting from horizontal and vertical dissections, respectively, are included in Fig. 8b.

Fig. 8

Hazard curves at Site class B, T = 0 for Champhai (Mizoram)

Variation in the ratio of mean annual rate of exceedance of IM to rate hazard curves (Fig. 8b) with respect to IM is presented in Fig. 9a. Similarly, Fig. 9b presents the variation in the ratio of intensity measures from IM to rate hazard curves (Fig. 8b) with respect to the mean annual rate of exceedance. As evident from the Figs. 9a and b, the choice of IM or rate hazard does not affect the fractile representation of MHC. Similar comparison is also included in Fig. 9 for the weighted mean representation of MHC which is somewhat sensitive to the definition of IM vs. rate hazard. Hence, care should be exercised while selecting and adopting the weighted mean representation of hazard, which is governed by the end objective such as characterization of seismic hazard and estimation of collapse fragility.

Fig. 9

Difference between weighted mean and fractile representation of hazard curves due to horizontal and vertical dissection at Site class B, T = 0 for Champhai (Mizoram)

The end objective in this paper is to estimate the design seismic hazard, and hence, the horizontal dissection is chosen with IM as a random variable conditioned to a mean annual rate of exceedance. Therefore, weighted mean and any percentile/fractile representation of IM will be referred to as weighted mean and percentile/fractile representation of hazard (dropping IM) hereafter for brevity.

6.2 Uniform Hazard Spectra

Given one terminal branch of the logic tree, the hazard curves are constructed using spectral ordinates at different periods as the IM. The spectral ordinates, when plotted against the time periods conditioned to a mean annual rate of exceedance, result in the UHS associated with the considered terminal branch of the logic tree. Similarly, UHS associated with all branches of the logic tree are constructed. Figure 10a presents a sample illustration of 2475 years UHS for the Champhai district in Mizoram with site class B while thick outer lines indicate the spread. Figure 10b presents the associated weighted mean and different fractile estimates (by vertical dissection) of the UHS. Similar studies are carried out in the companion paper for all of North-east India for all three site classes (B, C and D) and at both MCE and DBE levels.

Fig. 10

Uniform hazard spectra (UHS) at Site class B, 2%PE in 50 years, for Champhai (Mizoram)

6.3 Results Presented in the Companion Paper

This paper presents the framework for conducting PSHA considering possible sources of epistemic uncertainty using the logic tree approach. The framework is implemented over the north-east region of India. Only one sample illustration is presented here to explain the application of the proposed framework. Detailed comparison of results with previous studies and Indian standard recommendations, in terms of weighted mean representation of PGA hazard and UHS for NEHRP soil types B, C and D at DBE are presented in the companion paper. Further, a hazard map of the complete region is prepared by dividing the area in a grid spacing of 0.1° (about 10 km). Two return periods (MCE and DBE) with three soil types are considered and maps are presented in Appendix 2 of the companion paper. Ratio of fractile-to-weighted mean representation of hazard is presented as an alternative viewpoint of importance factor used in the seismic design. Weighted mean and fractile representation of target conditional spectra (CS) with different conditional time periods (0.2–1.6 s in increments of 0.2 s) are also estimated by two methods (GCR-CS and GCIM-CS, considering GMPE specific generalized causal rupture and all contributing causal ruptures, respectively) using the logic tree approach and results are compared. Weighted mean representation of target CS (mean and standard deviation) are calculated at 112 district headquarters, but only mean spectra (without standard deviation) are reported in the Appendix 3 of the companion paper.

7 Conclusion

A framework is developed for PSHA to account for the contribution from possible sources of epistemic uncertainty that includes (i) recurrence parameters, (ii) magnitude distribution, (iii) distance probability distribution, (iv) maximum magnitude and (v) selection of GMPEs. The log-likelihood approach is employed to arrive at the weights associated with various contributors of epistemic uncertainty. A somewhat different approach is applied for the recurrence parameters and weights are assumed to be inversely proportional to the mean squared error. A GMPE rule is proposed to be used with the PSHA framework to account for the propagation of epistemic uncertainty. A procedure is also developed for computing the weights associated with the MHCs. The weighted mean representation of hazard is calculated by taking weighted sum of IM as outcome from various branches of the logic tree. Similarly, fractile estimate is used to construct the fractile representation of hazard.

Following are the key contributions/conclusions of this paper based on the limited investigation carried out:

• 1. Relevant guidelines are proposed for the weight calculation at each node of the logic tree (except for GMPEs) to minimize the subjectivity based on the degree of belief of the analyst.

• 2. A GMPE rule is proposed to account for the propagation of epistemic uncertainty.

• 3. Characterization of seismic hazard in terms of weighted mean and fractile representation of hazard with a new interpretation of importance factor in seismic design is envisioned.

• 4. Horizontal or vertical dissection of the hazard curves should be determined based on the end objective. While the fractile representation of hazard remains insensitive, weighted mean representation of hazard is somewhat sensitive to the choice of dissection.

Some of the contributors of epistemic uncertainty such as Vs30 and fault rupture characteristics are not included in the proposed framework.