Keywords

1 Introduction

Flow-induced deformation of flexible plates is ubiquitous. There are plenty of natural and artificial examples of such systems: from aquatic vegetation to flexible blades. These systems inspire many engineering applications such as drag reduction by flow-induced reconfiguration, wind energy harvesting from flow over flexible blades. Many researchers have attempted to model and simulate these problems from both static and dynamic perspectives. For instance, [1] and [2] studied the drag variation as a function of the fluid flow velocity. For bluff bodies, the drag and square of velocity ratio scales as the zeroth velocity power, i.e., \(D/U^{2} \;\alpha \;U^{0}\), where D is the drag force, and U is flow velocity. They suggested that this relation gets modified for flexible bodies as \(D/U^{2} \;\alpha \;U^{e}\), where e is an exponent that can be treated as a measure of reconfiguration. They collected numerous data on plants, such as potted pines, and concluded that e = −1.13 for speeds above 6 m/s. Luhar and Nepf [3] worked in the same field by using a combination of experiments and theoretical models. They developed an Euler–Bernoulli beam model for static analysis of flexible plants. A balance between drag force, buoyancy, and beam inertia results in a second-order ordinary differential equation that can be solved to find the relation between drag force and flow velocity. Later, [4] modified the same model by adding the role of skin friction. Leclercq and de Langre [5] developed an analytical model to quantify the drag reduction for flexible cantilever beams. They predicted the value of the Vogel exponent that quantifies the drag reduction in such configurations.

The dynamic characteristics of these systems have also been explored vastly. Py et al. [6] studied the dynamic interaction between the waves and crop. They developed a lock-in mechanism model and compared its output with experimental results. De Langre [7] presented a review on the flow-structure interaction between plants and wind, where he examined the dynamics of plants when they are strongly coupled to the wind. He performed this analysis by modifying the elementary oscillator model using wind load to understand the modal response of plants. Luhar and Nepf [8] performed a combination of experimental and numerical studies to describe the motion of flexible blades that imitate the dynamic behavior of aquatic vegetation. They considered two main parameters in their study: (i) Cauchy number (Ca), and (ii) the blade length to wave travel ratio. The studies were performed for Ca << 1 and Ca >> 1. Zhang et al. [9] investigated the dynamic behavior of wall-mounted 2D flexible filaments (single and double). They demonstrated the frequency lock-in with different structural modes and explained the physical driving mechanisms.

With the understanding gained from these studies, there have been many attempts to develop energy harvesting models to utilize wave energy by applying these systems. Yu et al. [10] presented a review on the energy extraction from flag vibrations. They studied the vibration and vortex dynamics of the proposed system to understand their feasible practical applications. They assert that flag vibrations are a good energy solution to provide power in various industrial applications. Shoele and Mittal [11] developed a numerical model of an inverted piezoelectric flag. They examined the dynamic response of the inverted flag and investigated its energy harvesting performance.

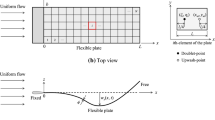
In most studies, the plate is analyzed in a wall-mounted configuration [5,6,7, 9]. We propose a fixed bottom of the plate, but not mounted to the wall as shown in Fig. 1. This arrangement allows the flow at both top and bottom of the plate, and the flow energy consumption in boundary layer formation near wall is eliminated. It results in a lower critical Re for the onset of flow-induced plate vibrations [9]. As a result, maximum flow energy is utilized in plate vibrations. Such arrangement is useful where intensive plate vibrations are required at low Re such as energy harvesting.

Fig. 1
An illustration depicts a rectangular computational domain with dimensions and boundary conditions marked for the four sides. A flexible plate with dimensions marked is displayed within the computational domain.

Schematic of the computational domain with respective dimensions and boundary conditions

Full size image

2 Computational Model

We use an in-house, partition approach-based fluid–structure interaction (FSI) solver with a two-way coupling between the fluid and solid domains. Fluid is solved over an Eulerian mesh while the structure solver uses the Lagrangian framework. Details of the fluid and structural solver used are as follows.

2.1 Fluid Dynamics

The 2D unsteady, incompressible Navier–Stokes equations are solved along with the continuity equation (Eqs. 1 and 2) using a sharp interface immersed boundary (IB) method-based flow solver developed by [12]. This IB method is based on the ghost cell methodology and uses a Cartesian grid for computations. Discretization in space is done on a cell-centered collocated grid using the finite difference method, and the fractional step method is used for time marching. The flow solver is implemented in two steps: (i) solving the advection–diffusion equation using the Crank-Nicolson scheme, and (ii) solving the pressure Poisson equation using the geometric multigrid method with divergence-free velocity constraint. The method is verified and tested for second-order accuracy [12].

$$\frac{{\partial u_{i} }}{\partial t} + u_{j} \frac{{\partial u_{i} }}{{\partial x_{j} }} = - \frac{\partial p}{{\partial x_{i} }} + \frac{1}{{\text{Re}}}\frac{{\partial^{2} u_{i} }}{{\partial x_{j} \partial x_{j} }}$$
(1)
$$\frac{{\partial u_{i} }}{{\partial x_{i} }} = 0$$
(2)

where \({\text{Re}} = \frac{{\rho_{{\text{f}}} U_{\infty } L}}{\mu }\).

2.2 Solid Dynamics

The structural solver is an open-source finite element solver [13] that was developed at Sandia National Labs, CA. Using it, we solve 2D Navier's equations of motion (Eq. 3) for plane strain condition. We use the Saint Venant-Kirchoff material model to simulate large solid deformations accurately. In this model, the solid is treated as a (i) geometrically nonlinear, (ii) linear elastic material. The constitutive relation and the Second Piola-Kirchoff stress expressed as a function of Cauchy stress is shown in Eq. 4. The Green-Lagrangian strain tensor is written as a function of the deformation gradient as shown in Eq. 5.

$$\rho_{{\text{s}}} \frac{{D^{2} d_{i} }}{{D t^{2} }} = \frac{{\partial \sigma_{ij} }}{{\partial x_{j} }} + \rho_{{\text{s}}} f_{i}$$
(3)
$$S = \lambda tr(E) I + 2 \mu E \hspace{0.2cm}; \hspace{0.4cm} S = JF^{ - 1} \sigma F^{ - T}$$
(4)
$$E = \frac{1}{2}(F^{{\text{T}}} F - I)$$
(5)

2.3 Coupling of the Flow and Structural Solvers

The fluid and structural solvers are coupled using an implicit strong coupling (see details in Ref. [14,15,16]). The FSI field is solved numerically using a partitioned approach where fluid and solid domains are solved alternately with interface boundary conditions. For the flow field, a one-time step is marched to obtain the updated pressure and velocity field with the current deformed shape of the solid. The updated flow field is used to solve the structural dynamics then. At the interface, the continuity of velocity and traction is maintained as given by Eqs. 6 and 7, respectively. These interface conditions are forced as boundary conditions while marching in time for fluid and solid.

$$u_{{\:i,\:{\text{fluid}}}} = \dot{d}_{{\:i,\:{\text{solid}}}}$$
(6)
$$\sigma_{{ij,\:{\text{fluid}}}} \,n_{j} = \sigma_{{ij,\:{\text{solid}}}} \,n_{j}$$
(7)

2.4 Key Parameters

The geometry and material properties of the plate primarily govern its dynamic response. We consider two such parameters viz. (i) bending stiffness (Eq. 8), and (ii) mass ratio (Eq. 9). We perform the simulations at different values of bending stiffness. These values are obtained by varying the non-dimensional Elasticity (E) and keeping all other parameters constant. We study this dynamic problem concerning reduced velocity, \(U_{{\text{R}}}\) (see Eq. 10). It's a dimensionless parameter representing the ratio of solid to fluid dynamics time scales. The chosen time scale for fluid is the convective time scale. For the solid, the dynamic time scale is the inverse of its natural frequency. Natural frequencies of the plate in vacuum are calculated by treating it as an Euler–Bernoulli beam (Eq. 11). We focus on the first and second modes and ignore the higher modes for the present work. It should be noted that the consideration of natural frequencies in vacuum is an approximation since the plate natural frequencies are modulated by various effects due to the presence of a surrounding fluid: (i) added mass effect, (ii) flow-induced damping effect, (iii) added stiffness due plate curvature in its mean position, and (iv) nonlinear effect due to large amplitude oscillations. Zhang et al. [9] argued that the added mass and flow-induced damping tend to decrease the plate natural frequency while added stiffness effect increases the same. Both cancel each other’s effect to some extent, however, implications of nonlinear effects are hard to analyze theoretically. As a result, the natural frequencies in vacuum are approximate plate natural frequency values that are used in this study to compare with the plate's oscillation frequency and analyze its response.

$$K_{{\text{b}}} = \frac{E}{{\rho_{{\text{f}}} U_{\infty }^{2} }}\frac{{h^{3} }}{{12L^{3} }}$$
(8)
$$M = \frac{{\rho_{{\text{s}}} h}}{{\rho_{{\text{f}}} L}}$$
(9)
$$U_{{\text{R}}} = \sqrt {\frac{M}{{K_{{\text{b}}} }}} \left( {\sim \frac{{fn_{{{\text{fluid}}}} }}{{fn_{{{\text{solid}}}} }}\sim \frac{{T_{{{\text{solid}}}} }}{{T_{{{\text{fluid}}}} }}} \right)$$
(10)
$$f_{ni} = \frac{{k_{i}^{2} }}{2\pi L}\sqrt {\frac{{K_{{\text{b}}} }}{M}}$$
(11)

For post-processing of the obtained data, we define an angle \(\theta\) concerning the probe point \((x,y)\) and reference coordinates of the beam \((x_{0} ,y_{0} )\) as shown in Fig. 2. This transformation is similar to the \(\theta\) definition presented by [9] in their study of wall-mounted flexible plates. However, they defined \(\theta\) from the X-axis while we take \(\theta\) as the angular deformation from its initial vertical position. The probe is installed at the tip of the plate with coordinates (x, y) = (20.05, 19.00) at time t = 0. As the solid deforms, the global coordinates of this point change, but it remains fixed locally to the solid. We use this transformation to move from XY space to the \(\theta\) space for calculating the plate frequency, \(f_{p}\) and amplitude of vibrations, \(A_{\theta }\). The amplitude is now defined as \(A_{\theta } ( = \Delta \theta /2)\) instead of \(\Delta X\) and \(\Delta Y\) separately, and it’s calculated as the peak to peak amplitude. Since \(\theta\) depends on both X and Y-coordinates of the probe point, it results in an advantage of accounting both X and Y parameters into one.

Fig. 2
An illustration presents a flexible plate that is bent with the location of the probe point indicated on the top, which is represented on a graph. The angles of theta bar and delta theta with respect to the mean position are indicated.

Location of the probe point, and moving from XY space to \(\theta\) space for the plate oscillation frequency \((f_{{\text{p}}} )\) and amplitude (\(A_{\theta }\)) calculation

Full size image

3 Validation and Testing

3.1 Grid and Domain Size Independence Test

The grid and domain independence tests are performed at Re = 100. The chosen parameters for the solid are: (i) modulus of Elasticity, E = 400, (ii) Poisson's ratio, \(\nu = 0.4\), (iii) Mass ratio, M = 1. The test cases are compared using the root means square (RMS) displacements (both X and Y) of the probe point (see Fig. 2). First, a benchmark case is simulated with a domain size of \(75 \times 50\), a minimum grid size of 0.01 \((\Delta x = \Delta y)\) close to the plate, and a time step size of 0.005. During both tests, it serves as the reference solution for computing the relative errors.

For the domain independence test, all the domains consist of a minimum grid size of 0.02 \((\Delta x = \Delta y)\) and a time step size of 0.01. The domain sizes are varied in both x and y directions, as shown in Table 1. For all simulations, the CFL number is retained well below 1 to ensure numerical stability. The chosen domain size for further simulations is \(60 \times 40\) with an error below 1%.

Table 1 Domain independence test for minimum grid size 0.02. % Error is computed with respect to the benchmark case
Full size table

The grid independence test is performed over a domain size \(60 \times 40\) and a time step size of 0.01. Three different grid sizes are chosen, and errors are compared with the benchmark case as shown in Table 2. The selected grid size for further simulations is min. \(\Delta x = \Delta y = 0.02\).

Table 2 Grid independence test for domain size 60x40. % Error is computed with respect to the benchmark case
Full size table

3.2 Code Validation

We use a FORTRAN code that is based on the sharp interface immersed boundary method developed by [12]: see Sect. 2.1 for details of the method. The code has been validated extensively in previous literature. The flow solver has been validated by [12] using a combination of 2D and 3D problems, to name a few, flow past: (i) circular cylinder, (ii) sphere, (iii) suddenly accelerated normal plate, etc. The solver has been further extended for flexible body deformation (see Sect. 2.2 for details) by [14]. Bhardwaj and Mittal [14] and Kundu [15] validated the same using the benchmark problem ‘flow over splitter plate attached to a cylinder’ proposed by Turek and Hron [17]. They demonstrated that the structural solver is capable of accurately simulating large-scale deformation problems.

4 Results and Discussion

We perform simulations by varying the plate's modulus of Elasticity, E in a range of [\(2 \times 10^{5} ,365\)] keeping all other parameters constant. It results in a variation of plate bending stiffness \((K_{{\text{b}}} )\) and reduced velocity (\(U_{{\text{R}}}\)). As these parameters change, the dynamic response of the plate changes. We track the coordinates of the probe point (see Fig. 2) and use this data to compute the oscillation frequency and amplitude of vibrations as explained in Sect. 2.4.

4.1 Frequency and Lock-In Characteristics

Flow over the plate results in vortex shedding from its top and bottom, as shown in Fig. 3. The vortices are shed in a C(2S) pattern at low values of \(U_{{\text{R}}}\) where coalesced vortices of similar signs are shed that are arranged in two distinct rows. At large values of \(U_{{\text{R}}}\), the plate becomes very soft and is streamlined to the flow. As a result, the vortex shedding modifies to a 2S pattern in which two single vortices are shed in an opposite sense of rotation per cycle. The alternately shedding vortices are a result of the competing inertia and viscous forces that impose a periodic forcing on the plate. Due to this phenomenon, the plate bends at a certain angle and starts to oscillate about a curved mean position as shown in Fig. 2. The mean position of plate, \(\theta\) depends on the chosen modulus of Elasticity (E): softer the plate (represents a low value of E), larger its mean position.

Fig. 3
Five contour models depict the intensity of reduced velocity for plate deformation at values of U R equals 1.55, U R equals 3.46, U R equals 8.28, U R equals 12.57, and U R equals 17.11.

Vorticity contours along with instantaneous plate deformation at selected values of reduced velocity, \(U_{{\text{R}}}\) for a fully developed flow

Full size image

The dynamic response of the plate is captured by the peak to peak amplitude (\(A_{\theta }\)) and frequency (\(f_{{\text{p}}}\)) of its vibrations as shown in Figs. 4 and 5, respectively. Figure 4 demonstrates the variation in plate amplitude (\(A_{\theta }\)) with \(U_{{\text{R}}}\). On the other hand, in Fig. 5, we plot the amplitude spectral density (ASD) of the displacement signal (\(\theta\)) without any normalization. The contours represent the spectrum of plate oscillation frequency (\(f_{{\text{p}}}\)) with varying reduced velocity (\(U_{{\text{R}}}\)). Histogram distribution is used on a uniform frequency scale (\(\Delta f = 0.025\)) for interpolating the frequencies. The cut off lowest frequency shown on the plot is 1% of the maximum oscillation frequency. A logarithmic scale is used for plotting the color map, and its normalized with the maximum frequency. Darker contour areas represent a dominant output frequency and vice-versa, at any value of \(U_{{\text{R}}}\). In addition to this, we compute the first and second-mode natural frequencies of the plate (\(f_{n1}\) and \(f_{n2}\), respectively) using Euler–Bernoulli beam theory (see Eq. 11) and plot them as solid red and blue lines, respectively, on the same plot. The resulting plot demonstrates the lock-in/de-synchronization behavior of the system with first/second natural modes as \(U_{{\text{R}}}\) changes. Both plots (i.e., Figs. 4 and 5) are shown on the same scale of the \(U_{{\text{R}}}\) to demonstrate the variations in plate amplitude as the frequencies lock-in or de-synchronize. We qualitatively identify four regions as follows:

Fig. 4
A line graph plots amplitude versus reduced velocity. The line plotted for A theta depicts a fluctuating pattern at the initial stage that spikes thereafter.

Variation in amplitude of the plate vibrations \(A_{\theta }\) with respect to reduced velocity, \(U_{{\text{R}}}\)

Full size image
Fig. 5
A line graph plots frequency versus reduced velocity. The lines plotted for f n 1 and f n 2. Both lines depict a downward trend.

Contour plot for plate's frequency response with \(U_{{\text{R}}}\). The first and second mode plate natural frequency lines (\(f_{n1}\) and \(f_{n2}\)) are drawn in red and blue, respectively

Full size image

Region 1: Lock-in with first mode: It’s a small reduced velocity, \(U_{{\text{R}}}\), region where the plate's modulus of Elasticity, E is high (order of \(10^{4}\)). Lock-in with the first mode occurs for a range \(U_{{\text{R}}} \approx (2.0,4.9)\). In this range, the amplitude starts to increase from a value of \(0.7^{^\circ }\). At \(U_{{\text{R}}} \approx 3.5\), the observed plate amplitude is maximum, i.e., \(3.52^{\circ }\).

Region 2: De-synchronization: As we further reduce E (order of \(10^{3}\)), the plate becomes softer and it de-synchronizes with its first mode. The amplitude drops back to around \(1^{\circ }\). This starts to occur at \(U_{{\text{R}}} \approx 4.9\). The plate keeps oscillating for a large range of \(U_{R}\) where it does not lock-in with any other mode. The observed range of this de-synchronized plate vibrations is \(U_{R} \approx (4.9,13.0)\). We also observe secondary dominant frequencies in the range \(U_{{\text{R}}} \approx (5.0,10.5)\). The physics behind the presence of these secondary dominant frequencies in this \(U_{{\text{R}}}\) range is yet to be explored.

Region 3: Lock-in with second mode: With a further reduction in E (order of \(10^{2}\)), the plate becomes very soft and starts to show large deformations. At \(U_{{\text{R}}} \approx 13.6\) the plate response frequency reaches closer to its second-mode natural frequency and lock-in with second mode is observed. As a result of this lock-in, amplitude of vibrations again starts to increase with \(U_{{\text{R}}}\). At \(U_{{\text{R}}} \approx 18.13\) plate completely locks in with its second mode and a peak amplitude of \(7.54^{^\circ }\) is noted. This amplitude is almost three times the amplitude in first-mode lock-in. This is understandable by the fact that the plate is softer in the second-mode lock-in as compared to the first-mode lock-in, and is expected to show larger deformations.

Region 4: De-synchronization: The plate remains locked in with its second mode for a larger range of \(U_{{\text{R}}} \approx (14.8 - 20)\). Above \(U_{{\text{R}}} = 20\) the plate becomes extremely soft (\(E \approx 150\)) and very large deformations occur. Due to a very low mass ratio (M) and modulus of Elasticity (E), the simulations become hard to be handled by our solver at very high \(U_{{\text{R}}}\). Due to this, for now, we limit our simulations to \(U_{{\text{R}}} = 20\) for maintaining accuracy. However, we are investigating other parametric combinations to achieve high \(U_{{\text{R}}}\) simulation cases as a part of our future plans. It is expected that the plate should de-synchronize with the second mode at a high value of \(U_{{\text{R}}}\).

5 Conclusions

In this study, we investigated the flow-induced vibrations of a flexible plate in a 2D incompressible flow field. The vortex shedding patterns were examined to understand the onset of plate vibrations. The amplitude and frequency response of these vibrations were plotted, and insights were given into the plate dynamics concerning its first and second-mode natural frequencies with reduced velocity. We found that the plate response is similar to the vortex-induced vibrations (VIV) of elastically mounted rigid cylinder. Similar to the VIV, plate response is divided into various regions. In these regions, the plate locks in and de-synchronizes with its first and second-mode natural frequencies as the reduced velocity changes. Overall, the plate exhibits rich dynamics that later has been further investigated [18] for potential practical applications such as energy harvesting and drag/lift optimization.