Modelling of a Cantilevered Flexible Plate Undergoing Large-Amplitude Oscillations Due to a High Reynolds-Number Axial Flow

Abstract

We present a new model of the nonlinear fluid-structure interaction of a cantilevered flexible plate with an ideal flow that can account for the effect of boundary-layer separation from the plate surface upstream of its trailing edge. Short plates are studied herein for which the behaviour is dominated by low-order structural modes. When the wake is forced to form from the trailing edge the typical sequence of amplitude growth to nonlinearly saturated oscillations at flow speeds above that of the onset of linear instability is found. However, if separation is included the system evidences the same sequence at a flow speed for which the system is neutrally stable to linear disturbances. This suggests that flow separation may be the cause of the sub-critical instability found in experimental studies of the system.

1 Introduction

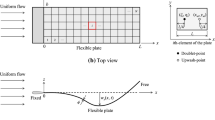
A new model is developed of the nonlinear fluid-structure interaction (FSI) of a cantilevered flexible plate of length L in uniform axial flow of velocity $U_{\infty }$ as depicted in Fig. 1. Inviscid flow is assumed and therefore the FSI model approximates the very high Reynolds number flows that predominate in engineering applications. However, viscous effects are implicitly incorporated either through the imposition of the Kutta condition at the plate’s trailing edge or through boundary-layer separation (as drawn in Fig. 1) that can occur in an adverse pressure gradient upstream of the trailing edge. Previous approaches have modelled this FSI system using the former whereby the wake forms from the trailing edge and in Tang and Païdoussis (2007, 2008) is assumed to follow a sinusoidal path following the spatio-temporal characteristics of the plate motion. Therefore, the main purpose of this paper is to determine the effect of flow separation on the nonlinear stability of the FSI system by comparing its results with those in which the boundary-layer vorticity is assumed to remain attached on both sides for the full length of the flexible plate.

Fig. 1

Schematic of the fluid-structure system studied and the approach taken to model separation

2 Method

The present solution of the Laplace equation utilises a non-linear boundary-element flow solution similar to that developed in Lucey et al. (1997) and is an extension of the second-order linear boundary-element method detailed in Howell et al. (2009) so as to capture finite-amplitude effects. The flexible plate is discretised into N panels each of length $\delta s=L/N$ and the vector of nonlinear vortex strengths, ${\gamma }$, for the N panels is found by imposing the no-flux condition giving

$$\begin{aligned} \lbrace \gamma \rbrace = [\mathbf {I^N}]^{-1}\lbrace U_\infty \sin \theta + \dot{\eta }\cos \theta - \dot{x}\sin \theta + u^{T_b}\sin \theta - u^{N_b}\cos \theta \rbrace , \end{aligned}$$

(1)

where $\theta$ is the panel angle relative to $y=0$ and $\dot{x}$ and $\dot{\eta }$ are respectively the velocities of each panel control point in the x- and y-directions. $u^{N_b}$ and $u^{Tb}$ are respectively the normal and tangential velocities induced at the panel control points by the discrete vortices of the wake. $[\mathbf {I^N}]$ comprises the normal influence coefficients. The nonlinear version of the Euler-Bernoulli beam equation, presented in Tang and Dowell (2002), is

$$\begin{aligned} \delta p&= \rho h \ddot{\eta }_s - \rho h \frac{\partial \eta }{\partial s} \int ^s_0 \left( \left( \frac{\partial ^2 \eta }{\partial t \partial s}\right) ^2 +\frac{\partial \eta }{\partial s}\frac{\partial ^3 \eta }{\partial t^2 \partial s}\right) \mathrm{d} s \nonumber \\&\quad - \rho h \frac{\partial ^2 \eta }{\partial s^2} \int ^L_s \int ^s_0 \left( \left( \frac{\partial ^2 \eta }{\partial t \partial s}\right) ^2 + \frac{\partial \eta }{\partial s}\frac{\partial ^3 \eta }{\partial t^2 \partial s} \right) \mathrm{d}s \mathrm{d}s \nonumber \\&\,\,\,\, \ \ + \ B \left[ \frac{\partial ^4 \eta }{\partial s^4} + \frac{\partial ^4 \eta }{\partial s^4} \left( \frac{\partial \eta }{\partial s}\right) ^2 + 4\frac{\partial \eta }{\partial s}\frac{\partial ^2 \eta }{\partial s^2}\frac{\partial ^3 \eta }{\partial s^3} + \left( \frac{\partial ^2 \eta }{\partial s^2}\right) ^3 \right] , \end{aligned}$$

(2)

where $\rho$, h, and B are the plate density, thickness, and stiffness respectively. This model is based upon the assumption that the plate is inextensible; thus, L and therefore $\delta s$ are constant. To determine the pressure difference across the plate, $\delta p$, the vortex-singularity strengths found from Eq. (1) are used to determine the flow perturbations (from the mean flow) and the velocity potential. These are then used in the unsteady Bernoulli equation (see Howell et al. 2009) applied along the upper and lower surfaces of the flexible plate. When separation occurs, the surface pressure downstream of the separation point is taken to be that at the point of separation.

We decompose the transmural pressure using $\delta p = \delta p' + \rho _\mathrm{f} [{\mathbf B}]\ddot{\eta }$ to separate out the fluid inertia; herein $\rho _\mathrm{f}$ is the fluid density and $[{\mathbf B}]$ is a matrix that contains the influence coefficients of the velocity potential. Combining this equation with Eq. (2) gives an equation for the coupled fluid-structure system. This equation is rearranged for plate acceleration and is solved using a semi-implicit Crank-Nicholson-type method of solution, detailed in Lucey and Carpenter (1992), that solves first for the plate acceleration at the next time step followed by integration to determine velocities and displacements. The wake formed by the separation of vorticity from the plate is modelled using a nonlinear version of the discrete-vortex method described in Howell et al. (2009) by Gaussian blobs of strength $\varGamma$ shown in Fig. 1. Separation from the plate surface is adjudged to occur downstream of the point at which an adverse pressure gradient first occurs and where it exceeds a threshold value of $5\,\%$ of the dynamic pressure; this value has been determined by using the present flow solution to model the known separation characteristics of oscillating aerofoils.

3 Results

Results are presented in terms of non-dimensional time $\bar{T} = T\rho _\mathrm{f}^2B^{1/2}/(\rho h)^{5/2}$, flow speed $\bar{U} = U_\infty (\rho h)^{3/2}/(\rho _\mathrm{f}B^{1/2}$) and fluid-to-plate mass ratio $\bar{L} = \rho _\mathrm{f}L/(\rho h)$ following the scheme presented in Howell et al. (2009). Herein, we use $\bar{L} = 1$ throughout that broadly corresponds to the short plates for which the FSI dynamics are dominated by low-order flexible-plate modes (Tang and Dowell 2002; Tang and Païdoussis 2008; Howell et al. 2009).

Initial results—not shown here—studied the behaviour of the coupled system at a flow speed approximately 40 % higher than the critical flow speed for linear instability determined in Howell et al. (2009) in the absence of a wake. When separation was forced to occur at the trailing edge, the results evidenced excellent agreement with the equivalent models of Tang and Païdoussis (2007, 2008); this served to validate our model and its implementation. When the effect of separation upstream of the trailing edge was included, it was found that the effect on system behaviour was negligible.

Fig. 2

Oscillation of a cantilevered plate in axial flow at $\bar{L}=1$ and $\bar{U} = 5.96$: the top row of sub-figures for wake formation from the plate trailing edge, and the bottom row when separation is included. The first column of sub-figures are snapshots in time of plate displacement; blue and red profiles are respectively the initial (imposed) deflection and the deflection at ${\bar{T}} = 4$. Second and third columns respectively show time series of plate-tip defection and plate energy, the latter normalised by the strain energy of the plate in its initial deflection

However, at lower flow speeds wake-separation effects are found to be very significant. Figure 2 shows the behaviour of the FSI system described for $\bar{U} = 5.96$, the critical flow speed for linear instability. The top row of figures pertains to the wake forced to form from the trailing edge while the bottom row are the corresponding results when flow separation is modelled. The simulations were initiated by releasing the flexible plate from an imposed deformation in the shape of in vacuo Mode 2. In both cases the FSI mode principally comprises components of in vacuo Modes 1 and 2. In the absence of separation, the top figure shows that after applying the initiating finite-amplitude deflection the plate motion settles quickly into low-amplitude neutrally-stable oscillations as predicted by linear studies. In contrast, the bottom figure shows amplitude growth followed by non-linear saturation at approximately $\bar{T}=1$ when the plate settles in to limit-cycle oscillations with the steady mode shape of the red line in the plate-deflection history captured at $\bar{T}=4$; these phenomena are also seen in the time series of both tip deflection (second column of sub-figures) and plate-energy (third column of sub-figures). The results of Fig. 2 demonstrate that flow separation can cause nonlinear instability at a flow speed for which the system is linearly stable. This type of nonlinear sub-critical instability, that causes hysteresis as flow speed is changed, is well known in experimental studies of cantilevered flexible-plate/flag flutter.

Fig. 3

Wake vorticity generated by a plate undergoing non-linear oscillations for $\bar{L} = 1$ with $\bar{U} = 5.59$: a wake vorticity is forced to separate at the trailing edge; b separation is modelled. Markers denote a wake vortex shed from either the trailing edge (•), or the separation point ($\triangle$). Colour denotes vorticity polarity: green positive, red negative

To understand the effect of separation on nonlinear motions and stability of the flexible plate, Fig. 3 shows the wake structures at the flow speed used to generate Fig. 2 when the flow is (a) forced to remain attached for the full length of the plate and (b) when separation is modelled. First, (a) demonstrates that the assumption, e.g. in the models of Tang and Païdoussis (2007, 2008), that wake vortices follow a sinusoidal path when separation occurs at the trailing edge is valid. Second, the effect of separation on stability, discussed above, can be deduced from the structure of the wake in (b). At high flow speed, it was observed that intense vortical structures form but that these convect downstream rapidly and have little effect on the plate behaviour. In contrast, for the lower flow speed that generated Fig. 2, roll-up occurs much closer to the trailing edge of the plate (located at $x/L = 1$ in these figures) and these structures can therefore exercise a significant effect on the flow field that drives the plate motion.

4 Conclusions

It is shown that at flow speeds much higher than the critical speed for linear instability the effects of separation are not significant. Amplification and subsequent nonlinear saturation at finite amplitudes can be adequately modelled by wake formation from the trailing edge of the plate as has been done in previous studies. At the flow speed for which the system is neutrally stable to linear disturbances, separation can lead to nonlinear instability and ensuing limit-cycle flutter. This suggests that flow separation may be a mechanism for the sub-critical instability that is observed in the experimental work of Eloy et al. (2008). Correctly modelling sub-critical instability relies upon choosing a threshold value of pressure gradient for separation that can only be found from experiment. However this does not negate the purpose of the present paper which was to show how separation can cause sub-critical instability.