Keywords

1 Context

For design and maintenance purposes, the knowledge of the flow in shallow water basins is relevant to highlight undesirable features such as stagnation areas, dead zones, separation and reattachment points and short-circuiting paths. In artificial dam reservoirs, large-scale flow patterns may have a strong influence on the rate of sediment deposited. If the sediment accumulated on the bottom reaches a certain threshold value, the water-storage capacity of the dam can be seriously compromised, with negative impact on the originally projected energy production. Moreover, the accumulation of sediments can contribute to the abrasion of the turbines and other components, with loss on their efficiency or even reduction in their life span.

Investigations on shallow, rectangular basins with sudden expansion at entrance and abrupt contraction at outlet have been recently reported in the literature [1–4]. Flow patterns in symmetric, finite-length basins have been studied numerically and experimentally. The main results have shown that, despite their simple configuration, symmetric flows in symmetric channels could become unstable under certain geometric and hydraulic characteristics. For these conditions, different types of flow patterns can emerge, namely channel-like flow, symmetric flow patterns characterized by two or four large eddies and asymmetric flow patterns [1].

Kantoush [4] conducted a number of experiments to study the effect of geometry on flow and sedimentation in symmetric shallow basins. Dewals et al. [3] performed numerical and theoretical analysis in a series of rectangular basins and compared their results with experimental data. By using a finite volume scheme with closure relationships for bottom friction and turbulent stresses, they showed that two-dimensional (2D) simulations performed with perfectly symmetric input data produce symmetric results and symmetric and non-symmetric flow patterns can be reproduced by a perturbation on the inflow conditions.

Dufresne et al. [2] extended the experimental database by considering a wider range of flow and geometric conditions. The impact of different flow and geometric parameters on the prediction of reattachment lengths was explored and a “shape parameter” was proposed to classify symmetric and asymmetric flows. For a large number of rectangular shallow reservoirs with different lateral expansion ratio and length, Camnasio et al. [1] conducted experimental studies to determine average velocity fields and streamlines. Their results were in agreement with previous work and confirmed the prediction of flow patterns based on the geometrical characteristics. Recently, Peng et al. [5] used the lattice Boltzmann model for shallow water equation and compared their results with the finite volume solver and laboratory experiences of Dewals et al. [3]. They also analyzed a determined range of values of Froude numbers and bed friction coefficients, concluding that larger values of Froude number and bed friction yield flows with a weaker asymmetry and longer reattachment length.

The aim of this work is the numerical simulation of shallow rectangular basins with sudden expansion and contraction. The capabilities of the TELEMAC modelling system to reproduce symmetric and asymmetric flows are evaluated by comparing two-dimensional finite element simulations with experiences by Kantoush [4] for a wide range of geometrical configurations. The sensitivity of the model is also discussed, with emphasis on the closure turbulence model and geometrical parameters.

The outline of this article is as follows. The mathematical and numerical models are presented in Sect. 2. In Sect. 3, the experimental setup of Kantoush [4] used to compare the numerical simulations is briefly presented and the observed flow patterns are introduced. Numerical results and comparisons with experimental results are given in Sect. 4. In Sect. 5, the results of this work are summarized and the conclusions are presented.

2 Mathematical and Numerical Model

2.1 Governing Equations and Closure Relationships

Many engineering problems involving water motion can be treated as shallow turbulent flows, where the shallowness condition h/l ≪ 1, valid whenever the depth h of the water layer is small compared to the wavelike extent l of the fluid motion, is achieved. In this work, numerical computations are based on the solution of the depth-averaged shallow water equations, expressed as function of the depth-averaged components of the flow velocity u( x , t) and v( x , t) with respect to Cartesian directions x = (x, y), the water depth h( x , t), the ground elevation measured from a reference altitude b( x ), the bed resistance terms τ bx and τ by in the x and y directions, respectively, the turbulent eddy viscosity ν t , the constant density ρ, the gravitational acceleration g, and the time t [6].

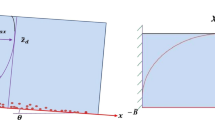
In this work, computations were performed in a symmetric, rectangular domain Ω = L × B; where L and B are the basin length and width, respectively, b is the inlet (outlet) channel width of length a, see Fig. 1.

Fig. 1
figure 1

General basin scheme (flow direction is from left to right)

Full size image

Computations are conducted using two different models for the turbulent flows, namely (1) a constant viscosity model, and (2) a two-length-scale turbulence model. The constant viscosity model is based on the assumption that the eddy viscosity ν t is constant throughout the domain. The two-length-scale turbulence model is a depth-averaged version of the standard k-ε model introduced by Launder and Spalding [6].

A relationship for the bed resistance term is specified according to the classical quadratic, nonlinear dependency on the depth-averaged velocity, as follows:

$$ \tau_{b} = \left( {\tau_{ bx} ,\;\tau_{ by} } \right) = \rho \;C_{f} \,\left( {u,\;v} \right)\left| U \right|, $$

where |U| = (u 2 + v 2)1/2 is the Euclidean norm of the horizontal velocity vector, and C f is the non-dimensional friction coefficient determined as function of the equivalent Nikuradse roughness k s .

2.2 Initial and Boundary Conditions

At t = 0, the water surface elevation is constant, that is, H = h(x, 0) + b( x ) = H 0; and the longitudinal and transversal velocity components are zero everywhere, that is, u(x, 0) = 0 and v(x, 0) = 0.

At the channel expansion inlet, a discharge is specified; at channel contraction outlet, the water depth is constant. A detail of the suitable boundary conditions is presented later in Sect. 4.

2.3 Dimensionless Parameters

The Vaschy-Buckingham theorem shows that 6 dimensionless parameters involving time, mass, and length can be obtained from 9 independent variables, namely the Reynolds number R = 4|U|h/υ, with υ the water kinematic viscosity; the Froude number F = |U|/(gh) 1/2; the dimensionless friction number k s /h; the lateral expansion ratio B/b; the dimensionless length L/B; and the dimensionless water depth H/B.

2.4 Numerical Solution

The computational framework for the solution of the shallow water equations is the TELEMAC modelling system.Footnote 1 This is an open-source, sequential and parallel free-surface solver based on the finite volume and finite element methods. Details of the numerical formulations for the models are given in Hervouet (2007) and not repeated here. The open-source TELEMAC modelling system was developed initially at the Laboratoire National d’Hydraulique et Environnement, a department of the research branch of Electricité de France. It is now a joint effort of several research teams in Europe (Telemac-Mascaret Consortium) and collaborations worldwide. For this work, numerical simulations were performed with the hydrodynamics module TELEMAC-2D of the TELEMAC modelling system.

Linear finite elements were chosen for the discretization of the water depth and quasi-bubble elements for the discretization of the velocity components [7]. The method used for solving the linear system is the conjugate gradient method with diagonal preconditioner.

3 Brief Description of the Experimental Setup and Flow Patterns

The numerical simulations presented in this work are compared with experimental results carried out by S. A. Kantoush at the laboratory of hydraulics constructions (LCH) of the Ecole Polytechnique Fédérale de Lausanne (EPFL) [2, 6]. Their tests were performed on an experimental facility consisting of a rectangular, PVC shallow basin with maximum length L = 6 m and width B = 4 m. Further details of the experimental setup, measurement techniques, and equipment can be consulted in [3, 4] and references therein.

Following [1], flow patterns can be classified according to the combined effects of the dimensionless length L/B and the lateral expansion ratio B/b. Channel-like flows (CH-L) occur on small expansion ratios and are independent of the length L. They are characterized by an unidirectional, symmetric flow, with a dominant central jet and the presence of two small eddies on both sides of the inlet expansion. This pattern was also analyzed by Abbot and Kline (1962). They found that for infinite length channels, the flow remains symmetric while the expansion ratio B/b < 2.67.

Symmetric flows without stagnation point (S0) occur in short basins (see Fig. 2b). A stagnation or reattachment point is defined as the point where a local fluid velocity is equal to zero [2]. The S0 flow pattern is characterized by two eddies placed symmetrically with respect to the channel centerline. Camnasio et al. [1] showed that this flow pattern develops if L/B < 1. Symmetric flows with one stagnation point (S1) are also generated for small L/B. For this case, a symmetric flow with four recirculation zones of unequal length develops. The eddies are symmetrically placed along the centerline of the channel and consist of two small eddies immediately upstream of the expansion and two larger eddies occupying approximately 2/3 of the basin length L.

Fig. 2
figure 2

Flow patterns classification. a CH-L/channel like, b S1/symmetric with one reattachment point R 1, and c A1/asymmetric with one reattachment point R 1. The flow is from left to right

Full size image

When increasing L/B, asymmetric flow patterns have been observed (see Fig. 2c). The development of this kind of pattern may be explained by the Coanda effect [8], resulting from a perturbation of the flow field that pushes the main flow toward one side of the channel while increasing the velocity magnitude near the wall and decreasing the pressure near that wall. Depending on the length of the basin, one reattachment point can appear after a distance R 1. For this case, the flow pattern is denoted as A 1. A fluctuating, unstable zone between the symmetric and asymmetric flow patterns has been observed by Dufresne et al. [2] and Camnasio et al. [1]. For this case, flow patterns have shown to be highly sensitive to external perturbations.

To quantify the limit between symmetric unstable zone asymmetric flow patterns, Dufresne et al. [2] proposed a non-dimensional shape parameter T, based on the geometrical characteristics of the channel: T = L(B−b) −0.6 b −0.4, see also [1]. Other patterns, such as asymmetric flows with two (A2) or three (A3) reattachment points have been analyzed by [1, 2, 4] and are not treated here. A sketch of flow patterns analyzed in this work is showed in Fig. 2.

4 Numerical Results and Discussion

In this section, numerical simulations are presented for shallow, rectangular basins with maximum length L = 6 m and maximum width B = 4 m. For all cases (except where indicated), the inlet and outlet channels were b = 0.25 m wide and a = 1 m long, see Fig. 1. At the inflow boundary, the discharge was set to q = 0.007 m3/s and at outflow boundary the water depth was fixed to h = 0.2 m, corresponding to subcritical flows with Froude number F = 0.10 and to a Reynolds number R = 112,000, based on the bulk velocity and water depth at the inlet of the expansion.

Numerical simulations were conducted up to steady state using non-structured triangular meshes with ∆x the representative element size. Sensitivity analysis of the time resolution has shown little impact on the results to approach to steady solutions for time steps ∆t on the range [0.01; 1 s]. All computations were run on 8 CPU cores of Xeon E5620 processors with 2.4 Ghz clock speed and 8 Gb of RAM. For cases CH-L, S1, and A1, the computational time required to reach the steady state was approximately 100, 1,200, and 6,000 s, respectively.

4.1 Case CH-L

This test case corresponds to a basin with length L = 6 m, width B = 0.5 m, and geometrical ratios B/b = 2 and L/B = 12. The influence of the mesh size on the results was verified for ∆x = 0.1 and 0.05 m and ∆t = 1 s. For both cases, comparison with experimental data shows good agreement with observed flow field, see Fig. 3. Moreover, for ∆x = 0.05 m, the model was able to capture the two small eddies on both sides of the inlet jet. By adopting ∆x = 0.05 m, comparison of simulations performed with the constant viscosity model with ν t  = 10−4 m2 s−1 and depth-averaged k-ε model showed little variations on the results. Finally, the influence of the bed roughness height was analyzed for k s  = 10−2 and 10−4 m. In both cases, the simulated flow field remains very close to the experimental observations of Kantoush [4].

Fig. 3
figure 3

Experiments (left) and numerical simulation (right) of velocity field and magnitude for the case CH-L (L = 6 m, B = 0.5 m and constant viscosity model)

Full size image

4.2 Case S1

This test case corresponds to a basin with length L = 5 m, width B = 4 m, and geometrical ratios B/b = 16 and L/B = 1.25. Preliminary computations performed with ∆x = 0.05 m, ∆t = 1 s, k s  = 10−3 m and the constant viscosity with ν t  > 10−5 m2 s−1 and k-ε turbulence models, showed that the main symmetric jet traversing the domain from the expansion at the inlet to the contraction at the outlet is well represented, but the observed four eddies structure does not develops [1, 4].

For similar numerical and physical parameters and constant turbulence model with ν t  = 10−5 m2 s−1, the model is able to represent the four circulation zones placed symmetrically with respect to the main jet, see Fig. 4. Furthermore, at approximately x = 2.50 m, the small deviation of the main jet due to the transfer of momentum toward the wall at right is well represented. A comparison between measured and simulated velocity profiles in two cross-sections of the basin, namely x = 0.05 m and x = 2.50 m, for a range of constant turbulent eddy-viscosity models with ν t  = [4.5 × 10−6; 1.5 × 10−5 m2 s−1] and for the depth-averaged k-ε model are shown in Fig. 5. The solution computed with a constant turbulence model with ν t  = 10−5 m2 s−1 compares very favorably with experimental data, despite an underestimation of about 5 % of the maximum observed velocity at x = 0.05 m.

Fig. 4
figure 4

Experiments (left) and numerical simulations (right) of velocity field and magnitude for the case S1 (L = 5 m and B = 4 m)

Full size image
Fig. 5
figure 5

Measured and simulated velocity profiles in two cross-sections of the basin at x = 0.5 m (left) and x = 2.50 m (right), for different values of ν t

Full size image

4.3 Case A1

This test case corresponds to a basin with length L = 6 m, width B = 4 m, and geometrical ratios B/b = 16 and L/B = 1.5. Preliminary computations performed with ∆x = 0.01 m, ∆t = 1 s; k s  = 10−3 m and the constant viscosity with ν t  > 10−5 m2 s−1 and k-ε turbulence models showed that simulations with a symmetric input data produce an erroneous, symmetric solution which does not correspond to physical reality [1, 4]. A simulation with constant turbulence model with ν t  = 10−5 m2 s−1 was able to predict the observed A1-type flow, with two large recirculation zones of unequal length as showed in Fig. 6. The asymmetric pattern can be explained by the Coanda effect, where a change in the momentum of the flow at the basin entrance yields to a reduction in the pressure which modifies the hydrodynamics field by projecting the jet toward the wall [8].

Fig. 6
figure 6

Experiments (left) and numerical simulation (right) of velocity field and magnitude for the case A1 (L = 6 m and B = 4 m)

Full size image

The numerical results showed remarkably good agreement with simulations by Dewals et al. [3]. It is worth noting that, in contrast to results of Dewals et al., the simulations performed here were able to reproduce the asymmetric pattern observed by Kantoush [4], despite the symmetry and stability of the inflow discharge. To reproduce the asymmetric patterns, Dewals et al. specified a linear perturbation at the basin inlet [3]. As for the Lattice Boltzmann simulations of Peng et al. [5], simulations with the depth-averaged k-ε model have showed poor results when comparing with experimental observations. Furthermore, model results have showed to be highly sensitive to the finite element mesh topology. These topics will be subject of further investigations.

4.4 Transition Zone S1/A1

Between symmetric (S1) and asymmetric (A1) flow patterns, an instability transition area characterized by flows highly sensitive to external perturbations was observed by [1, 2]. Preliminary results showed that basins with geometrical configurations in the limit symmetric-asymmetric S1/A1 were difficult to reproduce. To investigate the capabilities of the TELEMAC-2D to reproduce flow patterns in the transition zone, the number of geometrical configurations tested by [1–4] has been expanded with five new additional configurations, corresponding to lengths L = 6.3, 6.6, 8.4, 9.6, and 10.8 m with constant width B = 4 m and b = 0.25 m, see Fig. 7. For ∆x = 0.01 m, ∆t = 1 s, and k s  = 10−3 m, numerical simulations showed that the model is less predictive if the geometry is close to the transition zone.

Fig. 7
figure 7

Diagram of flow patterns classification (adapted from [1], see also Sect. 3). The numerical computations performed in Sect. 4.4 are indicated with the symbol “*”, see Table 1 for geometrical characteristics. Dash-dot lines represent the threshold values that delimit the symmetric unstable area asymmetric flow patterns calculated with the non-dimensional parameter T [1, 2]

Full size image

Computations performed near the asymmetric zone with the constant viscosity model with ν t  = 10−5 m2 s−1 developed asymmetric flows for a symmetric discharge input. Table 1 synthesizes the computed flow patterns for the zone S1/A1, reproduced with both constant eddy-viscosity and k-ε turbulence models. In Fig. 7, dash lines indicate the (fuzzy) limit between each flow pattern. Dash-dot lines represent the threshold value predicted with the non-dimensional parameter T of Dufresne et al. [2]. The critical values corresponding to the zone symmetric instability area asymmetric flow patterns are T = 4.09 and T = 4.48 [1]. Numerical computations presented in this section are consistent with the observations of Camnasio et al. [1] and with the forecasting capability of the non-dimensional parameter T of Dufresne et al. [2].

Table 1 Simulated flow patterns for the new geometrical characteristics
Full size table

5 Conclusions

In this paper, the capabilities of the 2D hydrodynamics model (TELEMAC-2D) to simulate large, recirculating flows in shallow turbulent basins are demonstrated by comparison with experiments of Kantoush [4]. Numerical simulations also show that flow patterns depend on the geometrical characteristics of the basin, in agreement with previous observations by Camnasio et al. [1] and Dusfresne et al. [2].

For CH-L-type basins, the unidirectional, symmetric flow with two small eddies near the inlet is well reproduced for both the constant viscosity and depth-averaged two-length-scale k-ε turbulence models. For S1-type basins, the symmetric jet with four large-scale eddies is well represented with the constant viscosity model. For this case, the depth-averaged k-ε model was not able to reproduce the observed eddies. For A1-type basins, the two large, asymmetric recirculation zones observed in A1-type basins are well predicted by the numerical simulations. The formation of this asymmetric pattern can be explained by the Coanda effect. Furthermore, the simulations are able to reproduce the asymmetric pattern even for a fully symmetric discharge at the inlet, in contrast to simulations of Dewals et al. [3]. As in the previous case, the k-ε turbulence model represented poorly the experiments, as was also observed by Peng et al. [5].

In the transition zone S1/A1, numerical simulations show that model results are highly sensitive to the choice of turbulence model and the model is therefore less predictive. Furthermore, computations performed nearby the asymmetric zone with the constant viscosity model developed the experimentally observed asymmetric flows. In general, numerical results compare qualitatively well with experimental data, whereas the k-ε model results develop symmetric pattern, possibly due to numerical diffusion of the first-order numerical scheme. Except for the CH-L-type, the 2D model shows strong dependency on the turbulence model. Further investigations on this topic are underway, on the basis of 3D numerical simulations. Further work will also include coupling with sediment transport model (Sisyphe) in order to reproduce large-scale sedimentary patterns in shallow basins at laboratory and field scale.