Point Set Registration of Large Deformation Using Auxiliary Landmarks

Abstract

We present a probabilistic non-rigid point set registration method to deal with large and uneven deformations. The registration is treated as a density estimation problem. The main ideas of our method are to add constraints to enforce landmark correspondences and preserving local neighborhood structure. Landmarks represent the salient points in point sets, which can be computed using feature descriptors such as scale-invariant feature transform. By enforcing landmark correspondences, we preserve the overall global shape of the point set with significant deformations. In addition, we incorporate constraints to preserve local neighborhood structure by leveraging Stochastic Neighbor Embedding (SNE), which penalizes incoherent transformation within a neighborhood. We evaluate our method with both 2D and 3D datasets and show that our method outperforms the state-of-the-art methods in a large degree of deformations. In particular, quantitative results show our method is 49% better than the second best result (from the state-of-the-art methods). Finally, we demonstrate the importance of using correct landmark correspondences in registration by showing good registration results in large and uneven deformations point sets.

1 Introduction

Point set registration identifies correspondences between two sets of points, from which a transformation function is derived to achieve alignment. It is a fundamental task in many computer vision applications such as range image-based human pose tracking and three-dimensional object reconstruction. In such applications, however, large deformations make point set registration a challenging task [8].

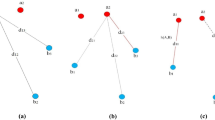
To address non-rigid deformation, Coherent Point Drift (CPD) was proposed to regulate the transformations of the points within a neighborhood [12]. This method assumes that the transformation for points that are in close vicinity is highly similar. Ge et al. [4] extended the CPD method by adding constraints to maintain local neighborhood structure. Ma et al. [11] used shape descriptors to ensure the local structure of point subsets. Despite the success demonstrated by the aforementioned methods, obtaining accurate correspondences between point sets and maintaining the shape and structure in the case of large and uneven deformation is still an open challenge in non-rigid point set registration. In the applications of tracking humans in actions, for example, deformation from movements of limbs is common. As a consequence, the body shape appears dramatically differently; whereas the local structure of a rigid body part remains unchanged (as shown in Fig. 1(a) and (b)). Such disparity makes the coherency assumption incomplete; registration results of CPD, LSP, and our method are shown in Fig. 1(c), (d), and (e), respectively.

Fig. 1.

Registration of human body with large and uneven deformation.

In this paper, we present a non-rigid point set registration method by incorporating constraints of corresponding landmarks to register point sets that represent large deformation. Landmarks represent the salient points in point sets, which can be identified using methods such as scale-invariant feature transform [10]. The correspondence between landmarks enables us to regulate the optimization process. In addition, by leveraging Stochastic Neighbor Embedding (SNE) [6], we aim to penalize incoherent transformation within a neighborhood and hence preserve the local structure.

The rest of this paper is organized as follows: Sect. 2 reviews the related methods for non-rigid point set registration. Section 3 presents our proposed method for non-rigid point set registration. Section 4 discusses our experimental results and comparisons with state-of-the-art methods. Section 5 concludes this paper with a summary.

2 Related Work

To register point sets, Chui et al. [3] proposed a general framework based on robust point matching (RPM) [5]. In this framework, the authors used thin-plate spline (TPS) as a non-rigid spatial mapping, which performs a soft assignment, instead of binary assignment, for point correspondence and employs deterministic annealing to favor global rigid transformations at the early stage of the optimization and local, non-rigid transformations in a later stage using thin-plate-splines. Tin et al. [16] proposed Kernel Correlation (KC) by extending the correlation technique to point set registration. This method also used soft correspondence assignment and the correlation of the two kernel density estimates is the main part of the cost function. A similar strategy was used by Jain et al. [7], in which the point sets are modeled as Gaussian mixtures, and the registration problem is formulated as minimizing the L2 distance between the two Gaussian mixtures.

One popular method for non-rigid registration is a probabilistic approach where the registration is mapped into density estimation based on GMM. In this approach, GMM centroids are represented by one point set (template or model) and other point set represents the input data. The template points are transformed with prior constraints so that the point sets are aligned as much as possible by maximum likelihood fashion. Coherent Point Drift (CPD) is a robust probabilistic point set registration method based on GMM and the key idea is moving points coherently to maintain the topological structure of the point set [12]. Extensions to the CPD have been proposed to preserve point set structure and the intrinsic geometry of the data [4, 11, 13, 17]. Panaganti et al. [13] proposed to use proximity weight between the points using shape context [1] to calculate correspondences and graph-Laplacian regularization term to preserve the intrinsic geometry of the point set. Ge et al. [4] extended the CPD method, called Local Structure Preservation (LSP), to handle complex non-rigid and articulated deformations by adding two regularization terms Local Linear Embedding (LLE) [14] and Laplacian coordinate (LC) to maintain the local neighborhood relationship and scale (size) respectively. Instead of using equal membership probabilities to the mixture model such as that in [4, 12], recent methods have assigned membership probabilities to the mixture model and show robustness to noises, outliers, occlusions [11, 17]. The idea is to match similar local neighborhood structures between point sets with the help of feature descriptors [1, 9, 15]. However, these methods are vulnerable to a local minimum in case of large and uneven deformations. Also, the assumption of similar local structure in both point sets is problematic as distortions and stretches are always present in real data.

3 Method

Our method takes two sets of points as inputs and corresponding landmarks are used as a strong constraint. The optimization process leverages the Gaussian mixture model that enforces both local coherence using SNE and global constraint through landmarks. Let X and Y denote two sets of points in a D dimensional space. We have $X = {\{ \mathbf{x}_1, \mathbf{x}_2, \ldots , \mathbf{x}_N \}}$ and $Y = {\{ \mathbf{y}_1, \mathbf{y}_2, \ldots , \mathbf{y}_M \}}$, where M and N denote the number of points of the respective set. Assume noise follows the uniform distribution, i.e., $p^*_n = \frac{1}{N}$, we have the probability density function of point $\mathbf{x}_n$ given Y as follows:

$$\begin{aligned} \begin{aligned} p(\mathbf{x}_n) = \sum _{m=1}^{M}p(\mathbf{x}_n|\mathbf{y}_m)p(\mathbf{y}_m) + p^*_n \end{aligned} \end{aligned}$$

(1)

where $p(\mathbf{y}_m) = \frac{1}{M}$. Given a set of landmarks $\dot{X} \in X$ and $\dot{Y} \in Y$, we have the correspondence between each pair of points $\dot{x}_j \leftrightarrow \dot{y}_j$, where $\dot{x}_j \in \dot{X}$ and $\dot{y}_j \in \dot{Y}$. Hence, our optimal transformation function must minimize the total distance between all pairs of the corresponding $\dot{x}_j$ and $\dot{y}_j$ as follows:

$$\begin{aligned} E_{G} = \sum _j{\Vert \dot{x}_j-\dot{y}_j \Vert }^2. \end{aligned}$$

(2)

To avoid possible singularity in the matrix inverting operation, we revise Eq. (2) as follows:

$$\begin{aligned} E_{G} = \sum _{m,n}^{M,N}{} \mathbf{A}_{m,n}{\Vert \mathbf{x}_n-\tau (\mathbf{y}_m) \Vert }^2 \end{aligned}$$

(3)

where $\mathbf{A} _{M \times N}$ is landmark coefficient matrix, $\mathbf{A}_{m,n} = 1$ if $(\mathbf{x}_n, \mathbf{y}_m) \in L$; otherwise 0, and L is a set containing all pairs of landmark correspondences.

To keep points within a neighborhood relatively close after transformation and points far apart remain distant, Stochastic Neighbor Embedding (SNE) [6] is employed. Let $r_{ij}$ be the probability that two points $\mathbf{y}_i$ and $\mathbf{y}_j$ are neighbors before transformation and $s_{ij}$ be the probability that these two points become neighbors after transformation $\tau$. A constraint on local structure is represented as the minimization of cost function which is the sum of Kullback-Leibler (KL) divergences between $r_{ij}$ and $s_{ij}$ distributions over neighbors of each point [6]:

$$\begin{aligned} E_{L} = \sum _{ij} r_{ij}\log \frac{r_{ij}}{s_{ij}} = \sum _i KL \left( \mathbf{R}_i \Vert \mathbf{S}_i \right) , \end{aligned}$$

(4)

where

$$r_{ij}=\frac{\exp (-\beta _2{\left\| \mathbf{y}_i-\mathbf{y}_j\right\| }^2)}{\sum _{k \ne i}\exp (-\beta _2{\left\| \mathbf{y}_i-\mathbf{y}_k\right\| }^2)}, $$

and

$$\begin{aligned} s_{ij}=\frac{\exp (-{\left\| \tau (\mathbf{y}_i)-\tau (\mathbf{y}_j)\right\| }^2)}{\sum _{k \ne i}\exp (-{\left\| \tau (\mathbf{y}_i)-\tau (\mathbf{y}_k)\right\| }^2)}. \end{aligned}$$

Following the GMM framework in [12], the objective function of our method integrates local and global constraints as follows:

$$\begin{aligned} Q(\varvec{\theta , \sigma ^2})= & {} \frac{1}{2\sigma ^2} \sum _{n,m=1}^{N,M} p^{i-1}(\mathbf{y}_m|\mathbf{x}_n){\Vert \mathbf{x}_n - \tau (\mathbf{y}_m)\Vert }^2 + \frac{N_PD}{2}\ln \sigma ^2\\\nonumber&+ \frac{\lambda _1}{2}tr(\mathbf{W} ^T\mathbf{GW} ) + \frac{\lambda _2}{2} E_L + \frac{\lambda _3}{2} E_G \end{aligned}$$

(5)

where

$$\begin{aligned} p^{(i-1)}(\mathbf{y}_m|\mathbf{x}_n) = \frac{\exp ^{(-\frac{1}{2} {\Vert \frac{\mathbf{x}_n - \tau (\mathbf{y}_m)}{\sigma _{(i-1)}} \Vert }^2)}}{\sum _{k=1}^M \exp (-\frac{1}{2} {\Vert \frac{\mathbf{x}_n - \tau (\mathbf{y}_k)}{\sigma _{(i-1)}} \Vert }^2) + C}, \end{aligned}$$

(6)

where $C = \gamma (2\pi \sigma _{(i-1)}^2)^{D/2}M/((1-\gamma )N)$, $\tau$ is a transformation function that maps a point $\mathbf{y}_m$ in Y to a new spatial location such that it coincides with a point $\mathbf{x}_n$ in X, i.e., $\mathbf{x}_n=\tau (\mathbf{y}_m)$, $\gamma \in [0,1]$ denotes the rate of noise and outlier in the observed dataset X, $tr(\cdot )$ refers to the trace of a matrix, and $N_P = \sum _{n,m=1}^{N,M} p^{(i-1)}(\mathbf{z}_n = m|\mathbf{x}_n) \le N$. We use transformation model which moves neighborhood points coherently and helps in maintaining topological structure of the point set [12]. $\mathbf{G} _{M \times M}$ is a kernel matrix with elements $g_{ij} = G(\mathbf{y}_i,\mathbf{y}_j) = \exp (-\frac{1}{2} {\Vert \frac{\mathbf{y}_i-\mathbf{y}_j}{\beta }) \Vert }^2$, $\mathbf{W} _{M \times D} = (\mathbf{w} _1, \ldots ,\mathbf{w} _M)^T$ is a coefficients matrix, $\lambda _1$, $\lambda _2$, and $\lambda _3$ are regularization weights for motion coherence, local structure, and correspondence constraints, respectively.

We obtain the coefficient matrix $\mathbf{W}$ by taking derivative of Eq. (5) with respect to $\mathbf{W}$ and set it equal to zero

$$\begin{aligned} (diag(\mathbf{P1} )\mathbf{G} + \sigma ^2\lambda _1\mathbf{I} + \sigma ^2\lambda _2\mathbf{JG} + \sigma ^2\lambda _{3}diag(\mathbf{A1} )\mathbf{G} ) \mathbf{W} = \\\nonumber (\mathbf{PX} - diag(\mathbf{P1} )\mathbf{Y} - \sigma ^2\lambda _2\mathbf{JY} - \sigma ^2\lambda _3diag(\mathbf{A1} )\mathbf{Y} + \sigma ^2\lambda _3\mathbf{AX} ) \end{aligned}$$

(7)

where $\mathbf{J} = (diag(\mathbf{R1} ) - 2\mathbf{R} + diag(\mathbf{1} ^T\mathbf{R} ))$, $\mathbf{1}$ refers to column vector of all ones, $\mathbf{I}$ refers to identity matrix, and $diag(\mathbf{v} )$ refers to the diagonal matrix created from the vector $\mathbf{v}$.

We define the transformation function, $\tau$, as the initial position, $\mathbf{y}_m$, plus a displacement function $\mathbf{f}(\mathbf{y}_m)$, $\tau (\mathbf{y}_m) = \mathbf{y}_m + \mathbf{f}(\mathbf{y}_m)$. We adopt the following transformation function [12]:

$$\begin{aligned} \mathbf{T} = \tau (\mathbf{Y}, \mathbf{W}) = \mathbf{Y} + \mathbf {GW} \end{aligned}$$

(8)

Similarly, we obtain $\sigma ^2$ by taking derivative of Eq. (5) with respect to $\sigma ^2$ and set to zero

$$\begin{aligned} \begin{aligned} \sigma ^2 = \frac{1}{N_PD}(tr(\mathbf{X} ^Tdiag(\mathbf{P} ^T\mathbf{1} )) - 2tr(\mathbf{PX} ^T\mathbf{T} ) + tr(\mathbf{T} ^Tdiag(\mathbf{P1} )\mathbf{T} )) \end{aligned} \end{aligned}$$

(9)

where $N_P = \mathbf{1}^T\mathbf{P1}$.

4 Results and Discussion

4.1 Experimental Data and Settings

In our experiments, we use publicly available 2D dataset [2] and 3D human pose dataset captured by Microsoft Kinect II [18]. The 2D dataset contains point sets of tools such as scissors, pliers, knives. Each tool has five different shapes. In our 2D tools data experiments, we set the parameters of our method as follows: $\lambda _1$ = 8.0, $\lambda _2$ = 1.0, $\lambda _3$ = 120.0, $\beta _1 = 1.0$, $\beta _2$ = 10.0, and maximum iterations of EM is 50. The 3D human body dataset includes four human subjects with different body shapes and sizes. Each point set consists of more than 12 thousands points. In our experiments on this dataset, the parameters of our proposed method are as follows: $\lambda _1$ = 2.0, $\lambda _2$ = 1.0, $\lambda _3$ = 150.0, $\beta _1 = 1.0$, $\beta _2$ = 15.0, and maximum iterations of EM is 50.

We compute the registration error with a normalized Euclidean distance between points of the input point set and corresponding points of the target point set as follows:

$$\begin{aligned} \varepsilon = \frac{1}{N} \sum _{i,j} {\left\| \mathbf{x}_i - \mathbf{y}_j \right\| }_2 \end{aligned}$$

(10)

where $\mathbf{x}_i \in \mathbf{X}$ and $\mathbf{y}_j \in \mathbf{Y}$ is the estimated corresponding point of $\mathbf{x}_i$ after registration, and N is the number of points in point set $\mathbf{X}$. We evaluate our method in the following three aspects: 1) different degrees of deformation, 2) the different number of landmarks, and 3) the impact of incorrect correspondences between landmarks.

4.2 Degree of Deformation

Figure 2 shows a qualitative registration results of both Fig. 2(a) 2D tools and Fig. 2(b) 3D human body datasets of three degrees of deformation (small, medium, and large) in the top, middle, and bottom rows, respectively. In this figure, the first two columns are input and template point sets while the rest of the three columns are the registration results of our method, CPD [12], and LSP [4]. For the 2D tools dataset, both our method and LSP have good registration results than CPD in a small degree of deformation. In the medium degree of deformation, CPD fails to maintain structure in the upper part of the tool. Our method and LSP exhibit better results than CPD in this case but the structure of the tip of the tool (upper part) from our method is better than LSP. Finally, in the large degree of deformation, our method shows good results than the other two methods where both CPD and LSP completely fail to maintain the shape of the tool. For the 3D human body dataset, our method and CPD generate accurate results than LSP in a small degree of deformation. In the medium degree of deformation, CPD fails to maintain the shape of the head and has twisted legs, LSP maintains the local structure but inflexible in this case, and our method generates an accurate result. For a large degree of deformation, both CPD and LSP fail to maintain human body shape but our method shows better results (but has some artifacts in the hand regions). In both datasets, our method shows significantly better results by maintaining both local and global structures especially in a large degree of deformation showing the importance of preserving local neighborhood structure and using landmark correspondences.

Fig. 2.

Exemplar registration results with three degrees of deformation. The left two columns of each figure are the inputs and the following three columns are results of our method, CPD, and LSP, respectively.

Table 1 lists the quantitative registration errors with respect to different degrees of deformation and a comparison with CPD [12] and LSP [4] methods for both 2D tools and 3D human body datasets. We have three degrees of deformation: small, medium, and large (an example of each case is shown in Fig. 2). For each degree of deformation, the best and the second best results are highlighted in bold and italic fonts, respectively. Each experiment was repeated five times. Our method exhibits the smallest registration error (and stds.) in almost all cases except the case of small deformation in 2D. In this one case, our method’s registration error is slightly higher than LSP’s registration error by 0.21. The average registration errors, by combining both 2D and 3D deformation results for each method, of our method, CPD, and LSP are 7.64, 15.18, and 83.76, respectively. Our method has the lowest average registration error and is 49% better than the second best result. It is evident that our method has a small registration error (std) than the other methods as the deformation degree increases.

Table 1. Average registration error with respect to three degrees of deformation.

4.3 Number of Landmarks

We test our method and compare registration accuracy with other methods to see the effect of the different number of corresponding landmark points in the point sets during registration. In each point set, we marked five landmarks and conducted experiments using $x, x\in \{1, 2, \ldots , 5\}$, number of corresponding pairs of landmarks. In this experiment, we have selected the point sets with large deformations between them (Fig. 3) and the order of corresponding landmark pairs are fixed. For example in human body point sets, we fixed the order of following five pairs of corresponding landmarks between two point sets: heads, right foot, left foot, right hands, and left hands, respectively. For each x, we selected the first x pairs of corresponding landmarks from the fixed order of landmark pairs and repeated the experiment five times. Figure 3 illustrates the registration results using different numbers of landmarks in our method. Figure 3(a) shows the registration results of human body dataset, and Fig. 3(b) shows the registration results of tools dataset. The template and input point sets depict large deformations. Each row depicts a case with the left two columns showing the input and the template point sets. The rest columns in a row show the registration results using an increasing number of landmark pairs from left to right. Figure 3(a) illustrates a challenging case with large and uneven deformations between the input and template point sets. When the number of landmark pairs is less than five, the method resulted in poor registration. In human cases, arms and head were fuzzy or ‘vaporized’. As the number of landmark pairs reaches five, the results gained significant improvement due to more precise shape constraints. This trend is also demonstrated in the registration of the Tools case as shown in Fig. 3(b) but shows good registration results even in less than five landmark pairs. In particular, Fig. 3(b) show improved registration results when the number of landmark pairs is four or more. Therefore, it is fair to say the minimum number of landmarks needed depends on the degree of disparity between the point sets.

Table 2 presents the average registration errors and standard deviations of our method using a different number of corresponding landmarks for both 2D tools and 3D human body datasets. As the landmark correspondences increases, the registration accuracy of our method also increases. In particular, registration errors start to decrease sharply after adding four or more landmark correspondences, especially in the case of the 3D human body dataset.

Fig. 3.

Registration results of our method using different number of landmarks. The first two left columns show the input and template point sets, respectively. Columns three to seven show the results using different number of landmarks. Row (a) shows the results of human body dataset, and row (b) shows the results of tools dataset.

Table 2. Average registration error of our method with different number of landmarks.

4.4 Incorrect Landmark Correspondence

To evaluate the impact of incorrect landmark correspondence, we create three incorrect correspondence cases for each dataset and repeated each registration five times. Figure 4 shows the results of using incorrect correspondences in our registration method. Figure 4(a) shows registration results of 2D tools point sets and Figure 4(b) shows the registration results of 3D human point sets. The first two columns show the inputs and the corresponding landmarks are shown in the same color. Third and fourth columns are the registration results of using correct and incorrect landmark correspondences respectively.

Fig. 4.

Exemplar registration results using incorrect landmark correspondences. The left two columns of each figure are the inputs (and corresponding landmarks have the same color). The third column shows the registration results using correct landmark correspondences and the last column shows the registration results. (Color figure online)

For the 2D tools dataset, the registration result of the first row shows the thin shape of the tool and is twisted in the middle part of the tool. This is because the left and right landmark correspondences at the top and bottom regions are swapped between input and template point sets. In particular, the left tip landmark (yellow) and right tip landmark (black) of the input point set correspond to the right tip landmark (yellow) and left tip landmark (black) of the template point set. Similar incorrect left and right correspondences between the landmarks at the bottom regions of the tool point set are used. In the second case (middle row), the registration result is similar to the result of the first row, i.e., twisted at the middle part of the tool and thin shape of the tool as a result of incorrect landmark correspondences. In the last case (bottom row), not only left and right landmark correspondences at the top regions but also landmark correspondences at the middle and lower right handle regions between input and template point sets are swapped. In this case, the registration result shows an inaccurate shape of the tool where points from different parts of the tool are mixed together.

Similarly, for the 3D human body dataset, head region points are fused with the right shoulder and the upper body is twisted in the top row. In the middle row, the upper body part is twisted and points from the head are mixed with the left shoulder. The last row is even highly inaccurate with twisted and fusion of the different parts of the body regions.

Table 3 lists the quantitative registration results of using incorrect landmark correspondences in the three different cases. For the 2D tools dataset, all three cases have similar registration errors (and stds.). For the 3D human body dataset, the first two cases have better results than the last case. The average registration errors, when all three cases are combined for each dataset, are 6.78 (2.4) for the 2D tools dataset and 19.74 mm (1.5) for the 3D human body dataset.

Table 3. Registration results (stds.) of our method with different combinations of incorrect landmark correspondences in 2D and 3D datasets.

5 Conclusion

In this paper, we present a probabilistic non-rigid point set registration method to register point sets that represent large and uneven deformation. Keys to our method are constraints for enforcing landmark correspondences and preserving local neighborhood structure. Landmarks represent the salient points in point sets, which can be computed using methods such as scale-invariant feature transform. The correspondence between landmarks enables us to regulate the optimization process. In addition, by leveraging Stochastic Neighbor Embedding, we preserve the local structure of the point set by penalizing incoherent transformation within a neighborhood.

We evaluate our method with three different aspects: different degrees of deformation, the number of landmarks in registration, and the impact of incorrect landmark correspondences in registration. Our method shows significantly better results in a large degree of deformation in both 2D and 3D datasets. Quantitative results show our method is 49% better than the second best result in deformation experiments. Our evaluation results show that as the number of landmark correspondences increases, the registration accuracy of our method also increases, highlighting the importance of landmark correspondences in a large degree of deformation. Also, using incorrect landmark correspondences in registration results in a significant degrade in registration accuracy based on our experiments.