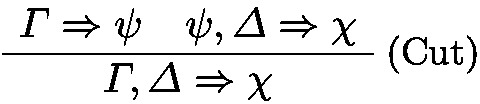Paraconsistent Rough Set Algebras

Abstract

Paraconsistent Pawlakian rough sets and paraconsistent covering based rough sets are introduced for modeling and reasoning about inconsistent information. Topological quasi-Boolean algebras are shown to be algebras for paraconsistent rough sets. We also give two sequent calculi as the modal systems for these paraconsistent rough sets.

This work was supported by Chinese National Funding of Social Sciences (Grant no. 18ZDA033).

1 Introduction

Rough sets by Pawlak [14, 15] was proposed as an approach to imprecise knowledge about objects in the field of knowledge representation. Knowledge and data differ in the way that the former is organized while the latter is loosely scattered. Pawlakian knowledge is based on the notion of classification. A knowledge base is understood as a relational structure $(U, \textbf{R})$ where $U\ne \varnothing$ is a set of objects and $\textbf{R}$ is a family of equivalence relations over U. Hence the logic for approximate reasoning in Pawlakian rough sets is indeed a multimodal logic $\textbf{S5}$. Later works focus on the generalization of Pawlak’s rough set theory by extending the equivalence relation to similarity relation [18], altering the equivalence relation to arbitrary binary relations [21, 22] or by replacing the partitions by coverings [6, 23]. Interactions between rough set theory and modal logic are presented in [9, 16].

In many practical scenarios, classifications of objects are given by a set of attributes. A usual assumption is that each attribute determines a set of objects. Given an object x in the universe and an attribute $\phi$, either $\phi (x)$ holds or not. This is usually called the consistency assumption. Thus in standard rough set systems we make the lower and upper approximations of a given set X of objects. However, in practice, there exist datebases which are inconsistent in the sense that there are contradictions or conflict. For example, a toy is classified into both round objects and square objects. In such a case, we need a paraconsistent rough set theory which can be used to deal with inconsistent information.

Previous work bridging paraconsistent logic and rough set theory can be found in [12, 20] where basic notions such as set, approximations and similarity relation are allowed to have four values. Later, paraconsistency was treated as membership function, set containment and set operations in [13, 19]. Four-valued logic was employed as the semantics to express approximate reasoning. However, bilattice in Belnap’s logic was discarded since Belnapian truth ordering was considered counterintuitive. Therefore, only knowledge ordering was retained in their framework and truth ordering was changed into a linear order in their approach.

Here, we consider an attribute $\phi$ as a pair of sets of objects $\langle \phi ^+, \phi ^- \rangle$ where $\phi ^+$ is the set of all objects having the attribute $\phi$ and $\phi ^-$ is the set of all objects lacking the attribute $\phi$. Then $\phi ^+\cap \phi ^-$ consists of those objects with inconsistent information, and the objects outside $\phi ^+\cup \phi ^-$ have no information with respect to the attribute $\phi$. Similar idea can be found in the Belnap-Dunn four-valued logic [3, 4]. We will introduce the notion of polarity in knowledge base and approximations of polarity. In such a way we obtain new paraconsistent rough sets. A polarity is simply a pair of sets of objects $\langle X,Y \rangle$ which are candidates for approximations. The following figure shows four cases of a polarity $\langle X,Y \rangle$ in a universe U of objects:

Fig. 1.

Polarity in a universe

Objects in $X\cap Y$ have inconsistent information, and those outside of $X\cup Y$ have no information. If $X\cap Y\ne \varnothing$, we say that $\langle X,Y \rangle$ is inconsistent; and if $X\cup Y\ne U$, we say that $\langle X,Y \rangle$ is incomplete. In the standard rough set theory, a set of objects X can be viewed as a polarity $\langle X, X^c \rangle$ where $X^c$ is the complement of X in U. It is clearly both consistent and complete.

Quasi-Boolean algebras and topological quasi-Boolean algebras are algebras for rough sets. Algebras for Pawlakian rough sets and covering based rough sets can be found in previous work such as [1, 2, 7, 11]. Recent development on the interrelations betwenn rough sets and logic is presented in [9, 17]. We construct the algebras for paraconsistent Pawlakian rough set and paraconsistent covering based rough sets respectively. Jonsson-Tarskian style [5] duality results are also provided.

In the present work, we shall introduce two types of paraconsistent rough sets. One is the Pawlakian, and the other is covering based. Lower and upper approximations in each type will be defined. Then paraconsistent rough set algebras for each type of paraconsistent rough sets will be proposed and representation theorems for these algebras will be proved. Finally we establish two sequent calculi for reasoning in these paraconsistent rough sets.

2 Paraconsistent Rough Sets

In this section, we introduce paraconsistent rough sets which are variants of the standard rough sets. We shall define the upper and lower approximations, and prove some basic properties of them.

Definition 1

A (Pawlakian) approximation space is a structure $\mathcal {K}=(U, R)$ where $U\ne \varnothing$ is the set of objects and R is an equivalence relation on U. For every $x\in U$, let $R(x)=\{y\in U: xRy\}$, i.e., the equivalence class of x.

A polarity in U is a paraconsistent pair of sets $\langle X, Y \rangle$ with $X, Y\subseteq U$ and $X\cap Y\ne \varnothing$. The set of all polarities in U is denoted by $\mathfrak {P}(U)$ which is exactly the product $\mathcal {P}(U)\times \mathcal {P}(U)$ of power sets of U. We use capital letters G, H etc. for polarities. For each $G\in \mathfrak {P}(U)$, if $G=\langle X, Y \rangle$, we write $G^+ =X$ and $G^-=Y$.

Let $\mathcal {K}=(U, R)$ be an approximation space. A polarity G is consistent in $\mathcal {K}$ if $G^+\cap G^- = \varnothing$; and G is complete in $\mathcal {K}$ if $G^+\cup G^- = U$. In the standard Pawlakian rough set theory, a set of objects X to be approximated can be viewed as a consistent and complete polarity $\langle X, X^c \rangle$ where $X^c=U\setminus X$ is the complement of X in U. Each polarity G can be viewed as an attribute or property of objects. The set $G^+$ stands for the set of all objects having the attribute G, and $G^-$ for the set of all objects lacking G. Then objects in $G^+\cap G^-$ both have G and do not have G. This part is the source of inconsistent information. Objects in the complement $(G^+\cup G^-)^c$ neither have nor lack the attribute G, namely no information is given for these objects.

Definition 2

Let $\mathcal {K}=(U, R)$ be an approximation space and $G, H\in \mathfrak {P}(U)$ be polarities. The operations $\sim$, $\sqcap$ and $\sqcup$ are defined as follows:

$$\begin{aligned} {\sim }G&= \langle G^-, G^+ \rangle \\ G\sqcap H&= \langle G^+\cap H^+, G^-\cup H^- \rangle \\ G\sqcup H&= \langle G^+\cup H^+, G^-\cap H^- \rangle . \end{aligned}$$

The binary relation $\sqsubseteq$ on $\mathfrak {P}(U)$ is defined by setting $G\sqsubseteq H$ if and only if $G^+\subseteq H^+$ and $H^-\subseteq G^-$. We define the following sets:

$$\begin{aligned} \underline{G}^+&= \{x\in U: R(x)\subseteq G^+\},&\underline{G}^-&= \{x\in U: R(x)\cap G^- \ne \varnothing \},\\ \overline{G}^+&= \{x\in U: R(x)\cap G^+\ne \varnothing \},&\overline{G}^-&= \{x\in U: R(x)\subseteq G^-\}. \end{aligned}$$

The lower approximation of G is defined as the polarity $\underline{G}=\langle \underline{G}^+, \underline{G}^- \rangle$, and the upper approximation of G is defined as the polarity $\overline{G}=\langle \overline{G}^+, \overline{G}^- \rangle$.

For every approximation space $\mathcal {K}=(U, R)$, it is clear that $\sqsubseteq$ is a partial order on the set $\mathfrak {P}(U)$ of all polarities. Moreover, for all $G, H\in \mathfrak {P}(U)$, $G=H$ if and only if $G\sqsubseteq H$ and $H\sqsubseteq G$.

Example 1

Let $\mathcal {K}=(U, R)$ be the approximation space where $U=\{x_1,x_2,x_3, x_4,x_5\}$ and R is an equivalence relation with classification $\{\{x_1\}, \{x_2,x_4\}, \{x_3,x_5\}\}$. Let $G^+ = \{x_1,x_2\}$ and $G^- = \{x_2, x_3, x_5\}$. Note that the polarity $G=\langle G^+,G^- \rangle$ is inconsistent and incomplete. Note that $R(x_1)=\{x_1\}$, $R(x_2)=R(x_4)=\{x_2,x_4\}$ and $R(x_3)=R(x_5) = \{x_3,x_5\}$. Then $\underline{G}$ and $\overline{G}$ are calculated as follows:

$$ \underline{G}^+ = \{x_1\};~\underline{G}^- = \{x_2,x_3,x_4,x_5\};~ \overline{G}^+ = \{x_1, x_2, x_4\};~\overline{G}^- = \{x_3, x_5\} $$

Note that $\underline{G}$ and $\overline{G}$ are consistent and complete.

Proposition 1

Let $\mathcal {K}=(U, R)$ be an approximation space and $G, H\in \mathfrak {P}(U)$ be polarities. Then the following conditions hold:

• (1) ${\sim }(G\sqcap H) = {\sim }G\sqcup {\sim }H$.

• (2) ${\sim }(G\sqcap H) = {\sim }Q\sqcup {\sim }H$.

• (3) ${\sim }{\sim }G = G$.

• (4) $\langle \varnothing , U \rangle \sqsubseteq G$ and $G\sqsubseteq \langle U, \varnothing \rangle$.

• (5) $\underline{\langle U,\varnothing \rangle } = \langle U,\varnothing \rangle$ and $\overline{\langle \varnothing ,U \rangle } =\langle \varnothing ,U \rangle$.

• (6) if $G\sqsubseteq H$, then $\underline{G}\sqsubseteq \underline{H}$ and $\overline{G}\sqsubseteq \overline{H}$.

• (7) $\underline{G\sqcap H} = \underline{G}\sqcap \underline{H}$ and $\overline{G\sqcup H} = \overline{G}\sqcup \overline{H}$.

• (8) ${\sim }\underline{G} = \overline{\sim G}$ and ${\sim }\overline{G} = \underline{\sim G}$.

• (9) $\underline{G}\sqcap \overline{H}\sqsubseteq \overline{G\sqcap H}$.

Proof

For (6), assume $G\sqsubseteq H$. Suppose $x\in \underline{G}^+$. Then $R(x)\subseteq G^+$. By the assumption, $G^+\subseteq H^+$. Hence $x\in \underline{H}^+$. Suppose $x\in \underline{H}^-$. Then $R(x)\cap H^-\ne \varnothing$. By the assumption, $H^-\subseteq G^-$. Then $R(x)\cap G^-\ne \varnothing$ and so $x\in \underline{G}^-$. Hence $\underline{G}\sqsubseteq \underline{H}$. Similarly $\overline{G}\sqsubseteq \overline{H}$. For (7), clearly $G\sqcap H\sqsubseteq G$ and $G\sqcap H\sqsubseteq H$. By (6), $\underline{G\sqcap H}\sqsubseteq \underline{G}$ and $\underline{G\sqcap H}\sqsubseteq \underline{H}$. Hence $\underline{G\sqcap H}\sqsubseteq \underline{G}\sqcap \underline{H}$. Conversely, $\underline{G}\sqcap \underline{H} = \langle \underline{G}^+\cap \underline{H}^+, \underline{G}^-\cup \underline{H}^- \rangle$ and $\underline{G\sqcap H} = \langle \underline{G^+\cap H^+}, \underline{G^-\cup H^-} \rangle$. Clearly $\underline{G}^+\cap \underline{H}^+\subseteq \underline{G^+\cap H^+}$ and $\underline{G^-\cup H^-}\subseteq \underline{G}^-\cup \underline{H}^-$. Hence $\underline{G}\sqcap \underline{H}\sqsubseteq \underline{G\sqcap H}$. Then $\underline{G\sqcap H} = \underline{G}\sqcap \underline{H}$. Similarly $\overline{Q\sqcup H} = \overline{G}\sqcup \overline{H}$. Other items are shown directly.    $\square$

Proposition 2

Let $\mathcal {K}=(U, R)$ be an approximation space and $G\in \mathfrak {P}(U)$. Then (1) $\underline{G} \sqsubseteq G\sqsubseteq \overline{G}$; (2) $\underline{G} \sqsubseteq \underline{\underline{G}}$ and $\overline{\overline{G}}\sqsubseteq \overline{G}$; and (3) $\overline{G} \sqsubseteq \underline{(\overline{G})}$ and $G\sqsubseteq \underline{(\overline{G})}$.

Proof

(1) Assume $x\in \underline{G}^+$. Then $R(x)\subseteq G^+$. Since R is an equivalence relation, we have $x\in R(x)$ and so $x\in G^+$. Hence $\underline{G}^+\subseteq G^+$. Assume $y\in G^-$. By the reflexivity of R, we have $y\in R(y)$. Then $R(y)\cap G^-\ne \varnothing$. Hence $y\in \underline{G}^-$. Then $G^-\subseteq \underline{G}^-$. It follows that $\overline{G}\sqsubseteq G$. Similarly $G \sqsubseteq \overline{G}$.

(2) Assume $x\in \underline{G}^+$. Then $R(x)\subseteq G^+$. Suppose $y\in R(x)$. Let $z\in R(y)$. By the transitivity of R, we have $z\in R(x)$. Then $z\in G^+$. Hence $R(y)\subseteq G^+$, i.e., $y\in \underline{G}^+$. Then $R(x)\subseteq \underline{G}^+$, i.e., $x\in \underline{\underline{G}}^+$. It follows that $\underline{G}^+\subseteq \underline{\underline{G}}^+$. Assume $x\in \underline{\underline{G}}^-$. Then $R(x)\cap \underline{G}^-\ne \varnothing$. Let $y\in R(x)$ and $y\in \underline{G}^-$. Then $R(y)\cap G^-\ne \varnothing$. Let $z\in R(y)$ and $z\in G^-$. By the transitivity of R, we have $z\in R(x)$. Then $R(x)\cap G^-\ne \varnothing$. Hence $x\in \underline{G}^-$. Then $\underline{\underline{G}}^-\sqsubseteq \underline{G}^-$. Similarly $\overline{\overline{G}}\sqsubseteq \overline{G}$.

(3) Assume $x\in \overline{G}^+$. Then $R(x)\cap G^+\ne \varnothing$. Let $y\in R(x)$ and $y\in G^+$. Suppose $z\in R(x)$. Since R is an equivalence relation, we have $y\in R(z)$. Then $R(z)\cap G^+\ne \varnothing$, i.e., $z\in \overline{G}^+$. Hence $R(x)\subseteq \overline{G}^+$, i.e., $x\in \underline{(\overline{G})}^+$. Then $\overline{G}^+\subseteq \underline{(\overline{G})}^+$. Assume $x\in \underline{(\overline{G})}^-$. Then $R(x)\cap \overline{G}^-\ne \varnothing$. Let $y\in R(x)$ and $y\in \overline{G}^-$. Then $R(y)\subseteq G^-$. Suppose $z\in R(x)$. Since R is an equivalence relation, $z\in R(y)$. Then $z\in G^-$. Hence $R(x)\subseteq G^-$, i.e., $x\in \overline{G}^-$. It follows that $\underline{(\overline{G})}^-\subseteq \overline{G}^-$. Moreover, by (1), we have $G\sqsubseteq \overline{G}\sqsubseteq \underline{(\overline{G})}$.    $\square$

Now we continue by introducing the paraconsistent covering based rough sets which are defined based on covering frames by a neighborhood function N.

Definition 3

Given a nonempty set of objects U, a covering of U is a nonempty collection $\mathscr {C}=\{C_i\subseteq U \mid i\in I\}$ such that $\bigcup \mathscr {C}=U$.

A covering frame is a pair $\mathscr {F}=(U,\mathscr {C})$ where $U\ne \varnothing$ and $\mathscr {C}$ is a covering of U. The neighborhood function $N: U\rightarrow \mathcal {P}(U)$ is defined by setting

$$ N(x)=\bigcap \{C \in \mathscr {C}\mid x\in C \}. $$

For every polarity $G\in \mathfrak {P}(U)$, we define the following sets:

$$\begin{aligned} \Box _N G^+&= \{x\in U: N(x)\subseteq G^+\},&\Box _NG^-&= \{x\in U: N(x)\cap G^- \ne \varnothing \},\\ \Diamond _NG^+&= \{x\in U: N(x)\cap G^+\ne \varnothing \},&\Diamond _NG^-&= \{x\in U: N(x)\subseteq G^-\}. \end{aligned}$$

The lower N-approximation of G is defined as $\Box _NG=\langle \Box _NG^+, \Box _NG^- \rangle$, and the upper N-approximation of G is defined as $\Diamond _NG=\langle \Diamond _NG^+, \Diamond _NG^- \rangle$.

An $\textbf{S4}$-frame is a pair $\mathfrak {F}=(U, R)$ where $U\ne \varnothing$ is a nonempty set of objects and $R\subseteq U\times U$ is a preorder, i.e., a reflexive and transitive relation on U. For every $x\in U$, let $R(x)=\{y\in U: xRy\}$ be the set of all objects related with x in $\mathfrak {F}$.

Example 2

Let $U=\{x_1,x_2,x_3,x_4,x_5\}$ and $R=\{\langle x_i,x_j \rangle \in U\times U: i\le j\}$. Then we have an $\textbf{S4}$ frame $\mathfrak {F}=(U,R)$. Consider the polarity $G=\langle G^+,G^- \rangle$ where $G^+ = \{x_1,x_2\}$ and $G^- = \{x_2, x_3, x_5\}$. Then we calculate $\Box _N G^+ = \varnothing , \Box _NG^- = U, \Diamond _NG^+ =\{x_1, x_2\}$ and $\Diamond _NG^- = \{x_5\}$. Note that $\Box _N G$ is consistent and complete, and $\Diamond _N G$ is consistent and incomplete.

Proposition 3

Let $\mathscr {F}=(U, \mathscr {C})$ be a covering frame and $G,H\in \mathfrak {P}(U)$ be polarities. Then the following conditions hold:

• (1) if $G\sqsubseteq H$, then $\Box _NG\sqsubseteq \Box _N{H}$ and $\Diamond _NG\sqsubseteq \Diamond _N{H}$.

• (2) $\Box _N{G\sqcap H} = \Box _N{G}\sqcap \Box _N{H}$ and $\Diamond _N(Q\sqcup H) = \Diamond _N{G}\sqcup \Diamond _N{H}$.

• (3) ${\sim }\Box _N{G} = \Diamond _N{\sim }G$ and ${\sim }\Diamond _N{G} = \Box _N{\sim G}$.

• (4) $\Box _N{G}\sqcap \Diamond _N{H}\sqsubseteq \Diamond _N(G\sqcap H)$.

• (5) $\Box _N{G} \sqsubseteq G\sqsubseteq \Diamond _N{G}$.

• (6) $\Box _N{G} \sqsubseteq \Box _N{\Box _N{G}}$ and $\Diamond _N{\Diamond _N{G}}\sqsubseteq \Diamond _N{G}$.

Proof

Items (1)–(4) are shown by the definition.

(5) Assume $x\in \Box _N{G}^+$. Then $N(x)\subseteq G^+$. Clearly $x\in N(x)$. Then $x\in G^+$. Hence $\Box _N{G}^+\subseteq G^+$. Assume $y\in G^-$. Then $y\in N(y)$ and so $N(y)\cap G^-\ne \varnothing$. Hence $y\in \Box _N{G}^-$. Then $G^-\subseteq \Box _N{G}^-$. Hence $\Box _N{G}\sqsubseteq G$. Similarly $G \sqsubseteq \Diamond _N{G}$.

(6) We show $\Box _N{G} \sqsubseteq \Box _N{\Box _N{G}}$. Assume $x\in \Box _N{G}^+$. Then $N(x)\subseteq G^+$. Suppose $y\in N(x)$. Let $z\in N(y)$. Then $z\in N(x)$ and so $z\in G^+$. Hence $y\in \Box _N G^+$. Then $N(x)\subseteq \Box _N G^+$, i.e., $x\in \Box _N\Box _N G^+$. Hence $\Box _N G^+\subseteq \Box _N\Box _N G^+$. Now assume $x\in \Box _N\Box _N G^-$. Then $N(x)\cap \Box _NG^-\ne \varnothing$. Let $y\in N(x)$ and $y\in \Box _NG^-$. Then $N(y)\cap G^-\ne \varnothing$. Let $z\in N(y)$ and $z\in G^-$. Then $z\in N(x)$. Hence $N(x)\cap G^-\ne \varnothing$, i.e., $x\in \Box _NG^-$. Then $\Box _N\Box _N G^-\subseteq \Box _N G^-$. Similarly $\Diamond _N{\Diamond _N{G}}\sqsubseteq \Diamond _N{G}$.    $\square$

3 Paraconsistent Rough Set Algebras

In this section, we show that algebras for paraconsistent Pawlakian rough sets are partition topological quasi-Boolean algebras, and algebras for paraconsistent covering based rough sets are topological quasi-Boolean algebras.

An algebra $\mathbb {A}=(A, \cdot , +,\ ', 0, 1)$ is a quasi-Boolean algebra (qBa) if $(A, \cdot , +, 0, 1)$ is a bounded distributive lattice(cf. [8, Definition 2.12]) and for all $a,b\in A$:

• (1) $(a\cdot b)' = a' + b'$.

• (2) $(a+ b)' = a'\cdot b'$.

• (3) $a''=a$

• (4) $0' = 1$ and $1'=0$.

Note that for simplicity, we will abbreviate ab for $a\cdot b$ hereafter. Quasi-Boolean algebras are often used as the fundamental part of rough algebras. If we add modal operators to a qBa satisfying additional conditions, we obtain various rough algebras [2].

Definition 4

An algebra $\mathbb {A}=(A, \cdot ,+,\ ', 0,1, \Box )$ is a topological quasi-Boolean algebra (tqBa) if $(A,\cdot , +,\ ',0,1)$ is a quasi-Boolean algebra, $\Box$ is a unary operations on A such that for all $a,b\in A$:

• $(\textrm{K}_\Box )$ $\Box (a b)=\Box a \Box b$

• $(\textrm{N}_\Box )$ $\Box 1=1$

• $(\textrm{T}_\Box )$ $\Box a\le a$

• $(4_\Box )$ $\Box a\le \Box \Box a$

where the lattice order $\le$ on A is defined by setting $a\le b$ if and only if $a b=b$. Let $\textbf{tqBa}$ be the variety of all topological quasi-Boolean algebras.

A partition topological quasi-Boolean algebra (tqBa5) is a topological quasi-Boolean algebra $\mathbb {A}=(A,\cdot , +,\ ', \Box , 0,1)$ such that for all $a\in A$:

• $(5_\Box )$ $\Diamond a\le \Box \Diamond a$

where $\Diamond$ is the unary operation on A defined by $\Diamond a:= (\Box a')'$. Let $\textbf{tqBa5}$ be the variety of all partition topological quasi-Boolean algebras.

Fact 1

Let $\mathbb {A}=(A, \cdot ,+,\ ', 0,1, \Box )$ be a tqBa. For all $a\in A$, (1) $\Diamond (a+b)=\Diamond a+\Diamond b$; (2) $\Diamond 0=0$; (3) $a\le \Diamond a$ and (4) $\Diamond \Diamond a\le \Diamond a$.

Now we define the dual algebras of approximation space and covering frame respectively.

Definition 5

The dual algebra of an approximation space $\mathcal {K}=(U, R)$ is defined as $\mathcal {K}^* = (\mathfrak {P}(U), \sqcap , \sqcup , {\sim }, \underline{(.)}, \langle \varnothing , U \rangle , \langle U, \varnothing \rangle )$ where $\mathfrak {P}(U)$ is the above defined polarities on U. The operation $\underline{(.)}$ stands for taking the lower approximation of quasicomplement. The dual algebra of a covering frame $\mathcal {F}=(U,\mathscr {C})$ is defined as $\mathcal {F}^\sharp = (\mathfrak {P}(U), \sqcap , \sqcup , {\sim }, \Box _N, \langle \varnothing , U \rangle , \langle U, \varnothing \rangle )$ where $\mathfrak {P}(U)$ is the above defined polarities on U.

By Proposition 1 (8), in the dual algebra $\mathcal {K}^*$ of an approximation space, we can define $\overline{G} := {\sim }(\underline{\sim G})$. By Proposition 3 (3), in the dual algebra $\mathcal {F}^\sharp$ of a covering frame $\mathscr {F}$, we can define $\Diamond _NG:= {\sim }\Box _N{\sim }G$.

Proposition 4

Let $\mathcal {K}=(U, R)$ be an approximation space and $\mathcal {F}=(U,\mathscr {C})$ be a covering frame. Then (1) $\mathcal {K}^*$ is a tqBa5; and (2) $\mathcal {F}^\sharp$ is a tqBa.

Proof

It suffices to show that both algebras defined satisfy the properties of tqBa5 and tqBa respectively. For (1), by Proposition 1 and Proposition 2, $\mathcal {K}^*$ is a tqBa5. For (2), by Proposition 3, $\mathcal {F}^\sharp$ is a tqBa.    $\square$

Let $\mathbb {A}=(A,\cdot , +,\ ', \Box , 0,1)$ be a tqBa. A filter in $\mathbb {A}$ is a subset $u\subseteq A$ such that the following conditions hold for all $a,b\in A$:

• (1) $ab\in u$ for all $a,b\in u$.

• (2) $a\in u$ and $a\le b\in A$ imply $b\in u$.

A filter u in $\mathbb {A}$ is proper if $0\not \in u$. A proper filter u in $\mathbb {A}$ is prime if $a+b\in u$ implies $a\in u$ or $b\in u$. Let U(A) be the set of all prime filters in $\mathbb {A}$. Let $\mathbb {A}=(A,\cdot , +,\ ', \Box , 0,1)$ be a tqBa. A subset $\varnothing \ne X\subseteq A$ has the finite meet property, if $a_1\ldots a_n\ne 0$ for all $a_1,\ldots , a_n \in X$. It is well-known that, by Zorn’s lemma, every subset $\varnothing \ne X\subseteq A$ with the finite meet property can be extended to a proper filter, and every proper filter can be extended to a prime filter.

Fact 2

Let $\mathbb {A}=(A,\cdot , +,\ ', \Box , 0,1)$ be a tqBa. For all $u\in U(A)$ and $a,b\in u$,

• (1) $ab\in u$ if and only $a,b\in u$; and

• (2) $a+b\in u$ if and only if $a\in u$ or $b\in u$.

Moreover, if $\mathbb {A}$ is a tqBa5, then $a\le \Box \Diamond a$ and $\Diamond \Box a\le \Box a$.

Definition 6

The dual space of a tqBa5 $\mathbb {A}=(A,\cdot , +,\ ', \Box , 0,1)$ is defined as the structure $\mathbb {A}_* = (U(A), R^A)$ where $R^A$ is defined as follows:

$uR^Av$ if and only if $\{a: \Box a\in u\}\subseteq v$.

Note that $uR^Av$ if and only if $\{\Diamond b: b\in v\}\subseteq u$.

Lemma 1

For every tqBa5 $\mathbb {A}$, the dual space $\mathbb {A}_*$ is an approximation space.

Proof

Let $\mathbb {A}=(A,\cdot , +,\ ', \Box , 0,1)$ be a tqBa5 and $\mathbb {A}_* = (U(A), R^A)$. It suffices to show that $R_A$ is an equivalence relation. By $(\textrm{T}_\Box )$, $R^A$ is reflexive. By $(4_\Box )$, $R^A$ is transitive. Suppose $uR^Av$ and $a\in v$. Then $\Diamond a\in u$. By $(5_\Box )$, $\Diamond a\le \Box \Diamond a$ and so $\Box \Diamond a\in u$. Then $\Diamond a\in u$. Hence $vR^Au$.    $\square$

Lemma 2

Let $\mathbb {A}=(A,\cdot , +,\ ', \Box , 0,1)$ be a tqBa5 and $u\in U(A)$. If $\Box a \not \in u$, then there exists $v\in R_A(u)$ with $a \not \in v$.

Proof

Assume $\Box a\not \in u$. Consider the set $X=\{b:\Box b\in u\}$ which is clearly closed under meet. Then $a\not \in X$. Now we show that X has the finite meet property. Suppose not. Then $\Box 0 \in u$. Clearly $\Box 0\le 0$ and so $0\in u$ which contradicts $u\in U(A)$. Then there exists a prime filter $v\in U(A)$ with $uR_A v$ and $a\not \in v$.

Let $\mathbb {A}$ and $\mathbb {B}$ be tqBas. A function $f: A\rightarrow B$ is an embedding from $\mathbb {A}$ to $\mathbb {B}$ if f is an injective homomorphism, i.e., for all $a,b\in A$, $f(ab)=f(a)f(b)$; $f(a+b)=f(a)+f(b)$; $f(a') = f(a)'$; $f(0)=0$ and $f(1)=1$; and $f(\Box a)=\Box f(a)$. We say that $\mathbb {A}$ is embedded into $\mathbb {B}$ if there is an embedding from $\mathbb {A}$ to $\mathbb {B}$.

Theorem 1

Every tqBa5 $\mathbb {A}$ is embedded into $(\mathbb {A}_*)^*$.

Proof

Let $\mathbb {A}=(A,\cdot , +,\ ', \Box , 0,1)$ be a tqBa5 and $\mathfrak {P}(U(A)) = \mathcal {P}(U(A))\times \mathcal {P}(U(A))$. Clearly $(\mathbb {A}_*)^* = (\mathfrak {P}(U(A)), \sqcap , \sqcup , \underline{(.)}, \langle \varnothing , U(A) \rangle , \langle U(A), \varnothing \rangle )$. We define the function $f: A\rightarrow \mathfrak {P}(U(A))$ by $f(a) = \langle \pi ^+(a), \pi ^-(a) \rangle$ where

$$ \pi ^+(a) = \{u\in U(A): a\in u\};~\pi ^-(a) = \{v\in U(A): a'\in v\}. $$

Now we show that f is injective. Suppose $a\ne b$. Without loss of generality, suppose $a\not \le b$. By Zorn’s lemma, there exists a prime filter $u\in U(A)$ such that $a\in u$ and $b\not \in u$. This implies that $u\in \pi ^+(a)$ and $v\not \in \pi ^+(b)$. Hence $f(a)\ne f(b)$.

Next we show the function f preserves operations:

(1) We have $\pi ^+(ab) = \{u\in U(A): ab\in u\} = \{u\in U(A): a\in u\}\cap \{u\in U(A): b\in u\} = \pi ^+(a)\cap \pi ^+(b)$. Moreover, $\pi ^-(ab) = \{u\in U(A): (ab)'\in u\} = \{u\in U(A): a' + b'\in u\} = \{u\in U(A): a'\in u\}\cup \{u\in U(A): b'\in u\} = \pi ^-(a)\cup \pi ^-(b)$. Hence $f(ab)=f(a)\sqcap f(b)$.

(2) We have $\pi ^+(a+b) = \{u\in U(A): a+b\in u\} = \{u\in U(A): a\in u\}\cup \{u\in U(A): b\in u\} = \pi ^+(a)\cup \pi ^+(b)$. Moreover, $\pi ^-(a+b) = \{u\in U(A): (a+b)'\in u\} = \{u\in U(A): a' b'\in u\} = \{u\in U(A): a'\in u\}\cap \{u\in U(A): b'\in u\} = \pi ^-(a)\cap \pi ^-(b)$. Hence $f(a+b)=f(a)\sqcup f(b)$.

(3) We have $\pi ^+(a') = \{u\in U(A): a'\in u\} = \pi ^-(a)$. Moreover, $\pi ^-(a') = \{u\in U(A): a''\in u\} = \{u\in U(A): a\in u\} = \pi ^+(a)$. Hence $f(a') = {\sim }f(a)$.

(4) We have $\pi ^+(\Box a) = \{u\in U(A): \Box a\in u\}$. Now we show $\pi ^+(\Box a) = \underline{\pi ^+(a)} = \{u\in U(A): R_A(u)\subseteq \pi ^+(a)\}$. Suppose $u\in \pi ^+(\Box a)$. Then $\Box a\in u$. If $v\in R_A(u)$, then $a\in v$ and so $v\in \pi ^+(a)$. Hence $R_A(u)\subseteq \pi ^+(a)$. Suppose $R(u)\subseteq \pi ^+(a)$. For a contradiction, assume $\Box a\not \in u$. By Lemma 2, there exists $v\in R_A(u)$ with $a\not \in v$. Then $v\in \pi ^+(a)$, i.e., $a\in v$ which contradicts $a\not \in v$. Hence $\pi ^+(\Box a) = \underline{\pi ^+(a)}$. Similarly we have $\pi ^+(\Box a) = \underline{\pi ^-(a)}$. Hence $f(\Box a) = \underline{f(a)}$.    $\square$

Definition 7

Let $\mathbb {A}=(A,\cdot , +,\ ', \Box , 0,1)$ be a tqBa. The binary relation $Q_A\subseteq U(A)\times U(A)$ is defined as follows:

$$uQ_Av \textrm{ if and only if} \{a: \Box a\in u\}\subseteq v. $$

Note that $uQ_Av$ if and only if $\{\Diamond b: b\in v\}\subseteq u$. The function $N_A : U(A)\rightarrow \mathcal {P}(U(A))$ is defined by $N_A(u) =\bigcup \{C\in \mathscr {C}_A: u\in C\}$. Note that $N_A(u)=Q_A(u)$. The dual frame of a tqBa $\mathbb {A}$ is defined as the structure $\mathbb {A}_\sharp = (U(A), \mathscr {C}_A)$ where $\mathscr {C}_A=\{Q_A(u): u\in U(A)\}$.

Lemma 3

For every tqBa $\mathbb {A}$, the dual frame $\mathbb {A}_\sharp$ is a covering frame.

Proof

Let $\mathbb {A}=(A,\cdot , +,\ ', \Box , 0,1)$ be a tqBa. It suffices to show $\bigcup \mathscr {C}_A = U(A)$. Clearly $\bigcup \mathscr {C}_A \subseteq U(A)$. Let $u\in U(A)$. By $(\textrm{T}_\Box )$, $u\in Q(u)$. Hence $u\in \bigcup \mathscr {C}_A$.    $\square$

Lemma 4

Let $\mathbb {A}=(A,\cdot , +,\ ', \Box , 0,1)$ be a tqBa and $u\in U(A)$. If $\Box a \not \in u$, then there exists $v\in Q_A(u)$ with $a \not \in v$.

Proof

The proof is similar to Lemma 2 and details are omitted.

Theorem 2

Every tqBa $\mathbb {A}$ is embeddable into $(\mathbb {A}_\sharp )^\sharp$.

Proof

Let $\mathbb {A}=(A,\cdot , +,\ ', \Box , 0,1)$ be a tqBa and $\mathfrak {P}(U(A)) = \mathcal {P}(U(A))\times \mathcal {P}(U(A))$. Clearly $(\mathbb {A}_\sharp )^\sharp = (\mathfrak {P}(U(A)), \sqcap , \sqcup , \Box _{N_A}, \langle \varnothing , U(A) \rangle , \langle U(A), \varnothing \rangle )$. We define the function $f: A\rightarrow \mathfrak {P}(U(A))$ by $f(a) = \langle \pi ^+(a), \pi ^-(a) \rangle$ where $\pi ^+(a) = \{u\in U(A): a\in u\}$ and $\pi ^-(a) = \{v\in U(A): a'\in v\}$. Like the proof of Theorem 1, the function f is an embedding.    $\square$

4 Logics for Paraconsistent Rough Sets

In this section, we introduce two sequent calculi for Pawlakian paraconsistent rough sets and covering based rough sets respectively.

Definition 8

Let $\mathbb {V}=\{p_i: i\in \omega \}$ be a denumerable set of variables. The set of all formulas Fm is defined inductively as follows:

$$ Fm\ni \phi \,::= p\mid \bot \mid \lnot \phi \mid (\phi _1\wedge \phi _2)\mid (\phi _1\vee \phi _2)\mid \Box \phi $$

where $p\in \mathbb {V}$. We define $\top :=\lnot \bot$ and $\Diamond \phi :=\lnot \Box \lnot \phi$. A sequent is an expression $\varGamma \Rightarrow \phi$ where $\varGamma$ is a finite multiset of formulas and $\phi$ is a formula. For every finite multiset of formulas $\varGamma$, let $\Box \varGamma =\{\Box \phi : \phi \in \varGamma \}$. If $\varGamma =\varnothing$, then $\Box \varnothing = \varnothing$.

Definition 9

The sequent calculus $\textbf{G4}$ consists of the following axiom schemata and inference rules:

• (1) Axiom schemata:

  $$ \mathrm {(Id)}~\phi ,\varGamma \Rightarrow \phi \quad (\bot )~\bot ,\varGamma \Rightarrow \phi \quad (\top )~\varGamma \Rightarrow \top $$
  $$ (T_\Box )~\Box \phi \Rightarrow \phi \quad (4_\Box )~\Box \phi \Rightarrow \Box \Box \phi $$

• (2) Logical rules:

  

  

  

  

  

• (3) Contraposition:

  

• (4) Modal Rules:

  

• (5) Cut rule:

  

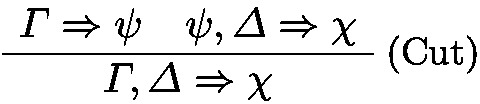
The sequent calculus $\textbf{G5}$ is obtained from $\textbf{G4}$ by adding the following axiom:

$$ (5)~\Diamond \phi \Rightarrow \Box \Diamond \phi . $$

A derivation in a sequent calculus is a finite tree of sequents in which each node is either an axiom or derived from child node(s) by a rule. The height of a derivation is defined as the maximal length of branches in it. For $\textbf{G}\in \{\textbf{G4}, \textbf{G5}\}$, let $\textbf{G}\vdash \varGamma \Rightarrow \psi$ denote that the sequent $\varGamma \Rightarrow \psi$ is derivable in $\textbf{G}$. A formula $\phi$ is $\textbf{G}$-equivalent to $\psi$ (notation: $\textbf{G}\vdash \phi \Leftrightarrow \psi$) if $\textbf{G}\vdash \phi \Rightarrow \psi$ and $\textbf{G}\vdash \psi \Rightarrow \phi$.

Proposition 5

The following hold:

• (1) $\textbf{G4}\vdash {\lnot }\top \Leftrightarrow \bot$ and $\textbf{G4}\vdash \phi \Leftrightarrow {\lnot }{\lnot }\phi$.

• (2) $\textbf{G4}\vdash {\lnot }(\phi \wedge \psi )\Leftrightarrow {\lnot }\phi \vee {\lnot }\psi$ and $\textbf{G4}\vdash {\lnot }(\phi \vee \psi )\Leftrightarrow {\lnot }\phi \wedge {\lnot }\psi$.

• (3) $\textbf{G4}\vdash {\lnot }\Box \phi \Leftrightarrow \Diamond \lnot \psi$ and $\textbf{G4}\vdash \lnot \Diamond \phi \Leftrightarrow \Box \lnot \phi$.

• (4) if $\textbf{G4}\vdash \phi \Rightarrow \psi$, then $\textbf{G4}\vdash \Box \phi \Rightarrow \Box \psi$ and $\textbf{G4}\vdash \Diamond \phi \Rightarrow \Diamond \psi$.

• (5) $\textbf{G4}\vdash \Box (\phi \wedge \psi )\Leftrightarrow \Box \phi \wedge \Box \psi$ and $\textbf{G4}\vdash \Diamond (\phi \vee \psi )\Leftrightarrow \Diamond \phi \vee \Diamond \psi$.

• (6) $\textbf{G4}\vdash \Box \phi \wedge \Diamond \psi \Rightarrow \Diamond (\phi \wedge \psi )$.

• (7) $\textbf{G4}\vdash \phi \Rightarrow \Diamond \phi$.

• (8) $\textbf{G4}\vdash \Box \phi \Leftrightarrow \Box \Box \phi$ and $\textbf{G4}\vdash \Diamond \phi \Leftrightarrow \Diamond \Diamond \phi$.

• (9) $\textbf{G5}\vdash \phi \Rightarrow \Box \Diamond \phi$ and $\textbf{G5}\vdash \Diamond \Box \phi \Leftrightarrow \Box \phi$.

Proof

We show $\textbf{G4}\vdash {\lnot }(\phi \wedge \psi )\Leftrightarrow {\lnot }\phi \vee {\lnot }\psi$. We have the following derivations:

We show $\textbf{G4}\vdash \Box (\phi \wedge \psi )\Leftrightarrow \Box \phi \wedge \Box \psi$. We have the following derivations:

The remaining items are shown regularly.    $\square$

An assignment in a tqBa $\mathbb {A}$ is a function $\theta : \mathbb {V}\rightarrow A$. A sequent $\varGamma \Rightarrow \phi$ is valid in a tqBa $\mathbb {A}$ (notation: $\mathbb {A}\models \varGamma \Rightarrow \phi$), if $\bigwedge _{\psi \in \varGamma }\theta (\psi )\le \theta (\phi )$. The notation $\textbf{tqBa}\models \varGamma \Rightarrow \phi$ denote that $\varGamma \Rightarrow \phi$ is valid in all tqBas, and the notation $\textbf{tqBa5}\models \varGamma \Rightarrow \phi$ denote that $\varGamma \Rightarrow \phi$ is valid in all tqBa5s.

Theorem 3

For every sequent $\varGamma \Rightarrow \phi$, (1) $\textbf{G4}\vdash \varGamma \Rightarrow \phi$ if and only if $\textbf{tqBa}\models \varGamma \Rightarrow \phi$; and (2) $\textbf{G5}\vdash \varGamma \Rightarrow \phi$ if and only if $\textbf{tqBa}\models \varGamma \Rightarrow \phi$.

Proof

This is shown by the standard Lindenbaum-Tarski method. The soundness part is shown directly by induction on the height of a derivation of $\varGamma \Rightarrow \phi$ in a sequent calculus. For $\textbf{G}\in \{\textbf{G4}, \textbf{G5}\}$, the binary relation $\equiv _\textbf{G}$ on the set of all formulas Fm is defined by setting

$$\phi \equiv _\textbf{G}\psi \textrm{ if and only if} \textbf{ G}\vdash \phi \Rightarrow \psi \textrm{ and} \textbf{ G }\vdash \psi \Rightarrow \phi.$$

One can easily show that $\equiv _\textbf{G}$ is a congruence relation on Fm. Let $Fm/_\textbf{G}=\{[\phi ]: \phi \in Fm\}$ where $[\phi ]=\{\psi \in Fm: \phi \equiv _\textbf{G}\psi \}$ is the equivalence class of $\phi$. The Lindenbaum-Tarski algebra for $\textbf{G}$ is defined as $\mathfrak {L}_\textbf{G}=(Fm/_\textbf{G}, \cdot , +,\ ', [\bot ], [\top ])$ where we have

$[\phi ][\psi ] = [\phi \wedge \psi ]$, $[\phi ]+[\psi ] = [\phi \vee \psi ]$ and $[\phi ]' = [{\sim }\phi ]$.

Obviously $\mathfrak {L}_\textbf{G4}$ is a tqBa and $\mathfrak {L}_\textbf{G5}$ is a tqBa5. Suppose $\textbf{G}\not \vdash \varGamma \Rightarrow \phi$. Let $\theta$ be the assignment in $\mathfrak {L}_\textbf{G}$ such that $\theta (p)=[p]$ for each $p\in \mathbb {V}$. By induction on the complexity of a formula $\chi$, we have $\theta (\chi )=[\chi ]$. Hence $\mathfrak {L}_\textbf{G}\not \models \varGamma \Rightarrow \phi$.    $\square$

Let $\mathcal {K}=(U, R)$ be an approximation space and $\mathscr {F}=(U, \mathscr {C})$ be a covering frame. A sequent $\varGamma \Rightarrow \phi$ is valid in $\mathcal {K}$ (notation: $\mathcal {K}\models \varGamma \Rightarrow \phi$), if $\mathcal {K}^*\models \varGamma \Rightarrow \phi$. Let $\textbf{AS}\models \varGamma \Rightarrow \phi$ denote that $\varGamma \Rightarrow \phi$ is valid in all approximation spaces. A sequent $\varGamma \Rightarrow \phi$ is valid in $\mathscr {F}$ (notation: $\mathscr {F}\models \varGamma \Rightarrow \phi$), if $\mathscr {F}^\sharp \models \varGamma \Rightarrow \phi$. Let $\textbf{CF}\models \varGamma \Rightarrow \phi$ denote that $\varGamma \Rightarrow \phi$ is valid in all covering frames.

Corollary 1

For every sequent $\varGamma \Rightarrow \phi$, (1) $\textbf{G4}\vdash \varGamma \Rightarrow \phi$ if and only if $\textbf{AS}\models \varGamma \Rightarrow \phi$; and (2) $\textbf{G5}\vdash \varGamma \Rightarrow \phi$ if and only if $\textbf{CF}\models \varGamma \Rightarrow \phi$.

Proof

It follows immediately from Theorem 3, Theorem 1 and Theorem 2.    $\square$

5 Concluding Remarks

The present work contributes new paraconsistent Pawlakian rough sets and paraconsistent covering based rough sets by introducing approximations of polarities in a universe of objects. Moreover, topological quasi-Boolean algebras are shown to be algebras for paraconsistent covering based rough sets, and partition topological quasi-Boolean algebras are shown to be algebras for paraconsistent Palwakian rough sets. Finally, we present sequent calculi as modal systems for these paraconsistent rough sets. There are some problems which need to be explored further. One problem is about the applications of these paraconsistent rough sets in practical scenarios. The other problem is extendeding the approach taken in the present paper to other types of rough sets. For example, as in [9, 10], we can consider the connections between Kripke structures, covering frames and algebras for various paraconsistent rough sets.