Abstract
A survey of approaches yielding paraconsistent logics is made and is summarised through a diagram. The rough set theoretic approach is included in the survey, and it is the focus in the second part of the work. Several new paraconsistent systems are presented, that are obtained by weakening existing rough modus ponens rules.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
In common sense reasoning, one often derives meaningful conclusions from contradictory information, that is, information which contains both a statement and its negation. Classical logic does not allow such inferences. Many researchers have tried to deal with the issue by formulating “inconsistency-tolerant systems” [26]. Such systems violate either of two classical properties: the principle of explosion or the law of non-contradiction. Violation of the principle of explosion forms the basis of paraconsistent logics. The paper presents a survey of various techniques which give rise to paraconsistent logics. There are several existing surveys of paraconsistent systems, for instance in [1, 24, 26, 31, 38, 40]. However, this survey is an attempt to compile almost all the major techniques by which paraconsistent systems are arrived at. Furthermore, we focus on paraconsistent logics arising out of rough set theory – this is not part of any of the other surveys. Utilising the notion of rough truth [36] and various forms of rough modus ponens [6, 17], paraconsistent systems have been obtained. Furthering this direction of work, we get new paraconsistent systems by weakening existing rough modus ponens rules.
Let us give the formal versions of the classical principles mentioned above. Define a logic \(\mathcal {L}\) as a tuple \((FOR, \vdash )\), where FOR represents the set of formulas, and \(\vdash \) is the consequence relationFootnote 1 \((\vdash \subseteq \mathcal {P}(FOR) \times FOR)\). FOR is based on an enumerable language with the connective negation \((\lnot )\). Let \(\varGamma \cup \{\alpha ,\beta \} \subseteq FOR\).
(I) The Principle of Explosion or Ex Contradictione Quodlibet (ECQ):
\(\forall \varGamma \forall \alpha \forall \beta (\varGamma \cup \{\alpha , \lnot \alpha \} \vdash \beta ).\)
(II) The Law of Non-contradiction (LNC): \(\vdash \lnot (\alpha \wedge \lnot \alpha )\).
A logic \(\mathcal {L}\) is said to be explosive if ECQ holds.
Łukasiewicz’s 3-valued logic [14] and Kleene’s 3-valued logic [30] are examples of inconsistency-tolerant systems that violate LNC. However, ECQ holds in both – so these are not referred to as paraconsistent systems. Note that in classical logic, ECQ and LNC are equivalent. The above two logics show that the principles may not be comparable in the context of inconsistency-tolerant logics. In fact, there are also logics, such as the Logic of Paradox [38], where ECQ fails but LNC holds.
The survey of approaches giving paraconsistent logics (i.e. where ECQ fails) is summarised by the diagram given in Fig. 1. In Sect. 2, we briefly outline the motivations behind each approach (including the rough set theoretic one), and cite some logics that are obtained by following the approach. In Sect. 3, new paraconsistent systems arising from the rough set theoretic approach are presented. Section 4 concludes the article.
2 Different Approaches to Paraconsistency
Let us now present the different approaches, mentioning how ECQ is violated in each case yielding paraconsistent logics. Figure 1 gives a brief representation of the complete survey. The rectangular nodes, other than the topmost node, represent different techniques of obtaining paraconsistent logics violating ECQ.
2.1 The 3-Valued Approach
Let the three truth-values be denoted as t, m, f, where t, f correspond to the classical truth values true and false respectively, and m represents the middle-value. The question of whether the third value should be regarded as “close” to the notion of truth or not is then addressed – in the former case, it is termed as a designated value. Paraconsistency may result, when m and t are both designated values. Let us see how. We assume that the logical connective of negation \((\lnot )\) in the language behaves classically on \(\{t, f\}\), i.e., \(\lnot t = f\), \(\lnot f= t\), while \(\lnot m= m\). So for any propositional variable p in the language, if p takes the value m, \(\lnot p\) also evaluates to m. The semantic consequence relation \(\vDash \) is defined such that whenever the premisses take designated values under any valuation, the conclusion must also get a designated value under that valuation. It is then clear that for any distinct propositional variables p, q and a valuation that gives p the value m and q the value f, \(\{p,\lnot p\} \nvDash q\). An example for this approach is provided by the Logic of Paradox (LP) mentioned earlier in Sect. 1. This 3-valued logic was proposed to deal with logical paradoxes; in this logic the truth-value m represents both true and false.
2.2 Non-adjunctive Approach
A non-adjunctive system is one that does not validate the law of adjunction, i.e. there exist formulas \(\alpha \), \(\beta \) such that \(\{\alpha , \beta \} \nvdash \alpha \wedge \beta \), where \(\wedge \) is the logical connective of conjunction. In particular, if \(\beta := \lnot \alpha \) then \(\{ \alpha , \lnot \alpha \} \nvdash \alpha \wedge \lnot \alpha \), which ensures that such a system violates ECQ. The first known non-adjunctive paraconsistent logic is the Discussive (or Discursive) logic (J) proposed by Jaśkowski [23, 29]. The motivation of not adopting the law of adjunction in J, arose from the perspective of a discussion where different participants may offer some contradictory information, idea or opinion. According to an individual participant, a statement in a discussion may be true and consistent, but may be discordant with the opinion of other participants. Let us imagine that each participant in the discussion is represented by a single world and the opinion of that participant is considered to be true in that very world; i.e. each such set of sentences is true in at least one world. This sense of world based semantics might have been the reason for which Jaśkowski considered the normal modal logic S5 to model the semantics for J. The language of J is that of S5 (see [23]). The semantic consequence relation \((\vDash _{J})\) is defined for J as follows: \(\varGamma \vDash _{J} \alpha ~\text{ if } \text{ and } \text{ only } \text{ if }~ \lozenge \varGamma \vDash _{S5} \lozenge \alpha \), where “\(\lozenge \)” is the possibility modal operator and \(\lozenge \varGamma := \{\lozenge \gamma : \gamma \in \varGamma \}\). For any propositional variable p, it is easy to show in S5 that \(\{\lozenge p, \lozenge \lnot p\} \nvDash _{S5}\lozenge (p\wedge \lnot p)\) and thus \(\{p,\lnot p\} \nvDash _{J} p\wedge \lnot p\).
2.3 Non-truth Functional Approach
Classically, the truth value of a compound formula, is wholly determined by the truth value(s) of the propositional variables that occur in the formula, and the logical connectives are referred to as being truth functional. In particular, if negation is not truth functional, the possibility of violation of ECQ arises – as we observe in the following examples. Consider Da-costa’s \(C_n\)-systems [22] and Diderik Batens’ system PI [8]. In both these logics, negation is taken to be weaker than that in classical logic. One direction of classical negation holds: if a statement is false then its negation is true. However, it is possible that a statement and its negation are both true. But then \(\{p,\lnot p\} \nvDash q\) for distinct propositional variables p, q. A non-truth functional semantics for negation is also considered by Tuziak [45] in case of the paraconsistent extensions of the positive fragment \(CPL^{+}\) of CPL, the classical propositional logic. Other than one extension that is explosive, one can argue that ECQ is violated in the rest, in a manner similar to the cases of \(C_n\) and PI.
2.4 Transformation Approach
The transformation approach gives us different ways to obtain a paraconsistent logic from an explosive logic. The basic principle is to define a new logic by restricting the inferences of the mother logic in such a manner that the new logic becomes non-explosive. We place under this approach, the methods defined in [7, 15, 25, 39]. For other methods of variable inclusion readers are referred to [16].
In [25] the authors have presented a method called paraconsistentization, where the consequence relation of the transformed system is based on those derivations of the parent consequence relation that are obtained from a consistent subset of the premise set. Let us describe this formally.
Given a logic \(\mathcal {L}:=(FOR, \vdash )\) and \(\varGamma \subseteq FOR\), the set \(C(\varGamma ) := \{\alpha : \varGamma \vdash \alpha \}\), is said to be the set of all consequences of \(\varGamma \). \(\varGamma \) is called C - consistent if \(C(\varGamma ) \ne FOR\), otherwise it is called C - inconsistent. The paraconsistentizaion consequence relation \(\vdash ^{ \mathbb {P}} \subseteq \mathcal {P}(FOR) \times FOR\) is defined as \(\varGamma \vdash ^{ \mathbb {P}} \alpha \), if and only if there is some C-consistent subset \(\varGamma ^{'}\) of \(\varGamma \) such that \(\varGamma ^{'} \vdash \alpha \). In [25], a set of conditions on C is imposed so that the corresponding \((FOR,\vdash ^{ \mathbb {P}}) \) becomes paraconsistent.
As examples, one can show that the consequence relations of Łukasiewicz’s 3-valued logic (Ł\(_3\)) [14], Gödel’s 3-valued logic \((G_3)\) [41] and Kleene’s 3-valued logic \((K_3)\) [30] (in all of which ECQ holds) satisfy the said conditions. Hence the paraconsistentization of these logics are indeed paraconsistent.
Two other methods for converting a system satisfying ECQ into one that violates the principle, have been presented in [7, 15]. These are termed as the left variable inclusion and restricted rules methods.
A new logic \(\mathcal {L}^{l}:=(FOR, \vdash ^{l})\), based on \(\mathcal {L}\), is defined as follows:
\(\varGamma \vdash ^{l} \alpha \) if and only if there is a \(\varGamma ^{'} \subseteq \varGamma \) such that \(Var(\varGamma ^{'}) \subseteq Var(\alpha )\) and \(\varGamma ^{'} \vdash \alpha \),
where \(Var(\gamma )\) is the set of all propositional variable(s) contained in \(\gamma \), and \(Var(\varGamma ) := \cup \{Var(\gamma ) : \gamma \in \varGamma \}\). The new logic \(\mathcal {L}^{l}\) is known as the left variable inclusion companion of \(\mathcal {L}\).
In the restricted rules method, one Hilbert-style logic is obtained from another by imposing restrictions on logical rules. Suppose \(\mathcal {L}\) is a Hilbert-style logic with \(A (\subseteq FOR)\) as the set of axioms and \(R_{\mathcal {L}}(\subseteq \mathcal {P}(FOR) \times FOR)\) as the set of rules of inference. Based on \(\mathcal {L}\), a new Hilbert-style logic \(\mathcal {L}^{re}:=(FOR, \vdash ^{re})\) is defined with the same set A of axioms and set of rules \(R_{\mathcal {L}^{re}}\) := \(\{\frac{\varGamma }{\alpha } \in R_{\mathcal {L}}\) | \(Var(\varGamma )\subseteq Var(\alpha )\}\). \(\mathcal {L}^{re}\) is known as the restricted rules companion of \(\mathcal {L}\).
In [7], it is shown that if \(\mathcal {L}\) is a Hilbert-style logic then \(\mathcal {L}^l\) is stronger thanFootnote 2 \(\mathcal {L}^{re}\) in the sense that for all \(\varGamma \) and \(\alpha \), \(\varGamma \vdash ^{re} \alpha \) implies \(\varGamma \vdash ^{l} \alpha \). Moreover, the authors showed that if the mother logic contains a formula \(\alpha \) such that \(\alpha \) is not a theorem and there is some propositional variable p which is not included in \(\alpha \), then both the logics, obtained by applying left variable inclusion and restricted rules, are paraconsistent. The same work also presents a sufficient condition specifying when \(\mathcal {L}^{l}\) and \(\mathcal {L}^{re}\), obtained from the same mother logic, would be identical. CPL serves as an example for which the left variable inclusion and restricted rules companions are identical, and paraconsistent.
Plurivalence [39] is another way of transforming an explosive logic to a non-explosive one. In this method a mother logic (two-valued or many-valued) with a univalent semantic consequence relation \(\models _{u}\) is converted to a logic by generating a plurivalent semantic consequence relation \(\models _{p}\). However, in [39], the author mainly focused on converting a many-valued logic with a univalent consequence relation to its “plurivalent” counterpart. A univalent interpretation (\(M, \mathcal {V}\)) is considered based on a structure M := (\(V, D, \delta \)), consisting of a non-empty set V of truth values, a designated set D (\(\subseteq V\)) of truth values, a set \(\delta \) of truth functions for the logical connectives, and a valuation \(\mathcal {V}\), assigning a unique truth value to each propositional variable. \(\mathcal {V}\) is extended over the set of all formulas in the usual recursive manner, and \(\models _{u}^{M}\) is also defined in the usual manner: \(\varGamma \models _{u}^{M} \alpha \) if and only if for all interpretations (\(M, \mathcal {V}\)), if \(\mathcal {V}(\gamma ) \in D\) for all \(\gamma \in \varGamma \) then \(\mathcal {V}(\alpha ) \in D\). Now given (\(M, \mathcal {V}\)), the respective plurivalent interpretation (\(M, \mathcal {R}\)) is obtained by replacing the valuation \(\mathcal {V}\) by a relation \(\mathcal {R}\) which relates every propositional variable to a subset of V, and the relation is suitably extended [39] over the whole set of formulas. Further, it is defined that \(\mathcal {R}\) designates \(\alpha \) if and only if there is some \(v\in D\) such that \(\alpha \mathcal {R} v\) holds. The plurivalent semantic consequence \(\vDash ^M_p\) is defined as follows: \(\varGamma \vDash ^M_p \alpha \) if and only if for all interpretations \((M, \mathcal {R})\), if \(\mathcal {R}\) designates every member of \(\varGamma \) then \(\mathcal {R}\) designates \(\alpha \). It is observed that for any plurivalent semantics which contains the truth-values t (true) and f (false) such that negation \((\lnot )\) behaves classically for t, f, ECQ is violated by \(\vDash ^M_p\). As an example, the plurivalent counterpart of CPL is in fact, LP (ref. Sect. 2.1).
2.5 Logics of Formal Inconsistency
The key feature of the logics of formal inconsistency (LFI) is to bring in a unary ‘consistency’ operator \(\circ \) in the object language so that some formulas can be segregated from those which are tolerant to inconsistency. The first reported such family of logics was proposed by Carnielli and Marcos in [18, 20]. A finite set of compound formula(s) involving only \(\alpha \), denoted as \(\ocircle (\alpha )\), is introduced. With respect to this set a contradictory premise may behave classically. If \(\ocircle (\alpha )\) is a singleton, it is simply denoted as \(\circ \alpha \).
Further, a notion of gentle explosion is defined. A set \(\varGamma \) of formulas is said to be \(\textit{gently explosive}\) if (i) there is \(\alpha \) such that \(\ocircle (\alpha ) \cup \{\alpha \}\) and \(\ocircle (\alpha ) \cup \{\lnot \alpha \}\) are both non-trivialFootnote 3, and (ii) for all \(\alpha , \beta \), \(\varGamma \cup \ocircle (\alpha ) \cup \{\alpha , \lnot \alpha \} \vDash \beta \). A logic \(\mathcal {L}\) is said to satisfy Gentle Principle of Explosion (gPPS) if all \(\varGamma (\subseteq FOR)\) are gently explosive. Then an LFI is defined as follows.
Definition 1
A logic \(\mathcal {L}\) is said to be LFI if ECQ does not hold but (gPPS) holds.
Thus, the definition of LFI allows explosion in a controlled way; it allows \(\{\alpha , \lnot \alpha \}\) to be explosive in the presence of \(\ocircle \alpha \), where neither \(\alpha \) nor \(\lnot \alpha \) alone leads to triviality in the presence of \(\ocircle \alpha \). Let us note that Da Costa’s hierarchy of \(C_{n}\)-systems, discussed in Sect. 2.3, are all examples of LFI. As mentioned in [18], Discussive logic (J) (ref. Sect. 2.2) is also an LFI, in which \(\ocircle (\alpha )= \circ \alpha := \lnot (\alpha \rightarrow _{d} \lnot (\alpha \vee \lnot \alpha )) \rightarrow _{d} (\lnot \alpha \rightarrow _{d} \lnot (\alpha \vee \lnot \alpha )) \).
A wide variety of paraconsistent logics fall under the general definition of LFIs. For instance, a fundamental LFI logic (mbC) is proposed as an extension of \(CPL^{+}\) by adding \(\circ \) in the language and axioms \(\circ \alpha \rightarrow (\alpha \rightarrow (\lnot \alpha \rightarrow \beta ))\) and \(\alpha \vee \lnot \alpha \), where the former one presents a form of gentle explosion.
Moreover, mbC also shares properties of the non-truth functional approach discussed in Sect. 2.3. A valuation \(\mathcal {V}\) for mbC is a function that assigns the values t and f to all formulas where the semantics for negation \((\lnot )\) and consistency operator \((\circ )\) is given below.
-
(1)
\(\mathcal {V}(\lnot \alpha ) = f\) implies \(\mathcal {V}(\alpha ) = t.\)
-
(2)
\(\mathcal {V}(\circ \alpha ) = t \) implies \(\mathcal {V}(\alpha ) = f\) or \(\mathcal {V}(\lnot \alpha ) = f\).
Clearly, both \(\lnot \) and \(\circ \) are non-truth functional. Thus, based on the usual definition of semantic consequence it can be shown that \(\{\circ p, p \}\nvDash _{mbC} q\) and \(\{\circ p, \lnot p\} \nvDash _{mbC} q\) for some distinct p, q; however, as \(\circ p\), p, \(\lnot p\) cannot be true together, \(\{\circ p, p, \lnot p\} \vDash _{mbC}\beta \) for all \(\beta \). So mbC satisfies (gPPS). Moreover, from Sect. 2.3 it is straightforward that mbC violates ECQ. Hence mbC is an LFI. In a step by step manner adding some further axiom schemes and imposing some further conditions on \(\circ \), Carnielli and Marcos have developed a series of interesting LFIs. For more details readers are referred to [19, 20].
2.6 Adaptive Approach
The adaptive approach aims to identify the appearance of inconsistency within a derivation and develop strategies to adapt changes in the derivation so that it violates ECQ. Diderik Batens is the forerunner in developing different strategies for adaptive reasoning [9], among which the strategies dealing with inconsistencies lead towards paraconsistent systems. An adaptive logic consists of three components, namely (i) a lower limit logic (LLL) (ii) a set of abnormalities, and (iii) an adaptive strategy. LLL consists of a number of inferential rules that are accepted as a basis for a particular adaptive system. The set of abnormalities consists of some formulas that help to decide when an already derived formula need not be a conclusion. An adaptive strategy describes how to handle the applications of inference rules based on the set of abnormalities. The LLL and the collection of abnormalities jointly define the strategy to be adapted in the derivation chain, and on the other hand the set of abnormalities and the strategies jointly define which formulas in the derivation chain are to be marked for throwing out of consideration. The upper limit logic (ULL) can be obtained by extending LLL with the condition that no abnormality is logically derivable. ULL includes the inferential rules (and/or axioms) of LLL as well as some supplementary rules (and/or axioms) that can be used during the reasoning process in the absence of abnormalities. Thus, based on the set of inference rules and axioms added to LLL, there can be different adaptive logics lying between LLL and ULL.
Let us consider an example of an adaptive logic CLuN\(^m\) which is obtained from the lower limit logic CLuNFootnote 4 [11, 12] where abnormal formulas are of the form \(\alpha \wedge \lnot \alpha \) and classical logic CPL is used as an ULL.
Let \(\varGamma := \{p,q, \lnot p, \lnot p \vee r, \lnot q \vee s \}\) be a premise set, where p, q, r, s are all propositional variables. In the logic CLuN, r cannot be deduced from \(\varGamma \) (see [10]). Below, let us present how the adaptive notion of derivation accommodates something additional in the logic CLuN\(^m\).
The first five steps of the derivation chain are obtained directly from \(\varGamma \). At step 6, r is derived from steps 1 and 4 under the condition p behaves consistently as the formula \(p\wedge \lnot p\) has not been derived till now in the derivation chain. Similarly at step 7, s is derived under the condition q behaves consistently. However at stage 8, \(p \wedge \lnot p\) is derived from the steps 1 and 3. That is, the inconsistent behaviour of p becomes prominent at stage 8 and thus r can no longer be guaranteed as a deduction under CLuN\(^m\). So, after the inconsistent behaviour of p becomes apparent at stage 8, the line 6 is marked with \((\surd )\) to indicate that a previously derived formula is no longer possible to derive. Hence ECQ fails to hold in CLuN\(^m\). In general, we have \(C_{{{\textbf {CLuN}}}}(\varGamma ) \subset C_{{\textbf {CLuN}}^m}(\varGamma ) \subset C_{CPL} (\varGamma )\), where C denotes a consequence operator.
2.7 Relevance Approach
T.J. Smiley, in 1959, attempted to impose a notion of relevance between the premisses and conclusion of an inference relation by defining the logical entailment [43] as follows: \(\{\alpha _1, \alpha _2, ... , \alpha _n\} \vdash \beta \) if and only if \((\alpha _1 \wedge \alpha _2 \wedge ...\wedge \alpha _n)\rightarrow \beta \) is a classical tautology and neither \(\lnot (\alpha _1 \wedge \alpha _2 \wedge ...\wedge \alpha _n)\) nor \(\beta \) is a tautology. Thus, \(\{\alpha , \lnot \alpha \} \vdash \beta \) fails to hold as \(\lnot (\alpha \wedge \lnot \alpha )\) is a classical tautology. Contrary to classical context here the semantic consequence is not defined based on the material implication which allows anything to follow from a false formula. The mentioned notion of entailment is not reflexive as clearly \(\{\alpha \wedge \lnot \alpha \} \nvdash \alpha \wedge \lnot \alpha \).
The relevant logics of Anderson and Belnap (1975), known as first-degree entailment (FDE), contains formulas of the form \(\alpha \rightarrow \beta \) called first-degree entailments, where \(\alpha , \beta \) do not contain any occurrence of the connective \(\rightarrow \). Belnap and Dunn around 1977 [13] proposed a four-valued semantics for FDE containing the truth values \(N=\emptyset \), \( T=\{t\}\), \(F=\{f\}\), \(B=\{t,f\}\) where T, F behave classically and \(\lnot B= B\), \(\lnot N= N\). Considering \(D:=\{T, B\}\) as the designated set of truth values, the semantic consequence for FDE is defined as: \(\varGamma \vDash _{fde} \alpha \) if and only if for all valuation \(\mathcal {V}\), if \(\mathcal {V}(\alpha ) \in D\) for all \(\alpha \in \varGamma \) then \(\mathcal {V}(\beta ) \in D\) [33, 42]. Clearly \(\{p, \lnot p\}\nvDash _{fde} q\), where p, q are distinct propositional variables.
2.8 Rough Set Approach
Rough sets were introduced by Pawlak in 1982 [35]. In literature, one finds different approaches linking rough sets and paraconsistency. For instance, in [47, 48], a notion of “paraconsistent set” is developed. Contrary to a set over a universe U, a paraconsistent set incorporates a four-valued membership function which also can be represented as a set over \(U \cup \lnot U\) where \(\lnot U\) = \(\{\lnot x: x \in U\}\) and for any \(X \subseteq U \cup \lnot U\), \(\lnot x \in X\) denotes that there is an evidence that x is not in X. Then, a notion of paraconsistent rough set is defined by bringing in rough approximation space in the context of paraconsistent set. Consequently, “whether an object is an instance of a certain concept” is approximated. Such approximations are often relevant in abstracting rules from a database.
Similar attempts can be found in the area of paraconsistent rough description logics [46], where typically the aim has been to develop a language which can represent assertions like “an object is an instance of a concept”, “two objects are related by a relation” etc., and design a reasoning strategy based on such assertions. As databases may contain inconsistent information and the rough set based approximations are defined based on a database, interpreting or evaluating the assertions generated from a database using the tools of paraconsistent set and paraconsistent rough set come naturally. However, in none of the above mentioned works the intention has been to develop a proof theory for deductive reasoning based on such a language.
In [32, 44, 49], some logics are developed based on the notion of paraconsistent rough sets. However, the consequence relation of most of them are explosive. Among the logics presented in [44], DDT is a first-order extension of Belnap’s logic involving two negations (weak and strong) and it can be shown that the consequence relation is non-explosive only with respect to the weak negation.
In contrast to the above-mentioned rough set approaches to paraconsistency, in [32] the authors developed a proof theory for the decision logic of rough sets based on a four-valued tableau calculi. The original work of decision logic of rough sets was by Pawlak [37], addressing consistent decision tables. This idea is extended in [32] by introducing a variable precision rough set model and respectively allowing four values, namely true, false, uncertain, inconsistent, to describe whether an object is an instance of a concept. In the tableau calculi, for four-valued logic two negations are introduced. With respect to the strong negation (\(\sim \)) the rule for explosion, denoted by \(\{Tp, T\sim p\}\), is dropped and with respect to the weak negation (\(\lnot \)) violation of LNC is shown. Although, in the work the authors presented a logic for decision systems which is paraconsistent in nature, the language and its interpretation are developed keeping decision systems in mind, and the logical inference is not defined for deriving a formula from a non-empty set of formulae – as is the focus of the present paper.
Relations between 3-valued systems (algebras, logics) and rough sets have been discussed in several papers, e.g. [3, 4, 21, 28, 34]. The 3-valued approach adopted in [3] in particular, yields a few deductive systems of reasoning including a paraconsistent logic \(\mathcal {L}^{I}\) which we briefly present here. The language of \(\mathcal {L}^{I}\) has a countable set of propositional variables \(P:=\{p,q,r,...\}\) and connectives \(\lnot , \rightarrow \). The formulas are defined using the scheme: \(p~|~\lnot \alpha ~|~ \alpha \rightarrow \beta \). Let \(FOR^{I}\) denote the set of all formulas. A sequent calculus for \(\mathcal {L}^{I}\) is formulated that is shown to be sound and complete with respect to a semantics based on a non-deterministic matrix (Nmatrix). Let us describe the semantics. The Nmatrix corresponding to \(\mathcal {L}^{I}\) is defined as \(\mathcal {M}^{I} := (\mathcal {T}^{I}, \mathcal {D}^{I}, \mathcal {O}^{I})\) where,
-
\(\mathcal {T}^{I} := \{t (true), f (false), u (unknown)\}\) is a set of truth values,
-
\( \mathcal {D}^{I} :=\{t,u\} \) is the set of designated values,
-
\(\mathcal {O}^{I} := \{ \lnot ^{\mathcal {M}}, \rightarrow ^{\mathcal {M} }\}\), with \(\lnot ^{\mathcal {M}}\) and \(\rightarrow ^{\mathcal {M} }\) as interpretations of \(\lnot \) and \(\rightarrow \) respectively given by the following tables:

A valuation v in an Nmatrix is a function \(v: FOR^{I} \rightarrow \mathcal {T}^{I}\) that satisfies the following condition: \(v(*(\alpha _1,...,\alpha _n)) \in *^\mathcal {M}(v(\alpha _1),..., v(\alpha _n))\) for any n-ary connective \(*\) in \(\mathcal {L}^{I}\).
-
A formula \(\alpha \) is satisfied by a valuation v, in symbols \(v\vDash \alpha \), if \(v(\alpha ) \in \mathcal {D}^{I}\).
-
A sequent \(\varGamma \Rightarrow \varDelta \) is satisfied by a valuation v, written as \(v\vDash \varGamma \Rightarrow \varDelta \), if and only if either v does not satisfy some formula in \(\varGamma \) or v satisfies some formula in \(\varDelta \).
-
A sequent \(\varGamma \Rightarrow \varDelta \) is valid (\(\vDash \varGamma \Rightarrow \varDelta \)), if it is satisfied by all valuations v.
-
The consequence relation \((\vdash _{\mathcal {M}})\) on \(FOR^{I}\) is defined as: for any \(T, S \subseteq FOR^{I}\), \(T \vdash _{\mathcal {M}}S \) if and only if there exist finite sets \(\varGamma \subseteq T\) and \(\varDelta \subseteq S\) such that the sequent \(\varGamma \Rightarrow \varDelta \) is valid.
Soundness and completeness of \(\mathcal {L}^{I}\) with respect to the consequence relation \(\vdash _{\mathcal {M}}\) is established. Now it is clear from the definition of \(\vdash _{\mathcal {M}}\) that \(\mathcal {L}^{I}\) violates ECQ. Indeed, if we choose two distinct propositional variables p, q and a valuation v such that \(v(p):=u\) and \(v(q):=f\) then \(\{p, \lnot p\} \nvdash _\mathcal {M} q\).
It should also be mentioned here that in [3], two kinds of determinizations of \(\mathcal {L}^{I}\) have been derived: “Łukasiewicz determinization” and “Kleene determinization”. It is shown that the Łukasiewicz determinization is equivalent to the paraconsistent logic \(J_3\), while the Kleene determinization is equivalent to the paraconsistent logic Pac [2]. Therefore \(\mathcal {L}^{I}\) may be looked upon as a “common denominator” of \(J_3\) and Pac.
It has been well-established over the years that rough set theory has many intricacies which cannot be captured by any single approach. We now turn to the notions of rough truth proposed in [36] and rough consequence introduced in [6], and paraconsistent deductive systems that have been obtained through work based on these notions.
A rough set may be viewed as a triple (X, R, A), where \(A \subseteq X\) and (X, R) is a Pawlakian approximation space, i.e. X is a non-empty set and R an equivalence relation on it. It was noticed early on that an S5 formula \( \alpha \) may be interpreted in an S5 model (X, R, v) as a rough set (X, R, A), with A being the set of possible worlds where \(\alpha \) is true under the valuation v, i.e. \( A = v(\alpha )\). Moreover, \(v(L\alpha ) =\underline{v(\alpha )}\), the lower approximation of \(v(\alpha )\), and \(v(M\alpha ) =\overline{v(\alpha )}\), the upper approximation of \(v(\alpha )\), where L, M denote the necessity and possibility operators respectively. One of the basic notions in rough set theory is that of rough equality: sets A and B are roughly equal if they have the same lower and upper approximations. In S5, one can see that rough equality of \(\alpha ,\beta \) would be represented by the formula \(\alpha \approx \beta := (L\alpha \leftrightarrow L\beta ) \wedge (M\alpha \leftrightarrow M\beta )\). This is because in any S5 model (X, R, v) with \( A = v(\alpha )\) and \( B = v(\beta )\), \(\alpha \approx \beta \) would be true under v if and only if A, B are roughly equal. Rough consequence was based on the idea of rough modus ponens, which, loosely put, stipulates that for any S5 formulas \(\alpha , \alpha ^{\prime }, \beta \), if \(\alpha \), \(\alpha \approx \alpha ^\prime \) and \(\alpha ^\prime \rightarrow \beta \) are all “derivable” from a set \(\varGamma \) of S5 formulas, then \(\beta \) should also follow from \(\varGamma \). Formally, the rough consequence relation \({ \vert \!\!\! \sim }\) was defined in the backdrop of S5:
\(\varGamma \ { \vert \!\!\! \sim }\ \alpha \), in case \(\alpha \) is a member of \(\varGamma \), or is an S5 theorem, or is derived through the rule (RMP): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \varGamma { \vert \!\!\! \sim } \beta \rightarrow \gamma \varGamma \vdash \alpha \approx \beta }{\varGamma { \vert \!\!\! \sim } \gamma }\),
where \(\vdash \) denotes the S5 consequence relation. One may notice that whenever \(\alpha = \beta \), the rule (RMP) becomes standard modus ponens (MP). A study was made in [5, 6, 17] by weakening RMP in different ways (again in the backdrop of S5), and considering logics based on the resulting rules. This included a rule based on the formula \(\alpha \sim > \beta := (L\alpha \rightarrow L \beta )\wedge (M\alpha \rightarrow M\beta )\), representing rough inclusion. Following is a summary of rules considered in these works:
(\(MP_{\approx }\)): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \varGamma { \vert \!\!\! \sim } \beta \rightarrow \gamma \vdash \alpha \approx \beta }{\varGamma { \vert \!\!\! \sim } \gamma }\) and (\(MP_{\sim >}\)): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \varGamma { \vert \!\!\! \sim } \beta \rightarrow \gamma \vdash \alpha \sim > \beta }{\varGamma { \vert \!\!\! \sim } \gamma }\)
(\(RMP_1\)): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \vdash \beta \rightarrow \gamma \vdash M\alpha \rightarrow M\beta }{\varGamma { \vert \!\!\! \sim } \gamma }\) and (\(RMP_2\)): \(\frac{\vdash \alpha \varGamma { \vert \!\!\! \sim } \beta \rightarrow \gamma \vdash L\alpha \rightarrow L\beta }{\varGamma { \vert \!\!\! \sim } \gamma }\)
(\(RMP_1\)) and (\(RMP_2\)) were used to define the logic Lr. It was seen later that (\(RMP_2\)), in fact, follows from (\(RMP_1\)), and (\(RMP_1\)) is equivalent to the rule:
(\(R_1\)): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \vdash M\alpha \rightarrow M\beta }{\varGamma { \vert \!\!\! \sim } \beta }\)
The logic Lr was extended in [5] by adding another rule:
(\(R_2\)): \(\frac{\varGamma { \vert \!\!\! \sim } M\alpha \varGamma { \vert \!\!\! \sim } M\beta }{\varGamma { \vert \!\!\! \sim } M \alpha \wedge M\beta }\)
This new logic is denoted by \(\mathcal {L}_{\mathcal {R}}\). In [5] it was shown that Jaśkowski’s discussive logic J (discussed in Sect. 2.2) is equivalent to \(\mathcal {L}_{\mathcal {R}}\).
The following are from [17]:
\(MP_1\): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \varGamma { \vert \!\!\! \sim } \beta \rightarrow \gamma \vdash M\alpha \rightarrow M\beta }{\varGamma { \vert \!\!\! \sim } \gamma }\) \(MP_2\): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \varGamma { \vert \!\!\! \sim } \beta \rightarrow \gamma \vdash L\alpha \rightarrow L\beta }{\varGamma { \vert \!\!\! \sim } \gamma }\)
\(MP_3\): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \varGamma { \vert \!\!\! \sim } \beta \rightarrow \gamma \vdash \alpha \rightarrow \beta }{\varGamma { \vert \!\!\! \sim } \gamma }\) \(MP_4\): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \varGamma { \vert \!\!\! \sim } \beta \rightarrow \gamma \vdash M\alpha \rightarrow \beta }{\varGamma { \vert \!\!\! \sim } \gamma }\)
\(MP_5\): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \varGamma { \vert \!\!\! \sim } \beta \rightarrow \gamma \vdash L\alpha \rightarrow M\beta }{\varGamma { \vert \!\!\! \sim } \gamma }\) \(MP_0\): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \varGamma { \vert \!\!\! \sim } \alpha \rightarrow \gamma }{\varGamma { \vert \!\!\! \sim } \gamma }\)
For each of the rules \(MP_i\), \(i=0,...,5, {\sim >}, \approx \), a rough consequence relation \({ \vert \!\!\! \sim }_i\) is defined as mentioned earlier. The corresponding logics are denoted as \(Lr_i\). In [5], it was shown that ECQ fails to hold in both Lr and \(\mathcal {L_R}\). ECQ also fails for the system \(Lr_4\), as observed in [17]. In all the other \(Lr_i\) systems, ECQ holds. However, we shall see in the next section that one can define several other rough consequence relations that yield paraconsistent logics.
3 Some New Paraconsistent Logics
Let us consider a set \(\varGamma \cup \{\alpha , \beta , \gamma \}\) of S5 formulas. We define new rules of inference by weakening \(MP_i\), \(i=1,...,5, {\sim >}, \approx \), as follows:
\(\frac{\varGamma { \vert \!\!\! \sim } \alpha \vdash \beta \rightarrow \gamma \vdash \alpha \rightarrow _i \beta }{\varGamma { \vert \!\!\! \sim } \gamma }\),
where \(\alpha \rightarrow _i \beta \) denotes the S5-implication in \(MP_i\) (e.g. \(\alpha \rightarrow _1 \beta := M\alpha \rightarrow M\beta \)).
Proposition 1
The new rule defined above is equivalent to \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \vdash \alpha \rightarrow _i \gamma }{\varGamma { \vert \!\!\! \sim } \gamma }\), for \(i=1,...,5, {\sim >}\).
Proof
We give the proof for \(i=1\). The other cases have similar proofs. Suppose the rule \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \vdash \beta \rightarrow \gamma \vdash M\alpha \rightarrow M\beta }{\varGamma { \vert \!\!\! \sim } \gamma }\) holds. Let \(\varGamma \ { \vert \!\!\! \sim }\ \alpha ,~ \vdash M\alpha \rightarrow M\gamma \). Since \(\vdash \gamma \rightarrow \gamma \), \(\varGamma \ { \vert \!\!\! \sim }\ \gamma \) holds as well.
Conversely, let \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \vdash M\alpha \rightarrow M\gamma }{\varGamma { \vert \!\!\! \sim } \gamma }\) hold, and \(\varGamma \ { \vert \!\!\! \sim }\ \alpha , ~ \vdash \beta \rightarrow \gamma ,~ \vdash M\alpha \rightarrow M\beta \). Now \(\vdash \beta \rightarrow \gamma \) implies \(\vdash M\beta \rightarrow M\gamma \). Therefore \(\vdash M\alpha \rightarrow M\gamma \) holds as well. Then by assumption, \(\varGamma \ { \vert \!\!\! \sim }\ \gamma \). \(\Box \)
Notation 1
Henceforth, \(\overline{MP_i}\) will denote the rule \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \vdash \alpha \rightarrow _i \gamma }{\varGamma { \vert \!\!\! \sim } \gamma }\), for \(i=1,...,5, {\sim >}, \approx \). In other words,
\(\overline{MP_1}\): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \vdash M\alpha \rightarrow M\gamma }{\varGamma { \vert \!\!\! \sim } \gamma }\) \(\overline{MP_2}\): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \vdash L\alpha \rightarrow L\gamma }{\varGamma { \vert \!\!\! \sim } \gamma }\)
\(\overline{MP_3}\): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \vdash \alpha \rightarrow \gamma }{\varGamma { \vert \!\!\! \sim } \gamma }\) \(\overline{MP_4}\): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \vdash M\alpha \rightarrow \gamma }{\varGamma { \vert \!\!\! \sim } \gamma }\)
\(\overline{MP_5}\): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \vdash L\alpha \rightarrow M\gamma }{\varGamma { \vert \!\!\! \sim } \gamma }\) \(\overline{MP_{\sim >}}\): \(\frac{\varGamma { \vert \!\!\! \sim } \alpha \vdash \alpha \ \sim > \ \gamma }{\varGamma { \vert \!\!\! \sim } \gamma }\)
\(\overline{MP_{\approx }}\): \(\frac{\varGamma \ { \vert \!\!\! \sim }\ \alpha \vdash \alpha \approx \gamma }{\varGamma \ { \vert \!\!\! \sim }\ \gamma }\).
For \(i= \ \approx \), we have one direction of Proposition 1.
Observation 1
\(\frac{\varGamma \ { \vert \!\!\! \sim }\ \alpha \vdash \beta \rightarrow \gamma \vdash \alpha \approx \beta }{\varGamma \ { \vert \!\!\! \sim }\ \gamma }\) implies \(\overline{MP_{\approx }}\).
3.1 The Systems \(\overline{Lr_i}\)
A logic is defined for each rule \(\overline{MP_i}\), \(i=1,...,5, {\sim >}, \approx ,\) as mentioned in Sect. 2.8. Formally, the consequence relation \({ \vert \!\!\! \sim }_{\overline{i}}~\) for \(\overline{Lr_i}\) is given as follows.
Definition 2
\(\varGamma \ { \vert \!\!\! \sim }_{\overline{i}}\ \alpha \) if and only if there is a sequence \(\alpha _1, \alpha _2,..., \alpha _n(=\alpha )\) such that for each \(\alpha _j(j=1,...,n)\), one of the following holds.
(i) \(\alpha _j \in \varGamma ~~\) ...(ov).
(ii) \(\alpha _j\) is an S5 theorem ...(S5).
(iii) \(\alpha _j\) is derived from some of \(\alpha _1,\ldots , \alpha _{i-1}\) by \(\overline{MP_i}\).
Let us consider the S5-implications in \(\overline{MP_i},~i=1,2,3\), namely \(M\alpha \rightarrow M \beta , L\alpha \rightarrow L \beta , \alpha \rightarrow \beta \). One may abbreviate these implications as \( \varDelta _i \alpha \rightarrow \varDelta _i \beta \), where \(\varDelta _i\) is respectively M, L and “1” for \(i=1,2,3\). We then have the following.
Theorem 1
For \(i=1,2,3\), \(\varGamma \ { \vert \!\!\! \sim }_{\overline{i}}\ \alpha \), if and only if \(~\vdash \varDelta _i \alpha \), or there is a \(\beta \) in \( \varGamma \) with \( \vdash \varDelta _i \beta \rightarrow \varDelta _i \alpha \).
Proof
By induction on the number n of steps of derivation of \(\alpha \) from \(\varGamma \).
Basis \(n=0\): \(\vdash \alpha \), or \(\alpha \in \varGamma \). If \(\vdash \alpha \), for case \(i = 3\), we are done. For the cases \(i=1,2\), observe that \(\vdash \alpha \) implies \(\vdash \varDelta _i \alpha \). So we are done in these cases as well. Now suppose \(\alpha \in \varGamma \). Since \( \vdash \varDelta _i \alpha \rightarrow \varDelta _i \alpha \), the result obtains.
Induction step: We sketch the proof. Suppose \(\alpha \) is derived by \(\overline{MP_i}\) from \(\varGamma \ { \vert \!\!\! \sim }_{\overline{i}} \ \gamma \) and \(\vdash \varDelta _i \gamma \rightarrow \varDelta _i \alpha \) for some \(\gamma \). Then by induction, either \(\vdash \varDelta _i \gamma \) or \( \vdash \varDelta _i \beta \rightarrow \varDelta _i \gamma \) for some \(\beta \in \varGamma \). If \(\vdash \varDelta _i \gamma \) holds, then from \( \vdash \varDelta _i \gamma \rightarrow \varDelta _i \alpha \), \(\vdash \varDelta _i \alpha \) holds as well. Otherwise \( \vdash \varDelta _i \beta \rightarrow \varDelta _i \gamma \) for some \(\beta \in \varGamma \), and then \( \vdash \varDelta _i \beta \rightarrow \varDelta _i \alpha \) holds.
Conversely, suppose \(\vdash \varDelta _i \alpha \). Then \(\varGamma \ { \vert \!\!\! \sim }_{\overline{i}} \ \varDelta _i \alpha \), by (S5). So we are done for \(i=3\). If \(i=1,2\), since \(\vdash \varDelta _i \varDelta _i \alpha \rightarrow \varDelta _i \alpha \), \(\varGamma \ { \vert \!\!\! \sim }_{\overline{i}} \ \alpha \) holds by \(\overline{MP_i}\). For the other case, suppose \( \vdash \varDelta _i \beta \rightarrow \varDelta _i \alpha \) for some \(\beta \in \varGamma \). Now \(\varGamma \ { \vert \!\!\! \sim }_{\overline{i}}\ \beta \) holds by (ov) and then \(\varGamma \ { \vert \!\!\! \sim }_{\overline{i}} \ \alpha \) holds by \(\overline{MP_i}\). \(\Box \)
Theorem 2
\(\overline{Lr_1}\), \(\overline{Lr_2}\), \(\overline{Lr_3}\) are paraconsistent logics.
Proof
Consider two distinct propositional variables p, q. We use Theorem 1.
-
(i)
Since \(\nvdash M q\), \(\nvdash M p \rightarrow Mq\) and \(\nvdash M (\lnot p) \rightarrow Mq\), therefore
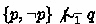 by Theorem 1. Hence \(\overline{Lr_1}\) is paraconsistent.
by Theorem 1. Hence \(\overline{Lr_1}\) is paraconsistent. -
(ii)
\(\nvdash L q\), \(\nvdash L p \rightarrow Lq\) and \(\nvdash L (\lnot p) \rightarrow Lq\) give
 .
. -
(iii)
\(\nvdash q\), \(\nvdash p \rightarrow q\) and \(\nvdash \lnot p \rightarrow q\) give
 . \(\Box \)
. \(\Box \)
Notation 2
For logics \(L_1\) and \(L_2\) with the same language, \(L_1 \preceq L_2\) denotes that \(L_2\) is stronger than \(L_1\), i.e. if \(\alpha \) is derivable from \(\varGamma \) in \(L_1\) then \(\alpha \) is derivable from \(\varGamma \) in \(L_2\), for all \(\alpha ,\varGamma \).
Lemma 1
\(\overline{Lr_4} \preceq \overline{Lr_3}\).
Proof
It suffices to show that \(\overline{MP_4}\) is derivable in \(\overline{Lr_3}\). Let \(\varGamma \ { \vert \!\!\! \sim }\ \alpha \) and \(\vdash M\alpha \rightarrow \gamma \). Since \(\vdash M\alpha \rightarrow \gamma \) implies \(\vdash \alpha \rightarrow \gamma \), then by \(\overline{MP_3}\), \(\varGamma \ { \vert \!\!\! \sim }\ \gamma \). \(\Box \)
Theorem 3
\(\overline{Lr_4}\) is paraconsistent.
Proof
Follows from Lemma 1 and Theorem 2. \(\Box \)
Theorem 4
-
(i)
\(\varGamma \ { \vert \!\!\! \sim }_{\overline{ {\sim >}}} \ \alpha \), if and only if either \(\vdash \alpha \) or there is a \(\beta \) in \( \varGamma \) with \(\vdash (M\beta \rightarrow M\alpha ) \wedge ( L\beta \rightarrow L\alpha )\).
-
(ii)
\(\varGamma { \vert \!\!\! \sim }_{\overline{\approx }} \ \alpha \), if and only if either \(\vdash \alpha \) or there is a \(\beta \) in \( \varGamma \) with \(\vdash (M\beta \leftrightarrow M\alpha ) \wedge ( L\beta \leftrightarrow L\alpha )\).
Proof
We give the proof of (i), which is by induction on the number n of steps of derivation of \(\alpha \) from \(\varGamma \). (ii) can be proved in a similar manner.
Basis: \(n=0\). Either \(\vdash \alpha \) or \(\alpha \in \varGamma \). If \(\vdash \alpha \), there is nothing to show. In the other case, \(\vdash (M\alpha \leftrightarrow M\alpha ) \wedge ( L\alpha \leftrightarrow L\alpha )\) gives the result.
In the induction step, we consider the possibility that \(\alpha \) is derived by \(\overline{MP_{ {\sim >}}}\) from \(\varGamma \ { \vert \!\!\! \sim }_{\overline{ {\sim >}}} \ \gamma \) and \(\vdash (M\gamma \rightarrow M\alpha ) \wedge (L\gamma \rightarrow L\alpha )\), for some \(\gamma \). Then by induction hypothesis, either \(\vdash \gamma \) or \( \vdash (M\beta \rightarrow M\gamma ) \wedge (L\beta \rightarrow L\gamma )\), for some \(\beta \in \varGamma \). If \(\vdash \gamma \) holds then \(\vdash L\gamma \) holds as well. Now \(\vdash L\gamma \rightarrow L\alpha \) holds as \(\vdash (M\gamma \rightarrow M\alpha ) \wedge (L\gamma \rightarrow L\alpha )\) holds. Therefore \(\vdash L\alpha \) as well as \(\vdash \alpha \) holds. Otherwise \( \vdash (M\beta \rightarrow M\gamma ) \wedge (L\beta \rightarrow L\gamma )\), for some \(\beta \in \varGamma \). Then \( \vdash (M\beta \rightarrow M\alpha ) \wedge (L\beta \rightarrow L\alpha )\) holds as, \( \vdash (M\gamma \rightarrow M\alpha ) \wedge (L\gamma \rightarrow L\alpha )\) holds.
Conversely, suppose \(\vdash \alpha \) holds, then \(\varGamma \ { \vert \!\!\! \sim }_{\overline{ {\sim >}}} \ \alpha \), by (S5). For the other case, suppose \( \vdash (M\beta \rightarrow M\alpha ) \wedge ( L\beta \rightarrow L\alpha )\) holds for some \(\beta \in \varGamma \). Now \(\varGamma \ { \vert \!\!\! \sim }_{\overline{ {\sim >}}} \ \beta \) holds by (ov) and then \(\varGamma \ { \vert \!\!\! \sim }_{\overline{ {\sim >}}} \ \alpha \) holds by \(\overline{MP_{ {\sim >}}}\). \(\Box \)
Theorem 5
\(\overline{Lr_{ {\sim >}}}\) and \(\overline{Lr_{\approx }}\) are paraconsistent logics.
Proof
Take two distinct propositional variables p, q. Since \(\nvdash q\), \(\nvdash (Mp \rightarrow Mq) \wedge ( Lp \rightarrow Lq)\) and \(\nvdash (M(\lnot p)) \rightarrow Mq) \wedge ( L(\lnot p)) \rightarrow Lq)\), therefore,
 as well as
as well as
 by Theorem 4. Hence \(\overline{Lr_{ {\sim >}}}\) and \(\overline{Lr_{\approx }}\) are both paraconsistent logics. \(\Box \)
by Theorem 4. Hence \(\overline{Lr_{ {\sim >}}}\) and \(\overline{Lr_{\approx }}\) are both paraconsistent logics. \(\Box \)
3.2 Paraconsistency of \(\overline{Lr_5}\)
The paraconsistency of \(\overline{Lr_5}\) is established using the fact that \(\overline{Lr_3}\) is paraconsistent (Theorem 2).
Let \(\mathcal {L}_{S5}\) and \(\mathcal {L}_{CPL}\) denote the languages of S5 and CPL respectively. We define a translation \(*: \mathcal {L}_{S5} \rightarrow \mathcal {L}_{CPL}\) as follows:
-
\(*(p) := p\), where p is a propositional variable.
-
\(*(\alpha \vee \beta ) := *(\alpha ) \vee *(\beta )\).
-
\(*(\alpha \wedge \beta ) := *(\alpha ) \wedge *(\beta )\).
-
\(*(\alpha \rightarrow \beta ) := *(\alpha ) \rightarrow *(\beta )\).
-
\(*(L\alpha ) := *(\alpha )\).
-
\(*(M\alpha ) := *(\alpha )\).
The image of a formula \(\alpha \) under the above translation, \(*(\alpha )\), is referred to as the PC-transform of \(\alpha \) in [27]. A modal logic Triv is defined in [27] such that \(S5 \preceq Triv\). Moreover Triv collapses into CPL, in the sense that every formula \(\alpha \) in Triv is equivalent to its PC-transform \(*(\alpha )\). Then for all \(\alpha \), \(\vdash _{Triv} \alpha \) if and only if \(\vdash _{CPL} *(\alpha )\). Thus one obtains
Lemma 2
For any S5 formula \(\alpha \), \(\vdash \alpha \) implies \(\vdash _{CPL} *(\alpha )\).
We are then able to establish
Lemma 3
\(\varGamma \ { \vert \!\!\! \sim }_{\overline{5}} \ \alpha \) implies \(*(\varGamma ) { \vert \!\!\! \sim }_{\overline{3}} *(\alpha )\), where \(*(\varGamma )= \{*(\gamma ): \gamma \in \varGamma \}\).
Proof
By induction on the number n of steps of derivation of \(\alpha \) from \(\varGamma \).
Basis: \(n=0\). Either \(\vdash \alpha \) or \(\alpha \in \varGamma \). If \(\vdash \alpha \) then \(\vdash _{CPL} *(\alpha )\) by Lemma 2, and so \(\vdash *(\alpha )\) holds. Hence \(*(\varGamma ) { \vert \!\!\! \sim }_{\overline{3}} *(\alpha )\), by (S5). Otherwise \(\alpha \in \varGamma \), then \(*(\alpha ) \in *(\varGamma )\), therefore \(*(\varGamma ) { \vert \!\!\! \sim }_{\overline{3}} *(\alpha )\), by (ov).
For the induction step, suppose \(\alpha \) is derived by \(\overline{MP_5}\) from \(\varGamma \ { \vert \!\!\! \sim }_{\overline{5}} \ \gamma \) and \(\vdash L\gamma \rightarrow M\alpha \), for some \(\gamma \). Then by the induction hypothesis, \(*(\varGamma ) { \vert \!\!\! \sim }_{\overline{3}} *(\gamma )\). Using Lemma 2, \(\vdash _{CPL} *(\gamma ) \rightarrow *(\alpha )\) holds, and therefore \(\vdash *(\gamma ) \rightarrow *(\alpha )\) holds as well. So by \(\overline{MP_3}\), \(*(\varGamma ) { \vert \!\!\! \sim }_{\overline{3}} *(\alpha )\). \(\Box \)
Theorem 6
\(\overline{Lr_5}\) is a paraconsistent logic.
Proof
Let p, q be two distinct propositional variables. Then
 , as shown in the proof of Theorem 2. Since \(*(\{p, \lnot p\} )= \{p, \lnot p\}\) and \(*(q) = q\), by Lemma 3,
, as shown in the proof of Theorem 2. Since \(*(\{p, \lnot p\} )= \{p, \lnot p\}\) and \(*(q) = q\), by Lemma 3,
 . \(\Box \)
. \(\Box \)
4 Conclusions
In this paper, we have presented a survey on the major approaches that yield paraconsistent logics. One of the salient features of this survey is the inclusion of the transformation approach and rough set approach. We focus on how new paraconsistent logics may be obtained, based on the rough set approach. Several new logics are proposed by considering a weakened version of rough modus ponens rules.
In [17], there is a study of the relationship between the logics that are based on the different kinds of rough modus ponens rules. An immediate task would be to investigate relations of the logics obtained in this work with the ones studied in [17]. Appropriate semantics for the new logics also need to be explored, to give a complete idea of these paraconsistent systems.
Notes
- 1.
The consequence relation \(\vdash \) is used as a meta-linguistic symbol. In the context of a particular logic this can be a relation obtained semantically or syntactically; moreover sometimes the same notion of consequence is represented by an operator from \(\mathcal {P}(FOR)\) to \(\mathcal {P}(FOR)\). The use of notation would be clear from the contexts.
- 2.
This notion is more formally introduced in Sect. 3.1.
- 3.
A subset \(\varGamma \subseteq FOR\) is said to be trivial if \(\varGamma \vdash \alpha \) for every formula \(\alpha \), otherwise it is called non-trivial.
- 4.
The logic CLuN, developed by Diderik Batens, is a predicative paraconsistent logic. The propositional part of CLuN is obtained by adding the axiom-schema \((\alpha \rightarrow \lnot \alpha ) \rightarrow \lnot \alpha \) to \(CPL^{+}\). The adaptive logic CLuN\(^{m}\) is obtained from CLuN based on a strategy, called minimal abnormality..
References
Arruda, A.I.: A survey of paraconsistent logic. In: Arruda, A., Chuaqui, R., Da Costa, N. (eds.) Mathematical Logic in Latin America. Studies in Logic and the Foundations of Mathematics, vol. 99. pp. 1–41. Elsevier (1980)
Avron, A.: Natural \(3\)-valued logics-characterization and proof theory. J. Symbolic Logic 56(1), 276–294 (1991)
Avron, A., Konikowska, B.: Rough sets and 3-valued logics. Stud. Logica. 90(1), 69–92 (2008)
Banerjee, M.: Rough sets and \(3\)-valued Łukasiewicz logic. Fund. Inform. 31(3–4), 213–220 (1997)
Banerjee, M.: Logic for rough truth. Fund. Inform. 71(2–3), 139–151 (2006)
Banerjee, M., Chakraborty, M.K.: Rough consequence. Bull. Polish Acad. Sci. (Math.) 41(4), 299–304 (1993)
Basu, S.S., Chakraborty, M.K.: Restricted rules of inference and paraconsistency. Log. J. IGPL 30(3), 534–560 (2022)
Batens, D.: Paraconsistent extensional propositional logics. Logique Anal. 23(90–91), 195–234 (1980)
Batens, D.: A universal logic approach to adaptive logics. Log. Univers. 1(1), 221–242 (2007)
Batens, D.: Tutorial on inconsistency-adaptive logics. In: Beziau, J.-Y., Chakraborty, M., Dutta, S. (eds.) New Directions in Paraconsistent Logic. SPMS, vol. 152, pp. 3–38. Springer, New Delhi (2015). https://doi.org/10.1007/978-81-322-2719-9_1
Batens, D., De Clercq, K.: A rich paraconsistent extension of full positive logic. Logique Anal. 47(185/188), 227–257 (2004)
Batens, D., De Clercq, K., Kurtonina, N.: Embedding and interpolation for some paralogics. The propositional case. Rep. Math. Log. 33, 29–44 (1999)
Belnap Jr, N.D.: A useful four-valued logic. In: Dunn, J.M., Epstein, G. (eds.), Modern Uses of Multiple-valued Logic. Episteme, vol. 2, pp. 5–37. Springer, Dordrecht (1977). https://doi.org/10.1007/978-94-010-1161-7_2
Boicescu, V., Filipoiu, A., Georgescu, G., Rudeanu, S.: Łukasiewicz-Moisil Algebras. North Holland (1991)
Bonzio, S., Moraschini, T., Pra Baldi, M.: Logics of left variable inclusion and Płonka sums of matrices. Arch. Math. Logic 60(1–2), 49–76 (2021)
Bonzio, S., Paoli, F., Pra Baldi, M.: Logics of variable inclusion. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-04297-3
Bunder, M.W., Banerjee, M., Chakraborty, M.K.: Some rough consequence logics and their interrelations. In: Peters, J.F., Skowron, A. (eds.) Transactions on Rough Sets VIII. LNCS, vol. 5084, pp. 1–20. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85064-9_1
Carnielli, W., Coniglio, M.E., Marcos, J.: Logics of formal inconsistency. In: Gabbay, D., Guenthner, F. (eds.) Handbook of Philosophical Logic, vol. 14, pp. 1–93. Springer, Dordrecht (2007). https://doi.org/10.1007/978-1-4020-6324-4_1
Carnielli, W., Coniglio, M.E.: Paraconsistent Logic: Consistency, Contradiction and Negation. LEUS, vol. 40. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-33205-5
Carnielli, W.A., Marcos, J.: A taxonomy of \({ C}\)-systems. In: Carnielli, W.A., Marcelo, C., D’ottaviano, I.M.L. (eds.) Paraconsistency, vol. 228, pp. 1–94. Dekker, New York (2002)
Ciucci, D., Dubois, D.: Three-valued logics, uncertainty management and rough sets. In: Peters, J.F., Skowron, A. (eds.) Transactions on Rough Sets XVII. LNCS, vol. 8375, pp. 1–32. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54756-0_1
da Costa, N.C.A., Alves, E.H.: A semantical analysis of the calculi \({ C}_{n}\). Notre Dame J. Formal Logic 18(4), 621–630 (1977)
da Costa, N.C.A., Doria, F.A.: On Jaśkowski’s discussive logics. Stud. Logica. 54(1), 33–60 (1995)
da Costa, N.C.A., Krause, D., Bueno, O.: Paraconsistent logics and paraconsistency. In: Jacquette, D. (ed.) Philosophy of Logic. Handbook of the Philosophy of Science, pp. 791–911. North-Holland, Amsterdam (2007)
de Souza, E.G., Costa-Leite, A., Dias, D.H.B.: On a paraconsistentization functor in the category of consequence structures. J. Appl. Non-Class. Log. 26(3), 240–250 (2016)
Dutta, S., Chakraborty, M.K.: Consequence–inconsistency interrelation: in the framework of paraconsistent logics. In: Beziau, J.-Y., Chakraborty, M., Dutta, S. (eds.) New Directions in Paraconsistent Logic. SPMS, vol. 152, pp. 269–283. Springer, New Delhi (2015). https://doi.org/10.1007/978-81-322-2719-9_12
Hughes, G.E., Cresswell, M.J.: A New Introduction to Modal Logic. Routledge, Milton Park (1996)
Iturrioz, L.: Rough sets and three-valued structures. In: Orłowska, E. (ed.) Logic at Work: Essays Dedicated to the Memory of Helena Rasiowa. Studies in Fuzziness and Soft Computing, vol. 24, pp. 596–603. Physica, Heidelberg (1999)
Kotas, J.: The axiomatization of S. Jaśkowski’s discussive system. Stud. Logica 33, 195–200 (1974)
Malinowski, G.: Kleene logic and inference. Bull. Sect. Logic 43(1/2), 43–52 (2014)
Middelburg, C.A.: A survey of paraconsistent logics. arXiv preprint arXiv:1103.4324 (2011)
Nakayama, Y., Akama, S., Murai, T.: Four-valued tableau calculi for decision logic of rough set. Procedia Comput. Sci. 126, 383–392 (2018)
Omori, H., Wansing, H.: 40 years of FDE: an introductory overview. Stud. Logica. 105(6), 1021–1049 (2017)
Pagliani, P.: Rough set theory and logic-algebraic structures. In: Orłowska, E. (ed.) Incomplete Information: Rough Set Analysis. Studies in Fuzziness and Soft Computing, vol. 13, pp. 109–190. Physica, Heidelberg (1998). https://doi.org/10.1007/978-3-7908-1888-8_6
Pawlak, Z.: Rough sets. Internat. J. Comput. Inform. Sci. 11(5), 341–356 (1982)
Pawlak, Z.: Rough logic. Bull. Polish Acad. Sci. (Tech. Sci.) 35(5–6), 253–258 (1987)
Pawlak, Z.: Rough Sets: Theoretical Aspects of Reasoning about Data. Kluwer Academic Publishers, Amsterdam (1991)
Priest, G.: Paraconsistent logic. In: Gabbay, D.M., Guenthner, F. (eds.) Handbook of Philosophical Logic, vol. 6, pp. 287–393. Springer, Netherlands, Dordrecht (2002). https://doi.org/10.1007/978-94-017-0460-1_4
Priest, G.: Plurivalent logics. Australas. J. Log. 11(1), 2–13 (2014)
Priest, G., Routley, R.: Introduction: paraconsistent logics. Stud. Logica. 43(1–2), 3–16 (1984)
Robles, G.: A Routley-Meyer semantics for Gödel 3-valued logic and its paraconsistent counterpart. Log. Univers. 7, 507–532 (2013)
Shramko, Y., Zaitsev, D., Belikov, A.: First-degree entailment and its relatives. Stud. Logica. 105(6), 1291–1317 (2017)
Smiley, T.J.: Entailment and deducibility. Proc. Aristot. Soc. 59, 233–254 (1959)
Tsoukiàs, A.: A first order, four-valued, weakly paraconsistent logic and its relation with rough sets semantics. Found. Comput. Decision Sci. 27(2), 77–96 (2002)
Tuziak, R.: Paraconsistent extensions of positive logic. Bull. Sect. Logic 25(1), 15–20 (1996)
Viana, H., Alcântara, J.A., Martins, A.T.: Searching contexts in paraconsistent rough description logic. J. Braz. Comput. Soc. 21(1), Art. 7, 13 (2015)
Vitória, A., Małuszyński, J., Szałas, A.: Modeling and reasoning with paraconsistent rough sets. Fund. Inform. 97(4), 405–438 (2009)
Vitória, A., Szałas, A., Małuszyński, J.: Four-valued extension of rough sets. In: Wang, G., Li, T., Grzymala-Busse, J.W., Miao, D., Skowron, A., Yao, Y. (eds.) RSKT 2008. LNCS (LNAI), vol. 5009, pp. 106–114. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-79721-0_19
Wu, H.: Paraconsistent rough set algebras. In: Chen, Y., Zhang, S. (eds.) AILA 2022. Communications in Computer and Information Science, vol. 1657, pp. 166–179. Springer, Singapore (2022). https://doi.org/10.1007/978-981-19-7510-3_13
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Saha, B., Banerjee, M., Dutta, S. (2023). Paraconsistent Logics: A Survey Focussing on the Rough Set Approach. In: Campagner, A., Urs Lenz, O., Xia, S., Ślęzak, D., Wąs, J., Yao, J. (eds) Rough Sets. IJCRS 2023. Lecture Notes in Computer Science(), vol 14481. Springer, Cham. https://doi.org/10.1007/978-3-031-50959-9_8
Download citation
DOI: https://doi.org/10.1007/978-3-031-50959-9_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-50958-2
Online ISBN: 978-3-031-50959-9
eBook Packages: Computer ScienceComputer Science (R0)






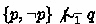 by Theorem
by Theorem  .
. .
.