Keywords

1 Introduction

Modern design always aims at reducing the mass, simplifying the structure, and reducing the energy consumption of systems, especially in robotics. A priority direction in robot design is to optimize structure with longer and thinner links. However, for these structures such as flexible robots, the rigidity and motion accuracy are usually reduced because of the elastic deformation of the links. Therefore, taking into account the effects of elastic factors is necessary when investigating the dynamics and control of flexible robots. In comparison with the traditional rigid robots, the flexible ones have potential advantages such as lower overall mass or energy consumption, small actuator, and greater payload-weight ratio. However, owing to the complex nature of such flexible systems, mathematical modeling has involved complex processes.

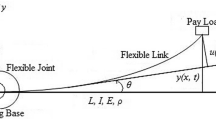
Since the modeling and control of the flexible robots are so complex, a simple robot structure with one or two-flexible links, connected by only rotational joints is mainly studied by most researchers. A few works consider the translational joints. Note that the use of different joint types when designing a flexible robot improves the flexibility for the robot. However, a robot model consisting of rotary and translation joints make the kinematic, dynamic modeling, and control become more complex than models which have only rotational joints. In the literature, there have been several studies focusing on the model of two-link flexible robots with all revolute joints [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] (Fig. 1).

Fig. 1
figure 1

Two-link manipulator with revolute joints

Full size image

Although there have been some researches considering the presence of the prismatic joint, they mainly focused on architectures of one or two links [16,17,18,19,20]. A few works consider the prismatic joints for multi-link manipulators [1, 13]. As for different configurations of the flexible manipulators, different modeling methods have been used. Two mainly modeling approaches, including the assumed modes method (AM method) [4, 7, 9, 20,21,22,23,24,25,26,27] and the finite elements method (FE method) [5, 6, 8, 17, 19, 28,29,30,31,32,33,34] have been applied to describe the motion of flexible manipulators. The governing equations for the flexible robots can be derived by using the Newton–Euler equation [3, 5, 16, 20, 35], the Lagrange-Euler equation [4, 6, 8, 9, 11, 12, 14, 17, 19, 21, 22, 30, 36,37,38], or the Gibbs-Appel equation [1, 13, 15, 39]. This paper presents an overview of the mathematical methods that have been exploited to model the kinematics and dynamics of flexible robots.

2 A Literature Review of Flexible Robot Modeling and Control

Due to the complexity of the formulation of the flexible robot dynamics, most of the works focus on a simplified robot mechanism consisting of one or two planar flexible links.

In recent decades, a number of researchers have made their great contributions and several approaches are now available to solve the mathematical modeling problem for the flexible robot. The surveys of the state of the art can be found out in [40,41,42,43,44,45,46,47]. The previous works in the literature, which have been focused on the modeling and analysis for different flexible robot’s types, can be categorized as the follow.

In particular, for the multi-link flexible robot, most of the researches emphasized the robot architectures with all revolute joints. As discussed earlier in the Introduction section, some of the works [1, 13] proposed the methods to model the dynamics of the robot with the multi-flexible links, of which the links are connected one another by prismatic joints. However, the work in [1] just considered the rotating and reciprocating motion of the flexible links with the predetermined length and revolute—prismatic joints, and the authors in [13] studied the dynamics of the robot structure with multi-flexible links connected by the sliding prismatic joints, but in this research, the effects of link’s time-variable length have not considered yet.

Note that there also exist some researches concerning with the flexible robot having prismatic joints. Wang and Wei [16] investigate the dynamics of a one-link flexible arm modeled by a moving slender prismatic beam. Al-Bedoor [17] addresses the dynamic modeling of one sliding link with a fixed prismatic joint. This joint in the two-link flexible robots was modeled by Ju [18] and Pan [19]. Wang [34] considers parallel robots having flexible links and sliding prismatic joints. The multi-link flexible robots with prismatic joints are considered in [1, 13]. For the kinematic and dynamic modeling, both the mentioned researches employed the assumed modes method which has proven the effectiveness to numerically simulate the single-link flexible arm [42].

Though the prismatic joint has been taken into account for the mathematical modeling, there was a little work, devoted to the flexible robot having two specific kinds of prismatic joint as shown in Fig. 2a and b.

Fig. 2
figure 2

Two kinds of prismatic joint

Full size image

The fixed prismatic joint can be characterized by the fixed and sliding motions between the joint and two consecutive links (\(i - 1\)) and link (\(i\)), respectively. The length of the link (\(i\)) varies in time (Fig. 2a), whereas when two links connecting by a sliding prismatic joint, the link (\(i - 1\)) is a variable length. Due to these characterizations, for a structure with the first case (Fig. 2a), the relative motion of the current link \(i\) depends on the joint’s motion and the elastic deformation at the distal end of the previous link \(\left( {i - 1} \right)\). Nonetheless, this deformation does not affect the link \(i\) motion in the configuration with the sliding prismatic joint. In this case, the effect of link (\(i - 1\)) deformation is considered through the elastic deformation at the coincide sliding element in the connection of the link \(\left( {i - 1} \right)\) and the joint. This element moves along the link \(\left( {i - 1} \right)\), , depending on the state of the flexible robot (Fig. 2b). The dynamic model of the flexible robot with those mentioned kinds of prismatic joint is built based on the basic assumption of the element having zero elastic deformation. It is noticeable that the elasticity effects involves the variable length of such links should be taken into account to propose a model for flexible robots consisting of all the joint types as discussed.

In theory, formulating the dynamics of the multi-link flexible robot with various joint types is a difficult task. A few works have been considered this issue to generalize the dynamic modeling and control for this robot’s kind [61, 62].

To formulate the flexible robot dynamics model, several analytical approaches and computational methods have been investigated. Generally, the flexible robot is investigated as continuous systems that are not confined by the number of freedom degrees, and described by nonlinear differential equations that cannot be solved exactly. To describe the dynamic motion of flexible robots, two discretized methods of the assume mode method (AM) and the finite element method (FE) are often used. Comparing the effectiveness of these methods, in [42, 43], the authors pointed out that the main disadvantage of the AM method is difficult to find the modes for non-regular cross-sections links and multi-link manipulators. Moreover, the authors in [42] also proved that the FE method is simple for the computations, resulting in suitable applications to model the multi-links flexible arms and the real-time control law computation. In practice, the FE method has been widely utilized to model the flexible robot’s dynamics [5, 6, 8, 17, 19, 28,29,30,31,32,33,34]. In the FM method-approach, the flexible links are discretized by finite elements with the same length. The dynamic model is built based on the global mass matrixes, stiffness matrixes of the entire system. These matrixes are constructed by the assembly of the mass and stiffness matrix of each element, which is formulated through the calculation of the kinetic and potential energy in the nodal coordinates. The assembled procedure is complicated, requires expensive computational time. Especially, with the flexible robots that consist of prismatic joints, this process is even more complicated due to the time-varying boundary conditions. Besides, there are many studies that has been focused on proposing the dynamic modeling for the flexible robots, combining the analytical approaches with the FE method or the AM method, such the approaches are:

  • Newton–Euler approach [3, 5, 6, 16, 20, 35, 63,64,65],

  • Approach based on Lagrange’s equations [4, 6, 8, 9, 11, 12, 14, 17, 19, 21, 22, 30, 36,37,38],

  • Approach based on Hamilton’s equations [18, 66],

  • Approach based on Gibbs–Appell equations [1, 13, 15, 39], and

  • Approach based on Kane’s equations [10, 53].

Note that the FE method has been widely used as an efficient approach to model complex structures. In [3], Augustynek proposed the dynamic modeling for flexible robot links—like beam with rotary joint, considering the assembly errors. Based on the FM method, Naganathan [5] presented the nonlinear model to investigate the effect of elastic deformations of the flexible links, coupling with the kinematics of joints. In [6], the authors incorporated a Newton–Euler analytical model with the FM method to model the flexible robot with all revolving joins. It was shown that, in the FE method, the elastic manner of a flexible robot is assessed through the overlay of elastic deformation of a rigid body. In [8], based on the Lagrangian approach and FM method, Usoro proposed the formulations of the mathematical equations for the dynamic of lightweight flexible links. In another approach, the authors in [10] developed a recursive formulation in the matrix form for flexible multi-link systems by combining the FM method with Kane’s equations. The modeling and controlling of the flexible manipulators with a prismatic joint were also developed in [17, 19]. The consideration of nonlinear behavior in the dynamic of the flexible was presented in [28] by Du. In this study, the dynamic was modeled in three-dimension by using the FM method, and the inertial of the link is consolidated at the element’s nodes. Tokhi [30] developed the experiments to validate the dynamic model of the flexible system. In [34], the dynamic of flexible link in the parallel foundation was described by the finite element coupling with Lagrangian equations. By using the FE method and Kane’s equations, comparing with other methods, Lochan [46] discussed the advantages of the FE method in the modeling of the flexible robot’s dynamic. In this research, the main benefits of the FE method were pointed out, including the ease to handle the nonlinear conditions and complicated boundary conditions and the independence of the dynamic modeling on the link’s shape.

In [61], the kinematics response of the joints and flexible links were described with a proposed transformation matrix. Also, the dynamic model was implemented by introducing a new recursive formulation. In the next developed step, the authors in [67] attempted to propose the dynamic model and its inverse analysis for a class of flexible robots, consisting of two-flexible links by using the FM-Lagrangian approach. The inverse dynamic analysis was then solved by the bisection method. Another attempt to propose new mathematical equations for flexible robot dynamics analysis, aiming at simplifying the computation process was presented in [62].

Based on the Lagrangian formulation, Tokhi [30], Al-Bedoor [31], Mahto [32] focused on one link—one rotary joint flexible robot, Karagulle [33] considered the manipulators, configured by two-links and two rotary joints, Al-Bedoor [17] and Pan [19] emphasized on the robot with one flexible link and one fixed prismatic joint. Wang [34] accounted for sliding prismatic joints in the architecture of a parallel robot, and Usoro [8] studied multi-link robot structure. In these researches, the matrix of each element was calculated based on the elastic deformation at its nodes and considering the previous joint variables and the elastic deformation of the nominal articulation. In [5, 6], the calculation of each element’s matrix was derived concerning the freedom degree of nodes. Global matrices were assembled from the elemental matrices. In particular, Karagulle [33] assembled directly the global mass matrix, entry by entry. In the study by My et al. [61, 62], a recursive kinematic and dynamic formulation has been developed for the multi-link flexible robot with respect to different joint types.

It is seen that the FEM Lagrangian approach has been mostly employed in the most recent works, such as Mahto [32], Karagulle et al. [33], and My et al. [61, 62, 67], in which the modeling and controlling of the flexible robots have been investigated. In these recent FEM formulations, a flexible robot consisting of \(n\) links is usually considered.

In Fig. 3, two links of a flexible manipulator are shown. The two links are connected by a joint \(i\) which is representative of different joint types.

Fig. 3
figure 3

General schematic of a flexible link’s pair

Full size image

For every element \(ij\), the elemental mass matrix was usually written as follows.

$${\varvec{M}}_{ij} = \left[ {m_{sp} } \right]_{ij} = \mathop \smallint \limits_{0}^{{l_{ie} }} m_{i} {\varvec{J}}_{ij}^{T} {\varvec{J}}_{ij} dx$$
(1)

where \(m_{i}\) is the mass of the element \(ij\), and the Jacobian \({\varvec{J}}_{ij}\) is calculated as follows

$${\varvec{J}}_{ij} = \frac{{\partial {\varvec{r}}_{0ij} }}{{\partial {\varvec{q}}}}$$
(2)

In Eq. (2), \({\varvec{r}}_{0ij}\) is a point on the beam element \(ij\), and \({\varvec{q}}\) is the vector of the generalized coordinates. As a consequence, the mass matrix can be cumulatively calculated as follow.

$${\varvec{M}} = \mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{j = 1}^{{n_{i} }} {\varvec{M}}_{ij}$$
(3)

In the same approach, the global stiffness matrix for the governing equation can be calculated as follow.

$${\varvec{K}} = \mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{j = 1}^{{n_{i} }} {\varvec{K}}_{ij}$$
(4)

When the matrices \({\varvec{M}}\) and \({\varvec{K}}\) are determined in a symbolic form, the governing equation for a flexible robot is expressed as follows.

$${\varvec{M}}\left( {\varvec{q}} \right)\user2{\ddot{q}} + {\varvec{C}}\left( {{\varvec{q}},\dot{\user2{q}}} \right)\dot{\user2{q}} + {\varvec{Kq}} + {\varvec{G}}\left( {\varvec{q}} \right) = {\varvec{F}}$$
(5)

Note that \(\user2{G }\) represents the gravity effects, the Coriolis and centrifugal matrix \({\varvec{C}}\) can be determined by using Christoffel method and \(\user2{F }\) is the forces/torques’ vector.

Besides the FM method, to model the flexible robot arms, the AM method also has been widely exploited. In this method, the link’s elasticity is modeled by a series of finite modes, in which spatial model eigenfunctions and time-varying amplitudes were truncated. Based on Lagrange’s equations, several investigations were carried out for the formulation of the dynamic equations in [4, 6, 8, 9, 11, 12, 14, 17, 19, 21, 22, 30, 36,37,38, 68,69,70,71,72,73]. Also, with the same purpose of dynamic formulation, Gibbs–Appell’s formulation was applied in the works by Korayem [1] and Khadem [13] derived, Hamilton’s principle was used in [18, 66], and Newton–Euler equations were adopted in [3, 5, 6, 16, 20, 35, 63,64,65].

Note that the modeling of the flexible robots has been also mentioned in some investigations on control law design [74,75,76,77]. Matsuno [78] designed the laws to control the one-link flexible robot based on analyzing the AM—Lagrangian dynamic model. Bolandi [79] proposed the nonlinear controlling law for tracking the exact tip of the flexible arm. Based on Hamilton’s equations, Zhang [80] formulated dynamic equations with the purpose of vibration control for one-link flexible robot. Apart from the aforementioned works, there have been many studies related to different aspects of modeling and analyzing flexible robotic systems. The inverse dynamics of the flexible arm were presented in [37, 48, 65, 81,78,83], the stiffness modeling and characteristics of robot were considered in [84,81,86], and the experiments were implemented in [61, 87,84,89].

3 Conclusion

Though flexible robots have many outstanding advantages in comparison with traditional rigid robots such as energy-saving, able to operate with a small actuator, and highly efficient load carrying. The stiffness of flexible robots is a critical issue for their design and control. The flexibility of the flexible robots increases the computational complexity of the kinematic and dynamic modeling for the robots, especially when considering a multi-link flexible robot with different joint types. There has been a massive amount of research work concerning flexible robots. Various configurations of flexible robots are taken into account but mainly focus on robots with a single-flexible link or two-flexible link. A few attempts consider the multi-link flexible robots. The rotational joint is a basic joint type that is considered in most studies. A few works are interested in prismatic joints. The combination of the revolute joint and translational joint in an elastic robot configuration is still problematic to deal with. The AM method and the FE method are mainly used for the formulation of the dynamic equation. However, the AM method is suitable for configurations with less elastic stitches. The FE method has many advantages to formulate the mathematical equations of the flexible multi-link robot even with different joint types. Besides, there have been several mathematical approaches for the derivation of the flexible robot’s dynamic equations. Nevertheless, the Newton–Euler method, Lagrangian formulation, Hamilton principle, and Kane equations are widely used for flexible robot modeling.