Keyword

1 General Consideration

Ionic transport processes in glasses and glass-nanocomposites have been a subject of deep scientific interest [1,2,3] for more than half a century, and to date, a large number of glass-forming systems had been investigated over a wide range of compositions with respect to the transport-related properties such as conductivity and its dependence on temperature and frequency, radio tracer diffusion, NMR, electrical and mechanical relaxation, etc.

The glasses possess certain advantage over their crystalline counterparts, which includes physical isotropy, the absence of grain boundaries, good workability and continuously variable composition. Moreover, the room temperature conductivity in these glasses can vary from as little as 10−15 to as much as 10−2Ω−1 cm−1, which makes them suitable for many electrochemical applications. The latter values of conductivity arise in fast-ion conductors in which the diffusing atoms are charged and carry electric current. This ionic contribution to the electric current exceeds the contribution from electrons. Various types of ions can diffuse in glasses which include the Li+ ion (the smallest) to Ag+ ion (the most deformable) having the highest conductivity [2, 3]. Some excellent review on the dynamic properties of the ions in the glasses can be found in the works of Ingram, Angell and Kahnt [3,4,5].

2 Transport Theory with Examples

The discovery of fast-ion conduction in oxide glass [6] and the energy crisis of the early 1970s stimulated much interest in using glasses as solid-state electrolytes in advanced battery systems. The microscopic mechanisms responsible for ionic conduction in glasses, however, are still not well understood due to the difficulty in independently determining the carrier concentration and mobility. The DC and AC conductivities of the ionically conducting glasses have been studied extensively for traditional glass formers [7,8,9]. The DC conductivity for materials with one type of carrier is given by

$$\sigma_{{{\text{dc}}}} = \left( {{\text{Ze}}} \right)n\,\mu$$
(6.1)

where Ze is the charge of the carrier, n is the concentration of mobile carriers, and μ is the mobility. The concentration of mobile ions may be thermally activated and can be written as

$$\begin{aligned} n & = N_{0} \exp \left( { - \Delta G_{c} /k_{{\text{B}}} T} \right) \\ & \; = N_{0} \exp \left( { - \Delta S_{c} /k_{{\text{B}}} } \right)\exp \left( { - \Delta H_{c} /k_{{\text{B}}} T} \right) \\ & \; = N_{e} \exp \left( { - \Delta H_{c} /k_{{\text{B}}} T} \right) \\ \end{aligned}$$
(6.2)

where ΔGc is the free energy necessary to impart a carrier population, ΔSc is the associated entropy, ΔHc is the enthalpy, kB is the Boltzmann constant, T is the absolute temperature, and Ne is the effective infinite temperature ion concentration which includes the entropy term. The mobility is related to the diffusivity (D) through Nernst-Einstein relation

$$\begin{aligned} \mu = {\text{Ze}}D/k_{{\text{B}}} T & = {\text{Ze}}\gamma \lambda ^{2} v_{{\text{H}}} /k_{{\text{B}}} T \\ & \; = \left( {{\text{Ze}}\gamma \lambda ^{2} v_{0} /k_{{\text{B}}} T} \right)\exp \left( { - \Delta G_{m} /k_{{\text{B}}} T} \right) \\ & \; = \left( {{\text{Ze}}\gamma \lambda ^{2} v_{0} /k_{{\text{B}}} T} \right)\exp \left( { - \Delta S_{m} /k_{{\text{B}}} } \right)\exp \left( { - \Delta H_{m} /k_{{\text{B}}} T} \right) \\ & \; = \left( {{\text{Ze}}\gamma \lambda ^{2} v_{{\text{e}}} /k_{{\text{B}}} T} \right)\exp \left( { - \Delta H_{m} /k_{{\text{B}}} T} \right) \\ \end{aligned}$$
(6.3)

where ΔGm is the free energy for ion migration, ΔSm is the associated entropy, ΔHm is the enthalpy, γ is the geometrical factor for ion hopping, λ is the average hop distance between the mobile ion sites, νH is the hopping frequency, ν0 is the jump attempt frequency of the ion, and νe is the effective jump attempt frequency including the entropy term. From the first law of thermodynamics under conditions of constant specimen volume and temperature, the enthalpy and energy state functions are equal. Thus, we replace ΔH by ΔE. Therefore, substituting Eqs. (6.2) and (6.3) to (6.1) yields

$$\sigma_{{{\text{dc}}}} = \left( {N_{e} \left( {{\text{Ze}}} \right)^{2} \gamma \lambda^{2} v_{{\text{e}}} /k_{{\text{B}}} T} \right)\exp \left\{ { - \left( {\Delta E_{c} + \Delta E_{m} } \right)/k_{{\text{B}}} T} \right\}$$
(6.4)

which agrees quite well with the experimental results in the limited temperature range.

Any discussion regarding the mechanism of ion transport in glasses must focus on two themes.

  • Strong electrolyte theories (Anderson-Stuart model)

  • Weak electrolyte theories (Ravaine-Souquet model).

2.1 Anderson-Stuart Model

The Anderson-Stuart [9] model is a structural model which considers the activation energy as the energy required to overcome electrostatic forces (ΔEB) plus the energy required to open up “doorways” in the structure large enough for the ion to pass through (ΔES). An atomic-level representation of this model by Martin and Angell [8] is shown in Fig. 6.1.

Fig. 6.1
An atomic level representation of energies of cation conduction process according to Anderson - Stuart model. B O and N B O are represented by circles with negative and positive sides are marked. Delta E subscript S and B distances are marked. Symmetrical peaks and depressions in the pattern can be seen on both sides.

Representation of the energies of cation conduction process according to the Anderson-Stuart model as interpreted by Martin and Angell [8]. Republished with permission from Martin and Angell [8]

Full size image

According to Anderson-Stuart model, the activation energy is

$$\Delta E_{{{\text{act}}}} = \Delta E_{B} + \Delta E_{S}$$
(6.5)

where the binding energy term is given as

$$\Delta E_{B} = \frac{{ZZ_{0} e^{2} }}{{\varepsilon_{\infty } }}\left[ {\frac{1}{{r + r_{0} }} - \frac{2}{\lambda }} \right]$$
(6.6)

and the strain energy term is given as

$$\Delta E_{s} = \pi G_{D} \lambda \left( {r - r_{D} } \right)^{2} /2$$
(6.7)

In these equations, GD is the shear modulus of the glass, and \(r_{D} ,\) \(r\) and \(r_{0}\) are the interstitial window, the mobile cation and the non-bridging anion radii, respectively; \(\lambda\) is the average jump distance; \(Z\) and \(Z_{0}\) are the number of charges on the mobile cation and the anion; and \(e\) is the charge on the electron [10, 11].

To make the Anderson-Stuart model more realistic, minor changes to the strain term have been proposed by McElfresh and Howitt [10]. Elliott [11] has pointed out that the Anderson-Stuart model neglects specific polarization and repulsion terms and includes these terms in the overall Coulomb potential. Other models describing the activation energy have been suggested, but nearly all follow the general principles of the Anderson-Stuart model.

The physical and structural parameters necessary to verify the validity of the Anderson-Stuart model and experimental methods for measuring these parameters are:

  • \(\Delta E_{{{\text{act}}}}\): determined from wide temperature-range ionic conductivity measurements

  • \(\lambda\): approximated from NMR static linewidth measurements or density measurements

  • G: determined from acoustic measurements

  • \(r_{D}\): the interstitial window radius determined from inert gas diffusion studies.

To test the validity of the Nernst-Einstein derivation for pre-exponent term, the following additional parameters are needed:

  • \(\sigma_{0}\): determined from wide temperature-range ionic conductivity measurements

  • \(\nu_{0}\): determined from the Far-IR ion vibrational frequency

  • \(\gamma\): usually taken as approximately equal to \(1/6\).

2.2 Ravaine-Souquet Model

The correlation between ionic conductivity and thermodynamic activity is the basis of weak electrolyte or Ravaine-Souquet model [12]. In glasses, the addition of M2O or M2S typically results in the added anions, becoming part of the glass structure by covalently bonding to the glass-forming cations, while the added alkali cations reside in a local region supporting charge neutrality. Most of these alkali cations are unionized and immobile, but a small fraction may dissociate from these sites to form ionized or dissociated “mobile” cations. These ions are proposed to contribute to the ionic conduction. The formation of mobile cations M+ from associated oxide complex in a glass is taken analogous to the dissociation of modifier salt added to the glass [13].

$${\text{M}}_{2} {\text{O}} = {\text{M}}^{ + } + {\text{OM}}^{ - }$$
(6.8)

and the concentration independent dissociation constant is given by

$${\text{K}} = \left[ {{\text{M}}^{ + } } \right]\left[ {{\text{OM}}^{ - } } \right]/\left[ {{\text{M}}_{2} {\text{O}}} \right]$$
(6.9)

From Eq. (6.8), the [M+] and [OM−] are equal, and the concentration of the free dissociated ion is, therefore, given by

$$\begin{aligned} \left[ {{\text{M}}^{ + } } \right] & = K^{1/2} \left[ {{\text{M}}_{2} {\text{O}}} \right]^{1/2} \\ & \; = K^{1/2} \left[ {{\text{a}}_{{{\text{M}}_{2} {\text{O}}}} } \right]^{1/2} \\ \end{aligned}$$
(6.10)

where aM2O is the thermodynamic activity equated to the M2O concentration. The equality is valid for very dilute solutions (Henry’s law). The ionic conductivity is proportional to the concentration of mobile ions, so that

$$\sigma \propto \left[ {{\text{M}}^{ + } } \right] = K^{1/2} \left[ {{\text{a}}_{{{\text{M}}_{2} {\text{O}}}} } \right]^{1/2}$$
(6.11)

Ravaine and Souquet performed both ionic conductivity and concentration cell emf measurements for various sodium and potassium silicate glasses. They plotted conductivity ratio versus activity ratio for various pairs of glasses and showed that the slope was ½ for this log plot.

3 DC Electrical Conductivity of Some Li Containing Glassy Systems Using Various Models

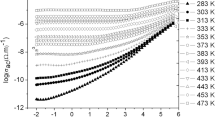
Glassy ceramics xLi2O–(1−x) (0.8V2O5–0.2ZnO) with x = 0.1, 0.2 and 0.3 have been developed in the laboratory by solid-state reaction. Complex impedance plots for x = 0.1 are presented in Fig. 6.2a at various temperatures. The DC electrical conductivity (σdc) has been computed from the semicircular portions of Fig. 6.2a. It is noted in Fig. 6.2a that grain boundary resistance as well as polarization effects are absent. Similar results are obtained for other samples. Yuan et al. [14] reveal that a small amount of doping is sensitive to the purity of the sample, which is reflected in the nature of the plot. Generally, the AC response of the system indicates a relation between the applied voltage and the current through the sample under consideration. The equivalent circuit containing ideal resistive and reactive components is presented in the inset of Fig. 6.2a. It may be proposed to explore AC response of the system.

Fig. 6.2
Dot plots represent various properties of glass systems. Image a: gives resistivity for different circuit measurements. Circuit with resistor and capacitor is given. b: shows temperature dependency for x equals 0.1, 0.2 and 0.3. c: gives fixed temperature conductivity and activation energy and d: givens low temperature D C conductivity plot.

a Cole–Cole plot of resistivity and corresponding equivalent circuit for measurement b temperature dependency of DC conductivity; c fixed-temperature (473 K) DC conductivity and activation energy and d low-temperature DC conductivity plot using Mott’s model. Republished with permission from Acharya et al. [15]

Full size image

In the equivalent circuit (parallel RC), the overall AC impedance of the present circuit can be represented as [14]:

$$\begin{aligned} \frac{1}{z} & = \frac{1}{{Z_{R} }} + \frac{1}{{Z_{C} }} \\ & = \left( {\frac{1}{R} + j\omega C} \right)^{ - 1} \\ & = \frac{R}{1 + j\omega RC} \\ & = \frac{R}{{1 + \left( {\omega RC} \right)^{2} }} - j\frac{{\omega R^{2} C}}{{1 + \left( {\omega RC} \right)^{2} }} \\ \end{aligned}$$
(6.12)

where \(Z_{R}\) and \(Z_{C}\) are the resistive and reactive components.

This result directly indicates the form of real (Zre) and imaginary (Zim) impedances of the parallel RC circuit as:

$$\begin{aligned} & Z_{{{\text{re}}}} = \frac{R}{{1 + \left( {\omega RC} \right)^{2} }} \\ & Z_{{{\text{im}}}} = - \frac{{\omega R^{2} C}}{{1 + \left( {\omega RC} \right)^{2} }} \\ \end{aligned}$$
(6.13)

and the phase angle φ can be presented as:

$${\text{tan}}\,\varphi = - \omega RC$$
(6.14)

At low frequency (ωRC ≪ 1), Zre ≈ R and Zim ≈ 0. This result implies that this RC circuit acts as a resistor. On the other hand, at high frequency (ωRC ≫ 1), Zre ≈ 0 and Zim ≈ 1/ωC, and the present circuit acts as a capacitor with time constant, equal to RC.

Equations (6.12) and (6.13) yield

$$\left( {Z_{{{\text{re}}}} - \frac{R}{2}} \right)^{2} + Z_{{{\text{im}}}}^{2} = \left( \frac{R}{2} \right)^{2}$$
(6.15)

Equation (6.15) indicates a half-circle in the complex plane, with a radius of R/2, which can be validated by Fig. 6.2a.

Figure 6.2b shows the variation of DC conductivity with reciprocal temperatures, which demonstrates thermally activated nature. It may be anticipated from the nature of variation of DC conductivity with temperature in Fig. 6.2b that the present glassy system must contain both ionic and electronic components, which may cause the total conductivity. However, semiconducting properties may arise due to presence of a small percentage of transition metals (vanadium), via polaron hopping, from lower cationic valence state to higher valence state [16, 17]. Similarly, ionic conductivity may arise due to transport of lithium ions in present glassy matrix, which may impart electrical conductivity of the present system [18].

4 Study of Temperature and Composition Dependency of Conductivity

It is also noteworthy from Fig. 6.2b that DC conductivity decreases with Li2O content in the compositions. It is quite clear from Fig. 6.2b that low-temperature DC conductivity data may arise due to polaron hopping process [19] and high-temperature DC conductivity data have been received mainly due to conduction of Li+ ions [20]. Here, the polaron conduction is achieved by the following conversion [21]:

$$V^{ + 5} \to V^{ + 6} + {\text{electron}}$$

Here, ZnO acts as a stabilizer [22]. As the Li2O content increases in the compositions (V2O5 decreases), more and more number of V+ ions are expected to take part into bonds of network, thereby contributing less number of polaron in the conduction process. As a consequence, conductivity drops down at low temperature.

High-temperature DC conductivity data as shown in Fig. 6.2b are found to increase with temperature linearly, which may be analyzed using Arrhenius equation:

$$\sigma_{{{\text{dc}}}} = \sigma_{0} \exp \left( { - E_{\sigma } /kT} \right)$$
(6.16)

where Eσ is the DC activation energy for present glassy ceramics under investigation, T is the absolute temperature, and k is the Boltzman constant. Figure 6.2c depicts the variation of σdc at 473 K with compositions. It is interestingly noted that the sample with x = 0.1 shows the highest DC conductivity. DC conductivity is found to decrease as the Li2O content increases in the compositions. Computed activation energy corresponding to σdc, obtained from the slopes of the best-fitted straight lines of Fig. 6.2a, is also presented in Fig. 6.2c, which shows opposite nature of DC conductivity.

To interpret DC conductivity data in low temperature ranges (below half of the Debye temperature), Mott’s variable-range hopping (VRH) model [23, 24] has been considered.

Here, a charge carrier (polaron) hops from one localized state to another. It is also assumed here that the density of states is finite and localized at the Fermi level. Mott’s VRH conductivity [23, 24] may be expressed as:

$$\sigma_{{{\text{dc}}}} = A\exp \left[ { - \left( {{\raise0.7ex\hbox{${T_{0} }$} \!\mathord{\left/ {\vphantom {{T_{0} } T}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$T$}}} \right)^{0.25 } } \right]$$
(6.17)

where A is pre-factor and T0 is the characteristic temperature coefficient, which takes the form:

$$T_{0} = \frac{{16 \alpha^{3} }}{{k\;N\left( {E_{{{\text{FM}}}} } \right)}}$$
(6.18)

Here, α−1 is the localization length, and N(EFM) is the density of states at the Fermi level. Low-temperature DC conductivity data with respect to T−0.25 are presented in Fig. 6.2d. The experimental data in Fig. 6.2d are fitted to Eq. (6.17). Here, α−1 is assumed to be 10 Å [25], which is relevant to the present glassy system with some localized states [25]. The slopes have been computed from the linear best-fit data as shown in Fig. 6.2d. The value of N(EFM) has been estimated from Eq. (6.18), which is presented in Table 6.1. The values of N(EFM) are found to decrease with composition (x), which show similar nature of DC conductivity. The above-mentioned outcomes convey the facts that decrement in V2O5 content in the compositions may be the most important factor for the conduction process in low temperature.

Table 6.1 Estimated values of density of states near Fermi level (N(EFM)) and fixed-temperature DC conductivity of xLi2O–(1−x)(0.5V2O5–0.5ZnO) glass–ceramics. Estimated errors of measurements are mentioned
Full size table

5 Conclusion

New Li2O-doped glassy ceramics have been prepared using melt-quenching route, and their electrical DC conductivity has been studied in wide temperature regime. It is anticipated from the nature of composition that Li+ conduction mostly contributes to electrical conductivity at high temperature, and Mott’s variable-range hopping (VRH) model has been utilized to analyze low-temperature DC conductivity data due to polaron hopping.