Electrical Transport Properties of Glass

Abstract

The aim of this chapter is to review the current understanding of various effects, both electronic and ionic transports, in oxide and chalcogenide glasses. Oxide and chalcogenide glasses are classified into an electronic or ionic transport materials depending on the composition of their constituents. Doping of transition metals or alkali atoms into oxide glasses produces electronic or ionic properties in electrical conduction processes. Free carriers (electron and hole) in rigid materials are transported via extended states (band conduction). Localized carriers are transported by a hopping mechanism through localized states. If carrier transport occurs in a deformable lattice, either with strong or weak carrier–phonon interaction, the carrier is accompanied by lattice distortion. This is regarded as a pseudoparticle and is called a polaron, producing a polaronic transport in these media, which is usually discussed for the transition-metal-oxide glasses (s). It is suggested in this article that an alternative explanation for the transport mechanism, instead of the traditional polaron model, is also possible in TMOG. When the conduction, either electronic or ionic, is thermally activated, it is pointed out that the Meyer–Neldel rule () or the compensation law plays the principal role in the transport process in glassy materials. A long-standing puzzle is the mixed alkali effect () in oxide glasses, together with the power-law conductivity behavior. A similar effect, i. e., the mixed cation effect, is also found in chalcogenide glasses. All of these are still matters of debate for electronic and/or ionic transport in glasses and there are many unsolved and important problems on electrical conductions in glasses, which will be finally summarized. Although the principal concern is with physics involved in electrical transport in glasses, nevertheless it should be mentioned at this juncture that electrical transport phenomena also have many technological ramifications.

Electronic and ionic transport phenomena in glasses are discussed in this chapter. The glasses discussed in this chapter are not limited to the so-called glass, usually prepared by the melt-quenched () technique, which experiences the glass transition. When we consider the materials (periodic table), there are two types: one is the oxide glass () based on silica, and the other is the chalcogenide glass (), which is composed of VI-group elements such as S, Se, and Te.

The electrically conducting materials can be classified into the electronic and ionic conductions, as outlined in Fig. 10.1. Both OG and ChG belong to the electronic or ionic transport materials, which depend highly on composition. Alloying of transition metals (V, W, Fe etc.) and alkali atoms (Na, Li etc.) with OGs leads to the electronic and ionic properties of electrical conduction, respectively [10.1]. If carrier transport occurs in a rigid lattice, electrons or holes are transported via extended states (band conduction) and/or conducted through localized states [10.2]. If a carrier is transported in a deformable lattice, the carrier is easily deforms the lattice (carrier–phonon coupling) and the carrier accompanied by such distortion is called a polaron. Polaronic transport occurs in these media [10.3, 10.4]. Note that the polaronic transport is further classified into the two limits: either strong or weak coupling [10.3].

Fig. 10.1

Electrical conduction processes in glasses. With some alkali or metallic additives into glasses, ionic (cation) diffusion dominates the electrical conduction

In ionic transport, on the other hand, it is remarkable that the mixing of different alkalis or cations in glass produces a pronounced minimum in the conductivity (or diffusion coefficient). This effect is called the mixed alkali effect (MAE) or mixed cation effect (). The MAE or MCE is an interesting issue in glass science and has been a matter of debate for long time. Together with the above issue, the power-law correlation between conductivity and cation contents in OGs and ChGs is also long-standing puzzling issue. A detailed discussion of this unsolved problem will be given in this review.

When the conduction, either electronic or ionic, is thermally activated, the Meyer–Neldel rule (MNR) or the compensation law plays the principal role in the transport process in glassy materials. This effect is also a long-unsolved issue.

In this chapter, the current understanding of electrical conduction processes, through both theories and experimental data, is discussed in ChGs and OGs. There are many unsolved and interesting problems in electrical conductions in glassy materials, which will be finally outlined in Sect. 10.6.

1 Electronic Transport Theory

The electronic transport in solids, in general, is controlled by phonons. We should therefore discuss the two extreme cases: the transport in a rigid lattice in which the electron–phonon coupling is ignored, or transport in a deformable lattice in which a carrier accompanies lattice distortion. In the following, we briefly review the theoretical background on these issues in disordered solids such as glassy or amorphous semiconductors.

1.1 Electronic Transport in a Rigid Lattice

In a rigid network of atoms in a disordered semiconductor, electrons (holes) are assumed to move through the band (extended) states and/or through the localized states, without being subjected to the lattice deformations. The electron–phonon coupling is therefore ignored in this case [10.2]. The electronic configuration of individual atoms in a solid remains the same in both crystalline and disordered solids. Therefore, the electronic density-of-states () for disordered solids in the region of extended states deviates little from that in crystalline solids and can be approximated by the square root of the energy in three-dimensional () configuration.

Figure 10.2 shows the electronic density of states. The electronic conduction, through the extended states (above $E_{\mathrm{c}}$ and below $E_{\mathrm{v}}$), occurs in disordered solids, similarly to crystalline solids. However, due to the lack of long-range orders, the carrier mean free path approaches the length scale of atomic separation, which may produce various anomalies in the electronic transport in disordered solids [10.5]. The lack of long-range order and presence of dangling-bond defects produces localized tail states (shaded region between $E_{\mathrm{v}}$ and $E_{\mathrm{c}}$) and localized gap states, respectively. The electronic hopping (or tunneling) transport occurs through these localized states at relatively low temperatures [10.2]. The nature of carriers gets altered when a charge carrier crosses the energies $E_{\mathrm{c}}$ and $E_{\mathrm{v}}$, which separate the extended and localized states and are called the mobility edge. The transport above $E_{\mathrm{c}}$ is the band conduction type for electrons and transport below $E_{\mathrm{v}}$ is the band conduction type for holes.

Fig. 10.2

Electronic density of states $D$ ($E$). The mobility edge divides the delocalized (above $E_{\mathrm{c}}$ and below $E_{\mathrm{v}}$) and localized states (shaded area)

1.1.1 Electronic Transport in Extended States

First, we discuss the band conduction in nondegenerate cases. The temperature-dependent number (density) of free electrons $n$ in the conduction band () beyond the energy $E_{\mathrm{c}}$ at high temperature $T$ (near room temperature) is given as

$$n=N_{\mathrm{c}}\exp\left(-\frac{E_{\mathrm{c}}-E_{\mathrm{F}}}{k_{\mathrm{B}}T}\right),$$

(10.1)

where $N_{\mathrm{c}}$ is the effective density-of-states for the conduction band, $E_{\mathrm{F}}$ the Fermi level and $k_{\mathrm{B}}$ the Boltzmann constant. The conductivity is therefore given by

$$\sigma=en\mu_{0}=eN_{\mathrm{c}}\mu_{0}\exp\left(-\frac{E_{\mathrm{c}}-E_{\mathrm{F}}}{k_{\mathrm{B}}T}\right),$$

(10.2)

where $\mu_{0}$ is the microscopic mobility. As $E_{\mathrm{c}}-E_{\mathrm{F}}$ can be approximated to vary linearly with the temperature as $E_{\mathrm{c}}-E_{\mathrm{F}}=E_{\mathrm{c}}-E_{\mathrm{F}}(0)-\gamma T$, where $E_{\mathrm{F}}(0)$ is the Fermi level at $T=0$ and $\gamma$ the temperature coefficient, the conductivity is given as

$$\begin{aligned}\displaystyle\sigma&\displaystyle=eN_{\mathrm{c}}\mu_{0}\exp\left(\frac{\gamma}{k_{\mathrm{B}}}\right)\exp\left(-\frac{E_{\mathrm{c}}-E_{\mathrm{F}}(0)}{k_{\mathrm{B}}T}\right)\\ \displaystyle&\displaystyle\equiv\sigma_{0}\exp\left(-\frac{E_{\mathrm{c}}-E_{\mathrm{F}}(0)}{k_{\mathrm{B}}T}\right).\end{aligned}$$

(10.3)

The conductivity is thermally activated with the activation energy $\Updelta E=E_{\mathrm{c}}-E_{\mathrm{F}}(0)$. For p-type transport, the activation energy should be given as $\Updelta E=E_{\mathrm{F}}(0)-E_{\mathrm{v}}$: $E_{\mathrm{F}}(0)$ lies between $E_{\mathrm{c}}$ and $E_{\mathrm{v}}$. Note that the above equations rely on the Boltzmann transport theory and hence depend on the assumption that the mean free path, for example, is large compared with the lattice constant. Equation (10.3) is therefore valid for ordered (crystalline) semiconductors. When the mean free path is of the order of a lattice constant the Boltzmann formula breaks down [10.5], in which $\sigma_{0}$ cannot be given by $eN_{\mathrm{c}}\mu_{0}\exp(\gamma/k_{\mathrm{B}})$.

Strictly speaking in glasses, a proper theoretical understanding of the prefactor $\sigma_{0}$ is still lacking.

For a degenerate electron in glasses (metallic glasses), i. e., Fermi energy $E_{\mathrm{F}}$ lies above $E_{\mathrm{c}}$, metallic behavior for electronic transport is expected. When it lies below $E_{\mathrm{c}}$, the transport can occur through localized states at low temperatures and the conductivity at zero temperature vanishes. Thus, when the Fermi level crosses the mobility edges, a discontinuous conductivity, i. e., a finite value to zero, is expected to occur. This finite value of conductivity is called the minimum metallic conductivity $\sigma_{\text{min}}$: the prefactor $\sigma_{0}$ was given by $\sigma_{\text{min}}$, being roughly estimated to be around ${\mathrm{200}}\,{\mathrm{S{\,}cm^{-1}}}$ [10.2, 10.5]. This famous idea of the minimum metallic conductivity proposed by Mott was alive by the beginning of 1980 in the field of localization theory [10.5]. However, the concept of minimum metallic conductivity is no longer supported by the scaling theory [10.6] and some experimental results in which conductivity tends continuously to zero at zero temperature [10.7, 10.8], while there was evidence to support the concept of minimum metallic conductivity [10.5, 10.9].

Finally, it should be stated what happens in carrier transport when the mean free path approaches the lattice constant or the mean distance between carriers. This condition should be met in glassy materials, in particular, when we discuss the conductivity prefactor. As will be discussed in Sect. 10.3.1, the conductivity prefactor involves another unknown factor (Meyer–Neldel rule). Therefore, the term of minimum metallic conductivity itself looked unattractive for most experimentalist in the field of oxide and chalcogenide glasses.

For amorphous metals where the resistivity is large, the temperature coefficient of the resistivity () is predicted to be negative as observed experimentally [10.5, 10.9]. A new idea with quantum corrections on the Boltzmann equation was introduced to explain this behavior [10.5]. Remember that the TCR is positive in conventional metals. We will discuss briefly the modified Boltzmann equation in Sect. 10.1

1.1.2 Electronic Transport in Localized States

Carrier transport occurs between localized states, in which a probability of tunneling (hopping) of localized carriers dominates the conductivity. The carrier transport via localized states is therefore completely different from that of the band conduction. The rate-determining process is the hopping of an electron from an occupied localized state (O) below the Fermi level to an empty state above (E). The probability $\nu$ per unit time for this event to occur is given by [10.2, 10.5]

$$\nu=\nu_{0}\exp\left(-\frac{2R}{a}-\frac{W}{k_{\mathrm{B}}T}\right),$$

(10.4)

where $R$ and $W$ are the spatial distance and the energy difference between the states O and E respectively, $a$ is the Bohr radius of a localized state, and the prefactor $\nu_{0}$ is of the order of phonon frequency ($\approx{\mathrm{10^{12}}}\,{\mathrm{s^{-1}}}$). Note that the factor $\exp(-2R/a)$ represents the extent of overlapping of the wavefunction and $\exp(-W/(k_{\mathrm{B}}T))$ is the Boltzmann factor.

The diffusion coefficient of localized carriers in 3-D space can be given as

$$D=\frac{R^{2}\nu}{6}\;.$$

(10.5)

The hopping conductivity $\sigma_{\mathrm{h}}$ using the Einstein relation, $\mu{}k_{\mathrm{B}}T=eD$, is given by

$$\sigma_{\mathrm{h}}=en_{\mathrm{h}}\mu=\frac{n_{\mathrm{h}}(eR)^{2}}{6k_{\mathrm{B}}T}\nu_{0}\exp\left(-\frac{2R}{a}-\frac{W}{k_{\mathrm{B}}T}\right),$$

(10.6)

where $n_{\mathrm{h}}$ is the density of hopping carriers. When the hopping occurs between the nearest neighbor sites, we call it nearest-neighbor hopping () [10.2]. The conduction in tail states at relatively low temperatures can be dominated by the NNH mechanism. This means that the conduction path moves from the band states to localized tail states with decreasing temperature.

At low temperatures transport near $E_{\mathrm{F}}$ may occur, since the number of carriers in the band and tail states decrease significantly. In the so-called Fermi glass, in which the Fermi level lies in localized states, the density of hopping electrons $n_{\mathrm{h}}$ can be given by $(NE_{\mathrm{F}})k_{\mathrm{B}}T$, where $N$ ($E_{\mathrm{F}}$) is the DOS at $E_{\mathrm{F}}$. Since there are $(4\uppi/3)R^{3}N(E_{\mathrm{F}})$ states available in a spherical region of radius $R$, the average separation of these energy levels can be given as

$$W=\left[\frac{4\uppi}{3}R^{3}N(E_{\mathrm{F}})\right]^{-1}\;.$$

(10.7)

The hopping distance $R$ is therefore correlated with the energy difference $W$. An optimal hopping distance $R_{\text{opt}}$ is defined at which the hopping rate will be maximum. This mechanism was proposed by Mott [10.10] and is called variable-range hopping (). It is known for a uniformly distributed DOS near $E_{\mathrm{F}}$ so that $\nu$ is proportional to $\exp(-(T_{0}/T)^{1/4})$ (non-temperature-activated process), where $T_{0}$ is the characteristic temperature related to the value of $N(E_{\mathrm{F}})$ [10.10, 10.2].

Here we implicitly assumed the single phonon process in which the Bohr radius $a$ is required to be comparable with the lattice parameter ($\approx$ phonon wavelength) and $W$ is comparable or less than phonon energy. If not, the hopping rate $\nu$ should be significantly small. The multiphonon transition may occur instead of a single phonon process [10.11, 10.2, 10.3], which will be discussed in the following section.

It is known that under an external AC field an energy loss can be induced by atomic or molecular dipole relaxation. A hopping of carrier resembles the dipolar relaxation, i. e., $eR$ in (10.6) can be equivalent to the electric dipole [10.12]. The complex dielectric constant $\varepsilon^{*}(\omega)$, e. g., for the Debye response in the field direction $\exp(\mathrm{i}\omega t)$, is given as

$$\varepsilon^{*}(\omega)=\varepsilon_{\infty}+\frac{\varepsilon_{\mathrm{s}}-\varepsilon_{\infty}}{1+\mathrm{i}\omega\tau}\equiv\varepsilon_{1}-\mathrm{i}\varepsilon_{2}\;,$$

(10.8)

where $\varepsilon_{\mathrm{s}}$ and $\varepsilon_{\infty}$ are the static (at low frequency) and background (high frequency) dielectric constants respectively, and $\tau$ is the dielectric relaxation time. The complex conductivity is defined as $\sigma^{*}(\omega)=\mathrm{i}\omega\varepsilon_{0}\varepsilon^{*}(\omega)$, where $\varepsilon_{0}$ is the dielectric constant in a vacuum. So-called AC conductivity or AC loss is the real part of the conductivity given by $\omega\varepsilon_{0}\varepsilon_{2}(\omega)$.

Impedance spectroscopy () is therefore useful to understand its dynamics through the relaxation time $\tau$. When the localized carrier is assumed to be confined within a pair of localized states, it is called the pair approximation () and AC hopping conductivity is given in the general form as [10.12]

$$\sigma(\omega)=N_{\mathrm{p}}\int\alpha(\tau)\frac{\omega^{2}\tau}{1+\omega^{2}\tau^{2}}P(\tau)\mathrm{d}\tau\;,$$

(10.9)

where $N_{\mathrm{p}}$ is the number of pairs (dipoles), $\alpha(\tau)$ is the polarizability, and $P(\tau)$ is the probability distribution function of $\tau$. It is known for the most disordered solids that $\sigma(\omega)$ is nearly proportional to $\omega$ when $P(\tau)$ is proportional to $1/\tau$ [10.13, 10.14]. Note, however, that $\sigma(\omega)$ in this PA approximation cannot give DC conductivity since $\sigma(\omega)$ becomes zero at $\omega=0$. In the context of the PA approximation in the IS technique, $\sigma(\omega)$ cannot account for the experimental data if both DC and AC transports occur by the same mechanism.

A proper approach to hopping AC (and DC) conductivity can be a continuous-time random-walk () approximation [10.15]. A simple form of the complex AC conductivity based on the CTRW, which is strongly correlated to DC conductivity, is presented as [10.16, 10.17]

$$\sigma^{*}(\omega)=\sigma(0)\frac{\mathrm{i}\omega\tau_{\mathrm{m}}}{\ln(1+\mathrm{i}\omega\tau_{\mathrm{m}})}\;,$$

(10.10)

where $\tau_{\mathrm{m}}$ is the maximum hopping time (inverse minimum hopping rate) and $\sigma$(0) is the DC conductivity given as (10.6) [10.11]

$$\sigma(0)=\frac{n_{\mathrm{h}}(eR)^{2}}{6k_{\mathrm{B}}T\tau_{\mathrm{m}}}\;.$$

(10.11)

Note here that the values of $R$ and/or $W$ in (10.6) are assumed to be randomly distributed and among them the maximum $R$ and/or $W$ produce the maximum hopping time.

Each hopping event is treated equivalently as electrical circuits, which are shown in Fig. 10.3a,b. The pair approximation, leading to zero conductivity at $\omega=0$, can be treated as a parallel circuit (Fig. 10.3a,ba). In this CTRW approximation, on the other hand, each hopping event is treated equivalently as a series sequence of parallel connections of capacitance and resistance, as shown in Fig. 10.3a,bb. The overall value of admittance (and hence complex conductivity) in a series sequence of hopping events is known to be dominated by the minimum value of the admittance [10.16, 10.17]. Note that the CTRW approximation predicts properly the DC conductivity (10.11).

Fig. 10.3a,b

Equivalent electrical circuits approximation for (a) pair approximation and (b) CTRW approximation

1.2 Electronic Transport in a Deformable Lattice

An extra electron or hole in crystalline and noncrystalline materials can distort its deformable surroundings. A carrier accompanied by such distortion lowers its overall energy and is called a polaron [10.18, 10.19, 10.2]. When the spatial extent of the wavefunction of such a carrier is less than or comparable to the interatomic or intermolecular separation, it is called a small polaron (strong electron–phonon interaction), otherwise it is a large polaron (weak electron–phonon interaction) [10.3]. It is known that small polarons exist, for example in alkali halides, molecular crystals, rare-gas solids and some glasses [10.2, 10.3, 10.5].

While it is believed that small polarons dominate the electronic transport in some disordered materials such as chalcogenides [10.20, 10.3] and transition metal oxide glasses [10.1, 10.21], the issue still remain a subject of debate. We discuss the two extreme cases for electronic transport for a deformable lattice in the following section.

1.2.1 Strong Carrier–Phonon Coupling Limit

Electrons are coupled with both optical and acoustic phonons in a deformable lattice. First we must define the terms adiabatic and nonadiabatic conditions. What do we mean by the adiabatic condition? A simple reply to this question is that the carrier follows atomic vibrations, resulting in a high probability of a carrier hopping to the adjacent site. The nonadiabatic case has an opposite meaning: the carrier cannot follow the atomic vibrations and hence its probability for transfer is much smaller than in the adiabatic case.

It is known that the adiabatic approximation cannot explain the overall features of the DC and AC conductivities in glasses [10.22]: the jump rate of a small polaron in the adiabatic approximation at a high temperature is temperature-independent and is simply thermally activated, which is actually not observed experimentally. We therefore review only the nonadiabatic regime in the following.

An exact formulation of the nonadiabatic multiphonon transition rate $\Gamma$ for strong coupling (small polaron) in disordered solids has been presented as [10.23]

$$\Gamma=\left(\frac{J_{ij}}{\hbar}\right)^{2}C(T)\exp\left(-\frac{E_{\mathrm{A}}^{\text{op}}+E_{\mathrm{A}}^{\mathrm{ac}}+\Delta/2}{k_{\mathrm{B}}T}\right),$$

(10.12)

where $J_{ij}$ and $\Delta$ are the electron transfer integral and the energy difference between site $i$ and $j$ respectively, and $C(T)$ is a weakly temperature-dependent function. $E_{\mathrm{A}}^{\text{op}}$ and $E_{\mathrm{A}}^{\text{ac}}$ are related to optical and acoustic phonons respectively, and are given as

$$E_{\mathrm{A}}^{\text{op}}=\frac{2kT}{\hbar\omega_{\mathrm{o}}}E_{\mathrm{b}}^{\mathrm{op}}\tanh\left(\frac{\hbar\omega_{\mathrm{o}}}{4k_{\mathrm{B}}T}\right),$$

(10.13)

and

$$E_{\mathrm{A}}^{\text{ac}}=\frac{1}{N}\sum_{g}\frac{2kT}{\hbar\omega_{g,\mathrm{ac}}}E_{\mathrm{b}}^{\mathrm{ac}}\tanh\left(\frac{\hbar\omega_{g,\text{ac}}}{4k_{\mathrm{B}}T}\right),$$

(10.14)

where $\omega_{\mathrm{o}}$ is the mean optical frequency (a small dispersion of optical modes is assumed), $\hbar\omega_{g,\text{ac}}$ is the acoustic phonon energy at wavevector $g$, $N$ is the number of phonon modes, and $E_{\mathrm{b}}^{\text{op}}$ and $E_{\mathrm{b}}^{\text{ac}}$ are the polaronic binding energies for optical and acoustic phonons respectively. The nonadiabatic treatment of small polarons requires $J_{ij}<{\mathrm{0.1}}\,{\mathrm{eV}}$ modes [10.18, 10.19].

1.2.2 Weak Carrier–Phonon Coupling Limit

The multiphonon jump rate $R(\Delta)$ of localized electrons coupled to one vibrational mode $\omega_{\mathrm{c}}$ in the weak coupling limit ($k_{\mathrm{B}}T\gg\hbar\omega_{\mathrm{c}}$) is derived as [10.3]

$$R(\Delta)=K\sum_{n=-\infty}^{\infty}I_{p}(z)\cos(p\phi_{n})\;,$$

(10.15)

where $K$ is a characteristic frequency in the order of $\omega_{\mathrm{c}}$, $p$ is the number of participating phonons ($=\Delta/(\hbar\omega_{\mathrm{c}}))$, ${\phi}_{n}$ is the lattice relaxation-phase shift, and $I_{p}(z)$ is the modified Bessel function given by

$$I_{p}(z)=\left(\frac{z}{2}\right)^{p}\sum_{k=0}^{\infty}\frac{(z^{2}/4)^{k}}{k!\,:\Gamma(p+k+1)}\;,$$

(10.16)

where $z$ is given by

$$z=\frac{2E_{\mathrm{b}}}{\hbar\omega_{\mathrm{c}}}A_{n}\,\text{cosech}\left(\frac{\hbar\omega_{\mathrm{c}}}{k_{\mathrm{B}}T}\right),$$

(10.17)

where $A_{n}$ is the lattice relaxation amplitude function.

In the weak coupling limit ($z\cong 0$; small polaronic binding energy, for example), $R(\Delta)$ is given by [10.24]

$$R(\Delta)\cong\omega_{c}\dfrac{\left[\left(\frac{4E_{\mathrm{b}}}{\hbar\omega_{\mathrm{c}}}\right)\left(\frac{k_{\mathrm{B}}T}{\hbar\omega_{\mathrm{c}}}\right)\right]^{p}}{p!}\;,$$

(10.18)

where $E_{\mathrm{b}}$ is the polaronic binding energy. When $p$ is a large number, the Stirling formula can be used to give

$$\frac{1}{p!}\cong\frac{1}{\sqrt{2\uppi p}}p^{-p}\exp(p)\;.$$

(10.19)

Using

$$\left(\frac{4E_{\mathrm{b}}}{\hbar\omega_{\mathrm{c}}}\right)^{p}=\exp\left[\frac{\Delta}{\hbar\omega_{\mathrm{c}}}\ln\left(\frac{4E_{\mathrm{b}}}{\hbar\omega_{\mathrm{c}}}\right)\right]$$

(10.20)

and

$$p^{-p}=\left(\frac{\Delta}{\hbar\omega_{\mathrm{c}}}\right)^{-\frac{\Delta}{\hbar\omega_{c}}}=\exp\left[-\frac{\Delta}{\hbar\omega_{\mathrm{c}}}\ln\left(\frac{\Delta}{\hbar\omega_{\mathrm{c}}}\right)\right],$$

(10.21)

the multiphonon jump rate given by (10.18) can be rewritten as

$$R(\Delta)\cong\omega_{\mathrm{c}}\exp(-\gamma\mathrm{p})\left(\frac{k_{\mathrm{B}}T}{\hbar\omega_{\mathrm{c}}}\right)^{p}\;,$$

(10.22)

where $\gamma$ is given by $\ln(\Delta/4E_{\mathrm{b}})-1$. The condition

$$G\equiv\left(\frac{4E_{b}}{\hbar\omega_{\mathrm{c}}}\right)\left(\frac{k_{\mathrm{B}}T}{\hbar\omega_{\mathrm{c}}}\right)\ll 1\;$$

(10.23)

should be satisfied in the weak coupling limit. However, when $p$ is large, the small argument approximation can still be valid even for $G\approx 1$ [10.24]. Note that $1/R(\Delta)$ should be equivalent to $\tau_{\mathrm{m}}$ in (10.11). We then obtain the DC conductivity given by (10.11) under the weak coupling limit.

2 Ionic Transport Theory

While ionic conductors have been studied for long time, the mechanism of transport in disordered materials is still not fully understood. There is no simple broadly accepted model, since ion motion in disordered solids is fundamentally different from electronic transport in crystalline solids. Below typical vibrational frequencies, ion motion can be described by thermally activated hopping between sites separated by a potential barrier. As shown in Fig. 10.4, ions must hop by surmounting potential barriers (dashed line): the potential-energy landscape for mobile ions in a glass is expected to be irregular and contains a distribution of depth and barrier heights in three-dimensional (3-D) space, while Fig. 10.4 is a simple one-dimensional () description.

Fig. 10.4

One-dimensional description of the potential-energy landscape. At high frequencies, a local motion (dashed line) contributes to the AC conductivity (loss). For DC transport to occur, ions must hop over the maximum potential barrier $U_{\mathrm{m}}$ in the transport path

2.1 DC and AC Transports

In disordered ionic conductors, the mobile ions show a subdiffusive behavior (dispersive or anomalous diffusion) in short time scales and show a normal diffusion in longer time scales. This means that the mean square displacement () of the mobile ions is given as [10.25, 10.26]

$$\langle r^{2}(t)\rangle=At^{\alpha}\;,$$

(10.24)

where $A$ is a constant, and $\alpha<{\mathrm{1.0}}$ in a short time range and $\alpha={\mathrm{1.0}}$ in a longer time range. As the time derivative of MSD is proportional to the diffusion coefficient $D$, $D$ on short timescales follows $t^{\alpha-1}$ and $D$ takes a constant value on longer timescales, which is related to the DC conductivity. The time-dependent diffusion coefficient $D(t)$ itself implies the frequency-dependent diffusion coefficient $D(\omega)$. Ionic conductivity therefore depends on the external frequency $\omega$, making the ansatz [10.26],

$$\sigma(\omega)=\sigma(0)+\mathrm{C}\omega^{s}\;,$$

(10.25)

where $\sigma(0)$ is the DC conductivity originating from the constant $D$, C is a constant, the exponent $s$ is less than $\mathrm{1.0}$, and the frequency-dependent term is from $D(\omega)$. This kind of feature can be attributed to a random distribution of potential barriers as shown in Fig. 10.4. Equation (10.25) is a just ansatz formula.

The CTRW approach already discussed in the previous section should give a nonansatz formula for ionic transport processes. The random barrier model (), in which mobile ions hop the potential barriers are distributed randomly, is mathematically the same as the CTRW of localized electrons under a certain condition. The complex ionic conductivity $\sigma_{\mathrm{i}}^{*}(\omega)$ based on the CTRW is given as

$$\sigma_{\mathrm{i}}^{*}(\omega)=\sigma_{\mathrm{i}}(0)\frac{\mathrm{i}\omega\tau_{\mathrm{m}}}{\ln(1+\mathrm{i}\omega\tau_{\mathrm{m}})}\;,$$

(10.26)

where $\sigma_{\mathrm{i}}(0)$ is the DC conductivity and $\tau_{\mathrm{m}}$ is the maximum hopping time among many jumping times. The jumping time $\tau$ required to surmount potential barrier $U$ is given as

$$\tau=\tau_{0}\exp\left(\frac{U}{k_{\mathrm{B}}T}\right),$$

(10.27)

where $\tau_{0}$ is a characteristic time. As will be discussed later, it is known that $\tau_{0}$ itself depends on $U$ and is given by

$$\tau_{0}=\tau_{00}\exp\left(\frac{-U}{E_{\text{MN}}}\right),$$

(10.28)

where $\tau_{00}$ is a constant and $E_{\text{MN}}$ is a characteristic energy (called the Meyer–Neldel energy). This type of relation in thermally activated processes is called the Meyer–Neldel rule or the compensation law [10.27]. The $\tau_{\mathrm{m}}$ in (10.26) is taken to be the maximum $\tau$ (written as $\tau_{\mathrm{m}}$) in (10.27) when we take $U=U_{\mathrm{m}}$ (maximum potential barrier).

Similar to the CTRW in the electronic processes discussed in Sect. 10.1, the DC ionic conductivity is given by

$$\sigma_{\mathrm{i}}(0)=\frac{N_{\mathrm{i}}(eR)^{2}}{6k_{\mathrm{B}}T\tau_{\mathrm{m}}H_{\mathrm{v}}}\;,$$

(10.29)

where $N_{\mathrm{i}}$ is the number of mobile ions, $H_{\mathrm{v}}$ is the Haven ratio [10.26], and $R$ is the hopping length. Note here in ionic transport that $H_{\mathrm{v}}$ is related to the geometry of the transport path.

It should be noted that the present CTRW approach leading to (10.26) is a zeroth-order approximation. More accurate analytical presentation of the RBM is given by [10.28]

$$\ln\tilde{\sigma}=\frac{\mathrm{i}\tilde{\omega}}{\tilde{\sigma}}\left(1+\frac{8}{3}\frac{\mathrm{i}\tilde{\omega}}{\tilde{\sigma}}\right)^{-1/3},$$

(10.30)

where $\tilde{\sigma}=\sigma_{\mathrm{i}}^{*}(\omega)/\sigma(0)$ and $\tilde{\omega}=\omega/\omega^{*}$ is a suitably scaled frequency ($\omega^{*}=1/\tau_{\mathrm{m}}$).

2.2 Power-Law Compositional Dependence

It is of interest to discuss the so-called power-law dependence of ionic conductivity and diffusion coefficient on metallic compositions to oxide [10.29, 10.30, 10.31] and chalcogenide glasses [10.32, 10.33, 10.34]. For example, in Ag-Ge-S glasses [10.32, 10.33, 10.34], the relations $\sigma_{\text{dc}}\propto(x_{\text{Ag}})^{\alpha}$ and $D_{\text{Ag}}\propto(x_{\text{Ag}})^{\beta}$ are found experimentally, where $x_{\text{Ag}}$ is the $\mathrm{at.\%}$ of Ag content (between $\mathrm{0.003}$ and ${\mathrm{5}}\,{\mathrm{at.\%}}$) in the system, $\sigma_{\text{dc}}$ is the DC conductivity, which is usually measured by the IS method, $D_{\text{Ag}}$ is the tracer diffusion coefficient, and the parameters $\alpha$ and $\beta$, are the temperature-dependent constants. Note that no significant structural change has been reported in this composition range. Thus, the power-law dependence itself cannot be a structure-related issue in moderate doping range and has been widely discussed [10.32, 10.33, 10.34].

There are several models [10.29, 10.30, 10.31, 10.32, 10.33, 10.34, 10.35] to interpret the power law. To explain the steep rise of conductivity (or diffusion coefficient) with cation or metallic elements, a percolation model has been proposed [10.29, 10.32]. Observations of conduction thresholds in mixtures of conducting and nonconducting materials are called the percolation thresholds. Roughly speaking in three-dimensional materials, when ${\mathrm{30}}\%$ by volume of the compact is metallic (random mixture), the material system gets its metallic nature from the insulator. Note that a percolation-like behavior occurs at very low concentration of silver atoms as stated above.

Under an exponential distribution of hopping site energy where ions accommodate, the occupation probability of mobile ions in sites is calculated. As the highest energy of occupied sites corresponds to the highest chemical potential, an increase of cation density reduces the energy required for surmounting potential barriers (lower activation energy $U$ in (10.27)). Another percolation approach [10.32] requires a much larger volume of ions, which is called the allowed volume, to explain a percolation threshold behavior, since in a classical percolation theory, in two- and three-dimensional spaces, the power-law exponent appears near a certain threshold in network conductivity. Another view is the dynamic structure model [10.29]: the principal assumption is that mobile ions themselves dominate a glass structure, which is not frozen-in until far below the glass transition temperature. Note that the power exponent is related to the energy difference between sites.

Among them, the simplest model to account for the experimental data may be the configuration entropy change () model [10.35], which is briefly discussed below. Cations, denoted here by $\mathrm{X^{+}}$, should surmount the potential barrier. The Gibbs free energy $G$ should be used for the potential barrier as

$$G=H-T_{0}S\;,$$

(10.31)

where $H$ is the enthalpy, $S$ is the entropy, and $T_{0}$ is the fictive temperature, which may lie between the glass transition temperature $T_{\mathrm{g}}$ and the melting temperature $T_{\mathrm{m}}$ in glasses. $H$ may keep a constant value through a moderate concentration of cations. The network with an ideal homogeneous mixture changes the entropy as

$$S=k_{\mathrm{B}}\ln\frac{N!}{n!(N-n)!}\;,$$

(10.32)

where $k_{\mathrm{B}}$ is the Boltzmann constant, $N$ is the total number of sites, and $n$ is the concentration of cation-provided atoms, e. g., $\text{Li}\rightarrow\mathrm{Li^{+}}$. Here, it is assumed that $\mathrm{[Li^{+}]}=c$[Li] with $c\approx 1$. Then the chemical potential $\mu_{\mathrm{X}}$ of X (the Gibbs energy for one X atom) is described as

$$\mu_{\mathrm{X}}=\frac{\partial G}{\partial n}=\mu_{\mathrm{X}}^{*}+k_{\mathrm{B}}T_{\mathrm{g}}\ln\frac{x}{1-x}\;,$$

(10.33)

where $\mu_{\mathrm{X}}^{*}$ is a constant, and $x$ (at.%) is $n/N$. When $x\ll 1$, the second term in (10.33) is given by $k_{\mathrm{B}}T_{0}\text{ln}(x)$. Then $G$ (activation energy for hopping) decreases by this amount with increasing $n$ (and hence $x$) as

$$\mathrm{G}=G_{0}-k_{\mathrm{B}}T_{0}\ln(|x|)\;,$$

(10.34)

where $G_{0}$ is a constant. Usually the term $U$ is used customarily as an activation energy and hence we use $U$ instead of $G$ in the following. Note that the free enthalpy $G$ here is given for one ion and hence the unit is given in eV.

We begin with the discussion of the diffusion coefficient of cations $D_{\mathrm{X}}$. Diffusion should be thermally activated and hence $D_{\mathrm{X}}$ can be given as

$$D_{\mathrm{X}}=D_{0}\exp\left(-\frac{U}{k_{\mathrm{B}}T}\right),$$

(10.35)

where $D_{0}$ is a constant. By combining the above two equations, $D_{\mathrm{x}}$ is given as

$$D_{\mathrm{X}}=D_{0}\exp\left(-\frac{U_{0}}{k_{\mathrm{B}}T}\right)(x)^{T_{0}/T}\;.$$

(10.36)

It is noted that the Meyer–Neldel (10.27) appears in the term $D_{0}$ and is given by [10.27, 10.36]

$$D_{0}=\frac{R^{2}}{6\tau_{0}}=\frac{R^{2}}{6\tau_{00}}\exp\left(\frac{U}{E_{\text{MN}}}\right)\equiv D_{00}(x)^{-k_{\mathrm{B}}T_{0}/E_{\text{MN}}}\;.$$

(10.37)

Then $D_{\mathrm{X}}$ is finally given as

$$D_{\mathrm{X}}=D_{00}\exp\left(\frac{-U_{0}}{k_{\mathrm{B}}T}\right)(x)^{T_{0}/T-k_{\mathrm{B}}T_{0}/E_{\text{MN}}}\;. $$

(10.38)

Using the Nernst–Einstein relation, $\sigma_{\text{dc}}$ is given by

$$\begin{aligned}\displaystyle\sigma_{\text{dc}}&\displaystyle=\frac{e^{2}Nx}{k_{\mathrm{B}}T}D_{\mathrm{X}}\\ \displaystyle&\displaystyle=\sigma_{0}\exp\left(\frac{-U_{0}}{k_{\mathrm{B}}T}\right)(x)^{1+T_{0}/T-k_{\mathrm{B}}T_{0}/E_{\text{MN}}},\end{aligned}$$

(10.39)

where $\sigma_{0}$ is a constant. We now see that the power law is simply understood by the compositional dependence of the Gibbs free energy change with mixing additives. The power exponent is therefore

$$\alpha=1+\beta=1+T_{0}/T-k_{\mathrm{B}}T_{0}/E_{\text{MN}}\;.$$

3 Experimental Results: Chalcogenide Glasses

The DC conductivity of most chalcogenide glasses (ChGs) (including amorphous chalcogenide thin films) near room temperature is thermally activated with the activation energy $\Updelta E$. It is known that $\Updelta E$ goes as $\approx E_{\mathrm{o}}$/2, where $E_{\mathrm{o}}$ is the bandgap (the optical gap or the Tauc gap) [10.2, 10.37]. In the following section, we discuss the detailed nature of the electrical conduction based on the experimental results reported in chalcogenide glasses.

3.1 Electronic Transport

In this section, we discuss the experimental results of the DC conduction, Hall effect, thermoelectric power, AC conduction, and electronic doping effects in ChGs.

3.1.1 DC Conduction

As stated already the DC conductivity at relatively high temperatures (near room temperature) is thermally activated and is given by

$$\sigma=\sigma_{0}\exp\left(-\frac{\Updelta E}{k_{\mathrm{B}}T}\right),$$

(10.40)

where $\sigma_{0}$ is a constant, and the relation $\Updelta E\approx E_{\mathrm{o}}/2$ suggests that the band transport dominates the DC electrical conduction. As will be discussed later, the p-type (hole) signature is reported in the thermoelectric power measurements and hence $\Updelta E$ is given as $E_{\mathrm{v}}-E_{\mathrm{F}}(0)$ (10.3). Most ChGs are known to be weakly p-type materials. It is believed that the significant density of charged defects ($\mathrm{D^{+}}$, $\mathrm{D^{-}}$) may pin the Fermi level closer to the valence band edge. As will be stated later, the determination of p- or n-type can be given by the thermopower measurement (not by the Hall measurement). A more important issue is the so-called $\mu\tau$ product in the primary photoconductivity, i. e., the time-of-flight () drift mobility study. In most ChGs, the photocurrent by holes is observed, indicating that the $\mu\tau$ product for holes is larger than that for electrons. Strictly speaking, this does not mean ChGs are p-type materials. The signature of carrier, p- or n-type, in semiconductors should be simply determined by the Fermi level position, i. e., p- or n-type is simply defined by which carrier is in the majority. In crystalline semiconductors, the Hall measurement gives a clear signature of carrier type. In a practical sense in glassy materials, the $\mu\tau$ product should be a more convenient physical parameter than p- or n-type when we discuss the signature of carriers.

Although the central issues concerning electronic transport have been widely discussed in the literature, there is still an important and interesting issue that is not properly understood. This is called the Meyer–Neldel rule (MNR) or the compensation law [10.27]; The prefactor in (10.39) $\sigma_{0}$ is actually not a constant and it correlates with the activation energy $\Updelta E$ as

$$\sigma_{0}=\sigma_{00}\exp\left(\frac{\Updelta E}{E_{\text{MN}}}\right),$$

(10.41)

where $E_{\text{MN}}$ is called the Meyer–Neldel characteristic energy and $\sigma_{00}$ is a constant. Examples of the MNR are shown in Fig. 10.5 for some ChGs [10.38]. The pre-exponential factor itself is a function of the activation energy $\Updelta E$. The MN energy, $E_{\text{MN}}$, has a value of around $40{-}50\,{\mathrm{meV}}$.

Fig. 10.5

The pre-exponential factor $\sigma_{0}$ plotted as a function of $\Updelta E$ in several chalcogenide glassy systems (after [10.37])

A similar effect is also found in hydrogenated amorphous silicon (a-Si:H), which is well explained by the statistical shift of the Fermi level (i. e., the temperature variation of the Fermi level) [10.39]. This statistical shift of the Fermi level applied to a-Si:H is not applicable to ChGs and the reason why the MNR is found in ChGs is still not clear. Figure 10.6 shows a surprising correlation between $\sigma_{00}$ and $E_{\text{MN}}$ reported in ChGs

$$\sigma_{00}=\sigma^{\prime}_{00}\exp\left(\frac{E_{\text{MN}}}{\varepsilon}\right),$$

(10.42)

where $\varepsilon$ is a constant (${\mathrm{1.7}}\,{\mathrm{meV}}$), meaning that a large $E_{\text{MN}}$ produces a larger pre-exponential term [10.38].

Fig. 10.6

Correlation between $\sigma_{00}$ and the Meyer–Neldel energy $E_{\text{MN}}$ for some chalcogenide glasses and a-Si:H (after [10.38])

It should be noted that the MNR is also found in some kinetics such as the reaction rate, which is thermally activated. The kinetic rate, for example the hopping rate $\nu$, is followed by

$$\begin{aligned}\displaystyle\nu&\displaystyle=\nu_{0}\exp\left(-\frac{U}{k_{\mathrm{B}}T}\right)\\ \displaystyle&\displaystyle=\nu_{00}\exp\left(\frac{U}{E_{\text{MN}}}\right)\exp\left(-\frac{U}{k_{\mathrm{B}}T}\right),\end{aligned}$$

(10.43)

where $U$ is the energy barrier. This kind of compensation law is found in ionic transport even for crystalline solids, and this can be explained in terms of phonon absorption and emission processes with lattice distortion [10.36]. As the MNR is universally observed in a wide class of materials, the multiexcitation entropy is suggested to be important in some kinetics and thermodynamics. As a general explanation, in multiphonon excitations for example, small polarons have been proposed for explaining the MNR, in which the prefactor $\sigma_{0}$ is proportional to the number of ways of assembling these excitations (entropy effect) [10.27] and hence $E_{\text{MN}}$ corresponds to the optical phonon energy. There is, however, no clear evidence that the small polarons exist and dominate the electronic transport in ChGs and or a-Si:H [10.27, 10.38].

The relation between ln $\sigma_{0}$ and $\Updelta E$, as shown in Fig. 10.5, produces $E_{\text{MN}}={\mathrm{43}}\,{\mathrm{meV}}$ and $\sigma_{0}={\mathrm{1\times 10^{-15}}}\,{\mathrm{S{\,}cm^{-1}}}$. Note for ChGs that $E_{\text{MN}}$ lies in the range $25{-}60\,{\mathrm{meV}}$ and $\sigma_{00}$ in the range $E-5{-}E-15\,{\mathrm{S\mskip 3.0mucm^{-1}}}$. Although $E_{\text{MN}}$ lies in almost the same range for both a-Si:H and ChGs, $\sigma_{00}$ for ChGs is very much smaller than that ($\approx{\mathrm{1}}\,{\mathrm{S{\,}cm^{-1}}}$) for a-Si:H. The $\sigma_{00}$ in a-Si:H is close in value to the microscopic conductivity, $e\mu_{0}N_{\mathrm{c}}$ (10.2), for the standard band transport model. Note that similar values of $\sigma_{00}$ ($E-3{-}E-15\,{\mathrm{S\mskip 3.0mucm^{-1}}}$) have been found in organic semiconductors [10.38]. The common features for small $\sigma_{00}$ between ChGs and organic semiconductors can be attributed to quantum tunneling through barriers that may exist in relatively low-dimensional soft materials.

As the kinetics and thermodynamics are different topics, each phenomenon therefore may have different origins. The definitive solution to this unresolved problem of the MNR is therefore extremely necessary, since this effect may contain unknown principles of physics.

One other important issue in electronic transport should be stated. As stated in Sect. 10.1.1, Electronic Transport in Extended States, the Boltzmann transport theory traditionally used in crystalline materials was applied here also for a-ChGs. However, if the carrier scattering time is very short ($<{\mathrm{10^{-15}}}\,{\mathrm{s}}$) or the carrier mean free path approaches the interatomic distance, the Boltzmann transport theory cannot be valid for analyzing the experimental data without some caution [10.5]. In fact, the importance of this issue is pointed out when we discuss, in particular, metallic transport or the Hall effect in disordered matters. In the following section, we discuss the Hall effect observed in ChGs.

3.1.2 Hall Effect

The Hall measurement usually taken in crystalline semiconductors is a fundamental technique for obtaining the carrier number $n$ and its signature (electron or hole). We apply a magnetic field in a perpendicular direction to the applied field, which is driving the electrons or holes. Because of the magnetic field, all moving charges experience the Lorentz force, which induces an electric field perpendicular to the applied field direction. This induced voltage is called the Hall voltage [10.40]. As the Hall voltage depends on the sample geometry, we customarily use the following Hall coefficient, which measures the resulting Hall field per unit transverse applied current and magnetic field. Therefore, the Hall coefficient is a gauge of the magnitude of the Hall effect. For n-type semiconductors, the Hall coefficient $R_{\mathrm{H}}$ is negative (positive for hole) and is given by [10.40]

$$R_{\mathrm{H}}=-\frac{r}{n|e|}\;,$$

(10.44)

where $r$ is the scattering factor, which is not much greater than one. From the conductivity $\sigma$ and $R_{\mathrm{H}}$ we get the mobility as

$$\mu_{\mathrm{H}}=|R_{\mathrm{H}}|\sigma=r\mu\;,$$

(10.45)

where $\mu_{\mathrm{H}}$ is called the Hall mobility. Note that (10.44) and (10.45) are valid when the mean free path is long enough compared with the interatomic spacing. Otherwise, the Boltzmann transport condition is broken, in which case the Hall coefficient does not have any physical meaning [10.41]. The Hall mobility in ChGs therefore cannot be a useful parameter when we discuss the number of carriers and its signature. Note, however, that the conductivity $\sigma$ itself remains a well-defined quantity even if the Boltzmann condition does not hold; the definition $\sigma=en\mu$ is universally used, since the conductivity itself is a macroscopic quantity. A problem is how to extract proper values of $n$ and $\mu$. The $\mu$ cannot be given by the well-known expression of $e\tau/m^{*}$ for free carriers. While the Hall measurements have been made on a limited number of ChGs, the Hall coefficient was found to be negative: the Hall effect has the opposite sign obtained from the thermoelectric power. Note that the signature of the thermoelectric power should be the same as that of the Hall coefficient; e. g., holes in ChGs should give positive signature for both the thermoelectric power and the Hall coefficient. We found the opposite and therefore call it the pn anomaly. The most anomalous behavior in the carrier transport in ChGs should be the Hall effect. As the thermoelectric power should be followed by the classical Boltzmann theory even when the carrier mean free path is comparable with a lattice parameter, the signature from this measurement correctly predicts the signature of carriers (either p- or n-type).

There are several attempts to explain the pn anomaly. Emin's small polaron [10.3] should be one candidate for explaining it, which will be discussed in Sect. 10.4.1, Polaronic Transport. The other one is a treatment of the quantum interference effect of electron transport, which should be taken into consideration when the carrier mean free path is shorter than a critical value [10.42].

3.1.3 Thermoelectric Power

Thermoelectric power $S$ is thought to not be directly related to electric conduction. However, as will be discussed below, measurement of $S$ produces important information on the carrier transport mechanism, not only the signature of the carrier. Thermoelectric power is related to the Peltier coefficient $\Pi$ by [10.5]

$$S=\frac{\Pi}{T}\;.$$

(10.46)

The Peltier coefficient is defined as the energy carried by electrons (holes) per unit charge and energy is measured relative to the Fermi level $E_{\mathrm{F}}$. Each electron (hole) contributes to $\Pi$ in proportion to its relative contribution to the total conductivity $\sigma$. Therefore $\Pi$ (and hence $S$) is directly related to $\sigma$ and is given by [10.5]

$$\Pi=-\frac{1}{e}\int(E-E_{\mathrm{F}})\frac{\sigma(E)}{\sigma}\frac{\partial f}{\partial E}\mathrm{d}E\;,$$

(10.47)

and

$$S=-\frac{k_{\mathrm{B}}}{e}\int\frac{E-E_{\mathrm{F}}}{k_{\mathrm{B}}T}\frac{\sigma(E)}{\sigma}\frac{\partial f}{\partial E}\mathrm{d}E\;,$$

(10.48)

where $\sigma$ is given by the energy dependent conductivity $\sigma(E)$ as

$$\sigma=e\int\mu(E)N(E)f(1-f)\mathrm{d}E=-\int\sigma(E)\frac{\partial f}{\partial E}\mathrm{d}E\;,$$

(10.49)

where $f$ is the Fermi distribution function and $f(1-f)=-k_{\mathrm{B}}T\mathrm{d}f/\mathrm{d}E$ and $\sigma(E)=e\mu(E)N(E)k_{\mathrm{B}}T$. Note that $S<0$ for electron at energies $E> E_{\mathrm{F}}$ and $S> 0$ for holes at energies $E<E_{\mathrm{F}}$. $S$ for holes associated with the valence band () (in the case of ChGs) is given by [10.41]

$$S=\frac{k_{\mathrm{B}}}{e}\left(\frac{E_{\mathrm{F}}-E_{\mathrm{v}}}{k_{\mathrm{B}}T}+1\right)=\frac{k_{\mathrm{B}}}{e}\left(\frac{E_{\mathrm{s}}}{k_{\mathrm{B}}T}+1\right),$$

(10.50)

where $E_{\mathrm{s}}=E_{\mathrm{F}}-E_{\mathrm{v}}$. It is of interest to point out that the value of $E_{\mathrm{s}}$, which appeared in $S$, should be the same as $E_{\sigma}$ ($=\Updelta E$), which appeared in conductivity (10.40). However, $E_{\mathrm{s}}$ is always smaller than $E_{\sigma}$, i. e., $E_{\sigma}=E_{\mathrm{s}}+\Updelta W$, in a-ChGs, similarly to a-Si:H. The value of $\Updelta W$ is reported to be around ${\mathrm{0.2}}\,{\mathrm{eV}}$ in ChGs. Why such a difference in $\Updelta W$ appears in a-Chs and a-Si:H is a matter of debate [10.40]. If the conduction or valence band edge fluctuates energetically for some reason, for example, the valence band edge $E_{\mathrm{v}}$ takes various energies as shown in Fig. 10.7. As already stated, the electrical conduction should occur at the percolation threshold $E_{\text{pc}}$ (not at $E_{\mathrm{v}}$), and $E_{\sigma}$ is given by $E_{\mathrm{F}}-E_{\text{pc}}$. For thermoelectric power, as discussed above, $E_{\mathrm{s}}$ is given by $E_{\mathrm{F}}-E_{\mathrm{v}}$, resulting in $E_{\sigma}=E_{\mathrm{s}}+\Updelta W$. Note here that the energy $\Updelta W$ can be canceled out through carriers up and down, when thermal energy (thermoelectric power) is measured, while for charge transport (conductivity) $\Updelta W$ should be involved [10.40].

Fig. 10.7

Schematic illustration of band edge fluctuations and the percolation threshold $E_{\text{pc}}$ for free holes

The above view is similar to the two-channel model of conduction, i. e., the carrier transport occurs via tail and band states, since hopping energy $\Updelta W$ (up and down) is not involved in the thermoelectric power as stated above [10.40]. If the small polarons dominate carrier transport, the relation $E_{\sigma}=E_{\mathrm{s}}+\Updelta W$ should be found, since the hopping energy is canceled out in thermoelectric power [10.20]. The $\Updelta W$ therefore corresponds to the hopping activation energy, and hence the small polaron binding energy is $2\Updelta W$ [10.20, 10.3]. It should be stressed that there is no direct argument to prove which mechanism, two-channel or small polaron, is valid. In the case of a-Si:H, a macroscopic potential fluctuation in the band state is considered to be a possible mechanism for this to occur [10.39].

3.1.4 AC Transport

As impedance spectroscopy is a useful technique to understand the dynamics of localized carriers in glasses, there are many reports on the AC conductivity in ChGs [10.13, 10.14]. In earlier stages of the AC conductivity study in ChGs, as shown in Fig. 10.8, the AC and DC losses were thought to have different origins; i. e., free holes in VB contribute to the DC transport and two electrons, as a bipolaron, can hop between oppositely charged coordination defect sites (e. g., using notations $\mathrm{C_{3}^{+}}$–$\mathrm{C_{1}^{-}}$ in Fig. 10.8b), which induces AC loss; two electrons (or holes) hopping between $\mathrm{C_{3}^{+}}$–$\mathrm{C_{1}^{-}}$ pairs means that $\mathrm{C_{3}^{+}}+2\mathrm{e}\rightarrow\mathrm{C_{1}^{-}}$ and $\mathrm{C_{1}^{-}}+2\mathrm{h}\rightarrow\mathrm{C_{3}^{+}}$, which accompany lattice relaxation [10.14, 10.43]. The interconversion of their places induces the AC loss. Note that the neutral dangling bond $\mathrm{C_{1}^{0}}$ is not stable, which is shown in a configurational coordinate diagram (Fig. 10.8c).

Fig. 10.8

(a,b) Formation of charged defects in a-Se and its configuration coordinate diagram. (c) The overall energy is lowered by the effective correlation energy $U_{\text{eff}}$. Interconversion of the states between $\mathrm{C_{1}^{-}}$ and $\mathrm{C_{3}^{+}}$ induces the AC loss

To understand the bipolaron hopping mechanisms in detail, readers need knowledge of the nature of defects, which are given elsewhere [10.2, 10.44]. In the following, a brief summary of the bipolaron hopping proposed for ChGs is presented.

The hopping time of a bipolaron that surmounts barrier $W$ is given as

$$\tau=\tau_{0}\exp\left(\frac{W}{k_{\mathrm{B}}T}\right),$$

(10.51)

where $\tau_{0}$ is a characteristic time ($\approx{\mathrm{10^{-12}}}\,{\mathrm{s}}$) and $W$ is the Coulombic potential energy between charged centers, which is correlated with site separation $R$. Therefore, this process is called the correlated barrier hopping () model [10.14]. Starting from (10.9), the real part of AC conductivity of bipolaron hopping is given as [10.14, 10.43]

$$\sigma(\omega)=\frac{\uppi^{3}}{6}N_{\mathrm{T}}^{2}\varepsilon_{0}\varepsilon_{\infty}\omega R_{\omega}^{6}\;,$$

(10.52)

Where $N_{\mathrm{T}}$ is the number of charged defects, $\varepsilon_{0}\varepsilon_{\infty}$ is the background dielectric constant, and $R_{\omega}$ is the hopping distance (site separation $R$) at $\omega\tau=1$. As $R_{\omega}$ is known to be changed approximately with $\omega^{s-1}$ ($s<1.0$) [10.13, 10.14], $\sigma(\omega)$ is proportional to $\omega^{s}$, which is experimentally observed in the radio frequency range.

As will be discussed later, the $N_{\mathrm{T}}$ estimated from the CBH model is larger than that deduced from the other defect spectroscopies [10.45]. Furthermore, the CBH model is based on the pair approximation (PA), predicting $\sigma(0)\rightarrow 0$, which is far from the experimental results. When the DC conductivity, $\sigma_{\text{DC}}$, is dominated by the band transport, then the overall conductivity can be obtained from the sum of $\sigma(\omega)+\sigma_{\text{DC}}$. If two contributions, DC and AC, are the same, i. e., the DC conductivity is dominated by the bipolaron hopping, the present CBH model may not be a proper approach.

As we stated in the previous section, a proper approach for overcoming the above drawback on the PA seems to be the CTRW approximation. A simple form of the AC conductivity based on CTRW is given by (10.10) [10.16, 10.17]. At high frequency (10.10) also predicts $\sigma(\omega)\propto\omega^{s}(s<{\mathrm{1.0}})$.

It is shown that the AC conductivity is directly related to DC conductivity $\sigma(0)$. Note again that the above equation can be applied when the DC and AC transports are due to the same hopping mechanism.

As shown in Fig. 10.9, the same experimental data for amorphous $\mathrm{As_{2}Se_{3}}$ were analyzed by the CTRW equation, i. e., a random walk of bipolarons was taken into consideration, and by the PA (CBH). The dashed lines indicate the prediction by the CBH model. Fitting the experimental data to (10.52) produces a value for $N_{\mathrm{T}}={\mathrm{2.4\times 10^{19}}}\,{\mathrm{cm^{-3}}}$, as given in Table 10.1. The density of defects $N_{\mathrm{T}}$, estimated from the CBH model, is found in the range of $4E18{-}4E19\,{\mathrm{cm^{-3}}}$ in ChGs. This is always found to be two orders of magnitude larger than that ($E16{-}5E17\,{\mathrm{cm^{-3}}}$) from the other measurements (e. g., drift mobility and light-induced electron spin resonance etc.). The CBH is based on the PA in which localized carriers are assumed to be confined on a pair of defects. As the carriers are not confined to a pair of centers at lower frequencies, the PA cannot be a proper approach at lower frequencies. It is thus suggested that the CTRW approach is more realistic than the PA. The solid curves in Fig. 10.9 indicate the prediction from the CTRW approach. Fitting of the PA model to the experimental data looks fairly good. However, as shown in Table 10.1, $N_{\mathrm{T}}$ estimated from the CTRW is consistent with the other measurements [10.41, 10.45].

Fig. 10.9

Temperature dependence of the AC conductivity at various frequencies in $\mathrm{As_{2}Se_{3}}$ glass. The solid and dashed curves represent the CTRW and the PA respectively (after [10.45])

Table 10.1 Extracted density of defect states $N_{\mathrm{T}}$ in some chalcogenide glasses

3.1.5 Impurity Doping into Chalcogenide Glasses

As we already stated, ChGs are p-type semiconductors and electronic applications are limited by the extraordinary difficulty in obtaining n-type ChGs. In some ChGs, e. g., Ge(S,Se,Te), i. e., Ge with each of the chalcogens with very high Bi or Pb doping ($\approx{\mathrm{10}}\,{\mathrm{at.\%}}$), n-type ChGs have been realized [10.46]. Amorphous Se with alkaline elements also shows n-type behavior [10.47]. None of these materials showed device quality pn-junctions.

Very recently, it was reported that ion implantation of Bi into GeTe and GaLaSO produces n-type conduction and pn junction (rectification) devices [10.48]. Note that both GeTe and GaLaSO are classified into the phase-change material family, as well as GeSbTe (), which is known to be the most useful material for the digital versatile disk (DVD) [10.49]. The electrical doping effect of Bi occurs at 100 times lower concentration than Bi melt-doped GeChGs. The Raman spectra of GeTe, for example, indicate that a ${\mathrm{38}}\%$ increase in Ge–Te bonds and a ${\mathrm{30}}\%$ reduction in a band associated with Te chains with Bi implanted to a peak concentration of ${\mathrm{1.4}}\,{\mathrm{at.\%}}$, while the ab initio model shows a ${\mathrm{4}}\%$ increase in Ge–Te bonds and a ${\mathrm{4}}\%$ decrease in Te–Te wrong bonds with ${\mathrm{2}}\,{\mathrm{at.\%}}$ Bi doping. This difference between the experiments and modeling can be due to the modeling being for a quenched system. XPS measurements indicate that the Bi species responsible for n-type in GeTe and GaLaSO are $\mathrm{Bi^{+}}$ or $\mathrm{Bi^{2+}}$, which provide free electrons. In fact, the Bi concentration at which the n-type transition occurs (thermoelectric power measurement) is too low for it to be caused by a percolation threshold, i. e., the transition is not interpreted in terms of a percolation theory, which requires $\approx 10{-}30\%$ of some inclusions (species).

3.2 Ionic Transport

Ag-doped ChGs have numerous potential applications as solid-state ion conductors (s), and possess high ionic conductivity such as two to three orders of magnitude higher than that of oxide glasses with the same mobile ion concentration [10.32, 10.33, 10.34]. A number of methods have been developed for characterization of SSICs, such as cyclic voltammetry, electrical polarization of solid state technique, four probe DC method, and impedance spectroscopy (IS). Among them, IS can be a powerful method of characterizing many electrical properties of materials [10.50, 10.51, 10.52, 10.53, 10.54].

In principle, there are two ways of analyzing IS. The most popular one is the conventional equivalent electrical circuit () analysis [10.52, 10.53]. The other one is the solution of the Poisson–Nernst–Planck () equation [10.54]. The EEC method has many merits leading to a fast data analysis from a complex impedance $Z_{1}$–$Z_{2}$ plane, where $Z_{1}$ is the real part of impedance and $Z_{2}$ the imaginary part. A number of physical parameters such as bulk resistance and capacitance can be extracted using EEC and therefore many IS data have been analyzed so far by this technique. The EEC approach has some drawbacks:

• 1. The arrangement of equivalent circuit elements in different ways can provide the same $Z_{1}$–$Z_{2}$ plane.

• 2. The EEC method does not provide physical parameters such as the relaxation time and the diffusion coefficient, and the number of mobile ions [10.50, 10.51].

The EEC analysis itself can be a macroscopic approach.

The PNP model should also be a macroscopic approach, since the relations between the electronic potential and the diffusing (drifting) ionic particles are derived macroscopically by using the Maxwell equation. The PNP approach is not so popular, even though the solution of PNP provides the important parameters such as diffusion coefficient and the number of mobile ions [10.52, 10.53]. This may be due to the complexity involved in solving the PNP equation.

A new approach based on a random walk () of mobile ions has been developed to overcome some drawbacks encountered in the traditional IS, which analyze the impedance data without using EEC and extract more physical parameters than the conventional methods mentioned above [10.50, 10.51]. The dynamics of mobile ions and the physical parameters are deduced from the RW approach, which should be a direct microscopic approach, in contrast with the EEC and PNP approaches.

Figure 10.10 is an example of a $\rho_{1}$–$\rho_{2}$ plane for $\mathrm{Ag_{25}As_{25}S_{50}}$ glass, where $\rho_{1}$ and $\rho_{2}$ are the real and imaginary parts of resistivity respectively [10.50, 10.51]. The open circles and square represent the experimental data at the applied voltage, $V_{\mathrm{a}}={\mathrm{0.1}}$ and ${\mathrm{0.3}}\,{\mathrm{V}}$ respectively, and the solid and dashed lines are the model calculations, which will be stated below. The observed curve shows a typical ionic conductivity behavior containing a high-frequency semicircle (smaller $\rho_{1}$ and $\rho_{2}$), which represents the bulk properties of the materials, and the low-frequency tail (higher resistivity side), which is the response of interfacial (electrode) polarization, which depends on the applied voltage. Note that the interfacial region is connected in series with the bulk and electrode and hence the overall complex conductivity $\sigma^{*}$($\omega$) can be given as

$$\frac{1}{\sigma^{*}(\omega)}=\frac{f}{\sigma_{\mathrm{i}}^{*}(\omega)}+\frac{1-f}{\sigma_{\mathrm{b}}^{*}(\omega)}\;,$$

(10.53)

where $f$ is the spectral weight of the interfacial conductivity, and the subscripts i and b indicate interface and bulk respectively. Note here that $\rho^{*}(\omega)=1/\sigma^{*}(\omega)$ is obtained from (10.26). Fitting of (10.26), (10.29), and (10.53) produces the physical parameters, $\tau_{\mathrm{m}}$, $\sigma(0)$, as listed in Table 10.2. The interfacial effect highly depends on the applied voltage and a large deviation between the fitting and the experimental data at ${\mathrm{0.1}}\,{\mathrm{V}}$ may be due to involving nonlinear effects at the interface.

Fig. 10.10

Complex $\rho_{1}$–$\rho_{2}$ plane in $\mathrm{Ag_{25}As_{25}S_{50}}$ glass. The solid and dashed lines are the model calculations, and the circles and squares are the experimental data at the applied voltage, $V_{\mathrm{a}}={\mathrm{0.1}}$ and ${\mathrm{0.3}}\,{\mathrm{V}}$ respectively (after [10.50])

Note that the diffusion coefficient $D$ is calculated from

$$D=\frac{R^{2}}{6\tau_{\mathrm{m}}}\;,$$

(10.54)

where $R$ is the hopping site separation and the Haven ratio $H_{\mathrm{v}}$ was assumed to be $\mathrm{1.0}$. Both the bulk and interfacial contributions can be separately discussed in the context of the RW approach.

Table 10.2 Physical parameters extracted from the IS data taken at ${\mathrm{300}}\,{\mathrm{K}}$ in $\mathrm{Ag_{25}As_{25}S_{50}}$ glass at the applied voltage of ${\mathrm{0.1}}\,{\mathrm{V}}$

In Sect. 10.2.2, the model for the power-law dependence of ionic conductivity and diffusion coefficient on metallic compositions into glasses has been discussed. When the potential barrier follows (10.34), the power law should be observed in the diffusion coefficient and hence conductivity. This is the essential feature of the power-law dependence [10.32, 10.33, 10.34]. Figure 10.11 shows the dependence of silver concentration on the activation energies (potential barrier for mobile Ag ions) for conductivity and diffusion coefficient in Ag-GeS glass [10.32, 10.33, 10.34, 10.35]. The solid line is a least-square fit to the experimental data and follows (10.34), producing $k_{\mathrm{B}}T_{0}={\mathrm{50}}\,{\mathrm{meV}}$ (fictive temperature $T_{0}\approx T_{\mathrm{g}}={\mathrm{580}}\,{\mathrm{K}}$).

Fig. 10.11

Dependence of Ag content on the activation energies for conductivity (circles) and diffusion coefficient (crosses) in Ag-Ge-S glass. The solid line is a least-square fit to the experimental data, producing $k_{\mathrm{B}}T_{0}={\mathrm{50}}\,{\mathrm{meV}}$ (after [10.32])

A deviation from the logarithmic dependence of the activation energy (given by the straight line) is observed in the highly doped range, which can be attributed to an alternation of the glass network in short- and/or medium-range orders [10.32, 10.33, 10.34, 10.35]. As stated in Sect. 10.2.2, the logarithmic dependence is predicted from an assumption of a homogeneous mixture and this assumption is broken in the highly doped range.

Figure 10.12a,ba,b shows the Ag content dependence of DC conductivity and the diffusion coefficient respectively, in an Ag-GeS glass system measured at $\mathrm{298}$ and ${\mathrm{373}}\,{\mathrm{K}}$ [10.32, 10.33, 10.34, 10.35]. Note that the diffusion coefficient is estimated by the tracer diffusion technique. As predicted by (10.38) and (10.39), the relations, $\sigma_{\text{dc}}\propto(x_{\text{Ag}})^{\alpha}$ and $D_{\text{Ag}}\propto(x_{\text{Ag}})^{\beta}$ are found experimentally, where $x_{\text{Ag}}$ is the at.% of Ag content (between $\mathrm{0.003}$ and ${\mathrm{5}}\,{\mathrm{at.\%}}$).

Fig. 10.12a,b

Dependence of Ag content on the DC conductivity (a) and on the diffusion coefficient (b) in Ag-Ge-S glass, measured at ${\mathrm{298}}\,{\mathrm{K}}$ (circles) and ${\mathrm{373}}\,{\mathrm{K}}$ (crosses), respectively. The solid lines are least-square fit to the experimental data (after [10.33, 10.34])

The observed power-law exponent $\alpha(=1+{T}_{\mathrm{g}}/{T}-{T}_{\mathrm{g}}/E_{\text{MN}})$ is $\mathrm{2.0}$ and ${\beta}(=T_{\mathrm{g}}/{T}-{T}_{\mathrm{g}}/E_{\text{MN}})={\mathrm{1.0}}$ at $T={\mathrm{298}}\,{\mathrm{K}}$ (Fig. 10.12a,ba,b), satisfying (10.38) and (10.39). The $E_{\text{MN}}$ is then estimated to be ${\mathrm{50}}\,{\mathrm{meV}}$, which is a reasonable value for the MN energy [10.27]. It is therefore suggested that the simple CEC model discussed in Sect. 10.2.2 is very useful to explain the power-law dependence of Ag mixing into ChGs. The power-law dependence observed in oxide glasses will be discussed again in the following section and we will find more large values of the exponents $\alpha$ and $\beta$, which can be due to different values of $T_{\mathrm{g}}$ and $E_{\text{MN}}$.

It should be noted that both the conductivity and the diffusion coefficient deviate from the power-law composition dependence in the highly doped range. The reason why is the same as stated above (change in the activation energy): a structural change in the highly doped range disturbs a homogeneous mixture of dopants.

There are also important contributions to the field of ionic transport in ChGs and some of them are listed here [10.55, 10.56, 10.57, 10.58, 10.59, 10.60]. One of these is the mixed cation effect in ChGs [10.60], which is similar to the mixed alkali effect on OGs, and these will be discussed in Sect. 10.4.2. This effect occurs in glassy alkali conductors of the general formula $x\mathrm{X_{2}O}(1-x)\mathrm{Y_{2}O}$-($\mathrm{SiO_{2}}$, $\mathrm{B_{2}O_{3}}$, $\mathrm{GeO_{2}}$ etc.) where $\mathrm{X_{2}O}$ and $\mathrm{Y_{2}O}$ are different alkali oxides. An increase in the activation energy of the conductivity of one type of ion is observed when it is replaced by a second type of ion, keeping total alkali concentration constant. The ionic conductivity therefore goes through a deep minimum as $x$ is varied. This is still a long-term mystery in glass sciences. This will be briefly discussed in Sect. 10.4.2, Mixed Alkali Effect.

4 Experimental Results: Oxide Glasses

Oxide glasses (OGs) are usually insulators. However, many OGs exhibit electrically conductive natures when we introduce transition metals [10.1, 10.21, 10.22] or alkali metals into OGs [10.1, 10.25, 10.26, 10.31]. These glasses are called transition-metal oxide glasses (TMOGs). TMOGs show relatively high conductivity, which is dominated by electronic processes [10.21, 10.22]. OGs containing alkali metals (s) (such as Li and Na etc.), on the other hand, show ionic transport in nature [10.1, 10.26]. In addition to these traditional OGs, a novel type of oxide glass semiconductor such as In-Ga-Zn-O () has been developed [10.61, 10.62, 10.63]. In reality, IGZO is prepared as films (not glassy materials) and the metal–insulator transition is reported in IGZO. The IGZO is now being applied to very useful devices such as thin-film transistors (TFTs). In the following section, we discuss detailed nature of the electrical conduction based on the experimental results reported in these glasses.

4.1 Electronic Transport

Two types of the experimental results, polaronic and nonpolaronic electronic conductions, are discussed in this section.

4.1.1 Polaronic Transport

Experimentally, the transition-metal oxide glasses (TMOGs) show semiconducting behavior with conductivities in the range $E-2{-}E-11\,{\mathrm{S\mskip 3.0mucm^{-1}}}$. The activation energy for the DC conductivity decreases gradually with decreasing temperature. The Seebeck coefficient between $\mathrm{300}$ and ${\mathrm{500}}\,{\mathrm{K}}$ generally has the n-type value $\approx{\mathrm{200}}\,{\mathrm{\upmu{}V{\,}K^{-1}}}$ (almost temperature-independent), suggesting that the number of carriers is independent of temperature. These features lead to the conclusion that the small polaron dominates the electronic transport in TMOGs [10.21].

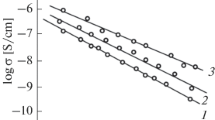
An example of the temperature dependence of the DC conductivity (solid circles) for ($\mathrm{V_{2}O_{5}}$)${}_{80}$($\mathrm{P_{2}O_{5}}$)${}_{20}$ is shown in Fig. 10.13. In the V-P-O system, hopping of electrons from $\mathrm{V}^{4+}$ to $\mathrm{V}^{5+}$ ions could dominate the charge transport (interconversion of V-sites). Assuming the formation of small polarons, the temperature dependence of DC conductivity is calculated using (10.11)–(10.14) [10.22, 10.23]. The phonon density of states is approximately $g(\omega)\propto\omega^{2}$ for acoustic phonons with a cutoff (Debye) frequency $\omega_{\mathrm{D}}$ and a mean optical phonon frequency $\omega_{\mathrm{o}}=3\omega_{\mathrm{D}}$ conventionally used [10.24]. One of the important physical parameters is the Debye frequency, which determines the shape of the curve: curves (a)–(c) in Fig. 10.13 are the calculated results for $\omega_{\mathrm{D}}={\mathrm{3.1\times 10^{13}}}$, $\mathrm{8.2\times 10^{13}}$, and ${\mathrm{1.3\times 10^{14}}}\,{\mathrm{s^{-1}}}$. Other physical parameters required for the calculation are taken to be $E_{\mathrm{b}}^{\text{ac}}=E_{\mathrm{b}}^{\text{op}}={\mathrm{0.7}}\,{\mathrm{eV}}$, $\Delta={\mathrm{0.03}}\,{\mathrm{eV}}$, $h_{\mathrm{h}}={\mathrm{1\times 10^{21}}}\,{\mathrm{cm^{-3}}}$, and $R={\mathrm{0.4}}\,{\mathrm{nm}}$ (average site separation of vanadium ions). The theory fits well to the experimental data (curve (b)), producing $J_{ij}={\mathrm{1.2}}\,{\mathrm{eV}}$. The other two curves, (a) and (c), are just for comparison of sensitivity of parameters.

Fig. 10.13

Temperature dependence of the DC conductivity in ($\mathrm{V_{2}O_{5}}$)${}_{80}$($\mathrm{P_{2}O_{5}}$)${}_{20}$ glass. Closed circles are the experimental data and the solid lines are calculated results for (a) $\omega_{\mathrm{D}}={\mathrm{3.1\times 10^{13}}}$, (b) $\mathrm{8.2\times 10^{13}}$, and (c) ${\mathrm{1.3\times 10^{14}}}\,{\mathrm{s^{-1}}}$ respectively (after [10.22])

The estimated $J_{ij}$ is very much larger than the required value of less than ${\mathrm{0.1}}\,{\mathrm{eV}}$, predicted from the nonadiabatic treatment of small polarons. A large value of $J_{ij}$ is also obtained for many other TMOGs and hence the small polaron hopping theory is inadequate quantitatively to explain the electronic transport in TMOGs [10.22]. Probably, the MNR should be related to this inconsistency of the pre-exponential term $J_{ij}$ [10.4]. As the temperature dependence of the jump rate of a small polaron in the adiabatic approximation is simply proportional to $\exp(-E_{\mathrm{b}}/(2{k_{\mathrm{B}}T}))$ at high temperature, where $E_{\mathrm{b}}$ is the polaron binding energy, the adiabatic approximation also cannot explain the experimental data that show the temperature-dependent hopping activation energy.

Alternatively, a weak coupling multiphonon hopping () of conduction electrons has been proposed [10.22].

Figure 10.14 shows the temperature variation of DC and AC conductivities in the same ($\mathrm{V_{2}O_{5}}$)${}_{80}$($\mathrm{P_{2}O_{5}}$)${}_{20}$ glass. The solid line for the DC conductivity (experimental data are the same as those shown in Fig. 10.13), instead of the strong-coupling limit, is the calculated result in the WCMH that predicts $\sigma_{\text{DC}}=CT^{m}$ (10.22). As discussed in Sect. 10.1.2, Weak Carrier–Phonon Coupling Limit, the $m$-value here should be taken to be an integer value given as $p$ ($=\Delta/(\hbar\omega_{\mathrm{c}})$) in (10.22). Experimentally, however, $m={\mathrm{13.4}}$ for the present material gives the best fit to the data. In fact, the p-value is expected to distribute around an average value and hence the noninteger $m$-value can be extracted experimentally.

Fig. 10.14

Temperature dependence of the DC and AC conductivities in ($\mathrm{V_{2}O_{5}}$)${}_{80}$($\mathrm{P_{2}O_{5}}$)${}_{20}$ glass. Solid lines are calculated results based on the CTRW approach (after [10.22])

The other solid lines in Fig. 10.14 are the calculated AC conductivity using (10.10), which is based on the CTRW approach [10.22]. The only fitting parameter here is the hopping time $\tau_{\mathrm{m}}$, which is equal to $1/R(\Delta)$. Fitting the experimental data produces $\omega_{\mathrm{c}}={\mathrm{2\times 10^{12}}}\,{\mathrm{s^{-1}}}$, which is much smaller than the Debye cutoff frequency $\omega_{\mathrm{D}}$ ($\approx{\mathrm{8\times 10^{13}}}\,{\mathrm{s^{-1}}}$), suggesting that long wavelength acoustic phonons contribute to the WCMH mechanism. The reason for the small $\omega_{\mathrm{c}}$ may originate from some delocalized nature of the electrons, since an electron in weakly localized states (large Bohr radii) can interact only for a longer wavelength of phonons [10.11, 10.2, 10.22]. Fitting also produces the number of electrons $n_{\mathrm{h}}={\mathrm{8\times 10^{18}}}\,{\mathrm{cm^{-3}}}$, which is a reasonable value [10.22, 10.64]. More detailed physical parameters extracted by the fitting are described elsewhere [10.22, 10.64].

4.1.2 Nonpolaronic Transport

Thin films of amorphous oxide semiconductors (s) are not technically categorized as glasses. However, throughout this chapter, the terms amorphous and glass are used interchangeably and hence we discuss AOSs in this section. The $\mathrm{P_{2}O_{5}}$-$\mathrm{V_{2}O_{5}}$ system discussed in the previous section shows a polaron-like conducting nature where the carrier mobility is very small ($\approx{\mathrm{10^{-4}}}\,{\mathrm{cm^{2}{\,}V^{-1}{\,}s^{-1}}}$) and hence no practical application in electronics has been found.

Among various AOSs a new type called amorphous $\mathrm{In_{2}O_{3}}$-ZnO-$\mathrm{Ga_{2}O_{3}}$ (IGZO), developed recently, is the best-known, which was sent to the market in flat-panel displays (s) [10.61, 10.62, 10.63]. Free carriers (electrons) are produced by chemical doping, i. e., by alternation of stoichiometry of oxygen ions by controlling the oxygen vapor pressure during deposition processes, it is possible to prepare metallic IZGO. Because AOSs are usually optically transparent, IGZO opened new and unique fields in oxide glasses.

Figure 10.15a,ba,b shows the temperature-dependent density of free electrons in IGZO films, extracted from the Hall measurement and conductivity respectively [10.62, 10.63]. One remarkable point of the Hall measurement in IGZO is that there is no sign anomaly, suggesting that the carrier mean free path is long, as compared with ChGs. While the number of electrons are independent of temperature for $n_{\text{Hall}}> {\mathrm{10^{17}}}\,{\mathrm{cm^{-3}}}$, the conductivity weakly depends on temperature except for $n_{\text{Hall}}\approx{\mathrm{10^{20}}}\,{\mathrm{cm^{-3}}}$. These results predict that the Hall mobility $\mu_{\text{Hall}}$ should be temperature dependent. Interestingly, the temperature-independent conductivity ($\approx{\mathrm{200}}\,{\mathrm{S{\,}cm^{-1}}}$) for a5 and a6 is the same as the predicted value of minimum metallic conductivity (Sect. 10.1.1, Electronic Transport in Extended States).

Fig. 10.15a,b

Temperature-dependent density of free electrons extracted from the Hall measurement (a) and conductivity (b) in IGZO films. a1–a2 are the doping levels, which may be almost the same as $n_{\text{Hall}}$ at high temperatures (after [10.62, 10.63])

Figure 10.16a,ba,b shows the Hall mobility as a function of carrier concentration and temperature, respectively, in IGZO films [10.62, 10.63]. The $\mu_{\text{Hall}}$ is actually thermally activated for the films of $n_{\text{Hall}}$ ($=N_{\mathrm{e}}$ in Fig. 10.16a,b) $<{\mathrm{2\times 10^{19}}}\,{\mathrm{cm^{-3}}}$. The $\mu_{\text{Hall}}$ increases with carrier concentration and reaches $\approx{\mathrm{10}}\,{\mathrm{cm^{2}{\,}V^{-1}{\,}s^{-1}}}$ at $n_{\text{Hall}}$ ($N_{\mathrm{e}}$ in Fig. 10.16a,b) $\approx 10^{18-19}{\mathrm{cm^{-3}}}$. The carrier scattering time is therefore estimated to be $\tau\approx{\mathrm{2\times 10^{-15}}}\,{\mathrm{s}}$, which is consistent with that estimated from the free carrier absorption measurement. The high electron mobility can be due to the $\mathrm{s}$ states forming the bottom of the conduction band, which are not sensitive to disorders such as angular distortion. Note that $\mathrm{p}$ or $\text{sp}^{3}$ states are affected by such disorder and hence much more band tail states are produced in this bond configuration. Interestingly, this trend, i. e., carrier mobility increases with carrier concentration (or dopant concentration), is opposite to that for conventional crystalline semiconductors. These behaviors in $\mu_{\text{Hall}}$ can be interpreted by a percolation argument in which the conduction band edge is modulated by long-range potential fluctuations. When the Fermi level reaches the percolation threshold level $E_{\text{pth}}$ ($n_{\text{Hall}}\approx{\mathrm{10^{20}}}\,{\mathrm{cm^{-3}}}$), the complete metallic transport behavior should be observed. The metal-insulator transition occurs at the critical number of free electrons $n_{\mathrm{c}}=n_{\text{Hall}}\approx{\mathrm{1\times 10^{17}}}\,{\mathrm{cm^{-3}}}$. It should be noted that the transport is metallic even when the conductivity decreases with decreasing temperature, which is frequently observed in so-called the dirty metals (disordered metals) [10.5].

Fig. 10.16a,b

Dependence of the Hall mobility $\mu_{\text{Hall}}$ on carrier concentration $N_{\mathrm{e}}$ (a) and on temperature (b) in IGZO films (after [10.62, 10.63])

As AOSs are generally n-type materials, there have been efforts to develop p-type oxides such as $\mathrm{CuAlO_{2}}$ [10.62].

4.2 Ionic Transport

The traditional ionic (oxide) glasses are network glasses, which consist of a network former ($\mathrm{SiO_{2}}$, $\mathrm{B_{2}O_{3}}$, $\mathrm{Al_{2}O_{3}}$ etc.) and a network modifier ($\mathrm{Na_{2}O}$, $\mathrm{K_{2}O}$, $\mathrm{Li_{2}O}$ etc.) [10.1, 10.31]. The alkali ions involved are mobile and therefore diffuse through the glassy network. The mobile ions may themselves interact with each other by Coulombic forces. Note, however, that the dynamic ionic motions, including the long-range Coulomb forces, are still not clear. We discuss three prominent topics in the following sections, which are of interest to understanding the dynamics of mobile ions in $\mathrm{SiO_{2}}$-based glasses.

4.2.1 Dynamics of Mobile Ions

It is believed that the diffusion of the mobile ions occurs via hopping motions between well-defined potential minima in glassy networks [10.26]. The mobile Ag-ion diffusion in ChGs has been discussed in this context (Sect. 10.3.2) by using the CTRW approach under the assumption of the random barrier model () [10.50, 10.51]. The RBM is a simple and easy to access dynamic formulation. In this section we will argue that the cation transport in oxide glasses (OGs) proceeds in the same way as in ChGs. What can be learned from impedance spectroscopy (IS) in OGs? In the field of OGs, the real part of frequency-dependent conductivity $\sigma_{1}(\omega)$, so-called AC conductivity, has been customarily taken into consideration. Use of the complex impedance plane, $Z_{1}$–$Z_{2}$, is not so popular for historical reasons. We hence discuss here the $\sigma_{1}(\omega)$ in OGs.

As already discussed in Sect. 10.2.1, experimentally observed $\sigma_{1}(\omega,T)$ obeys ansatz (10.25), and is also found to follow the scaling ansatz equation as [10.26]

$$\sigma_{1}(\omega,T)=\sigma(0,T)f\left[\frac{\omega}{\omega^{*}(T)}\right],$$

(10.55)

where $f$ is a scaled function and $\omega^{*}(T)$ ($=1/\tau_{\mathrm{m}}(T)$) is the onset angular frequency at which conductivity becomes frequency dependent (10.26). Note that (10.26) follows this scaling equation [10.16, 10.17].

An example for the scaling in sodium-borate (open circle) and lithium-phosphate (cross) glasses are shown in Fig. 10.17 [10.26]. The AC conductivities for both glasses drop onto a single curve. This feature is universally observed for all oxide glasses [10.26]. The solid line is obtained from (10.26), indicating that the experimental data are well explained by the CTRW approximation. Note again here that (10.26) holds under the extreme disorder limit, i. e., the highest potential barrier dominates the DC conductivity and hence AC behavior. As mentioned in Sect. 10.2.1, a scaled function, (10.30), is more accurate than the CTRW approach given by (10.26). Actually, however, the prediction from (10.26) is almost the same as that from (10.30), and (10.26) is very useful for extracting the important physical parameters [10.16, 10.17].

Fig. 10.17

Scaling of the AC conductivity with a characteristic frequency $\omega^{*}$ in sodium-borate (circles) and lithium-phosphate (crosses) glasses. The solid line is predicted from the CTRW approximation (after [10.26])

4.2.2 Power-Law Dependence

Figure 10.18 shows the compositional dependence of the conductivity activation energy in $x\mathrm{Li_{2}O}(1-x)\mathrm{SiO_{2}}$ and $x\mathrm{Li_{2}O}(1-x)\mathrm{B_{2}O_{3}}$ glasses [10.31, 10.65]. As discussed in Sect. 10.2.1 and 10.3.2, it follows (10.34), and $T_{0}={\mathrm{900}}$ and ${\mathrm{4500}}\,{\mathrm{K}}$ for $x\mathrm{Li_{2}O}(1-x)\mathrm{SiO_{2}}$ and $x\mathrm{Li_{2}O}(1-x)\mathrm{B_{2}O_{3}}$ respectively. The fictive temperature $T_{0}$ was taken to be the glass transition temperature as discussed in Sect. 10.2.2 and 10.3.2. However, $T_{0}={\mathrm{4500}}\,{\mathrm{K}}$ is too high for the glass transition temperature for $\mathrm{B_{2}O_{3}}$-based glasses. A careful discussion on the meaning of $T_{0}$ in oxide glasses is thus still needed.

Fig. 10.18

Composition-dependent activation energy for the DC conductivity measured at ${\mathrm{423}}\,{\mathrm{K}}$ in the $x\mathrm{Li_{2}O}(1-x)\mathrm{SiO_{2}}$ and $x\mathrm{Li_{2}O}(1-x)\mathrm{B_{2}O_{3}}$ (colored) systems (after [10.65])

Figure 10.19 shows the power-law dependence of the DC conductivity measured at $T={\mathrm{423}}\,{\mathrm{K}}$ in the same glasses discussed above [10.31]. Both the systems show the relation $\sigma_{\text{DC}}\propto(x)^{\alpha}$, where $\alpha$ is the power-law exponent and $\alpha={\mathrm{3.3}}$ and $\mathrm{15.8}$ for $x\mathrm{Li_{2}O}(1-x)\mathrm{SiO_{2}}$ and $x\mathrm{Li_{2}O}(1-x)\mathrm{B_{2}O_{3}}$ are extracted, respectively. These power-law exponents observed in OGs are larger than those in ChGs. This may be due to lower glass transition temperatures in ChGs than in OGs, since $\alpha$ is related to $T_{0}$ (Sects. 10.2.2 and 10.3.2).

Fig. 10.19

Composition-dependent DC conductivity measured at ${\mathrm{423}}\,{\mathrm{K}}$ in the $x\mathrm{Li_{2}O}(1-x)\mathrm{SiO_{2}}$ and $x\mathrm{Li_{2}O}(1-x)\mathrm{B_{2}O_{3}}$ (colored) systems (after [10.65])

4.2.3 Mixed Alkali Effect

The most prominent effect on ion-conducting glasses has been considered to be the mixed alkali effect () [10.26, 10.31, 10.66]. This effect occurs in glassy alkali conductors of the general formula $x\mathrm{X_{2}O}(1-x)\mathrm{Y_{2}O}$-($\mathrm{SiO_{2}}$, $\mathrm{B_{2}O_{3}}$, $\mathrm{GeO_{2}}$ etc.) where $\mathrm{X_{2}O}$ and $\mathrm{Y_{2}O}$ are different alkali oxides. An increase in the activation energy of the diffusion coefficient (and conductivity) of one type of ion is observed when it is replaced by a second type of ion, keeping total alkali concentration constant. The ionic conductivity therefore goes through a deep minimum as $x$ is varied. Note that the MAE occurs in other properties, e. g., thermal and mechanical ones [10.31]. Here we only discuss the MAE on ionic conduction. This issue is regarded as a long-term puzzle and as one of the most challenging subjects in glass science [10.31].

Figure 10.20 shows the typical example of MAE for the DC conductivity reported in the $x\mathrm{Na_{2}O}(1-x)\mathrm{Li_{2}O}$-$\mathrm{3B_{2}O_{3}}$ glass system. It is seen that the effect is more pronounced as the temperature is lowered [10.66]. As stated in Sect. 10.3.2, a similar cation effect has been observed in ChGs [10.60]. It is known that the local environment of any cation is not affected by the addition of a second cation. The evidence for this is produced by (extended x-ray absorption fine structure), (nuclear magnetic resonance), and (infrared), x-ray, and neutron scattering measurements, combined with some theoretical studies. One way to understand the MAE is a mismatch effect related to its structural origin, where sites in the glassy network favorable for one type of ion are not favorable for the other. In ionic hopping systems, the mismatch effect means that site energies are different for different types of ions, and therefore a low-energy site for one type is a high-energy site for other type of ion. Note also that the MAE becomes weaker with decreasing total ion content.

The model mentioned above suggests the independent moving (diffusion) of A and B ions: each ion (A or B) may each have a preferred conducting path, leading to the site memory effect. A simple approach may invoke the model of configuration entropy change (CEC), which is used to explain the power-law dependence of ionic conductivity: the increase in $x$ decreases the conductivity related to $\mathrm{Li^{+}}$ and increases the $\mathrm{Na^{+}}$-related conductivity [10.35]. It should be mentioned that a systematic theoretical study is still not yet completed on all main signatures of MAE.

Fig. 10.20

Mixed alkali effect on the DC conductivity in the $x\mathrm{Na_{2}O}(1-x)\mathrm{Li_{2}O}$-$\mathrm{3B_{2}O_{3}}$ glassy system measured at various temperatures (after [10.66])

5 Electrical Transport Property in Device-Related Materials

The excellent amorphous materials already sent to global markets are briefly discussed. As amorphous Se (a-Se) is a very sensitive photoconductor, especially for x-rays, due to its high atomic weight, it was possible to realize a direct x-ray imaging device for use in the medical field. The image of the human body (hand) recalls Röntogen's first x-ray photograph [10.67]. This device incorporates a large area of thick (${\mathrm{1}}\,{\mathrm{mm}}$) a-Se evaporated onto a thin-film transistor (TFT) made from an a-Si:H active matrix array. The x-ray induced carriers in a-Se travel along the electric field lines and are collected at their respective biased electrode and storage capacitor. The stored images are directly sent to the medical specialists through a computer network.

The avalanche photomultiplication effect has been utilized to create a very sensitive color sensor for broadcasting TV cameras whose sensitivity is over 100 times higher than a  (charge coupled device) camera [10.68]. Color pictures of rainbows at Mt. Fuji (Japan) and Iguaz falls (Brazil) under moonlight are the famous demonstration of TV cameras. The origin of the avalanche effect observed in a-Se is still not clear [10.69, 10.70], since the avalanche effect is believed to be unfeasible in glassy materials with short carrier mean free paths. How and why the avalanche occurs in glassy materials should be a very important issue related to a basic carrier transport mechanisms, which will be discussed in detail in in Chap. 19.

The famous acronym DVD (digital versatile disk) is an optical memory device and is one of the ChGs. This is a so-called phase-change material and the best known composition is $\mathrm{Ge_{2}Sb_{2}Te_{5}}$ [10.49]. Rewritable electrical memory devices will be commercially available that use a phase-change random access memory () [10.71, 10.72]. In addition, phase-change materials offer a promising route for the practical realization of new forms of brain-like computers that could learn, adapt, and change over time [10.73]. Instability, for example the resistance of device changes with time as $t^{\beta}$ ($\beta={\mathrm{0.03}}\approx{\mathrm{0.1}}$), is found in the amorphous phase. This unwanted instability is called the resistance drift. The reason for this occurring is still not clear and this difficulty should be overcome [10.74, 10.75, 10.76]. Probably, this is related to the nonthermal equilibrium glassy states.

6 Summary

The electronic and ionic transport properties in oxide and chalcogenide glasses were reviewed. Oxide glasses alloying with transition metals or alkali atoms into oxide glasses exhibit electronic or ionic transports respectively. Chalcogenide glasses doped with metallic elements exhibit ionic transport behavior. Free carriers in rigid materials are transported via extended states (band conduction) and localized carriers hop between localized states. Carriers in deformable lattices are self-trapped and either strongly or weakly coupled with phonons; these pseudoparticles are called polarons and a polaronic transport should occur in these media. In Sect. 10.1, we introduced briefly the classification of the types of transport in glasses.

Current understandings of the electrical conduction processes, through both theories and experimental data, were discussed in chalcogenide and oxide glasses, including a novel oxides semiconductor that opened up a new market.

Finally, the following unsolved issues in glass science, in particular the electronic and ionic transports on glasses, are summarized:

• 1. When the conduction, either electronic or ionic, is thermally activated (Arrhenius-type conduction), the factor of activation energy is always involved in the pre-exponential factor, which is called the Meyer–Neldel rule. While the reason for the occurrence of this rule has been a matter of debate for more than $\approx{\mathrm{80}}$ years, a proper discussion, for example extracting valid physical parameters from the experimental data, cannot be possible without taking this rule into the discussion. Thus we should not ignore the Meyer–Neldel law in the electronic and ionic transport in glasses.

• 2. The pn anomaly, a long-term puzzle ($\approx{\mathrm{50}}$ years), is found in ChGs as well as in other amorphous semiconductors such as hydrogenated amorphous silicon. However, there is no pn anomaly in the transparent oxide IGZO films. The short mean free path in glassy materials can be the origin of the anomaly. In fact, the mean free path for IGZO is reported to be long enough as compared with that for ChGs. Quantitative arguments taking into consideration the mean free path have yet to be formulated.

• 3. In ionic transport that involved alkali ions, the mixed alkali effect i. e., where one type of mobile alkali ion interferes the movement of another type of alkali ion, is also a long-term issue ($\approx{\mathrm{120}}$ years after the first discovery). This is regarded as the most important and interesting subject in glass science.

• 4. The power-law correlation between ion diffusion coefficient and cation content in glasses is found when the metallic elements are introduced into glasses. The diffusion coefficient follows the power law of metallic inclusions. The so-called traditional percolation argument cannot be applied to this issue, since this effect is found even when the metallic inclusion is less than ${\mathrm{1}}\,{\mathrm{at.\%}}$. Probably, the present power-law correlation can be related to the mixed alkali effect in OGs and the mixed cation effect in ChGs. Recall that the mixed alkali effect from this point may be of interest in renewing this issue.

Appendix

In Sect. 10.1.1, it is stated that the Boltzmann transport theory breaks down when carrier mean free path $l$ closes in on the atomic separation (Ioffe–Regel rule [10.77]). Kawabata [10.78] modified the Boltzmann conductivity by taking into account multiple scattering as follows

$$\sigma=\sigma_{\mathrm{B}}\left\{1-\frac{C}{(k_{\mathrm{F}}l)^{2}}\right\},$$

(10.B56)

where $\sigma_{\mathrm{B}}$ is the Boltzmann conductivity given by $ne^{2}\tau/m^{*}$, where $n$ is the density of the carrier, $\tau$ is the scattering time, $m^{*}$ is the effective mass, $C$ is a constant (order of unity), and $k_{\mathrm{F}}$ is the wave vector at the Fermi energy. Equation (10.B56) was generalized further as

$$\begin{aligned}\displaystyle\sigma&\displaystyle=\sigma_{\mathrm{B}}\left\{1-\frac{C}{(k_{\mathrm{F}}l)^{2}}\left(1-\frac{l}{L}\right)\right\}\\ \displaystyle&\displaystyle\equiv\mathrm{A}+\mathrm{B}\frac{l}{L}\;,\end{aligned} $$

(10.B57)

where $L$ is the inelastic diffusion length when the electron–phonon or electron–electron interaction dominates the electron transport [10.5]. Note that $L> l$ is required in (10.B57).

If electron–electron collisions dominate, the inelastic scattering time $\tau_{\mathrm{i}}$ is proportional to

$$\left(\frac{k_{\mathrm{B}}T}{E_{\mathrm{F}}}\right)^{-2}[10.5]\;,$$

and hence $L$ ($\propto\tau_{\mathrm{i}}^{1/2}$) should be proportional to $T^{-1}$, producing $\sigma\propto T$. If on the other hand electron–phonon collisions dominate, $\tau_{\mathrm{i}}$ is proportional to $T^{-1}$, leading to $L\propto T^{-1/2}$ and $\sigma\propto T^{1/2}$. In amorphous metals, the conductivity is found to follow the above prediction [10.5, 10.79, 10.80, 10.81, 10.82]

$$\sigma=\alpha+\beta T^{\frac{1}{2}}+\gamma T\;.$$

(10.B58)