Prologo

In this chapter, we focus on a particular branch of efficiency and productivity analysis that mostly relates to Network Data Envelopment Analysis (NDEA) models in their connection to what has been called the centralized allocation model or industry efficiency model. Both of these models may be thought as being part of an analytical approach that looks at productivity and efficiency analysis from a system perspective rather than the more traditional granular perspective of plant or firm efficiency analysis. From this point of view, the models can be better connected with issues of regulation of markets that present strong externalities or distortions, or issues of efficient allocation of limited resources in government centrally planned operations. The reason why we focus on NDEA models in particular is due to their astonishing growth in the last 5 to 10 years. A Google Scholar search dated 24/02/2021 with either "Network DEA" or "Network Data Envelopment Analysis" in the title returns 887 research papers. By limiting the same search to before year 1999, one obtains zero papers. Between year 2000 and 2005, 9 papers were published. Between year 2006 and 2010, 87 papers were published. Between 2011 and 2015, 252 papers were published. After 2015 until today, 572 papers have been published. This is an astonishingly exponential growth of what was a tiny little detail in productivity analysis. This search does not include papers that include “Network DEA” or “Network Data Envelopment Analysis” outside of the title. If we remove the requirement for these two sentences to appear in the title, 7,520 papers appear from the search, with a similar temporal distribution: 54 papers before 1999, 92 papers between 2000 and 2005, 419 papers between 2006 and 2010, 1,770 papers between 2011 and 2015, and 5,060 papers between 2016 and 2021. This is a huge amount of papers for such a specialized topic and, to the best of our knowledge, no other sub-field in efficiency and productivity analysis has undergone such miraculous growth. One is therefore left with a feeling of backwardness, as if the modern researcher in productivity and efficiency analysis is missing the biggest leap forward in our knowledge of the field. This motivated us to make a very selective review of this large body of literature. During this process, we stumbled across the contributions of Kantorovich (1939, 1965), Koopmans (1951) and Johansen (1972) and we formed the view that this field of study is far from being a specialized field within efficiency and productivity analysis, but it is rather the best effort to make a connection with economic policy issues associated with central planning and the regulation of markets. Since it is tedious, boring, and almost impossible to review all of these papers, we decided to focus on papers that received the highest number of citations, with a special focus on papers published after 2015. Having a bit of a bigger focus on what happened after 2015 would help in mitigating the distortions that could arise by the citation game. Although this is not necessarily the best way of reviewing the literature and there could be very good papers that received a small number of citations, we nevertheless decided to proceed this way. From the above search, we selected a bit more than 150 papers that we reviewed in order to gain an understanding of what is happening in the field. This chapter is an attempt at explaining in a succinct way our view of this growing body of literature (and we cite, from those 150, only papers that we think are relevant to our discussion, without having the ambition of providing an exhaustive literature review). During our search, we developed our independent modeling strategy to try to reconcile these papers. The outcome of this modeling strategy is contained in Peyrache and Silva (2019).

The origins of system models in efficiency and productivity analysis can be traced back to Kantorovich (1939). In essence, a system is a set of interacting or interdependent group of items forming a unified whole. The system has properties that its parts do not necessarily possess. As Senge (1990) mentions in his system thinking approach: a plane can fly while none of its parts can. Under production economics, systems can be considered groups of firms acting in an industry, or production processes acting within a firm.

Farrell (1957) is often cited as the father of modern efficiency and productivity analysis either through parametric or nonparametric techniques. In his seminal paper, he mentions the measurement of industry efficiency in the following words:

There is, however, a very satisfactory way of getting round this problem: that is, by comparing an industry’s performance with the efficient production function derived from its constituent firms. The ‘technical efficiency’ of an industry measured in this way, will be called its structural efficiency, and is a very interesting concept. It measures the extent to which an industry keeps up with the performance of its own best firms. It is a measure of what is natural to call the structural efficiency of an industry - or the extent to which its firms are of optimum size, to which its high cost-firms are squeezed out or reformed, to which production is optimally allocated between firms in the short run (p.262).

If one replaces in the above citation the word industry with the word firm and the word firm with the word process, it is clear that the issues arising in structural efficiency measurement for an industry are the same as those arising at the level of the firm when one wants to aggregate the efficiency of its processes.

In reviewing all this material, we discovered astonishing similarities between NDEA models and the forgotten contributions of Kantorovich, Koopmans and Johansen (KKJ). These authors were the first to explicitly state the problem of the efficient allocation of scarce resources in order to maximize production. These initial contributions are strictly connected with the early development of linear programming and the methods of solutions associated with the simplex method. The similarity goes beyond the fact that all these models are using linear programming. If one were to judge this literature in terms of its contribution to optimization theory, then there would be no much originality. To the optimization methodologist, there is nothing really new in any of these contribution, since, from a mathematical perspective, once you write down a linear program that is it. If the reader decides to apply the optimization theorist point of view to this field, then she can stop reading here. On the contrary, we think that there is an original contribution also in the writing and interpretation itself of the linear program at hand because this involves its connection to policy making. In this respect, the contribution of KKJ is substantial and the fact that it has been basically ignored by modern researchers in productivity analysis represents a great disservice to the broader scientific community. In particular, KKJ are using linear programming to give a mathematical and computational representation to policy problems associated with the optimal allocation of scarce resources in order to maximize output. These early authors had clearly in mind a system or network perspective in their approach. These early contributions were sophisticated enough to provide the basis for most of the system efficiency analysis that could be conducted on a modern dataset. They also provided a stringent economic and engineering interpretation of the model that could have formed the basis for a rich analysis. The fact that in the ’70s, ’80s and ’90s these contributions were basically ignored, means that authors started to develop the same model again in the last 10 to 20 years, with the explosion associated with NDEA that we observed in the last 10 years. The reasons why this happened are certainly complex, but a great deal of the explanation may come from the fact that economic, social and cultural thinking in those three decades switched the attention from central planning and government intervention toward a more granular view of society. Accordingly, productivity analysis switched the attention from a system perspective toward a more micro-approach, with an extreme focus on the measurement of efficiency and productivity at the firm level. The complexity of the methodologies associated with the measurement of firm level efficiency has grown in time to an incredible level of sophistication. This sophistication required the simplification of the object of study, and therefore, those early contribution that could have provided the bridge toward a more realistic system analysis have been basically disregarded in favor of a simpler object of inference. The best way of describing this forgotten early literature is to look at the citation count. For the sake of simplicity, we may consider Charnes et al. (1978) (CCR) and Banker et al. (1984) (BCC) the founding papers of DEA analysis and Aigner et al. (1977) the founding paper of stochastic frontier analysis (SFA). DEA and SFA represent the two main approaches to firm level efficiency analysis. These papers received respectively 37,556 citations (Charnes et al.,1978), 21,228 citations (Banker et al. 1984) and 13,213 citations (Aigner et al., 1977). Compare this with the citation count of KKJ. Kantorovich (1939) was published in English in Kantorovich (1960) and it received 990 citations. Koopmans (1953) published on the American Economic Review received 19 citations. The book on which this paper is based (Koopmans 1951) received 1,638 citations. Johansen (1972) book received 633 citations. Charnes and Cooper (1962) (32 citations) knew Kantorovich’s and Koopmans’ contributions, yet they were very critical of Kantorovich’s contribution, focusing their critic on methodological grounds (the reader should notice that any computational and methodological issue was relegated by Kantorovich in an appendix). The Sveriges Riksbank prize committee clearly disagreed with Charnes and Cooper (1962) when assigning the Nobel Prize in Economics to Kantorovich and Koopmans for their contributions to the optimal allocation of scarce resources. This is in line with the reviews of Gardner (1990) and Isbell and Marlow (1961) that stress the importance of Kantorovich’s contribution. It is a pity that Johansen was not included in the list of the prize recipients. Johansen’s contribution to productivity analysis is in some respects even more important than Kantorovich and Koopmans, in the sense that Johansen was basically proposing to use the KKJ model (based on linear programming) as the tool to be used in the definition of a macro- or aggregate production function based on firm level or micro-data on production. Johansen has a clear understanding of the use of such a tool for the micro-foundation of the aggregate production function.

Given that these early contributions are at risk of been completely forgotten by the modern researcher, we decided to organize our story by starting with the analysis of the KKJ model. We then make a leap forward from 1972 to basically 2000, when Fare and Grosskopf (2000) re-introduced a special case of the KKJ model naming it Network DEA. In the 30 years, from 1972 to 2001, nothing really happened in the system approach to productivity analysis except for the fact that researchers actively involved in this field provided a massive amount of methodological machinery for the estimation of firm level efficiency. Even theoretical work on production efficiency mostly focused on the “black box” approach. To be clear, we are not claiming that these 30 years were not useful. We are claiming that they did not advance the research agenda on the system perspective of productivity analysis, which is mostly based on the idea of efficiently allocating scarce resources. Hopefully, we are persuasive enough to show that there are still some quite big challenges in the system approach that are worth more attention than developing another 8 components stochastic frontier model.

The chapter is organized as follows: in section The Origins of Network DEA (1939–1975), we provide a description of the early contributions of Kantorovich, Koopmans and Johansen; in section Shephard, Farrell and the “Black Box” Technology (1977–1999), we very briefly describe the methodological development that happened in the years 1977–1999, by stressing the underlying common “black box” production approach; in section Rediscovery of KKJ (2000–2020), we describe recent developments in 3 apparently disconnected pieces of literature: Network DEA, multi-level or hierarchical models and allocability models; in section Topics for Future Research, we provide a summary of open problems that have not been addressed. Section Epilogo concludes.

The Origins of Network DEA (1939–1975)

In three separate and independent contributions, Kantorovich (1939), Koopmans (1951) and Johansen (1972) laid the foundation for the analysis of efficiency and productivity from a system perspective. Reading these early papers requires some imaginative effort, since the mathematical notation and the language are different from what we use today. The underlying mathematical object is nevertheless the same; therefore, it is just a matter of executing a good “translation”. We start this section by describing the model of Kantorovich and introduce the notation in this subsection. As it should result clear by the end of this section, Kantorovich proposed efficiency measurement in a system perspective without making explicit use of intermediate materials and under either variable or non-increasing returns to scale. In view of this fact, the major contribution of Koopmans (1951) is to explicitly account for the use of intermediate materials under constant returns to scale. The introduction of intermediate materials clearly makes the model more flexible and general. Johansen is included in this review because he proposed the same model of Kantorovich under variable returns to scale. Although the model is the same, Johansen interpretation of the model is strikingly different, since Johansen chief interest was in the micro-foundation of the short-run and long-run production function. Of course, it is impossible to make justice to all the details contained in these early papers and they should really be considered the classics of efficiency and productivity analysis that every researcher or practitioner in the field should read carefully. For example, Koopmans’ reduction of technology by elimination of intermediate materials has been subsequently used and rediscovered independently by Pasinetti (1973) to introduce the notion of a vertically integrated sector when using input-output tables. We should leave such details out of our review and only focus on the part that concerns the analysis of the production system efficiency.

Kantorovich (1939)

In 1939, Kantorovich presented a research paper (in Russian) proposing a number of mathematical models (and solution methods in the appendix) to solve problems associated with planning and organization of production. The aim of the paper was to help the Soviet centrally planned economy to reach efficiency in production by allocating resources efficiently. Kantorovich’s paper was published in English for the first time in 1960 in Management Science (Kantorovich, 1960), and we will refer to the English version of the paper due to our inability to read Russian, although we will refer to it as Kantorovich (1939). Kantorovich introduces his more complicated model (Problem C) in steps by first introducing two more basic models (Problem A and Problem B). In problem A, Kantorovich considers \(p=1,\ldots ,P\) machines each one producing \(m=1,\ldots ,M\) products. In problem A, the M outputs are produced non-jointly and each machine is used for a specified amount of time in the production of the single product m. This information can be collected in the following data matrix:

$$\mathbf {Y}=\left[ y_{mp}\right]$$

where \(y_{mp}\) is the quantity of product m that can be produced with machine p in a given reference unit of time. If a machine specializes in the production of a subset of the products, then the coefficients associated with the other products will be equal to zero. It should be noted that in modern terms we would call \(\mathbf {Y}\) a data matrix, but we can infer, by the wording Kantorovich is using, that this may just be information on the use of the machines that is obtained via consultation with engineers. Viewing the \(\mathbf {Y}\) matrix as a sample is somehow more restrictive than what these early authors had in mind. In general, the information can even come from a booklet of instruction associated with each machine. Kantorovich states his first planning problem in the following way:

$$\begin{aligned} \begin{array}{ll} \displaystyle {\max _{\theta , \lambda _{mp}}} &{} \theta \\ st &{} \theta g_{m}\le \sum _{p}\lambda _{mp}y_{mp}\,,\,\,\forall m\\ &{} \sum _{m}\lambda _{mp}=1\,,\,\,\forall p\\ &{} \lambda _{mp}\ge 0 \end{array} \end{aligned}$$
(4.1)

In this formulation \(\sum _{p}\lambda _{mp}y_{mp}\) is the overall amount produced of output m (by all machines jointly) and the coefficients \(g_{m}\) are given and used to determine the mix of the overall output vector produced. Maximizing \(\theta\) implies that the overall production is maximized in the given proportions \(g_m\). The constraint on the intensity variables \(\lambda _{mp}\) summing up to one is interpreted by Kantorovich as imposing that all machines must be used the whole time (\(\lambda _{mp}\) is the amount of time machine p is used in the production of product m). In modern terms, this constraint has been interpreted as a variable returns to scale constraint (Banker et al., 1984), although the authors proposing such an interpretation don’t make any mention of Kantorovich’s work. The overall meaning of problem A is to give the maximal production possible (in the given composition \(g_{m}\)) by using all machines at their full capacity level (fully loaded). Later on, in his book, Kantorovich (1965) relaxes this constraint to \(\sum _{p}\lambda _{pm}\le 1\), therefore allowing for partial use or shut down of machines. The reason for relaxing this constraint is due to the fact that Kantorovich discusses in the book problems associated with capital accumulation. This means that if used for intertemporal analysis, some machines may become economically obsolete if there are other factors that are limiting production. To the best of our knowledge, the use of the model for an analysis of depreciation of capital is still to be implemented along the lines suggested by Kantorovich. In more recent years, this constraint has been interpreted as a non-increasing returns to scale constraint. Because of the special setting of this problem, we want to delve a little bit more into potential interpretations from our point of view (Kantorovich gives several examples of practical problems that can be solved with this model and some of them are astonishingly relevant even today). In particular, if we interpret the P machines as being separate production processes, problem A is, in actual fact, a parallel production network, with a linear output set and free disposability of outputs and without inputs (in the basic model Kantorovich assumed that inputs such as energy or labor are available in the right quantities). In particular, this setting allows for the different P processes to specialize on different subsets of products, or for them to be just alternative methods of production of the same set of goods. This is in line with the modern approach to Network DEA. Each machine can be allocated to single line production processes, and the only limiting factor is the amount of time the machine can be used for. This means that the output set is linear and problem A can also be interpreted as a basic trade problem where each machine is specializing on the production of the good (or sub-set of goods) for which it has a comparative advantage. The connection with the comparative advantage idea went unnoticed as well, unfortunately, but it is the basis on which one can claim that in general if production units cooperate (or trade if they are in a complete free market) they can yield a bigger output. As a final note, we like to point out that the first constraint in the problem has been stated as an inequality constraint. Strictly speaking, Kantorovich uses an equality constraint, although he mentions that one could allow for “unused surpluses” of the products. Since this is basically a statement of free disposability of outputs, we prefer to state the constraint in its free disposability form.

In problem A, Kantorovich does not make any mention of inputs in the production process and only focuses on a given number of machines and their optimal use in producing given outputs. In problem B, Kantorovich introduces the use of inputs by including information on the use of each possible input (only the one input case is presented in the mathematical problem of Kantorovich’s paper, with a mention that extension to other factors is easy and left to the production engineers). In the given reference period of time of use, machine p will be using a given quantity \(x_{mp}\) of input (say energy, to follow Kantorovich’s example) in order to produce \(y_{mp}\) quantity of output m. Generalizing this on the lines proposed by Kantorovich, if the production process uses \(n=1,\ldots ,N\) inputs, then \(x_{nmp}\) is the quantity of input n used by machine p to produce the quantity of output \(y_{mp}\). If the overall quantity of input n available for production is given by \(\chi _{n}\) (notice that this can be equal to the observed overall quantity in the system, or it can be some other quantity set by the researcher), then problem B is:

$$\begin{aligned} \begin{array}{ll} \displaystyle {\max _{\theta ,\lambda _{mp}}} &{} \theta \\ st &{} \theta g_{m}\le \sum _{p}\lambda _{mp}y_{mp}\,,\,\,\forall m\\ &{} \sum _{p}\sum _{m}\lambda _{mp}x_{nmp}\le \chi _{n}\,,\,\,\forall n\\ &{} \sum _{m}\lambda _{mp}=1\,,\,\,\forall p\\ &{} \lambda _{mp}\ge 0 \end{array} \end{aligned}$$
(4.2)

The second constraint on the overall use of inputs means that the inputs can be a limitational factor for the production of the outputs. Since inputs may be specific to the use of some of the machines, this also means that inputs that are specific to the production of some outputs (output-specific inputs) can be accommodated with Kantorovich problem B. This line of reasoning was proposed recently in Cherchye et al., (2013). One limitation of problems A and B is given by the fact that no joint production of outputs is allowed: each machine is dedicated to the production of a single product at any given time and the overall time for which the machine is available can be allocated to the production of different products. Kantorovich tackles joint production in problem C (which he deems being the most difficult and general). In this problem, each machine p has available \(j=1,\ldots ,J\) alternative methods of production for the joint production of the output vector. Therefore, in the given reference time period, machine p can use method of production j to produce the following vector of output quantities \(\left( y_{1pj},\ldots ,y_{Mpj}\right) ^{T}\) jointly. Clearly, problems A and B can be embedded as special cases of this more general model by setting \(J=M\) and allowing the Y matrix to be diagonal. Problem C is stated by Kantorovich as follows:

$$\begin{aligned} \begin{array}{ll} \displaystyle {\max _{\theta ,\lambda _{pj}}} &{} \theta \\ st &{} \theta g_{m}\le \sum _{p}\sum _{j}\lambda _{pj}y_{mpj}\,,\,\,\forall m\\ &{} \sum _{p}\sum _{j}\lambda _{pj}x_{npj}\le \chi _{n}\,,\,\,\forall n\\ &{} \sum _{j}\lambda _{pj}=q_{p}\,,\,\,\forall p\\ &{} \lambda _{pj}\ge 0 \end{array} \end{aligned}$$
(4.3)

In problem C of Kantorovich, the activation levels \(\lambda _{pj}\) represent the “quantity of time” each machine p is used with production method j to produce the outputs jointly. Since each method of production j can produce different mixes of outputs, the single line production process can be embedded into this problem as a special case by selecting appropriate methods of production (i.e., one can list the single production line as an additional method of production). Kantorovich does not state explicitly the third constraint on the use of inputs, but by the way the problems are stated, it is clear that this was the intention. Problem C of Kantorovich tackles joint production in the sense that inputs are allocated to machines that can produce joint products.

Since Kantorovich uses in the book the weaker constraint that allows for partial use or shut down of machines, the overall system proposed by Kantorovich can be stated in terms of either variable returns to scale (VRS) or non-increasing returns to scale (NIRS). To the best of our knowledge, Kantorovich never mentioned the assumption of constant returns to scale. On page 375, he states: “Let there be n machines (or groups of machines) on which there can be turned out m different kinds of output”. “Groups of machines”? If we allow to have replicates of a given machine (let’s say we have 100 machines of a given vintage), then this would sum up to an assumption of replicability and we know that replicability together with the NIRS constraint (i.e., divisibility) implies constant returns to scale (CRS). Probably, Kantorovich did not have in mind CRS itself, but rather he was interested in the medium-term output (Soviet Union had 5 years production plans) in a situation where the number of machines is given. In his book later on, he talks about investment and the increase in the production capacity of the economy. Therefore, even if Kantorovich did not have in mind specifically CRS, he was aware of the limitational nature of replicability in the short or medium term and the necessity to deal with expansion in the long term. All in all, one could say that Kantorovich went really close to a notion of CRS by listing the divisibility and replicability assumption. He clearly did not use the axiomatic language that became dominant in the profession later on, but he clearly had in mind these notions and was using them in his examples. In the opening example on page 369 (Table I), Kantorovich gives a clear account of having more than one machine using the same set of technological coefficients. This is a clear cut case of what he means by “groups of machines”: those are replicates of the same machine, i.e., a given number of the same model of machine. Kantorovich gives this idea again in a more general setting on page 385 when he talks about the “Optimum Distribution of Arable Land”. Here, p indexes the different lots of land and each lot can have a different size \(q_{p}\). Since each lot of land varies in its size, the solution proposed by Kantorovich is equivalent to the constraint \(\sum _{j}\lambda _{pj}=q_{p}\) which implies that each lot of land needs to be used fully. According to Kantorovich, the \(q_{p}\) are either a natural number representing the number of replicates of machine p, or the size of the lot of land therefore a set of fixed real numbers. There is no account in the paper that makes one think that these fixed numbers can be regarded as decision variables in the optimization problem. If one were to assume them as non-negative decision variables on the real line, then this would sum up to a CRS assumption, but such an assumption is not explicitly stated. In the book, he proposed to relax the constraint to a lower inequality constraint that allows for partial use of the machine. This would amount to the following program:

$$\begin{aligned} \begin{array}{ll} \displaystyle {\max _{\theta ,\lambda _{pj}}} &{} \theta \\ st &{} \theta g_{m}\le \sum _{p}\sum _{j}\lambda _{pj}y_{mpj}\,,\,\,\forall m\\ &{} \sum _{p}\sum _{j}\lambda _{pj}x_{npj}\le X_{n}\,,\,\,\forall n\\ &{} \sum _{j}\lambda _{pj}\le q_{p}\,,\,\,\forall p\\ &{} \lambda _{pj}\ge 0 \end{array} \end{aligned}$$
(4.4)

What can we say in terms of interpretation of the Kantorovich model? The first point to make clear is that the model has two levels of decision making in problem C. One can easily grasp that the intensity variables \(\lambda _{pj}\) depend both on the machine used and on the selected method of production. Now, if we rename “machines” as “processes” and “methods of production” as “firms”, in all effects we have a model which is producing M outputs, using N inputs and each firm j is using P production processes to accomplish this production. This is the very first example of an attempt to open the black box of production, even before the black box of production idea was proposed. Kantorovich’s model is a fully fledged parallel production network under alternative specifications of returns to scale.

At this point, we should also notice that the data structure that Kantorovich had in mind is three dimensional. By looking at the input data, we have P matrices \(\mathbf {X}_p\) where the inputs are listed in the rows and the production methods in the columns. If we overlap all these matrices, we obtain a three-dimensional data structure:

We shall see in the next subsection that Koopmans (1951) is using the same data structure by stacking these matrices into a large two-dimensional matrix. Kantorovich does not discuss explicitly how many replicates of each machine we should use, but if we were to assume a long-term view and make the number of replicates a variable, then we could solve the previous problem for several values of \(q_p\) and choose the ones that maximize production for the given level of inputs available. This would make the number of “firms” in the industry a variable of choice like in Ray and Hu (1997) or Peyrache (2013, 2015). Moreover, the model also includes output-specific inputs (Cherchye et al., 2013) by designing the data \(\left( y_{mpj},x_{npj}\right)\) appropriately in order to make them specific to some of the processes.

If we account for the fact that this paper was published in Russian in 1939 and in English in 1960, this means that many production models recently proposed in the literature can be embedded as special cases of Kantorovich model and have been floating around for at least 60 years. The bottom line of this analysis is that in Kantorovich modeling J is the number of methods of production (this can be observed firms) and P is the entities we are evaluating. The coefficients \(\left( y_{mpj},x_{npj}\right)\) will determine the particular interpretation we want. Therefore, we can also obtain the widely celebrated output-oriented DEA models under VRS, NIRS (or CRS if we include replicability of the machines) by setting \(P=1\) and \(\left( y_{mpj},x_{npj}\right) =\left( y_{mj},x_{nj}\right)\) where the dependence on the process has been dropped in the notation because \(P=1\) and one is evaluating the efficiency of the production plan \(\left( \mathbf {y}_{0},\mathbf {x}_{0}\right)\). Output orientation is obtained as a special case by setting \(g_{m}=y_{0m}\). In fact, this is even more general than the output-oriented model because the projection is dictated by the \(g_{m}\) coefficients. One is left to wonder if the 37,000 citations of the CCR model or the 21,000 citations of the BCC model are better deserved than the less than 1,000 citations of Kantorovich’s work, especially considering the exponential growth in Network DEA that we observed over the past 5–10 years.

The chief interest of Kantorovich is into optimal allocation of resources in order to maximize the output of the system. He does not show any interest in the efficiency at a more granular level and he takes for granted that if a machine is not used efficiently then it should be used at the efficient level (this is implicit in the formulation of the problem). Since the objective function is maximizing the overall output produced, this corresponds to an industry model where firms have a network production structure and the production runs in parallel without any flow of intermediate materials from one process to another. The words of Kantorovich himself are better than any explanation:

There are two ways of increasing the efficiency of the work of a shop, an enterprise, or a whole branch of industry. One way is by various improvements in technology; that is, new attachments for individual machines, changes in technological processes, and the discovery of new, better kinds of raw materials. The other way - thus far much less used - is improvement in the organization of planning and production. Here are included, for instance, such questions as the distribution of work among individual machines of the enterprise or among mechanisms, the correct distribution of orders among enterprises, the correct distribution of raw materials, fuel, and other factors. (p. 367)

... I discovered that a whole range of problems of the most diverse character relating to the scientific organization of production (questions of the optimum distribution of the work of machines and mechanisms, the minimization of scrap, the best utilization of raw materials and local materials, fuel, transportation, and so on) lead to the formulation of a single group of mathematical problems.

I want to emphasize again that the greater part of the problems of which I shall speak, relating to the organization and planning of production, are connected specifically with the Soviet system of economy and in the majority of cases do not arise in the economy of a capitalist society. There the choice of output is determined not by the plan but by the interests and profits of individual capitalists. The owner of the enterprise chooses for production those goods which at a given moment have the highest price, can most easily be sold, and therefore give the largest profit. The raw material used is not that of which there are huge supplies in the country, but that which the entrepreneur can buy most cheaply. The question of the maximum utilization of equipment is not raised; in any case, the majority of enterprises work at half capacity.

Next I want to indicate the significance of this problem for the cooperation between enterprises. In the example used above of producing two parts (Section I), we found different relationships between the output of products on different machines. It may happen that in one enterprise, A, it is necessary to make such a number of the second part or the relationship of the machines available is such that the automatic machine, on which it is most advantageous to produce the second part, must be loaded partially with the first part. On the other hand, in a second enterprise, B, it may be necessary to load the turret lather partially with the second part, even though this machine is most productive in turning out the first part. Then it is clearly advantageous for these plants to cooperate in such a way that some output of the first part is transferred from plant A to plant B, and some output of the second part is transferred from plant B to plant A. In a simple case these questions are decided in an elementary way, but in a complex case the question of when it is advantageous for plants to co-operate and how they should do so can be solved exactly on the basis of our method.

This is an incredibly fascinating sentence in all respects, but Kantorovich goes on:

The distribution of the plan of a given combine among different enterprises is the same sort of problem. It is possible to increase the output of a product significantly if this distribution is made correctly; that is, if we assign to each enterprise those items which are most suitable to its equipment. This is of course generally known and recognized, but is usually pronounced without any precise indications as to how to resolve the question of what equipment is most suitable for the given item. As long as there are adequate data, our methods will give a definite procedure for the exact resolution of such questions. (p. 366, Kantorovich, 1939).

This is a clear statement and description of what we would call today an industry model, centralized allocation model or network model. Moreover, the statement is so clear (and does not involve formulas) that makes one wonder why we write the same sort of problems in a much more intrigued and cryptic fashion. Kantorovich goes on and discusses: optimal utilization of machinery, maximum utilization of a complex raw material, most rational utilization of fuel, optimum fullfilment of a construction plan with given construction materials, optimum distribution of arable land and best plan of freight shipments. Only a researcher fixated with finding the next generation of complicated models that will deliver improbable estimates of individual firm efficiencies could deny the practical and empirical relevance of these problems for the modern economy, half of which is run with centrally planned operations and the other half is regulated to solve some sort of market failure.

Kantorovich’s work was a major breakthrough in productivity and efficiency analysis. The solution methods for the associated linear programs developed around the same time by Dantzing in the west resulted to be more powerful. But from the perspective of organizing an economy, sector, industry or company in the best possible way (which is at the end the core of productivity analysis), Kantorovich’s contribution stands as being the most significant contribution of the last 80 years. It lays clearly the foundation for work related to optimal allocation of resources in order to maximize system output. In fact, computational issues are relegated by Kantorovich into an appendix. It is somehow puzzling that Charnes and Cooper (1962) were so critical of Kantorovich’s work and were focusing almost exclusively on the computational aspects rather than looking into the ways that the model could be used for empirical analysis and policy making. Johansen (1976) and Koopmans (1960) clearly recognize the importance of Kantorovich’s work. The “critique” of Charnes and Cooper (1962) is even more astonishing considering that some of the models proposed by these authors later on were actually embedded as special cases of Kantorovich’s model. Given the influence of the CCR and BCC models in efficiency analysis, it would have made sense to include Kantorovich work as one of the seminal papers that introduced a more intriguing production structure. In fact, Koopmans (1960) words on Kantorovich’s work are the best way of describing the importance of this contribution:

The application of problems “A”, “B” and “C” envisaged by the author include assignment of items or tasks to machines in metalworking, in the plywood industry, and in earth moving; trimming problems of sheet metal, lumber, paper, etc.; oil refinery operations; allocation of fuels to different uses; allocation of land to crops, and of transportation equipment to freight flows. One does not need to concur in the authors’ introductory remarks comparing the operation of the Soviet and capitalist systems to see that the wide range of applications perceived by the author make his paper an early classic in the science of management under any economic system. For instance, the concluding discussion anticipating objections to the methods of linear programming has a flavor independent of time and place.

There is little in either the Soviet or the Western literature in management, planning, or economics available in 1939, that could have served as a source for the ideas in this paper, in the concrete form in which they were presented. From its own internal evidence, the paper stands as a highly original contribution of the mathematical mind to problems which few at that time would have perceived as mathematical in nature - on a par with the earlier work of von Neumann on the proportional economic growth in a competitive market economy, and the later work of Dantzing well know to the readers of Management Science.

The Nobel Prize committee clearly listened to Koopmans’ words when assigning the 1975 economic prize to both of them for their major contribution in the science of the optimal allocation of scarce resources.

Koopmans

Kantorovich’s examples always involve one particular industry or a particular group of machines. In his 1965 book, there is a more general discussion on how one could potentially extend these ideas to the whole economy as well. As we shall see in this subsection, from the point of view of system efficiency, Koopmans’ most important contribution was to actually provide a way of measuring efficiency for the whole economy, by taking into explicit account the use and flows of intermediate materials across the different nodes of the network (the different sectors or activities of the economy). In 1951, Koopmans collected the proceeding of a conference in a book titled “Activity analysis of Production and Allocation”. In the opening statement of the book, Koopmans states:

The contributions to this book are devoted, directly or indirectly, to various aspects of a fundamental problem of normative economics: the best allocation of limited means toward desired ends.

There are various ways of presenting Koopmans’ contribution. The way we want to approach the presentation here is to have it in connection with the model of Kantorovich. Although the paper of Kantorovich was not known to Koopmans in 1951 (therefore Koopmans’ contribution is completely independent from Kantorovich’s contribution), the two papers approach the same empirical problem using very similar methods. Therefore, we see the two contributions as complementary rather than competing with each other.

As noted in Charnes and Cooper (1962), Kantorovich is ambiguous about the sign of the data. Quite in stark contrast, Koopmans is very clear about the underlying conditions under which the “efficient production set” is non-empty and this is a necessary condition for the model presented by Kantorovich to have a basic feasible solution. Koopmans presents all his results under the CRS assumption (although he mentions that CRS is not necessary and results can be generalized to variable returns to scale). If we make the coefficients \(q_{p}\) free non-negative decision variables in problem (4.3), then the intensity constraint \(\sum _p \lambda _{pj}=q_p\) is redundant and we can omit it (which is the equivalent to assume CRS). Before we proceed and write the model explicitly, it is useful to provide the classification of inputs and outputs proposed by Koopmans. Koopmans uses the same matrices of data for the inputs and the outputs, but he introduces an additional set of matrices, which are the matrices of intermediate materials. We will indicate intermediate products as \(z_{lpj}\) with \(l=1,\ldots ,L\). While Koopmans assumes that all input and output quantities are positive, the L intermediate materials can be both positive or negative. If \(z_{lpj}\) is negative, then it represents the quantity of intermediate l used as an input in process p with production method j. If \(z_{lpj}\) is positive, then it represents the quantity of intermediate l produced as an output in process p using method of production j. This is equivalent to adopting a netput notation for the intermediates. In particular, Koopmans is assuming that for each intermediate l, there is at least one process that is using it as an input (\(z_{lpj}<0\) for at least one p and one j) and is produced as an output by at least one process (\(z_{lpj}>0\) for at least one p and one j). If this condition does not hold, then the intermediate should be classified as either an input or an output (depending on its sign). Intermediate materials are produced within the system to be used within the system. Koopmans imposes explicitly that the overall net production of every given intermediate must be non-negative (otherwise production would be impossible because it would require some flow of the intermediate from outside the system), which amounts to adding the following constraint to model (4.3):

$$\begin{aligned} \sum _{p}\sum _{j}\lambda _{pj}z_{lpj}\ge \eta _l\,,\,\,\forall l=1,\ldots ,L \end{aligned}$$
(4.5)

In actual fact, Koopmans allows this constraints to be tightened by the quantities (\(\eta _l\)), by proposing that some of the intermediate materials may be flowing into the system. In other words, these coefficients allow for situations in which some intermediate materials must be available before starting production, or some intermediate materials must be produced as final outputs to be used in future production. The sign of the \(\eta _l\) coefficients is negative if the intermediate is an input that must be available before starting production, and they are positive if the intermediate must be produced above a certain quantity as a final output. These quantities play the same role here as the overall quantities \(\chi _n\) in Kantorovich’s model. Adding this constraint to problem (4.3) and omitting the intensity variable constraint to allow for CRS, returns the Koopmans’ model of production.

Koopmans introduces a more parsimonious way of representing the system and the underlying data of the problem. The best way of introducing such notation is by looking at the stacking of the three-dimensional matrices of Kantorovich. If we stack all the input matrices together and transpose them, we obtain:

$$\begin{aligned} \mathbf {X}=\left[ \mathbf {X}_1,\ldots ,\mathbf {X}_P\right] \end{aligned}$$
(4.6)

Although this makes the notation a bit more confusing, we will refer to \(\mathbf {X}_p\) as one particular two-dimensional matrix of inputs for process p as in the representation of Kantorovich. And we will refer to \(\mathbf {X}\) as the stacked two-dimensional matrix composed of the stacking of all of the P input matrices. Notice that each row of matrix \(\mathbf {X}\) represents now a particular input; that is, the dimension of the matrix is \(N\times (J+P)\). We can define in the same way the output matrix

$$\begin{aligned} \mathbf {Y}=\left[ \mathbf {Y}_1,\ldots ,\mathbf {Y}_P\right] \end{aligned}$$
(4.7)

and the matrix of intermediates

$$\begin{aligned} \mathbf {Z}=\left[ \mathbf {Z}_1,\ldots ,\mathbf {Z}_P\right] \end{aligned}$$
(4.8)

We can now stack these large matrices into the following one:

$$\begin{aligned} \mathbf {A}=\left[ \begin{array}{c} -\mathbf {X} \\ \mathbf {Z} \\ \mathbf {Y} \end{array}\right] \end{aligned}$$
(4.9)

In this matrix, each column represents the netput of a given production process. Koopmans calls the columns of this matrix “basic activities”. Notice that if the three-dimensional matrix of Kantorovich is sparse, then Koopmans’ representation provides a more parsimonious way of representing the data, since one can eliminate all the columns that have zero for all inputs and outputs (all columns filled with zeros only). In Koopmans, the technology matrix is dense, while in Kantorovich it could be sparse. On the other hand, if one were to introduce VRS constraints on the intensity variables for all processes, then Kantorovich’s representation is more exhaustive and general, since the processes are accounted for in a more explicit way. To do the same with the more succinct way of Koopmans, one need to introduce an indicator matrix with as many columns as the number of intensity variables and as many rows as the number of processes. This matrix will only contain indicator variables, i.e., zeros and ones. Then, the intensity variable constraints can be represented as:

$$\begin{aligned} \mathbf {W}\boldsymbol{\lambda } = \mathbf {1}_P \end{aligned}$$
(4.10)

where \(\mathbf {1}_P\) is a column vector of ones of dimension P. If we call \(\boldsymbol{\pi }\) a generic \((N+M+L)\) netput vector, then we can obtain the very parsimonious representation of the production possibilities set proposed by Koopmans:

$$\begin{aligned} \boldsymbol{\pi }=\mathbf {A}\boldsymbol{\lambda } \,,\,\,\boldsymbol{\lambda }\ge \mathbf {0} \end{aligned}$$
(4.11)

where \(\boldsymbol{\lambda }\) has all the \(\lambda _{pj}\) coefficients stacked together. If we call the intensity variables of process p, \(\boldsymbol{\lambda }_p=\left[ \lambda _{p1},\ldots ,\lambda _{pJ}\right] ^T\), then the stacked vector of intensity variables for the system is:

$$\begin{aligned} \boldsymbol{\lambda }=\left[ \begin{array}{c} \boldsymbol{\lambda }_1 \\ \vdots \\ \boldsymbol{\lambda }_P \end{array}\right] \end{aligned}$$
(4.12)

Although this is a parsimonious representation, Koopmans’ suggestion of introducing limitations on the primary factors of production is better written in formal terms by looking at the individual input, output and intermediate matrices. It should also be stressed that Koopmans’ interest is in determining efficient sets and he does not really propose (contrary to Kantorovich) an objective function to determine maximal or optimal production. If we were to choose the same objective function of Kantorovich, then we would write the optimization model as (where we omit non-negativity constraints on the decision variables \(\boldsymbol{\lambda }\ge \mathbf {0}\)):

$$\begin{aligned} \begin{array}{ll} \displaystyle {\max _{\theta ,\boldsymbol{\lambda }}} &{} \theta \\ st &{} \theta \mathbf {g}\le \mathbf {Y}\boldsymbol{\lambda }\\ &{} \boldsymbol{\eta }\le \mathbf {Z}\boldsymbol{\lambda }\\ &{} \boldsymbol{\chi }\ge \mathbf {X}\boldsymbol{\lambda }\\ \end{array} \end{aligned}$$
(4.13)

As said earlier, this program is expressed under the assumption of CRS (as in Koopmans). One can introduce VRS by adding the constraint \(\mathbf {W}\boldsymbol{\lambda }=\mathbf {1}_P\), or NIRS by adding the constraint \(\mathbf {W}\boldsymbol{\lambda }\le \mathbf {1}_P\). Alternatively, one can take the notion of replicability of Kantorovich and write this constraint as \(\mathbf {W}\boldsymbol{\lambda }=\mathbf {q}\) where \(\mathbf {q}\) are pre-specified levels of replication. The new explicit constraint on the intermediates states that given the activation levels represented by the intensity variables \(\lambda _{pj}\), the overall net production of intermediate material l of the system must be non-negative. This means that the system is producing enough intermediate material to satisfy the use of it in all production processes that require it as an input. It should be noted that under CRS the notation is simplified further because there are no restrictions on the \(\lambda _{pj}\), apart from non-negativity constraints.

What can we say about Koopmans’ model in connection with system efficiency? The intelligent reader will convince herself that Koopmans’ technology can embed a whole lot of network structures (actually the large majority) that have been produced in the last few years. We shall discuss this briefly in the next few sections, by giving some examples. We should also point out that Koopmans has an explicit discussion on the prices associated with the efficient subset of the production set. This set of prices (which is nothing more that the separating hyperplane at the optimal solution of problem 4.13) is discussed by Koopmans in connection with planning problems that involve decentralized decisions. In this sense, the price vector is used by Koopmans to incentivize individual production units to reach the optimal plan set out by the central planner. Kantorovich (1965) in his book takes up this discussion even in a more explicit way, by suggesting that this set of supporting prices would permit the fulfillment of the 5 year plan, by making the best use of the limited economic resources at hand. Of course, neither Koopmans or Kantorovich introduced the dual problem that would set the optimization problem directly in terms of supporting shadow prices. But both of them had clearly in mind that such a vector of supporting prices could play a key role in practice. Koopmans discussed this explicitly and Kantorovich implicitly by proposing his solution method based on the “resolving multipliers”. The issue of decentralization of the plan by providing individual production units with a set level of prices at which they could trade their inputs and outputs has not been used as a tool for implementation of the optimal solution.

All in all, Koopmans’ contribution, especially if read in connection with Kantorovich’s paper, represents another big leap forward in our ability to represent production systems. The introduction of the CRS assumption and the constraints associated with the use and flows of intermediate materials open up wide possibilities of applications and actually nest many of the current proposals in Network DEA analysis. Although Koopmans’ paper is well known within the productivity community (contrary to Kantorovich’s paper), his general representation of the technology set that basically includes network models has been widely neglected, with the scientific community posing excessive attention on the definition that Koopmans gives of an efficient set. This is a misplaced interpretation and minimizes the contribution of Koopmans to productivity and efficiency analysis, since the notion of efficiency of Koopmans was already proposed by Pareto. The main point of Koopmans’ analysis regards (in line with Kantorovich) the efficient allocation of a limited amount of resources to produce the maximal possible output. His representation of the technology set associated with this problem is so general and simple that puts to shame many modern representations (including the one of the authors, Peyrache and Silva, 2019). Everyone should read Koopmans’ book if interested in efficiency and productivity analysis in order to experience that feeling of satisfaction and fulfillment that only the reading (and studying) of the great classical thinkers of our time can provide—a feeling (to say this using Koopmans’ words) that “has a flavour independent of time and place”.

Johansen

Johansen (1972) had a chief interest in the micro-foundation of the aggregate production function. Johansen’s setting of the problem was an aggregation from the firm production function to the industry production function. If we call f(x) the firm production function and there are J firms in the industry, then Johansen defines the industry production function as:

$$\begin{aligned} F\left( \sum _j x_j\right) =\max _{x_{j}} \sum _j f(x_j) \end{aligned}$$
(4.14)

This means that if the overall quantity of input of the industry is \(\chi =\sum _j x_j\), then the industry overall maximal production is obtained by allocating the industry input \(\chi\) to individual firms optimally by choosing the appropriate allocations \(x_j\). Johansen notices that if the firm level production function is approximated by a piece-wise linear envelope of the observed data points, the previous maximization problem becomes a linear program. In fact, the linear program associated with such a specification is the same as in Kantorovich’s specification. This is not surprising since the objective of Johansen’s problem is to choose the allocation of resources (inputs) to the various firms in a way that maximizes the overall output produced by the industry. Johansen calls this approach the nonparametric approach to the micro-foundation of the aggregate production function. He goes on discussing notions of short-run vs long-run choices, and most importantly, he notices that if one is willing to make additional assumptions on how the inputs are distributed across firms one can make more explicit the parametric form of the aggregate production function. For example, he notices that the contribution of Houthakker (1955) is an example of such an approach: if one assumes that the inputs are distributed as a generalized Pareto, then the aggregate production function is Cobb-Douglas. Interestingly, Houthakker was making an explicit connection to the activity analysis model of Koopmans. This fact has been recently used by Jones (2005) in macroeconomic modeling.

Johansen further discusses issues associated with technical change and how to introduce it into the model. Johansen’s book is a source of inspiration for work in productivity analysis that still has to happen. All in all, Johansen is providing an explicit link to economics and he is suggesting a way of proceeding that makes use of the activity analysis model by looking at the distribution of inputs across firms. Interestingly, this did not give rise to a proper research program exploring how to use statistical methods to estimate density functions on data in order to obtain the industry production function. This work is still far from being accomplished, and in this sense, Johansen’s (1972) book is an important source of inspiration. This could help the scientific community in efficiency and productivity analysis to make a more explicit connection and build a bridge and a methodology that can be used in macroeconomic modeling. Among the three authors that we reviewed so far, Johansen is definitely extremely original and also the most neglected of the three.

Summing Up: The KKJ (Kantorovich-Koopmans-Johansen) Model

We shall refer to these early contributions as the Kantorovich-Koopmans-Johansen (KKJ) model and consider the specification of program (4.13) with the associated discussion on the constraints on the intensity variables to characterize returns to scale as the benchmark model. This model allows for various forms of returns to scale, and at the same time, it makes use of intermediate materials, therefore making it suitable to represent networks system, where the nodes of the system are connected by the flow of intermediate materials.

Before we close this long section on the KKJ model, it is useful to show its application to some of the current models proposed in the literature, just to give a flavor of the flexibility and generality of the KKJ model. Let us assume for simplicity that there are only two processes, 3 firms (or methods of production), two inputs and two outputs. If the two processes are independent, with input 1 producing output 1 in process 1, and input 2 producing output 2 in process 2, then the associated input and output matrices would be:

$$\mathbf {X}=\left[ \begin{array}{cccccc} x_{111} &{} x_{112} &{} x_{113} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} x_{221} &{} x_{222} &{} x_{223} \\ \end{array}\right]$$
$$\mathbf {Y}=\left[ \begin{array}{cccccc} y_{111} &{} y_{112} &{} y_{113} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} y_{221} &{} y_{222} &{} y_{223} \\ \end{array}\right]$$

The first 3 columns of these matrices represent process 1, and the second 3 columns process 2. Since input 1 enters with zeros in process 2 and so does output 1, this means that process 1 is producing output 1 using input 1; that is, input 1 is specific to the production of output 1. This is true for process 2 as well. This is an example of two single production lines working in parallel. If we wanted these two production lines to work sequentially in a series two-stage network, then the matrix of intermediates would be:

$$\mathbf {Z}=\left[ \begin{array}{cccccc} z_{111} &{} z_{112} &{} z_{113} &{} z_{123} &{} z_{123} &{} z_{123} \\ \end{array}\right]$$

with the caveat that the first 3 entries of this matrix would be positive (the intermediate material is an output of process 1) and the second 3 entries would be negative (the intermediate material is an input of process 2). This provides the KKJ representation of the widely “celebrated” two-stage Network DEA model. One can easily see that by building these basic matrices in an appropriate manner, it is possible to cover such a wide variety of network structure that we are not even sure any of the current proposals falls out of this representation. For example, the joint inputs model of Cherchye et al. (2013) requires that if an input is provided in a given quantity to one process, then it is available in the same quantity to all other processes (it is a public good). Suppose a third input is available, then we would change the input matrix to:

$$\mathbf {X}=\left[ \begin{array}{cccccc} x_{111} &{} x_{112} &{} x_{113} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} x_{221} &{} x_{222} &{} x_{223} \\ x_{311} &{} x_{312} &{} x_{313} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} x_{311} &{} x_{312} &{} x_{313} \\ \end{array}\right]$$

and as the reader can verify the quantity of input available to process 2 is the same as process 1. Even if rows 3 and 4 represent the same physical input, we separated them so that when summing up the total quantity of input available to the system, these quantities are not double counted. By splitting and creating additional rows and columns and creating fictitious inputs and outputs, one can accommodate so many structures that the only limitation is the creativity and imagination of the applied researcher. This would, for example, allow us to keep the level of the intermediate flows at the observed level, rather than making them change in the optimal solution, de facto nesting so-called fixed link Network DEA models. This can be accomplished by adding a fictitious number of rows to the matrices in order to preserve the current allocation.

Koopmans published his work in 1951, Kantorivich in English in 1960 and Johansen his book in 1972. The Nobel Prize was assigned to Kantorovich and Koopmans in 1975. Therefore, if a martian were to come to planet earth in 1976, she would have been provided with a strong mathematical model to deal with problems associated with the optimal allocation of resources in production systems. It is very likely that the martian would have started to look at issues associated with the use of such a model and the associated collection of data, and she would have delved into a list of issues that we are going to describe at the end of this chapter. But this is not what we have done on planet earth. With the contributions of Charnes et al. (1978), Banker et al. (1984), Aigner et al. (1977), Fare and Lovell (1978) and the associated work on duality theory of Ronald Shephard, the scene was set for studying production using the black box technology approach. To be fair, we should also point to the fact that at that time the available data was more limited and this may have contribute to shift the attention toward firm level analysis. Certainly, the boom in NDEA publications in the last 10 years has partly to do with the availability of more refined datasets that contain information at a lower level of aggregation and actually permit to go beyond black box analysis. Even so, it is puzzling that researchers focused on firm level efficiency, given that a firm level dataset allows at least the possibility of carrying out the industry model analysis so well presented and discussed in Johansen. At the very least, the Johansen model should have had become a basic analytical tool in the efficiency and productivity community.

In any event, starting in the late ’70s for about 30 years, an entire generation of researchers in efficiency and productivity analysis has worked on the basic assumption that input data and output data are available at the firm level and the main focus of the analysis should be the one of measuring the efficiency and productivity of individual firms. This paradigm laid the foundation for all subsequent work on stochastic frontier analysis, DEA, index numbers, economic theory of production and aggregation and duality. Very little if anything has been done during these 30 years in terms of looking “inside” the black box, which was what the KKJ model basically does. By saying this, we don’t want to minimize the impact of what has been done in terms of research in efficiency and productivity analysis. We just want to point out to the fact that in one way or another the memory of the KKJ model has been lost, and a lot of the effort that went into building Network DEA models could have been saved if the KKJ model were to be credited the correct amount of attention and importance in this field of study. In some sense, we lost a lot of the creativity and understanding of how to optimally organize and measure the efficiency of a system of production that these early authors so forcefully and elegantly described. In exchange for it, we greatly simplified the object of our study. After simplifying it, the research problem has been reduced to the measurement of the efficiency of a single individual firm. Starting at the end of the ’70s, the scene was set to research and deliver an impressive methodological machinery that keeps growing at the present day and allows the modern researcher to have very flexible strategies to estimate the black box production technology.

Shephard, Farrell and the “Black Box” Technology (1977–1999)

In two independent contributions, Farrell (1957) and Shephard (1970) laid the foundation for what would become the “black box” technology and the basis of the successive 30 years of research in efficiency and productivity analysis. This is clearly the case if one looks at the citation count of Farrell: with 23,879 citations, this is definitely the founding paper of modern productivity analysis. Shephard’s 1970 book received 4,887, but one should keep in mind that this is a theoretical contribution, and for being a theoretical contribution, this represents a high number of citations. From the perspective of our discussion, the main outcome of these two contributions is to set the scene for a simplified object of inquiry, shifting the attention from the optimal allocation of resources and the associated problems of measurement, toward the optimal use of those resources at the firm level. The firm is considered the basic unit of the analysis, and problems associated with reallocation of inputs and production across production units are rarely taken into consideration. These two contributions formed the basis for successive work on production frontier estimation, inference and theoretical development. The reference to the firm as the basic unit of analysis, without reference to the component production processes or the allocation problems across different firms, has given rise to the definition of such an approach as a “black box” approach. The firm is a “black box” in the sense that we only observe the inputs that are entering production and the outputs that are exiting as products, but we do not observe what happens inside the firm. This is in sharp contrast to both the KKJ approach and the Network DEA approach.

The best way of describing this is to look once again at citation count as a rough measure of the popularity of the main contributions in the field. Aigner et al. (1977) and Meeusen and van Den Broeck (1977) received respectively 13,229 and 7,811 citations, laying the foundation for the research program on stochastic frontier production function estimation and inference. Subsequent work (continuing today) made the model more and more flexible considering issues associated with functional form specification, panel data, additional error components and all the methodological machinery that is still under development, providing a large body of models and methods for estimation and inference. Charnes et al. (1978) and Banker et al. (1984) (after renaming the linear activity analysis model DEA) received respectively 37,581 and 21,240 citations, setting the agenda for research in DEA and estimation of production frontiers and technical efficiency at the firm level. This stream of literature saw the development of a plethora of efficiency measures (radial, slack based, directional, etc.) and alternative ways of specifying returns to scale, and relaxation of the convexity assumption. Fare and Lovell (1978), with a citation count of 1,459 (high for a theoretical contribution), made the connection between economic theory, duality and efficiency and productivity analysis; subsequent work will see the Shephard duality approach extended to various alternative notions of technical, cost, revenue and profit efficiency.

All of those contributions have a commonality in the fact that they are based on the black box technology and they lack any interest in the problems of allocation of resources that was the core of the early development of the KKJ model. Therefore, the subsequent work in efficiency analysis, at least until the first decade of this century, basically “forgot” the problem of optimal allocation of resources and took the route of simplifying the policy problem to the analysis of the firm and its efficiency in various forms. By no means, we are implying that this work was not useful: quite on the contrary, this work equipped the modern researcher with a tremendous set of tools to analyze firm level dataset and the various measures of efficiency associated with the black box technology idea. The side effect of this massive amount of work that went into estimation, inference and theoretical development of the black box technology is that the latest generation of researchers in productivity analysis has no memory of the early developments associated with the KKJ model. Starting with the contribution of Fare and Grosskopf (2000), the field started re-discovering the problem of optimal resource allocation, without the knowledge of the work of the KKJ model.

Rediscovery of KKJ (2000–2020)

The literature on system efficiency has grown disperse, and in fact, the name “production system” is rarely used. Instead, there are the following strands of the efficiency measurement literature that can be considered within this production system perspective:

  • Netowork DEA models;

  • Multi-Level or Hierarchical models;

  • Input-output allocability models.

It should be noted that in the literature we found a variety of names trying to describe the same sort of problems—for example, “industry models” have also been called “centralized allocation models”. The rationale we follow for our classification is based mainly on the separation between the decision problem of allocating resources to the different nodes of the system, from the efficient use of these resources in production. In Network DEA models, the focus is typically oriented toward the firm and its internal structure. Clearly, there are two layers of decision making here, and in this sense, these models could also be discussed under the multi-level models. We keep Network DEA models separated from the rest because of the large strand of the literature dealing with the internal structure of the firm. In multi-level models, there are various layers of decision making delivering the observed allocation of resources. In fact, in such a system, decision making happens at all the various levels: at the level of the production process, at the level of the firm and at the level of the industry or the economy as a whole (we include industry models in this class). When studying production system models, it is important to categorize the types of inputs and outputs that are used and produced. The literature has, most often than not, ignored this classification, except for certain cases where explicitly some inputs are considered allocatable and the optimal allocation is to be determined; or some cases where the specificity of some inputs in the production of only one or a subset of outputs is considered. As a result, we also consider this strand of literature separated from the rest because it explicitly deals with the definition itself of inputs and outputs. We call this stream “Input-output allocability models”. Note that this division or classification is arbitrary, as indeed are all classifications that can be found in the literature. This may be confusing, and in a sense, this could be one of the reasons why these different streams of literature are developing independently.

The KKJ model looks at optimality conditions for the system as a whole: the associated efficiency measure is computed for the whole system, being it an industry, a firm or the whole economy. One of the merits of the last 20 years of research on this topic has stressed the importance of assigning the overall inefficiency of the system to the different components. We shall not discuss these contributions in too much detail because that would be out of the scope of this chapter and would take excessive space. One could even make the argument that assigning efficiency to the different components of the system is not really useful, since the KKJ model is already providing targets for the different components that would make the whole system efficient. We rather focus on the connection between the KKJ model and this recent literature in terms of the structure of the underlying system.

In what follows, we will explain what each of the aforementioned strands of the literature aims to do in terms of efficiency measurement and we will explain how these various strands are in fact interconnected (and how they relate to the KKJ model). As a matter of fact, the relationship between the various strands of the literature is hardly acknowledged in the literature.

Network Models

Many network models (in particular those that do not allow for intermediate materials) are in all aspects similar to industry models, but authors have not recognized this link. This has happened mainly because the two types of analysis have somehow different objectives. Whereas in the multi-level model literature, it has been recognized that the aggregate is more than the sum of its parts because of allocation inefficiencies, in network models, most often than not, allocation issues are not even mentioned and the problem is mainly mathematical: that of providing an efficiency of the parts and of the whole and aggregating the parts to form the whole or disaggregating the whole into its parts. In this mathematical exercise, authors have missed the most important issue: that the whole is different from the sum of its parts and possesses characteristics that parts do not. In particular, as we saw with the KKJ model, allocation inefficiencies are somehow the core of this type of analysis.

As mentioned in the introduction, the Network DEA literature is growing at a very fast pace. Kao (2014) provides a review of Network DEA models and includes them into 7 types (basic two-stage structure, general two-stage structure, series structure, parallel structure, mixed structure, hierarchical structure and dynamic structure). It is interesting to verify that more than 170 studies in his Table 1 (pages 11 and 12) are two-stage models (representing more than 50% of the total number of studies). Another important remark is that allocation issues are not addressed in this literature. In the same year, Castelli and Pesenti (2014) also reviewed the Network DEA literature and classified papers into 3 categories: Network DEA; shared flow models; and multi-level models. Interestingly, Castelli and Pesenti (2014) claim that in Network DEA the subunits do not have the ability to allocate resources, and therefore, they assume that when this assumption is dropped models fall into the shared flow models (which are essentially network models where allocation of resources is allowed). Castelli and Pesenti (2014) basically recognized the fact that most network models are ignoring the resource allocation issue and solve the problem by assuming that the word “network” is unrelated with resource allocation issues. In addition, Castelli and Pesenti (2014) interpret dynamic models as network models, and therefore, no reallocation of resources is allowed. On the contrary, Kao (2014) considers dynamic models as a separate type of network model. Dynamic models have, indeed, been treated as a separate type of network models as the review by Fallah-Fini et al. (2014) testifies. In this review, the authors distinguish between alternative dynamic models by the way intertemporal dependencies are treated (as production delays, as inventories, as capital related variables, as adjustment costs and as incremental improvement and learning processes). Agrell et al. (2013) also reviewed series or supply chain network models in depth, pointing out the prevalence of two-stage network models and the fact that “most models lack a clear economic or technical motivation for the intermediate measures” (p. 581).

To the best of our knowledge, the term “Network DEA” was introduced in the literature with the work of Fare and Grosskopf (2000). This work is a follow up of Fare (1986), where dynamic models have been modeled as a network structure for the first time. In these models, a firm observed in different periods of time is analyzed as a whole entity since it is assumed that certain factors pass from period to period and work as a link between time periods. This means that the same firm in different time periods should be assessed as a whole entity, or as a system that is temporally interconnected. Clearly, this bears connections with supply chain or series models where some factors flow from one process to the next as intermediate factors. Therefore, dynamic models can be seen as series models of network structures. In what follows, we start by presenting dynamic network models. This choice is dictated by the fact that dynamic network models can be viewed as the more general class, of which the series and parallel network structures are special cases. This choice will also make the connection to the KKJ model more clear.

Dynamic Network DEA Models

Fare (1986) proposed models with separate reference technologies for each time period. The author classifies inputs into two categories: (i) inputs that are observed and allocated to each time period and (ii) inputs whose total amount (across all time periods) is given, but not its time allocation. The second class of inputs is also considered in some multi-level models, where the allocation of some inputs is not observed. Fare and Grosskopf (1996) take up on this work, and introduce the idea of intermediate factors linking time periods. This idea is at the basis of most series network models (dynamic or not).

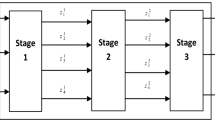
One of the first models to be employed for dynamic network models was that of Fare and Grosskopf (2000) (shown below in program 4.15). In this paper the authors propose the division of  total output  into a part that is final and a part that is kept in the system to be used in subsequent time periods. In this specification, we use a radial output expansion factor. Note that Fare and Grosskopf (2000) only propose a technology for dynamic models and do not discuss an efficiency measure. The use of the output radial expansion with this technology set has been proposed by Kao (2013), and we decided to follow this strategy to make the discussion more clear. If we were to evaluate the efficiency of the input-output combination \((x_{npo},y_{mpo},z_{lpo})\) (where o is indexing the DMU under evaluation), the program would be:

$$\begin{aligned} \begin{array}{ll} \displaystyle {\max _{\lambda _{pj},\theta }} &{} \theta \\ st &{} \sum _{j}\lambda _{pj} {x}_{npj} \le x_{npo} \,,\,\,\forall n,p\\ &{} \sum _{j} \lambda _{pj}{y}_{mpj}\ge \theta y_{mpo} \,,\,\,\forall m,p\\ &{} \sum _j \lambda _{pj} z_{l(p-1)j} \le z_{l(p-1)o} \,,\,\,\forall l,p\\ &{} \sum _j \lambda _{pj} z_{lpj} \ge z_{lpo} \,,\,\,\forall l,p \\ \end{array} \end{aligned}$$
(4.15)

In this program, the process index p can be interpreted as time and the intermediate factor (\(z_l\)) enters the network at the beginning node 0 and exits at node P. The index p can stand for time or for process, since dynamic models are identical to series models. Therefore, the flow of the intermediate in this network is sequential, flowing from \(p=1\) to \(p=2\), \(p=2\) to \(p=3\) and so on, until reaching node P where it exits as an output. The last two constraints on the intermediates allow for production feasibility by making sure that the activation level at node p is not using more intermediate input (\(z_{l(p-1)o}\)) than is available and is producing at least the observed amount of intermediate output (\(z_{lpo}\)). The reader can convince herself that by appropriately expanding Koopmans’ matrices to make all inputs and outputs process specific, program (4.15) becomes a special case of the KKJ model.

In program (4.15), output is maximized by keeping the level of the inputs at the observed level without allowing for reallocation of resources across the different nodes of the system. In Bogetoft et al. (2009) or Färe et al. (2018) the authors call model (4.15) the static model, where intermediates are treated as normal inputs and outputs. When they are considered as decision variables the dynamic nature of the system emerges, given that optimal allocation is determined. Kao (2013) proposes an alternative model in which the system is optimized as a whole, given constraints on the overall quantities of inputs. This means that reallocation of resources across the different nodes is possible and the program becomes:

$$\begin{aligned} \begin{array}{ll} \displaystyle {\max _{\lambda _{pj},\theta }} &{} \theta \\ st &{} \sum _p \sum _{j}\lambda _{pj} {x}_{npj} \le \sum _p x_{npo} \,,\,\,\forall n\\ &{} \sum _p \sum _{j} \lambda _{pj}{y}_{mpj}\ge \theta \sum _p y_{mpo} \,,\,\,\forall m\\ &{} \sum _p \sum _j \lambda _{pj} \left( z_{lpj}-z_{l(p-1)j}\right) \ge z_{lPo}-z_{l0o} \,,\,\,\forall l\\ \end{array} \end{aligned}$$
(4.16)

We should notice here that Kao (2013) is actually calling \(\theta\) the “system efficiency”. This means that the author is actually recognizing that these are “system efficiency” models. This specification can clearly be embedded into the KKJ model by noting that the intermediate material is really nothing more than a resource stock that can be depleted in time. Note that in this specification there is no constraint stating that the intermediate input that enters node p (\(\sum _j \lambda _{pj} z_{(p-1)j}\)) must be lower than the output exiting node \(p-1\) (\(\sum _j \lambda _{(p-1)j} z_{(p-1)j}\)). This is fine, as long as the overall underlying stock variable is big enough to compensate any shortages in a given time period (see Kao’s paper for an empirical example). Nevertheless, the most important characteristic of this model is that there is a measure of efficiency from the system perspective. In all respects, this model is a special case of the KKJ model, where the intermediate materials are interpreted as a depleting stock. In fact, as we shall see, if we omit the constraint on the depleting resources, this program is equivalent to the industry efficiency model (see model 4.19 in the next section). Such a model is also proposed in Kao (2012) for parallel production systems (which resemble in all respects industry models). Note that models (4.15) and (4.16) evaluate efficiency relative to different technologies. While in (4.15), technology is process/time dependent—i.e., there is a technology considered individually for each process or time period, in (4.16) a process meta-technology is employed, where the objective function does not yield process/time-specific efficiencies, but the efficiency of the system as a whole, like in the KKJ model. In order to recover process efficiency scores from the system efficiency score, Kao (2013) proposes to use the multiplier form and the associated optimal multipliers for deriving process/time period-specific efficiencies. This results in some problems of the approach, one of which related to the fact that multipliers are not unique and another being the inconsistency between targets obtained from the envelopment model and the efficiency scores obtained from the multiplier model.

Series Network Models

Series models are a special case of dynamic models where different processes within the same firm are connected through intermediate factors and inputs and outputs consumed at different stages may be different. For some reason, the literature has given particular emphasis to two-stage series models where the main focus has been the analysis of the aggregation of process efficiency scores. The general model presented in Kao (2014) for handling multi-stage series models is similar to model (4.16) for dynamic models. In the Kao (2014) model (4.15) is also proposed as an alternative method for solving series network models where “the technologies of all processes are allowed to be different” (p. 2). Note that the differences between these two models do not relate only to different technologies, but also different treatment of intermediates. Tone and Tsutsui (2009) noted that one can have two assumptions on the intermediate variables. The fixed link assumption is stating constraints on the intermediates as in program (4.15) by constraining these variables to their observed level. In the free link approach, they assume that the intermediate variables can be freely chosen (given some feasibility constraints as in the KKJ model). The model proposed by Tone and Tsutsui (2009) is similar to model (4.15), except that they use a slack-based efficiency measure and use equality variables for the intermediates, where under the free link intermediate factor targets from the succeeding stage are set equal to targets for the preceding stage, and under the fixed link the targets for intermediates are set equal to observed values. Fukuyama and Mirdehghan (2012) analyzed this model and concluded that the approach of Tone and Tsutsui (2009) did not account for inefficiencies from intermediate factors.

Kao and Hwang (2010) were among the first to propose two-stage network models. Under this special case of series network, the structures of models in the literature are very similar to those of models (4.15) and (4.16). The difference is that in this case where inputs and outputs are different across stages the use of the meta-technology is not possible and most models resemble model (4.15), with differences mainly in the treatment of intermediates. For example, Lim and Zhu (2016) or Chen et al. (2013) propose two-stage models where intermediates are decision variables, similarly to what is proposed in Nemoto and Goto (2003) (and similar to the free link approach).

The literature on the two-stage models is mainly concerned with decomposing the overall efficiency of the firm into stage 1 and stage 2 efficiencies. Kao (2013) provides some decomposition between process efficiencies and firm efficiency for the case of series systems. Various types of decompositions exist in the literature with the additive and multiplicative ones being the prevalent. Despotis et al. (2016) and Sotiros et al. (2019) point out existing problems and inconsistencies with the original decomposition such as the fact that the maximum firm efficiency score can be obtained from process efficiency scores that are not on the Pareto-frontier, and that could therefore be improved. They propose alternative approaches to solve the problem based on multi-objective linear programming. Li et al. (2018) also analyze two-stage models and provide alternative models for defining which of the processes is the leader or the follower.

Parallel Network Models

Parallel network models can be seen as a set of processes within a DMU that may share some resources. The main feature that distinguishes parallel networks is that there is no flow of intermediate materials between the processes. As a result, parallel networks can be represented using model (4.16), where the constraints regarding intermediates are deleted. Kao (2012) proposed this definition of parallel network models and studied them using the following multiplier form:

$$\begin{aligned} \begin{array}{ll} \displaystyle {\max _{u_m,v_n}} &{} \sum _m v_n \sum _p x_{npo} \\ st &{} \sum _m u_m y_{mpj} - \sum _n v_n x_{npj} \le 0 \,,\,\,\forall p,j\\ &{}\sum _n u_m \sum _p y_{mpo} = 1 \end{array} \end{aligned}$$
(4.17)

This is the dual of program (4.16), with the caveat that intermediate constraints have been omitted since we are dealing with a parallel network. The only difference with the program presented in Kao (2012) is that we are using output orientation instead of input orientation: this choice simplifies the discussion and makes the connection to the previous sections more transparent. In program (4.17), \(u_m\) is the weight assigned to output m and \(v_n\) is the input weight assigned to input n—weights are considered the same across subunits (i.e., the implicit value attributed to each input and output should be the same in each sub-unit). Note that the original model of Kao (2012) has more constraints, but some are redundant. As a result, we simplified it by excluding redundant constraints and ignoring slacks. This results in model (4.17).

According to Kao (2012), model (4.17) results in efficiency scores for each \(DMU_o\) ( \(E^*_o\)). The efficiency of sub-unit p in DMU j (\(e_{pj}\)) is determined using the optimal weights of model (4.17) (indexed with a \(*\) that means they are the optimal values from program [4.17]):

$$\begin{aligned} e_{pj} = \frac{\sum _{m}{u^*_m y_{mpj}}}{\sum _{n}{v^*_n x_{npj}}} \end{aligned}$$
(4.18)

The computation of subunit efficiencies in this way allows the DMU efficiency to be decomposed into the efficiency of the subunits, using appropriate weights. Being the dual of a model that is nested in the KKJ model implies that Kao (2012) is basically proposing to use the shadow prices associated with the KKJ model to assess the efficiency of the individual production units. This is in line with the intuitions provided by Kantorovich in his book and the use of shadow pricing as a decentralization mechanism to reach efficiency in Koopmans. If one were to allow production units to trade at the Kao (2012) prices, this would implement the central plan in a decentralized manner (as suggested by Kantorovich and Koopmans).

The use of a meta-technology in the parallel network model has some implicit assumptions, not always explicitly discussed. In particular the assumption that all inputs are perfectly allocatable. Under CRS, this assumption implies that the meta-frontier will be constituted by the most productive process, which implies at the optimal solution that inefficient processes are advised to closure (see also Pachkova, 2009). This provides inconsistencies between the multiplier and envelopment formulations since in the multiplier model all processes will have an efficiency score, where in the envelopment model targets for some processes will be zero. Most of these problems derive from misconceptions regarding what model (4.17) is supposed to measure. It is a firm model, assessing the average unit and assuming that complete reallocation of resources is possible (e.g., closure of some processes to replace them by the most efficient ones). In the disaggregation of the system efficiency proposed in (4.18) the reallocation of resources within firms is disregarded and the whole is considered the sum of the parts. In Peyrache and Silva (2019), these issues are discussed and the authors maintain that firm efficiencies are not simply the sum (or product) of processes efficiencies but include a reallocation component that is mostly disregarded in the literature.

Note that an alternative to solving parallel models would be to use model (4.15) without the intermediate constraints. This solution is not without problems too. In fact, a single expansion factor is used across processes in this model, implying that the solution equals the maximum of process efficiencies as assessed independently (which may be an inadequate aggregate measure for the firm).

As we will see in the next sections, the application of model (4.15) to parallel network models is closely linked with the literature on output-specific inputs and the application of model (4.16) is closely linked with the literature on industry models.

Multi-Level or Hierarchical Models

The term multi-level model has been used by Castelli et al. (2010) and Castelli and Pesenti (2014) to mean the assessment of production units at different levels of decision making. Another term has been used by Cook et al. (1998) and Kao (2014) to mean the same thing: hierarchical models. In this sort of models, firms are grouped into hierarchies, where for example different factories belong to the same plant, and different plants belong to the same company, and different companies belong to the same industry. In this type of models, the problem is that of aggregating the efficiency of factories to obtain the efficiency of plants and then aggregate the efficiency of plants to obtain the efficiency of companies, given that there may be inputs and outputs that are level specific. So these models include the industry models or centralized allocation model, where the problem is exactly the same: to aggregate firm efficiency to get the industry global or structural efficiency.

Multi-level structured data (data that are observed at a system level and cannot be disaggregated in lower levels) may arise in many settings. For example, in education grades are available at the student level, but the number of teachers is available at the school level. Multi-level data is in fact related to group frontiers and meta-frontiers (see, e.g., O’Donnell et al., 2008) where individual firms are usually grouped according to a higher-level characteristic (students may be grouped in private schools and public schools, firms may be grouped according to location or district, etc.). In this type of models, higher-level variables enter the analysis in the constitution of the homogeneous groups, but not as inputs or outputs of the higher-level production process.

In Cook et al. (1998), the authors consider different levels for the variables and solve multiplier models with different multiplier factors associated with each level. When solving the higher-level model, they include constraints for that level and also for the other levels, such that the optimal solution of multipliers for the higher level can also be applicable at lower levels. They assume that the higher-level variables are not allocatable. Cook and Green (2005), or Cook and Green (2004), assumed that these higher-level variables are allocatable, and the model resembles the one presented in Beasley (1995) (which we will refer to later on under [iii]). Castelli et al. (2004) also proposed models for hierarchical structures, but rather than being multi-level models, these are models with a series structure within a parallel structure.

Industry Models

The literature on industry models tries to aggregate the efficiency of each constituent firm to form the efficiency of the industry (or structural efficiency). It started as early as the work of Farrell (1957) and has been discussed also by Forsund and Hjalmarsson (1979) who advocate the use of the average firm for measuring structural efficiency. Ylvinger (2000) advocates that the average unit assessment is not equivalent to the efficiency of the industry, and Li and Cheng (2007), showed that the weighted average of firm efficiencies and the efficiency of the average unit are equivalent concepts under an identical convex individual technology set, and that differences between the two are related to allocative efficiency. Karagiannis (2015) explored in more depth the relationship between the efficiency of the average unit and structural efficiency. The authors conclude that the two concepts of efficiency will coincide only if size is uncorrelated with efficiency and if there are no reallocation inefficiencies. The efficiency of the average DMU has been explored by several authors under the denomination of “Industry models” (e.g., Lozano & Villa 2004; Peyrache & Zago (2016; Peyrache (2013, 2015), where allocation issues between firms in the industry are usually at the center of the discussion. Kuosmanen et al. (2006) also proposed similar models for analyzing the industry cost efficiency and named them top-down approaches. Note that industry models are also related to input-output tables which can be seen as industry models where the industry is an economy composed of various sectors of activity (see Prieto & Zofio, 2007).

The centralized resource allocation model discussed by Lozano and Villa (2004) somehow epitomizes the core of both the industry models and the multi-level models. We therefore discuss it a little more in depth. The model is presented in Lozano and Villa (2004) in input orientation under VRS. If we were, for sake of comparison, switch to output orientation, then the model would be:

$$\begin{aligned} \begin{array}{ll} \displaystyle {\max _{\lambda _{pj},\theta }} &{} \theta \\ st &{} \sum _p \sum _{j}\lambda _{pj} {x}_{nj} \le \sum _j x_{nj} \,,\,\,\forall n\\ &{} \sum _p \sum _{j} \lambda _{pj}{y}_{mj}\ge \theta \sum _j y_{mj} \,,\,\,\forall m\\ \end{array} \end{aligned}$$
(4.19)

where the P nodes of the system are the firms (which are also used in the definition of the technology). Model (4.19) is equivalent to Kantorovich’s problem C, reported in equation (4.3), by noting that we impose the restriction \(x_{npj}=x_{nj},y_{npj}=y_{nj}\) on the data matrices (i.e., all processes uses the same technology) and by setting \(g_m=\sum _j y_{mj}\), \(\chi _n=\sum _j x_{nj}\) and \(q_p=1\). In other words, the three-dimensional Kantorovich matrix of data is simplified by assuming \(x_{npj}=x_{nj}\) and \(y_{mpj}=y_{mj}\), with \(P=J\). This specification is also equivalent to a model where the efficiency of a virtual DMU with average inputs and outputs is assessed. In fact by dividing all constraints (left and right hand sides) by the number of firms J, one would obtain the average firm interpretation. The assessment of this average unit was first proposed by Forsund and Hjalmarsson (1979) for measuring the structural efficiency of an industry (see also Ylvinger, 2000). The solution of the model under this specification can yield results that are prima facie contradictory, since it is possible for an industry to be composed of only technically efficiency units (i.e., when assessed individually they all lie on the frontier) and, at the same time, the industry (composed by these technically efficient units) may be inefficiently organized (see, e.g., Ylvinger, 2000). Indeed, what happens is that when the average unit is used for assessing the industry, reallocation of resources is implicitly considered possible and therefore each firm may individually be performing at its best, but reallocations within the industry could still improve its overall efficiency (i.e., output). This is supposedly one of the reasons for Lozano and Villa (2004) calling their models centralized resource allocation models—since resource allocation between firms is at the heart of such models (see also Mar Molinero et al., 2014). Issues of aggregation and decomposition are also addressed in these models, particularly when they are used to assess industry structural efficiency. For example, Li and NG (1995) show that structural efficiency equals the product of aggregate efficiency and a component of reallocation efficiency, and Karagiannis (2015) decomposed additively structural efficiency into aggregate efficiency (or average efficiency) and a covariance term relating deviation in output shares and technical efficiencies from their averages.

Allocability Models

The last class of models that we want to discuss deals with the explicit definition of different types of inputs and/or outputs. This is a major issue in network models, since once the black box of production is open, one has to state which inputs can be allocated, which ones cannot and which ones are only available at higher level of aggregation. The precursor of these models can be considered the work of Fare (1986) since the author assumes that for some inputs time allocation is not known, and this allocation could be derived. The idea of unknown allocation of otherwise allocatable inputs was used by Beasley (1995). Castelli and Pesenti (2014) call this model the shared flow model. Beasley (1995) assesses the efficiency for two types of university functions (teaching and research) that have specific inputs and outputs but also share some inputs whose allocation is unknown. The author assesses the two functions separately and then considers the determination of the optimal allocation of the shared resource between the two functions (see Ding et al. 2015) for a recent review of this strand of literature). The most important feature of this models is that it implies a (a priori) classification of inputs (some are allocatable or shared between functions/processes and others are not). Following the same idea, in the output-specific input literature, different technologies are associated with different sets of inputs and outputs, and one cannot assume that all inputs are used in the production of all outputs. Cherchye et al. (2013) and Cherchye et al. (2017) propose models that can handle process-specific and shared inputs (or “joint inputs” as they named them). These models assume that joint inputs are simultaneously used by all processes and cannot be distributed (or allocated) to the different processes. Recently, Podinovski et al. (2018) propose a Multiple Hybrid Returns to Scale (MHRS) technology where it is assumed that shared inputs are allocated to different processes (in spite of the allocation not being observed).

Shared flow models imply the existence of shared allocatable resources, but the allocation is not observed (or there is no a priori information on the allocation). These models yield an efficiency score that is different from what would be obtained if one assumed that the shared resource was fully available to each process. But this difference only exists because prior information on allocation is provided through the form of weight constraints. Therefore, these models seem to classify shared resources into one category that is somewhere in the middle between “Full information on resource allocation is observed” and “No information on resource allocation is observed”, which should be the category “Partial information on resource allocation is known/desired”. The literature has also been very confusing on this matter as no such classification exists so far.

Summing Up

In general terms, we may characterize existing system models according to the technology employed, the treatment of intermediates and the type of efficiency measure proposed. For example, industry models and parallel network structures may be defined in relation to a meta-technology (the intersection of processes technologies), or in relation to process-specific technologies. Indeed, the model of Kao (2009) for parallel networks resembles the centralized industry model presented in Lozano and Villa (2004). In this type of model, the assessment is equivalent to “finding common input and output weights that maximize the efficiency of a virtual DMU with average inputs and outputs” (Lozano & Villa, 2004, p. 149). On the contrary, process-specific technologies, as those applied in output-specific input settings, in general yield the efficiency of the DMU as being the same as the maximum efficiency across its processes (and therefore, disregard completely inefficient processes).

Process-specific technologies can be also encountered in series models. The reason is in general obvious—if we have two stages, one consuming inputs and another producing outputs, then the assessment of each stage implies the consideration of process-specific technologies since variables are different in each stage. Interestingly, this does not happen in dynamic models, where in fact the variables repeat in each stage. This is the main reason behind two main ways available in the literature for assessing the efficiency under dynamic models: the Fare and Grosskopf (2000) model and the Kao (2013) model. Most existing models for dynamic network structures use the Fare and Grosskopf (2000) process technologies (or time-specific technologies) like those of Nemoto and Goto (2003) or Tone and Tsutsui (2014), but Kao (2013) models aggregate across time the DMUs inputs and outputs (and therefore use a meta-technology).

Another major distinction that one can find between models in the literature is on the treatment of intermediates. Tone and Tsutsui (2009) provide an interesting classification for intermediates: the free link approach and the fixed link approach. Most of the existing models use one way or another for dealing with intermediates. The main difference between them lies in the consideration of inefficiency sources on the use of intermediates in the overall efficiency of the DMU or not. Fukuyama and Mirdehghan (2012) noted this problem in relation to the Tone and Tsutsui (2009) model that did not include inefficiencies from intermediates and provided a way to fix that. Indeed, the type of efficiency measure considered is probably the major difference between models in the literature (e.g., in series models several papers exist that show different ways of computing overall efficiency and aggregating processes efficiencies as testifies Cook et al. [2010] in their review).

All in all, from our review of this large body of literature, we found that the distinctions between the KKJ model and the various strands of literature described in the previous sections are really minor. Most (if not all) of these differences reside in the definition of the efficiency measure. All of the other issues associated with allocability or not of inputs and outputs are really relegated in the building of appropriate data matrices in the KKJ model.

Topics for Future Research

As we saw in the previous sections, one way of rationalizing the growing body of literature on Network DEA models is to look at it from the perspective of the KKJ model. In this sense, the main problem is shifted from the measurement of firm level efficiency to the measurement of the efficiency of the system as a whole and attributing efficiency to possibly the different levels or hierarchies in the system. By looking at this literature from this perspective, one has also the advantage point of making connections to other methodologies in engineering that deal with allocation of resources. In fact, the KKJ model is useful to determine the level of inefficiency of the system, but the input and output targets set by the model can have multiple solutions. The literature is quite silent on how we choose among these alternative allocations, and ideas from the system thinking may help in selecting appropriate and realistic targets in each particular situation. In the rest of this section, we will look into what we think are the open problems associated with the KKJ model and therefore Network DEA models. As we saw, the field of productivity and efficiency analysis developed in the first 30 years (1939–1972) around the KKJ model; it then turned its attention to firm level efficiency estimation for another 30 years (1977–2001); although some papers dealt with resource allocation during this time, it is really only in the last 20 years that the field has been re-discovering the KKJ model and started progressing to solve some inherent problems associated with that type of modeling. In what follows, we are going to present an overview on the main problems associated with the KKJ model.

Efficiency Measurement vs Structure of the Network

It is possible to design the data matrices of the KKJ model in order to accommodate a great deal of network structures. In principle, one should separate the building of the technology reference set, from the measure of efficiency that can be used to measure the inefficiency of the system. Given that the reference set can be represented in a compact way by designing the associated input and output data matrices appropriately, in this section we consider what type of efficiency measure one should use. The literature developing in the last 20 years, as one would expect, has used both radial and slack-based measures of efficiency. From the point of view of our argument, the choice between these two classes of measures does not present any additional challenges compared to a simple and standard DEA model. Russell and Schworm (2009, 2011) have shown that from an axiomatic point of view the two measures of efficiency can be rationalized by looking at the axioms that they satisfy. In particular, radial measures will satisfy continuity, while slack-based measures will satisfy indication (Pareto efficiency). Depending on the particular application, one may choose one measure or the other, but the fact that we are dealing with a network structure is not really adding any additional arguments in favor of one or the other. The only additional argument one has to keep in mind is that hierarchical network models have decision making happening at various levels. Therefore, there is an issue of simplicity of aggregation of the measure of efficiency. In this sense, using a measure of efficiency which is simpler to aggregate will provide an easier way of assessing the efficiency of the system and its components.

Unobserved Allocations

In the KKJ model and in general in the recent Network DEA models, it is assumed that the allocation of the various inputs and outputs is observed. For example, if a firm is composed of P production plants, one observes in the dataset the allocation of each input and the production of each output at each node of the system. What happens if these allocations are not observed or only partially observed? Suppose that the allocation of raw materials to each different node p is observed, but the allocation of labor is not observed. In other words, suppose that we have a case where we know that a given input (labor for example) is allocatable, but we do not observe its allocation. Although this is likely to be a very common case in practice, the literature is quite silent on this point. Once could treat the input as a public good (a joint input), but this is clearly introducing a bias in the measurement of efficiency. Podinovski et al. (2018) propose a solution to this problem for the case of CRS technologies. The reader should refer to this very important contribution to gain a better perspective of the modeling strategy. For our purposes, it suffices to say that the Podinovski et al. (2018) model provides a technology reference set that is contained in the one that one would obtain if the allocations were observed. This has the great advantage of providing a conservative estimate of the inefficiency of the system. Extensions to VRS and other scale characterizations are yet to be made. In the absence of a model that extends the ideas of Podinovski et al. (2018) to the VRS case, one could use a suggestion of Farrell (1957). This consists of dividing up the dataset in clusters of observations that have the same “size” and then apply the Podinovski et al. (2018) model to these classes. Although this is less satisfactory than an extension of Podinovski et al. (2018) to the VRS case, it is really the only viable option to deal with unobserved allocations, unless one is willing to interpret the input as a public good (joint input).

In a very recent paper, Gong and Sickles (2021) adapt the stochastic frontier model to the case of a simple parallel network (they use a different wording). This paper is important in itself just because is the first attempt to propose a network model in the stochastic frontier tradition. But for our discussion it is also important because it is dealing with unobserved allocations of allocatable inputs. In particular, the authors make use of input price information to make inferences about the possible allocation of inputs across the different processes. Although the study assumes that price information is available, this is a first attempt at dealing with the problem in a stochastic frontier framework.

Costly Reallocation

In the KKJ model and subsequent work on Network DEA, it is implicitly assumed that either reallocation of inputs is not possible (i.e., inputs are process specific), or reallocation of inputs can happen at no cost. What if the reallocation is costly, but not prohibitively so? To the best of our knowledge, there is only one paper dealing with costly reallocations (Pachkova, 2009). This is likely to be a very important problem in practice, since reallocation of resources is likely to happen at some cost. In particular, one can look at inputs that are specific to a particular process as a resource that is allocatable but the cost of reallocation is either very high or prohibitive. For example, if we think of beds in a hospital, they are likely to be allocatable at negligible cost (i.e., the cost of transporting them from one department to another or one hospital to another). On the contrary, doctors, given their specialization, are unlikely to be allocatable at no cost. Even if one could retrain a cardiologist to become a radiologist, this is likely to take a lot of time, money and effort. Therefore, in the short run, at least the number of doctors in a hospital represents an input that is prohibitively costly to reallocate. In general terms, if information on the cost of reallocation is available, one should be able to introduce it into the KKJ model in order to take it into account. In this way, the model becomes a hybrid transportation-production model, where optimality is reached taking into account the actual possibilities and costs of reallocation of resources.

Connection Between Network Analysis and the Black Box Analysis

What happens if we run the analysis at the black box level rather than the network level? One formal way of stating this is the following. Call \(T_p\) the production possibilities set of process p and each process is allocated input \(x_p\) to produce output \(y_p\). The total for the firm is \(X=\sum _p x_p\) and \(Y=\sum _p y_p\). The firm production possibilities set is given by all the possible allocations of the inputs across the different P processes:

$$\begin{aligned} T=\left\{ \left( \sum _p x_p,\sum _p y_p\right) :\left( x_p,y_p\right) \in T_p\right\} \end{aligned}$$
(4.20)

Suppose now that we run the analysis at the firm level and we build the production possibilities set using the total inputs and outputs of the firm. Call this set \(T_F\). What is the relationship between T and \(T_F\)? In other words, if we know that the firm is composed of different departments (cardiology, radiology, etc.) but we run the analysis at the firm level ignoring the allocations to the various departments, can we still obtain meaningful efficiency scores? Is it possible to make general statements about their relationship? For example is the black box technology always underestimating efficiency? In general, we think the answer is no, and convexity plays a big role in addressing this issue. Is it possible to have general results? We found only one theoretical paper by Buccola and Fare (2008) dealing with this issue. This is actually an important area of research, since it is connected with the simplification of the analysis and it makes an explicit connection between the black box technology and the underlying process-specific technologies. In general, one may want to build \(T_F\) in such a way that it is contained in T. If so, the estimation of efficiency at the firm level using the black box technology is higher than the one estimated using T and this means that the KKJ model helps to increase discrimination power. In general, conditions for this to happen will involve some restrictive assumptions that we still don’t know.

Network Stochastic Frontiers

This is possibly the biggest missing point in the literature. With the exception of Gong and Sickles (2021), we could not find a single stochastic frontier paper that is dealing with some form of network structure. Stochastic frontier analysis applied to network production structures can bring about many benefits. Although the standard narrative is to say that the difference between SFA and DEA is coming from the noise component, it is important to stress that SFA allows the introduction of functional forms. If the dataset has a small number of observations, then it makes sense to parameterize the production frontier function and assume that it has some known parametric form. In general, SFA analysis may provide an advantage in this sense. One may use SFA as a noise-canceling device and once estimation is done, use the estimated coefficients to determine the optimal allocation of resources. As long as the functional form is convex, the KKJ would become a convex program rather than a linear program. Convex programming made some strong progress in computational terms. If one wants to stick with linear programming, then it is possible to follow the suggestion of Koopmans (1951) of approximating the known functional form with a piece-wise function. In fact, one could go a step further and estimate directly a spline function in a SFA framework and use it to retain a linear program specification for the KKJ model.

Micro-foundation of the Aggregate Production Function

Johansen (1972) had a chief interest in the micro-foundation of the macro- or aggregate production function. The KKJ model was interpreted by Johansen as a tool to describe the aggregate production possibilities set starting with observations at the micro-level or, in other words, from observation of the firm level input-output combinations. In this respect, the KKJ model is a nonparametric way of determining the aggregate production function. By making specific assumptions on the statistical distribution of the inputs and outputs across firms, one can infer specific functional forms for the aggregate production function. Johansen discusses a number of them. If we were to take this approach to its logical consequences, then one should start with the estimation of the distribution functions of the inputs and outputs and once these distributions are known determine the aggregate production function. This would open up the way to the use of flexible ways of estimating multivariate distribution functions such as copulas. Work in this space is very much limited, to the best of our knowledge, to the proposals of Johansen. Given the progress that has been made in the last 50 years in terms of estimation of multivariate distribution functions, it is quite clear that this is now a viable and potentially very fruitful avenue of research that is underexplored. The intuition of Johansen can be given more explicit content and it would be possible to specify a number of alternative ways of extending this idea to the more general setting of the KKJ model.

Epilogo

The previous pages provide a number of important unexplored topics that are relevant to the modern researcher in efficiency and productivity analysis, especially if she is willing to focus on problems associated with central planning and regulation of markets. We also provided a brief history of this field of study, and hopefully, we have provided evidence that many of the NDEA models developed in the last 10 years or so are just special cases of the KKJ model that can be dealt with by adjusting in a proper way the data matrices as presented in Koopmans and Kantorovich. As a result of separate developments, each of the above strands of literature tends to look at the same problem from different perspectives, like in the Indian elephant parable where each blind man guessed a different object depending on the body part of the elephant they were sensing (see Fig. 4.1)

Fig. 4.1
figure 1

Parable of the blind men and an elephant originated in India

Full size image

Given the current status of this field of research, the themes proposed in the last section to progress forward this field are unlikely to be explored at the same pace at which the NDEA literature has been growing in the last 10 years. This may be due to a number of factors, many of them having to do with the way research is structured today. A question one should really ask is why the sub-fields described in section Summing Up have been growing into almost completely separate streams of literature, even if they all are under the umbrella of system efficiency analysis (and mostly just variations of the KKJ model). In this last subsection, we should speculate on how the field arrived at such a state of affairs.

Clearly, the working environment of the modern researcher is very different from the one in which academics used to work in the past. The pressure to publish papers has become bigger and bigger. Universities value research output based on quantity rather than quality, in most cases. This means that researchers have a strong incentive to engage in salami slicing (the practice of taking a single piece of research and fragment it into smaller pieces that can be published). This prompted Wikipedia to have a page describing what this is (search on Wikipedia for “least publishable unit”). The “least publishable unit” has become definitely smaller in time. The interested reader can make a quick Google Scholar search with the keyword “publish or perish” to see that there are already a number of papers concerned with the distortions that this system is producing.

Universities require academics to be “leader” in their own field of research. This means that academics have a strong incentive and a tendency to create sub-fields and over-represent their contribution within these sub-fields. In particular, many of these sub-fields are not even so different from each other, at least for what we saw in the previous few sections. This state of things is creating a dangerous mentality, and we are breeding an entire generation of researcher that hyper-specialize, by teaching them how to best market their research in order for it to look original, so they can be “leader” in their respective fields of research. The quest for truth and knowledge has been replaced by the quest for publication at any cost. The collegiality and intellectual honesty of the scientific international community have been replaced by a grim citation count. This basically transformed international conferences from places where academics share and progress knowledge, into places where researchers put forward aggressive marketing campaigns (sometimes on the edge of bullying and harassment) to increase their citation count, h-index and impact factor. Journals have followed this trend, transforming editorial boards into lobbies that look after the “insiders”, instead of having their more traditional function of recognizing original and relevant work irrespective of where it is coming from. The ingenuity and fascination of true knowledge that drives many people into the search for academic jobs (and is so much needed for the advancement of truth and knowledge) are quickly replaced by a more mundane need to be competitive on the market for academic jobs. Instead of leaving small details associated with the development of models and results out of the papers, we create entire new papers out of these details. It is quite amusing that by reading Kantorovich work, many small details and intuition were left to “the production engineers” (this resembles the traditional role of the teacher that is leaving some details to be sorted out by the student as homework). Sorting out such details would of course imply that the “production engineers” (to stick with Kantorovich) have a good education in the first place that allows them to do so. Out of these details, we now build entire journals that are trying to “fill the gaps” in the literature. Roger Koenker, notably one of the most creative and prominent econometrician and statistician of our time (and the proponent of quantile regression; another field to which productivity analysis should have closer connections...), has suggested that we should all be part of the “Society for the Preservation of Gaps in the Literature” (the interested reader can visit: https://www.econ.uiuc.edu/roger/gaps.html). To use his words:

Gaps in the literature constitute the essential breathing spaces of academic life. The research and publication process poses an increasing threat to the well being of disciplines by gradually filling these gaps with meritless interpolation of existing results. The Society for the Preservation of Gaps in the Literature is dedicated to the preservation of the “intellectual green space” afforded by these gaps.

Rather than filling gaps in the literature one of the great accomplishments of serious research is to create gaps in the literature by debunking the nonsense of the past. Nowhere is this objective better formulated than in the introduction to the bibliography of Keynes’ (1921) Treatise on Probability:

“I have not read all these books myself, but I have read more of them than it would be good for any one to read again. There are here enumerated many dead treatises and ghostly memoirs. The list is too long, and I have not always successfully resisted the impulse to add to it in the spirit of a collector. There are not above a hundred of these which it would be worth while to preserve,–if only it were securely ascertained which these hundred are. At present a bibliographer takes pride in numerous entries; but he would be a more useful fellow, and the labours of research would be lightened, if he could practise deletion and bring into existence an accredited Index Expurgatorius. But this can only be accomplished by the slow mills of the collective judgment of the learned; and I have already indicated my own favorite authors in copious footnotes to the main body of the text.

There are no better words to describe the state of the literature on the system perspective in efficiency and productivity analysis (maybe to describe the state of the literature in general?). We definitely did not read all papers in NDEA and we have no intention to do so in the future, given that the ones we found are only minor incremental progresses to the KKJ model. In fact, it is hard enough to acknowledge that some of the models proposed by one of the authors of this chapter (Peyrache, 2013, 2015) are so close to the KKJ model to make one wonder if they were to be published in the first place or if they should have been left as homework exercises. We are starting to think that we have ourselves destroyed another gap in the literature and made our academic life less green by adding noise to noise (Peyrache & Silva, 2019).

How is it possible that the literature has grown so fragmented, by producing such an exponential growth in the number of published papers that basically deal with the same underlying problem? If every single author were to walk in the same conference room and read their paper, everyone would be reading the same material in a different “language”, creating a lot of chatter. We thought that we may call this effect “publication chatter”, like the chatter in the conference room. But this time we were smart enough to look out for a paper instead of re-inventing the wheel. We were surprised to find at least 4 papers on this topic (maybe these papers are also filling a gap in our knowledge?). Kozlov and Hurlbert (2006), in the Journal of Fundamental Biology, pushed the idea that we should learn from mistakes of the past; otherwise, we are going to reproduce the same mistakes in the current literature (we could not have said this better!). They cite the 1984 Dean of the Graduate School, Yale University:

Nowhere in all of scholarship has the book or shorter contribution (the ’paper’) become more thoroughly debased than in science ... the principal remedy is for everyone to write fewer and more significant works ... It seems to be a deeply held, quasi-philosophical position among contemporary scientists that publication, and lots of it, is an inalienable right ... it is no longer an honor to get a paper published ... publication of any and all results has become the norm ... the publication process has largely ceased to act as a quality control mechanism ... It is terribly important for students to appreciate the older literature in their field ... For scientists there is a danger that the vast tide of chatter in the current literature may isolate us from our intellectual underpinnings.

Given that researchers themselves don’t have incentives to limit the number of published papers, can we still hope for this to be accomplished by the refereeing process? Is this process really conducive to eliminate papers that only marginally contribute to the literature and really incentivize innovation? Lloyd (1985), in The Florida Entomologist, states:

Read on: “We share the opinion of Hall (1979), Stumpf (1980), and others that anonymous peer reviews may be more costly than beneficial. A system that could allow a reviewer to say unreasonable, insulting, irrelevant, and misinformed things about you and your work without being accountable hardly seems equitable. To some degree the reviewer is indeed accountable- to the editor-but the potential for abuse is still too great to be ignored" (Peters and Ceci 1982); Rules based on "empirical research,” for manuscript acceptance are as follows: “Authors should: (1) not pick an important problem, (2) not challenge existing beliefs, (3) not obtain surprising results, (4) not use simple methods, (5) not provide full disclosure, and (6) not write clearly” (Armstrong 1982; see also Harlow 1962).

To sum up, our peer/referee system, the piers of our academic sand castle, can sometimes amount to nothing more than an adversarial confrontation where the defendant is presumed guilty, has no counsel or friend in court by arrangement, cannot face his accusers, and there are no qualifications for judges. At other times, it can be the reverse, and a conspiracy of peers in a field to promote the field (and one another), or a network of master(s) and disciples. Shouldn’t we find out how bad it really is and try to fix it, and try to anticipate what will happen next to pervert it?

Thomson (1984) writes on the American Scientist:

Evidently our way of coping with the flow of minor publications is to ignore them, thereby making them even more trivial. All this work therefore represents the most senseless waste, especially when the occasional gem by an unknown author gets lost in the crowd. In short, nowhere in all of scholarship has the book or shorter contribution (the “paper”) become more thoroughly devased than in science (although apparently other fields are doing their best to catch up).

These are harsh words, and logically it will behooves any author to add another paper to the list in order to make the point, when the principal remedy is for everyone to write fewer and more significant works (physician, help thyself). But “less is more” may be hard to attain in this area. Publish or perish is deeply embedded in the subculture of science (and God forbid that we should have to find some more valid criterion in order to judge promotions).

It is somehow sad to see that many good researchers in efficiency and productivity analysis are so deeply entrenched with playing a game that is holding the field from progressing at the pace it should. While closing with this pessimistic note, we also notice that a new generation of researchers in productivity analysis is coming to the scene. With the old guard retiring from editorial boards, this will make it harder to publish, but maybe this will re-orient the research effort of the latest generation of researcher in productivity and efficiency analysis toward a more fruitful and useful path. We really hope so. Even if anecdotal evidence suggests the opposite.