Measurement of productivity changes for general network production systems with stochastic data

Abstract

Performance evaluation of network production systems has been widely studied in recent Data Envelopment Analysis (DEA) literature where internal relations of sub-units are taken into consideration. Most of prior work assumes network systems to have simple series or parallel structures. Complexities of some practical production processes require development of DEA models for their effective analysis. However; input, intermediate products and/or output data are often stochastic and linked to exogenous random variables in most applications. The current study extends Malmquist Productivity Index (MPI) for investigating productivity changes of general network production units with stochastic data in a DEA framework. The proposed stochastic performance analysis models are then transformed into deterministic equivalent non-linear forms so they could be simplified to deterministic programming with quadratic constraints. Numerical examples including an application to productivity evaluation of branches of a university system are presented to illustrate the applicability of the proposed framework.

1 Introduction

Data envelopment analysis is a powerful mathematical programming tool that is widely used for evaluating relative performance of a group of decision-making units (DMUs) where inputs are consumed to produce outputs. The first DEA model was introduced by Charnes et al [1] and then extended by Banker et al [2] for evaluating the technical efficiency of a set of homogenous DMUs. A considerable number of DEA studies have been rapidly developed since its inception in 1978. DEA methodology is utilized in many different scientific fields as reported in various systematic surveys; see Emrouznejad et al [3] for an extensive listing of 26 DEA “real-world” applications. In most of the traditional DEA models, input and output data sets are assumed to be exact and transformation of input to output takes place within a black-box structure where possible internal structures are completely ignored. Complexity of production processes impose more conditions in performance or productivity evaluation of DMUs in DEA applications to the top five industries of banking, health care, agriculture and farm, transportation and education, Emrouznejad and Yang [4].

Network DEA is considered to be the outcome of consideration of intermediate products along with intermediate exchanges within a decision-making unit and its effects on evaluating performance of the units. A considerable number of studies have been devoted to developing network DEA models in recent literature to address this issue. The review presented by Kao [5, 6] presents details of many related models and applications with regard to network DEA and provides a good overview on this topic.

In production economics, productivity evaluation and determining regress and progress of production systems is an important topic from both theory and application perspectives. Also, productivity analysis for network production system has also been a subject of research. For example, Kao and Hwang [7] analyzed efficiency and productivity analysis in two-stage series systems. Kao [8] introduced a network DEA model to calculate the MPI of a network system. His proposed approach makes it possible to identify sub-processes that improve system performance by providing the relation between system and the Malmquist productivity index. More recently, Kao [9] extended measured MPI for parallel system and also showed that system MPI is a linear combination of the processes MPIs.

Classic DEA and Network DEA models assume that input and output data of decision-making units are known with precision without any variations. Making this assumption is a productivity issue discussion. Information is not often certain in most production data sets. Using stochastic data in place of certain data creates a probability of presentation of models with more adaptability to real world environments. In this sense, in classic literature, DEA is called upon for stochastic data envelopment analysis.

A variety of DEA models have been developed for performance enhancement of DMUs based stochastic data assumptions. Charnes and Cooper’s stochastic programming [10] and Charnes and Cooper [11] chance-constrained programming (CCP) model are most commonly used techniques in this area. In CCP, the proposed stochastic linear programming problem is transformed into an equivalent deterministic non-linear programming problem to deal with stochastic input/output data in a DEA framework. Cooper et al [12, 13] further extended CCP technique and its applications.

As a novel contribution, this work develops a network MPI evaluation in the presence of stochastic data that aims to bridge the gap in previous work in the field of performance and productivity evaluation of general network production systems.

The reminder of this paper is organized as follows. Section 2 is devoted to present a relevant literature review. Section 3 presents a brief review of the two general network DEA models proposed by Lozano [14] and Kazemi Matin and Azizi [15] and states Malmquist index. Section 3 in addition presents the MPI concept for productivity analysis of a typical DMU at two time periods with stochastic data. Section 4 offers an extension of MPI DEA models for performance evaluation of general network systems in presence of stochastic input/output data. Two numerical examples are utilized to explain the proposed approach in section 5, and in section 6 conclusions are provided.

2 Relevant literature

Conventional DEA models emphasize technical efficiency measurement by utilizing radial measures, which are gauged relative to input/output isoquant by seeking the maximal equiproportional reduction/expansion in all input/outputs of the DMU that would be feasible for a given output/output vector. Basic DEA models are based on a set of mild assumptions regarding production possibility sets and production functions. For more reading see Cherchye et al [16] which introduces a DEA method to modify for multi-output efficiency measurement and Cherchye et al [17] for a new application for profit efficiency analysis in the context of multi-output production when prices are observed, among the others.

A particular issue with traditional DEA models is that they are only designed to evaluate whole-unit or black-box productions where inputs are directly transformed into final outputs. There are many practical applications however where the produced intermediate products and sub-processes participate in producing the final outputs. For example, banks could be considered a two-stage production system with profitability and marketability functions for a bank stock share value generation process; Seiford and Zhu [18], Lo and Lu [19]. Network DEA techniques is developed to deal with performance evaluation of production systems with network structure and has attracted a lot of attention in recent DEA literature. Some network system have a two-stage structure which first stage uses inputs for producing outputs and become the inputs to the second stage. Some other network systems have more complex internal structure, which are referred as general network in DEA literature.

Kao [20] and Kao and Hwang [21] introduced two-stage DEA models and a decomposition scheme of technical efficiency into two-stage network models. Kao [22] developed a model with a parallel structure in the production processes. He introduced a method to analyze the multi-step structure in order to calculate efficiency scores. Recently, Kao [22] also studied the productivity discussion on expansion of series and parallel network models.

One of the important challenges faced by researchers in this field is that some network models do not follow the simple series and parallel structure. Lozano [14] formally presented a comprehensive model for systems with network structure and discussed cost and scale efficiency. Kao [20] studied the efficiency analysis of a general multi-stage system where external inputs and internal products are used in order to produce internal outputs and products. Kazemi Matin and Azizi [15] introduced a radial and also a multiplier approach to model general network structures.

Traditional network DEA models assume that the inputs, intermediates and outputs are deterministic. However, it is well-known that data in the real-world problems are often stochastic. It is possible to encounter DEA applications where both of the traditional basic assumptions of simple production structure and exact-data are violated, i.e., we may face with the case of inexact data in a network structure production system. This study aims to tackle both these issues in a unified development fashion. For managers of modern economic entities, taking productivity measurement into account for network production processes is of great necessity because of utilization of more complex structures in production. However, achieving such objective may not be easy with uncertainty in data. Therefore, standard DEA models may not be able to produce a practical and reliable solution. This necessitates implementing stochastic data in productivity evaluation of general network systems and which is the aim of this study.

A very useful tool for productivity analysis in DEA is the Malmquist productivity index (MPI) introduced by Caves et al [23]. MPI calculates the relative efficiency of an observed unit at different periods of time using the technology of a base period. Färe et al [24] combined the technical efficiency measurement with the productivity measurement idea of Caves et al [23] to construct a DEA-based MPI and decomposed it into efficiency changes and technical changes. Walheer [25] presented a new productivity index to minimize cost producers in multi-output settings which takes the form of a cost Malmquist productivity index (CMPI). Walheer and Zhang [26] also used profit Luenberger and Malmquist-Luenberger indexes for multi-activity decision-making units and applied their technique to the star-rated industry for 30 provinces over the period 2005–2015. For a complete survey on MPI and its application see the DEA surveys by Emrouznejad and Yang [4], Färe et al [27].

For modelling uncertainty, CCP provides a useful tool for taking stochastic data into consideration in DEA framework. There is also considerable research conducted on the idea of CCP in DEA; for example see Khodabakhshi and Asgharian [28], Khodabakhshi [29], Khodabakhshi et al [30], Hosseinzadeh Lotfi et al [31], Ross et al [32], and Izadikhah et al [33] among others.

In this paper, a novel MPI DEA approach is proposed that directly treats stochastic input, intermediate and output data for the case of general network production systems in order to make productivity analysis more realistic and practical. To the best of our knowledge, this is the first study which directly aims to deal with MPI for general network DEA models in the presence of stochastic data by using CCP technique.

3 Preliminaries

In this section, DEA models for performance evaluation of general network systems are reviewed and then the MPI for productivity evaluation of an observed unit is presented.

3.1 Network system with general structure

Suppose that for each ${\text{DMU}}_{j} ,\;(j = 1, \ldots ,n),$ in general network systems, inputs $x_{ij} ,\;(i = 1, \ldots ,m)$ are to be used for producing intermediate products $z_{dj} ,\;(d = 1, \ldots ,D),$. Intermediate products are then consumed as inputs of other processes to produce final outputs $y_{rj} ,\;(r = 1, \ldots ,s)$.

Several studies have been presented in recent DEA literature for treating performance evaluation of general network production systems. Two recent approaches are discussed; Lozano [14] and Kazemi Matin and Azizi [15]. Lozano presented a method for general production systems that provide useful details on scale efficiency and allocative efficiency. Kazemi Matin and Azizi presented an approach to modeling comprehensive network structures. Their suggested model has the ability to analyze complex network structures.

Lozano [14] introduced and studied general network models without explicit series or parallel structures by utilizing a direct approach. Assuming constant returns to scale (CRS) technology, convexity and free (strong) disposability of inputs, intermediate products and outputs, Lozano introduced a linear programming model with envelopment form in order to calculate a system efficiency score for the unit under evaluation, DMU_k, as follows:

$$ \begin{aligned} & E_{k} = \hbox{min} \,\theta \\ & s.t\quad \quad \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} x_{ij}^{p} \le \theta x_{ik} ,} } \quad i = 1, \ldots ,m, \\ & \quad \quad \quad \sum\limits_{{p \in P_{O} (r)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} y_{rj}^{p} \ge y_{rk} ,} } \quad r = 1, \ldots ,s, \\ & \quad \quad \quad \sum\limits_{{p \in P^{out} (d)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} z_{dj}^{p} - \sum\limits_{{p \in P^{in} (d)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} z_{dj}^{p} \ge 0,} } } } \quad d = 1, \ldots ,D, \\ & \quad \quad \quad \quad \lambda_{j}^{p} \ge 0,\quad j = 1, \ldots ,n,\quad p = 1, \ldots ,q. \\ \end{aligned} $$

(1)

P_I(i) is the set of processes that consume i^th input, and, $x_{i}^{p}$is the i^th input consumed in p^th process. x_ik is the total consumed amount of initial input of DMU_k. P_O(r) is the set of processes which produce r^th output, and $y_{r}^{p}$ is the r^th output produced in the p^th process. y_rk is the total produced amount of the final output of DMU_k. P^out(d) is the set of processes which produce the d^th intermediate product $z_{d}^{p} \,,\,p \in P^{out} (d)$ is the d^th intermediate product produced in the p^th process. Pⁱⁿ(d) is the set of processes which consume the d^th intermediate product, and $z_{d}^{p} \,,\,p \in P^{in} (d)$is the d^th intermediate product consumed in the p^th process. It is assumed that intermediate products are not used as initial inputs or produced as final outputs.

Kazemi Matin and Azizi [15] model explored a relational model for network systems with general internal relations in CRS case. Using the above notation, their proposed model may be stated in envelopment form as follows:

$$ \begin{aligned} & E_{k} = \hbox{min} \,\theta \\ & s.t\quad \quad \sum\limits_{p = 1}^{q} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} x_{ij}^{p} \le \theta x_{ik}^{p} ,} } \quad i = 1, \ldots ,m \\ & \quad \quad \quad \sum\limits_{p = 1}^{q} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} y_{rj}^{p} - \sum\limits_{p = 1}^{q} {\sum\limits_{j = 1}^{n} {\sum\limits_{c = 1}^{q} {\lambda_{j}^{c} y_{rj}^{Ipc} } } } \ge \sum\limits_{p = 1}^{q} {y_{rk}^{kp} ,} } } \quad r = 1, \ldots ,s \\ & \quad \quad \quad \sum\limits_{c = 1}^{q} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} z_{dj}^{pc} \ge \sum\limits_{c = 1}^{q} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{c} z_{dj}^{pc} } } } } ,\quad d = 1, \ldots ,D,\quad p = 1, \ldots ,q \\ & \quad \quad \quad \quad \lambda_{j}^{p} \ge 0,\quad j = 1, \ldots ,n. \\ \end{aligned} $$

(2)

In Model (2), $x_{ij}^{p}$ is the consumed input of the j^th unit in the p^th process, $z_{dj}^{pc}$ is the d^th intermediate product of the j^th unit which is produced in the p^th process and all or part of it is used in the p^th process. $z_{dj}^{pc}$ is used to denote the d^th intermediate product of the j^th unit which is produced in the c^th process and all or part of it is used in the p^th process. Also note that $y_{rj}^{p}$ shows the r^th output of the j^th unit that is produced by the p^th process. It is assumed here that intermediate products are produced and consumed among the processes. Internal structure of sub-processes is not limited to series and parallel systems in Model (2) and the model can be used for performance evaluation and computing efficiency scores in network production with arbitrary internal relations, Kazemi Matin and Azizi [15].

Note that the above discussed Models (1) and (2) assume deterministic input, intermediate product, and output data for each DMU. However, data often involve uncertainty in many practical applications.

3.2 The Malmquist productivity index

Malmquist productivity change indices are a useful and widely used instrument for evaluating productivity at different time periods in production. Färe and Grosskopf presented an analysis of this index in technology and efficiency variations, Färe et al [24] and Färe and Grosskopf [34]. Yao et al [35] and Aparicio et al [36] introduced the cost-based Malmquist productivity index.

MPI introduced by Caves et al [23] is defined based on the ratio of technical efficiencies of a production unit at two different time periods as a measure of change in performance. The same DMUs at two different times and relative to two different production technologies are evaluated to compute MPI. This index helps to identify regress or progress of any observed unit in time.

MPI for the DMU_k as the unit under evaluation is shown by $M_{k}$. To calculate $M_{k}$, the following ratio of efficiencies at times t and t+1 need to be obtained:

$$ M_{k} ((\mathop {\mathbf{x}}\nolimits^{t} ,\mathop {\mathbf{y}}\nolimits^{t} ),\mathop {({\mathbf{x}}}\nolimits^{t + 1} ,\mathop {\mathbf{y}}\nolimits^{t + 1} )) = \frac{{\mathop E\nolimits_{k}^{t + 1} (\mathop {\mathbf{x}}\nolimits^{t + 1} ,\mathop {\mathbf{y}}\nolimits^{t + 1} )}}{{\mathop E\nolimits_{k}^{t} (\mathop {\mathbf{x}}\nolimits^{t} ,\mathop {\mathbf{y}}\nolimits^{t} )}}\left[ {\frac{{\mathop E\nolimits_{k}^{t} (\mathop {\mathbf{x}}\nolimits^{t + 1} ,\mathop {\mathbf{y}}\nolimits^{t + 1} )}}{{\mathop E\nolimits_{k}^{t + 1} (\mathop {\mathbf{x}}\nolimits^{t + 1} ,\mathop {\mathbf{y}}\nolimits^{t + 1} )}} \times \frac{{\mathop E\nolimits_{k}^{t} (\mathop {\mathbf{x}}\nolimits^{t} ,\mathop {\mathbf{y}}\nolimits^{t} )}}{{\mathop E\nolimits_{k}^{t + 1} (\mathop {\mathbf{x}}\nolimits^{t} ,\mathop {\mathbf{y}}\nolimits^{t} )}}} \right]^{{\frac{1}{2}}} $$

(3)

where, $M_{k} < 1$ indicates deterioration (regress) in the total productivity factor of DMU_k for the time interval t to t+1; $M_{k} > 1$ and $M_{k} = 1$ indicate the status progress and quo (indifference) in the productivity factor, respectively. The ratio outside the brackets, measures the technical efficiency change between the two time periods. The geometric mean of the two ratios inside the bracket captures the technological change (or frontier shift in technology) between the two time periods.

Note that although calculating MPI in (4) needs deterministic input and output data for each DMU at each time period, data often involve uncertainty in practical situations.

4 The Malmquist productivity index for general network production systems with stochastic data

As discussed before in measuring production unit productivity, data may involve stochastic variations and stochastic programming is one of the main approaches in handling uncertainty in many practical applications of DEA, Charnes and Cooper [11]. The remainder of this study attempts to evaluate production system productivity in the presence of a comprehensive network structure by considering stochastic data.

To do so, the stochastic version of MPI based on general network DEA Models (1) and (2) is extended. For formal presentation of the models, it is assumed that inputs, intermediate and final output of any observation are random vectors at two time periods t and t+1 as follows:

$$ \begin{aligned} & \tilde{\varvec{x}}_{j}^{t} = \left( {\tilde{x}_{1j}^{t} , \ldots ,\tilde{x}_{mj}^{t} } \right), \tilde{\varvec{z}}_{j}^{t} = \left( {\tilde{z}_{1j}^{t} , \ldots ,\tilde{z}_{dj}^{t} } \right), \tilde{\varvec{y}}_{j}^{t} = \left( {\tilde{y}_{1j}^{t} , \ldots ,y_{sj}^{t} } \right) \\ & \tilde{\varvec{x}}_{j}^{t + 1} = \left( {\tilde{x}_{1j}^{t + 1} , \ldots ,\tilde{x}_{mj}^{t + 1} } \right), \tilde{\varvec{z}}_{j}^{t + 1} = \left( {\tilde{z}_{1j}^{t + 1} , \ldots ,\tilde{z}_{dj}^{t + 1} } \right), \tilde{\varvec{y}}_{j}^{t + 1} = \left( {\tilde{y}_{1j}^{t + 1} , \ldots ,y_{sj}^{t + 1} } \right) \\ \end{aligned} $$

All inputs, intermediate, and outputs values are assumed to be jointly distributed normally. Choices of multivariate normal distributions are less restrictive than might at first appear to be the case. Transformations are available for bringing other types of distributions into approximately normal form—as was done in Charnes et al [10], for instance, when it was found necessary to treat highly skewed distributions with log-normal approximations [13].

When stochastic data is available, by assuming $l,f \in \{ t,t + 1\}$ for calculating MPI, the Lozano’s general Model (1) could be arranged as the following chance-constrained optimization model by considering $s_{i} \ge 0$ and $\,s_{r} \ge 0$ to represent slack variables:

$$ \begin{aligned} & (\tilde{E}_{k}^{f} )^{l} = \hbox{min}\, \theta \\ & s.t\quad \quad \Pr \left\{ {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} + s_{i} = \theta (\tilde{x}_{ik} )^{f} } } } \right\} \ge 1 - \alpha ,\quad i = 1, \ldots ,m \\ & \quad \quad \quad \Pr \left\{ {\sum\limits_{{p \in P_{O} (r)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{y}_{rj}^{p} )^{l} - s_{r} = (\tilde{y}_{rk} )^{f} } } } \right\} \ge 1 - \alpha ,\quad r = 1, \ldots ,s \\ & \quad \quad \quad \Pr \left\{ {\sum\limits_{{p \in P^{out} (d)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{z}_{dj}^{p} )^{l} - \sum\limits_{{p \in P^{in} (d)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{z}_{dj}^{p} )^{l} \ge 0} } } } } \right\} \ge 1 - \alpha ,\quad d = 1, \ldots ,D \\ & \quad \quad \quad \quad \lambda_{j}^{p} ,\;s_{i} ,\;s_{r} \ge 0,\quad j = 1, \ldots ,n,\quad p = 1, \ldots ,q. \\ \end{aligned} $$

(4)

Here, Pr indicates “probability” and “~” presents the data as random variables with a normal distribution and $\alpha \in \left( {0,1} \right]$indicates a predefined and reasonable minute size of a type one error; i.e., an allowable chance of failing to satisfy the constraints.

Definition

$DMU_{k}$ is stochastically efficient in model (4) if and only if the following conditions are satisfied; [12]:

• (i) $\theta_{k}^{*} = 1,$

• (ii) Slack variables are zero in all alternative optimal solutions.

$DMU_{k}$ is called stochastically inefficient if it does not fulfill the conditions of this definition. Following CCP approach, it is assumed that all inputs, intermediate products and outputs are independent random variables with normal distribution. For stochastic data and by applying cumulative distribution function denoted by $\varPhi ,$ it is possible to convert the chance constrained Model (4) into its corresponding deterministic equivalent model as follows (see Appendix A for more details):

$$ \begin{aligned} & (\tilde{E}_{k}^{f} )^{l} = \hbox{min}\, \theta \\ & s.t\quad \quad \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\left( {\lambda_{j}^{p} (x_{ij}^{p} )^{l} } \right) - \varPhi^{ - 1} (\alpha )(\omega_{i}^{l} ) \le \theta (x_{ik} )^{f} ,} } \quad i = 1, \ldots ,m \\ & \quad \quad \quad \sum\limits_{{p \in P_{O} (r)}} {\sum\limits_{j = 1}^{n} {\left( {\lambda_{j}^{p} (y_{rj}^{p} )^{l} } \right) + \varPhi^{ - 1} (\alpha )(\omega_{r}^{l} ) \ge (y_{rk} )^{f} ,} } \quad r = 1, \ldots ,s \\ & \quad \quad \quad \sum\limits_{{p \in P^{out} (d)}} {\sum\limits_{j = 1}^{n} {\left( {\lambda_{j}^{p} (z_{dj}^{p} )^{l} } \right) - \sum\limits_{{p \in P^{in} (d)}} {\sum\limits_{j = 1}^{n} {\left( {\lambda_{j}^{p} (z_{dj}^{p} )^{l} } \right) + \varPhi^{ - 1} (\alpha )(\omega_{d}^{OI} )^{l} \ge 0,} } } } \quad d = 1, \ldots ,D \\ & \quad \quad \quad \quad \lambda_{j}^{p} \ge 0,\quad j = 1, \ldots ,n,\quad p = 1, \ldots ,q. \\ \end{aligned} $$

(5)

where, $f,l \in \{ t,t + 1\}$, $\varPhi^{ - 1} (\alpha )$ is the inverse of cumulative distribution function. $\omega_{i}^{l} ,\omega_{r}^{l}$ and $(\omega_{d}^{OI} )^{l}$ refer to variance and covariance of inputs, outputs and intermediate products. They are respectively calculated as follows.

$$\begin{aligned} & \forall i:\quad (\omega _{i} ^{l} )^{2} = \left\{ \begin{array}{*{20}l} \sum\limits_{{p \in P_{I} (i)}} \sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{n} ((\lambda _{j} ^{p} )^{2} Var(\tilde{x}_{{ij}}^{p} )^{l} ) + (\lambda _{k} ^{p} - \theta )^{2} Var(\tilde{x}_{{ik}}^{p} )^{f} \quad {f = l} \hfill \\ \sum\limits_{{p \in P_{I} (i)}} \sum\limits_{{j = 1}}^{n} ((\lambda _{j} ^{p} )^{2} Var(\tilde{x}_{{ij}}^{p} )^{l} ) + (\theta )^{2} Var(\tilde{x}_{{ik}}^{p} )^{f} , \quad {f \ne l} \hfill \\ \end{array} \right. \\ & \forall r:\quad (\omega _{r} ^{l} )^{2} = \left\{ \begin{array}{*{20}l} \sum\limits_{{p \in P_{O} (r)}} \sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{n} ((\lambda _{j} ^{p} )^{2} Var(\tilde{y}_{{rj}}^{p} )^{l} ) + (\lambda _{k} ^{p} - 1)^{2} Var(\tilde{y}_{{rk}}^{p} )^{f} , \quad {f = l} \hfill \\ \sum\limits_{{p \in P_{O} (r)}} \sum\limits_{{j = 1}}^{n} ((\lambda _{j} ^{p} )^{2} Var(\tilde{y}_{{rj}}^{p} )^{l} ) + Var(\tilde{y}_{{rk}}^{p} )^{f} , \quad {f \ne l} \hfill \\ \end{array} \right. \\ & \forall d,\forall p,\forall c:\quad ((\omega _{d} ^{{OI}} )^{l} )^{2} = \sum\limits_{{p \in P^{{out}} (d)}} \sum\limits_{{j = 1}}^{n} (\lambda _{j} ^{p} )^{2} Var(\tilde{z}_{{dj}} ^{p} )^{l} - \sum\limits_{{p \in P^{{in}} (d)}} \sum\limits_{{j = 1}}^{n} (\lambda _{j} ^{p} )^{2} Var(\tilde{z}_{{dj}} ^{p} )^{l} , . \\ \end{aligned} $$

Model (5) is a non-linear optimization model due to its quadratic constraints. In order to calculate stochastic MPI, $\left( {\hat{E}_{k}^{f} } \right)^{l}$ for $f,l \in \{ t,t + 1\}$ are needed. They indicate stochastic efficiency of system for $DMU_{k}$ at time periods t and t+1 with respect to two different technologies associated with time periods t and t+1.

Note that for simplicity of calculations, all inputs, intermediate products and outputs are assumed to be independent, so the corresponding covariance values are zero in the above calculation of variances and the constraints take quadratic form in term of $\lambda$’s. Note that $\varPhi^{ - 1} \left( {0.5} \right) = 0$ and the same deterministic Model (1) is achieved.

Remark

For $\alpha > 0.5$ when $l = f \in \left\{ {t,t + 1} \right\}$, it is possible to obtain negative efficiency scores in Model (6), i.e., $\left( {\hat{E}_{k}^{t} } \right)^{t} < 0$ or $\left( {\hat{E}_{k}^{t + 1} } \right)^{t + 1} < 0$. Therefore, the stochastic efficiency scores of $DMU_{k}$ in the two time periods are calculated under the condition $\alpha \in \left( {0,5} \right)$.

To calculate the stochastic Malmquist productivity index of $DMU_{k}$ using the Lozano’s general network DEA model, relation (3) or its following equivalent form may be utilized by applying stochastic efficiency scores $\left( {\hat{E}_{k}^{f} } \right)^{l}$ at periods t and t+1:

$$ \tilde{M}_{k}^{S} \left( {(\mathop {\mathbf{x}}\nolimits^{t} ,\mathop {\mathbf{y}}\nolimits^{t} ),\mathop {({\mathbf{x}}}\nolimits^{t + 1} ,\mathop {\mathbf{y}}\nolimits^{t + 1} )} \right) = \left[ {\frac{{\mathop {\tilde{E}}\nolimits_{k}^{t} (\mathop {\mathbf{x}}\nolimits^{t + 1} ,\mathop {\mathbf{y}}\nolimits^{t + 1} )}}{{\mathop {\tilde{E}}\nolimits_{k}^{t} (\mathop {\mathbf{x}}\nolimits^{t} ,\mathop {\mathbf{y}}\nolimits^{t} )}} \times \frac{{\mathop {\tilde{E}}\nolimits_{k}^{t + 1} (\mathop {\mathbf{x}}\nolimits^{t + 1} ,\mathop {\mathbf{y}}\nolimits^{t + 1} )}}{{\mathop {\tilde{E}}\nolimits_{k}^{t + 1} (\mathop {\mathbf{x}}\nolimits^{t} ,\mathop {\mathbf{y}}\nolimits^{t} )}}} \right]^{{\frac{1}{2}}} $$

(6)

As before, $\tilde{M}_{k}^{S} < 1$indicates stochastic deterioration in productivity factor for the time period t to t+1, $\tilde{M}_{k}^{S} > 1$ demonstartes stochastically progress in productivity factor and $\tilde{M}_{k}^{S} = 1$ illustrates the quo case.

MPI may also be applied as an alternative approach for evaluating productivity factor with stochastic data based on Kazemi Matin and Azizi’s proposed model for performance evaluation of general network systems. Results are then used to make a comparison between the two alternatives general network models.

Again, following the CCP approach [13], under the same assumptions as above for stochastic data, and using the same significant level $\alpha$; the chance constrained version of Model (2) could be represented as the following deterministic non-linear optimization form:

$$ \begin{aligned} & (\tilde{E}_{k}^{f} )^{l} = \hbox{min}\, \theta \\ & s.t\quad \quad \sum\limits_{p = 1}^{q} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} - \varPhi^{ - 1} (\alpha )(\omega_{i} )^{l} \le \theta (x_{ik}^{p} )^{f} ,} } \quad i = 1, \ldots ,m \\ & \quad \quad \quad \sum\limits_{p = 1}^{q} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (y_{rj}^{p} )^{l} - \sum\limits_{p = 1}^{q} {\sum\limits_{j = 1}^{n} {\sum\limits_{c = 1}^{q} {\lambda_{j}^{c} (y_{rj}^{Ipc} )^{l} } } } + \varPhi^{ - 1} (\alpha )(\omega_{r} )^{l} \ge \sum\limits_{p = 1}^{q} {(y_{rk}^{p} )^{f} ,} } } \quad r = 1, \ldots ,s \\ & \quad \quad \quad \sum\limits_{c = 1}^{q} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (z_{dj}^{pc} )^{l} - \sum\limits_{c = 1}^{q} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{c} (z_{dj}^{pc} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{d}^{OI} )^{l} \ge 0} } } } ,\quad d = 1, \ldots ,D,\quad p = 1, \ldots ,q \\ & \quad \quad \quad \quad \lambda_{j}^{p} \ge 0,\quad j = 1, \ldots ,n. \\ \end{aligned} $$

(7)

where variances are calculated as follows:

$$ \begin{aligned} & \forall i:\quad (\omega_{i} )^{2} = \left\{ {\begin{array}{*{20}l} {\sum\limits_{p = 1}^{q} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{n} {((\lambda_{j}^{p} )^{2} Var(\tilde{x}_{ij}^{p} )) + (\lambda_{k}^{p} - \theta )^{2} Va(\tilde{x}_{ik}^{p} )} ,} } \quad {f = l} \hfill \\ {\sum\limits_{p = 1}^{q} {\sum\limits_{j = 1}^{n} {((\lambda_{j}^{p} )^{2} Var(\tilde{x}_{ij}^{p} )) + \theta^{2} Va(\tilde{x}_{ik}^{p} )} ,} } \quad {f \ne l} \hfill \\ \end{array} } \right. \\ & \forall r:\quad (\omega_{r} )^{2} = \left\{ {\begin{array}{*{20}l} {\sum\limits_{p = 1}^{q} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{n} {((\lambda_{j}^{p} )^{2} Var(\tilde{y}_{rj}^{p} ) - \sum\limits_{p = 1}^{q} {\sum\limits_{c = 1}^{q} {(\lambda_{j}^{c} )^{2} Var(\tilde{y}_{rj}^{Ipc} )) + \sum\limits_{p = 1}^{q} {(\lambda_{k}^{p} - 1)^{2} Va(\tilde{y}_{rk}^{kp} )} } } } ,} } \quad {f = l} \hfill \\ {\sum\limits_{p = 1}^{q} {\sum\limits_{j = 1}^{n} {((\lambda_{j}^{p} )^{2} Var(\tilde{y}_{rj}^{p} ) - \sum\limits_{p = 1}^{q} {\sum\limits_{c = 1}^{q} {(\lambda_{j}^{c} )^{2} Var(\tilde{y}_{rj}^{Ipc} )) + \sum\limits_{p = 1}^{q} {Va(\tilde{y}_{rk}^{kp} )} } } } ,} } \quad {f \ne l} \hfill \\ \end{array} } \right. \\ & \forall d,\forall p,\forall c:\quad (\omega_{d}^{OI} )^{2} = \sum\limits_{c = 1}^{q} {\sum\limits_{j = 1}^{n} {(\lambda_{j}^{p} )^{2} Var(\tilde{z}_{dj}^{pc} ) - \sum\limits_{c = 1}^{q} {\sum\limits_{j = 1}^{n} {(\lambda_{j}^{c} )^{2} Var(\tilde{z}_{dj}^{pc} )} } } } . \\ \end{aligned} $$

Covariance values become zero in the calculation of variances by assuming independent input, intermediate product, and output data. As the results of the above, Model (7) relaxes to an optimization problem with linear objective function and quadratic constraints. The optimal value of $\left( {\hat{E}_{k}^{f} } \right)^{l}$ indicates system stochastic efficiency score of the unit under evaluation, $DMU_{k}$, at time periods t and t+1. Then Eq. (6) is used to compute stochastic MPI productivity factor.

5 Illustrative examples

Two illustrative examples are considered in this section to demonstrate the technology and its novelty. The first example is based on a simple multi-stage series production system and the second one discusses productivity evaluation of university departments in academic year time periods 2015 and 2016.

5.1 Example 1: MPI evaluation for a simple three-stage production system

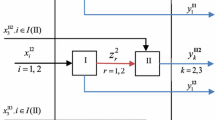
In this example, we assume three-stage network model and we write Lozano’s general model and Kazemi Matin and Azizi’s general model for evaluating this system. Assume eight production units in a typical three-stage network structure as depicted in figure 1. Each production unit includes three inputs ($\varvec{x}$), four intermediate products ($\varvec{z}$) and three final outputs ($\varvec{y}$). It is also assumed that all input/intermediate/output variables for the two time periods t and t+1 follow normal distribution with known mean and variance as given in tables 1 and 2.

Figure 1

Network structure for the three-stage series network.

Table 1 Random average data for example 1.

Table 2 Variance of data for example 1.

By assuming deterministic data and using the average values in table 1, deterministic system efficiency scores could be calculated by applying both Models (1) and (2). Using Eq. (3) then, values for deterministic Malmquist productivity index of the system are then computed. For illustration purposes, consider the associated optimization models for a typical DMU 1 in both mentioned network models.

• Lozano’s general model:

For the provided three-stage series network structure, the deterministic and stochastic version of Lozano’s general model could be represented as in expanded forms as follows. For an illustration purpose, $\alpha = 0.05$ is just considered in this example. Hence Model (5) is calculated by using $\varPhi^{ - 1} (0.05) = 1.645$. Note that DMUk is the under evaluation unit.

Model (1) for Example 1

Model (5) for Example 1

$\begin{aligned} & (E_{k}^{f} )^{l} = \hbox{min}\, \theta \\ & s.t\quad \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{1} (x_{1j}^{1} )^{l} } \right) \le \theta (x_{1k}^{1} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{1} (x_{2j}^{1} )^{l} } \right) \le \theta (x_{2k}^{1} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{1} (x_{3j}^{1} )^{l} } \right) \le \theta (x_{3k}^{1} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (y_{1j}^{3} )^{l} \ge (y_{1k}^{3} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (y_{2j}^{3} )^{l} \ge (y_{2k}^{3} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (y_{3j}^{3} )^{l} \ge (y_{3k}^{3} )^{f} } , \\ & \quad \quad \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{1} (z_{1j}^{1} )^{l} + \lambda_{j}^{2} (z_{1j}^{2} )^{l} } \right) - \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{2} (z_{1j}^{1} )^{l} + \lambda_{j}^{3} (z_{1j}^{2} )^{l} } \right) \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{1} (z_{2j}^{1} )^{l} + \lambda_{j}^{2} (z_{2j}^{2} )^{l} } \right) - \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{2} (z_{2j}^{1} )^{l} + \lambda_{j}^{3} (z_{2j}^{2} )^{l} } \right) \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{1} (z_{3j}^{1} )^{l} + \lambda_{j}^{2} (z_{3j}^{2} )^{l} } \right) - \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{2} (z_{3j}^{1} )^{l} + \lambda_{j}^{3} (z_{3j}^{2} )^{l} } \right) \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\,\left( {\lambda_{j}^{1} (z_{4j}^{1} )^{l} + \lambda_{j}^{2} (z_{4j}^{2} )^{l} } \right) - \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{2} (z_{4j}^{1} )^{l} + \lambda_{j}^{3} (z_{4j}^{2} )^{l} } \right) \ge 0,} } \\ & \quad \quad \quad \lambda_{j}^{1} ,\,\lambda_{j}^{2} ,\,\lambda_{j}^{3} \ge 0,\quad j = 1, \ldots ,8. \\ \end{aligned}$

$\begin{aligned} & (\tilde{E}_{k}^{f} )^{l} = \hbox{min}\, \theta \\ & s.t\quad \sum\limits_{\begin{subarray}{l} j = 1 \\ \end{subarray} }^{8} {\left( {\lambda_{j}^{1} (x_{1j}^{1} )^{l} } \right) - 1.645(\omega_{1}^{I} ) \le \theta (x_{1k}^{1} )^{f} ,} \\ & \quad \quad \sum\limits_{\begin{subarray}{l} j = 1 \\ \end{subarray} }^{8} {\left( {\lambda_{j}^{1} (x_{2j}^{1} )^{l} } \right) - 1.645(\omega_{2}^{I} ) \le \theta (x_{2k}^{1} )^{f} ,} \\ & \quad \quad \sum\limits_{\begin{subarray}{l} j = 1 \\ \end{subarray} }^{8} {\left( {\lambda_{j}^{1} (x_{3j}^{1} )^{l} } \right) - 1.645(\omega_{3}^{I} ) \le \theta (x_{3k}^{1} )^{f} ,} \\ & \quad \quad \sum\limits_{\begin{subarray}{l} j = 1 \\ \end{subarray} }^{8} {\lambda_{j}^{3} (y_{1j}^{3} )^{l} + 1.645(\omega_{1}^{O} ) \ge (y_{1k}^{3} )^{f} ,} \, \\ & \quad \quad \sum\limits_{\begin{subarray}{l} j = 1 \\ \end{subarray} }^{8} {\lambda_{j}^{3} (y_{2j}^{3} )^{l} + 1.645(\omega_{2}^{O} ) \ge (y_{2k}^{3} )^{f} ,} \\ & \quad \quad \sum\limits_{\begin{subarray}{l} j = 1 \\ \end{subarray} }^{8} {\lambda_{j}^{3} (y_{3j}^{3} )^{l} + 1.645(\omega_{3}^{O} ) \ge (y_{3k}^{3} )^{f} } , \\ & \quad \quad \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{1} (z_{1j}^{1} )^{l} + \lambda_{j}^{2} (z_{1j}^{2} )^{l} } \right) - \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{2} (z_{1j}^{1} )^{l} + \lambda_{j}^{3} (z_{1j}^{2} )^{l} } \right) + 1.645(\omega_{1}^{OI} ) \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{1} (z_{2j}^{1} )^{l} + \lambda_{j}^{2} (z_{2j}^{2} )^{l} } \right) - \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{2} (z_{2j}^{1} )^{l} + \lambda_{j}^{3} (z_{2j}^{2} )^{l} } \right) + 1.645(\omega_{2}^{OI} ) \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{1} (z_{3j}^{1} )^{l} + \lambda_{j}^{2} (z_{3j}^{2} )^{l} } \right) - \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{2} (z_{3j}^{1} )^{l} + \lambda_{j}^{3} (z_{3j}^{2} )^{l} } \right) + 1.645(\omega_{3}^{OI} ) \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{1} (z_{4j}^{1} )^{l} + \lambda_{j}^{2} (z_{4j}^{2} )^{l} } \right) - \sum\limits_{j = 1}^{8} {\left( {\lambda_{j}^{2} (z_{4j}^{1} )^{l} + \lambda_{j}^{3} (z_{4j}^{2} )^{l} } \right) + 1.645(\omega_{4}^{OI} ) \ge 0,} } \\ & \quad \quad \quad \lambda_{j}^{1} ,\lambda_{j}^{2} ,\lambda_{j}^{3} \ge 0,\quad j = 1, \ldots ,8. \\ \end{aligned}$

where, for the stochastic case;

$$ \begin{aligned} &(\omega_{i}^{l} )^{2} = \left\{ \begin{array}{l} \sum\limits_{j = 2}^{8} {((\lambda_{j}^{1} )^{2} Var(\tilde{x}_{ij}^{1} )^{l} ) + (\lambda_{1}^{1} - \theta )^{2} Va(\tilde{x}_{i1}^{1} )^{f} } ,\,\,i = 1,2,3\,\,\& \,\,f = l \hfill \\ \sum\limits_{j = 1}^{8} {((\lambda_{j}^{1} )^{2} Var(\tilde{x}_{ij}^{1} )^{l} ) + \theta^{2} Va(\tilde{x}_{i1}^{1} )^{f} } ,\,\,i = 1,2,3\,\,\& \,f \ne l\, \hfill \\ \end{array} \right. \hfill \\ &(\omega_{r}^{O} )^{2} = \left\{ \begin{array}{l} \sum\limits_{j = 2}^{8} {((\lambda_{j}^{3} )^{2} Var(\tilde{y}_{rj}^{3} )^{l} ) + (\lambda_{1}^{3} - 1)^{2} Va(\tilde{y}_{r1}^{3} )^{f} } ,\,\,r = 1,2,3\,\,\& \,\,f = l \hfill \\ \sum\limits_{j = 1}^{8} {((\lambda_{j}^{3} )^{2} Var(\tilde{y}_{rj}^{3} )^{l} ) + Va(\tilde{y}_{r1}^{3} )^{f} } ,\,\,r = 1,2,3\,\,\& \,\,f \ne l \hfill \\ \end{array} \right. \hfill \\ &(\omega_{d}^{OI} )^{2} = \sum\limits_{j = 1}^{8} {\,\left( {(\lambda_{j}^{1} - \lambda_{j}^{2} )^{2} Var(\tilde{z}_{dj}^{1} )^{l} + (\lambda_{j}^{2} - \lambda_{j}^{3} )^{2} Var(\tilde{z}_{dj}^{2} )^{l} } \right)\,\,,} \,\,d = 1,2,3,4. \hfill \\ \end{aligned} $$

A computational issue arises in solving the above optimization models for calculating efficiency scores for both time periods. As it is shown in the first two columns of table 3, these models fail to productively evaluate all units due to producing zero values for efficiency scores $\left( {E_{k}^{t} } \right)^{t} , \left( {E_{k}^{t + 1} } \right)^{t + 1} , \left( {\tilde{E}_{k}^{t} } \right)^{t}$ and $\left( {\tilde{E}_{k}^{t + 1} } \right)^{t + 1}$. This makes MPI ill-defined with both deterministic and stochastic data when using the above mentioned model in dealing with general network case.

Table 3 Deterministic and stochastic Malmquist indexes in two approaches.

The next alternative approach is considered now.

• Kazemi Matin and Azizi’s general model:

Using the same setting, the following optimization models are to be solved for any observed DMU:

Model (2) for example 1

Model (7) for example 1

$\begin{aligned} & (E_{k}^{f} )^{l} = \hbox{min}\, \theta \\ & s.t\quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{1} (x_{1j}^{1} )^{l} \le \theta (x_{1k}^{1} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{1} (x_{2j}^{1} )^{l} \le \theta (x_{2k}^{1} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{1} (x_{3j}^{1} )^{l} \le \theta (x_{3k}^{1} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (y_{1j}^{3} )^{l} \ge (y_{1k}^{3} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (y_{2j}^{3} )^{l} \ge (y_{2k}^{3} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (y_{3j}^{3} )^{l} \ge (y_{3k}^{3} )^{f} } , \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{1} (z_{1j}^{1} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{2} (z_{1j}^{1} )^{l} \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{1} (z_{2j}^{1} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{2} (z_{2j}^{1} )^{l} \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{1} (z_{3j}^{1} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{2} (z_{3j}^{1} )^{l} \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{1} (z_{4j}^{1} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{2} (z_{4j}^{1} )^{l} \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{2} (z_{1j}^{2} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (z_{1j}^{2} )^{l} \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{2} (z_{2j}^{2} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (z_{2j}^{2} )^{l} \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{2} (z_{3j}^{2} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (z_{3j}^{2} )^{l} \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\,\lambda_{j}^{2} (z_{4j}^{2} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (z_{4j}^{2} )^{l} \ge 0,} } \\ & \quad \quad \quad \lambda_{j}^{1} ,\,\lambda_{j}^{2} ,\,\lambda_{j}^{3} \ge 0,\quad j = 1, \ldots ,8. \\ \end{aligned}$

$\begin{aligned} & (\tilde{E}_{k}^{f} )^{l} = \hbox{min}\, \theta \\ & s.t\quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{1} (x_{1j}^{1} )^{l} - \varPhi^{ - 1} (\alpha )(\omega_{1}^{I} ) \le \theta (x_{1k}^{1} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{1} (x_{2j}^{1} )^{l} - \varPhi^{ - 1} (\alpha )(\omega_{2}^{I} ) \le \theta (x_{2k}^{1} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{1} (x_{3j}^{1} )^{l} - \varPhi^{ - 1} (\alpha )(\omega_{3}^{I} ) \le \theta (x_{3k}^{1} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (y_{1j}^{3} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{1}^{O} ) \ge (y_{1k}^{3} )^{f} ,} & \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (y_{2j}^{3} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{2}^{O} ) \ge (y_{2k}^{3} )^{f} ,} \\ & \quad \quad \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (y_{3j}^{3} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{3}^{O} ) \ge (y_{3k}^{3} )^{f} } , \\ & \quad \quad \sum\limits_{j = 1}^{8} {\,\lambda_{j}^{1} (z_{1j}^{1} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{2} (z_{1j}^{1} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{1}^{OI} ) \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\,\lambda_{j}^{1} (z_{2j}^{1} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{2} (z_{2j}^{1} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{2}^{OI} ) \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\,\lambda_{j}^{1} (z_{3j}^{1} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{2} (z_{3j}^{1} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{3}^{OI} ) \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\,\lambda_{j}^{1} (z_{4j}^{1} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{2} (z_{4j}^{1} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{4}^{OI} ) \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\,\lambda_{j}^{2} (z_{1j}^{2} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (z_{1j}^{2} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{1}^{OI} ) \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\,\lambda_{j}^{2} (z_{2j}^{2} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (z_{2j}^{2} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{2}^{OI} ) \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\,\lambda_{j}^{2} (z_{3j}^{2} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (z_{3j}^{2} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{3}^{OI} ) \ge 0,} } \\ & \quad \quad \sum\limits_{j = 1}^{8} {\,\lambda_{j}^{2} (z_{4j}^{2} )^{l} - \sum\limits_{j = 1}^{8} {\lambda_{j}^{3} (z_{4j}^{2} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{4}^{OI} ) \ge 0,} } \\ & \quad \quad \quad \lambda_{j}^{1} ,\lambda_{j}^{2} ,\lambda_{j}^{3} \ge 0,\quad j = 1, \ldots ,8. \\ \end{aligned}$

Where, for the stochastic case variances are calculated as follows:

$$ \begin{aligned} (\omega _{i} ^{l} )^{2} & = \left\{ {\begin{array}{*{20}l} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{8} {((\lambda _{j} ^{1} )^{2} Var(\tilde{x}_{{ij}}^{1} )^{l} ) + (\lambda _{k} ^{1} - \theta )^{2} Var(\tilde{x}_{{ik}}^{1} )^{f} } ,\quad i = 1,2,3\,\,\& \,\,f = l} \hfill \\ {\sum\limits_{{j = 1}}^{8} {((\lambda _{j} ^{1} )^{2} Var(\tilde{x}_{{ij}}^{1} )^{l} ) + \theta ^{2} Var(\tilde{x}_{{ik}}^{1} )^{f} } ,\quad i = 1,2,3\,\,\& \,\,f \ne l} \hfill \\ \end{array} } \right. \\ (\omega _{r} ^{l} )^{2} & = \left\{ {\begin{array}{*{20}l} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{8} {((\lambda _{j} ^{3} )^{2} Var(\tilde{y}_{{rj}}^{3} )^{l} ) + (\lambda _{k} ^{3} - 1)^{2} Var(\tilde{y}_{{rk}}^{3} )^{f} } ,\quad r = 1,2,3\,\,\& \,\,f = l} \hfill \\ {\sum\limits_{{j = 1}}^{8} {((\lambda _{j} ^{3} )^{2} Var(\tilde{y}_{{rj}}^{3} )^{l} ) + Var(\tilde{y}_{{rk}}^{3} )^{f} ,\quad r = 1,2,3\,\,\& \,\,f \ne l} } \hfill \\ \end{array} } \right. \\ (\omega _{d} ^{{OI}} )^{2} & = \sum\limits_{{j = 1}}^{8} {\,(\lambda _{j} ^{1} - \lambda _{j} ^{2} )^{2} Var(\tilde{z}_{{dj}} ^{1} )^{l} \,\,,} \,d = 1,2,3,4.\, \\ (\omega _{d} ^{{OI}} )^{2} & = \sum\limits_{{j = 1}}^{8} {\,(\lambda _{j} ^{2} - \lambda _{j} ^{3} )^{2} Var(\tilde{z}_{{2j}} ^{2} )^{l} \,\,,} \,d = 1,2,3,4.\, \\ \end{aligned} $$

As the results in table 3 indicate, these models successfully generate MPI values. Note that for the case of stochastic data, in order to calculate the efficiency scores of a production system in the depicted three-stage network structure, average values and variance data are used in both approaches. Covariance values are taken to be zero for calculation of variances. The value of $\alpha = 0.05$ is used which indicates a five percentage points of unsatisfied constraints of the Models (1) and (2). The associated Models (5) and (7) are used for computing stochastic efficiency scores. The corresponding computed MPIs are reported in the last two columns of table 3.

In the case of stochastic data, the computed efficiency scores for DMU1 are as follows: $(\tilde{E}_{1}^{t} )^{t} = 0.188$, $(\tilde{E}_{1}^{t} )^{t + 1} = 0.103$, $(\tilde{E}_{1}^{t + 1} )^{t} = 0.010$ and $(\tilde{E}_{1}^{t + 1} )^{t + 1} = 0.012$ and as a result $\tilde{M}_{1}^{S} \left( {(\mathop {\mathbf{x}}\nolimits^{t} ,\mathop {\mathbf{y}}\nolimits^{t} ),\mathop {({\mathbf{x}}}\nolimits^{t + 1} ,\mathop {\mathbf{y}}\nolimits^{t + 1} )} \right) = \left( {\frac{0.104}{0.188} \times \frac{0.012}{0.010}} \right)^{{\frac{1}{2}}} = 0.81.$

There are two noteworthy items in this example:

• (i) The proposed network DEA Model (1) may be unable to cover all general network production systems in efficiency and productivity analysis.

• (ii) It is possible to get a different MPI status when enhancing standard deterministic efficiency models by stochastic optimization models.

Results indicate that progress MPI status for almost all units turns to regression in stochastic MPI by allowing only five percentages of unsatisfied constraints. Here $\alpha$, as a predetermined acceptable risk, may additionally be utilized for planning purposes. We found that in this example, similar results are obtained when different values for α are utilized for $0 < \alpha < 0.2$. Therefore, it seems values of stochastic MPI offer a better and more accurate prediction of productivity status of production systems in this sample.

5.2 Example 2: An empirical application on education institutes for MPI evaluation with stochastic data

Assessing efficiency and analyzing productivity is an important issue in higher education institutions and universities. In recent decades, DEA techniques have been widely used in educational applications by taking into consideration educational institutions, universities, faculties, departments or programmes as DMUs. Most of the studies in literature analyze performance in terms of teaching and/or research from a variety of perspectives. Mohammad and Sanee [37] assessed academic performances by proving a network DEA model. They emphasized that it is important to have an acceptable methodology as well as a set of good performance indicators. In their presented network DEA model, they computed sub-functional efficiencies such as academic quality, research productivity and the overall efficiency.

Funetes et al [38] presented a three-stage DEA model for assessing higher education by considering the learning-teaching process. They used super efficient DEA models and sensitivity analysis to identify the effect of each key performance indicator. Kuah and Wong [39] used DEA models for an effective allocation and utilization of educational resources in performance evaluation of universities. Despotis et al [40] presents a multi-objective programming problem for deriving a unique and neutral efficiency score in academic research activities in DEA framework. They estimated the efficiencies of the stages without a prior definition of the overall efficiency of the system.

Ten branches of the Islamic Azad University (IAU) system for higher education in Iran is considered. Their productivity is evaluated in a general network DEA in a novel approach. Data for two academic years of 2015 and 2016 is collected from ISCS¹ and considered in this application.

IAU campus branches are comprised of different departments. The four major offices in managing the campuses are Education (stage 1), Research (stage 2), Graduate (stage 3) and Commercialization of Projects (stage 4). These sections cooperate with each other in a network system as depicted in figure 2.

Figure 2

General network structure of activities in a higher education institution.

Education office is responsible for graduating students from predefined courses while having non-academic personnel, academic personnel and other costs as the main factors. Research office provides the graduate students with training, laboratories, workshops and libraries with its products being published journal articles, conference papers, books, etc. Commercialization of Project office manages projects obtained from research office and acquiring industry support for projects of mutual interest. Graduate office has non-academic personnel for non- academic student support with its products being graduate students.

The standard black-box model is too limited to be used for evaluation of such a complex industry. Clearly, a general network production model is needed by design.

Inputs, intermediates and outputs data used in this evaluation follow normal distribution with known mean and variances as given in tables 4 and 5.

Table 4 Random average data for 10 university campuses.

Table 5 Variance of data for 10 university campuses.

• Inputs: Number of academic staff (x ¹₁ ), Number of non-academic staff for teaching office (x ¹₂ ), other costs (x ¹₃ ) (in billion Rials), Number of laboratories, studios, and libraries (x ²₄ ), Number of non-academic personnel for graduate office (x ³₅ ).

• Intermediate: Number of graduate students from offered courses (z ¹²₁ ), Number of graduate students from research (z ²³₂ ), Number of projects (z ²⁴₃ ).

• Outputs: Number of publications (y ²₁ ), Number of graduate students (y ³₂ ), Earnings (in billion Rials) (y ⁴₃ ).

For system efficiency evaluation of universities with an inter-relational structure as depicted in figure 2, the proposed Models (2) and (7) are utilized for deterministic and stochastic cases, respectively. Using provided details in [15], the adapted version of general network Models (2) and its stochastic version (7) could be represented in an expansive form as follows:

Model (2) for example 2

Model (7) for example 2

$\begin{aligned} & (E_{k}^{f} )^{l} = \hbox{min}\, \theta \\ & s.t\sum\limits_{j = 1}^{10} {\lambda_{j}^{1} (x_{ij}^{1} )^{l} \le \theta (x_{ik}^{1} )^{f} ,} \quad i = 1,2,3 \\ & \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{2} (x_{4j}^{2} )^{l} \le \theta (x_{4k}^{2} )^{f} ,} \\ & \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{3} (x_{5j}^{3} )^{l} \le \theta (x_{5k}^{3} )^{f} ,} \\ & \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{2} (y_{1j}^{2} )^{l} \ge (y_{1k}^{2} )^{f} ,} \\ & \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{3} (y_{2j}^{3} )^{l} \ge (y_{2k}^{3} )^{f} ,} \\ & \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{4} (y_{3j}^{4} )^{l} \ge (y_{3k}^{4} )^{f} ,} \\ & \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{1} (z_{1j}^{12} )^{l} \ge (z_{1j}^{12} )^{l} ,} \\ & \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{2} (z_{1j}^{12} )^{l} \le (z_{1j}^{12} )^{l} ,} \\ & \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{2} (z_{2j}^{23} )^{l} \ge (z_{2j}^{23} )^{l} ,} \\ & \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{3} (z_{2j}^{23} )^{l} \le (z_{2j}^{23} )^{l} ,} \\ & \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{2} (z_{3j}^{24} )^{l} \ge (z_{3j}^{24} )^{l} ,} \\ & \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{4} (z_{3j}^{24} )^{l} \le (z_{3j}^{24} )^{l} ,} \\ & \quad \quad \lambda_{j}^{1} ,\,\lambda_{j}^{2} ,\,\lambda_{j}^{3} ,\lambda_{j}^{4} \ge 0,\quad j = 1, \ldots ,10. \\ \end{aligned}$

$\begin{aligned} & (E_{k}^{f} )^{l} = \hbox{min}\, \theta \\ & s.t\quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{1} (x_{ij}^{1} )^{l} - \varPhi^{ - 1} (\alpha )(\omega_{i}^{1} )^{l} \le \theta (x_{ik}^{1} )^{f} ,} \quad i = 1,2,3 \\ & \quad \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{2} (x_{4j}^{2} )^{l} - \varPhi^{ - 1} (\alpha )(\omega_{4}^{2} )^{l} \le \theta (x_{4k}^{2} )^{f} } \\ & \quad \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{3} (x_{5j}^{3} )^{l} - \varPhi^{ - 1} (\alpha )(\omega_{5}^{3} )^{l} \le \theta (x_{5k}^{3} )^{f} } \\ & \quad \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{2} (y_{1j}^{2} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{1}^{2} )^{l} \ge (y_{1k}^{2} )^{f} } \\ & \quad \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{3} (y_{2j}^{3} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{2}^{3} )^{l} \ge (y_{2k}^{3} )^{f} } \\ & \quad \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{4} (y_{3j}^{4} )^{l} + \varPhi^{ - 1} (\alpha )(\omega_{3}^{4} )^{l} \ge (y_{3k}^{4} )^{f} } \\ & \quad \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{1} (z_{1j}^{12} )^{l} + \varPhi^{ - 1} (\alpha )((\omega_{1}^{12} )^{1} )^{l} \ge (z_{1j}^{12} )^{l} } \\ & \quad \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{2} (z_{1j}^{12} )^{l} - \varPhi^{ - 1} (\alpha )((\omega_{1}^{12} )^{2} )^{l} \le (z_{1j}^{12} )^{l} } \\ & \quad \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{2} (z_{2j}^{23} )^{l} + \varPhi^{ - 1} (\alpha )((\omega_{2}^{23} )^{2} )^{l} \ge (z_{2j}^{23} )^{l} } \\ & \quad \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{3} (z_{2j}^{23} )^{l} - \varPhi^{ - 1} (\alpha )((\omega_{2}^{23} )^{3} )^{l} \le (z_{2j}^{23} )^{l} } \\ & \quad \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{2} (z_{3j}^{24} )^{l} + \varPhi^{ - 1} (\alpha )((\omega_{3}^{24} )^{2} )^{l} \ge (z_{3j}^{24} )^{l} } \\ & \quad \sum\limits_{j = 1}^{10} {\lambda_{j}^{4} (z_{3j}^{24} )^{l} - \varPhi^{ - 1} (\alpha )((\omega_{3}^{24} )^{4} )^{l} \le (z_{3j}^{24} )^{l} } \\ & \quad \quad \lambda_{j}^{1} ,\,\lambda_{j}^{2} ,\,\lambda_{j}^{3} ,\lambda_{j}^{4} \ge 0,\quad j = 1, \ldots ,10. \\ \end{aligned}$

where $f,l \in \{ t,t + 1\}$ and

$$ \begin{aligned} (\,(\omega _{i} ^{1} )^{l} )^{2} & = \left\{ {\begin{array}{*{20}l} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{{10}} {((\lambda _{j} ^{1} )^{2} Var(\tilde{x}_{{ij}}^{1} )^{l} ) + (\lambda _{k} ^{1} - \theta )^{2} Var(\tilde{x}_{{ik}}^{1} )^{f} ,\quad i = 1,2,3\,\,\& \,\,f = l} } \hfill \\ {\sum\limits_{{j = 1}}^{{10}} {((\lambda _{j} ^{1} )^{2} Var(\tilde{x}_{{ij}}^{1} )^{l} ) + (\theta )^{2} Var(\tilde{x}_{{ik}}^{1} )^{f} } ,\quad i = 1,2,3\,\,\& \,\,f \ne l} \hfill \\ \end{array} } \right. \\ ((\omega _{4} ^{2} )^{l} )^{2} & = \left\{ {\begin{array}{*{20}l} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{{10}} {((\lambda _{j} ^{2} )^{2} Var(\tilde{x}_{{4j}}^{2} )^{l} ) + (\lambda _{k} ^{2} - \theta )^{2} Var(\tilde{x}_{{4k}}^{2} )^{f} } ,\quad f = l} \hfill \\ {\sum\limits_{{j = 1}}^{{10}} {((\lambda _{j} ^{2} )^{2} Var(\tilde{x}_{{4j}}^{2} )^{l} ) + (\theta )^{2} Var(\tilde{x}_{{4k}}^{2} )^{f} } ,\quad f \ne l} \hfill \\ \end{array} } \right. \\ (\omega _{5} ^{3} )^{l} )^{2} & = \left\{ {\begin{array}{*{20}l} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{{10}} {((\lambda _{j} ^{3} )^{2} Var(\tilde{x}_{{5j}}^{3} )^{l} ) + (\lambda _{k} ^{2} - \theta )^{2} Var(\tilde{x}_{{5k}}^{3} )^{f} } ,\quad f = l} \hfill \\ {\sum\limits_{{j = 1}}^{{10}} {((\lambda _{j} ^{3} )^{2} Var(\tilde{x}_{{5j}}^{3} )^{l} ) + (\theta )^{2} Var(\tilde{x}_{{5k}}^{3} )^{f} } ,\quad f \ne l} \hfill \\ \end{array} } \right. \\ ((\omega _{1} ^{2} )^{l} )^{2} & = \left\{ {\begin{array}{*{20}l} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{{10}} {((\lambda _{j} ^{2} )^{2} Var(\tilde{y}_{{1j}}^{2} )^{l} ) + (\lambda _{k} ^{2} - 1)^{2} Var(\tilde{y}_{{1k}}^{2} )^{f} } ,\quad f = l} \hfill \\ {\sum\limits_{{j = 1}}^{{10}} {((\lambda _{j} ^{2} )^{2} Var(\tilde{y}_{{1j}}^{2} )^{l} ) + Var(\tilde{y}_{{1k}}^{2} )^{f} } ,\quad f \ne l\,} \hfill \\ \end{array} } \right. \\ ((\omega _{2} ^{3} )^{l} )^{2} & = \left\{ {\begin{array}{*{20}l} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{{10}} {((\lambda _{j} ^{3} )^{2} Var(\tilde{y}_{{2j}}^{3} )^{l} ) + (\lambda _{k} ^{3} - 1)^{2} Var(\tilde{y}_{{2k}}^{3} )^{f} } ,\quad f = l} \hfill \\ {\sum\limits_{{j = 1}}^{{10}} {((\lambda _{j} ^{3} )^{2} Var(\tilde{y}_{{2j}}^{3} )^{l} ) + Var(\tilde{y}_{{2k}}^{3} )^{f} } ,\quad f \ne l} \hfill \\ \end{array} } \right. \\ ((\omega _{3} ^{4} )^{l} )^{2} & = \left\{ {\begin{array}{*{20}l} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{{10}} {((\lambda _{j} ^{4} )^{2} Var(\tilde{y}_{{3j}}^{4} )^{l} ) + (\lambda _{k} ^{4} - 1)^{2} Var(\tilde{y}_{{3k}}^{4} )^{f} } ,\quad f = l} \hfill \\ {\sum\limits_{{j = 1}}^{{10}} {((\lambda _{j} ^{4} )^{2} Var(\tilde{y}_{{3j}}^{4} )^{l} ) + Var(\tilde{y}_{{3k}}^{4} )^{f} } ,\quad f \ne l} \hfill \\ \end{array} } \right. \\ (((\omega _{1} ^{{12}} )^{1} )^{l} )^{2} & = \sum\limits_{{j = 1}}^{{10}} {\left( {(\lambda _{j} ^{1} )^{2} Var(\tilde{z}_{{1j}}^{{12}} )^{l} + (\lambda _{j} ^{1} - 1)^{2} Va(\tilde{z}_{{1j}}^{{12}} )^{l} } \right)} ,\,\, \\ (((\omega _{1} ^{{12}} )^{2} )^{l} )^{2} & = \sum\limits_{{j = 1}}^{{10}} {\left( {(\lambda _{j} ^{2} )^{2} Var(\tilde{z}_{{1j}}^{{12}} )^{l} + (\lambda _{j} ^{2} - 1)^{2} Va(\tilde{z}_{{1j}}^{{12}} )^{l} } \right)} ,\,\, \\ (((\omega _{2} ^{{23}} )^{2} )^{l} )^{2} & = \sum\limits_{{j = 1}}^{{10}} {\left( {(\lambda _{j} ^{2} )^{2} Var(\tilde{z}_{{2j}}^{{23}} )^{l} + (\lambda _{j} ^{2} - 1)^{2} Va(\tilde{z}_{{2j}}^{{23}} )^{l} } \right)} ,\, \\ (((\omega _{2} ^{{23}} )^{3} )^{l} )^{2} & = \sum\limits_{{j = 1}}^{{10}} {\left( {(\lambda _{j} ^{3} )^{2} Var(\tilde{z}_{{2j}}^{{23}} )^{l} + (\lambda _{j} ^{3} - 1)^{2} Va(\tilde{z}_{{2j}}^{{23}} )^{l} } \right)} ,\, \\ (((\omega _{3} ^{{24}} )^{2} )^{l} )^{2} & = \sum\limits_{{j = 1}}^{{10}} {\left( {(\lambda _{j} ^{2} )^{2} Var(\tilde{z}_{{3j}}^{{24}} )^{l} + (\lambda _{j} ^{2} - 1)^{2} Va(\tilde{z}_{{3j}}^{{24}} )^{l} } \right)} , \\ (((\omega _{3} ^{{24}} )^{4} )^{l} )^{2} & = \sum\limits_{{j = 1}}^{{10}} {\left( {(\lambda _{j} ^{4} )^{2} Var(\tilde{z}_{{3j}}^{{24}} )^{l} + (\lambda _{j} ^{4} - 1)^{2} Va(\tilde{z}_{{3j}}^{{24}} )^{l} } \right)} . \\ \end{aligned} $$

Deterministic MPI values are reported in the first column of table 6. Table 6 also presents the results of stochastic MPI, relation (6) for particular $\alpha$-levels. Comparison of the deterministic results with stochastic MPI values provides interesting insight. Although the chance constraint system efficiency scores for each DMU are always higher than (or equal to) the deterministic counterparts, the calculated MPIs may show different behavior.

Table 6 The stochastic MPI for 10 educational campuses with different acceptable risk levels.

For example, the computed deterministic and stochastic MPI values for universities U1, U2 and U6 indicate regression for every acceptable risk level of $\alpha \in \left[ {0.001, 0.4} \right]$. For the campuses U3, U4 results show progress in performance during time period 2015 to 2016 in every computed $\alpha$ level. Based on the provided stochastic MPI results, it seems reasonable to classify U5 in universities with indifference status in performance because their MPI values are very close to 1 during the entire period. U7, U8, U9 and U10 are the campuses with a notable difference between deterministic and stochastic MPIs. In this group, U7 could be considered as a potential candidate for the case of regression in performance during time period 2015 to 2016 because all of its stochastic MPI values are strictly less than 1. With the same reason, the other campuses U8, U9 and U10 are suggested to consider with progress in performance. Based on this analysis, there is more strong evidence now to decide on potential candidates for productive branches during the time period and offer improvement scenarios for the less productive candidates.

It needs to be emphasized that the results are quite dependent on the mean and variances of the sample but nature and type of data utilized in this application indicate the applicability of the proposed method to many practical situations. Stochastic MPI could assist policy makers in planning decisions in uncertain situations.

The novelty of the proposed models is that it enables managers in making more stable and accurate decisions about regress or progress of production systems with general network structures.

6 Conclusions

Assessment of productivity progress or regress is of significant importance to overall system management and optimization. In conventional deterministic view of productivity analysis, a traditional DEA evaluation is conducted for the case of deterministic and known prices. However, as many production and process planning decisions are made in anticipation of unknown and stochastic information, evaluation itself introduces a bias with unknown properties. In this work, Malmquist Productivity Indicator (MPI) is applied to productivity evaluation of production units with stochastic data. MPI is a close approach to practical environments in most actual production data sets.

The novelty of the current work lies in the analysis and study of progress and regress in productivity analysis of general network production systems in a Stochastic-DEA framework. The latest general network DEA models introduced by Lozano [14] and Kazemi Matin- Azizi model [15] are used to extend chance-constrained techniques to address stochastic input, intermediate, and output data. The chance-constrained technique proposed in this study requires the known mean and variance. It also assumes normal distribution of input/intermediate/output data for each unit.

Following the proposed method in Cooper et al [12], it is illustrated that a chance-constrained model may be converted into a deterministic equivalent quadratic optimization problem. A new stochastic version of MPI is introduced based on computed efficiency scores for general network production systems. The proposed technique is then demonstrated with a simple numerical example and an empirical application of data from 10 university campuses.

Computations demonstrate that the general stochastic DEA model suggested by Kazemi Matin and Azizi [15] produce more accurate results and adhere better to practice than a deterministic general network DEA. Results demonstrate that the introduced models could be readily implemented to practical applications. Further, distributions of estimates from the stochastic model more closely resemble practical productivity. Results also were coded using LINGO software.

As a future effort, a study is suggested to investigate whether statistical distribution could be used in place of normal distribution (for example, cases of skewed or truncated normally distributed data). Dealing with global and cost and also Luenberger-Malmquist productivity indexes with stochastic data could be considered as an interesting challenges for future studies.

Appendix A

To convert the chance-constrained optimization Model (4) to associate deterministic equivalent Model (5), we can proceed as follows. Note that the same argument could be presented for introducing Model (7). Here, $\Pr$ means ‘Probability’ and $\alpha$ is a predetermined value between 0 and 1.

The first constraint of Model (4) can be stated as follows:

$$ \Pr \left\{ {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} \le \theta (\tilde{x}_{ik} )^{f} } } } \right\} \ge 1 - \alpha ,\quad i = 1, \ldots ,m $$

By considering external slack value $s_{i}$, we have:

$$ \Pr \left\{ {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} \le 0} } } \right\} = (1 - \alpha ) + s_{i} ,\quad i = 1, \ldots ,m $$

So, there exist a positive slack variable $s_{i} > 0$ such that the above relation take this form:

$$ \Pr \left\{ {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} \le s_{i} } } } \right\} = 1 - \alpha ,\quad i = 1, \ldots ,m $$

Accordingly, by using the definition of expected value and variance of the elements, we may write the above equation as follows:

$$ \Pr \left[ {\frac{{\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } - E\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } } \right)}}{{\sqrt {var\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } } \right)} }} \ge \frac{{s_{i} - E\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } } \right)}}{{\sqrt {var\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } } \right)} }}} \right] = \alpha . $$

For the sake of simplicity let denote $\sqrt {var\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } } \right)}$by$\sigma_{i} \left( {\theta ,\lambda } \right)$. Therefore, we have:

$$ \Pr \left[ {\frac{{\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } - \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} + \theta (x_{ik} )^{f} } } }}{{\sigma_{i} \left( {\theta ,\lambda } \right)}} \ge \frac{{s_{i} - \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} + \theta (x_{ik} )^{f} } } }}{{\sigma_{i} \left( {\theta ,\lambda } \right)}}} \right] = \alpha $$

By denoting the left-hand side of the above inequality by $z_{j},$ it follows a normal standard distribution with zero mean and unit variance. Hence, we can write:

$\Pr \left[ {z_{j} \ge \frac{{s_{i} - \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} + \theta (x_{ik} )^{f} } } }}{{\sigma_{i} \left( {\theta ,\lambda } \right)}}} \right] = \alpha.$ Thus, we have $\varPhi \left[ {\frac{{ - s_{i} + \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} - \theta (x_{ik} )^{f} } } }}{{\sigma_{i} \left( {\theta ,\lambda } \right)}}} \right] = \alpha,$ where $\varPhi$ represent the normal cumulative distribution function. So, taking the inverse, we obtain $\left[ {\frac{{ - s_{i} + \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} - \theta (x_{ik} )^{f} } } }}{{\sigma_{i} \left( {\theta ,\lambda } \right)}}} \right] = \varPhi^{ - 1} (\alpha ),$ which could be stated as $- s_{i} + \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} - \theta (x_{ik} )^{f} } } = \varPhi^{ - 1} (\alpha )\sigma_{i} \left( {\theta ,\lambda } \right)$or equivalently as follows:

$\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\left( {\lambda_{j}^{p} (x_{ij}^{p} )^{l} } \right) - \varPhi^{ - 1} (\alpha )\sigma_{i} \left( {\theta ,\lambda } \right) \le \theta (x_{ik} )^{f} ,} } \quad i = 1, \ldots ,m.$ This is the first constraint of the model (5). The other constraints could be achieved in the same way.

For calculating $\left( {\sigma_{i} \left( {\theta ,\lambda } \right)} \right)^{2}$ we can write:

$$ \begin{aligned} & \text{var}\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{j = 1}^{n} {\lambda_{j}^{p} (\tilde{x}_{ij}^{p} )^{l} - \theta (\tilde{x}_{ik} )^{f} } } } \right) = \text{var}\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne o \end{subarray} }^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} + (\lambda_{j}^{p} - \theta )(x_{ik} )^{f} } } } \right) \\ & = \text{var}\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne o \end{subarray} }^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} } } } \right) + \text{var}\left( {(\lambda_{j}^{p} - \theta )(x_{ik} )^{f} } \right) + 2\text{Cov}\left( {\sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne o \end{subarray} }^{n} {\lambda_{j}^{p} (x_{ij}^{p} )^{l} } } ,(\lambda_{j}^{p} - \theta )(x_{ik} )^{f} } \right) \\ \end{aligned} $$

Therefore,

$$ \begin{aligned} \left( {\sigma_{i} \left( {\theta ,\lambda } \right)} \right)^{2} = \sum\limits_{{p \in P_{I} (i)}} {\sum\limits_{\begin{subarray}{l} j = 1 \\ j \ne k \end{subarray} }^{n} {((\lambda_{j}^{p} )^{2} Var(\tilde{x}_{ij}^{p} )^{l} ) + \sum\limits_{o \ne k} {\sum\limits_{j \ne k} {\lambda_{o}^{p} \lambda_{j}^{p} Cov(\tilde{x}_{io}^{p} ,\tilde{x}_{ij}^{p} )} } } \,\,\,\,} \hfill \\ + 2(\lambda_{k}^{p} - \theta )\sum\limits_{o \ne k} {\lambda_{k}^{p} Cov(\tilde{x}_{io}^{p} ,\tilde{x}_{ik}^{p} )} + (\lambda_{k}^{p} - \theta )^{2} Var(\tilde{x}_{ik}^{p} )^{f} \hfill \\ \end{aligned} $$

In the model (5), $\left( {\sigma_{i} \left( {\theta ,\lambda } \right)} \right)^{2}$ is denoted by non-negative variables $(\omega_{i}^{l} )^{2}$.