Nonlinear dynamics of a viscoelastic sandwich beam with parametric excitations and internal resonance

Abstract

Nonlinear dynamical behaviors of an axially accelerating viscoelastic sandwich beam subjected to three-to-one internal resonance and parametric excitations resulting from simultaneous velocity and tension fluctuations are investigated. The direct method of multiple scales is adopted to obtain a set of first-order ordinary differential equations and associated boundary conditions. The frequency and amplitude response curves along with their stability and bifurcation are numerically studied. A great number of dynamic behaviors are presented in the form of phase portraits, time traces, Poincaré sections, and FFT power spectra. Due to modal interaction, various periodic, quasiperiodic, and chaotic behaviors are displayed, depending on the initial conditions. The largest Lyapunov exponent is carried out to determine the midly chaotic response by the convergent form of exponents. Numerical results show various oscillatory behaviors indicating the influence of internal resonance and coupled effects of fluctuating axial velocity and tension.

1 Introduction

In recent years, axially moving structures have widely applications in many fields of engineering devices, such as power transmission belts, pipe conveying fluids, band saw blades, paper sheets, and other similar systems. So far, dynamical models of axially moving continua have been studied in many literatures. After a literature survey, different numerical methods are applied to the mechanical analysis of axially moving beams and their dynamical stability.

Fig. 1

Schematic of an axially moving viscoelastic sandwich beam with time-dependent axial tension and velocity

Perturbation method, especially the method of multiple scales, has found more practical and efficient among researchers. Based on the method of multiple scales, the parametric vibration and stability of an axially accelerating beam with hinged–hinged conditions was carried out by Öz and Pakdemirli [1]. Moreover, the fixed–fixed supported beam was studied by Öz [2]. Transverse vibrations of axially moving beams with harmonically varying velocity have been investigated, and the approximate boundary-layer-type solutions have been given by Özkaya et al. [3]. Stability of axially moving beams with parametric excitation was studied by using perturbation methods as well as single-term Galerkin truncation in Ref. [4]. In this study, the parametric excitation was resulted from simultaneous tension and speed fluctuations. By considering the subharmonic and combination parametric oscillations, dynamic stability in transverse vibration of axially accelerating viscoelastic beams has been discussed by Chen et al. [5] via the averaging method and the Galerkin method. Yang and Chen [6] established a nonlinear model to analyze the forced vibration of the traveling beam due to the motion of supporting foundation by the method of multiple scales. Stability of the viscoelastic beam studied by Chen and Wang [7] is based on the differential quadrature method and the asymptotic perturbation method. In Ref. [8], dynamic responses of an axially moving viscoelastic beam subjected to two-frequency parametric excitation with considering internal resonance were investigated. Also, a similar study on an axially moving beam with respect to single-frequency parametric excitation was done by Sahoo et al. [9]. By using the method of multiple scales, Tang et al. [10] estimated the nonlinear parametric vibration of an Euler–Bernoulli beam with axial motion on elastic foundation. In addition, a vibrational model was established to analyze stability of an axially moving viscoelastic beam in Ref. [11]. In this study, the three-to-one internal resonance and the primary resonance cases due to the external excitation were considered.

Galerkin method as an efficient tool for the transformation of the governing equation, is adopted to further investigation. By applying the Galerkin truncation method and the method of incremental harmonic balance, forced response of the axially moving beam in the presence of internal resonance was presented by Sze et al. [12]. A similar study was presented by Ghayesh [13] who exploited the Galerkin method to investigate the forced dynamical behaviors of translating viscoelastic beams with considering internal resonance. In addition to these, the Galerkin technique and the fourth-order Runge–Kutta method have been used to study dynamical behaviors of the axially moving beam with time-varying tension taken into consideration in Ref. [14]. And dynamic phenomenon such as attractors was observed in the form of Poincaré map and bifurcation diagram. In Ref. [15], vibration isolation of a viscoelastic beam with vertical elastic support was discussed. For the axially accelerating buckled beam, a closed form solution for the post-buckling configuration and its thermo-mechanical nonlinear dynamical behaviors were investigated by Kazemirad et al. [16]. And the post-buckling analysis of the beam with four different supercritical speeds in axial direction was given in Ref. [17]. In addition, an axially moving beam subjected to a harmonic external force was studied by Ghayesh et al. [18]. They considered coupled longitudinal and transverse displacements and a three-to-one internal resonance into the investigation of the thermo-mechanical nonlinear dynamical behaviors.

Table 1 Material properties of the viscoelastic sandwich beam

Fig. 2

Variation of the natural frequencies $\omega _{1}$, $\omega _{2}$, and $3\omega _{1}$ with varying moving velocity $v_{0}$

Besides the applications of the perturbation method and the Galerkin method, other numerical methods have been applied in the axially moving beam, including the differential quadrature method, the Lindstedt–Poincaré method, etc. By considering the application of artificial neural networks [19] and Lie group theory [20], the influence of harmonic velocity on stability boundaries of the beam was studied in these works. Another method for multidimensional Lindstedt–Poincaré was also used to investigate the axially moving beam by Chen et al. [21]. Dynamical behaviors of beams and plates have also been investigated by Gavete et al. [22] applying the generalized finite difference method. In order to analysis dynamical behaviors of axially moving viscoelastic beams, the Fourier differential quadrature method and the Runge–Kutta–Fehlberg method were employed to obtain discrete governing equations, respectively, in space and time regions [23]. On the basis of the full-state feedback boundary control, the hybrid partial–ordinary differential equations were derived to study control problems for a class of axially moving nonuniform system by Zhao et al. [24]. An axially translating beam with axial pretension was discussed by Mokhtari and Mirdamadi [25] via Timoshenko beam theory. Recently, the transporting belts are applied in many mechanical structures. However, the transporting belts with considering nonhomogeneous boundary conditions have been attractive to researchers. For example, free and forced vibration characteristics of a transporting belt were investigated by Ding and coworkers [26, 27] using the differential quadrature method.

Fig. 3

a Frequency response curves for the first mode when $v_{1}=10$ and $p=10$. Zoomed solutions corresponding to part A (b), part B (c), part C (d) and part D (e)

Fig. 4

a Frequency response curves for the second mode when $v_{1}=10$ and $p=10$. Zoomed solutions corresponding to part E (b), part F (c), and part G (d)

Fig. 5

a Frequency response curves for the first mode when $v_{1}=20$ and $p=10$. Zoomed solutions corresponding to part A (b), part B (c), and part C (d)

From the reviewed researches, the front contents involve viscoelastic beams with axial acceleration [5,6,7,8,9,10,11, 13, 14, 23, 25]. It is known that viscoelastic material has characteristics of viscous fluid and elastic solid. But for sandwich structures, there are several advantages in high stiffness and strength-to-weight ratios [28]. Therefore, sandwich structures with viscoelastic core have significant effects on the control and reduction of vibration. Recently, the researches on sandwich structures with viscoelastic material are only few in number, especially for beam models in linear and nonlinear vibrations analyses. Some investigators focused on their attention on studying nonlinear vibrations of the damped viscoelastic sandwich beam using the harmonic balance method with Galerkin approximation [29] and the harmonic balance method and the finite element method [30]. In addition, transient dynamic analysis of viscoelastic sandwich beams was presented by the fractional derivative operator [31] and the Galerkin-based state-space method [32]. Under these effects of the moving speed, thickness and internal damping of core material, dynamic responses of viscoelastic sandwich beams were performed in Ref. [33]. Dynamic analysis of a cantilevered viscoelastic sandwich beam with the effects of transverse shear deformation and rotational inertia was given by Alvelid [34]. Vibration and damping analysis were made by Jin et al. [35] for a sandwich beam based on Reddy’s higher-order theory and a modified Fourier–Ritz method. On the other hand, the forced harmonic response [36] and vibration characteristics and structural stability [37] of viscoelastic sandwich beams were investigated. With considering low- and high-frequency principal parametric oscillations, Li et al. [38] worked on investigating forced vibration and stability of the sandwich beam with viscoelastic core. Using differential quadrature method, vibration and damping characteristics of three-layered curved sandwich beams with composite face layers and viscoelastic core were developed by Demir et al. [39].

Fig. 6

a Frequency response curves for the second mode when $v_{1}=20$ and $p=10$. Zoomed solutions corresponding to part D (b), part E (c), and part F (d)

Fig. 7

a Frequency response curves for the first mode when $v_{1}=10$ and $p=40$. Zoomed solutions corresponding to part A (b), part B (c), and part C (d)

Fig. 8

a Frequency response curves for the second mode when $v_{1}=10$ and $p=40$. Zoomed solutions corresponding to part D (b), part E (c), part F (d) , part G (e) and part H (f)

Simultaneous effect resulting from parametric excitations as an importation part of dynamical analysis of mechanical systems has attracted attention in few researches. Several investigators have considered coupled effects into stability analysis of their models. By using the method of multiple scales, the modulation equations of amplitude and phase were determined in Ref. [40]. With considering the effects of damping, self-excitation, and two-frequency parametric excitation, vibrational behaviors of the system were also discussed. Along similar lines, a drillstring system was modeled by a nonlinear equation with time-varying axial velocity and axial load [41]. With considering harmonically varying axial speed and axial load simultaneously, dynamical behaviors of the axially moving beam were presented by Özhan [42]. Also, dynamic characteristics of an axially moving viscoelastic sandwich beam were studied by Lv et al. [43]. In the above-mentioned works, parametric resonance cases have been studied, including combined parametric oscillation (Both the two subharmonic types of parametric oscillations are of order 1/2 [40]) and so on. For the continuous system derived in Ref. [42], combined parametric vibration (simultaneous parametric resonance from parametric excitations) was given. It is worth mentioning that combined parametric oscillation and combined parametric vibration are both for discrete and continuous systems. Also, these references demonstrate that the simultaneous effect has significant influence in analyzing dynamical systems.

Fig. 9

a Frequency response curves for the first mode when $v_{1}=20$ and $p=40$. Zoomed solutions corresponding to part A (b), part B (c), and part C (d)

Fig. 10

a Frequency response curves for the second mode when $v_{1}=20$ and $p=40$. Zoomed solutions corresponding to part D (b), part E (c), part F (d), part G (e) and part H (f)

In the previously mentioned researches, the analysis of viscoelastic sandwich beams is mainly focused on time-varying axial load or axial moving velocity expect for the work [43]. Few literatures have studied the dynamical behaviors of axially moving viscoelastic sandwich beams subjected to parametric excitation resulting from the first two modes expect for the works [37, 38, 43]. Internal resonance as a typical nonlinear dynamical behavior, many complex dynamic behaviors such as bifurcations and chaos, are observed. However, there is no work considering it into viscoelastic sandwich beams in all available works.

Fig. 11

a, b Frequency response curves for the first and second modes when $\sigma _{1}=-48.06$

Fig. 12

a Frequency response curves for the first mode when $\sigma _{1}=5.6553\times 10^{-4}$. Zoomed solutions corresponding to part A (b), part B (c), and part C (d)

To resolve the lack of researches mentioned above, this paper is focused on the dynamical behaviors of axially accelerating viscoelastic sandwich beams subjected to three-to-one internal resonance and principal parametric resonances owing to the simultaneous effect of axial moving velocity and axial tension fluctuations. The direct method of multiple scales is used to the dimensionless governing equations and associated simply supported boundary conditions for both end. The obtained equations are complex modulation equations for the first two interacting modes. On the basis of Cartesian formulation, a set of first-order modulation equations are obtained to investigate nonlinear behaviors of the system. Using the pseudo-arclength continuation algorithm, the associated solutions are obtained to analyze stability and bifurcation. The simultaneous effect of harmonically varying velocity and tension is illustrated by the variation of pitchfork bifurcation points in trivial solution curves and the branch stability of nontrivial solutions. And the dynamic solutions of the system are presented in the form of periodic, quasiperiodic, and chaotic phenomena. The largest Lyapunov exponent is employed to reveal uncertain system responses. Finally, subcritical and supercritical Hopf bifurcation curves are given to find more interesting oscillatory behaviors associated with the coupled effect of harmonically varying components of velocity and tension by tracing codimension one bifurcation curves.

Fig. 13

a Frequency response curves for the second mode when $\sigma _{1}=5.6553\times 10^{-4}$. Zoomed solutions corresponding to part D (b), part E (c), and part F (d)

Fig. 14

a Amplitude response curves for the first mode when $p=10$ and $\sigma _{1}=57.87$. Zoomed solutions corresponding to part A (b) and part B (c)

Fig. 15

a Amplitude response curves for the second mode when $p=10$ and $\sigma _{1}=57.87$. Zoomed solutions corresponding to part C (b)

2 Governing equations

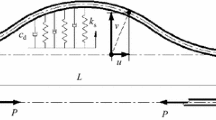
Consider an axially moving sandwich beam with viscoelastic core subjected to parametric oscillations in the presence of internal resonance. The model of the sandwich beam with length L and width b is depicted in Fig. 1. It is assumed that the uniform cross section takes the plane assumption. And the beam performs planar motion. On the basis of the Euler–Bernoulli beam theory, the transverse vibration analysis of the beam is studied. The surface layers and core layer are made of homogeneous and isotropic materials. The corresponding thickness of surface layers and core layer is $h_\mathrm{s}$ and $h_\mathrm{c}$, respectively. Assuming the axial tension to be a small harmonic fluctuation about initial tension, it is represented in the form of $P(T)=P_{0}+\varepsilon P_{1} \text {sin}(\overline{\varOmega }_{0}{T})$, where $P_{0}$ is the initial tension, $\varepsilon P_{1}$ is the amplitude and $\overline{\varOmega }_{0}$ is the frequency of the harmonically varying component. The axially moving velocity is assumed to be $V_e (T)$=$V_0+\varepsilon V_1 \text {sin}(\overline{\varOmega }_{1}{T})$, where $V_0$ is mean velocity, $\varepsilon V_1$ is the amplitude and $\overline{\varOmega }_{1}$ is the frequency of the harmonic component. The governing equation of transverse vibration of the sandwich beam in nondimensional form is given by Lv et al. [43]

$$\begin{aligned}&\dfrac{\partial ^{2} w}{\partial {t}^{2}}+2v\dfrac{\partial ^{2} w}{\partial x \partial t}+\left( v^2-1\right) \dfrac{\partial ^{2} w}{\partial {x}^{2}}+\dfrac{\partial v}{\partial t} \dfrac{\partial w}{\partial x}\nonumber \\&\quad +\,k_f^2 \dfrac{\partial ^{4} w}{\partial {x}^{4}}-\varepsilon p \,\text {sin}(\varOmega _{0}t) \dfrac{\partial ^{2} w}{\partial {x}^{2}}\nonumber \\&\quad +\,\alpha \varepsilon \left( \dfrac{\partial ^{5} w}{\partial {x}^{4} \partial t}+v\dfrac{\partial ^{5} w}{\partial {x}^{5}}\right) -\dfrac{3}{2} k_1\left( \dfrac{\partial w}{\partial x}\right) ^{2} \dfrac{\partial ^{2} w}{\partial {x}^{2}}\nonumber \\&\quad -\,k_2\left( 2\dfrac{\partial w}{\partial x} \dfrac{\partial ^{2} w}{\partial {x}^{2}} \dfrac{\partial ^{2} w}{\partial x \partial t}+2v\dfrac{\partial w}{\partial x} \left( \dfrac{\partial ^{2} w}{\partial {x}^{2}}\right) ^2\right. \nonumber \\&\quad \left. +\,\left( \dfrac{\partial w}{\partial x}\right) ^2 \dfrac{\partial ^{3} w}{\partial {x}^{2} \partial t}+v\left( \dfrac{\partial w}{\partial x}\right) ^2 \dfrac{\partial ^{3} w}{\partial {x}^{3}}\right) \nonumber \\&\quad +\,\dfrac{1}{2}\left( 1+\varepsilon p \,\text {sin}(\varOmega _{0}t)\right) \left( \dfrac{\partial w}{\partial x}\right) ^2 \dfrac{\partial ^{2} w}{\partial {x}^{2}}\nonumber \\&\quad +\,\dfrac{5}{12}k_{1}\left( \dfrac{\partial w}{\partial x}\right) ^4 \dfrac{\partial ^{2} w}{\partial {x}^{2}}\nonumber \\&\quad +\,6k_{2}\left( 4v \left( \dfrac{\partial w}{\partial x}\right) ^4 \dfrac{\partial ^{2} w}{\partial {x}^{2}}+v\left( \dfrac{\partial w}{\partial x}\right) ^4 \dfrac{\partial ^{3} w}{\partial {x}^{3}}\right. \nonumber \\&\quad \left. +\,4\left( \dfrac{\partial w}{\partial x}\right) ^3 \dfrac{\partial ^{2} w}{\partial {x}^{2}} \dfrac{\partial ^{2} w}{\partial x \partial t}+\left( \dfrac{\partial w}{\partial x}\right) ^4 \dfrac{\partial ^{3} w}{\partial {x}^{2} \partial t}\right) =0.\nonumber \\ \end{aligned}$$

(1)

Fig. 16

a Amplitude response curves for the first mode when $v_{1}=10$ and $\sigma _{1}=57.87$. Zoomed solutions corresponding to part A (b)

Fig. 17

a Amplitude response curves for the second mode when $v_{1}=10$ and $\sigma _{1}=57.87$. Zoomed solutions corresponding to part B (b), part C (c), and part D (d)

The corresponding dimensionless quantities are defined as

$$\begin{aligned} \begin{aligned}&x=\dfrac{X}{L},\;w=\dfrac{W}{L},\;t=T\sqrt{\dfrac{P_0}{\rho bHL^2}},\;\\&v_0=V_0\sqrt{\dfrac{\rho bH}{P_0}},\;v_1=V_1\sqrt{\dfrac{\rho bH}{P_0}},\\&\alpha =\dfrac{\eta bh_\mathrm{c}^3}{12\varepsilon L^3\sqrt{\rho bHP_0}},\;k_1=\dfrac{E_\mathrm{s} bh_\mathrm{s}+E_\mathrm{c} bh_\mathrm{c}}{P_0},\;\\&k_2=\dfrac{\eta bh_\mathrm{c}}{L\sqrt{\rho bHP_0}},\;p=\dfrac{P_1}{P_0},\\&k_f^2=\dfrac{E_\mathrm{s} b(h_\mathrm{s}^3+3h_\mathrm{c}^2 h_\mathrm{s}+3h_\mathrm{c} h_\mathrm{s}^2)+E_\mathrm{c} bh_\mathrm{c}^3}{12P_0 L^2},\;\\&\varOmega _{0}=\overline{\varOmega }_{0}\sqrt{\dfrac{\rho bHL^2}{P_0}},\;\varOmega _{1}=\overline{\varOmega }_{1}\sqrt{\dfrac{\rho bHL^2}{P_0}}. \end{aligned} \end{aligned}$$

(2)

where X is the longitudinal coordinate, W is the transverse displacement, and $E_\mathrm{s}$($E_\mathrm{c}$) and $\rho _\mathrm{s}$($\rho _\mathrm{c}$) are the Young’s modulus and density of surface layers(core layer), respectively. x, w, $\alpha$, $\varOmega _{0}$, and $\varOmega _{1}$, respectively, denote nondimensional longitudinal displacement, nondimensional transverse displacement, nondimensional viscoelastic coefficient, nondimensional frequency of axial tension, and nondimensional frequency of velocity.

Fig. 18

a, b Amplitude response curves for the first and second modes when $p=10$ and $\sigma _{1}=-48.06$

Fig. 19

a, b Amplitude response curves for the first and second modes when $p=10$ and $\sigma _{1}=5.6553\times 10^{-4}$

The dimensionless axial velocity is expressed as

$$\begin{aligned} v=v_0+\varepsilon v_1 \,\text {sin}(\varOmega _{1}t), \end{aligned}$$

(3)

where $v_0$ and $\varepsilon v_1$ denote nondimensional mean velocity and nondimensional amplitude, respectively, and $\varOmega _{1}$ is nondimensional frequency of harmonically varying component.

Fig. 20

a, c Amplitude response curves for the first and second modes when $v_{1}=10$ and $\sigma _{1}=-48.06$. Zoomed solutions corresponding to part A (b), and part B (d)

Fig. 21

a, d Amplitude response curves for the first and second modes when $v_{1}=10$ and $\sigma _{1}=5.6553\times 10^{-4}$. Zoomed solutions corresponding to part A (b), part B (c), part C (e), and part D (f)

To obtain the smallness of amplitude of the direction w, it can be scaled like

$$\begin{aligned} w\rightarrow \sqrt{\varepsilon }w \end{aligned}$$

(4)

where $\varepsilon$ is the book keeping parameter and used in the subsequent perturbation analysis. Substituting Eq. (4) into Eq. (1), the nonlinear equation of motion can be rewritten as

$$\begin{aligned}&\dfrac{\partial ^{2} w}{\partial {t}^{2}}+2v\dfrac{\partial ^{2} w}{\partial x \partial t}+\left( v^2-1\right) \dfrac{\partial ^{2} w}{\partial {x}^{2}}+\dfrac{\partial v}{\partial t} \dfrac{\partial w}{\partial x}\nonumber \\&\qquad +\,k_f^2 \dfrac{\partial ^{4} w}{\partial {x}^{4}}-\varepsilon p \,\text {sin}(\varOmega _{0}t) \dfrac{\partial ^{2} w}{\partial {x}^{2}} \nonumber \\&\qquad +\,\alpha \varepsilon \left( \dfrac{\partial ^{5} w}{\partial {x}^{4} \partial t}+v\dfrac{\partial ^{5} w}{\partial {x}^{5}}\right) -\dfrac{3}{2} k_1\varepsilon \left( \dfrac{\partial w}{\partial x}\right) ^{2} \dfrac{\partial ^{2} w}{\partial {x}^{2}} \nonumber \\&\qquad -\,k_2\varepsilon \left( 2\dfrac{\partial w}{\partial x} \dfrac{\partial ^{2} w}{\partial {x}^{2}} \dfrac{\partial ^{2} w}{\partial x \partial t}+2v\dfrac{\partial w}{\partial x} \left( \dfrac{\partial ^{2} w}{\partial {x}^{2}}\right) ^2\right. \nonumber \\&\qquad \left. +\,\left( \dfrac{\partial w}{\partial x}\right) ^2 \dfrac{\partial ^{3} w}{\partial {x}^{2} \partial t}+v\left( \dfrac{\partial w}{\partial x}\right) ^2 \dfrac{\partial ^{3} w}{\partial {x}^{3}}\right) \nonumber \\&\qquad +\,\dfrac{1}{2}\varepsilon \left( 1+\varepsilon p \,\text {sin}(\varOmega _{0}t)\right) \left( \dfrac{\partial w}{\partial x}\right) ^2 \dfrac{\partial ^{2} w}{\partial {x}^{2}}\nonumber \\&\qquad +\,\dfrac{5}{12}k_{1}\varepsilon ^{2} \left( \dfrac{\partial w}{\partial x}\right) ^4 \dfrac{\partial ^{2} w}{\partial {x}^{2}}\nonumber \\&\qquad +\,6k_{2}\varepsilon ^{2} \left( 4v \left( \dfrac{\partial w}{\partial x}\right) ^4 \dfrac{\partial ^{2} w}{\partial {x}^{2}}+v\left( \dfrac{\partial w}{\partial x}\right) ^4 \dfrac{\partial ^{3} w}{\partial {x}^{3}}\right. \nonumber \\&\qquad \left. +\,4\left( \dfrac{\partial w}{\partial x}\right) ^3 \dfrac{\partial ^{2} w}{\partial {x}^{2}} \dfrac{\partial ^{2} w}{\partial x \partial t}+\left( \dfrac{\partial w}{\partial x}\right) ^4 \dfrac{\partial ^{3} w}{\partial {x}^{2} \partial t}\right) =0.\nonumber \\ \end{aligned}$$

(5)

with simply supported boundary conditions

$$\begin{aligned} w(0,t)=w(1,t)=0,\,\dfrac{\partial ^{2}{w}}{\partial {x}^{2}}(0,t)=\dfrac{\partial ^{2}{w}}{\partial {x}^{2}}(1,t) =0. \end{aligned}$$

(6)

Fig. 22

a, c Amplitude response curves for the first and second modes when $p=10$ and $\sigma _{1}=57.87$. Zoomed solutions corresponding to part C (b), and part F (d)

Fig. 23

a, c Amplitude response curves for the first and second modes when $v_{1}=10$ and $\sigma _{1}=57.87$. Zoomed solutions corresponding to part A (b), and part B (d)

2.1 Perturbation Analysis

The solution to Eq. (5) is assumed to be an uniform solution of a first-order expansion in the following form

$$\begin{aligned} w(x,t,\varepsilon )=w_0 (x,T_0,T_1)+\varepsilon w_1 (x,T_0,T_1)+\cdots , \end{aligned}$$

(7)

where the timescales are $T_n=\varepsilon ^{n}t$, $n=0,1,2,\ldots$. By denoting the differential operators as $D_n={\partial }/{\partial T_n}$, $n=0,1,2,\ldots$, partial derivatives with respected to t are expressed as

$$\begin{aligned} \dfrac{\partial }{\partial t}=D_0+\varepsilon D_1+\cdots , \dfrac{\partial ^2 }{\partial {t}^{2}}=D_{0}^{2}+2\varepsilon D_{0}D_{1}+\cdots . \end{aligned}$$

(8)

Fig. 24

a Phase portrait and b projected Poincaré section for $\sigma _{2}=72.8159$. FFT power spectrum for $p_{1}$ is shown in (a)

Substituting Eqs. (7) and (8) into Eqs. (5) and (6) with the aid of Eq. (3), and balancing coefficients of $\varepsilon ^{0}$ and $\varepsilon ^{1}$, functional equations can be derived as

$$\begin{aligned}&O(\varepsilon ^{0}): D_0^2 w_0+2v_0 D_0 w_0^{\prime }+(v_0^2-1)w_0^{\prime \prime } \nonumber \\&\quad +k_f^2 w_0^{\prime \prime \prime \prime }=0,\nonumber \\&w_0(0,t)=w_0(1,t)=0,\, w_0^{\prime \prime }(0,t)=w_0^{\prime \prime }(1,t)=0 \end{aligned}$$

(9)

and

$$\begin{aligned}&O(\varepsilon ^{1}): D_0^2 w_1+2v_0 D_0 w_1^{\prime }+\left( v_0^2-1\right) w_1^{\prime \prime }+k_f^2 w_1^{\prime \prime \prime \prime }\nonumber \\&\quad =-2D_0 D_1 w_0-2v_0 D_1 w_0^{\prime }+p\,\text {sin}(\varOmega _{0}t) w_0^{\prime \prime }\nonumber \\&\qquad -2v_{1}\,\text {sin}(\varOmega _{1}t)\left( D_0 w_0^{\prime }+v_0 w_0^{\prime \prime }\right) \nonumber \\&\qquad -v_{1}\varOmega _{1}w_{0}^{\prime }\,\text {cos}(\varOmega _{1}t)-\alpha \left( D_0 w_0^{\prime \prime \prime \prime }+v_0 w_0^{\prime \prime \prime \prime \prime }\right) \nonumber \\&\qquad +\left( \dfrac{3}{2} k_1-\dfrac{1}{2}\right) \left( w_0^{\prime }\right) ^2 w_0^{\prime \prime }\nonumber \\&\qquad +k_2 \left( 2w_0^{\prime } w_0^{\prime \prime } D_0 w_0^{\prime }+2v_0 w_0^{\prime } \left( w_0^{\prime \prime }\right) ^2\right. \nonumber \\&\qquad \left. +\left( w_0^{\prime }\right) ^2 D_0 w_0^{\prime \prime }+v_0 \left( w_0^{\prime }\right) ^2 w_0^{\prime \prime \prime }\right) .\nonumber \\&w_1(0,t)=w_1(1,t)=0,\, w_1^{\prime \prime }(0,t)=w_1^{\prime \prime }(1,t)=0 \end{aligned}$$

(10)

The primes denote derivative with respect to nondimensional longitudinal coordinate x. It is assumed that the solution to Eq. (9) which is expressed as

$$\begin{aligned} w_0(x,T_0,T_1)=\sum _{n=1}^{\infty }\phi _n(x)A_n(T_1)e^{i\omega _{n}T_0}+cc, \end{aligned}$$

(11)

where $\phi _n(x)$ represent the mode shapes, $\omega _{n}$ denote the natural frequencies, and cc are complex conjugate terms. The nth complex mode shape $\phi _n(x)$ for simply supported boundary conditions is stated as follows [1]

Fig. 25

a Phase portrait and b projected Poincaré section for $\sigma _{2}=63.1816$. FFT power spectrum for $p_{1}$ is shown in (a)

$$\begin{aligned} \phi _n(x)&=C_{1n}\left\{ e^{i\beta _{1n}x}-\dfrac{\left( \beta _{4n}^{2}-\beta _{1n}^{2}\right) \left( e^{i\beta _{3n}}-e^{i\beta _{1n}}\right) }{\left( \beta _{4n}^{2}-\beta _{2n}^{2}\right) \left( e^{i\beta _{3n}}-e^{i\beta _{2n}}\right) }e^{i\beta _{2n}x}\right. \nonumber \\&\quad \left. -\,\dfrac{\left( \beta _{4n}^{2}-\beta _{1n}^{2}\right) \left( e^{i\beta _{2n}}-e^{i\beta _{1n}}\right) }{\left( \beta _{4n}^{2}-\beta _{3n}^{2}\right) \left( e^{i\beta _{2n}}-e^{i\beta _{3n}}\right) }e^{i\beta _{3n}x}\right. \nonumber \\&\quad +\,\left[ -1+\dfrac{\left( \beta _{4n}^{2}-\beta _{1n}^{2}\right) \left( e^{i\beta _{3n}}-e^{i\beta _{1n}}\right) }{\left( \beta _{4n}^{2}-\beta _{2n}^{2}\right) \left( e^{i\beta _{3n}}-e^{i\beta _{2n}}\right) }\right. \nonumber \\&\quad \left. \left. +\,\dfrac{\left( \beta _{4n}^{2}-\beta _{1n}^{2}\right) \left( e^{i\beta _{2n}}-e^{i\beta _{1n}}\right) }{\left( \beta _{4n}^{2}-\beta _{3n}^{2}\right) \left( e^{i\beta _{2n}}-e^{i\beta _{3n}}\right) }\right] e^{i\beta _{4n}x}\right\} , \end{aligned}$$

(12)

where $\beta _{mn}$ are the eigenvalues which are the roots of following relations

$$\begin{aligned}&k_{f}^{2}\beta _{mn}^{4}-(v_0^2-1)\beta _{mn}^{2}-2\omega _{n}v_{0}\beta _{mn}-\omega _{n}^{2}=0,\qquad \nonumber \\&\quad m=1,2,3,4,\, n=1,2,\ldots . \end{aligned}$$

(13)

and

$$\begin{aligned}&\left[ e^{i(\beta _{1n}+\beta _{2n})}+e^{i(\beta _{3n}+\beta _{4n})}\right] \left( \beta _{1n}^{2}-\beta _{2n}^2\right) \left( \beta _{3n}^{2}-\beta _{4n}^{2}\right) \nonumber \\&\qquad +\left[ e^{i(\beta _{1n}+\beta _{3n})}+e^{i(\beta _{2n}+\beta _{4n})}\right] \left( \beta _{2n}^{2}-\beta _{4n}^2\right) \left( \beta _{3n}^{2}-\beta _{1n}^{2}\right) \nonumber \\&\qquad +\left[ e^{i(\beta _{2n}+\beta _{3n})}+e^{i(\beta _{1n}+\beta _{4n})}\right] \left( \beta _{1n}^{2}-\beta _{4n}^2\right) \left( \beta _{2n}^{2}-\beta _{3n}^{2}\right) \nonumber \\&\quad =0. \end{aligned}$$

(14)

3 Principal parametric resonances and internal resonance

In the present investigation, the length and width of the beam are $L=2\,\text {m}$ and $b=0.05\,\text {m}$. The material properties as those in Ref. [37, 38, 43] are displayed in Table 1. The linear natural frequencies of the viscoelastic sandwich beam are solved from the above Eqs. (13) and (14). With the increasing of initial tension $P_{0}$, the flexural stiffness value $k_\mathrm{f}$ is decreased. Numerical simulation shows that the first and second natural frequencies are decreased by increasing the mean velocity $v_0$ for a fixed flexural stiffness value $k_\mathrm{f}=0.214$. As the mean velocity $v_0$ increases, the second natural frequency is close to three times as much as the first natural frequency when $v_{0}=v_\mathrm{c}=0.46199$, resulting in a three-to-one internal resonance (Fig. 2). At critical speed of buckling or divergence, the first natural frequency is close to zero. Since all other high modes except the first two modes decay with time for the damping and Coriolis terms [45], the internal resonance response is activated between the first two modes. According to this, the general solution to Eq. (9) can be rewritten as

$$\begin{aligned} w_0(x,T_0,T_1)= & {} \phi _{1}(x)A_{1}(T_1)e^{i\omega _{1}T_0} \nonumber \\&+\,\phi _{2}(x)A_{2}(T_1)e^{i\omega _{2}T_0}+cc. \end{aligned}$$

(15)

Fig. 26

a Phase portrait, b, c time trajectories, and d projected Poincaré section for $\sigma _{2}=68.0851$

Table 2 The parametric frequency detuning parameter values at a, b, c, and d

Fig. 27

a Phase portrait and b projected Poincaré section for $\sigma _{2}=68.1935$

Substituting Eq. (15) into Eq. (10) yields

$$\begin{aligned}&D_0^2 w_1+2v_0 D_0 w_1^{\prime }+\left( v_0^2-1\right) w_1^{\prime \prime }+k_f^2 w_1^{\prime \prime \prime \prime }\nonumber \\&\quad =\varGamma _{1} e^{i\omega _{1}T_0}+\varGamma _{2} e^{i\omega _{2}T_0}+\varGamma _{3} e^{i\left( -\omega _{1}+\varOmega _{0}\right) T_{0}}\nonumber \\&\qquad \quad +\,\varGamma _{4} e^{i\left( \omega _{1}+\varOmega _{0}\right) T_{0}}+\varGamma _{5} e^{i\left( -\omega _{1}+\varOmega _{1}\right) T_{0}}\nonumber \\&\qquad \quad +\,\varGamma _{6} e^{i\left( \omega _{1}+\varOmega _{1}\right) T_{0}}+\varGamma _{7} e^{i\left( -\omega _{2}+\varOmega _{0}\right) T_{0}}\nonumber \\&\qquad \quad +\,\varGamma _{8} e^{i\left( \omega _{2}+\varOmega _{0}\right) T_{0}}+\varGamma _{9} e^{i\left( -\omega _{2}+\varOmega _{1}\right) T_{0}}\nonumber \\&\qquad \quad +\,\varGamma _{10} e^{i\left( \omega _{2}+\varOmega _{1}\right) T_{0}}+\varGamma _{11} e^{3i\omega _{1}T_{0}}+\varGamma _{12} e^{i\left( 2\omega _{1}+\omega _{2}\right) T_{0}}\nonumber \\&\qquad \quad +\,\varGamma _{13} e^{i\left( \omega _{1}+2\omega _{2}\right) T_{0}}+\varGamma _{14} e^{3i\omega _{2}T_{0}}+\varGamma _{15} e^{i\left( 2\omega _{2}-\omega _{1}\right) T_{0}}\nonumber \\&\qquad \quad +\,\varGamma _{16} e^{i\left( \omega _{2}-2\omega _{1}\right) T_{0}}+cc, \end{aligned}$$

(16)

where the $\varGamma _{n}$ are defined in Appendix.

It is observed that Eq. (16) will contain secular terms when $\varOmega _{0}\approx 2\omega _{1}$ or $\varOmega _{1}\approx 2\omega _{2}$. Hence, frequency detuning parameters $\sigma _{1}$, $\sigma _{2}$ and $\sigma _{3}$ are used to describe the nearness of $\omega _{2}$ to 3$\omega _{1}$, $\varOmega _{0}$ to $2\omega _{1}$ and $\varOmega _{1}$ to $2\omega _{2}$. And then, the nearness relations of these frequencies can be expressed as

$$\begin{aligned} \omega _{2}=3\omega _{1}+\varepsilon \sigma _{1}, \varOmega _{0}=2\omega _{1}+\varepsilon \sigma _{2}, \text {and} \,\varOmega _{1}=2\omega _{2}+\varepsilon \sigma _{3}. \end{aligned}$$

(17)

Fig. 28

a Phase portrait and b projected Poincaré section for $\sigma _{2}=317.5002$

In this case, the combined parametric resonance type, $\varOmega _{0}=\omega _{2}-\omega _{1}+\varepsilon \left( \sigma _{2}-\sigma _{1}\right)$, is also considered. Substituting Eq. (17) into Eq. (16) yields

$$\begin{aligned}&D_0^2 w_1+2v_0 D_0 w_1^{\prime }+\left( v_0^2-1\right) w_1^{\prime \prime }+k_f^2 w_1^{\prime \prime \prime \prime }\nonumber \\&\quad =\varGamma _{1}e^{i\omega _{1}T_{0}}+\varGamma _{2}e^{i\omega _{2}T_{0}}+\varGamma _{3}e^{i\left( \omega _{1}T_{0}+\sigma _{2}T_{1}\right) }\nonumber \\&\qquad +\varGamma _{4}e^{i\left( \omega _{2}T_{0}-\sigma _{1}T_{1}+\sigma _{2}T_{1}\right) }+\varGamma _{9}e^{i\left( \omega _{2}T_{0}+\sigma _{3}T_{1}\right) }\nonumber \\&\qquad +\varGamma _{11}e^{i\left( \omega _{2}T_{0}-\sigma _{1}T_{1}\right) }+\varGamma _{16}e^{i\left( \omega _{1}+\sigma _{1}T_{1}\right) }+cc+\text {NST}, \end{aligned}$$

(18)

where NST stands for terms that do not bring secular or small-divisor terms into solution. The homogeneous part of Eq. (18) has a nontrivial solution, so the corresponding nonhomogeneous part will has a solution. For this, the solvability condition is only satisfied [46]. To achieve it, the right-hand side of Eq. (18) should be orthogonal to the solution of adjoint homogeneous problem. These conditions demand that

$$\begin{aligned} \int _{0}^{1}\left( \varGamma _{1}+\varGamma _{3}e^{i\sigma _{2}T_{1}} +\varGamma _{16}e^{i\sigma _{1}T_{1}}\right) \bar{\phi }_{1}\text {d}x=0, \end{aligned}$$

(19)

and

$$\begin{aligned}&\int _{0}^{1}\left( \varGamma _{2}+\varGamma _{4}e^{i\left( \sigma _{2}T_{1} -\sigma _{1}T_{1}\right) }+\varGamma _{9}e^{i\sigma _{3}T_{1}} \right. \nonumber \\&\quad \left. +\varGamma _{11}e^{-i\sigma _{1}T_{1}}\right) \bar{\phi }_{2}\text {d}x=0. \end{aligned}$$

(20)

Fig. 29

a, b Phase portraits, c, d time trajectories, and e, f projected Poincaré sections: a, c, e $\sigma _{2}=317.5934$; b, d, f $\sigma _{2}=320.2881$. FFT power spectra for $p_{1}$ are shown in (a) and (b)

Substituting $\varGamma _{n}(n=1,\,2,\,3,\,4,\,9,\,11,\,16)$ from Appendix into Eqs. (19) and (20), modulation equations are obtained as

$$\begin{aligned}&2A_{1}^{\prime }+8H_{1}A_{1}^{2}\bar{A}_{1}+8H_{2}A_{1}A_{2}\bar{A}_{2}+2\alpha E_{1}A_{1}\nonumber \\&\quad +2G_{1}\bar{A}_{1}e^{i\sigma _{2}T_{1}}+8K_{5}A_{2}\bar{A}_{1}^{2}e^{i\sigma _{1}T_{1}}=0, \end{aligned}$$

(21)

and

$$\begin{aligned}&2A_{2}^{\prime }+8H_{3}A_{2}^{2}\bar{A}_{2}+8H_{4}A_{1}A_{2}\bar{A}_{1}+2\alpha E_{2}A_{2}\nonumber \\&\quad +2G_{2}A_{1}e^{i\left( \sigma _{2}T_{1}-\sigma _{1}T_{1}\right) }+2G_{3}\bar{A}_{2}e^{i\sigma _{3}T_{1}}\nonumber \\&\quad +8K_{4}A_{1}^{3}e^{-i\sigma _{1}T_{1}}=0, \end{aligned}$$

(22)

where the prime denotes derivative with respect to the slow time $T_{1}$, overbar indicates the complex conjugate terms. The detailed representation of nonlinear coefficients of Eqs. (21) and (22) is presented in Appendix. For the stability of trivial state, the polar transform of complex amplitudes $A_{n}$ is impossibility [47]. In what follows, $A_{n}$ are expressed in Cartesian form as

$$\begin{aligned} A_{n}=\dfrac{1}{2}\left[ p_{n}\left( T_{1}\right) -iq_{n}\left( T_{1}\right) \right] e^{i\lambda _{n}\left( T_{1}\right) },\qquad n=1,2 \end{aligned}$$

(23)

Substituting Eq. (23) into Eqs. (21) and (22) yields

$$\begin{aligned} p_{1}^{\prime }&=-\mu _{1}q_{1}-H_{1R}\left( p_{1}^{3}+p_{1}q_{1}^{2}\right) -H_{1I}\left( p_{1}^{2}q_{1}+q_{1}^{3}\right) \nonumber \\&\quad -H_{2R}\left( p_{1}p_{2}^{2}+p_{1}q_{2}^{2}\right) -H_{2I}\left( q_{1}p_{2}^{2}+q_{1}q_{2}^{2}\right) \nonumber \\&\quad -\alpha p_{1}E_{1R}-\alpha q_{1}E_{1I}-p_{1}G_{1R}+q_{1}G_{1I}\nonumber \\&\quad -K_{5R}\left( p_{1}^{2}p_{2}-q_{1}^{2}p_{2}+2p_{1}q_{1}q_{2}\right) \nonumber \\&\quad +K_{5I}\left( 2p_{1}q_{1}p_{2}-p_{1}^{2}q_{2}+q_{1}^{2}q_{2}\right) , \end{aligned}$$

(24)

$$\begin{aligned} q_{1}^{\prime }&=\mu _{1}p_{1}-H_{1R}\left( p_{1}^{2}q_{1}+q_{1}^{3}\right) +H_{1I}\left( p_{1}^{3}+p_{1}q_{1}^{2}\right) \nonumber \\&\quad -H_{2R}\left( q_{1}p_{2}^{2}+q_{1}q_{2}^{2}\right) +H_{2I}\left( p_{1}p_{2}^{2}+p_{1}q_{2}^{2}\right) \nonumber \\&-\alpha q_{1}E_{1R}+\alpha p_{1}E_{1I}+q_{1}G_{1R}+p_{1}G_{1I}\nonumber \\&\quad +K_{5R}\left( 2p_{1}q_{1}p_{2}-p_{1}^{2}q_{2}+q_{1}^{2}q_{2}\right) \nonumber \\&\quad +K_{5I}\left( 2p_{1}q_{1}q_{2}+p_{1}^{2}p_{2}-q_{1}^{2}p_{2}\right) , \end{aligned}$$

(25)

$$\begin{aligned} p_{2}^{\prime }&=-\mu _{2}q_{2}-H_{3R}\left( p_{2}^{3}+p_{2}q_{2}^{2}\right) -H_{3I}\left( p_{2}^{2}q_{2}+q_{2}^{3}\right) \nonumber \\&\quad -H_{4R}\left( p_{1}^{2}p_{2}+q_{1}^{2}p_{2}\right) \nonumber \\&\quad -H_{4I}\left( p_{1}^{2}q_{2}+q_{1}^{2}q_{2}\right) -\alpha p_{2}E_{2R}-\alpha q_{2}E_{2I}\nonumber \\&\quad -p_{1}G_{2R}-q_{1}G_{2I}-p_{2}G_{3R}+q_{2}G_{3I}\nonumber \\&\quad -K_{4R}\left( p_{1}^{3}-3p_{1}q_{1}^{2}\right) +K_{4I}\left( q_{1}^{3}-3p_{1}^{2}q_{1}\right) , \end{aligned}$$

(26)

$$\begin{aligned} q_{2}^{\prime }&=\mu _{2}p_{2}-H_{3R}\left( p_{2}^{2}q_{2}+q_{2}^{3}\right) +H_{3I}\left( p_{2}^{3}+p_{2}q_{2}^{2}\right) \nonumber \\&\quad -H_{4R}\left( p_{1}^{2}q_{2}+q_{1}^{2}q_{2}\right) \nonumber \\&\quad +H_{4I}\left( p_{1}^{2}p_{2}+q_{1}^{2}p_{2}\right) -\alpha q_{2}E_{2R}+\alpha p_{2}E_{2I}\nonumber \\&\quad -q_{1}G_{2R}+p_{1}G_{2I}+q_{2}G_{3R}+p_{2}G_{3I}\nonumber \\&\quad +K_{4R}\left( q_{1}^{3}-3p_{1}^{2}q_{1}\right) +K_{4I}\left( p_{1}^{3}-3p_{1}q_{1}^{2}\right) , \end{aligned}$$

(27)

where

$$\begin{aligned} \mu _{1}&=\dfrac{\sigma _{2}}{2},\; \mu _{2}=\dfrac{3\sigma _{2}}{2}-\sigma _{1},\; \sigma _{3}=3\sigma _{2}-2\sigma _{1}, \end{aligned}$$

(28)

$$\begin{aligned} \lambda _{1}&=\dfrac{\sigma _{2}T_{1}}{2}-n\pi ,\; \lambda _{2}{=}\dfrac{3\sigma _{2}T_{1}}{2}-\sigma _{1}T_{1}{-}3n\pi +2m\pi . \end{aligned}$$

(29)

Fig. 30

a, b Phase portraits and c, d projected Poincaré sections: a, c $\sigma _{2}=378.00298$. FFT power spectra for $p_{1}$ are shown in (a) and (b)

4 Numerical results and discussions

In this section, a great number of numerical results are carried out to study the viscoelastic sandwich beam by considering flexural stiffness $k_\mathrm{f}=0.214$ and the book keeping parameter $\varepsilon =0.01$. In current research, the mean traveling velocity is considered as $v_{0}=0.6$ firstly. Depending on the value of the mean moving velocity, the related parameter values are internal detuning parameter $\sigma _{1}=57.87$ and the first two natural frequencies $\omega _{1}=3.1021$ and $\omega _{2}=9.8850$.

4.1 One parameter analysis

It is known that periodic motions of the beam are correspond to equilibrium solutions of Eqs. (24)–(27). These equilibrium solutions are numerically solved by setting $p_{i}^{\prime }=q_{i}^{\prime }=0$ in Eqs. (24)–(27). The frequency and amplitude response analyses are focused on the variation of system parameters including axially harmonic velocity and tension, and internal and parametric frequency detuning parameters of the beam. A pseudo-arclength continuation algorithm [48] is applied to obtain the branches of equilibrium solutions involving specific values of system variables. The bifurcation and stability of a fixed point is determined by the eigenvalues of the corresponding Jacobian matrix given by Eqs. (24)–(27). Note that the amplitudes of the first mode $a_{1}$ and second mode $a_{2}$ are calculated from $a_{k}=\left( p_{k}^{2}+q_{k}^{2}\right) ^{1/2}$.

Fig. 31

Lyapunov exponents for $\sigma _{2}=378.00298$

Obviously, the equilibrium analysis is confined to reveal system behavior [8]. In order to settle the limits of equilibrium solutions, dynamic solutions of the system such as periodic, quasiperiodic, and chaotic responses are taken into investigation.

Fig. 32

a, b Phase portraits, c time trajectory, and d projected Poincaré section for $\sigma _{2}=374.8555$. FFT power spectra for $p_{1}$ and $p_{2}$ are shown in (a) and (b), respectively

Fig. 33

a Phase portrait and b projected Poincaré section for $\sigma _{2}=63.6768$. FFT power spectrum for $p_{1}$ is shown in (a)

4.1.1 Stability and bifurcation analysis

Frequency response analysis Typical frequency response curves for first and second modes are shown in Figs. 3 and 4. The system parameters are considered as $v_{1}=10$ and $p=10$. In the following investigation, $P_{0}$ is assumed to be a fixed initial tension. Therefore, p denotes the influence of fluctuating tension, whereas $v_{1}$ represents the influence of harmonic velocity disturbance. According to the eigenvalues of the Jacobian matrix, equilibrium solutions are divided into three parts including stable solutions(solid lines), saddles(dashed lines), and unstable foci(bold lines). As we can see, the frequency response curves display a hardening-spring nonlinear feature. As $\sigma _{2}$ increases, the trivial solution loses stability at supercritical pitchfork bifurcation point a ($\sigma _{2}=-13.282079$), leading to two-mode equilibrium solutions. Also, the amplitude of the first mode is firstly increased and then decreased. On this branch, the equilibrium solution loses stability through a Hopf bifurcation at $\text {H}_{1}$ ($\sigma _{2}=13.653545$), where a pair of complex conjugate eigenvalues crosses the imaginary axis of complex plane from left side to right side. But it regains stability through a reverse Hopf bifurcation at $\text {H}_{2}$ ($\sigma _{2}=73.628133$), resulting the existence of limit cycles between $\text {H}_{1}$ and $\text {H}_{2}$. However, the stability of Hopf bifurcation points $\text {H}_{1}$ and $\text {H}_{2}$ are obtained by the application of normal form theory and the calculation of cubic coefficient given in Ref. [49]. It follows from Fig. 3b that, as $\sigma _{2}$ increases further, the amplitude of the first mode decreases at saddle-node bifurcation $\text {SN}_{1}$ ($\sigma _{2}=97.100664$). Then, the system response gives way to either a two-mode equilibrium solution, or a dynamic solution, or the trivial solution [50]. At $\sigma _{2}=116.065709$, the equilibrium solution encounters a limit point $\text {SN}_{2}$, resulting in the secondary reduction of amplitude of the first mode. Furthermore, this branch has another Hopf bifurcation at $\text {H}_{3}$ ($\sigma _{2}=173.066084$). The trivial solution loses stability at point b ($\sigma _{2}=13.282079$) through subcritical pitchfork bifurcation by increasing $\sigma _{2}$ from point a. Increasing $\sigma _{2}$ beyond $\text {SN}_{3}$ in the nontrivial state, the response jumps to stable solution and the amplitude of the first mode is decreased. The branch has Hopf bifurcation $\text {H}_{4}$ ($\sigma _{2}=42.883581$) and $\text {H}_{5}$ ($\sigma _{2}=41.553177$), as shown in Fig. 3d. In Fig. 3e, corresponding to part D of Fig. 3a, supercritical and subcritical pitchfork bifurcation points are, respectively, represented as c and d. Also, the numerical result presented in Fig. 3e illustrates other bifurcation information such as e ($\sigma _{2}=40.954068$) and f ($\sigma _{2}=52.825190$).

Figure 4a shows the amplitude of the second mode against frequency detuning parameter $\sigma _{2}$. The parts E, F, and G are zoomed in Fig. 4b–d, respectively. Comparing Fig. 3e with Fig. 4a and e, the branch from pitchfork bifurcation point c ($\sigma _{2}=32.407297$) obviously has supercritical and subcritical pitchfork bifurcation points e and f, respectively. Similarly, the nontrivial solution branch from subcritical pitchfork bifurcation point d ($\sigma _{2}=44.752703$) has two points g and h. But g ($\sigma _{2}=58.816441$) and h ($\sigma _{2}=70.687547$) are not supercritical or subcritical pitchfork point. And it is noted that the amplitudes of the second mode from points c and d are not equal to zero significantly, comparing with the variation of amplitudes of the first mode in Fig. 3. Physically speaking, this is related to energy transfer between the first two modes. Moreover, there are four pitchfork bifurcation points (a, b, c, and d) existing on trivial solution branch.

Fig. 34

a Phase portrait and b projected Poincaré section for $\sigma _{2}=51.9850$. FFT power spectrum for $p_{1}$ is shown in (a)

Fig. 35

a Eigenvalue movement and b Hopf bifurcation curves: a the arrows denote the direction of eigenvalue movement with increasing $\sigma _{2}$; b solid lines and dashed lines denote supercritical and subcritical Hopf bifurcation curves, respectively

Influence of amplitude of velocity harmonic component To further study the effect of the velocity harmonic component, the variations of the parametric frequency detuning parametric versus the amplitudes of the first two interacting modes are, respectively, discussed. Figures 5 and 6 show response amplitudes by considering $v_{1}=20$ and $p=10$. It can be observed that these response curves are similar to Figs. 3 and 4, respectively. In addition, there are still four pitchfork bifurcation points containing a, b, c, and d on the trivial solution branch. It is obvious that unstable interval ($\text {c}$–$\text {d}$) of trivial solution has broadened. However, unstable part ($\text {a}$–$\text {b}$) is invariant. And the interval between Hopf bifurcation points $\text {H}_{1}$ and $\text {H}_{2}$ has also broadened. Furthermore, points e ($\sigma _{2}=32.022876$) and f ($\sigma _{2}=43.893995$) appear between pitchfork bifurcation points c ($\sigma _{2}=26.234594$) and d ($\sigma _{2}=50.925406$), comparing to the case of c and d shown in Fig. 3e.

Influence of amplitude of fluctuating axial tension component The influence of amplitude of fluctuating axial tension component is shown in Figs. 7 and 8. For the case of $v_{1}=10$ and $p=40$, there are slight changes for the response curves, comparing to these curves shown in Fig. 3. Obviously, one may find an important difference about the number of pitchfork bifurcation points in the trivial state. There are only two pitchfork bifurcation points shown in Fig. 8e and f, corresponding to supercritical bifurcation ($\text {a}$) and subcritical bifurcation ($\text {b}$), respectively. In addition, some new Hopf bifurcation points appear, such as $\text {H}_{5}$ ($\sigma _{2}=394.073620$) and $\text {H}_{6}$ ($\sigma _{2}=403.434746$) in Fig. 7a or 8a and $\text {H}_{3}$ ($\sigma _{2}=163.405251$) in Fig. 7b or 8d. In contrast, some Hopf bifurcation points like $\text {H}_{4}$ and $\text {H}_{5}$ are vanish in Figs. 7 and 8. In which, by increasing the value of $\sigma _{2}$, the amplitudes of the first and second modes are monotonously increased from point b. It is obvious that the instability region ($\text {a}$–$\text {b}$) of trivial solution branch is broadened, comparing to a and b in Fig. 3a. It indicates that the harmonic component of axial tension increases the strength of nonlinear modal interaction.

Fig. 36

a Phase portrait and b projected Poincaré section for $v_{1}=6.3249$ and $p=2.5287\times 10^{-4}$. FFT power spectrum for $p_{1}$ is shown in (a)

Fig. 37

a, b Lyapunov exponents: a $v_{1}=6.3249$, $p=2.5287\times 10^{-4}$; b $v_{1}=3.2296$, $p=-\,0.3332$

Influence of amplitudes of fluctuating velocity and tension componentsIn this subsection, the coupled effects of amplitudes of fluctuating velocity and tension components on frequency response curves have been analyzed by the variation of frequency detuning parameter $\sigma _{2}$. Figures 9 and 10, respectively, show similar response curves with the previous case for $v_{1}=10$ and $p=40$. The unstable trivial solution region ($\text {a}$–$\text {b}$) keeps the same with the previous case. But the differences are the interval between Hopf bifurcation points $\text {H}_{5}$ and $\text {H}_{6}$ is broadened, and the stability associated with $\text {H}_{1}$ and $\text {H}_{2}$ is drastically reduced. As evident from Fig. 10e and f, the pitchfork bifurcation points in the trivial solution curve are still a and b.

In Table 2, the parametric frequency detuning parameter values (a, b, c, and d) are displayed. In contrast with the first case of $v_{1}=10$ and $p=10$, the pitchfork bifurcation points ($\text {c}$, $\text {d}$) in the second case are influenced by the fluctuating velocity $v_{1}$. It is noted that the instability range between c and d is substantially increased, comparing with the first case. In the light of the third case for $v_{1}=10$ and $p=40$, the pitchfork bifurcation points ($\text {a}$, $\text {b}$) are moved toward both sides, whereas the points $\text {c}$ and $\text {d}$ are not about pitchfork bifurcation, comparing with the first two cases. This is induced by the fluctuating tension component associated with axial tension. The similar phenomena can be observed from the last case for $v_{1}=20$ and $p=40$.

Fig. 38

a Projected Poincaré section and b time trajectory for $v_{1}=3.2296$ and $p=-\,0.3332$

Fig. 39

a Projected Poincaré section and b time trajectory for $v_{1}=3.2192$ and $p=-\,0.3364$

Influence of internal frequency detuning parameter Figures 11, 12 and 13 demonstrate frequency response curves with the variation of internal frequency detuning parameter. Also, $v=10$ and $p=10$ are considered to be used for analysis. For $\sigma _{1}=-48.06$ at mean velocity $v_{0}=0.3$, the trivial solution branch has four pitchfork bifurcation points (a and c are supercritical bifurcation, b and d are subcritical bifurcation), as shown in Fig. 11. It follows from Fig. 11 that, as $\sigma _{2}$ increases past a and b, the amplitude of the first mode $a_{1}$ is about zero and the amplitude of the second mode $a_{2}$ grows all the way. However, the amplitudes of both modes are monotonously increased on the nontrivial solution branches from c and d. Notice that the system response has not up to the condition of internal resonance, resulting in no bifurcation information (Hopf bifurcation, saddle-node bifurcation, and so on) does not appear. As we can observe in Fig. 12, it only has two pitchfork bifurcation points containing a ($\sigma _{2}=-13.085202$) and b ($\sigma _{2}=13.085202$) given by the symmetric form. Clearly, the results presented in Fig. 12 are similarly to the case shown in Fig. 7. It indicates that parameter variables are in the vicinity of points c and d; the amplitude of the first mode is about zero. It is worth mentioning that harmonically varying components of parametric excitation and internal resonance in the parametric study, the dynamical system will demonstrate the existence of pitchfork bifurcation phenomena in trivial solution curves. It is same with the analysis in Ref. [8]. Besides this, the saddle-node bifurcation $\text {SN}_{2}$ is changed into Hopf bifurcation $\text {H}_{4}$ comparing with these cases shown in Figs. 3a, 5a, 7b and 9a. In the following analysis, the amplitude response curves are discussed.

Fig. 40

a, b Phase portraits, c projected Poincaré section, and d time trajectory for $v_{1}=0.3796$ and $p=0.2211$

Amplitude response analysis By considering the variation of amplitude of the fluctuating axial velocity, the amplitude response curves are shown in Figs. 14 and 15. With decreasing fluctuating velocity $v_{1}$ from 30, the trivial solution loses stability at subcritical pitchfork bifurcation point a ($v_{1}=13.152531$). Figure 14c shows the amplitude of the first mode remains unchanged in the nontrivial solution curve. In contrast, a significant increasing in the amplitude of the second mode is observed before the saddle-node bifurcation $\text {SN}_{1}$ ($v_{1}=0.005714$) appears. After that, with the increasing of moving velocity $v_{1}$, the corresponding response amplitude for the second mode is continuously increased. It also obviously has isolated two-mode solutions, as shown in Fig. 15a. Corresponding to the two-mode solutions, some bifurcation points such as $\text {H}_{2}$ ($v_{1}=0.338328$), $\text {H}_{3}$ ($v_{1}=0.257388$), $\text {SN}_{2}$ ($v_{1}=0.231428$) and $\text {SN}_{3}$ ($v_{1}=1.774630$) are presented in Figs. 14b and 15b.

Figures 16 and 17 show amplitude response curves for $v_{1}=10$, $\sigma _{1}=57.87$, and $\sigma _{2}=100$. With the decrease in axially harmonic tension, the unstable trivial solution loses stability at subcritical pitchfork bifurcation point a ($p=75.289412$), resulting in the response jumps to nontrivial solution. In addition, as the fluctuating load p decreases, the amplitude of the second mode increases monotonically. But for the first mode, it remains unchanged. In addition to this, the majority of bifurcation information are zoomed in Figs. 16b and 17b, d, containing Hopf bifurcation point $\text {H}_{1}$ and limit points $\text {SN}_{i}$ ($i=1,2,3,4$). In contrast with the above case, the equilibrium solutions of the first and second modes display much more complexities. And it is shown that bifurcation points are mostly appearing in the vicinity of low values of p.

Fig. 41

a, b, c, d Projected Poincaré sections: a, b $v_{1}=0.2307$, $p=4.9121$; c $v_{1}=0.2322$, $p=5.0463$; d $v_{1}=0.2321$, $p=5.0298$

Fig. 42

a, b, c, d Phase portraits, e, f projected Poincaré sections: a, c, e $v_{1}=-5.4514$, $p=0.1112$; b, d, f $v_{1}=-5.3248$, $p=0.2004$

Influence of internal frequency detuning parameter In order to analyze the detuning parameter $\sigma _{1}$, the typical parameters are $-48.06$ and $5.6553\times 10^{-4}$ selectively. In Figs. 18 and 19, with the increasing of amplitude of fluctuating velocity component, some qualitative changes are depicted. The trivial solution loses stability through subcritical pitchfork bifurcation at a from $v _{1}=21.982532$ ($\sigma _{1}=-48.06$) to $v _{1}=16.649136$ ($\sigma _{1}=5.6553\times 10^{-4}$). Also, the stable trivial solution decreases through pitchfork bifurcation at a from $p =76.764052$ ($\sigma _{1}=-48.06$) to $p =76.422185$ ($\sigma _{1}=5.6553\times 10^{-4}$). Moreover, a new saddle-node bifurcation appears at $\text {SN}_{3}$ in Fig. 19, comparing with Fig. 18. Besides this, with increasing $\sigma _{1}$, these branches ($\text {H}_{1}$–$\text {H}_{2}$, $\text {SN}_{3}$–$\text {H}_{5}$) have broadened and new Hopf bifurcation point $\text {H}_{4}$ and limit point $\text {SN}_{2}$ appear in the vicinity of point b. All these phenomena are displayed in Figs. 20 and 21. Comparing with the case of $\sigma _{1}=57.87$, various bifurcation points containing saddle-node bifurcation point $\text {SN}_{3}$ and Hopf bifurcation point $\text {H}_{2}$ are displayed. Typically at lower values of p, the equilibrium solution has two limit points containing $\text {SN}_{4}$ and $\text {SN}_{5}$.

Influence of parametric frequency detuning parameter In the present study, the effect of the parametric frequency detuning parameter is discussed. The results presented herein are for $\sigma _{2}=20$, which are compared to numerical simulation obtained by the case of $\sigma _{2}=100$. From Fig. 22c, the amplitude of the second mode monotonously increases through supercritical pitchfork bifurcation at a ($v _{1}=6.953105$), displaying a hardening-spring behavior. It can be observed that increasing fluctuating velocity component results in supercritical and subcritical pitchfork bifurcation points displayed in parts E and D, respectively. In contrast with the case of $\sigma _{2}=100$, the amplitude of the second mode displays soft-spring feature firstly. For some certain ranges of parameter values, Hopf bifurcations at $\text {H}_{1}$ ($v _{1}=7.729802$) and $\text {H}_{2}$ ($v _{1}=7.738442$), and saddle-node bifurcation at $\text {SN}_{1}$ ($v _{1}=8.090234$) exist in region E. Also, there are Hopf bifurcation at $\text {H}_{5}$ ($v _{1}=10.799705$) and saddle-node bifurcation at $\text {SN}_{3}$ ($v _{1}=10.799570$) in region D. It follows from Fig. 23 that, as the fluctuating loading increases, the nontrivial amplitudes of both modes are increased monotonically. Comparing with the case of $\sigma _{2}=100$, the amplitude of the second mode is significantly reduced in the present case. Furthermore, the number of bifurcation points on the nontrivial equilibrium solutions is substantially reduced. And saddle-node bifurcation points ($\text {SN}_{1}$, $\text {SN}_{2}$) appear in the region of $0<p<0.1$. In addition, the nontrivial solution curves follow from Hopf bifurcation at $\text {H}_{1}$ that remain stability.

4.1.2 Dynamic solutions

The analysis of dynamic behavior of the system is focused on the phenomena in the form of periodic, quasiperiodic, and chaotic responses, depending on initial conditions. Firstly, the system variables are, respectively, taken as: $k_{f}=0.214$; $v_{0}=0.6$; $v_{1}=10$; $p=10$; $\sigma _{1}=57.87$. As indicated in Fig. 3, frequency response curves are displayed. By calculating the first Lyapunov coefficient [49], it is known that $\text {H}_{2}$ is a supercritical Hopf bifurcation point. Therefore, the stable limit cycles are resulted in the vicinity of $\text {H}_{2}$, corresponding to the quasiperiodic response of beam. For chaotic motion, system has least one positive Lyapunov exponent. So the largest Lyapunov exponent is always considered to indicate the existence of chaotic response in the parameter region of system. As $\sigma _{2}$ decreases to 72.8159, the system response is demonstrated in Fig. 24. It can be observed that the Poincaré section displayed in Fig. 24b is closed loops, indicating the system response is quasiperiodic. And its phase portrait and power spectrum are also displayed in Fig. 24a. By decreasing $\sigma _{2}$ further, typically at $\sigma _{2}=63.1816$, it leads to chaotic response, forming two large chaotic attractors. From Fig. 24 to Fig. 25, it is noted that nontrivial responses have continued to deform with decreasing $\sigma _{2}$. Finally, the chaotic attractors are formed. These are about the formation and breakdown of tori. The corresponding dynamic behaviors are sensitive to initial conditions. At typical parameter values of $\sigma _{2}$, the results called ‘periodic windows’ are obtained from the following study. Figure 26 shows period-two in both modes at $\sigma _{2}=68.0851$. Typically at $\sigma _{2}=68.1935$, the dynamical motion is depicted by the form of time trajectory and two-dimensional projection on the $p_{1}$–$q_{1}$ plane. From the Poincaré section, it can be identified that the response is period-three, as shown in Fig. 27b.

In the following analysis, complex dynamic behaviors are represented for higher values of fluctuating velocity and even fluctuating tension. Some similar behaviors are also displayed selectively when $k_{f}=0.214$, $v_{0}=0.6$, $v_{1}=20$, $p=40$ and $\sigma _{1}=57.87$. In Fig. 10, there are two supercritical Hopf bifurcation points, namely $\text {H}_{5}$ ($\sigma _{2}=317.313860$) and $\text {H}_{6}$ ($\sigma _{2}=410.245395$). Increasing $\sigma _{2}$ few from $\text {H}_{5}$, it is observed that the system response is periodic-one, as shown in Fig. 28. Also, the quasiperiodic response is observed by the four-torus feature of Poincaré section shown in Fig. 29e. At the right side of Fig. 29, the system exhibits chaotic behavior as illustrated by phase portrait, time trace and two-dimensional projection on $p_{1}$–$q_{1}$ plane at $\sigma _{2}=320.2881$. On the same branch, the system response encounters Neimark–Sacker bifurcation, typically at $\sigma _{2}=371.9448$, indicating a torus bifurcation. As can be seen from the Poincaré section in Fig. 30c, the corresponding dynamic motion of the beam is chaotic. A more pronounced difference is that FFT power spectrum is not always the critical tool for some special parameters, including the chaotic motion displayed in Fig. 30a. As already stated before, the largest Lyapunov exponent is always used to determine the existence of chaotic response when the chaotic behavior is not obvious. For this, the convergent form of the lyapunov exponents is shown in Fig. 31. Then, the system encounters Fold bifurcation of limit cycle at $\sigma _{2}=378.0029825$, resulting in a jump of the system response. Increasing $\sigma _{2}$ beyond it, the system shows a jump phenomenon as depicted by two-torus feature of Poincaré section shown in Fig. 30d. This means that the system is in a slow motion along the branch from $\text {H}_{5}$ until it reaches the bifurcation point, that is, at $\sigma _{2}=378.0029825$. And then, it follows from Fig. 30d that, as the detuning parameter $\sigma _{2}$ increases, the system response jumps to the branch from $\text {H}_{6}$ in a fast motion. As can be observed in Fig. 32c, there is the magnification of the time trace. In Fig. 32d, the Poincaré section is represented by three closed loops, which is agreement with the phenomenon shown in Fig. 32c. The above results are illustrated by high values of parametric frequency detuning parameter $\sigma _{2}$.

Similarly, for some lower values of detuning parameter $\sigma _{2}$, the system also has a wide range of dynamic behavior. For example, at $\sigma _{2}=63.6768$, the system exhibits a quasiperiodic motion as displayed by projected Poincaré section in Fig. 33b. On the same branch at $\sigma _{2}=51.9850$, the chaotic behavior of torus breakdown is shown in Fig. 34. These dynamic behaviors are attributed to internal resonance and the harmonically oscillation of parametric excitation.

4.2 Two parameters analysis

As seen before, a nonlinear autonomous system has various complex dynamic behaviors characterized in the vicinity of critical points. As discussed before, simultaneous effect has various interesting phenomena for dynamical systems. In the subsection, the parameter analysis is mainly focused on the analysis of two parameters (axial velocity and axial tension) by tracing bifurcation curves of codimension one. Figures 3a and 9a show the frequency response curves with coupled effects of fluctuating velocity component and axial tension component. Note that the same type of Hopf bifurcation point from Figs. 3a and 9a are, respectively, labeled as m and n, as shown in Fig. 35. The movement of relevant eigenvalues, starting from $\sigma _{2}=50$, is shown in Fig. 35a. Increasing $\sigma _{2}$, the unstable complex eigenvalues move toward the left half plane and cross the imaginary axis at $0-22.014i$(m) and $0-63.340i$(n), developing the occurrence of Hopf bifurcation. It follows from Fig. 35a that, as $\sigma _{2}$ increases to 90, the rest of eigenvalues are on the left side of complex plane. In the second study, Hopf bifurcation curves on p–$v_{1}$ plane are displayed in Fig. 35b. In which, the m and n denote the same Hopf bifurcation points in Fig. 35a. The solid lines denote supercritical Hopf bifurcation, and the dashed one for subcritical Hopf bifurcation. Clearly, various supercritical and subcritical Hopf bifurcation curves varying parameters $v_{1}$ and p are interweaved together. Specially, a more pronounced parameter region is observed in the vicinity of zero, indicating complex dynamic behaviors are resulted here. Therefore, the following discussions are carried out to investigate the simultaneous effect of parameters $v_{1}$ and p in some special parameter zones.

According to Jacobian matrix of the system, the characteristic roots of Jacobian matrix at critical points are calculated. For this, different types of codimension two singularities are found. Meanwhile, bifurcation phenomena can be found near these singularities. This section is focused on dynamic behaviors of the system by varying the dominant variables $v_{1}$ and p simultaneously. In Fig. 36, the value of fluctuating axial tension is sufficiently small, where the system response is dominated by velocity fluctuation. In this figure, chaotic phenomenon is exhibited at $v_{1}=6.3249$. It is clearly that the contours of tori are broken, as shown in Fig. 36b. Also, the convergent form of the lyapunov exponents is displayed in Fig. 37a, performing a small amplitude motion. However, the largest Lyapunov exponent is still greater than zero, indicating the chaotic motion. Here, the value of p is negative, namely the initial tension $P_{0}$ remains unchanged and associated harmonic component makes the total axial tension P less than the initial tension. Therefore, it has practical meaning for restricting axial tension. As indicated in Fig. 37b, at $v_{1}=3.2296$ and $p=-\,0.3332$, the corresponding largest Lyapunov exponent is beyond zero. However, from the projected Poincaré section displayed in Fig. 38a, there is no apparent change about the tori. For another bifurcation analysis at $v_{1}=3.2192$ and $p=-\,0.3364$, it leads to torus breakdown obviously, performing in Fig. 39.

For parametric frequency detuning parameter $\sigma _{2}=63.676910$, the system also presents dynamic solutions for typical system parameters. Here, a few of them are depicted selectively. Figure 40 shows an attracting invariant ellipse as described by two-dimension Poincaré section on $q_{2}$–$p_{2}$ plane, indicating quasiperiodic behavior. It can be seen that the phase portrait shown in Fig. 40b is complex when compared to other ones. This is due to its Floquet multipliers. In particular, the time trace has regions which are out of the boundaries of wave form. Results indicate that the coupled effects of tori may occur at special parameters. As shown in Fig. 41a and b, chaotic motion is observed at $v_{1}=0.2307$ and $p=4.9121$. However, for the values $v_{1}=0.2321$ and $p=5.0298$, one can observe that the existence of quasiperiodic solution. Thus, the system has a transient dynamic phenomenon which is depicted in Fig. 41c. In the following, the axial velocity is assumed to take low values associated with mean velocity. It is clear that the sign of parameter value $v_{1}$ influences the amplitude of mean velocity. However, the motion direction associated with axial velocity remains unchanged. Again at $v_{1}=-\,5.4514$ and $p=0.1112$, the phenomena are observed resulting from the coupled effects of tori. Similarly, one can obtain that at $v_{1}=-5.3248$ and $p=0.2004$. It is worth mentioning that the complex dynamic behaviors are resulted due to the combined influence of $v_{1}$ and p, and Floquet multipliers at critical points (Fig. 42). As in the description of bifurcation analysis, additional phenomena are described depending on sensitive parameter values. The main difference compared to the section of one parameter analysis is the coupled effects of velocity and tension fluctuations in the axial direction. So the simultaneous effect resulting from fluctuating velocity and tension components has significant effects on stability analysis of dynamical systems.

5 Concluding remarks

In the present study, the nonlinear dynamics of a viscoelastic sandwich beam with principal parametric resonances in the presence of three-to-one internal resonance are investigated. A set of first-order differential equations is obtained from the nondimensional partial differential equation using the method of multiple scales. While the pseudo-arclength continuation algorithm is applied to obtain the frequency response and amplitude response curves about the first two modes. Several bifurcations such as saddle-node bifurcation, subcritical and supercritical Hopf bifurcation, and pitchfork bifurcation are carried out in the equilibrium solutions of modulation equations. The parameter analysis is based on the amplitude and frequency detuning of harmonic disturbances. The frequency response curves related to single-mode equilibrium solutions exhibit a hardening-spring response. It is worth mentioning that the number of pitchfork bifurcation points is decreased to two on the trivial branches with respect to the effect of harmonically axial tension. Moreover, the instability zone between the two pitchfork bifurcation points is broadened due to the effect of axial velocity fluctuation. However, there is no bifurcation information when internal frequency detuning parameter value is negative. In amplitude response curves, system exhibits similar phenomena such as the variation of the number of saddle-node bifurcation and Hopf bifurcation points by considering different control parameters. It is found that the two-mode equilibrium solutions are isolated from single-mode equilibrium solutions for typical system parameters. With the help of phase portraits, time traces, Poincaré sections, and FFT power spectra, dynamic solutions are presented in terms of periodic, quasiperiodic, and chaotic responses, depending on initial conditions. Several dynamical phenomena such as jump phenomenon and ‘period windows’ are observed. In addition, the largest Lyapunov exponent is considered to decide the existence of midly chaotic parameters. In the bifurcation analysis varying amplitudes of fluctuating velocity and tension, rich and interesting nonlinear phenomena are depicted. It is shown that the time trajectories are complex compared to other ones, inducing by simultaneous effect of fluctuating velocity and tension and Floquet multipliers at special parameters. The numerical calculations illustrate that the system response is verified from periodic to chaotic through quasiperiodic route. Both the response curves and dynamic solutions indicate that the simultaneous effect of parameter excitations resulting from velocity and load fluctuations play an important role in stability and bifurcation of the sandwich beam with viscoelastic core.

Appendix

$$\begin{aligned} \varGamma _{1}=&-2i\omega _{1}\phi _{1}A_{1}^{\prime }-2v_{0}A_{1}^{\prime }\phi _{1}^{\prime }-A_{1}^{2}\bar{A}_{1}\phi _{1}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime }+3k_{1}A_{1}^{2}\bar{A}_{1}\phi _{1}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime }+2ik_{2}\omega _{1} A _{1}^{2}\bar{A}_{1}\phi _{1}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime }\nonumber \\&-A_{1}A_{2}\bar{A}_{2}\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{1}^{\prime \prime }+3k_{1}A_{1}A_{2}\bar{A}_{2}\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{1}^{\prime \prime }+2ik_{2}\omega _{1}A_{1}A_{2}\bar{A}_{2}\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{1}^{\prime \prime }+2k_{2}v_{0}A_{1}^{2}\bar{A}_{1}\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime 2}\nonumber \\&-A_{1}A_{2}\bar{A}_{2}\phi _{1}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime }+3k_{1}A_{1}A_{2}\bar{A}_{2}\phi _{1}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime }+2ik_{2}\omega _{1}A_{1}A_{2}\bar{A}_{2}\phi _{1}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime }+4k_{2}v_{0}A_{1}A_{2}\bar{A}_{2}\bar{\phi }_{2}^{\prime }\phi _{1}^{\prime \prime }\phi _{2}^{\prime \prime }\nonumber \\&-\dfrac{1}{2}A_{1}^{2}\bar{A}_{1}\phi _{1}^{\prime 2}\bar{\phi }_{1}^{\prime \prime }+\dfrac{3}{2}k_{1}A_{1}^{2}\bar{A}_{1}\phi _{1}^{\prime 2}\bar{\phi }_{1}^{\prime \prime }+ik_{2}\omega _{1}A_{1}^{2}\bar{A}_{1}\phi _{1}^{\prime 2}\bar{\phi }_{1}^{\prime \prime }+4k_{2}v_{0}A_{1}^{2}\bar{A}_{1}\phi _{1}^{\prime }\phi _{1}^{\prime \prime }\bar{\phi }_{1}^{\prime \prime }-A_{1}A_{2}\bar{A}_{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime \prime }\nonumber \\&+3k_{1}A_{1}A_{2}\bar{A}_{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime \prime }+2ik_{2}\omega _{1}A_{1}A_{2}\bar{A}_{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime \prime }+4k_{2}v_{0}A_{1}A_{2}\bar{A}_{2}\phi _{2}^{\prime }\phi _{1}^{\prime \prime }\bar{\phi }_{2}^{\prime \prime }+4k_{2}v_{0}A_{1}A_{2}\bar{A}_{2}\phi _{1}^{\prime }\phi _{2}^{\prime \prime }\bar{\phi }_{2}^{\prime \prime }\nonumber \\&+2k_{2}v_{0}A_{1}^{2}\bar{A}_{1}\phi _{1}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime \prime }+2k_{2}v_{0}A_{1}A_{2}\bar{A}_{2}\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{1}^{\prime \prime \prime }+2k_{2}v_{0}A_{1}A_{2}\bar{A}_{2}\phi _{1}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime \prime }+k_{2}v_{0}A_{1}^{2}\bar{A}_{1}\phi _{1}^{\prime 2}\bar{\phi }_{1}^{\prime \prime \prime }\nonumber \\&+2k_{2}v_{0}A_{1}A_{2}\bar{A}_{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime \prime \prime }-i\alpha \omega _{1}A_{1}\phi _{1}^{\prime \prime \prime \prime }-\alpha v_{0}A_{1}\phi _{1}^{\prime \prime \prime \prime \prime },\nonumber \\ \end{aligned}$$

$$\begin{aligned} \varGamma _{2}=&-2i\omega _{2}\phi _{2}A_{2}^{\prime }-2v_{0}A_{2}^{\prime }\phi _{2}^{\prime }-A_{1}A_{2}\bar{A}_{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime }+3k_{1}A_{1}A_{2}\bar{A}_{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime }+2ik_{2}\omega _{2}A_{1}A_{2}\bar{A}_{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime }\nonumber \\&-A_{1}A_{2}\bar{A}_{1}\phi _{1}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime }+3k_{1}A_{1}A_{2}\bar{A}_{1}\phi _{1}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime }+2ik_{2}\omega _{2}A_{1}A_{2}\bar{A}_{1}\phi _{1}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime }-A_{2}^{2}\bar{A}_{2}\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime }\nonumber \\&+3k_{1}A_{2}^{2}\bar{A}_{2}\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime }+2ik_{2}\omega _{2}A_{2}^{2}\bar{A}_{2}\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime }+4k_{2}v_{0}A_{1}A_{2}\bar{A}_{1}\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime }\phi _{2}^{\prime \prime }+2k_{2}v_{0}A_{2}^{2}\bar{A}_{2}\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime 2}\nonumber \\&-A_{1}A_{2}\bar{A}_{1}\phi _{1}^{\prime }\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime \prime }+3k_{1}A_{1}A_{2}\bar{A}_{1}\phi _{1}^{\prime }\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime \prime }+2ik_{2}\omega _{2}A_{1}A_{2}\bar{A}_{1}\phi _{1}^{\prime }\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime \prime }+4k_{2}v_{0}A_{1}A_{2}\bar{A}_{1}\phi _{2}^{\prime }\phi _{1}^{\prime \prime }\bar{\phi }_{1}^{\prime \prime }\nonumber \\&+4k_{2}v_{0}A_{1}A_{2}\bar{A}_{1}\phi _{1}^{\prime }\phi _{2}^{\prime \prime }\bar{\phi }_{1}^{\prime \prime }-\dfrac{1}{2}A_{2}^{2}\bar{A}_{2}\phi _{2}^{\prime 2}\bar{\phi }_{2}^{\prime \prime }+\dfrac{3}{2}k_{1}A_{2}^{2}\bar{A}_{2}\phi _{2}^{\prime 2}\bar{\phi }_{2}^{\prime \prime }+ik_{2}\omega _{2}A_{2}^{2}\bar{A}_{2}\phi _{2}^{\prime 2}\bar{\phi }_{2}^{\prime \prime }\nonumber \\&+4k_{2}v_{0}A_{2}^{2}\bar{A}_{2}\phi _{2}^{\prime }\phi _{2}^{\prime \prime }\bar{\phi }_{2}^{\prime \prime }+2k_{2}v_{0}A_{1}A_{2}\bar{A}_{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime \prime }+2k_{2}v_{0}A_{1}A_{2}\bar{A}_{1}\phi _{1}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime \prime }+2k_{2}v_{0}A_{2}^{2}\bar{A}_{2}\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime \prime }\nonumber \\&+2k_{2}v_{0}A_{1}A_{2}\bar{A}_{1}\phi _{1}^{\prime }\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime \prime \prime }+k_{2}v_{0}A_{2}^{2}\bar{A}_{2}\phi _{2}^{\prime 2}\bar{\phi }_{2}^{\prime \prime \prime }-i\alpha \omega _{2}A_{2}\phi _{2}^{\prime \prime \prime \prime }-\alpha v_{0}A_{2}\phi _{2}^{\prime \prime \prime \prime \prime },\nonumber \\ \varGamma _{3}=&-\dfrac{1}{2}ip\bar{A}_{1}\bar{\phi }_{1}^{\prime \prime },\nonumber \\ \varGamma _{4}=&-\dfrac{1}{2}ipA_{1}\phi _{1}^{\prime \prime },\nonumber \\ \varGamma _{5}=&\,v_{1}\omega _{1}\bar{A}_{1}\bar{\phi }_{1}^{\prime }-\dfrac{1}{2}v_{1}\varOmega _{1}\bar{A}_{1}\bar{\phi }_{1}^{\prime }+iv_{0}v_{1}\bar{A}_{1}\bar{\phi }_{1}^{\prime \prime },\nonumber \\ \end{aligned}$$

$$\begin{aligned} \varGamma _{6}=&-v_{1}\omega _{1}A_{1}\phi _{1}^{\prime }-\dfrac{1}{2}v_{1}\varOmega _{1}A_{1}\phi _{1}^{\prime }+iv_{0}v_{1}A_{1}\phi _{1}^{\prime \prime },\nonumber \\ \varGamma _{7}=&-\dfrac{1}{2}ip\bar{A}_{2}\bar{\phi }_{2}^{\prime \prime },\nonumber \\ \varGamma _{8}=&-\dfrac{1}{2}ipA_{2}\phi _{2}^{\prime \prime },\nonumber \\ \varGamma _{9}=&v_{1}\omega _{2}\bar{A}_{2}\bar{\phi }_{2}^{\prime }-\dfrac{1}{2}v_{1}\varOmega _{1}\bar{A}_{2}\bar{\phi }_{2}^{\prime }+iv_{0}v_{1}\bar{A}_{2}\bar{\phi }_{2}^{\prime \prime },\nonumber \\ \varGamma _{10}=&-v_{1}\omega _{2}A_{2}\phi _{2}^{\prime }-\dfrac{1}{2}v_{1}\varOmega _{1}A_{2}\phi _{2}^{\prime }+iv_{0}v_{1}A_{2}\phi _{2}^{\prime \prime },\nonumber \\ \varGamma _{11}=&-\dfrac{1}{2}A_{1}^{3}\phi _{1}^{\prime 2}\phi _{1}^{\prime \prime }+\dfrac{3}{2}k_{1}A_{1}^{3}\phi _{1}^{\prime 2}\phi _{1}^{\prime \prime }+3ik_{2}\omega _{1}A_{1}^{3}\phi _{1}^{\prime 2}\phi _{1}^{\prime \prime }+2k_{2}v_{0}A_{1}^{3}\phi _{1}^{\prime }\phi _{1}^{\prime \prime 2}+k_{2}v_{0}A_{1}^{3}\phi _{1}^{\prime 2}\phi _{1}^{\prime \prime \prime },\nonumber \\ \varGamma _{12}=&-A_{1}^{2}A_{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\phi _{1}^{\prime \prime }+3k_{1}A_{1}^{2}A_{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\phi _{1}^{\prime \prime }+4ik_{2}\omega _{1}A_{1}^{2}A_{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\phi _{1}^{\prime \prime }+2ik_{2}\omega _{2}A_{1}^{2}A_{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\phi _{1}^{\prime \prime }\nonumber \\&+2k_{2}v_{0}A_{1}^{2}A_{2}\phi _{2}^{\prime }\phi _{1}^{\prime \prime 2}-\dfrac{1}{2}A_{1}^{2}A_{2}\phi _{1}^{\prime 2}\phi _{2}^{\prime \prime }+\dfrac{3}{2}k_{1}A_{1}^{2}A_{2}\phi _{1}^{\prime 2}\phi _{2}^{\prime \prime }+2ik_{2}\omega _{1}A_{1}^{2}A_{2}\phi _{1}^{\prime 2}\phi _{2}^{\prime \prime }\nonumber \\&+ik_{2}\omega _{2}A_{1}^{2}A_{2}\phi _{1}^{\prime 2}\phi _{2}^{\prime \prime }+4k_{2}v_{0}A_{1}^{2}A_{2}\phi _{1}^{\prime }\phi _{1}^{\prime \prime }\phi _{2}^{\prime \prime }+2k_{2}v_{0}A_{1}^{2}A_{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\phi _{1}^{\prime \prime \prime }+k_{2}v_{0}A_{1}^{2}A_{2}\phi _{1}^{\prime 2}\phi _{2}^{\prime \prime \prime },\nonumber \\ \end{aligned}$$

$$\begin{aligned} \varGamma _{13}=&-\dfrac{1}{2}A_{1}A_{2}^{2}\phi _{2}^{\prime 2}\phi _{1}^{\prime \prime }+\dfrac{3}{2}k_{1}A_{1}A_{2}^{2}\phi _{2}^{\prime 2}\phi _{1}^{\prime \prime }+ik_{2}\omega _{1}A_{1}A_{2}^{2}\phi _{2}^{\prime 2}\phi _{1}^{\prime \prime }+2ik_{2}\omega _{2}A_{1}A_{2}^{2}\phi _{2}^{\prime 2}\phi _{1}^{\prime \prime }\nonumber \\&-A_{1}A_{2}^{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\phi _{2}^{\prime \prime }+3k_{1}A_{1}A_{2}^{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\phi _{2}^{\prime \prime }+2ik_{2}\omega _{1}A_{1}A_{2}^{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\phi _{2}^{\prime \prime }+4ik_{2}\omega _{2}A_{1}A_{2}^{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\phi _{2}^{\prime \prime }\nonumber \\&+4k_{2}v_{0}A_{1}A_{2}^{2}\phi _{2}^{\prime }\phi _{1}^{\prime \prime }\phi _{2}^{\prime \prime }+2k_{2}v_{0}A_{1}A_{2}^{2}\phi _{1}^{\prime }\phi _{2}^{\prime \prime 2}+k_{2}v_{0}A_{1}A_{2}^{2}\phi _{2}^{\prime 2}\phi _{1}^{\prime \prime \prime }+2k_{2}v_{0}A_{1}A_{2}^{2}\phi _{1}^{\prime }\phi _{2}^{\prime }\phi _{2}^{\prime \prime \prime },\nonumber \\ \varGamma _{14}=&-\dfrac{1}{2}A_{2}^{3}\phi _{2}^{\prime 2}\phi _{2}^{\prime \prime }+\dfrac{3}{2}k_{1}A_{2}^{3}\phi _{2}^{\prime 2}\phi _{2}^{\prime \prime }+3ik_{2}\omega _{2}A_{2}^{3}\phi _{2}^{\prime 2}\phi _{2}^{\prime \prime }+2k_{2}v_{0}A_{2}^{3}\phi _{2}^{\prime }\phi _{2}^{\prime \prime 2}+k_{2}v_{0}A_{2}^{3}\phi _{2}^{\prime 2}\phi _{2}^{\prime \prime \prime },\nonumber \\ \varGamma _{15}=&-A_{2}^{2}\bar{A}_{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime }+3k_{1}A_{2}^{2}\bar{A}_{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime }-2ik_{2}\omega _{1}A_{2}^{2}\bar{A}_{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime }+4ik_{2}\omega _{2}A_{2}^{2}\bar{A}_{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime }\nonumber \\&+2k_{2}v_{0}A_{2}^{2}\bar{A}_{1}\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime 2}-\dfrac{1}{2}A_{2}^{2}\bar{A}_{1}\phi _{2}^{\prime 2}\bar{\phi }_{1}^{\prime \prime }+\dfrac{3}{2}k_{1}A_{2}^{2}\bar{A}_{1}\phi _{2}^{\prime 2}\bar{\phi }_{1}^{\prime \prime }-ik_{2}\omega _{1}A_{2}^{2}\bar{A}_{1}\phi _{2}^{\prime 2}\bar{\phi }_{1}^{\prime \prime }\nonumber \\ \end{aligned}$$

$$\begin{aligned}&+2ik_{2}\omega _{2}A_{2}^{2}\bar{A}_{1}\phi _{2}^{\prime 2}\bar{\phi }_{1}^{\prime \prime }+4k_{2}v_{0}A_{2}^{2}\bar{A}_{1}\phi _{2}^{\prime }\phi _{2}^{\prime \prime }\bar{\phi }_{1}^{\prime \prime }+2k_{2}v_{0}A_{2}^{2}\bar{A}_{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime \prime }+k_{2}v_{0}A_{2}^{2}\bar{A}_{1}\phi _{2}^{\prime 2}\bar{\phi }_{1}^{\prime \prime \prime },\nonumber \\ \varGamma _{16}=&-\dfrac{1}{2}A_{2}\bar{A}_{1}^{2}\bar{\phi }_{1}^{\prime 2}\phi _{2}^{\prime \prime }+\dfrac{3}{2}k_{1}A_{2}\bar{A}_{1}^{2}\bar{\phi }_{1}^{\prime 2}\phi _{2}^{\prime \prime }-2ik_{2}\omega _{1}A_{2}\bar{A}_{1}^{2}\bar{\phi }_{1}^{\prime 2}\phi _{2}^{\prime \prime }+ik_{2}\omega _{2}A_{2}\bar{A}_{1}^{2}\bar{\phi }_{1}^{\prime 2}\phi _{2}^{\prime \prime }\nonumber \\&-A_{2}\bar{A}_{1}^{2}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\bar{\phi }_{1}^{\prime \prime }+3k_{1}A_{2}\bar{A}_{1}^{2}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\bar{\phi }_{1}^{\prime \prime }-4ik_{2}\omega _{1}A_{2}\bar{A}_{1}^{2}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\bar{\phi }_{1}^{\prime \prime }+2ik_{2}\omega _{2}A_{2}\bar{A}_{1}^{2}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\bar{\phi }_{1}^{\prime \prime }\nonumber \\&+4k_{2}v_{0}A_{2}\bar{A}_{1}^{2}\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime }\bar{\phi }_{1}^{\prime \prime }+2k_{2}v_{0}A_{2}\bar{A}_{1}^{2}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime \prime 2}+k_{2}v_{0}A_{2}\bar{A}_{1}^{2}\bar{\phi }_{1}^{\prime 2}\phi _{2}^{\prime \prime \prime }+2k_{2}v_{0}A_{2}\bar{A}_{1}^{2}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\bar{\phi }_{1}^{\prime \prime \prime },\nonumber \\ S_{1}=&\dfrac{\dfrac{1}{8}\left( 1-3k_{1}-2ik_{2}\omega _{1}\right) \int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime }\bar{\phi }_{1}\text {d}x}{i\omega _{1}\int _{0}^{1}\phi _{1}\bar{\phi }_{1}\text {d}x+v_{0}\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}\text {d}x},\nonumber \\ S_{2}=&\dfrac{\dfrac{1}{8}\left( \dfrac{1}{2}-\dfrac{3}{2}k_{1}-ik_{2}\omega _{1}\right) \int _{0}^{1}\phi _{1}^{\prime 2}\bar{\phi }_{1}^{\prime \prime }\bar{\phi }_{1}\text {d}x}{i\omega _{1}\int _{0}^{1}\phi _{1}\bar{\phi }_{1}\text {d}x+v_{0}\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}\text {d}x},\nonumber \\ S_{3}=&\dfrac{-\dfrac{1}{8}k_{2}v_{0}\left( 2\int _{0}^{1}\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime 2}\bar{\phi }_{1}\text {d}x+4\int _{0}^{1}\phi _{1}^{\prime }\phi _{1}^{\prime \prime }\bar{\phi }_{1}^{\prime \prime }\bar{\phi }_{1}\text {d}x+2\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime \prime }\bar{\phi }_{1}\text {d}x+\int _{0}^{1}\phi _{1}^{\prime 2}\bar{\phi }_{1}^{\prime \prime \prime }\bar{\phi }_{1}\text {d}x\right) }{i\omega _{1}\int _{0}^{1}\phi _{1}\bar{\phi }_{1}\text {d}x+v_{0}\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}\text {d}x},\nonumber \\ \end{aligned}$$

$$\begin{aligned} S_{4}=&\dfrac{\dfrac{1}{8}\left( 1-3k_{1}-2ik_{2}\omega _{1}\right) \left( \int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{1}^{\prime \prime }\bar{\phi }_{1}\text {d}x+\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime }\bar{\phi }_{1}\text {d}x+\int _{0}^{1}\phi _{1}^{\prime }\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime \prime }\bar{\phi }_{1}\text {d}x\right) }{i\omega _{1}\int _{0}^{1}\phi _{1}\bar{\phi }_{1}\text {d}x+v_{0}\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}\text {d}x},\nonumber \\ S_{5}=&\dfrac{-\dfrac{1}{2}k_{2}v_{0}\left( \int _{0}^{1}\bar{\phi }_{2}^{\prime }\phi _{1}^{\prime \prime }\phi _{2}^{\prime \prime }\bar{\phi }_{1}\text {d}x+\int _{0}^{1}\phi _{2}^{\prime }\phi _{1}^{\prime \prime }\bar{\phi }_{2}^{\prime \prime }\bar{\phi }_{1}\text {d}x+\int _{0}^{1}\phi _{1}^{\prime }\phi _{2}^{\prime \prime }\bar{\phi }_{2}^{\prime \prime }\bar{\phi }_{1}\text {d}x\right) }{i\omega _{1}\int _{0}^{1}\phi _{1}\bar{\phi }_{1}\text {d}x+v_{0}\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}\text {d}x},\nonumber \\ S_{6}=&\dfrac{-\dfrac{1}{4}k_{2}v_{0}\left( \int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{1}^{\prime \prime \prime }\bar{\phi }_{1}\text {d}x+\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime \prime }\bar{\phi }_{1}\text {d}x+\int _{0}^{1}\phi _{1}^{\prime }\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime \prime \prime }\bar{\phi }_{1}\text {d}x\right) }{i\omega _{1}\int _{0}^{1}\phi _{1}\bar{\phi }_{1}\text {d}x+v_{0}\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}\text {d}x},\nonumber \\ S_{7}=&\dfrac{\dfrac{1}{8}\left( 1-3k_{1}-2ik_{2}\omega _{2}\right) \int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime }\bar{\phi }_{2}\text {d}x}{i\omega _{2}\int _{0}^{1}\phi _{2}\bar{\phi }_{2}\text {d}x+v_{0}\int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}\text {d}x},\nonumber \\ S_{8}=&\dfrac{\dfrac{1}{8}\left( \dfrac{1}{2}-\dfrac{3}{2}k_{1}-ik_{2}\omega _{2}\right) \int _{0}^{1}\phi _{2}^{\prime 2}\bar{\phi }_{2}^{\prime \prime }\bar{\phi }_{2}\text {d}x}{i\omega _{2}\int _{0}^{1}\phi _{2}\bar{\phi }_{2}\text {d}x+v_{0}\int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}\text {d}x},\nonumber \\ S_{9}=&\dfrac{-\dfrac{1}{8}k_{2}v_{0}\left( 2\int _{0}^{1}\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime 2}\bar{\phi }_{2}\text {d}x+4\int _{0}^{1}\phi _{2}^{\prime }\phi _{2}^{\prime \prime }\bar{\phi }_{2}^{\prime \prime }\bar{\phi }_{2}\text {d}x+2\int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}^{\prime }\phi _{2}^{\prime \prime \prime }\bar{\phi }_{2}\text {d}x+\int _{0}^{1}\phi _{2}^{\prime 2}\bar{\phi }_{2}^{\prime \prime \prime }\bar{\phi }_{2}\text {d}x\right) }{i\omega _{2}\int _{0}^{1}\phi _{2}\bar{\phi }_{2}\text {d}x+v_{0}\int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}\text {d}x},\nonumber \\ \end{aligned}$$

$$\begin{aligned} S_{10}=&\dfrac{\dfrac{1}{8}\left( 1-3k_{1}-2ik_{2}\omega _{2}\right) \left( \int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime }\bar{\phi }_{2}\text {d}x+\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime }\bar{\phi }_{2}\text {d}x+\int _{0}^{1}\phi _{1}^{\prime }\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime \prime }\bar{\phi }_{2}\text {d}x\right) }{i\omega _{2}\int _{0}^{1}\phi _{2}\bar{\phi }_{2}\text {d}x+v_{0}\int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}\text {d}x},\nonumber \\ S_{11}=&\dfrac{-\dfrac{1}{2}k_{2}v_{0}\left( \int _{0}^{1}\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime }\phi _{2}^{\prime \prime }\bar{\phi }_{2}\text {d}x+\int _{0}^{1}\phi _{2}^{\prime }\phi _{1}^{\prime \prime }\bar{\phi }_{1}^{\prime \prime }\bar{\phi }_{2}\text {d}x+\int _{0}^{1}\phi _{1}^{\prime }\phi _{2}^{\prime \prime }\bar{\phi }_{1}^{\prime \prime }\bar{\phi }_{2}\text {d}x\right) }{i\omega _{2}\int _{0}^{1}\phi _{2}\bar{\phi }_{2}\text {d}x+v_{0}\int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}\text {d}x},\nonumber \\ S_{12}=&\dfrac{-\dfrac{1}{4}k_{2}v_{0}\left( \int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{1}^{\prime \prime \prime }\bar{\phi }_{2}\text {d}x+\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime \prime }\bar{\phi }_{2}\text {d}x+\int _{0}^{1}\phi _{1}^{\prime }\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime \prime \prime }\bar{\phi }_{2}\text {d}x\right) }{i\omega _{2}\int _{0}^{1}\phi _{2}\bar{\phi }_{2}\text {d}x+v_{0}\int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}\text {d}x},\nonumber \\ E_{1}=&\dfrac{\dfrac{1}{2}\left( i\omega _{1}\int _{0}^{1}\phi _{1}^{\prime \prime \prime \prime }\bar{\phi }_{1}\text {d}x+v_{0}\int _{0}^{1}\phi _{1}^{\prime \prime \prime \prime \prime }\bar{\phi }_{1}\text {d}x\right) }{i\omega _{1}\int _{0}^{1}\phi _{1}\bar{\phi }_{1}\text {d}x+v_{0}\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}\text {d}x},\nonumber \\ E_{2}=&\dfrac{\dfrac{1}{2}\left( i\omega _{2}\int _{0}^{1}\phi _{2}^{\prime \prime \prime \prime }\bar{\phi }_{2}\text {d}x+v_{0}\int _{0}^{1}\phi _{2}^{\prime \prime \prime \prime \prime }\bar{\phi }_{2}\text {d}x\right) }{i\omega _{2}\int _{0}^{1}\phi _{2}\bar{\phi }_{2}\text {d}x+v_{0}\int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}\text {d}x},\nonumber \\ G_{1}=&\dfrac{\dfrac{1}{4}ip\int _{0}^{1}\bar{\phi }_{1}^{\prime \prime }\bar{\phi }_{1}\text {d}x}{i\omega _{1}\int _{0}^{1}\phi _{1}\bar{\phi }_{1}\text {d}x+v_{0}\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}\text {d}x},\nonumber \\ \end{aligned}$$

$$\begin{aligned} G_{2}=&\dfrac{\dfrac{1}{4}ip\int _{0}^{1}\phi _{1}^{\prime \prime }\bar{\phi }_{2}\text {d}x}{i\omega _{2}\int _{0}^{1}\phi _{2}\bar{\phi }_{2}\text {d}x+v_{0}\int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}\text {d}x},\nonumber \\ G_{3}=&\dfrac{\dfrac{1}{2}\left( -v_{1}\omega _{2}\int _{0}^{1}\bar{\phi }_{2}^{\prime }\bar{\phi }_{2}\text {d}x+\dfrac{1}{2}v_{1}\varOmega _{1}\int _{0}^{1}\bar{\phi }_{2}^{\prime }\bar{\phi }_{2}\text {d}x-iv_{0}v_{1}\int _{0}^{1}\bar{\phi }_{2}^{\prime \prime }\bar{\phi }_{2}\text {d}x\right) }{i\omega _{2}\int _{0}^{1}\phi _{2}\bar{\phi }_{2}\text {d}x+v_{0}\int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}\text {d}x},\nonumber \\ K_{1}=&\dfrac{\dfrac{1}{8}\left( \dfrac{1}{2}-\dfrac{3}{2}k_{1}+2ik_{2}\omega _{1}-ik_{2}\omega _{2}\right) \int _{0}^{1}\bar{\phi }_{1}^{\prime 2}\phi _{2}^{\prime \prime }\bar{\phi }_{1}\text {d}x}{i\omega _{1}\int _{0}^{1}\phi _{1}\bar{\phi }_{1}\text {d}x+v_{0}\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}\text {d}x},\nonumber \\ K_{2}=&\dfrac{\dfrac{1}{8}\left( 1-3k_{1}+4ik_{2}\omega _{1}-2ik_{2}\omega _{2}\right) \int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\bar{\phi }_{1}^{\prime \prime }\bar{\phi }_{1}\text {d}x}{i\omega _{1}\int _{0}^{1}\phi _{1}\bar{\phi }_{1}\text {d}x+v_{0}\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}\text {d}x},\nonumber \\ K_{3}=&\dfrac{-\dfrac{1}{8}k_{2}v_{0}\left( 4\int _{0}^{1}\bar{\phi }_{1}^{\prime }\phi _{2}^{\prime \prime }\bar{\phi }_{1}^{\prime \prime }\bar{\phi }_{1}\text {d}x+2\int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime \prime 2}\bar{\phi }_{1}\text {d}x+\int _{0}^{1}\bar{\phi }_{1}^{\prime 2}\phi _{2}^{\prime \prime \prime }\bar{\phi }_{1}\text {d}x+2\int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{1}^{\prime }\bar{\phi }_{1}^{\prime \prime \prime }\bar{\phi }_{1}\text {d}x\right) }{i\omega _{1}\int _{0}^{1}\phi _{1}\bar{\phi }_{1}\text {d}x+v_{0}\int _{0}^{1}\phi _{1}^{\prime }\bar{\phi }_{1}\text {d}x},\nonumber \\ \end{aligned}$$

$$\begin{aligned} K_{4}=&\dfrac{\dfrac{1}{8}\left( \dfrac{1}{2}-\dfrac{3}{2}k_{1}-3ik_{2}\omega _{1}\right) \int _{0}^{1}\phi _{1}^{\prime 2}\phi _{1}^{\prime \prime }\bar{\phi }_{2}\text {d}x-\dfrac{1}{4}k_{2}v_{0}\int _{0}^{1}\phi _{1}^{\prime }\phi _{1}^{\prime \prime 2}\bar{\phi }_{2}\text {d}x-\dfrac{1}{8}k_{2}v_{0}\int _{0}^{1}\phi _{1}^{\prime 2}\phi _{1}^{\prime \prime \prime }\bar{\phi }_{2}\text {d}x}{i\omega _{2}\int _{0}^{1}\phi _{2}\bar{\phi }_{2}\text {d}x+v_{0}\int _{0}^{1}\phi _{2}^{\prime }\bar{\phi }_{2}\text {d}x},\nonumber \\ H_{1}=&\,S_{1}+S_{2}+S_{3},\nonumber \\ H_{2}=&\,S_{4}+S_{5}+S_{6},\nonumber \\ H_{3}=&\,S_{7}+S_{8}+S_{9},\nonumber \\ H_{4}=&\,S_{10}+S_{11}+S_{12},\nonumber \\ K_{5}=&\,K_{1}+K_{2}+K_{3}.\nonumber \end{aligned}$$