Keywords

1 Introduction

In recent years, a new class of composites namely functionally graded materials (FGMs) has gained great attention in many modern engineering applications such as military, aerospace, automotive, biomedical, marine and civil engineering. FGM is advanced class of composites which combines favourable properties of both ceramic and metal by providing smooth and gradual spatial variation of its constituents. Due to its superior properties over composites such as lower transverse shear stresses, high resistance to temperature shocks and no interface problems through the layer interfaces, the researchers have extensively examined the static, vibration and buckling responses of these structures.

The literature devoted to predict the structural response of FGMs can be characterized into study of FGM beams, plates and shells. It is also worth to notice that as compared to FGM plate and shell, a smaller number of studies are available on FEM study of continuous FGM beam. The literature on FGM beam can be segregated based on the used beam theories. It is well-known that the classical beam theory, known as Euler–Bernoulli theory, ignores the effects of shear deformation, is oldest beam theory. Studies such as [1,2,3] investigated the response of FGM beams using classical beam theory. In addition to this researchers [4,5,6,7,8,9,10,11] also used first-order beam theory or Timoshenko theory, which takes shear deformation into account in determining the flexural behaviour. For instance, Aydogdu and Taskin [9] examined the effect of material inhomogeneity on free vibration response of FGM beam using Timoshenko beam theory. The Young’s Modulus and density were varied along the thickness of beam while Poisson’s ratio was kept constant. Another study by Pradhan and Chakraverty [4] also investigated the effects of constituent volume fractions, slenderness ratios and the beam theories on the natural frequencies on FGM beam. Ziane, Meftah and Belhadj [12] analysed thin and thick functionally graded material box beams under free vibration. Chen, Kitipornchai and Yang [11] investigated the non-linear free vibration behaviour of shear deformable sandwich porous beam by employing Ritz method and von Kármán type non-linear strain–displacement relationships. The effects of porosity coefficient, slenderness ratio was observed in order to improve its vibration behaviour. Sharma [13] developed a generalized beam theory to study the linear-static behaviour of an Aluminium-Zirconia functionally graded beam under thermomechanical loading conditions. Celebi et al. [14] used complementary functions method to convert the problem into initial-value problem for free vibration analysis of FGM beams. Furthermore, functionally graded beams were analysed using shear deformation theories of different orders [5, 11, 15]. Li et al. [16] focused on vibration analysis of a variable thickness beam made of functionally graded materials, which are submerged in water. Babaei et al. [17] examined the effects of large amplitude free vibrations on FGM shallow arches on non-linear elastic foundations.

Present study highlights the effects of various material properties, boundary conditions and geometrical parameters on free vibration behaviour of FGM beam. The primary objective of the present study is to demonstrate an efficient and accurate solution method. Material properties, like Young’s Modulus and density, vary in thickness direction according to Mori–Tanaka scheme and power law. Poisson’s ratio is kept constant. Hamilton’s principle is used to derive the governing differential equations. The numerical solution of the derived differential equations is obtained by employing finite element formulation. Convergence study is conducted and accuracy of model is verified by comparing the results with that in literature. Also, vibration characteristics of the FGM beam are displayed in the form of mode shapes of natural frequencies.

FEM Formulation

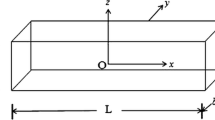
Material Gradation. A functionally graded beam with a uniform material distribution on a Cartesian coordinate system is shown in Fig. 1. The beam has a length L, width b and thickness he. Material properties of the beam are Young’s modulus E, Poisson’s ratio, shear modulus G and mass density ρ. It is assumed that the effective material properties P(z), satisfying all the material properties, vary continuously in the thickness direction (z) according to the following power law distribution [1, 2]:

$$P\left( z \right) = \left( {P_c --{ }P_m } \right){ }V_c + { }P_m$$
(1)
Fig. 1
figure 1

Material gradation of FGM beam

Full size image

where Pc and Pm are, respectively, the material properties at the top and bottom surfaces of the FG beam, Vc is the volume fraction of the top constituent ceramic of the beam defined as:

$$V_c = \left( {\frac{z}{h_e } + \frac{1}{2}} \right)^n \;{\text{for}}\;n \ge 0$$
(2)

Following governing equations for shear deformable are obtained using Hamilton’s principle

$$- I_0 \ddot{\nu } + A_0 \nu^{\prime \prime} + I_1 \ddot{\phi } - A_1 \phi^{\prime \prime} = 0$$
(3)
$$- I_0 + A_3 w^{\prime \prime} - A_3 \phi^{\prime} = 0$$
(4)
$$I_1 \ddot{\nu } - A_1 \upsilon^{\prime \prime} + A_3 w^{\prime} - I_2 \ddot{\phi } + A_2 \phi^{\prime \prime} - A_3 \phi = 0$$
(5)

wherein Ii (i = 0, 1, 2) and Aj (j =  0, 1, 2, 3) are defined as:

$$I_i = \smallint z^i \rho \left( z \right)dA,A_i = \smallint z^i E\left( z \right)dA(i = 0.1.2)\;A_3 \smallint G\left( z \right)dA$$
(6)

2 Convergence Study

A convergence study has been conducted to fix the number of elements in FEA model of FGM beam, and the results of convergence study are presented in Tables 1, 2. For instance, Table 1 shows the variation of the first five natural frequency parameters \(\left( {\lambda = \frac{\omega L^2 }{{h_e }}\sqrt {\frac{{{\text{rhom}}}}{E_m }} } \right)\) with the corresponding number of elements for FGM beam with simply supported edges (S–S). Similarly, the effect of number of elements on the calculated frequency parameters for functionally graded beam with both edges free (i.e. F–F) is shown in Table 2. It is to be noted that the convergence study is conducted with 20 slenderness ratios (i.e. L/he = 20) whereas the value of power law exponent is kept unity.

Table 1 Convergence of first five frequency parameters of S–S beam (slenderness ratio = 20; power law exponent = 1)
Full size table
Table 2 Convergence of first five frequency parameters of F–F beam (slenderness ratio = 20; power law exponent = 1)
Full size table

The frequency parameter (λ) is expressed by normalizing the obtained eigenfrequencies using the following expression:

$$\lambda = \frac{\omega L^2 }{{h_e }}\sqrt {\frac{\rho_m }{{E_m }}}$$

where

  • ω = Natural frequency of beam

  • L = Length of beam

  • he = Height of beam

    \(\rho_m\) = Mass Density of metal

  • \(E_m\) = Young’s Modulus of metal.

By this study, it is found that by increasing the number of discretized elements of either beam, the difference between the consecutive frequencies for any mode decreases considerably. This shows that the results obtained would be of higher accuracy when the number of discretized elements for FG beam is increased. Thus, it can be observed that the difference between frequency parameters becomes minimum as we consider higher values of ndiv. Conclusively, the number of discretized elements (ndiv) is set as ‘8’ for this complete study.

3 Validation Study

To perform the present study, the accuracy of FEM formulation must be validated with the results reported in the relevant literature.

In this section, first five frequency parameters for the free vibration of FGM beam subjected to different sets of boundary conditions are compared. To validate the analysis, results for simply supported (S–S) as well as Fixed (C–C) beam are compared with numerical convergence studies of frequency parameters with the literature published. The results for S–S FGM beam are compared with that reported by Aydogdu and Taskin [9] and presented in Table 3. Table 4 shows the comparison of natural frequencies for C–C FGM beam with Pradhan and Chakraverty [4].

Table 3 Comparison of natural frequency parameters for S–S Al/Al2O3FGM beam with Aydogdu and Taskin [9]
Full size table
Table 4 Comparison of natural frequency parameters for F–F Al/Al2O3FGM beam with Aydogdu and Pradhan and Chakraverty [4]
Full size table

Material and geometrical parameters for FGM beam are taken from references [9, 10] and mentioned below for ready reference.

$$\begin{aligned} & {\text{Al}}:E_m = 70\;{\text{GPa}}, \\ & {\text{rhom}} = 2702\;{\text{kg}}/{\text{m}}^3 \\ & {\text{Al}}_2 {\text{O}}_3 :E_c = 380\;{\text{GPa}} \\ & {\text{rhoc}} = 3800\;{\text{kg}}/{\text{m}}^3 \\ \end{aligned}$$

The Poisson’s ratio for both materials is kept constant as 0.3. From Tables 3 and 4, a good agreement between the results of the frequency parameters for different values of the power law exponent can be observed.

4 Present Study

In the present study, the first five frequency responses of a functionally graded (FG) beam for three different scenarios are investigated and presented. Functionally graded material of the beam is basically composed of Silicon Carbide at the top of the beam (i.e. z = +h/2) and Titanium Aluminide (Ti48Al2Cr2Nb) at the bottom of the beam (i.e. z = −h/2) with the following properties varying or as per the power law through the thickness of the beam.

$$\begin{aligned} {\text{Silicon}}\;{\text{Carbide}}:E_c & = 410\;{\text{GPa}} \\ \rho_c & = 3100\;{\text{kg}}/{\text{m}}^3 \\ {\text{Titanium}}\;{\text{Aluminide}}:E_m & = 160\;{\text{GPa}} \\ \rho_m & = 3600\;{\text{kg}}/{\text{m}}^3 \\ \end{aligned}$$

For the first study, the behaviour of frequency parameters against various values of power law exponent is observed as shown in Table 5. The value of L/he is set as 20 and boundary condition taken as simply supported. It can be clearly seen that the natural frequency of the FG beam for irrespective of mode shapes decreases with the increase in the value of n. This behaviour has been portrayed by a 1-D plot graph as shown in Fig. 2.

Table 5 Effect of material inhomogeneity on the first five natural frequencies parameters for a TiAl/SiC S–S FG beam with slenderness ratio = 20
Full size table
Fig. 2
figure 2

Variation of frequency parameters for different power law exponents

Full size image

For the second study, the behaviour of frequency parameters for four different boundary conditions is examined as shown in Table 6. Similar to the previous condition, the value of L/he is set as 20 and the value of power law exponent n is 1. Out of all four boundary conditions, the value of normalized frequency of C–C beam for any mode shapes is the largest.

Table 6 Effect of boundary conditions on the first five natural frequency parameters of TiAl/SiC FG beam (slenderness ratio = 20; power law exponent = 1)
Full size table

For the third study, the behaviour of frequency parameters for different values of slenderness ratio is examined as shown in Table 7. By keeping power law exponent as n = 1 and boundary condition as simply supported beam, the eigen frequencies (f) and respective dimensionless frequency parameters (λ) are evaluated for variable slenderness ratios. Values of eigenfrequencies vary considerably for this part of study.

Table 7 Effect of slenderness ratio on the first five natural frequency/frequency parameters of TiAl/SiC S–S FG beam WITH power law exponent = 1
Full size table
Fig. 3
figure 3

Variation of displacements for first five-mode shapes

Full size image

5 Conclusion

A finite element formulation for free vibration analysis of FGM beam is carried out in the present study. The accuracy of model is verified by comparing the present results with that available in the literature and various numerical studies are conducted to investigate the effect of material properties, boundary conditions and geometrical parameters on the free vibration behaviour of FGM beam. Based on the present study, following important conclusions can be drawn:

  • The behaviour observed in the first study showed the variation in the frequency parameter λ with respect to the power law exponent n for our parametric considerations. It is observed that with the increase in n, a subsequent decrease in λ is depicted. We can thus imply that when the volumetric fraction starts leaning more towards metal, then the corresponding natural frequency for the FG beam also increases.

  • It is found that out of four boundary conditions the highest natural frequency was attained by the C–C beam whereas the lowest natural frequency was attained by the C–F beam. This indicates that for lowest probability of resonance condition, an FG beam with highest possible natural frequency for any mode should be used, i.e. the C–C FG beam.

  • It is observed that the values of eigenfrequency for respective mode shapes were decreasing with increase in L/he ratio. This proves that a thin or slender beam has lower natural frequency compared to that of a thick or rigid beam and more susceptible towards failure.