Keywords

1 Introduction

Fractional derivatives are used in modeling of numerous important models in significant areas such as signal and systems, control theory, mechanics, chemical engineering, biological sciences, fluid dynamic traffic, acoustics, neurophysiology, plasma physics, and many engineering sciences. The universe is full of nonlinear fractional-order models, and it is not possible to find their exact solution due to their nonlinearity in nature. So, we have to choose some numerical methods for their convergent solution. In literature, there are few techniques for finding approximate solution to these models, e.g., homotopy perturbation [1,2,3,4] scheme, q-homotopy analysis [5] via the Laplace transform, iterative method via the Sumudu transform [6], variational iteration [7] scheme. For more methods, (see, for details, [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]).

This paper studies the merit of scheme HPSTT to get the numerical solution of nonlinear time-fractional Belousov-Zhabotinsky (BZ) equation. HPSTT is a smooth combination of homotopy perturbation scheme and Sumudu transform. This technique offers the numerical solution simply in a convergent series. It is evident that some semi-analytical methods, when combined with the Sumudu transform, take less CPU runtime in calculation than other techniques. Sumudu transform [54, 55] has an advantage of the “unity” feature over other transforms. Watugala [56] proposed the Sumudu transform, and Asiru [57] proved its properties. Weerakoon [58, 59] applied it in finding solution to wave equation.

Singh et al. [60] presented homotopy perturbation method via the Sumudu transform (HPSTM). It is largely due to the works of Ghorbani and Saberi-Nadjafi [61]. Ghorbani [62] used He’s polynomials in nonlinear term. The benefit of HPSTT is its power of embracing two robust computational schemes for tackling a fractional differential equation. These approaches can reduce the time and computation work more in comparison with other existing schemes, preserving efficiency of the results.

We examine the time-dependent nonlinear Belousov-Zhabotinsky (BZ) equation with fractional derivative in Liouville-Caputo sense in this paper. The Belousov-Zhabotinsky reaction is an experimental model for pattern formation and chemical oscillatory reaction. It is a famous example of the self-organizing chemical system. It is given as

$$\begin{aligned} D_{t}^{\alpha } u\left( {x,t} \right) & = u\left( {x,t} \right)\left( {1 - u\left( {x,t} \right) - rv\left( {x,t} \right)} \right) + u_{xx} \left( {x,t} \right), \\ D_{t}^{\alpha } v\left( {x,t} \right) & = - au\left( {x,t} \right)v\left( {x,t} \right) + v_{xx} \left( {x,t} \right), \\ \end{aligned}$$
(1)

where \(0 \le \alpha \le 1, 0 < t < R < 1\).

The fractional model given by Eq. (1) is studied for the first time by Ali Jaradat et al. [63] with generalized Taylor series and discussed the effects of arbitrary order on its solution. Our paper is prepared as follows.

After introduction in Sect. 1, we give few definitions and some properties of Liouville-Caputo arbitrary-order derivative and the Sumudu transform in next section. In Sect. 3, analysis of HPSTT is presented. Next section has the error analysis, and in Sect. 5, HPSTT is implemented on the time-fractional nonlinear BZ equation. In Sect. 6, we discuss the results and their importance using figures. Also, in last Sect. 7, we recap outcomes and find a conclusion.

2 Preliminaries

We write some definitions of fractional-order derivatives and integrals in Liouville-Caputo sense along with few properties of the Sumudu transform (see, for details, [64, 65]).

Definition 2.1

A real function \(g\left( \mu \right),\mu > 0,\) lies in spaces:

  1. (a)

    \(C_{\zeta } ,\zeta \in {\mathbb{R}}\) if there exists a real number \(p > \zeta\) in such a manner that

    $$g\left( \mu \right) = \mu^{p} g_{1} \left( \mu \right),\;\; {\text{while}}\;\;g_{1} \left( \mu \right) \in C\left[ {0,\infty } \right).$$
  2. (b)

    \(C_{\zeta }^{l}\) if \(g^{l} \in { }C_{\zeta } , l \in N\).

Definition 2.2

Liouville-Caputo arbitrary-order derivative of \(g\left( \mu \right),g \in C_{ - 1}^{m} ,m \in {\text{N}}, m > 0,\) is stated as

$$D^{\beta } g\left( \mu \right) = I^{m - \beta } D^{m} g\left( \mu \right) = \frac{1}{{r\left( {m - \beta } \right)}}\int \limits_{0}^{\mu } \left( {\mu - \eta } \right)^{m - \beta - 1} g^{\left( m \right)} \left( \eta \right){\text{d}}\eta ,$$

where \(m - 1 < \beta \le m.\)

The operator \(D^{\beta }\) has following basic properties:

  1. 1.

    \(D^{\beta } I^{\beta } g\left( \mu \right) = g\left( \mu \right),\)

  2. 2.

    \(I^{\beta } D^{\beta } g\left( \mu \right) = g\left( \mu \right) - \mathop \sum \limits_{k = 0}^{m - 1} g^{\left( k \right)} \left( {0^{ + } } \right)\frac{\mu }{{r\left( {k + 1} \right)}}, m > 0.\)

Definition 2.3

Sumudu transform [66, 67] is stated over a set of function.

$$A = \{ \left. {f\left( t \right)} \right|\exists M,t_{1} ,t_{2} {\text{ > }}0,\left| {f\left( t \right)} \right|{\text{ < }}Me^{{\frac{{\left| t \right|}}{{t_{j} }}}} \quad {\text{if}}\;\;t \in ( - 1)^{j} \times \left[ {0,\infty } \right)$$

by the following formula,

$$S\left[ {f\left( t \right)} \right] = \int \limits_{0}^{\infty } f\left( {ut} \right)e^{ - t} {\text{d}}t,\;\;u \in \left( { - t_{1} ,t_{2} } \right).$$

Definition 2.4

Sumudu transform [66, 67] of Liouville-Caputo derivative is

$$S\left[ {D_{x }^{m\alpha } u\left( {x,t} \right)} \right] = s^{ - m\alpha } S\left[ {u\left( {x,t} \right)} \right] - \mathop \sum \limits_{k = 0}^{m - 1} s^{{\left( { - m\alpha + k} \right)}} u^{k} \left( {0,t} \right), m - 1 < m\alpha \le m.$$

3 Analysis of Homotopy Perturbation Sumudu Transform Technique (HPSTT)

Ponder over a nonlinear time-fractional differential equation of arbitrary order is

$$D_{t}^{\beta } u\left( {x,t} \right) + Ru\left( {x,t} \right) + Nu\left( {x,t} \right) = f\left( {x,t} \right), l - 1 < \beta \le l,$$
(2)

with the condition

$$u^{m} \left( {x,0} \right) = f_{m} \left( x \right), m = 0, 1, 2, \ldots ,l - 1,$$
(3)

where \(D_{t}^{\beta } u\left( {x,t} \right)\) is \(\beta\)-order derivative of \(u\left( {x,t} \right)\) in Liouville-Caputo sense and \(R\) and \(N\) are used for linear and nonlinear differential operators, respectively. \(f\left( {x,t} \right)\) is actually the source term.

By Sumudu transform on Eq. (2),

$$\begin{aligned} & u^{ - \alpha } S\left[ {u\left( {x,t} \right)} \right] - \mathop \sum \limits_{k = 0}^{m - 1} u^{{ - \left( {\alpha - k} \right)}} u^{k} \left( {x,0} \right) \\ & \quad = - S\left( {Ru\left( {x,t} \right) + Nu\left( {x,t} \right) - f\left( {x,t} \right)} \right). \\ \end{aligned}$$

On simplification,

$$\begin{aligned} S\left[ {u\left( {x,t} \right)} \right] & = \mathop \sum \limits_{k = 0}^{m - 1} u^{k} u^{k} \left( {x,0} \right) \\ & \quad - u^{\alpha } \left\{ {S\left[ {Ru\left( {x,t} \right)} \right] + S\left[ {Nu\left( {x,t} \right)} \right] - S\left[ {f\left( {x,t} \right)} \right]} \right\} = 0. \\ \end{aligned}$$
(4)

Taking inverse Sumudu transform

$$\begin{aligned} u\left( {x,t} \right) &= S^{ - 1} \left[\mathop \sum \limits_{k = 0}^{m - 1} u^{k} u^{k} \left( {x,0} \right)\right] \\ & \quad- S^{ - 1} { }\left\{ {u^{\alpha } \left[ {S\left( {Ru\left( {x,t} \right) + Nu\left( {x,t} \right) - f\left( {x,t} \right)} \right)} \right]} \right\} = 0 \\ \end{aligned}$$
(5)

By homotopy perturbation method, we have

$$u\left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{\infty } p^{i} u_{i} \left( {x,t} \right).$$
(6)

The nonlinear term is expressed in He’s polynomials as

$$Nu\left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{\infty } p^{i} H_{i} \left( u \right),$$
(7)

where He’s polynomial \(H_{i} \left( w \right)\) is given as:

$$H_{i} \left( w \right) = \frac{1}{i!}\frac{{\partial^{i} }}{{\partial p^{i} }}\left[ {N\left( {\mathop \sum \limits_{j = 0}^{\infty } p^{j} w_{j} } \right)} \right]_{p = 0} ,\quad i = 0, 1, 2, 3, \ldots$$
(8)

Putting Eqs. (6) and (7) in Eq. (5), we write

$$\begin{aligned} & \mathop \sum \limits_{i = 0}^{\infty } p^{i} u_{i} \left( {x,t} \right) = S^{ - 1} \left( {\mathop \sum \limits_{k = 0}^{m - 1} u^{k} u^{k} \left( {x,0} \right) + S\left[ {f\left( {x,t} \right)} \right]} \right) \\ & \quad - p\left[ {S^{ - 1} \left\{ {u^{\alpha } S\left\{ {\left[ {R\mathop \sum \limits_{i = 0}^{\infty } p^{i} u_{i} \left( {x,t} \right)} \right] + \mathop \sum \limits_{i = 0}^{\infty } p^{i} H_{i} \left( u \right)} \right\}} \right\}} \right] \\ \end{aligned}$$
(9)

Equating on each side the coefficients of identical powers of \(p,\) we find

$$\begin{aligned} & p^{0} :u_{0} \left( {x,t} \right) = S^{ - 1} \left( {\mathop \sum \limits_{k = 0}^{m - 1} u^{k} u^{k} \left( {x,0} \right) + S\left[ {f\left( {x,t} \right)} \right]} \right), \\ & p^{1} :u_{1} \left( {x,t} \right) = - S^{ - 1} \left\{ {u^{\alpha } S\left\{ {\left[ {Ru_{0} \left( {x,t} \right)} \right] + H_{0} \left( u \right)} \right\}} \right\}, \\ & p^{2} :u_{2} \left( {x,t} \right) = - S^{ - 1} \left\{ {u^{\alpha } S\left\{ {\left[ {Ru_{1} \left( {x,t} \right)} \right] + H_{1} \left( u \right)} \right\}} \right\}, \\ & p^{3} :u_{3} \left( {x,t} \right) = - S^{ - 1} \left\{ {u^{\alpha } S\left\{ {\left[ {Ru_{2} \left( {x,t} \right)} \right] + H_{2} \left( u \right)} \right\}} \right\}, \\ \end{aligned}$$

In the same way, the next iterates can be found.

Hence, the solution is

$$u\left( {x,t} \right) = \mathop {\lim }\limits_{p \to 1} \mathop {\lim }\limits_{N \to \infty } \mathop \sum \limits_{i = 0}^{N} p^{i} u_{i} \left( {x,t} \right) = \mathop {\lim }\limits_{N \to \infty } \mathop \sum \limits_{i = 0}^{N} u_{i} \left( {x,t} \right).$$
(10)

4 Error Analysis

Now, we give the error analysis of presented approach found with HPSTT.

Theorem 4.1

If there exists \(0 < \gamma < 1\), such that

$$\left\|u_{i + 1} \left( {\tau ,\xi } \right)\right\| \le \gamma\left\| u_{i} \left( {\tau ,\xi } \right)\right\|, \forall i \in N,$$

then, the maximum value of absolute truncation error in HPSTT solution given by Eq. (10) of time-dependent nonlinear Belousov-Zhabotinsky equation is estimated as

$$\left| {u\left( {\tau ,\xi } \right) - \mathop \sum \limits_{i = 0}^{j} u_{i} \left( {\tau ,\xi } \right)} \right| \le \frac{{\gamma^{j + 1} }}{{\left( {1 - \gamma } \right)}}u_{0} \left( {\tau ,\xi } \right).$$

5 Applications

In this section, HPSTT is implemented on the fractional model of BZ equation.

Test Example. Consider the following fractional model of Belousov-Zhabotinsky equation

$$\begin{aligned} D_{t}^{\alpha } u\left( {x,t} \right) & = u\left( {x,t} \right)\left( {1 - u\left( {x,t} \right) - rv\left( {x,t} \right)} \right) + u_{xx} \left( {x,t} \right), \\ D_{t}^{\alpha } v\left( {x,t} \right) & = - au\left( {x,t} \right)v\left( {x,t} \right) + v_{xx} \left( {x,t} \right), \\ \end{aligned}$$
(11)

where \(0 \le \alpha \le 1, 0 < t < R < 1\). The initial conditions are

$$\begin{aligned} u\left( {x,0} \right) & = - \frac{1}{2}\left( {1 - \tanh^{2} \left( \frac{x}{2} \right)} \right), \\ v\left( {x,0} \right) & = - \frac{1}{2} + \tanh \left( \frac{x}{2} \right) + \frac{1}{2}\tanh^{2} \left( \frac{x}{2} \right). \\ \end{aligned}$$
(12)

The exact solution of Eq. (11) when \(\alpha = 1\), for \(r = 2,a = 3\) is given as

$$\begin{aligned} u\left( {x,t} \right) & = - \frac{1}{2}\left( {1 - \tanh^{2} \left( {\frac{x}{2} + t} \right)} \right), \\ v\left( {x,t} \right) & = - \frac{1}{2} + \tanh \left( {\frac{x}{2} + t} \right) + \frac{1}{2}\tanh^{2} \left( {\frac{x}{2} + t} \right) \\ \end{aligned}$$

Firstly, exerting Sumudu transform operator on Eq. (11)

$$\begin{aligned} S\left[ {D_{t}^{\alpha } u\left( {x,t} \right)} \right] & = S\left[ {u\left( {x,t} \right)\left( {1 - u\left( {x,t} \right) - rv\left( {x,t} \right)} \right) + u_{xx} \left( {x,t} \right)} \right], \\ S\left[ {D_{t}^{\alpha } v\left( {x,t} \right)} \right] & = S\left[ { - au\left( {x,t} \right)v\left( {x,t} \right) + v_{xx} \left( {x,t} \right)} \right]. \\ \end{aligned}$$

Applying the inverse Sumudu transform

$$\begin{aligned} u\left( {x,t} \right) & = u\left( {x,0} \right) - S^{ - 1} \left\{ {u^{\alpha } S\left[ { - u + u^{2} + ruv - u_{xx} } \right]} \right\}, \\ v\left( {x,t} \right) & = v\left( {x,0} \right) - S^{ - 1} \left\{ {u^{\alpha } S\left[ {auv - v_{xx} } \right]} \right\}, \\ \end{aligned}$$

By applying the homotopy perturbation method, using

$$u\left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{\infty } p^{i} u_{i} \left( {x,t} \right)\quad {\text{and}}\;\;v\left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{\infty } p^{i} v_{i} \left( {x,t} \right),$$

And, the nonlinear term is decomposed as

$$Nu\left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{\infty } p^{i} H_{i} \left( u \right)\quad {\text{and}}\;\;Nv\left( {x,t} \right) = \mathop \sum \limits_{i = 0}^{\infty } p^{i} H_{i} \left( v \right).$$

where \(H_{i} \left( u \right),H_{i} \left( v \right)\) are homotopy polynomials that are representing the nonlinear terms. So, Eq. (11) becomes

$$\begin{aligned} & \mathop \sum \limits_{i = 0}^{\infty } p^{i} u_{i} \left( {x,t} \right) = u\left( {x,0} \right) \\ & \quad - pS^{ - 1} \left\{ {u^{\alpha } S\left[ {\begin{array}{*{20}c} { - \mathop \sum \limits_{i = 0}^{\infty } p^{i} u_{i} \left( {x,t} \right)} \\ { \quad + \sum\limits_{i = 0}^{\infty } p^{i} H_{i} \left( u \right) - \left( {\mathop \sum \limits_{i = 0}^{\infty } p^{i} u_{i} \left( {x,t} \right)} \right)_{xx} } \\ \end{array} } \right]} \right\}, \\ & \mathop \sum \limits_{i = 0}^{\infty } p^{i} v_{i} \left( {x,t} \right) = v\left( {x,0} \right) - pS^{ - 1} \left\{ {u^{\alpha } S\left[ {\mathop \sum \limits_{i = 0}^{\infty } p^{i} H_{i} \left( v \right) - \left( {\mathop \sum \limits_{i = 0}^{\infty } p^{i} v_{i} \left( {x,t} \right)} \right)_{xx} } \right]} \right\}, \\ \end{aligned}$$
(13)

where

$$\mathop \sum \limits_{i = 0}^{\infty } p^{i} H_{i} \left( u \right) = u^{2} + ruv\quad {\text{and}}\;\,\mathop \sum \limits_{i = 0}^{\infty } p^{i} H_{i} \left( v \right) = auv.$$
$$H_{0} \left( u \right) = u_{0}^{2} + ru_{0} v_{0} ,\quad H_{0} \left( v \right) = au_{0} v_{0} ,$$
$$H_{1} \left( u \right) = 2u_{0} u_{1} + 2u_{0} v_{1} + 2v_{0} u_{1} ,\quad H_{1} \left( v \right) = a\left( {u_{0} v_{1} + v_{0} u_{1} } \right),$$

Solving above equations, we get

$$u_{0} \left( {x,t} \right) = - \frac{1}{2}\left( {1 - \tanh^{2} \left( \frac{x}{2} \right)} \right),\quad v_{0} \left( {x,t} \right) = - \frac{1}{2} + \tanh \left( \frac{x}{2} \right) + \frac{1}{2}\tanh^{2} \left( \frac{x}{2} \right),$$
$$\begin{aligned} & u_{1} \left( {x,t} \right) \\ & \quad = - \frac{{t^{\alpha } }}{{\Gamma \left( {\alpha + 1} \right)}}\left\{ {\frac{5}{4} - 2\tanh^{2} \left( \frac{x}{2} \right) + \frac{3}{4}\tanh^{4} \left( \frac{x}{2} \right) - \tanh \left( \frac{x}{2} \right){\text{sech}}^{2} \left( \frac{x}{2} \right)} \right. \\ & \quad \quad \left. { - \frac{1}{4}{\text{sech}}^{4} \left( \frac{x}{2} \right) + \frac{1}{2}\tanh^{2} \left( \frac{x}{2} \right){\text{sech}}^{2} \left( \frac{x}{2} \right)} \right\}, \\ \end{aligned}$$
$$\begin{aligned} v_{1} \left( {x,t} \right) & = - \frac{{t^{\alpha } }}{{\Gamma \left( {\alpha + 1} \right)}}\left\{ {\frac{3}{4} + \frac{3}{2}\tanh^{2} \left( \frac{x}{2} \right) + \frac{3}{4}\tanh^{4} \left( \frac{x}{2} \right) - \frac{3}{2}\tanh \left( \frac{x}{2} \right){\text{sech}}^{2} \left( \frac{x}{2} \right)} \right. \\ & \quad \left. { - \frac{1}{4}{\text{sech}}^{4} \left( \frac{x}{2} \right) + \frac{1}{2}\tanh^{2} \left( \frac{x}{2} \right){\text{sech}}^{2} \left( \frac{x}{2} \right) + \frac{1}{2}\tanh \left( \frac{x}{2} \right)} \right\}, \\ \end{aligned}$$
$$\begin{aligned} u_{2} \left( {x,t} \right) & = \frac{{t^{2\alpha } }}{{\Gamma \left( {2\alpha + 1} \right)}}\left\{ {\frac{9}{2} + \frac{43}{4}\tanh^{2} - \frac{34}{4}\tanh^{4} \left( \frac{x}{2} \right)} \right. \\ & \quad + \frac{9}{2}\tanh \left( \frac{x}{2} \right){\text{sech}}^{2} \left( \frac{x}{2} \right) \\ & \quad + 2{\text{sech}}^{4} \left( \frac{x}{2} \right) - 6\tanh^{2} \left( \frac{x}{2} \right){\text{sech}}^{2} \left( \frac{x}{2} \right) + \frac{9}{4}\tanh^{6} \left( \frac{x}{2} \right) \\ & \quad - \frac{3}{2}\tanh^{3} \left( \frac{x}{2} \right){\text{sech}}^{2} \left( \frac{x}{2} \right) - \frac{1}{4}\tanh^{2} \left( \frac{x}{2} \right){\text{sech}}^{4} \left( \frac{x}{2} \right) \\ & \quad + \frac{5}{2}\tanh^{4} \left( \frac{x}{2} \right){\text{sech}}^{2} \left( \frac{x}{2} \right) \\ & \quad + 2\tanh \left( \frac{x}{2} \right) - \frac{7}{2}\tanh^{3} \left( \frac{x}{2} \right) + \frac{3}{2}\tanh^{5} \left( \frac{x}{2} \right) - \frac{5}{2}\tanh \left( \frac{x}{2} \right){\text{sech}}^{4} \left( \frac{x}{2} \right) \\ & \quad\left. { - \frac{1}{2}{\text{sech}}^{6} \left( \frac{x}{2} \right)} \right\}, \\ \end{aligned}$$
$$\begin{aligned} v_{2} \left( {x,t} \right) &= \frac{{t^{2\alpha } }}{{\Gamma \left( {2\alpha + 1} \right)}}\left\{ { - \frac{3}{8} + \frac{43}{4}\tanh^{2} \left( \frac{x}{2} \right) - \frac{3}{8}\tanh^{4} \left( \frac{x}{2} \right)} \right. \hfill \\&\quad + \frac{9}{2}\tanh \left( \frac{x}{2} \right){\text{sech}}^{2} \left( \frac{x}{2} \right) + \frac{1}{4}{\text{sech}}^{4} \left( \frac{x}{2} \right) \hfill \\ &\quad- 6\tanh^{2} \left( \frac{x}{2} \right){\text{sech}}^{2} \left( \frac{x}{2} \right) + \frac{9}{4}\tanh^{6} \left( \frac{x}{2} \right) \hfill \\&\quad - \frac{3}{2}\tanh^{3} \left( \frac{x}{2} \right){\text{sech}}^{2} \left( \frac{x}{2} \right) - \frac{9}{4}\tanh^{2} \left( \frac{x}{2} \right){\text{sech}}^{4} \left( \frac{x}{2} \right) \hfill \\&\quad + \frac{5}{2}\tanh^{4} \left( \frac{x}{2} \right){\text{sech}}^{2} \left( \frac{x}{2} \right) \hfill \\&\quad + 2\tanh \left( \frac{x}{2} \right) - \frac{7}{2}\tanh^{3} \left( \frac{x}{2} \right) + \frac{3}{2}\tanh^{5} \left( \frac{x}{2} \right) - \frac{5}{2}\tanh \left( \frac{x}{2} \right){\text{sech}}^{4} \left( \frac{x}{2} \right) \hfill \\ &\quad- \left. { \frac{1}{4}{\text{sech}}^{6} \left( \frac{x}{2} \right)} \right\} + \cdots, \hfill \\ \end{aligned}$$

Hence, the next iterates of series solution can be calculated.

The HPSTT solution is given as

$$u\left( {x,t} \right) = \mathop {\lim }\limits_{N \to \infty } \mathop \sum \limits_{i = 0}^{N} u_{i} \left( {x,t} \right),\quad v\left( {x,t} \right) = \mathop {\lim }\limits_{N \to \infty } \mathop \sum \limits_{i = 0}^{N} v_{i} \left( {x,t} \right).$$

6 Results and Discussion

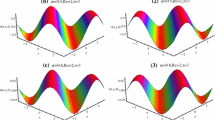
Figures 1a–f represent the behavior of solution at \(\alpha = 1\), the estimated solution for Eq. (11), and the absolute error. We can clearly see from the plots of solution that the proposed numerical approach is accurate. Figures 2a–d give 2D graphical representations of the numerical solution for varying fractional order, and we clearly observe from Figs. 2a, d that the oscillatory behavior of \(u\) and \(v\) with \(x\) as the order \(\alpha\) increases. Figures 2b, c show decreasing behavior of numerical solution with time for order.

Fig. 1
figure 1

a \(u_{{{\text{exact}}}} \left( {x,t} \right)\) when \(\alpha = 1\), b \(u_{{{\text{approx}}{.}}} \left( {x,t} \right)\) when \(\alpha = 1\), c absolute error \(= \left| {u_{{{\text{exact}}}} - { }u_{{{\text{approx}}{.}}} } \right|,\) when \(\alpha = 1\), d \(v_{{{\text{exact}}}} \left( {x,t} \right),\) when \(\alpha = 1\), e \(v_{{{\text{approx}}{.}}} \left( {x,t} \right),\) when \(\alpha = 1\), f absolute error = \(\left| {v_{{{\text{exact}}}} - { }v_{{{\text{approx}}{.}}} } \right|\) when \(\alpha = 1\)

Full size image
Fig. 2
figure 2

For different values of \(\alpha ,\) the plots of a \(u_{{{\text{approx}}{.}}} \left( {x,t} \right)\) with \(x\) when \(t = 0.1\), b \(u_{{{\text{approx}}{.}}} \left( {x,t} \right)\) with \(t\) when \(x = 0.5\), c \(v_{{{\text{approx}}{.}}} \left( {x,t} \right)\) with \(t\) when \(x = 0.5\), and d \(v_{{{\text{approx}}{.}}} \left( {x,t} \right)\) with \(x\), when \(t = 0.1\)

Full size image

7 Conclusion

In this work, we used a numerical scheme HPSTT to investigate the nonlinear time-dependent Belousov-Zhabotinsky system and to check effects of the fractional order on obtained solution. The simulation results are illustrated graphically. The results are derived using the third-order iterates, and the accuracy of the proposed technique can be enhanced by calculating further approximations. The supremacy of HPSTT is its quality of joining two strong methods for the possible solution of nonlinear differential equations. We conclude that this effective scheme reduces time and computation compared to the standard scheme simultaneously conserving the high accuracy of results.