Keywords

1 Introduction

Recent technological advancements have enabled engineers to develop new design methods, advanced materials, and advanced construction equipment to build lighter and more slender structures. Consequently, structures are becoming prone to dynamic loads, especially moving loads. Deflection and vibration induced by heavy and high-speed vehicles affect the safety and serviceability of bridges. Vibration control using mechanical control devices like a tuned mass damper and a fluid viscous damper is very effective to suppress the response of bridges to ensure safety and serviceability of the structure.

A Tuned Mass Damper (TMD) is a simple and effective device; hence, one of the most widely adopted vibration control devices. The TMD is tuned to the fundamental vibration frequency of the primary structure in such a way so that it resonates out of phase with the original structure to dissipate vibration energy. There are mainly two challenges in the implementation of this system in a bridge deck. One of the most critical challenges arises from considerable static stretching of the spring connected between the bridge deck and TMD mass due to gravity. Lower the frequency of the TMD (which is close to the fundamental frequency of the structure), more will be the static stretching of the TMD. Also, the vibrational energy of the primary structure is transferred to the TMD mass, which is responsible for large stroke of TMD. Streamlined bridge decks have very little space to accommodate this damper displacement. In recent times, a device named inerter, developed for the suspension system of Formula-1 racing cars, is found to be effective in controlling vibration of structures. It is used to amplify the physical mass of the system by transforming linear motion into high-speed rotational motion. Thus, it can generate an inertial force which is similar to force generated by inertia of physical mass.

To understand the bridge behavioural characteristics under moving loads, Biggs [1] derived the equations of motion of a simply supported bridge under a moving vehicle where the vehicle is modelled as a springing mass having one degree of freedom supported by a spring and a dashpot. Using this bridge vehicle model, Humar and Kashif [2] numerically analysed different bridges that consist of one or multiple simply supported spans and identified the influencing parameters for their response. Wang et al. [3] modelled the car-body as a flexible multi-body system and the bridge as a Euler Beam. They identified that though the car-body acceleration produces peak responses at certain speeds, the flexibility of the car-body does not significantly affect the bridge response. Salcher and Adam [4] considered the effect of rail irregularities during modal analysis of a train–bridge model and simulated the interaction between both subsystems. Paultre et al. [5] have given prime concern to the vertical acceleration of the bridge deck under pedestrian load to ensure structural safety and serviceability.

Extensive research has been conducted to control moving load-induced bridge vibrations and different solutions have been proposed for different situations. Kwon et al. [6] studied the vibration response of a three-span bridge induced by high-speed trains, considering the vehicle to be modelled as a moving mass model, which consists of the vehicle body and wheel, and designed a TMD to suppress the bridge vibrations. Sadek et al. [7] reviewed existing literature on the topic and suggested that in the choice of TMD parameters, large mass ratios must be used for heavy damping in the first two modes. Marian and Giaralis [8] used TMDI as a passive vibration control and energy harvesting device in a harmonically excited structure. Optimal TMDI parameters were obtained using Den Hartog’s [9] tuning approach. This system was reported to be more robust than the traditional TMD to detuning effects. Xu et al. [10] studied the reduction of undesirable vortex-induced vibrations that influences the fatigue life and serviceability of the bridge structure using the TMDI. Papageorgiou and Smith [11] presented experimental results on inerters and proposed a methodology for testing inerters as well.

In this paper, the focus is on controlling the vibration of a bridge deck produced by moving vehicles using TMD and TMDI. The work aims to present a comparison of the performances of the two devices and to highlight the greater practical applicability of the TMDI system in the bridge deck from the viewpoint of the limited space available to accommodate the stroke of the damper mass. In what follows, first, the working principle of the TMDI is discussed. Next, the modelling of the bridge–vehicle damper system is presented for various cases of the TMD and TMDI. This is followed by a numerical study into the performance of the damper systems in mitigating the bridge vibrations and the stroke lengths of the damper mass is carried out under different speed and frequency parameters of the moving vehicle and bridge systems.

2 Working Principle of the TMDI

Smith [7] developed the concept of the inerter. It is a linear two-terminal device with negligible physical mass which produces internal (resisting) force \(F\), proportional to the relative acceleration between its two terminals. That is,

$$F=b\left({\ddot{u}}_{1}-{\ddot{u}}_{2}\right)$$
(1)

where, \({u}_{1}\) and \({u}_{2}\)= the displacement coordinates of the inerter terminals,

\({\ddot{u}}_{1}-{\ddot{u}}_{2}\)= relative acceleration between the two terminals of the inerter,

b = constant of proportionality (inertance).

Figure 1 shows a device consisting of a flywheel linked to a rack-and-pinion via n gears (here n = 4) called inerter. The inertance of this device is given by

Fig. 1
figure 1

Rack-pinion-flywheel based inerter device with four gear

Full size image
$$b={m}_{f}\frac{{\gamma }_{f}^{2}}{{r}_{fp}^{2}}\left(\prod_{k=1}^{n}\frac{{r}_{k}^{2}}{{r}_{kp}^{2}}\right)$$
(2)

where \({m}_{f}=\) mass of the flywheel; \({\gamma }_{f}=\) radius of gyration of the flywheel; \({r}_{fp}=\) radius of flywheel pinion; \({r}_{k}=\) radii of the \(kth\) gear; and \({r}_{kp}=\) radii of the \(kth\) gear pinion (Fig. 2).

Fig. 2
figure 2

Single gear inerter

Full size image

Let \(\ddot{d}\) be the acceleration of the TMD and \({\alpha }_{1}\) and \({M}_{1}\) be the angular acceleration and torque at the centre of the gear; \({\alpha }_{1}=\frac{\ddot{d}}{{r}_{1p}}\).

Let \({\alpha }_{f}\) be the angular acceleration of the flywheel

$${\alpha }_{f}\cdot {r}_{fp}={\alpha }_{1}\cdot {r}_{1}$$
(3)

or

$${\alpha }_{f}=\frac{{\alpha }_{1}\cdot {r}_{1}}{{r}_{fp}}=\frac{\ddot{d}}{{r}_{fp}}\cdot \frac{{r}_{1}}{{r}_{fp}}$$

Now, torque at the centre of the flywheel

$${M}_{f}=I\cdot {\alpha }_{f}$$
(4)

where \(I=\) Moment of inertia of the flywheel and \({\alpha }_{f}=\) angular acceleration of the flywheel.

Now,

$${\alpha }_{f}={\alpha }_{1}$$

Or

$$\frac{{M}_{f}}{{r}_{f}}=\frac{{M}_{1}}{{r}_{1}}$$

Or

$${M}_{1}={M}_{f}\cdot \frac{{r}_{1}}{{r}_{f}}$$
(5)

The amount of force generated by the inerter due to acceleration of the TMD is then given by

$$F=\frac{{M}_{1}}{{r}_{1}}=\frac{{M}_{f}}{{r}_{fp}}\cdot \frac{{r}_{1}}{{r}_{1p}}=\frac{I\cdot {\alpha }_{f}}{{r}_{fp}}\cdot \frac{{r}_{1}}{{r}_{1p}}=\frac{I}{{r}_{fp}}\cdot \frac{\ddot{d}}{{r}_{fp}}\cdot \frac{{r}_{1}}{{r}_{fp}}\cdot \frac{{r}_{1}}{{r}_{1p}}$$

Or

$$F={m}_{f}\cdot \frac{{\gamma }_{f}^{2}}{{r}_{fp}^{2}}\left(\frac{{r}_{1}^{2}}{{r}_{fp}^{2}}\right)\cdot \ddot{d}$$
(6)

3 Modelling of Bridge–Vehicle Damper System

3.1 Modelling of the Bridge and the Vehicle

In Fig. 3, the bridge is modelled [1] as a uniform prismatic isotropic beam. Here, a simplified analytical technique is used to model the complex dynamic behaviour of a bridge to identify the response governing characteristics, which may help develop rational design procedures. The vehicle body is supported by a spring of stiffness\({k}_{v}\). \({m}_{b}\) is the mass per unit length of the bridge. The wheel load, damping of the vehicle body and damping of the bridge deck are ignored. The vehicle, as it rolls along, is assumed to be always in contact with the surface of the deck. In the beam and vehicle model of Fig. 3, the displacement of the sprung mass relative to its absolute position before deflection under self-weight is represented by\({u}_{v}\). \({u}_{b}=z\left(t\right)\mathrm{sin}\frac{\pi x}{l}\), represents the displacement of the sprung mass, that models the vehicle body, relative to its position of equilibrium when moving, where \(\mathrm{sin}\frac{\pi x}{l}\) is the first mode shape of the beam. Assuming the vehicle is moving at a constant speed\(v\), Biggs [2] derived the equation of motion of the position of the vehicle body along with the bridge deck, reproduced as follows:

Fig. 3
figure 3

Modelling of bridge vehicle system

Full size image
$$\left[\begin{array}{cc}{m}_{v}& 0\\ 0& \frac{{m}_{b}l}{2}\end{array}\right]\left[\begin{array}{c}{\ddot{u}}_{v}\\ \ddot{{z}_{c}}\end{array}\right]+\left[\begin{array}{cc}{k}_{v}& -{k}_{v}\mathrm{sin}\frac{\pi vt}{l}\\ -{k}_{v}\mathrm{sin}\frac{\pi vt}{l}& {k}_{v}{\mathrm{sin}}^{2}\frac{\pi vt}{l}+\frac{{\pi }^{4}EI}{2{l}^{3}}\end{array}\right]\left[\begin{array}{c}{u}_{v}\\ {z}_{c}\end{array}\right]=g\left[\begin{array}{c}0\\ {m}_{v}\mathrm{sin}\frac{\pi vt}{l}\end{array}\right]$$
(7)

We now define \(\chi =\frac{{m}_{v}}{{m}_{b}}\)= mass ratio, \({\omega }_{v}\)= bounce frequency of the vehicle, \({\omega }_{b}=\) frequency of the bridge model, \(\phi =\frac{{\omega }_{v}}{{\omega }_{b}}\)= frequency ratio, and \(\alpha =\frac{v{T}_{b}}{2L}\) as the speed parameter. Further, the following coordinates are defined.

$${\tilde{u }}_{v}=\frac{{u}_{v}}{\delta }=\frac{{u}_{v}{\omega }_{v}^{2}}{g}$$
(8)
$$\stackrel{\sim }{{z}_{c}}=\frac{{z}_{c}}{{\Delta }_{st}}=\frac{z{\omega }_{b}^{2}}{2\chi g}$$
(9)

\(\stackrel{\sim }{{z}_{c}}\) = dynamic amplification factor.

Transforming coordinates to a non-dimensional system, \({\tilde{u }}_{v}\) and \(\stackrel{\sim }{{z}_{c}}\), the equations reduce to

$$\begin{aligned}& \left[\begin{array}{cc}\frac{1}{{\omega }_{v}^{2}}& 0\\ 0& \frac{2{\phi }^{4}\chi }{{\omega }_{v}^{2}}\end{array}\right]\left[\begin{array}{c}{\ddot{\tilde{u }}}_{v}\\ \ddot{{\tilde{z }}_{c}}\end{array}\right]+\left[\begin{array}{cc}1& -2\chi {\phi }^{2}\mathrm{sin}\frac{\alpha }{\phi }{\omega }_{v}t\\ -2\chi {\phi }^{2}\mathrm{sin}\frac{\alpha }{\phi }{\omega }_{v}t& 4{\chi }^{2}{\phi }^{4}{\mathrm{sin}}^{2}\frac{\alpha }{\phi }{\omega }_{v}t+2\chi {\phi }^{2}\end{array}\right]\left[\begin{array}{c}{\tilde{u }}_{v}\\ {\tilde{z }}_{c}\end{array}\right]\\ & =\left[\begin{array}{c}0\\ 2\chi {\phi }^{2}\mathrm{sin}\frac{\alpha }{\phi }{\omega }_{v}t\end{array}\right]\end{aligned}$$
(10)

Equation 10 thereby represents a set of non-dimensional equations that are solved by the ode45 solver in MATLAB R2018b.

It is evident from Eq. 10 that the response of the bridge is controlled by the following four parameters, \({\omega }_{v}, \chi , \phi \, and \, \alpha \).

After introducing a new time variable \(\overline{t }={\omega }_{v}t\), we obtain

$$\frac{{\partial }^{2}{\tilde{u }}_{v}}{\partial {t}^{2}}={\omega }_{v}^{2}\frac{{\partial }^{2}{\tilde{u }}_{v}}{\partial {\overline{t} }^{2}}$$

and

$$\frac{{\partial }^{2}{\tilde{z }}_{c}}{\partial {t}^{2}}={\omega }_{v}^{2}\frac{{\partial }^{2}{\tilde{z }}_{c}}{\partial {\overline{t} }^{2}}$$

It can be concluded from the above equations that the response is independent of \({\omega }_{v}.\)

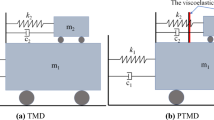
3.2 Modelling of the Bridge–Vehicle System with TMD

In Fig. 4, \({m}_{d}\) is the mass of TMD, \({k}_{d}\) is the stiffness of the spring of TMD and \(d\) is the relative displacement of the mass of TMD. Figure 4 shows the vehicle and bridge interaction with TMD at the mid-span of the bridge, can be derived as follows:

Fig. 4
figure 4

Modelling of vehicle bridge system with TMD

Full size image
Fig. 5
figure 5

Modelling of vehicle bridge system with TMDI (when an inerter device is connected between TMD mass and a fixed support/pier)

Full size image
Fig. 6
figure 6

Modelling of vehicle–bridge system with TMDI (when an inerter device is connected between TMD mass and the bridge deck)

Full size image
$$\begin{aligned} & \left[\begin{array}{ccc}{m}_{v}& 0& 0\\ 0& \frac{{m}_{b}l}{2}& 0\\ 0& 0& {m}_{d}\end{array}\right]\left[\begin{array}{c}{\ddot{u}}_{v}\\ {\ddot{z}}_{c}\\ \ddot{d}\end{array}\right]+\left[\begin{array}{ccc}{c}_{v}& -{c}_{v}\mathit{sin}\frac{\pi vt}{l}& 0\\ 0& {c}_{b}+{c}_{d}& -{c}_{d}\\ 0& -{c}_{d}& {c}_{d}\end{array}\right]\left[\begin{array}{c}{\dot{u}}_{v}\\ {\dot{z}}_{c}\\ \dot{d}\end{array}\right]\\ & \quad +\left[\begin{array}{ccc}{k}_{v}& -{k}_{v}\mathit{sin}\frac{\pi vt}{l}& 0\\ -{k}_{v}\mathit{sin}\frac{\pi vt}{l}& {k}_{v}{\mathit{sin}}^{2}\frac{\pi vt}{l}+\frac{{\pi }^{4}EI}{2{l}^{3}}& -{k}_{d}\\ 0& -{k}_{d}& {k}_{d}\end{array}\right]\left[\begin{array}{c}{u}_{v}\\ {z}_{c}\\ d\end{array}\right]=g\left[\begin{array}{c}0\\ {m}_{v}\mathit{sin}\frac{\pi vt}{l}\\ 0\end{array}\right]\end{aligned}$$
(11)

3.3 Modelling of the Bridge–Vehicle System with TMDI (When an Inerter Device is Connected Between TMD Mass and a Fixed Support/pier)

The second terminal of the inerter device is here considered fixed so that the maximum inertance effect can be achieved. The force generated by the inerter is given by \(F=b\left(\ddot{d}-0\right)=b\ddot{d}\). Figure 5 shows the vehicle and bridge interaction with a TMDI instead of a TMD at the mid-span of the bridge, represented in Eq. 12 can thus be derived.

$$\begin{aligned} & \left[\begin{array}{ccc}{m}_{v}& 0& 0\\ 0& \frac{{m}_{b}l}{2}& 0\\ 0& 0& {m}_{d}+b\end{array}\right]\left[\begin{array}{c}{\ddot{u}}_{v}\\ {\ddot{z}}_{c}\\ \ddot{d}\end{array}\right]+\left[\begin{array}{ccc}{c}_{v}& -{c}_{v}\mathit{sin}\frac{\pi vt}{l}& 0\\ 0& {c}_{b}+{c}_{d}& -{c}_{d}\\ 0& -{c}_{d}& {c}_{d}\end{array}\right]\left[\begin{array}{c}{\dot{u}}_{v}\\ {\dot{z}}_{c}\\ \dot{d}\end{array}\right]\\ & \quad+\left[\begin{array}{ccc}{k}_{v}& -{k}_{v}\mathit{sin}\frac{\pi vt}{l}& 0\\ -{k}_{v}\mathit{sin}\frac{\pi vt}{l}& {k}_{v}{\mathit{sin}}^{2}\frac{\pi vt}{l}+\frac{{\pi }^{4}EI}{2{l}^{3}}& -{k}_{d}\\ 0& -{k}_{d}& {k}_{d}\end{array}\right]\left[\begin{array}{c}{u}_{v}\\ {z}_{c}\\ d\end{array}\right]=g\left[\begin{array}{c}0\\ {m}_{v}\mathit{sin}\frac{\pi vt}{l}\\ 0\end{array}\right]\end{aligned}$$
(12)

3.4 Modelling of the Bridge–Vehicle System with TMDI (When an Inerter Device is Connected Between TMD Mass and the Bridge Deck)

There is a practical limitation in attaching the inerter between TMD mass and fixed support/pier, but it is easier to attach the second terminal to the bridge deck. As there is a large difference between the acceleration of the TMD mass and the mid-span of the bridge deck, we can make use of this relative acceleration to generate force in the inerter, though it will be lower than that in the case of attaching the inerter is connected between TMD mass and fixed support/pier. The force generated here is \(F=b(\ddot{d}-{\ddot{z}}_{c})\). Figure 6 shows the vehicle and bridge interaction with a TMDI when the inerter is connected between TMD mass and bridge deck at the mid-span of the bridge, which are represented by Eq. 13.

$$\begin{aligned} & \left[\begin{array}{ccc}{m}_{v}& 0& 0\\ 0& \frac{{m}_{b}l}{2}& -b\\ 0& -b& {m}_{d}+b\end{array}\right]\left[\begin{array}{c}{\ddot{u}}_{v}\\ {\ddot{z}}_{c}\\ \ddot{d}\end{array}\right]+\left[\begin{array}{ccc}{c}_{v}& -{c}_{v}\mathrm{sin}\frac{\pi vt}{l}& 0\\ 0& {c}_{b}+{c}_{d}& -{c}_{d}\\ 0& -{c}_{d}& {c}_{d}\end{array}\right]\left[\begin{array}{c}{\dot{u}}_{v}\\ {\dot{z}}_{c}\\ \dot{d}\end{array}\right]\\ & \quad +\left[\begin{array}{ccc}{k}_{v}& -{k}_{v}\mathrm{sin}\frac{\pi vt}{l}& 0\\ -{k}_{v}\mathrm{sin}\frac{\pi vt}{l}& {k}_{v}{\mathrm{sin}}^{2}\frac{\pi vt}{l}+\frac{{\pi }^{4}EI}{2{l}^{3}}& -{k}_{d}\\ 0& -{k}_{d}& {k}_{d}\end{array}\right]\left[\begin{array}{c}{u}_{v}\\ {z}_{c}\\ d\end{array}\right]=g\left[\begin{array}{c}0\\ {m}_{v}\mathrm{sin}\frac{\pi vt}{l}\\ 0\end{array}\right] \end{aligned}$$
(13)

4 Performance of TMDI Compared to the Classical TMD in Vibration Suppression

For reduction of the bridge deck response subjected to a moving springing mass, closed-form expressions for optimum tuning parameters of the TMD are given in Table 1, as suggested by Den Hartog [6] for harmonically excited structures. By replacing \(\mu \) with \(\mu +\beta \) as suggested by Marian and Giaralis [4], the expressions for the TMDI are derived.

Table 1 Optimum frequency ratio (\(\nu )\) and Optimum damping ratio (\(\zeta )\) for TMD and TMDI
Full size table

An example bridge [2] is now taken, that is a half through truss with following properties: weight = 1031.936 kN; length = 24.384 m; natural frequency of the bridge, \({f}_{b}\)= 3.95 Hz; the ratio of vehicle mass to bridge mass per unit length, χ = \({m}_{v}\)/\({m}_{b}\) = 0.517; frequency ratio, ϕ=\({\omega }_{v}\) /\({\omega }_{b}\) = 0.7. The variation of maximum mid-span acceleration of bridge deck with speed ratio, \(\alpha \), (a) with TMD (b) with TMDI when the inerter is connected between TMD mass and fixed support/pier and (c) with TMDI when the inerter is connected between TMD mass and bridge deck, for different values of damper mass ratio, \(\mu \), are presented in Fig. 7.

Fig. 7
figure 7

a Mid-span acceleration of bridge with and without TMD. b Mid-span acceleration of bridge with and without TMDI when the inerter is connected between TMD mass and fixed support/pier. c Mid-span acceleration of bridge with and without TMDI when the inerter is connected between TMD mass and pier bridge deck

Full size image

It can be seen from Fig. 7 that the peak acceleration of the bridge deck at mid-span is almost linearly increasing with the speed ratio, \(\alpha \). Further, increasing the mass of the TMD always achieves greater efficiency in the reduction of the mid-span acceleration response though the maximum mid-span acceleration does not improve much at μ = 10% from μ = 5%. In the case of the TMDI, when the second terminal of the inerter is grounded, it achieves higher efficiency at the same mass ratio as the TMD. However, if inerter is connected between TMD mass and bridge deck, the TMDI efficiency is lower than that in the case of the TMD.

At a higher mass ratio, \(\mu ,\) the dynamic displacement of the mass of TMD is smaller, but for lower \(\mu , \mathrm{the}\) stroke of the TMD is significant. When the TMDI is used, and the inerter is connected between TMD mass and fixed support/pier, the maximum displacement of the mass of TMDI is reduced. It may, however, be difficult to ground the second terminal of the inerter. Instead, if the inerter is connected between TMD mass and bridge deck, the stroke of the damper mass is substantially reduced, and this configuration would be easy to install within the bridge deck.

The variation of relative maximum stroke of the mass of TMDI to that of the TMD with inertance, \(\beta \) (a) when inerter is connected between TMD mass and fixed support/pier and (b) when inerter is connected between TMD mass and bridge deck, for different values of mass ratio, \(\mu \) is studied. It is observed from Fig. 8a that for very low mass ratios, such as \(\mu =0.5\%\), the effectiveness of the inerter in reducing the stroke of the TMDI with a grounded terminal as compared to the TMD at the same mass ratio is up to 23%. With increasing mass ratio, \(\mu \), the effect of inertance in reducing the stroke of the TMDI reduces and is hardly 2.5% for \(\mu =10\%\). However, it is seen from Fig. 8b that when inerter is connected between TMD mass and bridge deck, for mass ratio \(\mu =0.5\%\), the effectiveness of the inerter in reducing the stroke of the TMDI as compared to the TMD is up to 69% at same mass ratio; which is much higher as compared to the previous case. With increasing mass ratio, μ, the effect of inertance in reducing the stroke of the TMDI reduces. However, it is still as high as 35% for the case of \(\mu =10\%\). Thus, this system is highly effective in reducing the stroke of the damper mass while mitigating the bridge deck vibrations. Moreover, this system can be easily installed within a bridge deck, both for new as well as for existing structures.

Fig. 8
figure 8

a Maximum stroke of the mass of the TMDI (inerter is connected between TMD mass and fixed support/pier) normalised by the maximum stroke of the TMD at same mass ratio. b Maximum stroke of the mass of the TMDI (inerter is connected between TMD mass and bridge deck) normalised by the maximum stroke of the TMD at same mass ratio

Full size image

5 Conclusions

A TMD, which is very effective in controlling structural vibrations, has applicability in mitigating bridge deck vibrations induced by the moving vehicle. Increasing the mass of the TMD generally increases the efficiency of the TMD. However, the mass cannot be increased indiscriminately as the static deflection of the TMD also increases with the increase in mass and imposes a practical limitation on the installation of the TMD in bridge decks. Further, the large stroke of the TMD compounds the problem. In such cases, the TMDI configuration resolves these problems. The effectiveness of the TMDI compared to the TMD system when the inerter is connected between damper mass and fixed support/pier is significant. The following conclusions are drawn for this case.

  1. I.

    At the same mass ratio, this system is very effective in reducing the mid-span acceleration of the bridge as compared to the TMD. The inertance of the system acts as a virtual mass without adding additional static deflection to the system.

  2. II.

    For lower mass ratio (μ = 0.5%), the effectiveness of the inerter in reducing the stroke of the TMDI as compared to the TMD at the same mass ratio is up to 23%. The effect of the inertance with increasing mass ratio in reducing the stroke of the TMDI reduces and is hardly 2.5% for μ = 10%.

When the inerter is connected between TMD mass and bridge deck, the following conclusions are obtained from the study.

  1. I.

    In this configuration of the inerter, the efficiency of TMDI system is lower as compared to the TMD system. However, installing TMDI would be more feasible since the static deflection of the damper mass is drastically reduced.

  2. II.

    For lower mass ratio (μ = 0.5%), the effectiveness of the inerter in reducing the stroke of the damper mass as compared to the TMD is up to 69% at the same mass ratio; which is much higher as compared to the previous case of TMDI configuration. With increasing mass ratio, the effect of inertance in reducing the stroke of the TMDI reduces. However, it is as high as 35% for the case of μ = 10%.

Overall, the TMDI system is very effective in reducing the stroke of the damper mass. Though this system is less effective than the TMD in reducing the mid-span response of the bridge, it can be installed easily inside a bride deck. Further, another advantage of the proposed system is that it can be applied to new and existing bridge structures.