1 Introduction

The service loads including the traffic vehicles and wind exist on the long-span bridge structures and some severe extreme loads including earthquake loads may also happen. The coupling impact of the earthquake and service loads is likely to cause the dynamic response of long-span bridges to exceed the normal service value. Furthermore, these loads may not only cause damage to the bridge structure but also affect the comfort of the passenger (Zhou & Chen, 2015). Therefore, the suppression system should be deeply studied and had application in controlling the vibration of bridge structures.

Structural vibration control methods mainly include two forms, such as active control and passive control (Nikoo et al., 2020; Wang et al., 2021). According to previous studies, the passive control method was often used to suppress the vibration of large-scale structures (Ghorbanzadeh et al., 2023; Xing et al., 2014). The passive control method was to set additional devices on the structure to absorb the structure energy of motion through oscillation (Kim et al., 2021; Talyan et al., 2021). Therefore, the oscillation of the structure can be quickly suppressed. As an oscillation suppression device, the TMD system is widely used in actual bridge structures because of its simple manufacture and good economy (Alizadeh et al., 2021; Dai et al., 2022). Since Frahm investigated firstly the TMD concept in 1911, based on the applications of the different structures, many studies have been conducted to test and verify its reliability (Jiang et al., 2019). The suppression effects of the TMD system on bridge structure vibration under strong wind load through a wind tunnel test were studied by Fujino and Yoshida (2002). Li et al. (2020) suggested a special method considering the effect of TMD parameters to analyze the oscillation suppression effect of the bridges under the action of moving forces. Li et al. (2020) studied the nonlinear TMD by using the harmonic balance method and optimized the performance of TMD.

Previous studies are full of enthusiasm about the improvement of the TMD system performance and the suppression effect on the bridge vibration response under traffic and/or wind loads (Igusa & Xu, 1994; Matin et al., 2020; Wang et al., 2020; Cai et al., 2015; Yang et al., 2019). In recent years, a vibration suppression system (PTMD) was designed and studied (Ubertini et al., 2017; Lu et al., 2018; Li et al., 2015a, 2015b; Song et al., 2016; Yin et al., 2019). The PTMD system is made up of a sliding mass block and an additional limit device. The additional limit device is used to limit the vibration of the mass block, and the viscoelastic material on its surface can dissipate energy through impact or pounding. Compared with the conventional TMD system, the PTMD system can not only control oscillations in two directions at the same time but also it is easier to install and maintain (Sun et al., 2022). In addition, the PTMD system has better robustness than the conventional TMD system (Li et al., 2015a, 2015b; Wang et al., 2018a, 2018b). However, in the existing research, it is rarely found that the MPTMDs system was applied to the bridge vibration suppression under combined service and extreme loads.

In this work, a PTMD system was designed for the action of energy dissipation of long-span bridges under coupled loads. The numerical simulations of the bridge vibration under earthquake loads with MPTMDs were given. The parameters of MPTMDs on the suppression effect of bridge vibration response were studied, including different numbers, mass ratio, pounding stiffness, and the gap values.

2 Assembly of the Coupled System Under Earthquake Loads with MPTMDs

2.1 Simulation of Traffic Flow

2.1.1 Cell Automatic Traffic Model

The Cell Automatic (CA) traffic model can generate random traffic flow information by simulating the motion behavior of a single vehicle. Nagel and Schreckenberg (1992) first formally proposed the CA traffic flow model. In previous studies, the CA traffic flow model has been introduced into vehicle-bridge interaction under traffic flow, and its accuracy has been proved (Chen & Wu, 2011). To make the simulation results closer to the real traffic flow situation, the CA traffic flow model has been improved in various forms (Yin et al., 2016). In the car-following traffic vehicle model, the influence of the vehicle ahead was considered through the equation

$$\ddot{x}_{n} (t + T) = \lambda (\dot{x}_{n + 1} - \dot{x}_{n} )$$
(1)

where T denotes time-lag of the response and \(\lambda\) denotes the sensitivity coefficient; \(\ddot{x}_{n}\) and \(\dot{x}_{n}\) denotes the acceleration and velocity of the vehicle, respectively. Equation (1) indicates that the dynamic effect of the rear vehicle is influenced by the stimulation of the front vehicle. Based on the reference of Yin et al. (2016), Eq. (1) can be changed to:

$$\ddot{x}_{n} = \lambda_{1} (\dot{x}_{n + 1} - \dot{x}_{n} )_{{t - T_{1} }} + \lambda_{2} (\dot{x}_{n + 2} - \dot{x}_{n} )_{{t - T_{2} }}$$
(2)

where T1 and T2 represent the response time lag of two adjacent vehicles ahead, respectively; \(\lambda_{1}\) and \(\lambda_{2}\) denotes the sensitivity coefficient, \(\lambda_{1} > \lambda_{2}\), and \(\lambda_{1} ,\lambda_{2} \in (0,1)\).

Thus, the expression of the vehicle acceleration can be derived as:

$$\ddot{x}_{n} (t + 1) = \Theta (\Delta \dot{x}_{n + 1} (t),\Delta \dot{x}_{n + 2} (t - 1))$$
(3)

where \(\Theta = \lambda_{1} ({\dot{\text{x}}}_{{{\text{n}} + 1}} {\text{(t)}} - {\dot{\text{x}}}_{{\text{n}}} {\text{(t))}} + \lambda_{2} ({\dot{\text{x}}}_{{{\text{n}} + 2}} {\text{(t}} - {1)} - {\dot{\text{x}}}_{{\text{n}}} {\text{(t}} - {1))}\). The influence of the vehicle speed change can be considered in the CA traffic model through Eq. (3). Using Eqs. (2–3), the CA model was improved and simulated the traffic flow by considering the next-nearest neighbor vehicle.

2.1.2 Motion Equation of the Vehicle in Traffic Flow

The motion equation for a vehicle can be expressed by the following formula:

$$\left[ {{\text{M}}_{{\text{v}}} } \right]\left\{ {{\ddot{\text{Y}}}_{{\text{v}}} } \right\} + \left[ {{\text{C}}_{{\text{v}}} } \right]\left\{ {{\dot{\text{Y}}}_{{\text{v}}} } \right\} + \left[ {{\text{K}}_{{\text{v}}} } \right]\left\{ {{\text{Y}}_{{\text{v}}} } \right\} = \left\{ {{\text{F}}_{{\text{G}}} } \right\} + \left\{ {{\text{F}}_{{\text{v - b}}} } \right\}{ + }\left\{ {F_{vw} } \right\}$$
(4)

where \(\left[ {M_{v} } \right]\), \(\left[ {C_{v} } \right]\), and \(\left[ {K_{v} } \right]\) denote the vehicle mass, vehicle damping, and vehicle stiffness matrices, respectively; \(\left\{ {{\text{Y}}_{v} } \right\}\) represent the displacement vector of the vehicle; \(\left\{ {F_{G} } \right\}\) represent the gravity force vector, \(\left\{ {F_{{v - {\text{b}}}} } \right\}\) represent the wheel contact force vector, and \(\left\{ {F_{vw} } \right\}\) represent the wind forces vector.

2.2 Wind and Earthquake Forces on Traffic-Bridge Coupled System in Modal Coordinates

2.2.1 Wind Forces on the Bridge in Modal Coordinates

According to the finite element theory, the space calculation dynamic model of long-span bridges can be simulated by using beam element and truss element in accordance with its construction. The dynamic characteristics of the bridge can be solved in finite element software. Then, according to the obtained modal shapes, the response of any position on the bridge can be estimated in the time domain. Before the vibration response calculation of the bridge model, its nonlinear behavior was considered in the static analysis such as large deformation and stress stiffening. The motion equation of the bridge structure considering various external forces can be given as:

$$\left[ {{\text{M}}_{{\text{b}}} } \right]\left\{ {{\ddot{\text{Y}}}_{{\text{b}}} } \right\}{ + }\left[ {{\text{C}}_{{\text{b}}} } \right]\left\{ {{\dot{\text{Y}}}_{{\text{b}}} } \right\}{ + }\left[ {{\text{K}}_{{\text{b}}} } \right]\left\{ {{\text{Y}}_{{\text{b}}} } \right\}{ = }\left\{ {{\text{F}}_{{\text{b - v}}} {\text{ + F}}_{{\text{b - p}}} {\text{ + F}}_{{{\text{bw}}}} {\text{ + F}}_{{{\text{beq}}}} } \right\}$$
(5)

where \(\left[ {{\text{M}}_{{\text{b}}} } \right]\), \(\left[ {{\text{C}}_{{\text{b}}} } \right]\), and \(\left[ {{\text{K}}_{{\text{b}}} } \right]\) denote three matrices, i.e. the mass, damping, and stiffness of the bridge, respectively; \(\left\{ {{\text{Y}}_{{\text{b}}} } \right\}\) denotes the bridge displacement vector; \(\left\{ {{\dot{\text{Y}}}_{{\text{b}}} } \right\}\) and \(\left\{ {{\ddot{\text{Y}}}_{{\text{b}}} } \right\}\) represent the first derivative (velocity) and the second derivative (acceleration) of the \(\left\{ {{\text{Y}}_{{\text{b}}} } \right\}\), respectively; \(\left\{ {{\text{F}}_{{{\text{b}} - {\text{v}}}} } \right\}\) represents the vector of traffic flow; \(\left\{ {{\text{F}}_{{{\text{b}} - {\text{p}}}} } \right\}\) represents the force exerted by PTMD on the bridge; \(\left\{ {{\text{F}}_{{{\text{bw}}}} } \right\}\) and \(\left\{ {{\text{F}}_{{{\text{beq}}}} } \right\}\) are the vector of the wind and earthquake forces, respectively.

2.2.2 Earthquake Forces on the Bridge

Earthquake load is less considered in the traffic-bridge coupling system and it can cause a significant vibration response to long-span bridges. Therefore, we have to consider the influence of the earthquake load occurs on the bridge. In the work, the dynamic forces caused by earthquake ground movement were considered, and the equation of earthquake can be given by the following:

$${\text{F}}_{{{\text{beq}}}} { = } - \sum\limits_{{i{ = 1}}}^{n} {{\text{M}}_{{\text{b}}} {\text{R}}_{i} {\ddot{\text{U}}}_{i} {\text{(t)}}}$$
(6)

where \({\text{M}}_{{\text{b}}}\) represents bridge mass matrix; \(R_{i}\) denotes the influence vector about the bridge-pier; \({\ddot{\text{U}}}_{{\text{i}}}\) denotes the time history for motion acceleration of the ground.

2.3 Bridge Equations of Motion with MPTMDs System

2.3.1 The Mechanical Model of PTMD

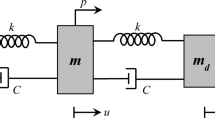
Considering the possibility of collisions between traditional TMD and the main structure, the working performance of the TMD device may decrease. In response to the practical engineering problem, an improved TMD device was designed by Song et al. (2016). As illustrated in Fig. 1, the working mechanisms of traditional TMD and PTMD were compared. The tuned mass m2 of traditional TMD can absorb some of the kinetic energy of the main structure, thus the vibration responses of the main structure were suppressed. There are two vibration reduction methods for PTMD. Firstly, when the kinetic energy of the main structure is low, PTMD reduces the main structural vibration by absorbing kinetic energy (similar to TMD). Second, when the main structure vibrates violently, the tuned mass m2 in PTMD will collide with the limiting devices on both sides, further dissipating the energy through collision.

Fig. 1
figure 1

The working mechanism of the damper

Full size image

2.3.2 Components of the Designed PTMD

In this work, the designed PTMD damper is composed of a sliding mass block similar to the conventional TMD and the additional limit device (Fig. 2a). The TMD system consists of a tuned mass connected by an L-shaped beam, which can oscillate in lateral and vertical directions. The additional limit device is used to limit the vibration of the tuned mass block, and the viscoelastic material on its surface can dissipate energy through impact or pounding. A piece of small-scale PTMD equipment was developed to get the technical parameters of the PTMD system, as shown in Fig. 2b. Furthermore, the PTMD system was applied to a long pipeline structure, and the effectiveness of the suppressing vibration was verified. More information about the details of experimental validation can be given by the references of Song et al. (2016).

Fig. 2
figure 2

The design of the PTMD equipment

Full size image

2.3.3 Equations of the Dynamic Balance of the PTMD

Each PTMD has an interactive relationship with the bridge, which can be given by the following dynamic balance equations:

$$m_{p} \ddot{y}_{pv} (t) + c_{pv} \dot{y}_{pv} (t) + k_{pv} y_{pv} (t) = - f_{p - b}^{v} (t) - Hf_{p - b}^{vp} (t)$$
(7)
$$m_{p} \ddot{y}_{pl} (t) + c_{pl} \dot{y}_{pl} (t) + k_{pl} y_{pl} (t) = - f_{p - b}^{l} (t) - Hf_{p - b}^{lp} (t)$$
(8)
$$\left[ {{\text{M}}_{{\text{p}}} } \right]\left\{ {{\ddot{\text{U}}}_{{\text{p}}} } \right\} + \left[ {{\text{C}}_{{\text{p}}} } \right]\left\{ {{\dot{\text{U}}}_{{\text{p}}} } \right\} + \left[ {{\text{K}}_{{\text{p}}} } \right]\left\{ {{\text{U}}_{{\text{p}}} } \right\}{ = }\left\{ {{\text{F}}_{{{\text{p}} - {\text{b}}}} } \right\} + {\text{H}}\Gamma \left\{ {{\text{F}}_{{{\text{p}} - {\text{b}}}}^{{\text{p}}} } \right\}$$
(9)

where \(m_{p}\) denotes the PTMD mass; \(c_{pv}\) and \(k_{pv}\) denote the vertical damping and stiffness of the PTMD, respectively; \(c_{pl}\) and \(k_{pl}\) denote the horizontal damping and stiffness of the PTMD, respectively; \(f_{p - b}^{v} (t)\) and \(f_{p - b}^{l} (t)\) are the relative motion force between the bridge and the PTMD in the vertical and horizontal direction, respectively; \(f_{p - b}^{vp} (t)\) and \(f_{p - b}^{lp} (t)\) represent the pounding forces in two directions, which are the vertical and horizontal direction, respectively; The variable H and Γ describe the direction and the location of the pounding force, respectively.

2.3.4 Equation of the Coupled System Under Earthquake Loads with MPTMDs

Based on the principle of coupling vibration, the vehicle-bridge coupling system was established through the geometric compatibility conditions and the equilibrium condition of forces at the contact point. Then, according to the coupling dynamic balance equations of the traffic vehicles and bridge, considering the quasi-static wind load, the earthquake/wind/traffic/bridge coupled system with MPTMDs can be assembled. The relevant formulas are as follows:

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {{\text{M}}_{{\text{b}}} } & {} & {} \\ {} & {{\text{M}}_{{\text{p}}} } & {} \\ {} & {} & {{\text{M}}_{{\text{v}}}^{{\text{N}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\ddot{\text{Y}}}_{{\text{b}}} } \\ {{\ddot{\text{Y}}}_{{\text{p}}} } \\ {{\ddot{\text{Y}}}_{{\text{v}}} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\text{C}}_{{\text{b}}} + {\text{C}}_{{{\text{bb}}}} + {\text{C}}_{{{\text{p}} - {\text{b}}}} } & {{\text{C}}_{{{\text{b}} - {\text{p}}}} } & {{\text{C}}_{{{\text{b}} - {\text{v}}}} } \\ {{\text{C}}_{{{\text{p}} - {\text{b}}}} } & {{\text{C}}_{{\text{p}}} + {\text{C}}_{{{\text{p}} - {\text{p}}}} } & {0} \\ {{\text{C}}_{{{\text{v}} - {\text{b}}}} } & {0} & {{\text{C}}_{{\text{v}}}^{{\text{N}}} + {\text{C}}_{{{\text{v}} - {\text{v}}}}^{{\text{N}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\dot{\text{Y}}}_{{\text{b}}} } \\ {{\dot{\text{Y}}}_{{\text{p}}} } \\ {{\dot{\text{Y}}}_{{\text{v}}} } \\ \end{array} } \right\} \\ & \quad + {\kern 1pt} \left[ {\begin{array}{*{20}c} {{\text{K}}_{{\text{b}}} + {\text{K}}_{{{\text{bb}}}} + {\text{K}}_{{{\text{p}} - {\text{b}}}} } & {{\text{K}}_{{{\text{b}} - {\text{p}}}} } & {{\text{K}}_{{{\text{b}} - {\text{v}}}} } \\ {{\text{K}}_{{{\text{p}} - {\text{b}}}} } & {{\text{K}}_{{\text{p}}} + {\text{K}}_{{{\text{p}} - {\text{p}}}} } & {0} \\ {{\text{K}}_{{{\text{v}} - {\text{b}}}} } & {0} & {{\text{K}}_{{\text{v}}}^{{\text{N}}} + {\text{K}}_{{{\text{v}} - {\text{v}}}}^{{\text{N}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\text{Y}}_{{\text{b}}} } \\ {{\text{Y}}_{{\text{p}}} } \\ {{\text{Y}}_{{\text{v}}} } \\ \end{array} } \right\}{ = }\left\{ {\begin{array}{*{20}c} {{\text{F}}_{{{\text{bp}}}}^{{\text{N}}} + {\text{F}}_{{{\text{b}} - {\text{v}}}}^{{\text{N}}} + {\text{F}}_{{{\text{bw}}}}^{{\text{N}}} + {\text{F}}_{{{\text{beq}}}}^{{\text{N}}} } \\ {{\text{F}}_{{{\text{p}} - {\text{b}}}}^{{\text{N}}} + {\text{H}}\Gamma {\text{F}}_{{{\text{p}} - {\text{b}}}}^{{\text{p}}} } \\ {{\text{F}}_{{{\text{v}} - {\text{b}}}}^{{\text{N}}} + {\text{F}}_{{\text{G}}}^{{\text{N}}} + {\text{F}}_{{{\text{vw}}}}^{{\text{N}}} } \\ \end{array} } \right\} \\ \end{aligned}$$
(10)

where N is the vehicle number; \({\text{M}}_{{\text{v}}}^{{\text{N}}}\), \({\text{C}}_{{\text{v}}}^{{\text{N}}}\), and \({\text{K}}_{{\text{v}}}^{{\text{N}}}\) represent matrices of traffic mass, damping, and stiffness, respectively; \({\text{C}}_{{{\text{b}} - {\text{vb}}}}^{{\text{N}}}\) and \({\text{K}}_{{{\text{b}} - {\text{vb}}}}^{{\text{N}}}\) denote the compensation damping and stiffness of the bridge structure due to the coupling effects, respectively; \({\text{C}}_{{{\text{b}} - {\text{v}}}}^{{\text{N}}}\) and \({\text{K}}_{{{\text{b}} - {\text{v}}}}^{{\text{N}}}\) denote the coupled stiffness and damping matrices of the bridge vibration caused by the traffic vehicles, respectively; \({\text{C}}_{{{\text{v}} - {\text{b}}}}^{{\text{N}}}\) and \({\text{K}}_{{{\text{v}} - {\text{b}}}}^{{\text{N}}}\) denote the coupled traffic/bridge damping and stiffness matrices, respectively; \({\text{C}}_{{{\text{v}} - {\text{v}}}}^{{\text{N}}}\) and \({\text{K}}_{{{\text{v}} - {\text{v}}}}^{{\text{N}}}\) denote the coupled matrices induced by other vehicles, respectively. The New-mark method can be used to solve Eq. (10).

To sum up, the flowchart of vibration suppression analysis of the bridge structure under combined service and extreme loads with MPTMDs can be illustrated in Fig. 3.

Fig. 3
figure 3

Framework of coupled system with MPTMDs dynamic analysis

Full size image

3 Numerical Analysis Example

3.1 The Simulation of Traffic, Wind, and Earthquake Loads

Considering the factors such as calculation efficiency and accuracy, in the traffic flow simulation, the heavy trucks with great influence on the traffic flow were modeled by the 18-DOFs vehicle model, and other types of the vehicle were modeled by the 3-DOFs vehicle model (Yin et al., 2019). In order to simulate different traffic conditions, according to the Eqs. (1–3), different traffic states are established through three different vehicle occupancy coefficients, including smooth traffic (\(\rho = 0.07\)), median traffic (\(\rho = 0.15\)), and heavy traffic (\(\rho = 0.3\)). The statistical characteristics of bridge traffic flow are illustrated in Fig. 4.

Fig. 4
figure 4

Traffic flow simulations with different traffic conditions: a smooth traffic, b median traffic, and c heavy traffic

Full size image

The wind velocities are simulated along the bridge span with the simulation interval Δ = 20 m, corresponding to the length of finite elements along the main span of the bridge. The average wind speed on the deck U = 20 m/s was set at the bridge. The EI Centro earthquake records in three directions were chosen as the scenario earthquake (Zhou and Chen 2015). The evolutionary power spectrum density functions were simulated for the vertical component, east–west component, and north–south component, respectively.

3.2 The Relevant Parameters of the Bridge/MPTMDs

In the work, an asymmetric cable-stayed bridge was taken as the case study, located at the border of Hunan province in China, and its span layout is 80 m + 208 m + 716 m + 70 m + 2 × 65 m from the north to the south. Based on the configuration of the bridge, the girder, towers, and railings of the bridge were all simulated by solid elements. The cable was modeled with link elements and a rigid connection was used between the cable and the girder of the bridge. Rigid connections were also used between both the girder and diaphragms and between the girder and bridge deck. The pavement parameters were: Young’s modules Ep = 1.5 GPa, thickness hp = 9.5 cm, Poisson’s ratio 0.25, and per-unit-length mass mp = 8778 kg/m. An analysis model was given using the FE method with numerical software, as seen in Fig. 5b.

Fig. 5
figure 5

Schematic modeling of the cable-stayed bridge

Full size image

According to the analysis results, the vibration suppression effect will be better if the MPTMDs were adjusted to the main vibration mode of the bridge in one direction and placed at the position with the maximal value for the displacement of the bridge (Chen et al., 2019). Based on the results of numerical analysis, the maximum bridge vibration displacement occurs in the midspan. Therefore, all the MPTMDs should preferably be placed at the midspan of the bridge. N numbers of single PTMD are shown in Fig. 5c.

According to the studies (Chen et al., 2019; Wang et al., 2018a, 2018b), the value of the damping ratio is set to 0.02. The value of 1% is the MPTMDs mass ratio. The value of 0.5 is the coefficient e, and the value of \(35,000\,{\text{N}}\,{\text{m}}^{ - 3/2}\) is the pounding stiffness \(\beta\).

To take the gauge of the reducing property of the MPTMDs, the definition of the dynamic reduction rate (\(\eta_{{_{Ctrl} }}\)) is introduced. The ratio of dynamic reduction is shown as:

$$\eta_{{_{Ctrl} }} { = }\frac{{Y_{O} - Y_{Ctrl} }}{{Y_{O} }} \times 100\%$$
(11)

where YO and YCtrl are the maximum responses of the coupled system without and with MPTMDs, respectively.

4 Numerical Analysis

4.1 Analysis of the Different Numbers of PTMD with the Coupled System

The time histories of the midspan vibration displacements with and without MPTMDs system under two load combinations (under traffic and wind, under traffic and earthquake) were illustrated in Fig. 6. From the comparison, it can be found that the values of the bridge vibration responses without MPTMDs system are greater than the marked by MPTMDs system, which shows that MPTMDs system can effectively suppress bridge vibration. For instance, the maximal value for the vertical displacement of the bridge is 33.88 cm under traffic and wind without the MPTMDs system, while the maximum values of the vertical vibration displacement are 29.57 cm (12.72%) and 26.61 cm (21.46%) for the cases with three PTMDs and nine PTMDs, respectively. In additional, Table 1 reveals the vibration reduction ratio of the vertical and lateral displacement can reach 21.46% and 19.71% under nine PTMDs system, respectively. It has been proven that the designed PTMD system has excellent bidirectional decreasing oscillation performance. Moreover, from Table 1, it can be found that the suppressing effectiveness for bridge vibration under traffic and earthquake is more than that under traffic and wind when using the MPTMDs system.

Fig. 6
figure 6

Comparison of the midspan vibration displacements with/without MPTMDs system

Full size image
Table 1 Maximum responses of the bridge with/without MPTMDs system
Full size table

4.2 Parametric Study of MPTMDs on Suppressing Effectiveness Under Traffic and Earthquake

4.2.1 Study of the Mass Ratio of MPTMDs on Suppressing the Effectiveness

The mass ratio is a momentous index affecting the vibration suppression performance of the MPTMDs system. Considering the various factors, such as economic cost and vibration suppression effecting, the value of the mass ratio is generally set to 0.5–2%. Figure 7 shows that there is a negative correlation between the vertical/lateral vibration displacement and the mass ratio. For example, the maximal value for the vertical vibration displacement is 44.5 cm and 74.1 cm, respectively, corresponding to the mass ratio of 2% and 0.5%. The vertical displacement was taken as an illustration from Table 2, with the mass ratio changing from 0.5 to 2%, and the vibration reduction ratio increasing from 22.23 to 53.30%.

Fig. 7
figure 7

Curve of the bridge vibration displacement under different mass ratios

Full size image
Table 2 Effect of mass ratio on suppressing effectiveness under traffic and earthquake
Full size table

4.2.2 Study of the Pounding Stiffness of MPTMDs on Suppressing the Effectiveness

The pounding stiffness \(\beta\) is also a key parameter affecting the ability of the MPTMDs system to mitigate pounding force. In this work, the value of the pounding stiffness was selected as from 15,000 to 75,000 \({\text{N}}\;{\text{m}}^{{ - {3/2}}}\). The comparison of the bridge vibration displacements with different pounding stiffness was indicated in Fig. 8. There is a positive relationship between the bridge vibration displacement and the pounding stiffness (as shown). For example, when the pounding stiffness is 15,000 \({\text{N}}\;{\text{m}}^{{ - {3/2}}}\) and 75,000 \({\text{N}}\;{\text{m}}^{{ - {3/2}}}\), the maximal value for the vertical vibration displacement is 64.5 cm and 77.3 cm, respectively. Table 3 shows the comparison of the suppressing effectiveness of pounding stiffness on the bridge dynamic response under traffic and earthquake. It is found that the method of changing the pounding stiffness of the MPTMDs system is very sensitive to suppressing the vibration response. As the pounding stiffness increases from 15,000 to 75,000 \({\text{N}}\;{\text{m}}^{{ - {3/2}}}\), the reduction ratio is decreased from 32.30 to 18.87%.

Fig. 8
figure 8

Curve of the bridge vibration displacement under different pounding stiffness

Full size image
Table 3 Effect of stiffness on suppressing effectiveness under traffic and earthquake
Full size table

4.2.3 Effect of the Gap Between L Shape Beam and Delimiter

The designed PTMD system needs to rely on the collision between the L-shaped beam and viscoelastic material to accelerate the dissipation of kinetic energy. Therefore, the parameter of the gap between the L-shaped beam and delimiter is also an important index in the PTMD system. The gap can be the mean relative displacement of the PTMD and the bridge, which is 3.5 cm. The gap parameters are selected from 0.6*3.5 cm (2.1 cm) to 1.2*3.5 cm (4.2 cm) at the interval of 0.2*3.5 cm (0.7 cm). Too larger gaps are not studied because the impact action between the L-shaped beam and delimiter may not happen. As indicated in Fig. 9 and Table 4, when the gap parameters increase from 0.6*3.5 to 1.2*3.5 cm, the effectiveness is degraded a lot from 40.29 to 18.94%. The reason for this phenomenon is that the L-shaped beam can collide with the delimiter at a high frequency in a smaller gap, so the efficiency of the dissipation of impact energy will be higher.

Fig. 9
figure 9

Curve of the bridge vibration displacement under different gaps

Full size image
Table 4 Effect of gap on suppressing effectiveness under traffic and earthquake
Full size table

5 Conclusions

In the study, a PTMD system was designed, which can be effectively used for the dissipation of impact energy. It is mainly composed of a tuned mass and an additional limit device. For the purpose of comparing the suppressing effect of the MPTMDs system, based on the earthquake/wind/traffic/bridge coupled system, different parameters of MPTMDs were studied, including different numbers, mass ratio, pounding stiffness, and the gap values. The numerical simulations demonstrate that:

  1. (1)

    The MPTMDs system is very effective in suppressing the displacements of the bridge caused by both the traffic/wind and traffic/earthquake. Furthermore, the suppressing effectiveness of bridge vibration under traffic and earthquake is more than that under traffic and wind.

  2. (2)

    The number of PTMDs has a significant influence in suppressing the bridge vibration under both traffic and earthquake. The number of PTMDs was increased from 3 to 9, and the vibration reduction ratio of the vertical displacements was increased from 25.39 to 48.05%.

  3. (3)

    The vibration suppression effectiveness of the MPTMDs system is positively correlated with the mass ratio. As the mass ratio changes from 0.5 to 2%, the vibration reduction ratio increases significantly from 22.23 to 53.30% under both traffic and earthquake.

  4. (4)

    The method of changing the pounding stiffness and gap of the MPTMDs system is very sensitive to suppressing the vibration response of the bridge. As the pounding stiffness increases from 15,000 to 75,000 N m−3/2, the reduction ratio decreases from 32.30 to 18.87%.