Keywords

1 Introduction

Inclusions greatly influence the physics and mechanics of materials. Hence, a deeper understanding of inclusions and research in the field of inclusions play a substantial role in the development of cutting-edge materials. Such research is also essential in the enhancement of already existing materials used in aerospace, marine, automotive, and numerous other applications [1]. The study of inclusions and inhomogeneities was pioneered by J. D. Eshelby. The theory of ellipsoidal inclusions has been widely used in homogenization schemes. These schemes, in turn, are utilized to predict failures in composite materials. This theory has also been used to accommodate imperfections and impurities inside material with significant thermal expansion in the detailed design of a machine and its components. Moreover, it has been used in a broad spectrum of research areas such as crack propagation and fatigue initiation from micro defects, semiconductors, biomechanics, and geomechanics. It has also been effectively used in the modeling of nanostructures like Quantum dots (QDs) and Quantum wires (QWRs). A comprehensive review of current studies and researches on this topic can be found in the work by Zhou et al. [1] (Fig. 1).

Fig. 1
figure 1

a Homogeneous inclusion (aka inclusion in general): The subregion \(\left(\varOmega \right)\) contains an eigenstrain \(\left({\varepsilon }_{ij}^{*}\right)\) and has the same elastic moduli as the matrix. b Inhomogeneous inclusion: The subregion \(\left(\varOmega \right)\) contains an eigenstrain \(\left({\varepsilon }_{ij}^{*}\right)\) and has different elastic moduli than the matrix. For zero eigenstrain, it is known as an inhomogeneity

Full size image

Eshelby formulated the elastic fields within an ellipsoidal inclusion subjected to some uniform eigenstrain and embedded inside a homogeneous isotropic elastic infinite matrix [2]. The eigenstrain is a non-elastic strain that the inclusion would show if it is not surrounded by the matrix on the outside. It is also called ‘strain without stress’ or ‘zero-stress strain.’ The non-elastic strain can be due to misfit, thermal deformation, plastic deformation, and phase transformation. If the elastic modulus of the subdomain \(\left(\varOmega \right)\) is the same as that of the matrix, then it is called a homogeneous inclusion or sometimes, inclusion in general. And if the elastic modulus of the inclusion is different from that of the matrix, then it is known as an inhomogeneous inclusion. When the eigenstrain inside the inhomogeneous inclusion is zero, it is called an inhomogeneity [3].

A huge number of studies on ellipsoidal inclusion problems are already done and published. However, a thorough literature review reveals that nearly all the studies deal with elastic inclusions, and semi-analytical methods are also developed for the same. Elasto-plastic inclusions under monotonic loading are discussed in the work by Jana and Chatterjee [4] while such problems under cyclic loading have not received any attention in the research. A potential application of such studies on elasto-plastic inclusions would be modeling of material damping and internal energy dissipation due to elasto-plastic flaws in the material [5].

In this paper, we investigate the stress–strain behavior inside a single elasto-plastic ellipsoidal inhomogeneous inclusion embedded within an infinite isotropic homogeneous elastic matrix under uniform sinusoidal far-field loading using ABAQUS. Two different material models namely elastic/perfectly plastic and elastic/linear isotropic hardening material behavior, along with J2 flow theory, are considered for the elasto-plastic inclusion in the finite element simulations. Details of the simulations are discussed in the following sections.

2 Finite Element Analysis

It is a fact in the literature that the stress state inside an ellipsoidal inclusion becomes uniform for an infinite unbounded matrix [2]. However, an infinite matrix is an imaginary concept and cannot be thought of in real-world applications. Thus, we work with limits, and hence the size of the inhomogeneity is taken very small such that the matrix behaves as an infinite solid surrounding the inhomogeneity.

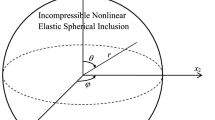
For finite element simulations in ABAQUS, the geometric model consists of a cube from the outside that acts as a matrix and an ellipsoid embedded inside the cube that acts as an inhomogeneity. The boundary condition is a uniform state of stress applied on all six faces of the cube on the outside. The nodes at the matrix–inhomogeneity, interface i.e., cube-ellipsoid boundary, are merged for appropriate load transfer. Simulations are carried out for two different aspect ratios of the ellipsoid and two different material models for inhomogeneity. Details of the geometry, finite element mesh, material models, and loading are discussed below. Figure 2 shows a schematic representation of an ellipsoidal inhomogeneity embedded inside a matrix, subjected to uniform far-field stresses.

Fig. 2
figure 2

Schematic of an elasto-plastic ellipsoidal \(\left(\frac{{x}^{2}}{{a}_{1}^{2}}+ \frac{{y}^{2}}{{a}_{2}^{2}}+\frac{{z}^{2}}{{a}_{3}^{2}}\le 1\right)\) inhomogeneity embedded in an elastic matrix under far-field stresses \({\sigma }_{ij}^{0}\)

Full size image

2.1 Geometry and Mesh Details of the Inhomogeneity

In this article, we have taken two different aspect ratios for the ellipsoidal inhomogeneity. The first one is a general ellipsoidal inhomogeneity while the other one is a spherical inhomogeneity. A cube is taken as the matrix and the size of the cube is taken considerably larger in comparison to that of the inclusion such that the cube behaves as an infinite material body for the inhomogeneity. Details of the geometry and mesh are discussed below.

2.1.1 Ellipsoidal Inhomogeneity

The first model consists of a general ellipsoidal inhomogeneity, which is an ellipsoid with semi-axes lengths of 1, 0.75, and 0.5 mm, centrally embedded inside the matrix represented by a cube with an edge length of \(20\,\mathrm{mm}.\) Figure 3a shows a quarter of the full meshed model. The mesh is highly refined near the matrix–inhomogeneity interface to capture the interaction and better the accuracy. The nodes are merged at the matrix–inhomogeneity interface. The complete meshed model consists of 84,032 eight-noded linear brick elements (C3D8R) (see ABAQUS documentation [6] for details). The final mesh with 84,032 elements is arrived at based on a convergence study, which is presented in Sect. 3.

2.1.2 Spherical Inhomogeneity

Similarly, the spherical inhomogeneity is a sphere with a radius of \(1\,\mathrm{mm},\) centrally embedded inside the matrix represented by a cube with an edge length of \(20\,\mathrm{mm}.\) One fourth of the full meshed model for the same is shown in Fig. 3b. The full meshed model consists of a total of 85,440 eight-noded linear brick elements (C3D8R), and high mesh refinement is used for reasons mentioned in the previous subsection. As mentioned earlier, the nodes at the matrix–inhomogeneity interface are merged.

Fig. 3
figure 3

a One quarter of the 3D meshed model consisting of an ellipsoidal inhomogeneity embedded in a matrix. b One quarter of the 3D meshed model consisting of a spherical inhomogeneity embedded in a matrix

Full size image

2.2 Material Models for the Inhomogeneity

The matrix and the inhomogeneity are considered to have isotropic material properties. Moreover, the matrix is considered to have purely elastic material behavior while that of the inhomogeneity is considered to have an elastic–plastic behavior. Simulations are carried out for two different elastic–plastic behaviors, viz., elastic/perfectly plastic behavior and elastic/linear isotropic hardening behavior. Schematic representations of both models are shown in Fig. 4a, b.

Fig. 4
figure 4

a Schematic representation of an elastic/perfectly plastic material model. b Schematic representation of elastic/linear isotropic hardening material model

Full size image

2.2.1 Elastic/Perfectly Plastic Inhomogeneity

In a material model with elastic/perfectly plastic behavior, the elastic behavior is linear and in the plastic region, the yield stress does not increase with plastic strain but remains constant throughout the loading process [7]. The material properties used for the combination of the elastic matrix and the elastic/perfectly plastic inhomogeneity are given in Table 1. These material properties are chosen from the earlier work by Jana and Chatterjee [4]. Moreover, it is assumed that the inhomogeneity material follows the J2 flow theory of plasticity.

Table 1 Material properties used in analyses of the elastic/perfectly plastic material model
Full size table

2.2.2 Elastic/Linear Isotropic Hardening Inhomogeneity

In an elastic/linear isotropic hardening material model, a linear elastic behavior is assumed and in the plastic region, the yield stress increases linearly with increasing plastic strain throughout the loading process [7]. Table 2 shows the material properties used for the combination of the elastic matrix and the elastic/linear isotropic hardening inhomogeneity. These material properties are chosen from the earlier work by Jana [5] and the inhomogeneity material is also assumed to follow the J2 plasticity flow theory.

Table 2 Material properties used in analyses of the elastic/linear isotropic hardening material model
Full size table

2.3 Loading

In ABAQUS, a pseudo-static analysis is carried out for the sinusoidally applied far-field stresses. We have used 200 steps for the sinusoidally applied far-field load in our analyses. The load steps starting from 1 to ending at 200 are represented using an artificial time that ranges from 0 to 1, and this representation of load steps is called a normalized load step. The load at a normalized load step depends on the frequency of the sinusoidally applied far-field load \(\left({\sigma }^{0}\right)\) and amplitude of each component of the far-field load. In this article, we have taken three cycles for the sinusoidally applied far-field stresses. A schematic of the sinusoidally applied far-field load is shown in Fig. 5a. The ordinate shown in the figure shows a multiplication factor \(k\). If \({\sigma }^{0}\) is the amplitude of a far-field stress component, then \(k{\sigma }^{0}\) will be the pseudo-statically applied far-field stress. Figure 5b shows the variation of a far-field stress component \(\left(k{{\varvec{\sigma}}}_{{\varvec{x}}{\varvec{x}}}^{0}\right)\) with \({{\varvec{\sigma}}}_{{\varvec{x}}{\varvec{x}}}^{0}=75\,\mathrm{MPa}\) used in the analyses.

Fig. 5
figure 5

a Schematic of a sinusoidally applied far-field load (three load cycles). b Variation of a far-field stress component \(\left({{\varvec{k}}{\varvec{\sigma}}}_{{\varvec{x}}{\varvec{x}}}^{0}\right)\) with \({{\varvec{\sigma}}}_{{\varvec{x}}{\varvec{x}}}^{0}=75\,\mathrm{MPa}\)

Full size image

The amplitude of the far-field stresses considered in the analyses for the elastic/perfectly plastic inhomogeneity and elastic/linear isotropic hardening inhomogeneity are given in Table 3 and Table 4, respectively.

Table 3 Far-field stresses used in analyses of the elastic/perfectly plastic material model
Full size table
Table 4 Far-field stresses used in analyses of the elastic/linear isotropic hardening model
Full size table

3 Results and Discussions

Several cases were simulated and studied for different aspect ratios of ellipsoid geometry, material models, and far-field stresses. Ellipsoidal and spherical elastic/perfectly plastic inhomogeneities were studied for far-field stresses given in Table 3. Ellipsoidal and spherical elastic/linear isotropic hardening inhomogeneities were studied for far-field stresses given in Table 4. The inputs for the material properties and the loadings are motivated and taken from the work done by Jana and Chatterjee [4]. The results from all the analyses reveal that the stress state within the inhomogeneity remains effectively uniform throughout the loading. This is true for both general ellipsoidal and spherical inhomogeneities. The surface plots of different stress components at a given normalized load step are shown in the following figures.

There is a slight non-uniformity in the stress values inside the inhomogeneity, mainly near the matrix–inhomogeneity interface, and this is a consequence of the discretization of the model.

We plot all the stress components in an arbitrarily chosen element near the centroid of the inhomogeneity against the normalized load step. All such plots from the analyses are shown below.

3.1 Elastic/Perfectly Plastic Inhomogeneity

Figures 6b and 7b show that after the transition from the elastic phase to the plastic phase, the normal stresses keep changing but the shear stresses tend to be constant (nearly flat lines). These results are in agreement with the J2 flow theory because yielding is a result of deviatoric stresses and not hydrostatic stresses. It is also seen that the amplitude of the stress components does not change. This is expected for an elastic/perfectly plastic material.

Fig. 6
figure 6

a Surface plot of \({{\varvec{\tau}}}_{{\varvec{y}}{\varvec{z}}}\) in a quarter of the model consisting of the ellipsoidal [1 mm, 0.75 mm, 0.5 mm] elastic/perfectly plastic inhomogeneity embedded in the elastic matrix, at a normalized load step of 0.2. b Stress components inside the inhomogeneity for the same model under sinusoidal far-field stresses are in Table 3

Full size image
Fig. 7
figure 7

a Surface plot of \({{\varvec{\sigma}}}_{{\varvec{x}}{\varvec{x}}}\) in a quarter of the model consisting of the spherical [1 mm] elastic/perfectly plastic inhomogeneity embedded in the elastic matrix, at a normalized load step of 0.4. b Stress components inside the inhomogeneity for the same model under sinusoidal far-field stresses are in Table 3

Full size image

3.1.1 Ellipsoidal Inhomogeneity

We studied mesh convergence for all the simulations. Table 5 details the mesh convergence study for elastic/perfectly plastic ellipsoidal inhomogeneity embedded inside an elastic matrix at 100th time step of the sinusoidal loading.

Table 5 Mesh convergence study of the elastic/perfectly plastic ellipsoidal inhomogeneity at 100th time step
Full size table

An element is chosen near the centroid in each of the coarser and the finer mesh models. The stress values in the element are taken at the 100th time step. It is clear from the table that the results obtained with the finer mesh are closer to those obtained with the coarser mesh. Thus, it is clear that the results have converged. Moreover, the results with finer mesh are shown in this paper.

3.1.2 Spherical Inhomogeneity

See Fig. 7.

3.2 Elastic/Linear Isotropic Hardening Inhomogeneity

Figures 8b and 9b show that even after the transition from the elastic phase to the plastic phase, the stresses behave in a non-linear fashion. It can be noticed that the amplitude of the stress components increases with the normalized load step. This behavior is expected for an elastic/linear isotropic hardening material.

Fig. 8
figure 8

a Surface plot of \({{\varvec{\tau}}}_{{\varvec{z}}{\varvec{x}}}\) in a quarter of the model consisting of the ellipsoidal [1 mm, 0.75 mm, 0.5 mm] elastic/linear isotropic hardening inhomogeneity embedded in the elastic matrix, at a normalized load step of 0.6. b Stress components inside the inhomogeneity for the same model under sinusoidal far-field stresses are in Table 4

Full size image
Fig. 9
figure 9

a Surface plot of \({\sigma }_{yy}\) in a quarter of the model consisting of the spherical [1 mm] elastic/linear isotropic hardening inhomogeneity embedded in the elastic matrix, at a normalized load step of 0.8. b Stress components inside the inhomogeneity for the same model under sinusoidal far-field stresses are in Table 4

Full size image

3.2.1 Ellipsoidal Inhomogeneity

See Fig. 8.

3.2.2 Spherical Inhomogeneity

Table 6 details the mesh convergence study for elastic/linear isotropic hardening plastic ellipsoidal inhomogeneity embedded inside an elastic matrix at 150th time step of the sinusoidal loading. An approach similar to the one adopted earlier is used in this case as well. Moreover, the results obtained with the finer mesh are closer to those with the coarser mesh, and hence it can be said that mesh convergence has been achieved.

Table 6 Mesh convergence study of the elastic/linear isotropic hardening plastic ellipsoidal inhomogeneity at 150th time step
Full size table

4 Conclusions and Future Work

In this paper, the stress–strain behavior in a single elasto-plastic ellipsoidal inhomogeneity embedded inside an infinite isotropic elastic matrix subjected to sinusoidal far-field stresses is investigated using ABAQUS. The study is done for two different material models, viz., elastic/perfectly plastic material model and elastic/linear isotropic hardening material model. The results for both material models are not shown in a single plot because the simulations are done for different loadings in each case, and the reason behind this approach is to validate this work with the work done by Jana and Chatterjee [4]. Nevertheless, this serves its purpose, i.e., we can easily distinguish between the two material behaviors from separate plots.

We also investigated two different shapes of the inhomogeneity namely a general ellipsoid and a sphere, i.e., a special ellipsoid. Moreover, the results for both geometric models, viz., ellipsoidal and spherical are not shown in the same plot because there is no difference in the mechanics since a sphere is a special case of an ellipsoid. Similar stress behaviors are observed for both geometric models. The major contribution of this work is the preliminary study of stress behavior inside the ellipsoidal inhomogeneity, and this work can be extended to other material models as well. In future, a semi-analytical method, based on Eshelby’s approach, can be developed to study the stress behavior, and in that case, this work would be used as validation for the results obtained from the semi-analytical method developed.