The investigation of the stress-strain state (SSS) of bodies with inclusions is important for the optimization of the processes of manufacturing of materials (powder metallurgy, ceramic production, casting, etc.) [1,2,3,4]. Inclusions can be used to model striated formations formed in the course of plastic prestraining in the microstructure of metals [5]. As one of directions in the investigation of the SSS of structural elements with inclusions of special types, we can mention the discrete hardening of materials [6].

Inclusions strongly affect the processes of deformation, lead to the concentration of stresses and the appearance of defects of the shape, and cause local fractures [7,8,9]. The processes of deformation may lead to phase transformations in materials, e.g., to the formation of martensitic structures [10]. It is especially important to study crack initiation in the course of phase transformations, which determines the onset of fracture of the material [11, 12]. Note that elongated inclusions can model the stiffening elements of thin-walled structures.

Inclusions and discontinuities in the form of cracks and pores play the role of local stress concentrators. In the study of the SSS of media containing these inclusions, it is reasonable to use numerical methods. They are fairly universal and applicable for the analyses of objects of various shapes and sizes and various types of loading, unlike the analytic methods, which are often cumbersome and, in some cases (noncanonical shapes of inclusions, complicated modes of deformation, etc.), inapplicable. Among the numerical methods, the finite-difference method, boundary-element method, and finite-element method (FEM) are used especially extensively [13,14,15]. We especially mention the urgency of development of projective-iterative schemes for the realization of grid methods capable of significant reduction of the computer time in numerous problems of the mechanics of deformable solid [16,17,18]. These schemes based on the FEM were also used for the media with inclusions [19,20,21,22]. We also indicate the possibility of construction of these schemes for the method of local variations, i.e., for the numerical method used for the solution of variational problems [23].

In design works, it is customary to apply the FEM as a part of various packages of applied programs, such as, ANSYS, NASTRAN, ABAQUS, etc. In the present work, by using the ANSYS program [24], we analyze the influence of the shape, parameters, and relative arrangement of elongated elliptic and rectangular inclusions in a plane element of the elastic medium (modeling its behavior in the indicated technological processes of manufacturing of structural elements or in the course of operation) on the SSS. We study two inclusions, which enables us to clarify the principal features of their interaction.

Computational Model

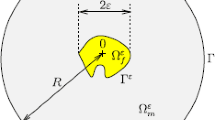
Consider an inhomogeneous plane element Ω of an elastic medium with two randomly located elastic inclusions Ω2 and Ω3 (Ω = Ω1 ∪ Ω2 ∪ Ω3) (Fig. 1). The sizes of the element are such that the boundary conditions do not affect the SSS in the vicinity of the inclusions. By L 1 and L 2 we denote the lengths of the sides of plane element, a i and b i are the sizes of the sides of the ith inclusion, s is the distance between the centers of the inclusions, α is the angle of rotation of one inclusion about the other, n i is the distance from the edge of the plane element to the ith inclusion, А–А and В–В are sections of the element used to analyze the SSS. Tensile forces

Fig. 1.
figure 1

Plane element used to model the behavior of a medium with inclusions.

Full size image
$$ P\left(x,y\right)={\left({P}_x\left(x,y\right),{P}_y\left(x,y\right)\right)}^T\left({P}_x\left(x,y\right)=0,{P}_y\left(x,y\right)=\mathrm{const}\right) $$

are given on the boundary γ of the domain Ω(y = 0,  0 ≤ x ≤ L 1 и y = L 2, 0 ≤ x ≤ L 1 ). On the remaining part of the boundary (x = 0, 0 ≤ y ≤ L 2 and x = L 1, 0 ≤ y ≤ L 2), the forces are absent.

It is necessary to find the fields of displacements and stresses in the element (matrix) with inclusions for different orientations of one inclusion relative to the other, study the influence of the mechanical characteristics and geometric parameters of the inclusions on the SSS of the element, and determine the safest possible configurations of their relative arrangements. Note that, by using the models of plane problems, it is possible to establish the principal features of the SSS, in particular, in the case of deformation of the media with regard for their interaction with inclusions of different shapes [9, 12, 20,21,22].

In the variational statement, the original problem leads to the minimization of functional of the potential strain energy [25]. In the analysis of the strain and stress fields near inclusions, it is customary to consider the problems in which the domains of perturbation of the SSS are much smaller than the characteristic sizes of the body. In the numerical analysis, the sizes of the body are assumed to be infinite. The classical variational principles were developed for finite domains and, hence, in order to extend them to infinite domains, it is necessary to change the formulation [21, 26].

The problem was solved by the FEM with the use of the ANSYS standard package of applied programs (licensed version) [24]. It is known [14, 15] that the main idea of the FEM is based on the discretization of the domain of continuous variation of arguments of the desired function (displacements, temperature, pressure, etc.) into a collection of finitely many subdomains, i.e., finite elements, and the approximation of continuous functions within the boundaries of each finite element by certain polynomials. As a result, the original variational problem is replaced by a discrete model, i.e. by a system of linear or nonlinear algebraic equations with unknown values of the required function at the nodes of a finite-element mesh.

In our numerical calculations, we use second-degree triangular (six-node) Lagrangian finite elements and approximate the unknown functions of displacements within each finite element by quadratic polynomials.

Results of Numerical Analysis

The calculations were performed for a plane element 0.4 × 0.4 m in size containing two elongated elliptic and rectangular inclusions a 1 × b 1 and a 2 × b 2 of the same material; the relative stiffness of the inclusions k = G 2/G 1 (G 1 and G 2 are the shear moduli of the materials of the matrix and inclusions, respectively) was taken to be either greater or smaller than one. The distance between the inclusions was s = 0.02 m, and the external tensile load was P = 10 MPa. As the materials of the inclusions and the media (matrix), it is possible to use aluminum and various steels, in particular, steels for hardening coatings, such as St3, R6M5, and other types of steel. The inclusions which are “softer” than the matrix can be used to endow binary systems with certain functional properties (conductivity and pore formation).

The numerical analyses were performed on an Intel Inside computer with Dual Core characterized by a clock frequency of 2.10 GHz, with a RAM of 3 GB, and a 32-bit operating system. The number of finite elements was 67,308. On the average, the calculation time was equal to 18 sec.

Figures 2 and 3 illustrate the distributions of the relative stress intensity σ i /P in the plane element depending on the angle of rotation of one inclusion about the second inclusion for k > 1 (Fig. 2; k = 3.2) and k < 1 (Fig. 3; k = 0.31). In all figures, the values of σ i /P on the segments of the axes [0; 0.2] and [0.8; 1] are constant and equal to the corresponding values for L = 0.2 and L = 0.8 (L is a dimensionless quantity, L = x/L 1 , 0 ≤ x ≤ L 1 , L 1 = L 2). For this reason, they are not presented.

Fig. 2.
figure 2

Distributions of the relative stress intensity σ i /p in a plane element with two rectangular (a, b) and elliptic (c, d, e, f) inclusions for k > 1: (а, с, e) in the А–А section (0 ≤ L ≤ L 2/L 2); (b, d, f) in the В–В section (0 ≤ L ≤ L 1/L 1); (1) α = 0°; (2) 45°; (3) 90°; (4) 135°; (5) 180°.

Full size image
Fig. 3.
figure 3

Distributions of the relative stress intensities σ i /p in the plane element for k < 1 (the notation is the same as in Fig. 2).

Full size image

In Figs. 2 а–d, we take the following sizes of inclusions: a 1 = 0.03 m; b 1 = 0.01 m; a 2 = 0.01 m; b 2 = 0.005 m; n 1 = n 2 = 0.0185 m. In the А–А section, the stresses with maximum magnitude are formed for an angle of rotation of the inclusion α = 135°. In the В–В section, the corresponding stresses are formed at an angle of 45°. In Figs. 3a, b, we present the distributions of the quantity σ i /P in these sections for “softer” inclusions depending on the angle between the inclusions.

The maximum stresses σ i in the А–А section appear at α = 90°, whereas in the В–В section, they are formed at 135°. Hence, for two rectangular inclusions of different lengths with higher relative stiffness, the stresses are higher. At the same time, “softer” inclusions decrease the stress concentration by 25%.

The angle of rotation α = 135° remains dangerous for both “soft” and “rigid” inclusions but, for “soft” inclusions, the peaks of stresses are also observed for the angle of rotation equal to 90°.

We studied (see Figs. 2c, d and 3 с, d) elliptic inclusions whose semiaxes are equal to the corresponding sizes of the inclusions depicted in Figs. 2 а, b and 3 а, b and investigated the influence of their shape on the changes in the SSS of the plate. The stresses with maximum magnitude σ i are formed in the А–А section for the angles of rotation equal to 135° and 45° and, in the В–В section, for the angles equal to 45° and 180° (Fig. 2c, d).

For the “soft” inclusion, we recorded their peak of stresses in the А–А section for α = 90° and 45° and, in the В–В section, for 90° (Figs. 3 с, d). The peaks of stresses in the В–В section for the other angles are practically equal (the difference is ~ 6%). Thus, for different combinations of materials, the elliptic inclusions cause lower peaks of stresses than the rectangular inclusions.

The difference between the maximum jumps of stresses becomes about two times higher for α = 135° (elliptic inclusions substantially decrease the peaks of stresses) (Figs. 2 а, с) and by about 30% higher for 90° (Figs. 3a, с). For 90° (Fig. 3d) and 135° (Fig. 3b), the differences between the peaks of stresses are insignificant (~ 2%).

In Figs. 2e, f and 3e, f, we present the results of investigations for two elliptic inclusions one of which is very long; the combination of materials is the same as in the previous cases; the sizes of the inclusions are as follows: a 1 = 0.07 m, b 1 = 0.017 m, a 2 = 0.02 m, b 2 = 0.023 m, n 1 = 0.0165 m, and n 2 = 0.019 m.

The stresses with maximum magnitude are formed in the А–А section at α = 135° and in the В–В section for all investigated angles of rotation (Figs. 2e, f). For the “soft” inclusion, the maximum stresses were recorded in the А–А section for α = 90° and, in the В–В section, as for the “rigid” inclusion, for all values of the angle α (Fig. 3e, f). The “softer” inclusion causes a higher stress intensity (~ 20%); the angle of orientation equal to 90° proves to be most dangerous in both cases. Moreover, for the “more rigid” inclusion, the angle equal to 135° is also dangerous.

Conclusions

The results of computer modeling of the SSS of plane elements of an elastic medium with elongated elliptic and rectangular inclusions of different sizes, orientations, and stiffnesses demonstrate that the stress intensity factor increases with the relative stiffness of the inclusions (for k > 1), which may lead to the appearance of plastic strains and the nuclei of fracture. By using the standard packages of finite-element analysis and varying the stiffness and geometric characteristics of the inclusions, their shapes, number, and orientations within broad ranges, we can also investigate the SSS for the other types of loading (biaxial tension–compression and torsion in combination with biaxial tension–compression).

The results of our investigations can be used to model the technological processes of powder metallurgy and ceramic production, in the study of the influence of discrete hardening and discretization of the microstructure of the material under phase transformations, and in analyzing the SSS of stiffened plate-like structural elements. By using a package of applied programs, it is possible to investigate the formation of irregularities in the form of cracks in the zone of location of the inclusions and the specific features of local loading formed in this case between the inclusion and the cracks.