1 Introduction

The moving mass problem, i.e., the problem of a continuously distributed system carrying a moving concentrated mass, has been an interest of research for more than a century [1]. It has broad applications in mechanics and engineering, including spacecraft stations, satellite antennas, robotic arms [2], machine tools, flexible manipulators [3], high-speed train railroads and highway bridges with moving vehicles [4].

The classical example of a moving mass problem is the idealisation of a vehicle-bridge system. In this case the moving vehicle is usually treated as a moving force, or load, of constant magnitude, while the bridge is modelled as a simply-supported beam. This problem is therefore more accurately described as a moving load problem [4]. Pesterev et al. [5] recently revisited the moving load problem to develop tools for finding the maximum beam deflection for a given velocity of the load. The moving load assumption does not take into account the inertial forces of the moving mass and the interactions between the moving mass and the continuous beam. The moving load treatment is therefore insufficient when the gravitational and inertial effects of the moving mass are not negligible compared to the mass of the structure. In [6] it was shown that the moving load solution is not an upper bound for the moving mass solution for the (simply-supported and clamped-clamped) boundary conditions considered there.

Ting et al. [7] were among the first to consider the inertial forces of the moving mass as an interaction between the mass and the beam. Ryu et al. [8] took all the inertial effects (including centrifugal and Coriolis effects) of a moving mass into account when deriving the equations of motion for an elastically restrained beam. A cantilever beam with a mass placed at its free end was investigated by Golnaraghi [9, 10]. A slider was placed at the free end of a cantilever beam as a controller to suppress the transient vibrations. A spring-mass subsystem coupled with a uniform cantilever beam was investigated by Khalily et al. [11], Siddiqui et al. [12–14] and Wu [15–18]. In [15–18] the spring-mass subsystem was replaced by massless equivalent springs and the corresponding normal mode shape solution that satisfied spring constraint conditions was derived. Perturbation [12, 13] and average acceleration [14] methods were used to analyse the distinctive oscillation features of the beam.

Here we consider the effects of a moving mass on vibration of a tapered beam (i.e., one of varying cross-section). This problem is for instance relevant for artillery and similar launch systems and to our knowledge has not been treated before. In artillery systems, for release and projection purposes one is particularly interested in tip deflections as these effect the initial conditions of the subsequent projectile motion of the launched mass. In this paper we ask the question whether the moving mass has a significant effect on the tip deflection of the beam. Vibrations of tapered beams have for instance been studied by Goel [19], Mabie and Rogers [20] and De Rosa and Auciello [21], who all considered linearly varying cross-sectional dimensions, and Zhou [22] who considered more general polynomial tapering. We choose the tapering to be parabolic, in which case we can obtain the mode shapes of the free beam, without a mass, exactly by using a transformation of the (spatial) independent variable similar to that used in [22]. We then expand the time-dependent solution of the moving mass problem in terms of these mode shapes and investigate the tip deflection as a function of the three important parameters of the problem: the relative mass of moving mass and beam, the velocity of the moving mass and the degree of tapering.

2 Modelling

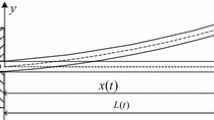
The system to be studied is shown schematically in Fig. 1. Here the constant parameters of the beam are its length \(l\), its mass density \(\rho \) and its modulus of elasticity \(E\), while the varying parameters are the cross-sectional area \(A(x)\) and the second moment of area about the \(z\)-axis \(I(x)\). The moving mass \(M\) slides along the length of the beam with local velocity \(v(t)\) and acceleration \(a(t)\). The beam deflection, in the \(y\) direction, is denoted by \(w(x,t)\).

Fig. 1
figure 1

Cantilever beam carrying a moving mass

Full size image

The beam is assumed to undergo small deflections. We can then write \(x(t)\) for the position of the mass along the axis of the beam and \(w(x(t),t)\) for the position of the mass in space. The vertical velocity of the moving mass is then computed as

$$\frac{{\rm d}w}{{\rm d}t}=v(t)\frac{\partial w}{\partial x}+\frac{\partial w}{\partial t}, $$
(1)

and the acceleration as

$$\frac{ {\rm d}^2 w}{{\rm d}t^2}=v^2(t)\frac{\partial ^2w}{\partial x^2}+2v(t)\frac{\partial ^2 w}{\partial x\partial t}+a(t)\frac{\partial w}{\partial x}+\frac{\partial ^2 w}{\partial t^2}.$$
(2)

The first and second terms on the right-hand side of (2) are the centrifugal and Coriolis terms, respectively.

We model the beam as an Euler–Bernoulli beam. The kinetic energy of the beam-mass system is then

$$ T=\frac{1}{2}\int _{0}^l \rho A(x) \left( \frac{\partial w}{\partial t} \right) ^2 {\rm d}x+\frac{1}{2}M\left( \frac{{\rm d}w}{{\rm d}t}\right) ^2, $$
(3)

while the potential energy is

$$ U=\frac{1}{2}\int _{0}^lEI(x)\left( \frac{\partial ^2w}{\partial x^2}\right) ^2 {\rm d}x, $$
(4)

and the gravitational energy is

$$W=\int _{0}^l\rho A(x)gw(x,t)\, {\rm d}x+Mgw(x,t),$$
(5)

where \(g\) is the acceleration due to gravity.

With the Lagrangian defined by

$$ L=W+T-U, $$
(6)

we then have the action functional of Hamilton’s principle in the form

$$ \begin{aligned} S& = \int _{t_1}^{t_2} \left\{ \int _{0}^l \left[ \frac{1}{2}\rho A(x) \left( \frac{\partial w}{\partial t}\right) ^2 \right. \right. \\&\left. \quad\,-\frac{1}{2}EI(x) \left( \frac{\partial ^2w}{\partial x^2}\right) ^2 +\rho A(x)gw\right] {\rm d}x \\&\left. \quad\,+\frac{1}{2}M \left( \frac{{\rm d}w}{ {\rm d}t}\right) ^2+Mgw\right\} {\rm d}t.\\ \end{aligned} $$
(7)

We consider deflections of the beam subject to the cantilever boundary conditions

$$ w\vert _{x=0}=0, \quad \left. \frac{\partial w}{\partial x}\right| _{x=0}=0 \quad {\text{ at }} {\text{ the }} {\text{ fixed }} {\text{ end }}, $$
(8)

and

$$ \left. \frac{\partial ^2w}{\partial x^2}\right| _{x=l}=0, \ \ \left. \frac{\partial ^3w}{\partial x^3}\right| _{x=l}=0 \quad {\text{ at }} {\text{ the }} {\text{ free }} {\text{ end }}.$$
(9)

We now use a Galerkin approximation to spatially discretise the problem and write the beam deflection as a truncated series \(w(x,t)=\sum _{i=1}^n\varPhi _{i}(x)Y_{i}(t)\), where the \(\varPhi _{i}(x)\) are (the first \(n\)) mode shapes of the free beam and the \(Y_{i}(t)\) are time-dependent dimensionless coefficients. After substitution of this series expansion into (7) the functional \(S\) becomes a function of the functions \(Y_i(t),\dot{Y_i}(t)\) and the application of Hamilton’s principle gives the Euler–Lagrange equations

$$ \frac{\partial L}{\partial Y_i}-\frac{\rm d}{{\rm d}t} \left( \frac{\partial L}{\partial \dot{Y_i}}\right) =0 \quad \quad (i=1,...,n), $$
(10)

taking the matrix form

$$ {\mathbf{M}}(t){\ddot{\mathbf{Y}}}(t)+{\mathbf{C}}(t){\dot{\mathbf{Y}}}(t)+{\mathbf{K}}(t){\mathbf{Y}}(t)={\mathbf{P}}(t), $$
(11)

where

$$ {\mathbf {Y}}(t) = [Y_{1}(t),Y_{2}(t),\dots ,Y_{n}(t)]^T, $$
(12)
$$ M_{ij} = \rho \int _{0}^lA(x)\varPhi _{i}(x)\varPhi _{j}(x) {\rm d}x+M\varPhi _{i}(x(t))\varPhi _{j}(x(t)),$$
(13)
$$C_{ij} = 2v(t)M\varPhi _{i}(x(t))\varPhi _{j}^\prime (x(t)),$$
(14)
$$\begin{aligned} K_{ij}&= E\int _{0}^lI^{\prime \prime }(x)\varPhi _{i}(x)\varPhi _{j}^{\prime \prime }(x) {\rm d}x\nonumber \\&\quad +2E\int _{0}^lI^\prime (x)\varPhi _{i}(x)\varPhi _{j}^{\prime \prime \prime }(x) {\rm d}x \\&\quad +E\int _{0}^lI(x)\varPhi _{i}(x)\varPhi _{j}^{\prime \prime \prime \prime }(x) {\rm d}x\\&\quad +v^2(t)M\varPhi _{i}(x(t))\varPhi _{j}^{\prime \prime }(x(t)) +a(t)M\varPhi _{i}(x(t))\varPhi _{j}^{\prime }(x(t)),\end{aligned}$$
(15)
$$ P_{i} = \rho g\int _{0}^lA(x)\varPhi _{i}(x){\rm d}x+Mg\varPhi _{i}(x(t)). $$
(16)

Here the prime indicates differentiation with respect to \(x\). The dimension of the system depends on the number of the assumed modes \(n\). The mass matrix \({\mathbf {M}}\) is symmetric. The matrix \({\mathbf {C}}\) in (14) comes from the Coriolis effect of the moving mass. Although taking the place of a damping matrix in the equation of motion (11), \({\mathbf {C}}\) is antisymmetric and therefore does not actually represent damping, in the sense that there is no dissipation. The stiffness matrix \({\mathbf {K}}\) in (15) varies with the beam coordinate \(x(t)\) as the mass moves along the beam and as a result it is nonsymmetric.

In the following section we derive the exact mode shapes \(\varPhi _i\) for the free tapered beam. Once these \(\varPhi _i\) are known the matrices \({\mathbf {M}}, \, {\mathbf {C}}\) and \({\mathbf {K}}\) and the vector \({\mathbf {P}}\) can be computed and Eq. (11) solved.

3 Exact mode shapes of the free tapered beam

3.1 Variation of the beam’s cross-section

The cross-section of the beam is assumed to be a circular ring with inner and outer radius varying parabolically with \(x\) (see Fig. 2). Denoting inner radius by \(r(x)\) and outer radius by \(R(x)\), we write \(r(x)=r_{0}(1-\alpha x/l)^2\) and \(R(x)=R_{0}(1-\alpha x/l)^2\), where the parameter \(\alpha \in [0,1]\) governs the degree of tapering of the beam and \(r_{0}\) and \(R_{0}\) are the inner and outer radius at the fixed end, respectively.

Fig. 2
figure 2

Cantilever beam with varying cross-section; a is the cross-section of the fixed end; b is the cross-section of the free end

Full size image

3.2 Mode shapes of the free beam

Based on the cross-sectional properties above, we have

$$ A(x) = \pi R^2(x)-\pi r^2(x)=A_0\left( 1-\frac{\alpha }{l}x\right) ^4,$$
(17)
$$ I(x) =\frac{\pi [R^4(x)-r^4(x)]}{4}=I_0\left( 1-\frac{\alpha }{l}x\right) ^8,$$
(18)

where \(A_{0}=\pi (R_{0}^2-r_{0}^2)\) and \(I_{0}=\pi (R_{0}^4-r_{0}^4)/4\).

The motion of the beam without a moving mass (and without gravity) is governed by

$$ E\frac{\partial ^2}{\partial x^2}\left[ I(x)\frac{\partial ^2 w}{\partial x^2} \right] +\rho A(x)\frac{\partial ^2 w}{\partial t^2}=0. $$
(19)

Using separation of variables in the form \(w(x,t)=\sum _{i=1}^n\varPhi _i(x){\rm e}^{{\rm i}\omega _i t}\), where the \(\omega _i\) are the first \(n\) natural circular frequencies of the beam, we find that the shape functions \(\varPhi _i\) solve the equation

$$ E\frac{{\rm d}^2}{{\rm d}x^2}\left[ I(x)\frac{{\rm d}^2\varPhi _i(x)}{{\rm d}x^2}\right] -\omega _i^2\rho A(x)\varPhi _i (x)=0. $$
(20)

By a transformation of the independent variable \(x\) according to \(x=l\xi , \, \zeta =1-\alpha \xi \) and \(\zeta ={\rm e}^z\), Eq. (20) is turned into the constant-coefficient equation

$$ \frac{{\rm d}^4\varPhi _{i}(z)}{{\rm d}z^4}+10\frac{{\rm d}^3\varPhi _{i}(z)}{{\rm d}z^3}+19\frac{{\rm d}^2\varPhi _{i}(z)}{{\rm d}z^2}-30\frac{{\rm d}\varPhi _{i}(z)}{{\rm d}z}-k_{i}^4\varPhi _{i}(z)=0, $$
(21)

where \(k_{i}^{4}=\rho A_{0}l^4\omega _{i}^2/EI_{0}\alpha ^4\).

Remarkably, the characteristic equation for (21), obtained on setting \(\varPhi_i ={\text{e}}^{\lambda _iz}\),

$$ {\lambda _{i}^{4}} + 10 {\lambda _{i}^{3}} +19 {\lambda _{i}^{2}}-30 {\lambda _{i}}-{k_{i}^{4}}=0, $$
(22)

has simple roots, as can be seen by noting that

$$ \left( \lambda _i^2+5\lambda _i-3\right) ^2=9+k_i^4 $$
(23)

and hence

$$ \left( \left( \lambda _i+\frac{5}{2}\right) ^2-\frac{37}{4}\right) ^2=9+k_i^4. $$
(24)

Thus the general solution of Eq. (21) can be written as

$$ \begin{aligned} \varPhi _{i}(z)&=\,{\text{e}}^{-5z/2}\left[ C_{i1}\cos (p_{i}z)+C_{i2}\sin (p_{i}z)\right. \\&\left. \quad+\, C_{i3}\sinh (q_{i}z)+C_{i4}\cosh (q_{i}z)\right] , \end{aligned}$$
(25)

where,

$$p_{i}=\sqrt{-\frac{37}{4}+\sqrt{9+k_i^4}},\qquad q_{i}=\sqrt{\frac{37}{4}+\sqrt{9+k_i^4}}$$

and the \(C_{ij}\) are coefficients yet to be determined. The \(p_i\) are real for \(k_i^4>76.5625\). In our numerical examples below this condition is always satisfied for all \(i=1,...,n\) (for instance, \(k_1^4=108\) for \(\alpha =0.9\) and larger for smaller \(\alpha \), and \(k_i\ge k_1\) for all \(i\)).

In terms of the original spatial variable \(x\) the solution (25) becomes

$$ \begin{aligned} \varPhi _{i}(x)=&\left( 1-\frac{\alpha }{l}x\right) ^{-5/2}\left\{ C_{i1} \cos \left[ p_{i}\log \left( 1-\frac{\alpha }{l}x\right) \right] \right. \\&+ C_{i2}\sin \left[ p_{i}\log \left( 1-\frac{\alpha }{l}x\right) \right] \\&+C_{i3}\cosh \left[ q_{i}\log \left( 1-\frac{\alpha }{l}x\right) \right] \\&\left. +\, C_{i4}\sinh \left[ q_{i}\log \left( 1-\frac{\alpha }{l}x\right) \right] \right\} . \end{aligned} $$
(26)

3.3 Determination of the coefficients \(C_{ij}\)

The coefficients \(C_{ij} \, (j=1,2,3,4)\) are determined by the boundary conditions (8) and (9), which yield the system of equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \varPhi _{i}(0)=0, \\ \varPhi _{i}^\prime (0)=0, \\ \varPhi _{i}^{\prime \prime }(l)=0, \\ \varPhi _{i}^{\prime \prime \prime }(l)=0. \end{array}\right. } \end{aligned}$$
(27)

Substituting the mode shapes (26) into (27), we obtain a system of linear homogeneous equations in the coefficients \(C_{ij}\), for each \(i=1,...,n\), in the form

$$\begin{aligned} S(k_{i})C_i:=&\left( \begin{array}{cccc} S_{11}(k_{i}) &{} S_{12}(k_{i}) &{} S_{13}(k_{i}) &{} S_{14}(k_{i})\\ S_{21}(k_{i}) &{} S_{22}(k_{i}) &{} S_{23}(k_{i}) &{} S_{24}(k_{i})\\ S_{31}(k_{i}) &{} S_{32}(k_{i}) &{} S_{33}(k_{i}) &{} S_{34}(k_{i})\\ S_{41}(k_{i}) &{} S_{42}(k_{i}) &{} S_{43}(k_{i}) &{} S_{44}(k_{i}) \end{array} \right) \left( \begin{array}{c} C_{i1}\\ C_{i2}\\ C_{i3}\\ C_{i4} \end{array} \right) \\ =&\left( \begin{array}{c} 0\\ 0\\ 0\\ 0 \end{array} \right) , \end{aligned} $$
(28)

where the \(S_{ij}(k_{i})\;(j=1,2,3,4)\) are functions of \(k_{i}\).

For non-trivial mode shapes we require the determinant of the matrix \(S(k_i)\) to be zero. This gives us a transcendental equation with infinitely many solutions the first \(n\) of which yield the \(k_i\) (and hence the natural circular frequencies \(\omega _{i}\)). We solve this equation using Newton iterations. For convergence it turns out to be sufficient to take the natural circular frequencies of the uniform beam \((\alpha =0)\) as initial guesses. Table 1 gives the first three natural frequencies for a number of \(\alpha \) values. We note that the first natural frequency increases with \(\alpha \), while the second and third natural frequencies decrease with \(\alpha \). Once the \(k_i\) have been obtained we can solve for the \(C_{ij}\), subject to a normalisation condition. Figure 3 shows the first three mode shapes of the cantilever beam for various values of \(\alpha \). Here we have used the normalisation that the absolute tip deflections \(|\varPhi _i(l)|\) are 1. It is found that when \(\alpha \) tends towards zero (uniform beam), the beam deflections (away from the end) become larger.

Fig. 3
figure 3

The first three mode shapes of a parabolically tapered cantilever beam with varying tapering parameter \(\alpha \)

Full size image
Table 1 First three natural frequencies of a pure beam with different tapering ratios \(\alpha \)
Full size table

4 Solutions of the moving mass problem

4.1 Example problem

In this section we consider a steel beam \((E=2.0\times 10^{11}\,{\rm Pa}, \rho =7{,}850\,{\rm kg/m^3})\) of length \(l=2\,{\rm m}\) and with \(R_{0}=0.1\,{\rm m}\) and \(r_{0}=0.05\,{\rm m}\). The tapering ratio \((\alpha )\), the magnitude \((M)\) and the velocity \((v)\) of the moving mass will be varied. We will focus on the effect of these parameters on beam tip and mass deflections as the beam is excited by the travelling mass. We compute expansions of the beam deflection in terms of the first three mode shapes \(\varPhi _i\), i.e., we take \(n=3\).

4.2 Numerical solutions and discussion

We discuss solutions for two different initial conditions. In the first the mass starts moving when the beam is in the static equilibrium configuration. We write the solution as

$$ {\mathbf Y}(t)=\widetilde{\mathbf Y}(t)+{\mathbf Y}_0, \quad \quad \widetilde{\mathbf Y}(0)=0 $$
(29)

and the load \( {\mathbf {P}}(t)\) as

$$ {\mathbf {P}}(t)=\widetilde{\mathbf {P}}(t)+ {\mathbf {P}}_0, $$
(30)

noting that \(P_{0i}=\rho g\int _0^l A(x)\varPhi _i(x)\,{\rm d}x\). The governing matrix Eq. (11) is then transformed into

$$ \left\{ \begin{aligned}&{\mathbf {M}}(t)\ddot{\widetilde{{\mathbf {Y}}}}(t)+{\mathbf{C}}(t)\dot{\widetilde{\mathbf {Y}}}+{\mathbf{K}}(t)\widetilde{{\mathbf {Y}}}(t)=\widetilde{\mathbf {P}}(t),\\&{\mathbf {K}}(t) {\mathbf {Y}}_0={\mathbf {P}}_0. \end{aligned} \right. $$
(31)

We solve the initial solution \({\mathbf Y}_0={\mathbf Y}(0)\) as \({\mathbf Y}_0={\mathbf K}^{-1}(0){\mathbf P}_0\) and obtain for the deflection \(w\) of the beam \(\sum _{i=1}^n\varPhi _i(x)Y_{0i}\) (with \(n=3\) in our case), which corresponds to the static deflection of the beam. This solution is displayed in Fig. 4.

Fig. 4
figure 4

Static deflection of a beam without mass at different tapering ratios \(\alpha \)

Full size image
Fig. 5
figure 5

Tip deflections at various values of \(M\) for different travelling velocities \(v\) and \(\alpha =0.1\). The ‘beam coordinate’ is the instantaneous position along the beam of the travelling mass

Full size image
Fig. 6
figure 6

Tip deflections at various values of \(v\), for a travelling mass \(M\) accounting for 20 % of the total mass and \(\alpha =0.1\)

Full size image

The remaining system of ordinary differential equations for \(\widetilde{\mathbf Y}\) in (31) is solved numerically using the fourth-order Runge–Kutta method. Solutions are given in the dynamic tip deflection plots of Figs. 5, 6 and 7. In each plot the tip deflection \(w(l,t)\) of the beam is given as a function of the instantaneous position \(x(t)\) of the moving mass. We call this the beam coordinate. It can be interpreted as a time coordinate when the speed is constant. When \(x(t)=l=2\), the mass has reached the end of the beam. Figure 5 shows three plots for three different velocities \(v\) and with varying mass \(M\) at fixed tapering ratio \(\alpha =0.1\). \(M\) is here specified as the percentage of the total mass of the beam-mass system. We see that the beam tip barely vibrates. Alternatively, in the case of a relatively low speed, such as \(v=100\,\hbox {m}/\hbox {s}\), we can say that the vibration frequency is so low that the tip has barely moved by the time the mass has traversed the length of the beam. In this case the static load effect of the moving mass dominates over the dynamic trigger effect. Tip deflection when the mass leaves the beam is almost proportional to the mass magnitude. At higher speeds, \(v=340\,\hbox {m}/\hbox {s}\) and \(v=1{,}800\,\hbox {m}/\hbox {s}\) in the figure, the mass movement triggers the beam tip to vibrate. Generally, the higher the velocity \(v\) and the larger the mass \(M\), the higher the vibration frequency of the beam tip. The tip deflections are no longer proportional to the mass magnitudes when the mass reaches the tip end. The amplitude of deflection reduces as the speed \(v\) increases.

Figure 6 presents the beam tip deflection when the mass travels along the beam (again with \(\alpha =0.1\)) at various velocities when the mass magnitude accounts for 20 % of the total mass of the system. Though the static load effect dominates the tip deflection at low velocities, in the range of \(v=10\,\hbox {m}/\hbox {s}\) to \(v=150\,\hbox {m}/\hbox {s}\), these velocities have different effects on the deflection trace. Again we note that generally the maximum tip deflection decreases as the velocity increases. In the last plot, at high velocities, we see that the tip deflection reaches its maximum when the mass is at about \(x=1.7\,\)m, almost independent of velocity.

Fig. 7
figure 7

Tip deflection for a mass accounting for 20 % of the total mass moving with velocity \(v=20\,\hbox {m}/\hbox {s}\) along a beam with different tapering ratios \(\alpha \). The uniform beam has \(\alpha =0\)

Full size image

Figure 7 shows the tip deflection under a travelling mass accounting for 20 % of the total mass and moving at a speed of \(v=20\,\hbox {m}/\hbox {s}\) along a beam at different tapering ratios \(\alpha \), including a uniform beam in the limit \(\alpha =0\). It is seen that a higher tapering ratio makes the beam effectively more slender: as \(\alpha \) increases, the maximum deflection of the tip increases.

Fig. 8
figure 8

Tip oscillations for a mass accounting for 20 % of the total mass moving along a beam with different tapering ratios \(\alpha \) from an initial non-equilibrium position at a velocity of \(v=20\,\hbox {m}/\hbox {s}\)

Full size image
Fig. 9
figure 9

Spectrogram of the tip oscillation for a mass accounting for 20 % of the total mass moving along a beam at a velocity of \(v=20\,\hbox {m}/\hbox {s}\) from an initial non-equilibrium position \((\alpha =0.1)\)

Full size image

In the second choice of initial conditions the beam is initially triggered to vibrate by both its own gravity and the moving mass. The situation can be described as follows. The beam is originally fixed at one end and simply supported at the other end. The simple support is then instantaneously removed at \(t=0\) when the mass starts moving from the fixed end. In this situation, the beam starts from a position of non-equilibrium. Beam gravity acts as an external load. It triggers vibration along with the moving mass. In this situation the tapering ratio matters significantly for the tip oscillation, as illustrated in Fig. 8. As the tapering ratio increases, the tip is more sensitive to the moving mass. Irregular oscillations occur when \(\alpha \) is large. The frequency content of the tip oscillation trace for \(\alpha =0.1\) in Fig. 8 is displayed in a spectrogram in Fig. 9. It shows the power spectral density (PSD) obtained by Fourier transformation (after multiplication by \(10^{4}\) and taking the logarithm for plotting purposes). The spectral decomposition is strongly dominated by frequencies close to, and slightly lower than, the first natural frequency of the corresponding free tapered beam (43 Hz according to Table 1). We find generally that the travelling mass has the effect to lower the frequency of vibration of the beam.

Fig. 10
figure 10

Tip (a) and mass (b) oscillations for different masses sliding along the beam at a constant velocity of \(v=10\,\hbox {m}/\hbox {s}\) from an initial non-equilibrium position \((\alpha =0.1)\)

Full size image
Fig. 11
figure 11

Tip (a) and mass (b) oscillations for different velocities \(v\) when a mass accounting for 20 % of the total mass moves along the beam from an initial non-equilibrium position \((\alpha =0.1)\)

Full size image

Having so far only considered the deflection of the beam tip, we now also focus on the deflection of the moving mass, or, equivalently, the position along the beam where the mass is instantaneously located. We call this the mass local deflection. Figures 10 and 11 display the effects on both tip and mass deflection of the magnitude of mass and its velocity at a low tapering ratio \((\alpha =0.1)\). We take again the second set of non-equilibrium initial conditions. The figures show that the oscillations are regular. Frequencies and tip amplitudes in Fig. 10a decrease slightly with the beam coordinate, which is due to the Coriolis acceleration \(\frac{\partial ^2w}{\partial x\partial t}\). We conclude that periods and amplitudes of vibration increase as we raise the magnitude of the travelling mass \(M\), and so does the deviation of the equilibrium position from the horizontal. When interpreting Fig. 11 it should be noted that the different periods for different velocities are the result of plotting deflections against a spatial coordinate (the beam coordinate). Plotted against time the curves would nearly fall on top of each other, with only a small divergence towards the right end (i.e., a slightly extended period for larger velocities).

Fig. 12
figure 12

Tip (a) and mass (b) oscillations when a mass accounting for 20 % of the total mass travels along the beam with an initial velocity \(v_0=10\,\hbox {m}/\hbox {s}\) and various constant accelerations \(a\) \((\alpha =0.1)\)

Full size image
Fig. 13
figure 13

Tip (a) and mass (b) oscillations when a mass accounting for 20 % of the total mass travels along the beam with an initial velocity \(v_0=10\,\hbox {m}/\hbox {s}\) and various constant decelerations \(a\) \((\alpha =0.1)\)

Full size image
Fig. 14
figure 14

Tip oscillations for different masses \(M\) sliding along the beam at constant velocity \(v=10\,\hbox {m}/\hbox {s}\) from an initial non-equilibrium position \((\alpha =0.8)\)

Full size image
Fig. 15
figure 15

Tip oscillations at different velocities \(v\) when a mass accounting for 20 % of the total mass moves along the beam from an initial non-equilibrium position \((\alpha =0.8)\)

Full size image

Figures 12 and 13 show oscillations when the moving mass is in constant acceleration, respectively deceleration (starting from an initial velocity \(v_0=10\,\hbox {m}/\hbox {s}\)), the beam again having tapering ratio \(\alpha =0.1\). For easier interpretation the deflections are here plotted against time rather than the beam coordinate. The period of both tip and mass oscillations is seen to vary slightly in time. This variation is in accordance with the slight extension of the period under increasing velocity of the moving mass observed in Fig. 11. In addition there is a small inertial effect: the periods of oscillation increase with increasing acceleration (and decreasing deceleration).

Note that there is a critical value for any realistic deceleration of the mass: the deceleration should be within the range \(-\frac{v_{0}^2}{2 l}\) to zero, otherwise the mass would go backwards before it reaches the tip end of the beam. The curves for \(a=-25\,\hbox {m}/\hbox {s}^{2}\) in Fig. 13 show the oscillations at this critical deceleration. Imposing a deceleration can be interpreted as a simple way of modelling friction between the moving mass and the beam.

We finally consider tip oscillations at large tapering ratio. Figures 14 (at constant mass \(M\)) and 15 (at constant velocity \(v\)) show that when \(\alpha =0.8\) these oscillations are very irregular.

5 Conclusion

In barreled launch systems the motion of the mass after it leaves the barrel (beam) is of obvious interest. However, after the moment of departure, the mass and beam motions are completely decoupled and can be studied by classical theory. In this paper we have studied the interaction between mass and beam while the former is travelling along the latter.

For this purpose approximate equations, in the form of a system of second-order ordinary differential equations with time-dependent coefficients, were derived from an energy formulation that takes into account dynamic mass-beam coupling due to inertial, Coriolis and centrifugal effects and uses an expansion in terms of the mode shapes of the free tapered beam, which can be obtained analytically. We consider cantilever boundary conditions, which are natural for launch applications, but other boundary conditions could be analysed as well. Using two different sets of initial conditions we then investigated the effect the travelling mass has on tip vibrations of the beam, important for the subsequent projectile motion of the released mass. Our results show that these tip vibrations become more irregular and grow in amplitude as the degree of tapering of the beam is increased.