Keywords

1 Introduction

The multi-layered sandwich beams are getting importance to get higher strengthening and economic structures. They can be also used to reduce unwanted vibrations of the load-carrying members especially using in automotive industry. In this study, a three-layered sandwich beam model is constructed with two thin layers made of more stiff materials for bottom and top, and a microstretch viscoelastic part for the middle layer. Thus, top and bottom layers sustain the major part of the bending loads, while the microstretch viscoelastic core absorbs the unwanted vibrations.

In literature, Kerwin [1] analyzed the flexural damped vibration of sandwich beams by considering traveling sinusoidal waves for the transverse displacement. Mead [2] generalized Kerwin’s though to simple supported plates. He showed that the standing waves or modes are uncoupled, even when damping was admitted in the core section. But when the beam supported in different ways such as clamped or free, the natural modes are coupled even for undamped core. Di Taranto [3, 4] has studied damped sandwich beams with viscoelastic core having a complex shear modulus with arbitrary boundary conditions. Mead and Markus [5] extended Di Taranto’s results to fixed-fixed beams. The Rayleigh–Ritz method is used to analyze the vibration characteristics of a sandwich beam with viscoelastic layer by Fasana et al. [6], and then Tang et al. analyzed the constrained damping layers, including normal strain effects [7].

More recently, Arikoglu and Ozkol studied vibration analysis of composite sandwich beam with viscoelastic core by using differential transform method. The core modeled with a complex shear modulus, and governing equations are derived by using Hamilton’s principle [8].

As it is well known, the material response to the external effects depends on to the material inner structure, especially for composite materials that possess granular structure, porous media, micro-damaged materials, etc. For such materials, the classical theory of elasticity is inadequate in the modeling. Higher order theories which include the micro-structure of the medium reflect the physical realities much better than the classical theories. For instance, Eringen’s micropolar [9] theory relies on the idea that every material particle can make micro-rotation in addition to the bulk deformation. The microstretch theory [10, 11] is a generalization of the micropolar theory and based on the assumption that every particle can undergo also volumetric micro-elongation together with micro-rotation, hence, it is a more convenient tool to model materials having micro-structures.

The theory of micropolar and microstretch viscoelastic materials are getting more attention of the researchers in recent years; Kumar and Partap studied vibrations of a microstretch viscoelastic plate [12, 13]. Ramazani et al. [14] analyzed micropolar elastic beams in a similar way as in [15]. Shaw used Hamiltonian principle to derive the governing equations and used Legendre’s transformation to solve the vibration problem of rectangular micropolar beams [16], while Svanadze gave the fundamental solutions of the system of equations of steady vibrations in micropolar viscoelastic medium [17].

In the present paper, we studied free vibrations of a typical sandwich beam structure containing two thin stiffer (high-strength) layers on top and bottom sides and a light (low-average strength) microstretch viscoelastic core in the middle part. Here the top and bottom stiff layers are considered as a classical elastic material, while the inner part is modeled as a microstretch viscoelastic material.

2 Fundamental Equations of Microstretch Viscoelastic Theory

The constitutive equations for a linear homogeneous and isotropic microstretch elastic solid are given as [10];

$$ \begin{aligned} & t_{kl} = \lambda \,\varepsilon_{mm} \,\delta_{kl} + (\mu + \kappa )\,\varepsilon_{kl} + \mu \,\varepsilon_{lk} + \lambda_{0} \,\bar{\theta }\,\delta_{kl} , \\ & m_{kl} = \alpha \,\gamma_{mm} \,\delta_{kl} + \beta \,\gamma_{kl} + \gamma \,\gamma_{lk} , \\ & m_{k} = a_{0} \,\bar{\theta }_{,k} , \\ & s - t = \lambda_{1} \,\bar{\theta } + \lambda_{0} \,\varepsilon_{kk} . \\ \end{aligned} $$
(1)

where \( t_{kl} ,\;m_{kl} \) are the stress and couple stress tensors, \( m_{k} \) is the microstretch vector and \( s = s_{kk} \), \( t = t_{kk} \), and the strain tensors are given as

$$ \varepsilon_{kl} = u_{l,k} + e_{lkm} \phi_{m} ,\quad \gamma_{kl} = \phi_{k,l} ,\quad \gamma_{k} = \bar{\theta }_{,k} $$
(2)

here, \( \lambda ,\,\,\mu \) are Lamé constant and shear modulus, \( \kappa ,\,\,\alpha ,\,\,\beta ,\,\,\gamma \) are the micropolar constants, \( \lambda_{0} ,\,\,\lambda_{1} \) and \( a_{0} \) are the microstretch constants, \( \rho \) is the mass density per unit volume, j is the micro-inertia, and \( {\mathbf{u}},\;{\varvec{\upphi}} \) and \( \bar{\theta } \) are the displacement and the micro-rotation vectors and the microstretch scalar, respectively.

The equations of motion of a microstretch elastic solid with no body forces, body couples, and body microstretch are given by

$$ \begin{aligned} & (c_{1}^{2} + c_{3}^{2} )\nabla \nabla \cdot {\mathbf{u}} - (c_{2}^{2} + c_{3}^{2} )\nabla \times \nabla \times {\mathbf{u}} + c_{3}^{2} \nabla \times {\varvec{\upphi}} + \bar{\lambda }_{0} \nabla \bar{\theta } = {{\ddot{\mathbf{u}}}} \\ & (c_{4}^{2} + c_{5}^{2} )\nabla \nabla \cdot {\varvec{\upphi}} - c_{4}^{2} \nabla \times \nabla \times {\varvec{\upphi}} + \omega_{0}^{2} \nabla \times {\mathbf{u}} - 2\omega_{0}^{2} {\varvec{\upphi}} = {{\ddot{\boldsymbol{\upphi} }}} \\ & c_{6}^{2} \Delta \bar{\theta } - c_{7}^{2} \theta - c_{8}^{2} \nabla \cdot {\mathbf{u}} = \ddot{{\theta}}, \\ \end{aligned} $$
(3)

where

$$ \begin{aligned} c_{1}^{2} & = \frac{(\lambda + 2\mu )}{\rho },\,\quad c_{2}^{2} = \frac{\mu }{\rho },\quad c_{3}^{2} = \frac{\kappa }{\rho },\quad c_{4}^{2} = \frac{\gamma }{\rho j},\quad c_{5}^{2} = \frac{(\alpha + \beta )}{\rho j}, \\ c_{6}^{2} & = \frac{{2a_{0} }}{\rho j},\quad c_{7}^{2} = \frac{{2\lambda_{1} }}{3\rho j},\quad c_{8}^{2} = \frac{{2\lambda_{0} }}{3\rho j},\quad \omega_{0}^{2} = \frac{{c_{3}^{2} }}{j},\quad \bar{\lambda }_{0} = \frac{{\lambda_{0} }}{\rho }. \\ \end{aligned} $$
(4)

To include the effects of viscoelastic character, we replace each one of the microstretch elastic constants

$$ \left( {\lambda ,\,\mu ,\,\kappa ,\,\alpha ,\,\beta ,\,a_{0} ,\,\lambda_{0} ,\,\lambda_{1} } \right) $$
(5)

by \( \left( {\lambda_{I} ,\,\mu_{I} ,\,\kappa_{I} ,\,\alpha_{I} ,\,\beta_{I} ,\,a_{I0} ,\,\lambda_{I0} ,\,\lambda_{I1} } \right) \). By representing each of the microstretch viscoelastic coefficients by \( b_{jI} \) which is a complex value such as \( b_{jI} = b_{j} \left( {1 + i\,\eta } \right) \), \( j = 1,2, \ldots 8 \). Here, \( \eta \) is the loss factor which also defines the ratio between the imaginal and real parts of the square of the nth frequency. With other way of saying it means the ratio of energy dissipation per cycle to maximum strain energy.

3 Formulation of the Problem

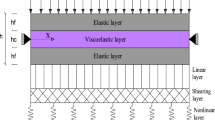
A sandwich beam is considered. The total length of the beam is L, total width is b and heights of the bottom and top layers are \( h_{1} \) and \( h_{3} \), while the core layer’s height is \( h_{2} \). The beam is constructed by two thin layers on top and bottom and a microstretch viscoelastic core in the middle. As it is well known, the top and bottom layers are assumed to be made of more high-strength material, thus it is supposed that they can be modeled as classical elasticity theory, while the softer (low-strength) part is assumed as microstretch viscoelastic to absorb the unwanted vibration.

The beam cross section is assumed to be symmetric with respect to the y-axis. The microstretch beam theory is constructed based on the following assumptions:

  • The beam height and its width are small as compared to the length.

  • No slip between layers.

  • Deflections are small.

  • Layers are incompressible though the thickness.

  • Transverse displacements are considered as unchanged between layers.

  • No torsion occurs in the beam.

  • The shear angle of the top and bottom layers is neglected.

  • The stress and the displacement fields do not vary severely across the height.

  • The contribution of the core layer is only by transverse shear stress.

  • Distributions of the body and surface force, couple and volumetric elongation, surface couple, strain, wryness, stress, and couple stress components are independent from y-axis.

In microstretch beam theory, the displacement vector, the micro-rotation vector, and the microstretch scalar are given as

$$ {\mathbf{u}} = \left( {u(x,z,t),\;0,\;w(x,z,t)} \right)^{T} ,\quad {\varvec{\upphi}} = \left( {0,\;\bar{\phi }(x,z,t),\;0} \right)^{T} ,\quad \bar{\theta } = \bar{\theta }(x,z,t) $$
(6)

The configuration of the sandwich beam is given in Fig. 1. Thus, the kinematic relations can be written as follows:

Fig. 1
figure 1

Geometry and displacement fields of the beam

Full size image
$$ \begin{aligned} & u_{1} (x,z,t) = u_{0} (x,t) - \frac{{h_{2} }}{2}\varphi (x,t) - \left( {z + \frac{{h_{1} }}{2}} \right)\frac{\partial w(x,t)}{\partial x},\quad \quad - \frac{{h_{1} }}{2} \le z \le \frac{{h_{1} }}{2}u_{1} (x,z,t) \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = u_{0} (x,t) - \frac{{h_{2} }}{2}\varphi (x,t) - \left( {z + \frac{{h_{1} }}{2}} \right)\frac{\partial w(x,t)}{\partial x},\quad \quad - \frac{{h_{1} }}{2} \le z \le \frac{{h_{1} }}{2} \\ & u_{2} (x,z,t) = u_{0} (x,t) - z\;\varphi (x,t),\quad \quad - \frac{{h_{2} }}{2} \le z \le \frac{{h_{2} }}{2} \\ & u_{3} (x,z,t) = u_{0} (x,t) + \frac{{h_{2} }}{2}\varphi (x,t) - \left( {z - \frac{{h_{3} }}{2}} \right)\frac{\partial w(x,t)}{\partial x},\quad \quad - \frac{{h_{3} }}{2} \le z \le \frac{{h_{3} }}{2} \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,w_{i} (x,z,t) = w(x,t)\quad \quad {\text{for}}\,{\text{all}}\quad \quad i = 1,2,3 \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\bar{\phi }(x,z,t) = \phi (x,t)\quad \quad {\text{and}}\quad \quad \bar{\theta }(x,z,t) = \theta (x,t) \\ \end{aligned} $$
(7)

where \( \varphi (x,t) =\Phi (x,t) + w^{\prime}(x,t) \), \( u_{0} (x,t) \) and \( w(x,t) \) are the total angular displacement, longitudinal, and transverse displacement of the centroid of microstretch elastic core, respectively. Similarly, \( u_{i} (x,z,t) \) and \( w_{i} (x,z,t) \) are longitudinal and transverse displacements of the ith layer for \( i = 1,2,3 \), while \( \bar{\phi }(x,z,t) \) and \( \bar{\theta }(x,z,t) \) stands for the nonzero component of the micro-rotation vector and microstretch scalar of the viscoelastic core.

Then, the strain quantities can be obtained from (2) by using (7) as

$$ \begin{aligned} \varepsilon_{xx}^{(1)} & = \frac{{\partial u_{0} }}{\partial x} - \frac{{h_{2} }}{2}\frac{\partial \varphi }{\partial x} - \left( {z + \frac{{h_{1} }}{2}} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }}, \\ \varepsilon_{xx}^{(3)} & = \frac{{\partial u_{0} }}{\partial x} + \frac{{h_{2} }}{2}\frac{\partial \varphi }{\partial x} - \left( {z - \frac{{h_{3} }}{2}} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }}, \\ \varepsilon_{xz}^{(2)} & = \frac{\partial w}{\partial x} + \phi ,\quad \varepsilon_{zx}^{(2)} = - \left( {\varphi + \phi } \right),\quad \gamma_{yx} = \frac{\partial \phi }{\partial x},\quad \gamma_{x} = \frac{\partial \theta }{\partial x}. \\ \end{aligned} $$
(8)

Thus, the stress–strain relations (1) become as

$$ \begin{aligned} t_{xx}^{(1)} & = E_{1} \;\varepsilon_{xx}^{(1)} ,\quad t_{xx}^{(3)} = E_{3} \;\varepsilon_{xx}^{(3)} , \\ t_{xz}^{(2)} & = \left( {\mu + \kappa } \right)\;\varepsilon_{xz}^{(2)} + \mu \;\varepsilon_{zx}^{(2)} ,\quad t_{zx}^{(2)} = \left( {\mu + \kappa } \right)\;\varepsilon_{zx}^{(2)} + \mu \;\varepsilon_{xz}^{(2)} , \\ m_{xy}^{(2)} & = \gamma \;\gamma_{yx}^{(2)} ,\quad m_{x} = a_{0} \;\gamma_{x} . \\ \end{aligned} $$
(9)

The assumptions used to derive the kinematic relations are taken as in [8]. The formulation procedure is similar to the one given by Kiris and Inan [18] and based on Hamilton principle;

$$ \int\limits_{0}^{T} {\left( {\delta U - \delta K} \right)} dt = 0, $$
(10)

where U and K show the elastic strain energy and the kinetic energy. For the present problem it becomes as

$$ \begin{array}{*{20}l} {\int\limits_{0}^{T} {\int\limits_{0}^{L} {\int\limits_{{ - h_{1} /2}}^{{h_{1} /2}} {\left[ {t_{xx}^{(1)} \;\delta \,\varepsilon_{xx}^{(1)} - \rho_{1} \left( {\frac{\partial w}{\partial t}\;\delta \frac{\partial w}{\partial t} + \frac{{\partial u_{1} }}{\partial t}\;\delta \frac{{\partial u_{1} }}{\partial t}} \right)} \right]} } } {\text{d}}z\;{\text{d}}x\;{\text{d}}t + \int\limits_{0}^{T} {\int\limits_{0}^{L} {\int\limits_{{ - h_{2} /2}}^{{h_{2} /2}} {\left[ {t_{xz}^{(2)} \;\delta \,\varepsilon_{xz}^{(2)} + t_{zx}^{(2)} \;\delta \,\varepsilon_{zx}^{(2)} } \right.} } } } \hfill \\ {\left. { + m_{x}^{(2)} \;\delta \,\gamma_{x}^{(2)} + (s - t)^{(2)} \;\delta \,\theta - \rho_{2} \left( {\frac{\partial w}{\partial t}\;\delta \frac{\partial w}{\partial t} + \frac{{\partial u_{2} }}{\partial t}\;\delta \frac{{\partial u_{2} }}{\partial t} + \frac{\partial \phi }{\partial t}\;\delta \frac{\partial \phi }{\partial t} + \frac{\partial \theta }{\partial t}\;\delta \frac{\partial \theta }{\partial t}} \right)} \right]{\text{d}}z\;{\text{d}}x\;{\text{d}}t} \hfill \\ { + \int\limits_{0}^{T} {\int\limits_{0}^{L} {\int\limits_{{ - h_{3} /2}}^{{h_{3} /2}} {\left[ {t_{xx}^{(3)} \;\delta \,\varepsilon_{xx}^{(3)} - \rho_{3} \left( {\frac{\partial w}{\partial t}\;\delta \frac{\partial w}{\partial t} + \frac{{\partial u_{3} }}{\partial t}\;\delta \frac{{\partial u_{3} }}{\partial t}} \right)} \right]} } } {\text{d}}z\;{\text{d}}x\;{\text{d}}t = 0.} \hfill \\ \end{array} $$
(11)

Substituting (8) and (9) into (11) and then applying partial integration give both the governing equations and boundary conditions. For governing equations, one must also set the coefficients of each variations, i.e., \( \delta u_{0} ,\;\delta \varphi ,\;\delta w,\;\delta \phi \) and \( \delta \theta \) to zero and get,

$$ \begin{aligned} & {\text{coeff}}(\delta u_{0} ): \\ & \left( {E_{1} h_{1} + E_{3} h_{3} } \right)\frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + \frac{{h_{2} }}{2}\left( {E_{3} h_{3} - E_{1} h_{1} } \right)\frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + \frac{1}{2}\left( {E_{3} h_{3}^{2} - E_{1} h_{1}^{2} } \right)\frac{{\partial^{3} w}}{{\partial x^{3} }} \\ & = \left( {\rho_{1} h_{1} + \rho_{2} h_{2} + \rho_{3} h_{3} } \right)\frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} + \frac{{h_{2} }}{2}\left( {\rho_{3} h_{3} - \rho_{1} h_{1} } \right)\frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + \frac{1}{2}\left( {\rho_{3} h_{3}^{2} - \rho_{1} h_{1}^{2} } \right)\frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}, \\ & {\text{coeff}}(h_{2} \;\delta \phi ):\quad \quad \kappa \left( {\frac{\partial w}{\partial x} + 2\phi + \varphi } \right) = - \rho_{2} \frac{{\partial^{2} \phi }}{{\partial t^{2} }} \\ & {\text{coeff}}(h_{2} \;\delta \theta ):\quad \quad a_{0} \frac{{\partial^{2} \theta }}{{\partial x^{2} }} - \lambda_{1} \theta = \rho_{2} \frac{{\partial^{2} \theta }}{{\partial t^{2} }} \\ \end{aligned} $$
(12)
$$ \begin{aligned} & {\text{coeff}}(\frac{{h_{2} }}{2}\delta \varphi ): \\ & \left( {E_{3} h_{3} - E_{1} h_{1} } \right)\frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + \frac{{h_{2} }}{2}\left( {E_{1} h_{1} + E_{3} h_{3} } \right)\frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + \frac{1}{2}\left( {E_{1} h_{1}^{2} + E_{3} h_{3}^{2} } \right)\frac{{\partial^{3} w}}{{\partial x^{3} }} - 2\left( {\mu + \kappa } \right)\left( {\varphi + \phi } \right) \\ & \quad + 2\mu \left( {\frac{\partial w}{\partial x} + \phi } \right) = \left( {\rho_{3} h_{3} - \rho_{1} h_{1} } \right)\frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} + \frac{{h_{2} }}{6}\left( {3\rho_{1} h_{1} + \rho_{2} h_{2} + \rho_{3} h_{3} } \right)\frac{{\partial^{2} \varphi }}{{\partial t^{2} }} \\ & \quad + \frac{1}{2}\left( {\rho_{1} h_{1}^{2} + \rho_{3} h_{3}^{2} } \right)\frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}, \\ & {\text{coeff}}(\delta w): \\ & \frac{1}{2}\left( {E_{3} h_{3}^{2} - E_{1} h_{1}^{2} } \right)\frac{{\partial^{3} u_{0} }}{{\partial x^{3} }} + \frac{{h_{2} }}{4}\left( {E_{1} h_{1}^{2} + E_{3} h_{3}^{2} } \right)\frac{{\partial^{3} \varphi }}{{\partial x^{3} }} + \frac{1}{3}\left( {E_{1} h_{1}^{3} + E_{3} h_{3}^{3} } \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} \\ & \quad - \left( {\mu + \kappa } \right)h_{2} \left( {\frac{\partial \phi }{\partial x} + \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + \mu \,h_{2} \left( {\frac{\partial \phi }{\partial x} + \frac{\partial \varphi }{\partial x}} \right) = \frac{1}{2}\left( {\rho_{3} h_{3}^{2} - \rho_{1} h_{1}^{2} } \right)\frac{{\partial^{3} u_{0} }}{{\partial t^{2} \partial x}} \\ & \quad - \left( {\rho_{1} h_{1} + \rho_{2} h_{2} + \rho_{3} h_{3} } \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + \frac{{h_{2} }}{4}\left( {\rho_{1} h_{1}^{2} + \rho_{3} h_{3}^{2} } \right)\frac{{\partial^{3} \varphi }}{{\partial t^{2} \partial x}} + \frac{1}{3}\left( {\rho_{1} h_{1}^{3} + \rho_{3} h_{3}^{3} } \right)\frac{{\partial^{4} w}}{{\partial t^{2} x^{2} }}. \\ \end{aligned} $$

The boundary conditions are

$$ \begin{aligned} & \left. {\left( {N_{x}^{(1)} + N_{x}^{(3)} } \right)\delta u_{0} } \right|_{0}^{L} = 0, \\ & \left. {\frac{{h_{2} }}{2}\left( {N_{x}^{(3)} - N_{x}^{(1)} } \right)\delta \varphi } \right|_{0}^{L} = 0, \\ & \left. {\left( {Q_{x}^{(2)} + \frac{\partial }{\partial x}M_{x}^{(1)} + \frac{\partial }{\partial x}M_{x}^{(3)} + \frac{{h_{1} }}{2}\frac{\partial }{\partial x}N_{x}^{(1)} - \frac{{h_{3} }}{2}\frac{\partial }{\partial x}N_{x}^{(3)} } \right)\delta w} \right|_{0}^{L} = 0, \\ & \left. {\left( {\frac{{h_{3} }}{2}N_{x}^{(3)} - \frac{{h_{1} }}{2}N_{x}^{(1)} - M_{x}^{(1)} - M_{x}^{(1)} } \right)\delta \frac{\partial w}{\partial x}} \right|_{0}^{L} = 0, \\ & \left. {\left( {a_{0} h_{2} \frac{\partial \theta }{\partial x}} \right)\delta \theta } \right|_{0}^{L} = 0, \\ \end{aligned} $$
(13)

where the cross-sectional moment and forces are

$$ N_{x}^{(i)} = \int\limits_{{ - h_{i} /2}}^{{h_{i} /2}} {t_{xx}^{(i)} dz} ,\quad ,Q_{x}^{(i)} = \int\limits_{{ - h_{i} /2}}^{{h_{i} /2}} {t_{xz}^{(i)} dz} ,\quad M_{x}^{(i)} = \int\limits_{{ - h_{i} /2}}^{{h_{i} /2}} {z\;t_{xx}^{(i)} dz} . $$
(14)

And their explicit forms are found from (11) as

$$ \begin{aligned} N_{x}^{(1)} & = E_{1} \left( {h_{1} \frac{{\partial u_{0} }}{\partial x} - \frac{1}{2}h_{1} h_{2} \frac{\partial \varphi }{\partial x} - \frac{1}{2}h_{1}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right),\quad N_{x}^{(3)} = E_{3} \left( {h_{3} \frac{{\partial u_{0} }}{\partial x} - \frac{1}{2}h_{2} h_{3} \frac{\partial \varphi }{\partial x} + \frac{1}{2}h_{3}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right), \\ Q_{x}^{(2)} & = \left( {\mu + \kappa } \right)h_{2} \left( {\frac{\partial w}{\partial x} + \phi } \right) - \mu \;h_{2} \left( {\varphi + \phi } \right),\;M_{x}^{(1)} = - \frac{1}{12}E_{1} h_{1}^{3} \frac{{\partial^{2} w}}{{\partial x^{2} }},\;M_{x}^{(3)} = - \frac{1}{12}E_{3} h_{3}^{3} \frac{{\partial^{2} w}}{{\partial x^{2} }}. \\ \end{aligned} $$
(15)

Considering harmonic vibrations, the displacement, micro-rotation and microstretch fields can be taken as follows:

$$ \begin{aligned} & \left\{ {u_{0} (x,t),\;\varphi (x,t),\;w(x,t),\;\phi (x,t)\;,\theta (x,t)} \right\} \\ & = \left\{ {\bar{U}(x,\omega ),\;\overline{\Phi } (x,\omega ),\;\bar{W}(x,\omega ),\;\overline{\Psi } (x,w)\;,\overline{\Theta } (x,t)} \right\}\,e^{{i{\kern 1pt} \omega {\kern 1pt} t}} \\ \end{aligned} $$
(16)

Then, the partial differential Eq. (12) will take the following ordinary differential equations:

$$ \begin{aligned} & \left( {E_{1} h_{1} + E_{3} h_{3} } \right)\bar{U}^{\prime\prime} + \frac{{h_{2} }}{2}\left( {E_{3} h_{3} - E_{1} h_{1} } \right)\bar{\varphi }^{\prime\prime} + \frac{1}{2}\left( {E_{3} h_{3}^{2} - E_{1} h_{1}^{2} } \right)\bar{W}^{{{\prime \prime \prime }}} \\ & = - \omega^{2} \left[ {\left( {\rho_{1} h_{1} + \rho_{2} h_{2} + \rho_{3} h_{3} } \right)\bar{U} + \frac{{h_{2} }}{2}\left( {\rho_{3} h_{3} - \rho_{1} h_{1} } \right)\bar{\varphi } + \frac{1}{2}\left( {\rho_{3} h_{3}^{2} - \rho_{1} h_{1}^{2} } \right)\bar{W}^{\prime}} \right], \\ & \left( {E_{3} h_{3} - E_{1} h_{1} } \right)\bar{U}^{\prime\prime} + \frac{{h_{2} }}{2}\left( {E_{1} h_{1} + E_{3} h_{3} } \right)\bar{\varphi }^{\prime\prime} + \frac{1}{2}\left( {E_{1} h_{1}^{2} + E_{3} h_{3}^{2} } \right)\bar{W}^{{{\prime \prime \prime }}} - 2\left( {\mu + \kappa } \right)\left( {\overline{\Phi } + \overline{\Psi } } \right) \\ & \quad + 2\mu \left( {\bar{W}^{\prime} + \overline{\Psi } } \right) = - \omega^{2} \left[ {\left( {\rho_{3} h_{3} - \rho_{1} h_{1} } \right)\bar{U} + \frac{{h_{2} }}{6}\left( {3\rho_{1} h_{1} + \rho_{2} h_{2} + \rho_{3} h_{3} } \right)\overline{\Phi } + \frac{1}{2}\left( {\rho_{1} h_{1}^{2} + \rho_{3} h_{3}^{2} } \right)\bar{W}^{\prime}} \right], \\ & \frac{1}{2}\left( {E_{3} h_{3}^{2} - E_{1} h_{1}^{2} } \right)\bar{U}^{{{\prime \prime \prime }}} + \frac{{h_{2} }}{4}\left( {E_{1} h_{1}^{2} + E_{3} h_{3}^{2} } \right)\overline{\Phi }^{{{\prime \prime \prime }}} + \frac{1}{3}\left( {E_{1} h_{1}^{3} + E_{3} h_{3}^{3} } \right)\bar{W}^{(4)} , \\ & \quad - \left( {\mu + \kappa } \right)h_{2} \left( {\overline{\Psi }^{{\prime }} + \bar{W}^{\prime\prime}} \right) + \mu \,h_{2} \left( {\overline{\Psi }^{{\prime }} + \overline{\Phi }^{{\prime }} } \right) = - \omega^{2} \left[ {\frac{1}{2}\left( {\rho_{3} h_{3}^{2} - \rho_{1} h_{1}^{2} } \right)\bar{U}^{\prime}} \right. \\ & \quad \left. { - \left( {\rho_{1} h_{1} + \rho_{2} h_{2} + \rho_{3} h_{3} } \right)\bar{W} + \frac{{h_{2} }}{4}\left( {\rho_{1} h_{1}^{2} + \rho_{3} h_{3}^{2} } \right)\overline{\Phi }^{{\prime }} + \frac{1}{3}\left( {\rho_{1} h_{1}^{3} + \rho_{3} h_{3}^{3} } \right)\bar{W}^{\prime\prime}} \right], \\ & \kappa \left( {\bar{W}^{\prime} + 2\overline{\Psi } + \overline{\Phi } } \right) = - \omega^{2} \rho_{2} \overline{\Psi } , \\ & a_{0} \overline{\Theta }^{{\prime \prime }} - \lambda_{1} \overline{\Theta } = - \omega^{2} \rho_{2} \overline{\Theta } . \\ \end{aligned} $$
(17)

The boundary conditions for clamped end are

$$ \bar{U} = 0,\quad \overline{\Phi } = 0,\quad \bar{W} = 0,\quad \overline{\Psi } = 0,\quad ,\overline{\Theta } = 0, $$
(18)

and for free end, they are

$$ \begin{aligned} & 2\left( {E_{1} h_{1} + E_{3} h_{3} } \right)\bar{U}^{\prime} + h_{2} \left( {E_{3} h_{3} - E_{1} h_{1} } \right)\overline{\Phi }^{{\prime }} + \left( {E_{3} h_{3}^{2} - E_{1} h_{1}^{2} } \right)\bar{W}^{\prime\prime} = 0, \\ & 2\left( {E_{3} h_{3} - E_{1} h_{1} } \right)\bar{U}^{\prime} + h_{2} \left( {E_{1} h_{1} + E_{3} h_{3} } \right)\overline{\Phi }^{{\prime }} + \left( {E_{1} h_{1}^{2} + E_{3} h_{3}^{2} } \right)\bar{W}^{\prime\prime} = 0, \\ & 12\left( {\mu + \kappa } \right)h_{2} \left( {\bar{W}^{\prime} + \overline{\Phi } } \right) - 12\mu \,h_{2} \left( {\overline{\Phi } + \overline{\Psi } } \right) + 6\left( {E_{1} h_{1}^{2} - E_{3} h_{3}^{2} } \right)\bar{U}^{\prime\prime} - 3h_{2} \left( {E_{1} h_{1}^{2} + E_{3} h_{3}^{2} } \right)\overline{\Phi }^{{\prime \prime }} \\ & \quad - 4\left( {E_{1} h_{1}^{3} + E_{3} h_{3}^{3} } \right)\bar{W}^{\prime\prime\prime} = 0, \\ & 6\left( {E_{3} h_{3}^{2} - E_{1} h_{1}^{2} } \right)\bar{U}^{\prime} + 3h_{2} \left( {E_{1} h_{1}^{2} + E_{3} h_{3}^{2} } \right)\overline{\Phi }^{{\prime }} + 4\left( {E_{1} h_{1}^{3} + E_{3} h_{3}^{3} } \right)\bar{W}^{\prime\prime} = 0, \\ & a_{0} h_{2} \overline{\Theta }^{{\prime }} = 0. \\ \end{aligned} $$
(19)

4 Solution Method

To solve the governing differential equations, we used Differential transform method [19]. The method based on Taylor Series expansion of the main variables and coefficients, but is different from higher order series method. Differential transform method provides an iterative procedure between different order derivatives which ends with less computational work. The basic definition is given as

$$ W(k,h) = \frac{1}{k!\;h!}\left[ {\frac{{\partial^{k + h} w(x,y)}}{{\partial x^{k} \,\partial y^{h} }}} \right]_{(0,0)} , $$
(20)

where \( w(x,y) \) is the original function and \( W(k,h) \) is the transformed function. The differential inverse transform of \( W(k,h) \) is defined as

$$ w(x,y) = \sum\limits_{k = 0}^{\infty } {\sum\limits_{h = 0}^{\infty } {W(k,h)} \;x^{k} y^{h} } . $$
(21)

Using above transformation in the governing Eq. (17) and the boundary conditions (18) in non-dimensional form gives an iterative procedure for the numerical solution.

$$ \begin{aligned} & \left( {E_{1} h_{1} + E_{3} h_{3} } \right)2U_{k + 2} + h_{2} \left( {E_{3} h_{3} - E_{1} h_{1} } \right)\varphi_{k + 2} + 3\left( {E_{3} h_{3}^{2} - E_{1} h_{1}^{2} } \right)W_{k + 3} \\ & = - \omega^{2} \left[ {\left( {\rho_{1} h_{1} + \rho_{2} h_{2} + \rho_{3} h_{3} } \right)U_{k} + \frac{{h_{2} }}{2}\left( {\rho_{3} h_{3} - \rho_{1} h_{1} } \right)\Phi _{k} + \frac{1}{2}\left( {\rho_{3} h_{3}^{2} - \rho_{1} h_{1}^{2} } \right)W_{k + 1} } \right], \\ & \left( {E_{3} h_{3} - E_{1} h_{1} } \right)2U_{k + 2} + h_{2} \left( {E_{1} h_{1} + E_{3} h_{3} } \right)\varphi_{k + 2} + 3\left( {E_{1} h_{1}^{2} + E_{3} h_{3}^{2} } \right)W_{k + 3} \\ & \quad - 2\left( {\mu + \kappa } \right)\left( {\Phi _{k} +\Psi _{k} } \right) + 2\mu \left( {W_{k + 1} +\Psi _{k} } \right) \\ & = - \omega^{2} \left[ {\left( {\rho_{3} h_{3} - \rho_{1} h_{1} } \right)U_{k} + \frac{{h_{2} }}{6}\left( {3\rho_{1} h_{1} + \rho_{2} h_{2} + \rho_{3} h_{3} } \right)\Phi _{k} + \frac{1}{2}\left( {\rho_{1} h_{1}^{2} + \rho_{3} h_{3}^{2} } \right)W_{k + 1} } \right], \\ & 3\left( {E_{3} h_{3}^{2} - E_{1} h_{1}^{2} } \right)U_{k + 3} + \frac{{3h_{2} }}{2}\left( {E_{1} h_{1}^{2} + E_{3} h_{3}^{2} } \right)\Phi _{k + 3} + 8\left( {E_{1} h_{1}^{3} + E_{3} h_{3}^{3} } \right)W_{k + 4} , \\ & \quad - \left( {\mu + \kappa } \right)h_{2} \left( {\Psi _{k + 1} + W_{k + 2} } \right) + \mu \,h_{2} \left( {\Psi _{k + 1} + \overline{\Phi }_{k + 1} } \right) = - \omega^{2} \left[ {\frac{1}{2}\left( {\rho_{3} h_{3}^{2} - \rho_{1} h_{1}^{2} } \right)U_{k + 1} } \right. \\ & \quad \left. { - \left( {\rho_{1} h_{1} + \rho_{2} h_{2} + \rho_{3} h_{3} } \right)W_{k} + \frac{{h_{2} }}{4}\left( {\rho_{1} h_{1}^{2} + \rho_{3} h_{3}^{2} } \right)\Phi _{k + 1} + \frac{2}{3}\left( {\rho_{1} h_{1}^{3} + \rho_{3} h_{3}^{3} } \right)W_{k + 2} } \right], \\ & \kappa \left( {W_{k + 1} + 2\Psi _{k} +\Phi _{k} } \right) = - \omega^{2} \rho_{2}\Psi _{k} , \\ & 2a_{0}\Theta _{k + 2} - \lambda_{1}\Theta _{k} = - \omega^{2} \rho_{2}\Theta _{k} \\ \end{aligned} $$
(22)

and the clamped boundary conditions (18) at \( x = 0 \) give

$$ U_{0} = 0,\quad\Phi _{0} = 0,\quad W_{0} = 0,\quad W_{1} = 0,\quad\Psi _{0} = 0,\quad ,\Theta _{0} = 0. $$
(23)

and the free boundary conditions (19) at \( x = L \) are given as in the followings:

$$ \begin{aligned} & \sum\limits_{k = 0}^{N} {2\left( {E_{1} h_{1} + E_{3} h_{3} } \right)kU_{k} L^{k - 1} + h_{2} \left( {E_{3} h_{3} - E_{1} h_{1} } \right)k\Phi _{k} L^{k - 1} + \left( {E_{3} h_{3}^{2} - E_{1} h_{1}^{2} } \right)k(k - 1)W_{k} L^{k - 2} } = 0, \\ & \sum\limits_{k = 0}^{N} {\left[ {2\left( {E_{3} h_{3} - E_{1} h_{1} } \right)kU_{k} L + h_{2} \left( {E_{1} h_{1} + E_{3} h_{3} } \right)k\,\Phi _{k} L + \left( {E_{1} h_{1}^{2} + E_{3} h_{3}^{2} } \right)k(k - 1)W_{k} } \right]L^{k - 2} } = 0, \\ & \sum\limits_{k = 0}^{N} {\left[ {12\left( {\mu + \kappa } \right)h_{2} L^{2} \left( {kW_{k} +\Phi _{k} } \right) - 12\mu \,h_{2} L^{2} \left( {\Phi _{k} +\Psi _{k} } \right) + 6\left( {E_{1} h_{1}^{2} - E_{3} h_{3}^{2} } \right)Lk(k - 1)U_{k} } \right.} \\ & \quad \left. { - 3h_{2} \left( {E_{1} h_{1}^{2} + E_{3} h_{3}^{2} } \right)Lk(k - 1)\Phi _{k} - 4\left( {E_{1} h_{1}^{3} + E_{3} h_{3}^{3} } \right)k(k - 1)(k - 2)W_{k} } \right]L^{k - 3} = 0, \\ \end{aligned} $$
(24)
$$ \begin{aligned} & \sum\limits_{k = 0}^{N} {\left[ {6\left( {E_{3} h_{3}^{2} - E_{1} h_{1}^{2} } \right)LkU_{k} + 3h_{2} \left( {E_{1} h_{1}^{2} + E_{3} h_{3}^{2} } \right)Lk\Phi _{k} + 4\left( {E_{1} h_{1}^{3} + E_{3} h_{3}^{3} } \right)k(k - 1)W_{k} } \right]} L^{k - 2} = 0, \\ & \sum\limits_{k = 0}^{N} {a_{0} h_{2} k\Theta _{k} L^{k - 1} } = 0. \\ \end{aligned} $$
(25)

The iterative governing Eqs. (22) and the end conditions (23) and (24) gives the following eigenvalue problem:

$$ {\mathbf{A}}(\omega ){\mathbf{D}} = {\mathbf{0}} $$
(26)

where the matrix A depends on to the frequencies and the material coefficients. The vector D contains \( U_{k} ,\Phi _{k} ,W_{k} ,\Psi _{k} ,\Theta _{k} \) for \( k = 1,2, \ldots ,N \). Here, the maximum number of terms is taken as N = 6. To find nontrivial solution, we write

$$ Det\left( {{\mathbf{A}}(\omega )} \right) = 0. $$
(27)

5 Results and Conclusions

In the Eq. (27), the material properties are taken as in [8] for the classical constants, and as in [18] for microstretch part. They are all given in Table 1.

Table 1 The beam properties and dimensions
Full size table

The obtained frequencies for the cantilever beam are given in Table 2. Here it must be noted that there are also additional frequencies between the classical frequencies due to the microstretch character of the core. For example for the loss factor \( \eta = 0.6 \), the spectrum of the frequencies are obtained as follows:

Table 2 The natural frequencies for clamped-free beam
Full size table
$$ \begin{aligned} & 0,\;65.108,\;65.214,\;65.225,\;65.241,\;65.255,\;297.504,\;297.472,\; \\ & 297.548,\;297.552,\;297.564,\;740.741,\;740.741,\;740.731,\;740.761, \\ & 740.779,\;1384.684,\;1384.652,\;1384.710,\;1384.738,\;1384.763,\; \\ & 2243.823,\;2243.897,\;2243.919,2243.931,\;2243.944,\;3316.421,\; \\ & 3316.456,\;3316.507,\;3316.507,\;3316.528 \\ \end{aligned} $$

But only the frequencies which give the minimum difference (given in Table 3) from the classical case given by [8] are assumed as deviated classical frequencies due to the microstretch effects. These frequencies are given in Table 2. The rest of the frequencies are considered as the additional frequencies due to the microstretch character.

Table 3 The minimum differences between deviated classical frequencies due to the microstretch character and classical frequencies
Full size table

The minimum differences between the classical frequencies given by [8] and the frequencies assumed as deviated classical frequencies are given in Table 3.

As we see, the values of the frequencies obtained for microstretch case are always greater than the classical ones as it is expected. Besides, the minimum differences between deviated classical frequencies due to the microstretch case and classical frequencies given in Table 3 are getting bigger for the large loss factors which is often used as a measure of damping in linear viscoelastic material.