Dynamic Analysis of Composite Sandwich Beams with a Frequency-Dependent Viscoelastic Core under the Action of a Moving Load

A dynamic analysis of the behavior of sandwich beams with a viscoelastic core under the action of a moving load is performed considering their geometrical asymmetry. The use of viscoelastic materials integrated into structures in front of the moving load is considered as a new suggestion to enhance their stability. A high-order theory, taking into consideration longitudinal and rotational inertias was used to examine the viscoelastic damping properties composite sandwich beams with account of their geometrical asymmetry and the frequency-dependent behavior of their viscoelastic core.

1. Introduction

Transport structures, in particular, bridges and railway lines, on which vehicles or trains run, are subjected to moving loads. Such loads usually cause vibrations, which that can lead to their structural damage and failure. This problem has been attacked by many researchers in order to investigate their behavior under the action of this type of loads. It was found that the use of viscoelastic materials is a good solution contributing to the attenuation of structural vibrations caused by various dynamical loads.

Therefore, the knowledge of their dynamic characteristics is very necessary and useful in the design and rehabilitation of structures made with viscoelastic materials. Several studies have been carried out using analytical approaches to investigate the vibratory behavior of structures with such materials [1,2,3,4,5]. Experimental and numerical procedures were used in the [6,7,8] to identify the damping properties of various test specimens. A model of the loss factor as a function of logarithmic decrement and strain amplitude was established for different materials, which was then used to identify the damping matrix of the Kelvin–Voigt–Thompson model. Different numerical approaches based on the finite-element method have also been considered in order to investigate structures with more complex geometries than those considered in the analytical approaches. Daya et al. [9] employed the numerical asymptotic method for solving the eigenvalue problem characterizing the free vibration of sandwich beams with a viscoelastic core. Daya et al. [10] applied a nonlinear theory to studying the nonlinear responses of viscoelastic sandwich beams. A generic approach, called “Diamond,” was developed by Bilasse et al. [11] in order to analyze the linear and nonlinear vibrations of viscoelastic sandwich beams. Arikoglu and Ozkol [12] investigated the vibration responses of a three-layer composite beam with a viscoelastic core. The Differential Transformation Method (DTM) was used to solve the equations of motion of the free vibration problem of sandwich beams obtained by the Hamilton principle. Irazu and Elejabarrieta [13] analyzed the influence of design parameters on the dynamic properties of thin sandwich beams.

Barbosa and Farage [14] carried out a numerical study based on the Golla–Hughes Method (GHM) to analyze the dynamic responses of sandwich beams with viscoelastic cores in the time domain. Arvin et al. [15] presented a high-order theory to examine the frequency and time responses of a sandwich beam with composite faces and a viscoelastic core. Time responses of the beam under the action of a transient excitation were described using a time-dependent modulus of the viscoelastic core. Moita et al. [16] developed another numerical model for the vibration analysis of beams in the time domain, in which a finite-element method was employed to analyze the passive and active damping of structures. Latifi and Kharazi [17] analyzed the nonlinear temporal responses of sandwich beams with a viscoelastic core and stratified composite skins subjected to a suddenly applied uniform load. The formulation was based on the Full Layerwise Theory (FLWT) and the Boltzmann superposition principle.

Much research has been conducted to explore the dynamic behavior of various structures under a moving load, and many studies have analyzed the impact of different dynamic parameters, but only few of them have considered structures with viscoelastic materials. In order to explore the vehicle–bridge interaction, Khadri et al.[18, 19] studied the influence of rail defects and its joints on the dynamic behavior of bridges. Tekili et al. [20] also studied the dynamic behavior of a sandwich beam, reinforced with two carbon/epoxy composite layers, under a moving load. It was found that the composite layers improved the damping performance of the aluminum central layer. Hilal and Zibdeh [21], Giunta et al. [22], Chen et al. [23], and Tao et al. [24] studied the dynamic behavior of sandwich beams with different configurations under a moving load. Sarvestanet al. [25] employed a quadratic equation for determining the vibratory responses of a cracked Timoshenko beam under a moving load. Kiral et al. [26] proposed a three-dimensional finite-element model based on the classical laminated beam theory to describe the dynamic response of a clamped-clamped beam. Based on the finite-element approach, Fuh-Gwo and Miller [27] proposed a dynamic analysis model for multilayer laminated composite beams subjected to a moving load. Kahya [28] employed the Timoshenko theory to consider the shear effect in each layer of a composite. Generally, results of these studies showed that the speed of a moving load and fiber orientation have a significant influence on the dynamic behavior of layered beams.

In this present paper, the efficiency of passive control of the effect of a moving load is examined using a numerical approach to study the dynamic behavior of asymmetrical composite sandwich beams with a viscoelastic core. For this reason, a high-order theory is employed taking into consideration the frequency dependence of its viscoelastic properties. The longitudinal and rotational inertias are considered by applying the Euler–Bernoulli beam theory to beam faces and the Timoshenko beam theory to the viscoelastic core. The numerical asymptotic method is presented as an efficient method to solve the complex eigenvalue problem. In addition, the effect of geometrical configuration of sandwich beams is thoroughly examined.

2. Mathematical Formulation

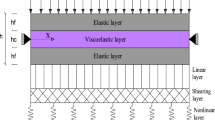
The linear vibration of the sandwich beam under a moving load will be investigated at small strains assuming that its core is made of a nonaging linear viscoelastic material [29, 30]. The assumptions considered by Bilasse et al. [11] will be modified in order to consider the effect of longitudinal and rotational inertia and asymmetry of the sandwich. The configuration of the asymmetric sandwich beam considered in this study is shown in Fig. 1, where h₁, h₂, and h₃ are thicknesses of its upper, middle, and lower layers, respectively. The displacement and strain fields of face layers are

$$ {\displaystyle \begin{array}{c}{u}_i\left(x,z,t\right)={u}_{0i}\left(x,t\right)-\left(z-{z}_i\right){w}_{,x},\kern1em {w}_i\left(x,z,t\right)=w\left(x,t\right),\\ {}{\varepsilon}_{ni}\left(x,z,t\right)={u}_{0i,x}\left(x,t\right)-\left(z-{z}_i\right){w}_{, xx},\kern1em i=1,3,\end{array}} $$

(1)

Fig. 1.

Asymmetric sandwich beam (a) and the geometry of its deformation (b): 1, 2 — upper and bottom faces and 3 — viscoelastic core.

where u,w, and ε_n are the longitudinal and transverse displacements and the normal strain, respectively; z₁ = h₁/2, z₂ = 0, and z₃ = −h₃/2 corresponding to the upper, middle, and lower layers, respectively, and u_0i is the longitudinal displacement of middle plane of an i th layer of sandwich beam (Fig. 1b). The displacement and strain fields of the viscoelastic layer are

$$ {\displaystyle \begin{array}{c}{u}_2\left(x,z,t\right)={u}_{02}\left(x,t\right)-(z)\beta, \kern1em w\left(x,z,t\right)=w\left(x,t\right),\\ {}{\varepsilon}_{n2}\left(x,z,t\right)={u}_{02,x}\left(x,t\right)-(z){\beta}_{,x},\kern1em {\varepsilon}_{c2}\left(x,z,t\right)=\beta \left(x,t\right)+{w}_{,x}\end{array}} $$

(2)

where ε_c2 is the shear strain in the viscoelastic layer and β is rotation of the middle layer.

The governing equation of motion of the beam is established by the Hamilton principle, but its total potential energy Π is expressed as [17, 31]

$$ \varPi =U-K-W $$

(3)

where U, K, and W are the strain energy, kinetic energy and the energy of external forces, respectively, are

$$ U=\sum \limits_{i=1}^3{\int}_v\frac{1}{2}{\sigma}_i{\varepsilon}_i dV,\kern1em K=-\sum \limits_{i=1}^3{\int}_v\frac{1}{2}\left({\rho}_i{\dot{u}}_i{\dot{u}}_i+{\rho}_i\dot{w}\dot{w}\right) dV,\kern1em W=\underset{V}{\int }{f}^v wdV+\underset{S}{\int }{f}^s wdS. $$

(4)

Here, σ, ${f}_i^v$, ${f}_i^s$, and ρ are the stress tensor, volume force, surface force, and density, respectively, of an i th layer. According to the variational formulation, based on the principle of virtual displacement, Eq. (3) can be written as

$$ \underset{0}{\overset{T}{\int }}\left(\delta \Pi \right) dt=\underset{0}{\overset{T}{\int }}\left(\delta U-\delta K-\delta W\right) dt $$

$$ =\underset{0}{\overset{T}{\int }}\underset{0}{\overset{L}{\int }}\left[\begin{array}{c}{N}_1\delta {u}_{1,x}+{N}_2\delta {u}_{2,x}+{N}_3\delta {u}_{3,x}+{M}_1\delta {w}_{, xx}+{M}_2\delta {\beta}_{,x}+{M}_3\delta {w}_{, xx}+T\left(\delta {w}_{,x}+\delta \beta \right)\\ {}+{\rho}_1{S}_1{\ddot{u}}_1\delta {u}_1+{\rho}_3{S}_3{\ddot{u}}_3\delta {u}_3+{\rho}_2{S}_2{\ddot{u}}_2\delta {u}_2\left({\rho}_1{S}_1+{\rho}_3{S}_3+{\rho}_2{S}_2\right)\ddot{w}\delta w-P\left(x,t\right)\delta w\end{array}\right] dxdt=0, $$

(5)

where N_i, M_i, and S_i are the normal force, bending moment, and cross-sectional area of an i th layer, respectively, and T is the shear force of the viscoelastic layer. The normal force and a bending moment in the face layers are expressed as:

$$ {N}_i={E}_i{S}_i{u}_{1,x},\kern0.5em {M}_i={E}_i{I}_i{w}_{, xx},\kern0.5em i=1,3, $$

(6)

where E_i and I_i are Young’s modulus and the quadratic moment of cross section of an i th layer, respectively. The normal force, moment, and shear force in the viscoelastic layer are

$$ {N}_2={E}_2^{\ast}\left(\omega \right){S}_2{u}_{2,x},{M}_2={E}_2^{\ast}\left(\omega \right){I}_2{\beta}_{,x},\kern0.5em T=\frac{S_2}{2\left(1+{\upsilon}_2\right)}{E}_2^{\ast}\left(\omega \right)\left(\beta +{w}_{,x}\right), $$

(7)

where ${E}_2^{\ast}\left(\omega \right)$ is the frequency-dependent complex Young’s modulus of the viscoelastic layer and I₂ and υ₂ are the quadratic moment of core cross section and Poisson’s ratio of the viscoelastic core. Inserting Eqs. (6) and (7) into Eq. (5), the dynamic equations of motion for the sandwich beam is derived in the form

$$ \underset{0}{\overset{T}{\int }}\underset{0}{\overset{L}{\int }}\left[\begin{array}{l}{E}_1{S}_1\left({\ddot{u}}_0+\frac{h_2}{2}\ddot{\beta}-\frac{h_1}{2}\ddot{w}\right)\left(\delta {u}_{0,x}+\frac{h_2}{2}\delta {\beta}_{,x}-\frac{h_1}{2}\delta {w}_{, xx}\right)+{E}_2^{\ast}\left(\omega \right){S}_2{u}_{0,x}\delta {u}_{0,x}\\ {}+{E}_3{S}_3\left({\ddot{u}}_0-\frac{h_2}{2}\ddot{\beta}+\frac{h_1}{2}\ddot{w}\right)\left(\delta {u}_{0,x}-\frac{h_2}{2}\delta {\beta}_{,x}+\frac{h_1}{2}\delta {w}_{, xx}\right){E}_1{I}_1{w}_{, xx}\delta {w}_{, xx}\\ {}\begin{array}{l}+{E}_2^{\ast}\left(\omega \right){I}_2{\beta}_{,x}\delta {\beta}_{,x}+{E}_2{I}_2{w}_{, xx}\delta {w}_{, xx}+\frac{S_2}{2\left(1+{\upsilon}_2\right)}{E}_2^{\ast}\left(\omega \right)\left(\beta +{w}_{,x}\right)\left(\delta \beta +\delta {w}_{,x}\right)\\ {}+\left({\rho}_1{S}_1+{\rho}_3{S}_3+{\rho}_2{S}_2\right)\ddot{w}\delta w+{\rho}_1{S}_1\left({\ddot{u}}_0+\frac{h_2}{2}\ddot{\beta}-\frac{h_1}{2}\ddot{w}\right)\left(\delta {u}_{0,x}+\frac{h_2}{2}\delta {\beta}_{,x}-\frac{h_1}{2}\delta {w}_{, xx}\right)\\ {}+{\rho}_3{S}_3\left({\ddot{u}}_0-\frac{h_2}{2}\ddot{\beta}+\frac{h_1}{2}\ddot{w}\right)\left(\delta {u}_{0,x}-\frac{h_2}{2}\delta {\beta}_{,x}+\frac{h_1}{2}\delta {w}_{, xx}\right)+{\rho}_2{S}_s{\ddot{u}}_0\delta {u}_0-P\left(x,t\right)\delta w\end{array}\end{array}\right] dxdt=0, $$

(8)

where u₀ = u₀₂ is the displacement of middle plane of the viscoelastic layer.

3. Finite-Element Formulation

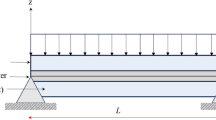
Discretization of Eq. (8) by the finite-element method and expression of the displacement field as a function of the nodal displacements U_e made it possible to construct the elementary matrices. A linear finite element (Fig. 2) of length L_e with two nodes and four degrees of freedom — the longitudinal u and transverse w displacements, the normal rotation β of the middle layer and the rotation θ = dw / dx — were considered, where

$$ w={N}_w{U}_e,\kern1em u={N}_u{U}_e,\kern1em \beta ={N}_{\beta }{U}_e,\kern1em {U}_e={\left\langle {U}_i\kern0.5em {\beta}_i\kern0.5em {\mathrm{w}}_i\kern0.5em {\theta}_i\right\rangle}^T,\kern1em i=1,2. $$

(9)

Fig. 2.

Finite element with two nodes and four degrees of freedom.

Here, N_w, N_u, and N_β are the interpolation functions

$$ {\displaystyle \begin{array}{c}{N}_w=\left[0\kern0.5em 0\left(1+2{\zeta}^3-3{\zeta}^2\right)\kern1em \left({\zeta}^3-2{\zeta}^2+\zeta \right){L}_e\kern0.5em 0\kern0.5em 0\kern0.5em \left(-2{\zeta}^3+3{\zeta}^2\right)\kern1em \left({\zeta}^3-{\zeta}^2\right){L}_e\right]\\ {}{N}_u=\left[\left(1-\zeta \right)\kern0.5em 0\kern0.5em 0\kern0.5em 0\kern0.5em \zeta \kern0.5em 0\kern0.5em 0\kern0.5em 0\right],\kern1em {N}_{\beta }=\left[0\left(1-\zeta \right)\kern0.5em 0\kern0.5em 0\kern0.5em 0\kern0.5em \zeta \kern0.5em 0\kern0.5em 0\right],\kern0.5em \xi =x/{L}_e.\end{array}} $$

(10)

The elementary matrix system describing the dynamic behavior of the sandwich beam can be obtained inserting the Eqs. (9) and (10) into Eq. (8), as a result of which we have

$$ {\left[M\right]}^e\left\{{\ddot{U}}_e\right\}+{\left[K\right]}^e\left\{{U}_e\right\}={\left\{F\right\}}^e, $$

(11)

where [M]^e, [K]^e, and {F}^e are the elementary mass matrix, stiffness matrix, and the nodal force vector, respectively. After assembly of the elementary matrices, the equation of motion that describes the vibratory behavior in the time domain were obtained by decomposing the stiffness matrix into two parts, K (ω) = K^R + iK^I, where K^R and K^I are its real and imaginary parts. Then, the general equation of motion of the composite sandwich structures with a viscoelastic core takes the form

$$ \left[M\right]\left\{\ddot{U}\right\}+\left({\left[K\right]}^R+\mathrm{i}{\left[K\right]}^{\mathrm{I}}\right)\left\{U\right\}=\left\{F\right\}, $$

(12)

where [K] and [M] are the global stiffness and mass matrices, respectively, {F} is the global external nodal load, and U is the global nodal displacement vector. Since $\dot{U}$ = iωU, Eq. (10) becomes

$$ \left[M\right]\left\{\ddot{U}\right\}+\left[C\right]\left\{\dot{U}\right\}+{\left[K\right]}^R\left\{U\right\}=\left\{F\right\} $$

(13)

where [C] is the equivalent damping matrix [32, 33]. The solution of Eq. (13) was found by the Newmark integration method. The simply supported sandwich beam is subjected to a moving load with a constant speed, v as shown in Fig. 1. The dynamic moving load appearing in the equation of motion Eq.(8), P(x,t) = P₀δ (x − vt) , where δ is the Dirac delta function, and P₀ is a concentrated force and the nodal force vector {F} for n nodes becomes

$$ \left\{F\right\}={\left\langle 0\dots {f}_i..\mathrm{0}\kern0.5em 0\right\rangle}^{\mathrm{T}}\kern0.5em \mathrm{with}\kern0.5em {f}_i={\int}_0^L{P}_0\delta \left(x- vt\right)\left[{N}_w(vt)\right] dx=\left\{\begin{array}{l}{P}_0\left[{N}_w(vt)\right],\kern0.5em \mathrm{t}\le \tau, \\ {}0,\kern0.5em \mathrm{t}>\tau, \end{array}\right. $$

(14)

where τ = L / v is the time necessary to traverse the beam. In the finite-element model, the nodal force f_i (i = 1, 2,..., n) moves over all mesh nodes when 0 ≤ t ≤ τ, as shown in Fig. 3; f_i=j = P₀ on a j th node at t_j = (j −1)L_e / v, but f_i≠j = 0 on the other nodes.

Fig. 3.

The moving load P_v in the finite-element model.

4. Eigenvalue Problem

In order to study the free vibration of the beam and construct the nodal basis, the complex eigenvalue problem

$$ \left(\left[K\right]-{\omega}^2\left[M\right]\right)\left\{U\right\}=0 $$

(15)

has to be solved. Its solution can be found by applying the set of techniques of the asymptotic numerical method starting with the decomposition of the complex Young’s modulus ${E}_2^{\ast}\left(\omega \right)$ of the viscoelastic layer dependent on the frequency in the form

$$ {E}_2^{\ast}\left(\omega \right)={E}_0+{E}_c\left(\omega \right), $$

(16)

where E₀ and E_c (ω) are the modulus of delayed elasticity and the dissipation modulus, respectively. Consequently, the stiffness matrix can be decomposed into two parts,

$$ \left[K\left(\omega \right)\right]=\left[{K}_0\right]+{E}_c\left(\omega \right)\left[{K}_c\right], $$

(17)

with [K₀] and [K_c] are real stiffness matrices. Inserting Eq. (17) into Eq. (15), the new eigenvalue can be written in the form

$$ R\left(U,\lambda \right)=\left[\left[{K}_0\right]+{E}_c\left(\omega \right)\left[{K}_c\right]-{\omega}^2\left[M\right]\right]\left\{U\right\}=0. $$

(18)

After decomposition of the problem, the perturbation technique was used to present the resident arguments in the form of power series [34–35]

$$ U={U}_0+\sum \limits_{n=1}^N{\left(\Delta \alpha \right)}^{\mathrm{n}}{U}_n,\kern1em \lambda ={\omega}^2\kern0.5em ={\omega}_0^2+\sum \limits_{n=1}^N{\left(\Delta \alpha \right)}^{\mathrm{n}}{\omega}_n,\kern1em E\left(\omega \right)={E}_0+\sum \limits_{n=1}^N{\left(\Delta \alpha \right)}^{\mathrm{n}}{E}_n, $$

(19)

where U₀, ω₀, and E₀ are the initial parameters of the eigenvector, frequency, and dissipative modulus, computed for each iteration. Considering the complexity of the eigenvalues problem due to the frequency dependence of its parameters, the homotopy procedure was employed by injecting the path parameter α_j + Δα into the problem Eq. (18), and the eigenvalue problem took the form

$$ R\left(U,\lambda \right)=\left[\left[{K}_0\right]+\left({\alpha}_j+\Delta \alpha \right){E}_c\left(\omega \right)\left({K}_c\right)-{\omega}^2\left[M\right]\right]\left\{U\right\}=0. $$

(20)

Inserting Eq. (19) into Eq. (20) and arranging them according to the powers of Δα, the following system of linear equations was obtained:

$$ {\displaystyle \begin{array}{c}\left[{A}_0\right]\left\{{U}_0\right\}=\left\{{F}_n\right\},\left\{{A}_0\right\}=\left[{K}_0\right]+\left({\alpha}_{\mathrm{max}}\right){E}_c\left(\omega \right)\left[{K}_c\right]-\lambda \left[M\right]\\ {}\left\{{F}_n\right\}=-{\alpha}_j\sum_{k=1}^{n-1}{E}_k\left[{K}_c\right]\left\{{U}_{n-k}\right\}-\sum_{k=0}^{n-1}{E}_k\left[{K}_c\right]\left\{{U}_{n-k-1}\right\}\\ {}-{\alpha}_j{E}_n\left[K\right]\left\{{U}_0\right\}+\sum_{k=1}^{n-1}{\lambda}_k\left[M\right]\left\{{U}_{j-k}\right\}+{\lambda}_n\left[M\right]\left\{{U}_0\right\}\end{array}} $$

(21)

Equation system (21) is still unsolved because there are m equations and m+1 unknowns, and an additional condition is necessary to solve it. The orthogonality property of the eigenmodes gives another equation for can solving the problem stated by Eq. (18), namely,

$$ {\left\{{U}_n\right\}}^T\left\{{U}_0\right\}=0. $$

(22)

The matrix A₀ is noninvertible, which implies that Eq. (18) at n ≥ 1 has no solution only if the following condition is satisfied Eq. (23):

$$ {\displaystyle \begin{array}{c}\left\{{F}_n\right\}{\left\{{U}_0\right\}}^T=-{\alpha}_j\sum_{k=1}^{n-1}{\mathrm{E}}_{\mathrm{k}}{\left\{{U}_0\right\}}^T\left[{K}_c\right]\left\{{U}_{n-k}\right\}\\ {}-\sum_{k=0}^{n-1}{\mathrm{E}}_k{\left\{{U}_0\right\}}^T\left[{K}_c\right]\left\{{U}_{n-k-1}\right\}-{\alpha}_j{E}_n{\left\{{U}_0\right\}}^T\left[{K}_c\right]\left\{{U}_0\right\}\\ {}+\sum_{k=1}^{n-1}{\lambda}_k{\left\{{U}_0\right\}}^T\left[M\right]\left\{{U}_{j-k}\right\}-{\lambda}_n{\left\{{U}_0\right\}}^T\left[M\right]\left\{{U}_0\right\}=0\end{array}} $$

(23)

The existence of this implicit equation is obliged due to the appearance of the terms λ_n and E_n simultaneously. To solve this type of problems, Faa di Bruno’s recursion formula was used for the high-degree differentiation of function Eq. (19). The term E_n was decomposed as

$$ {E}_n=\left\{{E}_{1\left|{\lambda}_1=1\right.}\right\}{\lambda}_n+\left\{{E}_{1\left|{\lambda}_1=0\right.}\right\}. $$

(24)

Insertion of Eq. (24) into Eq. (23) made it possible to express the coefficient λ_n (Eq. (25)) as

$$ {\displaystyle \begin{array}{c}{\lambda}_n=\frac{\alpha_j\sum_{k=1}^{n-1}{E}_k{\left\{{U}_0\right\}}^T\left[{K}_c\right]\left\{{U}_{n-k}\right\}+\sum_{k=0}^{n-1}{E}_k{\left\{{U}_0\right\}}^T\left[{K}_c\right]\left\{{U}_{n-k-1}\right\}}{{\left\{{U}_0\right\}}^T\left[M\right]\left\{{U}_0\right\}+{\alpha}_j\left\{{E}_{1\mid {\lambda}_1=1}\right\}{\left\{{U}_0\right\}}^T\left[{K}_c\right]\left\{{U}_0\right\}}\\ {}-\frac{\sum_{k=1}^{n-1}{\lambda}_k{\left\{{U}_0\right\}}^T\left[M\right]\left\{{U}_{j-k}\right\}+{\alpha}_j\left\{{E}_{1\mid {\lambda}_n=0}\right\}{\left\{{U}_0\right\}}^T\left[{K}_c\right]\left\{{U}_{n-k-1}\right\}}{{\left\{{U}_0\right\}}^T\left[M\right]\left\{{U}_0\right\}+{\alpha}_j\left\{{E}_{1\mid {\lambda}_1=1}\right\}{\left\{{U}_0\right\}}^T\left[{K}_c\right]\left\{{U}_0\right\}}.\end{array}} $$

(25)

After determination of λ_n, the n th Taylor coefficient of the vector U_n was deduced using Eq. (21). Integrating the Lagrange multiplier χ makes this equation more generic [11]:

$$ \left[\begin{array}{cc}{A}_0& {U}_0\\ {}{U}_0^T& 0\end{array}\right]\left[\begin{array}{c}{U}_0\\ {}\chi \end{array}\right]=\left[\begin{array}{c}{F}_n\\ {}0\end{array}\right]. $$

(26)

The problem was solved starting from the initial linear problem $R\left(U,\lambda \right)=\left[\left[{K}_0\right]-{\omega}_0^2\left[M\right]\right]{U}_0$ at α_j = 0 to the nonlinear problem $R\left(U,\lambda \right)=\left[\left[{K}_0\right]+{E}_n\left(\omega \right)\left[{K}_c\right]-{\omega}_0^2\left[M\right]\right]{U}_0$ at α_j = 1. To do this, a continuous procedure was employed, which consisted of taking a new step of solution from the starting point (U^j,λ^j) defined by

$$ {U}^j=\sum \limits_{n=0}^N{\left({\alpha}_{\mathrm{max}}\right)}^n{U}_n,\kern1em {\lambda}^j=\sum \limits_{n=0}^N{\left({\alpha}_{\mathrm{max}}\right)}^n{\lambda}_n. $$

(27)

Here, α_max is the convergence radius

$$ {\alpha}_{\mathrm{max}}={\left(\varepsilon \frac{\left\Vert {U}_1\right\Vert }{\left\Vert {U}_n\right\Vert}\right)}^{\frac{1}{N-1}}, $$

(28)

where ε is the precision parameter. The process continued with a new iteration

$$ {\alpha}_{j+1}={\alpha}_j+{\alpha}_{\mathrm{max}}. $$

(29)

The process ended when α_j > 1; at this step, eigenvalues and eigenvectors were calculated as

$$ {U}_s=\sum \limits_{n=0}^N{\left(1-{\alpha}_j\right)}^n{U}_n,\kern1em {\lambda}_s=\sum \limits_{n=0}^N{\left(1-{\alpha}_j\right)}^n{\lambda}_n. $$

(30)

5. Results and Discussion

Let us analyze the dynamic response of a sandwich beam under a moving load considering different frequency-dependent viscoelastic laws and different layer thickness ratios. At first, the natural frequencies and loss factors of a sandwich beam with constant Young’s modulus of the viscoelastic core are calculated and compared with the corresponding results obtained by Bilasse et al. [11]. A finite-element model with 50 elements and ε = 10⁻⁸ in Eq. (28) are assumed; a moving transverse load P₀ = 100 N with a constant speed v = 10 m/s operates on the beam.

5.1. Validation

In order to validate the numerical approach proposed, the results obtained for the natural frequencies ω and loss factors η of the sandwich beam with an viscoelastic core were compared with the corresponding results found in [11], where the Diamant approach was used to solve the eigenvalue problem. For the model of viscoelastic behavior, it was assumed that

$$ {E}_2={E}_0\left(1+\mathrm{i}{\eta}_{\mathrm{v}}\right), $$

(31)

where E₀ is the Young’s modulus of delayed elasticity and η_v is the viscoelastic loss factor. This model is widely used to simplify vibration studies. The mechanical and geometrical properties of the viscoelastic sandwich beam studied are given in Table 1. Comparison the results presented in Table 2, it is seen that the calculated natural frequencies and loss factors are close to those obtained in [11], which validated the numerical approach proposed.

Table 1. Mechanical and Geometrical Properties of the Viscoelastic Sandwich Beam

Table 2. Natural Frequencies and the Loss Factor of the Clamped-Clamped Sandwich Beam with Frequency Dependent Viscoelastic Modulus

5.2. Symmetrical composite sandwich beam with a viscoelastic PVB core

The configuration and the mechanical and geometrical properties of the composite sandwich beam considered are given in Fig. 1a and Table 3. The frequency-dependent shear modulus ${G}_c^{\ast}\left(\omega \right)$ of its viscoelastic polyvinyl butyral (PVB) core was described by the equation.

$$ {G}_c^{\ast}\left(\omega \right)={G}_{\mathrm{inf}}+\left({G}_0+{G}_{\mathrm{inf}}\right){\left[1+{\left(\mathrm{i}\omega \tau \right)}^{1-\alpha}\right]}^{-\beta }, $$

(32)

Table 3. Mechanical and Geometrical Properties of the Composite Sandwich with a PVB Core

where G₀ = 479·10³ Pa, G_inf = 2.35·10⁸ Pa , τ = 0.3979, α = 0.46, and β = 0.1946.

The dynamic deflections u of midspan point of sandwich beams with different thickness ratios h / H between their viscoelastic and face layers during forced (0 ≤ x / L ≤ 1) and free ( x / L > 1) vibrations are shown in Fig. 4, where x / L is the relative position of the moving load. It is seen that reducing the thickness of face layers increases the deflection amplitude especially in the region of forced vibrations. This is explained by the simultaneous reduction of the equivalent stiffness of the structure. The dynamic amplification factor (DAF) at different values of h / H are presented in Fig. 5. This factor is defined as the ratio between the maximum dynamic displacement under the moving load and the static displacement under the concentrated stationary force. The maximum values of DAF were reached for the critical speeds of moving load v_c = 150, 140, 120, and 110 m/s at h / H = 0.1, 0.3, 0.6, and 0.8, respectively. The critical speed decreases when the thickness ratio h / H increased. This fact supports the previous results that lowered natural frequencies increase vibration amplitudes.

Fig. 4.

Dynamic deflections u of viscoelastic sandwich beams with h / H = 0.1 (1), 0.3 (2), 0.4 (3), and 0.8 (4) under the action of a moving load.

Fig. 5.

The dynamic amplification factor DAF of viscoelastic sandwich beams with h / H = 0.1 (1), 0.3 (2), 0.6 (3), and 0.8 (4).

5.3. Dynamic behavior of composite sandwich beam with a PCDL

Beams with a Passive Constrained Damping Layer (PCDL) are employed to improve the attenuation of vibrations. In such sandwich beams, the upper layer is the constraining layer, which increases the shear in the viscoelastic core and improves its energy dissipation capacity. A sandwich beam with a PCDL is shown in Fig. 1. The viscoelastic core is made of an ISD112 viscoelastic polymer material. The frequency-dependent Young’s modulus is described by the generalized Maxwell model in the form [11, 33] (Table 4)

$$ {E}_2^{\ast}\left(\omega \right)=2{G}_0\left(1+{\upsilon}_2\right)\left(1+\sum \limits_{j=1}^3\frac{\Delta_j}{\omega -i{\Omega}_j}\right). $$

(33)

Table 4. Shear Modulus G₀ of the Viscoelastic ISD112 Core at 20 and 27°C

The mechanical and geometrical properties of the sandwich beam are presented in Table 5.

Table 5. Mechanical and Geometrical Properties of the Composite Sandwich Beam

The natural frequencies and loss factors as functions of the thickness ratios h₂ / h₃ between the viscoelastic and lower (basic) layers corresponding to the first three natural modes of a simply supported sandwich beam are presented in Fig. 6. The thickness ratio was varied by changing the thickness of the viscoelastic layer, while keeping the initial thickness of the lower layer constant. It can be concluded that the variation in the natural frequencies and core thickness are inversely proportional, especially for last two modes with the ISD112 core at 20°C. It is also seen that, at 27°C, the variation in the loss factor is inversely proportional to the variation in thickness of the viscoelastic layer, but this relationship becomes directly proportional at 20°C.

Fig. 6.

The natural frequencies ω (a) and loss factors η (b) of simply supported sandwich beams with a ISD112 viscoelastic core at 20°C as functions of the thickness ratio h₂ / h₃ between the viscoelastic and lower layers for the 1st (1), 2nd (2), and 3rd (3) modes.

In Fig. 7, the effects of different thickness ratios on the dynamic behavior of sandwich beams with a viscoelastic core at 20 and 27°C under the action of a moving load are evaluated and presented. It is seen that the attenuation of their vibrations noticeably depends on the ratio h₂ / h₃ between the thicknesses of the viscoelastic and basic layers.

Fig. 7.

Dynamic deflections u of the simply supported sandwich beams with a ISD112 viscoelastic core at 20 (a) and 27°C (b) under the action of the moving load h₂ / h₃ = 1/4 (1), 1/2 (1), 1 (3), and 3/2 (4).

5. Conclusion

A dynamic analysis of sandwich beams with a viscoelastic core subjected to a moving load has been carried out considering their geometrical asymmetry and frequency-dependent of viscoelastic behavior.

It was found that, for symmetric composite sandwich beams with a viscoelastic PVB core, vibration amplitudes increased with decreasing thickness of their composite face layers, owing to the lowering equivalent stiffness of the structures. This result was validated by an analysis of DAF, which showed the critical speed of the moving load decreased when the thickness ratio h / H grew.

For PCDL beams with an ISD112 viscoelastic core, considered at 20 and 27°C, the natural frequencies were inversely proportional to the thickness ratios h₂ / h₃. The loss factor of the ISD112 core at 27°C decreased as the thickness h₂ of the viscoelastic layer increased, but at 20°C, the loss factor increased as h₂ increases.