Keywords

1 Introduction

Vibration characteristics of sandwich structures are vital precise to study the dynamics analysis of structural members. The sandwich beam is one of the important structural members which is made up of two face sheets joined by viscoelastic core member as a middle layer. To reduce vibration, damping mechanism of a viscoelastic core is introduced for a sandwich beam. These sandwich structures have many applications such as railways, bridges, satellites, aeroplane wings and robotic arms etc.

Sandwich beam vibration analysis with exact solutions has been studied by Rao [1], and the various boundary conditions are used to calculate the frequency result, loss factors and the shear modulus assumed as a complex in the core model. Ganapathi et al. [2] studied the dynamic analysis of laminated composite and sandwich beam with loss factors. Arikoglu and Ozkol [3] examined the effect of viscoelastic core thickness on natural frequencies of three-layered sandwich beam model. A meshless method using penalty approach was studied by ChehelAmirani et al. [4] for vibration analysis of FG core sandwich beam with various boundary conditions. Abdoun et al. [5] studied the harmonic response of sandwich viscoelastic beam using an asymptotic numerical method.

Bilasse et al. [6] proposed a numerical solution using finite element approach for linear and non-linear vibration analysis of viscoelastic sandwich beam. Multi-layered sandwich beam modelled using finite element formulation for free vibration analysis has been presented by Mohanty [7]. Long et al. [8] where the finite element formulation is explained for sandwich structure and compared the obtained numerical simulation results of ANSYS with the reference results. Kpeky et al. [9] examined the solid-shell finite element formulation for sandwich structures modal analysis. Long [10] studied the active constraining layer of FG beam using finite element approach.

In the literature, there is no survey on bounds and soundness assortment of the sandwich structures damping responses. The numerical assessment related to this work is to improve a vibrant representation for vibration characteristics of damped sandwich beams. The main aim of the present work is to develop a finite element approach of a three-layered sandwich beam with cantilever and fixed–fixed boundary conditions and to investigate its vibration responses. The bottom and top face sheets are assumed to be FGM sheets, while the core is assumed as a viscoelastic layer. The FGM face sheets are made up of two materials, i.e. stainless steel and alumina, the viscoelastic core is assumed as polyurethane foam. The frequency response curves are obtained for various core loss factors, boundary conditions and different thickness ratios.

2 Mathematical Formulation

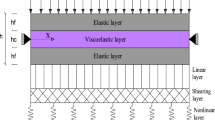
Sandwich beam with viscoelastic core as a middle is illustrated in Fig. 1. Timoshenko beam theory is adopted to model the bottom and top face FGM constraining layers.

Fig. 1
figure 1

Viscoelastic sandwich beam with FGM constraining layers

Full size image

The FGM constraining layer field variables are expressed as

$$ \begin{aligned} u\left( {x,z,t} \right) & = u\left( {x,t} \right) - z\phi \left( {x,t} \right) \\ w\left( {x,z,t} \right) & = w\left( {x,t} \right) \\ \end{aligned} $$
(1)

The displacement vector of an element can be represented as:

$$ q_{e}^{T} = \left[ {\begin{array}{*{20}l} {u_{t1} } \hfill & {w_{t1} } \hfill & {\phi_{t1} } \hfill & {u_{c2,1} } \hfill & {u_{c3,1} } \hfill & {w_{c,1} } \hfill & {u_{b,1} } \hfill & {w_{b,1} } \hfill & {\phi_{b,1} } \hfill \\ {w_{t2} } \hfill & {w_{c2} } \hfill & {w_{b2} } \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ {u_{t3} } \hfill & {w_{t3} } \hfill & {\phi_{t3} } \hfill & {u_{c2,3} } \hfill & {u_{c3,3} } \hfill & {w_{c3} } \hfill & {u_{b,3} } \hfill & {w_{b,3} } \hfill & {\phi_{b,3} } \hfill \\ \end{array} } \right] $$
(2)

The axial displacement of the viscoelastic core layer is denoted with a cubic function and the displacement of transverse direction is incorporated by the quadratic function.

Shape functions are represented as

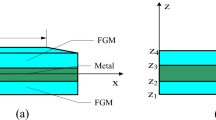
$$ \begin{aligned} N_{1} & = \frac{1 - \varsigma }{2},N_{2} = \frac{1 + \varsigma }{2}\quad {\text{for}} - 1 \le \varsigma \le 1 \\ N_{3} & = \frac{{\varsigma^{2} - \varsigma }}{2},N_{4} = 1 - \varsigma^{2} ,N_{5} = \frac{{\varsigma^{2} + \varsigma }}{2}\quad {\text{for}} - 1 \le \varsigma \le 1 \\ \end{aligned} $$
(3)

2.1 The Material Properties of FGM Face Sheet

The material properties of FGM face sheets are varying in the thickness direction, the effective material properties such as \( (E_{\text{FG}} ) \) Young’s modulus, \( (\rho_{\text{FG}} ) \) mass density and \( (\vartheta_{\text{FG}} ) \) Poisson’s ratio is obtained as.

$$ \begin{aligned} E_{\text{FG}} (z) & = E_{C} V_{C} + E_{M} V_{M} \\ \rho_{\text{FG}} (z) & = \rho_{C} V_{C} + \rho_{M} V_{M} \\ \vartheta_{\text{FG}} (z) & = \vartheta_{C} V_{C} + \vartheta_{M} V_{M} \\ \end{aligned} $$
(4)

The relationship between the \( (V_{M} ) \) metal and \( (V_{C} ) \) ceramic volume fractions is represented using simple rule of mixture obtained as

$$ V_{C} + V_{M} = 1 $$
(5)

The volume fraction of ceramic varies by using the simple power-law function is obtained as

$$ V_{C} = \left( {\frac{z + h}{2 \times h}} \right)^{k} $$
(6)

In which, k is an index of the power law and h is the thickness of face sheet. The variation of index value k varies the ceramic volume fraction content. It causes to change the material properties of the FGM constraining layer.

2.2 FGM Face Sheet

The constraining elemental FGM beam layer kinetic energy is expressed as:

$$ \begin{aligned} KE_{\text{FG}}^{\left( e \right)} & = \frac{1}{2}\rho_{\text{FG}} \iiint\limits_{v} {\left[ {\left( {\frac{\partial u}{\partial t}} \right)^{2} + \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right]}^{ 2} {\text{d}}v \\ & \quad = l_{b} \int\limits_{x} {\rho_{\text{FG}} } \partial u_{\text{FG}} \ddot{u}_{\text{FG}} {\text{d}}x + l_{b} \int\limits_{x} {\rho_{\text{FG}} } \partial w_{\text{FG}} \ddot{w}_{\text{FG}} {\text{d}}x + \alpha l_{b} \int\limits_{x} {\rho_{\text{FG}} } \partial \phi_{\text{FG}} \ddot{\phi }_{\text{FG}} {\text{d}}x \\ \end{aligned} $$
(7)

The kinetic energy of constraining layer of FGM beam element is expressed as

$$ \begin{aligned} {\text{KE}}_{\text{FG}}^{\left( e \right)} & = l_{b} \int\limits_{0}^{{l_{e} }} {\rho_{\text{FG}} } \left( {\delta q_{\left( e \right)}^{T} \left[ {N_{\text{FG}} } \right]^{T} \left[ {I_{\text{FG}} } \right]\left[ {N_{\text{FG}} } \right]\delta \ddot{q}_{\left( e \right)} } \right){\text{d}}x \\ & \quad = \delta q_{\left( e \right)}^{T} \left[ {M_{FG} } \right]^{\left( e \right)} \delta \ddot{q}_{\left( e \right)} \\ \end{aligned} $$
(8)

where \( \left[ {M_{\text{FG}} } \right]^{\left( e \right)} \) is mass matrix of FGM face sheet of beam element.

The stiffness matrix of FGM face sheet is expressed from the potential energy

$$ \begin{aligned} PE_{\text{FG}}^{\left( e \right)} & = \iiint\limits_{v} {\left( {\varepsilon^{T} \sigma } \right)}{\text{d}}v = l_{b} \int\limits_{0}^{{l_{e} }} {\left( {\delta q_{\left( e \right)}^{T} \left[ {B_{\text{FG}} } \right]^{T} \left[ {D_{\text{FG}} } \right]\left[ {B_{\text{FG}} } \right]\delta q_{\left( e \right)} } \right)} {\text{d}}x \\ & \quad = \delta q_{\left( e \right)}^{T} \left[ {K_{\text{FG}} } \right]^{\left( e \right)} \delta \ddot{q}_{\left( e \right)} \\ \end{aligned} $$
(9)

where \( \left[ {K_{\text{FG}} } \right]^{\left( e \right)} \) is element stiffness matrix of FGM face sheet.

2.3 Viscoelastic Core

Viscoelastic core element kinetic energy can be represented as

$$ \begin{aligned} {\text{KE}}_{C}^{\left( e \right)} & = l_{C} \int\limits_{0}^{{l_{e} }} {\rho_{C} } \left( {\delta q_{\left( e \right)}^{T} \left[ {N_{C} } \right]^{T} \left[ {I_{C} } \right]\left[ {N_{C} } \right]\delta \ddot{q}_{\left( e \right)} } \right){\text{d}}x \\ & \quad = \delta q_{\left( e \right)}^{T} \left[ {M_{C} } \right]^{\left( e \right)} \delta \ddot{q}_{\left( e \right)} \\ \end{aligned} $$
(10)

where \( \left[ {M_{C} } \right]^{\left( e \right)} \) is element viscoelastic core mass matrix.

The elemental strain energy of viscoelastic core is expressed as

$$ \begin{aligned} {\text{PE}}_{C}^{\left( e \right)} & = l_{b} \int\limits_{0}^{{l_{e} }} {\left( {\delta q_{\left( e \right)}^{T} \left[ {B_{C} } \right]^{T} \left[ {D_{C} } \right]\left[ {B_{C} } \right]\delta q_{\left( e \right)} } \right)} {\text{d}}x \\ & \quad = \delta q_{\left( e \right)}^{T} \left[ {K_{C} } \right]^{\left( e \right)} \delta \ddot{q}_{\left( e \right)} \\ \end{aligned} $$
(11)

where \( \left[ {K_{C} } \right]^{\left( e \right)} \) is viscoelastic core element stiffness matrix.

2.4 Governing Equation of Motion

Hamilton’s principle is used to derive the governing equation of motion of viscoelastic sandwich beam element.

$$ \delta \int\limits_{{t_{1} }}^{{t_{2} }} {\left( {{\text{KE}}^{\left( e \right)} - {\text{PE}}^{\left( e \right)} } \right)} {\text{d}}t = 0 $$
(12)

The equation of motion of sandwich beam element is represented as

$$ \left[ {M^{\left( e \right)} } \right]\left\{ {\ddot{q}^{\left( e \right)} } \right\} + \left[ {K^{\left( e \right)} } \right]\left\{ {q^{\left( e \right)} } \right\} = 0 $$
(13)

Sandwich beam element’s potential energy is equal to the sum of the potential energy of the constraining layers and viscoelastic layer. Similarly, the kinetic energy of sandwich beam element is the sum of a viscoelastic element and FGM face sheets.

The equation of motion of sandwich beam by assembling of mass and elastic stiffness matrix is obtained as

$$ \left[ M \right]\left\{ {\ddot{q}} \right\} + \left[ K \right]\left\{ q \right\} = 0 $$
(14)

3 Results and Discussion

Vibration response of sandwich beam with viscoelastic core can be studied using finite element method. The viscoelastic behaviour of a core material is assumed in a simple way by considering Young’s modulus E = Ev (1 + iηv), where Ev and ηv are constant. The derived equation of motion is used to determine the natural frequencies and loss factors for various modes. The first six modes of natural frequencies of a viscoelastic sandwich beam with a clamped-free boundary condition for various core loss factors are presented in Table 1. These results are reasonably good of those provided by the literature of references Bilasse et al. [6] and Abdoun et al. [5] observed in Table 1.

Table 1 Cantilever viscoelastic sandwich beam natural frequencies and loss factors
Full size table

Material properties which are used for this analysis are presented below.

  • Young’s modulus of elastic face sheet = 6.9 × 1010 Nm−2

  • Poisson ratio of elastic face sheet = 0.3

  • Density of elastic face sheet = 2766 kg m−3

  • Viscoelastic material properties:

  • Young’s modulus E = 1.794 × 106 Nm−2

  • Poisson ratio \( \upsilon_{c} = 0.3 \)

  • Density \( \rho_{c} = 968.1\;{\text{kg}}\;{\text{m}}^{ - 3} \)

The material properties of the ceramic and metal are as follows:

$$ \begin{aligned} {\text{SUS}}304,\rho_{\text{c}} & = 7800\,{\text{kg/m}}^{3} ,E = 201\;{\text{GPa}},\vartheta = 0.3 \\ {\text{Al}}_{2} {\text{O}}_{3} ,\rho_{\text{m}} & = 2707\,{\text{kg/m}}^{3} ,E = 380\;{\text{GPa}},\vartheta = 0.3 \\ \end{aligned} $$

Figure 2a, b represents the frequency variation with respect to the loss factor of the viscoelastic sandwich beam with FGM face sheets of a cantilever and both sides fixed boundary conditions, respectively. It is noticed that the first three mode frequencies are reduced with an increase of loss factor. The increase of loss factor reduces its overall stiffness matrix of the sandwich beam, which may cause marginally reduces its frequencies.

Fig. 2
figure 2

a First three-mode frequencies variation with loss factor for cantilever beam. b First three-mode frequencies variation with loss factor for fixed beam

Full size image

The variation of loss factor with respect to the core loss factor is shown in Fig. 3a, b, correspondingly. The loss factor is decreased with an increase of core loss factor. This is because of increase of core loss factor. The first mode loss factor decrease of variation can be observed in these figures. Similarly, the other two modes are also varied to a certain extent.

Fig. 3
figure 3

a First three-loss factors variation with a core loss factor of cantilever beam. b First three-loss factor variation with core loss factor of both sides fixed beam

Full size image

Figure 4a, b illustrated the frequency versus thickness ratio (FGM face sheet to the core) for cantilever and both sides fixed boundary conditions. It indicates that the increase of thickness ratio reduces the first three mode frequencies. There is no effect of the bending moment and displacement for fixed–fixed condition on the frequencies. Hence, higher frequency values.

Fig. 4
figure 4

a First three-mode frequencies variation with thickness ratio of cantilever beam. b First three-mode frequencies variation with thickness ratio of both sides fixed beam

Full size image

The variation of loss factor against thickness ratio of a sandwich beam for cantilever and both sides fixed boundary conditions is shown in Fig. 5a, b. Here, the increase of thickness ratio may decrease the first mode frequency; similarly, the increase of thickness ratio increases the second and third mode frequencies of FGM constraining layer sandwich beam. The reasons might be the effect of eigenvalues.

Fig. 5
figure 5

a Loss factor versus thickness ratio of cantilever beam. b Loss factor versus thickness ratio of both sides fixed beam

Full size image

4 Conclusions

Vibration responses and loss factors are obtained for a viscoelastic sandwich beam with various boundary conditions by using the present developed finite element modal. Timoshenko beam theory is assumed for basic kinematics. In the presently developed modal of the finite element method with three layer sandwich beam. The governing equation of motion of viscoelastic sandwich beam is derived by Hamilton’s principle. The influence of loss factor on the natural frequencies is observed. The natural frequencies are reduced with an increase of loss factor. The effect of loss factor on the thickness ratio also calculated. An increase of core thickness will decrease the first mode and correspondingly, increase the second and third mode frequency of cantilever sandwich beams.