Nonlinear Dynamics of Resonant Microelectromechanical System (MEMS): A Review

Abstract

Nonlinearity plays an important role in the dynamics of microelectromechanical resonator. On the one hand, presence of nonlinearity may lead to poor performance of the device. On the other hand, the same nonlinear terms can improve other characteristics of the system. Nonlinearity is, thus, sometimes unwanted while at the other occasions is welcome. Whatever be the reason is, nonlinear dynamics of MEMS device, especially resonator, needs further understanding. In this review work, different aspects of nonlinear dynamics of a single-degree-of-freedom MEMS resonators are discussed. Not only deterministic response under various kinds of excitation, but also noise characteristics of the nonlinear system have been scrutinized. Different methods, which are mostly of recent origin, of tailoring nonlinearity in MEMS resonators have been reviewed. Care has been taken to present a complete picture of the nonlinear dynamics of the simplest type of resonator, namely, the one which can be modelled as a single-degree-of-freedom oscillator.

1 Introduction

Miniaturized sensors, known as microsensors, are often actuated such that one or more component structures are driven to resonance. In macromechanical systems, resonance is generally avoided for safety of equipment. However, micromachined resonant sensors are used for high accuracy, long-term stability and quasidigital output. They are widely used in detection of chemical and biological substances [1], measurements of rheological properties of fluid [2], energy harvesting [3], measuring pressure [4] and in many other diverse fields [5]. In order to increase the sensitivity of the instrument, the dissipation is kept to a very small value. The accuracy of a well-designed resonator is good enough to use them as gyroscopes, timing references, frequency filters in cell phones and computers. In the field of metrology, resonators capable of detecting mass of 1 picogram have been fabricated.

One drawback associated with the resonant devices is that during large amplitude oscillation, when the system is excited to resonance, the effects of nonlinearities become pronounced. First, the resonant frequency of the flexible microstructure depends on the amplitude of excitation (amplitude-frequency effect or A-f effect). Second, nonlinearities make the interpretation of sensor data difficult. Finally, the noise characteristics of the device deteriorate as the participation of nonlinear term increases. Nevertheless, paradoxical though it seems, nonlinearities can sometimes be helpful. One example is that, the pull-in phenomenon resulted by the presence of nonlinear terms can be advantageously used in electrostatically driven MEMS switches [6]. Further, nonlinearities sometimes improve the noise behaviour of the device.

The study of nonlinear dynamics of resonant microsystems has emerged as an active field of research because of two reasons: (a) Since the nonlinear terms invariably show themselves up in the system’s response characteristics, an analysis based only on linear term does not predict correct results. (b) Nonlinear terms can be advantageously exploited to improve system’s performance and also to design new kinds of devices. Thus, whether good or bad, nonlinearities cannot be ignored altogether.

The effects of nonlinearities on the dynamics of resonant microdevices have been reviewed by many authors. Notable among them are the ones by Lifshitz and Cross [7], Rhoads et al. [8], Tiwari and Candler [9]. These reviews have emphasized on different aspects of nonlinearity. For example, Rhoads et al. [8] have studied effects of different types of excitation on the nonlinear dynamics of MEMS resonators, while Tiwari and Candler [9] have studied both types of devices where nonlinearity is undesirable and where it is to be exploited to the advantage.

The present review aims to provide a comprehensive overview of nonlinear effects on the response of resonant MEMS devices. Along with the usual sources of nonlinearity in a resonant MEMS, discussion has been made also on different ways by which nonlinearities are tailored to improve the system’s performance. The beneficial and undesirable effects of nonlinearity have been pointed out by means of simple models, which are valuable tools for getting insight into the design of such systems. The review is divided into several sections. The basic operating principal of resonant MEMS has been explained in Sect. 2 restricting to the linear theory. The effects of nonlinearity on differently excited resonators are discussed in Sect. 3. Only one kind of nonlinearity, namely, duffing-type nonlinearity has been treated in this section in order to highlight various roles that the nonlinearities can play in the dynamics of such systems. The real nature and origin of nonlinearities that appear in resonant MEMS devices are explained in the next section (Sect. 4). In Sect. 5, we compare the effects of nonlinearity and discuss the desirable and undesirable effects. In the final section (Sect. 6), various methods of modifying the nonlinearities of the device have been outlined.

2 Working Principle of Resonant MEMS Sensor

The working principal of a resonant device can be explained with the help of a forced single-degree-of-freedom (SDOF) oscillator, whose equation of motion can be written as

$$\begin{aligned} m\ddot{x}+c\dot{x}+kx=f(t) \end{aligned}$$

(1)

where the symbols have usual significance. In a resonant microsystem, the oscillator is driven to resonance by means of harmonic excitation $f(t)=f_0 \cos \omega t$. The steady-state response amplitude

$$\begin{aligned} X=\frac{F_0}{k \sqrt{\left( 1-\frac{\omega ^2}{\omega _n^2} \right) ^{2}+\left( 2\zeta \frac{\omega }{\omega _n} \right) ^2}}, \; \;\; \; \text {where,} \; \; \omega _n=\sqrt{\frac{k}{m}} \; \;\text {and}\; \; \zeta =\frac{c}{2\sqrt{mk}} \end{aligned}$$

(2)

attains a maximum value $X_{\max }=\frac{F_0/k}{2\zeta \sqrt{1-\zeta ^2}},$ when $\omega =\omega _n \sqrt{1-2\zeta ^2}$. Usually for resonant device the damping factor is kept small, so that $X_{\max }\approx \frac{F_0/k}{2\zeta }$ for $\omega \approx \omega _n$. It is customary to specify the damping factor in form of quality factor Q which is approximately equal to $\frac{1}{2\zeta }$. For resonant MEMS, the Q factor is very high.

In sensing devices, one of the physical parameters of the oscillator is changed depending on the external stimuli that need to be estimated. For example, in chemical gas sensor, the mass is altered when the gas is present near the vibrating body, in a pressure sensor the stiffness is changed. This change in inertia or stiffness causes the natural frequency to be shifted. The conditions for resonance of an initially resonating oscillator now get changed, resulting in significant change in the response amplitude and phase difference $\phi =\tan ^{-1}\left( \frac{2\zeta \omega /\omega _n}{1-\omega ^2/\omega _n^2} \right)$. Measurement of this change can enable one to quantitatively estimate the change in physical parameter and hence the stimuli.

For example, change of the mass from m to $m+\Delta m$ causes the steady-state amplitude to decrease by

$$\begin{aligned} \Delta X=\frac{F_0}{c \sqrt{k/m}}\left( 1-\frac{1}{\sqrt{1+\left( \frac{1}{2\zeta }\frac{\Delta m}{m} \right) ^2}} \right) \end{aligned}$$

(3)

or the phase angle is increased by

$$\begin{aligned} \Delta \phi =\tan ^{-1}\left( -\frac{c}{\Delta m \sqrt{k/m}} \right) - \frac{\pi }{2} = \cot ^{-1}\left( \frac{2\zeta }{\Delta m/m} \right) \end{aligned}$$

(4)

If the excitation frequency is tuned then it may be possible to bring the system again to resonance by changing the frequency from $\omega =\omega _n=\sqrt{\frac{k}{m}}$ to $\omega '=\sqrt{\frac{k}{m+\Delta m}}$. The change in the frequency $|\Delta \omega |=\sqrt{\frac{k}{m}}\left( 1-\frac{1}{\sqrt{1+\frac{\Delta m}{m}}} \right)$ can be measured to estimate $\Delta m$, provided the values of $\omega _n=\sqrt{\frac{k}{m}}$ and m are known. It may be noted that since $\Delta \omega \propto \omega _n$, the measurement becomes easy as the value of $\omega _n$ is increased. This explains why the microscale or nanoscale sensors are better suited for this purpose; the natural frequency of a system increases as the dimension is reduced.

The efficacy of the above-described sensing scheme depends on the ability of detecting change in the response amplitude or phase as the natural frequency is shifted, i.e. on the value of $\frac{\Delta X}{\Delta \omega _n}$, which should be sufficiently large. However, from (3) it may be easily established that

$$\begin{aligned} \frac{\Delta X}{\Delta m}&=\frac{F_0}{4\zeta ^2 k m }\frac{1}{\lambda }\left( 1-\frac{1}{\sqrt{1+\lambda ^2}} \right) , \; \;\; \; \lambda =\frac{1}{2\zeta }\frac{\Delta m}{m} \\&=\frac{F_0}{c^2} \frac{1}{\lambda } \left( 1-\frac{1}{\sqrt{1+\lambda ^2}}\right) \nonumber \end{aligned}$$

(5)

It is therefore required to have large excitation amplitude $F_0$ in order to increase the sensitivity for small value of $\Delta m$.

This limitation can be avoided if the oscillator is excited by parametric excitation rather than direct excitation. For the simplest situation, the following equation of motion is obtained:

$$\begin{aligned} m\ddot{x}+c\dot{x}+k\left( 1+2\varepsilon \cos 2\omega t \right) x=0 \end{aligned}$$

(6)

The response in this case shows two distinct behaviour depending on the values of the parameters $\varepsilon ,\, \omega /\omega _n$ and $\zeta$. The amplitude either increases exponentially if certain inequalities $\varepsilon > f\left( \omega /\omega _n,\, \zeta \right)$ are satisfied or gets reduced to zero when $\varepsilon < f\left( \omega /\omega _n,\, \zeta \right)$. Thus, the system can be conceived to be either in 0-state corresponding to low amplitude of oscillator or in the 1-state which corresponds to high amplitude of oscillation. When the natural frequency is changed, the system may be easily brought from one state to other. Next by proper adjustment of the excitation frequency $\omega$, the system can be restored to its original state. The measured value of $\Delta \omega$ required for that purpose is used to obtain the change in the mass or stiffness of the oscillator.

For example, when the excitation frequency $\omega$ is nearly equal to the natural frequency $\omega _n$, primary parametric resonance in an undamped system ($c=0$) occurs, if $1-\left( \frac{\omega }{\omega _n}\right) ^2<\,\varepsilon \,<1+\left( \frac{\omega }{\omega _n}\right) ^2$, i.e. within a narrow frequency zone of width, $1-\varepsilon<\, \left( \frac{\omega _n}{\omega }\right) ^2 \,<1+\varepsilon$ or approximately $1-\frac{\varepsilon }{2}<\, \left( \frac{\omega _n}{\omega }\right) \,<1+\frac{\varepsilon }{2}$. The state of the oscillator changes when $\omega _n$ is changed by amount $\frac{\varepsilon \omega }{2} \approx \frac{\varepsilon \omega _n}{2}$.

3 Nonlinearities in MEMS

The response amplitudes of resonant MEMS devices are generally large and hence the linear approximations are often insufficient to predict their correct behaviour. Also nonlinearities are sometimes introduced deliberately to gain some advantages. Presence of nonlinearities makes the analysis complicated because of two reasons, (a) the model becomes quite complex and (b) unlike linear systems there is no generic behaviour of system response. Every nonlinear system behaves differently depending on the type of nonlinearity, excitation or initial conditions. Thus, a complete discussion of nonlinear dynamics of MEMS devices will be too lengthy to be considered in a review of modest length.

Resonant MEMS devices can be broadly classified as shown in Fig. 1.

Fig. 1

A schematic explaining the classification of MEMS resonators

Nonlinear analysis of the system is different for different subsystem. Further each of the subsystem can be classified according to the mode of excitation in the following manner:

• 1. system with direct excitation,

• 2. system with parametric excitation,

• 3. system with combined direct and parametric excitations and

• 4. system with self-excitation.

In the following pages, only one type of nonlinear system, namely, the one which can be modelled as a single-degree-of-freedom oscillator is considered for discussion. Further, out of numerous kinds of nonlinear terms that may be present in the system, only the cubic type of nonlinearity is taken up. Different cases of excitation are now considered separately.

3.1 System with Direct Excitation

The equation of motion of a harmonically excited system with cubic-type nonlinear term can be written as

$$\begin{aligned} m\ddot{x}+kx+c\dot{x}+\alpha x^3 = f_0 \cos \omega t \end{aligned}$$

(7)

This quite simple looking system shows at times unexpected behaviour like sensitive dependence on initial conditions (chaos), although in most cases the behaviour is quite predictable. However, the behaviour depends on (i) the relationship between $\omega$ and $\omega _n$, (ii) the magnitude of $f_0$, (iii) the sign of $\alpha$, etc. Three cases can be distinguished.

Case 1: $\omega \approx \omega _n$. This is the case typically encountered in resonant MEMS [10]. The characteristic behaviour of the nonlinear system is mentioned here.

• (a) The frequency response curve for steady-state amplitude bends towards right or left (see Fig. 2) according to the sign of $\alpha$ is positive(hardening-type nonlinearity) or negative (softening-type nonlinearity). In fact, the natural frequency of unforced system depends on amplitude of oscillation as $\omega _n^2 = \frac{k}{m} + \frac{3}{4} \alpha a^2$, where a is the amplitude of oscillation. For a forced system, the response curve depends on the magnitude of $f_0$ and c.

• (b) The response amplitude can take any of the three possible values depending on the initial conditions, when the excitation frequency is within a zone in between $\omega _1$ and $\omega _2$ (shown in Fig. 3).

  The non-uniqueness in the amplitude gives rise to ‘jump phenomena’ when the frequency of excitation is quasistatically increased or decreased continuously. The direction of the jump (upward or downward) as well as its amount depends on the sign of $\alpha$. For example, a hardening-type nonlinearity exhibits downward jump in the frequency sweep up operations while a softening-type nonlinear system shows upward jump. However, if the frequency is not changed quasistatically, then significant transient oscillation takes place before the amplitude sets down to a new value.

Fig. 2

Frequency–amplitude curves for forced excitation

Fig. 3

Bifurcation frequency in case of softening and hardening nonlinearities

Case 2: $\omega \approx 3 \omega _n$. Although the predicted response is small according to linear analysis, the presence of cubic nonlinear term can make it large. The steady-state response has two frequencies, namely, the excitation frequency $\omega$ and the natural frequency $\omega _n$. The phenomena of large amplitude of oscillation is known as ‘subharmonic resonance’.

Case 3: $3\omega \approx \omega _n$. It is also possible to get large amplitude response because of ‘superharmonic resonance’.

When the oscillator is excited by force with two or more different frequencies then in addition to above, large amplitude oscillation may take place due to ‘combination resonance’.

3.2 System with Parametric Excitation

The effect of nonlinear terms in a parametrically excited system is to limit the oscillation amplitude to a finite value when the excitation causes instability to a linear system. For example, if the nonlinearity is of duffing type as in the following equation of motion:

$$\begin{aligned} m\ddot{x}+c\dot{x}+k(1+2\varepsilon \cos 2\omega t)x+\alpha x^3 = 0 \end{aligned}$$

(8)

one or two limit cycles may exist depending on the value of $\frac{\omega }{\omega _n}, \zeta =\frac{c}{2\sqrt{mk}}$ and the sign of $\alpha$. For a duffing-type nonlinearity, the limit cycle is stable if this is unique. For the system where two limit cycles exist, the one with higher amplitude of oscillation is stable. The instability region for a nonlinear system is shown in Fig. 4. The parametric space is divided into three regions. In the region I, both linear and nonlinear equations predict the same steady-state response which decays to insignificantly small value. In region II, the nonlinear equation predicts a stable limit cycle. However, the steady-state amplitude depends on initial condition in region III. For some initial conditions, the predictions of the nonlinear equation and the linear equations are identical, while for a different set of initial conditions a large amplitude of oscillation is predicted when the nonlinear term is present.

Fig. 4

Regimes for stable and unstable behaviours of parametrically excited system

3.3 System with Combined Direct and Parametric Resonances

When the stiffness term in a harmonically excited system is modulated periodically, the system shows often unexpected behaviour. Consider the following equation of motion [11]:

$$\begin{aligned} m\ddot{x}+c\dot{x}+k(1+2\varepsilon \cos 2\omega _p t)x = f_0 \cos (\omega _d t+ \phi ) \end{aligned}$$

(9)

If $\omega _d=\omega _p$, application of harmonic balance method gives the following steady-state response:

$$\begin{aligned} x=A \cos \omega _p t + B \sin \omega _p t \end{aligned}$$

(10)

where A and B satisfy the following equation:

$$\begin{aligned} \begin{bmatrix} k(1+\varepsilon )-m\omega _p^2 &{} c \omega _p\\ -c \omega _p &{} k(1-\varepsilon )-m\omega _p^2 \end{bmatrix} \begin{Bmatrix} A\\ B \end{Bmatrix} = f_0 \begin{Bmatrix} \cos \phi \\ -\sin \phi \end{Bmatrix} \end{aligned}$$

(11)

At resonance, i.e. $\omega _p=\omega _n=\sqrt{\frac{k}{m}}$, the response can be written in the following form provided the amplitude of parametric excitation remains below the threshold value:

$$\begin{aligned} x(t) = \frac{f_o \sqrt{4\zeta ^2+\varepsilon ^2}}{k \left( 4\zeta ^2-\varepsilon ^2 \right) } \left\{ \sin \left( \phi -\tan ^{-1}\frac{\varepsilon }{2\zeta } \right) \cos \omega _n t + \cos \left( \phi +\tan ^{-1}\frac{\varepsilon }{2\zeta } \right) \sin \omega _n t \right\} \end{aligned}$$

(12)

As $\varepsilon = 2\zeta$, the response amplitude becomes large leading to single amplification. Further, as $\tan ^{-1}\left( \frac{\varepsilon }{2\zeta } \right) = \frac{\pi }{4}$ when $\varepsilon = 2\zeta$, the amplitude becomes small for $\phi = \frac{\pi }{4}$. Amplitude becomes very large when $\phi = \frac{-\pi }{4}$. Thus, amplification or quenching of the signal during resonance depends on the value of the phase difference between direct and parametric excitations.

Above the threshold level of excitation, the parametrically excited linear system becomes unstable. In this case, the response can be written as

$$\begin{aligned} x(t)=x_1(t)+x_2(t) \end{aligned}$$

(13)

where $x_1(t)$ is obtained by the above analysis while $x_2(t)$ satisfies the damped Mathieu equation.

When $\omega _d \ne \omega _p$, the response can be written as

$$\begin{aligned} x(t)=A(t) \cos \omega _p t + B(t) \sin \omega _p t \end{aligned}$$

(14)

where A(t) and B(t) satisfy the following differential equation:

$$\begin{aligned} \begin{bmatrix} c &{} -2 m \omega _p\\ 2 m \omega _p &{} c \end{bmatrix} \begin{Bmatrix} \frac{\mathrm {d}A}{\mathrm {d}t} \\ \frac{\mathrm {d}B}{\mathrm {d}t} \end{Bmatrix} + \begin{bmatrix} k(1+\varepsilon )-m\omega _p^2 &{} c \omega _p\\ -c \omega _p &{} k(1-\varepsilon )-m\omega _p^2 \end{bmatrix} \begin{Bmatrix} A\\ B \end{Bmatrix} = f_0 \begin{Bmatrix} \cos \left\{ (\omega _d-\omega _p)t+\phi \right\} \\ -\sin \left\{ (\omega _d-\omega _p)t+\phi \right\} \end{Bmatrix} \end{aligned}$$

(15)

It is not difficult to see that if the solution is stable then the response consists of two harmonic terms, one with frequency $\omega _d$ and the other with frequency $2\omega _p-\omega _d$. When the nonlinear term is present, the response becomes generally quite complex. For a nonlinear oscillator driven by both parametric and external excitations (degenerate case), the equation of motion becomes [12]

$$\begin{aligned} m\ddot{x}+c\dot{x}+k(1+2\varepsilon \cos 2\omega _p t)x + \alpha x^3 = f_0 \cos (\omega t+ \phi ) \end{aligned}$$

(16)

The steady-state response can be obtained by assuming, as before

$$\begin{aligned} x(t)=A \cos \omega t + B \sin \omega t \end{aligned}$$

where A and B are obtained using balancing the harmonics after substituting x(t) into the governing equation of motion. When the system is driven below the parametric instability threshold, the system behaviour is the same as that of a duffing oscillator. When driven above the instability threshold, amplitude-frequency response shows five branches (unlike three in duffing oscillator) within certain frequency band, three of which are stable [12]. Two ‘active’ stable resonances are seen in this resonator. It is interesting to note that the maximum amplitude of the resonator does not depend on whether the parametric instability threshold is crossed or not. Thus, the parametric instability threshold is only of minor concern here, unlike in a linear resonator.

3.4 System with Self-Excitation

Some MEMS resonators are excited by itself through positive feedback mechanism [13]. Such systems are active and, of course, connected to an unlimited energy source. A simple mathematical model of a linear system with self-excitation is

$$\begin{aligned} m\ddot{x}-g \dot{x} + k x = 0 \end{aligned}$$

(17)

whose response grows exponentially with time. Examples of self-excited MEM resonators are optically heated mechanical resonators [14]. Presence of nonlinearity limits the amplitude of oscillation to a limit cycle. For example, the following equation exhibits limit cycle:

$$\begin{aligned} m\ddot{x}-g \left( \dot{x}- \frac{1}{3} \dot{x}^3 \right) + k x = 0 \end{aligned}$$

(18)

This equation can be written in another form, associated with the name of Van der Pol.

$$\begin{aligned} m\ddot{y}-g \left( 1 - y^2 \right) \dot{y} + k y = 0 \end{aligned}$$

(19)

by substituting $\dot{x} = y$.

If the oscillator is excited by harmonic excitation $f_0 \cos \omega t$, where $\omega \approx \omega _0 = \sqrt{\frac{k}{m}}$, then the steady-state motion becomes periodic with a frequency equal to that of excitation. Thus, the response gets synchronized at $\omega$. An interesting fact is that a small change in excitation frequency can cause large change in response behaviour. This happens when the excitation frequency falls outside the band in which ‘entrainment’ takes place.

4 Sources of Nonlinearity

Any vibrating system is generally nonlinear. Only under special operating conditions the effect of the nonlinear terms can be ignored. For example, the system is adequately modelled as a linear system when the amplitude of vibration is small. In resonant devices, this is not the case since the amplitude of vibration is kept to a very high level in order to increase the sensitivity of the device. Furthermore, the MEMS device is made by interconnecting different subsystems which have their own dynamics [15]. Hence, modelling the nonlinear terms is a very difficult task which can be achieved only with a detailed knowledge of the individual subsystems. In what follows some common sources of nonlinearity are discussed.

The sources of nonlinearity can be broadly classified as following:

• 1. nonlinearity in mechanical structure,

• 2. nonlinearity in actuation system,

• 3. nonlinearity in sensing (measuring) devices and

• 4. nonlinearity in feedback and electrical circuit.

4.1 Nonlinearity in Mechanical Structure

The nonlinear terms appearing in the equation of motion of the structural component of the resonant device (for example, beam, plate, wire, etc.) are of following types:

• (i) stiffness nonlinearity,

• (ii) damping nonlinearity and

• (iii) nonlinearity due to external forces.

4.1.1 Nonlinearity in Stiffness Terms

The stiffness or restoring force term in the equation of motion of the structure can be nonlinear because of (i) nonlinearity in strain–displacement relationship at large amplitude (geometric nonlinearity) [16], (ii) nonlinear constitutive relations of the material (material nonlinearity) and (iii) impact causing sudden change in the system behaviour [17].

In deriving the equation of motion of a vibrating structure, one needs the relationship between stress and strain components (constitutive equations) which can be mathematically expressed as

$$\begin{aligned} \sigma _{ij}=\sigma _{ij}\!\left( \epsilon _{kl} \right) ; \;\; i, j, k, l=1, 2, 3 \end{aligned}$$

Together with the relationship between strain and displacement gradient. In a linear system, both these are expressed as linear relations, namely,

$$\begin{aligned}&\sigma _{ij}=\sum _{k} \sum _{l}C_{ijkl} \nonumber \epsilon _{kl},\; \; \mathrm{where} \;C_{ijkl}=C_{jikl}=C_{ijlk}=C_{klij} \\ \mathrm{and} \;\;&\epsilon _{ij} = \frac{1}{2} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \end{aligned}$$

(20)

where $u_i(i=2,3)$ are the components of displacement field.

However, during large amplitude oscillation, significant deviations from the aforesaid relations occur. Even if the material nonlinearity can be ignored, the nonlinear relation between $\epsilon _{ij}$ and $\frac{\partial u_i}{\partial x_j}$ terms shows non-trivial effects. For example, the non-dimensional equation of motion of a MEMS beam fixed at both ends can be written as [16]

$$\begin{aligned} \frac{\partial ^2 w}{\partial t^2} + \frac{\partial ^4 w}{\partial x^4} - \left( \frac{Al^2}{2 I} \right) \frac{\partial ^2 w}{\partial x^2} \int \limits _{0}^{l}\left( \frac{\partial w}{\partial x} \right) ^2 \mathrm {d}x = 0, \;\; 0\le x\le l \end{aligned}$$

(21)

Here, even if the constitutive relations are assumed to be linear, the nonlinear relationship between strain and displacement, i.e. $\epsilon _{xx}=\frac{\partial u}{\partial x} + \frac{1}{2} (\frac{\partial w}{\partial x})^2$, where u(x, t) and w(x, t) are axial and transverse displacements, respectively, couples the longitudinal and transverse motion of the beam. The net effect is stretching of the neutral axis of the beam during large deformation, a fact which is often ignored during small amplitude oscillation.

In a cantilever beam, the above-mentioned mid-plane stretching does not take place but the geometrical nonlinear terms exist. The equation of motion can be written as [18]

$$\begin{aligned} \frac{\partial ^2 w}{\partial t^2} + \frac{\partial ^4 w}{\partial s^4} + \frac{\partial }{\partial s} \left[ \frac{\partial w}{\partial s} \frac{\partial }{\partial s} \left( \frac{\partial w}{\partial s} \frac{\partial ^2 w}{\partial s^2} \right) \right] + \frac{\partial }{\partial s} \left[ \frac{\partial w}{\partial s} \int \limits _{1}^{s}\frac{\partial }{\partial s} \left( \int \limits _{0}^{s} \frac{\partial w}{\partial s}\frac{\partial ^2 w}{\partial s \partial t} \mathrm {d}s \right) \mathrm {d}s \right] = 0 \end{aligned}$$

(22)

where s is the distance measured from the fixed end of the beam.

Fig. 5

Schematic of a compliant amplitude restraint

Material nonlinearity does not normally arise in MEMS devices unless special material is used. In systems where vibro-impact takes place, for example, the devices used in switching, positioning and tapping mode atomic force microscopy, the impacting process generates severe nonlinear behaviour. This kind of system is usually modelled as piecewise smooth (linear) system whose equations of motion are usually smooth. Specific rules, like Newtonian impact low, apply when the response crosses the regional boundaries. For example, for a cantilever beam with a compliant amplitude restraint (as shown in Fig. 5), the boundary conditions at the free end can be written as

$$\begin{aligned}&(i) \frac{\partial ^2 w}{\partial x^2}=0 \;\; \text {and} \;\; \frac{\partial ^3 w}{\partial x^3}=0 \;\; \text {when} \;\; |w(x=l,t)|<\delta \\ \nonumber&(ii) \frac{\partial ^2 w}{\partial x^2}=0 \;\; \text {and} \;\; \frac{\partial ^3 w}{\partial x^3}=\frac{k}{EI}(w-\delta ) \;\; \text {when} \;\; w(x=l,t) \ge \delta \\&(iii) \frac{\partial ^2 w}{\partial x^2}=0 \;\; \text {and} \;\; \frac{\partial ^3 w}{\partial x^3}=\frac{k}{EI}(w+\delta ) \;\; \text {when} \;\; w(x=l,t) \le -\delta \nonumber \end{aligned}$$

(23)

This system shows all the behaviour of a hard nonlinear system.

4.1.2 Nonlinear Damping Term

Different mechanisms are responsible for dissipation of energy from the vibrating structure in a resonant MEMS device. The sources of dissipation of energy can be broadly classified as follows:

• (i) structural/internal damping,

• (ii) support damping and

• (iii) fluidic and acoustic damping.

Various mechanisms of energy dissipation have been identified within the structure (bulk dissipation) [19, 20] or on its surface (surface dissipation) [21]. Of the former, the thermoelastic dissipation is the most dominant. Usually the damping is treated as linear. A major loss of energy from a resonatory microstructure takes place in the fluidic medium surrounding the structure. In many situations, the vibrating body is placed near a static structure. The fluid entrapped between these structure causes what is known as squeeze-film damping. As the amplitude of response increases, the effect of nonlinearity also becomes significant. For example, the equation of motion of a pined-pined beam vibrating near a fixed plate is

$$\begin{aligned} \rho A \frac{\partial ^2 w}{\partial t^2}+ c \frac{\partial w}{\partial t} +EI \frac{\partial ^4 w}{\partial x^4} - \frac{EA}{2 L} \left[ \int \limits _{0}^{l}\left( \frac{\partial w}{\partial x} \right) ^2 \mathrm {d}x \right] \frac{\partial ^2 w}{\partial x^2}= \int \limits _{-\frac{b}{2}}^{\frac{b}{2}} p\;\mathrm {d}y \end{aligned}$$

(24)

where p(x, y, t) is the pressure distribution on the beam surface which has width b. The pressure is calculated by solving the nonlinear version of Reynolds’s equation

$$\begin{aligned} \bigtriangledown \cdot \left[ w^3 p \bigtriangledown p \right] = \frac{12\mu }{1+6K} \frac{\partial \left( p w_0 \right) }{\partial t} \end{aligned}$$

(25)

where $\mu$ is the viscosity of the surrounding fluid and K is the Knudsen number (=mean free path of the gas/w). When the amplitude of vibration is small the damping is usually considered to be linear with damping coefficient, $C_\mathrm{squeeze}=\frac{b^3}{d^3} l \mu$, where b, d, l and $\mu$ are, respectively, the beam width, gap between plates, length of the plates and air/fluid viscosity. When the amplitude of vibration increases, the nonlinearity of damping is modelled by considering the damping coefficient as [16, 22]

$$\begin{aligned} C_\mathrm{squeeze}=\frac{\alpha }{(d-w)^3} \end{aligned}$$

(26)

4.1.3 Nonlinear External Forces

As the dimensions of the structure are reduced, some kinds of interaction forces with the nearby objects become pronounced which can introduce nonlinearity. For example, in scanning probe microscopy, the tip of the microcantilever often experiences electrostatic interactions or attractive van der Waals forces from the surface under observation. Most of the interaction forces are highly nonlinear function of the separating distance between tip and sample [23]. A very general model for tip–sample interaction force is given by

$$\begin{aligned} F_\mathrm{tip}=\left\{ \begin{array}{ccc} &{}&{} -\frac{C}{d^\alpha }, \,\, \text {for} \,\, d > a_0 \\ &{}&{} -\frac{C}{a_0^\alpha }+D(a_0-d), \,\, \text {for} \,\, d\le a_0 \end{array}\right. \end{aligned}$$

(27)

Here C, D, d and $a_0$ are general attractive force parameters, tip–sample separation and intermolecular distance at which contact is considered to be initiated. The parameters C and D are functions of tip radius. The forces are dependent on material of tip and sample. They are attractive (repulsive) for long (short) range.

4.2 Nonlinearity in Actuating System

MEMS resonators are excited by different mechanisms. The most common of which are

• (i) electrostatic actuation and

• (ii) piezoelectric actuation.

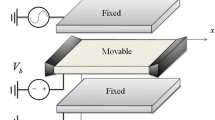
The forces of actuation in an electrostatically actuated MEMS (also called capacitive MEMS resonator) is calculated by solving the field equations in an electrostatic problem. However, under certain assumptions the force can be modelled as

$$\begin{aligned} F_\mathrm{actuation}=\frac{\epsilon A V^2}{2 g^2} \end{aligned}$$

where $\epsilon$ is the permittivity of the space, A is the area of the electrode, V is the voltage difference between the plates and g is the gap between the plates. For a capacitive actuation of the beam-type resonator, $g=d-w(t)$, where d is the initial gap and w is the transverse displacement of the beam. For a DC-driven system,

$$\begin{aligned} F_\mathrm{actuation}=\frac{\epsilon A V_{DC}^2}{2 (d-w)^2} \end{aligned}$$

However, resonant MEMS are excited by time-varying voltage $V=V_{DC}+V_{AC} \cos \omega t$. In this case, the actuation force leads to both ordinary nonlinear terms and nonlinear parametric excitations [24]. In this case

$$\begin{aligned} F_\mathrm{actuation}=\frac{\epsilon A}{2 (d-w)^2} \left( \left( V_{DC}^2+\frac{V_{AC}^2}{2} \right) + 2 V_{DC} V_{AC} \cos \omega t +\frac{V_{AC}^2}{2} \cos 2\omega t \right) \end{aligned}$$

(28)

The nonlinearity is usually softening type since

$$\begin{aligned} \frac{1}{(d-w)^2} \approx \frac{1}{d^2} \left( 1 + 2\frac{w}{d} + 3 \left( \frac{w}{d} \right) ^2 + 4\left( \frac{w}{d} \right) ^3 + --- \right) \end{aligned}$$

Usually in the model, the fourth- and fifth-order nonlinear terms are generally neglected. However, for very high amplitude oscillation they become effective [25].

In a piezoelectrically actuated resonator, electrical voltage is applied to the piezoelectric material to induce deformation (strain actuation) within the structure. Linear assumption provides adequate accuracy to the model as long as the applied electric field and stress are low. They become, however, increasingly inaccurate as the stress level and electric field strength increase. Pronounced nonlinearity and hysteresis in the strain–field relationship are observed in such case. Usually the nonlinearity is softening type.

4.3 Nonlinearity in Sensing System

Different response parameters like amplitude, phase, etc. are used in various ways in a resonant MEMS device. This requires sensing of the pertinent quantity with the help of suitable sensing device. Often the resolution of the MEMS device gets limited by the limitation of the sensing device. Different types of sensors are used, like capacitive sensor, piezoresistive sensor and optical sensor. It is desirable that the sensor should be linear for wide range of input. In practice they often show nonlinearity.

For example, in capacitive-type sensing scheme, the change in capacitance is measured to detect the displacement of the movable plate of parallel-plate capacitor [26]. As the capacitance of such a capacitor is given by

$$\begin{aligned}&C=\frac{\varepsilon A}{d-w} \nonumber \\ \text {one gets} \;\;\;&\frac{dC}{dw} = \frac{\varepsilon A}{(d-w)^2} \approx \frac{\varepsilon A}{d^2} \left( 1 + 2\frac{w}{d} + 3 \left( \frac{w}{d} \right) ^2 + \cdots \right) . \end{aligned}$$

(29)

Nonlinear terms in the aforementioned expression can be ignored if $w \ll d$. For large value of w, appreciable errors have been found out while using the linear relationship.

Apart from the sources of nonlinearity described above, the nonlinearities are deliberately introduced into the system by various mechanisms, like feedback, etc. Some of these methods are discussed later (see Sect. 6). In what follows the roles played by the nonlinearity are discussed. It will be seen that nonlinear terms sometimes enhance the performance measures of the device, while at other cases they play negative roles.

5 Effect of Nonlinearity on MEMS Performance

As mentioned earlier, nonlinearity can be the cause of performance degradation, or it can help to improve the device performance. Different effects of nonlinearities are discussed below.

5.1 Undesirable Effects of Nonlinearity

The following are the undesirable effects due to the presence of nonlinearities in the device:

• a. Frequency stability

  The resonant frequency (the frequency at which the amplitude becomes highest) of a nonlinear oscillator depends on the amplitude of the excitation force [9, 27]. This dependance of resonant frequency or amplitude limits the performance of the device where they are required to resonate at a particular frequency, for example, time device, frequency filters, resonant accelerometers, resonant energy harvesters, gravimetric sensors, etc.

• b. Noise performance

  High amplitude of response is preferred in resonant devices for increasing the signal-to-noise (S/N) ratio. However, the presence of nonlinear term limits the amplitude of oscillation for a given excitation level. To assess the noise performance of the oscillator, a block diagram of the open-loop system is used as shown in Fig. 6.

  In Fig. 6 $N_1(t)$, $N_2(t)$ are the noise in excitation and transducer, respectively, and y(t) is the measured output from the transducer. The maximum energy stored in the linear oscillator is

  $$\begin{aligned} E_{\max }=\frac{1}{2} k_1 X_{\max }^2 \end{aligned}$$

  While the maximum power that could be extracted from the oscillator is equal to

  $$\begin{aligned} P_\mathrm{sig}=\frac{\Delta E}{2\pi /\omega } = \frac{\omega E_{\max }}{Q} \end{aligned}$$

  The noise in y(t) is generated by two main sources, namely, the noise generated from excitation and the thermal noise generated due to motion resistance. With a properly designed excitation mechanism the contribution of the first term can be minimized. The thermal noise power can be written approximately as [28]

  $$\begin{aligned} p_\mathrm{noise}^\mathrm{mech}=4k_b T \left( \frac{\omega _0}{2Q\Delta \omega } \right) ^2 \end{aligned}$$

  where $\omega _0$ is the centre frequency and $\delta \omega$ is the offset from the former. The phase noise spectrum is obtained as

  $$\begin{aligned} L\left( \Delta \omega \right) = \frac{p_\mathrm{noise}^\mathrm{mech}+p_{N_2}}{2 p_\mathrm{sig}} = \frac{2k_b T}{p_\mathrm{sig}}\left( \frac{\omega _0}{2Q\Delta \omega } \right) ^2 + \frac{p_{N_2}}{2 p_\mathrm{sig}} \end{aligned}$$

  (30)

  where $p_{N_2}$ is the noise in the transducer. In the simplified analysis, the effect of 1/f noise has not been considered. It is seen from the above equation that a large value of $E_{\max }$ is required for improving the noise performance of the oscillator. However, the presence of the nonlinear term limits the value of $E_{\max }$ and hence decreases the S/N ratio. The limitation on amplitude of response due to nonlinearities puts a limit to the drive current that can be applied resulting in a far-from-carrier-phase noise. Also the frequency-amplitude dependence converts amplitude noise into phase noise [9, 29].

• c. Quality factor

  Nonlinearity often decreases the quality factor of the resonator in MEMS device. This affects adversely the sensitivity of the instrument [15, 30]. Also amplitude of response during parametric excitation gets limited to a low value if nonlinear terms are significant.

• d. Sensing

  Nonlinear terms introduce complexity in the sensing process [26, 31]. It is desirable to design and fabricate the resonator to drive in the linear regime. Nonlinear terms, for example, in capacitive sensing, affect the performance of the resonator. In optical sensing also the nonlinear effects are observed.

  Apart from the general effects of the nonlinearities present in almost all MEMS devices, some kinds of nonlinearities may degrade the quality of some special devices. For example, in dynamic atomic force microscopy, where near-resonant response of cantilever is measured to estimate topography of the sample, the nonlinear interaction strongly influences the resonant characteristics of the cantilever. Amplitude jump and hysteresis take place during forward and backward frequency sweeps. Transition between attractive-repulsive regime also leads to chaotic response. These effects have been found to affect the quality of image of the sample surface [32].

Fig. 6

Block diagram of a MEMS resonator considering the noise in excitation and detection

5.2 Desirable Effects of Nonlinearity

The desirable effects of nonlinearities are now listed below.

• a. Phase noise

  In the previous section, it has been pointed out how the phase noise increases because of nonlinearities present in the system. However, it has been found that if nonlinearity is judiciously introduced then the phase noise can be reduced [33]. It has been found, contrary to the conventional phenomenological wisdom, that there exist a special region in the parameter space, lying above the nonlinear threshold, where the phase noise is reduced. By operating the oscillator in this region the signal level can be increased to large value without degrading the oscillator performance. However, to achieve this objective a feedback with a phase delay is required. By properly selecting the gain and phase delay the nonlinear frequency shift is made comparable to the linear resonance line width, but small compared to the resonant frequency. This scheme is also known as phase feedback oscillator. Similar noise reduction has been experimentally demonstrated for a 2 DOF-coupled nonlinear oscillator [34].

• b. Frequency stability

  In timing devices, where stability of the output frequency is of greatest concern, the change in frequency, caused by increase in amplitude (i.e. amplitude-frequency, A-f effect), is a problem. However, the nonlinearity can help in achieving temperature compensation in silicon micromechanical resonator [35]. The main challenge in Si resonator is that Si has a temperature coefficient of frequency (TCF) near to 30 ppm/${}^{\circ }\text {C}$, which is large compared to that of a quartz oscillator (18 ppm/${}^{\circ }\text {C}$ at 25 ${}^{\circ }\text {C}$). With increasing temperature, both the resonant frequency and quality factor increase as follows:

  $$\begin{aligned}&f_r=f_0\left( 1+\,\mathrm{TCF}(T-T_0) \right) , \nonumber \\&Q_r=Q_0\left( 1+\,\mathrm{TCQ}(T-T_0) \right) , \end{aligned}$$

  (31)

  where $f_0$ and $Q_0$ are the resonant frequency and quality factor at 12.5 ${}^{\circ }\text {C}$ and TCQ is the temperature coefficient of quality factor. In the linear regime, operating at resonance, the amplitude is proportional to the quality factor, i.e.

  $$\begin{aligned} X=X_0\left( 1+\,\mathrm{TCQ}(T-T_0) \right) \end{aligned}$$

  where $X_0$ is the amplitude of MEMS at $T_0$. From the above equations, we get

  $$\begin{aligned}&\Delta f_T=\left( \frac{f_0}{X_0} \frac{\mathrm{TCF}}{\mathrm{TCQ}} \right) \Delta X \nonumber \\ \mathrm{or} \;\;\;&\frac{\Delta f_T}{f_0} = \frac{\mathrm{TCF}}{\mathrm{TCQ}} \frac{\Delta X}{X_0} \end{aligned}$$

  (32)

  i.e. there exists a linear relationship between $f_r$ and X. When nonlinearity is present the A-f dependence due to duffing-type nonlinearity can be written as

  $$\begin{aligned} \frac{\Delta f_D}{f_0} = \frac{3\alpha /4 (X_0+\Delta X)^2}{2 \pi f_0} \approx \frac{3\alpha }{4} \frac{X_0^2}{2 \pi f_0} + \frac{3\alpha }{4\pi } \frac{X_0^2}{f_0} \frac{\Delta X}{X_0} \end{aligned}$$

  (33)

  When both the effects are considered

  $$\begin{aligned} \frac{\Delta f}{f_0} = \frac{\Delta f_T}{f_0} + \frac{\Delta f_D}{f_0} = \frac{3}{4} \frac{\alpha X_0^2}{2\pi f_0} + \frac{\Delta X}{X_0} \left( \frac{TCF}{TCQ} + \frac{3\alpha X_0^2}{4\pi f_0} \right) . \end{aligned}$$

  (34)

  The effect of temperature variation can be nullified if $X_0$ is selected for $(\alpha <0)$ in such a way that the last term gets cancelled out. Thus, the temperature dependence of frequency is minimized. Further, electrostatic tuning is also used to suppress the temperature-frequency drift [36].

• c. Sensing devices

  Nonlinearity can be useful in many sensing devices. Some examples are given below:

  • (i) The pull-in phenomena of electrostatically driven MEMS, which is due to nonlinear nature of the interacting force, is desirable in MEMS switches for reducing switching voltage [6].

  • (ii) Jump phenomena (Bifurcation) in a nonlinear system have been advantageously used in mass sensing. In a linear system, sweeping of excitation frequency is carried out to detect resonant frequency. Performance of the sensor depends on the quality factor or damping. Further, the minimum detectable mass is also limited by noise. The strategy of exploiting bifurcation phenomena has been found giving better results. It has been found to be applied in different ways.

    • (a) One way is exciting microresonator at set point A$'$ (shown in Fig. 7a), close to the critical point, so that an addition of mass will cause a shift in the resonance frequency and also in the bifurcation frequency. If the change in bifurcation frequency is large enough, then it will cause saddle node bifurcation (jump to A) [10]. From the difference between set point and bifurcation frequency, minimum possible value of mass detected can be calculated. Such device has been used for switch-type operation, whether the minimum value of measurand is detected (1) or not (0).

    • (b) Another way found in literature is bifurcation tracking through sweeping a parameter [37]. Parametrically excited systems contain stable and unstable regimes. As shown in Fig. 7b, excitation frequency is swept towards the separating boundary of these regions. At critical point, amplitude of oscillations goes up. On mass detection, boundary will shift towards lower frequency and finding the shift, amount of mass detected can be calculated. Noise will be a dominating factor for uncertainty in sensing. Rate of frequency sweeping is an important factor for getting results with maximum precision [38]. If the rate is too fast, then bifurcation will happen after critical point, and, if it is too low, then noise activated jump can occur. Even influenced by noise, sensor based on bifurcation tracking has been found giving better results than resonant sensing.

    • (c) For continuous sensing, resonator has to be reset at low amplitudes, and again sensing can be carried out, which can be time-consuming. One technique was found very useful, which works on the phenomena of noise squeezing [39]. While approaching critical point, just before bifurcation, phase noise gets squeezed to a very small value. Considering it as sign of bifurcation gas sensing has been done with faster rate.

  • (iii) Nonlinear parametric resonance with broad driving range is useful in increasing the sensitivity of MEMS gyrosensor [40]. In a study, it has been demonstrated that by adjusting the electromagnetic and mechanical nonlinearities, a reduction in angle random walk (ARW) and bias instability is possible.

  • (iv) Nonlinear coupling between two modes of a micromechanical resonatory disc gyroscope introduces the parametric amplification of the Coriolis force without the need of externally applied parametric pumping [41]. The amplification increases the rate sensitivity of vibrating gyroscope.

  • (v) As described in previous section, large displacement reduces the sensor performance and detecting the displacement also becomes difficult. To limit the displacement, nonlinearity is introduced in the excitation loop [42]. In some of the mass-sensing strategies, microcantilever is operated in self-excitation loop. Tip deflection of cantilever beam is detected and (as shown in Fig. 8) base displacement is given as cubic polynomial function of the sensor output [43]. Self-excitation strategy has also been utilized for creating parametric resonance [15]. Here, the introduced nonlinearity will not cause any jumps in amplitude while sweeping of the excitation frequency.

• d. Memory devices

  In memory elements, bistability is introduced into the system to generate two states in the response amplitude, namely, 0 and 1 states, which correspond to the low and high values of the amplitude, respectively. Such bistability, through which amplitude is switched from one state to the other, is possible only because of nonlinearities [44].

Fig. 7

a Utilizing jump phenomena for sensing purpose. b Tracking the bifurcation frequency in parametrically excited systems

Fig. 8

Block diagram for self-excited MEMS resonator with induced nonlinearity in feedback

6 Tailoring Nonlinearity in MEMS Resonator

It is seen that adjustment of nonlinearity either by reducing it or enhancing may be required in MEMS resonator. Special arrangements are made to modify the nonlinearity in the existing microstructures. Some are listed below:

• (i) Microbeams with initially curved shape have been fabricated to utilize the bistable and snap through behaviour of arch beam [45]. Initially, curved shape causes softening quadratic nonlinearity in the governing equation of motion (Fig. 9).

• (ii) Nonlinearity may not be present due to geometric or actuation method, but for desirable results (as aforementioned in the previous section), it has been induced in artificial ways through applying nonlinear feedback [46]. Here, desired softening or hardening behaviour can be achieved via properly selecting feedback parameters.

• (iii) Adding or removing material at location (as shown in Fig. 10), where slope in the mode shape of resonator is maximum, cubic nonlinearity due to geometric effect can be increased or decreased, respectively. The coefficient has been increased or decreased up to more than 2.5 and 3 times, respectively, via varying the thickness of microbeam [47]. Here $\gamma$ is the coefficient for cubic nonlinearity. That influences the frequency-amplitude behaviour, by either broadening nonlinear resonance regime or making it nearly linear. Varying beam thickness, natural frequency also gets changed comparing to uniform beam.

• (iv) Electrostatically actuated comb drives are widely used in MEMS. Electrostatic force is dependent on distance separating electrodes and electrode surface area. Via shaping comb fingers, coefficients for nonlinear terms in governing differential equation can be changed [48]. Linear electrostatic force–displacement behaviour can also be achieved.

• (v) There is no mid-plane stretching in cantilever, but the stretching in the beam has been induced through a polymer attachment and similar effect is generated [49].

• (vi) Electrostatic force is a highly nonlinear function of the distance between electrodes and this electrical nonlinearity has been used advantageously for cancelling mechanical nonlinearity or tuning the overall nonlinear behaviour [50, 51].

Fig. 9

Microbeam with initially curved shape (arch beam)

Fig. 10

Modifying the cubic nonlinearity coefficient through varying the thickness

7 Conclusion

Different aspects of nonlinearities on the overall dynamics of MEMS resonators have been reviewed. Both desirable and undesirable effects of nonlinearities are discussed with the help of simple mathematical models. Although many facts of nonlinearities are dealt with, an exhaustive study is impossible because, unlike linear system, there is no general solution of nonlinear equation of motion. Consequently, different excitations have different effects. Furthermore, only one type of system, namely, the one which can be modelled as single-degree-of-freedom system has been considered here. Coupled array of micromachined oscillators or the MEMS where multiple modes interact due to nonlinearity has not been discussed. Any meaningful discussion of the dynamic behaviour of such system will make the size of the article too large to be within the limit.