Keywords

1 Introduction

Global environmental concern and the increasing cost of fossil fuels press scientists to make renewable energy sources more sustainable and cost effective. Solar energy has been found to be the most widely used renewable energy sources over the last few decades. The early researches on solar energy had been conducted in the early’ 40s by Hottel (1942). He (Hottel 1954; Zarem and Erway 1963; Hottel and Whillier 1955) continued his extensive research on solar energy, and all the early works are summarized by Duffie and Beckman (1974) in his book. Later Kalogirou (2004) presented a summary on various types of solar thermal collectors and their applications. Solar thermal collectors convert solar radiation into heat energy, which can be utilized in various applications. One of the promising application of thermal energy is cooling and dehumidification through the utilization of adsorption refrigeration technology.

With the rapid growth of the economy and development of infrastructure, energy consumption is increasing at a fast pace, and it is estimated to rise 28% within the next 20 years (Conti et al. 2016). Furthermore, according to the estimation of the International Institute of Refrigeration in Paris (Coulomb 2006), 15% of the world’s total produced electricity is spent on air-conditioning and refrigeration processes of various kinds. In the present scenario, vapor compression refrigeration technology is predominant in the market, which is highly energy intensive. Furthermore, it uses CFC, HCFC based refrigerants, which are being considered as the major culprits for global warming and ozone depletion. Adsorption based refrigeration technology is environmentally benign, as it can use natural refrigerants (e.g. water, CO2). Instead of electricity, it is primarily driven by low grade heat having a temperature of as low as 60 °C (Muttakin et al. 2018; Mitra et al. 2017; Saha et al. 2006). A typical low cost flat plate solar collector is able to provide heat at such low temperature. Hence solar thermal powered adsorption chiller is gaining considerable attention, particularly by the environmental scientists.

Scientists (Muttakin 2013) worked on the modeling and optimization of solar thermal systems utilizing various computer based simulation programs. Modelling of adsorption chiller (Wang 2001) is also necessary to make the system efficient and economically viable. The computer modelling of any system has numerous advantages (Kalogirou and Papamarcou 2000),

  • Prediction of system performance.

  • Optimization of the system to make it more economical and energy efficient.

  • Reduction or elimination of the cost of building prototypes.

  • Estimation of system performance under variable operating conditions.

  • Sensitivity analysis of different design parameters.

In this book chapter model equations of a solar thermal powered adsorption chiller are presented. First, the system is briefly explained in Sect. 8.2. In the next section, the construction of a flat plate collector is described, which is followed by the derivation of different heat transfer components to calculate its efficiency. Section 8.4 models an evacuated tube collector to estimate its dynamic performance. Next model equations of a typical commercial adsorption chiller are explained, and simulation results of a 10-RTon chiller are presented under specific operating conditions. Finally, the chapter ends with a conclusion.

2 System Description

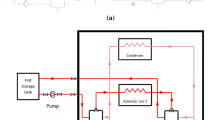
An adsorption chiller requires low grade heat for its operation. Hence the heat from flat plate collectors or evacuated tube collectors can drive the system. The main components of a two-bed adsorption chiller are two ad/de-sorption beds with adsorbents, one evaporator and one condenser. A schematic of a solar thermal powered adsorption chiller is shown in Fig. 8.1.

Fig. 8.1
figure 1

Schematic diagram of a solar thermal powered adsorption chiller

Full size image

A typical ad/de-sorption bed has finned tube heat exchanger, and the adsorbents are placed between the fins. The chiller works in cycles. The four major steps of an adsorption chiller are adsorption, mass recovery, heat recovery and desorption. During the adsorption phase, cold water flows through the tubes of the adsorbent bed and during the desorption phase, hot water from the hot water tanks flows through those tubes. The difference between the temperatures of hot and cold water is known as temperature swing. For a typical single stage silica gel—water adsorption chiller, the temperature of the hot water requires to be 60–80 °C. However, a multistage adsorption chiller can be operated at a temperature swing of 10 °C (Saha and Kashiwagi 1997). Theoretically, a temperature swing of 2.2 °C can be utilized to drive a 10-stage adsorption chiller (Saha et al. 2007).

In a solar thermal-powered adsorption chiller, heat is obtained primarily from the solar thermal collectors. However, an auxiliary electrical heater is often used to maintain the temperature in the hot water tank. This is required as the performance of the solar thermal collector strongly depends on the environmental condition. It is obvious that during rainy days, the output from the collector will be significantly lower when compared to the same during bright sunny days. The poor solar irradiance in rainy days results in lower absorbed energy by the solar thermal collector, which in turn reduces its output.

3 Model Equations of a Flat Plate Collector

A typical solar thermal system includes solar thermal collectors, water storage tanks and necessary piping. An adsorption chiller requires a low temperature heat source to be driven efficiently, and flat plate collectors (FPC) are the most popular solar thermal collectors considering low temperature application.

3.1 Components of an FPC

As can be seen in Fig. 8.2, the major components of a flat plate collector are;

Fig. 8.2
figure 2

Components of a flat plate collector

Full size image

  • Glazing: A glazing material is placed on the top of the FPC. Glass is the most widely used glazing material because of its ability to transmit 90% of the incoming shortwave solar irradiation while being opaque to longwave radiation emitted outward by the absorber plate (Duffie and Beckman 1974).

  • Absorber plate: The role of an absorber plate is to support the tubes and fins. In some collectors, it may be integrated with the tubes. The three most important materials that are used as absorber plates are copper, aluminium and stainless steel.

  • Tubes: Tubes provide the path for the flow of heat-transfer fluid from inlet to outlet.

  • Header: The header provides the passage for cold water inlet and hot water outlet.

  • Insulation: Insulation prevents the loss of heat from the collector through its bottom and its side.

  • Housing: The housing holds all the components as well as protects the system from moisture, dust etc.

An FPC is a non-concentrating type of solar thermal collector, i.e., its concentration ratio is one. The concentration ratio signifies the amount of transmitted solar energy that causes the rise of temperature of the heat-transfer fluid and can be defined as the ratio of aperture area of the collector to its absorber area.

Prior to modelling a flat plate collector, it is important to define two parameters that play vital roles in the performance of the collector; these are, absorptance α and emittance ε. The monochromatic, directional absorptance is a surface property, defined as the fraction of the incident radiation of wavelength ψ from the direction μ, φ, that is absorbed by the surface. Mathematically it can be shown as,

$$ \alpha_{\psi } (\mu ,\varphi ) = \frac{{I_{\psi ,abs} (\mu ,\varphi )}}{{I_{\psi ,inc} (\mu ,\varphi )}} $$
(8.1)

Here μ is the cosine of the polar angle and φ is the azimuth angle; I represents the radiant exposure and subscripts abs and inc stand for absorbed and incident, respectively.

On the other hand, the monochromatic directional emittance, of a surface is the ratio of the monochromatic intensity emitted by the surface in a specific direction to the same that would be emitted by a blackbody maintained at the same temperature (Duffie and Beckman 1980). Mathematically it can be written as,

$$ \varepsilon_{\psi } (\mu ,\varphi ) = \frac{{I_{\psi } (\mu ,\varphi )}}{{I_{\psi ,b} }} $$
(8.2)

where subscript b represents blackbody.

3.2 Efficiency of an FPC

An efficient solar collector should possess high absorptance for radiation in the solar energy spectrum. At the same time, in order to minimize the losses, it must have low emittance for long wave radiation. The efficiency (η) of an FPC is defined as the ratio of useful gain (Qu) to the incident solar radiation power (QT),

$$ \eta = \frac{{Q_{u} }}{{Q_{T} }} = \frac{{Q_{u} }}{{GA_{c} }} $$
(8.3)

where G represents the solar irradiance in W/m2, and Ac represents an aperture area of the collector. With Gs being the absorbed energy, the useful energy gain can be defined by,

$$ Q_{u} = A_{c} \left[ {G_{S} - U_{L} \left( {T_{c} - T_{a} } \right)} \right] $$
(8.4)

where UL is the overall heat transfer coefficient, Tc and Ta are the mean absorber plate temperature and ambient air temperature, respectively. Hence, UL(Tc – Ta) is the thermal energy lost from the collector to the ambient through conduction, convection and infrared radiation.

In order to determine the efficiency of the collector, all the parameters of Eq. (8.4) must be known. The parameters G, Ac, Tc and Ta can be measured through experiments. The absorbed energy Gs can be calculated from,

$$ G_{S} = G(\tau \alpha )_{eff} $$
(8.5)

where (τα)eff is called the effective transmittance-absorptance coefficient. It can be approximated from the known value of incidence angle modifier of a collector, as defined by,

$$ K_{\tau \alpha } = \frac{{(\tau \alpha )_{eff} }}{{(\tau \alpha )_{n} }} $$

where (τα)n is transmittance-absorptance normal to the collector surface. For FPC with flat covers, the incidence angle modifier depends on the angle of incidence θ following the below equation (Souka and Safwat 1966),

$$ K_{\tau \alpha } = 1 + b_{0} \left( {\frac{1}{\cos \theta } - 1} \right) $$

where b0 is the incidence angle modifier constant, and it has a positive value.

The thermal network of an FPC with two covers is shown in Fig. 8.3. The absorbed energy Gs is converted to useful energy gain Qu after losing a portion to the ambient environment through the top and bottom of the collector. At some typical location, let Tp be the absorber plate temperature. From the top of the collector, heat loss is due to convection and radiation heat transfer to the ambient. This heat loss is essentially the same as the steady state energy transfer between the plate at Tp and the first cover at Tc1 and is equal to the energy transfer between any other two adjacent covers. Hence, the heat loss through the top of the FPC can be expressed by,

Fig. 8.3
figure 3

Thermal model of an FPC having two covers

Full size image
$$ Q_{top,coll} = h_{c,p - c1} (T_{p} - T_{c1} ) + \frac{{\sigma (T_{p}^{4} - T_{c1}^{4} )}}{{\frac{1}{{\varepsilon_{p} }} + \frac{1}{{\varepsilon_{c1} }} - 1}} $$
(8.6)

where hc,p–c1 is the convection heat transfer coefficient between two inclined parallel plates, σ is the Stefan-Boltzmann constant which is equal to 5.6697 × 10−8 W/(m2 °C4), and εp and εc1 are the directional emittances of absorber plate and cover 1, respectively. Equation (8.6) can be written in terms of radiation heat transfer coefficient hr,p–c1 as,

$$ Q_{top,coll} = (h_{c,p - c1} + h_{r,p - c1} )(T_{p} - T_{c1} ) $$
(8.7)

hr,p–c1 can be calculated from,

$$ h_{r,p - c1} = \frac{{\sigma (T_{p} + T_{c1} )(T_{p}^{2} + T_{c1}^{2} )}}{{\frac{1}{{\varepsilon_{p} }} + \frac{1}{{\varepsilon_{c1} }} - 1}} $$
(8.8)

Thus the resistance R3 can be written as,

$$ R_{3} = \frac{1}{{h_{c,p - c1} + h_{r,p - c1} }} $$
(8.9)

The resistance, R2, between the two covers can have a similar expression, and the expression is essentially of the same form for further adjacent covers. However, considering practical applications, the maximum limit of the number of covers of an FPC is two. The resistance to heat loss, R1, from the top cover to the ambient, can be represented following the similar expression,

$$ R_{1} = \frac{1}{{h_{w} + h_{r,c2 - a} }} $$
(8.10)

where resistance to radiation heat transfer accounts for radiation exchange with the sky having a temperature Tsky;

$$ h_{r,c2 - a} = \frac{{\sigma \varepsilon_{c} (T_{c2} + T_{sky} )(T_{c2}^{2} + T_{sky}^{2} )(T_{c2} - T_{sky} )}}{{T_{c2} - T_{a} }} $$
(8.11)

For free-convection conditions, the minimum values of convection heat transfer coefficient are 5 and 4 W/(m2 °C) for temperature differences of 25 and 10 °C, respectively. But for forced-convection conditions, it can be calculated following the expression obtained from Mitchell’s (1976) experimental results,

$$ h_{w} = \frac{{c_{0} \left( {\frac{v}{{v_{0} }}} \right)^{0.6} }}{{\left( {\frac{L}{{L_{0} }}} \right)^{0.4} }} $$
(8.12)

where v0 = 1 m/s, c0 = 8.6 W/(m2 °C) and L0 = 1 m. L is the cubic root of the collector house volume in m and v represents the wind speed in m/s. For the simultaneous occurrence of free and forced convections, it is recommended (McAdams 1954) to use the larger value of the convection heat transfer coefficients; hence it can be expressed as,

$$ h_{w} = \hbox{max} \left[ {5,\frac{{8.6\left( {\frac{v}{{v_{0} }}} \right)^{0.6} }}{{\left( {\frac{L}{{L_{0} }}} \right)^{0.4} }}} \right]{\text{W}}/({\text{m}}^{2} \,{^\circ }{\text{C}}) $$
(8.13)

Thus, for an FPC having two covers, the mathematical expression of the top loss coefficient from the collector to the surroundings becomes,

$$ U_{top,coll} = \frac{1}{{R_{1} + R_{2} + R_{3} }} $$
(8.14)

On the other hand, losses through the back of the collector can be obtained from,

$$ U_{bot,coll} = \frac{1}{{R_{4} }} = \frac{{\kappa_{ins,coll} }}{{\delta_{ins,coll} }} $$
(8.15)

where κins,coll and δins,coll are the thermal conductivity and thickness of the insulation, respectively.

It needs mentioning that, for a well-designed system, the edge loss from the collector can be neglected as its value is very small compared to other heat losses from the collector. With edge loss coefficient-area product of (UA)edge, the losses through the edges of the collector can be calculated from,

$$ U_{edge,coll} = \frac{{(UA)_{edge,coll} }}{{A_{C} }} $$
(8.16)

The overall heat transfer coefficient, UL, is essentially the summation of all the loss coefficients. Adding Eqs. (8.14)–(8.16),

$$ U_{L} = U_{top,coll} + U_{bot,coll} + U_{edge,coll} $$
(8.17)

Putting the value of UL into Eq. (8.4), one can determine the useful energy gain Qu, which can be utilized to determine the FPC efficiency η using Eq. (8.3).

4 Model Equations of an Evacuated Tube Collector

An evacuated tube collector (ETC) comprises an absorber plate attached to a heat pipe, placed inside a vacuum-sealed tube, as can be seen in Fig. 8.4. Since the plate and the heat pipe are surrounded by the vacuum, the heat loss to the environment by convection and conduction is very minimal. This results in higher efficiency of ETC when compared to FPC.

Fig. 8.4
figure 4

Schematic of a heat pipe evacuated tube collector

Full size image

The solar energy absorbed by the plate, through both direct and diffuse radiation, is transferred to the heat-transfer fluid kept inside the heat pipe. Receiving heat, the fluid, e.g. methanol, evaporates and rises upward to the heat sink where it condenses again releasing heat to the flow-fluid, e.g. water. After condensing, the heat transfer fluid returns to the collector for receiving heat from the absorbed solar energy again. Thus it undergoes an evaporating—condensing cycle.

4.1 Efficiency of an ETC

The efficiency and useful energy gain of such a collector can be obtained using the same equations as used for FPC, i.e. Eqs. (8.3) and (8.4).

$$ \begin{aligned} \eta & = \frac{{Q_{u} }}{{Q_{T} }} = \frac{{Q_{u} }}{{GA_{c} }} \\ Q_{u} & = A_{c} \left[ {G_{S} - U_{L} \left( {T_{c} - T_{a} } \right)} \right] \\ \end{aligned} $$

Also from Eq. (8.5), we know, GS = G(τα)eff. For evacuated tube collectors, the overall incidence angle modifier Kτα is equal to the product of incidence angle modifier in transverse plane Kt and that in longitudinal plane Kl,

$$ K_{\tau \alpha } = K_{t} .K_{l} = \frac{{(\tau \alpha )_{eff} }}{{(\tau \alpha )_{n} }} $$

In order to determine the efficiency and useful energy gain, it is important to know the thermal model of an ETC, which is shown in Fig. 8.5. The energy absorbed by the plate is first transmitted to the heat-transfer fluid (e.g., methanol) placed inside the heat pipe, which transfers it to the manifold fluid (e.g., water). This causes the rise of the temperature of the manifold fluid.

Fig. 8.5
figure 5

Thermal model of a typical ETC

Full size image

Now, the steady state heat transfer rate from plate to heat transfer fluid can be represented by,

$$ Q_{c - h} = h_{e} A_{C} (T_{c} - T_{h} ) $$
(8.18)

where Th represents the mean temperature of the heat-transfer fluid, and he is the heat transfer coefficient. This heat transfer rate Qc–h is essentially the same as the useful energy gain Qu, i.e. Qc–h = Qu. Eliminating Tc and from Eqs. (8.4), (8.5) and (8.18), we can write,

$$ Q_{c - h} = \frac{{h_{e} /U_{L} }}{{h_{e} /U_{L} + 1}}A_{C} [G(\tau \alpha )_{eff} - U_{L} (T_{h} - T_{a} )] $$
(8.19)

The steady state energy transfer from the heat-transfer fluid to the manifold fluid can be expressed by,

$$ Q_{h - m} = h_{h - m} A_{h - m} \left( {T_{h} - T_{f} } \right) $$
(8.20)

where, hh–m represents the heat transfer coefficient for this heat flow, Ah–m is the area of the heat pipe in contact with the manifold fluid and Tf is the mean temperature of the working fluid.

Again, since Qc–h = Qh–m, eliminating Th from Eqs. (8.19) and (8.20) we can write,

$$ \begin{aligned} Q_{h - m} & = \frac{{A_{C} }}{{(U_{L} A_{C} /h_{h - m} A_{h - m} ) + (U_{L} /h_{e} + 1)}}[G(\tau \alpha )_{eff} - U_{L} (T_{f} - T_{a} )] \\ & \Rightarrow Q_{h - m} = F_{r} A_{C} [G(\tau \alpha )_{eff} - U_{L} (T_{f} - T_{a} )] \\ \end{aligned} $$
(8.21)

where

$$ F_{r} = \frac{1}{{(U_{L} A_{C} /h_{h - m} A_{h - m} ) + (U_{L} /h_{e} + 1)}} $$
(8.22)

Fr is known as the heat removal factor and can be defined as the ratio of the actual amount of heat transferred to the manifold fluid to the heat that would be transferred if the entire collector were at the fluid inlet temperature. From Eq. (8.22), it can be said that the value of Fr is dependent on three ratios, UL/he, UL/hh–m and Ah–m/Ac.

Since Qh–m = Qu, from Eqs. (8.3) and (8.21), collector efficiency can be written as,

$$ \eta = F_{r} (\tau \alpha )_{eff} - F_{r} U_{L} \frac{{(T_{f} - T_{a} )}}{G} $$
(8.23)

Thus the steady state efficiency of an ETC has a linear form; however, in real applications, it may not be linear and may be difficult to obtain solving all the parameters. To overcome this shortcoming, Cooper and Dunkle (1981) proposed a second order efficiency equation with the assumption,

$$ F_{r} U_{L} = a + b(T_{f} - T_{a} ) $$
(8.24)

Substituting Eq. (8.24) into the Eq. (8.23), we obtain,

$$ \eta = \underbrace {{F_{r} (\tau \alpha )_{eff} }}_{{\eta_{0} }} - a\frac{{\left( {T_{f} - T_{a} } \right)}}{G} - b\frac{{\left( {T_{f} - T_{a} } \right)^{2} }}{G} $$
(8.25)

where η0, a and b are constants and are usually furnished by the collector manufacturer. The mean manifold fluid temperature Tf can be considered as an average of the fluid temperatures at the inlet (Ti) and at the outlet (T0), i.e.,

$$ T_{f} = \frac{{T_{i} + T_{0} }}{2} $$

and thus the efficiency can be calculated from,

$$ \eta = \eta_{0} - a\frac{{\left( {T_{f} - T_{a} } \right)}}{G} - b\frac{{\left( {T_{f} - T_{a} } \right)^{2} }}{G} $$
(8.26)

It needs mentioning that the efficiency of an FPC can be expressed by the same equation as Eq. (8.26) shown above.

4.2 Dynamic Modelling of an ETC

In an evacuated tube collector, there are two fluids, heat transfer fluid or refrigerant and manifold fluid (water is considered in the current modelling). The current model is based on the assumption that there is no refrigerant present in the ETC, rather, water is assumed to flow directly through the heat pipes. The major assumptions are summarized below,

  • There is no presence of refrigerant. Water flows directly through the heat pipes.

  • The flow of water is only in the positive x direction.

  • The heat conduction in the fluid moving direction is neglected.

  • The temperature dependence of thermo-physical properties of water is considered.

  • Properties of glass and absorber do not depend on temperature and are assumed to be constant.

  • The infrared emissivity of the sky is unity (εsky = 1).

Based on the stated assumptions, the heat influx to various components of an ETC is depicted in Fig. 8.6. As shown in the figure, the model (Praene et al. 2005) consists of 3 thermal nodes. These are, the transparent glass cover, the absorber plate and the fluid (water) having temperatures Tg, Tc and Tf, respectively. The heat transfer between the sky and the glass cover is by radiation only. Again, since the absorber plate is surrounded by the vacuum, heat transfer between the glass cover and absorber plate, is entirely by radiation. Convective heat transfer is existent between the glass cover and the ambient environment, and between the absorber plate and water.

Fig. 8.6
figure 6

Assumed model of ETC

Full size image

Now, the governing equation that explains the time dependence of the temperature of the glass cover is,

$$ \begin{aligned} Cp_{g} \delta_{g} \rho_{g} \frac{{dT_{g} }}{dt} & = \varepsilon_{g} \sigma (T_{sky}^{4} - T_{g}^{4} ) + h_{g,a} (T_{a} - T_{g} ) \\ & \quad + \frac{{\varepsilon_{c} \varepsilon_{g} }}{{\varepsilon_{c} + \varepsilon_{g} - \varepsilon_{c} \varepsilon_{g} }}\sigma (T_{c}^{4} - T_{g}^{4} ) \\ \end{aligned} $$
(8.27)

where subscripts g, a, c and sky stand for glass cover, ambient, absorber plate and the sky, respectively. Cp represents the specific heat capacity, T is the temperature in K; δ stands for the thickness, and ρ represents the density. Using Swinbank’s formula (Swinbank 1963) \( T_{sky} = pT_{a}^{1.5} \) where p = 0.0552 K−1/2, the sky temperature can be obtained from the ambient temperature.

Now, for the absorber plate, the governing equation can be expressed as,

$$ Cp_{c} \delta_{c} \rho_{c} \frac{{dT_{c} }}{dt} = G(\tau \alpha ) + \frac{{\varepsilon_{c} \varepsilon_{g} }}{{\varepsilon_{c} + \varepsilon_{g} - \varepsilon_{c} \varepsilon_{g} }}\sigma (T_{g}^{4} - T_{c}^{4} ) + h_{f,c} (T_{f} - T_{c} ) $$
(8.28)

where subscript f stands for fluid (water). The plate receives radiative heat from the glass cover and transfers it to the working fluid predominantly in convective mode.

Finally, the temperature of the fluid, having a velocity of u along the positive x axis, depends on time and its position in the flow channel. The governing equation to describe the change in fluid temperature with time and position is,

$$ Cp_{f} \rho_{f} \frac{{\pi d_{in}^{2} }}{4}\left( {\frac{{dT_{f} }}{dt} + u\frac{{dT_{f} }}{dx}} \right) = \pi d_{in} h_{f,c} (T_{c} - T_{f} ) $$
(8.29)

where din represents the diameter of the absorber tube that contains the fluid.

Thus Eqs. (8.27)–(8.29) are the governing dynamic equations to determine the temperatures of the glass cover, absorber plate and working fluid (with both time and position) respectively.

5 Modelling of an Adsorption Chiller

The major components of a two-bed adsorption chiller are evaporator, condenser and two adsorber beds. An adsorber bed is necessarily a heat exchanger, filled with the adsorbent material, e.g., silica gel, packed between the fins of that finned tube heat exchanger. Adsorption and desorption are exothermic and endothermic processes, respectively. To extract the heat of adsorption, it is necessary to circulate cooling water through the tubes of the adsorber bed during the adsorption process. Furthermore, during this process, the bed is connected to the evaporator in order to receive the adsorbate vapor, e.g., water vapor, to be adsorbed by the adsorbent. Consequently, the other bed goes through the desorption process and is connected to the condenser. The hot water, flowing through its tubes, provide the necessary heat required for desorption.

Thus an adsorption chiller works in a cyclic manner. Each cycle consists of three operating modes (a) adsorption/desorption, (b) mass recovery and (c) heat recovery. This section will state the lumped analytical simulation model equations of an adsorption chiller that uses silica gel as the adsorbent and water as the adsorbate. The model is based on the following assumptions,

  • The porous properties of the adsorbent are constant.

  • The kinetics parameters, i.e. the diffusivity and activation energy, are independent of temperature and pressure.

  • At the first time step of any phase, the model does not consider the water flow condition within the bed in the previous time step.

  • The isotherm and kinetics equations for adsorption and desorption are same.

5.1 Description of Operating Modes

5.1.1 Mode (a): Adsorption/Desorption

In the operating mode (a) (see Fig. 8.7), Bed 1 goes through the desorption phase, and adsorption is taking place in Bed 2. Bed 1 is heated up by the hot water streams, which also raises the pressure of Bed 1.

Fig. 8.7
figure 7

Schematic of an adsorption chiller. Mode (a): Bed 1 goes through desorption and Bed 2 goes through adsorption

Full size image

The connecting valve between Bed 1 and condenser is open at this stage, and the desorbed vapor is then condensed in the condenser and returned back to the evaporator through an expansion valve. The other bed (Bed 2) is connected to the evaporator to adsorb the evaporated vapor, and this evaporation produces the desired cooling effect. The cooling water exiting from Bed 2 flows through the condenser to condense the desorbed vapor. The heated cooling water is usually cooled by a cooling tower.

5.1.2 Mode (b): Mass Recovery

At the end of ad/de-sorption, pressure in Bed 1 becomes higher than that in Bed 2. In the mass recovery mode (see Fig. 8.8), the bypass valve between the two beds is opened which causes flow of water vapor from hot Bed 1 to comparatively cooler Bed 2 by means of pressure swing. The mass recovery time is adjusted to attain the mechanical equilibrium between the two beds, while the excess time is not recommended.

Fig. 8.8
figure 8

Schematic of an adsorption chiller. Mode (b): Mass recovery. Water vapor flows from Bed 1 to Bed 2 due to the difference in pressure

Full size image

5.1.3 Mode (c): Heat Recovery

Due to the flow of hot and cooling water through Bed 1 and Bed 2, respectively, the temperature of Bed 1 becomes higher than that of Bed 2.

In the heat recovery mode (see Fig. 8.9) the cooling water first flows through Bed 1, extracting heat from the bed the water releases it to Bed 2. This causes an increase and reduction of temperatures of Bed 2 and Bed 1, respectively. Thus heat recovery reduces the total amount of heat required, which ultimately increases the system’s coefficient of performance (COP).

Fig. 8.9
figure 9

Schematic of an adsorption chiller. Mode (c): Heat recovery. Cooling water extracts heat from Bed 1 and releases it to Bed 2 before flowing through the condenser

Full size image

Thus one cycle is complete and in the next stage, the cycle is repeated, and the beds perform an alternating role. Bed 1 starts adsorbing and is connected to the evaporator and Bed 2 starts desorbing and gets connected to the condenser. The pressure of Bed 1 becomes essentially the same as that of evaporator and Bed 2 attains the same pressure as of condenser. Hence in the mass recovery mode, the desorbed vapor of Bed 2 is further passed to Bed 1 in order to achieve the mechanical equilibrium between the two beds. The heat is extracted from the hot Bed 2 by the cooling water and released to comparatively cooler Bed 1, during the heat recovery mode.

5.2 Model Equations for the Adsorbent—Adsorbate Pair

Prior to modelling different components (beds, evaporator, condenser) of an adsorption chiller, it is required to define the models of two most important parameters of an adsorbent—adsorbate pair; these are isotherm and kinetics.

5.2.1 Isotherm Model

Adsorption isotherm defines the maximum amount of adsorbate that can be adsorbed by the adsorbent at a particular pressure. The values of isotherm parameters are determined by correlating the experimental data of equilibrium uptake with the model. For silica gel—water pair, S-B-K model (Saha et al. 1995) can be used to determine the equilibrium adsorption uptake,

$$ w* = A\left( {T_{ads} } \right)\left[ {\frac{{P_{sat} \left( {T_{ref} } \right)}}{{P_{sat} \left( {T_{ads} } \right)}}} \right]^{{B\left( {T_{ads} } \right)}} $$
(8.30)

where,

$$ \begin{aligned} A\left( {T_{ads} } \right) & = A_{0} + A_{1} T_{ads} + A_{2} T_{ads}^{2} + A_{3} T_{ads}^{3} \\ B\left( {T_{ads} } \right) & = B_{0} + B_{1} T_{ads} + B_{2} T_{ads}^{2} + B_{3} T_{ads}^{3} . \\ \end{aligned} $$

Tads and Tref are the adsorption temperature and saturation temperature, respectively, and Psat is the saturation pressure. The values of the parameters A0, A1, A2, A3, B0, B1, B2, B3 are determined by fitting the model with experimental uptake data.

5.2.2 Kinetics Model

Adsorption kinetics can be defined as the rate of adsorption, which essentially determines the cycle time of the adsorption chiller. The faster the kinetics, the smaller the cycle time required, hence the greater the specific cooling produced. The most widely used kinetics models are linear driving force (LDF) model, Fickian diffusion (FD) model, Langmuir model, semi-infinite model etc. Some models are also proposed by implementing suitable modifications of the above mentioned models. In the current modelling of the adsorption chiller LDF model is utilized to simulate the adsorption kinetics, which assumes that the adsorption rate is proportional to the difference between the equilibrium uptake (w*) and the instantaneous uptake (w),

$$ \frac{dw}{dt} = k_{s} a_{v} \left[ {w* - w(t)} \right] $$
(8.31)

where ksav is the overall mass transfer coefficient. Due to the spherical shape of silica gel adsorbent, the overall mass transfer coefficient can be written as,

$$ k_{s} a_{v} = \frac{{15D_{s} }}{{R_{p}^{2} }}, $$

where Ds is the diffusion time constant, and Rp is the adsorbent particle radius. Ds depends on the temperature T, following equation,

$$ D_{s} = D_{so} \exp \left( {\frac{{ - E_{a} }}{RT}} \right) $$

where Dso is the pre-exponential constant, Ea is the activation energy, and R is the universal gas constant. The values of Dso and Ea can be obtained from the experimental data by plotting lnDs against \( 1/T \) as described by the equation stated below,

$$ \ln D_{s} - \ln D_{so} = \left( {\frac{{ - E_{a} }}{RT}} \right) $$

This plot is known as the Arrhenius plot. The slop yields \( - E_{a} /R \) and the intercept provides the constant, Dso. Hence, for an adsorption chiller comprising silica gel—water pair, Eq. (8.31) can be rewritten as,

$$ \frac{dw}{dt} = \frac{{15D_{so} }}{{R_{p}^{2} }}\left\{ {\exp \left( {\frac{{ - E_{a} }}{RT}} \right)} \right\}\left( {w* - w} \right) $$
(8.32)

5.3 Model Equations of the Chiller

The energy balance equations of different components (beds, evaporator, condenser) can be generalized as follows,

$$ \left[ {MC_{p} } \right]_{H.Ex} \frac{{dT_{k} }}{dt} = M_{bed} h_{ads} \frac{dw}{dt} + \left[ {\dot{m}C_{p} \left( {T_{in} - T_{out} } \right)} \right]_{H.Ex.fluid} $$
(8.33)

where M is the mass, Cp is specific heat capacity, Mbed is the mass of adsorbent used, and hads is the isosteric heat of adsorption/desorption. k indicates various components of adsorption chiller, i.e., adsorbing/desorbing bed, evaporator and condenser. Subscripts H.Ex and H.Ex.fluid stand for heat exchanger and heat transfer fluid respectively; in and out represent inlet and outlet respectively. The left-hand side of Eq. (8.33) represents the rate of change of enthalpy of the particular heat exchanger component (adsorbing/desorbing bed, evaporator, condenser). The first term on the right-hand side indicates the amount of heat released or absorbed by the adsorbent during the process of adsorption or desorption. And the last term indicates the sensible heat transfer between the heat transfer fluid and the respective component.

The solution of Eq. (8.33) provides the temperature Tk of the heat exchanger components. But that requires the outlet temperature Tout to be known. In order to determine Tout, the log mean temperature difference (LMTD) of the energy balance equation for heat transfer fluid is employed. According to that method, the amount of heat transfer,

$$ \dot{Q} = UA\Delta T_{\ln } $$
(8.34)

where U and A are the overall heat transfer coefficient and heat transfer surface area of the heat exchanging component respectively, and ∆Tln represents LMTD. Again \( \dot{Q} = \dot{m}C_{p} \left( {T_{out} - T_{in} } \right) \) gives,

$$ \Delta T_{\ln } = \frac{{\dot{m}C_{p} \left( {T_{out} - T_{in} } \right)}}{UA} $$
(8.35)

But ∆Tln is defined by the equation,

$$ \Delta T_{\ln } = \frac{{\left( {T - T_{in} } \right) - \left( {T - T_{out} } \right)}}{{\ln \left( {\frac{{T - T_{in} }}{{T - T_{out} }}} \right)}} $$
(8.36)

Hence, from Eqs. (8.35) and (8.36), we can determine Tout, as given in the equation below,

$$ T_{out} = T - \left[ {\left( {T - T_{in} } \right)\exp \left( { - \frac{UA}{{\dot{m}C_{p} }}} \right)} \right] $$
(8.37)

Substituting Tout into Eq. (8.33), it can be written as,

$$ \left[ {MC_{p} } \right]_{H.Ex} \frac{{dT_{k} }}{dt} = M_{bed} h_{ads} \frac{dw}{dt} + \left[ {\dot{m}C_{p} \left( {T_{in} - T_{k} } \right)\left\{ {1 - \exp \left( { - \frac{UA}{{\dot{m}C_{p} }}} \right)} \right\}} \right]_{H.Ex.fluid} $$
(8.38)

Thus, Eq. (8.38) is the energy balance equation, which is valid for all the heat exchanger components of the chiller.

5.3.1 Modelling of Adsorber/Desorber Bed

An adsorber/desorber bed comprises several modules where each module is necessarily a finned tube heat exchanger, and the adsorbents are packed between the fins. The mass of adsorbent loaded in each bed depends on the cooling capacity of the chiller. Figure 8.10 represents a typical module of a finned-tube heat exchanger.

Fig. 8.10
figure 10

A module of a finned-tube heat exchanger

Full size image

Let us consider a bed containing Nm number of modules. Length of each module is Lm, and each module contains Nt a number of tubes having outside and inside diameters Dm,o and Dm,i respectively. If the tube material density is denoted by ρt, the total mass of the tubes can be determined by,

$$ M_{t} = \frac{\pi }{4}\left( {D_{m,o}^{2} - D_{m,i}^{2} } \right)L_{m} N_{t} \rho_{t} $$
(8.39)

If Lf, Hf and Wf are the fin’s length, height and width respectively, the fin surface area that is in contact with the adsorbent can be calculated from,

$$ A_{f} = L_{f} H_{f} - \frac{\pi }{4}D_{m,o}^{2} N_{t} $$
(8.40)

If there are Nf number of fins in each module and the density of the fin material is ρf, the total mass of the fins can be expressed by,

$$ M_{f} = A_{f} W_{f} \rho_{f} N_{f} $$
(8.41)

Now, let us assume Cp,t, Cp,f and Cp,s are the specific heat capacities of tube material, fin material and silica gel. If Mbed is the amount of adsorbent used in each bed, we can write,

$$ \left[ {MC_{p} } \right]_{bed} = \left( {M_{t} C_{p,t} + M_{f} C_{p,f} } \right)N_{m} + M_{bed} C_{s} $$
(8.42)

The adsorbent bed goes through adsorption, desorption, mass recovery and heat recovery phases. Hence the model equations for each phase is narrated in the following sub-sections.

5.3.1.1 Bed Equations During Adsorption-Desorption

Let us assume, at a certain point of time, Bed 1 is at the desorption phase, and Bed 2 is at adsorption phase. The desorber bed, i.e., Bed 1, is then connected to the condenser. Hot water flows through the tubes of the heat exchanger, providing the necessary heat for the process of desorption. The hot water outlet temperature depends on the rate of heat transfer between the tubes and the adsorbent bed. For the desorber bed, Eq. (8.38) can be written as,

$$ \begin{aligned} \left[ {MC_{p} } \right]_{bed,des} \frac{{dT_{bed,des} }}{dt} & = M_{bed} h_{ads} \left( {\frac{dw}{dt}} \right)_{des} \\ & \quad + \dot{m}_{hot} C_{p,hot} (T_{in,hot} - T_{bed,des} )\left\{ {1 - \exp \left( { - \frac{{\left( {UA} \right)_{bed} }}{{\dot{m}_{hot} C_{p,hot} }}} \right)} \right\} \\ \end{aligned} $$
(8.43)

where, Tbed,des is the temperature of the desorbing bed, \( \dot{m}_{hot} \) and Cp,hot are the flow rate and specific heat capacity of hot water. \( \left( {\frac{dw}{dt}} \right)_{des} \) is the rate of desorption and can be calculated using Eq. (8.32). The equilibrium uptake w* at any time step can be determined using Eq. (8.30). It needs mentioning that in the case of a desorber bed, Psat(Tref) is essentially the condenser pressure and Psat(Tads) corresponds to the saturation pressure of water at the bed temperature. \( \left[ {MC_{p} } \right]_{bed,des} \) can be obtained from,

$$ \left[ {MC_{p} } \right]_{bed,des} = \left[ {MC_{p} } \right]_{bed} + wM_{bed} C_{p,des} $$

where, Cp,des is the specific heat capacity of water vapor at the desorber bed temperature. Tin,hot is the inlet temperature of hot water, and the hot water outlet temperature can be determined from,

$$ T_{out,hot} = T_{bed,des} - \left[ {\left( {T_{bed,des} - T_{in,hot} } \right)\exp \left( { - \frac{{\left( {UA} \right)_{bed} }}{{\dot{m}_{hot} C_{p,hot} }}} \right)} \right] $$
(8.44)

Similar to desorber bed, the model equation for adsorber bed, i.e., for Bed 2, can be written as,

$$ \begin{aligned} \left[ {MC_{p} } \right]_{bed,ads} \frac{{dT_{bed,ads} }}{dt} & = M_{bed} h_{ads} \left( {\frac{dw}{dt}} \right)_{ads} \\ & \quad + \dot{m}_{cool} C_{p,cool} \left( {T_{in,cool} - T_{bed,ads} } \right)\left\{ {1 - \exp \left( { - \frac{{\left( {UA} \right)_{bed} }}{{\dot{m}_{cool} C_{p,cool} }}} \right)} \right\} \\ \end{aligned} $$
(8.45)

where subscripts ads and cool represent adsorption and cooling water, respectively. The outlet temperature of cooling water can be calculated from,

$$ T_{out,cool} = T_{bed,ads} - \left[ {\left( {T_{bed,ads} - T_{in,cool} } \right)\exp \left( { - \frac{{\left( {UA} \right)_{bed} }}{{\dot{m}_{cool} C_{p,cool} }}} \right)} \right] $$
(8.46)

Since the adsorber bed is connected to the evaporator, the equilibrium uptake w* is a function of evaporator pressure and saturation pressure of water at the bed temperature.

5.3.1.2 Bed Equations During Mass Recovery

In the mass recovery stage, there is no water flow through any of the bed, as can be seen in Fig. 8.8. Hence the outlet temperatures of hot and cooling water will remain the same as their inlet temperatures. The beds are also isolated from the evaporator and condenser. At the end of the ad/de-sorption phase, the pressure at Bed 1 becomes higher than that at Bed 2. The opening of the by-pass valve in the mass recovery stage initiates the flow of excess vapor from Bed 1 to Bed 2 due to pressure swing, and the process is usually continued (accomplished by appropriate determination of cycle time) until the mechanical equilibrium between the two beds is attained. The flow rate of vapor, from Bed 1 to Bed 2, during this stage can be determined from Thu et al. (2017),

$$ \frac{dw}{dt} = 1.41576YA_{bp} \sqrt {\frac{{\Delta P\rho }}{K}} $$
(8.47)

where Y is the expansion factor (Shashi Menon 2015), Abp is the cross-section area of the bypass valve, ∆P is the pressure difference between the two beds and K is the total resistance coefficient. It needs mentioning that the reversed vapor flow due to pressure changes is also accounted for in the above model. K can be calculated from,

$$ K = f\frac{L}{D} + \sum\limits_{i} {\xi_{i} } $$

where ξ is the minor loss coefficient for different components, L and D are the length and width of the bypass valve, respectively. f is the friction factor given as,

$$ f = \left\{ {\begin{array}{*{20}l} {\frac{64}{\text{Re}}\,for\,\text{Re} < 2300} \hfill \\ {\frac{1.325}{{\left[ {\ln \left( {\frac{e}{3.7D} + \frac{5.74}{{\text{Re}^{0.9} }}} \right)} \right]^{2} }}\,for\,5000 \le \text{Re} \le 10^{8} \& 10^{ - 6} \le \frac{e}{D} \le 10^{ - 2} } \hfill \\ \end{array} } \right. $$

The energy balance equations for mass recovery can be written as follows;

for Bed 1,

$$ \left[ {MC_{p} } \right]_{bed,des} \frac{{dT_{bed,des} }}{dt} = - M_{bed} h_{ads} \frac{dw}{dt} $$
(8.48)

and for Bed 2,

$$ \left[ {MC_{p} } \right]_{bed,ads} \frac{{dT_{bed,ads} }}{dt} = M_{bed} h_{ads} \frac{dw}{dt} $$
(8.49)
5.3.1.3 Bed Equations During Heat Recovery

In the heat recovery stage, the beds are isolated from evaporator, condenser and also from each other. As a result, there is no flow of water vapor through the beds. The temperature of hot water at the outlet remains the same as it is at the inlet since there is no flow of hot water through the bed (see Fig. 8.9). The cooling water extracts heat from the desorbed bed (Bed 1) and heats up the adsorbed bed (Bed 2) on its way to the condenser. The cooling water outlet temperature from Bed 1 can be written as,

$$ T_{out,des} = T_{bed,des} - \left[ {\left( {T_{bed,des} - T_{in,cool} } \right)\exp \left( { - \frac{{\left( {UA} \right)_{bed} }}{{\dot{m}_{cool} C_{p,cool} }}} \right)} \right] $$
(8.50)

And the cooling water outlet temperature from Bed 2 can be calculated from,

$$ T_{out,ads} = T_{bed,ads} - \left[ {\left( {T_{bed,ads} - T_{out,des} } \right)\exp \left( { - \frac{{\left( {UA} \right)_{bed} }}{{\dot{m}_{cool} C_{p,cool} }}} \right)} \right] $$
(8.51)

The energy balance equations for the two beds can be expressed by;

for Bed 1,

$$ \left[ {MC_{p} } \right]_{bed,des} \frac{{dT_{bed,des} }}{dt} = \dot{m}_{cool} C_{p,cool} \left( {T_{in,cool} - T_{bed,des} } \right)\left\{ {1 - \exp \left( { - \frac{{\left( {UA} \right)_{bed} }}{{\dot{m}_{cool} C_{p,cool} }}} \right)} \right\} $$
(8.52)

for Bed 2,

$$ \left[ {MC_{p} } \right]_{bed,ads} \frac{{dT_{bed,ads} }}{dt} = \dot{m}_{cool} C_{p,cool} \left( {T_{bed,des} - T_{bed,ads} } \right)\left\{ {1 - \exp \left( { - \frac{{\left( {UA} \right)_{bed} }}{{\dot{m}_{cool} C_{p,cool} }}} \right)} \right\} $$
(8.53)

5.3.2 Modelling of the Evaporator

An evaporator is usually a shell and tube type heat exchanger comprising a series of tubes. Chilled water flows through the tubes while the refrigerant vapor evaporates from the shell side. During the ad/de-sorption phase, the evaporator is connected to the adsorber bed, and the evaporated vapor gets adsorbed by the adsorbent. Let us assume, the evaporator has Nt,evap number of tubes and mass, length and inside diameter of each tube are Mt,evap, Lt,evap, and De,i respectively. Hence, at any instant, the amount of chilled water present within the tubes of the evaporator is,

$$ M_{ch,evap} = \frac{\pi }{4}D_{e,i}^{2} L_{t,evap} N_{t,evap} \rho_{ch} $$
(8.54)

where ρch is the density of chilled water. \( \left[ {MC_{p} } \right]_{bed,des} \) can be calculated from,

$$ \left[ {MC_{p} } \right]_{evap} = M_{ch,evap} C_{p,ch} + M_{t,evap} N_{t,evap} C_{p,t,evap} $$
(8.55)

where, Cp,ch and Cp,t,evap are the specific heat capacities of chilled water and evaporator tube material respectively.

Let hfg,evap be the latent heat of evaporation of water at the evaporation temperature. The energy balance equation for the evaporator during ad/de-sorption phase can be written as,

$$ \begin{aligned} \left[ {MC_{p} } \right]_{evap} \frac{{dT_{evap} }}{dt} & = - M_{bed} \left( {\frac{dw}{dt}} \right)_{ads} \left\{ {h_{fg,evap} + C_{p,ads} \left( {T_{bed,ads} - T_{evap} } \right)} \right\} \\ & \quad + \dot{m}_{ch} C_{p,ch} \left( {T_{in,ch} - T_{evap} } \right)\left\{ {1 - \exp \left( { - \frac{{\left( {UA} \right)_{evap} }}{{\dot{m}_{ch} C_{p,ch} }}} \right)} \right\} \\ \end{aligned} $$
(8.56)

where subscript ch stands for chilled water. UA value of the evaporator, i.e., (UA)evap, is determined to utilize the LMTD method, as mentioned in Sect. 5.3.

The chilled water outlet temperature is determined from,

$$ T_{out,ch} = T_{evap} - \left[ {\left( {T_{evap} - T_{in,ch} } \right)\exp \left( { - \frac{{\left( {UA} \right)_{evap} }}{{\dot{m}_{ch} C_{p,ch} }}} \right)} \right] $$
(8.57)

During mass and heat recovery stages, the evaporator is isolated from the beds. Hence, the temperature of the evaporator and chilled water remain unchanged at these stages.

5.3.3 Modelling of the Condenser

Cooling water flows through the tubes of the condenser condensing the desorbed vapor that comes from the desorber bed. Similar to evaporator modelling, let us assume, the condenser has Nt,cond number of tubes and mass, length and inside diameter of each tube are Mt,cond, Lt,cond, and Dc,i respectively. Then for condenser, Eqs. (8.54) and (8.55) can be written as,

$$ M_{cool,cond} = \frac{\pi }{4}D_{c,i}^{2} L_{t,cond} N_{t,cond} \rho_{cool} $$
(8.58)

and,

$$ \left[ {MC_{p} } \right]_{cond} = M_{cool,cond} C_{p,cool} + M_{t,cond} N_{t,cond} C_{p,t,cond} $$
(8.59)

where subscripts cool and cond represent cooling water and condenser, respectively. During the ad/de-sorption stage, the cooling water from the outlet of Bed 1 enters the condenser. Hence, the energy balance equation can be written as,

$$ \begin{aligned} \left[ {MC_{p} } \right]_{cond} \frac{{dT_{cond} }}{dt} & = - M_{bed} \left( {\frac{dw}{dt}} \right)_{des} \left\{ {h_{fg,cond} + C_{p,des} \left( {T_{bed,des} - T_{cond} } \right)} \right\} \\ & \quad + \dot{m}_{cool} C_{p,cool} \left( {T_{out,cool} - T_{cond} } \right)\left\{ {1 - \exp \left( { - \frac{{\left( {UA} \right)_{cond} }}{{\dot{m}_{cool} C_{p,cool} }}} \right)} \right\} \\ \end{aligned} $$
(8.60)

The water temperature at the outlet of the condenser can be expressed as,

$$ T_{out,cond} = T_{cond} - \left[ {\left( {T_{cond} - T_{out,cool} } \right)\exp \left( { - \frac{{\left( {UA} \right)_{cond} }}{{\dot{m}_{cool} C_{p,cool} }}} \right)} \right] $$
(8.61)

In the mass recovery stage, the condenser is not connected to any bed. Thus, the temperatures of the condenser and cooling water don’t change at this stage.

During the heat recovery stage, the condenser is isolated from the beds and water from Bed 1 first flows through Bed 2, before entering the condenser. Thus the energy balance for this stage can be modeled as,

$$ \left[ {MC_{p} } \right]_{cond} \frac{{dT_{cond} }}{dt} = \dot{m}_{cool} C_{p,cool} \left( {T_{out,ads} - T_{cond} } \right)\left\{ {1 - \exp \left( { - \frac{{\left( {UA} \right)_{cond} }}{{\dot{m}_{cool} C_{p,cool} }}} \right)} \right\} $$
(8.62)

The water temperature at the outlet of condenser is,

$$ T_{out,cond} = T_{cond} - \left[ {\left( {T_{cond} - T_{out,ads} } \right)\exp \left( { - \frac{{\left( {UA} \right)_{cond} }}{{\dot{m}_{cool} C_{p,cool} }}} \right)} \right] $$
(8.63)

5.3.4 Performance Parameters

An adsorption chiller is usually specified by its cooling capacity and coefficient of performance (COP). The cooling capacity can be defined as the amount of cooling effect that an adsorption chiller is able to produce. For a chiller having a cycle time of tcycle, the cooling capacity can be defined by,

$$ Q_{c} = \frac{{\int_{0}^{{t_{cycle} }} {\dot{m}_{ch} C_{p,ch} \left( {T_{in,ch} - T_{out,ch} } \right)} dt}}{{t_{cycle} }} $$
(8.64)

The rate of heat input to drive an adsorption chiller can be expressed by,

$$ Q_{h} = \frac{{\int_{0}^{{t_{cycle} }} {\dot{m}_{hot} C_{p,hot} \left( {T_{in,hot} - T_{out,hot} } \right)} dt}}{{t_{cycle} }} $$
(8.65)

The COP of the chiller is defined by the ratio of useful cooling capacity produced to the heat input to the chiller. Mathematically it can be shown as,

$$ COP = \frac{{Q_{c} }}{{Q_{h} - Q_{rec} }} $$
(8.66)

where Qrec is the rate of heat recovered during the heat recovery stage.

5.4 Typical Simulation Results

In this subsection, simulation results of a typical 10-ton capacity adsorption chiller are shown. Let us consider the inlet temperatures of the cold water, hot water and chilled water are 27, 80 and 13 °C respectively and their flow rates are 10, 15 and 6 m3/h respectively. These values are assumed to be constant throughout the operation of the chiller. However, they may not be such a uniform in real-life application. The chiller uses silica gel as the adsorbent and water as the refrigerant. The isotherm parameters of the S-B-K model are furnished in Table 8.1 (Rezk and Al-Dadah 2012). The isosteric heat of ad/de-sorption for the pair is found to be, hads = 2.8 × 104 J/kg.

Table 8.1 Isotherm properties of the silica gel—water pair
Full size table

The particle radius of the silica gel adsorbent is considered as Rp = 0.17 mm. The adsorption rate is determined using the LDF model and the values of its kinetics parameters (Saha et al. 1995) are Dso = 2.54 × 10−4 m2/s and Ea = 4.2 × 104 J/mol. The assumed specifications of different components of the chiller are shown in Table 8.2.

Table 8.2 Specifications of different components of the adsorption chiller
Full size table

In the current simulation, the time required for the ad/de-sorption, mass recovery and heat recovery are considered as 300 s, 20 s and 10 s, respectively. The typical simulation results are shown in Figs. 8.11, 8.12 and 8.13. The average cooling capacity of the chiller is found to be 10.03 RTon with a COP of 0.51.

Fig. 8.11
figure 11

Typical simulation results showing the variation of temperature with time of different components of an adsorption chiller

Full size image
Fig. 8.12
figure 12

Simulation results showing the temperature of beds and uptakes at different stages of operation of an adsorption chiller

Full size image
Fig. 8.13
figure 13

The instantaneous cooling capacity of the chiller

Full size image

Figure 8.11 shows the variation of temperature of different components of the chiller obtained from the simulation results. The experimental data can be obtained from the test results of commercial adsorption chiller and can be utilized to validate the model. The variation of temperature and uptake of the beds is depicted in Fig. 8.12. As expected, the bed temperature increases during desorption and decreases during adsorption. The instantaneous cooling capacity at different stages of cycle time can be seen in Fig. 8.13. It needs mentioning that in determining the average cooling capacity and COP, the simulation result of the first cycle is ignored. It is done as the initial results are strongly influenced by the values used for initialization, and the model requires a few time steps to stabilize.

6 Conclusion

Flat plate collectors have widely been used for domestic water heating. On the other hand, the evacuated tube collector is the cheapest and most preferred option for boiler water preheating. In this chapter, the model equations of these two types of collectors are presented. Furthermore, a commercial adsorption chiller is modelled, and the simulation results of the model are presented. The design parameters of the chiller may be varied to observe their effects on its performance. The model can be utilized to predict the performance of the chiller under variable operating conditions. It can also play a vital role in designing different components of the chiller to make the system more efficient and cost effective.