Keywords

PACS

1 Introduction

Today, the works carried on the solutions of mathematical models are of an outstanding area among scientists because solitons provides more information into the relevant from nonlinear sciences to engineering applications [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54]. The first soliton model proposed by Korteweg and de Vries was KdV equation in 1895. Afterwards, Zabusky and Kruskal have presented an important paper on the interaction of “solitons” in a collisionless plasma in 1965 [26]. More recently, many scientific and engineering applications including vital real world problems on solitons have been presented to the literature. Bogoyavlenskii has presented some important models, which are entirely integrable solitons and N-solitons [27]. He has derived the connection with the Kadomtsev–Petviashvili equation with the help of the Painlevé method. One of the most important properties of integrable models is that these models produce many soliton solutions. Therefore, many experts have focused on the investigations of solitons arising in real world problems. Moreover, they have changed general structures of models for getting more and clear understanding of the models. This plays a major role in solitary waves theory and soliton theory. In this sense, Wazwaz has investigated the negative-order breaking soliton equations by using simplified Hirota’s method [28]. Fei and Cao have observed explicit soliton-cnoidal wave interaction solutions for the (2+1)-dimensional negative-order breaking soliton equation (NOBSE) [29] defined as

$$\begin{aligned} u_{t}-v_{x}=0, \quad \, u_{y}+v_{xxx}-4uv_{x}-2u_{x}v=0. \end{aligned}$$
(1.1)

This model was used to symbolize the (2+1)-dimensional interaction of the Riemann wave propagated along the y-axis with a long wave propagated along the x-axis [28,29,30,31,32]. Fei et al. [29] have derived the explicit soliton-cnoidal wave interaction solutions to the Eq. (1.1) by using an analytic method. The paper is organized as follows. In Sect. 2, we present the Improved bernoulli sub-equation function method (IBSEFM) in a comprehensive manner. Section 3 is devoted to obtain new complex travelling wave soliton solutions to the NOBSE. A conclusion and discussion is given in the last section.

2 General Properties of IBSEFM

The general properties of IBSEFM are given as follows:

Step 1. It can be considered that the following nonlinear model in two variables and a dependent variable \(v \);

$$\begin{aligned} \displaystyle P(u,u_{x},u_{y},u_{t},\ldots )=0. \end{aligned}$$
(2.1)

and take the wave transformation;

$$\begin{aligned} u(x,y,t)=U(\eta ),\eta =\mu (x+\alpha y-kt). \end{aligned}$$
(2.2)

where \(\mu , \alpha , k\) are constants and can be determined later. By substituting Eq. (2.2), Eq. (2.1) converts a nonlinear ordinary differential equation (NODE) as following;

$$\begin{aligned} N(U,U',U'',U''',\ldots )=0. \end{aligned}$$
(2.3)

Step 2. Considering trial equation of solution in Eq. (2.3), it can be written as following;

$$\begin{aligned} U(\eta )=\frac{\sum _{i=0}^{n}a_{i}F^{i}(\eta )}{\sum _{j=0}^{m}b_{i}F^{j}(\eta )}=\frac{a_{0}+a_{1}F(\eta )+a_{2}F^{2}(\eta )+\cdots +a_{n}F^{n}(\eta )}{b_{0}+b_{1}F(\eta )+b_{2}F^{2}(\eta )+\cdots +b_{m}F^{m}(\eta )}. \end{aligned}$$
(2.4)

According to the Bernoulli theory, we can consider the general form of Bernoulli differential equation for \(F'\) as following;

$$\begin{aligned} F'=wF+\lambda F^{M}, w \ne 0,\lambda \ne 0,\,M\in \mathbb {R}-\{0,1,2\}. \end{aligned}$$
(2.5)

where \(F=F(\eta )\) is Bernoulli differential polynomial. Substituting above relations in Eq. (2.3), it yields us an equation of polynomial \(\Omega (F)\) of F as following;

$$\begin{aligned} \Omega (F)=\rho _{s}F^{s}+\cdots +\rho _{1}F+\rho _{0}=0. \end{aligned}$$
(2.6)

According to the balance principle, we can determine the relationship between n, m and M.

Step 3. The coefficients of \(\Omega (F)\) all be zero will yield us an algebraic system of equations;

$$\begin{aligned} \rho _{i}=0,i=0,\ldots ,s. \end{aligned}$$
(2.7)

Solving this system, we will specify the values of \( a_{0},a_{1},\ldots ,a_{n} \) and \( b_{0},b_{1},\ldots ,b_{n}\).

Step 4. When we solve nonlinear Bernoulli differential equation Eq. (2.6), we obtain the following two situations according to b and d,

$$\begin{aligned} F(\eta )=\left[ \frac{-\lambda }{w}+\frac{E}{e^{w(M-1)\eta }}\right] ^{\frac{1}{1-M}}, w\ne \lambda . \end{aligned}$$
(2.8)
$$\begin{aligned} F(\eta )=\left[ \frac{(E-1)+(E+1)tanh(w(1-M)\frac{\eta }{2})}{1-tanh(w(1-M)\frac{\eta }{2})}\right] ,w=\lambda ,E\in \mathbb {R}. \end{aligned}$$
(2.9)

Using a complete discrimination system for polynomial of F, we solve this system with the help of computer programming and classify the exact solutions to Eq. (2.3).

3 Application of the IBSEFM

In this section, IBSEFM has been successfully considered to the NOBSE to obtain more and novel complex solutions.

Example

Taking the travelling wave transformation as

$$\begin{aligned} u(x,y,t)=U(\xi ), \xi = kx+wy-ct, \quad v(x,y,t)=V(\xi ), \xi = kx+wy-ct, \end{aligned}$$
(3.1)

which k, w, c are real constants and non-zero in Eq. (1.1), we get the following nonlinear ordinary differential equation;

$$\begin{aligned} wU'-ck^{2}U'''+6cUU'=0. \end{aligned}$$
(3.2)

with

$$\begin{aligned} V=\frac{-c}{k}U. \end{aligned}$$
(3.3)

Integrating once and getting to the zero of integration constants, Eq. (3.2) can be rewritten as

$$\begin{aligned} wU-ck^{2}U''+3cU^{2}=0. \end{aligned}$$
(3.4)

With the help of balance principle for \(U''\) and \(U^{2}\), relationship between M, m and n can be obtained as follows;

$$\begin{aligned} 2M+m=n+2. \end{aligned}$$
(3.5)

Case 1: Choosing \(M=3,n=5\) and \(m=1\), we can find and its derivatives from Eq. (3.5) as follows:

$$\begin{aligned} U=\frac{a_{0}+a_{1}F+a_{2}F^{2}+a_{3}F^{3}+a_{4}F^{4}+a_{5}F^{5}}{b_{0}+b_{1}F}=\frac{\Upsilon }{\Psi }, \end{aligned}$$
(3.6)
$$\begin{aligned} U'=\frac{\Upsilon '\Psi -\Upsilon \Psi '}{\Psi ^{2}}, \end{aligned}$$
(3.7)
$$\begin{aligned} U''=\ldots , \end{aligned}$$
(3.8)

where \(F'=pF+dF^{3}, a_{5}\ne 0,b_{1}\ne 0, p\ne 0, d\ne 0\). Substituting Eq. (3.6) with Eq. (3.8) into Eq. (3.4), a system of algebraic equations including various power of F can be found. Solving the system by using different computer programming such as Mathematica, Maple, and Matlap gives the complex structures;

Case-1a: For \(p\ne d\) the following coefficients;

$$\begin{aligned} \begin{aligned} a_{0}=\frac{-wb_{0}}{3c},a_{1}=\frac{-wb_{1}}{3c}&,a_{2}=\frac{i\sqrt{2}\sqrt{w}\sqrt{a_{4}}\sqrt{b_{0}}}{\sqrt{c}}, a_{3}=\frac{i\sqrt{2}\sqrt{w}\sqrt{a_{4}}b_{1}}{\sqrt{b_{0}}\sqrt{c}},a_{5}=\frac{b_{1}a_{4}}{b_{0}}, \\&p=\frac{i\sqrt{2}d\sqrt{w}\sqrt{b_{0}}}{\sqrt{a_{4}}\sqrt{c}},k=\frac{\sqrt{a_{4}}}{2\sqrt{2}d\sqrt{b_{0}}}, \end{aligned} \end{aligned}$$
(3.9)

we have the following new complex travelling wave solution

$$\begin{aligned} \begin{aligned} u_{1}= \frac{-w}{3c}+&4wa_{4}(i\sqrt{2}\sqrt{c}\sqrt{a_{4}}+2e^{\frac{i\sqrt{w}}{\sqrt{2}\sqrt{c}\sqrt{a_{4}}}(\sqrt{2}x\sqrt{a_{4}}+4d(ct-wy)\sqrt{b_{0}})}E\sqrt{b_{0}}\sqrt{w})^{-2}\\&+\frac{1}{\frac{c}{2w}-\frac{i\sqrt{c}E\sqrt{b_{0}}}{\sqrt{w}\sqrt{a_{4}}\sqrt{2}}e^{\frac{i\sqrt{w}}{\sqrt{2}\sqrt{c}\sqrt{a_{4}}}(\sqrt{2}x\sqrt{a_{4}}+4d(ct-wy)\sqrt{b_{0}})}}, \end{aligned} \end{aligned}$$
(3.10)
$$\begin{aligned} v_{1}=\frac{-2c\sqrt{2}d\sqrt{b_{0}}}{\sqrt{a_{4}}}u_{1}. \end{aligned}$$
(3.11)

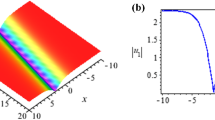
For better understanding of wave propagation meaning of via Eq. (3.10), and also, for suitable values of parameters, 2D and 3D figures along with contour graphs may be observed in Figs. 1, 2, 3 and 4.

Fig. 1
figure 1

The periodic wave surfaces of Eq. (3.10) for \(w=0.9\), \(c=0.2\), \(a_{4}=0.3\), \(b_{0}=0.5\), \(d=0.6\), \(E=0.1\), \(y=3\), \(-4<x<4\), \(-4<t<4\)

Full size image
Fig. 2
figure 2

The contour graphs of Eq. (3.10) for \(w=0.9\), \(c=0.2\), \(a_{4}=0.3\), \(b_{0}=0.5\), \(d=0.6\), \(E=0.1\), \(y=3\), \(-120<x<120\), \(-120<t<120\)

Full size image
Fig. 3
figure 3

The periodic wave surfaces of Eq. (3.10) for \(w=0.9\), \(c=0.2\), \(a_{4}=0.3\), \(b_{0}=0.5\), \(d=0.6\), \(E=0.1\), \(y=3,t=0.85\), \(-4<x<4\)

Full size image
Fig. 4
figure 4

The combination of contour graphs of both side of Eq. (3.10) for \(w=0.9\), \(c=0.2\), \(a_{4}=0.3\), \(b_{0}=0.5\), \(d=0.6\), \(E=0.1\), \(y=3\), \(-120<x<120\), \(-120<t<120\)

Full size image

Case-1b: When

$$\begin{aligned} \begin{aligned} a_{0}=\frac{-wb_{0}}{3c},&\; a_{1}=\frac{-wb_{1}}{3c},a_{2}=\frac{4idk\sqrt{w}\sqrt{b_{0}}}{\sqrt{c}}, a_{3}=\frac{4dki\sqrt{w}b_{1}}{\sqrt{c}}, \\&a_{4}=8d^{2}k^{2}b_{0},a_{5}=8d^{2}k^{2}b_{1},p=\frac{i\sqrt{w}}{2k\sqrt{c}}, \end{aligned} \end{aligned}$$
(3.12)

we have the following new complex bright soliton solution to the Eq. (1.1)

$$\begin{aligned} \begin{aligned}&u_{2}= \frac{8d^{2}k^{2}sech^{2}(\frac{-i\sqrt{w}}{k\sqrt{c}}f(x,y,t))}{(E+E\sqrt{1-sech^{2}(\frac{-i\sqrt{w}}{k\sqrt{c}}f(x,y,t))}+\frac{2idk\sqrt{c}}{\sqrt{w}}sech(\frac{-i\sqrt{w}}{k\sqrt{c}}f(x,y,t)))^{2}} \\&+\frac{4idk\sqrt{w}sech(\frac{-i\sqrt{w}}{k\sqrt{c}}f(x,y,t))}{(E\sqrt{c}+\sqrt{1-sech^{2}(\frac{-i\sqrt{w}}{k\sqrt{c}}f(x,y,t))}E\sqrt{c}+\frac{2icdk}{\sqrt{w}}sech(\frac{-i\sqrt{w}}{k\sqrt{c}}f(x,y,t)))}-\frac{w}{3c}, \\&v_{2}=\frac{-c}{k}u_{2} \end{aligned} \end{aligned}$$
(3.13)

in which \(f(x,y,t)=kx+wy-ct\). With a view to the deeper investigation of complex travelling wave structure of Eq. (3.13) along with suitable values of parameters, 2D and 3D figures along with contour graphs may be seen in Figs. 5, 6, 7 and 8.

Fig. 5
figure 5

The 3D graphs of Eq. (3.13) for \(w=0.9\), \(c=0.2\), \(d=0.3\), \(k=0.5\), \(E=0.1\), \(y=3\), \(-6<x<6\), \(-6<t<6\)

Full size image
Fig. 6
figure 6

The contour graphs of Eq. (3.13) for \(w=0.9\), \(c=0.2\), \(d=0.3\), \(k=0.5\), \(E=0.1\), \(y=3\), \(-120<x<120\), \(-120<t<120\)

Full size image
Fig. 7
figure 7

The periodic wave surfaces of Eq. (3.13) for \(w=0.9\), \(c=0.2\), \(d=0.3\), \(k=0.5\), \(E=0.1\), \(y=3\), \(t=0.85\), \(-6<x<6\)

Full size image
Fig. 8
figure 8

The combination of contour graphs of both side of Eq. (3.13) for \(w=0.9\), \(c=0.2\), \(d=0.3\), \(k=0.5\), \(E=0.1\), \(y=3\), \(-120<x<120\), \(-120<t<120\)

Full size image

Case-1c: Once we consider as

$$\begin{aligned} \begin{aligned} b_{0}=&\frac{-3ca_{0}}{w},a_{1}=\frac{-wb_{1}}{3c},a_{2}=\frac{-3ca_{0}a_{3}}{wb_{1}}, a_{4}=\frac{3c^{2}a_{0}a^{2}_{3}}{2w^{2}b^{2}_{1}}, \\&a_{5}=\frac{-ca^{2}_{3}}{2wb_{1}},p=\frac{i\sqrt{w}}{2k\sqrt{c}},d=\frac{-i\sqrt{c}a_{3}}{4k\sqrt{w}b_{1}}, \end{aligned} \end{aligned}$$
(3.14)

we have the following new complex dark soliton solution to the Eq. (1.1);

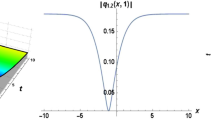
$$\begin{aligned} \begin{aligned}&u_{3}= \frac{a_{3}\sqrt{-1+tanh(-if(x,y,t))}}{\frac{c}{2w}a_{3}\sqrt{-1+tanh(-if(x,y,t))}+Eb_{1}\sqrt{-1-tanh(-if(x,y,t))}}\\&-\frac{ca^{2}_{3}(-1+tanh(\frac{-i\sqrt{w}}{k\sqrt{c}}(kx+wy-ct)))}{2w(\frac{ca_{3}}{2w}\sqrt{-1+tanh(-if(x,y,t))}+Eb_{1}\sqrt{-1-tanh(-if(x,y,t))})^{2}}-\frac{w}{3c}, \\&v_{3}=\frac{-c}{k}u_{3}, \end{aligned} \end{aligned}$$
(3.15)

in which \(f(x,y,t)=\frac{\sqrt{w}}{k\sqrt{c}}(kx+wy-ct)\). For suitable values of parameters, 2D and 3D figures along with contour graphs of Eq. (3.15) may be observed in Figs. 9, 10, 11, 12 and 13.

Fig. 9
figure 9

The 3D graphs of Eq. (3.15) for \(w=0.9\), \(c=0.2\), \(a_{3}=0.3\), \(k=-0.5\), \(b_{1}=-0.6\), \(E=0.1\), \(y=3\), \(-6<x<6\), \(-6<t<6\)

Full size image
Fig. 10
figure 10

The contour graphs of Eq. (3.15) for \(w=0.9\), \(c=0.2\), \(a_{3}=0.3\), \(k=-0.5\), \(b_{1}=-0.6\), \(E=0.1\), \(y=3\), \(-120<x<120\), \(-120<t<120\)

Full size image
Fig. 11
figure 11

The periodic wave surfaces of Eq. (3.15) for \(w=0.9\), \(c=0.2\), \(a_{3}=0.3\), \(k=-0.5\), \(b_{1}=-0.6\), \(E=0.1\), \(y=3\), \(t=0.85\), \(-6<x<6\)

Full size image
Fig. 12
figure 12

The combination of contour graphs of both side of Eq. (3.15) for \(w=0.9\), \(c=0.2\), \(a_{3}=0.3\), \(k=-0.5\), \(b_{1}=-0.6\), \(E=0.1\), \(y=3\), \(-120<x<120\), \(-120<t<120\)

Full size image
Fig. 13
figure 13

Periodic wave surfaces of combination of real and imaginary part of Eq. (3.15) for \(w=0.9\), \(c=0.2\), \(a_{3}=0.3\), \(k=-0.5\), \(b_{1}=-0.6\), \(E=0.1\), \(y=3\), \(-120<x<120\), \(-120<t<120\)

Full size image

4 Conclusion

In this manuscript, the complex dark and bright soliton solutions to the Eq. (1.1) have been obtained by using IBSEFM. It has been observed that all solutions found in this paper have been satisfied the Eq. (1.1) considered. With the suitable values for parameters, based on the physical meanings and properties of model taken, and also, for better understanding of the physical meanings of the dark and bright soliton solutions, the three- and two-dimensional graphs and contour simulations have been plotted with the help of several computer programs. The solitons of wave propagations can be observed from 3D Figs. 1, 5 and 9 along with 2D Figs. 3, 7 and 11. Moreover, high points of the mixed dark and bright soliton solutions, being Eqs. (3.10), (3.13) and (3.15), can be seen from contour surfaces of Figs. 2, 6 and 10, as an alternative and new perspective to the 3D graph. Combinations of contour graphs of real and imaginary parts of mixed dark and bright soliton solutions can be also viewed from Figs. 4, 8 and 12. Furthermore, more reality surfaces of solitons can be observed from Fig. 13 being combination of 2D graphs of real and imaginary parts of mixed dark and bright soliton solutions of Eq. (3.15). After all simulations, it can be understood that complex mixed dark and bright soliton solutions have shown the expected physical properties. Comparing some paper existing in literature [29], it can bee viewed that solutions of Eqs. (3.10), (3.13) and (3.15) are entirely new complex mixed dark and bright soliton solutions to the Eq. (1.1). To the best of our knowledge, the application of IBSEFM to the negative-order breaking soliton model with (2+1)-dimensional has been not submitted in advance.