Keywords

1 Introduction

Functional electrical stimulation (FES) is an important technique to restore movement in people with paralyzed limbs. However, a difficulty in the FES field is to identify the mathematical model parameters and consequently to perform a smooth control for the paralyzed limb movement and with the least muscular fatigue possible.

The system’s mathematical model to be controlled is fundamental to controllers design. Particularly in the FES, the dynamic relationship between the voltage or current applied in the muscle and joint position must be well understood. However, this process involves biomechanical interactions and several complex physiological phenomena, which are dynamic, non-linear and uncertains.

Ferrrarin and Pedotti [1] presented experimental results of a second order nonlinear model to represent the dynamics lower limb movement, from electrically stimulated quadriceps. One limitation of this model is not to consider the muscular delay in the relation between active torque and pulse width.

Another important study was by Previdi [2], who used NARX models through polynomial structures and with neural networks to describe the nonlinear relationship between quadriceps stimuli with knee joint movement, both in isometric and isotonic conditions. A practical limitation of this technique was to perform the identification in offline mode (simulation) without experimental results with controllers.

Schauer et al. [3] proposed an online approach to identify the parameters. The dynamics of the muscle was represented by a product between nonlinear activation dynamics and a nonlinear static contraction function, described by a neural network. In addition, an extended Kalman filter was implemented to estimate model parameters. By varying the parameter of muscle strength (in simulation mode), the obtained results showed robustness in position control for closed loop response. Although the proposed technique is valid, obviously the implementation of this technique is a challenge for embedded systems.

Teixeira et al. [4] showed that the nonlinear dynamics of the knee joint movement as a result of the electric stimulation applied to the quadriceps can be represented by the Takagi-Sugeno fuzzy model. A practical limitation of this approach is to monitor the torque variation in real time.

Most models consider position, velocity, and muscle torque variables as variables. However, obtaining the corresponding torque variation is a difficult process for experimental validation.

To overcome this problem, Sanches [5] proposed a novel model, where position, velocity and angular acceleration are considered as state variables. The state variables proposed in [5] are easily measurable.

We present for the first time in the literature an experimental protocol to obtain the polytopic uncertainties of the dynamic model of lower limbs using the Sanches model. The results obtained in this work contribute significantly to the approach of robust controllers design using the technique of linear matrix inequalities (LMI). The obtained results consider a uncertainty polytope with four vertices for tests in situations of non-fatigue, forced recruitment and fatigue around a desired angle of the knee joint.

2 Modeling of the Lower Limb with Polytopic Uncertainties

In a system that presents parametric uncertainties, these uncertainties can be restricted by a convex linear combination belonging to the set described as polytope.

2.1 State-Space Model

Sanches [5] in his study proposed a state-space model modification to facilitate practical implementation with accelerometers. Using elegant deduction, the torque state variable was replaced by acceleration. Further details of this technique can be found in [5].

Thus, the movement of the knee joint due to electrical stimulation applied in the quadriceps can be represented in state space as follows:

$$ \left[ {\begin{array}{*{20}c} {{{\dot{\text{x}}}}_{{1{\text{N}}}} } \\ {{{\dot{\text{x}}}}_{{2{\text{N}}}} } \\ {{{\dot{\text{x}}}}_{{3{\text{N}}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ 0 & 0 & 1 \\ {\frac{{{\tilde{\text{f}}}_{{21}} \left( {{\text{x}}_{1} } \right)}}{{\uptau }}} & {{\text{z}}\left( {{\text{x}}_{1} } \right) - \frac{{\text{B}}}{{{\uptau }{\text{J}}}}} & { - \frac{{\text{B}}}{{\text{J}}} - \frac{1}{{\uptau }}} \\ \end{array} } \right]~\left[ {\begin{array}{*{20}c} {{\text{x}}_{{1{\text{N}}}} } \\ {{\text{x}}_{{2{\text{N}}}} } \\ {{\text{x}}_{{3{\text{N}}}} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\frac{{\text{G}}}{{{\uptau }{\text{J}}}}} \\ \end{array} } \right]{\text{P}}_{{{\text{N}}~}} , $$
(1)

where \( {\text{x}}_{{1{\text{N}}}} \left( {\text{t}} \right) \) is the angular position of the knee joint, \( {\text{x}}_{{2\text{N}}} \left( {\text{t}} \right) \) is the angular velocity, \( {\text{x}}_{{3{\text{N}}}} \left( {\text{t}} \right) \) is the angular acceleration, B is the viscous friction coefficient, J is the moment of inertia, G and τ are parameters that express the first-order relation of the torque as a function of the pulse width \( {\text{P}}_{\text{N}} \) of the electric stimulus. The function \( {\tilde{\text{f}}}_{21} \left( {{\text{x}}_{1} } \right) \) is a non-linearity of the system which can be described by:

$$ {\tilde{\text{f}}}_{21} \left( {{\text{x}}_{1} } \right) = \frac{1}{{{\text{Jx}}_{1} }}\left[ { - {\text{mglsin}}\left( {{\text{x}}_{1} +\uptheta_{{{\text{v}}0}} } \right) -\uplambda{\text{e}}^{{ - {\text{E}}\left( {{\text{x}}_{1} +\uptheta_{{{\text{v}}0}} + \frac{\uppi}{2}} \right)}} \left( {{\text{x}}_{1} +\uptheta_{{{\text{v}}0}} + \frac{\uppi}{2} -\upomega} \right) + {\text{M}}_{{{\text{a}}0}} } \right], $$
(2)

where m is the mass of the foot-leg complex; g is the gravitational acceleration; l is the distance between the knee and the center of the mass of the foot-leg complex; \( \theta_{v0} \) is the angle of the shank, that is, the angulation formed between the shank and the vertical direction in the sagittal plane; λ and E are coefficients of the exponential term; ω the elastic resting angle of the knee; \( {\text{M}}_{{{\text{a}}0}} \) the active torque produced by the electrical stimulation at the desired operating point, given by:

$$ {\text{M}}_{{{\text{a}}0}} = {\text{mglsin}}\left( {{\text{x}}_{1} +\uptheta_{{{\text{v}}0}} } \right)\uplambda{\text{e}}^{{ - {\text{E}}\left( {\uptheta_{{{\text{v}}0}} + \frac{\uppi}{2}} \right)}} \left( {{\text{x}}_{1} +\uptheta_{{{\text{v}}0}} + \frac{\uppi}{2} -\upomega} \right), $$
(3)

and

$$ {\text{z}}\left( {{\text{x}}_{1} } \right) = \left( {\frac{{\partial {\tilde{\text{f}}}_{21} \left( {{\text{x}}_{1} } \right)}}{{\partial {\text{x}}_{1} }}} \right){\text{x}}_{1} + {\tilde{\text{f}}}_{21} \left( {{\text{x}}_{1} } \right). $$
(4)

The system control input \( {\text{P}}_{\text{N}} \) at the equilibrium point is given by:

$$ {\text{P}}_{\text{N}} = {\text{P}} - {\text{P}}_{0} , $$
(5)

where P is the pulse width in µsec, and \( {\text{P}}_{0} = \frac{{{\text{M}}_{{{\text{a}}0}} }}{\text{G}} \).

For convenience, we rewrite the expression (1) as follows:

$$ \left[ {\begin{array}{*{20}c} {{\dot{\text{x}}}_{{1{\text{N}}}} } \\ {{\dot{\text{x}}}_{{2{\text{N}}}} } \\ {{\dot{\text{x}}}_{{3{\text{N}}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\\upalpha \\ \end{array} \begin{array}{*{20}c} { 1 } \\ { 0} \\\upbeta \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\\upgamma \\ \end{array} } \right] \left[ {\begin{array}{*{20}c} {{\text{x}}_{{1{\text{N}}}} } \\ {{\text{x}}_{{2{\text{N}}}} } \\ {{\text{x}}_{{3{\text{N}}}} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ 0 \\\Psi \\ \end{array} } \right]{\text{P}}_{\text{N}} , $$
(6)

With the position and pulse width data, the transfer function was estimated for third-order system without delay. With the input and output data, the transfer function of the model was identified. Therefore the linearized system is identified.

$$ {\text{H}}\left( {\text{s}} \right) = \frac{\Psi }{{{\text{s}}^{3} - {\text{s}}^{2}\upgamma - {\text{s}}\upbeta -\upalpha}}. $$
(7)

The parameters were identified from the step-type signal. These parameters correspond to a third order uncertain linear model whose state variables are angular position, angular velocity and acceleration.

In this paper, we adopt the uncertainties in a polytope composed of four vertices. Thus, it is the controllable, linear and time-invariant system described by:

$$ {\dot{\text{x}}}\left( {\text{t}} \right) = {\text{A}}\left(\upalpha \right){\text{x}}\left( {\text{t}} \right) + {\text{B}}\left(\upalpha \right){\text{u}}\left( {\text{t}} \right), $$
(8)

being \( {\text{A}}\left(\upalpha \right) \in {\mathbb{R}}^{\text{nxn}} \) the state matrix, \( {\text{B}}\left(\upalpha \right) \in {\mathbb{R}}^{\text{nxm}} \) the input matrix, \( {\text{x}} \in {\mathbb{R}}^{\text{n}} \) the state vector, \( {\text{u}}\left( {\text{t}} \right) \in {\mathbb{R}}^{\text{m}} \) the input control.

The system (8) can be described as a convex combination of the polytope vertices, with parameters belonging to the unitary simplex :

$$ {\mathfrak{U}} \triangleq \left\{ {\left( {{\text{A}},{\text{B}}} \right)\left(\upalpha \right){:}\sum\limits_{{{\text{i}} = 1}}^{\text{n}} {\upalpha_{\text{i}} \left( {{\text{A}},{\text{B}}} \right)_{\text{i}} } ; \sum\limits_{{{\text{i}} = 1}}^{\text{n}} {\upalpha_{\text{i}} = 1} ;\upalpha_{\text{i}} \ge 0;{\text{i}} = 1, 2, \ldots ,{\text{n }}} \right\}. $$
(9)

in which n represents the vertices.

It is noticed that the system is described as a convex combination of the vertices, which consists in a convex region that delimits all possible parameters variations within maximum and minimum ranges.

3 Protocol for Parameters Identification

3.1 Subject

The present study was authorized through a research ethics committee involving human beings (CAAE: 79219317.2.1001.5402) in the São Paulo State University (UNESP), Ilha Solteira campus. An able-bodied male subject, 26 years old, participated in the study.

3.2 Test Platform

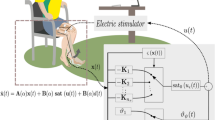
Experiments were performed on a test platform shown in Fig. 1. Figure 2 shows the identifications made in the volunteer. The platform is composed of a chair instrumented by an electrogoniometer (Lynx®), gyroscope LPR510AL (ST Microelectronics®), two triaxial accelerometers MMA7341 (Freescale®), a NI myRIO controller (National Instruments®), a current-based neuromuscular electrical stimulator (more details can be found in [5]), and an user interface developed in the LabVIEW Student Edition.

Fig. 1
figure 1

Instrumentated chair for neuromuscular electrical stimulation tests, present at the laboratory of instrumentation and biomedical engineering—UNESP, FEIS

Full size image
Fig. 2
figure 2

Identification curves of the non-fatigued (solid line), forced recruitment (dotted line), and fatigued trials (dashed line)

Full size image

The stimulation intensity is controlled by setting the pulse amplitude to the quadriceps and controlling the pulse width. The stimulus frequency were fixed in 50 Hz. In a preliminary test, pulse amplitude was determined at about 70 mA. The muscular electrostimulator delivers rectangular, biphasic, symmetrical pulse to the individual’s muscle, and allows an adjustment of the pulse width in a range of 0–400 μs.

3.3 Experimental Setup

Before applying the stimuli to the quadriceps, a muscle analysis determines the motor point for proper positioning of the surface electrodes. Then, scraping and cleansing procedures are performed at the motor point. The electrodes used are rectangular self-adhesive size 50 × 90 mm.

As a measure of safety and comfort, a stop button deactivates the stimulation pulses. The chair backrest and the knee joint position are adjustable for each volunteer.

After the motor-point identification, open-loop experimental tests are performed. The open-loop test consists of applying a stepping-type signal corresponding to a constant pulse width \( {\text{P}}_{0} \). The test duration is about four seconds. Thereafter, approximately 2-min time interval is timed for muscle rest. After the rest period, the step-type test is applied again for four seconds.

The pulse width, position, velocity and angular acceleration data are automatically recorded at the end of the step-type signal.

At each test the measured angular position should be the closest to the desired position. It is observed, however, that as the stimulation is applied the error between the measured angular position and the desired angular position becomes greater. After a large number of tests, the error becomes very large. Our hypothesis is that the muscle fibers recruited locally by the surface electrodes are saturated which leads to the fatigue state. The criterion used to determine the saturation condition of the fibers was defined by the evaluation of the error obtained between the desired and measured position. The initials trials have a small error, so we called non-fatigued situation. After ten trials, a 1 kg weight was added to the volunteer’s leg to induce fatigue. Consequently, ten step-type tests were performed, which in the so-called forced recruitment. After these tests, we observed a fatigue situation in the muscles. Finally, the weight was removed and muscular behavior was evaluated again for step-type signals. In these trials the obtained results were referred as fatigued situation. Therefore, a total of thirty experimental run were conducted, being ten for each test.

4 Results and Discussion

The data obtained in the thirty tests are shown in Fig. 2, considering results for non-fatigued, forced-recruitment, and fatigued trials.

The position, velocity and acceleration data were obtained from the application of the step-type signal in a period of 4 s. The recording of the data was initially performed 20 ms before the application of the step-type signal.

The model identification was based on output (position) and input data (pulse width) considering a sampling rate of 0.02 s, and the entire procedure was performed in open-loop.

A 10th-order moving average digital filter was applied to attenuate noisy signals of the accelerometer. The identification parameter corresponding to the know uncertainties in the plant were obtained are detailed in Table 1.

Table 1 Uncertain parameters of the model
Full size table

The vertices of the polytope are:

$$ \begin{aligned} A_{1} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{min} } \\ \end{array} \begin{array}{*{20}c} 1 \\ { 0} \\ { \beta_{min} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{min} } \\ \end{array} } \right]; B_{1} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{min} } \\ \end{array} } \right];\quad A_{2} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{min} } \\ \end{array} \begin{array}{*{20}c} 1 \\ 0 \\ {\beta_{min} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{min} } \\ \end{array} } \right]; B_{2} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{max} } \\ \end{array} } \right]; \\ A_{3} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{min} } \\ \end{array} \begin{array}{*{20}c} 1 \\ 0 \\ {\beta_{min} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{max} } \\ \end{array} } \right]; B_{3} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{min} } \\ \end{array} } \right];\quad A_{4} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{min} } \\ \end{array} \begin{array}{*{20}c} 1 \\ 0 \\ {\beta_{min} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{max} } \\ \end{array} } \right]; B_{4} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{max} } \\ \end{array} } \right]; \\ A_{5} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{min} } \\ \end{array} \begin{array}{*{20}c} 1 \\ 0 \\ {\beta_{max} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{min} } \\ \end{array} } \right]; B_{5} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{min} } \\ \end{array} } \right];\quad A_{6} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{min} } \\ \end{array} \begin{array}{*{20}c} 1 \\ { 0} \\ {\beta_{max} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{min} } \\ \end{array} } \right]; B_{6} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{max} } \\ \end{array} } \right]; \\ A_{7} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{min} } \\ \end{array} \begin{array}{*{20}c} 1 \\ 0 \\ {\beta_{max} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{max} } \\ \end{array} } \right]; B_{7} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{min} } \\ \end{array} } \right];\quad A_{8} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{min} } \\ \end{array} \begin{array}{*{20}c} 1 \\ 0 \\ {\beta_{max} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{max} } \\ \end{array} } \right]; B_{8} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{max} } \\ \end{array} } \right]; \\ A_{9} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{max} } \\ \end{array} \begin{array}{*{20}c} { 1 } \\ { 0} \\ { \beta_{min} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{min} } \\ \end{array} } \right]; B_{9} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{min} } \\ \end{array} } \right];\quad A_{10} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{max} } \\ \end{array} \begin{array}{*{20}c} 1 \\ 0 \\ {\beta_{min} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{min} } \\ \end{array} } \right]; B_{10} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{max} } \\ \end{array} } \right]; \\ A_{11} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{max} } \\ \end{array} \begin{array}{*{20}c} { 1 } \\ { 0} \\ { \beta_{min} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{max} } \\ \end{array} } \right]; B_{11} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{min} } \\ \end{array} } \right];\quad A_{12} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{max} } \\ \end{array} \begin{array}{*{20}c} 1 \\ 0 \\ {\beta_{min} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{max} } \\ \end{array} } \right]; B_{12} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{max} } \\ \end{array} } \right]; \\ A_{13} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{max} } \\ \end{array} \begin{array}{*{20}c} 1 \\ 0 \\ {\beta_{max} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{min} } \\ \end{array} } \right]; B_{13} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{min} } \\ \end{array} } \right];\quad A_{14} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{max} } \\ \end{array} \begin{array}{*{20}c} 1 \\ 0 \\ {\beta_{max} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{min} } \\ \end{array} } \right]; B_{14} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{max} } \\ \end{array} } \right]; \\ A_{15} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{max} } \\ \end{array} \begin{array}{*{20}c} 1 \\ 0 \\ {\beta_{max} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{max} } \\ \end{array} } \right]; B_{15} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{min} } \\ \end{array} } \right];\quad A_{16} & = \left[ {\begin{array}{*{20}c} 0 \\ {0 } \\ {\alpha_{max} } \\ \end{array} \begin{array}{*{20}c} 1 \\ 0 \\ {\beta_{max} } \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ {\gamma_{max} } \\ \end{array} } \right]; B_{16} & = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\Psi _{max} } \\ \end{array} } \right]; \\ \end{aligned} $$

Figure 3 shows the parameters behavior for each situation studied. The median of the parameters \( \alpha \), \( \beta \), \( \gamma \) tend to increase after the forced recruitment and fatigued test. On the other hand, the parameter \( \psi \) presents a decay behavior as the intensity of muscular effort increases. In the non-fatigued trials, a greater dispersion of the data was observed among all tests.

Fig. 3
figure 3

Comparison between model parameters given in (6) for the cases: non-fatigued, forced recruitment, and fatigued. On each box, the central mark is the median, the edges of the box are the 25th and 75th percentiles, the whiskers extend to the most extreme data points not considered outliers, and outliers are plotted individually

Full size image

The maximum and minimum parameters obtained by FES application in open-loop delimit the boundary for controller design. In the convex polytope approach, properties present in the vertices extend to all the points contained in the set itself, guaranteeing the controllability and robustness action of the controller designed for that region [6].

The polytopic matrix can be used by exploring its vertex, as an example is the application of the switched controller designed to operate around a desired point of operation.

Another interesting factor is that the non-repeatability in time-domain of the angular position can be mapped to a parametric analysis corresponding to the system model. Thus, the different external situations that the electrically stimulated muscle was subjected externally is characterized by the variation of the \( \alpha \), \( \beta \), \( \gamma \), \( \psi \) values.

This identification technique that allows to obtain the vertices of the polytope can be used to design controllers for linear and non-linear plants.

Identification techniques such as the one being proposed in this work allows to know in detail the region to be controlled and the uncertainties present in the plant.

One limitation of this identification technique is the impossibility of mathematically identifying muscular stress when electrical stimuli are applied for an indeterminate time.

It is important to note that for each section the plant identification is made. Identification is performed for each volunteer, that is, each identification presents its own uncertainties, justifying the non-linearity in the plant. It is important to note that for each test section, the identification of the plant is carried out.

5 Conclusion

The identification tests carried out in a healthy volunteer demonstrated that the technique used allows a good strategy to perform polytopic uncertainties identification of the electrically stimulated lower limbs model. The bounded convex polytope is considered one of the most general forms of representation of parametric uncertainties. This identification technique enables robust control design with known plant uncertainties.

This study can be extended with a statistical significance analysis of the parameters for a large number of individuals.