1 Introduction

Every year, thousands of people around the world suffer from spinal cord injuries resulting from traffic accidents, acts of violence, or falls. A widely used method for motor rehabilitation is neuromuscular electrical stimulation, promoting the health and welfare of these individuals.

Current research efforts in this field are focused on enhancing the stimulation systems by improving the controllers used in the closed-loop system. Electrical stimulation can act under different purposes and application to the body. For example, in the case of lower limbs, functional electrical stimulation (FES) can be used for motor rehabilitation through knee joint control [1,2,3,4,5,6,7], standing up [8,9,10,11], sitting pivot transfer [12,13,14], walking [15,16,17,18,19,20,21,22], swimming [23, 24], rowing [25, 26], and cycling [27,28,29,30], among others. In the current state-of-the-art, even simple motor activities still present great challenges and arouse interest due to the therapeutic benefits derived from electrical stimulation [31].

In this sense, several studies have been recently proposed to regulate knee joint using techniques such as proportional-integral-derivative (PID) control [1, 32], neural networks [33, 34], fuzzy [3, 4, 35], predictive [5, 36], adaptive [7, 37], sliding-mode control [1, 38, 39], robust control [6, 7], switched control [6], among others. About the recent papers, a robust parallel distributed compensation (RPDC) was proposed by Covacic et al.  [35] considering norm-bounded uncertainties. However, it does not deal with uncertain nonlinear functions. Gaino et al.  [3] presented a PDC discretized by emulation around a single operating point. However, it has limitations for practical applications, and its design does not consider plant uncertainties. Teodoro et al.  [6] evaluated the performance of switched and robust controllers, for an uncertain linear model of electrical stimuli applied to the angular position control of a knee, which presents an uncertain term added to the control signal. Although these authors obtained interesting results, the technique is linear and does not consider the saturation and fault of the actuator. Kirsch et al.  [5] presented a predictive control model for knee extension aiming to minimize muscular fatigue. However, the performance of the predictive controller for steady-state regulation was not been satisfactory for a longer time. Finally, Gaino et al.  [4] proposed a PDC based on the TS fuzzy model that is capable of regulation at different operating points. However, it assumes ideal conditions in its simulations and does not consider the uncertainties of the plant and other practical aspects.

The major challenge addressed by this paper is the achievement of regulation in the presence of nonlinear behavior and/or uncertainties in the musculoskeletal complex. Another significant issue is the nonlinear effect of actuator saturation in the control design. Most authors do not consider the saturation effects. The absence of saturation effects in the control design impacts the performance results. The current trend in medical devices is miniaturization, wearability, and low energy consumption. Therefore, it is important to consider the system behavior when the actuator fails or experiences a decrease in power due to limitations in the power source.

This study contributes to the state-of-the-art by improving the steady-state regulation results by switched control, considering fatigue, spasms, tremor, muscular recruitment, and actuator fault as plant uncertainties in an operating region. Although the system has several nonlinearities and uncertainties, the proposed technique uses an exact TS fuzzy model, but does not depend on the membership functions, which are uncertain in this case.

To the best of our knowledge, this is the first study in which a switched controller subject to saturation using TS fuzzy models was used in electrical stimulation of lower limbs under nonideal conditions. The control design is based on linear matrix inequalities (LMIs) for a nonideal uncertain plant described by TS fuzzy model with inaccurate membership functions. In relation to the literature, the nondependence of uncertain membership functions is a differential of this study for electrical stimulation applications. For the first time, the robust switched control technique is proposed for electrical stimulation applications considering saturation and fault in the actuator. Moreover, severe intensity levels of fatigue, spasms, and tremor are presented. In addition, the results of other TS fuzzy control techniques are reproduced and evaluated. Finally, we compare our results with those obtained with other important techniques. The results indicate that the proposed switched control presents the lowest RMS error.

The rest of this paper is organized as follows. Sect. 2 presents the derivation of the torque-based nonlinear dynamic model for leg extension, using electrical stimulation, and the TS fuzzy modeling technique. Sect. 3 describes the switched control design subject to actuator saturation using LMIs conditions. Sect. 4 presents the simulation results that demonstrate the controller performance improvement when compared with PDC in dealing with actuator fault, muscle activation uncertainty, and nonidealities like fatigue, spasms, and tremor. Sect. 5 concludes this study.

1.1 Notations

For a matrix \(\mathbf {X}\), \(\mathbf {X}^{-1}\) and \(\mathbf {X}^{T}\) denote the inverse and the transpose of \(\mathbf {X}\), respectively. The symbol \(\otimes\) denotes the Kronecker product. The symbol \(\mathbf {sl}_{p,j} \in \mathbb {R}^{1 \times p}\) denotes a row vector whose j-th element is 1 and the others are equal to zero, and \(\overset{\rightleftharpoons }{p}=p2^{p-1}\), \(p \geqslant 1\). For a symmetric matrix, the symbol \(*\) denotes the symmetric blocks in relation to the main diagonal. The set \(\mathbb {I}_{k}=\left\{ 1, \; 2, \; \cdots , \; k \right\}\), \(k \in \mathbb {N}\). \(\left\| \breve{\varvec{v}} \right\| _{\infty } = \underset{i \in \mathbb {I}_{k}}{\max }|\breve{\varvec{v}}_{i}|\) is the infinity norm of the vector \(\breve{\varvec{v}}\). Let \(\text {co} \left\{ \varvec{\upnu }_{1}, \;\varvec{\upnu }_{2},\; \cdots \; , \varvec{\upnu }_{p}\right\}\) denote the convex hull of the vectors \({\varvec{\upnu }}_{i}\), that is, \({\varvec{\upnu }} \in {\text{co}}\{{\varvec{\upnu }}_{1}, {\varvec{\upnu }}_{2}, \cdots , {\varvec{\upnu }}_{p}\}\) if and only if \(\varvec{\upnu } =\sum _{i=1}^{p} \lambda _{i} {\varvec{\upnu }}_{i}\), \(\lambda _{i} \geqslant 0\) and \(\sum _{i=1}^{p} \lambda _{i} = 1\), \(\; i \in \mathbb {I}_{p}=\left\{ 1,\;2,\;\cdots ,p\right\}\). Besides that, \(\varsigma =\arg ^{*} \underset{i\in \mathbb {I}_{n_r}}{\min } \left\{ \mathbf {x_i} \right\}\) denotes the smallest index \(\varsigma \in \mathbb {I}_{n_r}\), such that, for the set \(\left\{ \mathbf {x}_1,\; \mathbf {x}_2,\; \cdots , \mathbf {x}_{n_r} \right\}\), \(\mathbf {x}_{\varsigma }=\underset{i \in \mathbb {I}_{n_r}}{\min }\left\{ \mathbf {x}_i\right\}\).

2 Nonlinear Dynamic Model for Leg Extension using Electrical Stimulation

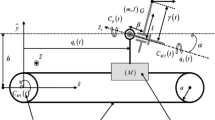
Consider the leg extension system using electrical stimulation with load cell added in the experimental apparatus, whose mathematical model is given by

$$\begin{aligned} J\ddot{\theta }=H_{g}(\theta )+\varLambda _{p}(\theta ,\dot{\theta })+\varGamma _{ke}(M_a); \end{aligned}$$
(1)

where \(\theta , \dot{\theta }, \ddot{\theta },\) and \(M_a \in \mathbb {R}\) are angular position, velocity, acceleration, and torque of the lower limb (shank-foot complex), respectively; \(J \in \mathbb {R}\) is the moment of inertia, and \(H_{g}(\theta )\) is the gravitational torque, which is given by

$$\begin{aligned} H_{g}(\theta )=-mgl\sin (\theta ), \end{aligned}$$

where m, and \(l \in \mathbb {R}\) are the mass and the distance between the knee and the shank-foot complex mass center, respectively, and g is the gravitational acceleration.

The passive musculoskeletal torque of the knee \(\varLambda _{p}(\theta ,\dot{\theta })\) is expressed as

$$\begin{aligned} \varLambda _p(\theta ,\dot{\theta })=-\lambda e^{-E_v\left( \theta +\frac{\pi }{2}\right) }\left( \theta +\frac{\pi }{2}-\omega \right) -B\dot{\theta }, \end{aligned}$$

where \(\lambda\) and \(E_v \in \mathbb {R}\) are the coefficients of the exponential terms related to knee stiffness, \(\omega \in \mathbb {R}\) is elastic rest angle of the knee, and \(B \in \mathbb {R}\) is the viscous friction coefficient [40].

Concerning the worst scenarios that can occur during electrically stimulated contractions, we incorporate nonidealities indicated in [39, 41]. The FES-induced muscle contraction produces muscular torque \(\varGamma _{ke}(M_a)\), which is expressed as

$$\begin{aligned} \varGamma _{ke}(M_a)=\left( 1+\kappa _{sp}+\kappa _{tr}\right) \kappa _{fat} M_a = \kappa _{stf}M_a \text {,} \end{aligned}$$

where \(\kappa _{sp},\;\kappa _{tr}\), and \(\kappa _{fat} \in \mathbb {R}\) are related to spasms, tremor, and fatigue, respectively. Three levels of spasms, tremor, and fatigue were taken into account, that is, mild, moderate, and severe. The criterion adopted for the classification of tremor waveforms and muscle spasm was chosen considering its importance in functional movement. For example, the occurrence of spikes in the angular position of the knee referring to spasms is classified as (i) mild, for amplitudes less than \(10^{\circ }\); (ii) moderate, for amplitudes between \(10^{\circ }\) and \(20^{\circ }\); and (iii) severe, for amplitudes greater than \(20^{\circ }\). Oscillations in the knee position are due to tremors and are classified as: (i) mild, those that modify knee dynamics in amplitude less than \(7.5^{\circ }\); (ii) moderate, for amplitude less than \(15^{\circ }\); and (iii) severe, for amplitude greater than \(15^{\circ }\). The fatigue severity rating was established in such a way that (i) \(\kappa _{fat}=1\) indicates the absence of fatigue; (ii) \(0< \kappa _{fat} < 1\) corresponds to partially fatigued muscle; and (iii) \(\kappa _{fat}=0\) suggests completely fatigued muscle.

Muscle activation \(M_a\) can be modeled by a first-order system as follows:

$$\begin{aligned} \frac{M_a}{\check{u}_{f}}=\frac{\hat{G}}{\tau s+1} \;\;\;\; \Longleftrightarrow \;\;\;\; \dot{M}_a=\frac{1}{\tau }\left( -M_a+\hat{G}\check{u}_{f}\right) \text {,} \end{aligned}$$

where \(\check{u}_{f} \in \mathbb {R}\) is the current amplitude of the electrical stimulation, \(\tau \in \mathbb {R}\) is time constant of muscle activation, and \(\hat{G} \in \mathbb {R}\) is an uncertain parameter [40].

Furthermore, a possible actuator fault is also considered in this paper. The actuator fault is a power loss from the stimulator power supply. In the model, this is represented by \(\check{u}_{f}\left( t\right) =\kappa _{flt}\check{u}(t)\), which may correspond to the following operating conditions of the actuator: (i) \(\kappa _{flt}=1\) implies that the actuator has no fault; (ii) \(0< \kappa _{flt} < 1\) implies that there is a partial fault in the actuator; and (iii) \(\kappa _{flt}=0\) represents a complete fault in the actuator.

Defining the state variables \(\check{x}_1=\theta\), \(\check{x}_2=\dot{\theta }\), and \(\check{x}_3=M_a\). Then, (1) can be written as follows:

$$\begin{aligned} \left\{ \begin{array}{rl} \dot{\check{x}}_1 =&{} \check{x}_2\\ \dot{\check{x}}_2 =&{} \frac{1}{J}[-mgl\sin (\check{x}_1)-\lambda e^{-E_v\left( \check{x}_1+\frac{\pi }{2}\right) }\left( \check{x}_1+\frac{\pi }{2}-\omega \right) \\ &{} \qquad \qquad \qquad \qquad \qquad \qquad \qquad -B\check{x}_2+\kappa _{stf}\check{x}_3]\\ \dot{\check{x}}_3 =&{} -\frac{1}{\tau }\check{x}_3+\frac{\kappa _{flt}\hat{G}}{\tau }\check{u}\text {.} \end{array} \right. \end{aligned}$$
(2)

The goal is to maintain the leg angle in a desired position \(\check{x}_1=\theta =\theta ^{d}\). Considering that the equilibrium point of the system (2) is \(\check{{x}}_e=[\check{x}_1 \quad \check{x}_2 \quad \check{x}_3]^{T}=[\theta ^d \quad 0 \quad M^{d}_{a}]^{T}\); therefore \(\dot{\check{x}}_1=0\), \(\dot{\check{x}}_2=0\), \(\dot{\check{x}}_3=0\), and \(\check{u}=\check{u}^d\). From (2) it follows that

$$\begin{aligned} \begin{aligned} 0=&\frac{1}{J}\left[ -mgl\sin (\theta ^{d})-\lambda e^{-E_v\left( \theta ^{d}+\frac{\pi }{2}\right) }\left( \theta ^{d}+\frac{\pi }{2}-\omega \right) \right. \\&\qquad \qquad \qquad \left. +\kappa _{stf}M^{d}_{a}\right] \text {,}\\ M^{d}_{a}=&\frac{mgl\sin (\theta ^{d})+\lambda e^{-E_v\left( \theta ^{d}+\frac{\pi }{2}\right) }\left( \theta ^{d}+\frac{\pi }{2}-\omega \right) }{\kappa _{stf}}. \end{aligned} \end{aligned}$$

Moreover, define \(\check{u}^{d}_{f}=k_{flt} \check{u}^{d}\), from (2) one can also obtain

$$\begin{aligned} 0&=-\frac{1}{\tau }M^{d}_{a}+\frac{\hat{G}}{\tau }\check{u}^{d}_f,\nonumber \\ \check{u}^{d}&=\frac{\check{u}^{d}_{f}}{k_{flt}}=\frac{M^{d}_{a}}{\kappa _{flt}\hat{G}}\text {,}\nonumber \\&=\frac{mgl\sin (\theta ^{d})+\lambda e^{-E_v\left( \theta ^{d}+\frac{\pi }{2}\right) }\left( \theta ^{d}+\frac{\pi }{2}-\omega \right) }{\kappa _{stf}\kappa _{flt}\hat{G}}. \end{aligned}$$
(3)

In addition, note that the equilibrium point is not the origin \([\check{x}_1 \quad \check{x}_2 \quad \check{x}_3]^{T}=[0 \quad 0 \quad 0]^{T}\). Thus, for stability analysis, it is necessary to modify the coordinates as

$$\begin{aligned} \begin{matrix} x_1=\check{x}_1-\theta ^{d}, &{} x_2=\check{x}_2, &{} x_3=\check{x}_3-M^{d}_{a}, &{} u=\check{u}-\check{u}^{d} &{} i.e.,\\ \check{x}_1=x_1+\theta ^{d}, &{} \check{x}_2=x_2, &{} \check{x}_3=x_3+M^{d}_{a}, &{} \check{u}=u+\check{u}^{d}. \\ \end{matrix} \end{aligned}$$

It follows that \(\dot{x}_1=\dot{\check{x}}_1\), \(\dot{x}_2=\dot{\check{x}}_2\), and \(\dot{x}_3=\dot{\check{x}}_3\), so

$$\begin{aligned} \dot{\mathbf {x}}(t)&=\begin{bmatrix} 0 &{} 1 &{} 0\\ {f}_{21}(\mathbf {z}) &{} -\frac{B}{J} &{} {f}_{23}(\mathbf {z})\\ 0 &{} 0 &{} -\frac{1}{\tau } \end{bmatrix} \mathbf {x}(t)+ \begin{bmatrix} 0\\ 0\\ {g}_{31}(\mathbf {z}) \end{bmatrix}{u}(t),\nonumber \\ {f}_{21}(\mathbf {z})&=\frac{1}{Jx_1} \left[ -mgl\sin (x_1+\theta ^{d}) \right. \nonumber \\&\left. -\quad\lambda e^{-E_v\left( x_1+\theta ^{d}+\frac{\pi }{2}\right) }\left( x_1+\theta ^{d}+\frac{\pi }{2}-\omega \right) \right. \nonumber \\&\left. \quad+mgl\sin (\theta ^{d})+ \lambda e^{-E_v\left( \theta ^{d}+\frac{\pi }{2}\right) }\left( \theta ^{d}+\frac{\pi }{2}-\omega \right) \right] , \nonumber \\ {f}_{23}(\mathbf {z})&=\frac{\left( 1+\kappa _{sp}+\kappa _{tr}\right) \kappa _{fat}}{J}=\frac{\kappa _{stf}}{J}, \nonumber \\ {g}_{31}(\mathbf {z})&=\frac{\kappa _{flt}\hat{G}}{\tau }\text {,} \end{aligned}$$
(4)

where \({z}=[x_{1} \quad x_{3} \quad \hat{G} \quad \theta ^{d} \quad \kappa _{stf} \quad \kappa _{flt}]^T \in \mathbb {R}^{6}\) and \(\mathbf {x}=\left[ x_1 \quad x_2 \quad x_3 \right] ^{T}\).

Note that \(\dot{x}_3 = -\frac{1}{\tau }x_3+g_{31}\left( \mathbf {z}\right) \check{u}\), \(u=\check{u}-\check{u}^{d}\), and \(x_3=\check{x}_3-M^{d}_{a}\), where \(\check{u}^{d}\) and \(M^{d}_{a}\) are uncertain values for different operating points \(\theta ^{d}\). Section 3 presents the analysis of the control system design, considering the uncertainties in the plant (4).

2.1 TS Fuzzy Models for the Exact Representation of Nonlinear Systems

Consider an uncertain nonlinear system described by

$$\begin{aligned} \dot{\mathbf {x}}(t)={\mathbf {f}\left( \mathbf {z}(t)\right) }\mathbf {x}(t)+{\mathbf {g}\left( \mathbf {z}(t)\right) }\;\varvec{\text{sat}}\left( \mathbf {u}(t)\right) , \end{aligned}$$
(5)

where \(\mathbf {x}(t) \in \mathbb {R}^{n_x}\) is the state vector, \(\mathbf {u}(t) \in \mathbb {R}^{n_u}\) is the input vector, \(\mathbf {f}(\cdot ): \mathbb {R}^{n_z} \rightarrow \mathbb {R}^{n_x \times n_x}\), \(\mathbf {g}(\cdot ): \mathbb {R}^{n_z} \rightarrow \mathbb {R}^{n_x \times n_u}\), \(\mathbf {z}(t) \in \mathbb {R}^{n_z}\) is a vector with premise variables that depends on the state vector \(\mathbf {x}(t)\) and uncertain parameters or unknown variables, and \(\varvec{\text {sat}}(\mathbf {u}(t)) \in \mathbb {R}^{n_u}\) is the saturation function of the control input.

The sector nonlinearity approach usually employed to construct an exact TS model of a nonlinear system is adequate in a bounded validity domain [42]. A low performance or system instability may occur when the state trajectories do not belong to the validity domain of the model. The validity domain can be represented by a polyhedral set

$$\begin{aligned} \mathcal {O} \triangleq \left\{ \mathbf {x}(t) \in \mathbb {R}^{n_x}: \left| \mathbf {N}_{(h)}\mathbf {x}(t)\right| \leqslant \phi _{(h)} , h \in \mathbb {I}_{p} \right\} \text {,} \end{aligned}$$
(6)

where \(\mathbf {N}=\left[ \mathbf {N}_{(1)}^{T} \; \mathbf {N}_{(2)}^{T} \cdots \mathbf {N}_{(p)}^{T} \right] ^{T} \in \mathbb {R}^{p \times n_x}\) and \(\varvec{\phi }= \left[ \phi _{(1)} \; \phi _{(2)} \cdots \phi _{(p)} \right] ^{T} \in \mathbb {R}^{p}\) are known.

In region \(\mathcal {O}\), consider that the system (2) can be exactly represented by a TS fuzzy model, described by the IF-THEN rules, where the \(\varphi\)-th fuzzy rule \({R}^{\varphi }\) is given by

$$R^{\varphi } :\;{\text{IF}}\;\;z_{1} (t){\text{ is }}M_{1}^{\varphi } {\text{ AND }} \cdots {\text{ AND }}z_{{n_{z} }} (t){\text{ is }}M_{{n_{z} }}^{\varphi } ,\;\;{\text{THEN}}\;\;\begin{array}{*{20}l} {\mathop {\mathbf{x}}\limits^{.} (t) = {\mathbf{A}}_{\varphi } {\mathbf{x}}(t) + {\mathbf{B}}_{\varphi } u(t),} \hfill \\ \end{array}$$

such that \(\varphi \in \mathbb {I}_{n_r}\), \(M_j^{\varphi }\) is the j-th fuzzy set of the \(\varphi\)-th fuzzy rule, \(j \in \mathbb {I}_{n_z}\) and \({z_1}(t),\;\cdots ,\;{z_{n_z}}(t)\) are the premise variables.

More details about the exact representation of a nonlinear system by TS fuzzy models can be found in [43]. From this method, one obtains the following representation for the system (5):

$$\begin{aligned} \dot{\mathbf {x}}(t)= & {} {\mathbf {A}\left( \alpha \right) }\mathbf {x}(t)+{\mathbf {B}\left( \alpha \right) }\;\varvec{\text {sat}}\left( \mathbf {u}(t)\right) , \end{aligned}$$
(7)
$$\begin{aligned} \mathbf {A}\left( \alpha \right)= & {} \sum _{i=1}^{n_r}\alpha _i \mathbf {A}_i,\;\mathbf {B}\left( \alpha \right) =\sum _{i=1}^{n_r}\alpha _i \mathbf {B}_i,\; \sum _{i=1}^{n_r}\alpha _i=1, \end{aligned}$$
(8)

where \(i \in \mathbb {I}_{n_r}\), \(\mathbf {A}_{i} \in \mathbb {R}^{n_x \times n_x}\), \(\mathbf {B}_{i} \in \mathbb {R}^{n_x \times n_u}\) and \(\alpha _i=\alpha _i (\mathbf {z}(t))\).

Remark 1

The exact representation of an uncertain nonlinear system by a TS fuzzy model is guaranteed by the procedure presented in [44,45,46,47]. This procedure uses the lower and upper bounds of the system nonlinearities and uncertain linear terms considering the given operation region of the state vector and the known range of the plant uncertain parameters. Therefore, the TS fuzzy models obtained with this procedure can exactly represent uncertain nonlinear systems described in (5) by a TS fuzzy model (7), which presents known local models and uncertain normalized weights.

The next section shows the switched control design subject to saturation and presents LMIs conditions that are used to determine the feedback gains.

3 Robust Switched Control Design Subject to Actuator Saturation and Fault (RSwASF) for Fuzzy Systems

The robust switched control for the lower limb electrical stimulation is proposed considering the actuator saturation and fault under nonideal muscular conditions (fatigue, spasm and tremor).

The idea is to design a set of feedback gains, with only one gain used at each time, chosen based on a switching law that depends on the state vector of the controlled system. Fig. 1 shows the schema of the switched control for electrical stimulation.

Fig. 1
figure 1

Electrical stimulation system of the lower limbs using robust switched controller subject to actuator saturation and fault

Full size image

Consider a nonlinear system subject to actuator saturation described by the following TS fuzzy model:

$$\begin{aligned} \dot{\mathbf {x}}=\mathbf {A}(\alpha )\mathbf {x}(t)+\mathbf {B}(\alpha ) \varvec{\text {sat}}\left( \mathbf {u}(t)\right) +\mathbf {B}(\alpha )d(t)\text {,} \end{aligned}$$
(9)

where \(\mathbf {A}(\alpha )\) defined in (8), \(\mathbf {B}(\alpha )=\mathbf {B}_0 g(\alpha )\), \(g(\alpha )\geqslant 0\), for all \(\alpha\),

$$\begin{aligned} \varvec{\text {sat}}\left( \mathbf {u}(t)\right)= & {} \left[ {\text {sat}}\left( u_{(1)} (t) \right) \cdots {\text {sat}}\left( u_{(n_u)}(t)\right) \right] ^{T}\text {,} \nonumber \\ {\text {sat}}\left( u_{(l)}(t)\right)= & {} \text {sgn}\left( u_{(l)}(t)\right) \text {min}\left\{ \rho _{(l)},|u_{(l)}(t)| \right\} \text {,} \end{aligned}$$
(10)

\(\forall l \in \mathbb {I}_{n_u}\), \(\vartheta _{1} \leqslant d(t) \leqslant \vartheta _{2}\), \(\rho _{(l)}\) is the actuator saturation values.

We propose the application of the robust switched control law subject to actuator saturation. The proposed procedure uses a switching index \(\varsigma\), as described in (12, 13), which selects a state-feedback controller gain that belongs to the set \(\left\{ \mathbf {K}_{j} \in \mathbb {R}^{n_u \times n_x},\; j \in \mathbb {I}_{n_r} \right\}\) and an index \(\psi\) that compensates uncertainty in the signal control, as defined in (13). An index \(\varsigma\) is determined by auxiliary symmetric matrices \({Q}_j\), obtained by the design procedure. The control law is defined as follows [44]:

$$\begin{aligned} \mathbf {u}(t)&=\varvec{\text {sat}}_{0}\left( \mathbf {u}_{\varsigma }(t)\right) -\vartheta _{\psi }(t)\text {,} \end{aligned}$$
(11)
$$\begin{aligned} \mathbf {u}_{\varsigma }(t)&=-\mathbf {K}_{\varsigma }\mathbf {x}(t)\text {,} \;\; \end{aligned}$$
(12)
$$\begin{aligned} \varsigma&=\arg ^{*}\underset{j \in \mathbb {I}_{n_r}}{\min }\left\{ \mathbf {x}^{T}(t)\mathbf {Q}_{j}\mathbf {x}(t)\right\} \text {,} \;\; \varsigma \text {,}\; j \in \mathbb {I}_{n_r} \text {,} \end{aligned}$$
(13)
$$\begin{aligned} \psi&=\arg ^{*} \underset{m \in \mathbb {I}_{2}}{\min }\left\{ -\mathbf {x}^{T}\mathbf {P}\mathbf {B}_0 \vartheta _{m} \right\} \text {,} \end{aligned}$$
(14)

where \(\varvec{\text {sat}}_{0}\left( \mathbf {u}_{\varsigma }(t)\right) =\left[ {\text {sat}}_{0}\left( u_{\varsigma (1)} (t) \right) \cdots {\text {sat}}_{0}\left( u_{\varsigma (n_u)}(t)\right) \right] ^{T}\), and

$$\begin{aligned} {\text {sat}}_{0}\left( u_{\varsigma (l)}(t)\right) =\text {sgn}\left( u_{\varsigma (l)}(t)\right) \text {min}\left\{ \rho _{0(l)},|u_{\varsigma (l)}(t)| \right\} \text {,} \end{aligned}$$
(15)

where \(\rho _{0(l)}=\rho _{(l)}-\underset{m \in \mathbb {I}_2}{\max }\left\{ \left| \vartheta _{m} \right| \right\}\), \(\forall l \in \mathbb {I}_{n_u}\), \(m \in \mathbb {I}_2\), and \(\vartheta _{m}\), \(\rho\), \(\rho _0\), \(\mathbf {B}_0\) will be defined later. The state-feedback matrices \(\mathbf {K}_{j}\) and decision matrices \(\mathbf {Q}_j\) will be obtained in the design procedure, ensuring the local stability of the system (9, 10, 11, 12, 13, 14 and 15) with decay rate.

In addition, consider the quadratic Lyapunov function \(V(\mathbf {x})=\mathbf {x}^{T}\mathbf {P}\mathbf {x}\), and let the ellipsoid \(\mathcal {E}(\mathbf {P},\delta )\)

$$\begin{aligned} \mathcal {E}(\mathbf {P},\delta )=\{\mathbf {x}(t)\in \mathbb {R}^{n_x}: \mathbf {x}(t)^{T}\mathbf {P}\mathbf {x}(t)\leqslant \delta \}\text {,} \end{aligned}$$
(16)

where the constant \(\delta >0\).

An invariant region related to operating of the system is considered. The initial condition of the system, initiated in a suitable region within an operating region, will remain in this region for all \(t \geqslant 0\). In other words, determining an invariant region, say \(\mathcal {E} \subset \mathcal {O}\), \(\forall \mathbf {x}(0) \in \mathcal {E}\), the state vector \(\mathbf {x}(t)\) of (9) remains in the operating region \(\mathcal {O}\), \(\forall t \geqslant 0\). Consequently, (7) exactly represents system (5) for \(t \geqslant 0\) and all \(\mathbf {x}(0) \in \mathcal {E}\), following the procedure described in Sect. 2.1.

Lemma 1

[42, 44] Consider a nonlinear system described by (5) and an operating region \(\mathbf {x}(t) \in \mathcal {O}\), for \(t \geqslant 0\), given in (6). Assume a symmetric positive definite matrix \(\mathbf {X} \in \mathbb {R}^{n_x \times n_x}\) exists, such that

$$\begin{aligned} \begin{aligned} \begin{bmatrix} \phi _{(h)}^{2} &{} \mathbf {N}_{(h)}\mathbf {X} \\ *&{} \mathbf {X} \end{bmatrix} \geqslant {0}, \end{aligned} \end{aligned}$$
(17)

holds \(\forall i\) and \(h \in \mathbb {I}_{p}\), and \(\mathbf {x}(t_{1})^{T} \mathbf {P} \mathbf {x}(t_{1})^{T} < \mathbf {x}(t_{0})^{T} \mathbf {P} \mathbf {x}(t_{0})^{T}\) for all \(t_{1}>t_{0}>0\), where \(\mathbf {P} = \mathbf {X}^{-1}\). Therefore, if \(\mathbf {x}(0) \in \mathcal {E}(\mathbf {P},1)\), given in (16), then \(\mathbf {x}(t) \in \mathcal {O}\), \(t \geqslant 0\).

Proof

More details are found in [42, 44]. \(\square\)

Consider the polyhedral set \(\mathcal {L}\left( \mathbf {H}_{k}\right)\)

$$\begin{aligned} \mathcal {L}\left( \mathbf {H}_{k}\right)&:=\left\{ \mathbf {x}(t) \in \mathbb {R}^{n_x}: \left| \mathbf {H}_{k(l)} \mathbf {x}(t)\right| \leqslant \breve{\rho }_{(l)},\; k \in \mathbb {I}_{n_r},\; \right. \nonumber \\&\qquad \quad \left. \text {and}\; l \in \mathbb {I}_{\overset{\rightleftharpoons }{n}_u} \right. \Big \}\text {,} \end{aligned}$$
(18)

where \(\breve{\varvec{\rho }}=\left[ \breve{\rho }_{(1)} \cdots \breve{\rho }_{(\overset{\rightleftharpoons }{n}_u)} \right] ^{T} \in \mathbb {R}^{\overset{\rightleftharpoons }{n}_u}\), \(\breve{\rho }_{(l)}>0\), \(\mathbf {H}_{k}=\left[ \mathbf {H}^{T}_{k(1)} \cdots \mathbf {H}^{T}_{k(\overset{\rightleftharpoons }{n}_u)} \right] \in {R}^{\overset{\rightleftharpoons }{n}_u \times n_x}\) are known.

Consider the set \({\mathcal {D}}_{n_u}\) composed of \(2^{n_u}\) diagonal matrices \({\mathbf {D}_s} \in \mathbb {R}^{n_u \times n_u}\), \(s \in \mathbb {I}_{2^{n_u}}\), whose diagonal elements are either 1 or 0. For any \({\mathbf {D}_s} \in {\mathcal {D}}_{n_u}\), consider that \({\mathbf {D}}^{-}_{s}= \mathbf {I}_{n_u}-{\mathbf {D}_s}\).

Now, the function \(q_{n_u}: \mathbb {I}_{2^{n_u}} \rightarrow \mathbb {I}_{2^{n_u-1}}\) is defined as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} q_{n_u}(i_s)=q_{n_u}(i_s-1)+1, &{}\mathbf {D}_{i_s}+\mathbf {D}_{j_s} \ne \mathbf {I}_{n_u}, \\ &{}\; \forall j_s \in \mathbb {I}_{i_s}\text {,}\; i_s \in \mathbb {I}_{2^{n_u}}\text {,}\\ q_{n_u}(i_s)=q_{n_u}(i_s), &{}\mathbf {D}_{i_s}+\mathbf {D}_{j_s} = \mathbf {I}_{n_u},\\ &{} \; \exists j_s \in \mathbb {I}_{i_s}\text {,}\; i_s \in \mathbb {I}_{2^{n_u}}\text {.} \end{array}\right. } \end{aligned}$$
(19)

This function will be useful for convex hull representation of saturation nonlinearity. In this paper, we adopted the saturation representation provided by [48].

Lemma 2

[48] Let \(n_u \geqslant 1\) be a given integer and \(\breve{\varvec{v}} \in \mathbb {R}^{\overset{\rightleftharpoons }{n}_u}\) be such that \(\left\| \breve{\varvec{v}} \right\| _{\infty } \leqslant \rho\), where \(\left\| \breve{\varvec{v}} \right\| _{\infty } = \underset{i \in \mathbb {I}_{\overset{\rightleftharpoons }{n_u}}}{\max }|\breve{\varvec{v}}_{i}|\). Let the elements in \(\mathcal {D}_{n_u}\) be labeled as \(\mathbf {D}_s\), \(s \in \mathbb {I}_{2^{n_u}}\) and the vector \(\mathbf {sl}_{2^{n_u-1},\;q_{n_u}(i_s)}\), where the function \(q_{n_u}(i_s)\) be defined in (19). Then, for any \(\mathbf {u} \in \mathbb {R}^{n_u}\), there holds

$$\begin{aligned} \varvec{\text {sat}}(\mathbf {u}) \in \text {co}\left\{ \mathbf {D}_{s}\mathbf {u}+\breve{\mathbf {D}}_{s}^{-}\breve{\varvec{v}}\right\} , \; s \in \mathbb {I}_{2^{n_u}}\text {,} \end{aligned}$$
(20)

if and only if, for any \(\varvec{\varrho } \in \mathbb {R}^{n_u}\)

$$\begin{aligned} \langle \varvec{\varrho },\mathbf {sat}(\mathbf {u}) \rangle\le & {} \underset{s \in \mathbb {I}_{2^{n_u-1}}}{\max } \left\{ \langle \varvec{\varrho },\mathbf {D}_{s}\mathbf {u}+\left( \mathbf {sl}_{2^{n_u-1},\;s}\otimes \mathbf {D}_{s}^{-}\right) \breve{\varvec{v}}\rangle , \right. \nonumber \\&\left. \langle \varvec{\varrho },\mathbf {D}_{s}^{-}\mathbf {u}+\left( \mathbf {sl}_{2^{n_u-1},\;s}\otimes \mathbf {D}_{s}\right) \breve{\varvec{v}} \rangle \right\} \text {,} \end{aligned}$$
(21)

where \(\langle a_1,a_2 \rangle\) denotes the inner product of the vectors \(a_1\) and \(a_2\), \(\breve{\mathbf {D}}_{s} \in \mathbb {R}^{n_u \times \overset{\rightleftharpoons }{n}_u}\), which is defined as

$$\begin{aligned} \breve{\mathbf {D}}_{s}=\mathbf {sl}_{2^{n_u-1},\;q_{n_u}(i_s)}\otimes \mathbf {D}_{s}^{-}, \; \forall s, i_s \in \mathbb {I}_{2^{n_u}}\text {.} \end{aligned}$$
(22)

Proof

Further details are found in [48]. \(\square\)

Remark 2

Note that Lemma 2 contains \(\overset{\rightleftharpoons }{n}_u=n_u2^{n_u-1}\) slack variables for the representation of the convex hull and usually offers less conservative conditions than that presented in [49].

For example, if \(n_u=2\), then \(\overset{\rightleftharpoons }{n}_u=4\), \(\mathbf {D}_s\), \(s \in \mathbb {I}_{2^{n_u}}\) are the matrices as follows:

$$\begin{aligned}&\varvec{\text {sat}}(\mathbf {u}) \in \text {co}\left\{ \mathbf {D}_{s}\mathbf {u}+\mathbf {D}_{s}^{-}\varvec{v}\right\} , \; s \in \mathbb {I}_{2^{n_u}} \text {.}\nonumber \\&{\mathcal {D}}_{2}=\left\{ {\mathbf {D}}_1, \; {\mathbf {D}}_2, \; {\mathbf {D}}_3, \; {\mathbf {D}}_4\right\} \text {,}\nonumber \\&{\mathcal {D}}_{2}=\left\{ \begin{bmatrix} 1 &{} 0\\ 0 &{} 1 \end{bmatrix}, \; \begin{bmatrix} 1 &{} 0\\ 0 &{} 0 \end{bmatrix}, \; \begin{bmatrix} 0 &{} 0\\ 0 &{} 1 \end{bmatrix}, \; \begin{bmatrix} 0 &{} 0\\ 0 &{} 0 \end{bmatrix}\right\} \text {.} \end{aligned}$$
(23)

From (19), adopting \(q_{2}(0)=0\), the associated function to elements of the set \({\mathcal {D}}_{2}\) is expressed as \(q_{2}(1)=1\), \(q_{2}(2)=2\), \(q_{2}(3)=q_{2}(2)=2\), and \(q_{2}(4)=q_{2}(1)=1\). Consequently, the row vectors are \(\mathbf {sl}_{2,\;q_{2}(1)}=\left[ 1 \quad 0\right]\), \(\mathbf {sl}_{2,\;q_{2}(2)}=\left[ 0 \quad 1\right]\), \(\mathbf {sl}_{2,\;q_{2}(3)}=\left[ 0 \quad 1\right]\), and \(\mathbf {sl}_{2,\;q_{2}(4)}=\left[ 1 \quad 0\right]\).

From (22) one obtains:

$$\begin{aligned} \breve{\mathbf {D}}^{-}_{s}= & {} \mathbf {sl}_{2,\;q_{2}(i_s)}\otimes \mathbf {D}_{s}^{-}, \; \forall s,\; i_s \in \mathbb {I}_{4} \text {,}\\ {\breve{\mathcal {D}}}^{-}_{2}= & {} \left\{ {\breve{\mathbf {D}}}^{-}_1, \; {\breve{\mathbf {D}}}^{-}_2, \; {\breve{\mathbf {D}}}^{-}_3, \; {\breve{\mathbf {D}}}^{-}_4\right\} \text {,}\\ {\breve{\mathcal {D}}}^{-}_{2}= & {} \left\{ \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 \end{bmatrix}, \; \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 \end{bmatrix}, \begin{bmatrix} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 \end{bmatrix}, \; \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0 \end{bmatrix}\right\} \text {.} \end{aligned}$$

Thus, (20) can be written as

$$\begin{aligned} \mathbf {sat}(\mathbf {u}) \in \text {co}\left\{ \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}, \; \begin{bmatrix} u_1 \\ \breve{v}_4 \end{bmatrix}, \; \begin{bmatrix} \breve{v}_3 \\ u_2 \end{bmatrix}, \; \begin{bmatrix} \breve{v}_1 \\ \breve{v}_2 \end{bmatrix}\right\} \text {.} \end{aligned}$$

Remark 3

If \(\mathbf {x}(t) \in \mathcal {L}(\mathbf {H}_k)\) defined in (18), \(k \in \mathbb {I}_{n_r}\), then \(\mathbf {x}(t) \in \mathcal {L}{\left( \mathbf {K}_j \right) }\), \(j \in \mathbb {I}_{n_r}\), and \({\text {sat}}\left( {u}\right)\) can be rewritten as

$$\begin{aligned} \mathbf {sat}\left( \mathbf {u}\right) =\sum _{s=1}^{2^{n_u}}\lambda _{s}\left[ \mathbf {D}_s \mathbf {u}+\breve{\mathbf {D}}^{-}_s\breve{\varvec{v}}\right] \text {,} \end{aligned}$$
(24)

where \(\mathbf {D}_{s} \in \mathcal {D}\), \(\breve{\mathbf {D}}^{-}_s \in \breve{\mathcal {D}^{-}}\), \(\breve{\mathbf {D}}^{-}_{s}=\mathbf {sl}_{2,\;q_{2}(i_s)}\otimes \mathbf {D}_{s}^{-}\), \(s \in \mathbb {I}_{2^{n_u}}\), and \(\lambda _{s} \geqslant 0\), \(\sum _{s=1}^{2^{n_u}}\lambda _s=1\).

Considering (15), \(\rho _{0(l)}=\rho _{(l)}- \underset{m \in \mathbb {I}_{2}}{\max }\left\{ \left| \vartheta _{m(l)} \right| \right\}\), from (11) one obtains \(\left| u_{(l)}(t) \right| = \left| {\text {sat}}_{0} \left( u_{\varsigma (l)}(t) \right) -\vartheta _{\psi (l)} \right| \leqslant \left| {\text {sat}}_{0} \left( u_{\varsigma (l)}(t) \right) \right| + \left| \vartheta _{\psi (l)} \right| \leqslant \rho _{0(l)} + \max \left\{ \vartheta _{i(l)} \right\}\), \(\rho _{0(l)} + \max \left\{ \vartheta _{i(l)} \right\} = \rho _{(l)}+\max \left\{ \left| \vartheta _i \right| \right\} -\max \left\{ \left| \vartheta _i \right| \right\} =\rho _{(l)}\). Therefore

$$\begin{aligned} {\text {sat}}\left( u_{(l)}(t)\right)&= {\text {sat}}_{0}\left( u_{\varsigma (l)}(t) \right) -\vartheta _{\psi (l)}\text {,\;and}\\ \mathbf {sat}\left( \mathbf {{u}}(t)\right)&= \mathbf {sat}_{0}\left( \mathbf {{u}}_{\varsigma }(t) \right) -\vartheta _{\psi }. \end{aligned}$$

Similarly to (24), if \(\mathbf {x}(t) \in \mathcal {L}\left( \mathbf {H}_k\right)\), \(k \in \mathbb {I}_{n_r}\), then \(\mathbf {x}(t) \in \mathcal {L}\left( \mathbf {K}\varsigma \right)\) and \(\mathbf {sat}_0\left( -\mathbf {K}_{\varsigma }\mathbf {x}\right)\) one obtains

$$\begin{aligned} \mathbf {sat}_0\left( -\mathbf {K}_{\varsigma }\mathbf {x}\right) =\sum _{s=1}^{2^{n_u}}\lambda _{s}\left[ \mathbf {D}_s\left( -\mathbf {K}_{\varsigma }\mathbf {x}\right) +\breve{\mathbf {D}}^{-}_s\left( \mathbf {H}_{\varsigma }\mathbf {x}\right) \right] \text {.} \end{aligned}$$
(25)

The following lemma provides a sufficient condition for the constraint \(\mathcal {E}(\mathbf {P},\delta ) \subset \mathcal {L}(\mathbf {H}_k)\).

Lemma 3

[44, 49] Let the sets \(\mathcal {E}(\mathbf {P},\delta )\) and \(\mathcal {L}(\mathbf {H}_k)\), the constraint \(\mathcal {E}(\mathbf {P},\delta ) \subset \mathcal {L}(\mathbf {H}_k)\) is enforced if the LMI

$$\begin{aligned} \begin{bmatrix} \rho ^{2}_{0(l)}\delta ^{-1} &{} \mathbf {G}_{k(l)}\\ *&{} \mathbf {X} \end{bmatrix} \geqslant 0 \text {,} \end{aligned}$$
(26)

holds for all \(k \in \mathbb {I}_{n_r}\), and \(l \in \mathbb {I}_{\overset{\rightleftharpoons }{n}_u}\), where \(\mathbf {X}=\mathbf {P}^{-1}\) and \(\mathbf {G}_{k(l)}=\mathbf {H}_{k(l)}\mathbf {X}\).

Proof

See [44, 49]. \(\square\)

With all ellipsoids that satisfy the invariance condition, a less conservative choice of the largest ellipsoid inside the domain of attraction can be guaranteed considering its shape. Let \(\mathcal {W}_0 \subset \mathbb {R}^{n_x}\) be defined as follows:

$$\begin{aligned} \mathcal {W}_0=\text {co}\left\{ \mathbf {w}^{1}_0,\;\mathbf {w}^{2}_0, \cdots , \mathbf {w}^{q}_0 \right\} \text {,} \end{aligned}$$
(27)

where \(\mathbf {w}^{i_w}_0 \in \mathbb {R}^{n_x}\), \(\forall i_w \in \mathbb {I}_q\) are a priori given vectors.

A guarantee that a convex hull (27) is contained in the invariant region \(\mathcal {E} (\mathbf {P},1)\) is described in Lemma 4.

Lemma 4

The constraint \(\bar{\omega }\) \(\mathcal {W}_0 \subset \mathcal {E} (\mathbf {P},1)\), where \(\mathcal {W}_0=co \left\{ \mathbf {w}^{1}_0,\mathbf {w}^{2}_0, \cdots , \mathbf {w}^{q}_0 \right\}\), \(\mathbf {w}^{i_w}_0 \in \mathbb {R}^{n_x}\) for all \(i_w \in I_{q}\), is the convex hull of known vectors \(\mathbf {w}^1_0\), \(\mathbf {w}^2_0\), \(\cdots\), \(\mathbf {w}^q_0\), and the constant \(\bar{\omega } > 0\), is enforced if

$$\begin{aligned} \begin{aligned} \begin{bmatrix} \bar{\omega }^{-2} &{} \mathbf {w}^{kT}_0 \\ \mathbf {w}^{i_w}_0 &{} \mathbf {X} \end{bmatrix} \geqslant {0}\text {,} \end{aligned} \end{aligned}$$
(28)

holds for all \(i_w \in \mathbb {I}_q\). Thus, \(\bar{\omega }\) can be used as a variable to obtain a less conservative estimate of the domain of attraction and to search the “largest” ellipsoid \(\mathcal {E} \left( \mathbf {P},1 \right)\).

Proof

See [49, 50]. \(\square\)

On the other hand, constraints may be adopted to avoid that the controller assumes a large norm, e.g., using Lemma 5.

Lemma 5

[44, 49] It is possible to reduce the norm of the gain matrix \(\mathbf {K}_j\), \(j \in \mathbb {I}_{n_r}\), increasing the region \(\mathcal {L}(\mathbf {K}_j)\) selecting appropriately \(\xi\) such that \(\mathcal {E}(\mathbf {P},\xi ^{-1}) \subset \mathcal {L}(\mathbf {K}_j)\) is imposed if the LMI

$$\begin{aligned} \begin{bmatrix} \xi \rho ^{-2}_{0(k)} &{} \mathbf {M}_{j(k)}\\ *&{} \mathbf {X} \end{bmatrix} \geqslant 0\text {,} \end{aligned}$$
(29)

holds for all \(j \in \mathbb {I}_{n_r}\), and \(k \in \mathbb {I}_{n_u}\).

Proof

See [44, 49, 51]. \(\square\)

Theorem 1

[44] Let the sets \(\mathcal {E}(\mathbf {P},1)\), \(\mathcal {L}(\mathbf {H}_k)\), and \(\mathcal {W}_0\) defined in (16), (18), and (27), respectively. Consider a nonlinear system subject to actuator saturation defined in (9) and (10), an operating region \(\mathbf {x}(t) \in \mathcal {O}\), described by (6), \(t \geqslant 0\), \(\varvec{\rho } \in \mathbb {R}^{n_u}, \; \varvec{\phi } \in \mathbb {R}^{p}\) and \(\mathbf {N} \in \mathbb {R}^{p \times n_x}\) are known. Assume that there exist a symmetric positive definite matrix \(\mathbf {X} \in \mathbb {R}^{n_x \times n_x}\), symmetric matrices \(\bar{\mathbf {Q}}_{i}\) and \(\bar{\mathbf {Z}}_{i} \in \mathbb {R}^{n_x \times n_x}\), matrices \(\mathbf {{G}}_{j}= \left[ {G}_{j(1)}^{T} \; {G}_{j(2)}^{T} \; \cdots {G}_{j(\overset{\rightleftharpoons }{n}_u)}^{T}\right]\), \(\mathbf {M}_{i} \in \mathbb {R}^{n_u \times n_x}\) and a scalar \(\beta > 0\) such that

$$\begin{aligned}&\mathbf {A}_i\mathbf {X}+\mathbf {X}\mathbf {A}_i^T+\bar{\mathbf {Z}}_i+\bar{\mathbf {Q}}_{i}+2\beta \mathbf {X}<0, \end{aligned}$$
(30)
$$\begin{aligned}&-\mathbf {B}_{i}\mathbf {D}_{s}\mathbf {M}_{j}+\mathbf {B}_{i}\breve{\mathbf {D}}^{-}_{s}\mathbf {G}_{j}-\mathbf {M}_{j}^{T}\mathbf {D}_{s}^{T}\mathbf {B}_{i}^{T}\nonumber \\&\quad +\mathbf {G}_{j}^{T}\breve{\mathbf {D}}^{-T}_{s}\mathbf {B}_{i}^{T}-\bar{\mathbf {Z}}_i-\bar{\mathbf {Q}}_{j} \leqslant 0, \end{aligned}$$
(31)
$$\begin{aligned}&\begin{bmatrix} \rho ^{2}_{0(l)} &{} \mathbf {G}_{j(l)}\\ *&{} \mathbf {X} \end{bmatrix} \geqslant 0 \text {,} \end{aligned}$$
(32)
$$\begin{aligned}&\begin{bmatrix} \phi ^{2}_{(h)} &{} \mathbf {N}_{(h)}\mathbf {X}\\ *&{} \mathbf {X} \end{bmatrix} \geqslant 0 \text {,} \end{aligned}$$
(33)
$$\begin{aligned}&\begin{bmatrix} \xi \rho ^{-2}_{0(k)} &{} \mathbf {M}_{i(k)}\\ *&{} \mathbf {X} \end{bmatrix} \geqslant 0 \text {,} \end{aligned}$$
(34)
$$\begin{aligned}&\begin{bmatrix} \bar{w}^{-2} &{} *\\ \mathbf {w}^{i_w}_{0} &{} \mathbf {X} \end{bmatrix} \geqslant 0 \text {,} \end{aligned}$$
(35)

hold for all i and \(j \in \mathbb {I}_{n_r}\), \(k \in \mathbb {I}_{{n}_u}\), \(l \in \mathbb {I}_{\overset{\rightleftharpoons }{n}_u}\) \(h \in \mathbb {I}_{p}\), \(i_w \in \mathbb {I}_q\), \(s \in \mathbb {I}_{2^{n_u}}\), \(\mathbf {D}_{s} \in \mathcal {D}\) and \(\breve{\mathbf {D}}^{-}_{s} \in \breve{\mathcal {D}}\). Then, the control law (11, 12, 13, 14 and 15), where \(\mathbf {K}_{i}=\mathbf {M}_{i}\mathbf {X}^{-1}\) and \(\mathbf {Q}_{i}=\mathbf {X}^{-1} \bar{\mathbf {Q}}_{i}\mathbf {X}^{-1}\) for all \(i \in \mathbb {I}_{n_r}\), makes the system (9) locally asymptotically stable with a decay rate equal to or greater than \(\beta\), \(\forall \mathbf {x}(0) \in \mathcal {E} \left( \mathbf {P}, 1 \right)\), where \(\mathbf {P} = \mathbf {X}^{-1}\). Furthermore, \(\mathbf {x}(t) \in \mathcal {O}, \; t \geqslant 0\).

Proof

Based on [44], consider as Lyapunov function candidate \(V(\mathbf {x}(t)) = \mathbf {x}(t)^{T}\mathbf {P}\mathbf {x}(t)\), \(\mathbf {P} = \mathbf {P}^{T} \in \mathbb {R}^{n_x \times n_x}, \; \mathbf {P} > 0\). Therefore, from the system (9) and the control law (12)

$$\begin{aligned} \dot{V}(\mathbf {x})&=2\mathbf {x}^{T}\mathbf {P}\dot{\mathbf {x}}\text {,}\nonumber \\&= 2\mathbf {x}^{T}\mathbf {P}\left[ \mathbf {A}(\alpha )\mathbf {x}+\mathbf {B}(\alpha )\varvec{\text {sat}}(\mathbf {u})+\mathbf {B}(\alpha )d\right] \text {.} \end{aligned}$$
(36)

Replacing (11, 12) in (36)

$$\begin{aligned} \dot{V}(\mathbf {x})&=2\mathbf {x}^{T}\mathbf {P}\mathbf {A}(\alpha )\mathbf {x}+2\mathbf {x}^{T}\mathbf {P}\mathbf {B}(\alpha )\left[ \varvec{\text {sat}}_0\left( \mathbf {u}_{\varsigma }(t)\right) -\vartheta _{\psi }(t)\right] \nonumber \\&\quad +2\mathbf {x}^{T}\mathbf {P}\mathbf {B}(\alpha )d\text {,}\nonumber \\ \dot{V}(\mathbf {x})&=2\mathbf {x}^{T}\mathbf {P}\mathbf {A}(\alpha )\mathbf {x}+2\mathbf {x}^{T}\mathbf {P}\mathbf {B}(\alpha )\mathbf {sat}_0\left( -\mathbf {K}_{\varsigma }\mathbf {x}\right) \nonumber \\&\quad +2\mathbf {x}^{T}\mathbf {P}\mathbf {B}(\alpha )\left[ d-\vartheta _{\psi }(t)\right] \text {.} \end{aligned}$$
(37)

Considering (25), (37) can be rewritten as

$$\begin{aligned} \dot{V}\left( \mathbf {x}\right)&=2\mathbf {x}^{T}\mathbf {P}\mathbf {A}(\alpha )\mathbf {x} +2\mathbf {x}^{T}\mathbf {P}\mathbf {B}(\alpha )\left[ d-\vartheta _{\psi }\right] \\&\quad +2\mathbf {x}^{T}\mathbf {P}\mathbf {B}(\alpha )\left\{ \sum _{s=1}^{2^{n_u}}\lambda _{s}\left[ \mathbf {D}_s\left( -\mathbf {K}_{\varsigma }\mathbf {x}\right) +\breve{\mathbf {D}}^{-}_s\left( \mathbf {H}_{\varsigma }\mathbf {x}\right) \right] \right\} \text {.} \end{aligned}$$

Note that \(\vartheta _1 \leqslant d(t) \leqslant \vartheta _2\) can be described as a convex combination \(\sum _{m=1}^{2}\gamma _{m}(t)=1\text {,}\;\; \gamma _1(t)\text {,} \; \gamma _2(t) \geqslant 0\), \(\gamma _2(t)=\frac{d(t)-\vartheta _1}{\vartheta _2-\vartheta _1}\text {,} \;\; \gamma _1(t)=1-\gamma _2(t)\).

Therefore, replacing \(\mathbf {B}(\alpha )=\mathbf {B}_{0}g(\mathbf {x})\), \(g(\mathbf {x}) \geqslant 0\), \(\forall \mathbf {x} \ne 0\), from (14), it follows that

$$\begin{aligned}&\mathbf {x}^{T}\mathbf {P}\mathbf {B}(\alpha )\left[ d-\vartheta _{\psi }\right] \nonumber \\&\quad = \mathbf {x}^{T}\mathbf {P}\mathbf {B}_{0}\left[ \sum _{m=1}^{2}\gamma _{m}(t)\vartheta _{m}+\underset{m \in \mathbb {I}_2}{\min }\left\{ -\mathbf {x}^{T}\mathbf {P}\mathbf {B}_0 \vartheta _{m} \right\} \right] \nonumber \\&\quad \leqslant \mathbf {x}^{T}\mathbf {P}\mathbf {B}_{0}\sum _{m=1}^{2}\gamma _{m}(t)\vartheta _{m} -\mathbf {x}^{T}\mathbf {P}\mathbf {B}_{0}\sum _{m=1}^{2}\gamma _{m}(t)\vartheta _{m}=0\text {.} \end{aligned}$$
(38)

Then, from (38) one obtains

$$\begin{aligned}&\dot{V}\left( \mathbf {x}\right) \leqslant \mathbf {x}^{T}\left[ \mathbf {A}(\alpha )^{T}\mathbf {P}+\mathbf {P}\mathbf {A}(\alpha )\right] \mathbf {x}\nonumber \\&\quad +\left\{ \sum _{s=1}^{2^{n_u}}\lambda _{s}\left[ \mathbf {D}_s\left( -\mathbf {K}_{\varsigma }\mathbf {x}\right) +\breve{\mathbf {D}}^{-}_s\left( \mathbf {H}_{\varsigma }\mathbf {x}\right) \right] \right\} ^{T}\mathbf {B}(\alpha )^{T}\mathbf {P}\mathbf {x}\nonumber \\&\quad +\mathbf {x}^{T}\mathbf {P}\mathbf {B}(\alpha )\left\{ \sum _{s=1}^{2^{n_u}}\lambda _{s}\left[ \mathbf {D}_s\left( -\mathbf {K}_{\varsigma }\mathbf {x}\right) +\breve{\mathbf {D}}^{-}_s\left( \mathbf {H}_{\varsigma }\mathbf {x}\right) \right] \right\} \text {.} \end{aligned}$$
(39)

Now, assume that there exist symmetric matrices \(\mathbf {Z}_{i}\) and \(\mathbf {Q}_{j}\) such that

$$\begin{aligned}&\left[ -\mathbf {D}_s\mathbf {K}_{j}+\breve{\mathbf {D}}^{-}_s\mathbf {H}_{j}\right] ^{T}\mathbf {B}_{i}^{T}\mathbf {P}\nonumber \\&\quad +\mathbf {P}\mathbf {B}_{i}\left[ -\mathbf {D}_s\mathbf {K}_{j}+\breve{\mathbf {D}}^{-}_s\mathbf {H}_{j}\right] \leqslant \mathbf {Z}_{i}+\mathbf {Q}_{j}\text {,} \end{aligned}$$
(40)

\(\forall i,\;j \in \mathbb {I}_{n_r}\), \(\forall \mathbf {D}_s \in \mathcal {D}\), and \(\forall \breve{\mathbf {D}}^{-}_s \in \breve{\mathcal {D}}^{-}\) . Then, for \(j = \varsigma\), multiplying by \(\alpha _{i}\), where \(\alpha _{i}\geqslant 0\), and taking the sum from \(i = 1\) to \(n_r\), \(\sum _{i=1}^{n_r} \alpha _{i}=1\) and then multiplying the result by \(\lambda _{s}\), \(\lambda _{s} \geqslant 0\) and taking the sum from \(s = 1\) to \(2^{n_u}\), \(\sum _{s=1}^{2^{n_u}} \lambda _{s}=1\), considering \(\mathbf {B}(\alpha )=\sum _{i=1}^{n_r}\alpha _i \mathbf {B}_i\), \(\alpha _i \geqslant 0\), \(\sum _{i=1}^{n_r} \alpha _i=1\), \(i \in \mathbb {I}_{n_r}\) one has

$$\begin{aligned}&\sum _{s=1}^{2^{n_u}}\lambda _s \left\{ \left[ -\mathbf {D}_s\mathbf {K}_{\varsigma }+\breve{\mathbf {D}}^{-}_s\mathbf {H}_{\varsigma }\right] ^{T}\mathbf {B}(\alpha )^{T}\mathbf {P}\right. \nonumber \\&\quad \left. +\mathbf {P}\mathbf {B}(\alpha )\left[ -\mathbf {D}_s\mathbf {K}_{\varsigma }+\breve{\mathbf {D}}^{-}_s\mathbf {H}_{\varsigma }\right] \right\} \leqslant \mathbf {Z}(\alpha )+\mathbf {Q}_{\varsigma }\text {,} \end{aligned}$$
(41)

where \(\mathbf {Z}(\alpha )=\sum _{i=1}^{n_r}\alpha _{i}\mathbf {Z}_{i}\). Note that, from the control law (13), \(\mathbf {x}^{T}\mathbf {Q}_{\varsigma }\mathbf {x}=\underset{i \in \mathbb {I}_{n_r}}{\min }\left\{ \mathbf {x}^{T}\mathbf {Q}_{i}\mathbf {x}\right\} \leqslant \sum _{i=1}^{n_r}\alpha _i\mathbf {x}^{T}\mathbf {Q}_{i}\mathbf {x}=\mathbf {x}^{T}\mathbf {Q}(\alpha )\mathbf {x}\).

Thus, from (39) and (41),

$$\begin{aligned} \dot{V}(\mathbf {x})\leqslant \mathbf {x}^{T}\left\{ \mathbf {A}(\alpha )^{T}\mathbf {P}+\mathbf {P}\mathbf {A}(\alpha )+\mathbf {Z}(\alpha )+\mathbf {Q}(\alpha ) \right\} \mathbf {x}\text {.} \end{aligned}$$
(42)

Aiming to achieve a decay rate greater than or equal to \(\beta\) it is sufficient that \(\dot{V}(\mathbf {x})\leqslant -2\beta V(\mathbf {x})\) [51]. Hence, from (42) is sufficient that, \(\forall i \in \mathbb {I}_{n_r}\),

$$\begin{aligned} \mathbf {A}^{T}_{i}\mathbf {P}+\mathbf {P}\mathbf {A}_{i}+\mathbf {Z}_{i}+\mathbf {Q}_{i} + 2 \beta \mathbf {P} \leqslant 0 \text {.} \end{aligned}$$
(43)

Premultiplying and postmultiplying (40) and (43) by \(\mathbf {X} = \mathbf {P}^{-1}\) and performing the change of variables \(\mathbf {G}_{j}=\mathbf {H}_{j}\mathbf {X}\), \(\mathbf {M}_{j}=\mathbf {K}_{j}\mathbf {X}\), \(\bar{\mathbf {Z}}_{i}=\mathbf {X}\mathbf {Z}_{i}\mathbf {X}\) and \(\bar{\mathbf {Q}}_{i}=\mathbf {X}\mathbf {Q}_{i}\mathbf {X}\), one obtains (30) and (31). Note that as \(V(\mathbf {x}) = \mathbf {x}^{T}\mathbf {P}\mathbf {x}\) and \(\dot{V}(\mathbf {x}) < 0\), \(\mathbf {x} \ne 0\), from (16), if \(\mathbf {x}(0) \in \mathcal {E}\left( \mathbf {P},\delta \right)\) then \(\mathbf {x}(t) \in \mathcal {E}\left( \mathbf {P},\delta \right)\), \(\forall t \geqslant 0\). Considering Lemma 3 with \(\delta = 1\), LMI (32) ensure \(\mathcal {E}(\mathbf {P},1) \subset \mathcal {L}\left( \mathbf {H}_k\right)\), a sufficient condition such that (25) holds. And considering Lemma 1, LMI (33) ensure \(\mathcal {E}(\mathbf {P},1) \subset \mathcal {O}\), a sufficient condition for a state trajectory started with an initial condition \(\mathbf {x}(0) \in \mathcal {E}(\mathbf {P},1)\) remains in \(\mathcal {O}\) for all \(t \geqslant 0\). In addition, considering Lemma 4, LMI (35) guarantees that the convex hull (27) is contained in the invariant region \(\mathcal {E} (\mathbf {P},1)\), and LMI (34) minimizes the norm of the matrices \(\mathbf {K}_i\), selecting appropriately \(\xi\) such that \(\mathcal {E} (\mathbf {P},\xi ^{-1}) \subset \mathcal {L}(\mathbf {K}_i)\). The proof is complete. \(\square\)

Table 1 Parameters from healthy and paraplegic individuals [40]
Full size table

Remark 4

The Gaino et al. approach [4] treated the plant model without uncertainties. Consequently, the values of \(\check{u}^{d}\) and nominal torque \(M_a\) are not uncertain. Now, assuming nonidealities, the state vector becomes an estimate, since \(M_a^{d}\) is uncertain. However, a term \(\vartheta _{\psi }(t)\) that will dominate the error from the uncertainty of the desired torque, was added to the control signal. Thus,

$$\begin{aligned} \check{u}=-\mathbf {K}_{\varsigma }\mathbf {x}_e(t)+\vartheta _{\psi }(t)\text {,} \end{aligned}$$
(44)

where \(\mathbf {x}_e(t)=\left[ x_1(t) \; x_2(t) \; x_{3e}(t) \right] ^{T}\), \(x_{3e}(t)=\check{x}_3-M_{a \; nom}^{d}\), \(M_{a \; nom}\) is the nominal torque and \(\mathbf {K}_{\varsigma }=\left[ {K}_{\varsigma 1} \; {K}_{\varsigma 2} \; {K}_{\varsigma 3}\right]\).

Considering the following relationship \(x_{3e}(t)=\check{x}_3-M_a^d+\varDelta M_a\), \(\varDelta M_a = M_a^d - M_{a \; nom}^{d}\), (44) can be rewritten as

$$\begin{aligned} \check{u}=-\left[ {K}_{\varsigma 1} \quad {K}_{\varsigma 2} \quad {K}_{\varsigma 3}\right] \begin{bmatrix} x_1\\ x_2\\ x_3+\varDelta M_a \end{bmatrix}+\vartheta _{\psi }(t)\text {,} \end{aligned}$$

Therefore,

$$\begin{aligned} u&=\check{u}-\check{u}^{d}_e\text {,}\\ u&=-\left[ {K}_{\varsigma 1} \quad {K}_{\varsigma 2} \quad {K}_{\varsigma 3}\right] \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}-{K}_{\varsigma 3}\varDelta M_a-\check{u}^d_e+\vartheta _{\psi }(t)\text {,} \\ u&=-\mathbf {K}_{\varsigma }\mathbf {x}-\check{u}^d+u_{error}+\vartheta _{\psi }(t)\text {,} \end{aligned}$$

where \(u_{error}=\left( \check{u}^d-\check{u}^d_e-{K}_{\varsigma 3}\varDelta M_a\right)\) will be dominated by the term \(\vartheta _{\psi }(t)\) from the control law (11), where \(\vartheta _1 \leqslant \vartheta _{\psi }(t) \leqslant \vartheta _2\), \(\vartheta _{1}=\min \{\check{u}^{d}\}\) and \(\vartheta _{2}=\max \{\check{u}^{d}\}\), \(\check{u}^{d}\) defined in (3).

3.1 Example: Paraplegic Individual P3

Table 1 presents the parameter values for healthy and paraplegic individuals, corresponding to experimental tests conducted by Ferrarin et al.  [40].

Consider the operating region defined in the interval \(0 \leqslant \check{x}_1(t) \leqslant \frac{7\pi }{18}\), desired position belongs to set \(\theta ^{d} \in [\pi /6 \quad \pi /3]\), \(\max \{M_a^d\}=9.16\), and the uncertain parameters \(\hat{G} \in [0.9G_n \quad G_n]\), \(\kappa _{stf} \in \left[ 0.1 \quad 1\right]\), and \(\kappa _{flt} \in \left[ 0.8 \quad 1\right]\).

Observe that the system (4) has three uncertain nonlinear functions \(\tilde{f}_{21}(\mathbf {z}(t))\), \(\tilde{f}_{23}(\mathbf {z}(t))\), and \(\tilde{g}_{31}(\mathbf {z}(t))\), consequently one obtains \(n_r=2^3=8\).

To find the local models, the maximum and minimum values of the uncertain nonlinear functions must be obtained.

Considering the paraplegic individual P3, whose parameters can be found in Table 1, and taking \(\mathbf {x}=\check{\mathbf {x}}-\check{\mathbf {x}}_e\), the set \(\mathbb {D}\) is obtained

$$\begin{aligned} \mathbb {D}= & {} \left\{ z \in \mathbb {R}^6: -\frac{\pi }{3} \leqslant {x}_1 \leqslant \frac{4\pi }{18}, \; -M_a^d \leqslant {x}_3 \leqslant M_a^d, \right. \\&\qquad \qquad \left. 0.9G_n \leqslant \hat{G} \leqslant G_n,\; 0.1 \leqslant \kappa _{stf} \leqslant 1, \right. \\&\qquad \qquad \left. \; 0.8 \leqslant \kappa _{flt} \leqslant 1,\frac{\pi }{6} \leqslant \theta ^{d} \leqslant \frac{\pi }{3}\right\} \text {.} \end{aligned}$$

Consequently, one obtains the local models for exact representation of system (4) through TS fuzzy models (7), \(\rho = 150\), and

$$\begin{aligned} \mathbf {A}_{1}&=\mathbf {A}_{2}=\begin{bmatrix} 0&{}1&{}0\\ 25.7877&{}-0.7335&{}2.5381\\ 0&{}0&{}-4.6512 \end{bmatrix}\text {,}\;\\ \mathbf {A}_{3}&=\mathbf {A}_{4}=\begin{bmatrix} 0&{}1&{}0\\ 25.7877&{}-0.7335&{}0.2538\\ 0&{}0&{}-4.6512 \end{bmatrix}\text {,}\\ \mathbf {A}_{5}&=\mathbf {A}_{6}=\begin{bmatrix} 0&{}1&{}0\\ 1.6826&{}-0.7335&{}2.5381\\ 0&{}0&{}-4.6512 \end{bmatrix}\text {,}\;\\ \mathbf {A}_{7}&=\mathbf {A}_{8}=\begin{bmatrix} 0&{}1&{}0\\ 1.6826&{}-0.7335&{}0.2538\\ 0&{}0&{}-4.6512 \end{bmatrix}\text {,}\\ \mathbf {B}_{1}&=\mathbf {B}_{3}=\mathbf {B}_{5}=\mathbf {B}_{7}=\begin{bmatrix} 0\\ 0\\ 1.4264\times 10^{3} \end{bmatrix}\text {,}\\ \mathbf {B}_{2}&=\mathbf {B}_{4}=\mathbf {B}_{6}=\mathbf {B}_{8}=\begin{bmatrix} 0\\ 0\\ 1.0270\times 10^{3} \end{bmatrix}\text {.} \end{aligned}$$

The operating region \(\mathcal {O}\) is described by (6), where \(p=3\), \(\mathbf {N} = \mathbf {I}_3\), and \(\varvec{\phi }=[\frac{\pi }{3} \quad 4 \quad 10]^{T}\). Moreover, note that \(\mathbf {B}(\alpha )=\mathbf {B}_0 g(\mathbf {z})\), where \(\mathbf {B}_0=\left[ 0 \quad 0 \quad 1\right] ^{T}\), and \(g(\mathbf {z}) \geqslant 0\), \(g_0(\mathbf {z})=\underset{\mathbf {z} \in \mathbb {D}}{\max }\left\{ g(\mathbf {z})\right\} =1.4264\times 10^{3}\).

The LMIs (30) were solved using the \(\hbox {MATLAB}^{\textregistered }\) software, and the modeling language YALMIP [52] with the solver LMILab [53]. Solving the LMIs (27) presented in Theorem 1, the aforementioned parameters, \(\beta =4.0\), \(q=4\), \(\mathbf {w}_0^1=\left[ \frac{\pi }{6} \quad 0 \quad 9.16\right] ^T\), \(\mathbf {w}_0^2=\left[ \frac{\pi }{6} \quad 0 \quad -9.16\right] ^T\), \(\mathbf {w}_0^3=\left[ -\frac{\pi }{18} \quad 0 \quad 9.16\right] ^T\), \(\mathbf {w}_0^4=\left[ -\frac{\pi }{18} \quad 0 \quad -9.16\right] ^{T}\), \(\vartheta _{1}=\min \{\check{u}^{d}\}=0.0149\), \(\vartheta _{2}=\max \{\check{u}^{d}\}=0.0332\), \(\rho _0=0.150\) minimizing \(\bar{w}\), one obtains the gains of the proposed RSwASF control procedure:

$$\begin{aligned} \mathbf {P}&=\begin{bmatrix} 7.8226\times 10^4 &{}1.1754\times 10^4 &{}196.7513\\ 1.1754\times 10^4 &{}2.0495\times 10^4 &{}33.6308\\ 196.7513 &{}33.6308 &{}0.8309 \end{bmatrix}\text {,}\\ \mathbf {K}_{1}&=\begin{bmatrix} 0.5406&0.0956&0.0027 \end{bmatrix}\text {,} \\ \mathbf {K}_{2}&=\begin{bmatrix} 0.5365&0.0967&0.0028 \end{bmatrix}\text {,} \\ \mathbf {K}_{3}&=\begin{bmatrix} 0.6319&0.1082&0.0026 \end{bmatrix}\text {,} \\ \mathbf {K}_{4}&=\begin{bmatrix} 0.6511&0.1128&0.0027 \end{bmatrix}\text {,} \\ \mathbf {K}_{5}&=\begin{bmatrix} 0.5220&0.0954&0.0027 \end{bmatrix}\text {,} \\ \mathbf {K}_{6}&=\begin{bmatrix} 0.5129&0.0963&0.0027 \end{bmatrix}\text {,} \\ \mathbf {K}_{7}&=\begin{bmatrix} 0.6165&0.1091&0.0026 \end{bmatrix}\text {,}\\ \mathbf {K}_{8}&=\begin{bmatrix} 0.6238&0.1120&0.0027 \end{bmatrix}\text {.} \end{aligned}$$

The TS fuzzy control techniques PDC and RPDC were comparated using the LMIs presented by Gaino et al. [4] and Covacic et al. [35], respectively. Solving the LMIS presented by Covacic et al. [35], considering the values \(\mu =150\) mA, \(\beta = 4.0\), and the constraint of the operating region (17), one obtains the following:

$$\begin{aligned} \mathbf {Q}&=\begin{bmatrix} 1.9071 \times 10^{12} &{}2.7137 \times 10^{11} &{}3.5540 \times 10^{7}\\ 2.7137 \times 10^{11} &{}5.0976 \times 10^{10} &{}6.7066 \times 10^{6}\\ 3.5540 \times 10^{7} &{}6.7066 \times 10^{6} &{}5.3648 \times 10^{5} \end{bmatrix}\text {,}\\ \mathbf {K}_{1}&=\mathbf {M}_{1}\mathbf {X}=\begin{bmatrix} 48.7925&9.1864&0.7267 \end{bmatrix}\text {,}\\ \mathbf {K}_{2}&=\mathbf {M}_{2}\mathbf {X}=\begin{bmatrix} 47.4738&8.9370&0.7230 \end{bmatrix}\text {,}\\ \epsilon _{11}&=1.9786\times 10^{-10} \text {,}\;\;\epsilon _{12}=1.9415\times 10^{-10} \text {,}\\ \epsilon _{22}&=1.8969\times 10^{-10} \text {.} \end{aligned}$$

The LMIs presented by Gaino et al.  [4] were solved considering the values \(\mu =150\) mA, \(\beta = 4.0\), and constraint for operating region (17). Consequently, one obtains the following:

$$\begin{aligned} \mathbf {P}&=\begin{bmatrix} 40.6894&{}7.1150&{}1.4004\\ 7.1150&{}1.3163&{}0.2534\\ 1.4004&{}0.2534&{}0.0621 \end{bmatrix}\text {,}\\ \mathbf {F}_{1}&=\mathbf {M}_{1}\mathbf {X}=\begin{bmatrix} 0.0058&0.0011&2.3611 \times 10^{-4} \end{bmatrix}\text {,}\\ \mathbf {F}_{2}&=\mathbf {M}_{2}\mathbf {X}=\begin{bmatrix} 0.0047&0.0010&2.1859 \times 10^{-4} \end{bmatrix}\text {.} \end{aligned}$$

4 Results and Discussion

Usually, the results of controllers from simulation consider ideal conditions for electrical stimulation of the lower limbs, i.e., without fatigue, tremor, spasms, and other uncertainties. First, we present the results under ideal conditions. Next, we evaluated the nonideal conditions. A priori, the comparative study was carried out using TS fuzzy-based control techniques. The results obtained from other techniques in the literature were then compared.

4.1 Ideal Conditions

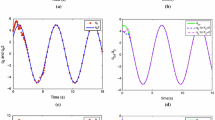
Three operating points in the time interval \(0 \leqslant t \leqslant 30\) s were evaluated considering the plant in ideal conditions. Fig. 2 shows the regulation performance of PDC [4], RPDC [35], and RSwASF (proposed) control techniques, using the gains designed in Sect. 3.1.

The root-mean-squared error value in the steady state (SSRMSE) was rated. For the three studied controllers, considering all individuals, the steady-state performance was satisfactory for regulation to the desired operating point. The null steady-state error was obtained.

Fig. 2
figure 2

Lower limb dynamic behavior for muscle nonidealities (fatigue, spasms, and tremor) in a mild and b severe conditions and considering actuator fault (80% of the nominal)

Full size image

4.2 Nonideal Conditions

The actuator fault, parametric uncertainty in the muscular recruitment function, and the different levels of fatigue, spasms, and tremor were simulated.

4.2.1 Muscle Fatigue, Tremor and Spasms

Muscle nonidealities (fatigue, spasms, and tremor) alter muscle torque. These nonidealities were evaluated in the time interval \(30 < t \leqslant 60\) s (Fig. 3). Note that the muscle fatigue profile is a decreasing function in the temporal domain, indicating a reduced muscular torque. Spasms profiles are described as torque impulses, which change the dynamics of the system for a short time. The tremor indicates damped torque oscillations, and its amplitude is strictly related to the degree of severity.

Fig. 3
figure 3

Muscle behavior in different nonidealities levels inserted during the tests: a fatigue, b spasms, and c tremor

Full size image

Figure 2a and b illustrate the system performance considering mild and severe condition of muscular nonidealities, respectively.

Fig. 4
figure 4

Comparison of RMS error between PDC [4], RPDC [35], and RSwASF (this paper) control techniques, considering healthy (Hi) and paraplegic (Pj) individuals in different scenarios of nonidealities: a fatigue—mild; b fatigue—moderate; c fatigue—severe; d fatigue, spasms, and tremor—mild; e fatigue, spasms and tremor—moderate; and f fatigue, spasms, and tremor—severe

Full size image

The nonideality situations due to fatigue are listed first. Fatigue, spasms, and tremor were assessed at three levels: mild, moderate and severe.

Note that although the RSwASF controller reduces the steady-state error, the fatigue precludes the null error. The muscle torque is substantially reduced. Consequently, maintaining the angular position and muscular activation applied to a single motor point is a difficult task, because the fatigue effect modifies the musculoskeletal system to null torque. One way to get better results is to stimulate more than one muscle activation point, switching the channels by detecting fatigue [2] or other events.

For all individuals, the highest RMS error was obtained for the severe fatigue situation (Fig. 4). This condition presents a greater error than considering all nonidealities in maximum severity degree. This behavior is due to spasticity [41]. In this case, spasticity effectively increases the knee joint stiffness, contributing to a smaller error in the controllers’ performance.

4.2.2 Actuator Fault and Parametric Uncertainty in the Muscle Recruitment

The actuator fault was considered as a decrease in energy (80% of the nominal) applied to the muscles. An uncertainty in the muscular recruitment function, expressed by parameter \(\hat{G}\), was also assumed.

The RSwASF controller reached the desired operating point, even in the presence of parametric uncertainties (Fig. 2b).

Regarding the results obtained among the TS fuzzy techniques, the RSwASF controller presented the best performance.

4.3 Comparative Analysis with Literature

The comparison between control techniques considering the nonidealities in the plant model is considered for isometric application of electrical stimulation. The knee joint controlled in a single angular position is a therapy to obtain muscle strength through electrical stimuli [31]. In this sense, the goal of the closed-loop system to obtain regulation with the smallest RMS error in different angular positions.

Table 2 lists the RMSE between different control techniques in the literature. Control techniques whose plant model considered parametric uncertainties in severe conditions were evaluated. Lynch and Popovic [41] initiated this modeling approach. First, the PID and sliding-mode (SMC) controllers were compared. In severe conditions of fatigue, spasms, and tremor, the RMS errors were large for both controllers. Next, Lynch and Popovic [39] proposed a comparative analysis with the gain-scheduling controller (GSC). Among the controllers, the PDC [4] had the worst performance. The PDC [4] obtained a large RMS error and was more sensitive to parametric variation. The SMC produced a relatively large RMS error. Although it is a robust technique, it was sensitive to parametric variation. This result may be due to the use of the boundary layer control, which compromised the convergence properties. In turn, the GSC produced a better response and less sensitivity to uncertainties, because it used integral control. An unfavorable point of the GSC refers to lengthy tuning process the multiple local controllers.

Benahmed et al.  [1] proposed an analysis with other controllers. The double-PID (DPID) reduced RMSE, when compared to the PID, but errors persisted due to sensitivity to plant parameters. Regarding sensitivity, backstepping (BC), integral-backstepping (IBC), and super-twisting (ST) were also evaluated. The sensitivity of BC to variations in parameters was lower than IBC and ST. On the other hand, adding integral action, there is a reduction in the RMSE index, but the sensitivity deteriorates.

Before this study, the technique that established the least RMSE was the ST [1]. The RSwASF controller surpassed the ST and obtained the best result, achieving the lowest RMSE for the angular position, considering all individuals and in all nonideal conditions.

About TS fuzzy technique, the PDC and RPDC controllers, proposed by Gaino et al.  [4] and Covacic et al.  [35], respectively, present unsatisfactory behavior (Fig. 2), since they do not deal with plant uncertainties. Although Covacic et al.  [35] proposed a norm-bounded uncertainty control, it is worth mentioning that the authors did not consider that the moment of inertia parameter is an uncertainty in the nonlinear function \(f_{21}(z)\). Consequently the TS model of the system is inaccurate.

In relation to actuator fault and parametric uncertainty, the results indicate a discrepancy between the knee angular position and the desired value using the PDC [4] and RPDC [35]. The incompatibility between the model and control design explains the degraded performance.

Table 2 RMS error between control techniques for healthy (\(RMSE_{h}\)) and paraplegic (\(RMSE_{p}\)) individuals considering nonidealities (severe). BC backstepping control, DPID double-proportional-integral-derivative, GSC gain-scheduling control, IBC integral-backstepping control, PDC parallel distributed compensation, PID proportional-integral-derivative control, SMC sliding-mode control, ST super-twisting, RSwASF robust switched control subject to actuator saturation and fault. \(N_h\) and \(N_p\) denote the numbers of the healthy and paraplegic individuals. Bold font indicates best result obtained
Full size table

4.4 Advantages and Limitations of the RSwASF

The RSwASF handled uncertainties inherent in the individual, such as muscle fatigue, spasms, tremor, and also features of the system such as saturation and actuator failure. Under ideal conditions, the performance of the PDC [4], RPDC [35], and RSwASF are similar. However, under nonideal conditions, the RSwASF controller performed better in the tests compared with the PDC [4].

Considering a nonlinear system described by the TS fuzzy model, the PDC controller depends on the known membership functions. The expressions of the membership functions can be extensive and demand a high computational cost to calculate them. When dealing with uncertain systems, the result obtained with PDC becomes unsatisfactory, because the membership functions become unsuitable for model uncertainties. Thus, the RSwASF controller is presented as an advantageous proposal, since it does not depend explicitly on the membership functions for the convex combination of controller gains. Other switched control applications for uncertain nonlinear plants can be found in [44, 45, 47].

It is worth mentioning that there is chattering in the control signal from the RSwASF under ideal conditions. However, this behavior can be smoothed using a smooth function, proposed by Alves et al.  [44]. Nonetheless, this function was not needed in relation to nonideal conditions.

5 Conclusions

The uncertainty of the recruitment function, actuator fault, and other nonideality parameters add an error to the model, specifically to nominal torque \(M^d_{a \; nom}\) and in the value of \(\check{u}^d\). This analysis explains why different muscle torque estimation-based control techniques yield regulation error.

The novelty of this study was the RSwASF control law applied to compensate plant uncertainties. This technique was compared to other control techniques in the literature. Among control techniques, the PDC presented the highest RMSE, followed by the PID and GSC. The RMS error has been reduced through a robust approach based on TS fuzzy models; however, its performance was below the sliding-mode control, ST, and backstepping control. The best performance among all reported techniques was presented by RSwASF, which using TS fuzzy models properly dealt with uncertainties and nonidealities of the system.

The contribution of this study was the improvement of the performance of the isometric contraction evoked by electrical stimuli dealing under nonideal conditions (fatigue, spasms, tremor, muscular activation and actuator saturation, and fault), as uncertainties in the control design.

Future works may investigate a new mathematical model for the plant, relating muscle activation and kinematic variables appropriately without relying on muscle torque estimation. From this study, hybrid FES systems such as powered ankle–foot prostheses [54] can be investigated, as well as isotonic applications with insertion of the delay effect in the plant through an approach proposed by [55].