Performance of Semi-actively Controlled Building Frame Using MR Damper for Near-Field Earthquakes

Abstract

Most of the studies on the control of building frame using MR damper are investigated for far-field earthquake records, and a considerable reduction in responses is shown. However, MR dampers have some significant drawbacks like the saturation of MR dampers and its performance variability with respect to the ground motions. It has been found that when the predominant frequency of the earthquake is much away from the natural frequency of the structure, the response reduction becomes significantly less. The reason for this may be attributed to the less values of relative displacement and velocities of the floors which primarily influence the force generated in the damper for a given voltage. The characteristics of the near-field ground motion are distinctly different from the far-field ground motion. The performance of the MR damper for the near-field earthquake is not well investigated. In the present study, the performance of the MR dampers is studied for two types of near-field earthquakes, namely Bam (directivity effect) and Chichi (fling step effect) earthquakes. A limited number of MR dampers are employed for response reduction.

1 Introduction

Controls of structural responses during natural calamities like earthquakes, tsunami, blast, fire, and cyclone have been a favorable research topic for the structural engineers. Many control systems have been proposed and studied by the researchers. The control systems are classified into four categories—passive system, active system, semi-active system, and hybrid system. Out of all the control systems, semi-active control system has gained a considerable attention due to its low power requirement and ability to generate control forces of same order as that produced by active systems. Among all the semi-active devices, MR damper has gained considerable attention as it is fail-safe.

Jansen and Dyke [1] evaluated the performance of different control algorithms using multiple MR dampers. In the numerical example, two MR dampers were installed at lower two floors of a six-story structure and the structure was subjected to El Centro excitation. Xu et al. [2] compared the optimal displacement control strategies with the optimal force control strategy using MR/ER dampers. Yoshida and Dyke [3] investigated the performance of a 20-story nonlinear benchmark building equipped with MR dampers. Kori and Jangid [4] studied the performance of MR dampers under different control algorithms and excitations. Christenson et al. [5] performed a real-time hybrid testing of a large-scale MR damper at University of Colorado, USA. Bahar et al. [6] proposed a hybrid control system combining a nonlinear base isolator and MR damper. In the MR damper, the voltage was updated by a feedback control loop. Chang and Zhou [7] used recurrent neural network models for structural control. They emulated the inverse dynamics of MR damper to produce required command voltage. Two examples of structural control were taken: optimal prediction control of a single degree of freedom system and LQR control of a multi-degree of freedom system to illustrate the proposed scheme. Lee et al. [8] applied the neuro-controller to a base-isolated benchmark problem. The training algorithm based on minimizing the cost function was used. A clipped optimal algorithm was then employed to produce the desired control force. Das et al. [9] used an ANN-cum-fuzzy control scheme for structural response mitigation. Bharti et al. [10] investigated the behavior of an asymmetric building plan with MR dampers.

All the researches published on structural control using MR dampers have mostly used far-field earthquake. In the present study, the performance of the MR dampers is studied for two types of near-field earthquakes, namely Bam (directivity effect) and Chichi (fling step effect) earthquakes. Three MR dampers are employed at the bottom three floors for response reduction.

2 Theory

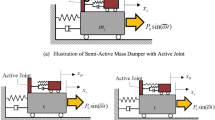
The equation of motion for the building frame fitted with MR dampers in Fig. 1 takes the form:

Fig. 1

Structural model equipped with three MR dampers

$$ \left[ {\mathbf{M}} \right]\left\{ {{\ddot{\mathbf{x}}}} \right\} + \left[ {\mathbf{C}} \right]\left\{ {{\dot{\mathbf{x}}}} \right\} + \left[ {\mathbf{K}} \right]\left\{ {\mathbf{x}} \right\} = \left[ {\mathbf{G}} \right]\left\{ {{\mathbf{f}}_{{\mathbf{m}}} } \right\} - \left[ {\mathbf{M}} \right]\left[ {\mathbf{r}} \right]\left\{ {{\ddot{\mathbf{u}}}_{{\mathbf{g}}} } \right\} $$

(1)

where M, C, and K are the mass, damping, and stiffness matrices of the system, respectively; f_m is the MR damper force vector; G is the damper location matrix of ones and zeroes; z is the displacement vector with respect to the ground; r is an influence coefficient vector; and $\ddot{\varvec{u}}_{\varvec{g}}$ is the earthquake ground acceleration. The governing Eq. (1) is expressed in the state-space form as below:

$$ \left\{ {{\dot{\mathbf{z}}}} \right\} = \left[ {\mathbf{A}} \right]\left\{ {\mathbf{z}} \right\} + \left[ {\mathbf{B}} \right]\left\{ {{\mathbf{f}}_{{\mathbf{m}}} } \right\} + \left[ {\mathbf{E}} \right]\left\{ {{\ddot{\mathbf{u}}}_{{\mathbf{g}}} } \right\} $$

(2)

$$ {\mathbf{y}} = \left[ {\mathbf{C}} \right]\left\{ {\mathbf{z}} \right\} + \left[ {\mathbf{D}} \right]\left\{ {{\mathbf{f}}_{{\mathbf{m}}} } \right\} + {\mathbf{v}} $$

(3)

where A is a 2n × 2n system matrix, B is a 2n × n_C control matrix, E is a 2n × 1 disturbance (excitation) matrix, C is a 2n × 2n identity matrix, D is a 2n × n_C matrix, x is a 2n × 1 state vector, y is a 2n × 1 vector of measured outputs, and v is a 2n × 1 measurement noise vector; n is the number of states, n_C is the number of controllers, and p is the number of measurements.

2.1 Linear Quadratic Regulator (LQR) Algorithm

The LQR estimates the control force by minimizing the following quadratic cost function:

$$ {\mathbf{J}} = {\mathbf{E}}[{\mathbf{x}}^{{\mathbf{T}}} \left( {{\mathbf{T}}_{{\mathbf{f}}} } \right){\mathbf{Fx}}\left( {{\mathbf{T}}_{{\mathbf{f}}} } \right)] + \int\limits_{0}^{{{\mathbf{T}}_{{\mathbf{f}}} }} {{\mathbf{x}}^{{\mathbf{T}}} ({\mathbf{t}}){\mathbf{Qx}}({\mathbf{t}})} + {\mathbf{u}}^{{\mathbf{T}}} ({\mathbf{t}}){\mathbf{Ru}}({\mathbf{t}}){\mathbf{dt}} $$

(4)

where E denotes the expected value; T_f denotes the final time which may be finite or infinite, and when T_f tends to infinity, the first term of the cost function ${\mathbf{x}}^{{\mathbf{T}}} \left( {{\mathbf{T}}_{{\mathbf{f}}} } \right){\mathbf{Fx}}\left( {{\mathbf{T}}_{{\mathbf{f}}} } \right)$ becomes negligible; Q and R are the positive definite matrices. The control force is given by the following equation:

$$ {\mathbf{u}}({\mathbf{t}}) = - {\mathbf{L}}({\mathbf{t}}){\hat{\mathbf{x}}}({\mathbf{t}}) $$

(5)

where L(t) is the feedback gain matrix and it is defined using A, B, Q, and R matrices and F by solving the following Riccati equation:

$$ - \mathop {\mathbf{S}}\limits^{.} ({\mathbf{t}}) = {\mathbf{A}}^{{\mathbf{T}}} {\mathbf{S}}({\mathbf{t}}) + {\mathbf{S}}({\mathbf{t}}){\mathbf{A}} - {\mathbf{S}}({\mathbf{t}}){\mathbf{B}}^{{\mathbf{T}}} {\mathbf{R}}^{ - 1} {\mathbf{B}}^{{\mathbf{T}}} {\mathbf{S}}({\mathbf{t}}) + {\mathbf{Q}} $$

(6)

$$ {\mathbf{L}}({\mathbf{t}}) = {\mathbf{R}}^{ - 1} {\mathbf{B}}^{{\mathbf{T}}} {\mathbf{S}}({\mathbf{t}})\;{\text{and}}\;{\mathbf{S}}({\mathbf{T}}) = {\mathbf{F}} $$

(7)

3 Generation of Control Forces Using MR Damper

Force in the MR damper is generated based on the movement of the piston and the viscosity of the MR fluid which is manipulated by applying the voltage to the magnetic coil of the MR damper. While the actuation of the piston is governed by the vibration of the structure, the applied voltage is governed by the control algorithm. The control algorithm is shown in Fig. 2. Modified Bouc–Wen model [11] is used for predicting the MR damper force. Inputs to the model are the inter-story drifts and velocities. By comparing the generated control force with the desired control force, voltage is held constant or set to zero using clipped optimal control. The reference time history of force used for clipped optimal control is obtained using LQR algorithm. The entire numerical scheme is carried out using Simulink toolbox of MATLAB.

Fig. 2

Control algorithm

Fig. 3

Comparison of uncontrolled and controlled time histories of base shear for Bam (2003) earthquake

3.1 Modified Bouc–Wen Model

Equations governing the MR damper force predicted by this model are given as [11]:

$$ {\mathbf{f}}_{{\mathbf{m}}} = {\mathbf{c}}_{1} {\dot{\mathbf{x}}} + {\mathbf{k}}_{1} \left( {{\mathbf{u}}_{{\mathbf{d}}} - {\mathbf{x}}_{0} } \right) $$

(8)

where the evolutionary variable z is given as:

$$ {\dot{\mathbf{z}}} = - {\varvec{\upgamma}}\left| {{\mathbf{v}}_{{\mathbf{d}}} - {\dot{\mathbf{x}}}\left| {({\mathbf{z}})} \right|{\mathbf{z}}} \right|^{{\left( {{\mathbf{n}} - 1} \right)}} - {\varvec{\upbeta}}\left( {{\mathbf{v}}_{{\mathbf{d}}} - {\dot{\mathbf{x}}}} \right)\left| {\mathbf{z}} \right|^{{\mathbf{n}}} + {\mathbf{A}}_{{\mathbf{m}}} \left( {{\mathbf{v}}_{{\mathbf{d}}} - {\dot{\mathbf{x}}}} \right) $$

(9)

and $\dot{x}$ is given as

$$ {\dot{\mathbf{x}}} = \left\{ {\frac{1}{{{\mathbf{c}}_{0} + {\mathbf{c}}_{1} }}} \right\}\left\{ {{\varvec{\upalpha}}_{0} {\mathbf{z}} + {\mathbf{c}}_{0} {\mathbf{v}}_{{\mathbf{d}}} + {\mathbf{k}}_{0} \left( {{\mathbf{u}}_{{\mathbf{d}}} - {\mathbf{x}}} \right)} \right\} $$

(10)

where u_d is the displacement of the damper; x is the internal pseudo-displacement of the damper; z is the evolutionary variable that describes the hysteretic behavior of the damper; k₁ is the accumulator stiffness; c₀ is the viscous damping at large velocities; c₁ is viscous damping for force roll-off at low velocities; k₀ is the stiffness at large velocities; and x₀ is the initial stiffness of spring k₁; $\alpha_{0}$ is the evolutionary coefficient; γ, β, η, and A_m are shape parameters of the hysteresis loop. The model parameters dependent on command voltage $c_{0} ,c_{1} ,\alpha_{0}$ are expressed as follows:

$$ {\mathbf{c}}_{0} = {\mathbf{c}}_{{0{\mathbf{a}} }} + {\mathbf{c}}_{{0{\mathbf{b}}}} {\mathbf{U}} $$

(11)

$$ {\mathbf{c}}_{1} = {\mathbf{c}}_{{1{\mathbf{a}} }} + {\mathbf{c}}_{{1{\mathbf{b}}}} {\mathbf{U}} $$

(12)

$$ {\varvec{\upalpha}}_{0} = {\varvec{\upalpha}}_{{0{\mathbf{a}} }} + {\varvec{\upalpha}}_{{0{\mathbf{b}}}} {\mathbf{U}} $$

(13)

where U is given as output of first-order filter following the condition as below

$$ \dot{U} = - \eta \left( {U - V} \right) $$

(14)

3.2 Clipped Optimal Control Law

The input voltage to the MR damper is obtained using clipped optimal law [12]. When the absolute value of MR damper force is greater than the absolute value of LQR force, then the voltage is set to maximum, and when the absolute value of MR damper force is less than the absolute value of LQR force, then the voltage is set to zero. The mathematical form of clipped optimal law is:

$$ {\mathbf{V}} = {\mathbf{V}}_{\hbox{max} } {\mathbf{H}}\left\{ {\left( {{\mathbf{F}}_{{\mathbf{d}}} - {\mathbf{F}}_{{{\mathbf{mr}}}} } \right){\mathbf{F}}_{{{\mathbf{mr}}}} } \right\} $$

(15)

where V is the input voltage to the MR damper, H is the Heaviside function, V_max is the maximum input voltage, F_d is the LQR force, and F_mr is the MR damper force. The voltage is maximum when Heaviside function is one and zero when Heaviside function is zero.

4 Numerical Study

The details of building frame are shown in Fig. 1. Mass of each story is 18,000 kg, and stiffness of each floor is 24,965 kN/m. Three MR dampers are used to control the response and are placed at the bottom the story of the frame where maximum drifts are expected to take place for uncontrolled vibration. The time histories of uncontrolled and controlled responses of top floor displacement for Bam and Chichi earthquakes are shown in Figs. 4 and 6, respectively. Similarly, time histories of uncontrolled and controlled responses of base shear for Bam and Chichi earthquakes are shown in Figs. 3 and 5, respectively. Force–displacement and force–velocity plots of the MR damper located at third floor are shown in Figs. 7, 8, 9, and 10.

Fig. 4

Comparison of uncontrolled and controlled time histories of top floor displacement for Bam (2003) earthquake

Fig. 5

Comparison of uncontrolled and controlled time histories of base shear for Chichi (1999) earthquake

Fig. 6

Comparison of uncontrolled and controlled time histories of top floor displacement for Chichi (1999) earthquake

Fig. 7

Force–displacement plot of MR damper for Bam (2003) earthquake

Fig. 8

Force–velocity plot of MR damper for Bam (2003) earthquake

Fig. 9

Force–displacement plot of MR damper for Chichi (1999) earthquake

Fig. 10

Force–velocity plot of MR damper for Chichi (1999) earthquake

It is seen from the above figures that the control characteristics for the two earthquakes are distinctly different. The differences in the two responses are largely due to the presence of the directivity effect in one and the fling step effect in the other. The fling step causes large displacement in the structure. The peak values for different response quantities of interest for uncontrolled and controlled conditions are shown in Table 1. The percentage reductions for different responses of interest are shown in Table 2. The percentage reduction is calculated as shown below

Table 1 Peak responses for Bam and Chichi earthquakes for uncontrolled and controlled conditions

Table 2 Percentage response reduction for Bam and Chichi earthquakes

$$ {\text{Percentage}}\;{\text{reduction}} = \frac{{{\mathbf{UN}}_{{{\mathbf{pr}}}} - {\mathbf{CO}}_{{{\mathbf{pr}}}} }}{{{\mathbf{UN}}_{{{\mathbf{pr}}}} }} $$

(16)

where UN_pr is the uncontrolled peak response; CO_pr is the controlled peak response.

5 Conclusions

Numerical studies lead to the following conclusion:

• 1. The controlled responses of the frame for the two earthquakes have distinctly different characteristics.

• 2. The fling step effect induces a large displacement in the structure as compared to the directivity effect.

• 3. The percentage reduction of response quantities of interest for an earthquake with directivity effect is comparable to those for far-field earthquake.

• 4. Fling step effect provides a very less reduction in response quantities of interest, and thus it appears that semi-active control using MR dampers is not suitable for the control of buildings for the near-field earthquake with fling step effect.