Keywords

1 Introduction

The installation of vibration control mechanisms in structures subjected to the effects of dynamic forces aims to reduce the magnitudes of displacement and interstory drift, providing a greater level of comfort and safety to users. These devices have different varieties and operating principles, with their specific characteristics and their application is determined by the type of structure designed and the possible events it will be subjected to [1].

These devices can be classified into three types, the active ones that need an external energy power to be activated, the semi-actives that require a small source of external energy for operation and use the movement of the structure to develop control forces, and the passive ones that stand out for consuming a minimum amount of power compared to the others [2]. The operation of passive mechanisms consists of energy dissipation using the oscillation of the main structure, with a secondary system that reduces the unwanted kinetic energy of the system, some examples of passive systems are friction dampers, viscoelastic dampers and tuned mass dampers [3].

The device model implanted in this work for vibration control is the tuned mass damper (TMD), whose operating principle consists of a mass, a spring and a viscous damper system coupled to the main structure [4]. This mechanism has a positive point which is the low waste of energy as it is a passive system, being a cheap and effective device. The TMD is dimensioned mainly to tune with the first vibration mode of the structure [5]. In this work, the TMD is able to reduce the vibrations of the building against seismic events.

Second [6], one of the most famous applications of the tuned mass damper is in the Taipei 101 skyscraper, in Taiwan, whose implementation is a milestone of modern engineering in the field of mechanical vibrations, serving as a basis for studies of new scientific projects. The application of this damping system in the building took into account that the city of Taipei is often hit by earthquakes and the TMD contributes to reducing the recurring vibrations of these unwanted events.

It is of great importance to note that the uncertainties in the structural properties of mass, stiffness and damping together with the parameters of the random dynamic excitation that take into account the peak ground acceleration, ground frequency and ground damping can change the optimal solution of the stipulated problem. Thus, it is extremely important to take into account uncertainties in the procedure in order to avoid damage to the structure, reduced performance and failures [7].

Within this context, the main objective of the present work is to propose a methodology to verify the effectiveness of installing a tuned mass damper at the top of a ten-story structure subject to random earthquakes, considering uncertainties and with the aim of reducing the maximum interstory drift of the building.

2 Methodology

In this chapter, the main concepts necessary for carrying out the case study are discussed. Therefore, as the focus is on the area of mechanical vibrations, the analysis of equations of motion as well as basic notions of vibrating elements are essential foundations for the work. Other factors such as methods of numerical integration and analysis of seismic events are also theorized throughout the chapter. In addition, in the area of probability and statistics, the input of random variables, among other fundamentals are necessary concepts for the work.

2.1 Equation of Motion

According to [8], the equation of motion for a vibrating system with the action of an external force and with n degrees of freedom (DOF) is formulated to provide, from numerical calculations, the amplitudes of displacement, velocity and acceleration of the system. To obtain the response of the equation of motion in the case of a structure subjected to an earthquake, it must be considered that the force vector is a base acceleration. The description of this formula is shown by Eq. (1).

$$\left[ M \right]{\ddot{\text{x}}}\left( t \right) + \left[ C \right]{\dot{\text{x}}}\left( t \right) + \left[ K \right]x\left( t \right) = - \left[ M \right]{\ddot{\text{x}}}_{g} (t)$$
(1)

where [M] is the mass matrix, [C] is the damping matrix and [K] is the stiffness matrix, all with dimensions (n x n). The term ẍ(t) represents the acceleration vector as a function of time, ẋ(t) represents the velocity vector as a function of time, x(t) represents the displacement vector as a function of time and ẍg(t) is the acceleration vector of the soil as a function of time, generated by the Kanai-Tajimi spectrum, which multiplied by the matrix [M] gives the forces of the seismic event.

In the numerical resolution of a shear building system considering the vectors in the transverse orientation of the structure, with n degrees of freedom, there is a need to formulate matrices containing the vibratory parameters of the structure for the calculation. The sizing of the matrices follows a pattern linked to the number of DOFs in the structure, forming square matrices of dimensions (n x n) [9]. The mass matrix, stiffness matrix and damping matrix are cited below (see Eqs. 2, 3 and 4).

$$[M]=\left[\begin{array}{c}\begin{array}{cc}{m}_{1}& 0\\ 0& {m}_{2}\end{array} \begin{array}{cc} \cdots & 0\\ \cdots & 0\end{array}\\ \begin{array}{cc} \vdots & \vdots \\ 0& 0\end{array} \begin{array}{cc} \ddots & \vdots \\ \cdots & { m}_{n}\end{array}\end{array}\right]$$
(2)

where [M] is the mass matrix, m1 is mass 1, m2 is mass 2, and mn is the mass of the last inertia element of the system.

$$[K]= \left[ {\begin{array}{*{20}l} {k_{1} + k_{2} } \hfill & { - k_{2} } \hfill & \cdots \hfill & 0 \hfill & 0 \hfill \\ { - k_{2} } \hfill & {k_{2} + k_{3} } \hfill & \cdots \hfill & 0 \hfill & 0 \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill \\ 0 \hfill & 0 \hfill & \cdots \hfill & {k_{{n - 1}} + k_{n} } \hfill & { - k_{n} } \hfill \\ 0 \hfill & 0 \hfill & \cdots \hfill & { - k_{n} } \hfill & {k_{n} } \hfill \\ \end{array} } \right]$$
(3)

where [K] is the stiffness matrix, k1 is the spring 1, k2 is the spring 2, and kn is the stiffness of the last element of the system.

$$[C]= \left[ {\begin{array}{*{20}l} {c_{1} + c_{2} } \hfill & { - c_{2} } \hfill & \cdots \hfill & 0 \hfill & 0 \hfill \\ { - c_{2} } \hfill & {c_{2} + c_{3} } \hfill & \cdots \hfill & 0 \hfill & 0 \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill \\ 0 \hfill & 0 \hfill & \cdots \hfill & {c_{{n - 1}} + c_{n} } \hfill & { - c_{n} } \hfill \\ 0 \hfill & 0 \hfill & \cdots \hfill & { - c_{n} } \hfill & {c_{n} } \hfill \\ \end{array} } \right]$$
(4)

where [C] is the damping matrix, c1 is the damping 1, c2 is the damping 2, and cn is the damping of the last element of the system.

To solve Eq. (1), a program developed in Matlab based on Newmark's method of numerical integration was used, which is an implicit method used to solve displacement, velocity and acceleration equations in the time domain [10].

2.2 Random Parameters of the Structure

In this work, the parametric probabilistic approach was used to obtain the uncertainties of the system parameters, in order to take into account, the uncertainties in the mass, stiffness and damping parameters of the main structure and the TMD installed at the top. These three stochastic variables are modeled as uncorrelated random variables with Lognormal distribution, as they cannot assume negative values, due to physical aspects, with known mean and coefficient of variation. Thus, in each run of the routine, the structure presents different parameters. Since the system's response depends on these random variables, it becomes random [11].

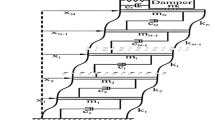
The structure to be studied was defined as a ten-story building equipped with a single tuned mass damper at the top. The building is simplified for the case study, simulating it as a shear building with ten tranversal DOFs, the mass is concentrated in each slab and the columns are springs of a certain stiffness, with viscous damping, the demonstration of this structure with the TMD installed is illustrated in Fig. 1:

Fig. 1.
figure 1

Ten-degree-of-freedom building with a single tuned mass damper at the top, (adapted from [15]).

Full size image

The work was analyzed for the case situation where a single TMD is installed at the top of the structure, considering it has a mass of 3% of the total mass of the building. The mass, stiffness and damping parameters for each of the ten floors of the structure, with the TMD parameters and their respective mean values and coefficient of variation of 5%, representing the uncertainties of the application, are described in Table 1.

Table 1. Mean value and coefficient of variation of structure and TMD random parameters.
Full size table

Considering the mean values of the parameters in Table 1 and assuming coefficients of variation equal to zero for the random variables, the first three natural frequencies of the present structure are 1.01, 3.00, and 4.94 Hz.

2.3 Random Seismic Excitations

According to [11], to solve Eq. (1) it is necessary to define the seismic loading. In this study, the seismic load is defined as a force of a one-dimensional seismic event that is simulated through the Kanai-Tajimi spectrum [12, 13] with a power spectral density function given by Eq. (5):

$$S\left(\omega \right)={S}_{0}\left[\frac{{\omega }_{g}^{4}+4{\omega }_{g}^{2}{\xi }_{g}^{2}{\omega }^{2}}{{\left({\omega }^{2}-{\omega }_{g}^{2}\right)}^{2}+4{\omega }_{g}^{2}{\xi }_{g}^{2}{\omega }^{2}}\right], { S}_{0}=\frac{0.03{\xi }_{g}}{\pi {\omega }_{g}\left(4{\xi }_{g}^{2}+1\right)}$$
(5)

where S0 is the constant spectral density, related to the peak ground acceleration (PGA), \({\omega }_{g}\) is the ground frequency and \({\xi }_{g}\) is the ground damping. Uncertainties in the ground and in the seismic excitation itself, which cannot be predicted, interfere with the optimal solution of the Kanai-Tajimi spectrum, therefore the excitation must be considered taking into account uncertainties. In the case of the seismic excitation, two levels of uncertainty can be observed, first the uncertainty of the random phase angle of the Tanai-Kajimi formula and finally the uncertainties of the soil of the dynamic excitation, in this case, the frequency of the soil, the soil damping and the PGA are assumed as independent Lognormal variables with known mean and coefficient of variation, as well as structure parameters, so the excitation has uncertainty over uncertainty [5]. The random variables of the problem, their mean values and their respective coefficient of variation of 10%, representing the uncertainties of the excitation, are described in Table 2.

Table 2. Mean value and coefficient of variation of seismic random parameters.
Full size table
Fig. 2.
figure 2

The Kanai-Tajimi spectral intensity in relation to the frequency for the soil scenario of Table 2.

Full size image

In this study, the earthquake was generated for a duration of 20 s with an integration step of 0.02 s. Following the mean values mentioned in Table 2 this graph was generated and plotted in Matlab, and the demonstration of the earthquake is illustrated in Fig. 3.

Fig. 3.
figure 3

Accelerogram of the artificial seismic event generated with Kanai-Tajimi spectrum of the mean values in Table 2.

Full size image

2.4 Monte Carlo Simulation and Latin Hypercube Sampling

The Monte Carlo Simulation (MCS) is a numerical method based on sampling random values with a large number of observations in order to acquire statistical results for probabilistic situations. The simulation starts from an average value with a specific variation to obtain the observations, where first it is assumed that all random variables are unrelated to each other, adjusting the problem in terms of these variables, and characterizing the probabilities as a probability density function to finally generate their determined values [14].

Thus, to generate the random variables for MCS was used Latin Hypercube Sampling (LHS). The LHS reduces the computational cost and provides an efficient way to generate variables from their distributions, taking samples from equal intervals, and selecting different values of a random variable where the domain of the random variable is divided into n intervals of equal probability. A value from each range is chosen at random with respect to the probability density in the interval, the choice must be made in a random way with respect to the density in each interval, so the selection must reflect the height of the density across the range [5].

3 Results and Discussions

Completing the studies of this work and considering the case of the proposed ten-story-building with a TMD at the top, subjected to random artificial earthquakes, the Matlab computational routine was executed providing, from the application of the Newmark method, the values of displacement, velocity and acceleration for each instant of time. For this situation, the results obtained of maximum interstory drift are the ones desired for the vibration analysis of the problem, being able to obtain them from the difference between the displacement values of each floor. Therefore, the values of the structural model with TMD can be compared with the model without vibration control, analyzing the effectiveness of installing this device. Considering that each story of the building is a DOF, these are the values of maximum drift, described in Table 3.

Table 3. Values of maximum inter-story drift in uncontrolled structure and structure with TMD.
Full size table

Analyzing Table 3, it is notable that there is a considerable reduction in the maximum drift values per floor, reaching values around 55%, the expected reduction values are due to the installation of the tuned mass damper in the structure. The maximum interstory drift value has occurred on the second floor of the building, so this will be used for general analysis as it is the most critical situation in this case. Then it becomes necessary to define the number of samples to be used in the course of the study, so a graph of convergence of the mean of the maximum interstory drift values is drawn up to define the ideal number to be used for the work, it is shown in Fig. 4.

Fig. 4.
figure 4

Convergence of the mean of maximum interstory drift.

Full size image

Analyzing Fig. 4, it was decided to use the amount of 300 samples, as this is where the line tends to stabilize, providing greater credibility of results. Based on this definition, a probability density function was created in relation to the maximum drift for the number set of samples, in the situation without vibration control and in the case with TMD installed, the results can be compared and analyzed in Fig. 5.

Fig. 5.
figure 5

Probability density function of maximum interstory drift for uncontrolled structure (red curve) and structure with TMD (blue curve). (Color figure online)

Full size image

Figure 5 demonstrates the frequency diagrams in unit area histograms constructed for the uncontrolled structure case (red histogram) and for the controlled structure case (blue histogram) for maximum drift. Looking at the graph, it can be seen that the blue curve is slender compared to the red curve, this is due to the variance has been reduced after installing the TMD, thus showing the effectiveness of the proposed methodology.

For a better demonstration of the vibration control event, an analysis graph was plotted for the maximum interstory drift values obtained on the second floor of the building in relation to the time of action of the seismic forces, which is equivalent to 20 s. Thus, the data can be analyzed in another way, and the demonstration of the reduction of amplitudes can be better visualized, as illustrated in Fig. 6.

Fig. 6.
figure 6

Interstory drift on the second floor for uncontrolled structure (red curve) and structure with TMD (blue curve). (Color figure online)

Full size image

Looking at the graph in Fig. 6, it is possible to visualize a notable reduction of the amplitudes of the structure, the reduction occurs mainly after 12 s of earthquake action, where the amplitudes of the structure without control (red curve) increase, but those of the structure with vibration control (blue curve) are reduced. The values refer to the second floor of the structure because, as already mentioned, it is the worst point for interstory drift in this case.

4 Conclusions

One of the positive points of a TMD is that it is a passive energy dissipation device that do not need mechanisms for activation, so it become cheaper compared to active ones, this is one of the advantages of the tuned mass damper, together with its effectiveness and reliability.

With the results obtained in the numerical simulation, a technical analysis was carried out based on theoretical references in order to prove the values that define the effectiveness of the tuned mass damper. The responses of the comparison between the structure with TMD installed and the structure without a vibration control device, as seen in Fig. 6, demonstrate that over time the seismic event was active, there was a visible drop in interstory drift amplitudes. In percentage values, this vibration control device was effective in reducing interstory drift by about 55% in its most critical case, as shown in Table 3, thus being able to be considered a passive control system applicable to the case study of this work.

In this study, the installation of the vibration control device also contributed to reducing the variance arising from uncertainties in the system, visible in the probability density function in Fig. 5. Uncertainties of the structure, the TMD and the seismic force that are common in real cases, due to human actions and of nature, uncertainties are always present and must be considered because they affect the final results of the study.

Thus, it can be concluded from the values obtained the effectiveness of the proposed methodology and the installation of the vibration control mechanism, which showed that a passive energy dissipation device was effective in reducing the interstory drift of this building, bringing safety in critical earthquake situations that may pose a danger to individuals of the place.