Keywords

1 Introduction

Damage sometimes manifests itself as the introduction of nonlinearity into a linear system. The damage that introduces nonlinearity into structures includes post-buckled structures (duffing nonlinearity), fatigue or breathing cracks (bilinear stiffness effect), and rattling joints (impacting systems with discontinuities). Damage detection can be significantly enhanced if one accounts for nonlinear characteristics of the structure during extraction of damage sensitive feature [1,2,3,4].

A complete list of nonlinear identification techniques developed is very exhaustive and hence to give a reasonable flavor of the range of techniques developed a few of them, with a reasonable success, are mentioned here. The comprehensive list of techniques includes time-series models [5], reverse path spectral methods [6], describing function [7], Volterra and Wiener series [8], adaptive Volterra filter [9], meta-heuristic algorithms [10], time–frequency analysis [11, 12] and so on.

In this paper, a nonlinear system identification method based on correspondence between the analytical and empirical slow-flow equation of the dynamics of the systems is presented. This nonlinear system identification technique using empirical slow-flow model requires only input–output measurement and need not know about the type of nonlinearities present in the system. A numerical simulation study has been carried out on a beam with breathing crack and investigations carried out in this paper clearly indicate that the empirical slow-flow method is an effective scheme for nonlinear parameter estimation even with noisy measurements.

2 Nonlinear System Identification Using Empirical Slow-Flow Model

The slow-flow-based system identification technique (SFMI) is based on multiscale dynamic partitions and the direct analysis of the measured time history response without any knowledge about the system [13]. It partitions the system response in terms of slow and fast components. Generally, a time history response of a structure is composed of a number of well-separated dominant frequency components called fast frequencies of the response and slow dynamic components that are represented by the slowly varying modulations of the fast-frequency components.

The slow-flow model of a nonlinear system provides a good approximation to the original dynamic system and also it governs the long-term behavior of the response. The reduced slow-flow model is easier to analyze than the traditional equations of motion and its parameters such as slowly varying amplitudes and phases provide clear-cut information about the characteristics of the system than the original time history response. This is usually performed by Complexification-Averaging (Cx-A) technique [14].

On the other hand, Hilbert transform to the actual time history response can be applied in order to obtain the instantaneous parameters such as instantaneous amplitude and instantaneous phase/instantaneous frequency. These can be easily related to the slow-flow model parameters obtained analytically through complexification-averaging technique from which the system parameters can be obtained.

3 Complexification-Averaging (Cx-A) Technique

The actual time history response is decomposed into slow and fast dynamics components using the Complexification-Averaging (Cx-A) technique

The Complexification-Averaging Method (CX-A) basically involves the following four steps:

  1. (i)

    complexification of the equations of motion

  2. (ii)

    partition of the dynamics into slow and fast component

  3. (iii)

    averaging of the fast-varying terms and

  4. (iv)

    extraction of the slow-flow variables from the averaged system.

In order to demonstrate the method, a nonlinear single degree of a system exhibiting a polynomial form of nonlinearity up to fourth order is considered.

$$ \begin{aligned} & {\ddot{x}} + {c}{{\dot{x}}} + {k}_{1} {x} + {k}_{2} {x}^{2} + {k}_{3} {x}^{3} + {k}_{4} {x}^{4} = 0 \\ & {\text{with}}\quad {x(0)} = {X,}\;\,{\dot{x}}(0) = 0,{ m} = {1} \\ \end{aligned} $$
(1)

For complexification, complex change of variable \( {{{\Psi} (t) = }}\dot{x}(t) + {\text{j}}{\upomega x(t)} \) is carried out

$$ x = \frac{\Psi -\Psi^{\prime}}{2{\text{j}}{\omega}};\quad\dot{x} = \frac{\Psi -\Psi^{\prime}}{2};\quad{\ddot{\text{x}}}(\text{t}) = \dot{\Psi} - \text{j}\omega\frac{\Psi -\Psi^{\prime}}{2} $$
(2)

where superscript \( ^{\prime } \) indicates complex conjugate.

The equation of motion (Eq. 1) in terms of complex variable (Eq. 2) can be written as

$$ \begin{aligned} & {{\dot{{\Psi} } - {\text{j}}\omega }}\frac{{{{{\Psi} + {\Psi} }}^{{\mathbf{\prime }}} }}{2} + c\frac{{{{{\Psi} + {\Psi} }}^{{\mathbf{\prime }}} }}{2} + k_{1} \frac{{{{{\Psi} - {\Psi} }}^{{\mathbf{\prime }}} }}{{2{\text{j}}{\omega }}} + k_{2} \left(\frac{{{{{\Psi} - {\Psi}^{\prime}}} }}{{2{\text{j}}{\omega }}}\right)^{2} \\ & \quad + k_{3} \left(\frac{{{{{\Psi} - {\Psi}^{\prime}}} }}{{2{\text{j}}{\omega }}}\right)^{3} + k_{4} \left(\frac{{{{{\Psi} - {\Psi}^{\prime}}} }}{{2{\text{j}}{\omega }}}\right)^{4} = 0 \\ \end{aligned} $$
(3)

The second step of the partitioning of the dynamics Ψ(t) = φ(t)ejωt into slow, φ(t), and fast, ejωt, components having a single frequency with modulated amplitude and phase is performed.

By averaging out the fast-frequency component, ejωt, Eq. (3) is transformed into Eq. (5) with the help of Eq. (4) by eliminating higher order terms (square-, cubic-, and fourth-order terms)

$$ {{\dot{{\Psi} } = \dot{\varphi }{\text{e}}}}^{{\text{j}}\omega {t}} {{ + \varphi {\text{j}}\omega \text{e}}}^{{{{{\text{j}}\omega {t}}}}} $$
(4)
$$ \begin{aligned} & {{\dot{\varphi } + {\text{j}}\omega }}\frac{\varphi }{2} + c\frac{\varphi }{2} - \frac{{{\text{j}}k_{1} {\varphi }}}{{2{\omega }}} + \frac{{k_{2} }}{{{2\omega }^{2} }}\left| {\varphi } \right|{\varphi } \\ & - \frac{{3{\text{j}}k_{3} }}{{8{\omega }^{3} }}\left| {\varphi } \right|^{2} {\varphi } - \frac{{k_{4} }}{{{4\omega }^{4} }}\left| {\varphi } \right|^{3} {\varphi } = 0 \\ \end{aligned} $$
(5)

On carrying out the third step of CX-A, the equation of motion represents an approximation to the actual dynamics. After averaging, the corresponding envelope and phase variables will be extracted by rewriting the variable φ(t) in polar form, φ(t) = a(t)ejβ(t) as

$$ \begin{aligned} & \dot{a} + {\text{j}}a{{\dot{\beta } + }}\frac{{{\text{j}}{\omega a}}}{2} + \frac{ca}{2} - \frac{{{\text{j}}k_{1} {a}}}{{2{\omega }}} + \frac{{k_{2} a^{2} }}{{{2\omega }^{2} }} \\ & \quad - \frac{{3{\text{j}}k_{3} a^{3} }}{{8{\omega }^{3} }} - \frac{{k_{4} a^{4} }}{{{4\omega }^{4} }} = 0 \\ \end{aligned} $$
(6)

The real and the imaginary parts of Eq. (6) are

$$ \dot{a} + \frac{ca}{2} + \frac{{{k}_{2} {a}^{2} }}{{2{\omega }^{2} }} - \frac{{{k}_{4} {a}^{4} }}{{{4\omega }^{4} }} = 0 $$
(7a)
$$ {{\dot{\beta } + }}\frac{\omega }{2} - \frac{{k_{1} }}{{2{\omega }}} - \frac{{3k_{3} a^{2} }}{{8{\omega }^{3} }} = 0 $$
(7b)

The boundary conditions can be determined by

$$ {\varphi }\left( {t} \right) = {a}\left( {t} \right){\text{e}}^{{{\text{j}\beta }\left( {t} \right)}} $$
(8)
$$ {{\Psi}} ({t}) = \varphi ({t}){\text{e}}^{{\text{j}}\omega {t}} = \dot{x}(t) + {\text{j}}\omega {x}({t}) $$
(9)

Hence β(t) = π/2 and a(0) = Xω

On solving the real and the imaginary part (Eq. 7), the slow-flow parameters can be obtained as

$$ a(t) = X{\upomega }e^{{[ - \frac{ct}{2} - \frac{{{k}_{2} t^{2} }}{{2{\omega }^{2} }} + \frac{{{k}_{4} t^{4} }}{{{4\omega }^{4} }}]}} $$
(10a)
$$ {{\beta ({t}) }} = \frac{{3k_{3} X^{2} }}{{8{\omega c}}}(1 - e^{ - ct} )- \left(\frac{\omega }{2} - \frac{{k_{1} }}{{2{\omega }}}\right)t + \frac{\pi }{2} $$
(10b)

Therefore, Eqs. (10a) and (10b) are the approximate and simplified slow-flow equations of the considered dynamical system. The system response predicted by the Cx-A method can be written in general form as

$$ x(t) = \frac{a(t)}{\omega }\sin ({\omega }t+{{ \beta ({t}))}} $$
(11)

which shows that the total phase variable is θ = \( {\omega }t+ \beta ({t}) \);

The slow-flow model of the system after performing Cx-A is given by

$$ \begin{aligned} x(t) & = \frac{a(t)}{\omega }\sin ({\omega }t + {{\beta ({t}))}} \hfill \\ {\text{where }}a(t) & = X{\omega }{\text{e}}^{{\left[ - \frac{ct}{2} - \frac{{{k}_{2} t^{2} }}{{2{\omega }^{2} }} + \frac{{{k}_{4} t^{4} }}{{{4\omega }^{4} }}\right]}} \hfill \\ {\text{and}} \quad \beta (t) & =\frac{{3k_{3} X^{2} }}{{8{\omega c}}}(1 - {\text{e}}^{ - ct} )- \left(\frac{\omega }{2} - \frac{{k_{1} }}{{2{\omega }}}\right)t + \frac{\pi }{2} \hfill \\ \end{aligned} $$
(12)

It is recommended to use the sub- and super-harmonics instead of frequency ‘ω’ during partitioning for systems exhibiting strong nonlinearities to improve the predictive capacity of the Cx-A model.

4 Numerical Study—Breathing Crack Problem

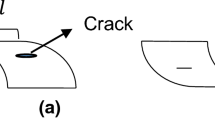
A cantilever beam with a breathing crack is considered as an example as shown in Fig. 1. The breathing crack introduces bilinear stiffness effect corresponding to the opening and closing state. The equation of motion (bilinear oscillator) of the beam with a breathing crack can be written as

Fig. 1
figure 1

Cantilever beam with breathing crack

Full size image
$$ {m}\ddot{x}({t}) + {c}\dot{x}({t}) + {g}[{x}({t})] = {f}({t});\,\,{g}({x}) = \left\{ {\begin{array}{*{20}l} {{\upalpha }{kx}} \hfill & {{x} \ge 0} \hfill \\ {kx} \hfill & {{x} < 0} \hfill \\ \end{array} } \right. $$
(13)

where g(x) is the restoring force and m, k, c, and f are the mass, stiffness, damping, and force respectively. The stiffness ratio α is defined as the ratio of squares of the cracked frequency to uncracked frequency. It lies in the range 0 ≤ α ≤ 1. The bilinear frequency ωB of the undamped free vibration of bilinear oscillator [15] is given by

$$ \omega_{\text{B}} = \frac{{2\omega_{0} \omega_{1} }}{{(\omega_{0} + \omega_{1} )}} = \frac{{2\sqrt {\alpha } }}{{(1 + \sqrt {\alpha } )}}\omega_{0} $$
(14)

where ω0 and ω1 are the natural frequencies of the uncracked and cracked beam, respectively, k and k′ (\( {k}^{{\mathbf{\prime }}} = {\alpha }{k} \)) are the stiffness of the uncracked and cracked states of the beam.

In the present work, the bilinear nature of the beam with a breathing crack is approximated by an amplitude dependent polynomial model of order 4 using the Weierstrass Approximation theorem [16]. Then a slow-flow model is established for the approximated polynomial system through Cx-A technique and its slowly varying parameters are determined.

The Weierstrass approximation theorem states that: “If f(x) is a continuous real-valued function on [a, b] and if any ε > 0 is given, then there exists a polynomial P(x) on [a, b] such that |f(x)-P(x)| < ε for all x ε [a, b]. Since the restoring force g(x) is a continuous function of displacement x, it can be well approximated by a polynomial.”

The restoring force of the fourth-order-approximated polynomial-type nonlinear system is given by

$$ \begin{aligned} & {m}{\ddot{x}}({t}) + {c}{\dot{x}}({t}) + {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }}[{x}({t})] = {f}({t}){\mkern 1mu} {\text{with}}{\mkern 1mu} \widehat{g}[{x}({t})] \\ & \quad = {g}_{0} + {c}_{1} {kx} + {c}_{2} {kx}^{2} + {c}_{3} {kx}^{3} + {c}_{4} {kx}^{4} \\ \end{aligned} $$
(15)

where g0 indicates the constant term and can be neglected when no static force is applied to the structure and k indicates the uncracked stiffness and c1kx represents the linear component and the additional higher order terms indicate the nonlinear components of the approximated polynomial nonlinear system. The coefficients, c1, c2, c3, c4 are evaluated by minimizing the error function E between the actual and approximated polynomial nonlinear system using the above-mentioned Weierstrass approximation theorem in the domain [–X, X] as

$$ {E}({c}_{1} ,{c}_{2} ,{c}_{3} ,{c}_{4} ) = \int\limits_{{ - {X}}}^{X} {g}[{x}({t})] - \hat{g}[{x}({t})]\}^{2} {\text{d}}x; $$
(16)
$$ \frac{{\partial {E}}}{{\partial {c}_{i} }} = {0,}\,\quad{\text{for}}\,{{i} = 1,2,3,4} $$
(17)

By applying the above equation, the coefficients are obtained [17, 18] as

$$ {c}_{1} = \frac{{(1{ + \alpha })}}{2},\quad{c}_{2} = - \frac{{105(1{ - \alpha })}}{{128{X}}},\quad{c}_{3} = 0,\quad{c}_{4} = \frac{{105(1{ - \alpha })}}{{256{X}^{3} }} $$
(18)

The actual system equation of motion is given by

$$ \ddot{y}({t}) + 23.5619 \dot{y}({t}) + 3.5{e}4\underbrace { ( 0. 7 5 )}_{\alpha }{y(t) = 0;\quad y}_{0} { = 0}.25;\quad{\dot{y}}_{0} = 0 $$
(19)

where \( {\alpha } \) is the stiffness ratio varying between 0 and 1 such that \( {\alpha } \) = 1 for x(t) < 0 and \( {\alpha } \) < 1 for x(t) ≥ 0. Further, the system can be idealized as a system with polynomial terms having coefficients up to fourth order depending on the value of the stiffness ratio, as discussed earlier.

$$ \begin{aligned} & {{\ddot{y}(t) + 23}}{.5619}\dot{y}(t){ + 3}{.5e04c}_{1} {y(t) + 3}{.5e04c}_{2} {y}^{2} {(t)} \\ & \quad { + 3}{.5e04c}_{3} {y}^{3} {(t) + 3}{.5e04c}_{4} {y}^{4} {(t) = 0} \\ \end{aligned} $$
(20)

The value of X is chosen as 2e-4 for this problem.

The system parameters considered are m = 1, c = 23.5619 Ns/m, k = 3.5e4. The time history responses are measured using Runge–Kutta integration scheme. The natural frequency of the system is found to be 30 Hz. The nonlinear system response will exhibit sub- and super-harmonics of excitation frequency into addition to the fundamental harmonic.

The displacement time history response obtained using Runge–Kutta (RK) integration scheme and the corresponding power spectrum (PSD) of the actual system are shown in Fig. 2. The white Gaussian noise in the form of signal to noise ratio (SNR = 50) is added to the time history response before processing. It can be observed from Fig. 2b that the spectrum exhibits peaks at the excitation frequency and at second and fourth-order super-harmonic resonances. This clearly indicates the presence of nonlinearity in the structure.

Fig. 2
figure 2

a Displacement time history response; b power spectrum of breathing crack problem

Full size image

Hilbert Transform (HT) on the displacement time history response can be applied to obtain the instantaneous amplitude and instantaneous frequency. The Hilbert transform of response x(t) can be defined as

$$ {\bar{x}}({t}) = {\text{HT}}({x}({t})) = \frac{1}{\pi }{\text{PV}}\int\limits_{ - \infty }^{\infty } {\frac{{{x}(\tau )}}{{{t} - \tau }}{\text{d}}\tau } $$
(22)

where PV indicates the principal Cauchy value. The corresponding analytical signal z(t) is then given by

$$ z(t) = x(t) + {\text{i}}{\bar{x}}(t) = A(t){\text{e}}^{{{\text{i}}\theta (t)}} $$
(23)
$$ A(t) = \left[ {\left( {[x(t)]^{2} + [\bar{x}(t)]^{2} } \right)} \right]^{1/2} $$
(24a)
$$ \omega (t) = \frac{{{\text{d}}\theta (t)}}{{{\text{d}}t}};\quad \, \theta (t) = { \tan }^{ - 1} \frac{{\bar{x}(t)}}{x(t)} $$
(24b)

where A(t) is instantaneous amplitude, \( \theta (t) \) is the phase angle and \( \omega (t) \) is the instantaneous frequency.

The instantaneous parameters (i.e., instantaneous amplitude and instantaneous frequency) obtained using HT of time history response is shown in Fig. 3a, b respectively. Once the instantaneous parameters are obtained through the Hilbert transform, it can be easily related to the slow-flow equations of the system.

Fig. 3
figure 3

HT of response a instantaneous amplitude b instantaneous frequency

Full size image

Through Slow-Flow Model Identification, the instantaneous phase given in Eq. (10b) after eliminating k3 (i.e. c3 = 0) becomes

$$ \beta ({t}) = - \left(\frac{\omega }{2} - \frac{{k_{1} }}{{2{\omega }}}\right)t + \frac{\pi }{2} $$
(25)

The slow-flow instantaneous phase equation (Eq. 25) obtained through complexification-averaging and the Hilbert transform (Eq. 24) are compared. As the system frequency and mass are known a priori, the time-dependent linear stiffness coefficient k1 can be estimated. A single value of k1 is then estimated using the least square procedure. The final single value of k1 is then related to stiffness ratio \( {\alpha } \) and then the value is determined.

Further, the instantaneous amplitudes given in Eqs. (10a) and (24a) are compared and the system damping parameter is estimated using the least square procedure.

The identified system parameters are shown in Table 1. It can be verified from Table 1 that the parameters obtained using slow-flow model compare well with the actual parameters even with measurement noise. The extension of the slow-flow model formulations to multi-degree of freedom is rather straightforward and Hilbert–Huang Transform (HHT) is used instead of HT for instantaneous parameter extraction. The advantage of the slow-flow model technique is that it is applicable for both linear and nonlinear systems which might include systems with smooth and non-smooth nonlinearities

Table 1 System identification by SFMI
Full size table

5 Conclusion

In this paper, the physics-based interpretation of instantaneous parameters derived using Hilbert transform and the slow-flow equation of the dynamics of the system is demonstrated. Based on the correspondence between the HT approach and slow-flow model, a nonlinear system identification strategy using the empirical slow-flow model in the time domain is presented. The analysis is based on input–output response measurements of the system and is applicable for both smooth and non-smooth nonlinear systems. The Hilbert transform approach gives sharper frequency and time resolutions compared to other time–frequency decomposition and helps in accurate estimation of instantaneous parameters for strongly nonlinear systems.

The extension of the approach to multi-degree of freedom is rather straightforward and Hilbert–Huang transform needs to perform on the time history response instead of Hilbert transform.

Numerical investigations have been carried out to verify the presented empirical slow-flow model for nonlinear parameter estimation by solving a beam with a single-edged breathing crack problem. Numerical studies presented in this paper clearly indicate that the proposed identification strategy using slow-flow model can identify nonlinear coefficients accurately even with noisy measurements.