Introduction

Identification of fatigue-breathing cracks at an early stage offers critical information about the health of structures, aiding in the prevention of catastrophic failure and saving human lives. The identification of breathing cracks using vibration data has been the subject of much research over the last three decades. Researchers have employed different analytical and numerical methods for nonlinear vibration analysis of beam structures [1] and mechanical components [2]. Bayat et al. [3] developed a homotopy perturbation method for finding the analytical solution for the vibration of electrostatically actuated micro-beams. The higher order approximations obtained by the method provide very accurate results for the large-amplitude vibration of electrostatically actuated micro-beams. Alternatively, Bayat et al. [4] used the Hamiltonian Approach for large-amplitude free vibrations of axially loaded Euler–Bernoulli beams. The results of the study reveal that the Hamiltonian approach is quickly convergent and accurate, and only one iteration leads to high accuracy of solutions for the whole domain. Payat et al. [5] demonstrated He's max–min approach for the nonlinear vibration of axially loaded Euler–Bernoulli beams. Their study concluded that the max–min approach does not necessitate small perturbation unlike other periodic solutions approaches based on a Fourier series, complicated numerical integration, and traditional perturbation methods. Chintha and Chaterjee [6] employed the Volterra series for nonlinear parameter estimation of both symmetric and non-symmetric systems utilizing harmonic probing principles considering higher order frequency functions. Prawin et al. [7] employed an improved version of the conditioned time- and frequency-domain method for nonlinear parameter estimation of multi-degree of freedom systems. Andreaus et al. [8] analyzed theoretically and experimentally both the free and forced harmonic vibration response of the beam with breathing crack (damage-induced nonlinearity) and concluded the presence of superharmonics in the response. Bovsunovsky and Surrace [9] provide a detailed state-of-the-art on the non-linearities in the vibrations of elastic structures with a closing crack. Besides presenting the studies on the nonlinear effects caused by breathing cracks in the response, the article also discussed the potential and prospects of using nonlinear behaviour to detect damage. Among the nonlinear effects, the sensitivity of the superharmonics, subharmonics, and intermodulations for localization of breathing crack is highlighted and investigations exploiting it by various researchers using harmonic vibration data are discussed. It should be mentioned here that all of the existing algorithms characterize breathing crack based on the amplitude or energy of the spectrum of super harmonics (single-tone)/sidebands (bitone) extracted from vibration response. For example, Broda et al. [10] proposed the ratio of spectral amplitudes of superharmonic-to-fundamental harmonic for breathing crack localization. Giannini et al. [11] compared the experimental response with the harmonic damage surface based on the normalized spectrum (i.e., the ratio of second harmonic to main harmonic) developed from the numerical model to locate and quantify the severity of the breathing crack. Kim et al. [12] used the concept of multi-scales exploiting the intermodulations for fatigue crack localization using bitone harmonic vibration data. Yelve et al. [13] proposed a damage index (DI) based on the first sidebands on either side of probing frequency for breathing crack diagnosis. The detailed review also concluded that bitone harmonic vibration is preferable over single-tone harmonic excitation due to the absence of pseudo-input force harmonics and timely breathing crack identification.

The challenge in the identification of breathing crack is the extraction of nonlinear sensitive features, i.e., super harmonics and intermodulation from the measured vibration response. The amplitude of these nonlinear features is significantly low when compared to linear components and becomes weak in a noisy environment. The conventional power spectrum cannot be employed directly on the measured response to extract nonlinear features and very challenging to track down the amplitudes of super harmonics/intermodulation. In view of this, Prawin et al. [14] proposed weighting-function enhanced curvature approach utilizing the power spectrum of the response to reliably extract low amplitude super harmonics and intermodulation for breathing crack diagnosis. However, the choice of zone factor in the proposed approach influences the damage index and the method is also sensitive to the spatial location of the load in addition to the requirement of reference data. Al-hababi et al. [15] utilized dual Fourier transform spectra for the identification of breathing crack in beam-like structures. However, location is not attempted. Alternatively, Prawin et al. [16, 17] used multi-variate analysis like singular spectrum analysis (SSA) [16] and singular value decomposition (SVD) [17] to isolate and reconstruct the nonlinear components before the power spectrum. The major limitation of the above signal decomposition approaches for breathing crack diagnosis is the high computational cost (associated with Hankel Matrix formation and decomposition using SVD/SSA for each sensor) which also increases largely with the increase in the number of sensors. It should also be mentioned here that the power spectrum is unsuitable for nonlinear and non-stationary signals. In view of this, Douka et al. [18] and Prawin et al. [19] employed time–frequency analysis based on the Hilbert–Huang transform (HHT) and empirical slow flow model for nonlinear system identification exploiting slow dynamics of the structure. Similarly, Cui et al. [20], Sinha [21], and Jiang et al. [22] proposed Higher order spectral analysis techniques, including Bispectrum, Trispectrum, and wavelet bicoherence, for breathing crack diagnosis. However, the majority of the studies on higher order spectral analysis related to fatigue-breathing crack identification are limited to rotating machinery components and simple spring–mass–damper systems.

Spectral correlation has been recently employed by researchers [23,24,25,26,27,28,29] in the field of SHM and NDE by combining with other ultrasonic inspection techniques for fatigue-breathing crack identification exploiting the cyclo-stationary nature of the response. The measured dynamic signatures (acceleration signals) obtained from the structure with breathing crack are generally non-stationary and bilinear in nature [23]. The bilinear behaviour is due to the opening-closing behaviour of the breathing crack. It was theoretically proved by Bouillaut and Sidahmed [24] that there is a strong link between cyclo-stationary and bi-linearity (i.e., opening and closing behaviour). It was also shown by the authors in their work that the cyclo-stationary approach offers more facilities in terms of computational time and flexibility of use for handling those signals. Boungou et al. [25] have used the second order of cyclo-stationary to inspect the nonlinearity of the breathing crack during fatigue damage. They have reported that the magnitude of the cyclic frequency, corresponding to the frequency of the nonlinear breathing crack model, increases with crack depth following definite trends. The nonlinearity of the breathing crack during fatigue deterioration is investigated using spectral correlation by Sohn et al. [26] and Liu et al. [27] based on nonlinear ultrasonic principles. In addition, their studies concluded that the selection of the pumping frequency as the resonant frequency boosts the spectral correlation's sensitivity to the identification of breathing cracks. Lim et al. [28] employed spectral correlation for damage detection under changing temperature conditions. The spectral correlation approach is a more robust and reliable approach to extract nonlinear features, especially in the case of a highly corruptive environment over the above-mentioned conventional spectral analysis, higher order spectral analysis, signal decomposition, and multi-variate analysis techniques. The spectral correlation is zero for Gaussian white noise signal corresponding to cyclic frequency \(\alpha > 0\) [29]. This motivates the present work to apply spectral correlation (i.e., second-order cyclo-stationarity or cyclic spectral density function) on the measured noisy vibration response of the beam with multiple breathing crack and derive a damage index based on spectral correlation for damage diagnosis. This paper contributes to the development of a generalized procedure of multiple breathing crack localization in beams based on spectral correlation through numerical simulations and lab-level experimentation.

Localization of multiple breathing cracks using the measured dynamic responses is a highly complex inverse problem as the number of breathing cracks present in the structure is not known beforehand. Only very limited studies are available in the literature based [31,32,33,34,35] on the identification of multiple breathing cracks in beams using vibration data. Pugno et al. [30] investigated the nonlinear dynamic response of the beam with several breathing cracks and concluded that the presence of multiple cracks leads to complex vibration patterns and increased amplitude of vibration. Sekhar et al. [31] have proposed a technique combining wavelets and eigenfrequencies for multiple breathing crack identification and to get more physical insights. However, the studies were performed on beam structures when compared to a detailed investigation of the rotor in the research study on multiple crack effects. In addition, the method used by Sekhar et al. [31] requires the proper selection of the parameters, such as the mother wavelet and the scale of wavelet decomposition and the finite-element model. Chomelette [32] makes use of the direct zeros of the higher order transfer function for the identification of multiple breathing cracks. However, the method is less accurate in localizing the crack close to the support (cantilever beam). Identifying the cracks closer to the support from the vibration response is challenging in the case of beams with multiple breathing cracks. Kharzan et al. [33] investigated the beams with multiple breathing cracks and concluded that the spatial location of the breathing crack has a greater role in the nonlinear dynamic characteristics of the response. Bovsunovsky et al. [34, 35] have concluded that the degree of nonlinearity due to the presence of breathing cracks depends on factors such as the size of the crack and the location along the cracked beam where the harmonic force is applied. For example, the degree of nonlinearity in the response will be higher if the input harmonic force is applied at a position closer to the breathing crack when compared to the case when the same input is applied at the farthest point from the position of the breathing crack. Hence it is essential to use more than one excitation point (in fact several excitation points) on the beam to identify all the breathing cracks which is not practical.

Due to the high level of nonlinear vibrations, structures with multiple breathing cracks exhibit more softening behaviour than a structure with a single breathing crack. The individual contribution of the degree of nonlinearity of each of the breathing cracks present summed to the total damage severity. In addition, the degree of nonlinearity contribution of each breathing crack depends on the state of the breathing crack, depth, and spatial location. Apart from this, the breathing cracks present in the structure need not be in the same state at any particular time instant, i.e., while a set of breathing cracks may be in an open state, while others may be in a semi-open or closed state at any particular time instant. It can also be noted here that the degree of nonlinearity exhibited by breathing crack(s) present at a particular spatial location will be high for a particular mode of vibration when compared to breathing cracks present at other spatial locations and is well dependent on the excitation position. Hence, it is essential to vary the excitation frequency and/or vary the spatial location of harmonic excitation to localize multiple breathing cracks. This whole exercise will be computationally very expensive. The conventional methods cannot establish the relationship between the superharmonics or intermodulation to several breathing cracks.

This paper presents a spectral correlation approach for multiple breathing crack diagnosis using the vibration response to overcome the above limitations and achieve early damage detection. The uniqueness of the proposed spectral approach for multiple breathing crack localization over the traditional approaches is

  1. (i)

    No need to vary the structure excitation position.

  2. (ii)

    No need to excite the structure multiple times with varied frequencies of harmonic excitation for localizing multiple breathing cracks.

  3. (iii)

    Localization of multiple breathing cracks including cracks closer to support and closely spaced cracks.

  4. (iv)

    Robustness to measurement noise.

  5. (v)

    Reliable extraction of nonlinear components of all cracks irrespective of varied intensity and the spatial location.

  6. (vi)

    Completely data-based and baseline-free approach.

The rest of the article is structured as: the sections “Spectral Correlation” and “Generalized Methodology of Spectral Correlation-Based Breathing Crack Localization” briefly describe the spectral correlation function and the generalized methodology of breathing crack diagnosis in multi-crack beam structures using the proposed approach. Modeling of multiple breathing cracks is presented in the section “Breathing Crack Model Description”. The sections “Numerical Investigations” and “Experimental Investigation” present the numerical simulation and lab experimentation studies and ended with conclusions in the section “Conclusion”.

Spectral Correlation

Spectral correlation is a powerful second-order cyclo-stationarity tool that is frequently used to analyze and characterize vibration signals. The spectral correlation function \(S_{x}^{\alpha } \left( \omega \right)\) computed at a specific cyclic frequency α, and spectral frequency ω [29] is mathematically given by

$$S_{x}^{\alpha } \left( \omega \right) = {\raise0.7ex\hbox{${FT}$} \!\mathord{\left/ {\vphantom {{FT} {t,\tau }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${t,\tau }$}}\left\{ {R_{x} \left( {t,\tau } \right)} \right\} = \iint {R_{x} \left( {t,\tau } \right){\text{ e}}^{ - i2\pi \alpha t} {\text{e}}^{ - i2\pi \omega \tau } {\text{d}}t{\text{d}}\tau },$$
(1)

where FT represents the Fourier Transform and Rx(t,τ) indicates the autocorrelation function of the time-history signal ‘x’ with respect to time ‘t’ and time lag τ.

The spectral correlation (SC) function computation using the Fourier spectrum of x(t) and expectation operator (E) is given by

$$S_{x}^{\alpha } \left( \omega \right) = E\left[ {X\left( {\omega + \frac{\alpha }{2}} \right)X^{*} \left( {\omega - \frac{\alpha }{2}} \right)} \right].$$
(2)

The cyclic spectral energy (CSE) estimated at a cyclic frequency ‘\(\alpha\)’ over a frequency band [\(\omega_{1} ,\omega_{2}\)] is mathematically given by

$${\text{CSE}}(\alpha ) = \int\limits_{{\omega_{1} }}^{{\omega_{2} }} {\left| {{\text{SC}}\left( {\omega_{k} ,\alpha } \right)} \right|{\text{d}}\omega } .$$
(3)

Spectral correlation estimated at a zero cyclic frequency results in spectral density function and spectral correlation exhibits multiple peaks at various spectral frequencies estimated at a non-zero cyclic frequency [17]. Specifically, the spectral correlation can be used to easily extract the sidebands or intermodulation produced by the modulation effect of two input frequency components during vibration. When the cyclic frequency is not zero (equal to the difference of input frequencies), the spectral correlation shows a peak at the average of the two input frequencies. The spectral correlation peak is not only caused by interactions between the input frequencies but also by interactions between noise components and their harmonics and intermodulation frequencies. This is because many different frequency combinations lead to the same cyclic frequency, which results in multiple SC peaks at various frequencies. The amplitudes of these peaks, however, depend on the energy of the various components present in the signal, including sidebands and harmonics, which are nonlinear components. As cyclic frequencies vary, so does the spectral correlation.

Generalized Methodology of Spectral Correlation-based Breathing Crack Localization

The following are the steps involved in generalized breathing crack localization using the spectral correlation technique in a multi-crack beam:

  1. 1.

    The beam is subjected to bitone harmonic excitation (ωpump + ωprob). The pumping frequency (ωpump) is chosen as near to the fundamental frequency of the target beam. The probing frequency (ωprob) is generally higher than the pumping frequency (ωpump). 

  2. 2.

    The acceleration time-history measurements are collected at considered “N” sensor locations throughout the beam span.

  3. 3.

    Compute the cyclic spectral energy (CSE) of each sensor for a selected non-zero cyclic frequency (α). The damage index (DI) for sensor ‘i’ is mathematically given by

    $${\text{DI}}(i) = {\text{CSE}}(i,\alpha ).$$
    (4)
  4. 4.

    The sensor nodes with the higher magnitude of damage index are those that are spatially near the position of the breathing cracks along the length of the beam.

Breathing Crack Model Description

The equation of motion of the beam model is

$$\left[ M \right]\left\{ {\ddot{y}} \right\} + \left[ C \right]\left\{ {\dot{y}} \right\} + \left[ K \right]\left\{ y \right\} = \left[ F \right],$$
(5)

where [M], [C], and {K} are the mass, damping, and stiffness matrix and {F} is the force matrix. The terms \(\left\{ {\ddot{y}} \right\}, \, \left\{ {\dot{y}} \right\},\left\{ y \right\}\) represent the acceleration, velocity, and displacement time-history response. The beam is discretized using 1D Euler-type finite elements.

The material and geometric parameters are Young’s modulus (E), length (L) moment of Inertia Iu, and Id for healthy and cracked beam. The stiffness [K] of the cracked beam (considering “M” number of cracks and total "N" number of elements) is given by

$$[K] = \mathop {\rm A}\limits_{e = 1}^{N} [K_{e} ] + \sum\limits_{m = 1}^{M} {\left[ {\Delta K^{(m)} } \right]} \, Cr^{(m)} (\{ y\} ).$$
(6)

The undamaged and cracked element stiffness [Ke, Kc] is mathematically given by

$$K_{e} = \frac{E}{L}\left[ {\begin{array}{*{20}c} {\frac{{12l_{u} }}{{L^{2} }}} & {\frac{{6l_{u} }}{L}} & { - \frac{{12l_{u} }}{{L^{2} }}} & {\frac{{6l_{u} }}{L}} \\ {} & {4l_{u} } & { - \frac{{6l_{u} }}{L}} & {2l_{u} } \\ {} & {} & {\frac{{12l_{u} }}{{L^{2} }}} & { - \frac{{6l_{u} }}{L}} \\ {} & {sym} & {} & {4l_{u} } \\ \end{array} } \right];\quad K_{c} = \frac{\mu E}{L}\left[ {\begin{array}{*{20}c} {\frac{{12l_{u} }}{{L^{2} }}} & {\frac{{6l_{u} }}{L}} & { - \frac{{12l_{u} }}{{L^{2} }}} & {\frac{{6l_{u} }}{L}} \\ {} & {4l_{u} } & { - \frac{{6l_{u} }}{L}} & {2l_{u} } \\ {} & {} & {\frac{{12l_{u} }}{{L^{2} }}} & { - \frac{{6l_{u} }}{L}} \\ {} & {sym} & {} & {4l_{u} } \\ \end{array} } \right], \begin{array}{*{20}c} {\mu = \frac{{\left( {l_{u} - l_{d} } \right)}}{{l_{u} }}} \\ {(0 < \mu < 1} \\ \end{array} ,$$
(7)
$$\Delta K^{m} = - H\left( {{\text{Cr}}^{(m)} (\{ y,\theta \} )} \right)K_{c} ;\left\{ {\begin{array}{*{20}l} {H\left( {{\text{Cr}}^{(m)} (\{ y,\theta \} )} \right) = 1, {\text{Cr}}^{(m)} > 0} \hfill \\ {H\left( {{\text{Cr}}^{(m)} (\{ y,\theta \} )} \right) = 0, {\text{Cr}}^{(m)} < 0} \hfill \\ \end{array} } \right.,$$
(8)
$${\text{Cr}}^{(m)} (\{ y,\theta \} ) = \frac{{\Delta \phi^{m} }}{{\max (\left| {\Delta \phi^{1} } \right|,\left| {\Delta \phi^{2} } \right|,......,\left| {\Delta \phi^{m} } \right|,....,\left| {\Delta \phi^{M} } \right|)}};\Delta \phi^{m} = \theta_{L}^{m} - \theta_{R}^{m} ,$$
(9)

where A represents the assembly operator and H is the Heaviside step function. In the above eqn. (9), the subscripts 'L' and 'R' indicate the left and right rotational degree of freedom and the superscript "m" represents the element number. More information on breathing crack modeling can be found in [11, 30].

Numerical Investigations

This section presents the numerical simulation studies on the vibration of beams containing multiple breathing cracks with varying parameters. Using a numerically generated simply supported and cantilever beam structure, the sensitivity of the spectral correlation approach to varied multiple breathing crack positions along the span, different crack depths, the spatial location of crack identification with limited sensors, and noisy measurements is studied.

Numerical Example-1: Simply Supported Beam

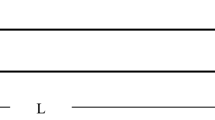
A steel simply supported beam with a dimension of 5 m × 0.3 m × 0.2 m shown in Fig. 1 is the first numerical example. For the first two modes, damping ratios of 1.5% and 2% are used to consider Rayleigh damping. Forty 1D Euler beam elements are used in the beam's modeling. The sampling frequency(fs) is 2500 Hz. The healthy beam's initial few frequencies are 18.77, 75.08, 168.95, 300.36, and 469.31 Hz. The beam is subjected to bitone harmonic excitation of 20 Hz and 500 Hz. The breathing crack is simulated at two locations, i.e., element no. 4 and 15 with both locations exhibiting a similar crack depth of 3% of the overall depth of the beam. Two breathing cracks of the same magnitude are simulated in the beam. While the first crack is closer to the support, the second crack is simulated in the middle third span of the span. The Newmark algorithm is used to compute acceleration time histories at all nodes. The measured time signals are corrupted with 5% Gaussian noise.

Fig. 1
figure 1

Cracked simply supported beam

Full size image

Spectral Correlation

The time-domain and frequency-domain (i.e., Fourier Spectrum) response corresponding to sensor node no. 15 of the cracked beam are presented in Fig. 2a, b for the breathing crack simulated at element no. 4 and 15, respectively. The Fourier Spectrum shown in Fig. 2b exhibits peaks at input excitation frequencies, i.e., 20 Hz (ωpump).and 500 Hz (ωprob), superharmonics of individual excitation frequencies, i.e., 40 Hz, 60 Hz, 80 Hz,100 Hz, 120 Hz (n ωpump with n = 2,3,4,…)etc., 1000 Hz, 1500 Hz (n ωprob) and intermodulation, i.e., 480 Hz, 520 Hz, 460 Hz, 540 Hz, etc. (ωprob ± mωpump). However, the Fourier spectrum amplitude corresponding to super harmonics and intermodulation is of very low order when compared to 20 Hz and 500 Hz (input frequencies). Therefore, the conventional Fourier spectrum cannot be employed to extract nonlinear features. It becomes much more difficult in the case of a highly corrupted environment.

Fig. 2
figure 2

Response of 15th node: a time-domain response and b Fourier spectrum

Full size image

The spectral correlation and the cyclic spectral energy (CSE)-based damage indicator for the measured vibration response of the beam with two breathing cracks are presented in Fig. 3a, b, respectively. The spectral correlation computed at different values of cyclic frequency of 20 Hz, 100 Hz, and 500 Hz using the true response is presented in Fig. 3a. The intermodulation is visible in Fig. 3a. However, the plot presented in Fig. 3b based on CSE fails to localize the breathing cracks, although the nonlinear features are enhanced through spectral correlation response. This can be explained as follows: The high-amplitude linear components still dominate and DI based on CSE cannot identify the true locations of breathing cracks. The choice of cyclic frequency also influences breathing crack identification using spectral correlation. In view of this, if nonlinear components are isolated and reconstructed at the first step, it is possible to develop a reliable multiple breathing crack diagnosis algorithm. For this purpose, the Linear Response Subtraction (LRS) scheme is employed.

Fig. 3
figure 3

True response: a spectral correlation and b DI based on the cyclic spectral energy

Full size image

Linear Response Subtraction Scheme

As the superharmonics and sidebands are buried in the total response and their amplitudes are much smaller than the linear component, they may not be easily distinguished from the background noise. In addition, it is highly difficult to extract the individual nonlinear contribution of each crack being present at varied locations with different intensities to identify multiple breathing cracks. To overcome the above limitations and to account for the evaluation of the nonlinear contribution of each crack in the measured total response of the system, it is proposed to apply linear response subtraction (LRS) scheme to the total response of each sensor to extract only the nonlinear intermodulation components at the first step. Sohn et al. [26] and Lim et al. [28] used the LRS scheme for the extraction of modulation components from bitone harmonic vibration data for improved breathing crack identification.

The response of the two distinct input harmonic excitation is eliminated by the linear response subtraction and the resulting response contains only nonlinear features. This is done in an experimental setting as follows:

  1. 1.

    First, using low- and high-frequency harmonic excitation (pumping and probing frequency, ωpump + ωprob) independently, two distinct responses are obtained.

  2. 2.

    By simultaneously exciting both frequencies, the response with modulation components is obtained.

  3. 3.

    The modified response is computed as the consequence of subtracting the response obtained under simultaneous and individual harmonic excitation (i.e., step 2–step 1)

As a result, only the intermodulation components are present in the response of the structure with breathing crack following the application of the linear response scheme. The LRS-modified response is then post-processed using spectral correlation for breathing crack diagnosis in multi-crack beams. With this background, a generalized procedure is devised for the localization of multiple breathing cracks using bitone harmonic vibration data.

Spectral Correlation with Linear Response Subtraction

The modified time-history response (i.e., after LRS application) and its corresponding Fourier spectrum are presented in Fig. 4a, b. Figure 4b depicts that the intermodulations are visible. However, the peaks at input excitation frequencies are visible as their amplitude is a higher order than intermodulation. Hence, these components cannot be completely removed. This investigation concludes that the modified response (i.e., after LRS) is more sensitive to breathing crack as it enhances the hidden harmonics and intermodulation when compared to the original total bitone harmonic vibration response. The Fourier spectrum amplitudes at nonlinear intermodulation extracted from the modified response cannot be directly employed for multiple breathing crack diagnosis. This is because even though nonlinear features are enhanced using LRS, the corresponding amplitudes are still lesser, and in the case of a highly corruptive environment, the amplitudes will get buried and more intermodulation cannot be extracted.

Fig. 4
figure 4

Modified response of 15th node (after LRS): a time response and b Fourier spectrum

Full size image

The spectral correlation is estimated at a varied cyclic frequency of 20 Hz, 100 Hz, and 500 Hz using the nonlinear intermodulation response (i.e., modified response after LRS). The corresponding result in Fig. 5a shows that all the nonlinear harmonics and intermodulation components are enhanced using Spectral correlation. The cyclic spectral energy-based damage indicator plot presented in Fig. 5b exhibits the peaks at element no. 4 and 15 (i.e., nodes 3 and 4, 14 and 15). This demonstrates the sensitivity of the LRS-modified response over the true response in multiple breathing crack diagnosis using spectral correlation and the proposed cyclic spectral energy-based damage indicator.

Fig. 5
figure 5

LRS-modified response: a spectral correlation and b DI based on CSE

Full size image

Generalized Methodology of Spectral Correlation-Based Breathing Crack Localization with Modified Response Through LRS Scheme

Based on the above investigation and the effectiveness of the Linear Response Subtraction (LRS) scheme in multiple breathing crack diagnosis, the process of damage-sensitive feature extraction is described below:

The vibration measurement in the present work is the acceleration time-history signals (using accelerometers) measured spatially at “N” locations with certain spacing longitudinally along the beam. The acceleration time-history signals at N locations are obtained for three loading scenarios: (i) simultaneous harmonic excitation of probing and pumping frequency (bitone, ωpump + ωprob); (ii) individual excitation of pumping frequency (ωpump); iii) individual excitation of probing frequency (ωprob). As a pre-processing step, Linear Response Subtraction scheme is applied using some algebraic operations on the above said measurements as outlined in the earlier section and the modified response is obtained for each sensor (i.e., “N” sensors”). The cyclic spectral energy (CSE) is estimated assuming an arbitrary cyclic frequency using Eq. (4). The cyclic spectral energy is computed through the application of spectral correlation, i.e., second-order cyclo-stationary on the modified response. The sensor feature is the cyclic spectral energy. The sensor nodes with the higher magnitude of damage index or sensor feature based on CSE are those that are spatially near the position of the breathing cracks along the length of the beam.

Breathing Crack Localization: Varied Breathing Crack Locations and Varied Crack Depths

Multiple breathing cracks complicate the study a little bit and need two different situations to be addressed: beams with all cracks open or closed, and beams with some cracks open and the rest closed. To investigate the efficiency of the cyclic spectral energy-based damage indicator in identifying multiple cracks with varied crack depth and at different locations, distinct circumstances of opening and closing states of multiple cracks, and different test cases considered are given in Table 1. The results of the DI are estimated using Eq. (4) for the distinct cases of Table 1 are presented in Fig. 6a–f, respectively, for test cases S1–S6. The beam is subjected to individual single-tone and bitone harmonic excitation of 20 Hz and 500 Hz at node no. 6. The LRS-modified response is post-processed for spectral correlation estimation.

Table 1 Simply supported beam—test cases
Full size table
Fig. 6
figure 6

DI (spectral correlation): a test case-S1, b test case-S2, c test case-S3, d test case-S4, e test case-S5, and f test case-S6

Full size image

To verify the efficiency of DI based on CSE with different choices of cyclic frequencies, i.e., 7 Hz, 14 Hz, 40 Hz, 100 Hz, and 500 Hz, the corresponding results are also presented in Fig. 6. The sensitivity of the cyclic spectral energy-based damage indicator in localizing multiple breathing cracks for the beam (Test Case S6) subjected to bitone harmonic excitation at any location, i.e., varied nodes 6, 16, and 22, are investigated. The results of sensitivity of DI of the SS beam with input force applied at different nodes, i.e., node numbers 6, 16, and 22, are presented in Figs. 6f, 7a, b, respectively.

Fig. 7
figure 7

DI (spectral correlation): test case S6 a load at node 16 and b load at node 22

Full size image

The observations made from Figs. 6 and 7 are as follows:

  1. (i)

    For Test case-S1 of two cracks with the same crack depth, it can be observed from Fig. 6a that DI based on cyclic spectral energy shows the peak corresponding to nodes of both crack locations, i.e., elements 4 and 15 including the different choice of cyclic frequency. It should be mentioned here that as the crack depth is the same and smaller, a high level of nonlinearity in vibration is expected at all the spatial locations of the breathing crack (several instances of opening and closing of cracks). In addition, the magnitude of the DI peak at element no. 4 is slightly higher when compared to the DI peak corresponding to element no. 15. This is because Test case-S1 depicts that as the load is applied at node no. 6, identification of crack closer to node no. 6, i.e., crack at element no. 4 should be simpler.

  2. (ii)

    For Test case-S2 of two closer centre cracks, it can be observed from Fig. 6b that the DI based on cyclic spectral energy shows peaks at both crack locations, i.e., elements 15 and 22. However, the magnitude of the DI of element no. 15 is higher when compared to element no. 22. This might be due to the varied crack depth: even though element no. 15 comes in the mid-region of the beam similar to element no. 22, it has a high crack depth of 10% over crack 2. The nonlinearity due to the opening-closing action of breathing crack may be more predominant for crack1 than crack 2.

  3. (iii)

    Figure 6b shows that the DI based on cyclic spectral energy is robust regardless of the selected cyclic frequency. However, for the cycle frequency selected in a higher frequency range, the DI magnitude corresponding to a lower crack depth is larger.

  4. (iv)

    The DI plot presented in Fig. 6c shows a peak corresponding to nodes of elements 4 and 34. Besides, the magnitude DI corresponding to element no. 4 is higher than element no. 34 due to higher crack depth.

  5. (v)

    It is clear from Fig. 6d–f that the proposed DI, regardless of cyclic frequency, can identify multiple breathing cracks present at various positions along the beam span.

  6. (vi)

    Figure 7 demonstrates that the proposed DI can identify multiple breathing cracks irrespective of bitone harmonic excitation being applied at any spatial location along the beam span.

  7. (vii)

    The cyclic spectral energy-based damage indicator relatively quantifies the severity of the crack.

Impact of Noise

The noise or interference, which is spectrally overlapped with the nonlinear modulation components in the vibration response, is effectively removed or reduced by spectral correlation. The spectral correlation value is zero estimated at cyclic frequency greater than zero, i.e., α ≠ 0 for a white Gaussian noise signal. Various researchers have already demonstrated the superiority of the nonlinear spectral correlation over the conventional spectral density function in terms of its sensitivity to nonlinear damage and robustness against noise [23,24,25].

To investigate the effect of the noise level on the performance of the proposed damage index based on cyclic spectral energy, measurement noise (i.e., white noise) is added to the acceleration time history before it is processed. The polluted measured acceleration response \(\ddot{x}_{p}\) is mathematically given by

$$\ddot{x}_{p} = \ddot{x}_{m} + E_{p} N_{{{\text{noise}}}} \sigma (\ddot{x}_{m} ),$$
(10)

where \(\ddot{x}_{m}\) denotes the responses without noise and Ep is the percentage noise level. Nnoise is a standard normal distribution vector with zero mean and unit standard deviation \(\sigma (\ddot{x}_{m} )\) is the standard deviation of the acceleration.

Three different levels of noise, that is, 3%, 6%, and 10% noise levels, and the test case S5 of the earlier Section, are considered for investigation. The results of the damage index based on spectral correlation of noise-free and noisy measurements (three levels of noise) are presented in Fig. 8a–d, respectively. It is clear from Fig. 8 that the proposed DI, regardless of levels of noise, can identify multiple breathing cracks present at various positions along the beam span (i.e., three cracks at elements 4, 18, and 34) by its maximum value at those respective sensor nodes.

Fig. 8
figure 8

DI (spectral correlation): a 0% noise, b 3% noise, c 6% noise, and d 10% noise

Full size image

Impact of Numerical Model Errors

The test case S5 of the earlier section is considered for the investigations on the impact of numerical model errors in breathing crack identification using spectral correlation. The elastic modulus, density, and damping coefficients are randomized by drawing samples randomly from a Gaussian distribution with the mean as the true values. The mean values are 2.1e11 Mpa, 7800 kg/m3, and 1%. The variances of the parameters are set as 1e−4, 50, and 0.1% for elastic modulus, density, and damping coefficients, respectively. About 50 datasets are simulated for the test case S5 assuming the above said Gaussian distribution. The results of the damage index based on cyclic spectral energy for the above 50 datasets (simulated randomly) concluded that it robustly localizes all the breathing cracks.

Comparison with Traditional Approaches

For comparing the proposed spectral correlation approach with the existing techniques in the literature, i.e., SSA and weighting function augmented curvature approach, test case S1 is considered. The results of DI computed based on the weighting function augmented curvature approach and SSA approach as given in [14, 17] are presented in Fig. 9a, b, respectively. It is reported that the weighting function augmented curvature approach is sensitive to the application of load. It should be also mentioned here that the weighting function augmented curvature approach involves subtracting the cracked beam response from the underlying healthy beam response before the computation of DI.

Fig. 9
figure 9

a Weighting function augmented curvature approach and b SSA approach

Full size image

It can be observed from Fig. 9a that the proposed DI based on the weighting function augmented curvature approach [14] only identifies the crack at element no. 15 when the bitone harmonic force is applied at Node no. 22. In other words, the DI plot shows a peak only at element no. 15 (nodes 15 and 16). This might be due to the fact the nonlinear contribution of a crack at element no. 15 might be higher than a crack at element no. 4 in the total response due to the force being applied at node no.22. However, when the load is applied at node no. 6, both the cracks are localized using the DI based on weighting function augmented curvature approach. This is due to the spatial location of load (node no. 6) closer to the breathing crack at element no. 4. Hence, it is evident that the spatial location of the harmonic force plays an important role in multiple breathing crack diagnosis.

Unlike the weighting function approach, the SSA approach does not need reference healthy data measurements. SSA using signal decomposition principles isolates and extracts the nonlinear features using the measurements of the beam with a breathing crack only. It can be observed from Fig. 9b that similar conclusions can be drawn from Fig. 9a for multiple breathing crack localization using DI based on SSA [17]. The major limitation of the existing approaches in localizing multiple breathing cracks is that it is essential to vary input harmonic excitation of the structure and/or vary the spatial location of excitation to localize multiple breathing cracks. This whole exercise will be computationally very expensive.

From the results presented in Figs. 6 and 7 and in comparison, with Fig. 9, it can be concluded that the spectral correlation approach overcomes the above limitations and enable multiple breathing crack diagnosis irrespective of the choice of cyclic frequency. In addition, the cyclic spectral energy-based damage indicator can localize multiple breathing cracks closer to supports, closely spaced cracks and spatially located far apart multiple breathing cracks. The cyclic spectral energy-based damage indicator also relatively quantifies the damage severity. The LRS scheme used in the proposed spectral correlation approach is effective in the extraction and enhancement of nonlinear sensitive damage features in the vibration response for multiple breathing crack identification in beams and overcomes the limitations of reference healthy data measurements.

Breathing Crack Localization: Limited Sensor Measurements

Four different sensor configurations with 20, 15, 12, and 10 sensors are investigated to demonstrate the reliability of the proposed spectral correlation technique in diagnosing breathing cracks utilizing limited sensor data. The present work uses the principal components-based effective independence method for the identification of optimal sensor locations. More details related to it can be found in [36]. The four optimal sensor configurations arrived through the above algorithm are presented in Table 2. The test case S4 of Table 1 (i.e., SS beam with three cracks) is considered for evaluation of the proposed cyclic spectral energy-based indicator towards identification of breathing cracks with limited measurements.

Table 2 Sensor placement optimization
Full size table

The results of the DI corresponding to single-tone and bitone harmonic excitations for the considered 4 different sensor configurations of Table 2 are shown in Table 3. The proposed cyclic spectral approach localizes three breathing cracks closer to the simulated actual locations using limited sensors, as evident from Table 3. The proposed spectral correlation approach is applicable for the identification of multiple breathing cracks even with limited sensor measurements. However, the number of sensors must be sufficient enough to detect all the multiple breathing cracks spread across the beam. However, it should be mentioned that for robust detection, using the proposed spectral correlation approach, the number of sensors required for localizing multiple breathing cracks is higher than to detect a single breathing crack. This is due to significantly varied nonlinear contributions (depending upon the spatial location and intensity) from each breathing crack to the total structural response.

Table 3 Damage localization—limited sensors
Full size table

Numerical Example-2: Cantilever Beam

The second example, a cantilever beam, is taken into consideration to investigate the sensitivity of the proposed cyclic spectral energy-based damage indicator in locating multiple breathing cracks in beam-like structures with different boundary conditions. The parameters are E = 2.1e11 N/m2; ρ = 7850 kg/m3. Rayleigh damping is considered with damping ratios of 1.5% and 2% for the first two modes. The cantilever beam is discretized with 40 elements. The first four natural frequencies of the intact cantilever beam are 5 Hz, 30 Hz, 82 Hz, and 160 Hz. The beam is subjected to either single-tone or bitone harmonic excitation at the free end of the cantilever beam, i.e., node 40. The different test cases of the cantilever beam are presented in Table 4. The results of the DI based on cyclic spectral energy for the test cases C1–C4 of Table 4 are presented in Fig. 10a–d, respectively. Figure 10 illustrates that the cyclic spectral energy-based damage indicator shows peaks at all the simulated crack locations irrespective of a varied choice of cyclic frequency for test cases C1–C4.

Table 4 Cracked cantilever beam—different test cases
Full size table
Fig. 10
figure 10

DI-Cantilever beam—cyclic spectral energy: a test case C1, b test case C2, c test case C3, and d test case C4

Full size image

Applicability of the Proposed Spectral Correlation Technique to Complex Structure with Multiple Beams

In practice, the majority of bridges are simply supported bridges. Even bridges with multiple spans typically have noncontinuous designs with simply supported end conditions for each span. When diagnosing damage in bridges, the simply supported beam model is commonly used. In view of this, the present work focuses on detecting multiple breathing cracks using a numerical model of the simply supported beam.

For a complex structure containing multiple beams, i.e., bridges with multiple girders, each girder plays a critical role in supporting the weight of the bridge and the vehicles that pass over it. Damage to any of the girders influences the structural integrity of the bridge (as each girder being a load carrying member), making it essential to identify damage at their incipience. By placing accelerometers (sensors) on each girder of multiple girder bridges, it would be possible to use vibration-based damage localization techniques to detect any damage that may have occurred. By comparing the vibration data from the different girders, it would be possible to localize the damage to a specific girder or area of the bridge. In the present work, the proposed spectral correlation-based breathing crack localization technique is developed for a single girder, which can be extended directly for bridges with multiple girders.

The challenges such as the sensitivity of the number of cracks in each girder, their spatial location, and crack depth towards breathing crack identification are already handled by the proposed spectral correlation approach. In addition, the applicability of the proposed spectral correlation algorithm in localizing breathing cracks in beam structures with varied boundary conditions and identification of minimum crack depth of 3% is already demonstrated in this section. Therefore, the proposed technique will work reliably for a structure containing multiple beams.

Experimental Investigation

To evaluate and validate the proposed spectral correlation technique, laboratory experiments were conducted on a cantilever beam fabricated by bonding aluminium plates, as shown in Fig. 11. The dimension is 1 m × 0.0254 m × 0.0191 m. The specimen and experimental setting are identical to those described in the literature [13, 15, 18]. The sensors arrangement is presented in Fig. 12. There are about 4 plates (3 plates at the top, 1 plate at the top) The three upper parts are interconnected to the bottom one, while the top faces forming the breathing crack are only in contact. Two equivalent beams are bonded together to form the healthy beam (0% crack depth). The beam is securely fixed to a stand using a C-Clamp. The breathing crack is simulated at 0.23 m and 0.7 m from the fixed end. The two cracks are located between sensors 2 and 3 (closer to sensor 2) and as well as between sensors 5 and 6 (closer to sensor 6). The crack depth is the same at both locations and accounts for 16% of the beam’s entire depth. The sampling frequency is 2400 Hz. Only limited experiments have been carried out due to the paucity of the facility. The first three natural frequencies of the specimen computed through numerical simulations and experiments without crack and with crack (given inside brackets) are presented in Table 5.

Fig. 11
figure 11

Experimental specimen: a experimental setup and b zoomed view of crack

Full size image
Fig. 12
figure 12

Sensor arrangement—experimental specimen

Full size image
Table 5 Natural frequencies—experimental specimen
Full size table

The cracked beam is subjected to 4N harmonic excitation (single tone) of 8 Hz and 145HZ and as well as the simultaneous application of harmonic excitation (bitone) of 8 Hz and 145 Hz at the free end. To extract the nonlinear intermodulation response by the LRS approach, single-tone excitations are necessary. Figure 13a displays the Fourier Power Spectra of the sensor 4. Figure 13a depicts the peaks of power spectra corresponding to excitation frequencies (i.e., 8 Hz and 145 Hz), super harmonics (i.e., 8 Hz, 16 Hz, 24 Hz, 145 Hz, 290 Hz, 435 Hz, and so on) and intermodulations (i.e., 121 Hz, 129Hz, 137Hz, 153Hz, 161Hz, 169Hz, and so on). Figure 13a shows that sidebands (or intermodulation), as well as superharmonics of two distinct excitation frequencies, are present. This demonstrates that the structure has a breathing crack. Additionally, it is concluded that the amplitude of intermodulation and nonlinear harmonics is significantly lower than the basic excitation harmonic. The Fourier power spectrum plots corresponding to nonlinear intermodulation response (i.e., modified response after LRS application) are shown in Fig. 13b. Since the power spectrum is not expected to exist for nonlinear intermodulation response obtained using the LRS procedure for an undamaged beam, the presence of intermodulation and superharmonics in Fig. 13b gives very conclusive evidence of breathing crack detection. Further, Fig. 13b reveals that the excitation frequencies cannot be eliminated effectively as discussed earlier while presenting the numerical simulation example.

Fig. 13
figure 13

Experimental specimen—Fourier power spectrum: a actual response and b modified response using LRS

Full size image

For breathing crack diagnosis, the cyclic spectral energy must be assessed at each sensor node (i.e., nodes 1 through 8). For illustration purposes, the SC function is evaluated for sensor node-6 and the corresponding plot is shown in Fig. 14a. The cyclic frequency chosen is equal to response frequency components (i.e., excitation frequency, superharmonics of pumping and probing frequency, and as well as sidebands). The damage index (DI) based on CSE is evaluated using the nonlinear intermodulation response (i.e., after LRS) for chosen varied cyclic frequencies are shown in Fig. 14b. The observations drawn from Fig. 14 are as follows:

  1. 1.

    It is clear from Fig. 14a that several frequency possibilities for the response of the beam with a breathing crack produce the same cyclic frequency. As a result, several spectral correlation peaks at various frequencies can be seen for the sensor 6 response.

  2. 2.

    Figure 14a depicts that the spectral correlation estimated at α = 137 Hz exhibits a peak at ω = 77 Hz. In other for α chosen as the difference of input low and high frequency, i.e., 8 Hz and 137 Hz, SC exhibit a peak at an average of 137 Hz and 8 Hz. This also holds valid for other selected cyclic frequencies. The energy of the frequency components of the measured acceleration time-history response determines how large these peaks are.

  3. 3.

    Regardless of the cyclic frequency used, the cyclic spectral energy-based damage indicator presented in Fig. 14b exhibits the peak at both spatial positions of the breathing crack.

Fig. 14
figure 14

a Spectral correlation and b CSE-based damage index—lab-level experimentation

Full size image

Conclusion

This paper proposes a cyclic spectral energy-based breathing-crack damage indicator based on spectral correlation in beam structures in two stages. In the first stage, the LRS scheme is used to compute responses with only sideband components. In the second stage, the modified response is post-processed by spectral correlation (i.e., estimate of cyclic spectral energy-based damage index) for identifying breathing cracks. The proposed spectral correlation technique is validated using both numerical simulations and lab-scale experimentation. The following are the main findings of the analysis:

  1. 1.

    The spectral correlation approach is data-driven and does not require reference structure measurements for multiple breathing crack diagnosis in beam structures.

  2. 2.

    Linear response subtraction is essential to isolate nonlinear intermodulation components before the computation of spectral correlation function to develop a simple and effective generalized multiple breathing crack localization procedure with an unknown number of cracks.

  3. 3.

    From the investigations in the paper, it is evident that the proposed DI based on cyclic spectral energy (CSE) exhibits improved robustness to noise and identifies the breathing cracks of smaller sizes. It also exhibits greater sensitivity for localizing closer cracks, centre cracks, and cracks closer to supports.

  4. 4.

    Numerical and experimental investigations concluded that spectral correlation does not involve tedious computational and experimental efforts unlike SSA and weighting function augmented curvature approach. In other words, there is no need to vary input harmonic excitation of the structure and/or vary the spatial location of excitation to localize multiple breathing cracks using spectral correlation.

  5. 5.

    The proposed spectral correlation approach is applicable for the identification of multiple breathing cracks even with limited sensor measurements. However, the number of sensors must be sufficient enough to detect all the multiple breathing cracks spread across the beam. However, it should be mentioned that for robust detection, using the proposed spectral correlation approach, the number of sensors required for localizing multiple breathing cracks is higher than to detect a single breathing crack. This is due to significantly varied nonlinear contributions (depending upon the spatial location and intensity) from each breathing crack to the total structural response.