Fines Migration in Aquifers and Oilfields: Laboratory and Mathematical Modelling

Abstract

Migration of natural reservoir fines is one of the main causes of formation damage in oil and gas fields. Yet, fines migration can be employed for enhancing reservoir sweep and water production control. Permeability decline due to fine particles’ detachment from reservoir rocks, mobilisation, migration and straining has been widely reported in the petroleum industry since the 1960s and is being researched worldwide. The topic of colloidal-suspension flows with particle detachment is also of wide interest in environmental, chemical and civil engineering. The current work begins with a detailed introduction on laboratory and mathematical modelling of fines migration, along with new mathematical models and experimental results. Each of the next three sections explores a particular cause of fines mobilisation, migration and straining. Section 2 covers high flow velocity that causes particle detachment accompanied by consequent permeability decline. Section 3 covers low-salinity water injection, where the decreased electrostatic attraction leads to particle mobilisation. Section 4 covers the effect of high temperature on production rate and low-salinity water injection in geothermal reservoirs. We attribute the long permeability stabilisation period during coreflooding with fines migration, to slow fines rolling and sliding and to diffusive delay in particle mobilisation. We derive the analytical models for both phenomena. Laboratory fines-migration coreflood tests are carried out, with the measurement of breakthrough fines concentration and pressure drop across the whole core and the core’s section. Treatment of the experimental data and analysis of the tuned coefficients show that the slow-particle model contains fewer coefficients and exhibits more typical strained concentration dependencies of the tuned parameters than does the delay-release model.

1 Introduction

Fines migration with consequent permeability reduction has been widely recognised to cause formation damage in numerous petroleum, environmental and water resource processes (Noubactep 2008; Noubactep et al. 2012; Faber et al. 2016). Fines migration takes place during oil and gas production in conventional and unconventional reservoirs, significantly reducing well productivity (Sarkar and Sharma 1990; Byrne and Waggoner 2009; Byrne et al. 2014; Civan 2014). Natural and induced fines migration has occurred in the waterflooding of oilfields. It also causes drilling and completion fluids to invade the formation (Watson et al. 2008; Fleming et al. 2007, 2010). Despite significant progress in the above-mentioned technologies, clogging of production and injection wells remains a major operational issue.

The distinguishing features of natural reservoir fines migration are mobilisation of the attached particles, their capture by straining in the rock, permeability reduction and consequent decline in well productivity and injectivity (Fig. 1). Several laboratory studies observed permeability decline during coreflooding with piecewise-constant increase in velocity in (Ochi and Vernoux 1998). Similar effects occur during piecewise-constant change in water salinity or pH during coreflooding (Lever and Dawe 1984). Numerous authors attribute the permeability reduction during velocity increase, salinity decrease and pH increase, to mobilisation of the attached fine particles and their migration into pore spaces until size exclusion in thin pore throats (Muecke 1979; Sarkar and Sharma 1990). Figure 1 shows a schematic for attached and size-excluded fine particles in the porous space, along with definitions of the concentrations of attached, suspended and strained particles. Detachment of fines from the grain surfaces yields an insignificant increase in permeability, whereas the straining in thin pore throats and consequent plugging of conducting paths causes significant permeability decline. The main sources of movable fine particles in natural reservoirs are kaolinite, chlorite and illite clays; quartz and silica particles can be mobilised in low-consolidated sandstones (Khilar and Fogler 1998). Usually, the kaolinite booklets of thin slices cover the grain surfaces (Fig. 2). Detachment of a thin, large slice from the booklet can result in plugging of a large pore.

Fig. 1

Schematic for fines detachment, migration and straining with consequent permeability decline

Fig. 2

Kaolinite particles attached to the grain surface (SEM image): a leaflet shape and b leaflets in the pore space

Figure 3a, e show typical decreasing permeability curves during velocity increase.

Fig. 3

Normalised permeability, flow rate, critical fine radius and drift delay factor against time, during coreflood with piecewise increasing velocity during test I (first column) and test II (second column): a, e experimentally determined permeability decline with time; b, f increasing velocity during the test; c, g decrease of the mobilised fines radius as velocity increases as calculated from torque balance; and d, h drift delay factor from the model adjustment

The laboratory-based mathematical modelling supports planning and design of the above-mentioned processes. Classical filtration theory applied to particle detachment includes a mass balance equation for suspended, attached and strained particles:

$$ \frac{\partial }{\partial t}\left[ {\phi c + \sigma_{\text{a}} + \sigma_{\text{s}} } \right] + U\frac{\partial c}{\partial x} = 0 $$

(1)

where c, σ_a and σ_s are the concentrations of suspended, attached and strained particles, respectively, and U is flow velocity of the carrier fluid, which coincides with particle speed.

The kinetics of simultaneous particle attachment and detachment is given by the relaxation equation (Bradford and Bettahar 2005; Tufenkji 2007; Bradford et al. 2012, 2013; Zheng et al. 2014; Bai et al. 2015b)

$$ \frac{{\partial \sigma_{\text{a}} }}{\partial t} = \lambda_{\text{a}} cU - k_{\det } \sigma_{\text{a}} $$

(2)

where λ_a is the filtration coefficient for attachment and k_det is the detachment coefficient.

The irreversible fines straining rate in thin pore throats is expressed by the linear kinetics equation where the straining rate is proportional to the advective flux of suspended particles (Herzig et al. 1970; Yuan and Shapiro 2011a, b; You et al. 2013; Sacramento et al. 2015):

$$ \frac{{\partial \sigma_{\text{s}} }}{\partial t} = \lambda_{\text{s}} cU $$

(3)

Modified Darcy’s law accounts for permeability damage due to both attachment and straining (Pang and Sharma 1997; Krauss and Mays 2014):

$$ U = - \frac{k}{{\mu \left( {1 + \beta_{\text{s}} \sigma_{\text{s}} + \beta_{\text{a}} \sigma_{\text{a}} } \right)}}\frac{\partial p}{\partial x} $$

(4)

Figure 1 illustrates the common assumption that the coating of grain by attached particles causes significantly lower permeability damage than does straining: $\beta_{\text{s}} \gg \beta_{\text{a}}$, i.e. the combination of particle detachment and straining is the primary cause of the decline in permeability. Therefore, the term $\beta_{\text{a}} \sigma_{\text{a}}$ in Eq. (4) that accounts for permeability increase due to detachment is negligible.

Civan (2010, 2014) presented numerous generalisations of the governing Eqs. (1)–(4), to account for non-Newtonian behaviour of suspension fluxes, non-equilibrium for deep-bed filtration of high-concentration suspensions and colloids, and particle bridging at thin pore throats.

Quasi-linear system of partial differential Eqs. (1)–(3) exhibits the delayed reaction to an abrupt injection rate alteration, whereas laboratory tests show an instant permeability and breakthrough concentration response (Ochi and Vernoux 1998; Bedrikovetsky et al. 2012a, b). This discrepancy between the modelling and laboratory data, and the corresponding shortcoming in the theory, has been addressed in the modified model for particle detachment, by introducing the maximum attached concentration as a velocity function σ_a = σ_cr(U) (Bedrikovetsky et al. 2011a, b). If the attached concentration exceeds this maximum value, particle detachment occurs and the detached particles follow the classical filtration Eq. (3); otherwise, the maximum attached concentration holds. The dependency σ_a = σ_cr(U) is called the maximum retention function. The following set of equations captures the above attachment–detachment scenario:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{\partial \sigma_{\text{a}} }}{\partial t} = \lambda_{\text{a}} Uc,\quad \sigma_{\text{a}} < \sigma_{\text{cr}} \left( U \right)} \hfill \\ {\sigma_{\text{a}} = \sigma_{\text{cr}} \left( U \right)} \hfill \\ \end{array} } \right. $$

(5)

The maximum retention function decreases as the flow velocity increases. Therefore, the velocity increase causes instant release of the excess attached fine particles.

The maximum retention function σ_cr(U) is an empirically based (material) function of the model and can be determined only by the inverse-problem approach applied to fines-migration tests (Figs. 4 and 5). However, it can be calculated theoretically for a simplified geometry of porous space, using the conditions of mechanical equilibrium of particles attached to the rock surface.

Fig. 4

Velocity and salinity dependencies of maximum retention function with introduction of critical velocity and salinity

Fig. 5

Strained concentration σ_s in large-scale approximation is determined by the maximum retention function σ_cr(γ). Here, concentrations σ_s and σ_cr(γ) are extrapolated by the vanishing function into the domain σ < σ_cr(γ), where no particles are mobilised

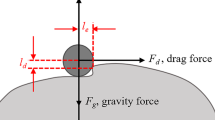
Freitas and Sharma (2001), Bergendahl and Grasso (2003), and Bradford et al. (2013) discussed the torque balance of attaching and detaching forces exerting on a particle situated at the rock or internal cake surface (Fig. 6):

$$ F_{\text{d}} (U,r_{\text{scr}} )l(r_{\text{scr}} ) = F_{\text{e}} (r_{\text{scr}} ) - F_{\text{l}} (U,r_{\text{scr}} ) + F_{\text{g}} (r_{\text{scr}} ),\quad l = l_{\text{d}} /l_{\text{n}} $$

(6)

Fig. 6

Scenarios involving particle detachment in monolayer on the grain surface and forces exerting on the particles. Torque and force balance on a fine particle attached to the pore wall: a the lever arm is equal to the contact area radius, deformation due to attracting electrostatic force. b The lever arm is determined by the asperity size. c Velocity distribution in Hele–Shaw flow in a pore

Here, F_d, F_e, F_l and F_g represent drag, electrostatic, lift and gravitational forces, respectively; l_d and l_n are the lever arms for drag and normal forces, respectively. Substitution of the expressions for drag, electrostatic, lift and gravitational forces into the torque balance equation (6) yields an expression of the maximum retention function (Bedrikovetsky et al. 2011a). The maximum retention function (5) for the case of poly-layer attachment of single-radius particles in rock having mono-sized cylindrical capillaries is a quadratic polynomial with flow velocity as the variable. The maximum retention function for a monolayer of polydispersed particles is expressed via size distribution for fine particles (You et al. 2015, 2016).

Expression (5) substitutes the equation for simultaneous attachment and detachment (2) in the mathematical model for colloidal-suspension transport (1)–(3). The modified model consists of three Eqs. (1), (3) and (5) for three unknown concentrations c, σ_a and σ_s. Equation (4) for pressure is separated from system (1), (3) and (5). Let us discuss the case of low straining concentration, where size exclusion does not affect the probability of particle capture. In this case, the filtration coefficient λ_s is constant, whereas it should be a σ_s-function in the general case. We also discuss the case of injection with timely decreasing rate, where the attached concentration is equal to the maximum retained concentration [second line in Eq. (5)]. The one-dimensional flow problem with attachment and detachment allows for exact solution, yielding suspended, attached and strained concentrations and pressure drop across the core. The laboratory- and theoretically determined maximum retention functions are in high agreement, which validates the maximum retention function as a mathematical model for particle detachment (Zeinijahromi et al. 2012a, b; Nguyen et al. 2013).

In the case of large stained concentration, λ_s = λ_s(σ_s). Suspended concentration can be expressed from Eq. (4) as a time derivative of a σ_s-dependent potential. Its substitution into Eq. (1) and integration in t reduces the system to one non-linear first-order partial differential equation, which is solved analytically using the method of characteristics (Alvarez et al. 2006, 2007).

Usually, fines-migration tests are performed under piecewise-constant decreasing velocity (Ochi and Vervoux 1998; Bedrikovetsky et al. 2011a; Oliveira et al. 2014, 2016). The amount of released particles during abrupt velocity alteration forms the initial suspended concentration for system (1), (3) and (4) with unknowns c, σ_s and p. Thus, the basic governing equations for deep-bed filtration and fines migration are the same (Herzig et al. 1970). The initial suspended concentration for deep-bed filtration in clean beds is zero, whereas for fines migration the initial suspended concentration is defined by the velocity alteration. Inlet boundary condition for deep-bed filtration is equal to concentration of the injected suspension, whereas it equals zero for fines migration. Therefore, the methods of exact integration of direct problems and regularisation of inverse problems, developed by Alvarez et al. (2006, 2007) for deep-bed filtration, can be applied for fines migration also.

The axisymmetric analogue of Eqs. (1), (3)–(5) describes the near-well flows, allowing estimating the well inflow performance accounting for fines migration. Zeinijahromi et al. (2012a, b) derive an analytical model for intermediate times with steady-state suspension concentration. Bedrikovetsky et al. (2012b) present an analytical steady-state model for late times, when all fines are either produced or strained. Marques et al. (2014) derive the analytical transient model for the overall well inflow period.

However, the exact solution of system (1), (3), (4) and (5) shows stabilisation of the pressure drop after injection of one pore volume (Bedrikovetsky et al. 2011a, b), whereas numerous laboratory studies have exhibited periods of stabilisation within 30–500 PVI (here PVI stands for pore volume injected) (Ochi and Vernoux 1998; Oliveira et al. 2014). Figure 3a shows the permeability stabilisation within 70–3000 PVI, for various injection velocities (Ochi and Vernoux 1998). The stabilisation times for flow exhibited in Fig. 3e vary from 300 to 1200 PVI. Therefore, the modified model for colloidal-suspension transport in porous media (1), (3) and (5) approximates well the stabilised permeability but fails to predict the long stabilisation period.

Several works have observed slow surface motion of the mobilised particles and simultaneous fast particle transport in the bulk of the aqueous suspension. Li et al. (2006) attributed the slow surface motion to particles in the secondary energy minimum. Yuan and Shapiro (2011a) and Bradford et al. (2012) introduced slow particle velocity into the classical suspension flow model, resulting in a two-speed model that matched their laboratory data on breakthrough concentration. Navier–Stokes-based simulation of colloids’ behaviour at the pore scale, performed by Sefrioui et al. (2013), also exhibited particle transport speeds significantly lower than the water velocity. However, classical filtration theory along with the modified particle detachment model assumes that particle transport is at carrier fluid velocity (Tufenkji 2007; Civan 2014).

Oliveira et al. (2014) attributed long stabilisation periods to slow drift of fine particles near the rock surface in the porous space. However, a mathematical model that depicts slow-particle migration and accurately reflects the stabilisation periods is unavailable in the literature.

Application of nanoparticles (NPs) can significantly decrease migration of the reservoir fines and the consequent permeability impairment (Habibi et al. 2012). Under certain salinity and pH, NPs attract both fines and grain. Low size of NPs causes high mobility and diffusion, spreading them over the grain surfaces. NPs ‘glue’ the fines and significantly increase the electrostatic fine-grain attraction (Ahmadi et al. 2013; Sourani et al. 2014a, b). The basic system of equations includes two mass balance equations for NPs and salt. Yuan et al. (2016) solved the system by the method of characteristics (Qiao et al. 2016). Combination of low-salinity and NP waterfloods in oilfields adds the above-mentioned mass balance and deep-bed filtration equations to Buckley–Leverett equation for two-phase flow in porous media (Bedrikovetsky 1993; Arab and Pourafshary 2013; Assef et al. 2014; Huang and Clark 2015; Dang et al. 2016).

Mahani et al. (2015a, b) observed delay between salinity alteration and corresponding surface change. This delay was attributed to saline water diffusion from the contact area between the deformed particle and rock surface. The Nernst–Planck diffusion in the thin slot between two plates subject to molecular-force action is significantly slower than the Brownian diffusion, so the Nernst–Planck diffusion can bring significant delay. The diffusive delay in particle mobilisation due to water salinity decrease can serve as another explanation for the long stabilisation period. Yet, a mathematical model that accounts for delay in particle mobilisation due to salinity alteration also seems absent from the literature.

In the current work, the long times for permeability stabilisation are attributed to slow surface motion of mobilised fine particles. The governing system (1), (3) and (5) is modified further by replacing the water flow velocity U by the particle velocity U_s < U (Fig. 1). We also introduce a maximum retention function with delay, which corresponds to the Nernst–Planck diffusion from the grain–particle contact area into the bulk of the fluid. We derive the maximum retention function for a monolayer of size-distributed fines, which accounts for its non-convex form. We found that during continuous velocity/pH/temperature increase or salinity decrease, the largest particles were released first. The obtained system with slow fines migration and delayed maximum retention function allows for exact solution for cases of piecewise-constant velocity/pH/temperature increase or salinity decrease. High agreement between the laboratory and modelling data validates the proposed model for slow surface motion of released fine particles in porous media.

The structure of the text is as follows. Section 2 presents the laboratory study of fines migration due to high velocities and presents the mathematical model for slow-particle migration that explains the long stabilisation periods. The derived analytical model provides explicit formulae for concentration profiles, histories and the pressure drop. Section 3 presents the laboratory study of fines migration due to low salinities, and it derives the mathematical model that accounts for slow-particle migration and for delayed fines mobilisation. Here, we also derive the analytical model. Section 4 presents the analytical model for fines mobilisation at high temperature. The recalculation method for varying salinity, temperature, pH, or velocity is developed. Section 5 presents fines migration in gas and coal-bed-methane reservoirs. Section 6 presents the conclusions.

2 Fine Particles Mobilisation, Migration and Straining Under High Velocities

This section presents the modelling and laboratory study of fine particles that migrate after having been detached by drag and lift forces at increased velocities. Section 2.1 presents a brief physical description of fines detachment in porous media and introduces the maximum retention function for a monolayer of size-distributed particles. A qualitative analysis of the laboratory results on long-term stabilisation gives rise to a slow-particle modification of the mathematical model for fines migration in porous media. Section 2.2 presents those basic equations accounting for slow-particle transport. Section 2.3 derives the analytical model for one-dimensional flow under piecewise increasing flow velocity with consequent fines release and permeability impairment. Section 2.4 describes the laboratory coreflood tests with fines mobilisation and examines how closely the analytical model matches the experimental data. Section 2.5 discusses the model’s validity, following the results of the laboratory and analytical modelling.

2.1 Physics of Fines Detachment, Transport and Straining in Porous Media

In this section, we discuss the physics of fines detachment/mobilisation on a micro-scale. In the presence of low ionic strength or high flow velocity, reservoir fines are detached from the rock surface, mobilise and flow through the porous media as shown in Fig. 1. Four forces act on a fine particle attached to the surface of the grain: drag, lift, electrostatic and gravity (Fig. 6). For calculation of drag, we use the expression proposed by Bergendahl and Grasso (2003) and Bradford et al. (2013); lift is calculated using the formula of Akhatov et al. (2008); and the electrostatic forces are calculated using DLVO (Derjaguin–Landau–Verwey–Overbeek) theory (Khilar and Fogler 1998; Israelachvili 2011; Elimelech et al. 2013).

Elastic particles located on the grain surface undergo deformation due to gravitational, lift and electrostatic forces acting normal to the grain surface. The right side of Eq. (6) contains the resultant of these forces (normal force). We assume that at the mobilisation instant, a particle rotates around the rotation-touching point in the boundary of the particle–grain contact area (Fig. 6a). Also assumed is that the lever arm is equal to the radius of the contact area of particle deformation, which is subject to the normal force (Freitas and Sharma 2001; Schechter 1992; Bradford et al. 2013). The contact area radius is equal to the lever arm l_n and is calculated using Hertz’s theory of mutual grain–particle deformation:

$$ l_{\text{n}}^{3} = \frac{{F_{\text{n}} r_{\text{s}} }}{4K}\quad l_{\text{d}} = \sqrt {r_{\text{s}}^{2} - l_{\text{n}}^{2} } \;\;K \equiv \frac{4}{{3\left( {\frac{{1 - \nu_{1}^{2} }}{{E_{1} }} + \frac{{1 - \nu_{2}^{2} }}{{E_{2} }}} \right)}} $$

(7)

Here, K is the composite Young modulus that depends on Poisson’s ratio ν and Young’s elasticity modulus E of the particle and of the surface. Indices 1 and 2 refer to the particle and solid matrix surfaces, respectively.

Figure 6b depicts the scenario in which a particle revolves around the contacting roughness (asperity) on the surface of a grain. The elastic properties of rock and particle determine the value of l_n in the first scenario (Fig. 6a). In the second scenario (Fig. 6b), the value of l_n is determined by the surface roughness.

Two coreflood tests (I and II) at piecewise-constant increasing fluid velocity on Berea sandstone cores were carried out by Ochi and Vernoux (1998) and resulted in mobilisation of kaolinite particles (Fig. 3). We used the following electrostatic constants and parameters for quartz and kaolinite in order to calculate F_e in Eq. (6): surface potentials ψ₀₁ and ψ₀₂ (−55, −50 mv) for test I and (−70, −80 mv) for test II (Ochi and Vernoux 1998); the Hamaker constant 2.6 × 10⁻²⁰ J (Welzen et al. 1981); atomic collision diameter 0.4 × 10⁻⁹ m (Das et al. 1994); and salinity 0.1 mol/L for test I and 0.01 mol/L for test II. The Hamaker constant was calculated using dielectric constant for water D = 78.0 and permittivity of free space (vacuum) ε₀ = 8.854 × 10⁻¹² C⁻² J⁻¹ m⁻¹ (Israelachvili 2011; Khilar and Fogler 1998). Electron charge was e = 1.6 × 10⁻¹⁹ C, Boltzmann’s constant was k_B = 1.3806504 × 10⁻²³ J/K and temperature was T = 25 °C. Young’s modulus for kaolinite was 6.2 GPa and for quartz was 12 GPa (Prasad et al. 2002), and Poisson’s ratios were 0.281 and 0.241 (Gercek 2007) and were used to evaluate the lever arm ratio according to Eq. (7). The above parameters were used to construct graphs for electrostatic potential and force versus separation particle–grain distance (Fig. 7a, b).

Fig. 7

Measured values for tests I and II: a energy potential and b electrostatic force

The total potential of interaction V determines electrostatic force F_e. Zero values for F_e correspond to energy extremes V_max and V_min, and the minimum value of electrostatic force is obtained from the inflection point of the total potential of interaction curve. The first test of Ochi and Vernoux (Fig. 3a–d) was favourable for attachment of kaolinite particles to the grain surface, which resulted in the absence of the secondary minimum on the total potential of interaction curve. For the second test (Fig. 3e–h), the values of the primary and secondary energy minima equalled 550 and 19 kT, respectively. The energy barrier was 87 kT, exceeding the values of the secondary minimum and allowing a particle to jump from secondary minimum to primary minimum (Elimelech et al. 2013). Therefore, the second test was unfavourable for kaolinite particle attachment to the grain surface.

Under the condition of mechanical equilibrium given by the torque balance Eq. (6), fluid flow velocity affects lift and drag forces, whereas particle size determines the magnitudes of all forces in the equation. Therefore, the critical radius of the particle mobilised by fluid flow with velocity U can be determined as follows: $r_{\text{scr}} = r_{\text{scr}} \left( U \right)$. This is an implicit function from Eq. (6), i.e. Equation (6) is a transcendent equation for implicit dependency r_scr = r_scr(U). The stationary iterative numerical procedure can be used to solve Eq. (6) (Varga 2009). The graph of the function r_scr = r_scr(U) obtained using the above parameters shows that the size of each mobilised particle r_scr(U) decreases monotonically as fluid velocity increases. Therefore, those particles that remained immobilised on the grain surface at fluid velocity U have sizes r < r_scr(U). The magnitude of F_e increases as the Hamaker constant increases (see Fig. 8), resulting in the right-shift of the r_scr(U)-curve.

Fig. 8

Critical particle size (minimum size of the fine particles lifted by the flux with velocity U)

Assume that the attached particles form a monolayer on the rock surface. The initial concentration distribution of attached particle sizes is denoted as Σ_a(r_s). Particles are mobilised by descending size, as mentioned above. Thus, the critical retention concentration in Eq. (5) includes all particles with radii smaller than r_scr(U):

$$ \sigma_{\text{cr}} \left( U \right) = \sigma_{{{\text{a}}0}} \int\limits_{0}^{{r_{\text{scr}} \left( U \right)}} {\sum\limits_{\text{a}} {\left( {r_{\text{s}} } \right){\text{d}}r_{\text{s}} } } $$

(8)

Now assume that the attached particles are size-distributed according to the breakage algorithm (i.e. log-normal distribution for attached particle sizes Σ_a(r_s) holds (Jensen 2000). The forms of the maximum retention function as calculated by Eq. (8) for different size distributions of the attached particles, using the above values for electrostatic and elastic constants, are shown in Fig. 9.

Fig. 9

Maximum retention function for the attached fines forming a monolayer on the pore surface: a for log-normal particle-size distributions with varying mean particle size. b For log-normal particle-size distributions with varying variance coefficient. c Determining the maximum retention function from the number of particles released at each abrupt velocity alteration

Bedrikovetsky et al. (2011a, b) found that σ_cr(U) for mono-sized particles that form the poly-layer coating on the surface of cylindrical pores is a quadratic polynomial. The corresponding curves σ_cr(U) are convex. The model for the poly-layer coating can be modified by the introduction of size distributions for spherical particles and cylindrical pores; the resulting maximum retention curves can contain the concave parts (Fig. 9).

Figure 9 indicates that the maximum retention function for monolayer fines is not convex. The calculated σ_cr(U)-curves for three particle-size distributions characterised by equal variance coefficients support the above observation that the larger the particle, the higher the drag on the particle and the fewer the remaining particles (Fig. 9a). Similar calculations for log-normal distributions with the same average particle size and different variance coefficients result in the σ_cr(U)-curves shown in Fig. 9b. The higher fraction of mobilised large particles corresponds to larger coefficient of variation C_v. For the low-velocity range, σ_cr(U)-curves having high standard deviation lie lower; whereas with the increase in fluid velocity, σ_cr(U)-curves shift to higher σ_cr-values. Equation (8) shows that the σ_cr(U)-curve has a step shape for mono-sized particles (C_v → 0), meaning that the maximum retention function is a step function. The wider the attached particle-size distribution, the wider the transitional spread of the σ_cr(U)-curves. The phenomenological model for fines detachment in porous media (1), (3)–(5) assumes the existence of a maximum retention function whose form is unconstrained.

Now consider particle-free water being injected with increasing piecewise-constant velocity into a core. The movable attached fines concentration is σ_a0. There is no particle mobilisation at low fluid velocities (see Fig. 9c), because the attaching torque from Eq. (6) exceeds the detaching torque for all size particles: points (U < U₀, σ_a0) are located below the maximum retention curve. Concentration of attached particles remains constant along the horizontal arrow from the point U = 0 to critical velocity U = U₀. Value U₀ corresponds to the minimum velocity that results in mobilisation of particles and the consequent first fine appearance in the core effluent.

The initial concentration of attached fines σ_a0 determines the critical velocity U₀ (Miranda and Underdown 1993; Hassani et al. 2014) as follows:

$$ \sigma_{{{\text{a}}0}} = \sigma_{\text{cr}} (U_{0} ) $$

(9)

Movement along the σ_cr(U)-curve corresponds to velocity increase above the critical value U > U₀. An instant rate change from U₁ to U₂ is accompanied by instant particle mobilisation with concentration ∆σ_a1 = σ_cr(U₁) − σ_cr(U₂) and increase in suspended concentration by [σ_cr(U₁) − σ_cr(U₂)]/ϕ. The mobilised particle moves along the rock surface with velocity U_s < U until it is strained by a pore throat smaller than the particle size. This results in rock permeability decline due to plugging of the pores. The increased strained particle concentration yields the permeability decline according to Eq. (4). The stabilised damaged permeability values at various fluid velocities, due to increasing strained particle concentration for tests I and II, is presented in Fig. 10a, b.

Fig. 10

Stabilised normalized permeability versus velocity: a test I and b test II

Let us introduce the non-dimensional pressure drop across the core, normalised by the initial pressure drop. This is denoted as the impedance J:

$$ J\left( T \right) = \frac{\Delta P\left( T \right)U\left( 0 \right)}{U\left( T \right)\Delta P\left( 0 \right)} = \frac{{k_{0} }}{\left\langle k \right\rangle \left( T \right)} $$

(10)

where 〈k〉(T) is the average core permeability and T is dimensionless time (pore volume injected). The permeability decline curves in Fig. 3a, e are recalculated to yield the impedance growth curves in Fig. 11a, b, respectively.

Fig. 11

Comparing the pressure drop across the core obtained from coreflood against the mathematical model: a test I and b test II

The increase in pressure drop across the core from Δp_n−1 to Δp _n , or permeability decline from k_n−1 to k _n , is caused by increasing fluid velocity U _n , n = 1, 2, 3…, which leads to particle mobilisation.

Permeability decline during the increase in fluid velocity is shown in Fig. 3. According to the data from tests I (Fig. 3a) and II (Fig. 3b), rock permeabilities stabilise after injection of many pore volumes. Classical filtration theory implies that for a mobilised particle to appear at the end of the core, it must traverse the overall core length. Each fine particle is transported by the carrier fluid; it is strained in the core or must arrive at the outlet after injection of at most one pore volume. According to Fig. 3a, e, permeability stabilisation times are significantly higher than 1 PVI. This can be explained by slow-particle drift along the rock surface: the mobilised particles move along the rock with velocity U_s that is significantly lower than the carrier fluid velocity U.

The next section introduces the basic governing equations for the transport of suspended colloids in porous media. The basic system includes the maximum retention function σ_cr which models particle detachment and its slow drift along the porous medium with low velocity U_s < U.

2.2 Governing System for Suspension-Colloidal Transport and Detachment in Porous Media

The following assumptions are introduced for the development of the mathematical model for detachment/mobilisation of particles and transport of suspended colloids in porous media (Yuan and Shapiro 2011a; Yuan et al. 2012, 2013):

• the mobilised fine particles cannot reattach to the rock surface;

• the mobilised particles do not diffuse in long micro-homogeneous cores;

• the carrier fluid is incompressible;

• small concentrations of suspension in flowing fluid do not change the density or viscosity of the carrier fluid, which equal those of injected water;

• there exists a phenomenological maximum retention function for particles attached to the rock surface;

• volume balance of the incompressible carrier fluid is not affected by the presence of small concentrations of suspended, attached or strained particles; and

• the mobilised particles move with velocity U_s which is smaller than fluid velocity U.

Mobilised particles move along the surface of grains with velocity U_s < U, meaning that the drifted particle concentration is significantly higher than the suspended concentration of fine particles carried by water stream (see Fig. 1). The drift speed U_s is a phenomenological constant of the model.

The slow-fines-drift assumption U_s < U determines the difference between the above formulated assumptions and those for modified model (1), (3)–(5). Thus, the system of governing equations includes a mass balance equation for suspended, attached and strained fines, where the suspended particles are transported by water flux with reduced velocity U_s:

$$ \frac{{\partial \left( {\phi c + \sigma_{\text{s}} + \sigma_{\text{a}} } \right)}}{\partial t} + U_{\text{s}} \frac{\partial c}{\partial x} = 0 $$

(11)

The straining rate is assumed to be proportional to particle advection flux, cU_s (Herzig et al. 1970; Xu 2016):

$$ \frac{{\partial \sigma_{\text{s}} }}{\partial t} = \lambda \left( {\sigma_{\text{s}} } \right)U_{\text{s}} c $$

(12)

If the maximum retention concentration is greater than attached concentration, the particle attachment rate of Eq. (5) is also assumed to be proportional to the particle advection flux cU_s:

$$ \begin{aligned} & \frac{{\partial \sigma_{\text{a}} }}{\partial t} = \lambda_{\text{a}} U_{\text{s}} c,\quad \sigma_{\text{a}} < \sigma_{\text{cr}} \left( U \right) \\ & \sigma_{\text{a}} = \sigma_{\text{cr}} \left( U \right) \\ \end{aligned} $$

(13)

Otherwise, the attached particle concentration is expressed by the maximum retention function given by Eq. (8).

Four Eqs. (4), (11), (12) and (13) with four unknowns c, σ_a, σ_s and p constitute a closed system and a mathematical model for fine-particle migration in porous media.

Now we introduce the following dimensionless parameters:

$$ \begin{aligned} & S_{\text{a}} = \frac{{\sigma_{\text{a}} }}{{\sigma_{{{\text{a}}0}} }},\quad S_{\text{s}} = \frac{{\sigma_{\text{s}} }}{{\sigma_{{{\text{a}}0}} }},\;\;C = \frac{c\phi }{{\sigma_{{{\text{a}}0}} }},\;\;\Lambda _{\text{a}} = \lambda_{\text{a}} L,\;\;\Lambda _{\text{s}} = \lambda_{\text{s}} L, \\ & T = \frac{{\int\nolimits_{0}^{t} {U\left( y \right){\text{d}}y} }}{\phi L},\quad X = \frac{x}{L},\;\;\alpha_{n} = \frac{{U_{{{\text{s}}n}} }}{{U_{n} }},\;\;P = \frac{kp}{\mu LU} \\ \end{aligned} $$

(14)

Here, the particle drift velocities U_sn and delay factors α _n , n = 1, 2, 3… correspond to flow velocities U _n ; T is the accumulated non-dimensional volume of injected water. For the case of piecewise-constant flow velocity U(t), the dimensionless accumulated injected volume T(t) is piecewise linear.

Substitution of dimensionless parameters (14) into governing Eqs. (4), (11)–(13) yields the following dimensionless system, which consists of the particle balance:

$$ \frac{{\partial \left( {C + S_{\text{s}} + S_{\text{a}} } \right)}}{\partial T} + \alpha_{n} \frac{\partial C}{\partial X} = 0 $$

(15)

particle straining kinetics (Xu 2016),

$$ \frac{{\partial S_{\text{s}} }}{\partial t} =\Lambda _{\text{s}} \alpha_{n} C $$

(16)

particle attachment–detachment kinetics,

$$ \begin{array}{*{20}l} {\frac{{\partial S_{\text{a}} }}{\partial T} =\Lambda _{\text{a}} \alpha_{n} C,\quad S_{\text{a}} < S_{\text{cr}} \left( U \right)} \hfill \\ {S_{\text{a}} = S_{\text{cr}} \left( U \right)} \hfill \\ \end{array} $$

(17)

and the modified Darcy’s law that accounts for permeability damage due to fines retention

$$ 1 = - \frac{1}{{1 + \beta_{\text{s}} \sigma_{{{\text{a}}0}} S_{\text{s}} }}\frac{\partial P}{\partial X} $$

(18)

In the next section, we solve non-dimensional governing system (15)–(18) for the conditions of laboratory tests with piecewise-constant increasing velocity.

2.3 Analytical Model for One-Dimensional Suspension-Colloidal Flow with Fines Mobilisation and Straining

During coreflood when velocity U₁ is higher than critical velocity U₀, i.e. σ_a0 > σ_cr(U₁), the excess of the attached concentration is instantly released into the colloidal suspension. Particle straining in the proposed model is irreversible; therefore, it is assumed that initial porosity and permeability already account for the strained particle initial concentration. Coreflood with constant fluid velocity results in constant attached concentration S_a given by the maximum retention function. Thus, the initial conditions are

$$ T = 0{:}\;\;C = \Delta S_{{{\text{a}}1}} = S_{{{\text{a}}0}} - S_{\text{cr}} \left( {U_{1} } \right),\;\;S_{\text{s}} = 0,\;\;S_{\text{a}} = S_{\text{cr}} \left( {U_{1} } \right) $$

(19)

The inlet boundary condition corresponds to injection of water without particles:

$$ X = 0:\;\;c = 0 $$

(20)

Substituting the expression for straining rate (16) into mass balance Eq. (15) and accounting for steady-state distribution of attached particles S_a yields the linear first-order hyperbolic equation

$$ \frac{\partial C}{\partial T} + \alpha_{1} \frac{\partial C}{\partial X} = -\Lambda _{\text{s}} \alpha_{1} C $$

(21)

The next section uses the method of characteristics to solve Eq. (21).

2.3.1 Exact Analytical Solution for Injection at Constant Rate

The characteristic velocity in Eq. (21) is equal to α₁. The solution C(X, T) is presented in Table 1, and integration of Eq. (16) over T determines the strained concentration profile S_s(X, T).

Table 1 Exact analytical solution for 1-D fines migration during the increase in piecewise-constant velocity

As illustrated in Fig. 12a, the concentration front of the injected particle-free fluid moves along the path X = α₁T. Behind the concentration front, suspended particle concentration is zero and the ‘last’ mobilised particle arrives at the core outlet at T = 1/α₁. The mobilised particles are assumed to be uniformly distributed: they move with the same velocity and have the same probability of capture by pore throats. Therefore, the profile of suspended particle concentration is uniform during fluid flow, and concentration of suspension at X > α₁T is independent of X (as indicated by the second line in Table 1). This leads to the conclusion that the concentration of particles strained in thin pores is independent of X ahead of the concentration front. Particle straining occurs for non-zero concentration of suspended particles. Therefore, the strained particles accumulate at a reservoir point X until the arrival of the concentration front, after which the concentration of suspended particles remains unchanged. Therefore, the concentration of strained particles behind the concentration front is steady-state.

Fig. 12

Schematic for the analytical solution of 1-D fines migration under piecewise increasing velocity at times before and after the breakthrough (moments T _a and T _b , respectively): a trajectory of fronts and characteristic lines in (X, T) plane. b Suspended concentration profiles in three moments T = 0, T _a , and T _b . c Strained concentration profiles at three instants

The profiles of suspended particle concentration at T = 0, T _a (before the arrival of the concentration front at the outlet of the core) and T _b (after the arrival of the concentration front) are shown in Fig. 12b. We denote ∆S_a1 as the initial concentration of the released suspended particles. The profile of the concentration of suspended particles equals zero behind the concentration front and is constantly ahead of the front. After the front’s arrival, the breakthrough concentration of suspended particles equals zero because all mobilised particles either are strained in thin pore throats or emerge at the rock effluent.

Three profiles of concentration of strained particles, for times 0, T _a and T _b , are shown in Fig. 12c. No strained particles are present in the rock before particle mobilisation. The concentration of strained particles continues to grow until the front’s arrival, after which it remains constant. The duration of particle straining during the flow becomes longer with X. Therefore, the profiles of strained particle concentration grow as X increases. The probability of particle capture ahead of the front remains constant. Thus, the particle advective flux is uniform, and the strained profile is uniform.

Figure 13 shows the history of particle breakthrough concentration. The later the arrival, the higher the particle capture probability. According to Herzig et al. (1970), the coefficient of filtration λ_s equals the probability of particle straining per unit length of the particle trajectory. Therefore, the number of particles captured by thin pore throats increases with time, and breakthrough concentration C(1, T) decreases with time. All mobilised fine particles either are strained or exit the core at time T_st,1, i.e. concentration of suspended particles becomes zero and the rock permeability stabilises at time T_st,1.

$$ T_{{{\text{st}},1}} = \frac{1}{{\alpha_{1} }} $$

(22)

Fig. 13

Histories for dimensionless pressure drop across the core J and breakthrough concentration C, with strained concentration S_s at the outlet

The impedance can be calculated directly from Eq. (10). Impedance for the time interval having the constant fluid velocity from Eq. (18) equals

$$ J(T) = \int\limits_{0}^{1} {\left( { - \frac{\partial P}{\partial X}} \right)} {\text{d}}X = 1 + \beta_{\text{s}} \sigma_{{{\text{a}}0}} \int\limits_{0}^{1} {S_{\text{s}} } (X,T){\text{d}}X $$

(23)

Substituting the solution for the concentration of the retained particles (rows 4 and 5 in Table 1) into Eq. (23) and integrating over X results in the following explicit formula for impedance increase with time:

$$ J\left( T \right) = 1 + \beta_{\text{s}} \sigma_{{{\text{a}}0}} \Delta S_{\text{a1}} \left[ {1 - \frac{1}{{\Lambda _{\text{s}} }} - \left( {1 - \frac{1}{{\Lambda _{\text{s}} }} - \alpha_{1} T} \right)e^{{ - \alpha_{1}\Lambda _{\text{s}} T}} } \right],\quad T < \alpha_{1}^{ - 1} $$

(24)

Substituting the expression for stabilisation time (22) into Eq. (24) yields the stabilised value of the impedance

$$ J\left( {T_{{{\text{st}}1}} } \right) = 1 + \beta_{\text{s}} \sigma_{{{\text{a}}0}} \Delta S_{{{\text{a}}1}} \left( {1 - \frac{1}{{\Lambda _{\text{s}} }} + \frac{{e^{{ -\Lambda _{\text{s}} }} }}{{\Lambda _{\text{s}} }}} \right),\quad T \ge \alpha_{1}^{ - 1} $$

(25)

Monotonic increase of dimensionless pressure drop from one to the maximum stabilised value is achieved at time equal to 1/α₁, which coincides with the arrival of the ‘last’ mobilised particle at the core outlet.

2.3.2 Analytical Solution for Multiple Injections

The solution of problem (15)–(18) where fluid velocity has changed from U_n−1 to U _n is similar to that of the first stage under U₁. The only difference is that the concentration of strained particles for T > T _n equals the total of the concentration of strained particles before the fluid velocity alteration at time T = T _n  − 0 and the concentration of particles that have been strained during time T > T _n . We discuss the case where the change in fluid velocity occurs after permeability stabilisation.

When the fluid velocity changes from U_n−1 to U _n at instant T = T _n , the attached particles are immediately mobilised. The mobilised particle concentration is ΔS_an = S_cr(U_n−1) − S_cr(U _n ). The strained concentration at T = T _n equals that before velocity alteration at T = T _n  − 0:

$$ T = T_{n} :\quad C = \Delta S_{{\text{a}n}} = S_{\text{cr}} \left( {U_{n - 1} } \right) - S_{\text{cr}} \left( {U_{n} } \right),\;\;S_{\text{s}} = S_{\text{s}} \left( {X,T_{n} - 0} \right),\;\;S_{\text{a}} = S_{\text{cr}} \left( {U_{n} } \right) $$

(26)

Substituting the strained concentration (see Table 1) into Darcy’s law (18) and integrating for pressure gradient over X along the core yields the impedance for T > T _n :

$$ \begin{aligned} & T < T_{n} + \alpha_{n}^{ - 1} : \\ & J\left( T \right) = J_{0n} + \beta_{\text{s}} \sigma_{a0} \Delta S_{an} \left[ {1 - \frac{1}{{\Lambda _{\text{s}} }}} \right. \\ & \quad\quad - \left. {\left( {1 - \frac{1}{{\Lambda _{\text{s}} }} - \alpha_{n} \left( {T - T_{n} } \right)e^{{ - \alpha_{n}\Lambda _{\text{s}} \left( {T - T_{n} } \right)}} } \right)} \right] \\ \end{aligned} $$

(27)

Substituting stabilised time T = T _n  + 1/α _n into Eq. (27) gives the stabilised impedance after the n-th injection with velocity U _n .

The analytical model-based formulae for impedance (rows 12 and 13 in Table 1) will be validated against the laboratory tests in the next section.

2.4 Using the Laboratory Results to Adjust the Analytical Model

In order to replicate water injection in a well, Ochi and Vernoux (1998) performed two laboratory corefloods using Berea cores at conditions similar to bottom-hole pressures and temperatures and at various fluid velocities. Permeability and flow velocity for test I are shown in Fig. 3a, b, respectively, and for test II in Fig. 3e, f, respectively. Initial and boundary conditions (19) and (20) correspond to injection of particle-free water with piecewise-constant increasing velocity. Pressure drop along the core was measured. Both tests used Berea sandstone cores prepared from the same block, so that the rock properties for both cores would be similar. As fluid velocity increased, kaolinite particles detached from the grain surface. The mobilised fines migrated and were strained by the rock. Pressure drop predicted by the analytical model proposed in Sect. 2.3 was compared to the actual pressure drop across the cores during the tests. Minimisation of the difference between the modelled and measured pressure drop was used to adjust the phenomenological constants of the model: α, Δσ, λL and β.

2.4.1 Tuning the Rheological Model Parameters from Laboratory Coreflooding Data

Formation damage and filtration coefficients were assumed to remain constant for the duration of the experiment. Therefore, these parameters would be independent of fluid velocity and concentration of the retained particles. The drift delay factor was assumed to vary, i.e. the alteration of rock surface during detachment/mobilisation of particles affects drift velocity.

For stabilised permeability, according to Eq. (4), the permeability values k _n fulfil the following relationship:

$$ \beta \left[ {\sigma_{\text{cr}} \left( {U_{n - 1} } \right)} \right]\Delta \sigma_{{\text{a}n}} = \frac{{k_{n - 1} }}{{k_{n} }} - 1 $$

(28)

Pressure drops along the core, which define the permeabilities k _i , were measured during coreflood tests with varying fluid velocities U _i . The least-squares method was used to tune the above experimental pressure drop data and obtained filtration coefficient λ_s, the products β_sΔσ_cr(U _n ), n = 1, 2…, and the drift delay factors α _n for different fluid velocities U _n . The optimisation problem (Coleman and Li 1996) was solved using the reflective trust region algorithm in Matlab (Mathworks 2016).

The average core permeabilities (Fig. 3a,e) were used to calculate the impedances in Fig. 11. For Berea sandstone, we assumed typical porosity of 0.2 and typical concentration of kaolinite particles of 0.06 (Khilar and Fogler 1998). The attached volumetric concentration is equal to σ_a0 = 0.06 × 0.8 = 0.048, which is equivalent to σ_cr for U₀ < U₁ (see Eq. (9)). We calculated the formation damage coefficient for the condition of total removal of all attached particles at the maximum fluid velocity, during the last fluid injection:

$$ \beta_{\text{s}} = \frac{{\sum\limits_{n = 1}^{N} {\left( {\beta_{\text{s}} \Delta \sigma_{{\text{a}n}} } \right)} }}{{\sigma_{{\text{a}0}} }} $$

(29)

Substituting formation damage coefficient (29) into the products β_sΔσ _an results in the values of released concentrations Δσ_an. The maximum retention concentrations at different fluid velocities can be calculated as follows:

$$ \sigma_{\text{cr}} \left( {U_{n} } \right) = \sigma_{{\text{a}0}} - \sum\limits_{n = 1}^{N} {\Delta \sigma_{{\text{a}n}} } $$

(30)

2.4.2 Results

Table 2 and Fig. 11 show results for history matching of impedance for the two coreflood tests by Ochi and Vernoux (1998). Tuning the model parameters resulted in monotonically decreasing dependency of the drift delay factor α = α(S) for corefloods in cores I and II (Fig. 3d, h, respectively). The higher the strained concentration, the higher the rock tortuosity, which decelerates particle drift. Also, the higher the strained concentration, the smaller the mobilised particles, which drifted at lower velocity.

Table 2 Tuned values of the model parameters

The experimental data closely matched the model (R² values of 0.99 and 0.98 for cores I and II, respectively). Fixing the drift delay factor for the overall period of fluid injection and then comparing the impedance data resulted in significantly lower R² values during adjustment of the proposed model. Using Eq. (30) to tune the model for two cores yielded the maximum retention function shown in Fig. 14. The increase in fluid velocity resulted in the increase in drag and lift forces, which detached the kaolinite particles from the surface of the rock grains and reduced the concentration of kaolinite particles remaining immobilised on the rock grain surface. If a monolayer of poly-sized kaolinite particles is attached to the surface of rock grains, mechanical equilibrium model (6) and (8) indicates that the obtained σ_cr-curves would not be convex.

Fig. 14

Maximum retention curves σ_cr(U) obtained from a test I and b test II

The proposed model can be used to calculate the size distribution of attached fine particles Σ_a(r_s) from the maximum retention function σ_cr(U): the minimum mobilised size r_scr(U) is determined from Eq. (6), and size distribution function Σ_a(r_s) is calculated from Eq. (8) by regularised numerical differentiation (Coleman and Li 1996).

Because the fluid velocity was changing stepwise during coreflood tests (seven velocities for test I, and four velocities for test II), the calculated kaolinite particle distributions are given in the form of a histogram (Fig. 15). As follows from Fig. 3c, g, the minimum radius of detached particles decreases as fluid velocity increases. This observation agrees with the shape of the velocity dependency of the critical radius exhibited in Fig. 8.

Fig. 15

Size distributions of movable fine particles on the matrix surface: a test I and b test II

Figure 16a, b compare the various forces acting on a particle at the critical instant of its mobilisation. According to Fig. 15, the ranges of particle radii cover the ranges of size distributions for particles attached to the surface of rock grains. The drag force was two orders of magnitude smaller than the electrostatic force. The drag force was significantly larger than the gravitational or lift force. Because lever arm ratio l significantly exceeded one, the small drag torque exceeded the torque developed by electrostatic force.

Fig. 16

Forces exerting on the attached particles: a test I and b test II

The maximum retention function can be parameterised by the critical particle radius σ_cr(U) = σ_cr(r_scr(U)). Considering the value σ_cr(r_scr) as an accumulation function of retained concentration for all particles with radius smaller than r_scr yields the corresponding histogram (Fig. 15), representing the concentration distribution of initial reservoir fines for various radii. Thus, the maximum retention function, σ_cr, for various sized particles attached to the grain surface can be explained: if particles attached to the grain surface cannot be mobilised by fluid flowing with velocity U, then their radii are smaller than r_scr(U) and their concentration is expressed as σ_cr(U). Increasing fluid velocity U results in the decrease of minimum radius of particles detached by flow with velocity U.

The calculated values of filtration and formation damage coefficients (Table 2) fall within the common ranges of these coefficients reported by Pang and Sharma (1997). The orders of magnitude of drift delay factor, which vary between 10⁻³ and 10⁻⁴ in the present work, are the same as those reported by Oliveira et al. (2014).

2.5 Summary and Discussion

According to mathematical model (1), (3) and (5), which accounts for the maximum retention function for detachment and migration of particles at velocity equal to carrier fluid velocity, rock permeability should stabilise after 1 PVI. However, the experimental data showed that the permeability stabilisation periods are significantly greater than 1 PVI. Such behaviour can be explained only if a mobilised particle moves significantly slower than the flowing fluid. This behaviour could be described by a two-speed particle-transport model (Yuan and Shapiro 2011a, b; Bradford et al. 2012).

The model contains six constants of mass exchange between particles moving slow and fast, detachment coefficient and filtration coefficient for fast particles, corresponding coefficients for slow particles and velocity of slow particles. The model tuning for the experimental breakthrough curves is not unique. Complete characterisation of the two-speed model would require complex experiments in which pressure drops along a core and along the particle breakthrough curve are measured and the retained particle concentrations are calculated. Yet, most coreflood studies have reported data for pressure drop along the core only. For this reason, the present study considers a rapid exchange between populations of particles migrating with fast and slow velocities along each rock pore, yielding a unique particle drift velocity. Also, this exchange is assumed to occur significantly faster than the capture of particles by the rock after a free run in numerous pores, resulting in equal concentrations of particles moving with fast and slow velocities. The above assumptions translate to a single-velocity model (You et al. 2015, 2016).

Proposed model (15)–(18) is applied to the data treatment of laboratory tests. The modelling results show that the migrating particles move significantly slower than the carrier fluid. Hence, there is a delay in the permeability stabilisation due to fines migration. The delay time is 500–1250 PVI, which corresponds to the drift delay factor α _n varying within 0.0008–0.002.

Migrating particles can be divided into two groups according to the velocity. One group of particles travel with the same velocity as the carrier fluid; while the other group drifts along the grain surfaces with significantly lower velocity (slow particles). The percentage of slow particles depends on particle-size distribution, velocity of the carrier fluid and electrostatic forces between the particles and grains (both magnitude of the electrical forces and whether they are repulsive or attractive). The slow particles can slide or roll on the grain surfaces, or temporarily move away from grain surface to the bulk of the fluid, before colliding with grain surface asperities again (Li et al. 2006; Yuan and Shapiro 2011b; Sefrioui et al. 2013).

The largest size of particles that can stay attached to the grain surface at each velocity can be calculated using torque balance Eq. (6), i.e. there exists a critical particle radius for each velocity such that all particles with larger radii will be mobilised by the carrier fluid: r_scr = r_scr(U) (see Fig. 6).

The maximum retention function, σ_cr(U), can be defined for a monolayer of attached particles as the concentration of attached particles with r < r_scr. The minimum size of mobilised particles as a function of fluid velocity follows from torque balance given by Eq. (6). It allows calculation of σ_cr using size distribution of the particles that can be mobilised at each fluid velocity. The function σ_cr depends on particle-rock electrostatic constants, Young’s moduli, Poisson’s ratio and size distribution of the attached particles.

Maximum retention is a monotonically decreasing function of mean particle size (Fig. 9a). The higher the variance coefficient of particle-size distribution, the lower the σ_cr at low fluid velocities, and the higher the σ_cr at high velocities (Fig. 9b).

The σ_cr curve for a monolayer of multi-sized particles has a convex shape at low fluid velocities and a concave shape at high velocities (Fig. 9c). However, for a multilayer attachment of mono-sized particles, that curve has a convex shape for all velocities.

For 1-D (one-dimensional) suspension flow with piecewise increase of the fluid velocity, the exact analytical solution can be obtained. The process includes particle migration and subsequent capture (straining) at the pore throats. Changing the fluid velocity creates a particle concentration front that starts moving from the core inlet. The concentration front coincides with the trajectory of the drifting particles and separates the particle-free region (behind the front) from particle-migration region (ahead of the front). The concentration profiles of the suspended and strained particles are uniform ahead of the front.

The drift delay factor α _n is a function of the particle size and the geometry of the porous media, which undergoes a continuous change during straining of migrating particles at the pore throats. Small particles move along the grain surface more slowly than do large particles. Hence, the drift delay factor is smaller for small particles than for large particles. Because larger particles are detached at lower fluid velocities, the size of the released particles decreases during the coreflood test with piecewise increase of fluid velocity. This explains the decrease in drift delay factor during the experiment (Fig. 3d, h). Hence, the introduction of a phenomenological function of the form α _n  = α _n (r_s,σ_s) can further improve the proposed model for colloidal-suspension transport in porous media with instant particle release and slow drift (Eqs. 15–18).

The proposed mathematical model has been found to yield pressure data that closely approximate those from coreflood tests with piecewise increase of velocity. To completely validate the model for where velocity of the migrating particles differs significantly from that of the carrier fluid, parameters such as particle retention profiles, breakthrough concentration of particles and size distribution of produced particles should also be measured. Then, these measured data would be compared against the analytical solutions presented in Table 1. Such a test with measurement of all required parameters is not available in the literature.

3 Fines Detachment and Migration at Low Salinity

Salinity alteration affects the electrostatic forces between fines and the rock surface, thereby influencing fines detachment. Decreasing salinity of the flowing brine increases the repulsive component of the electrical forces (double-layer electrical force). This weakens the total attraction between the attached fines and rock surface, which may cause fines to be mobilised by the viscous forces from flowing brine (Eq. 6). The detached fine particles migrate with the carrier fluid and plug pore throats smaller than they are, leading to a significant permeability reduction.

Section 3.1 describes the methodology and experimental setup for coreflood tests with piecewise salinity decrease. Section 3.2 presents the experimental results. Section 3.3 derives a mathematical model for fines detachment and migration in porous media, accounting for slow fines migration and delayed fines release during salinity alteration. Section 3.4 compares the experimental data and the mathematical model’s prediction.

3.1 Laboratory Study

This section presents the experimental setup, properties of the core and fluids, and the experimental methodology.

3.1.1 Experimental Setup

A special experimental setup was developed to conduct colloidal-suspension flow tests in natural reservoir rocks. The core permeability and produced fines concentration were measured. In addition, an extra pressure measurement was taken at the midpoint of the core, which complements the routine core inlet and outlet pressure measurements. The schematic drawing and the photograph of the apparatus are shown in Figs. 17 and 18, respectively. The system consisted of a Hassler type core holder, a high-pressure liquid chromatography pump (HPLC) and a dome back-pressure regulator to maintain a constant pressure at the core outlet. Three Yokogawa pressure transmitters were used to record the pressure data at the core inlet, outlet and the intermediate point, and a fraction collector was used to collect samples of the produced fluid. The overall volumetric concentration of solid particles at the effluent was measured using a PAMAS SVSS particle counter with a particle-size range of 1–200 µm. Prior to the tests, the concentration of solid particles in the solution was measured and used as the background particle concentration in the calculations.

Fig. 17

Schematic of laboratory setup for fines migration in porous media: (1) core plug. (2) Viton sleeve. (3) Core holder. (4) Pressure generator. (5, 9, 14, 15, 16) Manual valves. (6, 10, 11, 17) Pressure transmitters. (7) Suspension. (8) HPLC pump. (12) Back-pressure regulator. (13) Differential pressure transmitter. (18) Data acquisition module. (19) Signal converter. (20) Computer. (21) Beakers. (22) PAMAS particle computer/sizer

Fig. 18

Photo of laboratory setup for fines migration in porous media

3.1.2 Materials

A sandstone core plug was used to perform a coreflood test with piecewise salinity decrease. The core was taken from the Birkhead Formation (Eromanga Basin, Australia) and had a permeability of 34.64 mD. A water-cooled diamond saw was used to fashion several core plugs, each having a diameter of 37.82 mm and a length of 49.21 mm. These were subsequently dried for 24 h.

The XRD test showed that the core sample contains a considerable amount of movable clay, including 9.2 w/w% of kaolinite and 18.6 w/w% of illite (see Table 3 for the full mineral composition).

Table 3 Mineralogical composition of the rock

The ionic composition of the formation fluid (FF) is listed in Table 4a (supplied by Amdel Laboratories, Adelaide, Australia). The ionic composition was expressed as salt concentration in order to prepare an artificial formation fluid (AFF) with similar ionic strength (0.23 mol/L) to the formation water (Table 4b). The AFF was prepared by dissolving the calculated salt concentrations in deionized ultrapure water (Millipore Corporation, USA; later in the text it is called the DI water). NaCl was then added to the AFF, in order to increase the ionic strength of the solution to 0.6 mol/L, equivalent to the ionic strength of the completion fluid. The composition of high-salinity AFF is listed in Table 4b (AFF (NaCL)). In order to decrease salinity of the injected fluid during the experiment, the AFF was diluted using DI water to obtain the desired ionic strength for each injection step (maintaining the salinity 0.6, 0.4, 0.2, 0.1, 0.05, 0.025, 0.01, 0.005, 0.001 mol/L).

Table 4 a Ionic compositions for formation fluid (FF), and b ionic compositions for artificial formation fluid (AFF)

3.2 Methodology

Prior to the experiment, the air was displaced from the core by saturating the core sample with 0.6 M AFF under a high vacuum. Then, the core plug was installed inside the core holder, and the overburden pressure was gradually increased to 1000 psi and maintained during the experiment. Afterwards, the 0.6 M AFF was injected into the core sample with a constant volumetric flow rate of 1.0 mL/min (superficial velocity: 1.483 × 10⁻⁵ m/s). The pressure drop was recorded at three points: inlet, outlet and the intermediate point. The intermediate pressure point was placed 25.10 mm from the core inlet.

Fluid injection continued until permeability stabilisation was achieved with uncertainty of 3.2% or less (Badalyan et al. 2012). The test then proceeded by stepwise decreasing the ionic strength of injected brine in nine consecutive steps: 0.4, 0.2, 0.1, 0.05, 0.025, 0.01, 0.005, 0.001 mol/L and DI water. Permeability stabilisation was achieved at each step. The produced fluid was sampled using an automatic fraction collector. The sampling size was 0.17 PV at the beginning and then increased to 0.86 PV after 2 PVI.

The overall solid particle concentration in the produced samples was measured using a PAMAS particle counter, which uses laser scattering in a flow-through cell to measure the number and size distribution of the solid particles (from 0.5 to 5.0 µm) in the suspension, assuming spherical particles. Multiplying the size distribution function by the sphere volume and integrating with respect to radius yields the overall volumetric particle concentration. The electrolytic conductivity of the produced samples was also measured, to calculate breakthrough ionic strength.

3.3 Experimental Results

The initial core permeability and porosity were 34.64 mD and 0.13, respectively. This allowed calculation of mean pore radius (r_p = 6.62 µm, $r_{\text{p}}^{2} = k/(4.48\phi^{2} )$) (Katz and Thompson 1986). The analysis of effluent samples shows that the mean size of produced particles was 1.47 µm. The so-called 1/7–1/3 rule of filtration was introduced by Van Oort et al. (1993). They suggested that particles larger than 1/3 of the pore size cannot enter the porous media and form an external filter cake, but that particles smaller than 1/7 of the pore size can travel through porous media without being captured. Particles between 1/3 and 1/7 of the pore size can enter the porous media; however, they can be retained at the pore throats, which impairs permeability. In the current experiment, the particle-to-pore size ratio (jamming ratio) was 0.22 (between 1/3 and 1/7), implying that particles can be captured at pore throats after being released by reduction of fluid salinity. This explains the observed impedance growth (Fig. 19a) during reduction of injection fluid salinity (ionic strength).

Fig. 19

Matching the coreflood data by the slow-particle model: a impedance growth along the whole core and the first core section. b Accumulated fine particle production

If all mobilised particles were released instantly and moved at the same velocity as the carrier fluid, permeability would be expected to stabilise in 1 PVI after each salinity alteration. However, the measured pressure data show that permeability stabilisation takes much longer (Fig. 19a). This delay in permeability stabilisation could be attributed to delay in particle detachment after salinity alteration or to the slow migration of released particles drifting along the rock surface (Yuan and Shapiro 2011a; You et al. 2015).

Figure 20 shows the cumulative produced particles and effluent ionic strength. The salinity and produced particle fronts coincide after each salinity alteration. The salinity alteration is accompanied by fine particle production and permeability reduction. This confirms that the fines mobilisation during salinity alteration is the mechanism for the permeability impairment. Similar to permeability behaviour, the fines were produced for a much longer period than 1 PVI.

Fig. 20

Variation in effluent ionic strength and cumulative produced particle volume versus PVI during injection of water with piecewise-constant decreasing salinity: a for salinities 0.4, 0.2 and 0.1 M; b for salinities 0.05, 0.025 and 0.01 M; and c for salinities 0.005, 0.001 M and MilliQ water

3.4 Analytical Model for Slow Fines Migration and Delayed Particle Release

The impedance (reciprocal of permeability) growth curve presented in Fig. 19a indicates that after each salinity alteration, permeability stabilisation was achieved in tens to hundreds of PVI rather than the expected 1 PVI. As mentioned previously, one possible mechanism for the slow permeability stabilisation is the delay in particle detachment after salinity alternation. This phenomenon can be explained by electrokinetic ion-transport theory (Nernst–Planck model). It describes the diffusion of ions between the bulk fluid and the particle–grain area (Mahani et al. 2015a, b, 2016), which is not considered in slow-migration model (15)–(18). In this section, the slow-migration model is modified to account for both slow fines migration and delayed particle release.

Introducing a delay τ into the maximum retention function results in an expression for delayed fines detachment: σ_a(x, t + τ) = σ_cr(γ(x,t)), where γ(x, t) is the fluid salinity at time t. Retaining the first two terms of Taylor’s expansion for a small value of τ results in

$$ \tau \frac{{\partial \sigma_{\text{a}} }}{\partial t} = \sigma_{\text{cr}} \left( {\gamma_{1} } \right) - \sigma_{\text{a}} $$

(31)

The equation for maximum retention function (13) can now be replaced by kinetic Eq. (31). The system of three Eqs. (11), (12) and (31) describes suspension transport in porous media and accounts for delayed release of the reservoir fines during salinity reduction. This system can be solved for the unknown values c, σ_a and σ_s.

Replacing σ_a0 with released particles concentration Δσ_cr in dimensionless group (14) yields a dimensionless system of equations for suspension transport in porous media that accounts for delayed release of reservoir fines:

$$ \frac{{\partial \left( {C + S_{\text{s}} + S_{\text{a}} } \right)}}{\partial T} + \alpha \frac{\partial C}{\partial X} = 0 $$

(32)

$$ \varepsilon \frac{{\partial S_{\text{a}} }}{\partial T} = S_{\text{cr}} \left( {\gamma_{1} } \right) - S_{\text{a}} $$

(33)

$$ \frac{{\partial S_{\text{s}} }}{\partial T} = \alpha\Lambda C $$

(34)

where the delay factor ε is defined as $\varepsilon = {{U\tau } \mathord{\left/ {\vphantom {{U\tau } {\phi L}}} \right. \kern-0pt} {\phi L}}$.

Because it takes significantly longer than 1 PVI for the mobilised particles to reach the core outlet (1/α ≫ 1), i.e. α ≪ 1, the initial and boundary conditions for injection of particle-free fluid with salinity γ₁ are

$$ \begin{aligned} & C\left( {X,0} \right) = 0,\;\;\gamma \left( {X,0} \right) = \gamma_{1} ,\;\;S_{s} \left( {X,0} \right) = 0, \\ & \quad S_{a} \left( {X,0} \right) = S_{a0} = \frac{{\sigma_{a0} }}{{\Delta \sigma_{a} }} \\ & C\left( {0,T} \right) = 0,\;\;\gamma \left( {0,T} \right) = \gamma_{1} \\ \end{aligned} $$

(35)

where γ₀ and γ₁ are initial and injected salinities, respectively. The initial concentration of attached particles is σ_a0 = σ_cr(γ₀) for γ₀ > γ₁.

The solution to linear ordinary differential Eq. (33) with initial condition (35) is

$$ S_{\text{a}} = S_{\text{acr}} \left( {\gamma_{1} } \right) - \left[ {S_{\text{acr}} \left( {\gamma_{1} } \right) - S_{{{\text{a}}0}} } \right]\exp \left( { - \frac{T}{\varepsilon }} \right) $$

(36)

It yields the following equation for the detaching rate:

$$ \frac{{\partial S_{\text{a}} }}{\partial T} = \frac{1}{\varepsilon }\left[ {S_{\text{acr}} \left( {\gamma_{1} } \right) - S_{{{\text{a}}0}} } \right]\exp \left( { - \frac{T}{\varepsilon }} \right) $$

(37)

Substituting the equations for straining rate (34) and detaching rate (37) into overall particle balance equation (32) results in the following equation for suspended concentration:

$$ \frac{\partial C}{\partial T} + \alpha \frac{\partial C}{\partial X} = - \alpha\Lambda C + \frac{1}{\varepsilon }\left[ {S_{{{\text{a}}0}} - S_{\text{acr}} \left( {\gamma_{1} } \right)} \right]\exp \left( { - \frac{T}{\varepsilon }} \right) $$

(38)

Introduction of the following constants:

$$ y = \frac{1}{\varepsilon }\left[ {S_{{{\text{a}}0}} - S_{\text{acr}} \left( {\gamma_{1} } \right)} \right],\quad b = 1/\varepsilon $$

(39)

simplifies Eq. (38) as

$$ \frac{\partial C}{\partial T} + \alpha \frac{\partial C}{\partial X} = - \alpha\Lambda C + y\exp \left( { - bT} \right) $$

(40)

Ahead of the front of the mobilised fines (T ≤ X/α), the characteristic form of the linear hyperbolic Eq. (40) is

$$ \frac{{{\text{d}}x}}{{{\text{d}}T}} = \alpha $$

(41)

$$ \frac{{{\text{d}}C}}{{{\text{d}}T}} = - \alpha\Lambda C + y\exp \left( { - bT} \right),\quad C(X,0) = 0 $$

(42)

If αΛ ≠ b, the solution to the linear ordinary differential Eq. (42) is

$$ C\left( T \right) = \frac{y}{{\alpha\Lambda - b}}\left( {e^{ - bT} - e^{{ - \alpha\Lambda T}} } \right) $$

(43)

If αΛ = b, the solution to (42) is

$$ C\left( T \right) = yTe^{ - bT} $$

(44)

Similar to fines migration due to abrupt velocity increase (row 3 in Table 1), the initial uniform profile of the suspended particles moves with an equal capture probability for all the suspended particles. Thus, the profile of the suspended particles remains uniform, and the suspended concentration is time-dependent only.

Behind the front of mobilised fines (T > X/α), the characteristic form of Eq. (38) with a zero boundary condition is

$$ \frac{{{\text{d}}T}}{{{\text{d}}X}} = \frac{1}{\alpha },\quad T\left( 0 \right) = \eta $$

(45)

$$ \frac{{{\text{d}}C}}{{{\text{d}}X}} = -\Lambda C + \frac{y}{\alpha }\text{e}^{ - bT} ,\quad C\left( 0 \right) = 0 $$

(46)

If αΛ ≠ b, the solution to the linear ordinary differential Eq. (46) is

$$ C(X) = \frac{m}{{\Lambda - \frac{b}{\alpha }}}\left( {e^{{ - \frac{b}{\alpha }X}} - e^{{ -\Lambda X}} } \right),\quad m = \frac{y}{\alpha }e^{{\left( { - b\eta } \right)}} $$

(47)

Substituting the constant η along the characteristic line

$$ \eta = T - \frac{X}{\alpha } $$

(48)

into solution (48) yields the following expression for the suspended concentration behind the front:

$$ C(X,T) = \frac{y}{{\alpha\Lambda - b}}e^{ - bT} \left( {1 - e^{{\left( {\frac{b}{\alpha } -\Lambda } \right)X}} } \right) $$

(49)

If αΛ = b, the solution to Eq. (46) is

$$ C(X) = mXe^{{ -\Lambda X}} $$

(50)

Substituting the constant η along the characteristic line (48) into solution (50) yields the following expression for the suspended concentration behind the front:

$$ C(X,T) = \frac{y}{\alpha }{e}^{ - bT} Xe^{{\left( {\frac{b}{\alpha } -\Lambda } \right)X}} $$

(51)

Formulae for strained concentration S_s are obtained by substituting suspended concentration from Eqs. (43), (44), (49) and (51) into the equation for straining rate (34) and then integrating with respect to T. This solution is listed in Table 5 for αΛ ≠ b and in Table 6 for αΛ = b. The profiles of suspended and strained concentrations are shown in Fig. 21.

Table 5 Analytical model for fines mobilisation, migration and suspension ($\alpha\Lambda \ne b$)

Table 6 Analytical model for fines mobilisation, migration and suspension ($\alpha\Lambda = b$)

Fig. 21

Analytical slow-fines delay-release model: a trajectory of fronts and characteristic lines in (X, T) plane. b Suspended concentration profiles at three instants. c Strained concentration profiles at three instants

3.5 Treatment of Experimental Data

The result of the coreflood test with piecewise salinity decrease (presented in Sect. 3.1) is modelled in this section. The three models that have been presented in previous sections are applied to the experimental data treatment: the slow-particle migration model (Table 1), the delayed-particle-release model (Tables 5 and 6 with α = 1), and the general model that accounts for both effects (Tables 5 and 6). The pressure drop along the core (whole core) and between inlet and midpoint (half-core), and the accumulated produced fines are matched separately by all three models. The reflective trust region algorithm (Coleman and Li 1996) is applied for optimisation using Matlab (Mathworks 2016).

Figure 19 presents the treatment of impedance and cumulative produced fines data using the slow-particle migration model. The coefficient of determination R² is 0.9902. The model tuning parameters are formation damage coefficient β, filtration coefficient λ, released concentration Δσ, delay factor ε, and drift delay factor α. The pore space geometry and values of the tuning parameters change during coreflood, as a result of pore throat plugging by mobilised fines. Hence, the tuning parameters vary with change in injected fluid salinity, which causes fines mobilisation and permeability impairment. Table 7 and Fig. 22 show the values of the tuning parameters at each salinity.

Table 7 Fitted parameters for the slow-particle model

Fig. 22

Tuned values of the slow-particle model parameters: a drift delay factor, b formation damage coefficient, c filtration coefficient and d maximum retention function

The drift delay factor α decreases as salinity decreases (Fig. 22a). This can be attributed to the decreasing size of released particles during the salinity decrease. Smaller particles are subject to lower drag force and therefore move at lower velocity. Also, the rock tortuosity increases due to straining, so that the fines move at lower velocity. Regarding formation damage coefficient β, there are two competing factors during the salinity decrease. The first is permeability, which inversely affects the formation damage coefficient. The other is particle size, with which the formation damage coefficient varies. The retained-concentration dependency for the formation damage coefficient, shown in Fig. 22b, is attributed to particle size’s dominating the permeability effect. The filtration coefficient for straining, λ, increases with rock tortuosity increase during salinity reduction (Fig. 22c). Yet, it should decrease due to decrease in released particle size. Figure 22d presents the salinity dependency of the maximum retention function, which exhibits a typical form (Bedrikovetsky et al. 2012a, b; Zeinijahromi et al. 2012a, b).

The results of comparison with the delayed-particle-release model are presented in Fig. 23a for impedance, and in Fig. 23b for accumulated particle concentration. Table 8 shows the tuning parameter values. The values of tuned parameters β, λ, ε and Δσ versus the salinity injected are also presented in Fig. 24a–d, respectively. The coefficient of determination is equal to R² = 0.9874 and is slightly lower than that for the slow-particle model.

Fig. 23

Matching the coreflood data by the delayed-particle-release model: a impedance growth along the whole core and the first core section; b accumulated fine particle production

Table 8 Fitted parameters for the delayed-particle-release model

Fig. 24

Tuned values of the delayed-particle-release model parameters for 10 different-salinity stages: a formation damage coefficient, b filtration coefficient, c delay factor and d concentration of detached fines

Figure 24a shows that formation damage coefficient β increases as salinity declines, which contradicts the above conclusion for the slow-particle model. We attribute this to the dominant role of permeability decline on the formation damage coefficient: the lower the permeability, the higher the formation damage. Yet, this explanation contradicts the observation made above for the slow-particle model, where the formation damage coefficient decreases with the deposit increase.

The filtration coefficient λ decreases during salinity reduction (Fig. 24b), which also contradicts the above observation for the slow-particle model. We attribute this to the blocking filtration function, where λ is proportional to the vacancy concentration: the filtration function approaches zero as the number of pores smaller than particles approaches zero. Also, the released particle size decreases during salinity decrease, so the probability of particle straining declines, which is another explanation why the filtration coefficient declines during the injection.

The delay factor ε decreases with increase in strained concentration (Fig. 24c), which we attribute to more confined porous space and smaller diffusive path. Also, the interstitial velocity increases during straining, resulting in higher effective (Taylor’s) diffusion in each pore and yielding the delay decline.

The maximum retention function (Fig. 24d) is unlike the usual release of fine particles at very low salinity, which is close to freshwater. The effect of fines release decrease during salinity decrease might be explained by low concentration of small particles on the rock surface. This hypothesis could be tested by measuring particle-size distributions in the breakthrough fluid.

Mahani (2015a, b) measured the delay period, which is 10–20 times longer than that expected by diffusion alone and is explained by slow electrokinetic Nernst–Planck ion-diffusion in the field of electrostatic DLVO forces. The delay time t _τ varies from 10,800 to 363,600 s, which corresponds to dimensionless time (ε = Ut _τ /ϕL) varying from 15.49 to 521.62 PVI for conditions of the test presented in Sect. 3.1 (ϕ = 0.13, U = 1.48 × 10⁻⁵ m/s). These values have the same order of magnitude as those obtained by tuning the parameter ε from laboratory tests and are presented in Tables 8 and 9.

Table 9 Fitted parameters for the slow-particle delayed-release model

Figure 25a presents the results of impedance matching by the general model that accounts for both phenomena of slow-particle migration and delayed particle release. Figure 25b presents the results for accumulated particle concentration. Table 9 shows the tuning parameter values. The coefficient of determination is equal to R² = 0.9899. The modelling data are in close agreement with the laboratory results, with deviation observed only for freshwater injection. The strained concentration dependencies for α, β, λ and Δσ (Fig. 26a–c, e, respectively) follow the same tendencies as those exhibited by the slow-particle model. The delay factor ε (Fig. 26d) has the same form as that for the delay-detachment model. Thus, the tendencies for tuned values as obtained by the general model agree with the results of both particular models.

Fig. 25

Matching the coreflood data by the slow-particle delayed-release model: a impedance growth along the whole core and the first core section. b Accumulated fine particle production

Fig. 26

Tuned values of the slow-particle delayed-release model parameters for 10 different-salinity stages: a drift delay factor, b formation damage coefficient, c filtration coefficient, d delay factor and e concentration of detached fines

3.6 Summary and Discussion

The laboratory study of fines migration due to decreasing brine salinity provided three measurement histories during each injection step with constant salinity: impedance across the half-core, impedance across the whole core and the outlet concentration of fine particles. Each pressure curve and each concentration curve has at least two degrees of freedom. Thus, the three measured curves have six degrees of freedom for constant-salinity periods.

The slow-particle migration model has four independent coefficients; therefore, a six-dimensional dataset was compared to the model with four tuned coefficients, and the latter was found to be highly accurate. We explained the strained saturation dependencies of the tuned parameters by the well-known dependencies for formation damage parameters of particle and pore sizes. Under the conditions where the degree of freedom for the experimental data are higher than the number of tuned constants, close agreement between the experimental data and the model allows concluding the validity of the slow-particle migration model. The delay-release model has five independent coefficients. This is higher than that for the slow-particle migration model, but still lower than the six degrees of freedom of the laboratory dataset. The agreement coefficient is also very high between the laboratory data and the model-predicted data. The obtained delay periods have the same order of magnitude as do those observed in laboratory tests by Mahani et al. (2015a, b). However, the model does not exhibit a common form of the maximum retention function after the laboratory-data adjustment.

Thus, the advantages of the slow-particle model over the delay-release model are the smaller number of tuned parameters and common form of the revealed maximum retention function.

The general model has five independent coefficients, which is lower than the six degrees of freedom of the laboratory dataset. The agreement coefficient is also very high. The obtained delay periods have the same order of magnitude as do those observed in laboratory tests. The model exhibits a common form of the maximum retention function.

The slow-fines-migration model with four free parameters already exhibits very close agreement with laboratory data. Adding the delay factor into the slow-fines model does not change its accuracy.

The proposed interpretation of the model-parameter variations with the salinity decrease includes several competitive factors. It is impossible to declare a priori which factor dominates. Therefore, the proposed explanations must be verified by micro-scale modelling.

4 Fines Detachment and Migration at High Temperature

This section discusses the temperature dependency of fine particle detachment and migration in geothermal reservoirs (Rosenbrand et al. 2015).

As previously discussed, the DLVO theory is used for calculating the electrostatic forces. Because the electrostatic forces are temperature-dependent, fines mobilisation is also a function of temperature. The temperature-dependent parameters of the DLVO forces are listed in Table 10.

Table 10 Temperature effects on the parameters in DLVO interaction energy model

Figure 27 presents the effect of temperature on critical particle size according to Eq. (6). Because electrical attraction decreases with temperature increase, particles can be mobilised at a lower velocity if the temperature is increased (illustrated by the curve for 25 °C being above the curve for 80 °C).

Fig. 27

Critical particle size for monolayer of size-distributed particles mobilised by the fluid flow at various velocities

4.1 Experimental Results and Model Prediction

The experimental study was undertaken to help analyse formation damage due to fines migration in the Salamander-1 geothermal well (Pretty Hill Formation, Otway Basin, South Australia). However, there is no core from the Salamander-1 well, and only drilling cuttings are available. Thus, a core with analogous mineral characteristics from the same formation and basin (Ladbroke Grove-1 well) was used for this study. This core was taken from depth 2557.12 m and has porosity of 17.2%. The core is 6.33 cm long and has a diameter of 3.92 cm.

In order to characterise the mineralogy of fines present in the core sample, the produced fines were collected by filtering the effluent fluid through a 0.45 μm Nylon filter. The collected volume of produced fines was insufficient for performing an XRD analysis. Thus, SEM-EDX analyses were performed on the produced fines, the results of which are shown in Fig. 28. The plate-like ‘booklets’ on the SEM image show the typical characteristic of kaolinite fines (Fig. 28a). The ‘peak height ratio’ (ratio of relative molar proportions) for Al and Si are shown in the EDX spectrum (Fig. 28b). The similar ratios between Al and Si indicate that the observed booklets on the SEM image are kaolinite, where the compound Al₂(Si₂O₅)(OH)₄ is typical.

Fig. 28

SEM-EDX results for the core sample (Ladbroke Grove-1 well): a SEM image and b EDX spectra for kaolinite

A coreflood test with piecewise salinity (ionic strength) decrease was performed using the Ladbroke Grove-1 core, using the methodology given in Sect. 3.

Figure 29a presents the normalised permeability of the core for each salinity versus time (black circles). Figure 29b shows that reduction in injection fluid salinity resulted in decrease of the core permeability and production of fine particles. As expected, the graph shows a similar trend as those presented in Figs. 20, 23 and 25. The core permeability drops instantly after each salinity reduction, implying that a significant fraction of attached fine particles are mobilised when salinity is reduced. The mobilised particles then plug pore throats gradually.

Fig. 29

Results of tuning the laboratory data from corefloods with varying fluid ionic strength at T = 25 °C, using the analytical model and prediction for Salamander geothermal field (T = 129 °C): a decrease of core permeability during tests with piecewise-decreasing ionic strength. b Cumulative breakthrough concentration at different fluid ionic strengths

The analytical model presented in Sect. 2.3 (rows 12 and 13 in Table 1) was used to treat the experimental data from the Ladbroke Grove-1 core. A typical log-normal distribution of particle sizes is assumed.

Because quartz and kaolinite are the most abundant minerals in the studied sandstone core, the following DLVO parameters were used in the calculations: refractive index of kaolinite n₁ = 1.502 (Egan and Hilgeman 1979), refractive index of quartz $n_{2}$ and brine $n_{3}$ as functions of temperature (Leviton and Frey 2006; Aly and Esmail 1993), dielectric constant of quartz $\varepsilon_{2} = 4.65$ (Stuart 1955), dielectric constant of kaolinite $\varepsilon_{1} = 6.65$ at $T = 25\,^{ \circ } {\text{C}}$ and $\varepsilon_{1} = 6.35$ at 80 °C (Leluk et al. 2010; see Table 10), and dielectric constant of brine $\varepsilon_{3}$ (Leluk et al. 2010; see Table 11). The zeta potentials for fines and grains were calculated using the correlation presented by Schembre and Kovscek (2005), and the water viscosity as a function of temperature was calculated using $\mu \left( T \right) = 2.414 \times 10^{ - 5} \times 10^{{247.8/\left( {T - 140} \right)}}$ (Al-Shemmeri 2012).

Table 11 Dielectric constant of kaolinite ε₁ [interpolated from data in Leluk et al. (2010)]

No available data were found for temperature dependency of the characteristic wavelength of interaction $\lambda$, refractive index of clay $n_{1}$, or collision diameter $\sigma_{\text{c}}$. Therefore, it was assumed that the parameters mentioned above are constant with temperature (Schembre and Kovscek 2005; Schembre et al. 2006; Lagasca and Kovscek 2014). These constant values were taken from Egan and Hilgeman (1979) and Elimelech et al. (2013).

The model tuning parameters are as follows: filtration coefficient λ, formation damage coefficient β, drift delay factor α, variance coefficient for particle-size distribution C _v , and mean particle size 〈r_s〉. As discussed previously, the sizes of particles that are mobilised depend on the injected fluid velocity and ionic strength (salinity). The DLVO calculation showed that particles with smaller sizes can be mobilised during the reduction of injected fluid salinity (Fig. 27). We assume that particles of only one size can be mobilised during each salinity step. This allows the following parameters to remain unchanged during each salinity step: filtration coefficient, formation damage coefficient and drift delay factor.

A least-square goal function was used to tune the analytical model. The minimisation of the difference between model prediction and the experimental data was carried out using the Levenberg–Marquardt minimisation algorithm (Matlab 2016). The obtained values of the tuning parameters are presented in Table 12. Figure 29 presents the results of modelling for permeability and effluent concentration. It shows high agreement between modelling results and experimental data for both core permeability (R² = 0.997) and produced particle concentration (R² = 0.943).

Table 12 Dielectric constant of brine $\varepsilon_{3}$^a

We now calculate the number of degrees of freedom for the experimental dataset. Assuming that pressure drop is exponential with time during each constant-salinity injection, we obtain three degrees of freedom for each time interval in Fig. 29a. Yet, the initial permeability for each time interval is equal to the final permeability from the previous interval, which results in 2 × 4 = 8 degrees of freedom of the pressure drop measurements. Four independent breakthrough particle concentrations, averaged over the constant-salinity injection periods, add four degrees of freedom, giving a total of 12. Table 13 shows 15 independent constants tuned from the experimental data, which exceeds the number of degrees of freedom of the laboratory dataset. There is close agreement between the experimental and modelling data. We conclude that the model matches the laboratory results with high accuracy.

Table 13 Values of the model tuning parameters in the coreflood test

However, validating the proposed model would require significantly more laboratory data. Such data could include online measurements of breakthrough particle concentration against time. Another possibility is the three-point pressure measurement discussed in Sect. 3. Pressure measurements in an intermediate core port will double the number of degrees of freedom of the pressure drop information. It would allow increasing the number of degrees of freedom for the experimental dataset and validating the mathematical model.

The sensitivity analysis was performed using the following tuning parameters: drift delay factor, formation damage coefficient and filtration coefficient. Figure 29a, b presents the results of the sensitivity calculations. The blue curve in Fig. 29a indicates that α-increase yields stabilisation-time decrease, because the particles move faster. The light-blue curve indicates that lower probability of particle capture by thin pores translates to lower values of λ, leading to higher values for permeability stabilisation period. The green curve shows that smaller values of β correspond to decrease in permeability damage with time. The only modelling parameter that has a significant effect on breakthrough concentration of mobilised particles is the filtration coefficient λ, because it reflects the probability of mobilised particle capture by thin pore throats (Fig. 29b). The light-blue curve in Fig. 29b shows that the lower values of λ correspond to higher breakthrough particle concentrations. The blue curve indicates that breakthrough particle concentration is insensitive to drift delay factor. The green curve shows that the breakthrough concentration is insensitive to β. The obtained values of λ and β presented in Table 13 along with the drift delay factor fall within their common intervals given by Nabzar and Chauveteau (1996), Pang and Sharma (1997), and Civan (2010, 2014).

The tuned data allow predicting the maximum retention function using Eq. (8). Maximum retention functions for a monolayer of multi-sized particles versus fluid velocity and fluid ionic strength are shown in Fig. 30a, b, respectively. Point I in Fig. 30a corresponds to initial attached particle concentration. While fluid velocity increases from 0 to U _A under the ambient temperature, the state point moves along the path I → A without particle mobilisation. Increasing fluid velocity from U _A to U _B (represented by migrating from point A to point B) leads to initiation of particle mobilisation at critical fluid velocity U = U _B . If fluid velocity further increases from U _B to U _C , the state point moves down along the maximum retention curve from point B to point C. Figure 30a, b depict the typical shape of the maximum retention function with gradual decrease in fluid ionic strength corresponding to increase in fluid velocity. This results in similarity between the critical ionic strength γ _B and the critical fluid velocity U _B . Miranda and Underdown (1993) reported that critical velocity corresponds to the first-particle release when fluid velocity increases. Khilar and Fogler (1998) reported that critical ionic strength corresponds to the first-particle release when fluid ionic strength decreases. The maximum retention function allows predicting the amount of the released fines as a result of altering the critical parameters. The amount of mobilised particles during alteration of fluid velocity or salinity is denoted as ∆σ in Fig. 30a, b.

Fig. 30

Temperature, velocity, and salinity dependence of maximum retention function: a maximum retention concentration versus velocity at different temperatures. b Ionic strength dependency of maximum retention concentration ($\gamma_{1} = 0.2\;{\text{M}}$ NaCl) at different temperatures. c Ionic strength dependency at geothermal reservoir temperature and different velocities

Electrostatic attractive force decreases with increasing temperature, thereby somewhat decreasing the maximum retention function. On the contrary, reduction in water viscosity with temperature results in decrease in (detaching) lift and drag forces, yielding an increase in the maximum retention function. These two competing effects determine whether the maximum retention function increases or decreases.

Figure 30a, b show that the dominance of temperature influence on electrostatic attaching forces leads to decrease in the maximum retention function and consequent permeability decline with temperature rise. σ_cr-curves were calculated for the following temperatures: room temperature (25 °C), 80, 100, and 129 °C (curves 1–4, respectively, in Fig. 30a, b). Comparing these curves shows decline in the maximum retention function with temperature increase. The geothermal well from the Salamander-1 field is characterised by a moderate temperature of T = 129 °C and ionic strength equivalent to 0.2 M NaCl. At these field conditions, according to curve 4 (Fig. 30b), almost all fines were mobilised when the maximum retention function has decreased to zero.

Fluid velocity alteration also affected particle mobilisation within a porous medium. Figure 30c shows σ_cr-curves for the following fluid velocities: wellbore velocity r_w, 50 r_w, and 100 r_w (curves 1–3, respectively). A decrease in fluid velocity yielded the maximum retention concentration increase, due to reduced detaching drag force acting on the attached particles.

4.2 Using Sensitivity of Ionic Strength to Characterise Fines Mobilisation

Torque balance equation (6) shows that the critical concentration of the attached particle σ_cr is a function of drag and lift forces. These detaching forces highly depend on the fluid velocity and viscosity. In a geothermal reservoir, both fluid velocity and viscosity change with time and position.

Consider inflow performance in a geothermal production well. The production rate per unit of the reservoir thickness is $q = 2\pi rU\left( r \right)$, where U(r) is fluid velocity and r is radius of the drainage contour.

During production, the fluid velocity decreases significantly with radius (two or more orders of magnitude) in the direction from the wellbore toward the drainage contour. Therefore, the rheological dependence of σ_cr on temperature should be studied in a wide range of fluid velocities. Having studied this relationship, one can reliably estimate well fines migration and consequently the productivity index.

Experimental study of fines migration at very high velocities is limited by injection pump capacity. However, coreflood tests can be performed at a wide range of fluid ionic strength. Therefore, in the laboratory, it is more practical to perform fines mobilisation tests by varying fluid ionic strength than by varying velocity alteration. Torque balance Eq. (6) has solutions $\sigma_{\text{cr}} = \sigma_{\text{cr}} \left( \gamma \right)$ and $\sigma_{\text{cr}} = \sigma_{\text{cr}} \left( U \right)$. This allows the effect of fluid ionic strength on fines mobilisation ($\sigma_{\text{cr}} = \sigma_{\text{cr}} \left( \gamma \right)$) to be translated into the effect of fluid velocity on fines mobilisation ($\sigma_{\text{cr}} = \sigma_{\text{cr}} \left( U \right)$, and vice versa. From $\sigma_{\text{cr}} \left( {\gamma_{0} } \right) = \sigma_{\text{cr}} \left( {U_{0} } \right)$, the translation formula is

$$ \sigma_{\text{cr}} \left( {U,\gamma_{0} } \right) = \sigma_{\text{cr}} \left( {U_{0} ,\gamma } \right) $$

(52)

The methodology of this translation is described below for a monolayer of multi-sized particles (see Eq. (8)). Performing a coreflood test at constant velocity $U_{0}$ with varying fluid ionic strength γ yields critical concentration of attached particles $\sigma_{\text{cr}} \left( {U_{0} ,\gamma } \right)$. Equation (6) determines critical attached particle radius at each salinity $r_{\text{scr}} \left( {U,\gamma } \right)$. The critical radius for varying velocity at a constant ionic strength can be recalculated using Eq. (6): $r_{\text{scr}} \left( {U_{0} ,\gamma } \right) = r_{\text{scr}} \left( {U,\gamma_{0} } \right)$. This allows translating the experimentally obtained $\sigma_{\text{cr}} \left( {U_{0} ,\gamma } \right)$ into $\sigma_{\text{cr}} \left( {U,\gamma_{0} } \right)$. Figure 30a, b show such a translation. Curve 1 in Fig. 30a presents the critical particle concentration at constant ionic strength $\sigma_{\text{cr}} \left( {U,\gamma_{0} } \right)$ that is equivalent to curve 1 in Fig. 30b, the critical particle concentration at constant velocity $\sigma_{\text{cr}} \left( {U_{0} ,\gamma } \right)$.

Figure 30b presents the maximum retention function (critical concentration of the attached fine particles) that corresponds to the permeability decline curve presented in Fig. 29a. The cumulative produced particle concentration is presented in Fig. 29b. Point I in Fig. 30b corresponds to the initial condition (injection of high-salinity fluid γ₁). A negligible volume of fines was produced at this salinity (point I in Fig. 29b). The path for reduction of injection fluid salinity (ionic strength) from point I to III on the maximum retention function curve goes through point II (horizontally from I → II and then along the curve II → III, indicated by arrows in Fig. 30b). Reduction in fluid salinity (ionic strength) from point I to point III results in a significant mobilisation of fines and a sharp increase in produced fines (points II and III in Fig. 29b). This sharp increase in fines mobilisation can be explained by the increase of slope of the maximum retention function curve from point II to point III. Further decrease of fluid ionic strength to point IV is accompanied by a smaller increase of released and produced fines. This corresponds to the inflection of the maximum retention function curve.

4.3 Summary and Discussion

This laboratory study on fines migration at high temperatures and micro-scale modelling of fines mobilisation allows drawing the following conclusions:

• For geothermal reservoir conditions, the lifting and gravity forces are two to four orders of magnitude weaker than the drag and electrostatic forces. Mechanical equilibrium of attached fines and the maximum retention function is determined by drag and electrostatic forces; the lift and gravity forces are negligible.

• The fines release capacity—maximum retention function—for a monolayer deposit of multi-sized particles, as well as for a poly-layer of single-size particles, can be expressed by explicit formula.

• Experiment-based model predictions for high-temperature geothermal conditions showed that the electrostatic attraction weakens with temperature increase, and the detaching drag force reduces with water viscosity decrease. The former effect dominates, resulting in the decrease of the maximum retention function with temperature. Therefore, geothermal reservoirs are more susceptible to fines migration than conventional aquifers or oilfields.

• The laboratory ‘temperature-ionic strength’ transformation procedure along with mechanical equilibrium modelling allows determining temperature dependency of the maximum retention concentration from the tests with varying ionic strength; it allows predicting particle detachment at high temperatures based on laboratory tests with salinity variation.

• Laboratory-measured permeability history is consistent with the model prediction.

• The prediction from laboratory-based mathematical modelling closely approximates geothermal-well index history from field data.

• Kaolinite and illite/chlorite, as main clay minerals presented in released fines from coreflood in the present study, are responsible for formation damage.

5 Fines Migration in Gas and CBM Reservoirs

Byrne et al. (2009, 2014) reported the intensive fines production and associated formation damage in high-rate gas wells. Possible explanation of this phenomenon is drying-up the rock in well vicinity. Despite negligible equilibrium vapour concentration in methane, numerous gas volumes pass via the near-well zone, resulting in evaporation of the connate water. The adhesion grain–grain attraction (bridging between two particles by capillary menisci) consolidates the rock. As water saturation decreases below its connate value, the capillary water bridge between some grains disappeared, the capillary component of stress decreases, yielding rock dis-consolidation. It causes the release of some particles by the drag force, exerting on the particle by the flowing gas.

The maximum retention function can model the phenomenon of fines release during water saturation decreasing below the connate value. Lazouskaya et al. (2013) account for two-phase fines mobilisation in torque balance Eq. (6). The adhesive force attracts water-wet particles and repulses hydrophobic fines (Muecke 1979). Accounting for capillary forces makes maximum retention function saturation-dependent (Yuan and Shapiro 2011b). However, matching the laboratory or field data on fines migration in two-phase environment by mathematical model is not available.

Besides salinity decreasing and increase in velocity, pH and temperature, stress increasing can also be a cause of fines mobilisation (Bai et al. 2015a; Han et al. 2015). Fines migration has been reported during well fracturing. Another area of fines migration due to increase in the reservoir stress is methane production from coal beds (Yao et al. 2016). The mathematical model for fines lifting is a kinetic equation for detachment rate, where the kinetics coefficient (relaxation time) is stress-dependent (Civan 2010; Guo et al. 2015; Mitchell and Leonardi 2016). Validation of the fines detachment rate under stress-increase by laboratory testing and theoretical derivation of kinetics rate equation from entropy production (Onsager principle) are still not available in the literature.

6 Conclusions

This analytical modelling and laboratory study of fines migration due to velocity, salinity, temperature and pH alteration during coreflooding allows drawing the following conclusions:

• 1. Mechanical equilibrium of attached fines is determined mainly by drag and electrostatic forces. Neglecting lift and gravitational forces eliminates half of the tuning parameters in the torque balance equation.

• 2. Low-velocity fines’ drifting along the rock surface (rolling, sliding) explains the long permeability stabilisation periods. Stabilisation time greatly exceeds the expected one pore volume injected, suggesting that the fine particles migrate at a velocity that is two to three orders of magnitude lower than the carrier water velocity.

• 3. Another explanation of long permeability stabilisation periods might be the delay in particle release due to slow diffusion of salt from the grain–particle deformed contact area into the bulk of the fluid.

• 4. One-dimensional problems for slow fines migration with delayed particle release after velocity, salinity or pH alteration allow for exact solution. The analytical model contains explicit formulae for breakthrough and retained concentrations and pressure drop history.

• 5. Matching the measured permeability and cumulative outlet particle concentration by the analytical model, accounting for both slow fines migration and delayed release, shows strong agreement between the measured data and modelling results.

• 6. The slow-particle model matches the experimental data with higher accuracy than does the delay-release model. The straining concentration and salinity dependencies for model parameters obtained from tuning the laboratory data by the slow-particle model have typical forms observed in other studies. Using the delay-release model for laboratory-data tuning reveals a non-typical form of the maximum retention function.

• 7. Fine particles mobilisation occurs in order of decreasing particle size during velocity, temperature and pH increase, or salinity decrease.

• 8. The maximum retention function for size-distributed fine particles attached to pore walls as a monolayer is expressed by an explicit formula that includes the size distribution of attached particles and the critical detached-size curve. This function is equal to accumulated concentration of particles smaller than those mobilised by the flux with a given flow velocity U.

• 9. Size distribution of the attached movable particles can be determined from the maximum retention function and the critical-size curve.

• 10. The laboratory ‘velocity-ionic strength’ and ‘temperature-ionic strength’ translation procedures along with mechanical equilibrium modelling allow determining velocity- and temperature dependencies of the maximum retention concentration from tests that vary ionic strength.

• 11. Temperature effect on reduction of electrostatic attractive forces exceeds the effect of (detaching) drag-force reduction induced by viscosity decrease. This results in the maximum retention function decrease with temperature increase. Therefore, geothermal reservoirs are more susceptible to fines migration than are conventional aquifers or oil and gas fields.