Novel Modeling of Non-Isothermal Flow-Induced Fine Particle Migration in Porous Media Based on the Derjaguin-Landau-Verwey-Overbeek Theory

Abstract

Mobilization of in situ fine particles in geothermal reservoirs is a key contributor to permeability damage and clogging of the reservoir rock, leading to a decline in well productivity during enhanced geothermal operations. This phenomenon is a result of disturbance in the mechanical equilibrium of the forces acting on a given fine particle, most significant of which are electrostatic and drag forces. These forces are affected by changes in fluid flow velocities, in situ temperatures, or ionic strength of in situ fluids. Theoretical formulation of migration of fine particles in porous media driven by non-isothermal flow remains challenging, and requires a considerable number of parameters to quantify the characteristics of a given colloidal particle-pore fluid–solid grain system. The identification of all the involved parameters often necessitates costly, intricate, and time-consuming physical experiments. Moreover, implementing the complete form of the Derjaguin-Landau-Verwey-Overbeek (DLVO) theory, commonly adopted to evaluate changes in electrostatic forces, is complicated, computationally demanding, and impractical, particularly when applied to evaluate fines migration at a reservoir scale. This study presents a theoretical framework for accurate and practical prediction of fine particle migration driven by non-isothermal flow in a clay-NaCl-quartz system. The novel contributions of this study are twofold. Firstly, a new numerical model is developed based on the complete DLVO theory, which integrates for the first time the effects of both thermal and hydraulic loads on all underlying parameters including both the static dielectric constant and the refractive index of the pore fluid. Secondly, an innovative simplified DLVO-based model has been introduced, requiring notably fewer parameters compared to existing models, thus offering a practical and efficient solution. The proposed models are utilized to conduct a comprehensive assessment of the fundamental mechanisms involved in fine particle liberation. Findings are key to predict fines-migration-induced permeability damage in geothermal reservoirs to achieve a sustainable design of energy storage/production operations as well as to develop effective strategies to prevent or mitigate the decline in well productivity in time.

1 Introduction

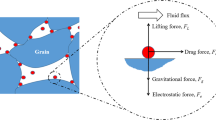
Decline in well productivity during enhanced geothermal operations is a widely reported challenge that has adverse effects on the sustainable extraction of heat (Baudracco 1990a, b; Baudracco and Aoubouazza 1995; Priisholm et al. 1987; Rosenbrand and Fabricius 2012; Rosenbrand et al. 2012, 2014, 2015). The release of in situ fine particles is a major factor contributing to this issue. These liberated particles move through the porous formation and become trapped in narrow pore throats, causing damage to permeability (Lever and Dawe 1984; Muecke 1979; Sarkar and Sharma 1990). Liberation of fines occurs when the mechanical equilibrium of the attaching forces (i.e., electrostatic and gravity forces) and the detaching forces (i.e., drag and lifting forces) exerted on the particle is disturbed (Fig. 1). In geological reservoirs, the equilibrium of in situ fines can be disturbed as a result of fluid flow velocities, temperature alterations in the porous formation, or reduced ionic strength of the in situ fluids (Bradford et al. 2013; Sharma et al. 1992a, b).

Fig. 1

Forces exerted on a fine particle situated on a solid surface in a porous medium

Non-isothermal injection of fluids deep into geological reservoirs is a frequent process during energy related operations including enhanced geothermal projects, and thermal energy storage in aquifers. Such operations generate spatiotemporal alterations in in situ pore pressures as well as temperatures, resulting in a coupled thermo-hydro-mechanical (THM) response of the reservoir formation (Chen and Ewy 2005; Tao and Ghassemi 2010; Zhai and Atefi-Monfared 2020a, b, c), in addition to liberation and migration of the in situ fine particles (Yu et al. 2019; Zhai and Atefi-Monfared 2021a, b). In situ stresses can be tightly coupled with pore pressure and temperature changes, while the reduction in permeability due to straining of the liberated particles also impacts in situ pore pressures and flow. As a result, in a porous formation containing in situ fines, a complex coupling exists between the THM response of the formation and the liberation, migration, and straining of the fine particles. It is critical to predict fines-migration-induced permeability damage in aquifers and geothermal reservoirs to achieve a sustainable design of energy operations and to develop effective strategies to prevent or mitigate the decline in well productivity in time.

Numerous laboratory experiments and theoretical studies have been conducted to evaluate the fundamental mechanisms behind fine-migration-induced permeability reduction in porous formations. Many studies have focused on fines migration induced as a result of high fluid flow velocities, and/or a reduced ionic strength of in situ fluids (e.g., Alem et al. 2015; Bedrikovetsky et al. 2012; Kia et al. 1987a, b; Liu et al. 2016a, b; Zhai and Atefi-Monfared 2020a, b). A number of studies have also been looking into temperature-induced particle mobilization (e.g., Schembre and Kovscek 2005a, b; Wang et al. 2021; You et al. 2019, 2016). The impact of temperature loads on the stability of in situ fines in a saturated porous formation introduces further intricacies as it generates various competitive mechanisms. An increase in reservoir temperatures results in a decline in the attaching electrostatic forces between fine particles and the solid surface. At the same time, the viscosity of the pore fluid decreases with an increase in in situ temperatures, leading to a reduction in the detaching drag and lifting forces (Yang et al. (2016). Theoretical formulation and investigation of problems of such intricate nature remains challenging.

Variations of the electrostatic force with temperature is often explained through the Derjaguin-Landau-Verwey-Overbeek (DLVO) theory (Schembre and Kovscek 2005a, b). Based on the DLVO theory, an increase in temperature in a saturated porous formation––consisting of quartz sand as the solid skeleton––with in situ clay particles present in the porous space, leads to a decrease in the dielectric permittivity of the pore fluid. As a result, the thickness of the electrical double layer (EDL) is reduced. Furthermore, an increase in temperature results in an increase in the negative surface charge of both clay particles and sand (Ramachandran and Somasundaran 1986; Rosenbrand et al. 2014), further enhancing particle-grain repulsion and contributing to the detachment of fine particles. Consequently, higher temperatures lead to decreased attaching electrostatic forces.

One of the key theoretical studies on temperature-induced fines migration was conducted by You et al. (2019) who studied liberation of in situ fines in geothermal reservoirs for low concentrations of fines. They proposed a solution for axisymmetric water flow toward the wellbore derived based on the DLVO theory. The reservoir domain was divided into two zones: a damaged zone, where the fluid is assumed to be incompressible and the fluid velocity was assumed to be constant; and an undamaged zone where fluid is compressible and the pore pressures are taken to be temporal. The proposed model involved many parameters related to the physical, chemical and mechanical properties of the solid grain, pore fluid, and in situ fine particles. Likewise, other pertinent research based on the DLVO theory involves a multitude of parameters to depict the detachment, mobilization, and straining of fines induced by thermal effects (e.g., Oliveira et al. (2014) Wang et al. (2021); Yu et al. (2019); Khilar and Fogler (1998).

Electrostatic force is the force acting between a charged colloidal particle and a given surface in an electrolyte solution. In the context of DLVO theory, colloidal particles are assumed to possess a significantly larger size compared to electrolyte ions. Consequently, the electrostatic force can be estimated by considering the summation of the London–van der Waals potential, short-range repulsive electrical double layer interactions, and Born potential (Schembre and Kovscek 2005a, b). The London–van der Waals potential is related to the separation distance between the colloidal particle and the solid grain surface, the Hamaker constant, and the characteristic wavelength of interaction. The interaction deriving from the electrical double layer between the colloidal particle and solid surface relies on factors such as the separation distance, surface charges, ion concentration, and zeta potential of the interacting system. The short-range repulsive Born potential is related to the separation distance, collision diameter, the Hamaker constant, and particle size of the porous matrix. This comprehensive analysis necessitates a considerable number of experiments to determine the relative factors within the colloidal particle-pore fluid–solid grain system, ultimately enabling the prediction of the electrostatic force. The identification of all the parameters involved often necessitates costly, intricate, and time-consuming physical experiments. Moreover, implementing the complete DLVO theory is complicated and computationally demanding requiring sophisticated numerical modeling techniques. These techniques might encounter challenges related to convergence and runtime, particularly when applied to evaluate fines migration at a reservoir scale. As a result, the practicality of this theory in field applications is limited. Current numerical studies on migration of fine particles in porous media driven by non-isothermal flow have been established based on a number of simplifying assumptions (e.g., Bedrikovetsky et al. (2012), You et al. (2019), Wang et al. (2021)). Hence, the development of a simplified DLVO theory is crucial to facilitate accurate yet practical predictions of fines migration’s impact on the THM behavior of geological reservoirs.

The goal of this study is to develop a novel theoretical framework for accurate and practical prediction of fine particle migration driven by non-isothermal flow. This work contains two novel components: Firstly, a new numerical model is developed based on the full DLVO theory. The proposed model integrates the influence of thermal and hydraulic loads on all the involved parameters, including both the static dielectric constant and the refractive index of the pore fluid. Subsequently, a comprehensive analysis utilizing this developed model is undertaken to gain new insights into the impacts of temperature, velocity, and ionic strength of in situ fluids on electrostatic forces. The newly acquired knowledge is then utilized to develop an innovative simplified DLVO-based model which requires notably fewer parameters compared to existing models, thus offering a practical and efficient solution. This model is then verified against the proposed model presented in the first part of this paper. The final part of the paper presents a sensitivity analysis conducted using the proposed simplified model, aimed at obtaining a better understanding of the impact of the key parameters on mobilization of in situ fines.

2 Methodology

The first part of this paper presents a new theoretical and numerical model based on the complete DLVO theory aimed at evaluating the mechanical equilibrium of fine particles in saturated porous media under induced temperatures and fluid velocities, while incorporating the effects from the ionic strength of in situ fluids. The second part of the paper presents a novel simplified DLVO-based model considering the effects of fluid velocity, temperature, and the ionic strength of in situ fluids. The assumptions behind the full theoretical model presented in the first part of the paper are primarily typical assumptions adopted in previous studies (You et al. 2016; Zhai and Atefi-Monfared 2021a, b), including constant porosity; trivial changes in permeability due to particle mobilization, thus incorporating particle straining as the main source of permeability change; and negligible gravity and uplift forces compared to the other existing forces. The in situ fine particles examined in this study are kaolinite clay (Leluk et al. 2010a, b). The clay particles are not considered mono-sized, and the grain size distribution of these in situ fines has been integrated in the proposed models. The solid skeleton of the porous medium is assumed to be of quarts, and the pore fluid is considered to be NaCl solution (i.e., clay-water–sand system). The proposed theoretical framework is developed for a temperature range of 5–170 °C (where variations in the static dielectric constant of clay particles ($\varepsilon_{2}$) with temperature can be assumed negligible), in situ pore pressures < 100 MPa, and for NaCl solution concentrations below 2 M. Following the approach of previous studies (e.g., Bedrikovetsky et al. 2011a, b; You et al. 2015; Yuan et al. 2012), a maximum retention function has been adopted as a mathematical means to examine fine particle liberation.

3 Mechanical Equilibrium of Fines Using the Complete DLVO Theory

3.1 Drag Force

The drag force acting on in situ fine particles situated within a porous medium subjected to a flowing fluid can be estimated using the following expression derived from the analytical solution of the Navier–Stokes equations obtained for flow around a finite size particle fixed on a plane (Goldman et al. 1966a, b; O'Neill 1968; Sharma et al. 1992a, b)

$$ F_{{\text{d}}} = \omega \pi \mu r_{s} u_{t} $$

(1)

where the drag factor $\omega = 6 \times 1.7$ is adopted in this study ($\omega = 6$ corresponds to the Stokes formula for a particle in the uniform boundary-free flux) (Yang et al. 2016).

The following empirical relation from AL-Shemmeri, T., 2012), also adopted by previous researchers (e.g., You et al. 2019), has been utilized in this study to describe the temperature dependency of water viscosity

$$ \mu = 2.414 \times 10^{ - 5} \times 10^{{\frac{247.8}{{T + 133.15}}}} $$

(2)

Equation 2 is valid for a temperature range of 0 °C–370 °C. Figure 2 presents variations of water viscosity with temperatures according to Eq. (2) and shows a decrease in water viscosity with increasing temperature which leads to a decline in the drag force. This reduction rate is notably higher under lower temperatures and reduces as the temperature rises.

Fig. 2

Variation of water viscosity with temperatures based on Eq. (2)

For Hele-Shaw flow in a slot, $u_{t}$ can be estimated as (Yang et al. 2016)

$$ u_{t} = \frac{{3r_{s} \overline{u}}}{H} $$

(3)

where the average velocity $\overline{u}$ is related to fluid flux U, as a function of formation’s porosity $\phi$(assumed to be constant in this study)

$$ \overline{u} = \frac{U}{\phi } $$

(4)

By substituting Eqs. (3) and (4) in Eq. (1), the drag force can be expressed as

$$ F_{{\text{d}}} = \frac{{\omega \pi \mu r_{s}^{2} U}}{\phi H} $$

(5)

3.2 Electrostatic Force

In studies concerned with colloid stability or particle deposition on a solid surface, the van der Waals attraction force between the fine particle and the solid grain is computed as a function of the separation distance between the solid grain and the fine particle, $h^{ * }$ (m). Two approaches have been commonly adopted to predict electrostatic forces between macroscopic bodies: applying a pairwise summation of all relevant intermolecular interactions (widely known as Hamaker (1937a, b) based approach); a more rigorous approach based on Lifshitz theory (Lifshitz and Hamermesh 1992) which depends entirely on macroscopic electrodynamic properties of the interacting media. Despite a number of limitations, the Hamaker approach continues to be widely adopted (e.g., You et al. (2016) due to simplicity of use while providing reasonably accurate results for practical systems (Bedrikovetsky et al. 2011a, b). In the current study, the Hamaker approach is adopted to compute the total electrostatic force ($F_{{\text{e}}}$, N) acting on a fine particle

$$ F_{{\text{e}}} = - \frac{\partial V}{{\partial h^{ * } }} $$

(6)

According to the DLVO theory, total energy is the sum of the London-van-der-Waals attraction ($V_{{{\text{LW}}}}$, J), the double electric layer repulsion ($V_{{{\text{EDL}}}}$, J), and the Born repulsion ($V_{{\text{B}}}$, J) potentials (Derjaguin and Landau 1993; Elimelech et al. 1995)

$$ V = V_{{{\text{LW}}}} + V_{{{\text{EDL}}}} + V_{{\text{B}}} $$

(7)

London-van-der-Waals Attraction $V_{{{\text{LW}}}}$ is computed as

$$ V_{{{\text{LW}}}} = - \frac{{A_{132} r_{s} }}{{6h^{ * } }}\left[ {1 - \frac{{5.32h^{ * } }}{\lambda }\ln \left( {1 + \frac{\lambda }{{5.32h^{ * } }}} \right)} \right] $$

(8)

where $\lambda = 100{\text{nm}}$ is adopted (Gregory 1981a, b); $A_{132}$ for a clay-water–sand system can be estimated as (Israelachvili 2011)

$$ A_{132} = \frac{3}{4}k_{{\text{B}}} \left( {T + 273.15} \right)\left( {\frac{{\varepsilon_{1} - \varepsilon_{3} }}{{\varepsilon_{1} + \varepsilon_{3} }}} \right)\left( {\frac{{\varepsilon_{2} - \varepsilon_{3} }}{{\varepsilon_{2} + \varepsilon_{3} }}} \right) + \frac{{3h\nu_{e} }}{8\sqrt 2 }\frac{{\left( {n_{1}^{2} - n_{3}^{2} } \right)\left( {n_{2}^{2} - n_{3}^{2} } \right)}}{{\left( {n_{1}^{2} + n_{3}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {n_{2}^{2} + n_{3}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left[ {\left( {n_{1}^{2} + n_{3}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} + \left( {n_{2}^{2} + n_{3}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right]}} $$

(9)

where the constant value of absorption frequency $\nu_{e} = 3 \times 10^{15} s^{ - 1}$ is taken from Israelachvili (2011). The static dielectric constants for clay and NaCl solution are temperature sensitive, while variations in $\varepsilon_{2}$ with temperature can be assumed negligible for $T < 170^\circ {\text{C}}$ (Stuart 1955). To explain the sensitivity of $\varepsilon_{1}$ with temperature, the following empirical relationship is adopted based on the results reported by Leluk et al. (2010a, b), also utilized by some previous studies (e.g., You et al. (2019)

$$ \varepsilon_{1} \approx \varepsilon_{10} - 0.005\left( {T - T_{0} } \right) $$

(10)

$\varepsilon_{3}$ is believed to be sensitive to both temperature and fluid pressure. For simplicity, some previous studies have assumed $\varepsilon_{3}$ to be linearly related to temperature (e.g., You et al. (2019). In order to obtain a higher accuracy, a more rigorous approach is adopted in this study. According to Hasted (1948), for solution concentrations less than 2 M, the relation between $\varepsilon_{3}$ and salt concentration could be expressed as

$$ \varepsilon_{3} = \varepsilon_{3,w} + 2\overline{\delta }c_{n} $$

(11)

A value of $\overline{\delta }$ = -11 has been adopted (Hasted 1948). The following empirical equation by Fernández et al. (1997) has been utilized to predict the temperature dependency of $\varepsilon_{3}$ for saturated formations

$$ \left\{ \begin{gathered} \varepsilon_{3,w} = 5.36058\left( {1 + \sum\limits_{i = 1}^{8} {L_{i} \theta^{i} } } \right) \hfill \\ \theta = \left( {1 - \frac{T + 273.15}{{T_{{{\text{ref}}}} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} \hfill \\ \end{gathered} \right. $$

(12)

where $T_{{{\text{ref}}}} = 647.096K$. The values for the parameter $L_{i}$ are presented in Table 1. Equation (11) can predict $\varepsilon_{3}$ with high accuracy (99.95%) for ${\text{T}} < 360.85^\circ {\text{C}}$ (Fernández et al. 1997).

Table 1 $L_{i}$ values to be implemented in Eq. 11 (Fernández et al. 1997)

The effect of fluid pressure (P, Pa) on $\varepsilon_{3}$ can be expressed as (Fernández et al. 1997)

$$ \frac{{\partial \varepsilon_{3} }}{\partial P} \approx 0.035 \times 10^{ - 6} $$

(13)

It is important to note that the impact of pressure on the static dielectric constant of NaCl solution is dependent on both the in situ temperature and the initial in situ pressure. The abovementioned relation has been provided for an in situ temperature of ~ 126 °C and a reference pressure $P_{{{\text{ref}}}}$ of 10 MPa. A sensitivity analysis was conducted in the current study and results suggest minimal changes when utilizing the various relations proposed by Fernández et al. (1997) for a wide range of in situ temperatures and initial pressures applicable for the study of interest.

The effect of temperature variations on $n_{1}$ is unknown, and the authors were not able to find any references studying this effect. The variation of $n_{2}$ over temperature can be estimated as (Radhakrishnan 1951)

$$ \frac{{\partial n_{2} }}{\partial T} \approx - 0.3 \times 10^{ - 5} $$

(14)

The dependence of $n_{3}$ on temperature is given by Leyendekkers and Hunter (1977)

$$ \left\{ \begin{gathered} n_{3} = \sqrt {\frac{{2f\left( {n_{3} } \right) + 1}}{{1 - f\left( {n_{3} } \right)}}} \hfill \\ f\left( {n_{3} } \right) = A\Psi_{w}^{ - B} \exp \left( { - CT} \right) + \Delta f\left( {n_{3} } \right) \hfill \\ \end{gathered} \right. $$

(15)

where $A$, $B$ and $C$ are only related to the wavelength, and adopted to be $A = {0}{\text{.2057691}}$, $B = {0}{\text{.88542}}$ and $C = {6}{\text{.0835}} \times {10}^{ - 5}$; $\Psi_{w}$ is the apparent specific volume of water present in the solution, computed as

$$ \left\{ \begin{gathered} \Psi_{w} = v_{w} \left[ {1 - 0.315\log \left( {\frac{{B_{T} + P_{{\text{e}}} + P}}{{B_{T} + 1 \times 10^{5} }}} \right)} \right] \hfill \\ B_{T} = 1 \times 10^{5} \left[ {2671.8 + 19.454T - 0.27028T^{2} + 0.0009798T^{3} } \right] \hfill \\ v_{w} = \frac{1}{{d_{w} }}1.000028 \hfill \\ d_{w} = 1 - \left( {T - a_{1} } \right)^{2} \left( {T + a_{2} } \right)/a_{4} /\left( {T + a_{3} } \right) \hfill \\ \end{gathered} \right. $$

(16)

where $a_{1} = 3.9863$, $a_{2} = 288.9414$, $a_{3} = 68.12963$ and $a_{4} = 508929.2$. The “effective pressure” $P_{{\text{e}}}$ is

$$ P_{{\text{e}}} = h_{0} + h_{1} x + h_{2} x^{2} + h_{3} x^{3} $$

(17)

where $h_{0} = - 0.03$, $h_{1} = {5078}{\text{.65}}$, $h_{2} = {2}{\text{.022}}$ and $h_{3} = {11206}{\text{.30}}$ for NaCl solution; $x$ is the grams of solute present in 1 g solution. $\Delta f\left( {n_{3} } \right)$ in Eq. (14) can be computed as (Leyendekkers and Hunter 1977)

$$ \Delta f\left( {n_{3} } \right) = c_{1} x + c_{2} x^{2} $$

(18)

where $c_{1} = {5}{\text{.69338}} \times 10^{ - 2}$ and $c_{2} = {0}{\text{.00433}} \times 10^{ - 2}$ for NaCl solution.

Double Electric Layer Repulsion. $V_{{{\text{EDL}}}}$ is estimated as a function of temperature as (Gregory 1975a, b)

$$ V_{{{\text{EDL}}}} = \frac{{128\pi r_{s} n_{\infty } k_{{\text{B}}} T}}{{\kappa^{2} }}\gamma_{s} \gamma_{{{\text{pm}}}} \exp \left( { - \kappa h^{ * } } \right) $$

(19)

where $n_{\infty } = 1000N_{{\text{A}}} c_{n}$ (m⁻³) and $\kappa$ (m.⁻¹) is computed as (Elimelech et al. 1995)

$$ \kappa = \sqrt {\frac{{e^{2} \sum\limits_{i} {n_{i0} z_{i}^{2} } }}{{\varepsilon_{0} \varepsilon_{3} k_{{\text{B}}} \left( {T + 273.15} \right)}}} $$

(20)

where $\gamma_{s}$ and $\gamma_{{{\text{pm}}}}$ (V) are computed as

$$ \left\{ \begin{gathered} \gamma_{s} = \tanh \left[ {\frac{{ze\zeta_{s} }}{{4k_{{\text{B}}} \left( {T + 273.15} \right)}}} \right] \hfill \\ \gamma_{{{\text{pm}}}} = \tanh \left[ {\frac{{ze\zeta_{{{\text{pm}}}} }}{{4k_{{\text{B}}} \left( {T + 273.15} \right)}}} \right] \hfill \\ \end{gathered} \right. $$

(21)

where $\zeta_{s}$ and $\zeta_{{{\text{pm}}}}$ (V) are related to temperature (Schembre and Kovscek 2005a, b)

$$ \zeta_{i} \left( T \right) = \left[ {0.01712\left( {T - T_{0} } \right) + 1} \right]\zeta_{i} \left( {T_{0} } \right) $$

(22)

Born Potential. $V_{{\text{B}}}$ is computed as

$$ V_{{\text{B}}} = \frac{{A_{132} \sigma_{c}^{6} }}{7560}\left[ {\frac{{8r_{s} + h^{ * } }}{{\left( {2r_{s} + h^{ * } } \right)^{7} }} + \frac{{6r_{s} - h^{ * } }}{{\left( {h^{ * } } \right)^{7} }}} \right] $$

(23)

where $\sigma_{c} = 0.5{\text{nm}}$ is adopted in this study (Elimelech et al. 1995).

By substituting Eqs. (7), (8), (19), and (23) in Eq. (6), the electrostatic force is obtained to be

$$ F_{{\text{e}}} = F_{{e,{\text{LW}}}} + F_{{e,{\text{EDL}}}} + F_{e,B} $$

(24)

where

$$ \left\{ \begin{gathered} F_{{e,{\text{LW}}}} = - \frac{{A_{132} r_{s} \lambda }}{6} \times \frac{1}{{\left( {h*} \right)^{2} \left( {5.32h* + \lambda } \right)}} \hfill \\ F_{{e,{\text{EDL}}}} = \frac{{128\pi r_{s} n_{\infty } k_{B} \left( {T + 273.15} \right)}}{\kappa }\gamma_{s} \gamma_{pm} e^{ - \kappa h*} \hfill \\ F_{e,B} = \frac{{A_{132} \sigma_{c}^{6} }}{7560}\left[ {\frac{{54r_{s} + 6h*}}{{\left( {2r_{s} + h*} \right)^{8} }} + \frac{{42r_{s} - 6h*}}{{\left( {h*} \right)^{8} }}} \right] \hfill \\ \end{gathered} \right. $$

(25)

3.3 Mechanical Equilibrium of In situ Fine Particles

The stability status of in situ fine particles can be determined using the equilibrium of the attaching and detaching torques exerted on the particle (Bedrikovetsky et al. 2011a, b). Assuming negligible gravity and uplift forces, the torque balance equation results in

$$ \frac{{F_{{\text{d}}} }}{{\left| {F_{{\text{e}}} } \right|}} = \frac{{l_{{\text{e}}} }}{{l_{{\text{d}}} }} \approx \varepsilon_{p} $$

(26)

The lever arm ratio $\varepsilon_{p}$ for a solid fine particle situated on a solid substrate is believed to be in the order of 10^–2–10^–3 (Bradford et al. 2013; Kalantariasl 2014, 2015).

The electrostatic force is of an attractive nature where F_e < 0, and of a repulsive nature for F > 0. F_e is a function of the fine-solid matrix separation distance (h*) (Eq. 6), and thus varies depending on the separation distance of the fine particle with respect to the solid matrix. In the context of mechanical equilibrium of fines, Eq. (25), the electrostatic force corresponds to the maximum negative F_e value. Once the equilibrium of a fine particle positioned on a solid matrix is disrupted, the particle will begin to move (either detaches or rotates on the surface surrounding the tangent point depending on in situ conditions). During this period, the separation distance h* between the particle and the solid surface will begin to increase from its minimum value to a certain value after which the electrostatic attraction between the fine particle and the solid matrix becomes negligible. The latter state corresponds to the particle dislodging stage, where the torque from the drag force exceeds that of the maximum attractive electrostatic forces. It is thus important to have a correct understanding of the complex variations in the electrostatic force between fines and the solid matrix.

Figure 3 presents variations of the total potential energy and the electrostatic force exerted on a fine particle as a function of the separation distance parameter computed using Eqs. (7) and (24), under three different in situ temperatures. Input parameters given in Table 2 have been adopted for these analyses.

Fig. 3

Variations of the total potential energy and electrostatic force as a function of the fine-solid matrix separation distance at three different in situ temperatures

Table 2 Input parameters adopted in this study (You et al. 2019)

Results indicate that the maximum attractive electrostatic force is indeed temperature dependent. Therefore, to accurately assess fine particle mobilization, F_e should be identified incorporating h* and in situ temperatures. The aforementioned parameters are both time-dependent under non-steady-state conditions. These graphs show one absolute value for F_e (Fig. 3a) in case of low in situ temperatures, while under higher in situ temperatures two local maximum values (negative) (F_emax) exist for the electrostatic force as h* varies (Fig. 3b, c).

Figure 4a illustrates variations in the two probable F_emax values along with the absolute maximum value of the electrostatic force (F_e) with temperature, under different salt concentrations in the range of 0.025 M–0.6 M. Figure 4b presents the corresponding h* for F_emax⁽¹⁾ and F_emax⁽²⁾ reported in Fig. 4a as a function of temperature for various salt concentrations. Results reveal that F_emax⁽¹⁾ corresponds to a smaller separation distance and decreases rapidly with an increase in temperature, while F_emax⁽²⁾ corresponds to a larger separation distance and seems to be insensitive to temperature changes. The electrostatic force adopted in Eq. (25) corresponds to the overall F_emax for various h*, which will be: F_emax⁽¹⁾ in case of lower in situ temperatures, is temperature dependent, and occurs under a smaller h* where the fines are very close to the solid skeleton; and F_emax⁽²⁾ in case of higher in situ temperatures, undergoes trivial changes with temperature variations maintaining a negative value close to zero, and occurs at a larger h*. Results from Fig. 4b suggest that the separation distance corresponding to F_emax⁽¹⁾ is practically not sensitive to temperature, while those corresponding to F_emax⁽²⁾ can vary with temperature.

Fig. 4

a Variations in F_{e, max} under different temperatures. b The corresponding h*

Looking at F_emax variations with temperature under a wide range of solution concentration (0.025 M–0.6 M) in Fig. 4, it is clear that F_emax⁽¹⁾ variation with temperature is sensitive to salt concentration, while F_emax⁽²⁾ is not affected by the aforementioned parameter. Overall, an increase in solution concentration resulted to a higher negative value for F_emax⁽¹⁾ and thus an overall increase in F_emax under lower temperatures. Furthermore, under higher temperatures, the h* corresponding to the maximum electrostatic force drops substantially with an increase in salt concentration.

Another key parameter for assessing fine particle liberation is the critical particle radius $r_{sc}$, defined as the minimal particle size that can detach from solid surface under a given in situ condition. Particles with radius greater than the critical particle radius ($r > = r_{sc}$) will detach from solid surface, while particles with a radius smaller than the critical particle radius ($r < r_{sc}$) will remain affixed to the solid surface. The critical particle radius can be estimated using the torque equilibrium equation (Eq. 25) under different fluid velocities, in situ temperatures, and solution concentration. It should be restated that the electrostatic force adopted for these analyses is F_emax obtained from Eq. (24).

Figure 5 presents variations in the critical particle radius as a function of temperature and fluid velocity using input parameters provided in Table 2. Results indicate that for a given in situ temperature, the critical radius decreases with an increase in fluid flow velocity. On the other hand, for a given fluid flow velocity, an increase in in situ temperatures initially results in an increase in the critical radius up to a certain temperature, after which further increase in in situ temperatures will decrease this parameter. Ultimately, there exists a temperature threshold beyond which the temperature’s influence on the critical particle radius becomes minimal. This threshold temperature is referred to in this paper as the ultimate temperature, T_ult. For $T < T_{{{\text{ult}}}}$, the electrostatic force equals to F_emax⁽¹⁾ and varies drastically with temperature (Fig. 3a), having a significant effect on the critical radius with temperature changes. However, for temperatures greater than the ultimate temperature ($T > T_{{{\text{ult}}}}$), the electrostatic force equals to F_emax⁽²⁾ which maintains a trivial value (≈0) independent of temperature, leading to the infinitesimal value of the critical radius. In other words, for $T > T_{{{\text{ult}}}}$, almost all particles have already detached from the solid grain surface and are in a mobilized state within the pore space.

Fig. 5

Critical particle radius as a function of a fluid velocity, and b in situ temperatures

As illustrated in Fig. 5, the impact of temperature on the critical radius under a given fluid flow velocity is complex. In case of in situ temperatures $T < T_{{{\text{ult}}}}$, the electrostatic force decreases with increasing temperature, which favors fine particle liberation (Fig. 4a). On the other hand, the drag force experiences an initial rapid decline as the temperature rises. However, beyond a certain threshold, the rate of change in the drag force decreases substantially with further temperature increase (Fig. 2). Hence, the critical particle radius first increases with temperature increase before decreasing beyond a certain temperature threshold. In case of high in situ temperatures $T > T_{{{\text{ult}}}}$, the variation of electrostatic force with temperature is very small (Fig. 4a), while the drag force decreases with increasing temperature due to variations in the fluid viscosity (Fig. 2). Thus, the critical particle radius exhibits a slight increasing trend for $T > T_{{{\text{ult}}}}$, particularly under lower fluid flow velocities.

4 Proposed Simplified DLVO Theory

4.1 Simplification of Electrostatic Force

The objective of this section is to present a simplified DLVO-based theory to explain fine liberation due to non-isothermal flow. Based on Eq. (24) and Eq. (25), the maximum attractive electrostatic force can be expressed as

$$ F_{e\max } = \left\langle {F_{e\max } } \right\rangle^{{{\text{LW}}}} + \left\langle {F_{e\max } } \right\rangle^{{{\text{EDL}}}} + \left\langle {F_{e\max } } \right\rangle^{B} $$

(27)

As explained earlier in the paper, in situ temperatures, pore pressures, and solution concentration impact the electrostatic force and are incorporated in the DLVO theory. To develop a simplified DLVO-based model, the sensitivity of the electrostatic force to in situ pressures, temperature variations, and solution concentrations is investigated next.

To better understand the impact of in situ pore pressures on the electrostatic force, variations in F_emax are plotted versus pore pressures, considering a wide range of in situ temperatures (Fig. 6). Results reveal that the electrostatic force changes less than 4% when pore pressures vary in the range of 0.1 MPa to 100 MPa. This observation suggests that the impact of pore pressures on the electrostatic force is negligible for pore pressures < 100 MPa. Accordingly, pore pressure effects on the electrostatic force are disregarded in the proposed simplified DLVO-based theory in the current study for simplicity.

Fig. 6

Variations of the electrostatic force with in situ pore pressures for a wide range of in situ temperatures

The effects from temperature alterations on the electrostatic force are studied in Fig. 7. This figure presents F_e and its components (Eq. 27) as a function of in situ temperatures using input parameters presented in Table 2. For in situ temperatures smaller than the ultimate temperature ($T < T_{{{\text{ult}}}}$), an increase in in situ temperature results in a linear decrease in the electrostatic force and $\left\langle {F_{e\max } } \right\rangle^{{{\text{EDL}}}}$ while generating a slight linear increase in $\left\langle {F_{e\max } } \right\rangle^{{{\text{LW}}}}$ and $\left\langle {F_{e\max } } \right\rangle^{B}$. Where in situ temperatures exceed the ultimate temperature ($T > T_{{{\text{ult}}}}$), the electrostatic force yields zero.

Fig. 7

Variations of the electrostatic force and its components as a function of temperature

Based on the trends detected in Fig. 7, quadratic and linear functions are proposed in this study to simplify the DLVO theory for explaining the attractive electrostatic force between fine particles and the solid matrix as a function of temperature. First, the component $\left\langle {F_{e\max } } \right\rangle^{{{\text{EDL}}}}$ is simplified to explain its sensitivity to temperature changes. According to Eq. (25), $\left\langle {F_{e\max } } \right\rangle^{{{\text{EDL}}}}$ is computed based on the product of zeta potentials of the fine particles and the porous matrix ($\gamma_{s} \cdot \gamma_{{{\text{pm}}}}$), as well as the Debye length ($\kappa$). Thus, to simplify the expression for $\left\langle {F_{e\max } } \right\rangle^{{{\text{EDL}}}}$, the aforementioned two terms will be simplified. First, variations in the zeta potentials with respect to temperature are evaluated. Using input values from Table 2 and Table 3 obtained from experimental data reported by You et al. (2019), the normalized product of the two reduced zeta potentials is computed using the theoretical Eq. (21) and plotted as a function of temperature (Fig. 8). Results suggest a fairly linear relationship between the normalized product of the reduced zeta potential values and temperature variations. Based on the results presented in Fig. 8, the following fitting relationship is proposed to estimate the normalized product of the reduced zeta potential values as a function of temperature

$$ \gamma_{s} \cdot \gamma_{{{\text{pm}}}} = \left( {a_{\gamma 0} + a_{\gamma 1} T} \right)\left( {\zeta_{s0} \cdot \zeta_{{{\text{pm0}}}} } \right) $$

(28)

where $a_{\gamma 0}$ and $a_{\gamma 1}$ are related to the salt concentration, pressure and pH values.

Table 3 Zeta potentials of fines and porous medium under different salt concentrations (You et al. 2019)

Fig. 8

a Variations in the product of the reduced zeta potentials of the fine and porous matrix as a function of temperature for a given range of salt concentration. b Proposed expression for the fitting coefficient $a_{\gamma 1}$ and m_i coefficients

$a_{\gamma 1}$ obtained from the data presented from You et al. (2019) under different salt concentrations presented in Fig. 8 can be fitted using $a_{\gamma 1} = m_{1} - m_{2} \times m_{3}^{{c_{n} }}$. $a_{\gamma 0}$ is found to be 36 for sand-clay-NaCl solution. Results obtained from the proposed simplified Eq. (29) (Fig. 8a) suggest a good approximation obtained for a temperature range of 5°C–170°C, particularly for higher salt concentrations. The proposed values for m₁, m₂, m₃ have been determined using curve fitting from Fig. 8a, as depicted in Fig. 8b.

Next, a simplified relation is proposed for the Debye length as a function of temperature. To achieve this, the Debye length versus temperature (Eq. 20) is plotted in Fig. 9. Results suggest the Debye length to vary in the order of ~ 10% with temperatures < 170°C. Therefore, the Debye length can be assumed insensitive to temperature changes for T < 170°C. Ignoring temperature effects, the expression of the Debye length for the NaCl solution (Eq. 20) can be simplified as

$$ \kappa^{ - 1} \approx \sqrt {\frac{{273.15k_{{\text{B}}} \varepsilon_{0} \varepsilon_{30} }}{{2 \times 10^{3} \times e^{2} N_{{\text{A}}} c_{n} }}} $$

(29)

Fig. 9

Variations of the Debye length with temperature for solutions with different salt concentrations

The Debye length computed using the simplified Eq. (29) presented in Fig. 8 confirms a fairly reasonable approximation in case of temperatures in the range of 5–170 °C. The precision of this simplified equation increases for solutions with higher salt concentrations.

Substituting the two simplified Eqs. (28) and (29) in Eq. (25b), the following approximation is obtained for $\left\langle {F_{e\max } } \right\rangle^{{{\text{EDL}}}}$

$$ \left\langle {F_{e\max } } \right\rangle^{{{\text{EDL}}}} = 128\pi r_{s} n_{\infty } k_{{\text{B}}} \kappa^{ - 1} \zeta_{s0} \zeta_{{{\text{pm}}0}} \left[ {273.15a_{\gamma 0} + \left( {a_{\gamma 0} + 273.15a_{\gamma 1} } \right)T + a_{\gamma 1} T^{2} } \right]e^{ - \kappa h*} $$

(30)

where $\kappa^{ - 1}$ is calculated using Eq. (29) independent of temperature.

Another temperature-sensitive parameter present in the DLVO theory is h*. Based on Fig. 4b, the separation distance appears not sensitive to temperature changes where T < T_ult. As a result, h* can be assumed temperature independent when calculating the maximum value of attractive electrostatic force where T < T_ult. Based on this assumption, $e^{ - \kappa h*}$ is taken to be constant ($B_{{{\text{EDL}}}}$) for $T \le T_{{{\text{ult}}}}$ and therefore Eq. (30) is further simplified as

$$ \begin{array}{*{20}c} {\left\langle {F_{e\max } } \right\rangle^{{{\text{EDL}}}} = 128B_{{{\text{EDL}}}} \pi r_{s} n_{\infty } k_{{\text{B}}} \kappa^{ - 1} \zeta_{s0} \zeta_{{{\text{pm}}0}} \left[ {273.15a_{\gamma 0} + \left( {a_{\gamma 0} + 273.15a_{\gamma 1} } \right)T + a_{\gamma 1} T^{2} } \right],} & {T \le T_{{{\text{ult}}}} } \\ \end{array} $$

(31)

where $B_{{{\text{EDL}}}}$ is related to material properties and independent of temperature and fluid velocity.

The Hamaker constant $A_{132}$ defined in Eq. (9) is related to temperature, salt concentration and pore pressure. The effect of pore fluid pressure on Hamaker constant is very small and can be neglected compared with the effects of temperature and salt concentration. The variation of Hamaker constant is quadratic under different temperatures, as shown in Fig. 10. Based on Tayler series, the following approximation of Hamaker constant is obtained

$$ A_{132} = \hat{A}_{132} + a_{h1} T + a_{h2} T^{2} - c_{n} \left( {a_{h3} T + a_{h4} T^{2} } \right) $$

(32)

where ${\hat{\text{A}}}_{132}$ is computed as follows:

$$ \begin{aligned} {\hat{\text{A}}}_{132} = \frac{3}{4}k_{{\text{B}}} \left( {T_{0} + 273.15} \right)\left( {\frac{{\varepsilon_{10} - \varepsilon_{30} }}{{\varepsilon_{10} + \varepsilon_{30} }}} \right)\left( {\frac{{\varepsilon_{2} - \varepsilon_{30} }}{{\varepsilon_{2} + \varepsilon_{30} }}} \right) \\ & \quad \quad + \frac{{3h\nu_{e} }}{8\sqrt 2 }\frac{{\left( {n_{1}^{2} - n_{30}^{2} } \right)\left( {n_{20}^{2} - n_{30}^{2} } \right)}}{{\left( {n_{1}^{2} + n_{30}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {n_{20}^{2} + n_{30}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left[ {\left( {n_{1}^{2} + n_{30}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} + \left( {n_{20}^{2} + n_{30}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right]}} \\ \end{aligned} $$

(33)

Fig. 10

Variations of the Hamaker constant A₁₃₂ under different temperatures and salt concentrations

The fitting parameters for the Hamaker constant are determined using the least square method and presented in Table 4. The results shown in Fig. 10 suggest that the simplified Eq. (32) can adequately predict the Hamaker constant under various temperatures and salt concentrations.

Table 4 Fitting parameters for the Hamaker constant (Eq. 32) obtained using the least square method

Applying Eq. (32) into Eqs. (25a, c), the following equations are proposed to estimate $\left\langle {F_{e\max } } \right\rangle^{LW}$ and $\left\langle {F_{e\max } } \right\rangle^{B}$

$$ \begin{array}{*{20}c} {\left\{ \begin{gathered} \left\langle {F_{e\max } } \right\rangle^{{{\text{LW}}}} = - \frac{{r_{s} \lambda }}{6}\left( {B_{{{\text{LW}}0}} + B_{{{\text{LW}}1}} T + B_{{{\text{LW2}}}} T^{2} } \right) \hfill \\ \left\langle {F_{e\max } } \right\rangle^{B} = \frac{{r_{s} \sigma_{c}^{6} }}{7560}\left( {B_{B0} + B_{B1} T + B_{B2} T^{2} } \right) \hfill \\ \end{gathered} \right.} & {\begin{array}{*{20}c} {for} & {} \\ \end{array} T \le T_{{{\text{ult}}}} } \\ \end{array} $$

(34)

where $B_{{{\text{LW}}i}}$ and $B_{Bi}$ (i = 0, 1, 2) are computed as follows.

$$ \left\{ \begin{gathered} B_{{{\text{LW}}0}} = \frac{{{\hat{\text{A}}}_{132} }}{{\left( {h*} \right)^{2} \left( {5.32h* + \lambda } \right)}} \hfill \\ B_{{{\text{LW}}1}} = \frac{{a_{h1} - a_{h3} c_{n} }}{{\left( {h*} \right)^{2} \left( {5.32h* + \lambda } \right)}} \hfill \\ B_{{{\text{LW2}}}} = \frac{{a_{h2} - a_{h4} c_{n} }}{{\left( {h*} \right)^{2} \left( {5.32h* + \lambda } \right)}} \hfill \\ \end{gathered} \right. $$

(35)

$$ \left\{ \begin{gathered} B_{B0} = \frac{42}{{\left( {h*} \right)^{8} }}{\hat{\text{A}}}_{132} \hfill \\ B_{B1} = \frac{42}{{\left( {h*} \right)^{8} }}\left( {a_{h1} - a_{h3} c_{n} } \right) \hfill \\ B_{B2} = \frac{42}{{\left( {h*} \right)^{8} }}\left( {a_{h2} - a_{h4} c_{n} } \right) \hfill \\ \end{gathered} \right. $$

(36)

Substituting Eqs. (31) and (34) in Eq. (27), the approximate equation for the attractive electrostatic force in obtained for T $\le$ T_ult

$$ \begin{array}{*{20}c} {F_{e\max } = - \left( {B_{0} - B_{1} T - B_{2} T^{2} } \right)r_{s} ,} & {T \le T_{{{\text{ult}}}} } \\ \end{array} $$

(37)

where

$$ \left\{ \begin{gathered} B_{0} = {3}{\text{.4963}} \times 10^{4} \times B_{{{\text{EDL}}}} \pi n_{\infty } k_{{\text{B}}} \kappa^{ - 1} a_{\gamma 0} \zeta_{s0} \zeta_{{{\text{pm}}0}} + \frac{\lambda }{6}B_{{{\text{LW}}0}} - \frac{{\sigma_{c}^{6} }}{7560}B_{B0} \hfill \\ B_{1} = 128\left( {a_{\gamma 0} + 273.15a_{\gamma 1} } \right)B_{{{\text{EDL}}}} \pi n_{\infty } k_{{\text{B}}} \kappa^{ - 1} \zeta_{s0} \zeta_{{{\text{pm}}0}} - \frac{\lambda }{6}B_{{{\text{LW}}1}} + \frac{{\sigma_{c}^{6} }}{7560}B_{B1} \hfill \\ B_{2} = 128a_{\gamma 1} B_{{{\text{EDL}}}} \pi n_{\infty } k_{{\text{B}}} \kappa^{ - 1} \zeta_{s0} \zeta_{{{\text{pm}}0}} - \frac{\lambda }{6}B_{{{\text{LW2}}}} + \frac{{\sigma_{c}^{6} }}{7560}B_{B2} \hfill \\ \end{gathered} \right. $$

(38)

For in situ temperatures $T > T_{{{\text{ult}}}}$, the electrostatic force remains relatively constant with temperature variations (Fig. 2). Therefore, the proposed simplified expressions for the maximum attractive electrostatic force based on in situ temperatures are as follows

$$ F_{e\max } = \left\{ \begin{gathered} \begin{array}{*{20}c} { - \left( {B_{0} - B_{1} T - B_{2} T^{2} } \right)r_{s} ,} & {T \le T_{{{\text{ult}}}} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} { - \left( {B_{0} - B_{1} T_{{{\text{ult}}}} - B_{2} T_{{{\text{ult}}}}^{2} } \right)r_{s} ,} & {T > T_{{{\text{ult}}}} } \\ \end{array} \hfill \\ \end{gathered} \right. $$

(39)

Figure 11 presents a comparison between the maximum attractive electrostatic force computed using the exact solution at $c_{n} = 0.2{\text{M}}$ and the values obtained using the proposed simplified model (Eqs. 39). The separation $h*$ value for $T < T_{{{\text{ult}}}}$ is $3.63 \times 10^{ - 10}$ based on the results shown in Fig. 4. Other parameters are calculated based on Eqs. (35, 36, 38) using the values provided in Tables 2 and 3. Figure 11 indicates that the proposed simplified equations exhibit a high level of accuracy for predicting the electrostatic force. As depicted in Fig. 11, the maximum electrostatic force exhibits continuity across temperature. However, there is an abrupt change in its slope at T = T_ult: denoted as F_emax⁽¹⁾ for T < T_ult, and F_emax⁽²⁾ for T > T_ult (as shown in Figs. 3 and 4). The key determinant of the maximum electrostatic force, along with its primary components, is h*. Notably, T_ult marks the temperature threshold beyond which the electrostatic force diminishes to a negligible value (≈0), regardless of temperature. This condition denotes the detachment of the fine particle from the solid grain surface (higher h*) and its transition to a mobilized state within the pore space. Consequently, this explains the observed discontinuity in the < F_emax > ^B, < F_emax > ^EDL, < F_emax > ^LW curves.

Fig. 11

Maximum attractive electrostatic force computed using the exact and simplified solutions ($r_{s} = 1\mu m$)

4.2 Critical Radius Based on the Proposed Simplified F _emax

The expression for the drag force given in Eq. (5) can be rewritten as

$$ F_{{\text{d}}} = A_{{\text{d}}} r_{s}^{2} U \times 10^{{\frac{247.8}{{T + 133.15}}}} $$

(40)

where

$$ A_{d} = 7.242 \times 10^{ - 5} \times \frac{\omega \pi }{{\phi H}} $$

(41)

Substituting Eq. (39) and Eq. (40) into Eq. (26) results in

$$ r_{s} = \left\{ {\begin{array}{*{20}c} {\frac{{A_{0} - A_{1} T - A_{2} T^{2} }}{U} \times 10^{{\frac{ - 247.8}{{T + 133.15}}}} ,} & {T \le T_{{{\text{ult}}}} } \\ {\frac{{A_{0} - A_{1} T_{{{\text{ult}}}} - A_{2} T_{{{\text{ult}}}}^{2} }}{U} \times 10^{{\frac{ - 247.8}{{T + 133.15}}}} ,} & {T > T_{{{\text{ult}}}} } \\ \end{array} } \right. $$

(42)

where

$$ \begin{array}{*{20}c} {A_{i} = \frac{{B_{i} }}{{A_{{\text{d}}} }}\varepsilon_{p} ,} & {i = 0,1,2} \\ \end{array} $$

(43)

Figure 12 presents variations in the critical radius as a function of temperature under different fluid flow velocities obtained using the exact solution (Eqs. 5, 24, and 26) and the proposed new simplified equations (Eq. 42). The results indicate that the proposed simplified Eq. (42) provides a satisfactory approximation, especially for temperatures below the ultimate temperature. However, for temperatures above T_ult, the simplified model slightly underestimates the r_s values, although it still captures the overall trend. This discrepancy is attributed to the assumption adopted in the simplified model that alterations in the electrostatic force are negligible for T > T_ult.

Fig. 12

Critical radius obtained using the simplified DLVO-based model versus the full DLVO theory

5 Summary of the Assumptions behind the Proposed Simplified DLVO Theory

To provide a better understanding of the proposed simplified DLVO-based model, a summary of all the adopted assumptions is presented next: negligible fluid pressure impacts on electrostatic force; a linear change in the reduced zeta potential function with temperature, with the curve slope attributed solely to the salt concentration of the solution; minimal temperature influence on the Debye length; constant separation distance at lower temperatures (T < T_ult); a parabolic assumption regarding temperature impacts on the Hamaker constant; minimal and temperature-independent electrostatic force under higher temperatures (T > T_ult).”

6 Maximum Retention Function

The Beerkan estimation of soil transfer (BEST) (Bayat 2015) model is adopted in this study to describe the particle size distribution of in situ fines, as shown below

$$ P_{psd} \left( {d \le d_{s} } \right) = \left[ {1 + \left( {\frac{{d_{g} }}{{d_{s} }}} \right)^{n} } \right]^{ - m} $$

(44)

where $d_{g}$, $m$, and $n$ are model parameters. Adopting the input parameters given in Table 2, the particle size distribution of in situ fines considered in this study is obtained and plotted in Fig. 13.

Fig. 13

The particle size distribution curve of in situ fines used in this study

Based on the proposed simplified DLVO-based model, the general form of the maximum retention function can be expressed as

$$ \frac{{\sigma_{cr} }}{{\sigma_{0} }} = \left\{ \begin{gathered} \begin{array}{*{20}c} {\left[ {1 + \left( {\frac{{0.5d_{g} U}}{{A_{0} - A_{1} T - A_{2} T^{2} }}} \right)^{n} 10^{{\frac{247.8n}{{T + 133.15}}}} } \right]^{ - m} ,} & {T \le T_{{{\text{ult}}}} } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\left[ {1 + \left( {\frac{{0.5d_{g} U}}{{A_{0} - A_{1} T_{{{\text{ult}}}} - A_{2} T_{{{\text{ult}}}}^{2} }}} \right)^{n} 10^{{\frac{247.8n}{{T + 133.15}}}} } \right]^{ - m} ,} & {T > T_{{{\text{ult}}}} } \\ \end{array} \hfill \\ \end{gathered} \right. $$

(45)

6.1 Model Verification

The proposed model presented in the first part of this paper (developed based on the full DLVO theory) along with the proposed DLVO-based simplified model is verified against the theoretical results presented by You et al. (2019). The input parameters adopted for this verification are those presented in Table 2. The maximum retention concentration of fines using the proposed full DLVO-based model is simulated using Eqs. (24), (26), (40) and (44) and that of the simplified model is simulated using Eq. (45). Figure 14 presents the maximum retention concentration of fines under various in situ temperatures. Parameters $A_{0}$, $A_{1}$, and $A_{2}$ of the simplified model are obtained Based on Eqs. (41) and (43). $T_{ult}$ is determined according to variations of the electrostatic force, as explained earlier in this paper. With regard to the grain size distribution data, the values for parameters $d_{g}$, $m$ and $n$ in Eq. 44 were determined by fitting the fine particle size distribution curves such to obtain the mean particle size and variance coefficient reported by You et al. (2019).

Fig. 14

Maximum retention functions for various temperatures from You et al. (2019) and the corresponding values obtained using the proposed model based on the complete DLVO theory, as well as the simplified DLVO-based model

In an earlier study, You et al. (2016) presented variations of the maximum retention function with respect to fluid velocities under different particle size distribution curves. Figure 15 presents a comparison between the results obtained using the proposed simplified model and findings from You et al. (2016), adopting input parameters from Table 2. The parameters of the BEST model are determined such to obtain the mean particle size ($r_{s}$) and variance coefficient ($C_{v}$) values reported by You et al. (2016). Results show that the simplified model (Eq. 45) is able to nicely predict the maximal retention concentration of fine particles under different fluid velocities and temperatures.

Fig. 15

Comparison of the proposed simplified DLVO-based model and the experimental results presented by You et al. (2016)

7 Sensitivity Analysis

To obtain a comprehensive understanding of fine particle detachment in a porous skeleton under non-isothermal flow, the proposed simplified DLVO-based model has been adopted to conduct a sensitivity analysis. Key model parameters have been selected for this analysis, and the remaining input parameters have been chosen based on Table 2. The typical ranges of the parameters selected for this sensitivity analysis have been obtained from the relevant literature. For each case scenario, the electrostatic force is obtained based on the proposed simplified model using Eqs. (38), (41) and (43), and the maximum retention function for concentration of fines is computed using Eq. (45).

7.1 Static Dielectric Constant of Clay

In the current study, in situ fine particles are assumed to be clay. The static dielectric constant of clay ($\varepsilon_{10}$) can vary from 5 to 40 (Davis and Annan (1989a, b). Variations of the electrostatic force with temperature computed using the proposed simplified model are presented in Fig. 16a. Results show higher electrostatic forces under a larger $\varepsilon_{10}$ value. Figure 16b presents the maximum retention concentrations of fines at two different temperatures (25 °C and 60 °C) as a function of fluid flow velocity. Overall, a higher $\varepsilon_{10}$ results in an increase in the detachment of fines independent of in situ temperatures or velocities. A higher static dielectric constant of clay minerals implies that they have a greater ability to polarize the surrounding water molecules, leading to a more extended EDL. This extended EDL can weaken the attractive forces between clay particles and surrounding surfaces, facilitating the detachment of fines.

Fig. 16

The impact of $\varepsilon_{10}$ on: a electrostatic force; b maximum retention concentration. (T_ult = 76.2 °C, 90.9 °C at ε₁₀ = 5, 40, respectively)

7.2 Refractive Index of Clay

The refractive index of clay ($n_{1}$) varies between 1.5 and 1.6 (You et al. (2019). Figure 17a shows a higher electrostatic force under a larger $n_{1}$. The maximum retention concentrations of fines under 25 °C and 60 °C are calculated with different $n_{1}$ values and presented in Fig. 17b. A larger percentage of clay particles detach from the solid surface under smaller $n_{1}$ values. In case of $T = 60^\circ C$, the effect of $n_{1}$ on the maximum retention concentration of fines seems to be minimal. The main reason is the decrease in the drag force with an increase in temperature due to the changes in the fluid viscosity (Eq. 2).

Fig. 17

The effect of $n_{1}$ on: a electrostatic force; b maximum retention concentration. (T_ult = 68.6 °C, 104.4 °C at n₁ = 1.5, 1.6, respectively)

A comparison between Figs. 16b and 17b suggests that the refractive index of clay has a higher impact on fine particle mobilization compared to the static dielectric constant.

7.3 Refractive Index of Sand

Current study assumes the solid skeleton of the porous medium to be composed of quartz sand. The refractive index of quartz is in the range of 1.54–1.68 (Radhakrishnan 1951). This range is adopted to evaluate the sensitivity of fine particle liberation based on the $n_{20}$ parameter. Results from Fig. 18a reveal a higher electrostatic force under a larger $n_{20}$ value. Figure 18b shows a higher percentage of fines detachment from the surface of the solid skeleton under smaller $n_{20}$ values, due to lower electrostatic forces (Fig. 18a). In case of higher $n_{20}$ values, the resulting higher electrostatic forces limit fine particle migration.

Fig. 18

The effect of $n_{20}$ value on: a electrostatic force; b maximum retention concentration. (T_ult = 90.8 °C, 142.4 °C at n₂₀ = 1.54, 1.68, respectively)

7.4 Salt Concentration

The characteristic properties of the pore fluid and the Debye length change substantially under different salt concentrations present in the pore fluid, affecting the electrostatic forces and fine particle mobilization. The zeta potential values under 0.11 M, 0.2 M and 0.6 M given by You et al. (2019) are chosen to evaluate the sensitivity of fine liberation based on salt concentrations. Figure 19a shows a higher electrostatic force under higher salt concentrations. The impact of salt concentration on the electrostatic force is less significant under lower temperatures. Figure 19b shows a minimal effect of salt concentration on the maximum retention concentrations of fines under lower temperatures (25 °C).

Fig. 19

The effect of $c_{n}$ value on: a electrostatic force; b maximum retention concentration. (T_ult = 85.2 °C, 89.3 °C at c_n = 0.025 M, 0.2 M, respectively)

7.5 Characteristic Wavelength of Interaction

The characteristic wavelength of interaction has a direct impact on the London-van-der-Waals Attraction and the electrostatic force. The range of the characteristic wavelength adopted in this section is 10 ~ 1000 nm following You et al. (2019). There is an increase in the electrostatic force with an increase in $\lambda$ for $\lambda < 100{\text{nm}}$ (Fig. 20a). In case of smaller $\lambda$ values, a lower electrostatic force is detected resulting in a higher percentage of fine particle detachment. Figure 20b shows a higher percentage of fine particle migration under higher fluid temperatures, especially for smaller $\lambda$ values.

Fig. 20

The effect of $\lambda$ on: a electrostatic force; b maximum retention concentration. (T_ult = 64.6 °C, 89.9 °C at λ = 10 nm, 100 nm, respectively)

7.6 Collision Diameter

The collision diameter has a significant effect on the short-range repulsive Born potential. The range of collision diameter adopted for the current sensitivity analysis is 0.4–0.6 nm (You et al. (2019). As shown in Fig. 21a, the electrostatic force decreases under larger collision diameters. Figure 21(b) shows a higher percentage of fine particle liberation under larger $\sigma_{c}$ values.

Fig. 21

The effect of $\sigma_{c}$ value on: a electrostatic force; b maximum retention concentration. (T_ult = 110.1 °C, 91.5 °C at σ_c = 0.4 nm, 0.5 nm, respectively)

8 Conclusions

This study presents a novel theoretical framework aimed at accurate yet practical prediction of migration of fine particles in geological reservoirs driven by non-isothermal fluid flow. The novel contributions are twofold. Firstly, a new numerical model is developed based on the complete DLVO theory, which integrates for the first time the effects of both thermal and hydraulic loads on all underlying parameters including both the static dielectric constant and the refractive index of the pore fluid. This model, similar to previous DLVO-based models presented in the literature, involves a considerable number of characteristic parameters related to the colloidal particle-pore fluid–solid grain system. The identification of all these parameters often necessitates costly, intricate, and time-consuming physical experiments. The second part of the paper presents an innovative simplified DLVO-based model which involves only 7 input parameters as opposed to the full DLVO-based model containing 23 input parameters, thus offering a practical and efficient solution. Finally, a sensitivity analysis was conducted using the simplified model to evaluate the impact of the key input parameters on particle liberation. Findings reveal that salt concentration had the least impact compared to the other parameters. Furthermore, the maximum retention concentration of fines is seen to be more sensitive to input parameters in case of higher in situ temperatures.