Keywords

1 Introduction

Unmanned powered parafoil (UPP) is a kind of flexible wing vehicle, consisting of traditional parafoil system and power plant. Because of its high ratio of lift and drag, perfect stability and operability, UPP has been applied in both military and civil areas, such as precision aerial delivery systems and aerial photography [1, 2]. Based on such advantages, UPP will expand applications in many fields [3,4,5]. In all this projects, fulfilling the task of tracking the target trajectory is the most important work [6, 7].

Some remarkable results have been investigated about UPP studies. Slegers created a simplified six-degree-of-freedom (dof) model and designed a trajectory tracking controller based on the model predictive strategy [8]. Aoustin designed a nonlinear control law based on the partial feedback linearization for controlling the longitudinal motion [9]. Ochi identified parameters and reduced a given plant model to a second-order system for the designed eight-dof powered parafoil model, and created a three-term PID controller [10]. Tao proposed a homing trajectory planning scheme based on the linear active disturbance rejection control of unmanned powered parafoil [7]. The total disturbance was estimated via ESO using input and output information, and compensated by real-time dynamic feedback in ADRC. However, in the existing studies, the control gain is mostly obtained by trial and error method, and the robustness of the control strategy under the wind disturbance and model uncertainties is not considered.

Therefore, in this paper, a precise longitudinal control approach of UPP based on ADRC and accurate control gain is proposed. In order to enhance the anti-disturbance ability and tracking precision simultaneously, the linear ESO and state error feedback with precise control gain are constructed. The controller designed in this paper can work well under various atmospheric wind environments. The validity of controller is verified by the semi-physical experiments.

2 Mathematical Model

The existing studies of the dynamic model for parafoil system mainly focused on three, four, and six dof models [11]. In the UPP, the relative pitch angle and yaw angle between the parafoil and payload should be taken into account, since they affect the payload attitude, which in turn determines the thrust direction. In the case where apparent mass and the relative motions are involved, the eight-dof model of UPP based on Kirchhoff motion equation is built and described.

Fig. 1
figure 1

Structure of unmanned powered parafoil

Full size image

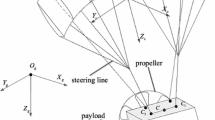
In order to facilitate analysis, three main coordinate systems to be used are established: geodetic coordinate \({O_d}{x_d}{y_d}{z_d}\), parafoil coordinate \({O_s}{x_s}{y_s}{z_s}\) and payload coordinate \({O_w}{x_w}{y_w}{z_w}\), shown as Fig. 1.

2.1 Motion Equations of Parafoil and Payload

The forces acting on the parafoil and payload include aerodynamic force, gravity, tension of suspension lines, and thrust provided by the power plant. Since the gravity and thrust can be reasonably assumed to act upon the mass center of payload, the angular momentums due to gravity and thrust are negligible. Considering the momentum theorem and angular momentum theorem, we analyze the forces on the parafoil and payload respectively:

$$\begin{aligned} \frac{{\partial {P_w}}}{{\partial t}} + {W_w} \times {P_w} = F_w^{aero} + F_w^G + F_w^t + F_w^{th} \end{aligned}$$
(1)
$$\begin{aligned} \frac{{\partial {H_w}}}{{\partial t}} + {W_w} \times {H_w} = M_w^{aero} + M_w^f + M_w^t \end{aligned}$$
(2)
$$\begin{aligned} \frac{{\partial {P_s}}}{{\partial t}} + {W_s} \times {P_s} = F_s^{aero} + F_s^G + F_s^t \end{aligned}$$
(3)
$$\begin{aligned} \frac{{\partial {H_s}}}{{\partial t}} + {W_s} \times {H_s} + {V_s} \times {P_s} = M_s^{aero} + M_s^G + M_s^t + M_s^f \end{aligned}$$
(4)

where P and H are the momentum and angular momentum respectively; F and M denote the force and moment acting on the parafoil and payload respectively; \(V = {\left[ {\begin{array}{*{20}{c}} u&v&w \end{array}} \right] ^T}\), \(W = {\left[ {\begin{array}{*{20}{c}} p&q&r \end{array}} \right] ^T}\) denote the velocity and angular velocity respectively; subscript w, s denote the payload coordinate and parafoil coordinate respectively; areo is the aerodynamic force; t is the tension of suspension lines; G is the gravity; f is the friction; th is the thrust, \(F_w^{th} = {\left[ {\begin{array}{*{20}{c}} {{T_x}}&0&0 \end{array}} \right] ^T}\) acting on the payload and the direction is along the positive x-axis. \( \times \) means the cross-product of two vectors.

Considering the apparent mass and the caused moment of inertia, the momentum and angular momentum of two bodies are summarized as follows:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{P_w} = {m_w}{V_w}}\\ {{H_w} = {J_w}{W_w}} \end{array}} \right. \end{aligned}$$
(5)
$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{P_s}}\\ {{H_s}} \end{array}} \right] = \left[ {{A_a} + {A_r}} \right] \left[ {\begin{array}{*{20}{c}} {{V_s}}\\ {{W_s}} \end{array}} \right] \end{aligned}$$
(6)

where \({m_w}\) is the mass of payload and \({J_w}\) is the matrix of moment of inertia; \({A_a}\) and \({A_r}\) represent the inertia matrix of apparent mass and real mass of parafoil.

2.2 Constraint of Velocity and Angular Velocity

The velocity and angular velocity between parafoil and payload are not independent of each other. The middle point c of two steering lines hanging on the payload is treated as the connection point between the parafoil and payload. The velocity and angular velocity constraint at the point c satisfies:

$$\begin{aligned} {V_w} + {W_w} \times {L_{wc}} = {V_s} + {W_s} \times {L_{sc}} \end{aligned}$$
(7)
$$\begin{aligned} {W_w} = {W_s} + {\tau _s} + {\kappa _w} \end{aligned}$$
(8)

where the distances from parafoil centroid and payload centroid to the point c are expressed as \({L_{sc}}\) and \({L_{wc}}\) respectively; \({\tau _s} = {\left[ {\begin{array}{*{20}{c}} 0&0&{{\psi _r}} \end{array}} \right] ^T}\), \({\kappa _w} = {\left[ {\begin{array}{*{20}{c}} 0&{{\theta _r}}&0 \end{array}} \right] ^T}\), \({{\psi _r}}\) and \({{\theta _r}}\) denote relative yaw angle and pitch angle respectively.

Based on above formulas, the eight-dof mathematical model of UPP can be well built. For detailed modeling process, please refer to the literature [5].

3 Longitudinal Altitude Controller Using ADRC with Precise Control Gain

3.1 Precise Control Gain

For the complex nonlinear characteristic of the UPP system, the control gain is mostly obtained from trial and error method, probably resulting in the loss of tracking precision. Then, in this section, this parameter is obtained precisely by the longitudinal dynamic of the UPP rather than a trial value.

According to the transformation of position and velocity between geodetic and parafoil coordinate, the vertical velocity and vertical acceleration of the geodetic coordinate can be obtained:

Note: for arbitrary angle \(\alpha \), \(\sin \alpha \equiv {s_\alpha }\), \(\cos \alpha \equiv {c_\alpha }\).

$$\begin{aligned} \dot{H} = T_{d - s}^T{V_s} = {u_s}{s_\theta } - {v_s}{s_\phi }{c_\theta } - {w_s}{c_\phi }{c_\theta } \end{aligned}$$
(9)
$$\begin{aligned} \begin{aligned} \ddot{H} =&{{\dot{u}}_s}{s_\theta } + ({u_s}{c_\theta } + {v_s}{s_\phi }{s_\theta } + {w_s}{c_\phi }{s_\theta })\dot{\theta }- {{\dot{v}}_s}{s_\phi }{c_\theta }\\&- {{\dot{w}}_s}{c_\phi }{c_\theta } + ({w_s}{c_\theta }{s_\phi } - {v_s}{c_\theta }{c_\phi })\dot{\phi }\end{aligned} \end{aligned}$$
(10)

where \({T_{d - s}}\) is the transformation from the geodetic to parafoil coordinateis, which is represented by Euler angles \((\phi ,\theta ,\psi )\). Since the principle of force interaction, the tension of suspension lines satisfies,

$$\begin{aligned} F_s^t = - {T_{w - s}}F_w^t \end{aligned}$$
(11)

where \({T_{w - s}}\) is the transformation from the payload to parafoil coordinate which is represented by \({{\psi _r}}\) and \({{\theta _r}}\). From Eq. 10, the relation between velocity components and thrust is required. Thus, substituting Eq. 11 into Eqs. 1 and 3 yields:

$$\begin{aligned} \begin{aligned} {A_1}{{\dot{V}}_s} + {A_2}{{\dot{W}}_s} + {T_{w - s}}{m_w}{{\dot{V}}_w} =\,&{T_{w - s}}(F_w^{aero} + F_w^G + F_w^{th}) - {T_{w - s}}{W_w} \times ({m_w}{V_w})\\&+ F_s^G+ F_s^{aero} - {W_s} \times ({A_1}{V_s} + {A_2}{W_s}) \end{aligned} \end{aligned}$$
(12)

where \({A_i}(i = 1, \cdot \cdot \cdot ,4)\) represents the third-order submatrix of \(({A_a} + {A_r})\).

In order to obtain the direct relationship between the control input and the altitude with the variable \({f_1},{f_2},{f_3}\) being irrelevant portions from Eq. 12, Eq. 12 can be rewritten as:

$$\begin{aligned} \left\{ {\begin{aligned} {{{\dot{u}}_s} = \frac{{\cos {\theta _r}\cos {\psi _r}}}{{{m_s} + {m_{a,11}}}}{T_x} + {f_1}}\\ {{{\dot{v}}_s} = \frac{{\cos {\theta _r}\sin {\psi _r}}}{{{m_s} + {m_{a,22}}}}{T_x} + {f_2}}\\ {{{\dot{w}}_s} = \frac{{ - \sin {\theta _r}}}{{{m_s} + {m_{a,33}}}}{T_x} + {f_3}} \end{aligned}} \right. \end{aligned}$$
(13)

where \({m_s}\) denotes parafoil mass; \({m_{a,11}},{m_{a,22}},{m_{a,33}}\) denote components in the apparent mass matrix.

The relationship between control input and output can be required by substituting Eq. 13 into 10.

$$\begin{aligned} \ddot{H} = f + b{T_x} \end{aligned}$$
(14)
$$\begin{aligned} \begin{aligned} b =&\frac{{\sin \theta \cos {\theta _r}\cos {\psi _r}}}{{{m_s} + {m_{a,11}}}} - \frac{{\sin \phi \cos \theta \cos {\theta _r}\sin {\psi _r}}}{{{m_s} + {m_{a,22}}}} + \frac{{\cos \phi \cos \theta \sin {\theta _r}}}{{{m_s} + {m_{a,33}}}} \end{aligned} \end{aligned}$$
(15)

From Eq. 15, the accurate control gain is obtained. Now the control gain b is applied to ESO and state error feedback for improving the control performance.

3.2 Principle of ADRC

ESO and SEF control law are utilized in ADRC, and the unknown system can be reduced to an integral series system. For the traditional second-order controlled object, the mathematical expression can be written as follow.

$$\begin{aligned} \ddot{y} = f(\dot{y},y,w) + bu \end{aligned}$$
(16)

where y is the output, u is the input, b is the control gain of input, which is set as a trial value mostly in the UPP, w is the external disturbance, f is the unknown function of the system.

Based on the disturbance concept in the ADRC, unknown disturbance f can be estimated and then cancelled. Thus, we choose to estimate f in real time via an observer instead of relying on its mathematical representation. So we define,

$$\begin{aligned} h = \dot{f}(\dot{y},y,w) \end{aligned}$$
(17)

And we convert Eq. 16 into the extended state space form:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{{\dot{x}}_1} = {x_2}}\\ {{{\dot{x}}_2} = {x_3} + bu}\\ {{{\dot{x}}_3} = h}\\ {y = {x_1}} \end{array}} \right. \end{aligned}$$
(18)

Because h is unknown and not available, it can be assumed to be zero. The total disturbance of the system can be observed by linear ESO as shown in Eq. 19.

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{e_1} = y - {z_1}}\\ {{{\dot{z}}_1} = {z_2} - {\beta _1}{e_1}}\\ {{{\dot{z}}_2} = {z_3} + bu - {\beta _2}{e_1}}\\ {{{\dot{z}}_3} = - {\beta _3}{e_1}} \end{array}} \right. \end{aligned}$$
(19)

where \({z_i}\) is the observed states of \({x_i}\); \(L = \left[ {\begin{array}{*{20}{c}} {{\beta _1}}&{{\beta _2}}&{{\beta _3}} \end{array}} \right] \) is the ESO error feedback gain matrix. Gao simplifies the ESO parameterization, by assigning the characteristic roots of observer at \( - {\omega _\mathrm{{o}}}\), and defines \(L = \left[ {\begin{array}{*{20}{c}} {3{\omega _\mathrm{{o}}}}&{3{\omega _\mathrm{{o}}}^2}&{{\omega _\mathrm{{o}}}^3} \end{array}} \right] \) [12].

With the parameter adjustment, \({x_i}\) can be accurately estimated by ESO. Ignoring the estimation error in \({z_3}\), and the control quantity is designed as:

$$\begin{aligned} u = {u_0} - \frac{{{z_3}}}{b} \end{aligned}$$
(20)

Substituting Eq. 20 into 16, the system can be expressed as:

$$\begin{aligned} \ddot{y} = b{u_0} \end{aligned}$$
(21)

Utilizing linear PD form of the SEF control law, we have:

$$\begin{aligned} {u_0} = {k_p}(r - {z_1}) + {k_d}(\dot{r} - {z_2}) \end{aligned}$$
(22)

where \({k_p}\) and \({k_d}\) denote the control parameters respectively.

Referring to Eq. 21, the nonlinear UPP system can be transformed into a linear system with the proper parameters of ESO and SEF control law. With this method the longitudinal altitude controller is constructed.

4 Semi-physical Experiment

In this section, the semi-physical experiments are carried out. The parameters of UPP are shown in Table. 1. The following is the introduction of semi-physical experimental setup and the analysis of experimental results.

Table 1 Parameters of unmanned powered parafoil
Full size table

The semi-physical experiment platform is composed of the host computer and the lower computer. The host computer consists of the dynamic model of UPP and various wind disturbance models established in the MATLAB. The lower computer is the embedded ARM microprocessor executing the ADRC algorithm mainly. The system structure is shown as Fig. 2. From Figs. 2, 4 is the thrust motor; 5 is the propeller; 7 is the motor driver; 8 is the ARM microprocessor; 9 and 10 is serial line, as the communication protocol between the controller and model. The other parts are horizontal tracking device.

Fig. 2
figure 2

Structure of semi-physical experiment platform

Full size image
Fig. 3
figure 3

Precise control gain b

Full size image

The working conditions are set as follows: the initial position is \((0, - 300,2000)\mathrm{{m}}\), and the initial velocity \({V_s} = (14.9,0,2.1)\,\mathrm{{m/s}}\); the reference altitude is \(1950\,\mathrm{{m}}\). The transverse average wind with a speed of 3 m/s and direction along the y-axis is added; NASA’s classic gust model [13] is also added into the environment. The simulation time is 250 s and simulation step is 0.025s. The ADRC controller parameters are tuned to be: \({\omega _\mathrm{{o}}} = 30\), \({k_p} = 0.0134\), \({k_d} = 0.3\).

Through the flight experiment data the time-varying b is acquired. Figure 3 indicates curve of the control gain b, the gain b becomes stable gradually after an initial fluctuation. The value is about 0.013 finally. Therefore, in the semi-physical experiments, b is selected as the stable value.

Fig. 4
figure 4

Altitude and thrust under different wind disturbance

Full size image

To simulate the disturbance under the actual flight environment, the wind disturbance of Fig. 4a, b is set as follows: the constant wind with a speed of 3 m/s is added at 50 s, and gust wind is added at 100 s along the y-axis, which the velocity is set to 5 m/s, the duration is 15 s. The gust wind affects the parafoil altitude by less than 0.7 m. The control quantity is quickly adjusted to reduce the error and suppress the disturbance of gust, and restore stability rapidly. The controller can track the reference altitude well, and the control quantity goes stable gradually. The average error finally converges to zero.

The wind environment of Fig. 4c, d is set as: the mixture of constant and turbulent wind are added at 50 s persistently. Even under the influence of various wind, the UPP can achieve reference altitude without overshoot. The adjustment time is shorter, the thrust is regulated to keep the flight path. There is no obvious oscillation on the whole control process.

5 Conclusion

Aiming at the nonlinear characteristic of unmanned powered parafoil, this paper proposes an accurate longitudinal control method based on ADRC with precise control gain. Rather than the trial and error method or experience value, the control gain is accurately obtained by the longitudinal dynamics of the unmanned powered parafoil system. Through semi-physical experiments with various wind disturbance, this control approach realizes the altitude control precisely with zero margin for error. This research provides an effective method for the trajectory tracking study of unmanned powered parafoil.